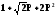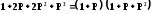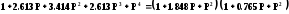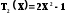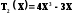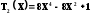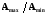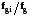2 Правила расчёта фильтров нижних частот
2.1 ОБЩИЕ ПРАВИЛА РАСЧЁТА ФИЛЬТРОВ НИЖНИХ ЧИСТОТ
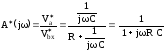
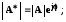



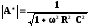 ;
;
 Положив:
Положив: 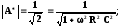
получим
частоту среза 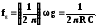 Фазовый сдвиг на этой частоте – 450.
Фазовый сдвиг на этой частоте – 450.
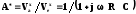
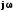 заменим на
заменим на 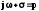 .
.
Передаточная функция фильтра:
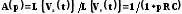
 Передаточная
функция определяет зависимость
преобразований Лапласа выходного и
входного напряжений для произвольных
временных сигналов. Переход от передаточной
функции
Передаточная
функция определяет зависимость
преобразований Лапласа выходного и
входного напряжений для произвольных
временных сигналов. Переход от передаточной
функции 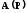 к частотной характеристики
к частотной характеристики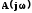 для синусоидальных входных сигналов
можно выполнить, положив
для синусоидальных входных сигналов
можно выполнить, положив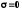 .
.

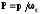 при
при 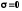
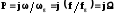
Частота
среза фильтра 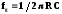
Тогда 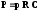
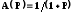
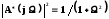 при W
>>
1;
т.е. f >>fg
при W
>>
1;
т.е. f >>fg
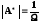 это соответствует
снижению коэффициента передачи фильтра
20дБ / декаду.
это соответствует
снижению коэффициента передачи фильтра
20дБ / декаду.
Для последовательно включенных n фильтров нижних частот:
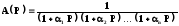 .
.
Где a1, a2….. an — действительные положительные коэффициенты.
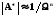 при W
>>
1.
при W
>>
1.
Уменьшение коэффициента передачи характеризуется величиной n × 20дБ на каждую декаду. Корни передаточной функции являются отрицательными и действительными. Такими свойствами обладают пассивные RC фильтры n – ного порядка.
В общем, виде передаточная функция фильтра нижних частот:
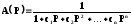 (2.1.1)
(2.1.1)
где c1, c2,×××× cn – положительные действительные коэффициенты.
Порядок фильтра определяется максимальной степенью переменной Р.
Для реализации фильтра необходимо разложить полином знаменателя на множители. Если среди корней полинома есть комплексные, то в этом случае вместо этого представления следует записать в виде произведения сомножителей второго порядка.
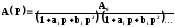 (2.1.2)
(2.1.2)
где ai и bi – положительные действительные коэффициенты. Для нечетных порядков полинома bi = 0.
2.2 ФИЛЬТР НИЖНИХ ЧАСТОТ БАТТЕРВОРТА
Модуль 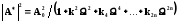 .
.
График функции | А* |2 должен быть по возможности горизонтальным на частотах входного сигнала, меньше частоты среза. Т.к. в этой области W < 1, необходимо, чтобы функция | А* |2 зависела только от старшей степени W.
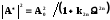 .(2.2.1)
.(2.2.1)
Коэффициент К2n определяется из условий нормировки, связанного с необходимостью обеспечения снижения коэффициента передачи фильтра на 3дБ при частоте среза W = 1.
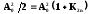 откуда К2n = 1.
откуда К2n = 1.
Тогда для фильтра Баттерворта n – ного порядка выражение имеет следующий вид:
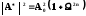 (2.2.2)
(2.2.2)
Для расчета | А* | необходимо знать соответствующий выражению (2.2.2) комплексный коэффициент передачи.
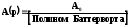
n | Полином Баттерворта |
1 | 1 + Р |
| |
3 | |
4 | |
Аналитические выражения для коэффициентов аi и bi передаточной функции (1.1.2) для фильтра Баттерворта.
Коэффициенты ai и bi :
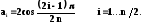
bi = 1.
Для нечетных n
а1 = 1 b1 = 0

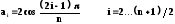
 bi = 1
bi = 1
2.3 ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА
Характеристика фильтра Чебышева спадает более круто за частотой среза. В полосе пропускания она имеет волнообразный характер с постоянной амплитудой. При задании порядка фильтра более резкому спаду амплитудно-частотной характеристики соответствует большая неравномерность в полосе пропускания.

В
области 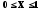 функция
функция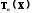 колеблется между 0 и 1, а при Х > 1 монотонно
возрастает.
колеблется между 0 и 1, а при Х > 1 монотонно
возрастает.
N | |
1 | |
2 | |
3 | |
4 | |
Выражение для фильтров нижних частот на основе полиномов Чебышева:
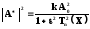
Постоянный
коэффициент k выбирается так, чтобы при
Х = 0 выполнялось условие 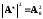 ,
т.е. k = 1 для полиномов нечетного порядка;
k= 1 +e2
для четных n. Множитель e
определяет степень неравномерности
характеристики фильтра..
,
т.е. k = 1 для полиномов нечетного порядка;
k= 1 +e2
для четных n. Множитель e
определяет степень неравномерности
характеристики фильтра..
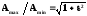
Отсюда 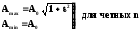
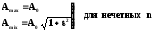
Неравномерность дБ | ||||
0,5 | 1 | 2 | 3 | |
| 1,059 | 1,122 | 1,1259 | 1,413 |
К | 1,122 | 1,259 | 1,585 | 1,935 |
e | 0,349 | 0,509 | 0,765 | 0,998 |
Однако, удобно вычислять полюсы передаточной функции фильтра непосредственно по:
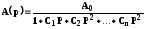 ;
;
и используя выражение для коэффициентов Баттерворта. Объединяя комплексно сопряженные полюсы передаточной функции для коэффициентов аi и bi:
Для четных n
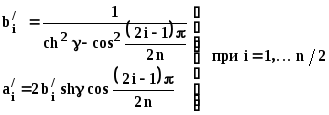
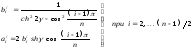
для нечетных n :

 b/I
= 0
b/I
= 0
a/I = 1/ sh g
где 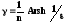
подставив а/i ; b/i вместо аi и bi в выражение
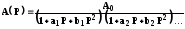
получим
передаточную функцию фильтра Чебышева
нижних частот, в котором Р нормировано
не относительно g
(соответствующую коэффициенту передачи
3дБ), а относительно с
– при котором коэффициент передачи в
последний раз принимает значение Аmin.
После заменим Р на Р,
и выберем постоянную нормирования
так, чтобы коэффициент передачи P = j
имел значение 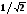 ;
тогда
;
тогда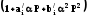 ,
где
,
где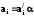 ;
;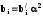 .
Коэффициенты для аi и bi передаточных
функций для фильтров до 5 порядка для
значений неравномерности АЧХ равных
0,5; 1; 2; 3дБ приведены в таблице 2.3.1.
.
Коэффициенты для аi и bi передаточных
функций для фильтров до 5 порядка для
значений неравномерности АЧХ равных
0,5; 1; 2; 3дБ приведены в таблице 2.3.1.
Таблица 2.3.1 Коэффициенты для расчётов ФНЧ.
N | аi | Bi | | Qi |
Фильтр Баттерворта | ||||
1 | 1,0000 | 0,0000 | 1,000 | — |
2 | 1,4142 | 1,0000 | 1,000 | 0,71 |
3 | 1,000 | 0,0000 | 1,000 | — |
1,0000 | 1,0000 | 1,272 | 1,00 | |
4 | 1,8478 | 1,0000 | 0,719 | 0,54 |
0,7654 | 1,0000 | 1,390 | 1,31 | |
5 | 1,0000 | 0,0000 | 1,000 | — |
1,6180 | 1,0000 | 0,859 | 0,62 | |
0,6180 | 1,0000 | 1,448 | 1,62 | |
Фильтр Чебышева с неравномерностью 1дБ | ||||
1 | 1,0000 | 0,0000 | 1,000 | — |
2 | 1,3022 | 1,5515 | 1,000 | 0,96 |
3 | 2,2156 | 0,0000 | 0,451 | — |
0,5442 | 1,2057 | 1,363 | 2,02 | |
4 | 2,5904 | 4,1601 | 0,540 | 0,78 |
0,3039 | 1,1697 | 1,417 | 3,56 | |
5 | 3,5711 | 0,0000 | 0,280 | — |
1,1280 | 2,4896 | 0,894 | 1,40 | |
0,1872 | 1,0814 | 1,486 | 5,56 | |
МОДЕЛИРОВАНИЕ ФИЛЬТРОВ НИЖНИХ ЧАСТОТ
ФИЛЬТР НИЖНИХ ЧАСТОТ БАТТЕРВОРТА
Исследование ФНЧ Баттерворта проведём по схеме с рис.1.2.1
Выберем следующие параметры схемы:
R1=1.2 kOm;
R2=R3=2.5 kOm;
C1=C3=0.0078 uF;
C2=0.001 uF.
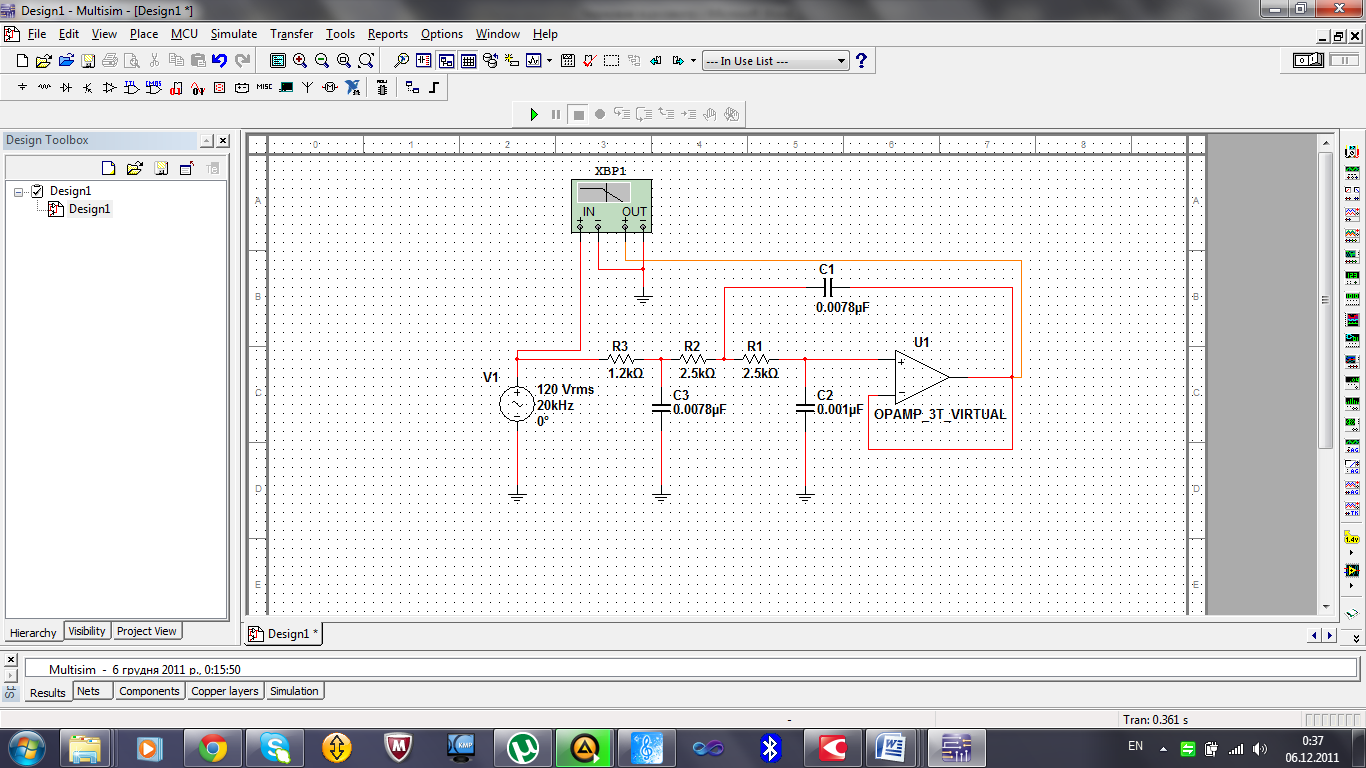
Рис.3.1.1 – Модель ФНЧ Баттерворта на ОУ
Используя блок body plotter снимем АЧХ вида:
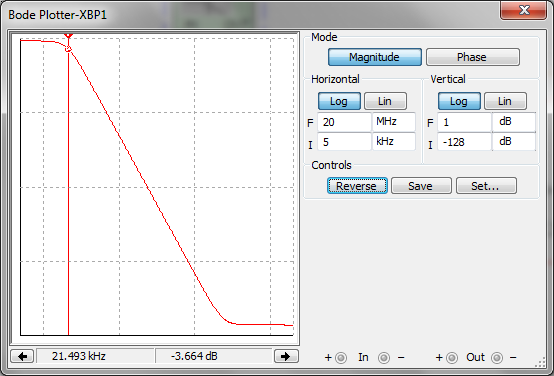
Рис. 3.1.2 – АЧХ ФНЧ Баттерворта при fср=20кГц и А=1 дБ
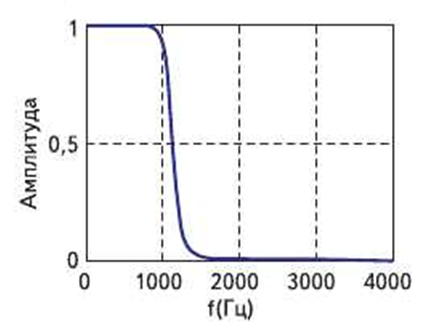
Рис. 3.1.3 – идеальная АЧХ для ФНЧ Баттерворта
Так, как полученная экспериментальным путем АЧХ подобная идеальной АЧХ для ФНЧ Баттерворта, изображенной на рисунке 3.1.3, то параметры схемы были расчитаны верно.
3.2 ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА
Исследование ФНЧ Чебышева проведём по схеме 3.2.1.
Выберем следующие параметры схемы:
R1=13 kOm;
R2=11 kOm;
R3=6 kOm;
C1=0.007 uF;
C2=0.001 uF.
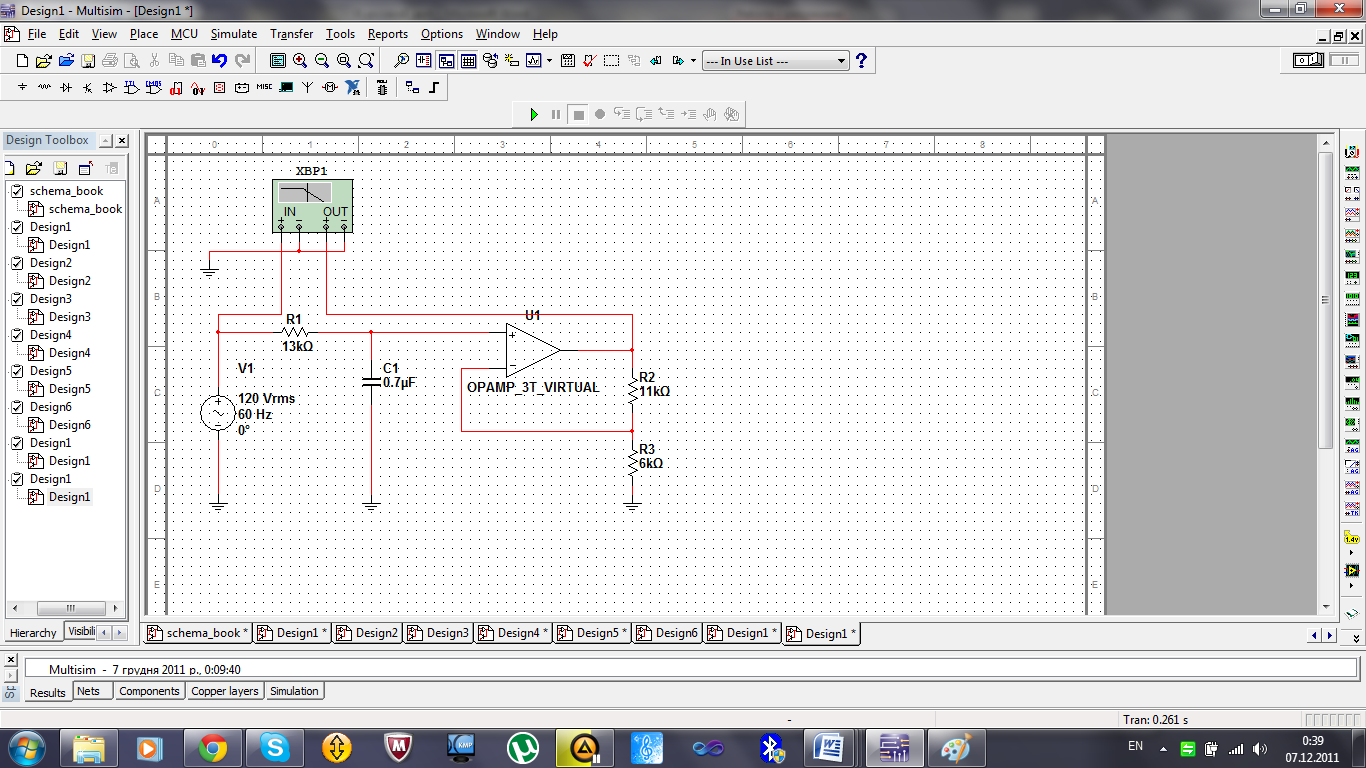
Рис.3.2.1 – Модель ФНЧ Чебышева
Используя блок body plotter снимем АЧХ вида:
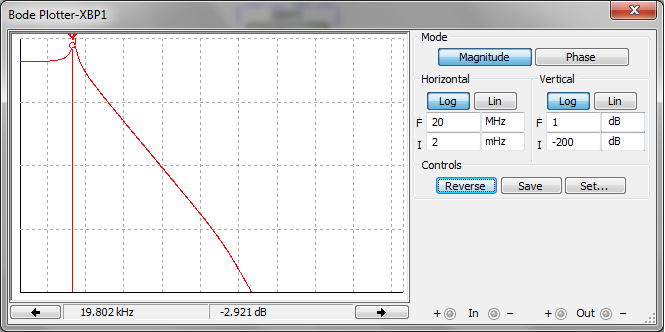
Рис. 3.2.2 – АЧХ ФНЧ Чебышева при fср=20кГц и А=1 дБ
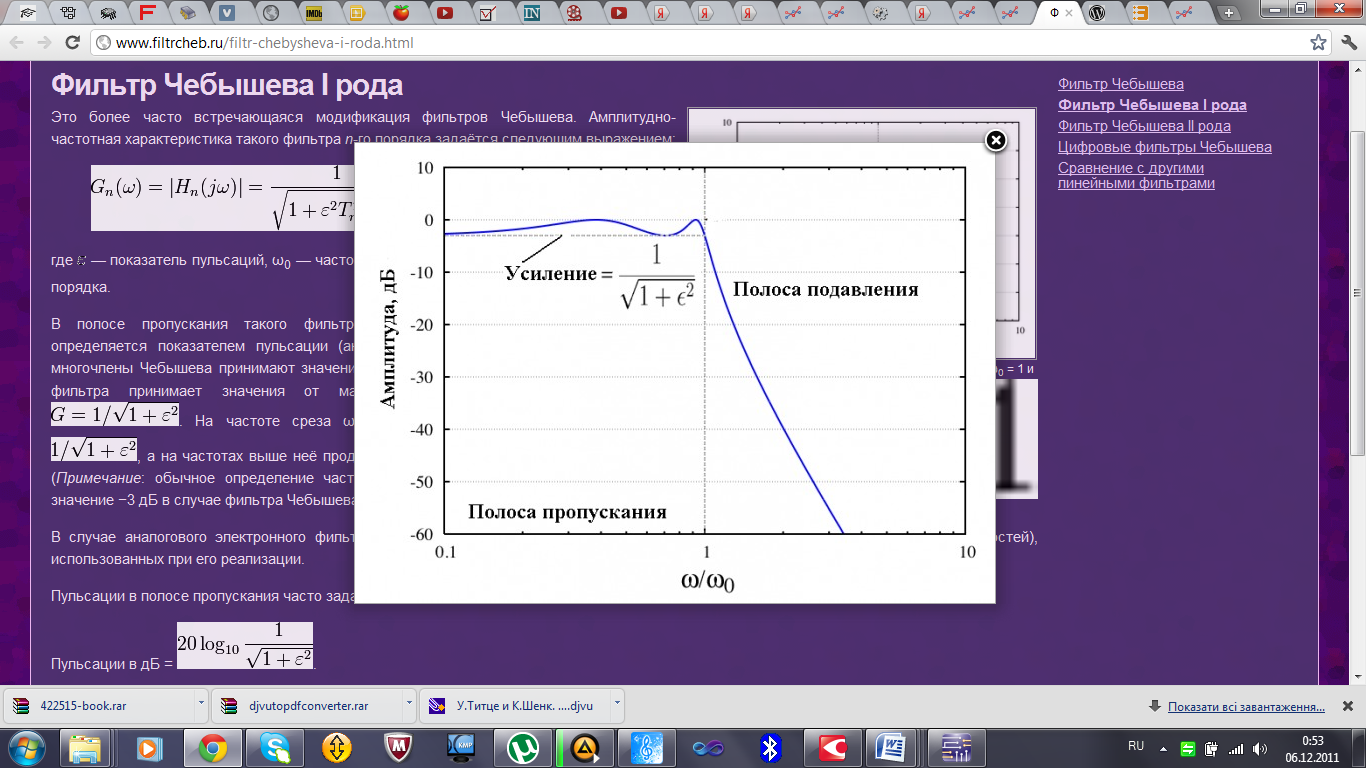
Рис. 3.2.3 – идеальная АЧХ для ФНЧ Чебышева
Так, как полученная экспериментальным путем АЧХ подобная идеальной АЧХ для ФНЧ Чебышева, изображенной на рисунке 3.2.3, то параметры схемы были расчитаны верно.
ВЫВОДЫ
В результате выполнения курсового проектирования по предмету «Схемотехника аналоговых компонентов компьютерных систем» были рассмотрены следующие вопросы:
— фильтры нижних частот (ФНЧ) и их назначение;
— основные сведения об ФНЧ Баттерворта и Чебышева;
— порядок расчёта ФНЧ Баттерворта и Чебышева.
Было выполнено моделирование вышеназванных фильтров нижних частот. Как для моделирования ФНЧ Баттерворта, так и для моделирования ФНЧ Чебышева использовались схемы на операционном усилителе.
В результате моделирования были сняты амплитудно-частотные характеристики фильтров, которые близки к идеальным характеристикам, описывающим каждый из видов исследуемых фильтров.
На основании полученных результатов можно предположить, что проектирование было выполнено успешно.
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
Титце У., Шенк К. Полупроводниковая схемотехника: Справочное руководство. — М.: Мир, 1982. – 512 с.
Справочник по активным фильтрамЖ Пер.с англ../Д.Джонсон, Дж.Джонсон, Г.Мур. – М.: Энергоатоммиздат, 1983 – 128 с.
Карлащук В.И. Электронная лаборатория на IBM PC. Программа Electronics Workbench и её преминение. – М.; Салон-Р, 1999, 506 с.
Методические указания по курсу «Схемотехника аналоговых».Раздел «Фильтры». Для студентов заочной формы обучения. – Харьков, 2003 – 33 с.
2. Фильтры нижних частот | 8. Фильтры | Часть2
2. Фильтры нижних частот
Фильтры нижних частот
Фильтр нижних частот — это схема, которая эффективно пропускает частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшает (подавляет) частоты сигнала выше этой частоты. Существует два основных типа схем, способствующих достижению данной цели: индуктивные фильтры нижних частот и емкостные фильтры нижних частот:
Индуктивный фильтр нижних частот.
С увеличением частоты импеданс катушки индуктивности возрастает. Этот высокий импеданс, при последовательном включении, имеет тенденцию блокировать высокочастотные сигналы от поступления на нагрузку. Проверить данное утверждение можно при помощи SPICE анализа:
inductive lowpass filter v1 1 0 ac 1 sin l1 1 2 3 rload 2 0 1k .ac lin 20 1 200 .plot ac v(2) .end
Емкостной фильтр нижних частот.
С увеличением частоты импеданс конденсатора уменьшается. Этот низкий импеданс, при параллельном включении с сопротивлением нагрузки, имеет тенденцию «закорачивать» высокочастотные сигналы, пропуская большую часть напряжения через последовательный резистор R1.
capacitive lowpass filter v1 1 0 ac 1 sin r1 1 2 500 c1 2 0 7u rload 2 0 1k .ac lin 20 30 150 .plot ac v(2) .end
Индуктивный фильтр нижних частот является вершиной простоты — он содержит всего один компонент — катушку индуктивности. Емкостной фильтр немного сложнее, для его работы нужны резистор и конденсатор. Однако, несмотря на более сложную конструкцию, в подавляющем большинстве случаев используются именно емкостные фильтры. Связано это с тем, что конденсаторы являются более «чистыми» реактивными компонентами, чем катушки индуктивности, а следовательно, они более предсказуемы в своем поведении. Под «чистотой» понимаются меньшие резистивные эффекты конденсаторов в сравнении с катушками индуктивности, что делает их почти 100% реактивными компонентами. Катушки индуктивности, с другой стороны, обладают значительными рассеивающими эффектами (подобно резисторам), которые связаны с длинными проводами (из которых они состоят) и магнитными потерями сердечников. Конденсаторы, помимо всего прочего, меньше катушек индуктивности «участвуют» в паразитных связях с другими компонентами схемы, и они дешевле.
Однако, в источниках питания AC-DC предпочтительнее использовать индуктивные фильтры нижних частот. Они позволяют отфильтровать переменную составляющую напряжения при преобразовании переменного напряжения в постоянное (оставляя на выходе только чистое постоянное напряжение). Основной причиной такого положения дел является требование к низкому сопротивлению фильтра на выходе источника питания. Емкостной фильтр нижних частот содержит дополнительное последовательное (источнику напряжения) сопротивление, в то время как индуктивный фильтр в таком сопротивлении не нуждается. При проектировании таких сильноточных цепей, как источники постоянного напряжения, в которых дополнительное последовательное сопротивление нежелательно, индуктивный фильтр будет лучшим решением. С другой стороны, если приоритетом для вас является низкий вес и компактный размер (а не низкое внутреннее сопротивление), то предпочтение стоит отдать емкостному фильтру.
Все фильтры нижних частот имеют определенную частоту среза. Частота среза — это такая частота, при превышении которой величина выходного напряжения падает ниже 70,7% по отношению к входному напряжению. Число 70,7 не является произвольным. В простом резистивно-емкостном фильтре нижних частот этому числу соответствует частота, при которой реактивное сопротивление конденсатора (в Омах) равно активному сопротивлению (в Омах). Рассчитать частоту среза простого емкостного фильтра можно по следующей формуле:
Подставив значения R и С из последнего SPICE моделирования в эту формулу, мы получим частоту среза 45,473 Гц. Однако, если мы посмотрим на график, созданный программой SPICE, то увидим, что напряжение на нагрузке достигнет значения 70,7% от исходного напряжения (1 вольт) только на частоте 30 Гц, которая значительно ниже рассчитанной нами частоты среза. В чем же здесь проблема? А проблема заключается в том, что сопротивление нагрузки 1 кОм оказывает непосредственное влияние на частотную характеристику фильтра, «отклоняя» ее вниз от рассчитанного по формуле значения. Если мы проведем SPICE анализ без учета сопротивления нагрузки, то получим более реальный график:
capacitive lowpass filter v1 1 0 ac 1 sin r1 1 2 500 c1 2 0 7u * note: no load resistor! .ac lin 20 40 50 .plot ac v(2) .end
Напряжение на выходе емкостного фильтра нижних частот достигнет 70,7% от исходного напряжения на частоте 45,473 Гц.
fсреза = 1/(2πRC) = 1/(2π(500 Ом)(7 мкФ)) = 45.473 Гц
При работе с фильтрующими схемами всегда важно знать, что характеристики фильтра зависят от величин компонентов этого фильтра и от импеданса нагрузки. Поскольку рассмотренное выше уравнение расчета частоты среза не учитывает импеданс нагрузки, оно не может дать точные результаты для реального фильтра, подключенного к нагрузке.
Емкостные фильтры нижних частот находят широкое применение в конструкции схем, имеющих компоненты или секции, чувствительные к электрическому “шуму”. В одной из предыдущих статей мы с вами рассматривали, что иногда сигналы переменного тока могут «передаваться» из одной цепи в другую при помощи паразитной емкости (Cпаразит.) и / или взаимной индукции, возникающих между двумя наборами проводов. Яркий пример такой «случайной связи» можно увидеть в промышленных предприятиях, где сигнальные кабели постоянного напряжения прокладываются в непосредственной близости от питающих проводов переменного напряжения:
Осциллограф слева показывает «чистое» напряжение источника постоянного напряжения. После возникновения паразитной связи с переменным напряжением источника «шума» (через паразитные индуктивность и емкость), в напряжении на нагрузке будет присутствовать как постоянная, так и переменная (нежелательная) составляющая. Рассуждая логически, следовало бы ожидать, что Uисточника будет равно Uнагрузки, поскольку два множества точек, между которыми измеряются напряжения, являются электрически общими. Однако, импеданс питающих проводов позволяет этим двум напряжениям отличаться, вследствие чего величина «шума» может изменяться в различных точках системы постоянного напряжения.
Если мы хотим оградить нагрузку цепи постоянного напряжения от поступления данного «шума», то единственное, что нам нужно сделать — это подключить вблизи нагрузки фильтр нижних частот, который будет блокировать любые паразитные сигналы. В своей простейшей форме этот фильтр представляет собой конденсатор, подключенный к силовым клеммам нагрузки. Очень низкий импеданс данного конденсатора закоротит любой «шум» переменного напряжения на землю. Называется такой конденсатор развязывающим:
Беглый взгляд на печатную плату, содержащую большое количество компонентов, позволит вам без труда выявить развязывающие конденсаторы, расположенные, как правило, поблизости с чувствительной к постоянному току нагрузкой. Минимальное значение емкости, способной произвести достаточно низкий импеданс, составляет 0,1 мкФ и более. Большая емкость будет лучше фильтровать шумы, но размеры и экономическая целесообразность ограничивают развязывающие конденсаторы небольшими величинами.
Фильтр Бесселя — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 мая 2015; проверки требуют 9 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 мая 2015; проверки требуют 9 правок.Фильтр Бесселя — в электронике и обработке сигналов один из наиболее[источник не указан 2841 день] распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика). Фильтры Бесселя чаще всего используют для аудио-кроссоверов. Их групповая задержка практически не изменяется по частотам полосы пропускания, вследствие чего форма фильтруемого сигнала на выходе такого фильтра в полосе пропускания сохраняется практически неизменной.
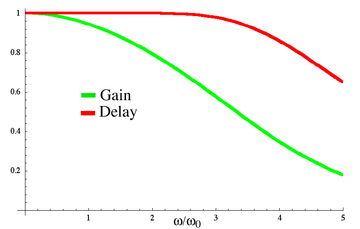 График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.
График амплитудно-частотной характеристики и групповой задержки для низкочастотного фильтра Бесселя четвёртого порядка. Спад амплитудно-частотной характеристики значительно менее крутой, чем у других линейных фильтров, однако групповая задержка практически не меняется по частотам полосы пропускания.Передаточная функция фильтра Бесселя низких частот определяется следующим выражением:
- H(s)=θn(0)θn(s/ω0){\displaystyle H(s)={\frac {\theta _{n}(0)}{\theta _{n}(s/\omega _{0})}}}
где θn(s){\displaystyle \theta _{n}(s)} — обратный многочлен Бесселя, из-за чего фильтр и получил своё название; ω0{\displaystyle \omega _{0}} — частота среза.
Дана передаточная функция низкочастотного фильтра Бесселя третьего порядка
- H(s)=15s3+6s2+15s+15{\displaystyle H(s)={\frac {15}{s^{3}+6s^{2}+15s+15}}}
с амплитудно-частотной характеристикой
- G(ω)=|H(jω)|=15ω6+6ω4+45ω2+225{\displaystyle G(\omega )=|H(j\omega )|={\frac {15}{\sqrt {\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}}
и фазо-частотной характеристикой
- ϕ(ω)=−arg(H(jω))=−arctg(15ω−ω315−6ω2){\displaystyle \phi (\omega )=-\mathrm {arg} (H(j\omega ))=-\mathrm {arctg} \left({\frac {15\omega -\omega ^{3}}{15-6\omega ^{2}}}\right)}
Групповая задержка такого фильтра:
- D(ω)=−dϕdω=6ω4+45ω2+225ω6+6ω4+45ω2+225{\displaystyle D(\omega )=-{\frac {d\phi }{d\omega }}={\frac {6\omega ^{4}+45\omega ^{2}+225}{\omega ^{6}+6\omega ^{4}+45\omega ^{2}+225}}}
Разложение групповой задержки в ряд Тейлора по степеням частоты:
- D(ω)=1−ω6225+ω81125+⋯{\displaystyle D(\omega )=1-{\frac {\omega ^{6}}{225}}+{\frac {\omega ^{8}}{1125}}+\cdots }
Из последнего выражения видно, что коэффициенты перед степенями ω2{\displaystyle \omega ^{2}} и ω4{\displaystyle \omega ^{4}} равны нулю, а перед более высокими степенями весьма малы, вследствие чего групповая задежка близка к единице на низких частотах.
Сравнение с другими линейными фильтрами[править | править код]
Ниже представлены графики амплитудно-частотных характеристик некоторых наиболее распространённых линейных электронных фильтров с одинаковым количеством коэффициентов:
Фильтра Бесселя нет на графике, но он имеет наименьшую крутизну характеристики (ещё более пологий, чем фильтр Баттерворта), в то же время он не имеет пульсаций АЧХ ни в полосе пропускания, ни в полосе подавления.
Поиск частоты среза фильтра по уровню 3 дБ. Определение типа фильтра, построение графика АЧХ, страница 2
Рис. 11.11
На рис. 11.12 приведена АЧХ цифрового фильтра при частоте дискретизации 10000 Гц.
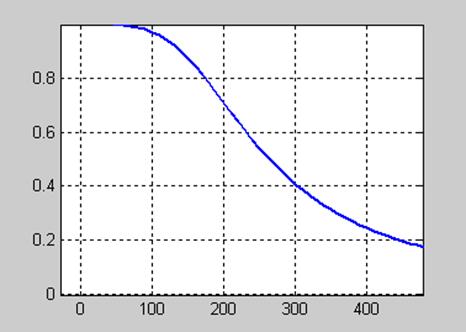
Рис. 11.12
10. Используя метод билинейного преобразования, рассчитать передаточную функцию цифрового ФНЧ с частотой среза по уровню 3 дБ ωС =100 Гц и частотой дискретизации Т = 1 кГц, аппроксимирующего передаточную функцию аналогового ФНЧ второго порядка Баттерворта.
Решение.
Передаточная функция нормированного (с единичной
угловой частотой среза) ФНЧ Баттерворта второго порядка имеет вид 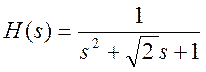 .
.
Определим критическую частоту (частоту среза) аналогового прототипа с помощью тангенциального преобразования
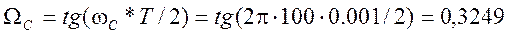 .
.
С помощью формулы частотного преобразования трансформируем нормированный ФНЧ в ФНЧ с частотой среза ΩС
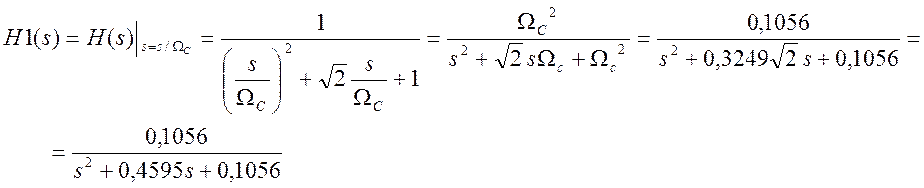
h2(s) является передаточной функцией аналогового прототипа для цифрового фильтра.
На рис. 11.13 показана АЧХ фильтра с передаточной функцией h2(s)
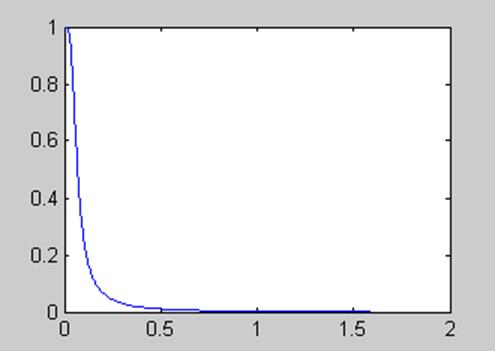
Рис. 11.13
Переход к цифровому фильтру
выполним с помощью билинейного преобразования путем подстановки 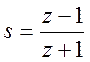 в передаточную функцию h2(s)
в передаточную функцию h2(s)
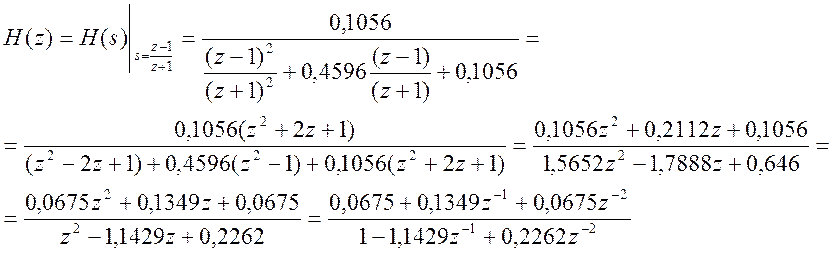
На рис. 11.14 представлена АЧХ цифрового ФНЧ с передаточной функцией H(z) при частоте дискретизации 1000 Гц
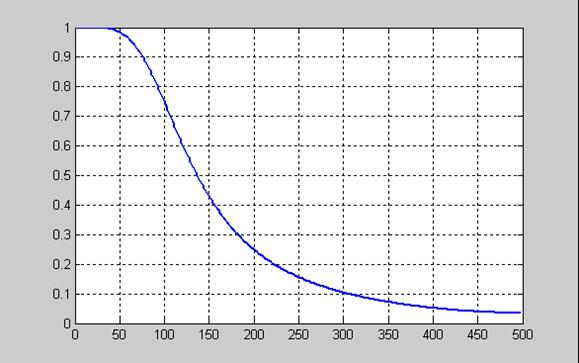
Рис. 11.14
Уравнение фильтра 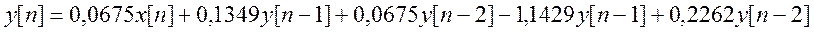 .
.
11. На основе метода билинейного преобразования спроектировать цифровой фильтр верхних частот Баттерворта с частотой среза ωС = 50 Гц и частотой дискретизации
500 Гц.
Решение.
Передаточная функция
нормированного ФНЧ 1-го порядка Баттерворта имеет вид 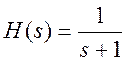 .
.
Находим нормированную граничную частоту полосы пропускания аналогового фильтра – прототипа с помощью тангенциального преобразования
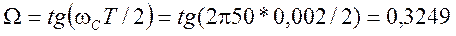 .
.
С помощью преобразования «ФНЧ -> ФВЧ» определим передаточную функцию аналогового прототипа
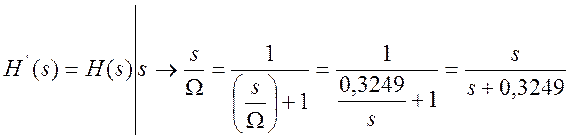 .
.
Для получения передаточной функции цифрового ФВЧ применим билинейное преобразование
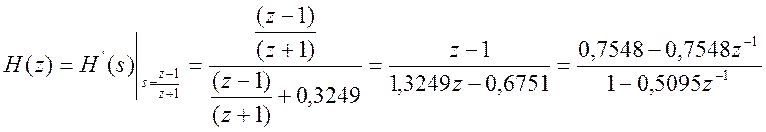 .
.
Уравнение фильтра
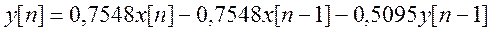 .
.
На рис. 11.15 показана АЧХ полученного ФВЧ с передаточной функцией H(z)
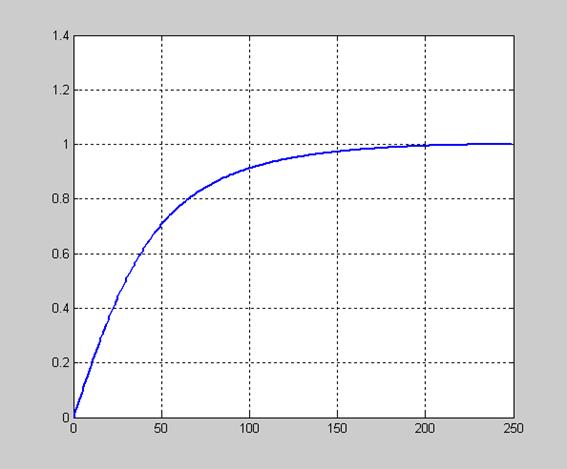
Рис. 11.15
12. Используя метод
сглаживающих окон, спроектируйте КИХ — фильтр нижних частот со следующей
спецификацией:
— допустимый уровень отклонений АЧХ в полосе пропускания 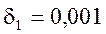 ;
;
— допустимый уровень отклонений
АЧХ в полосе задерживания 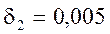 ;
;
— граничная частота полосы пропускания 500 Гц;
— граничная частота полосы задерживания 800 Гц.
Решение.
Проектирование фильтра на основе метода взвешивающих окон заключается в выборе типа окна, определении порядка и коэффициентов (значений импульсной характеристики) уравнения фильтра.
1.
Выберем частоту дискретизации (отсчетов) в соответствии с требованиями
теоремы отсчетов равной 2000 Гц, при этом частота Найквиста равна 1000 Гц.
Нормированные граничные частоты полосы пропускания и полосы задерживания
окажутся равными 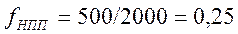 Гц/отсчет и
Гц/отсчет и 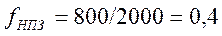 Гц/отсчет соответственно. Частота
среза фильтра
Гц/отсчет соответственно. Частота
среза фильтра 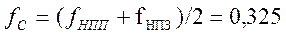 Гц/отсчет, соответственно
Гц/отсчет, соответственно 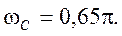 Ширина переходной полосы фильтра
Ширина переходной полосы фильтра 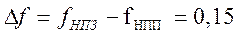 Гц/отсчет, нормированная угловая
переходная полоса
Гц/отсчет, нормированная угловая
переходная полоса 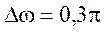 .
.
2.
Определим допустимый уровень пульсаций как 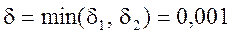 или
в децибелах
или
в децибелах 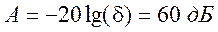 . Такому уровню ошибки
аппроксимации идеальной АЧХ фильтра соответствует окно Блэкмана, для которого допустимый
уровень пульсаций A = 74 дБ. Поэтому для дальнейшей
реализации фильтра выбираем окно Блэкмана.
. Такому уровню ошибки
аппроксимации идеальной АЧХ фильтра соответствует окно Блэкмана, для которого допустимый
уровень пульсаций A = 74 дБ. Поэтому для дальнейшей
реализации фильтра выбираем окно Блэкмана.
3. Определяем порядок фильтра с окном Блэкмана по выражению
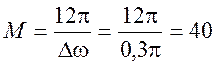
4.
Окно Блэкмана для фильтра 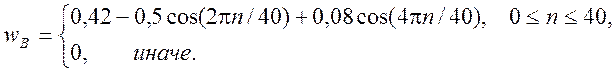
5.
Импульсная характеристика рассчитанного фильтра 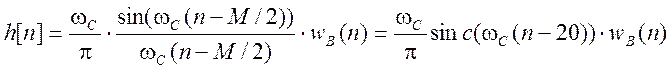
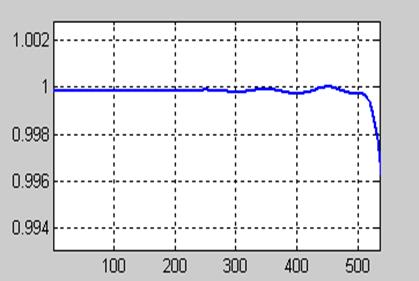
На рис. 11.16 представлена АЧХ спроектированного фильтра в линейном масштабе, а справа –график пульсаций в полосе пропускания.
|
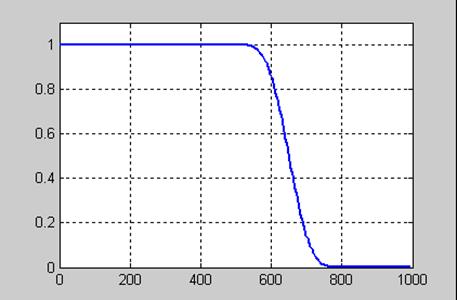
Рис. 11.16
Приведенные на графиках результаты свидетельствуют, что спроектированный фильтр удовлетворяет исходным требованиям.
Задачи для самостоятельного решения.
1.
Найдите частоту среза на уровне 3 дБ фильтра с передаточной функцией 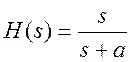
Ответ: 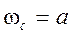 .
.
2.
Найдите импульсную характеристику, передаточную функцию, АЧХ и ФЧХ разностного
фильтра с уравнением 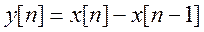 . Изобразите и
объясните график АЧХ.
. Изобразите и
объясните график АЧХ.
Ответ: 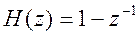 .
.
3.
Найдите порядок ФНЧ Баттерворта, который должен иметь ослабление Amax=1 дБ на частоте 10 Гц и Amin=45
дБ на частоте 20 Гц.
Ответ. N = 9.
4.
Определите тип и АЧХ фильтра с уравнением 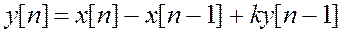 .
.
Ответ. ФВЧ, 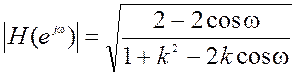 .
.
5. Фильтр нижних частот Чебышева 1-го рода имеет следующие параметры:
ΩP = 2,1 , ΩS = 8 , Amax = 0,5 дБ , Amin = 60 дБ. Определите необходимый порядок фильтра.
Ответ: N = 3.
6. Найдите минимально необходимый порядок для инверсного режекторного чебышевского фильтра с параметрами :
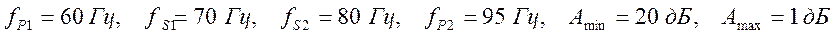 .
.
Ответ: для РФ N = 4 (для ФНЧ, как прототипа, N = 2).
7.
Определите тип фильтра и найдите частоту среза на уровне 3 дБ. Уравнение
фильтра
а) 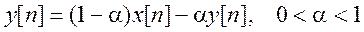 ,
,
б) 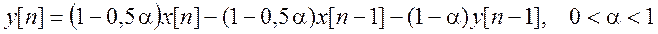 .
.
8. Рассчитайте аналоговый ФНЧ Чебышева 1-го рода со спецификацией:
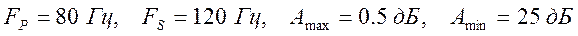 .
.
9. Рассчитайте цифровой ФНЧ Баттерворта с частотой среза на уровне 3 дБ = 800 Гц, минимальным затуханием на граничной частоте полосы задерживания 1000 Гц, равным 30 дБ, частотой отсчетов 4000 Гц.
10.
Выходной сигнал КИХ — фильтра формируется с помощью усреднения текущего
и предыдущего отсчетов. Определите для такого фильтра
а) импульсную характеристику,
б) АЧХ,
в) выходной сигнал, если входной дискретный синусоидальный
сигнал имеет частоту
10 Гц и частоту отсчетов 100 Гц.
11. Используя сглаживающее окно Хэмминга длиной М = 31, получите импульсную характеристику нерекурсивного фильтра нижних частот с частотой среза 200 Гц и частотой отсчетов 1000 Гц. Постройте АЧХ сглаженного фильтра и объясните её поведение.
12. Рассчитайте КИХ — фильтр нижних частот с исходными требованиями
· Нормированная граничная частота полосы пропускания ΩP = 0,45π
· Нормированная граничная частота полосы задерживания ΩS = 0,6π
·
Допустимые пульсации в полосе пропускания 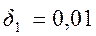
·
Допустимые пульсации в полосе задерживания 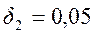 .
.
 Составил: доц.
Щетинин Ю.И.
Составил: доц.
Щетинин Ю.И.