Частота среза — это… Что такое Частота среза?



Частота среза

Частота́ сре́за (f_c) в электронике — частота, выше или ниже которой мощность выходного сигнала электронной схемы уменьшается вполовину от мощности в полосе пропускания.

См. также

Ссылки

Категория:

• Обработка сигналов

Wikimedia Foundation. 2010.

• Полоса подавления
• Чьерна Вода

Смотреть что такое «Частота среза» в других словарях:

• частота среза — граничная частота 1. Частота, при которой амплитуда сигнала составляет определенную часть от максимальной (например, на 3 дБ меньше). 2. Частота, при которой амплитуда передаваемых колебаний на 3 дБ меньше, чем на частоте максимума. [BS EN 1330 4 …   Справочник технического переводчика

• частота среза — ribinis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Dažnis, kuriam esant tam tikros grandinės ar įtaiso perdavimo faktoriaus vertė sumažėja tam tikru dydžiu jo vertės dažnių srityje, kurioje ji nepriklauso nuo dažnio,… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• частота среза — kraštinis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Dažnis, kuriam esant stiprintuvo galios stiprinimo koeficientas sumažėja iki 50 % didžiausios jo vertės. atitikmenys: angl. cut off frequency vok. Grenzfrequenz, f;… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• частота среза — ribinis dažnis statusas T sritis fizika atitikmenys: angl. boundary frequency; cut off frequency; limiting frequency vok. Grenzfrequenz, f; Schnittfrequenz, f rus. граничная частота, f; предельная частота, f; частота среза, f pranc. fréquence de… …   Fizikos terminų žodynas

• частота среза — atkirtos dažnis statusas T sritis automatika atitikmenys: angl. cut off frequency vok. Grenzfrequenz, f; Schnittfrequenz, f rus. частота отсечки, f; частота среза, f pranc. fréquence de coupure, f …   Automatikos terminų žodynas

• частота среза — kirtimo dažnis statusas T sritis automatika atitikmenys: angl. cut off frequecy vok. Abschaltfrequenz, f rus. частота среза, f pranc. fréquence de coupure, f …   Automatikos terminų žodynas

• частота среза — предельная частота; критическая частота …   Словарь русских синонимов по технологиям автоматического контроля

• частота среза интегральной микросхемы — частота среза Частота, на которой модуль коэффициента усиления напряжения интегральной микросхемы при разомкнутой цепи обратной связи уменьшается до 0,707 значения на заданной частоте. Обозначение fсзз fCO [ГОСТ 19480 89] Тематики микросхемы… …   Справочник технического переводчика

• частота среза фильтра — частота среза Частота полосы пропускания (задерживания), на которой затухание передачи фильтра достигает заданного значения. [ГОСТ 24375 80] Тематики радиосвязь Обобщающие термины фильтры Синонимы частота среза …   Справочник технического переводчика

• частота среза пьезоэлектрического (электромеханического) фильтра — (fc) Частота полосы пропускания или задерживания, на которой относительное затухание пьезоэлектрического (электромеханического) фильтра достигает заданного значения. [ГОСТ 18670 84] Тематики электрические фильтры EN cut off frequency FR fréquence …   Справочник технического переводчика

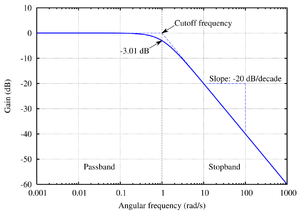
Частота среза

Частота срезаопределяется как частота, на которой значение АЧХ фильтра падает до 1/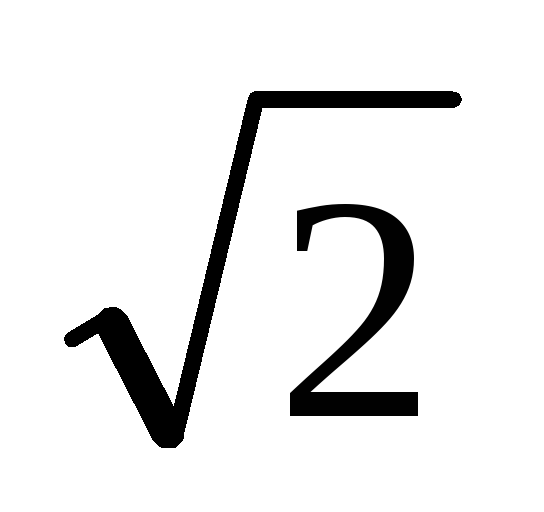= 0.707от своей величины в полосе пропускания. Она также называется «точкой 3 дБ» (поскольку 20lg (0.707) = -3).

12. Полоса пропускания, полоса задерживания и переходная полоса

Полоса пропускания– это частотная область, внутри которой сигналы проходят сквозь фильтр фактически без затухания.

Полоса задерживаниявыбирается проектировщиком такой, чтобы обеспечить уровень затухания не ниже заданного. Частотную область между точкой 3 дБ и полосой задерживания называютпереходной полосой. Переходная полоса характеризуется своей скоростью спада, которая обычно выражается в дБ/декада.

13. Пульсации

АЧХ некоторых фильтров имеют пульсации как в полосе пропускания, так и в полосе задерживания. Пульсации в полосе пропускания более значимы, поскольку они вносят определенные искажения в интересующий нас сигнал. Некоторый уровень пульсаций в полосе пропускания бывает допустимым, это зависит от конкретной задачи. Можно проектировать фильтры с произвольным уровнем пульсаций, но, как правило, имеет место компромисс между уровнем пульсаций в полосе пропускания, скоростью спада в переходной полосе и затуханием в полосе задерживания.

1. Требования к характеристикам фильтра:

• пульсации в полосе пропускания,

• скорость спада в переходной полосе,

• затухание в полосе задерживания,

• ФЧХ (наша следующая тема).

15. ФЧХ

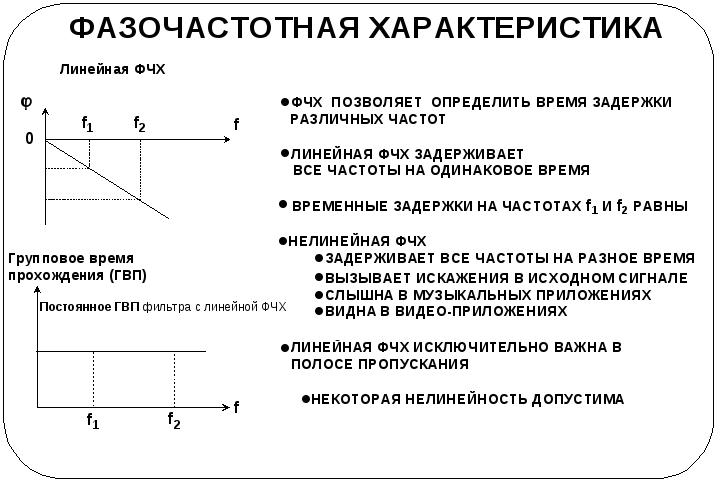
Вид ФЧХ является одним из важнейших показателей фильтра при принятии решения о его пригодности для конкретного приложения. ФЧХ позволяет определить временную задержку, вносимую в сигнал.

16. Линейная и нелинейная фчх

Фильтр с линейной ФЧХ задерживает все частоты на одно и то же время. Следовательно, выходной сигнал не искажается, а лишь задерживается на соответствующее время. Поскольку реальный сигнал содержит много частот, задержка каждой частоты на разное время приводит к искажению выходного сигнала.

В некоторых приложениях, таких как музыка или видео, нелинейная ФЧХ недопустима.

Линейная ФЧХ исключительно важна в полосе пропускания, поскольку тот диапазон, в котором происходит выделение интересующих нас частотных составляющих сигнала. Обычно имеет место компромисс между линейной ФЧХ в полосе пропускания и другими требованиями к фильтру, такими как крутизна спада и затухание в полосе задерживания.

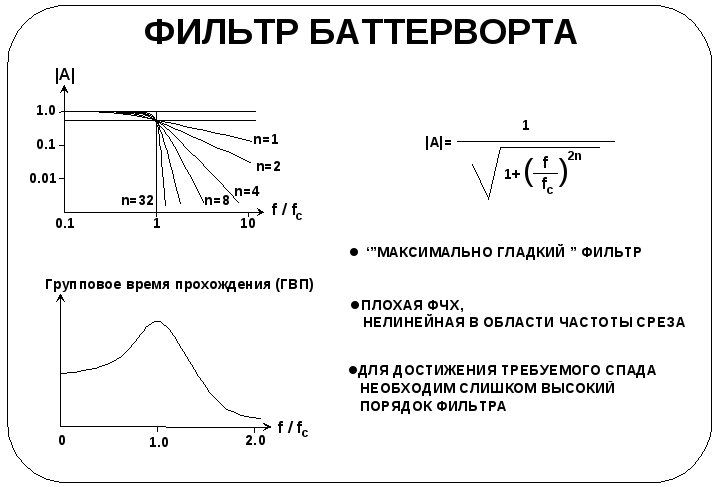
17. Практически используемые аналоговые фильтры

Существует много схем аналоговых фильтров с различными характеристиками АЧХ и ФЧХ. Рассмотрим более подробно фильтр Баттерворта.

18. Фильтр Баттерворта

Этот тип фильтра обычно называют «максимально гладким» вследствие плавности АЧХ в полосе пропускания. У фильтров Баттерворта действительно нет пульсаций в полосе пропускания, однако им присущи два недостатка:

1. Нелинейная ФЧХ в полосе пропускания исключает их применение в тех приложениях, где требуется линейная ФЧХ. График группового времени прохождения (ГВП)^)в нормированной шкале частот иллюстрирует нелинейность ФЧХ. Ненормированная частота среза при этом равнаf/f_c= 1.0. Задержка, вносимая в сигнал, существенно увеличивается, когда значение нормированной частоты приближается к частоте среза.

2. В переходной полосе АЧХ фильтра Баттерворта имеет пологий спад. Для того, чтобы достичь заданной крутизны спада, потребуется каскадное соединение большого числа звеньев. На графике представлено семейство АЧХ для фильтров Баттерворта различного порядка.

Частота среза — Википедия

Материал из Википедии — свободной энциклопедии

Частота́ сре́за (частота отсе́чки) fc{\displaystyle f_{c}} — частота, выше или ниже которой мощность выходного сигнала некоторого линейного частотно-зависимого объекта, например, электронной схемы уменьшается в два раза^[2] от мощности в полосе пропускания при воздействии на вход неизменного по амплитуде сигнала.

Амплитудно-частотная характеристика на частоте среза имеет спад до уровня −log10⁡2{\displaystyle -\log _{10}2} (приблизительно −3 дБ) относительно уровня в полосе пропускания.

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка

Фильтр нижних частот (ФНЧ) 1-го порядка имеет комплексную передаточную функцию H(s){\displaystyle H(s)} вида:

H(s)=11+αs,{\displaystyle H(s)={\frac {1}{1+\alpha s}},}

где s{\displaystyle s} — комплексная переменная преобразования Лапласа;

α{\displaystyle \alpha } — параметр фильтра, константа.

В случае подачи на вход фильтра гармонического сигнала с частотой ω{\displaystyle \omega } в установившемся режиме комплексная передаточная функция имеет вид:

H(jω)=11+αjω,{\displaystyle H(j\omega )={\frac {1}{1+\alpha j\omega }},}

где буквой j{\displaystyle j} обозначена мнимая единица;

ω{\displaystyle \omega } — угловая частота.

Эта функция имеет единственный полюс (частота, при которой знаменатель дроби обращается в 0) на частоте ωc=2πfc=1/α,{\displaystyle \omega _{c}=2\pi f_{c}=1/{\alpha },} fc{\displaystyle f_{c}} — частота среза.

Модуль коэффициента передачи этого ФНЧ в зависимости от частоты (эту функцию принято называть амплитудно-частотной характеристикой) имеет вид:

|H(jω)|=|11+αjω|=11+α2ω2.{\displaystyle \left|H(j\omega )\right|=\left|{\frac {1}{1+\alpha j\omega }}\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega ^{2}}}}.}

Модуль коэффициента передачи на частоте полюса:

|H(jωc)|=11+α2ωc2=12.{\displaystyle \left|H(j\omega _{\mathrm {c} })\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega _{\mathrm {c} }^{2}}}}={\frac {1}{\sqrt {2}}}.}

То есть, на частоте полюса коэффициент передачи уменьшается в 2.{\displaystyle {\sqrt {2}}.} В рассмотренном примере частота среза равна частоте полюса.

См. также

Примечания

1. ↑ Порядок фильтра равен порядку (степени алгебраического уравнения) знаменателя передаточной функции (ЛАФЧХ) фильтра. Как правило^{[уточнить]}, порядок фильтра равен количеству входящих в него сосредоточенных реактивных элементов.
2. ↑ При этом амплитуда сигнала на частоте среза равна 12≈0,707{\displaystyle {\frac {1}{\sqrt {2}}}\approx 0,707} от амплитуды сигнала в полосе пропускания.

Ссылки

Что такое частота среза ачх?

АЧХ- показывает зависимость коэффициента передачи (усиления) фильтра от частоты

Частота среза– точка, где ачх пересекает уровень 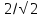, примерно 0.7, что соответствует передаче половины мощности сигнала. (частота, на которой значение АЧХ фильтра падает до 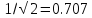от своей величины в полосе пропускания. Она также называется «точкой 3 дБ» (поскольку ).)

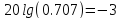35. Что такое переходная полоса, полоса пропускания и полоса задержки ачх цф?

Переходная полоса — диапазон частот, в котором АЧХ фильтра переходит от полосы пропускания к полосе задерживания.

Полоса задерживания – диапазон частот, где ачх близка к нулю.(диапазон частот, в котором фильтр ослабляет сигналы.)

Полоса пропускания –диапазон частот ачх, где ее значения близки к единице. (диапазон частот сигнала, в котором фильтр пропускает энергию сигнала на выход с минимальным ослаблением (частотная область, внутри которой сигналы проходят сквозь фильтр фактически без затухания). Обычно определяется как диапазон частот, в котором АЧХ фильтра не выходит за пределы заданной неравномерности.)

36. Что такое добротность цф?

— свойство колебательной системы, определяющее полосу резонанса и показывающее, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний.

— параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан.

Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

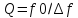f0 — центральная частота резонанса; ∆f — полоса пропускания по уровню 0,707 (- 3 дБ) от уровня f0, принятого за 1. Соответственно: ниже добротность — шире полоса пропускания, резонансный пик более пологий; выше добротность — уже полоса пропускания, острее резонансный пик.

37. Почему ачх цф рассматривают только в полосе от 0 Гц до частоты Найквиста?

Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если (спектральная плотность) наивысшая частота полезного сигнала равна половине или меньше частоты дискретизации (в англоязычной литературе под обозначением половины частоты дискретизации употребляют термин частота Найквиста). В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (маскировка частот), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то сигнал может быть (теоретически) продискретизирован и затем восстановлен без искажений. Фактически «оцифровка» сигнала (превращение аналогового сигнала в цифровой) сопряжена с квантованием отсчётов — каждый отсчёт записывается в виде цифрового кода конечной разрядности, в результате чего к отсчетам добавляются ошибки квантования (округления), при определенных условиях рассматриваемые как «шум квантования».

Частота среза — Википедия

Пример ЛАЧХ фильтра Баттерворта 1-го порядка^[1] с отмеченной частотой среза −3 дБ.

Частота́ сре́за (частота отсе́чки) fc{\displaystyle f_{c}} — частота, выше или ниже которой мощность выходного сигнала некоторого линейного частотно-зависимого объекта, например, электронной схемы уменьшается в два раза^[2] от мощности в полосе пропускания.

Амплитудно-частотная характеристика на частоте среза имеет спад до уровня −log102{\displaystyle -log_{10}2} (примерно −3 дБ) относительно уровня в полосе пропускания.

Содержание

• 1 Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка
• 2 См. также
• 3 Примечания
• 4 Ссылки

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка

Фильтр нижних частот (ФНЧ) 1-го порядка имеет передаточную функцию H(s){\displaystyle H(s)} вида:

H(s)=11+αs=11+αjω.{\displaystyle H(s)={\frac {1}{1+\alpha s}}={\frac {1}{1+\alpha j\omega }}.}

где s{\displaystyle s} — комплексная переменная преобразования Лапласа, в частотной области равна jω,{\displaystyle j\omega ,} ω{\displaystyle \omega } — круговая частота.

Эта функция имеет единственный полюс (знаменатель дроби обращается в 0) на частоте ωc=2πfc=1/α

Частота среза — Википедия

Пример ЛАЧХ фильтра Баттерворта 1-го порядка^[1] с отмеченной частотой среза −3 дБ.

Частота́ сре́за (частота отсе́чки) fc{\displaystyle f_{c}} — частота, выше или ниже которой мощность выходного сигнала некоторого линейного частотно-зависимого объекта, например, электронной схемы уменьшается в два раза^[2] от мощности в полосе пропускания.

Амплитудно-частотная характеристика на частоте среза имеет спад до уровня −log102{\displaystyle -log_{10}2} (примерно −3 дБ) относительно уровня в полосе пропускания.

Содержание

• 1 Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка
• 2 См. также
• 3 Примечания
• 4 Ссылки

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка

Фильтр нижних частот (ФНЧ) 1-го порядка имеет передаточную функцию H(s){\displaystyle H(s)} вида:

H(s)=11+αs=11+αjω.{\displaystyle H(s)={\frac {1}{1+\alpha s}}={\frac {1}{1+\alpha j\omega }}.}

где s{\displaystyle s} — комплексная переменная преобразования Лапласа, в частотной области равна jω,{\displaystyle j\omega ,} ω{\displaystyle \omega } — круговая частота.

Эта функция имеет единственный полюс (знаменатель дроби обращается в 0) на частоте ωc=2πfc=1/α.{\displaystyle \omega _{c}=2\pi f_{c}=1/{\alpha }.}

Модуль коэффициента передачи этого ФНЧ в зависимости от частоты (эту функцию принято называть амплитудно-частотной характеристикой) имеет вид:

|H(jω)|=|11+αjω|=11+α2ω2.{\displaystyle \left|H(j\omega )\right|=\left|{\frac {1}{1+\alpha j\omega }}\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega ^{2}}}}.}

Коэффициент передачи на частоте полюса:

|H(jωc)|=11+α2ωc2=12.{\displaystyle \left|H(j\omega _{\mathrm {c} })\right|={\sqrt {\frac {1}{1+\alpha ^{2}\omega _{\mathrm {c} }^{2}}}}={\frac {1}{\sqrt {2}}}.}

То есть на частоте полюса коэффициент передачи уменьшается в 2.{\displaystyle {\sqrt {2}}.} В рассмотренном примере частота среза равна частоте полюса.

См. также

• Фильтр нижних частот
• Фильтр верхних частот
• Постоянная времени
• Круговая частота

Примечания

1. ↑ Порядок фильтра равен порядку (степени уравнения) передаточной функции (ЛАФЧХ) фильтра. Как правило^{[уточнить]}, порядок фильтра равен количеству входящих в него реактивных элементов.
2. ↑ При этом амплитуда сигнала на частоте среза равна 12≈0,707{\displaystyle {\frac {1}{\sqrt {2}}}\approx 0,707} от амплитуды сигнала в полосе пропускания.

Ссылки

• Преобразование частоты среза f_c и постоянной времени τ (англ.)
• Основные характеристики и параметры фильтров

Это заготовка статьи об электронике. Вы можете помочь проекту, дополнив её.

Частота среза Википедия

Пример ЛАЧХ фильтра Баттерворта 1-го порядка^[1] с отмеченной частотой среза −3 дБ. 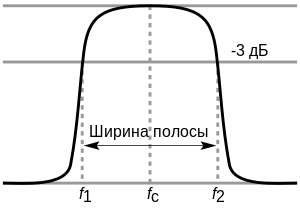Верхняя (f2{\displaystyle f_{2}}) и нижняя (f1{\displaystyle f_{1}}) частоты среза некоторого полосового фильтра.

Частота́ сре́за (частота отсе́чки) fc{\displaystyle f_{c}} — частота, выше или ниже которой мощность выходного сигнала некоторого линейного частотно-зависимого объекта, например, электронной схемы уменьшается в два раза^[2] от мощности в полосе пропускания при воздействии на вход неизменного по амплитуде сигнала.

Амплитудно-частотная характеристика на частоте среза имеет спад до уровня −log10⁡2{\displaystyle -\log _{10}2} (приблизительно −3 дБ) относительно уровня в полосе пропускания.

Содержание

• 1 Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка
• 2 См. также
• 3 Примечания
• 4 Ссылки

Пример вычисления частоты среза и коэффициента передачи на частоте среза фильтра нижних частот 1-го порядка[ | ]

Фильтр нижних частот (ФНЧ) 1-го порядка имеет комплексную передаточную функцию H(s){\displaystyle H(s)} вида:

H(s)=11+αs,{\displaystyle H(s)={\frac {1}{1+\alpha s}},}

где s{\displaystyle s} — комплексная переменная преобразования Лапласа;

α{\displaystyle \alpha }