Формула частоты в физике
Формула частоты в физикеОпределение
Частота — это физический параметр, которые используют для характеристики периодических процессов. Частота равна количеству повторений или свершения событий в единицу времени.
Чаще всего в физике частоту обозначают буквой $\nu ,$ иногда встречаются другие обозначения частоты, например $f$ или $F$.
Частота (наряду со временем) является самой точно измеряемой величиной.
Формула частоты колебаний
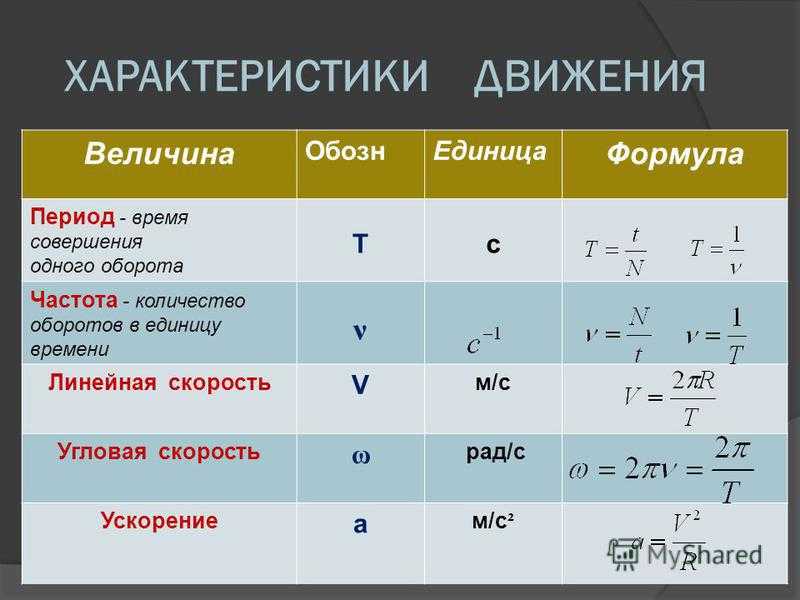
При помощи частоты характеризуют колебания. В этом случае частота является физической величиной обратной периоду колебаний $(T).$
\[\nu =\frac{1}{T}\left(1\right).\]
Частота, в этом случае — это число полных колебаний ($N$), совершающихся за единицу времени:
\[\nu =\frac{N}{\Delta t}\left(2\right),\]
где $\Delta t$ — время за которое происходят $N$ колебаний.
{-1}=Гц.\]
Герц — это единица измерения частоты периодического процесса, при которой за время равное одной секунде происходит один цикл процесса. Единица измерения частоты периодического процесса получила свое наименование в честь немецкого ученого Г. Герца.
Частота биений, которые возникают при сложении двух колебаний, происходящих по одной прямой с разными, но близкими по величине частотами (${\nu }_1\ и\ {\nu }_2$) равна:
\[{\nu =\nu }_1-\ {\nu }_2\left(3\right).\]
Еще одно величиной характеризующей колебательный процесс является циклическая частота (${\omega }_0$), связанная с частотой как:
\[{\omega }_0=2\pi \nu \left(4\right).\]
Циклическая частота измеряется в радианах, деленных на секунду:
\[\left[{\omega }_0\right]=\frac{рад}{с}.\]
Частота колебаний тела, имеющего массу$\ m,$ подвешенного на пружине с коэффициентом упругости $k$ равна:
\[\nu =\frac{1}{2\pi \sqrt{{m}/{k}}}\left(5\right).
\]
Формула (4) верна для упругих, малых колебаний. Кроме того масса пружины должна быть малой по сравнению с массой тела, прикрепленного к этой пружине.
Для математического маятника частоту колебаний вычисляют как: длина нити:
где $g$ — ускорение свободного падения; $\ l$ — длина нити (длина подвеса) маятника.
Физический маятник совершает колебания с частотой:
\[\nu =\frac{1}{2\pi \sqrt{{J}/{mgd}}}\left(7\right),\]
где $J$ — момент инерции тела, совершающего колебания относительно оси; $d$ — расстояние от центра масс маятника до оси колебаний.
Формулы (4) — (6) приближенные. Чем меньше амплитуда колебаний, тем точнее значение частоты колебаний, вычисляемых с их помощью.
Формулы для вычисления частоты дискретных событий, частота вращения
дискретных колебаний ($n$) — называют физическую величину, равную числу действий (событий) в единицу времени.
\[n=\frac{1}{\tau }\left(8\right).\]
Единицей измерения частоты дискретных событий является обратная секунда:
\[\left[n\right]=\frac{1}{с}.\]
Секунда в минус первой степени равна частоте дискретных событий, если за время, равное одной секунде происходит одно событие.
Частотой вращения ($n$) — называют величину, равную количеству полных оборотов, которое совершает тело в единицу времени. Если $\tau $ — время, затрачиваемое на один полный оборот, то:
\[n=\frac{1}{\tau }\left(9\right).\]
Примеры задач с решением
Пример 1
Задание. Колебательная система совершила за время равное одной минуте ($\Delta t=1\ мин$) 600 колебаний. Какова частота этих колебаний?
Решение. Для решения задачи воспользуемся определением частоты колебаний: Частота, в этом случае — это число полных колебаний, совершающихся за единицу времени.
\[\nu =\frac{N}{\Delta t}\left(1.1\right).\]
Прежде чем переходить к вычислениям, переведем время в единицы системы СИ: $\Delta t=1\ мин=60\ с$. Вычислим частоту:
\[\nu =\frac{600}{60}=10\ \left(Гц\right).\]
Ответ. $\nu =10Гц$
Пример 2
Задание. На рис.1 изображен график колебаний некоторого параметра $\xi \ (t)$, Какова амплитуда и частота колебаний этой величины?
Решение. Из рис.1 видно, что амплитуда величины $\xi \ \left(t\right)={\xi }_{max}=5\ (м)$. Из графика получаем, что одно полное колебание происходит за время, равное 2 с, следовательно, период колебаний равен:
\[T=2\ \left(c\right).\]
Частота — величина обратная периоду колебаний, значит:
\[\nu =\frac{1}{T}=0,5\ \left(Гц\right).\]
Ответ.
1) ${\xi }_{max}=5\ (м)$. 2) $\nu =0,5$ Гц
Читать дальше: формулы математического маятника.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||
01.12
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
В вершинах правильного треугольника расположены точечные заряды +q, -q, -Q, как показано на рисунке. Как направлена результирующая сила, действующая на заряд (-Q)?
Решено
Термопара с сопротивлением r1 = 6 Ом
Решено
Дано уравнение гармонических колебаний: x=0.
..
Ракета после старта в течении 5 мин..
Задачи по физике 9 класс
Пользуйтесь нашим приложением
Частота | Определения, символы и формулы
- Связанные темы:
- диапазон частот основная частота угловая частота собственная частота мода третьей гармоники
Просмотреть весь связанный контент →
Популярные вопросы
Что такое частота в физике?
В физике термин частота относится к числу волн, которые проходят фиксированную точку в единицу времени. Он также описывает количество циклов или колебаний, совершаемых в единицу времени телом, находящимся в периодическом движении.
Что такое символ частоты?
Чаще всего для обозначения частоты используются символы f и греческие буквы ню (ν) и омега (ω). Nu чаще используется при описании электромагнитных волн, таких как свет, рентгеновские лучи и гамма-лучи.
Омега обычно используется для описания угловой частоты.
Как выражается частота?
Частота обычно выражается в герцах, сокращенно Гц. Один килогерц (кГц) равен 1000 Гц, а один мегагерц (МГц) равен 1 000 000 Гц. В спектроскопии иногда используется еще одна единица частоты — волновое число, число волн на единицу расстояния.
частота , в физике количество волн, проходящих фиксированную точку в единицу времени; также число циклов или колебаний, совершаемых в единицу времени телом, находящимся в периодическом движении. Говорят, что тело в периодическом движении претерпело один цикл или одну вибрацию после прохождения ряда событий или положений и возвращения в исходное состояние. См. также угловая скорость; простые гармонические колебания.
Если период или интервал времени, необходимый для завершения одного цикла или вибрации, составляет 1 / 2 секунды, частота 2 в секунду; если период составляет 1 / 100 часов, частота составляет 100 в час.
В общем, частота является обратной величиной периода или временного интервала; т. е. частота = 1/период = 1/(интервал времени). Частота обращения Луны вокруг Земли чуть больше 12 оборотов в год. Частота струны ля скрипки составляет 440 колебаний или циклов в секунду.
Britannica Quiz
Физика и естественное право
Чаще всего для обозначения частоты используются символы f и греческие буквы ню (ν) и омега (ω). Nu чаще используется при описании электромагнитных волн, таких как свет, рентгеновские лучи и гамма-лучи. Омега обычно используется для описания угловой частоты, то есть того, насколько объект вращается или вращается в радианах в единицу времени. Обычно частота выражается в герцах, названных в честь немецкого физика 19 века Генриха Рудольфа Герца, где один герц равен одному циклу в секунду, сокращенно Гц; один килогерц (кГц) равен 1000 Гц, а один мегагерц (МГц) равен 1 000 000 Гц. В спектроскопии иногда используют другую единицу частоты — волновое число — число волн на единицу расстояния.
Редакция Британской энциклопедии Эта статья была недавно отредактирована и обновлена Эриком Грегерсеном.
Частота букв в английском языке
Частота букв в английском языке| Это нужно было знать изобретателю азбуки Морзе Сэмюэлю Морзе (1791-1872), чтобы он мог давать простейшие коды наиболее часто употребляемым буквам. Он сделал это, просто подсчитав количество букв в наборах типографского шрифта. Цифры, которые он придумал, были: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Однако это дает частотность букв в английском тексте, в котором преобладает относительно небольшое количество общеупотребительных слов.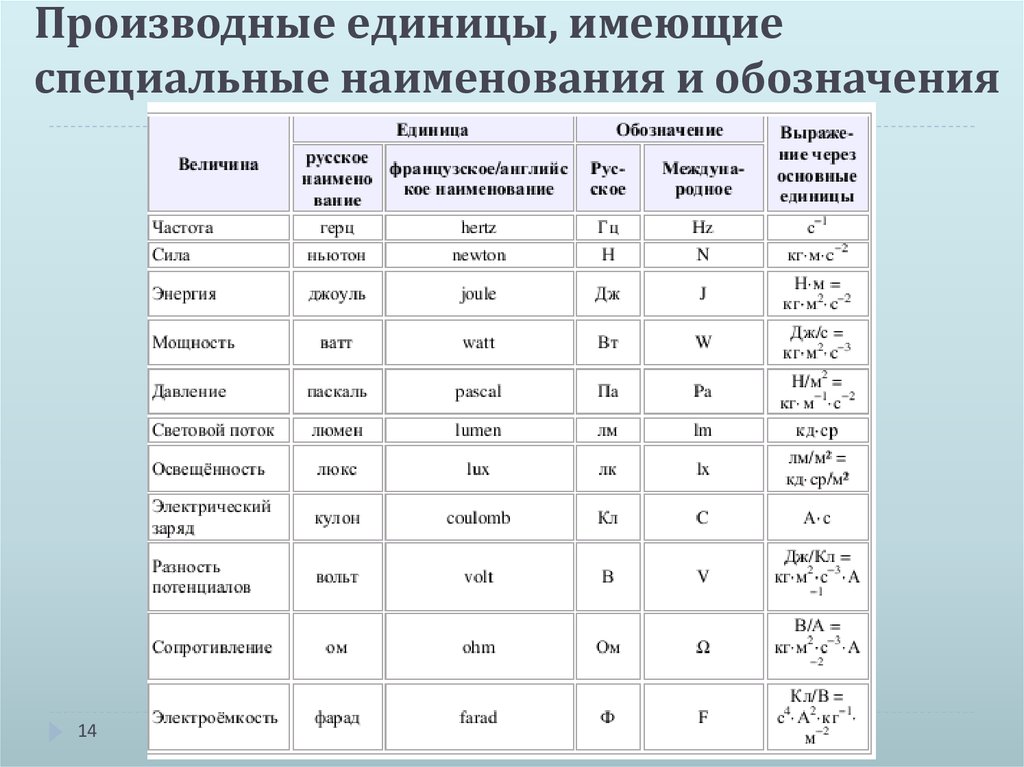 Для словесных игр чаще всего интерес представляет частота букв в английской лексике, независимо от частоты слов. Ниже приводится результат анализа букв, встречающихся в словах, перечисленных в основных статьях Concise Oxford Dictionary (9-е издание, 1995 г.) и получил следующую таблицу: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В третьем столбце представлены пропорции, в которых наименее распространенная буква (q) принимается равной 1. Буква E более чем в 56 раз чаще встречается, чем Q, при образовании отдельных английских слов. Частота букв в начале слов снова другая. В английском языке больше слов, начинающихся с буквы «s», чем с любой другой буквы. (В основном это связано с тем, что кластеры, такие как «sc», «sh», «sp» и «st», действуют почти как независимые буквы.  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
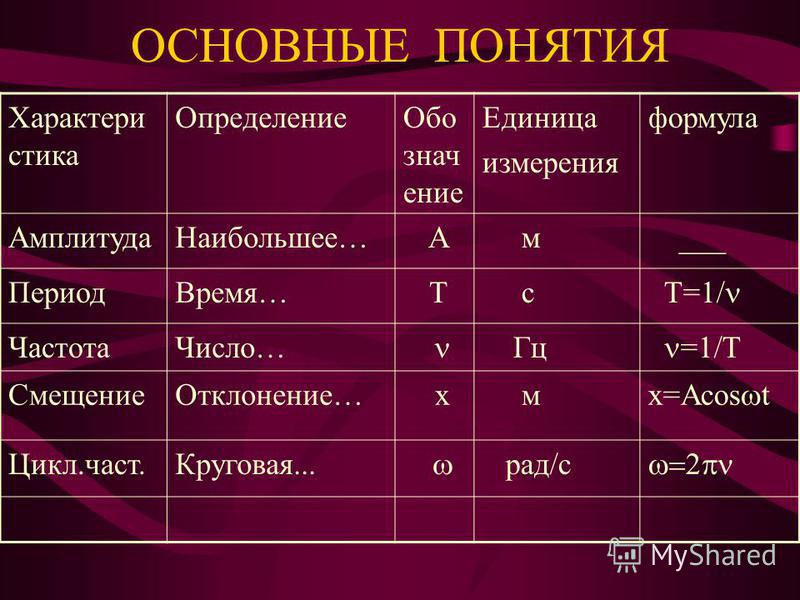
13