3 Переходные процессы в цепи Rl( короткое замыкание)
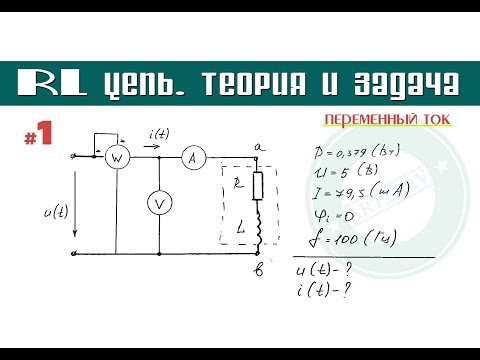
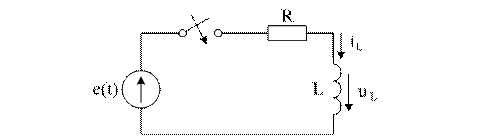
В схеме (рис. 6.3) контакт переключается из положения 1 в положение 2.
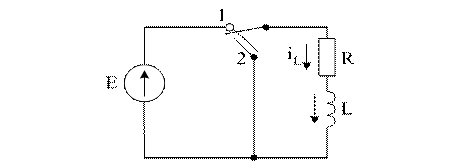
Рисунок 6.3
До коммутации, при t < 0, в цепи под действием постоянной ЭДС, протекал постоянный ток:
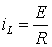 .
.
Напряжение
на индуктивности при постоянном токе
равно нулю: 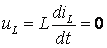 ,
т.е. при постоянном токе индуктивность
не оказывает сопротивления току, она
равносильна закоротке.
,
т.е. при постоянном токе индуктивность
не оказывает сопротивления току, она
равносильна закоротке.
После
коммутации, при t>0, цепь описывается
уравнением: 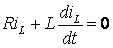 .
.
В такой
цепи iL
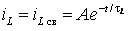 ,
,
где 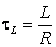 .
.
Определим постоянную интегрирования А с помощью первого закона коммутации:
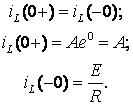
Следовательно, 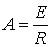 и
и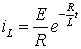 (6.13).
Найдем напряжения на индуктивности:
(6.13).
Найдем напряжения на индуктивности:
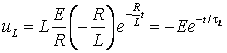
В первый
момент после коммутации 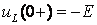 .
Это объясняется тем, что для поддержания
тока в цепи на прежнем уровне должна
возникнуть ЭДС самоиндукции
.
Это объясняется тем, что для поддержания
тока в цепи на прежнем уровне должна
возникнуть ЭДС самоиндукции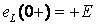 ,
а напряжение
,
а напряжение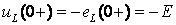 .
.
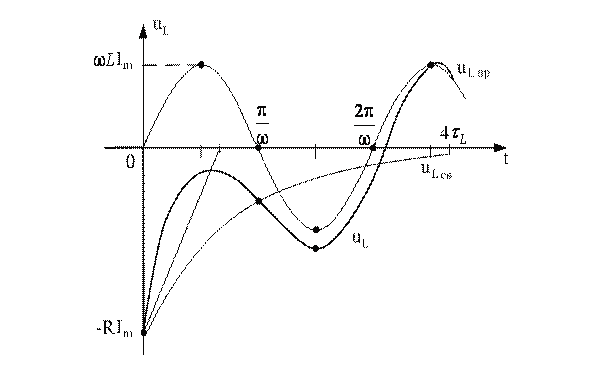
Графики iL и uL построены по уравнениям (6.13) и (6.14) и представлены на рис. 6.4.
Физический смысл переходного процесса состоит в том, что за его время энергия, которая была накоплена в магнитном поле до момента коммутации, выделяется в виде тепла в резисторе. Для доказательства вычислим энергию, которая выделяется в виде тепла за время переходного процесса:
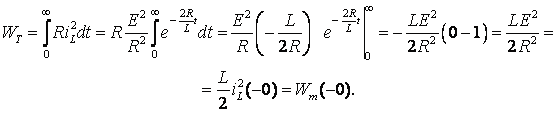
| |
4 Включение rL цепи на постоянное напряжение
Пусть
дана цепь (рис.1.1), которая подключается
к источнику постоянного напряжения.
Параметры цепы заданы: r, L, 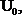
Определить ток i (t).
Решение:
В последний момент времени перед замыканием ключа ток в цепи отсутствовал
i(0-) = 0,
где t = 0-.
При t = 0+ ключ замыкается. Здесь t = 0+ – первый момент времени после совершения события (замыкания ключа).
Ключ замкнулся, образовался контур. Составим для него уравнение второго закона Кирхгофа:
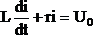
Это уравнение аналогично математическому дифференциальному уравнению первого порядка (ax’ + bx = y).
Решение для тока имеет вид:
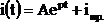 ,
,
где 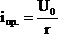 –
–
принужденная составляющая решения, А – постоянная интегрирования, которая может быть найдена из граничных условий.
По характеристическому уравнению: Lp + r = 0
определим
корень: 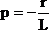
Обратная величина модуля корня называется постоянной переходного процесса (?):
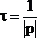 ,
,
а время переходного процесса равно: tп.п = (4…5) ?.
В
момент времени 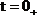 определим
постоянную интегрирования А.
определим
постоянную интегрирования А.
Подставим в решение для тока этот момент:
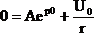
Отсюда А равно:
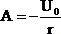 .
.
Окончательное решение для тока:
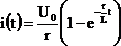 .
.
Напряжение на индуктивности можно определить по формуле:
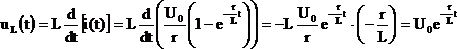 .
.
Мгновенная мощность источника:
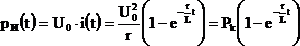 .
.
Мгновенная мощность нагрузки (r):
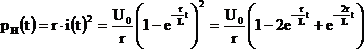 .
.
Мгновенная мощность нагрузки (L):
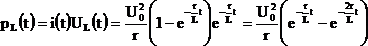 .
.
Для расчета переходных процессов в цепях классическим методом необходимо знать законы коммутации. В электрических цепях этих законов два.
5 Вкл цепи rl под синусоидальное напряжение.
К схеме (рис. 6.6) при нулевых начальных условиях подключается синусоидальная ЭДС:
| |
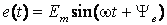 .
.
Рисунок 6.6
При t < 0 iL = 0, uL = 0.
При t > 0 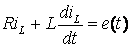 .
(6.17)
.
(6.17)
Решение этого уравнения состоит из двух составляющих:
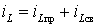
Поскольку в правой части уравнения (6.17) имеется синусоидальная ЭДС, то после окончания переходного процесса в цепи установится синусоидальный ток:
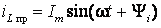 ,
(6.19)
,
(6.19)
где 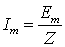 ;
;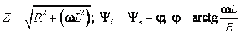 .
.
Для расчета принужденных составляющих iL пр и uL пр можно применить также комплексную форму записи. Эта методика будет показана при расчете цепи R, C.
Свободная составляющая не зависит от наличия и вида источника:
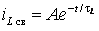 ;
(6.20)
;
(6.20)
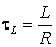 .
.
Подставляем (6.19) и (6.20) в (6.18) и применим первый закон коммутации для определения постоянной А
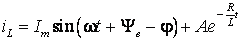 .
(6.21)
.
(6.21)
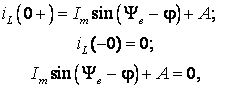
откуда
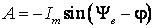 .
(6.22)
.
(6.22)
Подставив (6.22) в (6.21) получим:
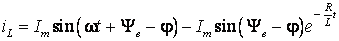 .
(6.23)
.
(6.23) Напряжение
на катушке индуктивности тоже состоит
из двух составляющих: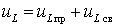 ,
причем
,
причем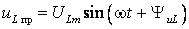 ,
где
,
где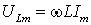 ,
а
,
а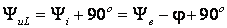 .
.
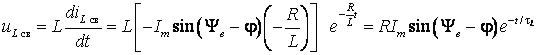 .
.
Таким образом,
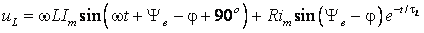
Поскольку в выражения iL (6.23) и uL (6.24) входит величина Ye, то интенсивность переходного процесса зависит от момента подключения синусоидальной ЭДС. Рассмотрим два крайних случая.
1) Если
Ye =
j, то YI =
0; 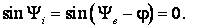
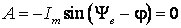 –
в этом случае не возникает
переходный процесс.
–
в этом случае не возникает
переходный процесс.
Графики iL, uL для этого случая представлены на рис. 6.7.
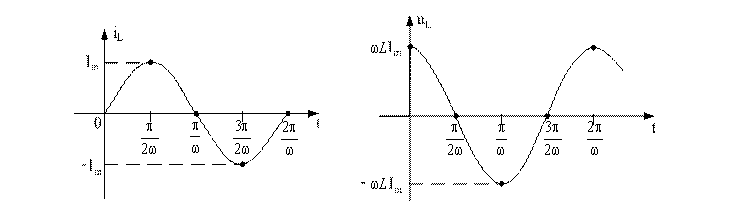
Рисунок 6.7
2) 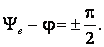 Выберем
значение
Выберем
значение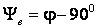 .
.
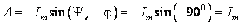 ;
;
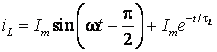 (6.25)
(6.25)
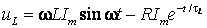 (6.26)
(6.26)
График тока , построенный согласно (6.25). представлен на рис. 6.8.
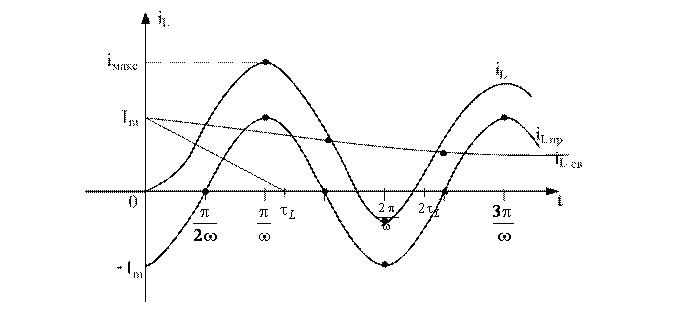
Рисунок 6.8
Если свободная составляющая затухает медленно, что возможно при малом значении R, через полпериода после включения ток достигает наибольшего значения iмакс., которое в пределе стремится к 2Im, если t®¥. В реальных цепях свободная составляющая всегда затухает, и для выбора электрической аппаратуры принимают iмакс = 1,8 Im.
График напряжения uL показан на рис. 6.9.
| |
Рисунок 6.9
Если R >>
wL.
то в первый момент после включения
возможен значительный скачок напряжения
на катушке: 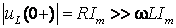 .
Изоляция электроустановок должна быть
выбрана с учетом этого возможного скачка
напряжения.
.
Изоляция электроустановок должна быть
выбрана с учетом этого возможного скачка
напряжения.
Таким образом, при синусоидальной ЭДС в цепи R, L при определенных условиях возникает сверхток iмакс и перенапряжение на катушке индуктивности.
Входные характеристики цепи rl

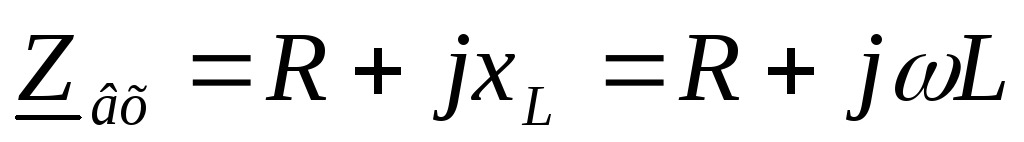
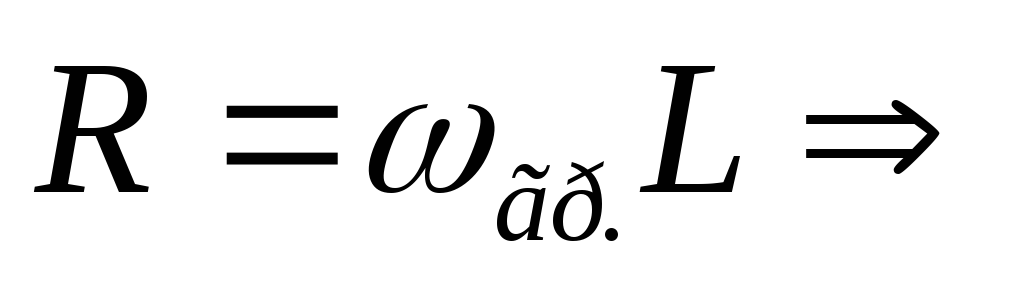
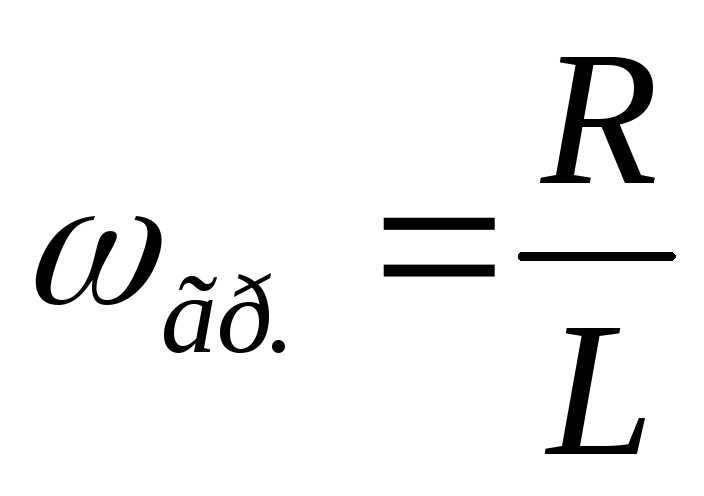 — формула граничной частоты цепиRL
— формула граничной частоты цепиRL
Порядок построения характеристик:
записываем комплексное входное сопротивление:
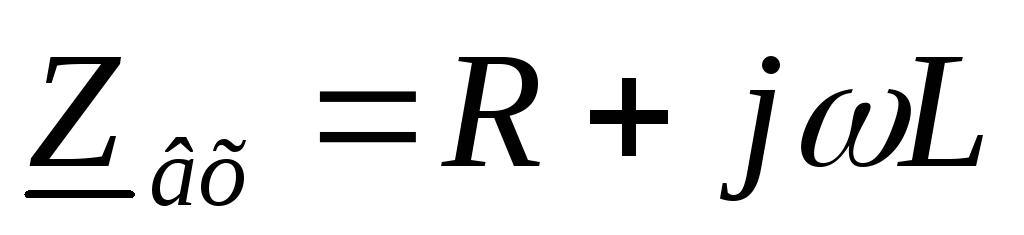
записываем модуль комплексного входного сопротивления:
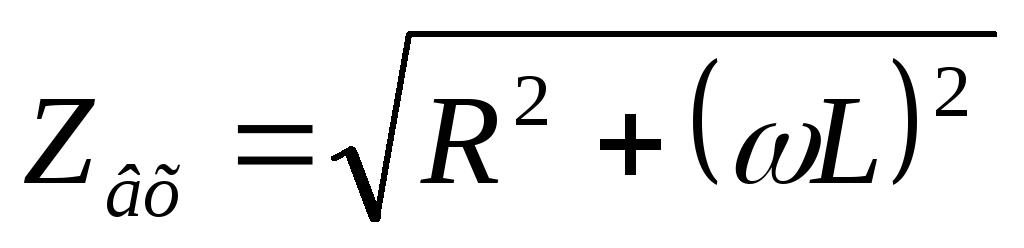
в
 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
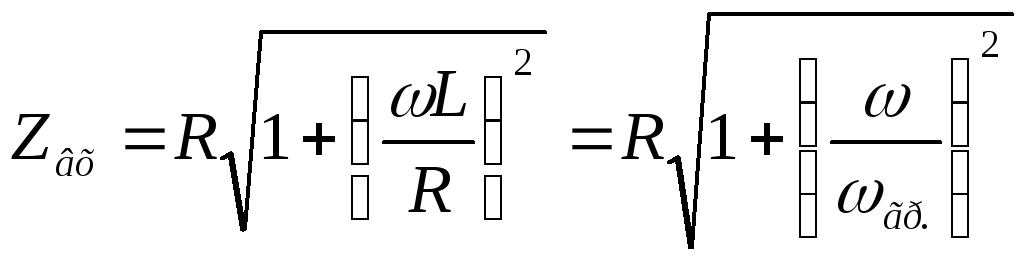
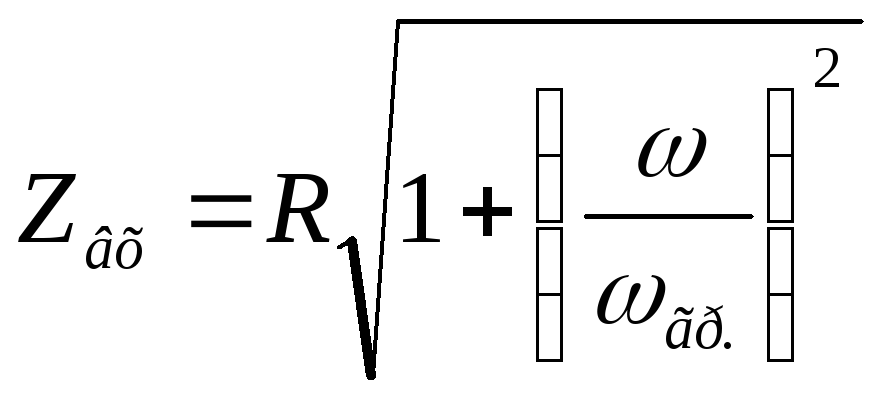 — формула входной АЧХ цепиRL
— формула входной АЧХ цепиRL
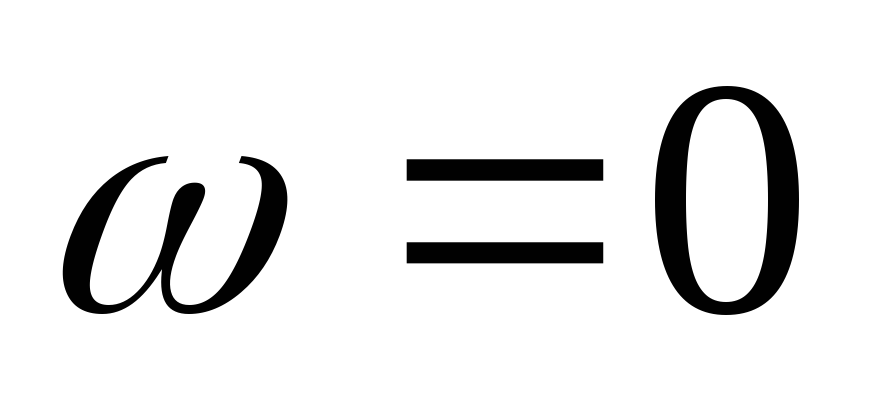
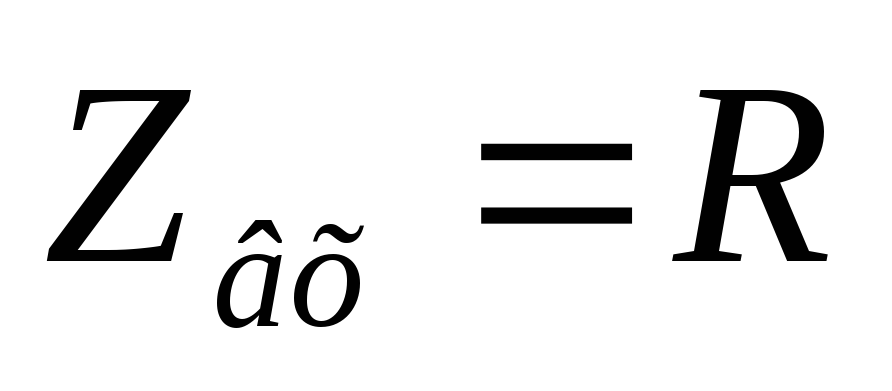
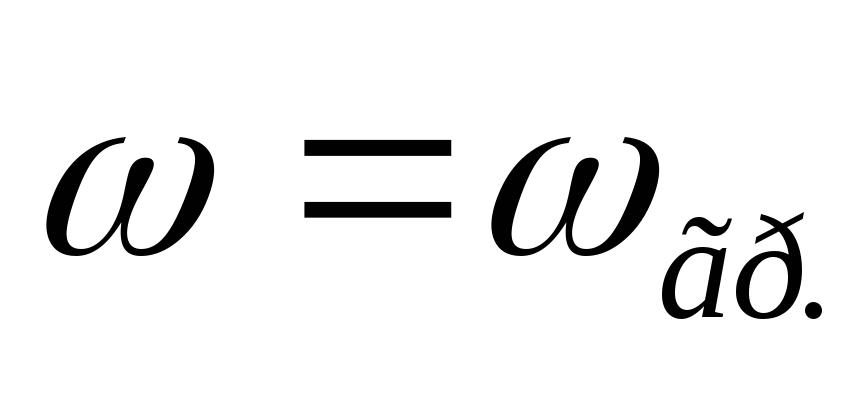
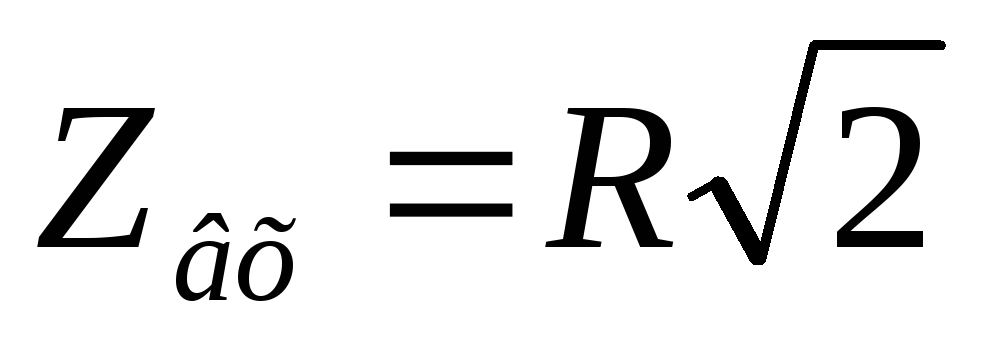
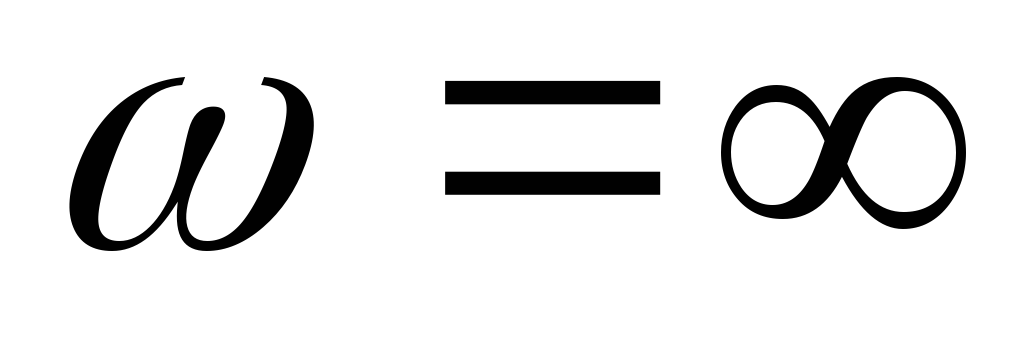
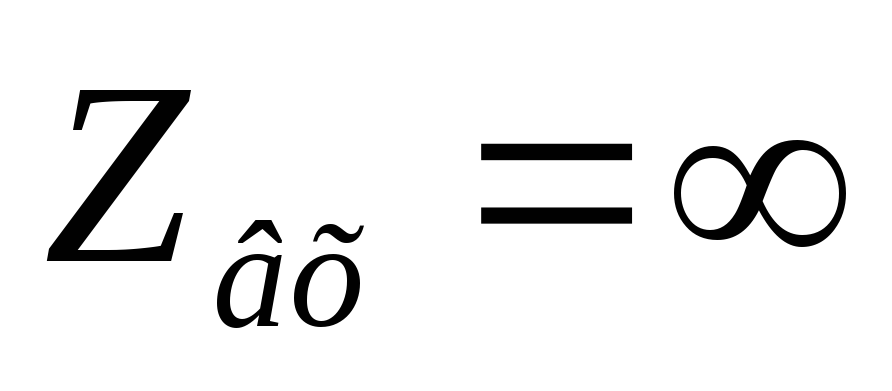
з
 апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ:
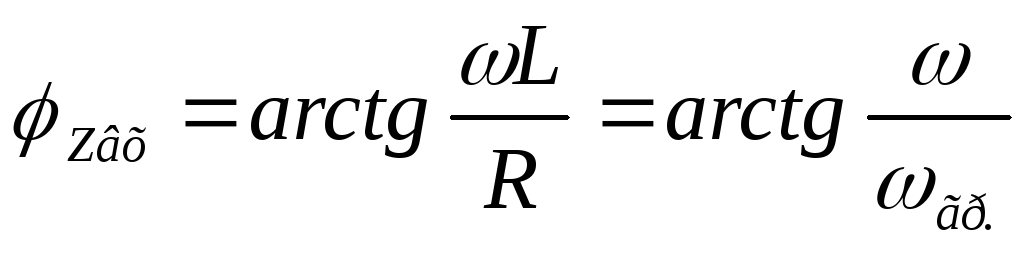
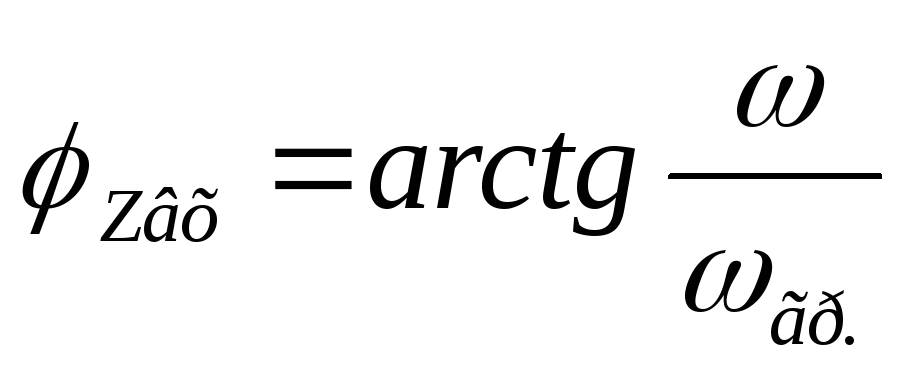 — формула входной ФЧХ цепиRL
— формула входной ФЧХ цепиRL
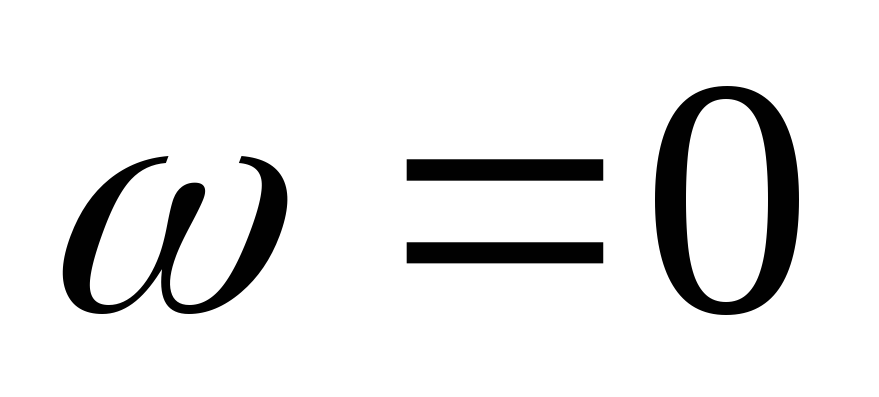
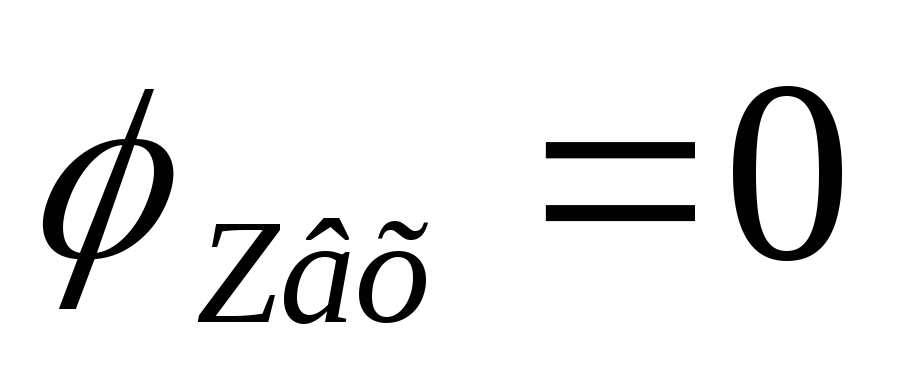
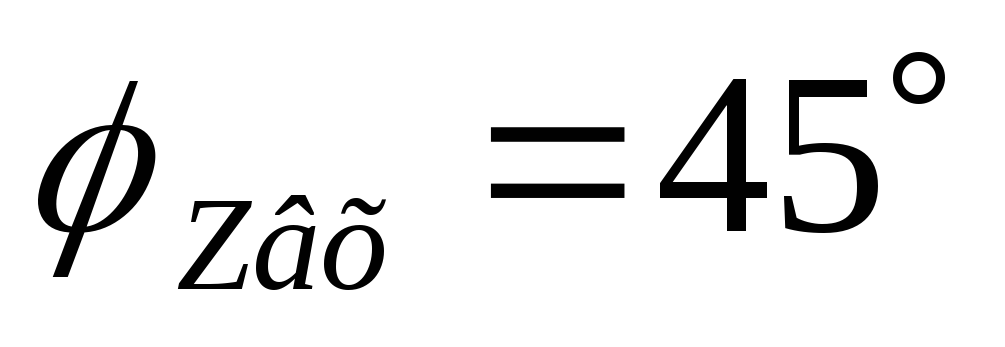
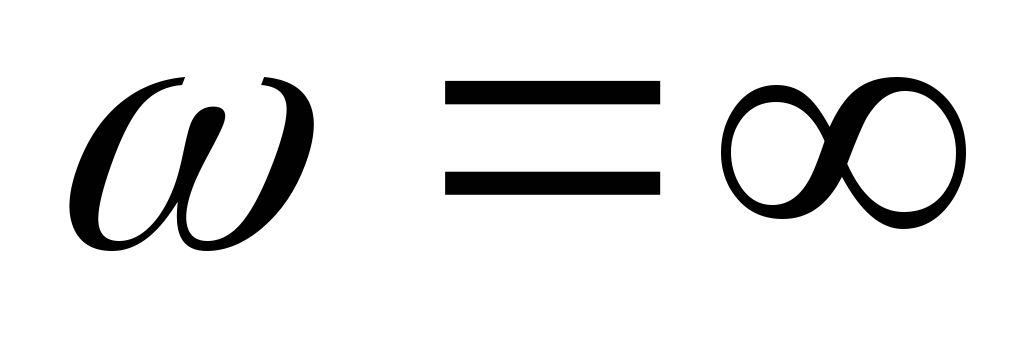
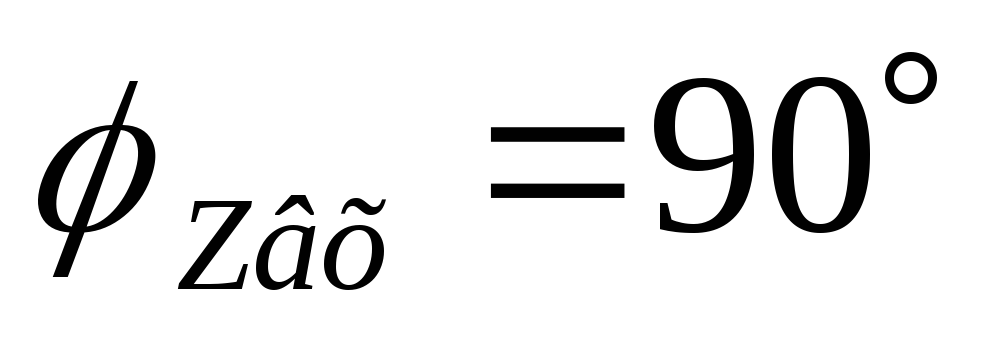
Выводы:
В цепи RLс ростом частоты входное сопротивление растёт.
Входная ФЧХ имеет линейный участок на частотах от
 до
до .
.
Построение входных характеристик качественно
Для сложных электрических цепей
характеристики можно строить только
с помощью вычислительной техники. Можно
построить характеристики качественно,
рассмотрев цепь на двух частотах: 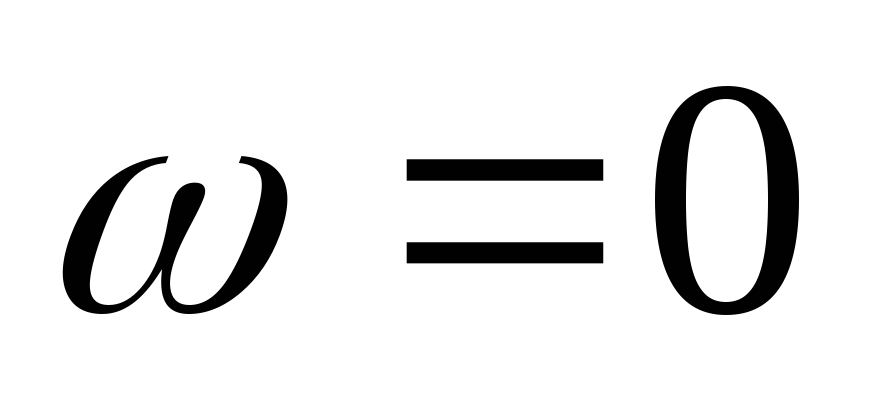 и
и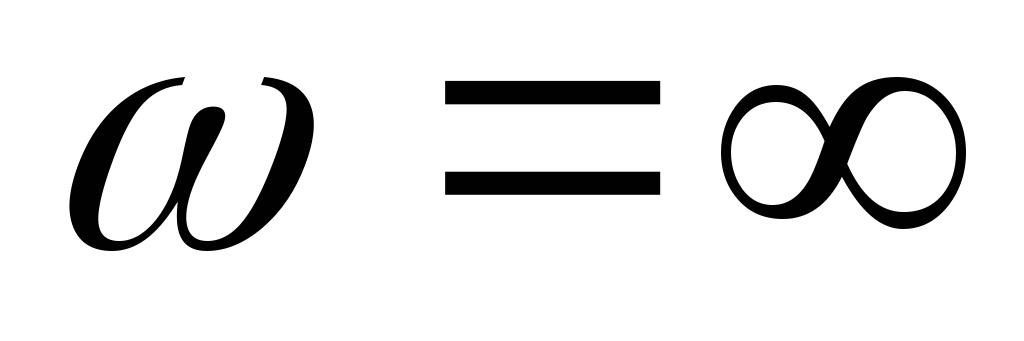 .
.
Надо помнить:
АЧХ и ФЧХ всегда нелинейные
Если в цепи есть индуктивность, то АЧХ возрастает, если ёмкость — АЧХ убывает.
Построим качественно АЧХдля цепи:

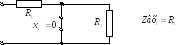
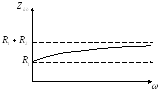
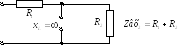
Построим качественно ФЧХдля той же цепи:
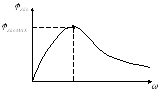
Т. к. цепь RL, то угол — положителен, и если при
— положителен, и если при 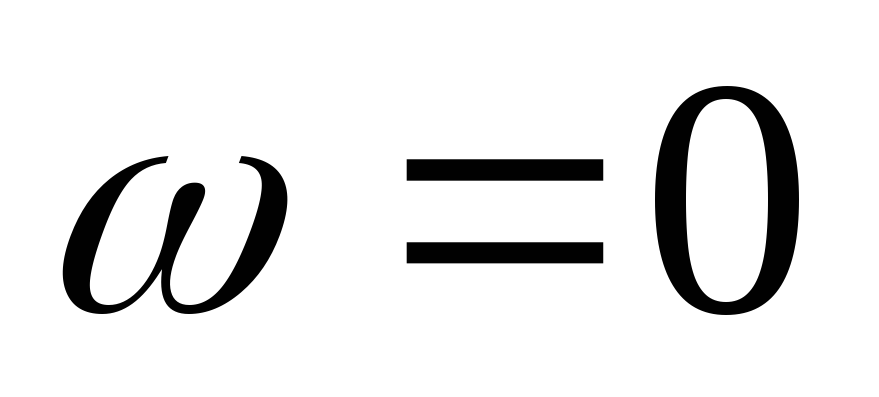 и
и 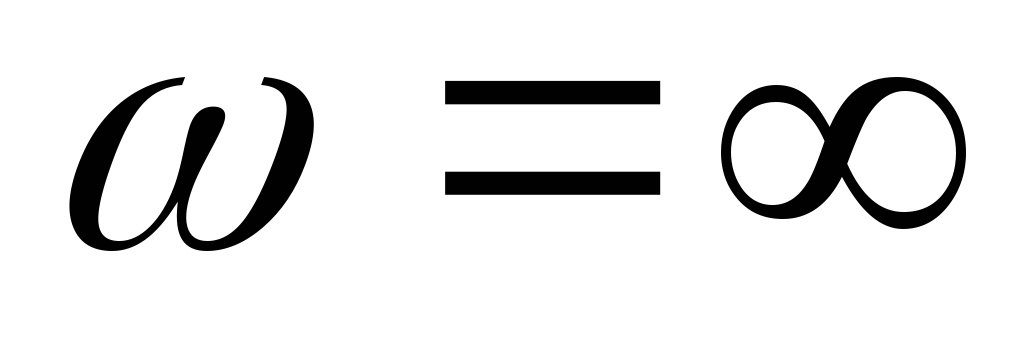
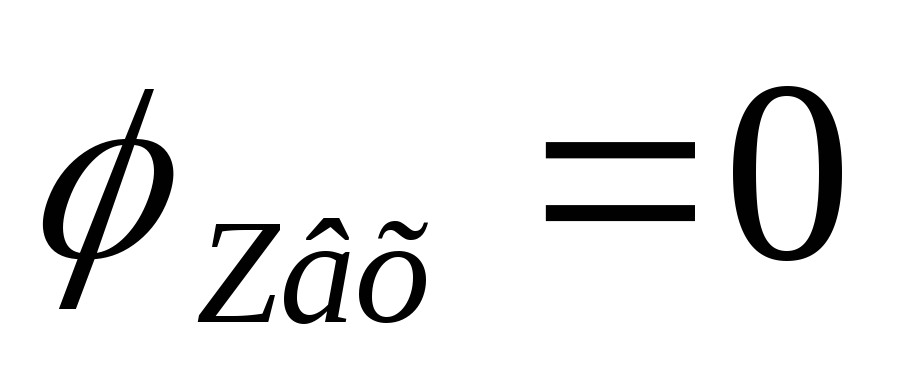 ,
то где-то есть максимум
,
то где-то есть максимум 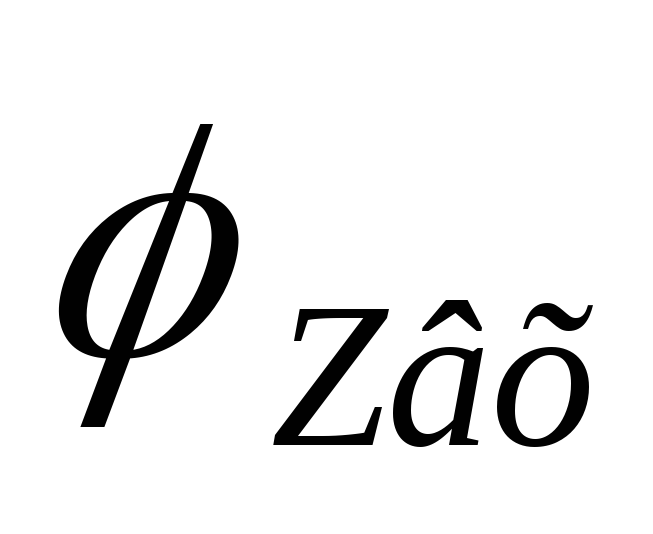 :
:
Вопрос 41. Входные ачх и фчх rc неразветвлённых и разветвлённых цепей. Определение и понятие граничной частоты. Поверхностный эффект. Построение входных характеристик.
Понятие входных АЧХ и ФЧХ, граничной частоты, а также порядок построения характеристик рассмотрены в предыдущем вопросе (см. вопрос 40).
Входные характеристики цепи rc
И спользуем
порядок построения характеристик:
спользуем
порядок построения характеристик:
записываем комплексное входное сопротивление:
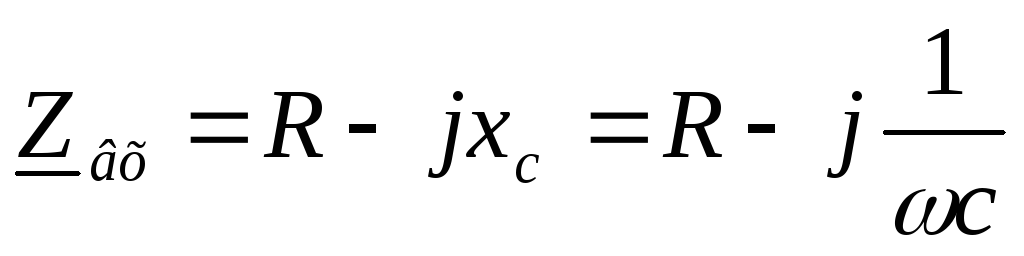
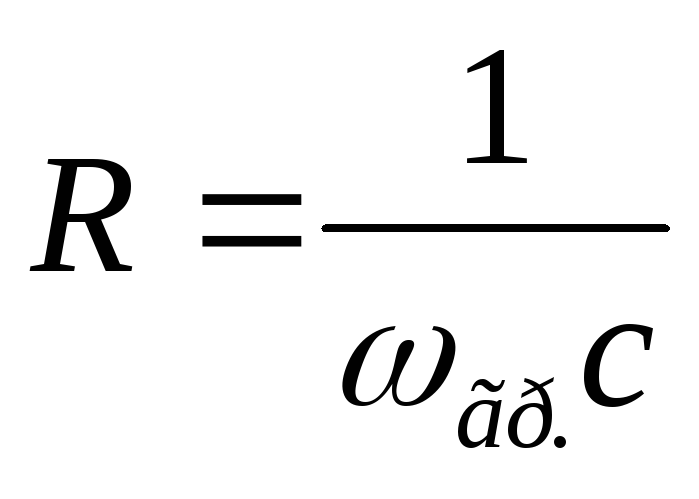
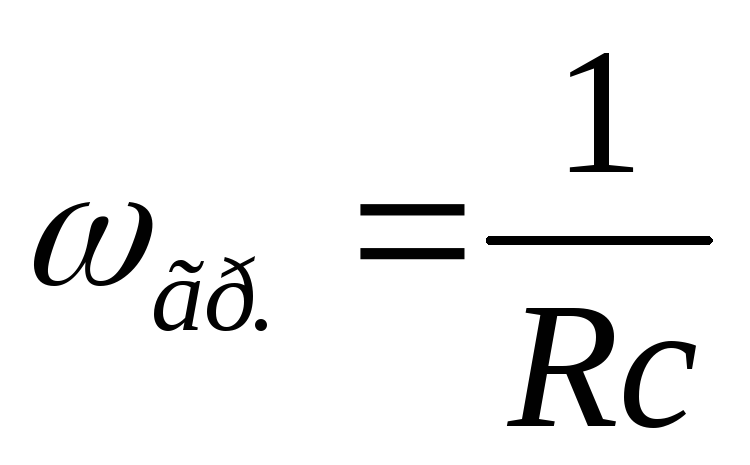 — формула граничной частоты цепиRC
— формула граничной частоты цепиRC
записываем модуль комплексного входного сопротивления:
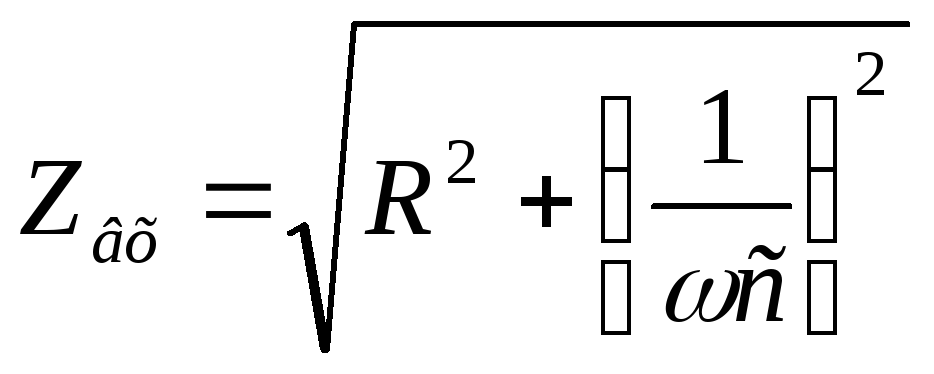
в
 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
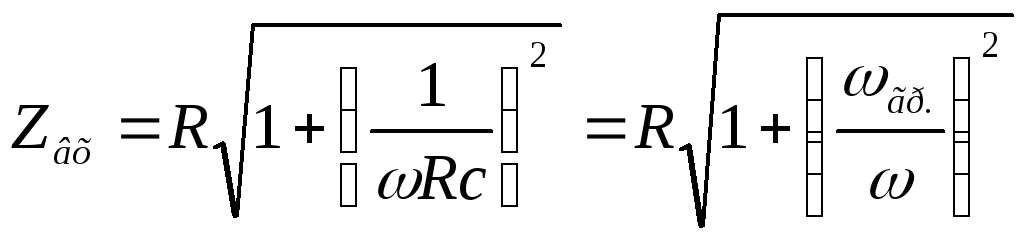
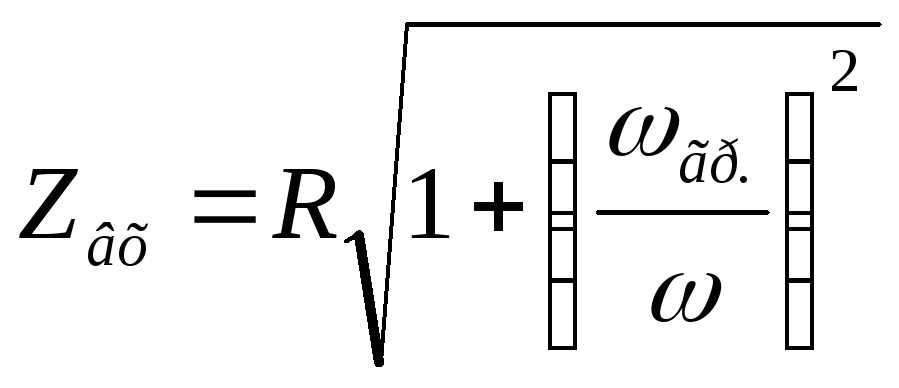 — формула входной АЧХ цепиRС
— формула входной АЧХ цепиRС
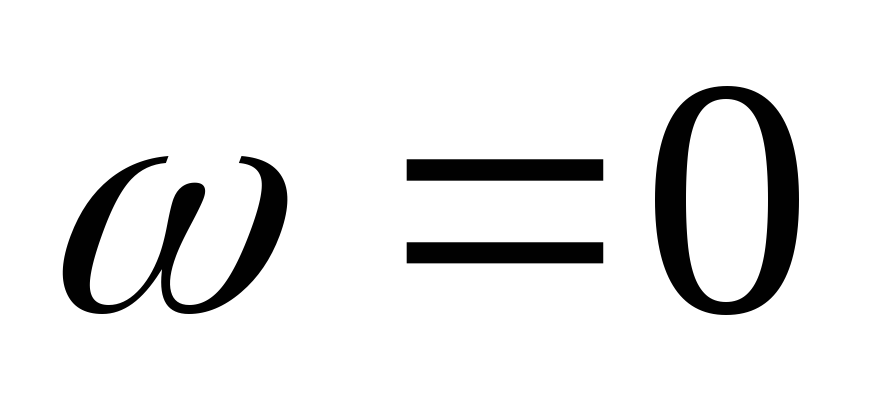
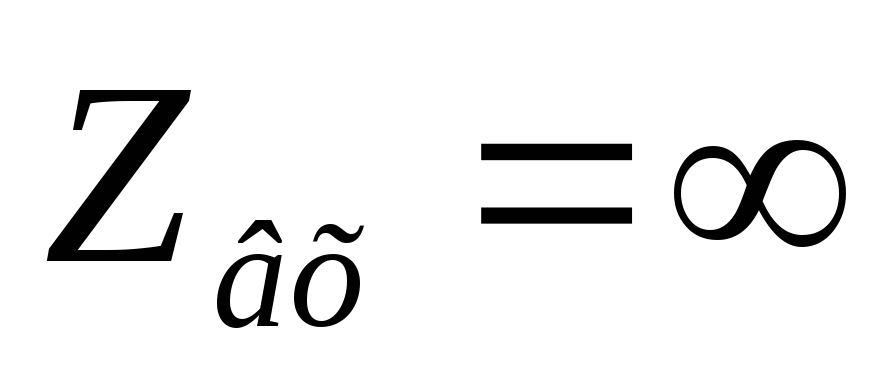
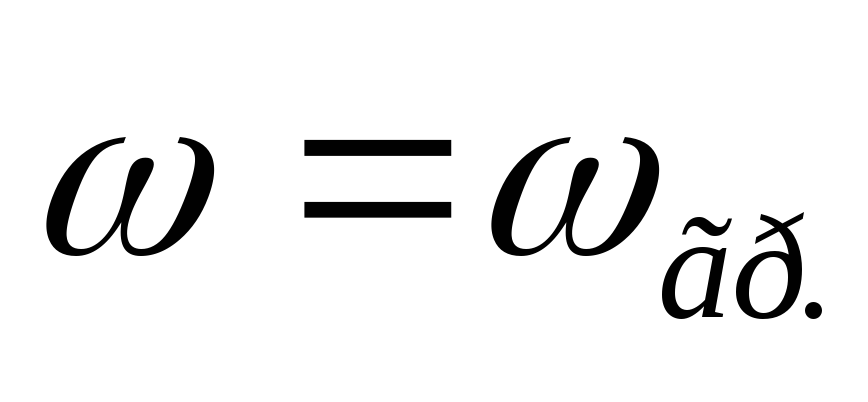
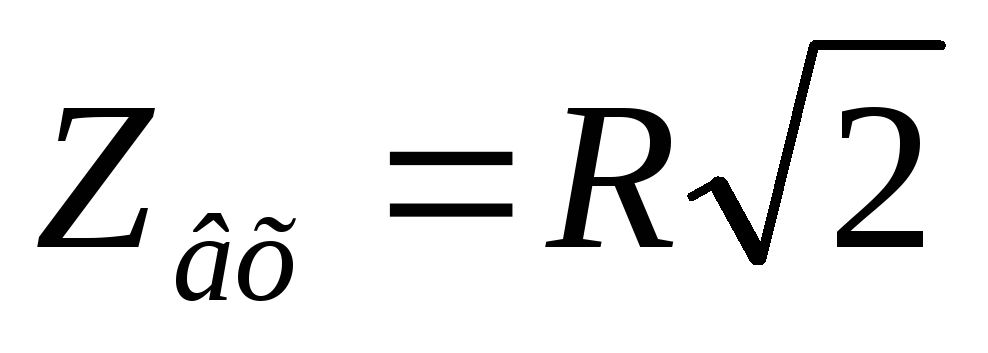
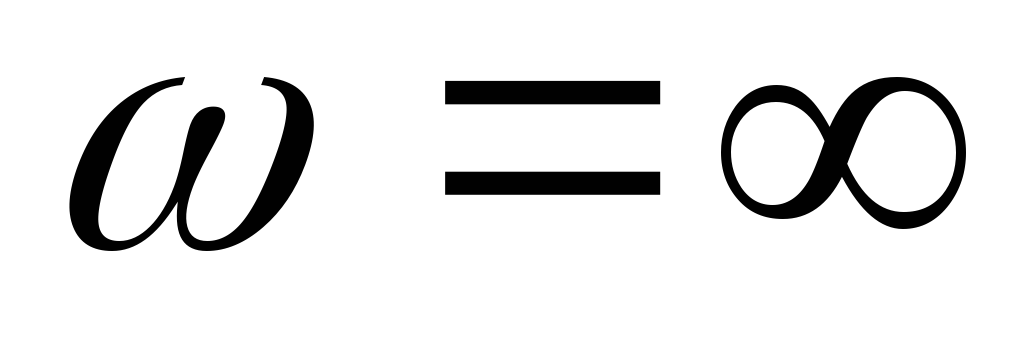
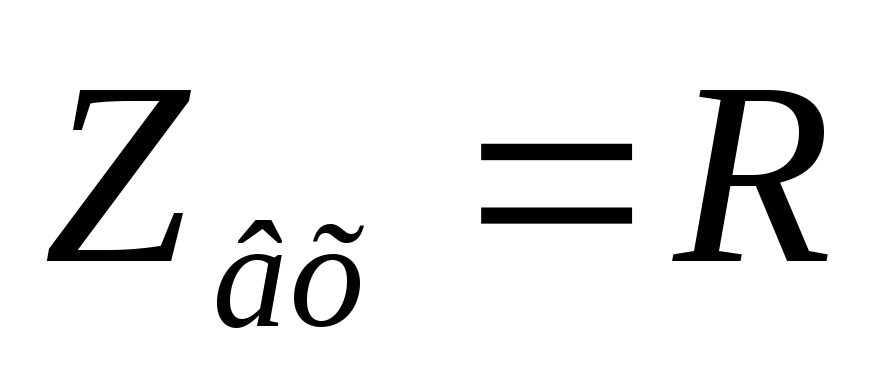
Вывод:
С ростом частоты входное сопротивление цепи RCуменьшается.
з
 апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ:
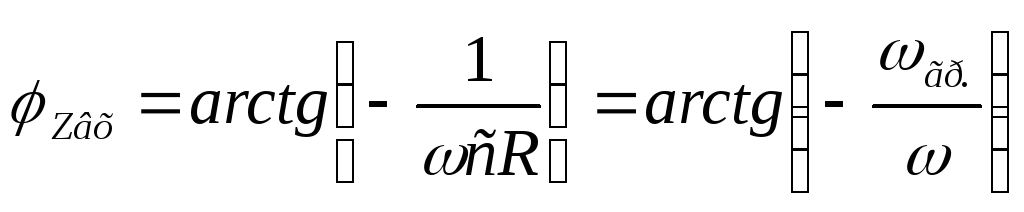
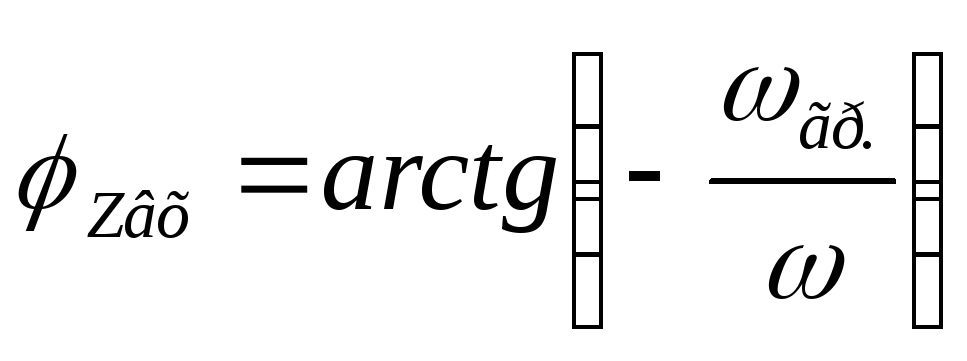 — формула входной ФЧХ цепиRС
— формула входной ФЧХ цепиRС
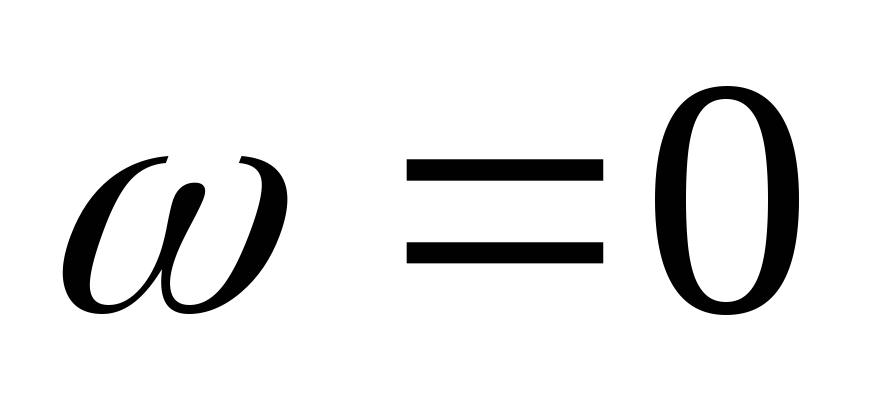
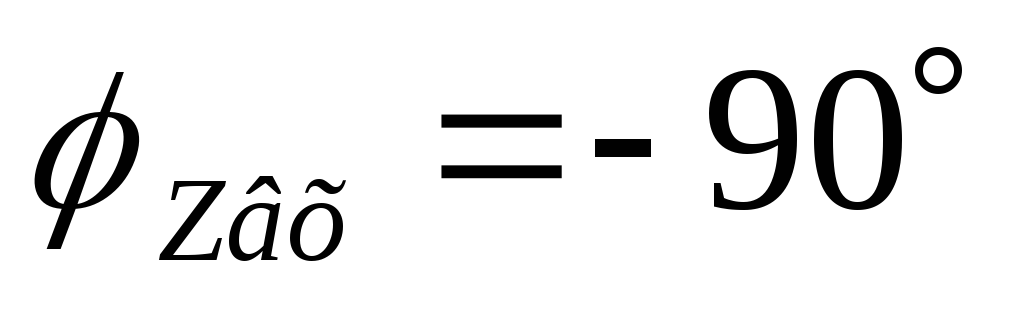
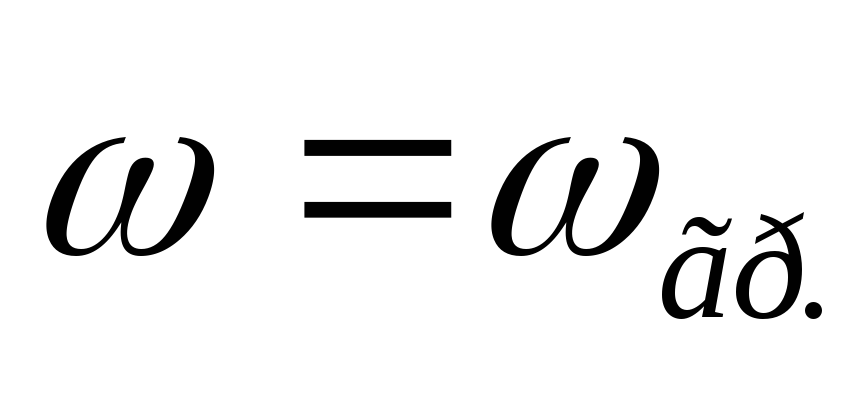
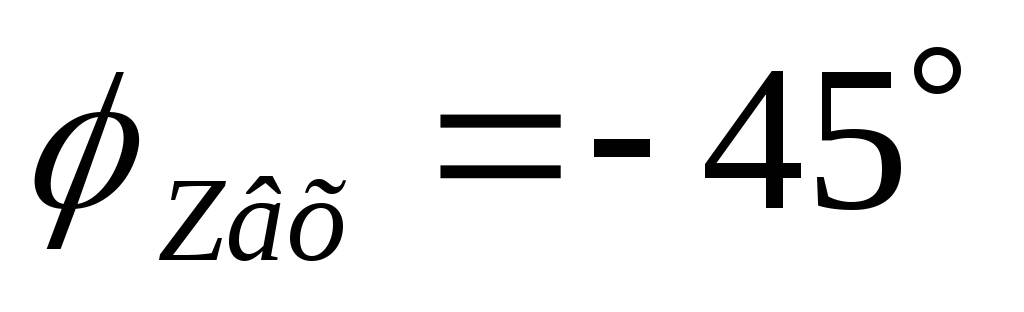
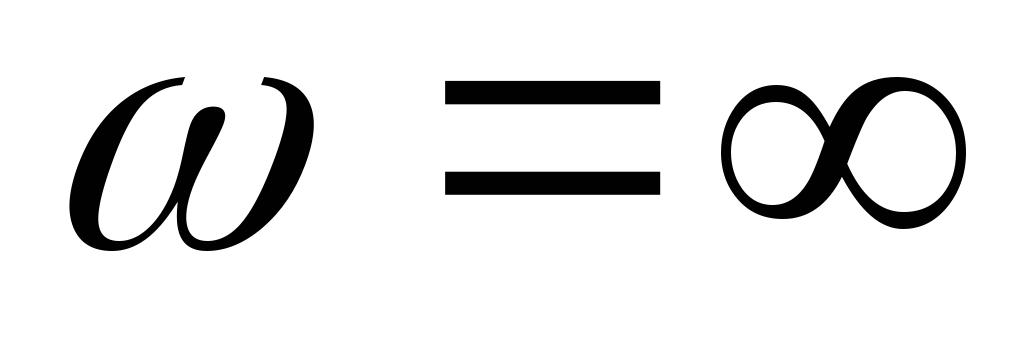
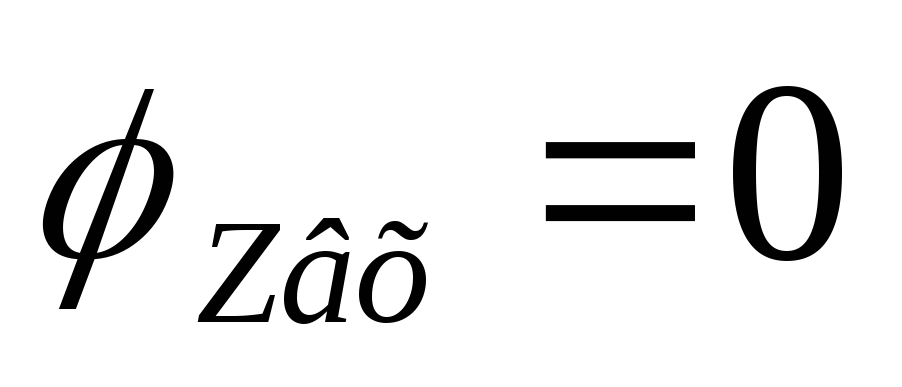
Вывод:
В цепи RCвходная ФЧХ имеет линейный
участок на частотах от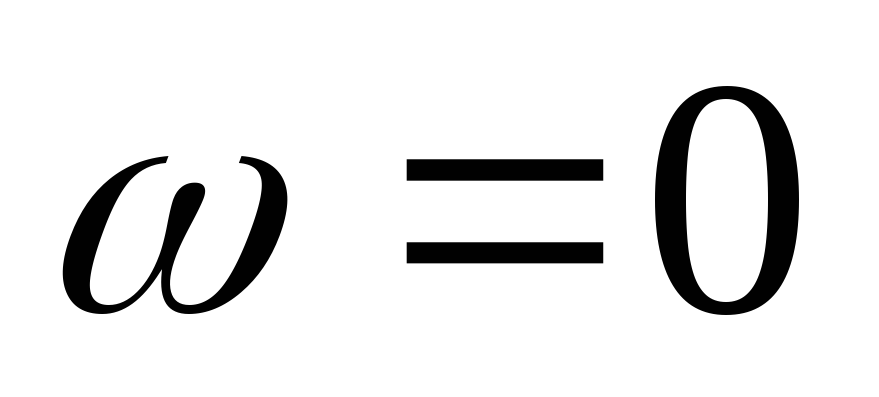 до
до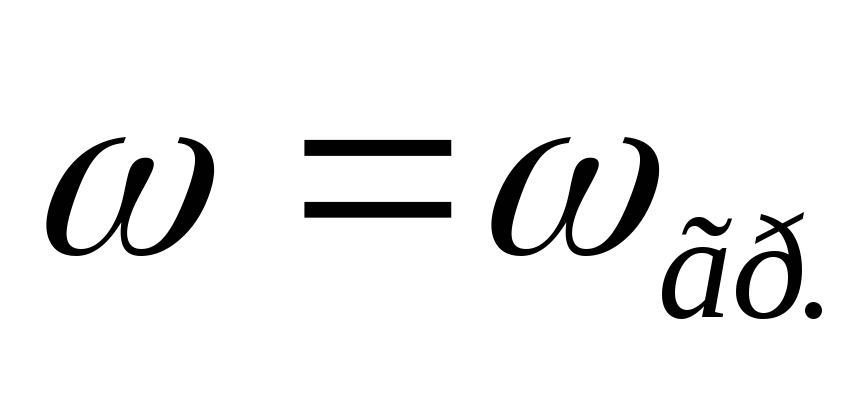 .
.
Вывод (к вопросам 40 – 41): на
граничной частоте в цепях первого
порядка 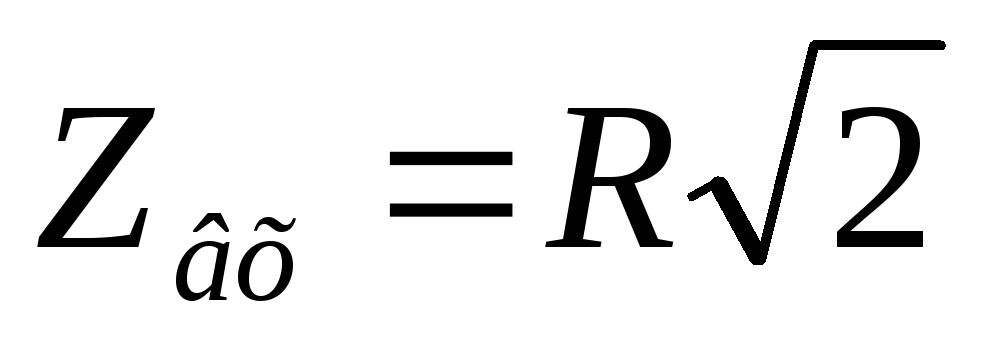 ,
, 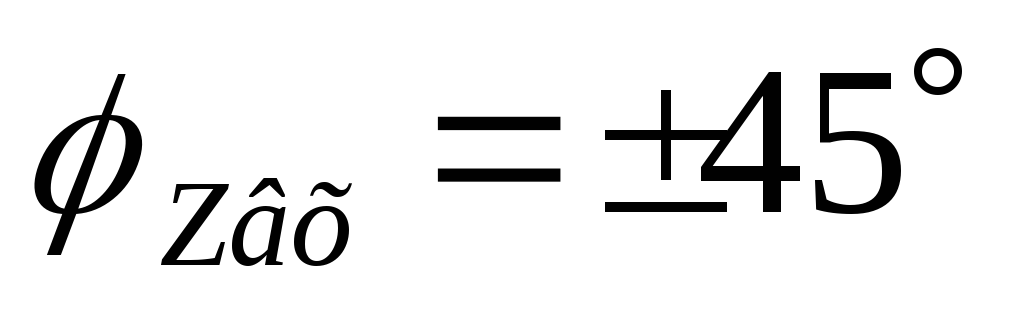 .
.
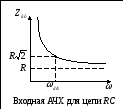
Построим качественно входные характеристики для цепи:

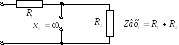
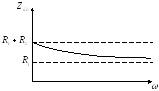
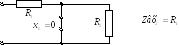
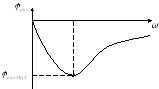
Т. к. цепь RС, то угол — отрицателен, и если при
— отрицателен, и если при 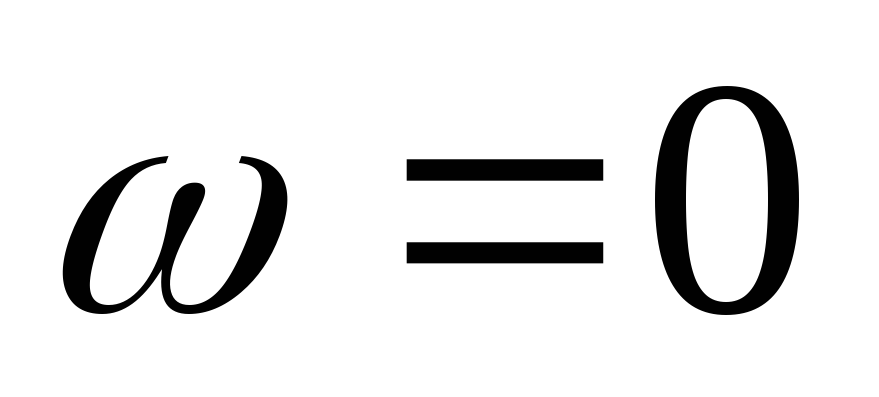 и
и 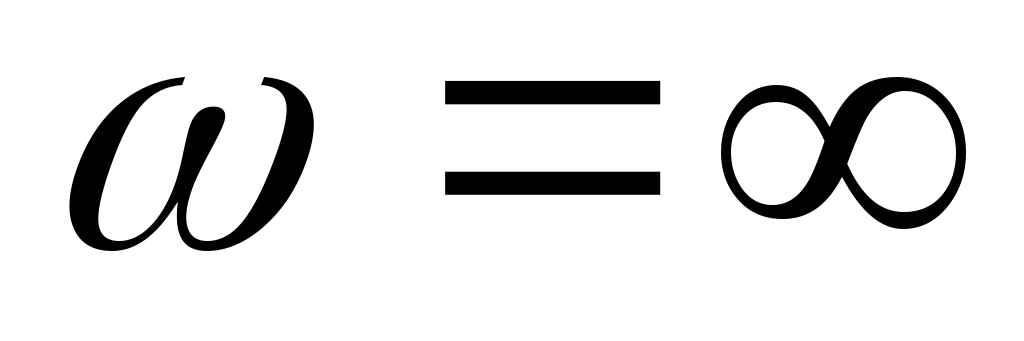
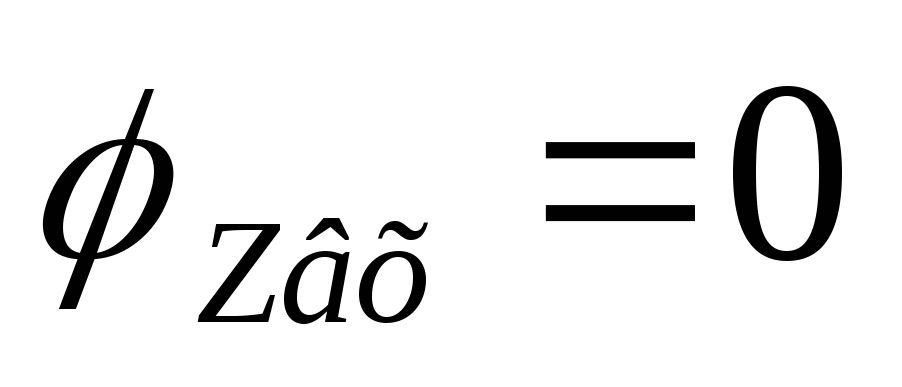 ,
то где-то есть максимум
,
то где-то есть максимум 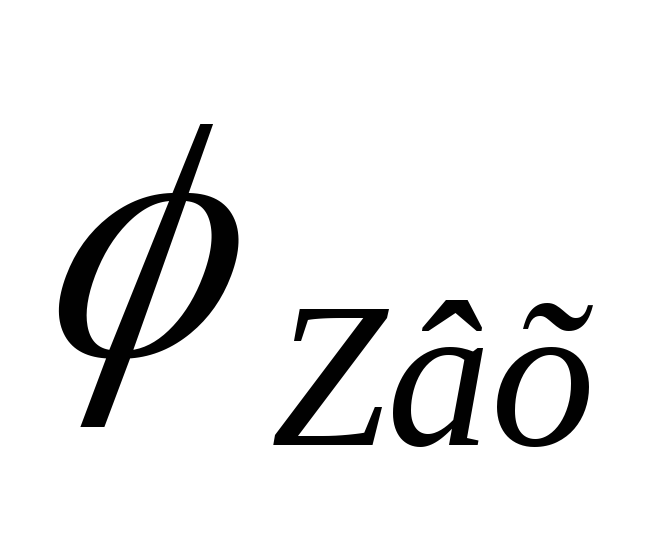 :
:
Поверхностный эффект
Поверхностный эффект(ПЭ) заключается
в том, что плотность переменного тока
оказывается наибольшей у поверхности
проводника, а по мере удаления от
поверхности вглубь сечения проводника
она убывает. Это связано с различной
индуктивностью внешних и внутренних
слоёв проводника (внутри индуктивность
больше). Вытеснение тока к поверхности
проводника равносильно уменьшению
сечения, а т. к. ,
значит увеличивается сопротивление.
,
значит увеличивается сопротивление.
ПЭ при переменном токе выражается тем резче, чем выше частота колебаний и чем больше диаметр провода.
При промышленной частоте 50 Гц ПЭ существенно влияет, когда диаметр провода выше 1 см. На высоких частотах (ВЧ) часто применяют вместо проводов трубки, т. к. внутри провода тока нет.
Параллельные цепи rl и rc при гармоническом воздействии
Если цепь параллельна, то векторную диаграмму начинают строить с вектора напряжений, т.к. напряжение участков при параллельном соединении одинаково.
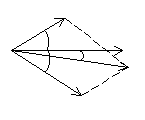
Ток 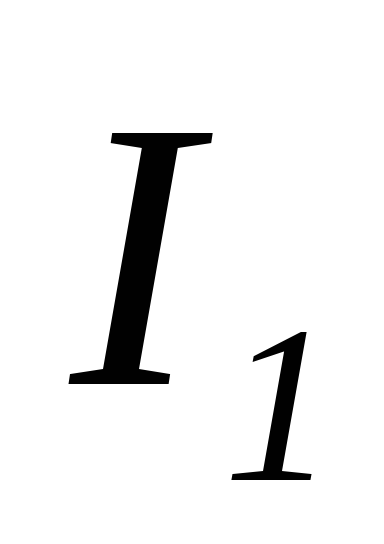 отстает от напряжения на угол
отстает от напряжения на угол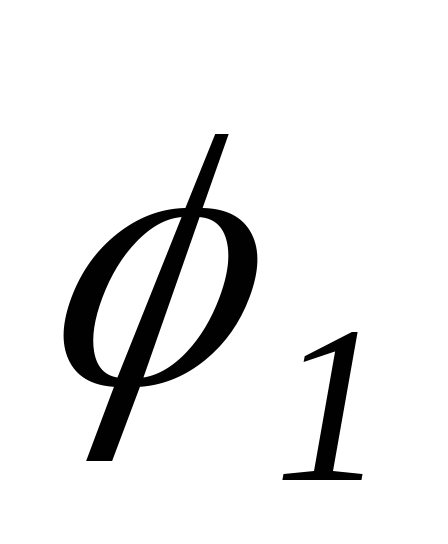 (цепьRL),
ток
(цепьRL),
ток 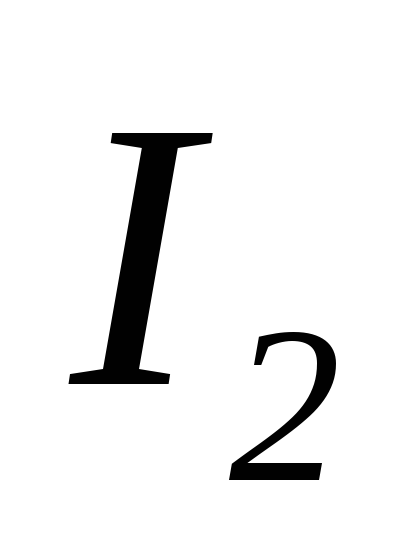 опережает напряжение на угол
опережает напряжение на угол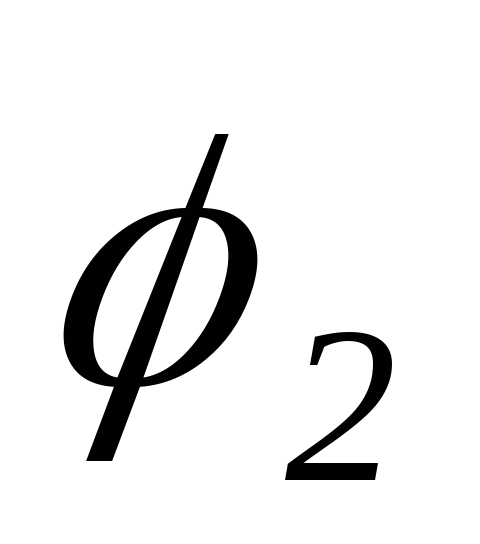 (цепьRC).
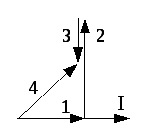
Общий ток равен векторной сумме этих
токов. Из диаграммы видно, что найти
общий ток можно только специальным
методом расчета. Этот метод называется
метод составляющих токов. Построим
подробную векторную диаграмму этой
цепи. Строим вектор напряжений и токи
(цепьRC).
Общий ток равен векторной сумме этих
токов. Из диаграммы видно, что найти
общий ток можно только специальным
методом расчета. Этот метод называется
метод составляющих токов. Построим
подробную векторную диаграмму этой
цепи. Строим вектор напряжений и токи 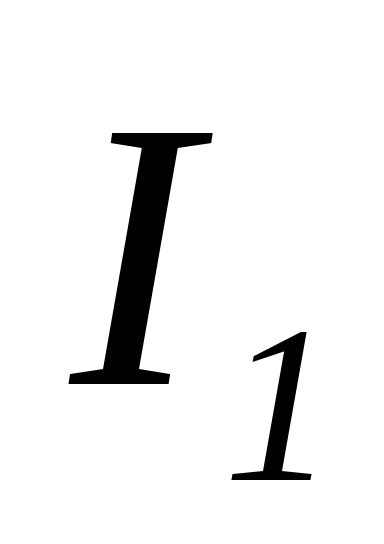 и
и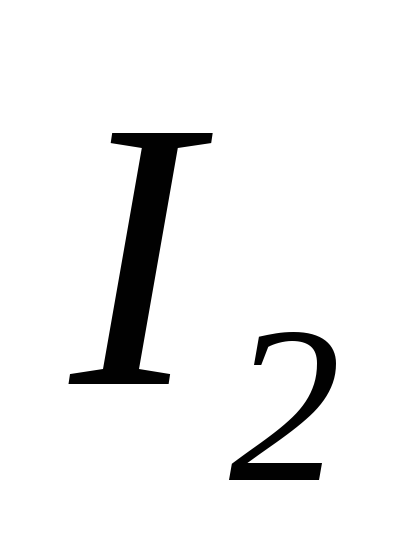 .
.
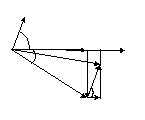
Разложим ток 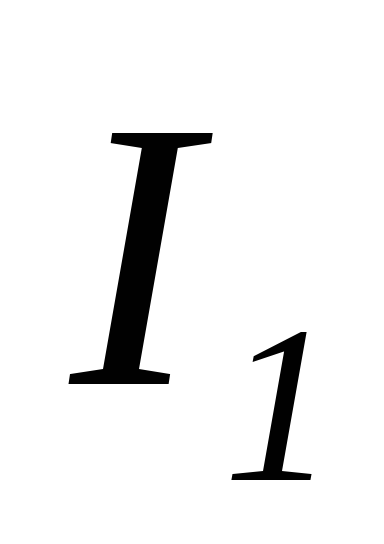 на две составляющие: активную
на две составляющие: активную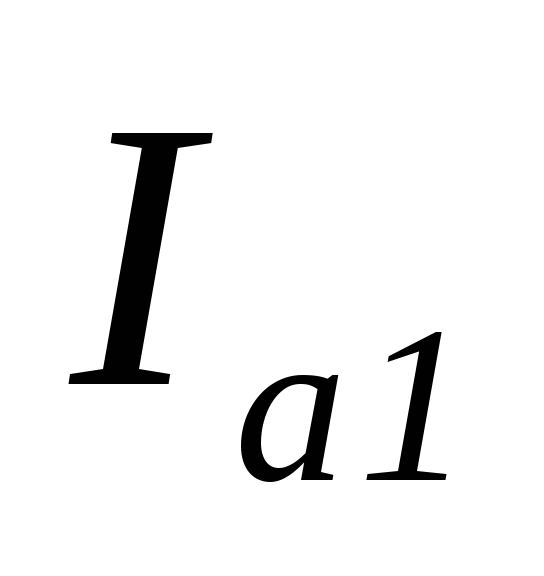 ,
которая совпадает по фазе с напряжением
и индуктивную
,
которая совпадает по фазе с напряжением
и индуктивную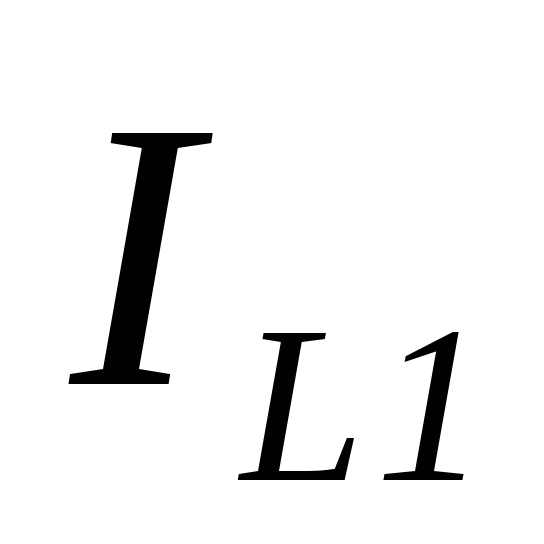 ,
которая отстающее по фазе от напряжения
на угол
,
которая отстающее по фазе от напряжения
на угол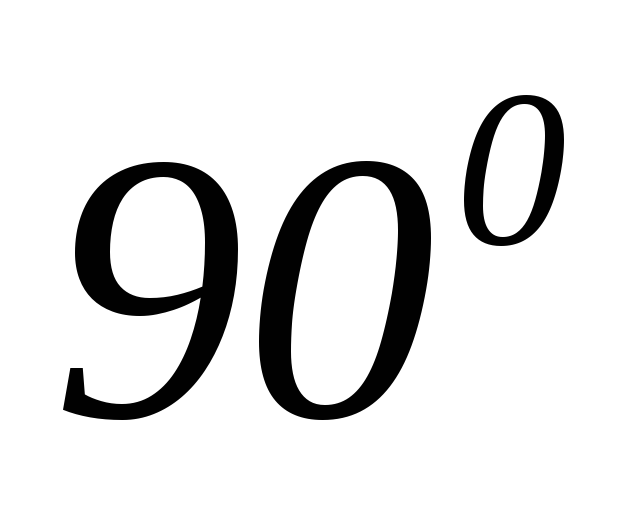 .
.
Эти составляющие
определяем по формулам прямоугольного
треугольника. 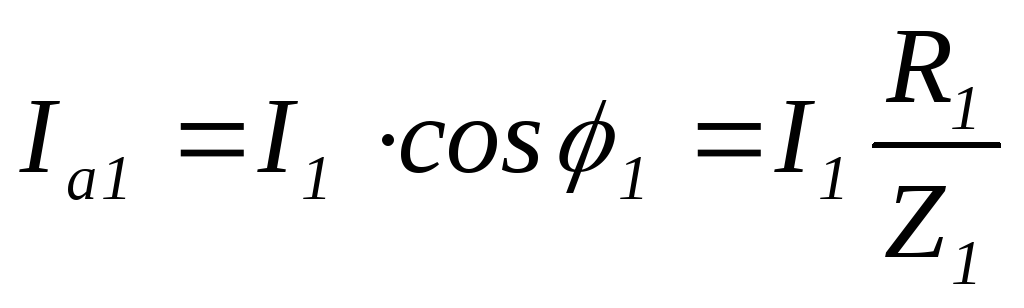 ,
,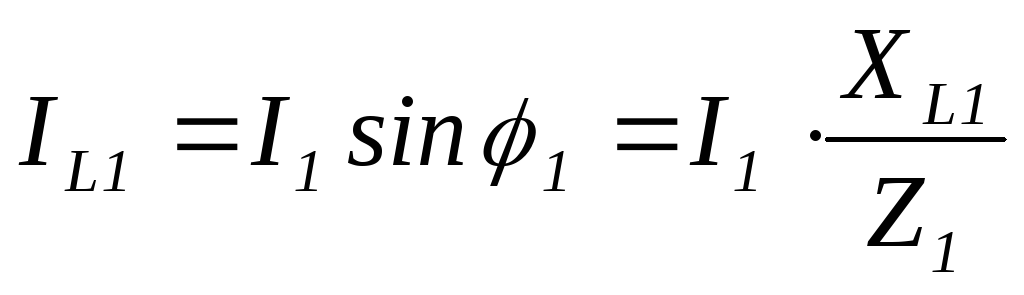 ,
где
,
где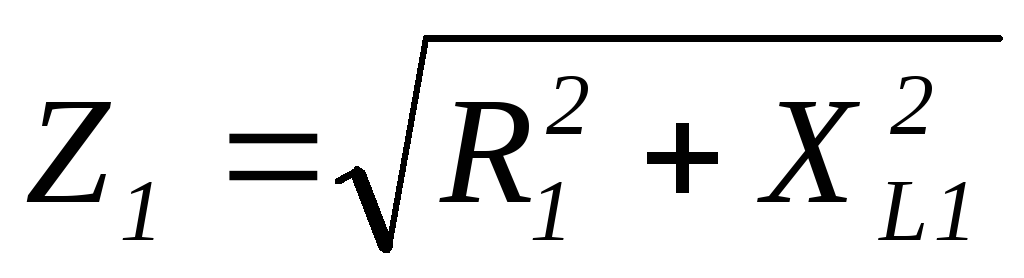 ;
;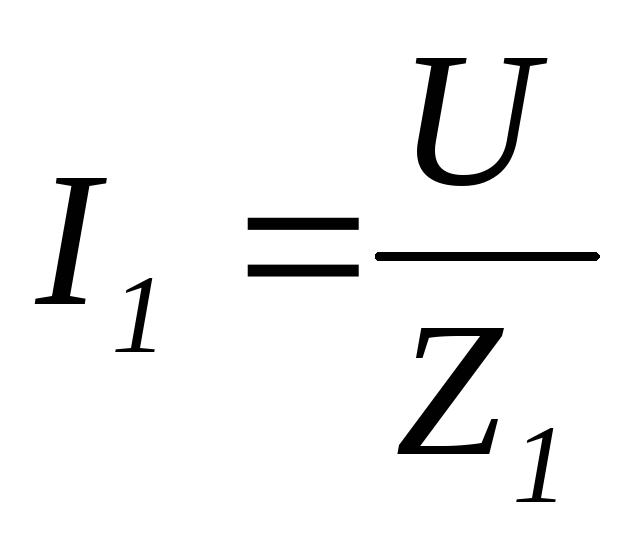
Разложим ток 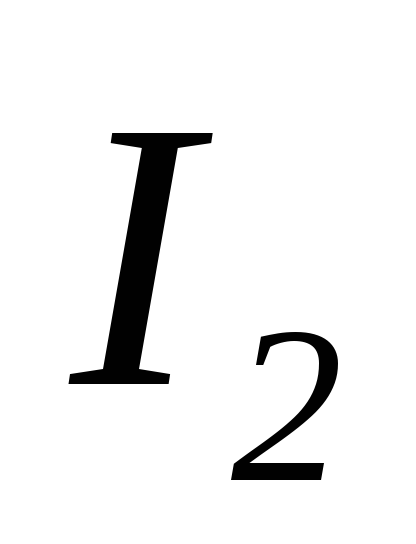 на две составляющие: активную
на две составляющие: активную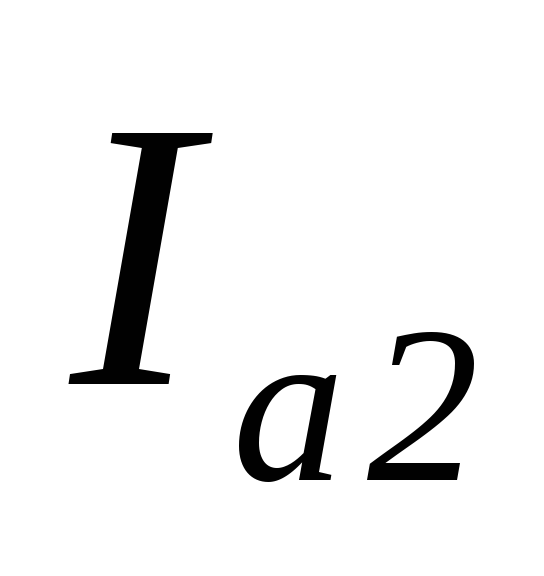 ,
которая совпадает по фазе с напряжением
и индуктивную
,
которая совпадает по фазе с напряжением
и индуктивную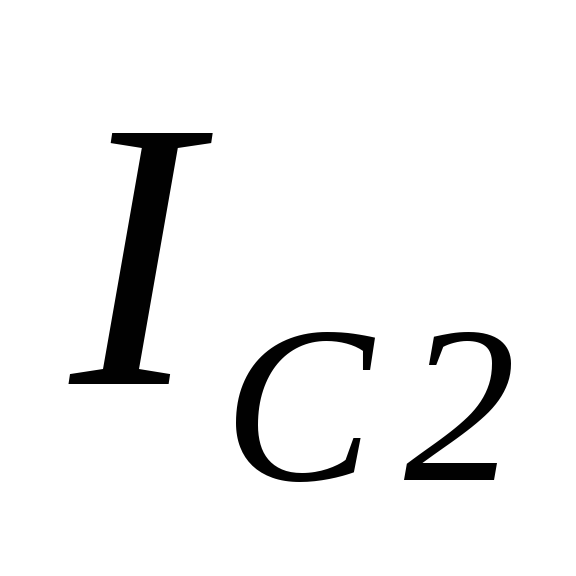 ,
которая опережает по фазе от напряжения
на угол
,
которая опережает по фазе от напряжения
на угол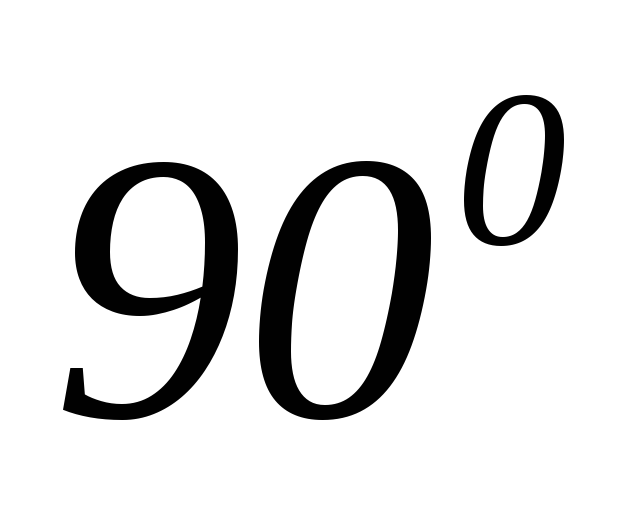 .
.
Эти составляющие
определяем по формулам прямоугольного
треугольника 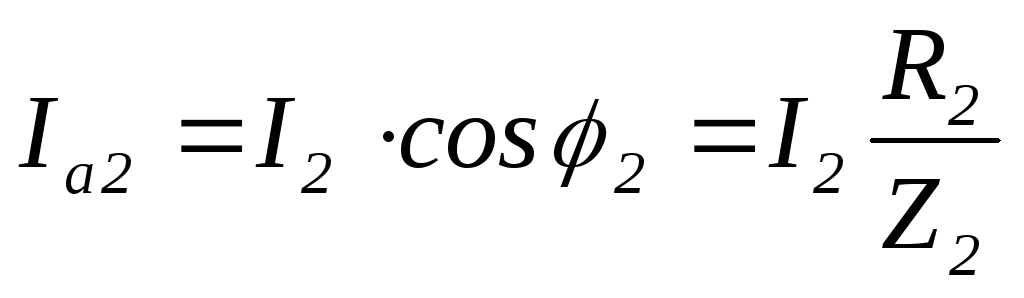 ,
,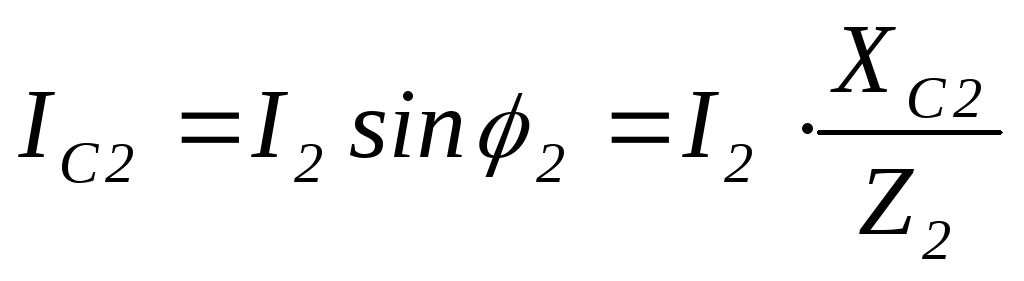 ,
где
,
где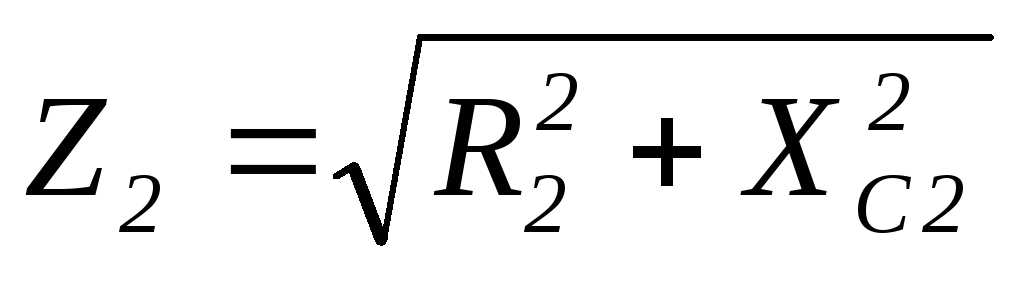 ;
;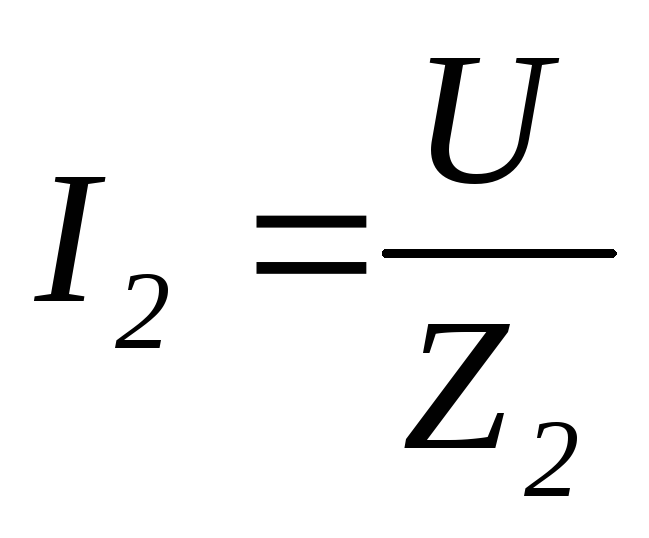
Складываем токи 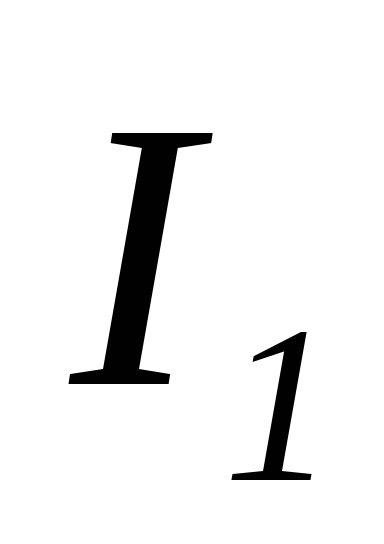 и
и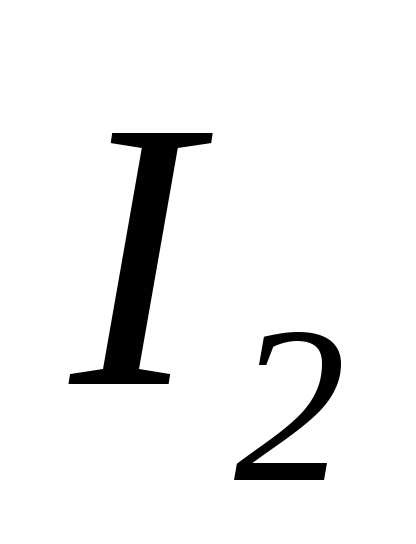 на векторной диаграмме и получаем общий
ток
на векторной диаграмме и получаем общий
ток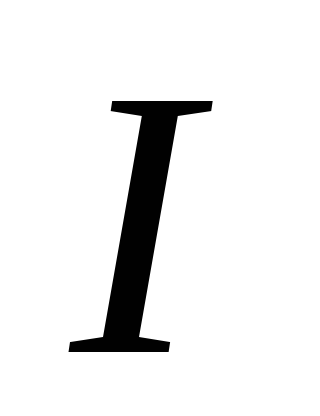
Из треугольника
АВС следует 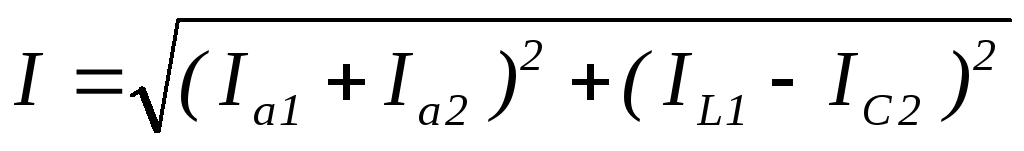
Проводимости при гармоническом воздействии
Отношение активной
составляющей тока к напряжению называется активной
проводимостью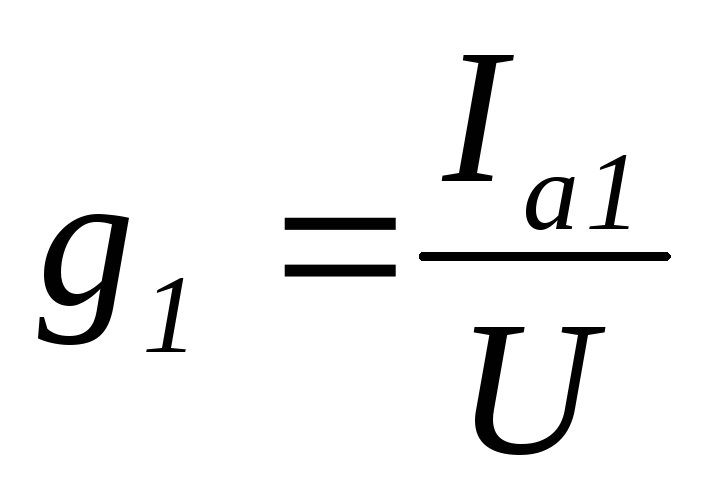
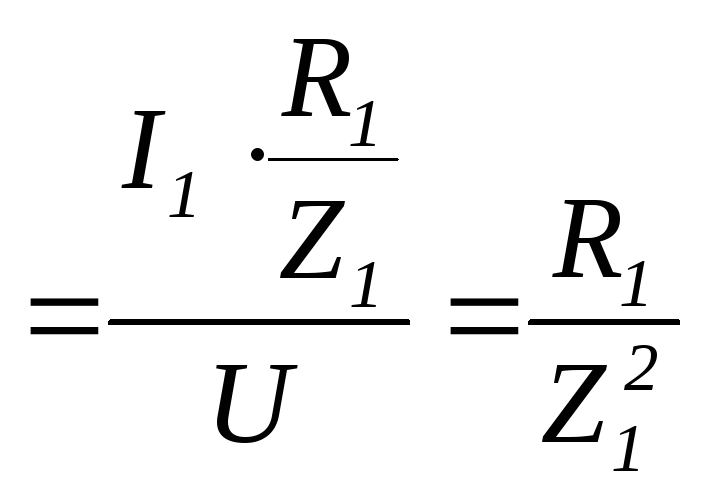 ,единица измерения
всех проводимостей Сименс (См)
,единица измерения
всех проводимостей Сименс (См)
Аналогично 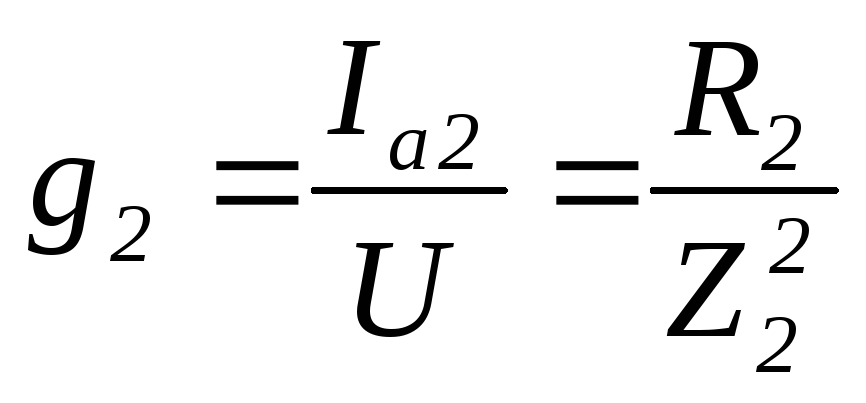
Отношение индуктивной или емкостной составляющей тока к напряжению называется реактивной проводимостью.
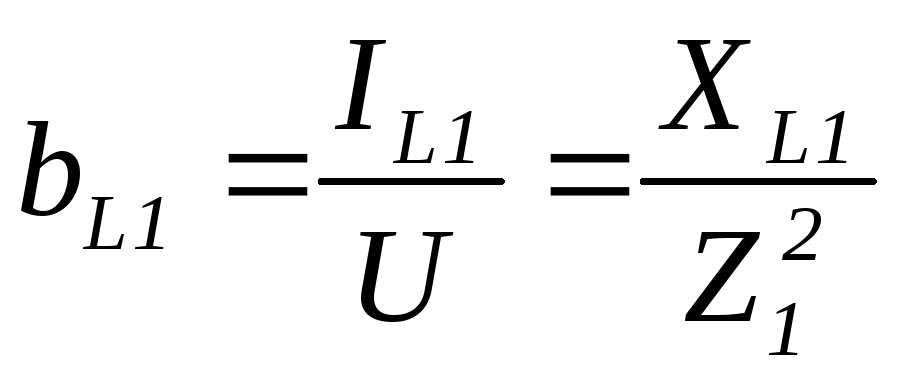
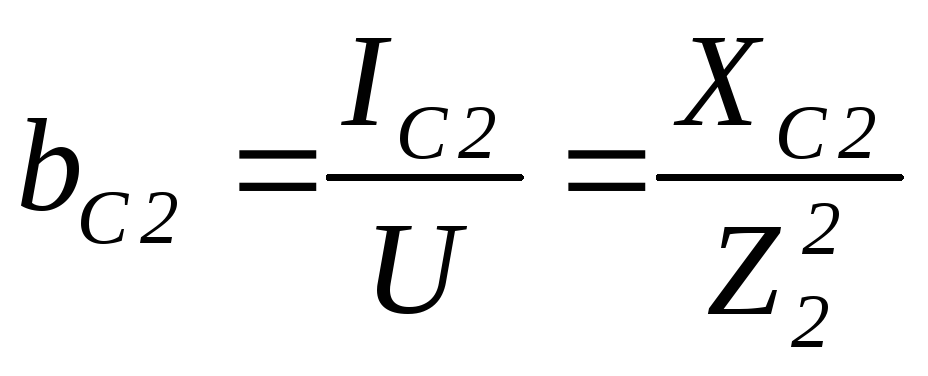
Отношение тока ветви или общего тока к напряжению называется полной проводимостью.
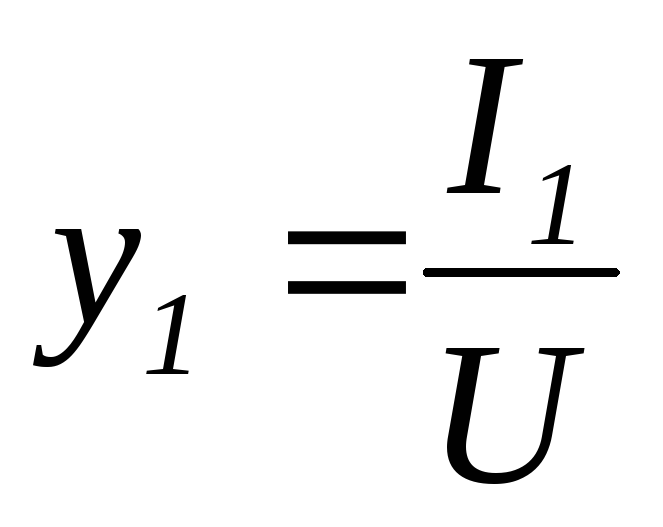
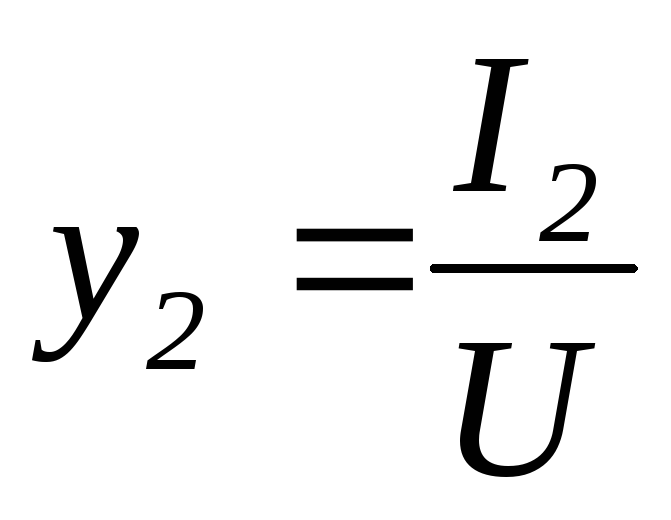
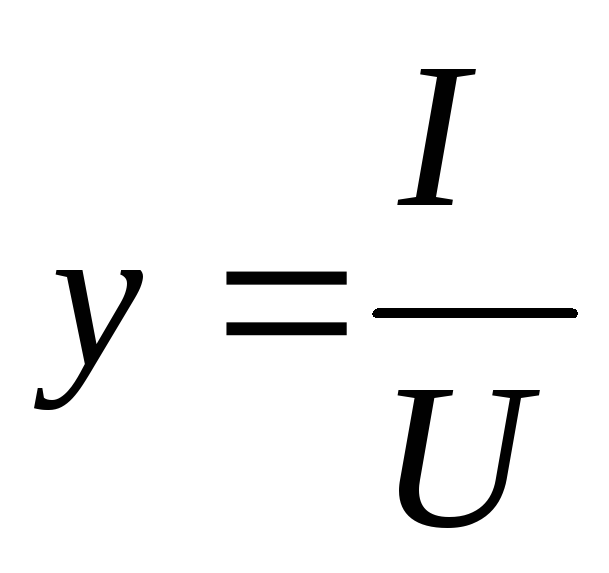 Отсюда
Отсюда 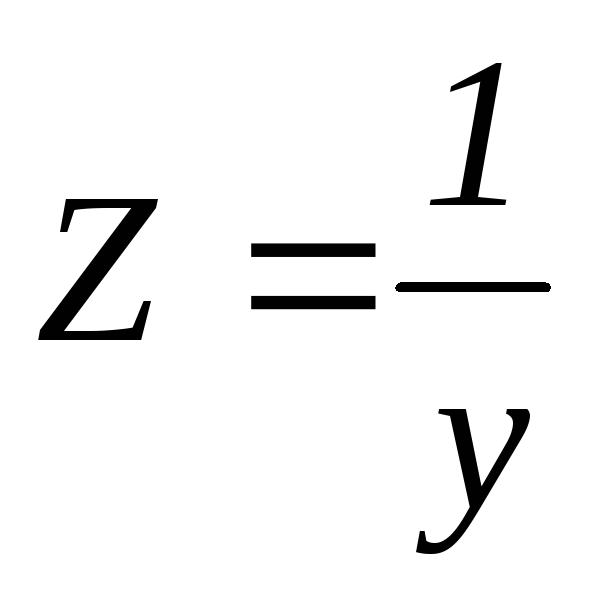
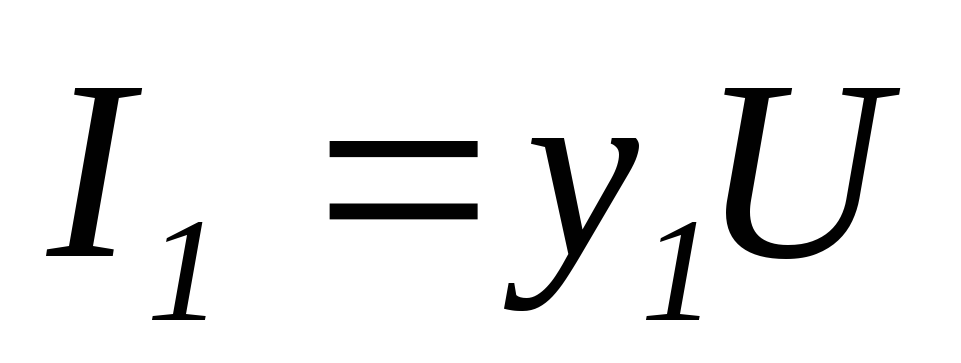
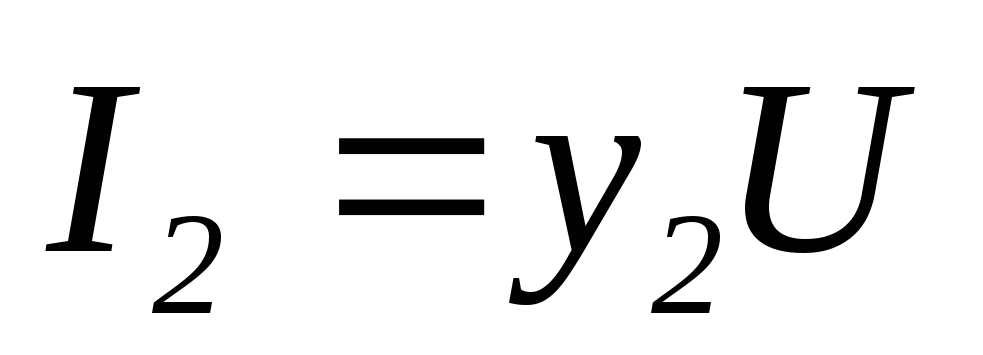
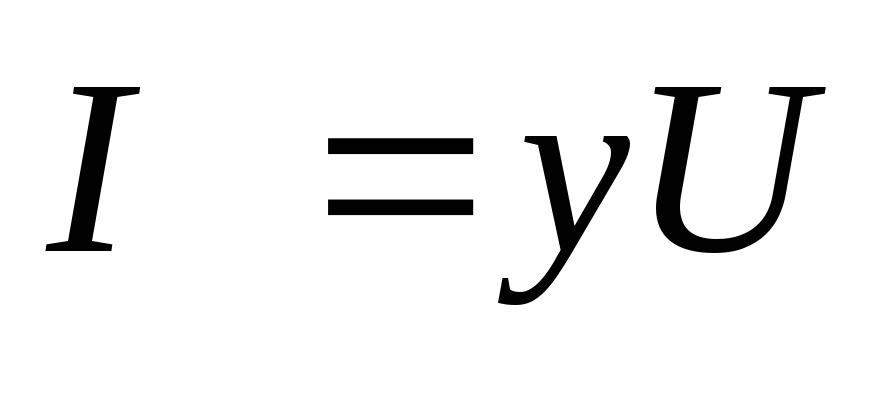 —
полное сопротивление
—
полное сопротивление
Разделим все стороны диаграммы токов на напряжение и получим диаграмму проводимости.
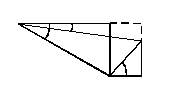 Из
треугольника АВС получим
Из
треугольника АВС получим 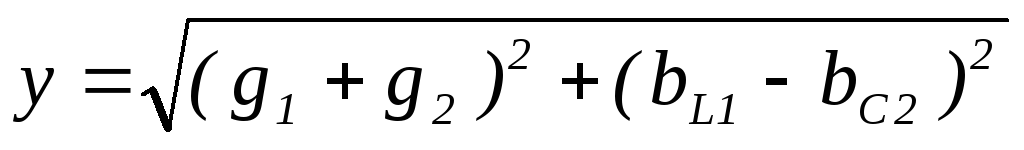
Если параллельно соединить по одному элементу, то формулы проводимости упрощаются:
проводимость
обратна величине сопротивления. 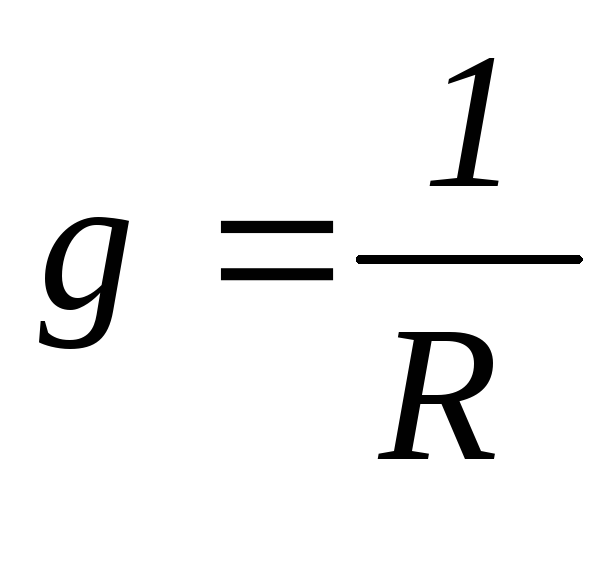 ,
,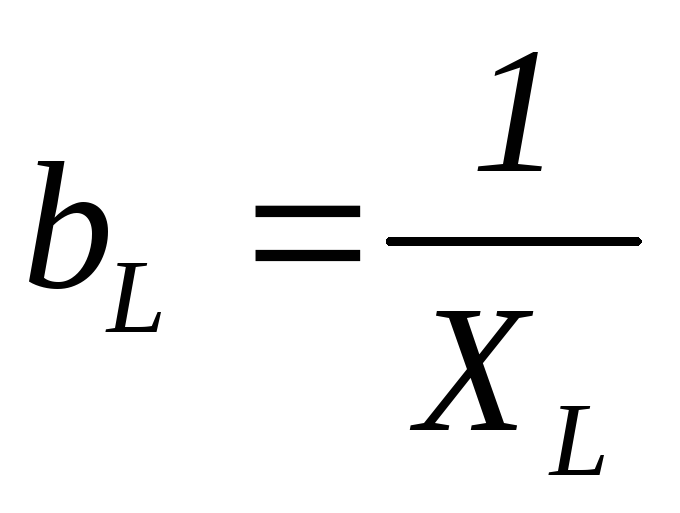 ,
,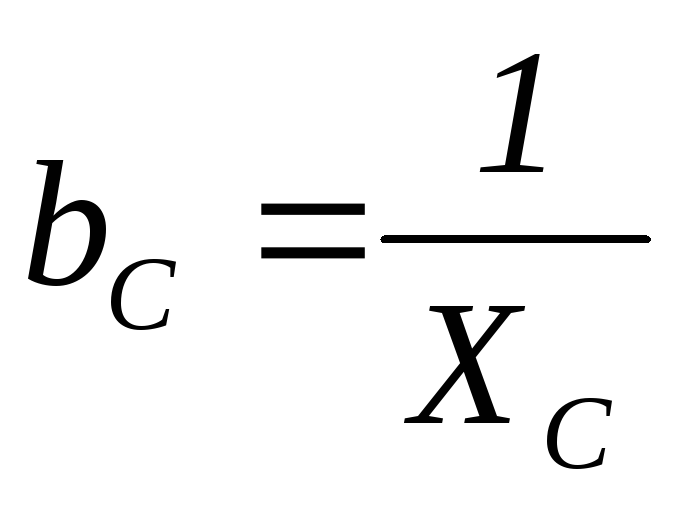 Пример решения задачи
Пример решения задачи
Д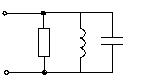 ано:
ано:
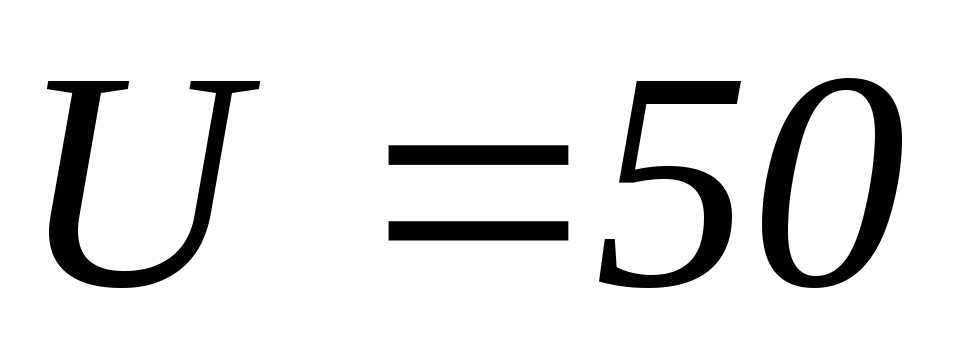 В
В
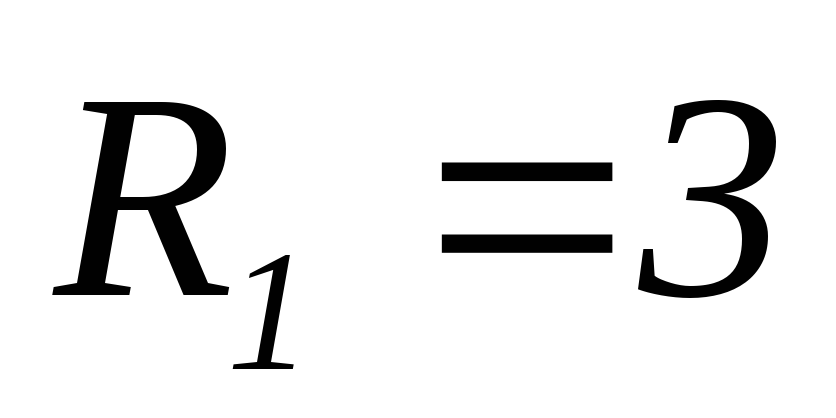 Ом
Ом
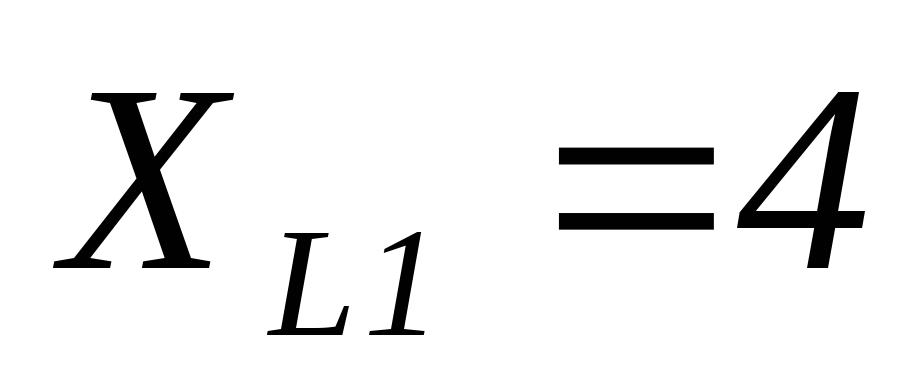 Ом
Ом
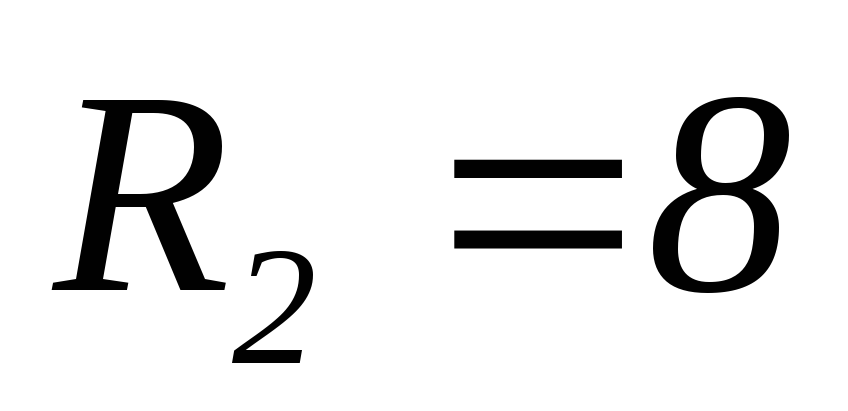 Ом
Ом
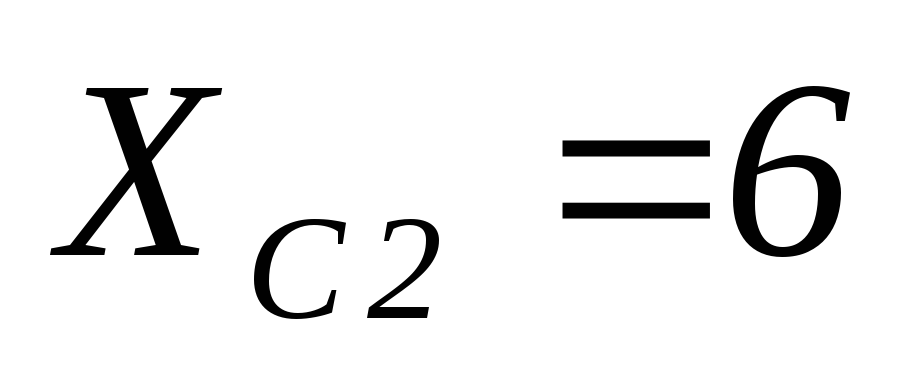 Ом
Ом
Найти: 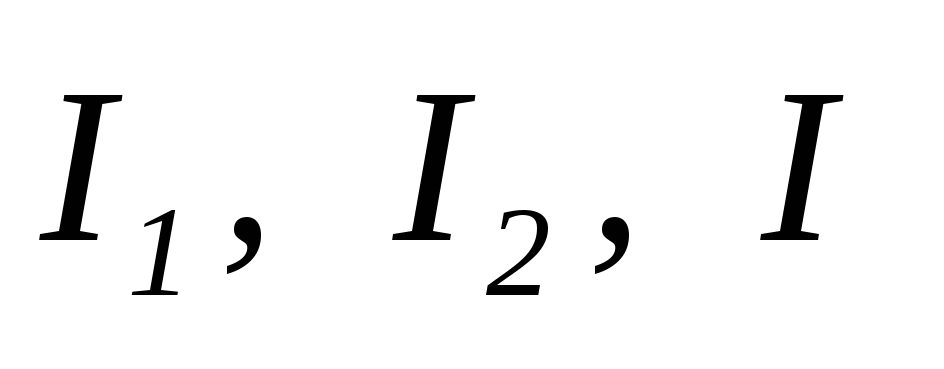 методом составляющих токов
методом составляющих токов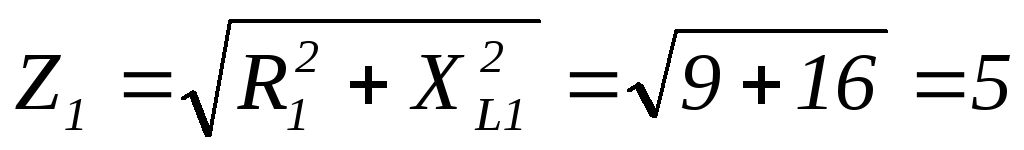 Ом
Ом
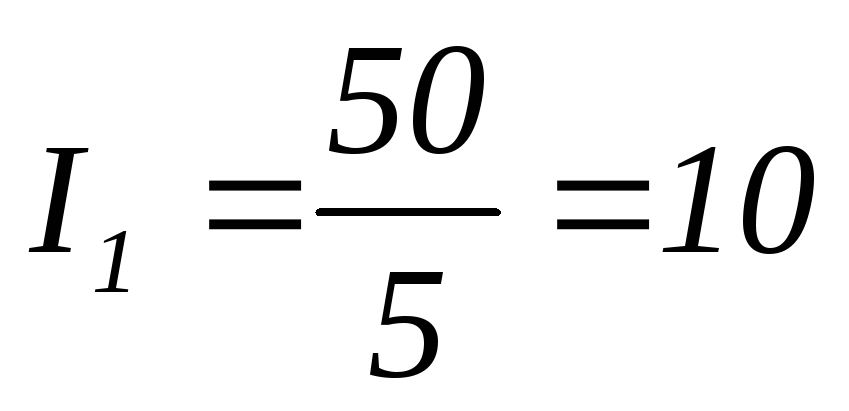 А
А
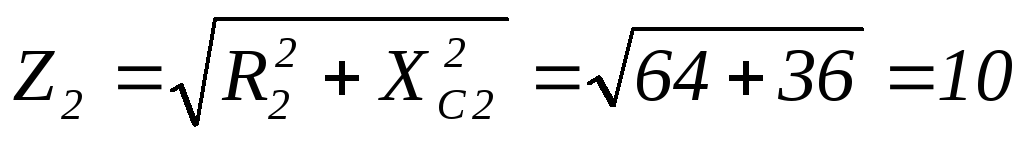 Ом
Ом
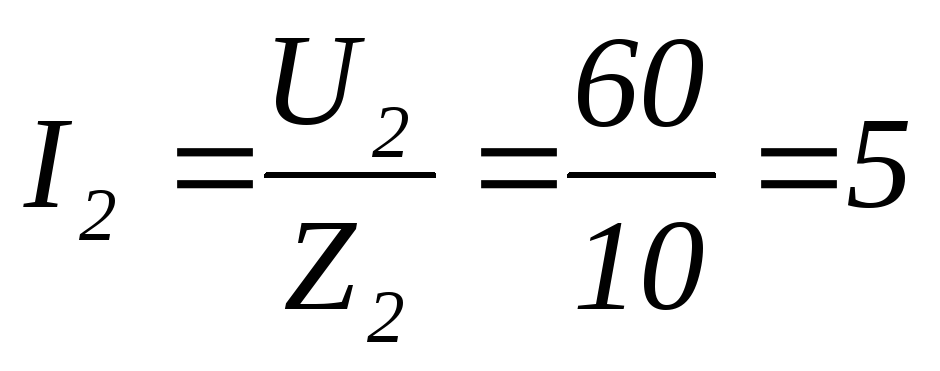 А
А
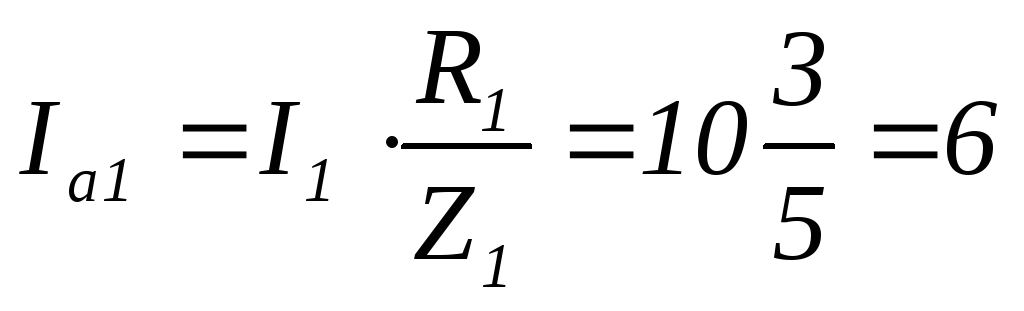 А
А 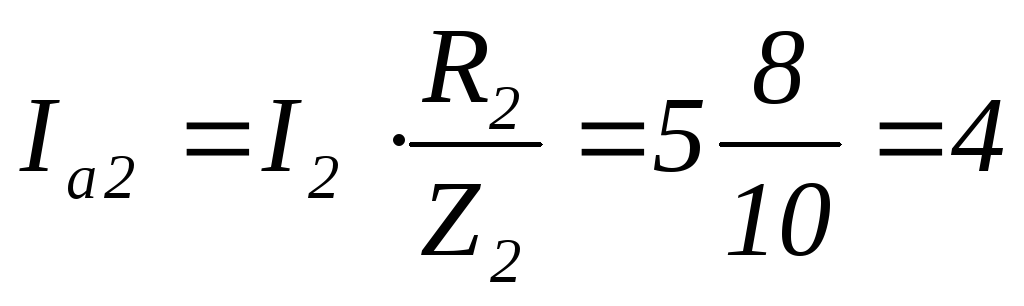 А
А
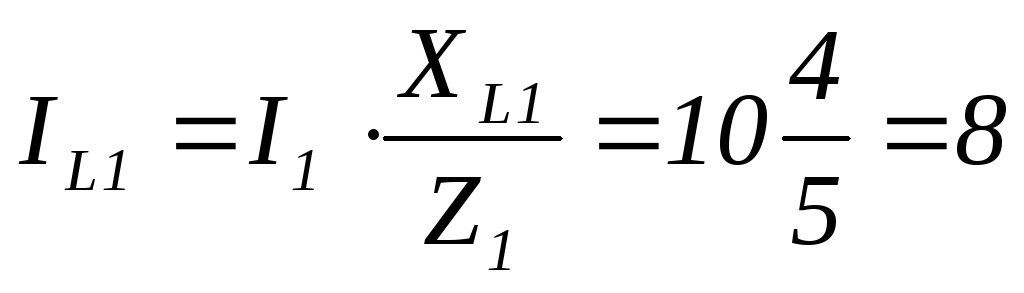 А
А 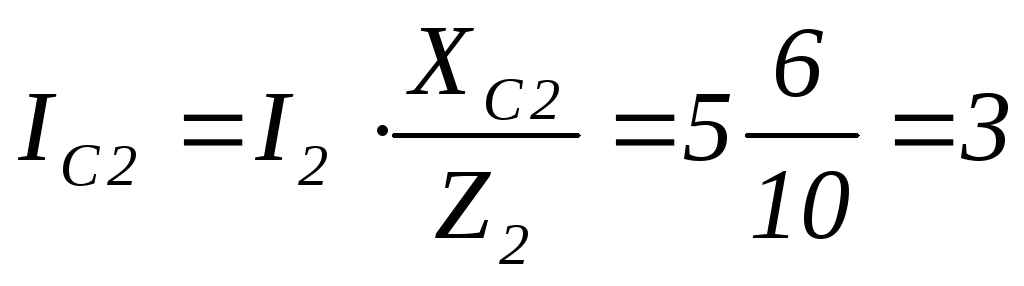 А
А
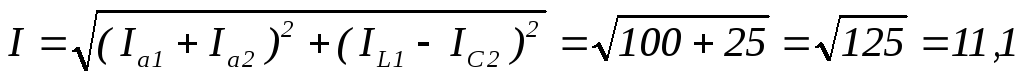 А
А
Чтобы рассчитать комплексное входное сопротивление при параллельном соединении используют формулу параллельного соединения резисторов. Вместо сопротивлений ставят их комплексные величины.
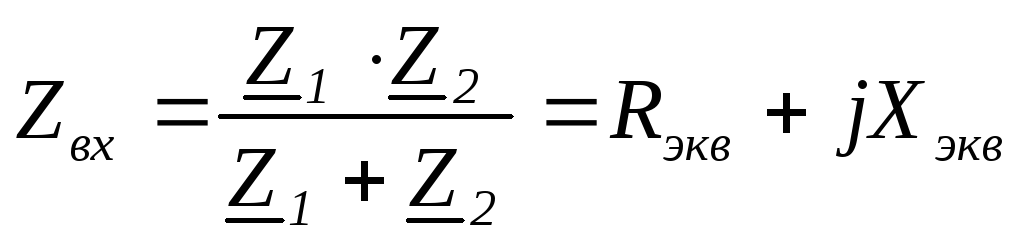
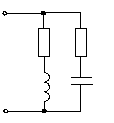
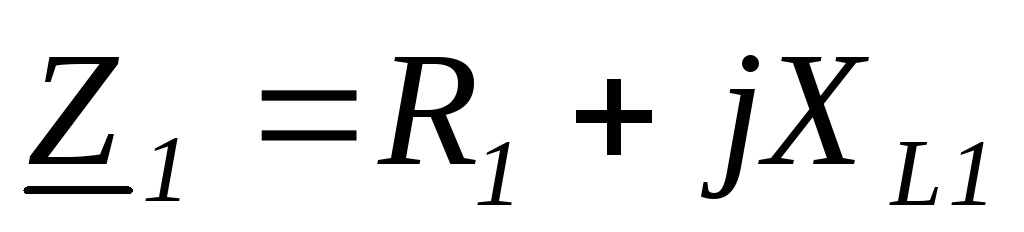
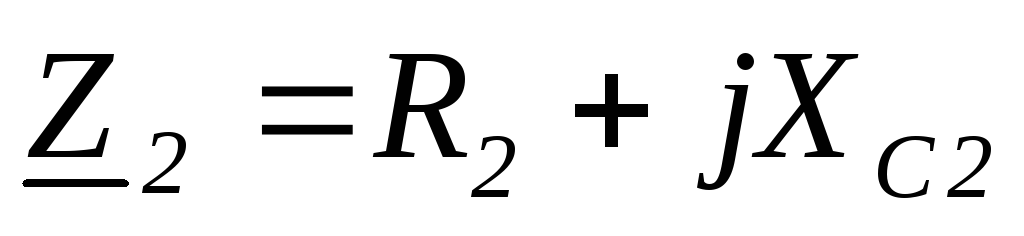
В числителе подставляем выражение в показательной форме, а в знаменатель в алгебраической.
Действительная
часть комплексного входного сопротивления
— это 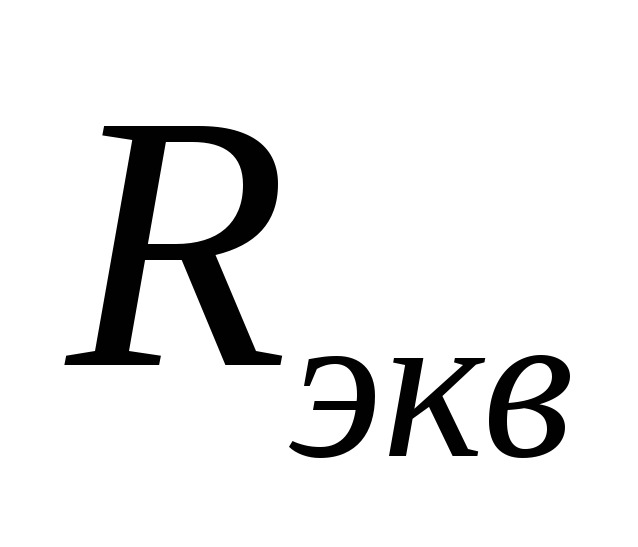 ,
мнимая-
,
мнимая-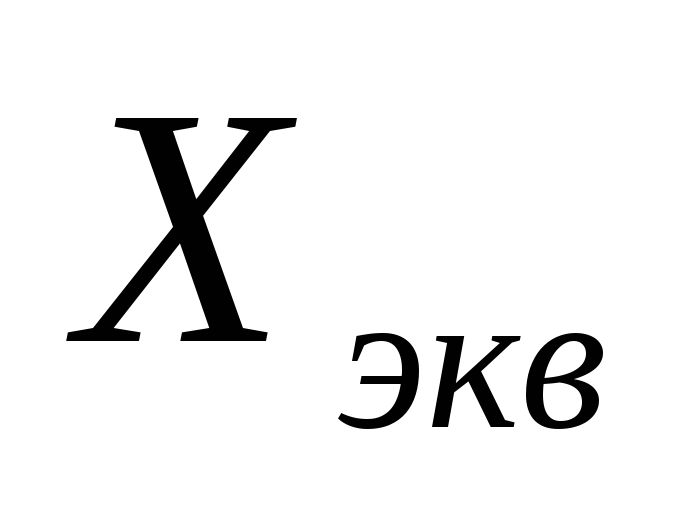 .
Вывод: любую параллельную цепь можно
заменить эквивалентной последовательной
с параметрами
.
Вывод: любую параллельную цепь можно
заменить эквивалентной последовательной
с параметрами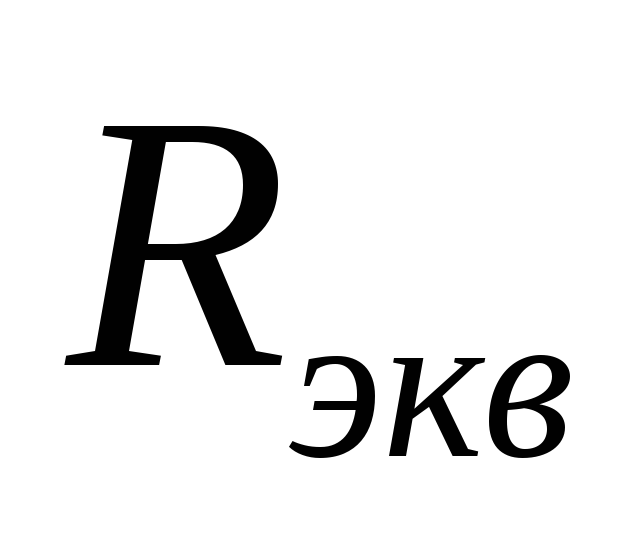 ,
,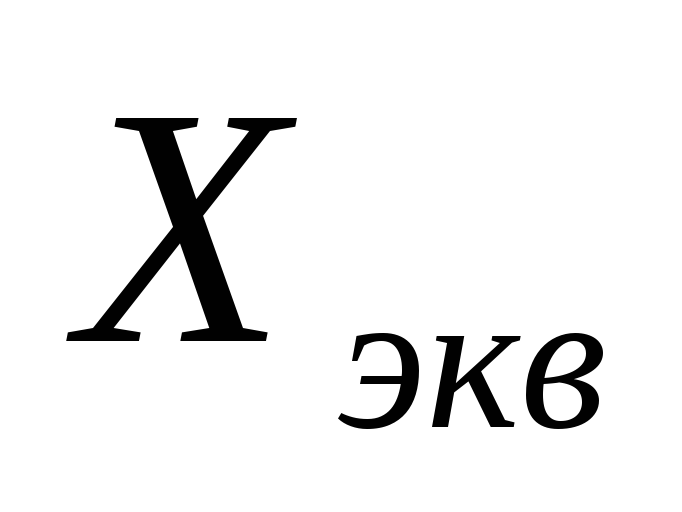 .
.
Тестовые задания:
Задание | Схема | Варианты ответов |
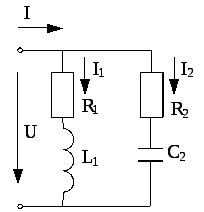
1. Какое из приведенных математических выражений для расчета общего тока данной схемы является неверным? |
| а) в) г) |
Символический метод расчета электрических цепей
Комплексная
мощность равна произведению комплексного
напряжения на сопряженный комплекс
тока, где сопряженный комплекс тока по
модулю равен комплексу тока и
противоположен по знаку аргумента 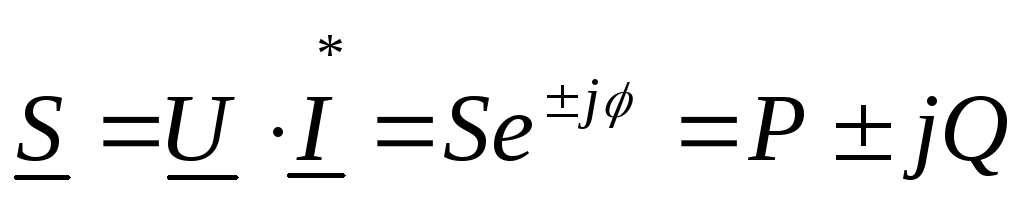 .
.
Модуль комплексной мощности – это полная мощность цепи S
Действительная часть – это активная мощность цепи Р.
Мнимая часть — это реактивная мощность цепи Q.
Пример решения задачи.
Дано:
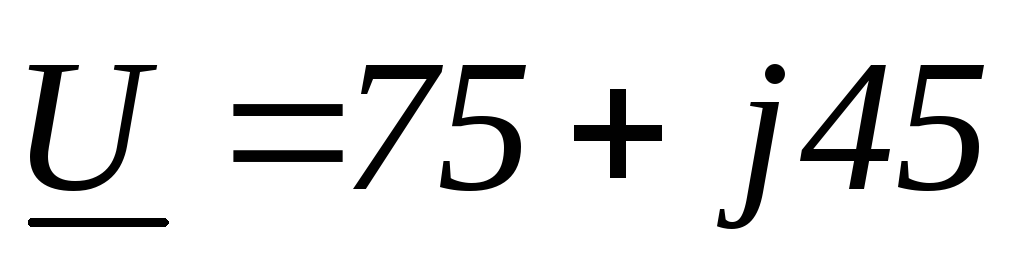
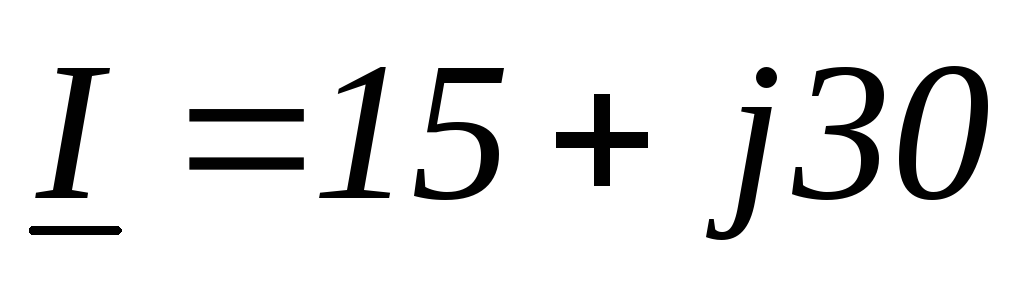
Найти: 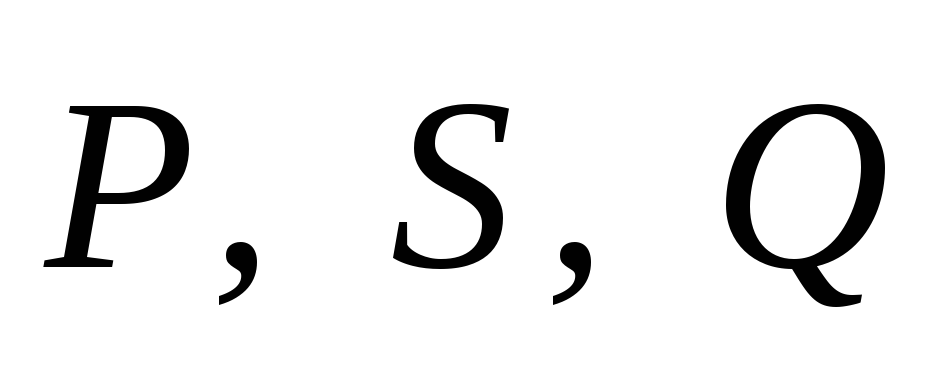
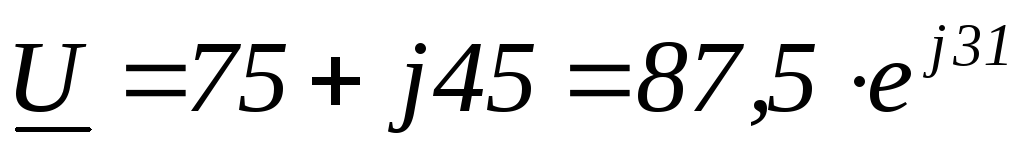
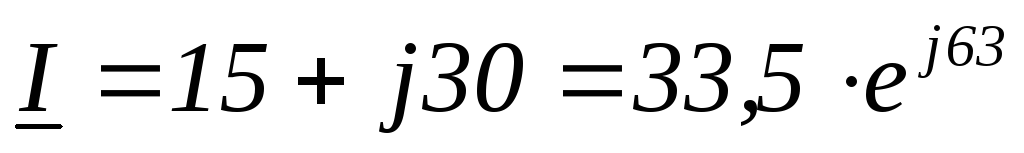
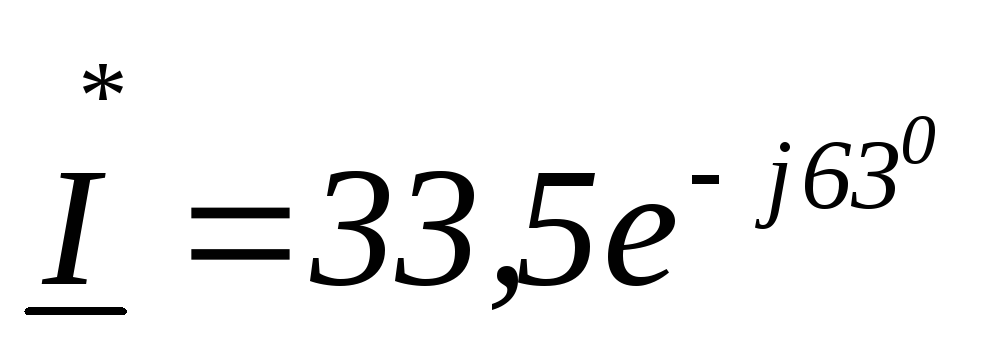
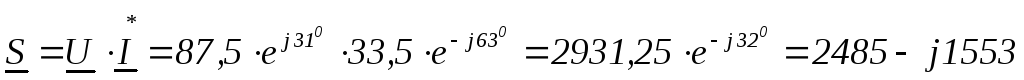
Отсюда: полная
мощность цепи S=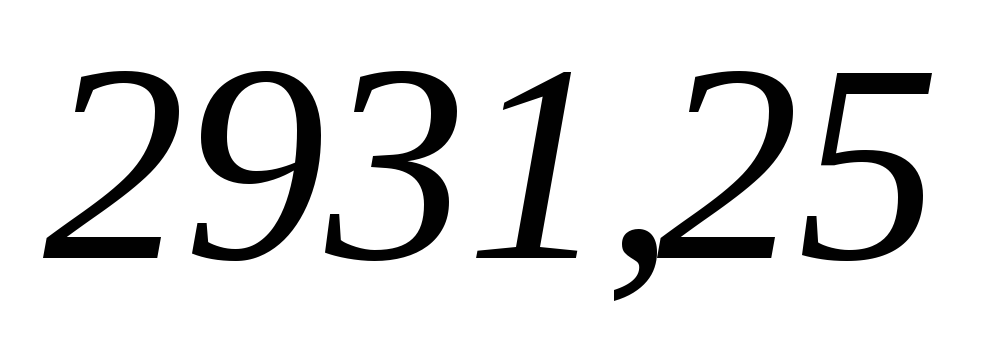 В∙А,
активная мощность цепи
В∙А,
активная мощность цепи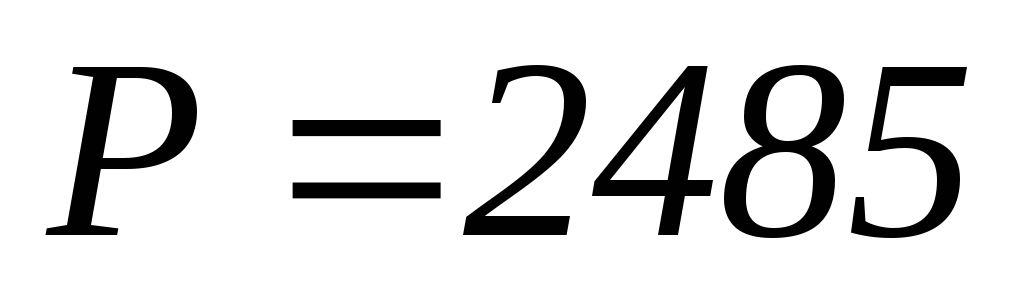 Вт,
реактивная мощность цепи
Вт,
реактивная мощность цепи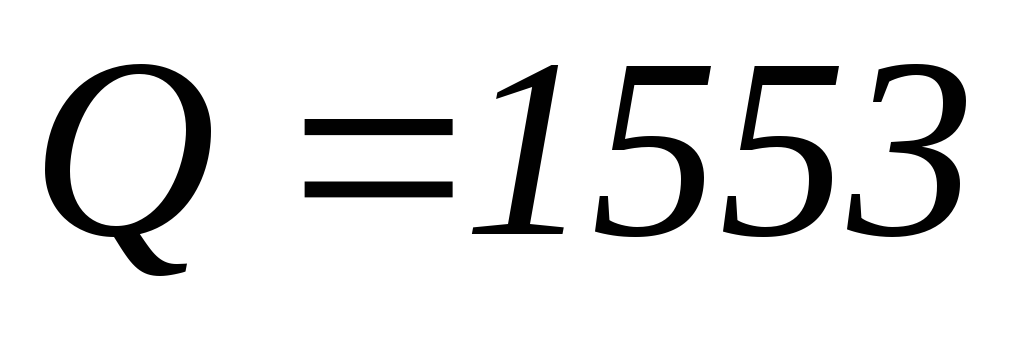 вар
вар
Расчет электрических цепей символическим методом производится по формулам смешанного соединения резисторов, только вместо сопротивлений резисторов подставляется комплексное сопротивление участков.
Пример решения задачи.
Дано
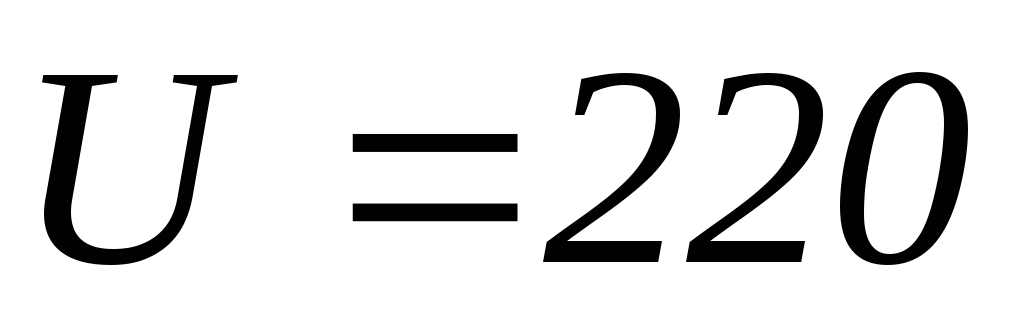
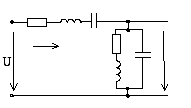 В
В
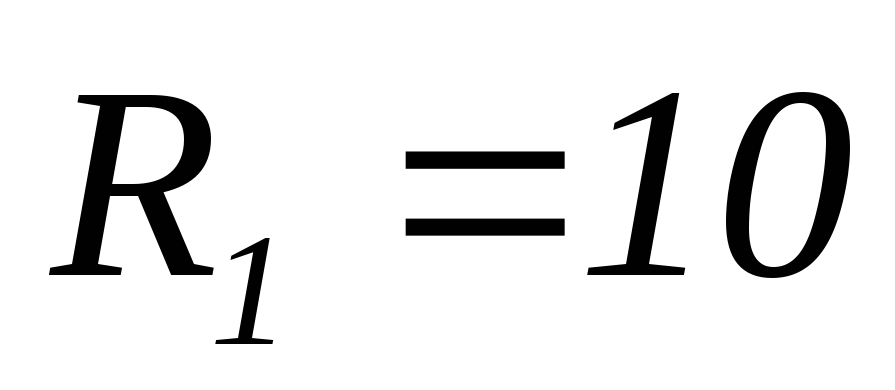 Ом
Ом
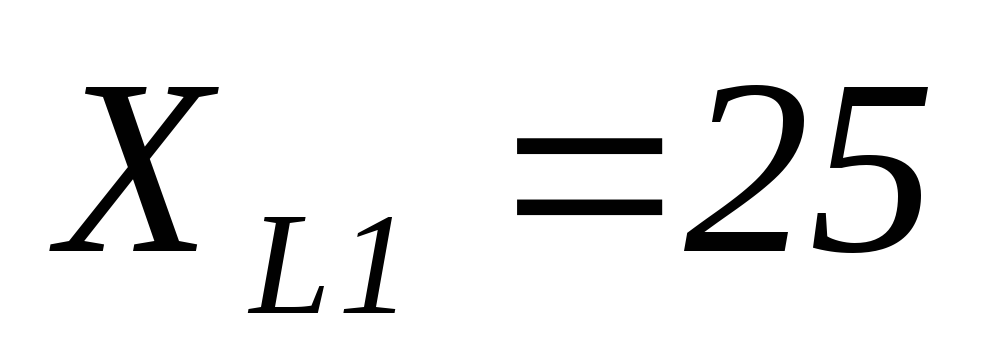 Ом
Ом
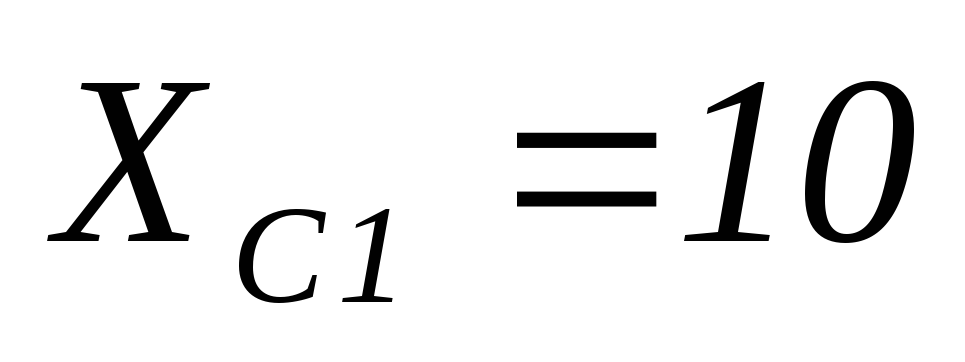 Ом
Ом
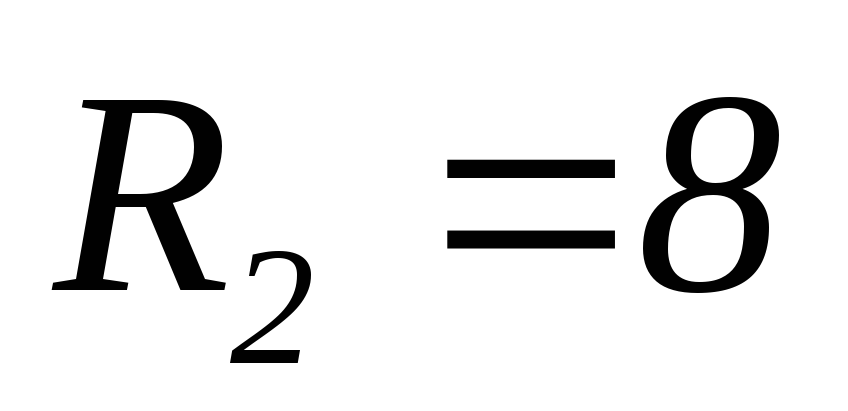 Ом
Ом
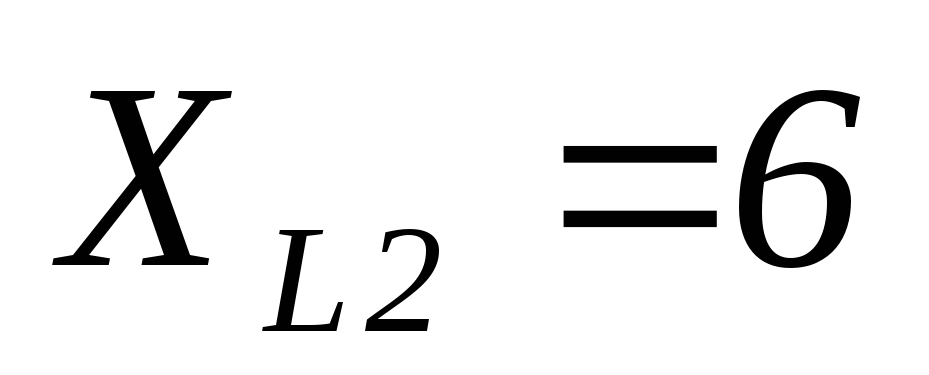 Ом
Ом
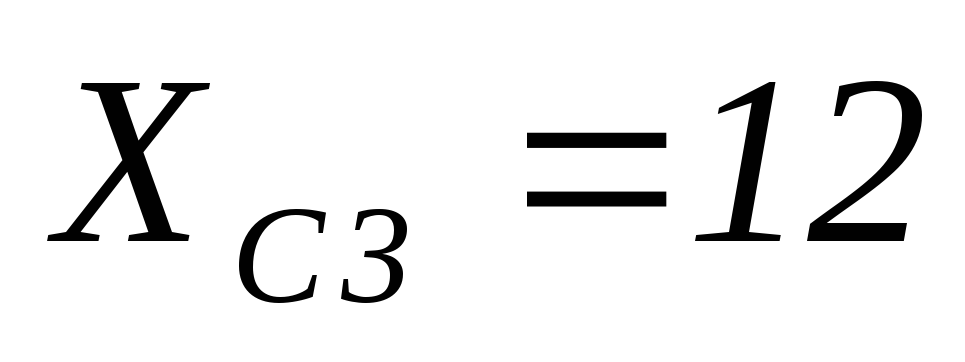 Ом
Ом
Найти: 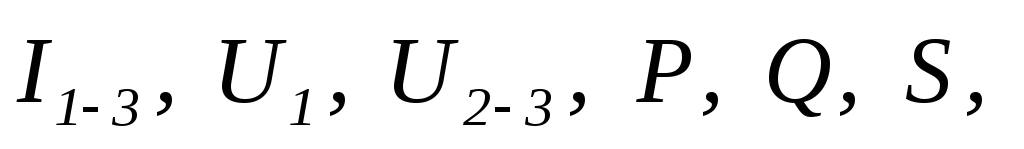 ,
построить векторную диаграмму напряжений.
,
построить векторную диаграмму напряжений.
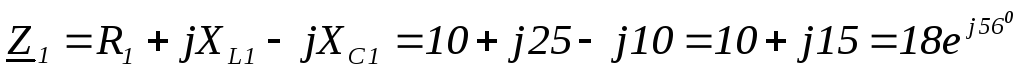
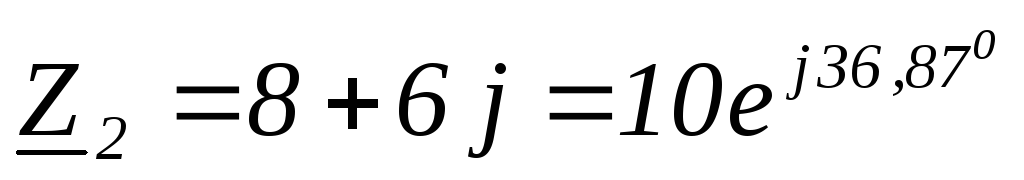
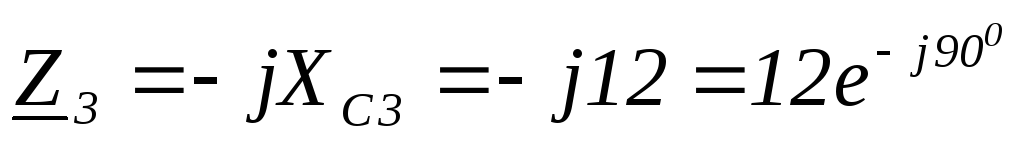
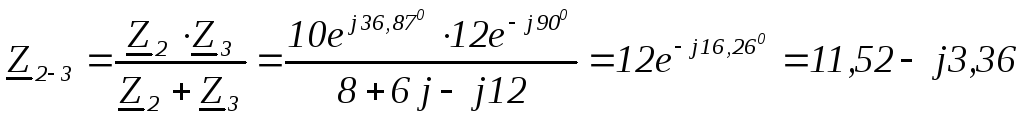
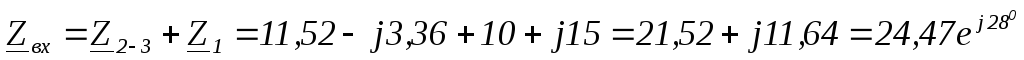
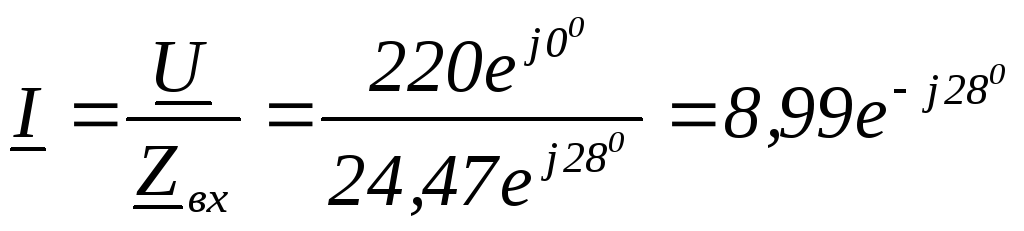
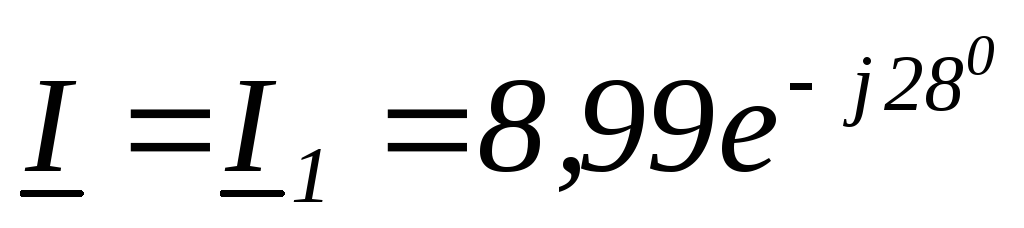
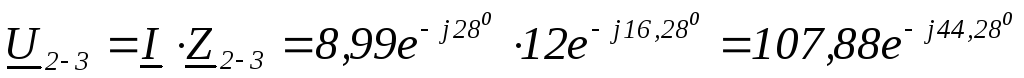
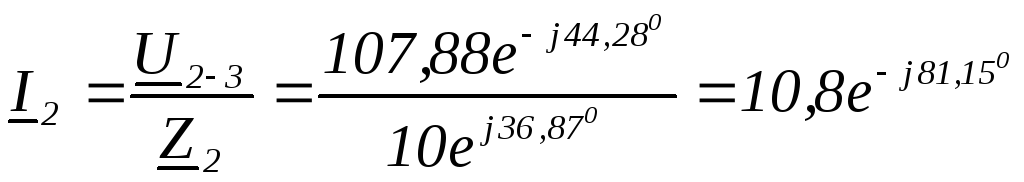
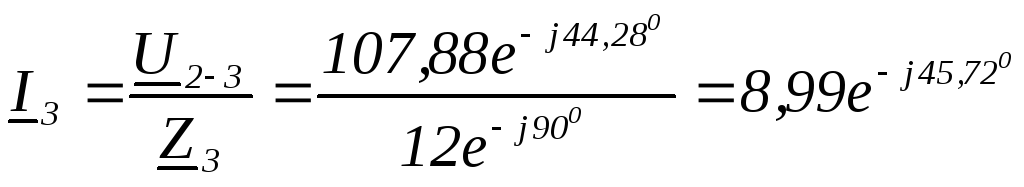
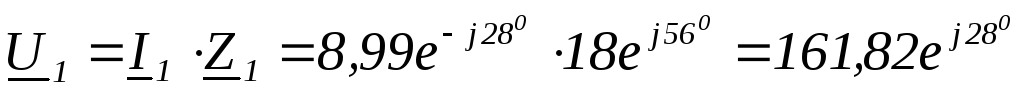
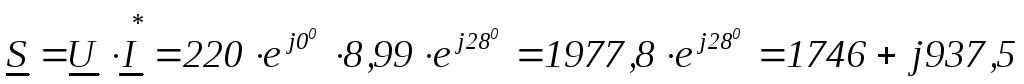
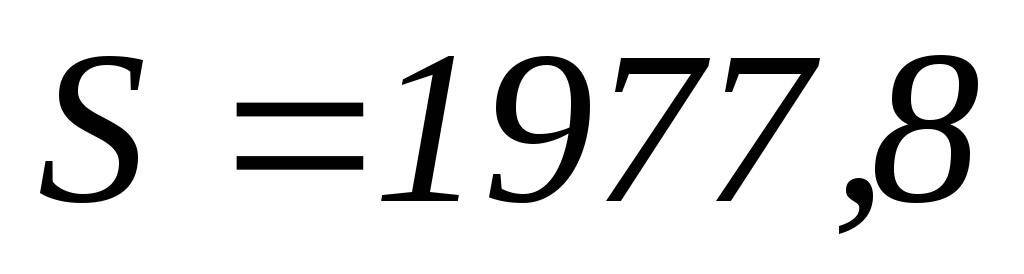 В∙А
В∙А
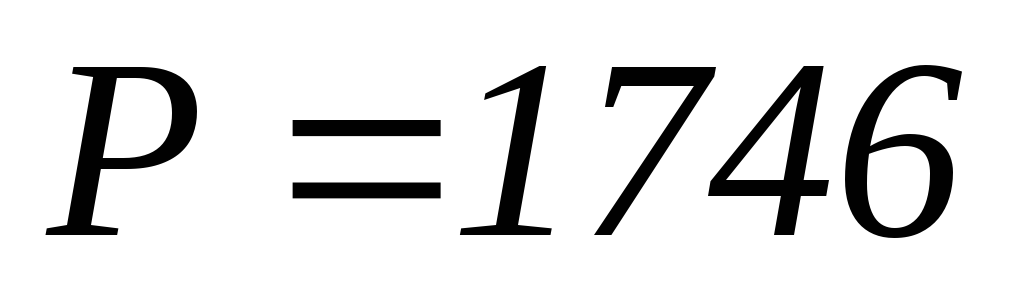 Вт
Вт
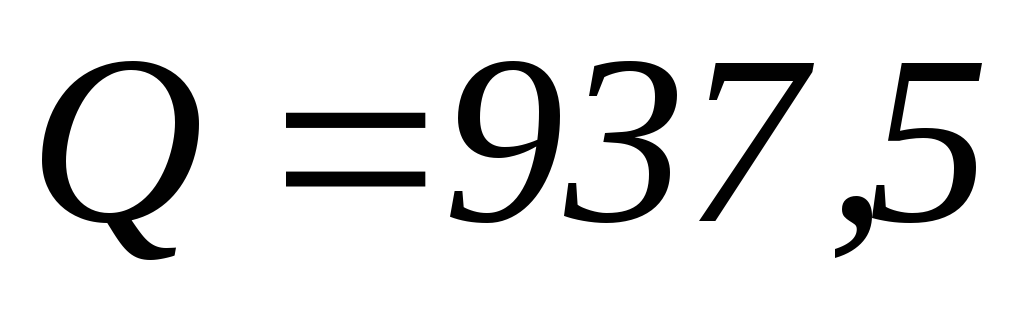 вар
вар
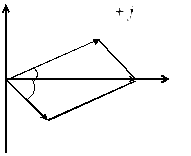
Квазистационарные процессы. Rc- и Rl-цепи
В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Электромагнитное поле в таких цепях состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Эти поля существуют независимо друг от друга.
Если на каком-то участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через некоторое время, которое по порядку величины равно времени τ распространения электромагнитного возмущения от одной точки цепи к другой. Так как электромагнитные возмущения распространяются с конечной скоростью, равной скорости света c , то 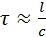 , где l – расстояние между наиболее удаленными точками цепи. Если это время τ много меньше длительности процессов, происходящих в цепи, то можно считать, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях а также сами цепи, называются квазистационарными.
, где l – расстояние между наиболее удаленными точками цепи. Если это время τ много меньше длительности процессов, происходящих в цепи, то можно считать, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях а также сами цепи, называются квазистационарными.
Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи.
Из-за огромного значения скорости света время установления в цепи электрического равновесия оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные.
Простыми примерами квазистационарных процессов могут служить процессы, происходящие в RC— и RL-цепях при подключении и отключении источника постоянного тока.
На рис. 2.1.1 изображена электрическая цепь, состоящая из конденсатора с емкостью C, резистора с сопротивлением R и источника тока с ЭДС, равной 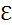 .
.
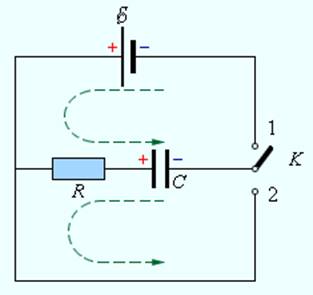
|
Рисунок 2.1.1. Цепи зарядки и разрядки конденсатора через резистор |
Если замкнуть ключ K в положение 1, то начинается процесс зарядки конденсатора через резистор. Для квазистационарной цепи по закону Ома можно записать:
RJ + U = |
где J – мгновенное значение силы тока в цепи, U – мгновенное значение напряжения на конденсаторе. Сила тока J в цепи равна изменению заряда q конденсатора в единицу времени: 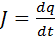 . Напряжение U на конденсаторе в любой момент времени равно q / C. Из этих соотношений следует
. Напряжение U на конденсаторе в любой момент времени равно q / C. Из этих соотношений следует
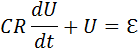
Мы получили дифференциальное уравнение, описывающее процесс зарядки конденсатора. Если конденсатор вначале не был заряжен, то решение этого уравнения имеет вид
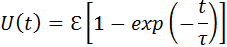
где τ = RC – так называемая постоянная времени цепи, состоящей из резистора и конденсатора. Величина τ является характеристикой скорости процесса. При t → ∞, U (t) → 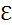 . Процесс зарядки конденсатора через резистор изображен на рис. 2.1.2 (I).
. Процесс зарядки конденсатора через резистор изображен на рис. 2.1.2 (I).
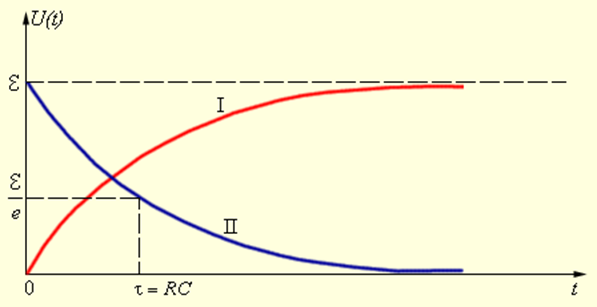
|
Рисунок 2.1.2. Зарядка (I) и разрядка (II) конденсатора через резистор |
Если после того, как конденсатор полностью зарядился до напряжения 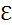 , ключ K перебросить в положение 2, то начнется процесс разрядки. Внешний источник тока в цепи разрядки отсутствует (
, ключ K перебросить в положение 2, то начнется процесс разрядки. Внешний источник тока в цепи разрядки отсутствует (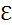 = 0). Процесс разрядки описывается выражением
= 0). Процесс разрядки описывается выражением
U (t) = |
Зависимость U (t) в процессе разрядки изображена на рис. 2.1.2 (II). При t = τ напряжение на конденсаторе уменьшается в e ≈ 2,7 раз.
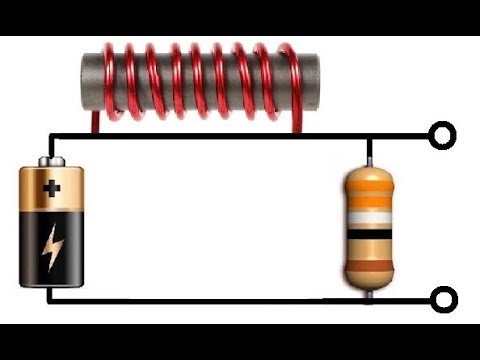
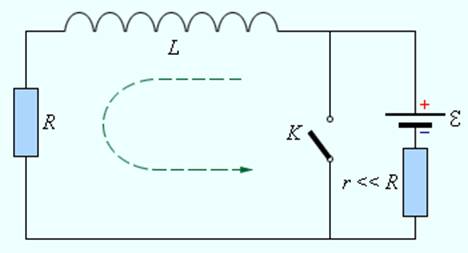
Аналогично протекают процессы в цепи, содержащей катушку с индуктивностью L и резистор с сопротивлением R (рис. 2.1.3).
|
Рисунок 2.1.3. Цепь, содержащая катушку с индуктивностью L, резистор с сопротивлением R и источник тока с ЭДС, равной |
Если в цепи, изображенной на рис. 2.1.3, ключ K сначала был замкнут, а затем внезапно разомкнут, то начнется процесс установления тока. Следует обратить внимание на то, что в схему последовательно с источником тока включен резистор r с малым сопротивлением, чтобы при замкнутом ключе K батарея не оказалась закороченной. Поскольку r << R, при написании уравнения для процесса установления тока этим сопротивлением можно пренебречь. Этот процесс описывается уравнением
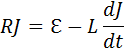
Это уравнение по виду совпадает с уравнением, описывающим зарядку конденсатора, только теперь переменной величиной является сила тока J. Решение этого уравнения имеет вид
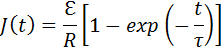
где постоянная времени τ = L / R. Аналогичным образом можно получить закон убывания тока в RL-цепи после замыкания ключа K:
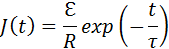
Следует отметить, что процессы в RC— и RL-цепях аналогичны механическим процессам при движении тела в вязкой жидкости.
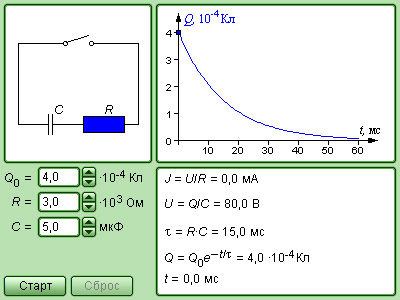 |
Модель. RC-контур |
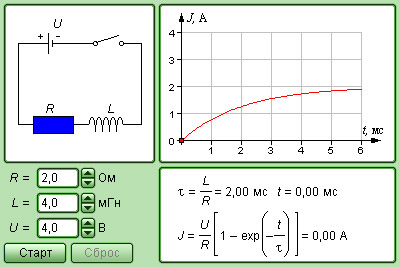 |
Модель. RL-контур |
Передаточные ачх и фчх в цепях первого порядка.
Отношение
комплексного входного напряжения к
комплексному входному току называют
комплексным коэффициентом передачи 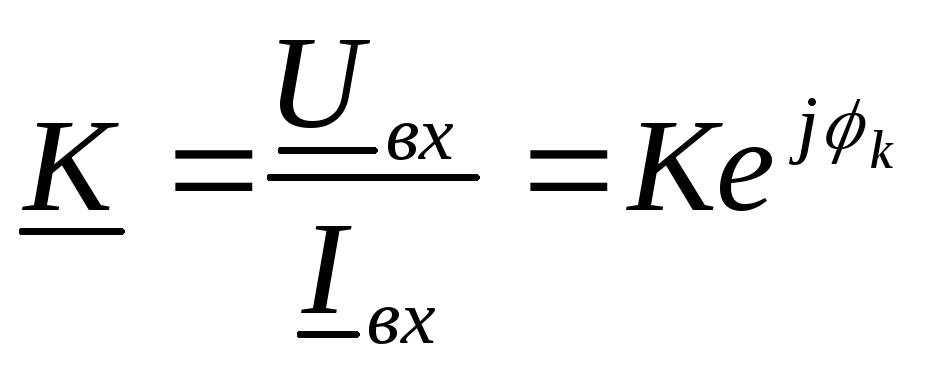
Зависимость модуля
комплексного коэффициента передачи
от частоты называется передаточная
АЧХ, 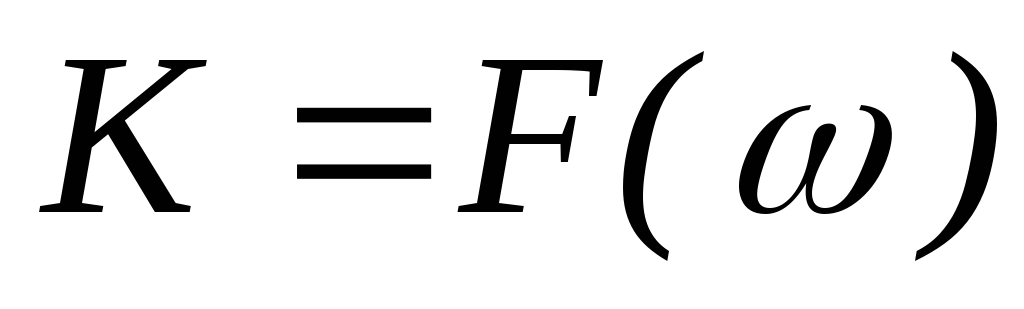 —
передаточная АЧХ.
—
передаточная АЧХ.
Зависимость
аргумента комплексного коэффициента
передачи от частоты называется
передаточная ФЧХ, 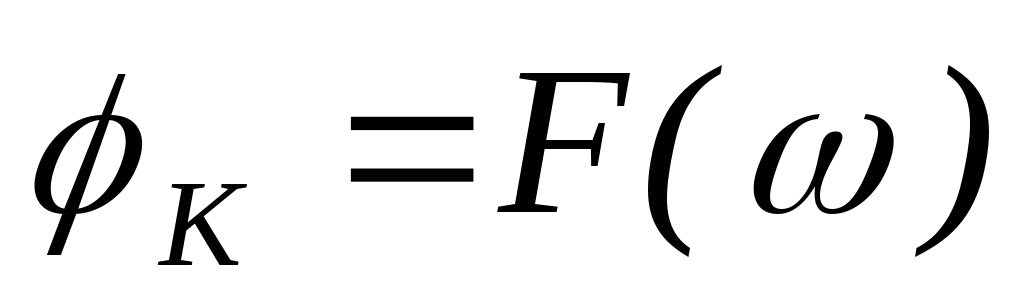 —
передаточная ФЧХ.
—
передаточная ФЧХ.
Модуль коэффициента передачи изменяется от 0 до 1.
Передаточные характеристики цепи rl
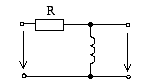 Выведем
формулы передаточных АЧХ и ФЧХ цепи RL. Комплексный
коэффициент передачи
Выведем
формулы передаточных АЧХ и ФЧХ цепи RL. Комплексный
коэффициент передачи 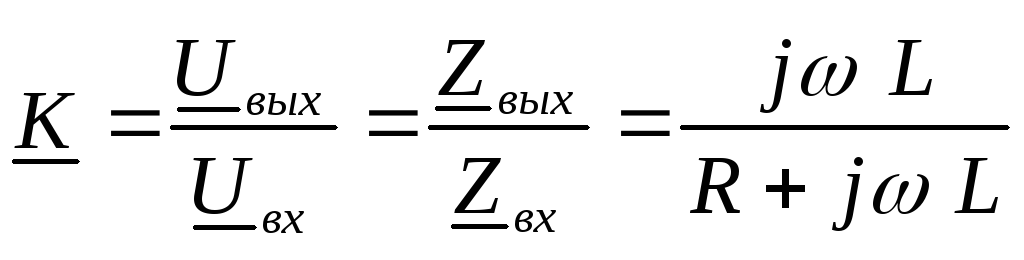
Домножим числитель и знаменатель на комплексно сопряженное число знаменателю.
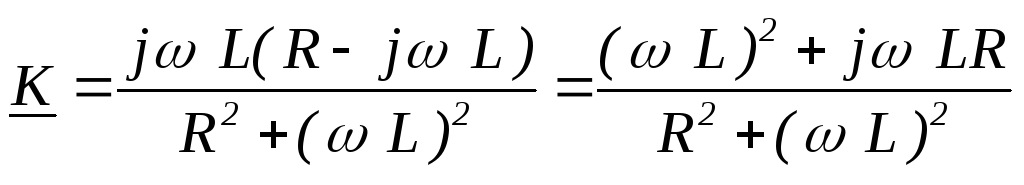
Выделим отдельно
действительную и мнимую часть 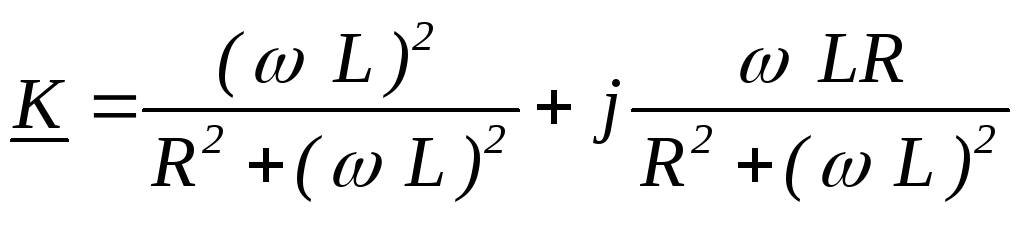
Разделим числитель
и знаменатель на 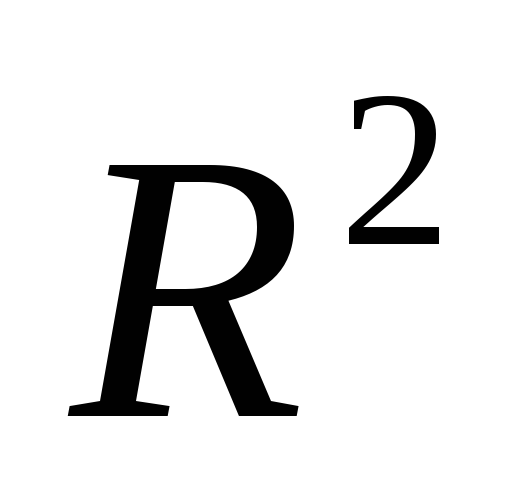
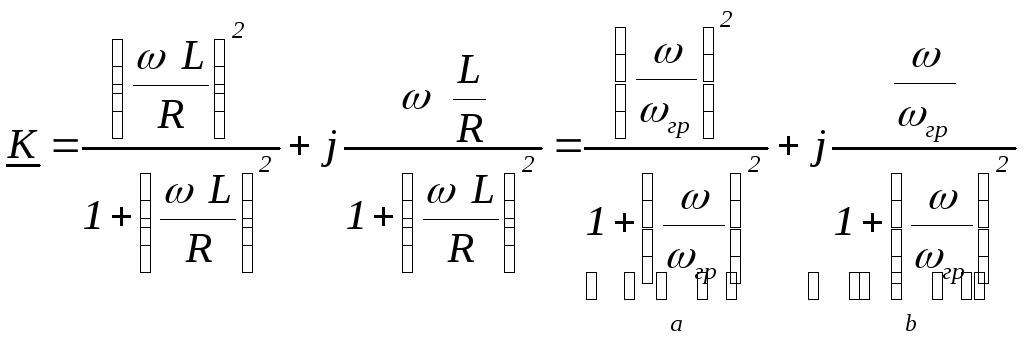
Воспользовавшись
формулой 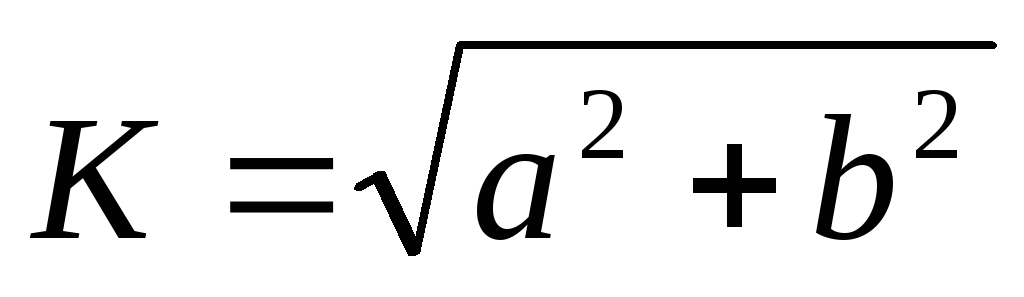 получим передаточную АЧХ цепиRL
получим передаточную АЧХ цепиRL
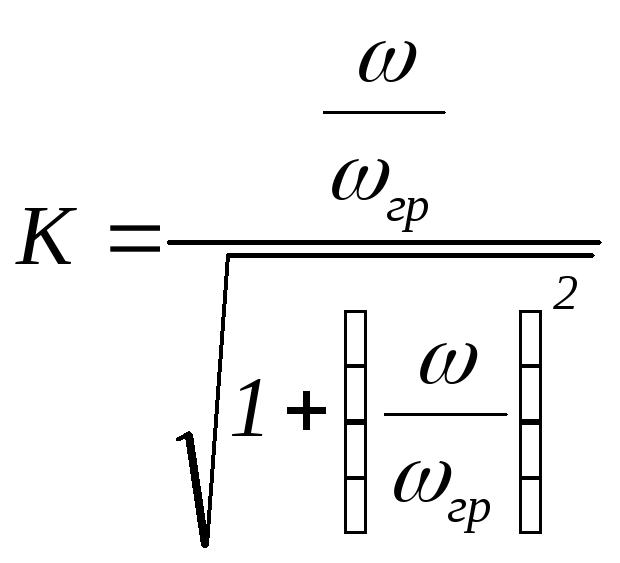 —
передаточная АЧХ цепи RL
—
передаточная АЧХ цепи RL
Передаточную ФЧХ
получаем по формуле: 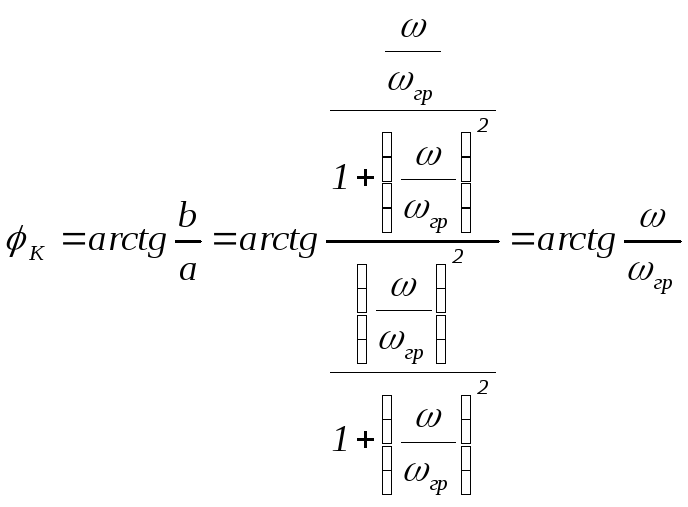
Зададимся несколькими частотами, чтобы построить передаточные характеристики.
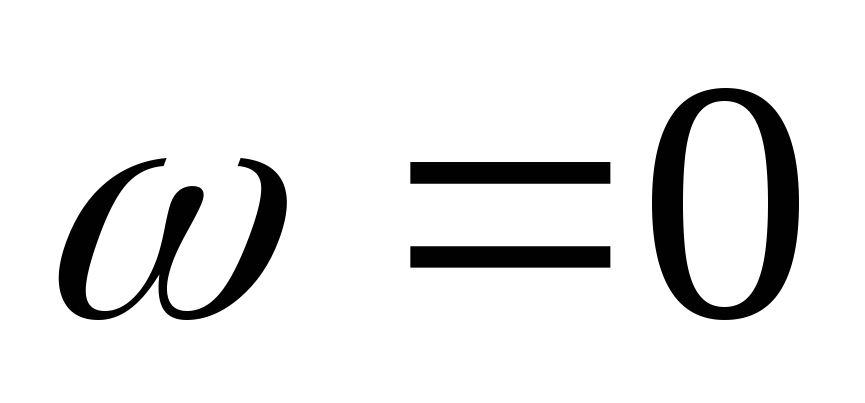
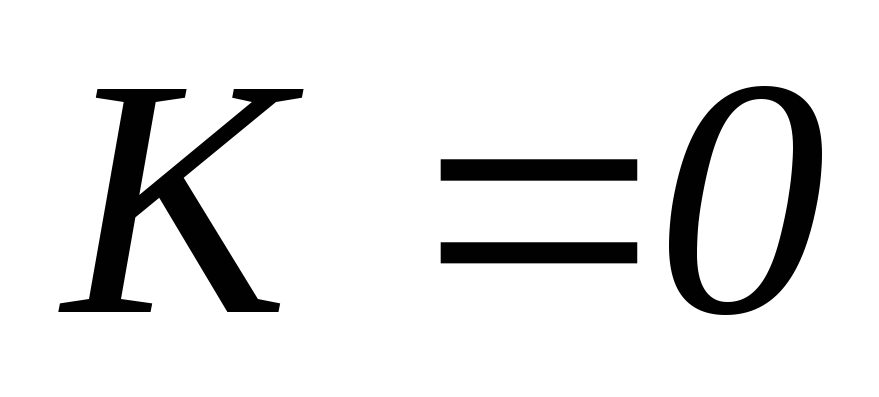
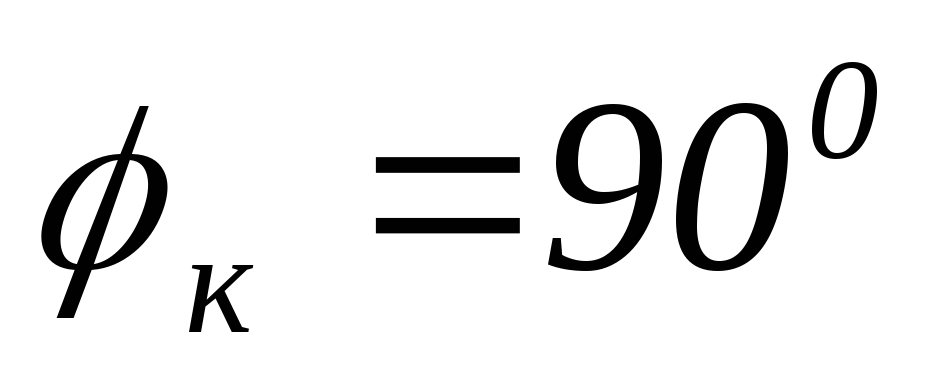
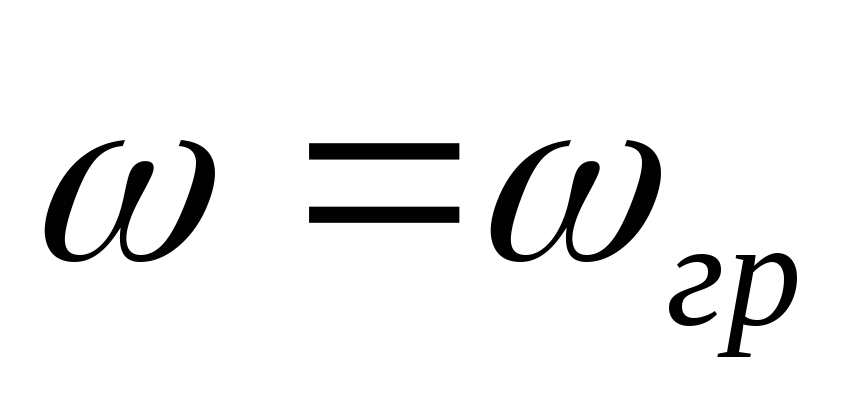
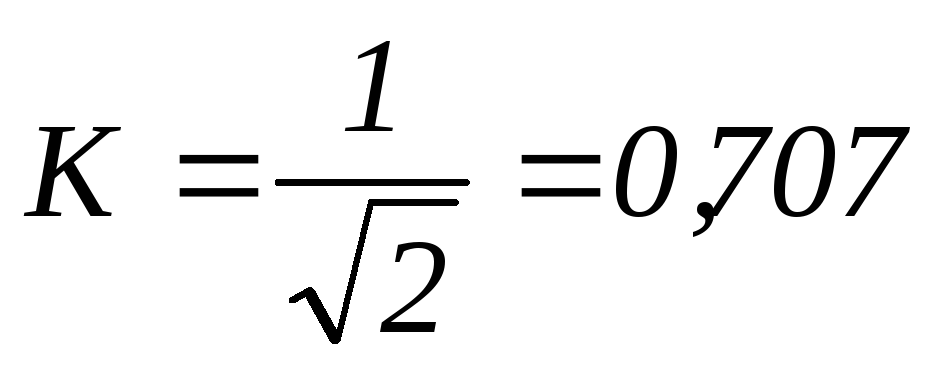
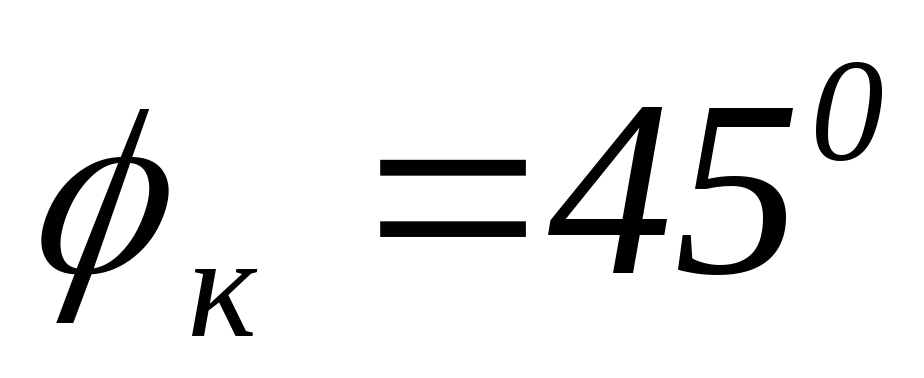
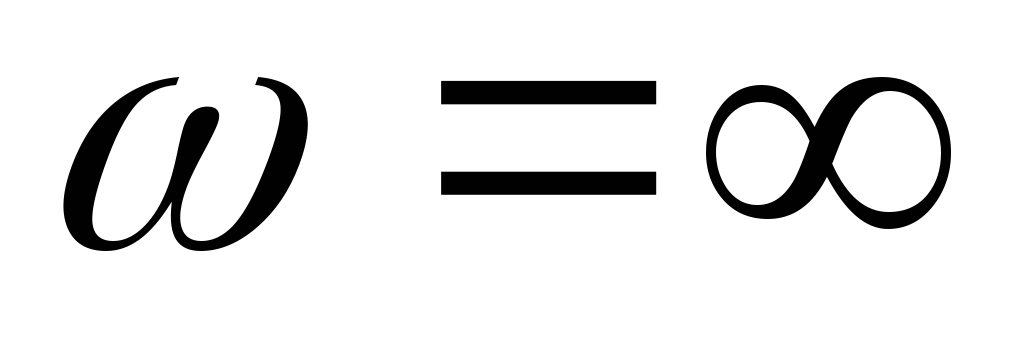
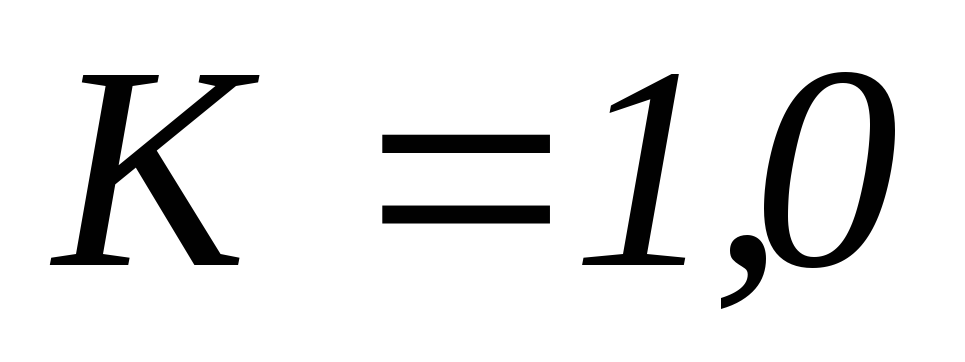
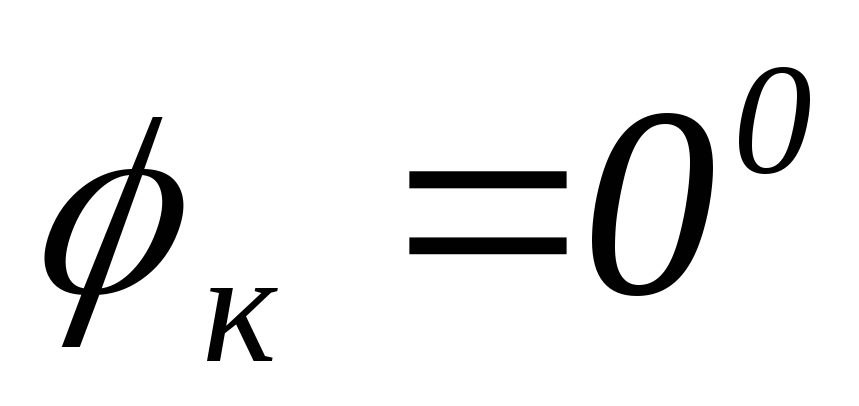
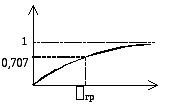
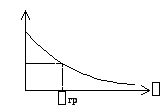
Вывод:
1) передаточная АЧХ в цепи RL зависит от того какой элемент стоит на выходе.
2) передаточная
ФЧХ имеет линейный участок на частотах
от 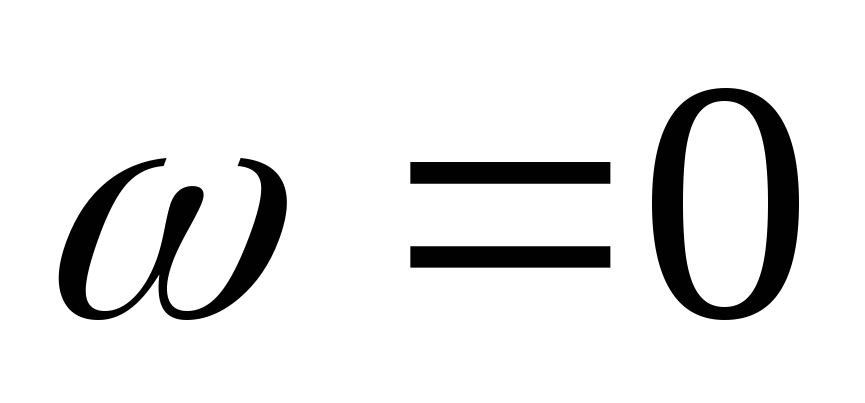 до
до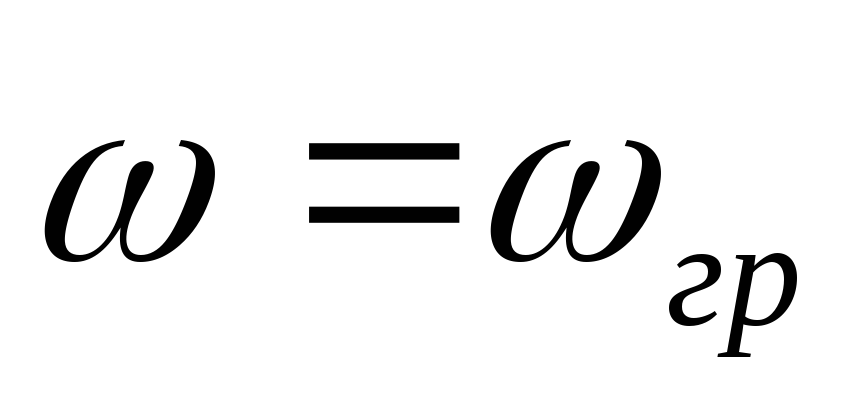 .
.
Передаточные характеристики цепи rс
 Выведем формулы
передаточных АЧХ и ФЧХ цепи RL. Комплексный
коэффициент передачи
Выведем формулы
передаточных АЧХ и ФЧХ цепи RL. Комплексный
коэффициент передачи 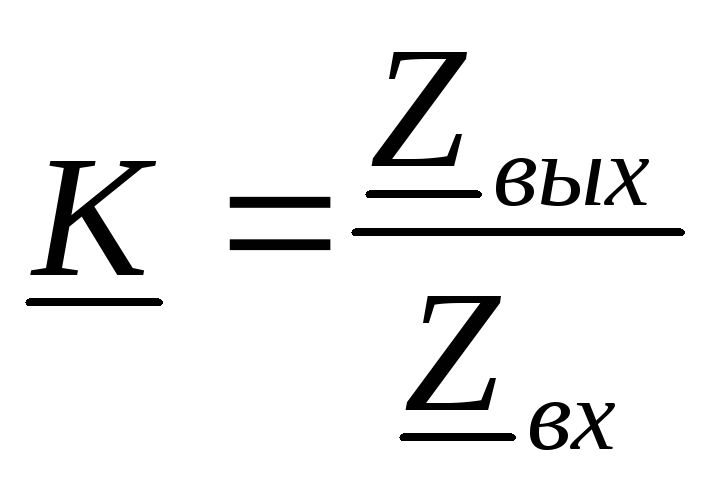
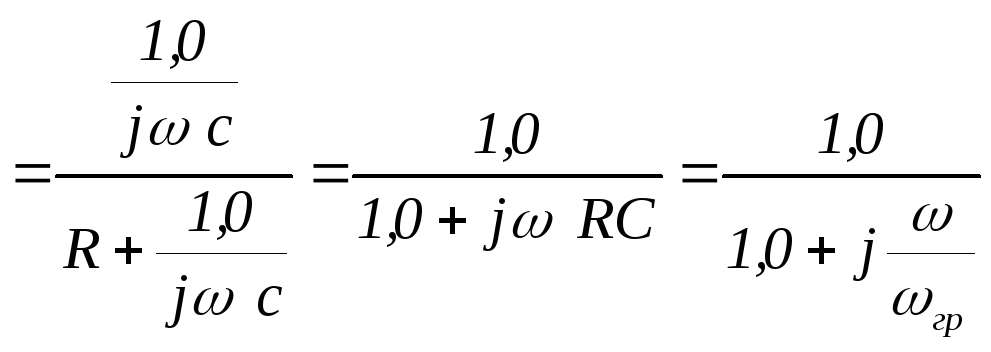 ,
где
,
где 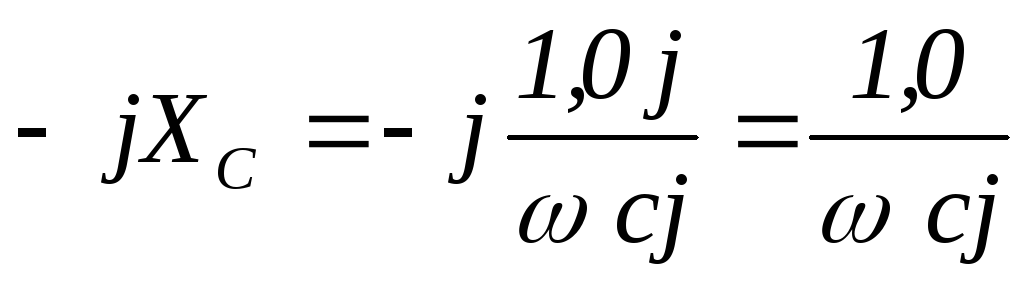 .
.
Домножим числитель и знаменатель на комплексно сопряженное число знаменателю.
Выделим отдельно действительную и мнимую часть
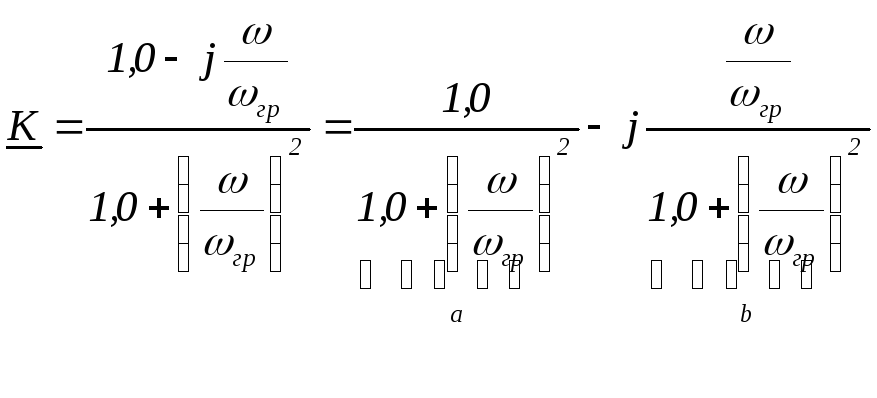
Воспользовавшись
формулой 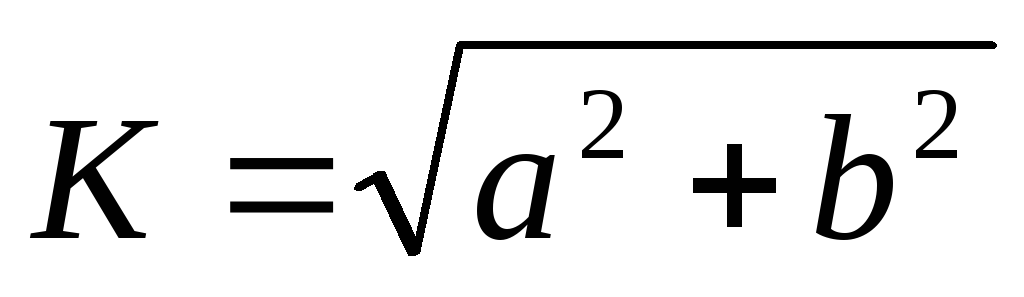 получим передаточную АЧХ цепиRС
получим передаточную АЧХ цепиRС
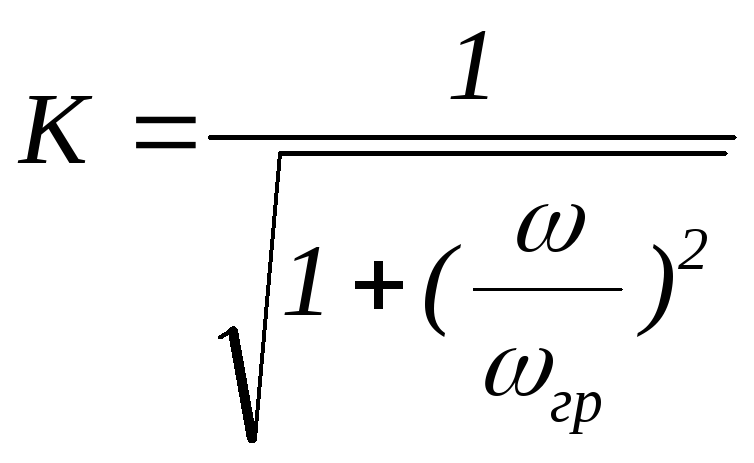 —
передаточная АЧХ цепи RС
—
передаточная АЧХ цепи RС
Передаточную ФЧХ
получаем по формуле: 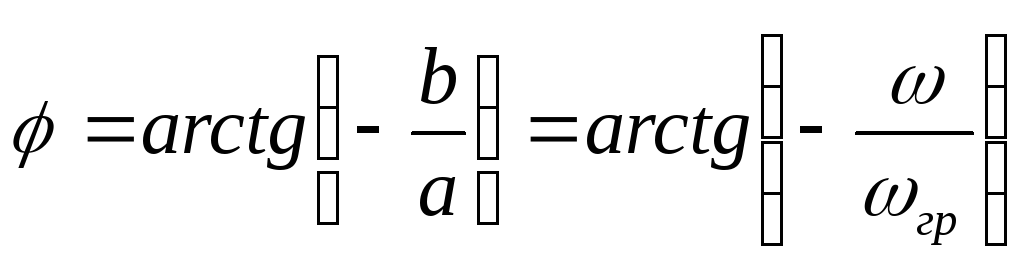
Зададимся несколькими частотами, чтобы построить передаточные характеристики.
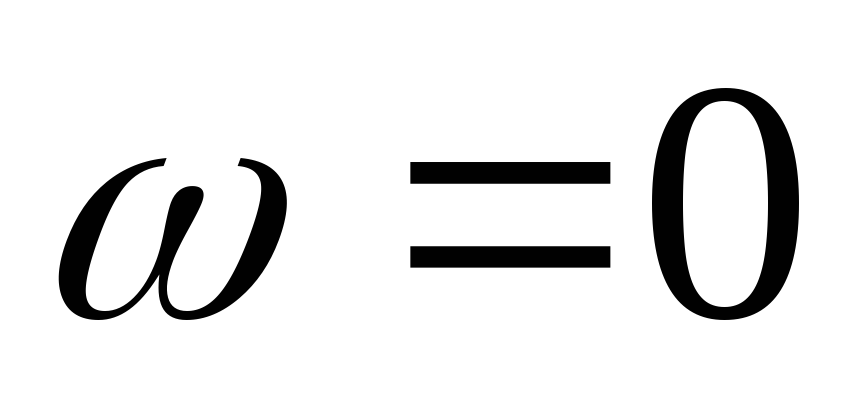
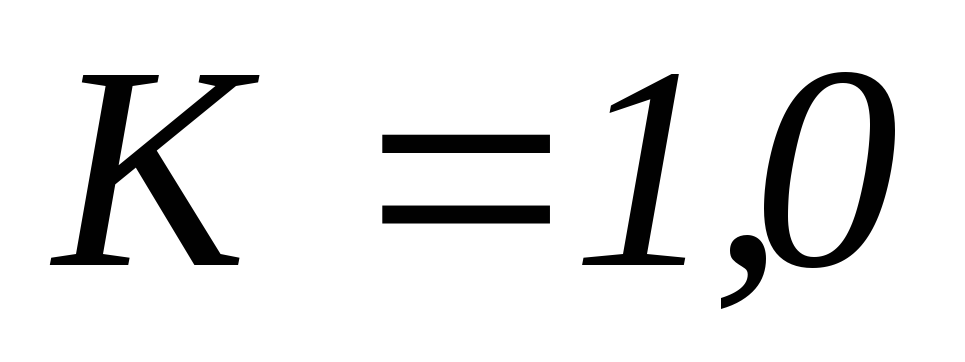
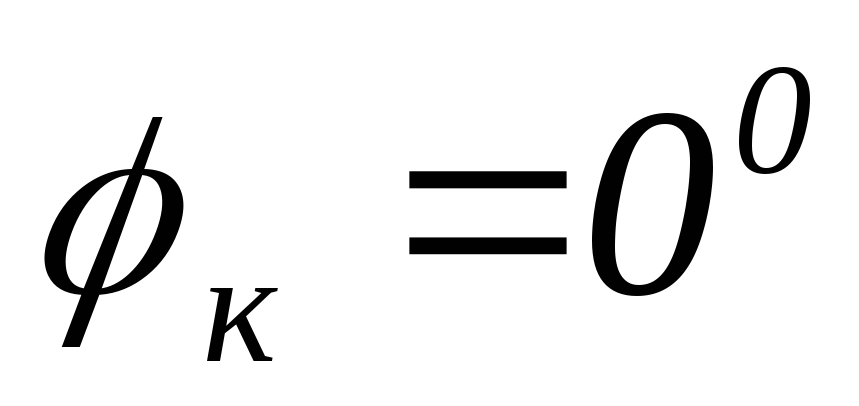
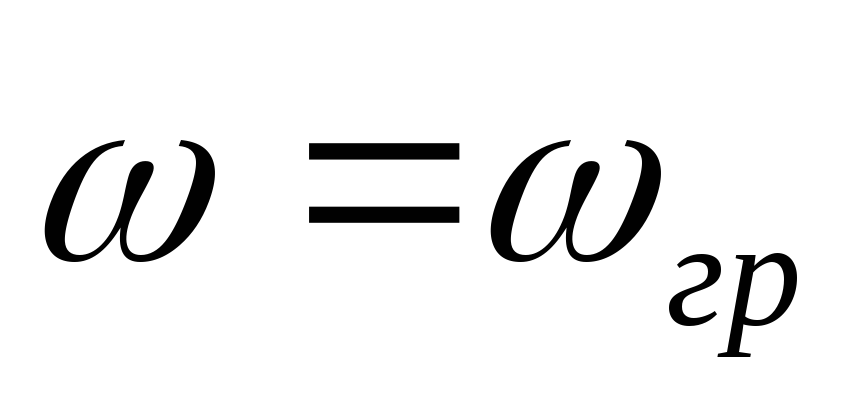
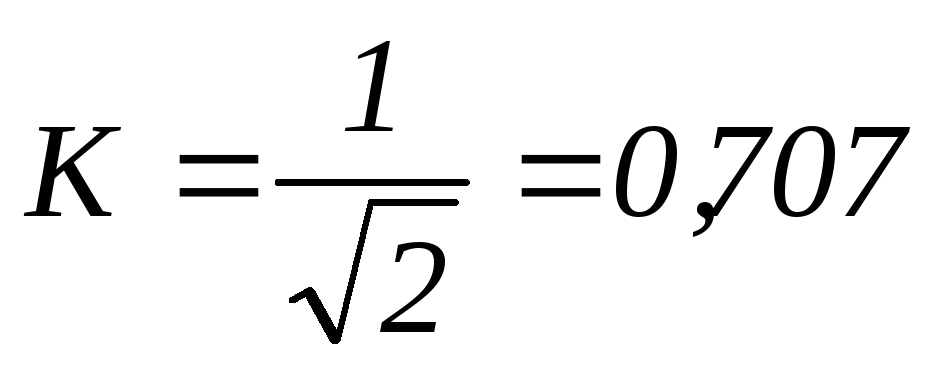
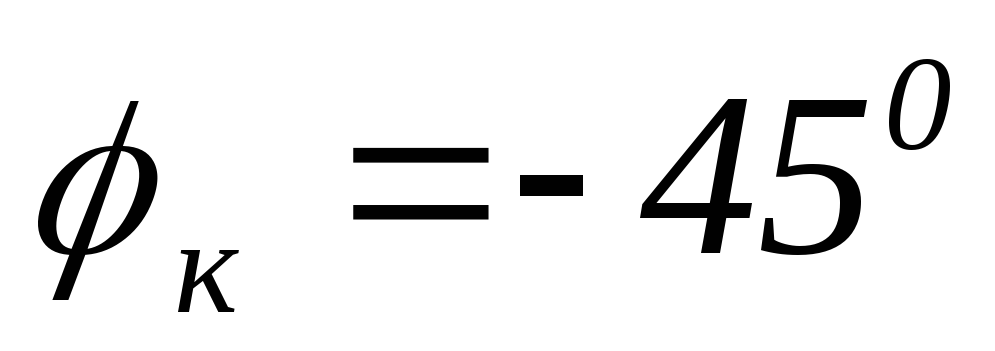
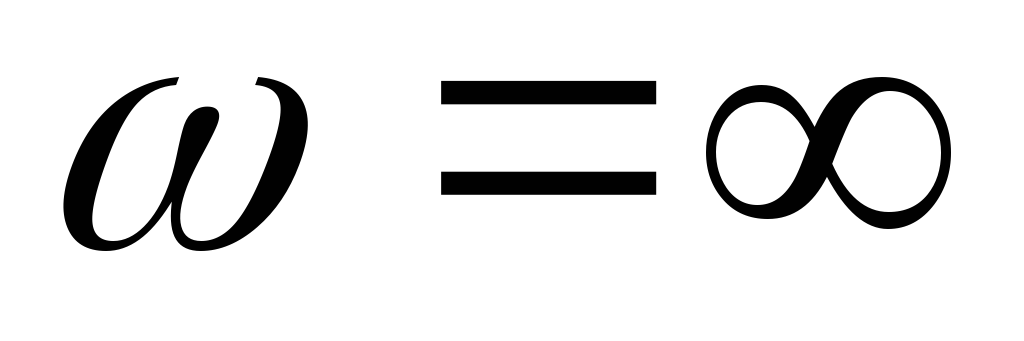
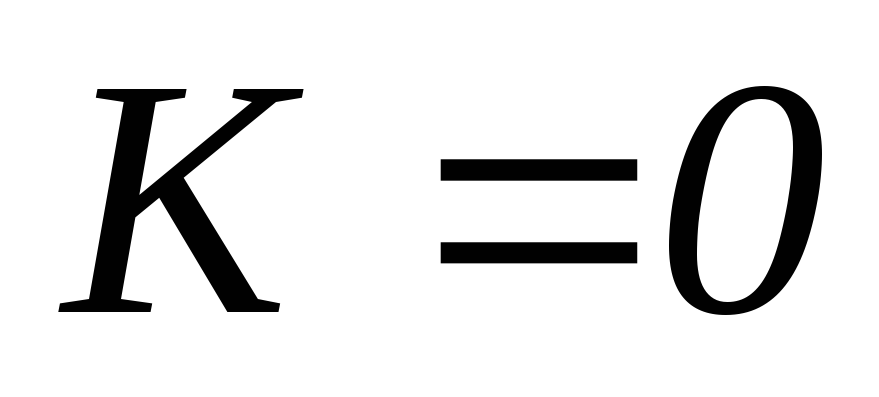
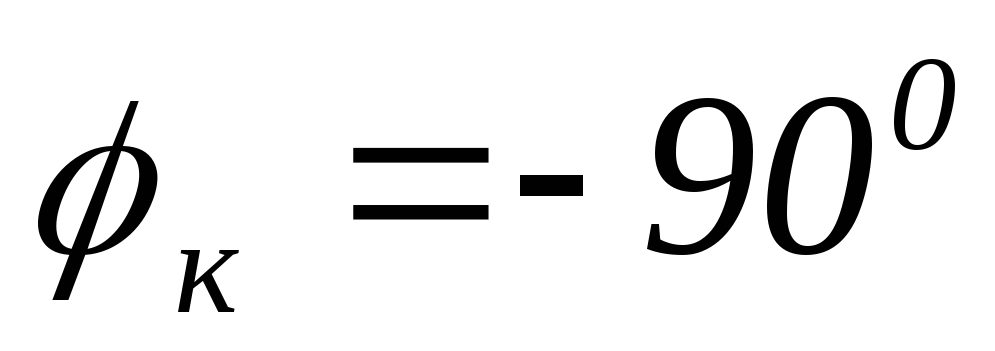
АЧХ ФЧХ
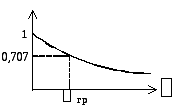
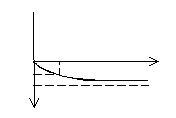
Вывод:
1) цепи RC передаточная АЧХ зависит от того, какой элемент стоит на выходе.
2) передаточная
ФЧХ имеет линейный участок на частотах
от 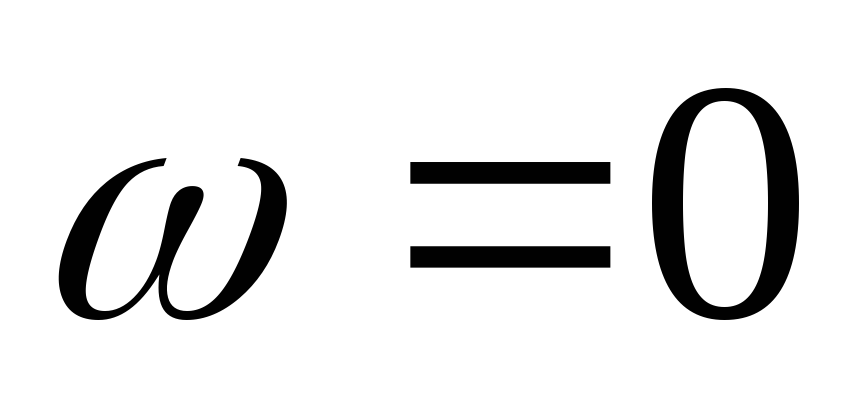 до
до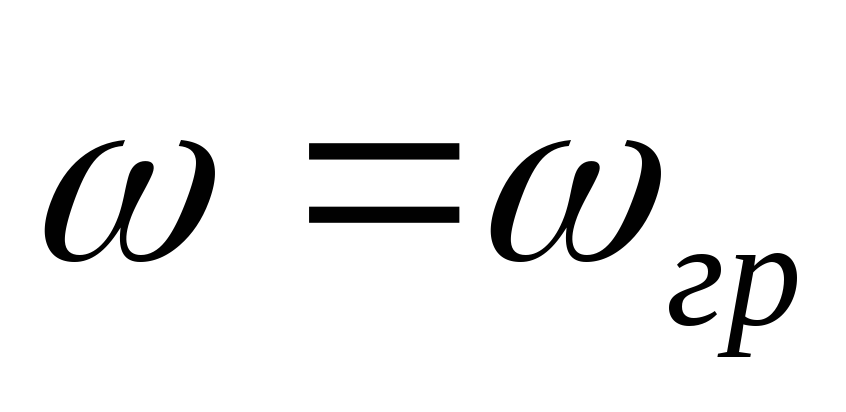 .
.
Тестовые задания:
Задание | Слова для вставки |
Вставьте пропущенные в определениях слова,взяв их из столбца «Слова для вставки» /одно слово – три точки/: 1).Входная АЧХ –это зависимость … комплексного … … от … . 2).Входная ФЧХ –это зависимость … … входного … от … . 3).Передаточная АЧХ –это зависимость … комплексного … … от … . 4).Передаточная ФЧХ –это зависимость … … коэффициента … от … . | модуль, сопротивление, входной, комплексный, частота, коэффициент передачи, аргумент |
Неразветвленная цепь rlc при гармоническом воздействии
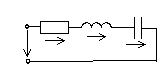 Пусть
по цепи течет ток
Пусть
по цепи течет ток 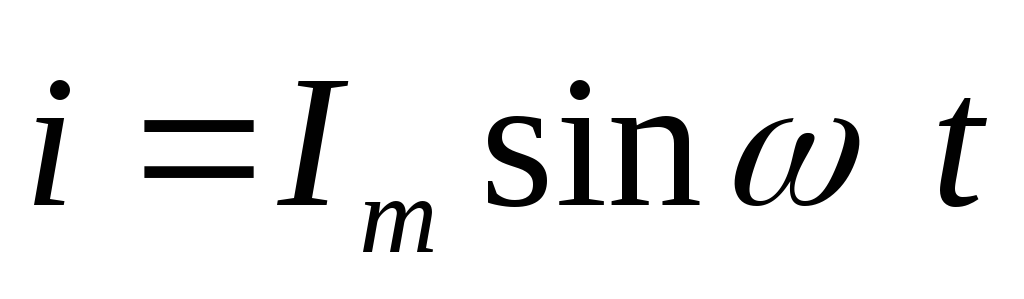 . Запишем уравнения мгновенных значений
напряжений на каждом элементе
. Запишем уравнения мгновенных значений
напряжений на каждом элементе
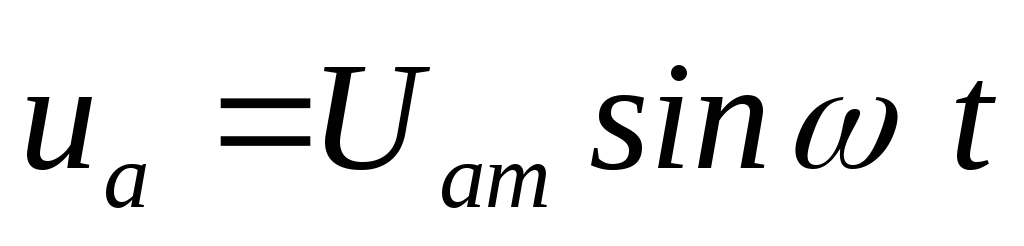
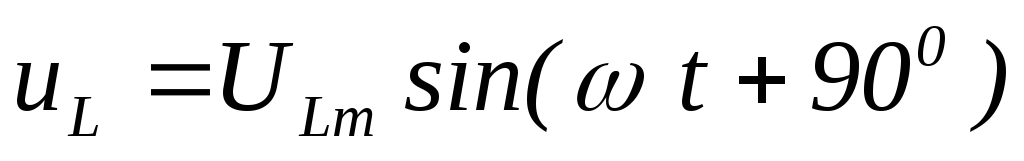
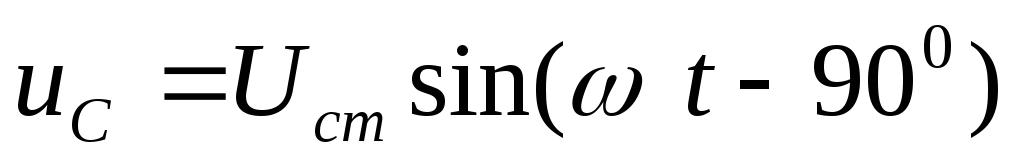
Общее напряжение
равно сумме напряжений отдельных
участков (справедливо для мгновенных
значений и векторов) 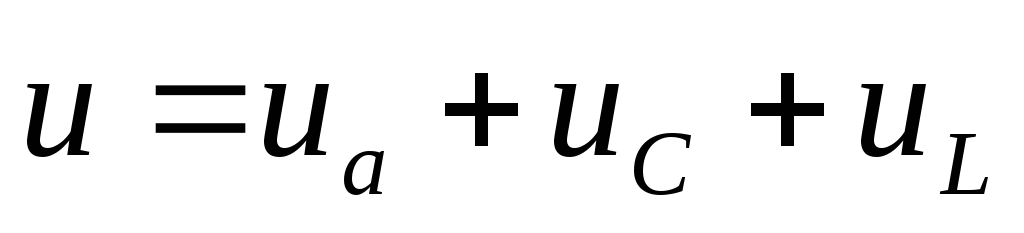 .
.
Построим векторную
диаграмму для случая 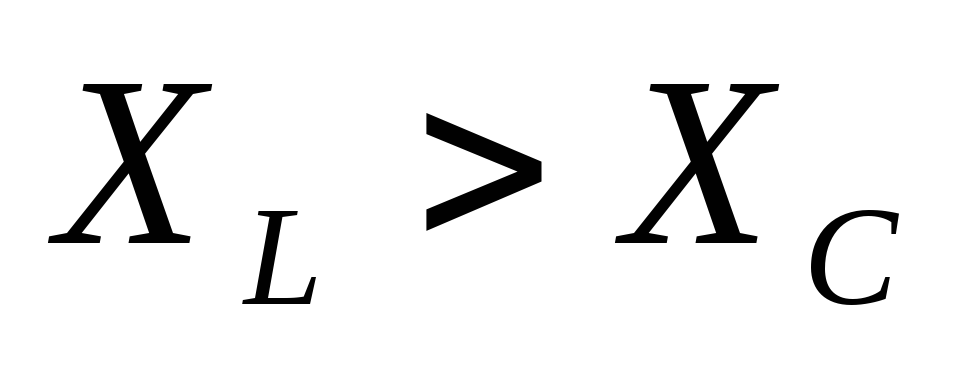
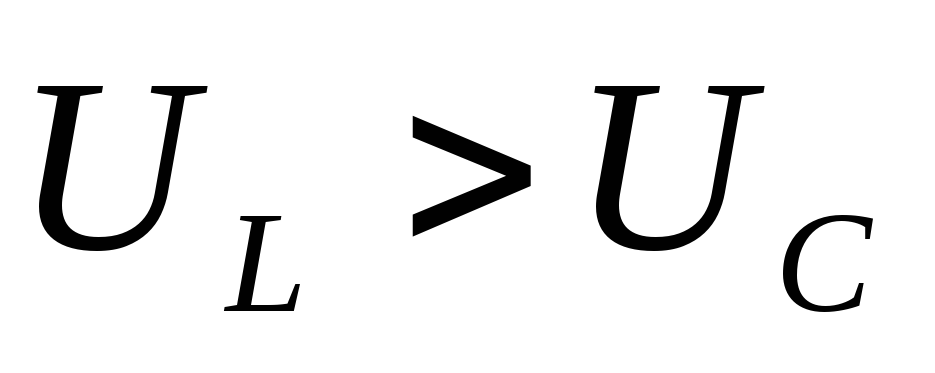
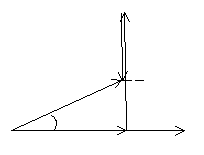
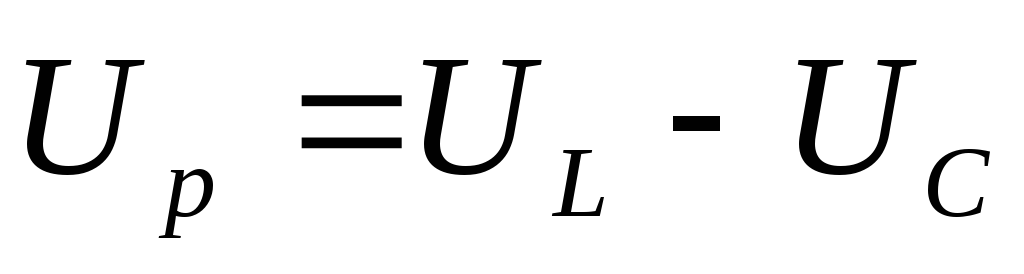 —
реактивная составляющая напряжения.
—
реактивная составляющая напряжения.
Выведем закон Ома для цепи RLC
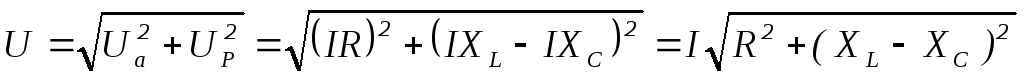
Обозначим 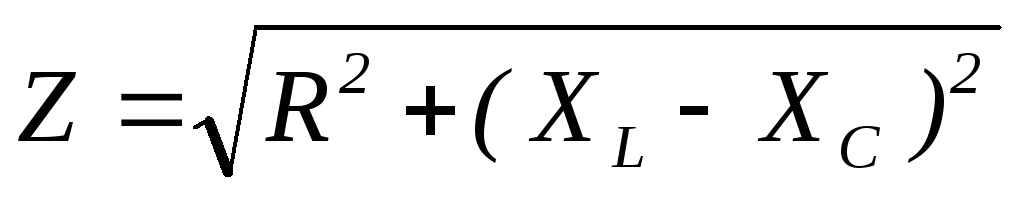 полное сопротивление цепиRLC и получим
закон Ома для цепи RLC
полное сопротивление цепиRLC и получим
закон Ома для цепи RLC 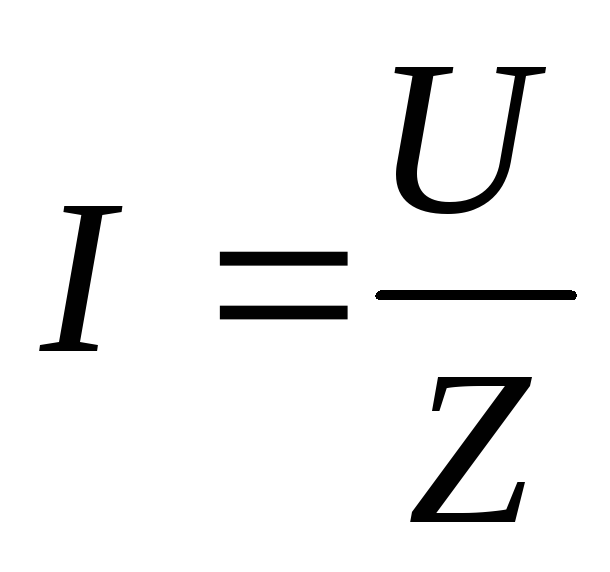
Разделим все стороны диаграммы напряжений на ток и получим диаграмму сопротивлений
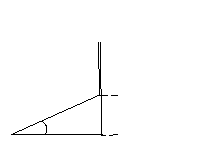 Обозначим
Обозначим 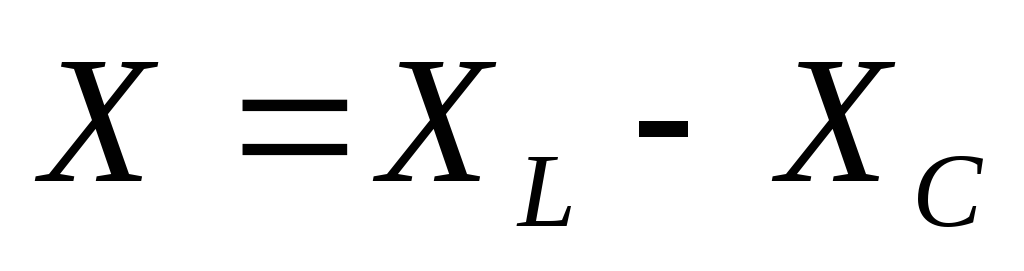 —
реактивное сопротивление цепи.
—
реактивное сопротивление цепи.
Если 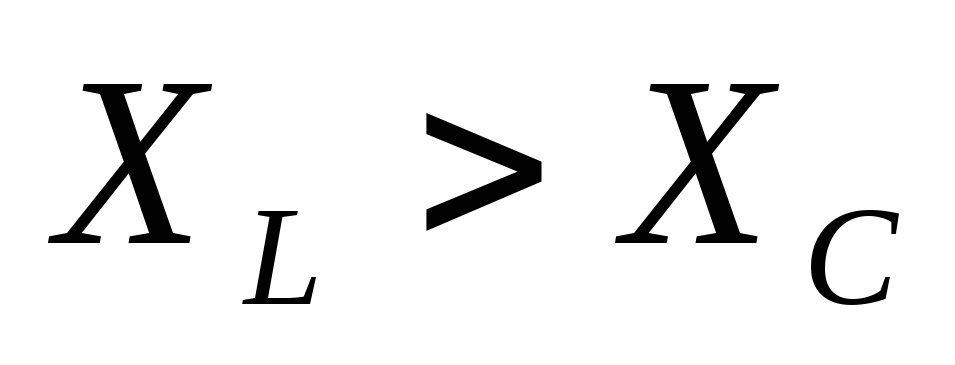
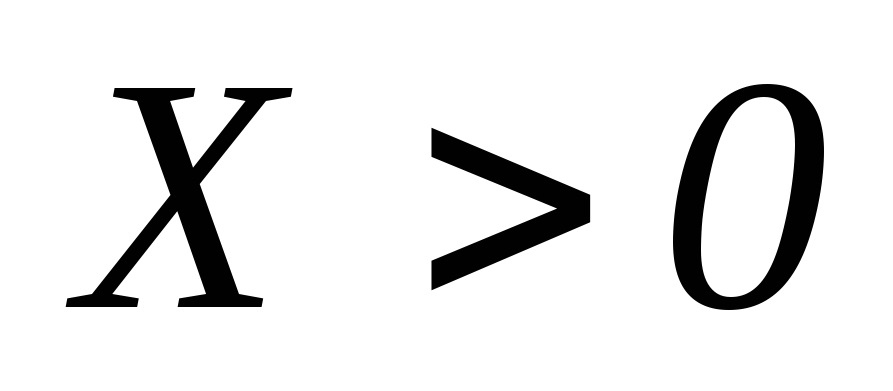 сопротивление цепи носит индуктивный
характер,
сопротивление цепи носит индуктивный
характер,
если 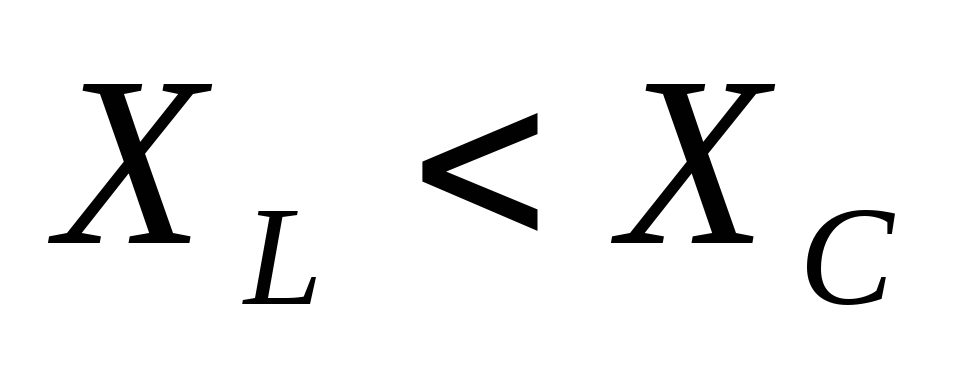
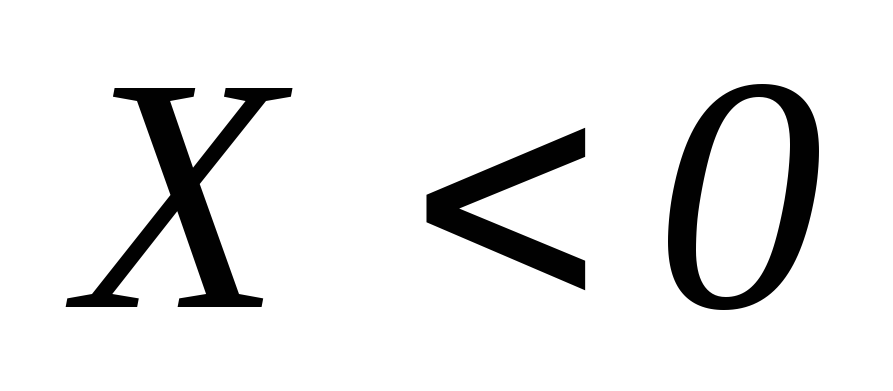 сопротивление цепи носит емкостной
характер
сопротивление цепи носит емкостной
характер
Умножим все стороны диаграммы напряжений на I и получим диаграмму мощностей
 Обозначим
Обозначим 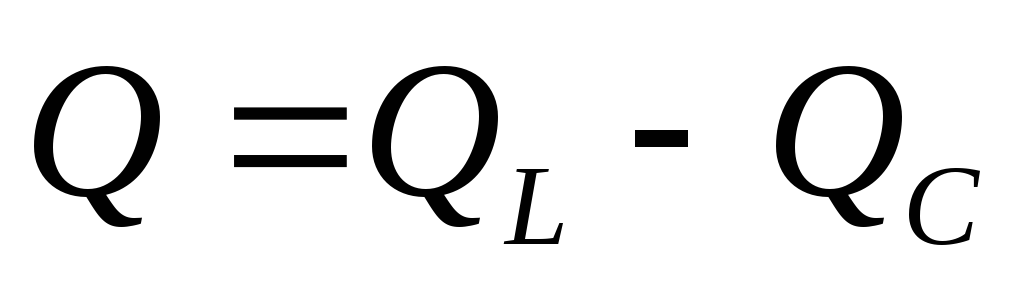 реактивная мощность цепи
реактивная мощность цепи
Построим диаграммы
для случая 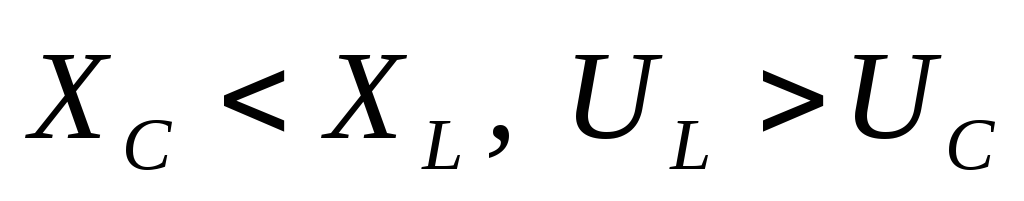
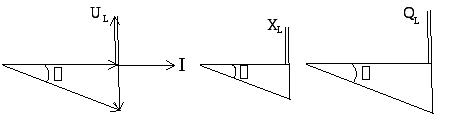
Пример решения задачи
Дано:
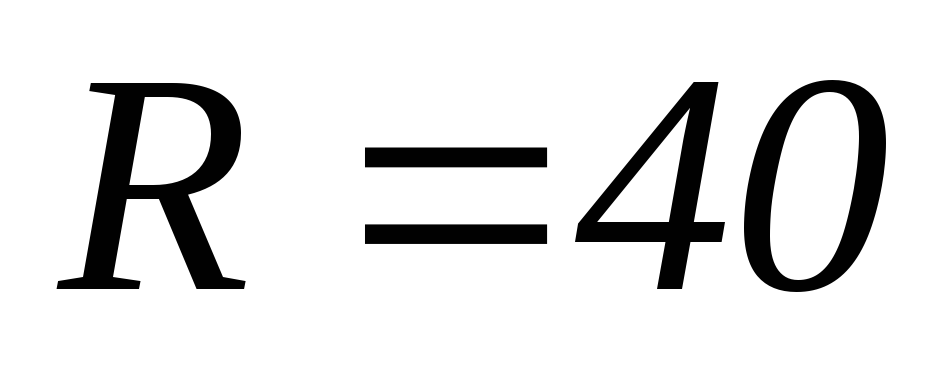
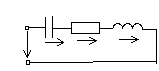 Ом
Ом
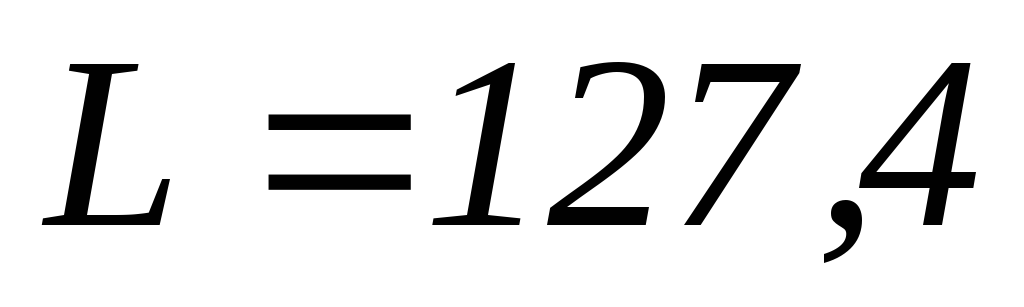 мГн
мГн
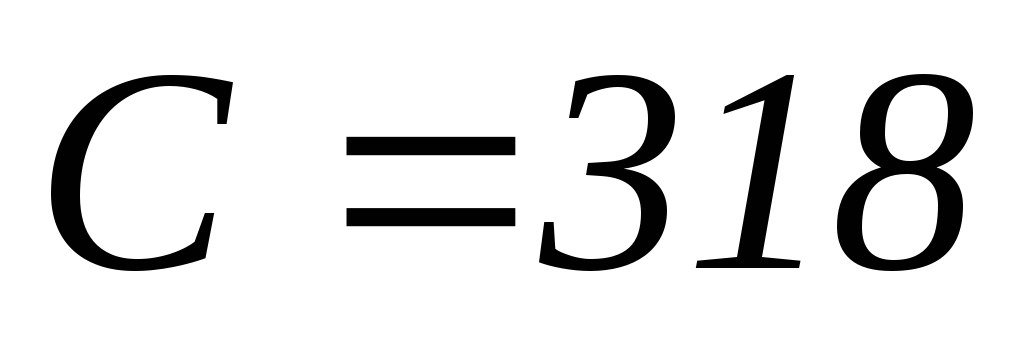 мкФ
мкФ
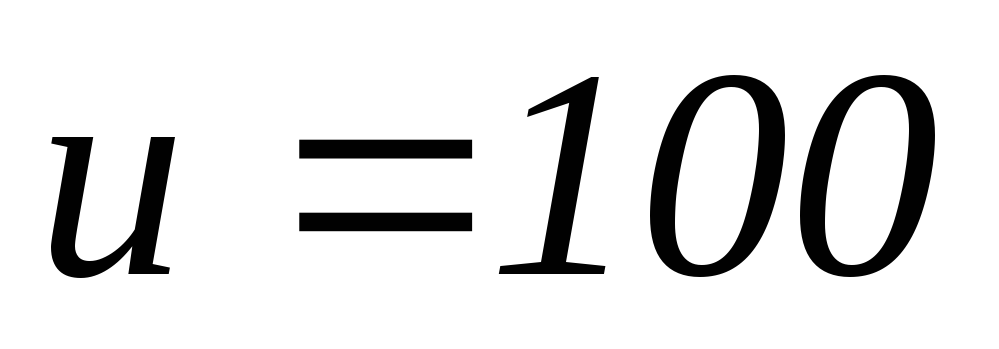 В
В
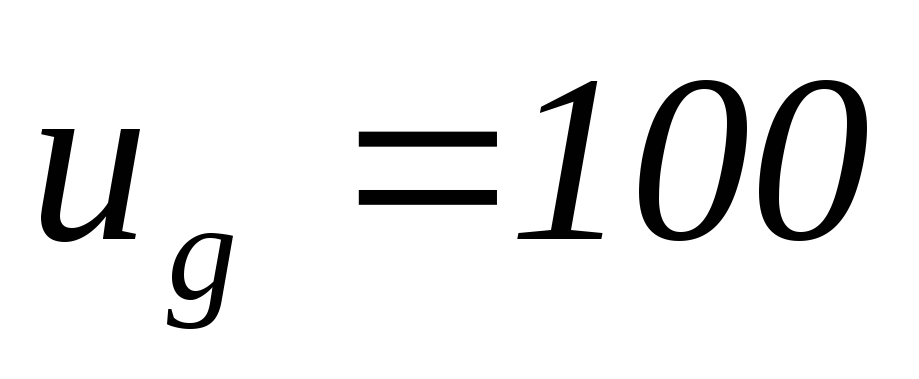 В
В
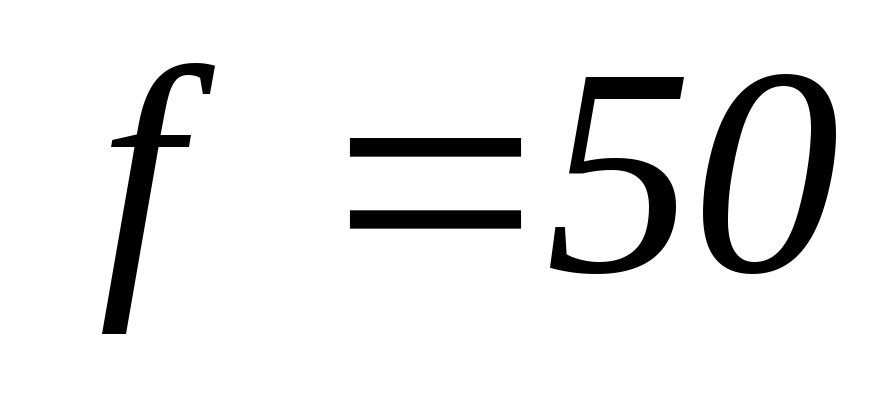 Гц
Гц
Найти: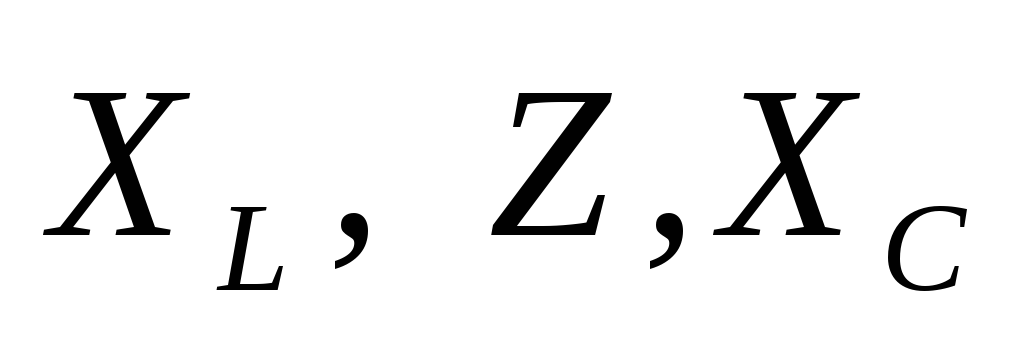
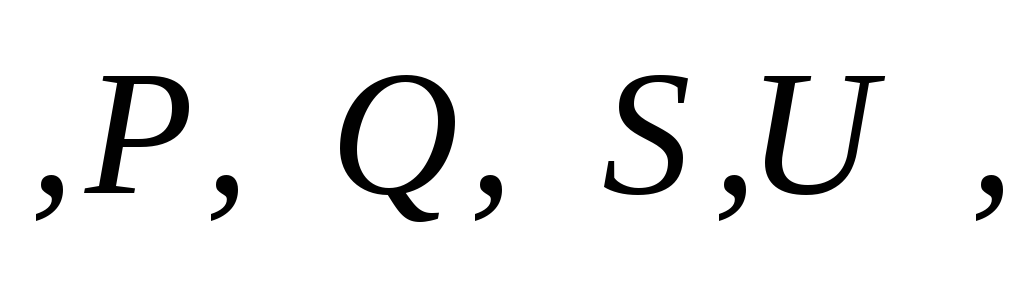
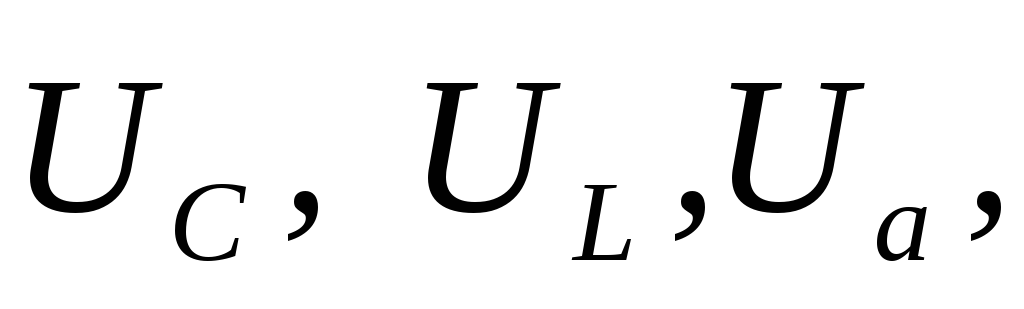
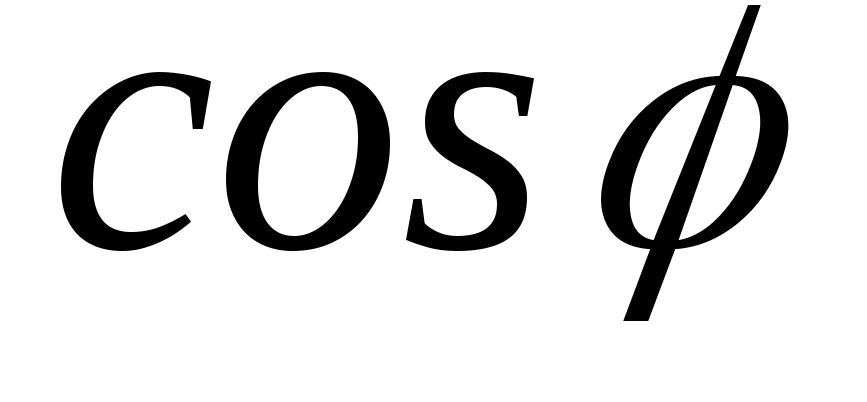
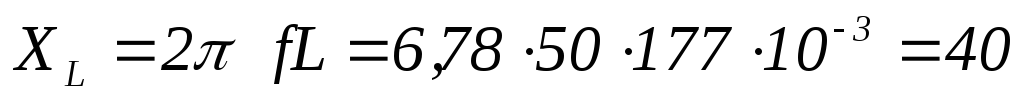 Ом
Ом
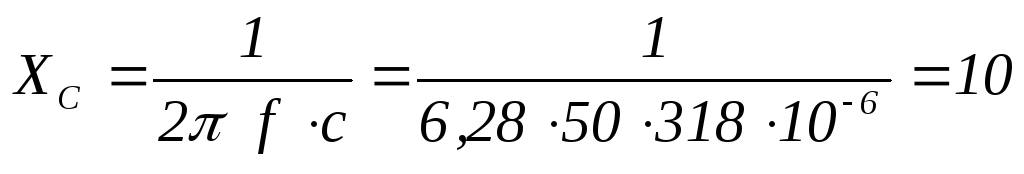 Ом
Ом
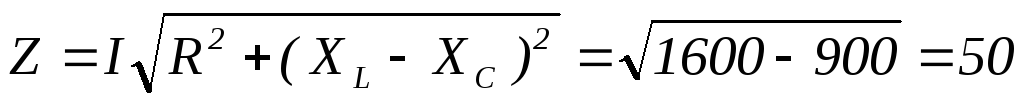 Ом
Ом
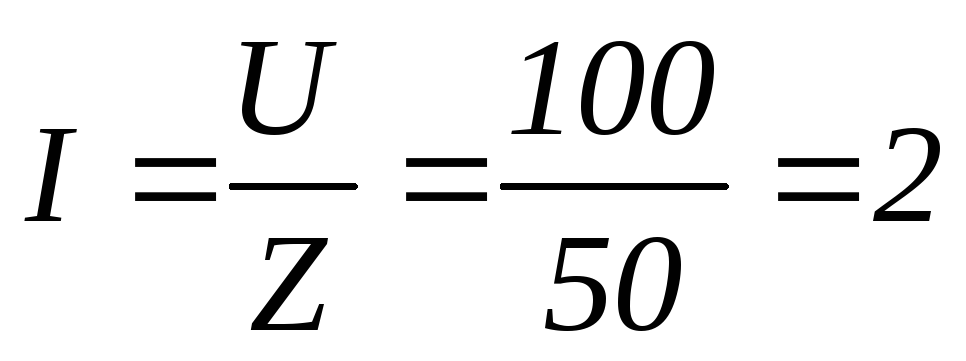 А
А
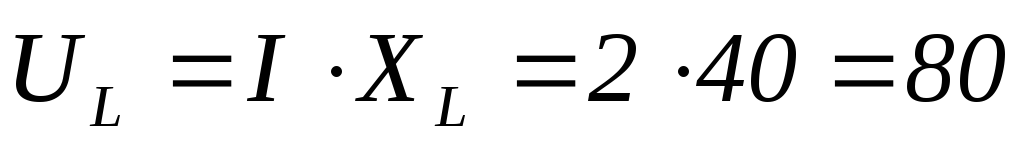 В
В 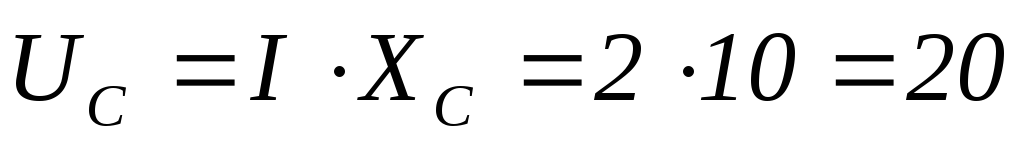 В
В
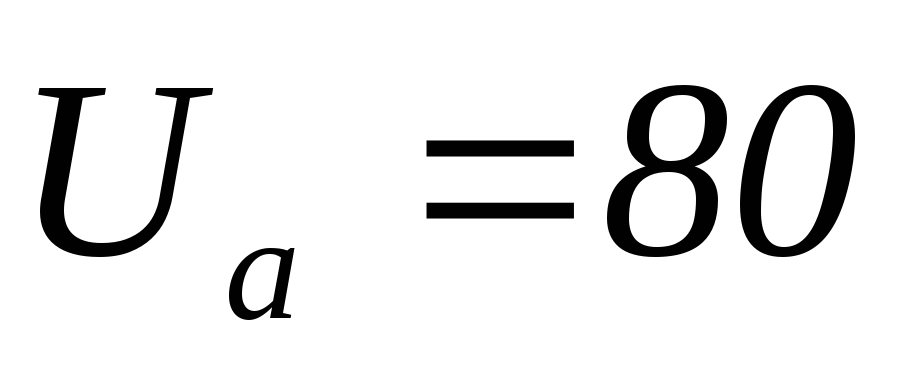 В
В
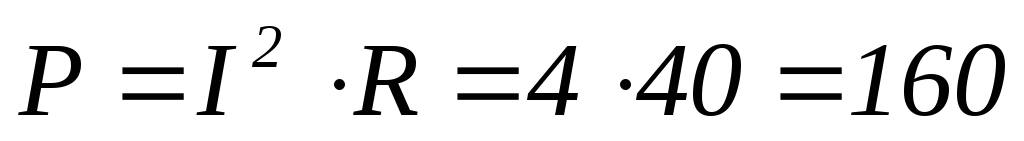 Вт
Вт 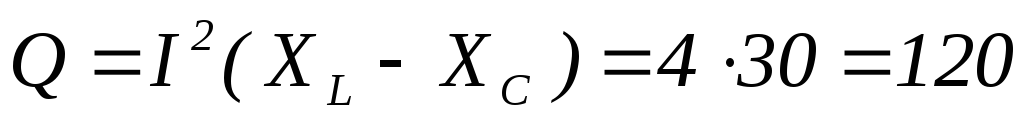 вар
вар
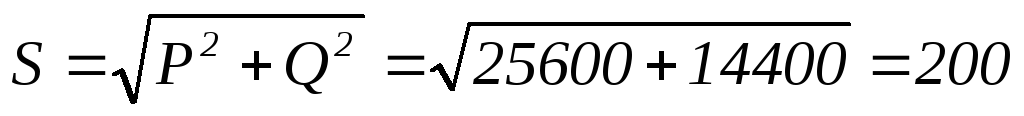 ВА
ВА
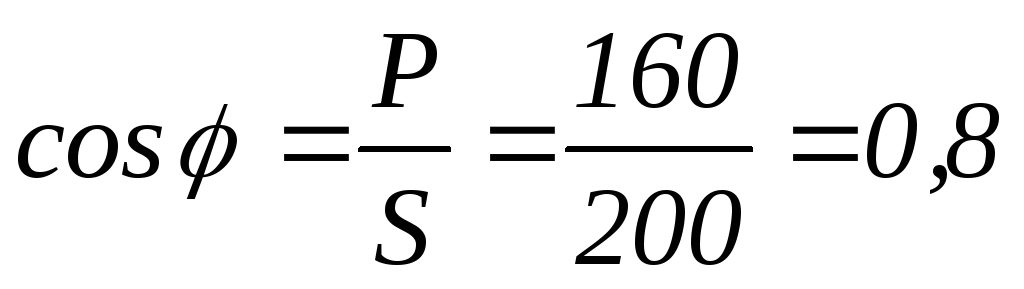
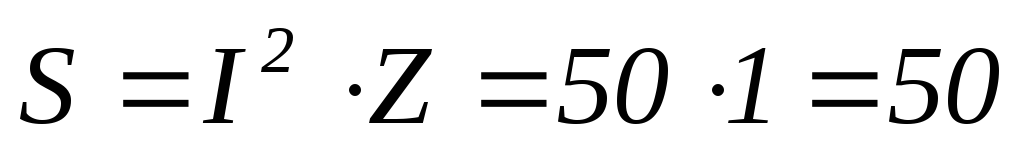 Вт
Вт
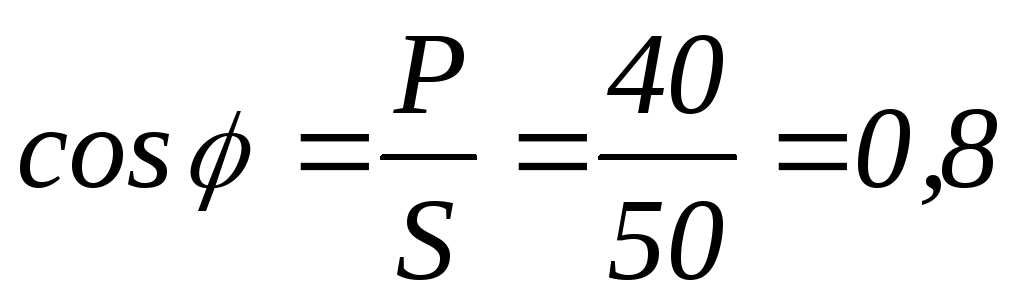
Тестовые задания:
Задание | Варианты ответов | ||
1.Укажите какое из математических выражений не относится к цепи последовательного соединения RLC. | а) в) | ||
Задание | Варианты ответов | ||
2.Укажите какое из приведенных математических выражений является законом Ома для цепи RLC. | а) | ||
Задание | Векторная диаграмма | Варианты ответов | |
3.Укажите какой вектор на векторной диаграмме соответствует перечисленным в ответах напряжениям. |
| а) напряжение на катушке; индуктивности б) напряжение на резисторе; в) напряжение на конденсаторе; г) общее напряжение цепи. | |
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
38. Включение rlc-цепи на постоянное напряжение. Апериодический характер процесса.
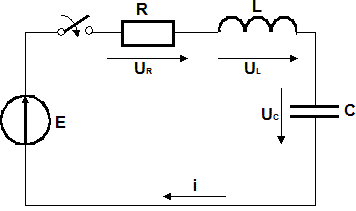
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности, подключенных к источнику постоянной ЭДС. Такую цепь будем называть RLC-цепью или цепью второго порядка.
Сумма всех напряжений в цепи равна сумме всех ЭДС:
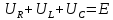
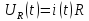
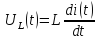
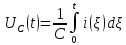
Тогда 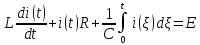
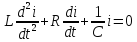
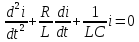
Решим это уравнение.
Составим характеристическое уравнение:
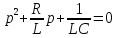
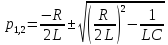
Рассмотрим
случай, когда 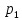 и
и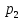 – отрицательные, действительные и
различные. Тогда переходный процесс в
цепи будет иметь апериодический характер.
– отрицательные, действительные и
различные. Тогда переходный процесс в
цепи будет иметь апериодический характер.
При этом сила тока в цепи зависит от времени по следующему закону:

Найдем
постоянные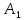 и
и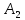 .
.
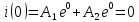
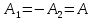
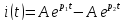
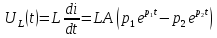
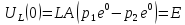
Теперь можно записать уравнение тока в цепи при переходном процессе:
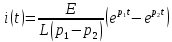
Уравнение переходного процесса на резисторе:
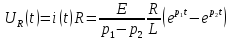
Уравнение переходного процесса на индуктивности:
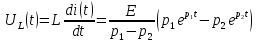
Уравнение переходного процесса на емкости:
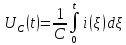
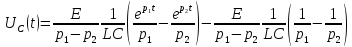
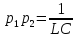
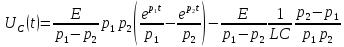
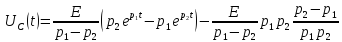
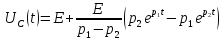
Таким образом, переходный процесс в цепи второго порядка можно описать с помощью следующей системы уравнений:

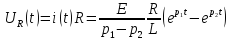
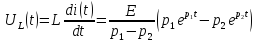
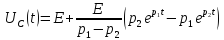
39. Включение rlc – цепи на постоянное напряжение. Граничный характер процесса.
В цепи нет источника, но зато содержится 2 реактивных элемента: катушка и емкость, обладающая напряжением в начальный момент времени:
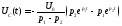 ,
где
,
где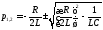 .
.
Данный частный случай характеризуется следующим соотношением:
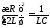 ,
,
т.е.
значение подкоренного выражения в
формуле для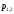 равняется нулю. Но тогда
равняется нулю. Но тогда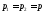 ,
и в выражениях для тока и напряжений
получаем неопределенность вида
,
и в выражениях для тока и напряжений
получаем неопределенность вида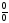 :
:
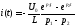 .
.
В
этом случае принимают 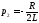 и находят предел выражения для тока
при
и находят предел выражения для тока
при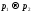 :
:
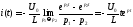 .
.
Теперь найдем все напряжения, исходя из полученной зависимости тока от времени:
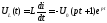
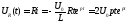 ,
,
где
мы учли, что 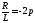 .
Тогда напряжение на конденсаторе имеет
вид:
.
Тогда напряжение на конденсаторе имеет
вид:
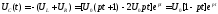 .
.
Как и для 1 случая, можно найти максимумы значений тока в контуре и напряжения на индуктивности:
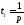
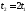 ,
,
40. Включение rlc – цепи на постоянное напряжение. Колебательный характер процесса.
В цепи нет источника, но зато содержится 2 реактивных элемента: катушка и емкость, обладающая напряжением в начальный момент времени:
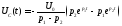 ,
где
,
где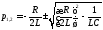 .
.
Данный случай характеризуется выражением
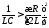 ,
,
т.е. корни характеристического уравнения 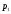 и
и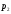 — комплексно сопряженные величины.
Введем следующие обозначения:
— комплексно сопряженные величины.
Введем следующие обозначения:
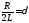 ,.
,.
Тогда
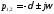
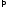
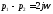 .
.
Найдем выражение для тока в контуре:
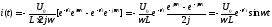 .
.
Получили периодическую зависимость тока от времени, отсюда и название случая.
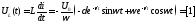 .
.
Введем
новые переменные 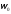 и
и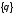 следующим образом:
следующим образом:
1) 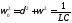
2) 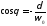
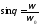
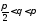 .
.
Разделим
и умножим выражение для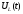 на
на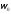 :
:
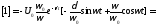
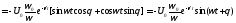 .
.
Найдем оставшуюся временную зависимость на конденсаторе. Имеем:
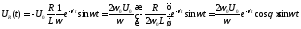 ,
,
тогда
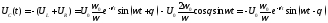 .
.
Заметим, что в данном случае мы имеем две постоянных времени.
График зависимости тока от времени будет иметь вид:
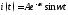 .
.
В общем виде график такого плана строится следующим образом. Очевидно, у этого графика есть 2 асимптоты – огибающие синусоиды, ведь график функции представляет собой синусоиду, амплитуда которой уменьшается по экспоненциальному закону.
Первая постоянная времени  характеризует асимптоты-экспоненты, а
вторая —
характеризует асимптоты-экспоненты, а
вторая — — частоту синусоидальной функции.
— частоту синусоидальной функции.
Теперь займемся построением графиков непосредственно токов и напряжений. Выпишем для наглядности полученные временные зависимости:
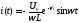
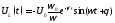
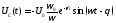
График тока (а значит и напряжения на резисторе) будет иметь такую же структуру, как только что рассмотренный, только взятый с противоположным знаком (действительно, при замыкании контура конденсатор начинает разряжаться).
Из формулы следует, что график напряжения на индуктивности начинается из отрицательной области (в начальный момент времени), а график напряжения на конденсаторе – из такого же по модулю и противоположного по знаку значения. Напряжение на индуктивности уже достигло своего максимального значения и после коммутации спадает (по модулю), а на емкости – только приближается к максимальному значению. Исходя из этих соображений, можно качественно построить графики.

Отметим, что если 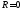 ,
то
,
то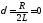 ,
,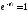 ,
т.е. график будет без затуханий:
действительно, мощность не будет
рассеиваться на активном элементе.
,
т.е. график будет без затуханий:
действительно, мощность не будет
рассеиваться на активном элементе.


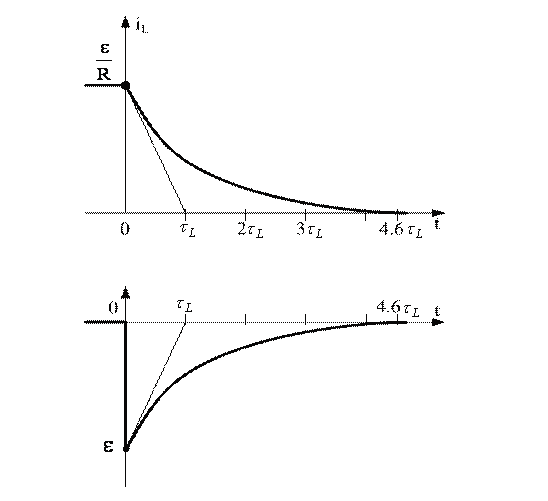
 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту: апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ: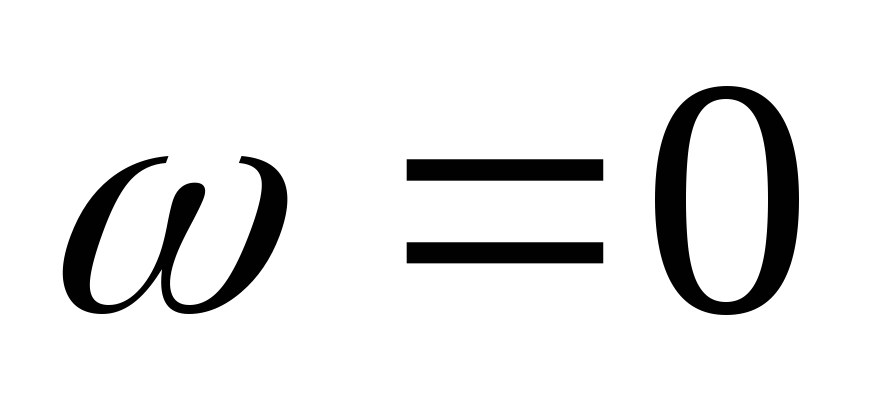 до
до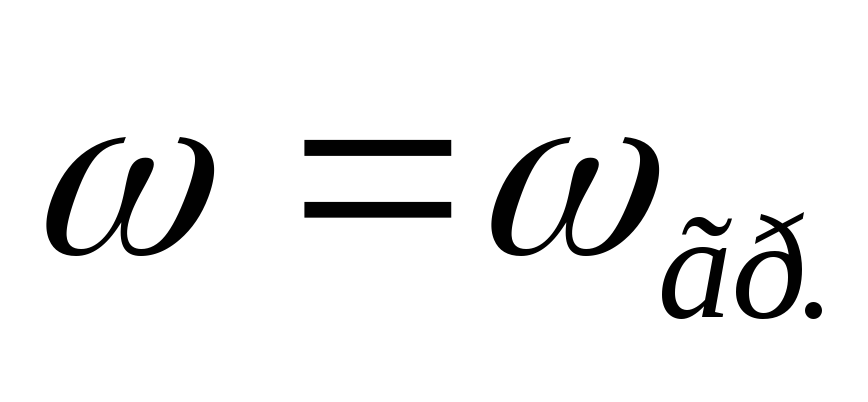 .
.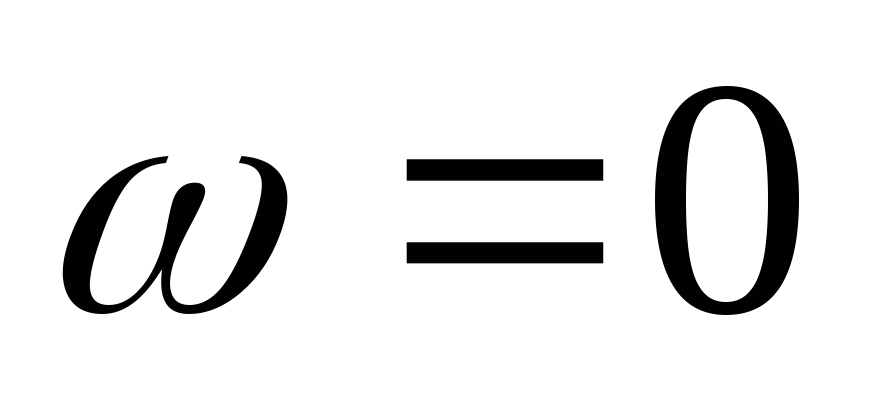
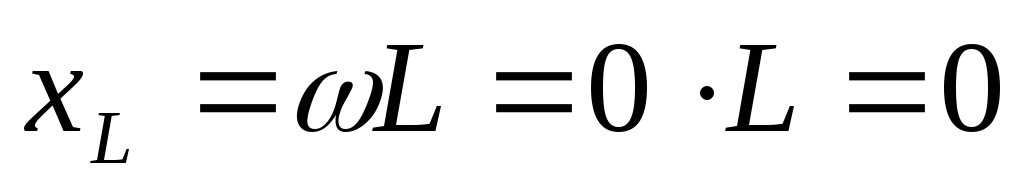
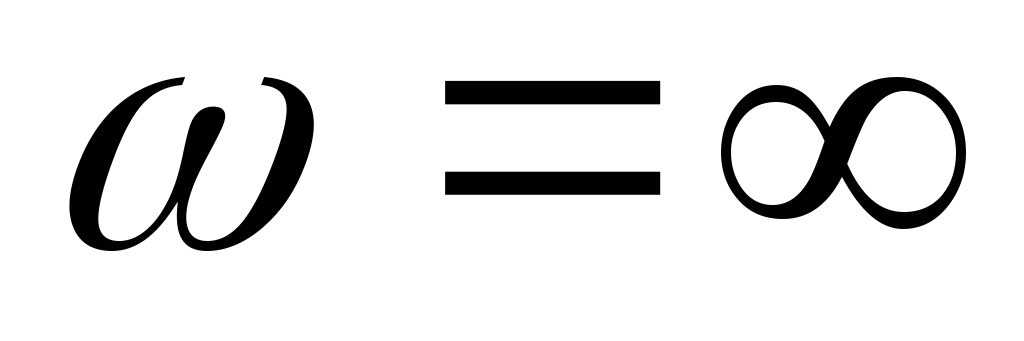
 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту: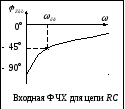 апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ: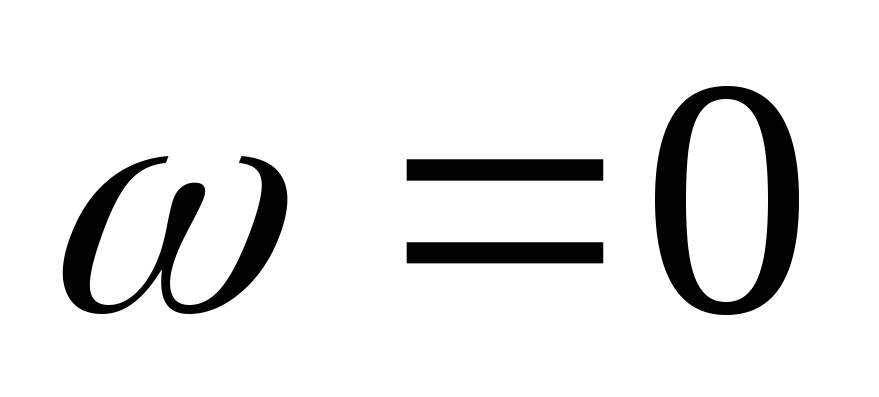
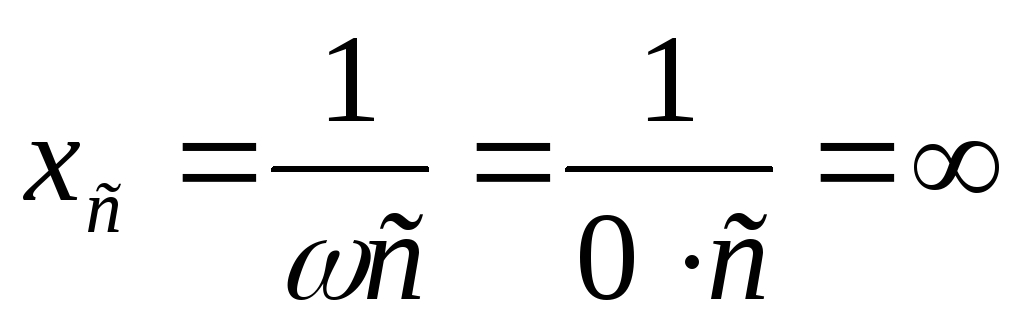
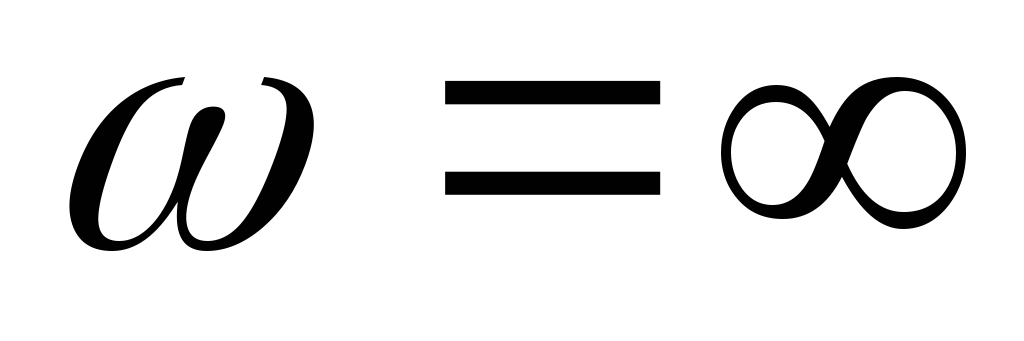
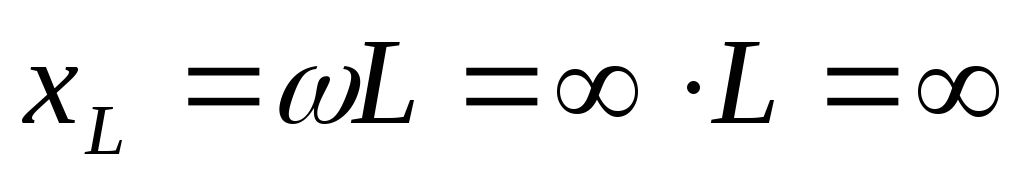
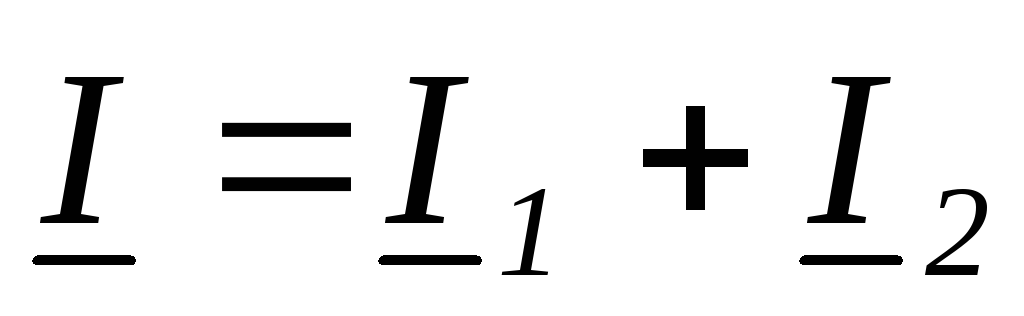 ;
б)
;
б)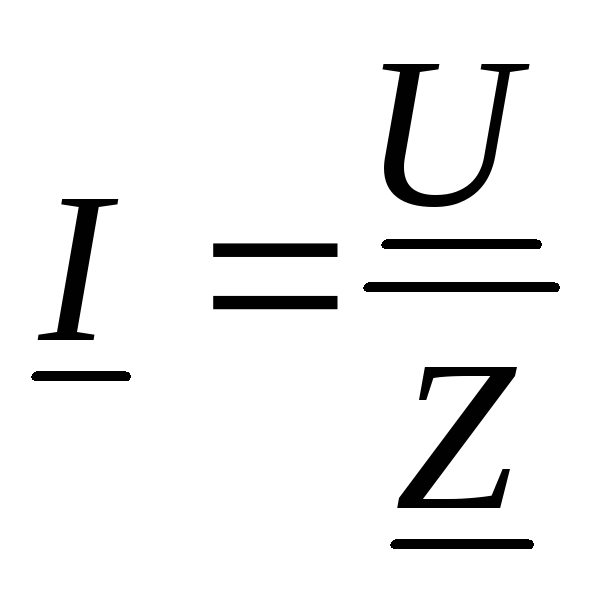 ;
;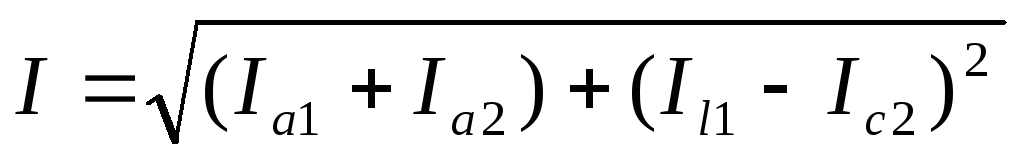 ;
;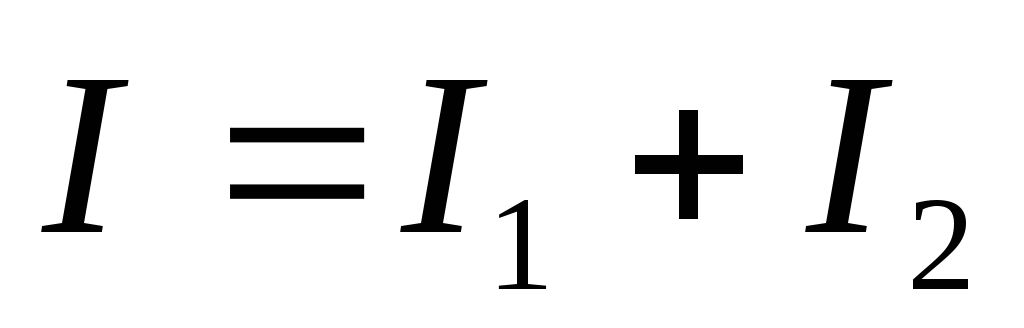 .
.
 ;
б)
;
б) ;
; ;
г)
;
г)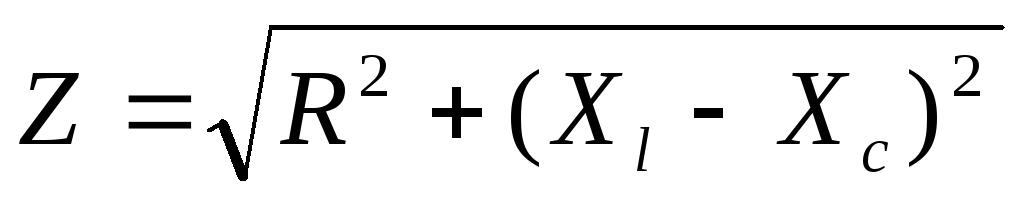
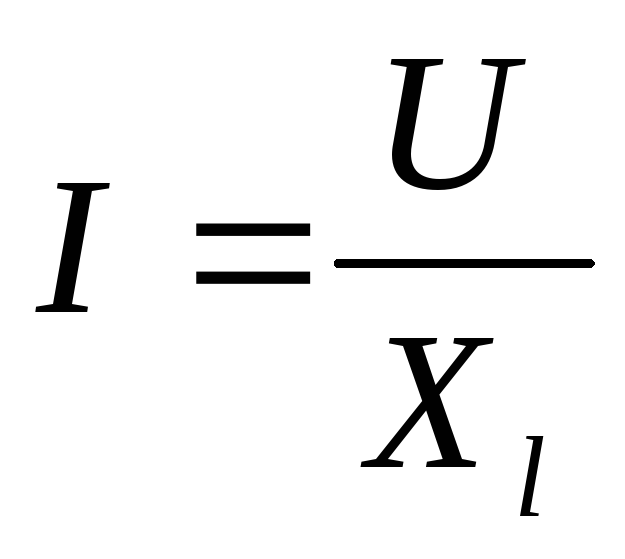 ;
б)
;
б)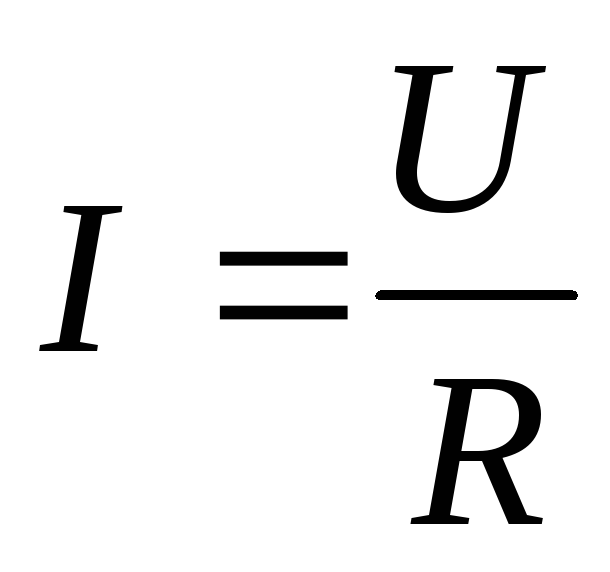 ;
г)
;
г)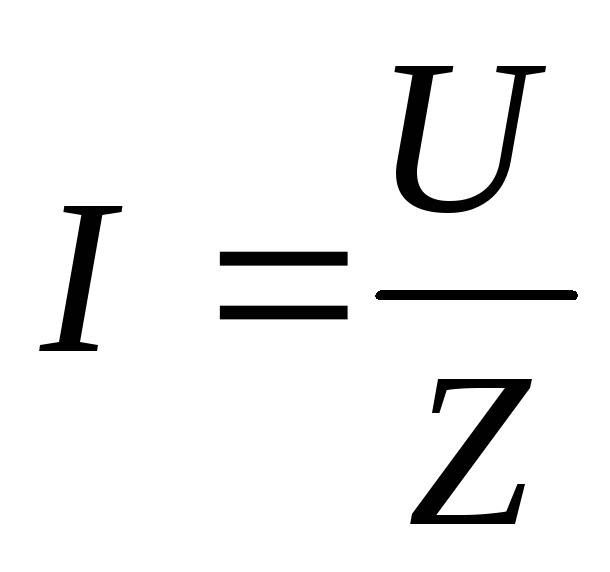 ;
д)
;
д) .
.