Электрическая цепь представляет собой средства и объекты, образующие, в совокупности, путь для прохождения электрического тока. Электромагнитные процессы, происходящие в них, могут получить свое определение при помощи таких понятий, как сила тока, напряжение, сопротивление и электродвижущая сила.
Цепи постоянного токаВ состав входят отдельные устройства, которые выполняют свои определенные функции. Они называются элементами электрической цепи. Основными элементами считаются источники электроэнергии и устройства, принимающие эту энергию. Во всех источниках, с не электрическими материалами происходит преобразование в электрическую энергию. Наиболее распространенными источниками являются аккумуляторы, гальванические элементы, электромагнитные генераторы, солнечные батареи и другие. С помощью приемников электроэнергия может преобразовываться в иные виды энергии. К основным видам таких приемников можно отнести нагревательные элементы и приборы, электродвигатели, гальванические ванны, приборы освещения и прочие. Кроме того, в электрической цепи содержатся элементы вспомогательного назначения. Например, с помощью реостатов, регулируется величина, напряжение регулируется при помощи потенциометров и делителей. От перегрузок цепь защищают предохранители, коммутацию обеспечивают выключатели. Контроль над режимом работы осуществляется контрольно измерительными приборами.
Цепи переменного токаПеременным называют электрический ток, способный менять направление своего движения периодически, за определенные промежутки времени. Поскольку у него происходит изменение во времени, здесь невозможно применять расчеты, подходящие для цепей постоянного тока. При наличии высокой частоты, заряды совершают колебательное движение. Они переходят в цепи из одних мест в другие и в обратном направлении. При переменном в отличие от постоянного, последовательно соединенные проводники могут иметь неодинаковые значения. Этот эффект усиливается наличием емкостей в цепи. Здесь же наблюдается эффект самоиндукции, возникающий при использовании катушек с большой индуктивностью даже при низкой частоте. Рассмотрим свойства цепи, подключаемой к генератору с переменным синусоидальным током. Роль конденсатора при подключении его в цепи постоянного и переменного тока совершенно различная. При постоянном, конденсатор заряжается до тех пор, пока его напряжение не сравняется с ЭДС источника тока. В этом случае зарядка прекращается и он падает до нуля. Если такую же цепь подключить к генератору переменного тока, то электроны будут перемещаться из одной части конденсатора в другую. Эти электроны и есть переменный ток с одинаковой силой с обеих сторон конденсатора. В случае необходимости, с помощью выпрямителя, происходит преобразование переменного тока в постоянный. |
Постоянная и переменная электрическая цепь
В электротехнике изучаются принципы действия и устройства основных электротехнических приборов, которые используются в быту и промышленности. Чтобы любое электротехническое устройство работало, должна создаваться электрическая цепь. Основное задачей цепи является передача электрической энергии и обеспечение устройству необходимого режима работы.
Электрическая цепь: понятие и основные элементы
Электрическая цепь – это совокупность различных объектов и устройств, которые образуют путь для нормального протекания электрического тока. Электромагнитные процессы в цепях могут описываться при помощи понятий об электродвижущей силе, электрическом токе и электрическом напряжении.
Для того чтобы проводить расчеты и анализ, электрическую цепь можно представить в виде электрической схемы, которая состоит из условных обозначений ее элементов и способов их соединения.
Все устройства и элементы, которые входят в состав электрической цепи, условно можно классифицировать на несколько групп:
- Источники электрического питания (энергии). Общее свойство всех источников питания – это преобразование любых видов энергии в электрическую. Источники, в которых осуществляется трансформация неэлектрической энергии в электрическую, называются первичными. Вторичными источниками являются те, в которых и на выходе, и на входе электрическая энергия. В качестве примера можно привести выпрямительные устройства.
- Потребители электроэнергии. Общее свойство всех потребителей электрической энергии – это трансформация электроэнергии в другие виды энергии. Пример – нагревательный прибор. Иногда потребители электроэнергии называют нагрузкой.
- Вспомогательные элементы электрической цепи. Сюда можно отнести коммуникативные устройства, соединительные провода, защитную аппаратуру, а также измерительные приборы, без которых электрическая цепь не функционирует.
Все элементы электрической цепи охватываются одним электромагнитным процессом.
Электрическая цепь с постоянным током
В электрической цепи постоянного тока электродвижущая сила, которая направлена внутрь источника электроэнергии от отрицательного полюса к положительному, возбуждает электрический ток такого же направления. Его можно определить по закону Ома для всей цепи:
$I = \frac {E}{R + R_{BT}}$, где:
- $R$ — это сопротивление внешней цепи, которая состоит из соединительных проводов и приемника;
- $ R_{BT} $ — сопротивление внутренней цепи, которая состоит из источника электрической энергии.
Определение 1
Если все элементы электрической цепи и их сопротивления не зависят от направления и значения тока и электродвижущей силы, то такие элементы называют линейными.
Стоит отметить, что в одноконтурной постоянной электрической цепи, что имеет один источник электрической энергии, ток прямо пропорционален электродвижущей силе и обратно пропорционален сопротивлению цепи.
Из этого следует, что $E-R_{BT} L = RI$, откуда:
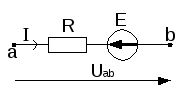
$I = \frac {(E – R_{BT} l)}{R}$ или $I = \frac {U}{R} $, где:
$U = E – R_{BT} l$ — это напряжение источника электроэнергии, которое направляется от положительного полюса к отрицательному.
При неизменной электродвижущей силе, напряжение зависит только от электрического тока, который определяет падение напряжения $ R_{BT} l$ внутри источника электроэнергии, но только в том случае, если сопротивление внутренней электрической цепи $ R_{BT} = const $.
Выражение $I = \frac {U}{R} $ — это закон Ома для участка электрической цепи, к зажимам которого приложено напряжение $U$, что совпадает с электрическим током $I $ этого же участка цепи.
Зависимость напряжения от электрического тока $U (I)$ при $E — const$ и $ R_{BT} = const $ называется внешней (вольтамперной характеристикой линейного источника электроэнергии). По данной характеристике можно определить соответствующее напряжение для любого тока, а по формулам, что приведены ниже, — рассчитать мощность приемника электроэнергии:
$P_2 = RI^2 = \frac {E2R}{(R + R_{BT} )^2}$
Мощность источника электроэнергии:
$P_1 = (R + R_{BT} ) I^2 = \frac {E^2}{R + R_{BT} }$
КПД установки в цепи постоянного тока:
$\eta = \frac {P_2}{P_1} = \frac {R}{R + R_{BT} } = \frac {1}{ 1 +\frac {R_{BT} }{R}} $
Точка Х вольтамперной характеристики источника электроэнергии соответствует режиму холостого хода при разомкнутой электрической цепи. В таком случае электрический ток $l_X = 0$, а напряжение $U_X = E$.
Точка К необходима для того, чтобы охарактеризовать режим короткого замыкания, который возникает при соединении зажимов источников электроэнергии. Внешнее сопротивление приравнивается нулю $R=0$. В этом случае формируется электрический ток короткого замыкания $I_K = \frac {E}{R_{BT} }$, который в несколько раз превышает номинальный ток $I_HOM$. Это случается по причине того, что внутреннее сопротивление источника электроэнергии $R_{BT}
Точка С соответствует согласованному режиму, при котором сопротивление внешней электрической цепи приравнивается сопротивлению внутренней цепи $ R_{BT} $ источника электроэнергии. В таком режиме формируется электрический ток $I_c = \frac {E}{2R_{BT} }$ внешней цепи и отвечает наибольшей мощности $R2_max = \frac {E2}{4R_{BT} }$. Коэффициент полезного действия в таком случае приравнивается нулю: $\eta c = 0$.
Учитывая все вышеизложенное, согласован режим, при котором:
$\frac {P2}{P2_max} = \frac {4R^2}{(R + R_{BT} )^2} = 1$ и $I_c = \frac {E}{2R} = 1$
Режимы электрических цепей в электроэнергетических установках значительно отличаются от согласованного режима и характеризуются токами, которые обуславливают сопротивление приемников $R$ и $ R_{BT} $. В результате этого работа систем на высоком КПД.
Изучение явлений, которые протекают в электрических цепях, упрощается, если происходит их замена на схемы замещения. Эти схемы представлены в виде математических моделей с идеальными элементами. Данные схемы подробно отображают свойства электрической цепи и при соблюдении конкретных условий делают анализ электрического состояния цепей значительно проще.
Электрическая цепь с переменным током
Практически во всех случаях электрическая энергия производится, перераспределяется и потребляется в виде электрической энергии переменного тока.
Замечание 1
Переменный ток нашел широкое применение в различных областях техники. Это все объясняется легкостью его получения, распределения, преобразования, а также простотой устройства двигателей и генераторов переменного тока, удобством их эксплуатации и надежностью работы.
Переменный ток меняет свое направление и значение определенное количество раз в секунду. Электроны при переменном токе движутся сначала в одном направлении вдоль провода, после чего останавливаются на мгновение и движутся в обратную сторону. В проводе электроны совершают колебательные движения. Из-за своей малой скорости ($V_{эл} = 10^{-4} м/с = 0,1 мм/с$) при таких колебаниях электроны успевают сделать лишь небольшие передвижения вдоль провода.
Чаще всего встречается синусоидальный переменный ток: изменение электрических величин (силы тока, электродвижущей силы, напряжения) показывают со временем плавную кривую линию, что называется синусоидой.
Определение 2
Электрические цепи, в которых направление электродвижущей силы, тока и напряжения периодически изменяются по синусоидальному закону, получили название «цепи синусоидального тока». Иногда их называют цепями переменного тока.
Для переменного тока выбирается синусоидальная форма, поскольку она обеспечивает экономное производство, распределение, использование и передачу электрической энергии. Именно переменная форма электрических величин остается неизменной во всех участках цепи. Иными словами, все емкостные и индуктивные элементы, которые входят в состав электрической цепи, не меняют синусоидальной формы напряжения и тока.
Электрические цепи с переменным током, по сравнению с цепями постоянного тока, имеют множество особенностей, которые определяются:
- в первую очередь тем, что в состав электрических цепей переменного тока входят новые элементы: конденсаторы, трансформаторы, индуктивные катушки;
- тем, что переменный ток и напряжение в данных элементах порождают переменные магнитные и электрические поля, которые приводят к формированию явления самоиндукции, токов смещения и взаимной индукции.
Все вышеперечисленные особенности оказывают ощутимое воздействие на процессы, протекающие в электрической цепи. Анализ процессов в таких цепях значительно усложняется. Большое значение для цепи переменного тока играет частота f. От ее значения зависит влияние индуктивностей и емкостей на процессы в электрической цепи.
Особенности цепей переменного тока обуславливают ряд специфических и новых явлений:
- явление резонанса;
- сдвиг фаз;
- возникновение реактивных мощностей.
Цепь постоянного тока
Постоянный ток – такой ток, который с течением времени не меняется ни по величине ни по направлению. (Аналогично постоянное напряжение и эдс).220
Электрическая цепь – совокупность источника энергии, приемника энергии и соединительных проводов.
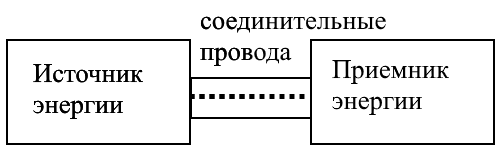
В источниках электрической энергии происходит преобразование различных видов энергии в электрическую.
В приемниках электрической энергии наоборот, электрическая энергия преобразуется в другие виды. Например, в механическую или тепловую.
Соединительные провода в некоторых электрических цепях играют очень важную роль (их диаметр). Правильный выбор проводов обеспечивает надежное и долговременное функционирование схем.
I=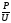 =110/220=0,5A
=110/220=0,5A
I=2200/220=10A
Обязательное условие для протекания электрического тока в цепях это наличие замкнутого контура.
I – ток (сила тока) [A] Ампер
U – напряжение [B] Вольт
R – сопротивление [Oм]
G=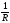 – проводимость [См] Сименс
– проводимость [См] Сименс
E – электро движущая сила ЭДС источника [B] Вольт
P – мощность активная [Вт] Ватт
Ток, напряжение и сопротивление связаны между собой законом Ома
I=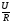 – закон Ома
– закон Ома
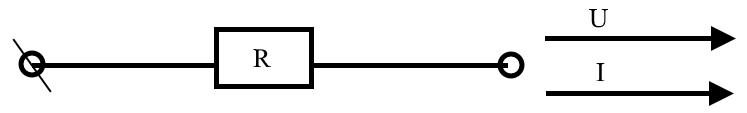
Сила тока, протекающего через сопротивление R прямо пропорционально падению напряжения на нем и обратно пропорционально величине этого сопротивления.
В электрических схемах принято изображать ток протекающем от «+» источника к «-».
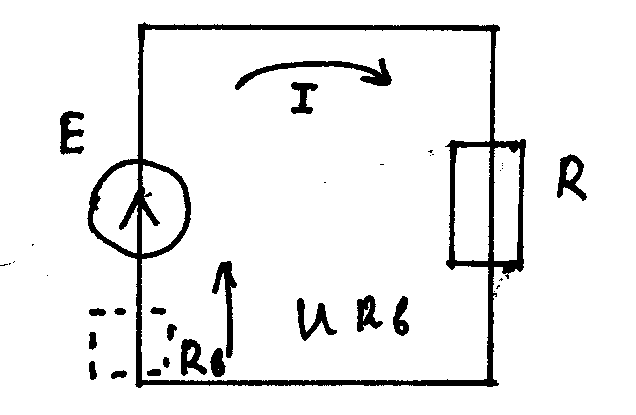
В источнике стрелка показывает направление увеличения потенциала и ток течет от + к – по внешней цепи.
U=I*R
U=E=I*R
В изображенной схеме источник является идеальным, т.е. его внутреннее сопротивление равно 0. Реальные источники всегда имеют внутреннее сопротивление.
Rв – внутреннее сопротивление источника. Оно точно так же ограничивает ток как и сопротивление нагрузки R.
Uрв=I*Rв => U≠E в реальных источниках.
Если в задачах указана величина Rв учитывать ее обязательно и U≠E тем больше, чем больше это Rв.
Замечание.
В изображенных примерах ток и напряжение
совпадают по направлению и равно I=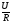
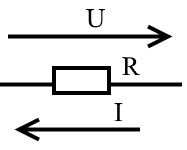
Если ток и напряжение не совпадают, то в формуле появляется знак минус. I= -U/R
Закон Ома для участка цепи с ЭДС
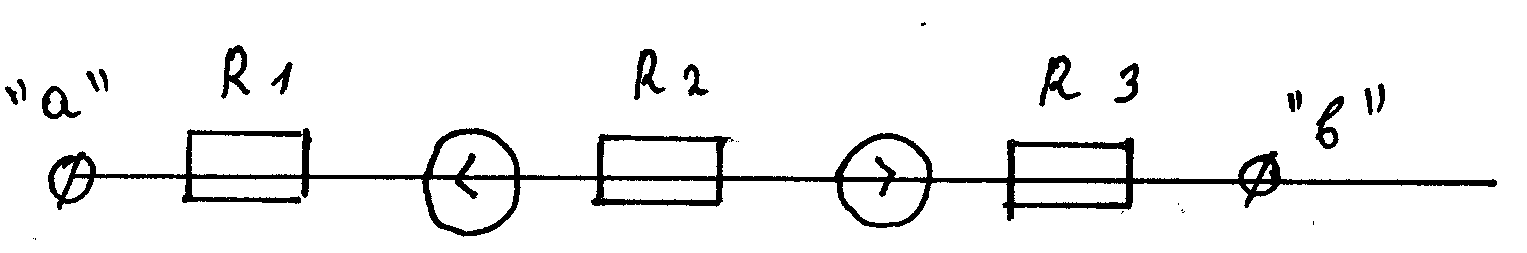
I=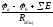
На участке содержащий несколько сопротивлений и источников ток равен дроби в числителе которой находится разность потенциалов взятое по направлению тока и алгебраическая сумма всех ЭДС источников, а в знаменателе общее сопротивление всей ветви.
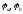 —
потенциалы зажимов ветви “a”
и ‘b’
—
потенциалы зажимов ветви “a”
и ‘b’
E “+” если I и E совпадает по направлению, и “-“ , если не совпадают.
∑ E=E2-E1
Общее сопротивление этой ветви определяется тремя сопротивлениями соединёнными последовательно, а значит их общее сопротивление является суммой этих сопротивлений
Rобщ=R1+R2+R3
I=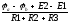
Чаще
всего могут быть заданы не потенциалы
этих узлов, а напряжения на ветви.
Например Uab
совпадающая с направлением тока или
Uba
встречное ему, тогда ток будет равен
I=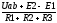
 I=
I=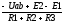
Применение законов Кирхгофа для расчета электрических цепей постоянного тока
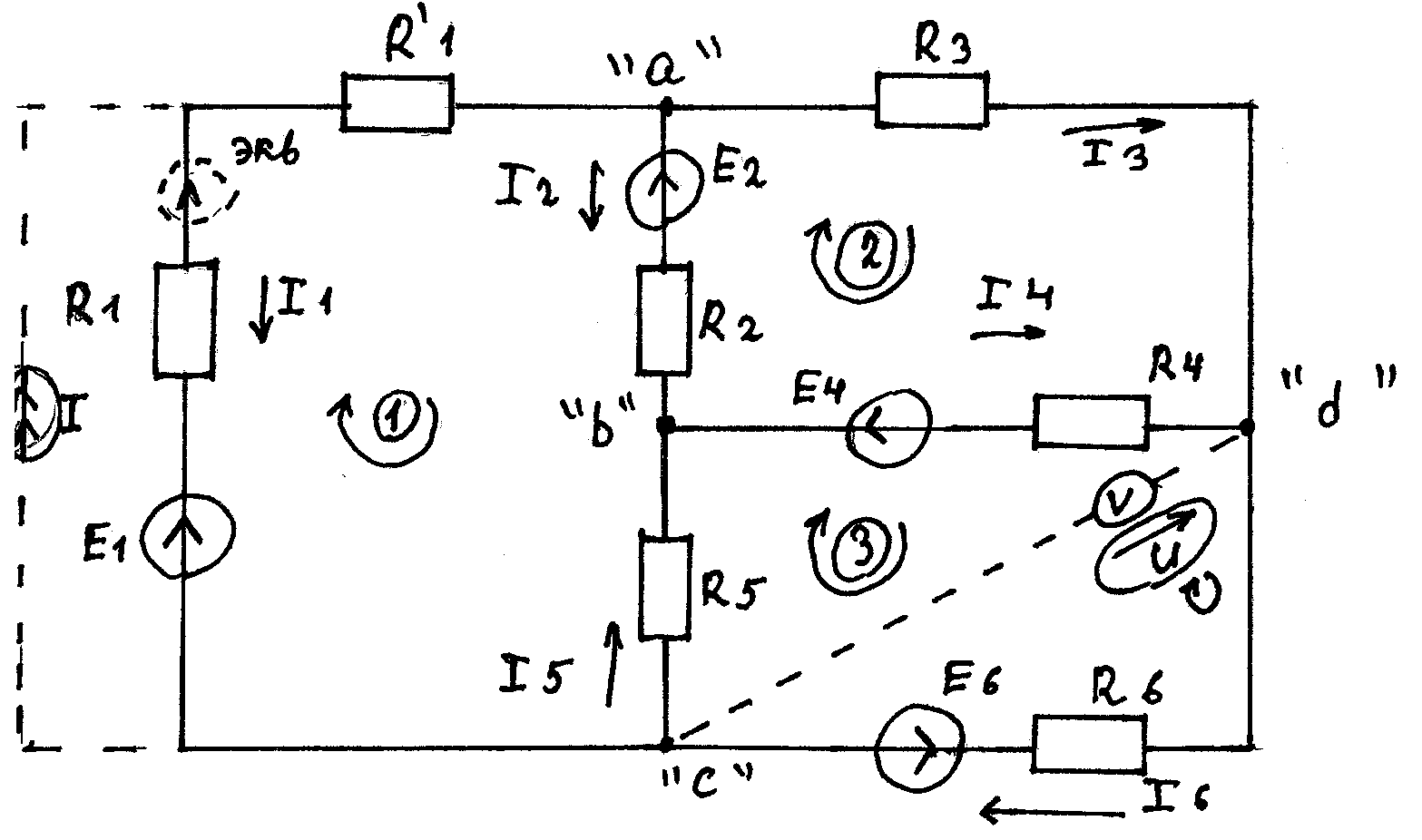
6
ветвей  4
узла
4
узла
Ветвь электрической цепи — это часть схемы, в которой все элементы соединены последовательно или есть один элемент. По всем элементам ветви протекает один и тот же ток. Направления этих токов проставляются произвольно, если изначально они не заданы.
Узел электрической цепи — это точка, в которой соединяется не менее 3 ветвей.
Замкнутым контуром называется контур схемы, ограниченный несколькими ветвями
Электрические цепи переменного тока
Электрическая энергия почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока.
Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации.
Переменный ток, меняет свое значение и направление, определенное число раз в секунду. При переменном токе электроны движутся вдоль провода сначала в одном направлении, затем на мгновение останавливаются, далее движутся в обратную сторону, опять останавливаются и снова повторяют движение вперед и назад. То есть электроны совершают в проводе колебательное движение. Вследствие своей малой скорости движения (Vэл= 10-4м/с = 0,1 мм/с) электроныпри таких колебаниях успевают сделать лишь небольшие перемещения вдоль провода.
Наиболее часто встречается, так называемый синусоидальный переменный ток. Изменение электрических величин (силы тока, напряжения, ЭДС) со временем показывает плавная кривая линия, называемая синусоидой).
Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.
Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии.
Кроме того, именно синусоидальная форма электрических величин остается неизменной во всех участках сколь угодно сложной электрической цепи, то есть индуктивные и емкостные элементы, входящие в состав электрических цепей не изменяют синусоидальной формы тока и напряжения.
Электрические цепи переменного тока по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются:
во-первых, тем, что в состав цепей переменного тока входят новые элементы: трансформаторы, конденсаторы, катушки индуктивности;
во-вторых, тем, что переменные токи и напряжения в этих элементах порождают переменные электрические и магнитные поля, которые в свою очередь приводят к возникновению явления самоиндукции, взаимной индукции и токов смещения.
Все это оказывает существенное влияние на протекающие электрической цепи процессы. Анализ процессов в цепях усложняется.
Для цепи переменного синусоидального тока большое значение имеет частота f. От частоты зависит влияние емкостей и индуктивностей на процессы в цепи.
Особенности цепей синусоидального тока обуславливают ряд новых, специфических для этих цепей явлений: сдвиг фаз, явление резонанса, появление реактивных мощностей.
Коэффициент мощности.
На современных промышленных предприятиях большинство потребителей электрической энергии переменного тока представляют собой активно-индуктивную нагрузку в виде асинхронных электродвигателей, силовых трансформаторов, сварочных трансформаторов, преобразователей и так далее. В такой нагрузке в результате протекания переменного тока индуктируются ЭДСсамоиндукции, обуславливающие сдвиг по фазе между током и напряжением. Этот сдвиг по фазе обычно увеличивается, аcos уменьшается при малой нагрузке. Например, еслиcos двигателей переменного тока при полной нагрузке составляет 0,75 — 0,8, то при малой нагрузке он уменьшается до 0,2 — 0,4.
Если мощность, потребляемая всеми приемниками в данных цепях, является вполне определенной, то при неизменном напряжении на зажимах приемника их ток: I = P / (Ucos )
С уменьшением cos ток нагрузки электростанций и подстанций будет увеличиваться при одной и той же отдаваемой мощности.
Вместе с тем электрические генераторы, трансформаторы и линии электропередачи рассчитываются на определенное напряжение и ток. Увеличение тока потребителя при снижении cosне должно превышать определенных пределов, так как питающие их генераторы рассчитываются на определенную номинальную мощность
cos, характеризующий использование установленной мощности, часто называют коэффициентом мощности.
Коэффициентом мощности определяют как отношение активной мощности к полной:
cos = P/S.
(2.71)
2.25 Коэффициент мощности (Адрес Блок 4) Коэффициентом мощности определяют как отношение активной мощности к полной:cos = P/S. Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы. |
Коэффициент мощности (2.25)показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы. Нормальным считаетсяcos 0,85 — 0,9. При низком коэффициенте мощности на предприятия, потребляющие электроэнергию, накладывается штраф, при высоком — предприятия премируются.
Для улучшения коэффициента мощности проводится ряд мероприятий:
2.заменяются двигатели переменного тока, нагруженные относительно мало, двигателями меньшей мощности;
2.включаются параллельно приемникам конденсаторы.
1_Эл_цепи постоянного тока
Электротехника, электроника и электропривод
Лекция 1. Электрические цепи постоянного тока
Основные понятия и определения
Электрическая цепь – совокупность устройств и объектов, электромагнитные процессы в которых могут быть описаны с помощью таких понятий, как электродвижущая сила (ЭДС), ток, напряжение, сопротивление.
Элемент электрической цепи – отдельное устройство, входящее в состав электрической цепи и выполняющее в ней определенную функцию.
Основные элементы электрической цепи – источники и приемники электроэнергии.
В источниках электроэнергии различные виды энергии (химическая – в гальванических элементах; механическая – в генераторах; световая; тепловая) преобразуются в электромагнитную или электрическую.
В приемниках электроэнергии электромагнитная энергия преобразуется в другие виды энергии (химическую – гальванические ванны; тепловую – нагревательные приборы; механическую – электрические двигатели).
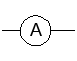
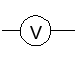
Вспомогательные элементы электрической цепи – резисторы, емкости, индуктивности, выключатели, предохранители, измерительные приборы.
Условные графические обозначения:
источник напряжения или ЭДС | гальванический элемент | выключатель |
| | |
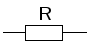
резистор | емкость | индуктивность |
| | |
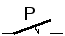
амперметр | вольтметр | |
| |
Электрические цепи принято изображать в виде различных схем, на которых показываются основные и вспомогательные элементы и их соединения. Различают монтажные, принципиальные схемы и схемы замещения.
На монтажных схемах изображают рисунок (эскиз) элементов цепи и соединения проводов, на принципиальных — условное графическое изображение элементов и схему их соединения. Схема замещения – расчетная модель электрической цепи. На ней реальные элементы заменяются идеальными и исключаются все элементы, не влияющие на результаты расчета.
Классификация электрических цепей
По виду тока (рис. 1):
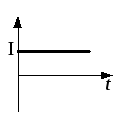
а) цепи постоянного тока – электрический ток не изменяется во времени;
б) цепи переменного тока:
а) постоянный ток | б) переменный синусоидальный ток |
| |
в) переменный несинусоидальный ток | |
Рис. 1
По характеру параметров элементов:
а) линейные цепи – цепи, у которых сопротивления не зависят от значений и направлений токов;
б) нелинейные.
В зависимости от наличия или отсутствия источника электроэнергии:
а) активные – содержащие источники электроэнергии;
б) пассивные.
Топологические понятия теории электрических цепей
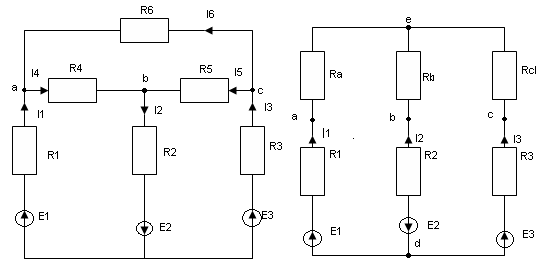
Топологические понятия электрических цепей рассмотрим на примере схемы рис. 2.
Ветвь электрической цепи – участок, элементы которого соединены друг за другом, т.е. последовательно. Ток в элементах один и тот же (adc, aeb).
Узел электрической цепи – место соединения ветвей (a,b,c).
Контур – любой замкнутый путь вдоль ветвей электрической цепи (cbadc, dabcd).
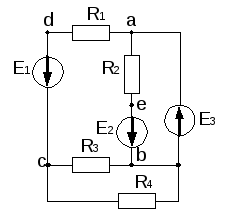
Рис. 2
Основные законы электрических цепей постоянного тока
Электрические цепи постоянного тока — цепи, в которых протекает электрический ток, не изменяющийся во времени ни по величине, ни по направлению. В электрических цепях действуют следующие основные законы: закон Ома и I и II законы Кирхгофа
Закон Ома.
а) Закон Ома для участка цепи без
источника. Сила тока на участке
электрической цепи прямо пропорциональна
напряжению на концах этого участка и
обратно пропорциональна сопротивлению
этого участка (рис. 3): 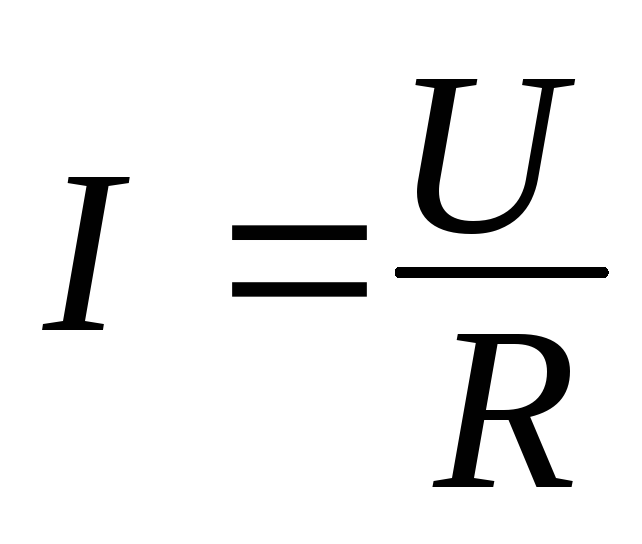
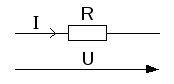
Рис. 3
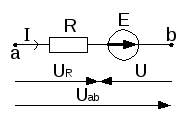
б) Обобщенный закон Ома (для участка цепи с ЭДС) (рис. 4):
а) | б) |
Рис. 4 | |
Если направление тока в ветви совпадает с направлением ЭДС источника (рис. 4а), то
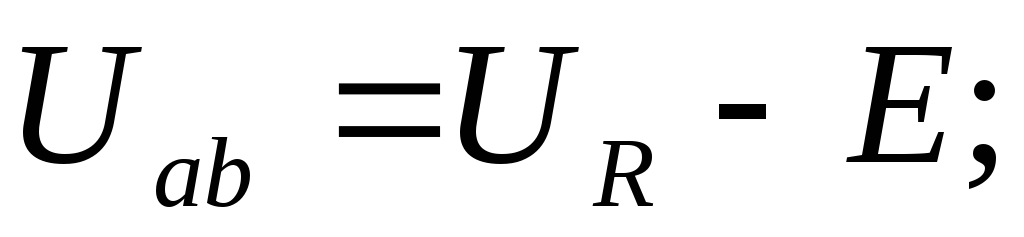
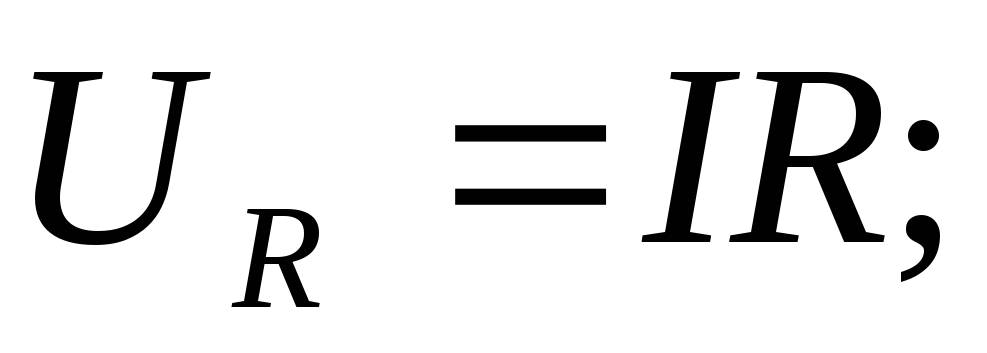
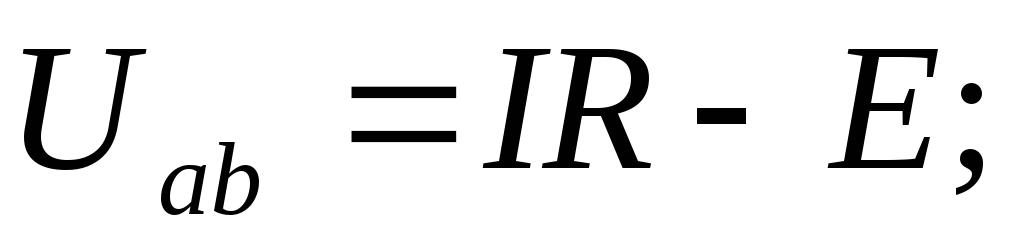
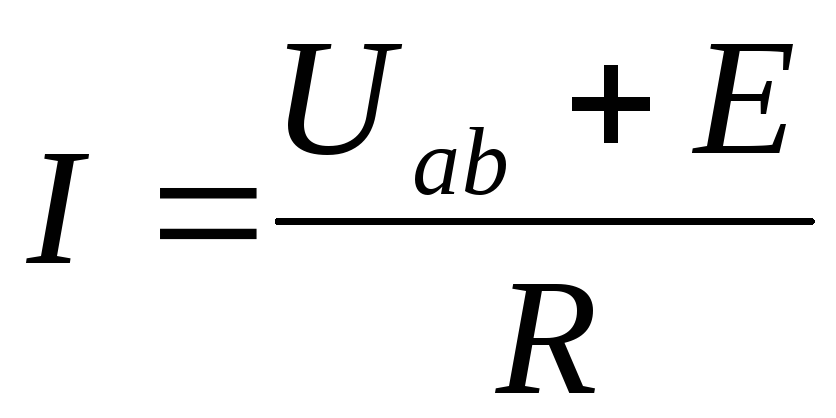 .
.
Если направление тока в ветви не совпадает
с направлением ЭДС источника (рис. 4б),
то 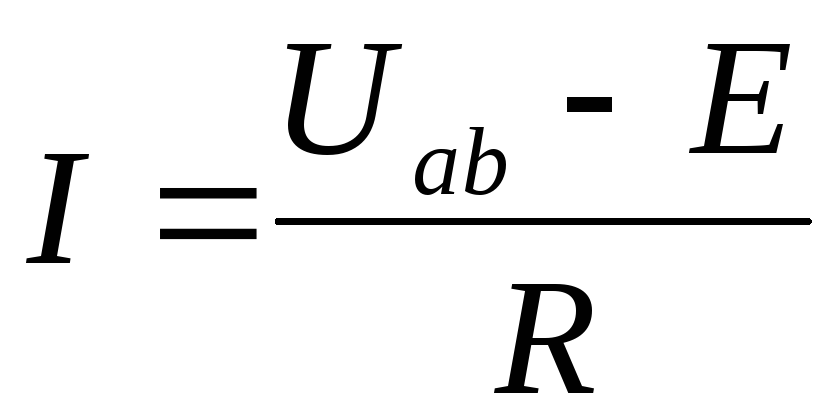 .
.
Законы Кирхгофа (рис. 5).
а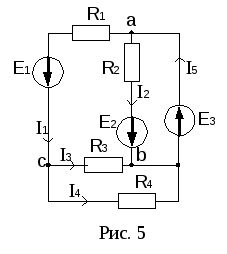 )
I закон Кирхгофа:
алгебраическая сумма токов в узле
электрической цепи равна нулю, при этом
токи, одинаково направленные относительно
узла, записываются с одинаковым знаком.
)
I закон Кирхгофа:
алгебраическая сумма токов в узле
электрической цепи равна нулю, при этом
токи, одинаково направленные относительно
узла, записываются с одинаковым знаком.
Для узла а: 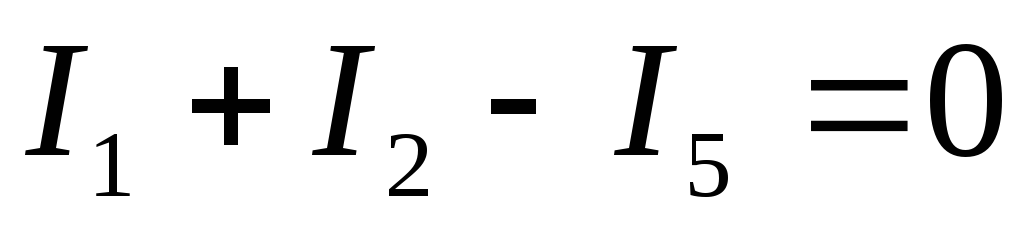 .
.
б) II закон Кирхгофа: алгебраическая сумма падений напряжений любого контура равна алгебраической сумме ЭДС этого контура.
Правило знаков: падения напряжения записываются со знаком «+», если направления тока совпадает с направлением обхода контура; ЭДС записываются со знаком «+», если направления ЭДС и обхода контура совпадают.
Рассмотрим схему электрической цепи, приведенную на рис. 5. Направление обхода контура abca выберем по часовой стрелке. Тогда уравнение II закона Кирхгофа будет иметь следующий вид:
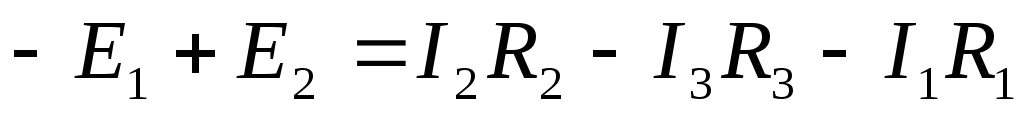 .
.
Баланс мощности.
Мощность характеризует интенсивность преобразования энергии одного вида в другой за единицу времени.
Для
цепи постоянного тока мощность источника: 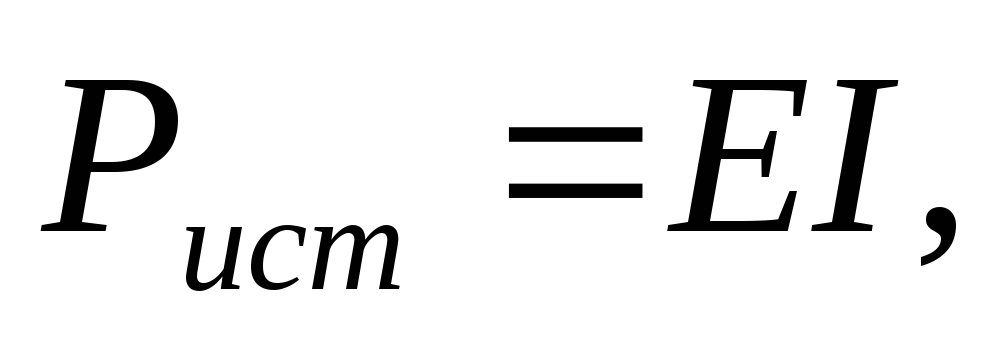 а приемника —
а приемника — 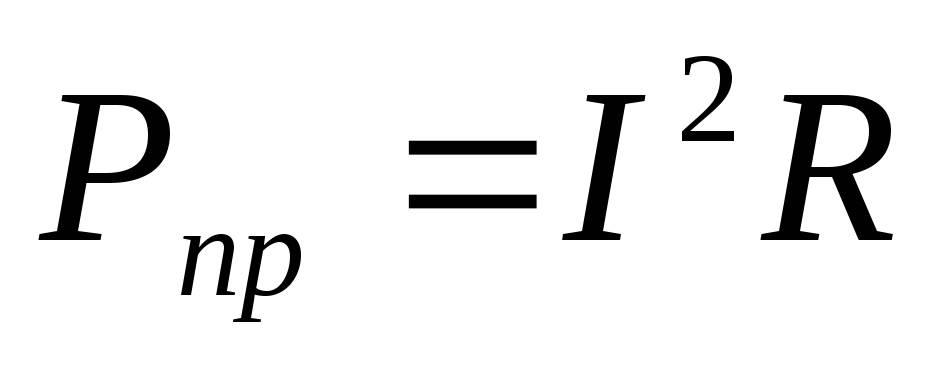 ,
(
,
( =Вт).
На основании закона сохранения энергии
мощность, развиваемая источниками
электроэнергии, должна быть равна сумме
мощностей всех приемников и потерь в
источниках из-за внутренних сопротивлений.
При этом: если направление ЭДС и тока
совпадают, то EI в сумме записываются со знаком «+». Для
схемы рис. 5 при выбранных направлениях
токов:
=Вт).
На основании закона сохранения энергии
мощность, развиваемая источниками
электроэнергии, должна быть равна сумме
мощностей всех приемников и потерь в
источниках из-за внутренних сопротивлений.
При этом: если направление ЭДС и тока
совпадают, то EI в сумме записываются со знаком «+». Для
схемы рис. 5 при выбранных направлениях
токов:
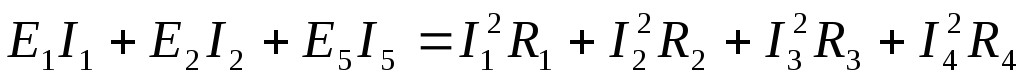 .
.
М етоды
расчета электрических цепей
етоды
расчета электрических цепей
Постановка задачи: в известной схеме цепи с заданными параметрами необходимо рассчитать токи, напряжения, мощности на отдельных участках. Для этого можно использовать следующие методы:
преобразования цепи;
непосредственного применения законов Кирхгофа;
контурных токов;
узловых потенциалов;
наложения;
эквивалентного генератора.
Будем рассматривать первых два метода.
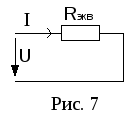
Метод преобразования цепи. Суть метода: если несколько последовательно или (и) параллельно включенных сопротивлений заменить одним, то распределение токов в электрической цепи не изменится.
а) Последовательное соединение резисторов. Сопротивления включены таким образом, что начало следующего сопротивления подключается к концу предыдущего (рис. 6).
Ток во всех последовательно соединенных элементах одинаков.
З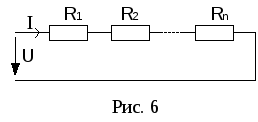 аменим
все последовательно соединенные
резисторы одним эквивалентным
аменим
все последовательно соединенные
резисторы одним эквивалентным  (рис. 7.).
(рис. 7.).
По II закону Кирхгофа:
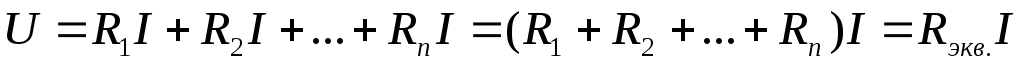 ;
;
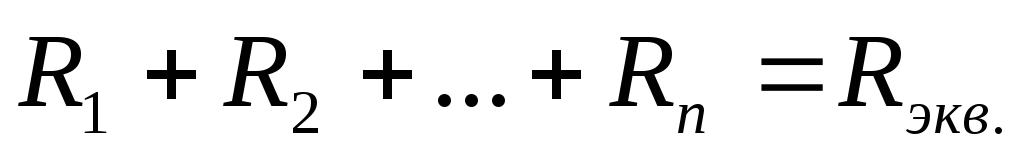 ;
;
т.е. при последовательном соединении резисторов эквивалентное сопротивление участка цепи равно сумме всех последовательно включенных сопротивлений.
б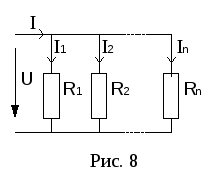 )
Параллельное соединение резисторов.
При этом соединении соединяются вместе
одноименные зажимы резисторов (рис. 8).
)
Параллельное соединение резисторов.
При этом соединении соединяются вместе
одноименные зажимы резисторов (рис. 8).
Все элементы присоединяются к одной паре узлов. Поэтому ко всем элементам приложено одно и тоже напряжение U.
По I закону Кирхгофа: 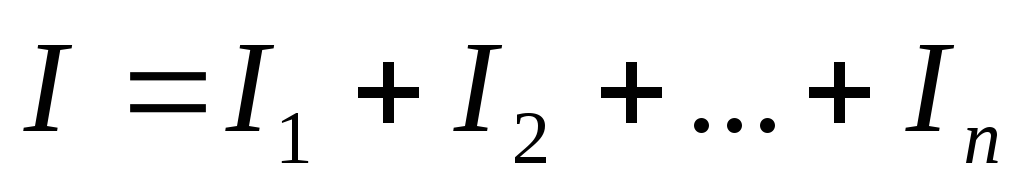 .
.
По
закону Ома 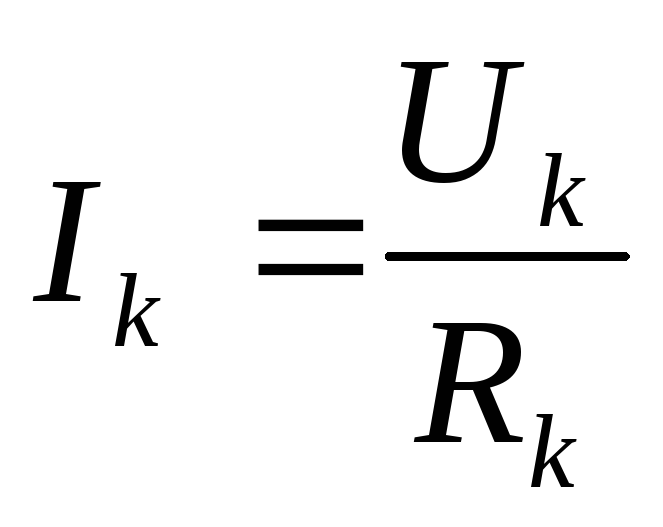 .
Тогда
.
Тогда 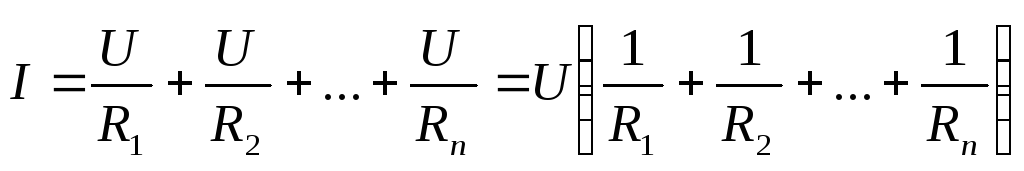 .
.
Для
эквивалентной схемы (см рис. 7): 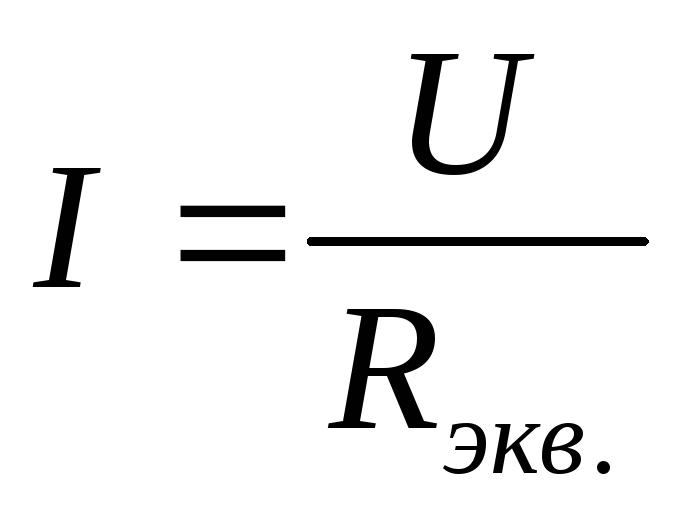 ;
; 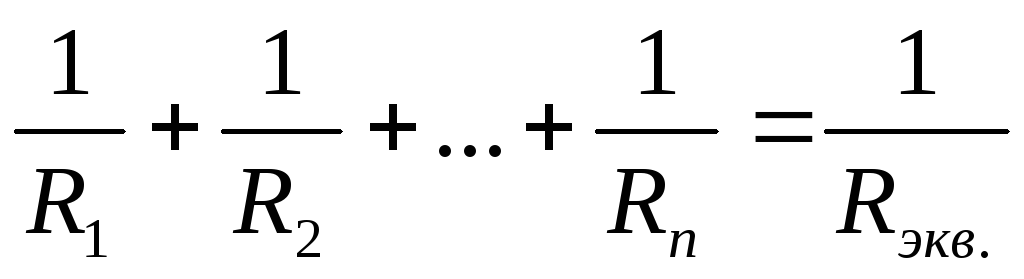 .
.
Величина 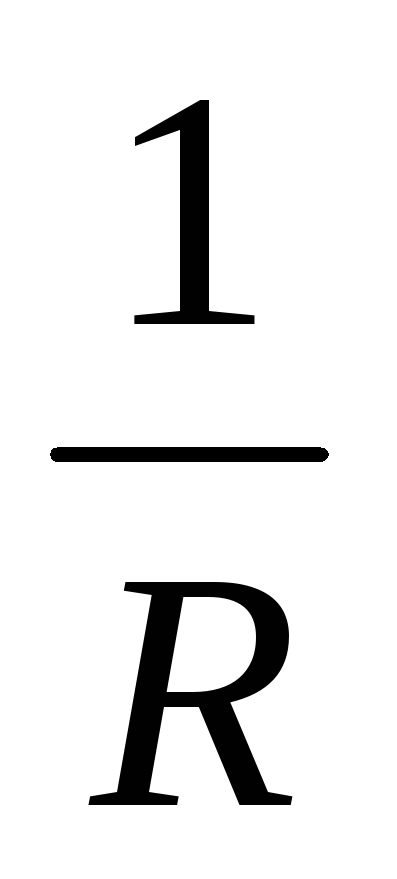 ,
обратная сопротивлению, называется
проводимостью G.
,
обратная сопротивлению, называется
проводимостью G.
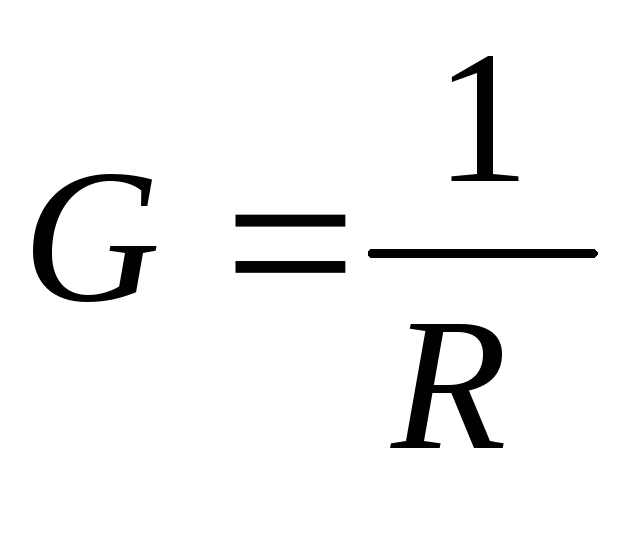 ;
; 
 =
Сименс (См).
=
Сименс (См).
Ч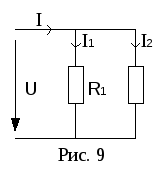 астный
случай: параллельно соединены два
резистора (рис. 9).
астный
случай: параллельно соединены два
резистора (рис. 9).
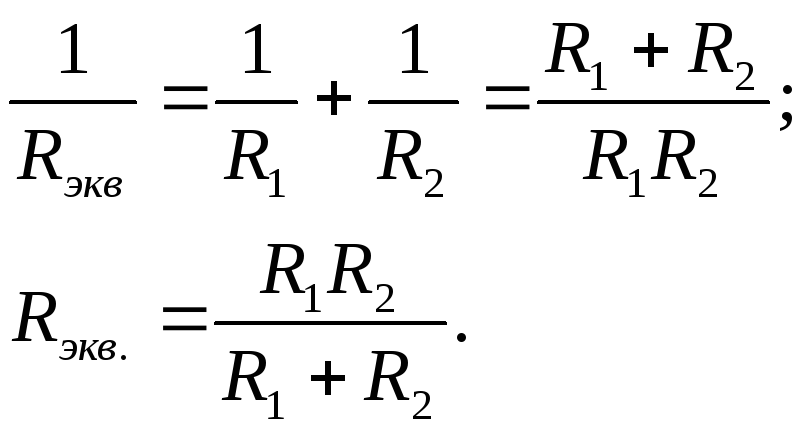


в) Взаимное преобразование звезды (рис.10а) и треугольник сопротивлений (рис. 10б).
— преобразование звезды сопротивлений в треугольник:
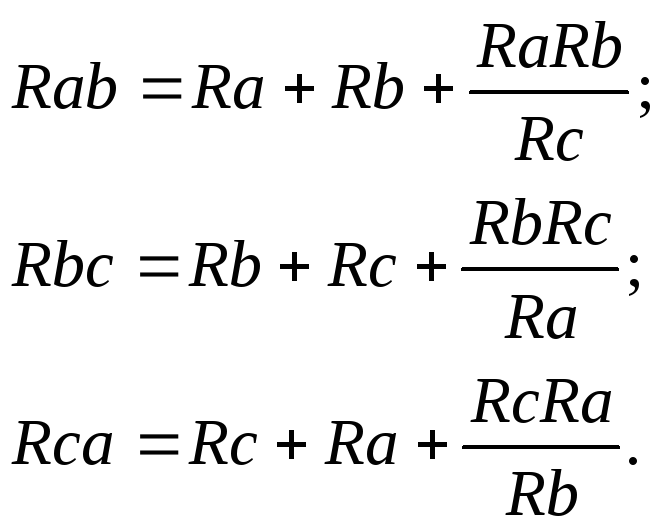
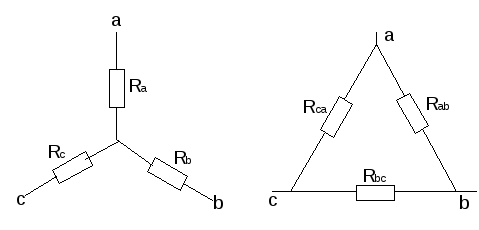
— преобразование «треугольника» сопротивлений в «звезду»:
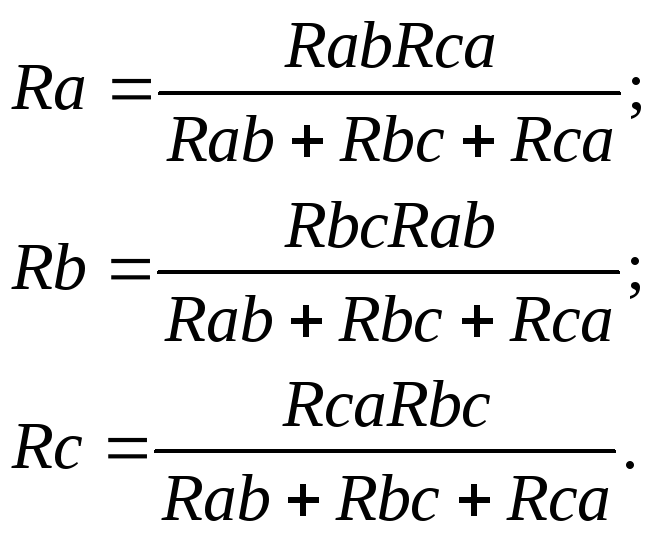
Метод непосредственного применения законов Кирхгофа. Порядок расчета:
Определить число ветвей (т.е. токов) и узлов в схеме.
Произвольно выбрать условно-положительные направления токов. Общее число уравнений должно быть равно числу неизвестных токов.
Определить, сколько уравнений должно быть составлено по I закону Кирхгофа, а сколько — по II закону Кирхгофа.
Составить уравнения для
 узлов
по I закону Кирхгофа и
для
узлов
по I закону Кирхгофа и
для  независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — по II
закону Кирхгофа.
независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — по II
закону Кирхгофа.Решить система уравнений относительно токов. Если в результате ток получился отрицательным, то его действительное направление противоположно выбранному.
Проверить правильность решения задачи, составив уравнение баланса мощности и смоделировав электрическую цепь средствами моделирующего пакета Electronics Workbench.
Примечание: если есть возможность, то перед составлением системы уравнений по законам Кирхгофа, следует преобразовать «треугольник» сопротивлений в соответствующую «звезду».
Закон Ома для полной цепи переменного тока. | |
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае:
|
|
| |
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: |
|
Сдвиг фаз в цепи переменного тока определяется характером нагрузки:
|
|
Мощность в цепи переменного тока. | |
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): |
|
или, переходя к действующим значениям, |
|
Величина |
коэффициент мощности |
Резонанс в электрической цепи. | |
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии
|
|
Следовательно, |
|
Амплитуды колебаний напряжения на индуктивности и емкости будут равны и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
Следовательно, |
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением |
|
При этом если величина то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! |
|
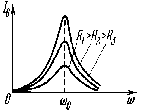
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. | |
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа |
|
В случае резонанса |
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.). |
|
Referat. Переменный ток — PhysBook
Переменный ток
Как известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток.
Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток.
Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника
или
Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.
Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:
\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,где u – мгновенное значение напряжения, Um – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае
\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,где φc – разность (сдвиг) фаз между колебаниями силы тока и напряжения.
Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.
Резистор в цепи переменного тока
Пусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление R называется активным потому, что, только на нем выделяется энергия, т.е.
Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением.
Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 1).
Рис. 1
Пусть напряжение на концах цепи меняется по гармоническому закону
\(~u = U_m \cdot \sin \omega t\) .Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:
\(~i = \frac{U}{R} = \frac{U_m \cdot \sin \omega t}{R} = I_m \cdot \sin \omega t\) .Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление:
Рис. 2
При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока.
Катушка в цепи переменного тока
Индуктивность влияет на силу переменного тока в цепи. Это можно обнаружить с помощью простого опыта. Составим цепь из катушки большой индуктивности и лампы накаливания (рис. 3). С помощью переключателя можно присоединять эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть одинаковы. Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы тока в рассматриваемой цепи меньше силы постоянного тока.
Рис. 3
Объясняется это самоиндукцией. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь по прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех установившихся значений, которые она приобрела бы с течением времени при постоянном напряжении, равном максимальному значению переменного напряжения. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью L цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.
Докажем это математически. Пусть в цепь переменного тока включена идеальная катушка с электрическим сопротивлением провода, равным нулю (рис. 4). При изменениях силы тока по гармоническому закону
\(~i = I_m \cdot \cos \omega t\) .в катушке возникает ЭДС самоиндукции
\(~e = -L \cdot i’ = I_m \cdot L \cdot \omega \cdot \sin \omega t\) ,где L – индуктивность катушки, ω – циклическая частота переменного тока.
Рис. 4
Так как электрическое сопротивление катушки равно нулю, то ЭДС самоиндукции в ней в любой момент времени равна по модулю и противоположна по знаку напряжению на концах катушки, созданному внешним генератором:
\(~u = -e = -I_m \cdot L \cdot \omega \cdot \sin \omega t\) .Следовательно, при изменении силы тока в катушке по гармоническому закону напряжение на ее концах изменяется тоже по гармоническому закону, но со сдвигом фазы:
\(~u = I_m \cdot L \cdot \omega \cdot \cos (\omega t + \frac{\pi}{2})\) .Следовательно, колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (рис. 5). В момент, когда напряжение становится равным нулю, сила тока максимальна по модулю.
Рис. 5
Произведение \(I_m \cdot L \cdot \omega\) является амплитудой колебаний напряжения на катушке:
\(~U_m = I_m \cdot L \cdot \omega\) .Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний силы тока в ней называется индуктивным сопротивлением (обозначается XL):
\(~X_L = \frac{U_m}{I_m} = L \cdot \omega\) .Связь амплитуды колебаний напряжения на концах катушки с амплитудой колебаний силы тока в ней совпадает по форме с выражением закона Ома для участка цепи постоянного тока:
\(~I_m = \frac{U_m}{X_L}\) .В отличие от электрического сопротивления проводника в цепи посто-янного тока, индуктивное сопротивление не является постоянной величиной, характеризующей данную катушку. Оно прямо пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в катушке при постоянном значении амплитуды колебаний напряжения должна убывать обратно пропорционально частоте. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю (XL = 0).
Зависимость амплитуды колебаний силы тока в катушке от частоты приложенного напряжения можно наблюдать в опыте с генератором пере-менного напряжения, частоту которого можно изменять. Опыт показывает, что увеличение в два раза частоты переменного напряжения приводит к уменьшению в два раза амплитуды колебаний силы тока через катушку.
Конденсатор в цепи переменного тока
Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.
При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения.
Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.
Рис. 6
Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону
\(~u = U_m \cdot \cos \omega t\) ,заряд на его обкладках изменяется по закону:
\(~q = C \cdot u = U_m \cdot C \cdot \cos \omega t\) .Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону:
\(~i = -U_m \cdot \omega \cdot C \cdot \sin \omega t = U_m \cdot \omega \cdot C \cdot \cos (\omega t + \frac{\pi}{2})\) .Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на π/2 или колебания силы тока опережают по фазе колебания напряжения на π/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д.
Рис. 7
Произведение \(U_m \cdot \omega \cdot C\) является амплитудой колебаний силы тока:
\(~I_m = U_m \cdot \omega \cdot C\) .Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается ХC):
\(~X_C = \frac{U_m}{I_m} = \frac{1}{\omega \cdot C}\) .Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора:
\(~I_m = \frac{U_m}{X_C}\) .Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.
Закон Ома для электрической цепи переменного тока
Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки (рис. 8). Если к выводам этой электрической цепи приложить электрическое напряжение, изменяющееся по гармоническому закону с частотой ω и амплитудой Um, то в цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой Im. Установим связь между амплитудами колебаний силы тока и напряжения.
Рис. 8
В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения:
\(~u = u_R + u_L + u_C\) . (1)Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону:
\(~i = I_m \cdot \cos \omega t\) . (2)Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, а колебания напряжения на катушке опережают по фазе колебания силы тока на π/2. Поэтому уравнение (1) можно записать так:
\(~u = U_{Rm} \cdot \cos \omega t + U_{Lm} \cdot \cos (\omega t + \frac{\pi}{2}) + U_{Cm} \cdot \cos (\omega t — \frac{\pi}{2})\) , (3)где URm, UCm и ULm – амплитуды колебаний напряжения на резисторе, конденсаторе и катушке.
Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм.
При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения URm, совпадает по направлению с вектором, изображающим амплитуду силы тока Im. Колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, поэтому вектор \(~\vec U_{Cm}\) отстает от вектора \(~\vec I_{m}\) на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на π/2, поэтому вектор \(~\vec U_{Lm}\) опережает вектор \(~\vec I_{m}\) на угол 90° (рис. 9).
Рис. 9
На векторной диаграмме мгновенные значения напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) , вращающихся с одинаковой угловой скоростью ω против часовой стрелки. Мгновенное значение напряжения во всей цепи равно сумме мгновенных напряжений uR, uC и uL на отдельных элементах цепи, т. е. сумме проекций векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) на горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов:
\(~\vec U_m = \vec U_{Rm} + \vec U_{Cm} + \vec U_{Lm}\) .Из рисунка 9 видно, что амплитуда напряжений на всей цепи равна
\(~U_m = \sqrt{U^2_{Rm} + (U_{Lm} — U_{Cm})^2}\) , (4)или
\(~U_{m} = \sqrt{(I_m R)^2 + (I_m X_L — I_m X_C)^2} = I_m \cdot \sqrt{R^2 + (X_L — X_C)^2} = I_m \cdot \sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}\) .Отсюда
\(~I_m = \frac{U_m}{\sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}}\) . (5)Введя обозначение для полного сопротивления цепи переменного тока
\(~Z = \sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}\) , (6)выразим связь между амплитудными значениями силы тока и напряжения в цепи переменного тока следующим образом:
\(~I_m = \frac{U_m}{Z}\) . (7)Это выражение называют законом Ома для цепи переменного тока.
Из векторной диаграммы, приведенной на рисунке 9, видно, что фаза колебаний полного напряжения равна ω∙t + φ. Поэтому мгновенное значение полного напряжения определяется формулой:
\(~u = U_m \cdot \cos (\omega t + \varphi)\) . (8)Начальную фазу φ можно найти из векторной диаграммы:
\(~\cos \varphi = \frac{U_{Rm}}{U_m} = \frac{I_m \cdot R}{I_m \cdot \sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}} = \frac{R}{Z}\) . (9)Величина cos φ играет важную роль при вычислении мощности в электрической цепи переменного тока.
Мощность в цепи переменного тока
Мощность в цепи постоянного тока определяется произведением напряжения на силу тока:
\(~P = U \cdot I\) .Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U∙I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой:
\(~p = u \cdot i\) .Пусть напряжение на концах цепи меняется по гармоническому закону
\(~u = U_m \cdot \cos \omega t\)(с тем же успехом, разумеется, вместо \(~u = U_m \cdot \cos \omega t\) можно было бы записать \(~u = U_m \cdot \sin \omega t\)), то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения:
\(~i = I_m \cdot \cos (\omega t + \varphi_c)\) ,где φc – сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать:
\(~p = u \cdot i = U_m \cdot I_m \cdot \cos \omega t \cdot \cos (\omega t + \varphi_c)\) .При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период.
Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов:
\(~\cos \alpha \cdot \cos \beta = \frac{\cos (\alpha — \beta) + \cos (\alpha + \beta)}{2}\) .В рассматриваемом случае α = ω∙t и β = ω∙t + φc. Поэтому
\(~p = \frac{U_m \cdot I_m}{2} [\cos \varphi_c + \cos (2 \omega t + \varphi_c)] = \frac{U_m \cdot I_m}{2} \cos \varphi_c + \frac{U_m \cdot I_m}{2} \cos (2 \omega t + \varphi_c)\) .Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю. Следовательно, средняя мощность Р за период равна первому члену, не зависящему от времени:
\(~P = \frac{U_m \cdot I_m}{2} \cos \varphi_c\) . (10)При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно:
\(~P = \frac{U_m \cdot I_m}{2} = \frac{I^2_m \cdot R}{2}\) .Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = I∙U = I2∙R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим
\(~P = \frac{I^2_m \cdot R}{2} =I^2 \cdot R\) или \(~\frac{I^2_m}{2} =I^2\) .Действующим значением силы тока называют величину, в \(~\sqrt{2}\) раз меньшую ее амплитудного значения:
\(~I = \frac{I_m}{\sqrt{2}}\) .Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.
Аналогично можно доказать, что
действующее значение переменного напряжения в \(~\sqrt{2}\) раз меньше его амплитудного значения:
\(~U = \frac{U_m}{\sqrt{2}}\) .Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать:
\(~P = \frac{U_m}{\sqrt{2}} \cdot \frac{I_m}{\sqrt{2}} \cos \varphi_c = U \cdot I \cos \varphi_c\) . (10)Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φc между напряжением и током. Множитель cos φc в формуле называется коэффициентом мощности.
В случае, когда φc = ± π/2 , энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при φc = — π/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.
Рис. 10
Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит.
При проектировании цепей переменного тока нужно добиваться, чтобы cos φc не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов.
Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φc в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φc является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φc < 0,85.
Литература
- Мякишев Г.Я., Синяков А.З. Физика: Колебания и волны. 11 кл.: Учеб. для углубленного изучения физики. – М.: Дрофа, 2002. – 288 с.
- Физика: Учеб. пособие для 11 кл. шк. и классов с углубл. изуч. физики / А.Т. Глазунов, О.Ф. Кабардин, А.Н. Малинин и др.; Под ред. А.А. Пинского. – М.: Просвещение, 1995.– 432 с.


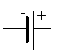
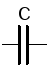
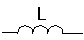
 етоды
расчета электрических цепей
етоды
расчета электрических цепей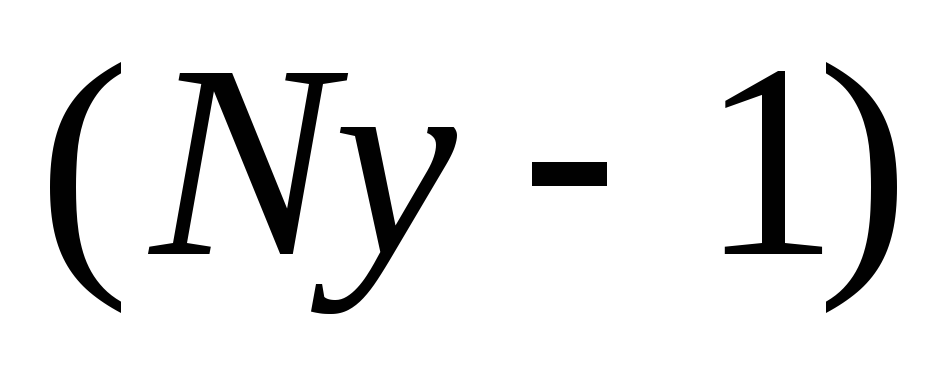 узлов
по I закону Кирхгофа и
для
узлов
по I закону Кирхгофа и
для 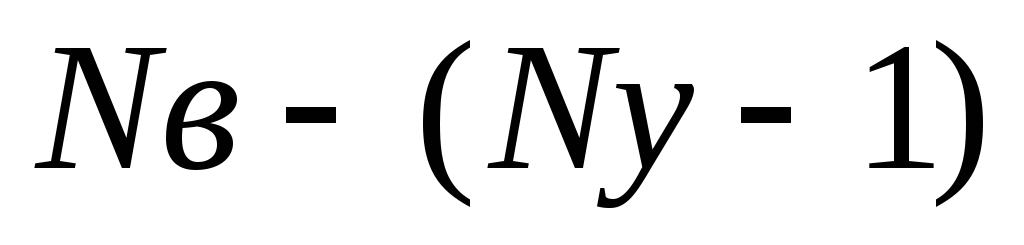 независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — по II
закону Кирхгофа.
независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — по II
закону Кирхгофа.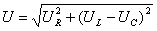
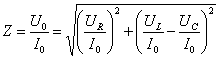 — полное сопротивление переменному току.
— полное сопротивление переменному току.
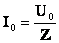
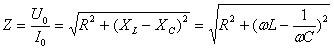 .
.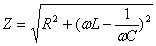
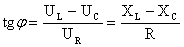 или
или 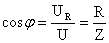 .
.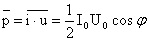
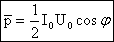
 .
.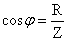 наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач.
наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач.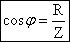
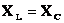 или
или 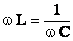 .
.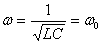 — т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.
— т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.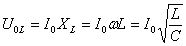
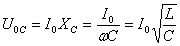
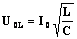
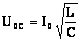
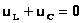 .
.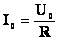 . В этом и состоит смысл явления резонанса.
. В этом и состоит смысл явления резонанса. ,
,
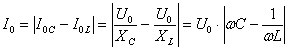 .
.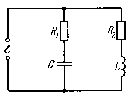
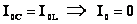 . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.
. Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.