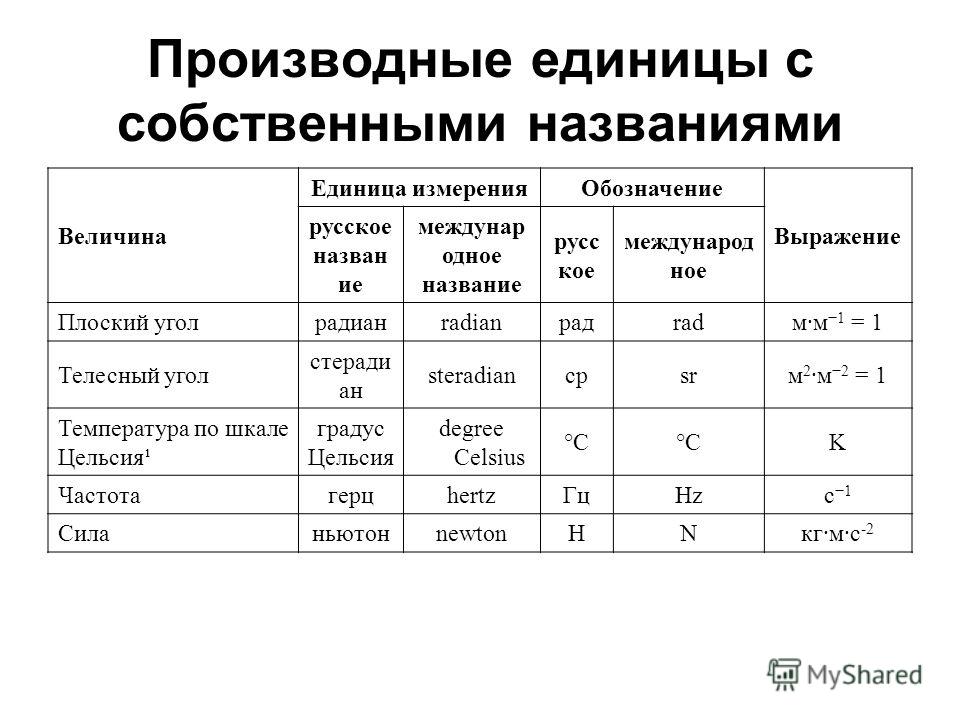
Формулы по физике 10 класса. Все формулы по физике за 10 класс с пояснениями и определениями

Закон	Формула	Определение	Единицы измерения
МЕХАНИКА
Вычисление перемещения	АВ2 = АС2 + ВС2	Перемещение – вектор, соединяющий начальную точку движения тела с его конечной точкой.
Проекция вектора перемещения	Sx = x2 – x1		x1 – начальная координата, [м] x2 – конечная координата, [м] Sx – перемещение, [м]
Формула расчета скорости движения тела	v = s/t	Скорость – физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло.	v – скорость, [м/с] s – путь, [м] t – время, [c]
Уравнение движения	x = x0 + Vxt		x0– начальная координата, [м] x – конечная координата, [м] v – скорость, [м/с] t – время, [c]
Формула для вычисления ускорения движения тела	a ⃗ = v ⃗- v0⃗ /t	Ускорение – физическая величина, которая характеризует быстроту изменения скорости.	a – ускорение, [м/с2] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] t – время, [c]
Уравнение скорости	v ⃗ = v0 ⃗ + a ⃗t		v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Уравнение Галилея	S = v0t + at2 / 2		S – перемещение, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Закон изменения координаты тела при прямолинейном равноускоренном движении	x = x0 + v0t + at2/2		x0 – начальная координата, [м] x – конечная координата, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Первый закон Ньютона		Если на тело не действуют никакие тела либо их действие скомпенсировано, то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно.
Второй закон Ньютона	a= F ⃗ / m	Ускорение, приобретаемое телом под действием силы, прямо пропорционально величине этой силы и обратно пропорционально массе тела.	a – ускорение, [м/с2] F – сила, [Н] m – масса, [кг]
Третий закон Ньютона	|F1⃗ |=|F2⃗| F1⃗ = -F2⃗	Сила, с которой первое тело действует на второе, равна по модулю и противоположна по направлению силе, с которой второе тело действует на первое.	F – сила, [Н]
Формула для вычисления высоты, с которой падает тело	H = g*t2/2		Н – высота, [м] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления высоты при движении вертикально вверх	h=v0t -gt2/2		h – высота, [м] v0 – начальная скорость, [м/с] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления веса тела при движении вверх с ускорением	P = m (g + a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2]
Формула для вычисления веса тела при движении вниз с ускорением	P = m (g – a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2]
Формула закона всемирного тяготения	F = Gm1m2/r2	Закон всемирного тяготения: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.	F – сила, [Н] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная m – масса тела, [кг] r – расстояние между телами, [м]
Формула расчета ускорения свободного падения на разных планетах	g = GMпл/Rпл2		g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная M – масса планеты, [кг] R – радиус планеты, [м]
Формула расчета ускорения свободного падения	g = GMз/(R з+H)2		g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная M – масса Земли, [кг] R – радиус Земли, [м] Н – высота тела над Землей, [м]
Формула расчета центростремительного ускорения	а = υ2/r		a – центростремительное ускорение, [м/с2] v – скорость, [м/с] r – радиус окружности, [м]
Формула периода движения по окружности	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота вращения, [с-1] t – время, [с] N – число оборотов
Формула расчета угловой скорости	ω = 2π/T = 2πν =υr		ω – угловая скорость, [рад/с] υ – линейная скорость, [м/с] Т – период, [с] ν – частота вращения,[с-1] r – радиус окружности, [м]
Формула импульса тела	p = mv	Импульсом называют произведение массы тела на его скорость.	p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость, [м/с]
Формула закона сохранения импульса	p1 + p2 =p1’ + p2’ m1 v + m2u = m1v’ + m1u’
Формула импульса силы	P = Ft		p – импульс тела, [кг·м/с] F – сила, [Н] t – время, [c]
Формула механической работы	A = Fs	Механическая работа – физическая величина, равная произведению модуля силы на величину перемещения тела в направлении действия силы.	A – работа, [Дж] F – сила, [Н] s – пройденный путь, [м]
Формула расчета мощности	N = A/t	Мощность – физическая величина, характеризующая быстроту совершения механической работы.	N – мощность, [Вт] A – работа, [Дж] t – время, [c]
Формула для нахождения коэффициента полезного действия (КПД)	η = Aп/Aз∙ 100%	КПД – отношение полезной работы к затраченной работе.	Aп – полезная работа, [Дж] Aз – затраченная работа, [Дж]
Формула расчета потенциальной энергии	Eп = mgh	Потенциальная энергия – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.	Eп – потенциальная энергия тела, [Дж] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения h – высота тела над поверхностью земли, [м]
Формула расчета кинетической энергии	Ek= mv2/2	Кинетическая энергия – энергия, которой обладает тело вследствие своего движения.	Ek – кинетическая энергия тела, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с]
Формула закона сохранения полной механической энергии	mv12/2 + mgh1=mv22/2 + mgh2	Закон сохранения полной механической энергии: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.	m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения v1 – скорость тела в начальный момент времени, [м/с] v2 – скорость тела в конечный момент времени, [м/с] h1 – начальная высота, [м] h2 – конечная высота, [м]
Формула силы трения	Fтр = μ mg	Сила трения – сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.	Fтр – сила трения, [Н] μ – коэффициент трения m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения
Уравнение колебаний	x = A cos (ωt + φ0)		А – амплитуда колебаний, [м] х – смещение, [м] t – время, [c] ω – циклическая частота, [рад/с] φ0 – начальная фаза, [рад]
Формула периода	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота колебании, [с-1] t – время колебании, [с] N – число колебаний
Формула периода для математического маятника	T= 2π √L/g		Т – период, [с] g ≈ 9,81 м/с2 – ускорение свободного падения L – длина нити, [м]
Формула периода для пружинного маятника	T= 2π √m/K		Т – период, [с] m – масса груза, [кг] К – жесткость пружины, [Н/м]
Формула длины волны	λ = υТ = υ/ν		λ – длина волны, [м] Т – период, [с] ν – частота, [с-1] υ – скорость волны, [м/с]
Формула полной механической энергии колебательного движения	E = kA2/2		E – энергия, [Дж] А – амплитуда колебаний, [м] k – жесткость пружины, [Н/м]
Радиус Шварцшильда	R = 2GM/c2	Радиус Шварцшильда – радиус «горизонта событий» черной дыры, из которого ничто не может вырваться.	R – радиус Шварцшильда, [м] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная М – масса черной дыры, [кг]
Собственное время	t = T/√1-v2/c2	Собственное время – время, измеренное наблюдателем, движущимся вместе с часами.	t – собственное время, [с] T – время в движущейся системе отсчета, [с] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Масса покоя	m = M/√1-v2/c22	Масса покоя – масса тела в СО, относительно которой оно покоится.	m – масса тела в СО, относительно которой оно покоится, [кг] M – масса тела в подвижной СО, [кг] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Формула Эйнштейна	E = mc2		E – энергия, [Дж] m – масса, [кг] c – скорость света, [м/с
МОЛЕКУЛЯРНАЯ ФИЗИКА 10 класс
Массовое число	M = Z + N		M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов
Формула массы ядра	МЯ = МА – Z me		MЯ – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг]
Формула дефекта масс	∆m = Zmp + Nmn – MЯ	Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.	∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг]
Уравнение Менделеева-Клапейрона	pV = m/M RT	Уравнение состояния идеального газа	p – давление, [Па] V – объем, [м3] m – масса, [кг] M – молярная масса, [кг] R = 8,31 [Дж/мольК] – молярная газовая постоянная T – температура, [°С]
Формула давления газа			p – давление, [Па] n – концетрация молекул E – средняя кинетическая энергия молекулы, [Дж] T – температура, [°С] k = 1,38 · 10-23, [Дж/К] – постоянная Больцмана
Закон Бойля-Мариотта	p1V1 = p2V2		p – давление, [Па] V – объем, [м3]
Закон Гей-Люссака	V1/T1 = V2/T2		T – температура, [°С] V – объем, [м3]
Закон Шарля	p1/T1= p2/T2		T – температура, [°С] p – давление, [Па]
Внутренняя энергия идеального газа	U = i/2 pV		U – энергия, [Дж] p – давление, [Па] V – объем, [м3] i – число степеней свободы молекул газа
Работа, совершаемая газом	A = pΔV		p – давление, [Па] V – объем, [м3] А – работа, [Дж]
Первый закон термодинамики	Q = ΔU + A		Q – количество теплоты, [Дж] А – работа, [Дж] U – энергия, [Дж]
Формула для нахождения коэффициента полезного действия (КПД) теплового двигателя	η = A/Q∙100%		А – работа, [Дж] Q – количество теплоты, полученное от нагревателя, [Дж]
Сила поверхностного натяжения	F = ϭl		F – сила поверхностного натяжения, [Н] ϭ – поверхностное натяжение, [Н/м] l – длина участка поверхности слоя, [м]
Закон Гука	ϭ = Eε	При упругой деформации тела напряжение пропорционально относительному удлинению тела.	ϭ – механическое напряжение, [Па] Е – модуль Юнга, [Па] ε – относительное удлинение тела, [м]
ЭЛЕКТРОДИНАМИКА
Закон Кулона	F = kq1q1/r2	Определяет силу электростатического взаимодействия двух точечных зарядов	F – сила Кулона, [Н] k = 9·109 [Нм2/Кл2] q – заряд, [Кл] r – расстояние между зарядами, [м]
Напряженность поля	E = F/q E = kQ/r2		Е – напряженность поля, [Н/Кл] q – пробный положительный заряд, [Кл] F – сила Кулона, [Н] k = 9·109 [Нм2/Кл2]
Потенциал электростатического поля	φ = W/q φ = Q/4πεr		φ – потенциал, [В] W – энергия, [Дж] q – заряд, [Кл]
Потенциальная энергия заряда	W = qφ		W – энергия, [Дж] q – заряд, [Кл] φ – потенциал, [В]
Работа силы электростатического поля	A = qU		А – работа сил, [Дж] q – заряд, [Кл] U – разность потенциалов, [В]
Разность потенциалов в однородном поле	U = Ed		U – разность потенциалов, [В] Е – напряженность поля, [Н/Кл] d – расстояние, [м]
Электроемкость уединенного проводника	C = Q/φ		C – электроемкость, [Ф] φ – потенциал, [В] Q – заряд, [Кл]
Электроемкость конденсатора	C = Q/U		C – электроемкость, [Ф] U – разность потенциалов, [В] Q – заряд, [Кл]
Энергия ЭСП	W = CU2/2		C – электроемкость, [Ф] U – разность потенциалов, [В] W – энергия ЭСП, [Дж

Удельная теплоемкость | 8 класс

Содержание

Вам уже известно, что количество теплоты зависит от массы вещества, разности температур и рода вещества. Количество теплоты ($Q$) в СИ измеряется в джоулях ($Дж$).

Возьмем два тела одинаковой массы и температуры, но из разных веществ. Логично, что для их нагрева на $1 \degree C$ потребуется разное количество теплоты. В этом случае у нас разный род веществ, из которых состоят тела. Здесь мы вводим новое понятие — удельная теплоемкость вещества. 

На данном уроке мы рассмотрим это новое для нас определение, узнаем его физическое значение, познакомимся с удельной теплоемкостью различных веществ.

Удельная теплоемкость вещества

Удельная теплоемкость вещества — это физическая величина, численно равная количеству теплоты, которое необходимо передать телу массой $1 \space кг$ для того, чтобы его температура изменилась на $1 \degree C$

Рассмотрим на примерах, как удельная теплоемкость характеризует вещество.

Возьмем $1 \space кг$ воды и нагреем его на $1 \degree C$ (рисунок 1). 

Рисунок 1. Определение удельной теплоемкости воды.

Для этого нам понадобится $4200 \space Дж$. Именно это количество теплоты и будет определять удельную теплоемкость воды.

А теперь нагреем на $1 \degree C$ кусок свинца массой $1 \space кг$ (рисунок 2).

Рисунок 2. Определение удельной теплоемкости свинца.

В этот раз нам потребуется затратить $140 \space Дж$. Это значение ожидаемо отличается от количества теплоты, затраченное на нагревание воды. Тем не менее, это количество теплоты так же будет характеризовать удельную теплоемкость свинца.

{"questions":[{"content":"Удельная теплоемкость определяет количество теплоты, которое необходимо для нагрева тела[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["массой $1 \\space кг$ на $1 \\degree C$","массой $1 \\space кг$ в течение $1 \\space мин$","на  $1 \\degree C$ в течение $1 \\space с$"],"answer":[0]}},"hints":[]}]}

Единица измерения удельной теплоемкости

Удельная теплоемкость обозначается буквой $c$.

Измеряется удельная теплоемкость вещества в $\frac{Дж}{кг \cdot \degree C}$.

Рассмотрим эту единицу измерения на примере графита. Его удельная теплоемкость равна $750 \frac{Дж}{кг \cdot \degree C}$. Что это означает?

Из этого значения мы можем сказать, что:

1. Для нагревания куска графита массой $1 \space кг$ на $1 \degree C$ нам необходимо затратить количество теплоты, равное $750 \space Дж$
2. При охлаждении куска графиты массой $1 \space кг$ на $1 \degree C$ будет выделяться количество теплоты, равное $750 \space Дж$
3. При изменении температуры куска графита массой $1 \space кг$ на $1 \degree C$ он будет или поглощать, или выделять количество теплоты, равное $750 \space Дж$

Табличные значения удельной теплоемкости

Существуют уже известные значения удельной теплоемкости различных веществ. Они представлены таблице 1.

Вещество	$c, \frac{Дж}{кг \cdot \degree C}$	Вещество	$c, \frac{Дж}{кг \cdot \degree C}$
Золото	130	Песок	820
Ртуть	140	Стекло	840
Свинец	140	Кирпич	880
Олово	230	Алюминий	920
Серебро	250	Масло подсолнечное	1700
Медь	400	Лед	2100
Цинк	400	Керосин	2100
Латунь	400	Эфир	2350
Железо	460	Дерево (дуб)	2400
Сталь	500	Спирт	2500
Чугун	540	Вода	4200
Графит	750	Гелий	5200

Таблица 1. Удельные теплоемкости некоторых веществ.

{"questions":[{"content":"Чему равна теплоемкость олова? [[input-1]] $\\frac{Дж}{кг \\cdot \\degree C}$.","widgets":{"input-1":{"type":"input","inline":1,"answer":"230"}},"hints":[]}]}

Вода имеет почти самую большую теплоемкость в таблице — $4200 \frac{Дж}{кг \cdot \degree C}$. Это означает, что вода, находящаяся в морях и океанах, поглощает большое количество теплоты, нагреваясь летом. Зимой воды начинает остывать и отдавать большое количество теплоты. Поэтому, в местностях, которые расположены в непосредственной близости от воды, летом не бывает очень жарко, а зимой не бывает очень холодно. По этой же причине воду широко используют в технике (например, охлаждение деталей во время их обработки) и быту (отопительный системы помещений).

Песок имеет небольшую теплоемкость — $820 \frac{Дж}{кг \cdot \degree C}$. Он быстро нагревается и быстро остывает. Поэтому в пустыне днем очень жарко, а ночью температура может опуститься почти ниже $0 \degree C$.  

Удельная теплоемкость и агрегатные состояния вещества

Давайте взглянем в таблицу 1 и сравним значения удельной теплоемкости льда и воды.

Удельная теплоемкость льда — $ 2100 \frac{Дж}{кг \cdot \degree C}$, а воды — $4200 \frac{Дж}{кг \cdot \degree C}$. Но мы знаем, что одно и то же вещество в разных агрегатных состояниях.

Удельная теплоемкость вещества, находящегося в различных агрегатных состояниях, различна.

{"questions":[{"content":"Удельная теплоемкость зависит от[[choice-1]]","widgets":{"choice-1":{"type":"choice","options":["агрегатного состояния вещества","массы тела","времени нагревания тела"],"answer":[0]}},"hints":[]}]}

Например, при $-120 \degree C$ ртуть будет находиться в твердом состоянии. Ее удельная теплоемкость будет равна $129 \frac{Дж}{кг \cdot \degree C}$. В жидком же состоянии удельная теплоемкость ртути равна $138 \frac{Дж}{кг \cdot \degree C}$.

Скорость света — как измерить, чему равна в вакууме, воздухе, воде

Ничто во Вселенной не может быть быстрее скорости света. Узнайте в этой статье, что представляет собой эта особая величина и как на самом деле можно измерить скорость света.

Скорость света c – это одна из самых важных фундаментальных констант в физике. Значение скорости света – 299 792 458 м / (с точностью до ±1,2 м/с) [1] (что примерно равно 300 000 километров в секунду). Это означает, что за одну секунду свет преодолевает расстояние в 300 000 километров. Например, если вы стоите на Луне и светите сильным источником света в сторону Земли, свет проходит 1,25 секунды, прежде чем его можно будет увидеть здесь.

На самом деле, это значение скорости является точным, поскольку, по международному соглашению, определение метра гласит, что один метр – это длина, которую свет проходит в вакууме за 1 / 299792458 секунд.

Заметим, однако, что это действительно только скорость света в вакууме. Если свет проходит через среду, даже если это всего лишь воздух, эта скорость уменьшается.

Помните! Скорость света c точно определена как 299 792 458 метров в секунду. Ничто не движется быстрее света.

Насколько велика скорость света?

Трудно представить, насколько велика скорость света. Лучше всего представить себе это в сравнении со скоростями, которые вам более знакомы. В следующей таблице рассмотрим, как быстро движутся другие вещи в нашей повседневной жизни по сравнению со скоростью света.

Объект	Скорость в м/с (с округлением)
Человек	1,5
Гоночный автомобиль	100
Звуковые волны	343
Сверхзвуковой самолет	400
Скорость света	300 000 000

Однако это скорость света в вакууме (например, в космическом пространстве). Если свет движется в среде, такой как воздух, его скорость иногда значительно уменьшается.

Скорость света – это максимальная скорость всей материи и информации. На обычных путях ничто не движется быстрее, чем скорость света в вакууме c. Это означает, что не только свет, но и все остальное подчиняется этому ограничению скорости. К ним относятся, например, электромагнитное излучение и гравитационные волны. Такие волны и частицы движутся со скоростью света, независимо от скорости и направления их источника. Это относится и к движущемуся объекту. Например, если поезд едет с включенными фарами, свет все равно будет двигаться со скоростью света, независимо от того, насколько быстро движется поезд. Частицы и материя, чья масса не равна нулю, могут приближаться к скорости света, но никогда не достигают ее.

Скорость света в различных средах

В прозрачных средах, таких как воздух или стекло, свет распространяется медленнее, чем скорость света в вакууме. То же самое относится и к электромагнитным волнам в проводниках. Они также движутся медленнее скорости света. Это отношение скорости света c к скорости в среде v называется показателем преломления n= c / v.

Скорость света в воздухе.

В воздухе этот показатель преломления для видимого света составляет 1,0003. Поэтому в воздухе свет проходит на около 90 километров в секунду медленнее, чем в вакууме, то есть c / 1,0003 ≈ 299910 км / с .

Скорость света в воде.

В воде коэффициент преломления составляет около 1,3 , поэтому скорость света снижается до 230 769 километров в секунду, то есть c / 1,3 ≈ 230 769 км / с .

Скорость света в стекле.

В стекле коэффициент преломления равен 1,5. Если вы рассчитаете это, как и раньше, то получите скорость около 200 000 километров в секунду, то есть c / 1,5 ≈ 200 000 км / с .

Измерение скорости света

Когда вы включаете дома свет, кажется, что свет сразу же заполняет комнату. Но если смотреть на него на очень больших расстояниях и с помощью более совершенных измерительных приборов, чем ваш невооруженный глаз, конечная скорость света становится очевидной.

Существует множество подобных экспериментов. Однако в одном интересном варианте в качестве мишени используется наша Луна.

Представьте, что вы поместили зеркало на поверхность Луны. Теперь вы используете лазер, чтобы направить свет с Земли на это зеркало, и ждете, сколько времени пройдет, пока вы увидите отраженный свет. Только примерно через 2,5 секунды вы увидите вспышку зеркала.

Так с какой скоростью v движется свет вашего лазера?

Вы можете рассчитать её. Луна находится на расстоянии 384 400 километров от Земли. Ваш лазерный свет должен преодолеть это расстояние дважды. Один раз, чтобы добраться от вашего местонахождения до Луны, а затем еще раз, чтобы вернуться от Луны обратно к вам. Лазеру требуется 2,5 секунды, чтобы преодолеть это расстояние.

v = расстояние / время = 2 * 384 400 км / 2,5 с = 307 520 км / с .

Это не совсем соответствует реальному значению около 300 000 километров в секунду, но очень близко. С помощью более точных измерительных приборов можно более точно определить скорость света.

Кстати, свету требуется еще больше времени, чтобы пройти путь от Солнца до Земли. Свету, излучаемому Солнцем, требуется в среднем 8 минут и 17 секунд, чтобы достичь нас на Земле.

Солнечному свету требуется в среднем 8 минут 17 секунд, чтобы достигнуть Земли [1]

Определение скорости света сыграло в науке очень важную роль. Была не только выяснена природа света, но и установлено, что никакое тело не может двигаться со скоростью, превышающей скорость света в вакууме. Это стало ясно после создания теории относительности.

[2]

Единицы измерения

Теперь вы увидели, что скорость указывается в метрах в секунду, а также в километрах в секунду или километрах в час. С помощью простых вычислений вы можете самостоятельно перевести значения в соответствующие единицы измерения.

Чтобы было легче вычислить, мы округлим и скажем, что скорость света составляет 300 000 000 метров в секунду (300 000 000 м/с).

Скорость света в км / с .

Пересчет в километры в секунду относительно прост. В одном километре 1000 метров. Вы знаете, что свет распространяется со скоростью 300 000 000 метров в секунду, тогда 300 000 000 м / 1000 = 300 000 км.

Это означает, что за одну секунду ваш свет распространяется на 300 000 километров.

Скорость света в км / ч .

Теперь вы знаете, какое расстояние проходит свет за одну секунду. Теперь вам просто нужно экстраполировать это на часы. В часе 60 минут. В одной минуте 60 секунд, тогда 60 * 60 с = 3600 с. Таким образом, в одном часе 3600 секунд.

В итоге получаем: ( 300 000 км * 3600 ) / ( 1 c * 3600 ) = 1 080 000 000 км / 3600 с = 1 080 000 000 км / ч.

Поэтому свет распространяется в вакууме со скоростью примерно 1 080 000 000 000 км/ч (километров в час).

Скорость света в электродинамике

Классическая физика описывает свет как тип электромагнитной волны. Кроме того, уравнения Максвелла описывают классическое поведение электромагнитных волн.  

Законы Максвелла предскажут волны в пустоте со скоростью: c = 1 / ε₀ * μ₀ , где ε₀ – электрическая постоянная и μ₀ – магнитная постоянная.

В современной квантовой физике теория квантовой электродинамики (КЭД) описывает электромагнитное поле. В этом случае свет является фундаментальным возбуждением (также называемым квантом) электромагнитного поля. Это возбуждение принимает форму фотона. В рамках КЭД фотоны являются безмассовыми частицами. Поэтому, согласно специальной теории относительности, они движутся через вакуум со скоростью света.

Список использованных источников

• Википедия
• Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ Г. Я. Мякишев, Б. Б. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. — 19-е изд. — М. : Просвещение, 2010. — 399 с.
• Касьянов В. А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.

Измерение — Словарь единиц A-E

Измерение — Словарь единиц A-E

 

---

---

Далее следует словарь единиц, возникающих в Физика, быт и олимпиады. это , а не означает исчерпывающий список всех тайных единица, когда-либо использовавшаяся какой-либо из когда-либо существовавших цивилизаций, однако ваш предложения, комментарии и исправления приветствуются по адресу jstanbro@venus. net.

Этот словарь густо, безумно и, возможно, раздражающе перекрестные ссылки. Выбор подчеркнутой единицы приведет вас к словарная статья для этой единицы.

---

Щелкните букву ниже, чтобы перейти непосредственно к этой букве в толковый словарь.
А Б В Г Э Ф Г ЗДРАВСТВУЙ Дж К Л М НЕТ П К Р С Т У В Вт Х Г Z

---

-А-

АБАМПЕРЕ

Единица силы тока. 1 абампер = 10 ампер.

АКРЕ

Единица площади в «английской» системе единиц. Первоначально, акр был одной из единиц измерения, используемых для представления количество земли, которое человек может вспахать вручную за единицу время, обычно сутки. Сегодня акр равен 43 560 футов ² . или 4 840 ярдов ² .

АМПЕР (А)

Единица тока в СИ. 9-я Генеральная конференция по весам и мер (CGPM-1948) принял ампер за единицу электрический ток со следующим определением:

Ампер – это такой постоянный ток, который, если его поддерживать в два прямых параллельных проводника бесконечной длины, пренебрежимо малой круглого поперечного сечения и размещенного 1 метра друг от друга в вакууме, между этими проводниками возникнет сила равно 2 х 10 ^-7 ньютон на метр длины.

АМПЕР НА МЕТР (А/м)

Единица СИ для напряженности магнитного поля. Один ампер/метр это напряженность магнитного поля внутри вытянутого, равномерно намотанный соленоид, который возбуждается линейным током плотность в его обмотке 1 ампер на метр осевого расстояния.

АМПЕР ^. ЧАС (Ач)

Единица количества электрического заряда. Ан Ампер ^. час — это количество электроэнергии представлено током в 1 ампер, протекающим в течение 1 час.

ANGSTROM (А с кружком сверху)

Единица длины. Один ангстрем равен 10 ^-10 метров.

АПОСТИЛЬ (asb)

Единица яркости. Один люмен за квадратный метр выходит поверхность, яркость которой составляет 1 апостильб во всех направлениях в пределах полушарие.

АРЕ

Единица площади в системе СИ. Один равен 100 метрам ² (площадь 10 метров х 10 метр квадратный). гектар (= 100 ар = 10 ⁴ метр ² ) чаще используется.

АСТРОНОМИЧЕСКАЯ ЕДИНИЦА (а.е.)

Единица длины в системе СИ, равная среднему радиусу Земли. орбита. Одна астрономическая единица равна 1,495 х 10 ¹¹ метров.

АТМОСФЕРА, СТАНДАРТНАЯ (атм)

Единица давления. Одна стандартная атмосфера равна 101 325 ньютонов на квадрат метр.

ЕДИНИЦА АТОМНОЙ МАССЫ, ЕДИНАЯ (u)

Атомная единица массы (унифицированная) равна 1/12 массы атом углерода-12 ( ¹² C) нуклида.

-В-

БАР (бар)

Единица давления. Один бар равен 100 000 (10 ⁵ ) ньютонов на квадрат метр.

САМОЙ (б)

Единица поперечного сечения ядра (площадь). Один сарай равен 10 ^-28 кв.м.

БОЧКА (баррель)

Единица объема. Один баррель равен 9 702 кубическим дюймам; или 0,158 99 куб.

БОД (Бод)

Единица скорости передачи сигналов. Один бод равен одному элементу ( бит в секунду.

БЕЛ (Б)

Безразмерная единица для выражения отношения двух значений мощность, являющаяся логарифмом по основанию 10 отношения мощностей. ( более часто используемая единица измерения — децибел (дБ). 10-кратный логарифм по основанию 10 отношения мощностей. Бел это 10 децибел.)

БИТ (б)

Единица информации, обычно представленная импульсом. Немного является двоичной цифрой, то есть 1 или 0 в компьютерных технологиях.

БИТ В СЕКУНДУ (б/с)

Единица скорости передачи сигналов. Скорость передачи 1 бит на второй. Один бит/сек = 1 бод.

БРИТАНСКАЯ ТЕПЛОВАЯ ЕДИНИЦА (БТЕ) ​​

Единица тепла. Теплота, необходимая для нагревания 1 фунта чистого воды через интервал в 1 градус по Фаренгейту.

-С-

КАЛОРИИ (Международная таблица) (кал. _It )

Единица тепла. Одна международная таблица калорий равна 4,1868. джоули. (9-я конференция Generale des Poids et Mesures принял джоуль как единица тепла.)

КАЛОРИЯ (термохимическая калория) (кал)

Единица тепла. Одна калория равна 4,1840 Дж.

КАНДЕЛА (кд)

Единица силы света в СИ. Агрегат на основе пламени или Стандарты нити накаливания до 1948 года были заменены изначально блоком на основе планковского излучателя (черного тела) при температура замерзания платины. Из-за трудностей с этим измерениям и новым экспериментальным методам, 16-я Генеральная Конференция по мерам и весам (CGPM 1979) приняла следующее определение:

Кандела – это сила света в данном направлении, источника, излучающего монохроматическое излучение с частотой 540x 10 ¹² Гц и имеет интенсивность излучения в этом направлении 1/683 Вт на стерадиан .

Ранее этот элемент назывался свечой.

СВЕЧА (с)

Устаревшая единица силы света. Использование единицы СИ, кандела предпочтительнее.

ЦЕЛЬСИЙ ( ^или С)

Единица измерения температуры. См. СТЕПЕНЬ ЦЕЛЬСИЙ

сантиметр (см)

Единица длины СГС. Один сантиметр равен (1) 0,01 дюймы.

САНТИПУАЗ (сП)

Единица динамической вязкости. 1 сантипуаз = 10 ^-2 пуаз.

СЕНТИСТОКС (сСт)

Единица кинематической вязкости. 1 сантистокс равен 10 ^-2 тактов.

КРУГЛЫЙ МИЛ (смил)

Площадь круга диаметром 0,0001 (10 ^-4 ) дюймов. Один круговой мил равен 1,4 x 10 ^-6 квадратных дюймов.

КУЛОН (К)

Количество электрического заряда, проходящего через любое поперечное сечение проводника за 1 секунду при постоянном токе на 1 ампер. Кулон – это единица СИ электрический заряд. (См. также Основные ед.)

КУБИТ

Исторически известная единица длины. Первоначально один локоть определяется как расстояние от локтя человека до конца его вытянутые кончики пальцев. Существовали различные локтевые длины во всем древнем мире. Один локоть равен примерно 20 дюймы.

ЧАШКА (с)

Единица объема в «английской» системе. Одна чашка = 0,5 пинта. Чашка , а не рекомендуется для научных целей.

КЮРИ (Ci)

Единица деятельности в области радиационной дозиметрии. Один Кюри равно 3,7 х 10 ¹⁰ распадов в секунду.

ЦИКЛ (с)

Интервал пространства времени, в котором завершается 1 раунд события или явления.

ЦИКЛ В СЕКУНДУ (Гц, цикл/с)

Количество циклов в секунду. (название герц (Гц) является общепринятым международным термином. Аббревиатура Гц предпочтительнее к/с.)

-Д-

ДАРСИ (Д)

Единица проницаемости пористой среды. Один дарси равен 1 сП(см/ с)( см/ атм) равняется 0,986 923 квадратных микрометра. (Проницаемость в 1 дарси позволит потоку в 1 куб. сантиметр в секунду жидкости вязкостью 1 сантипуаз через площадь 1 квадратный сантиметр при градиенте давления в 1 атмосферу за сантиметр.)

ДЕНЬ (д)

Единица времени, точное определение которой зависит о какой системе измерения времени идет речь, т. е. кажущееся солнечное время, среднее солнечное время, всемирное время, кажущееся звездное время, эфемеридное время или атомное время. За исключением атомное время, отсчет времени отсчитывается от вращения Земли. Для общих целей днем ​​считается период, принимаемый за 1 оборот Земли вокруг своей оси.

ДЕЦИБЕЛ (дБ)

Безразмерная единица для выражения отношения двух значений мощность, в 10 раз превышающая логарифм по основанию 10 степени соотношение. 1 децибел равен 10 бел.)

ГРАДУС ЦЕЛЬСИЯ ( ^o С)

Единица измерения температуры. Температурная шкала Цельсия это производное от термодинамического или Кельвина шкала температуры. Они связаны: температурой по Цельсию равна температуре Кельвина минус 273,15 (C = K — 273,15). Немного обычно используемые температуры Цельсия:

• абсолютный ноль равен -273,15 ^o C
• вода замерзает при 0 ^o С (при 1 атм)
• «комнатная температура» примерно равна 20 ^или С
• «нормальная» температура тела составляет примерно 37 ^или С
• вода кипит при 100 ^o С (при 1 атм)

СТЕПЕНЬ ФАРЕНГЕЙТА ( ^o F)

Единица измерения температуры. Температурная шкала Фаренгейта это относится к температурной шкале Цельсия по Фаренгейту температура равна 1,8 x температура по Цельсию плюс 32 (F = 1,8C + 32 ^или ). Некоторые часто используемые температуры по Фаренгейту:

• абсолютный ноль равен -459,69 ^o F
• вода замерзает на 32 ^o F
• «комнатная температура» примерно 70 ^или F
• «нормальная» температура тела составляет примерно 98.6 ^или F
• вода кипит при 212 ^o F (при 1 атм)

ГРАДУСОВ КЕЛЬВИНА ( ^или )

Устаревшая единица измерения температуры. Предпочтительной единицей является кельвин.

СТЕПЕНЬ РАНКИНА ( ^o R)

Единица измерения температуры. Температурная шкала Ренкина связан с температурной шкалой Фаренгейта: Ренкином температура равна температуре по Фаренгейту минус 459,69

ДИНА (дин)

Единица силы. Одна дина равна силе, необходимой для придания 1 грамм массы ускорение 1 сантиметр в секунду в секунду. 1 дина = 10 ^-5 ньютонов. Дина — единица измерения силы в системе СГС.

-Е-

ЭЛЕКТРОНВОЛЬТ (эВ)

Единица энергии. Один электронвольт равен энергии, полученной электроном, когда он проходит через разность потенциалов 1 вольт в вакууме. Один электронвольт равен 1,602 х 10 ^-12 эрг.

ЭЛЕКТРОСТАТИЧЕСКИЙ БЛОК (ЭСУ)

Единица количества электроэнергии.

ЭРГ (эрг)

Единица энергии. Один эрг – это работа, совершаемая при постоянном сила в 1 дин приложена на расстоянии от 1 сантиметра. 1 эрг = 10 ^-7 джоулей. Кроме того, 1 эрг = 7,376 х 10 ^-8 фут ^. фунтов = 9,481 x 10 ^-11 БТЕ. Эрг – это единица энергии в системе СГС.

---

Щелкните букву ниже, чтобы перейти непосредственно к этой букве в толковый словарь.
А Б В Г Э Ф Г ЗДРАВСТВУЙ Дж К Л М НЕТ П К Р С Т У В Вт Х Г Z

---

---

---

последнее обновление 7 октября 2000 г. автор JL Стэнбро

C. Точность и оценка :: Физика

Во многих случаях измеряемые нами величины (длина, углы, токи и т. д.) не точно соответствуют делениям наших весов. Показанная здесь линейка используется для измерения ширины w заштрихованной области. Обратите внимание, что ширина чуть больше трех единиц, но не точно 3,2 единицы (что в данном случае является следующей градацией шкалы).

В таких случаях мы должны оценить между градациями. Есть два подхода к этой ситуации. Первый заключается в оценке значения при однократном отсчете, а второй – в самостоятельном измерении ширины несколько раз и составлении среднего значения.

Оценка и точность делений шкалы

При оценке важно, чтобы наша оценка была максимально точной. Однако независимо от того, насколько хорошо мы можем произвести оценку, в нашем чтении всегда присутствует некоторая неопределенность. Есть два независимых источника этой неопределенности. Первый возникает из-за самого процесса оценки, а второй — из-за точности измерительного прибора.

Оценка:

В данном случае простейшей оценкой является присвоение значения посередине интервала. Затем мы могли бы сообщить показания как 3,1 +/- 0,1 единицы. Это основано на наблюдении, что измерение больше 3,0 единиц, меньше 3,2 единиц, а также на том факте, что добавление или вычитание 0,1 единицы приведет нас по крайней мере к одному из ближайших делений шкалы.

Тем не менее, мы могли бы сделать лучше, чем это. В расширенном представлении мы видим, что край рисунка достигает только примерно трети пути за пределы 3,0 единиц. Таким образом, одна треть интервала составляет 0,0666… единицы (здесь мы округляем до 0,07), что дает оценку w как w = 3,07 +/- 0,07 единицы. В этом случае прибавление или вычитание 0,07 единицы приведет нас к известному делению шкалы. Вы можете возразить, что добавление 0,03 единицы даст нам 3,1 единицы, что, как мы уверены, слишком велико, так что оценка нашей неопределенности может быть всего лишь 0,03 единицы. Хотя это правда, эту небольшую неопределенность следует рассматривать как наиболее оптимистичный отчет о нашем процессе оценки. Разумный компромисс можно найти, сообщив w как w = 3,07 +/- 0,05 единицы.

Точность прибора:

Точность любого измерительного прибора зависит от точности производственного процесса. На этом рисунке две линейки одного производителя показаны рядом. Хотя разница может показаться преувеличенной, некоторые различия всегда будут частью любого производственного процесса. Большинство производителей качественных измерительных приборов придерживаются соглашения о прецизионности (точности) своих приборов. Уровень или степень точности в процессе производства и контроля качества определяется размером делений шкалы, показанных на устройстве. Предполагается, что неопределенность составляет половину (1/2) наименьшего показанного деления шкалы. Для нашей линейки это означает, что при сравнении любых двух линеек, изготовленных в этом производственном процессе, наибольшая разница в общей длине никогда не должна превышать 0,1 единицы. Если это так, то никакое измерение с помощью этой линейки не следует считать более точным, чем 0,1 единицы. Теперь вы понимаете, почему линейка не показывает больше делений шкалы. Если бы это устройство было более точным, чем 0,1 единицы, производитель включил бы деления шкалы между показанными делениями.

Этот факт означает, что приведенный выше результат довольно оптимистичен в отношении точности произведенного измерения. Должны ли мы вернуться к исходному утверждению для w? Возможно нет. Наибольшая неопределенность возникает, когда при измерении используется вся длина линейки. Также случайным образом можно предположить, что у нас, вероятно, не самая плохая линейка в производственной партии. Таким образом, наше оценочное измерение, вероятно, лучше, чем w = 3,1 +/- 0,1 единицы, но не так хорошо, как w = 3,07 +/- 0,05 единицы.

Если устройство имеет цифровое считывание, такое как цифровой вольтметр, ответственные производители указывают точность числом отображаемых разрядов. Общее правило — плюс или минус одна из наименее значащих отображаемых цифр. Наиболее авторитетные производители добиваются большего успеха, сохраняя неопределенность на уровне половины наименее значащей цифры. Но если у вас нет доступа к руководству пользователя или опыту работы с продуктом, это небезопасное предположение.

Общее правило: Нередко при выполнении одного измерения можно избежать всего этого кропотливого процесса и просто назначить половину наименьшего деления шкалы в качестве неопределенности. Например, наименьшее деление шкалы обычных чашечных весов составляет 0,1 г. В этом случае мы предполагаем погрешность +/- 0,05 g.

Выполнение нескольких измерений

Есть и другой подход к этой проблеме. Хотя это занимает больше времени, настоятельно рекомендуется, когда мы заботимся о точности результата. Для этого метода просто измерьте ширину много раз и усредните результаты. При проведении нескольких измерений величины неопределенность можно оценить, вычислив среднее отклонение. Математика для этого разработана в следующих двух разделах; найти среднее и среднее отклонение.

При повторных измерениях следует стараться сделать каждое испытание независимым от предыдущего, насколько это возможно. Пусть измерения проводят разные люди, используют несколько разных устройств (например, новые линейки). Делайте каждое измерение как можно точнее и начинайте каждое измерение с нуля (например, берите линейку между измерениями).

Последнее обновление 26 ноября 2014 г.

AP Physics C: Mechanics Course – AP Central

Курс

Войти в AP Classroom

Беглый взгляд на курс

AP Physics C: Mechanics — это односеместровый курс физики на уровне колледжа, который особенно подходит для студентов, планирующих специализироваться или специализироваться в одной из физических или инженерных наук. Учащиеся развивают свое понимание физики посредством изучения и занятий в классе, а также практической лабораторной работы, когда они изучают такие понятия, как изменение, взаимодействие сил, поля и сохранение.

Лабораторные требования и лабораторные тетради

Лабораторный опыт должен быть частью обучения студентов AP Physics C и должен быть включен во все курсы AP Physics. Колледжи могут потребовать, чтобы студенты представили свои лабораторные материалы из научных курсов AP, прежде чем предоставить колледжу кредит на лабораторные работы, поэтому студентам рекомендуется сохранять свои лабораторные тетради, отчеты и другие материалы .

Описание курса и экзамена

Ресурсы курса

Доступен проект пересмотренной структуры учебного плана

Учителя приглашаются для предварительного ознакомления с пересмотренной структурой учебного плана по физике C: Механика и физика C: Электричество и магнетизм. Он был разработан для создания более унифицированного подхода ко всем четырем курсам AP Physics и для более точного отражения текущих ожиданий от вводных курсов колледжа. Осенью 2022 года мы предоставим дополнительную информацию о сроках и запуске пересмотренной платформы.

Предварительный просмотр пересмотренной структуры

Содержание курса

На основе модели Understanding by Design® (Wiggins and McTighe) эта структура курса содержит четкое и подробное описание требований к курсу, необходимых для успешной учебы учащихся. Структура определяет, что учащиеся должны знать, уметь делать и понимать, с акцентом на большие идеи, которые охватывают основные принципы, теории и процессы дисциплины. Структура также поощряет обучение, которое готовит учащихся к установлению связей между областями посредством более широкого мышления о физическом мире.

Структура AP Physics C: Mechanics состоит из семи общеизвестных учебных модулей, которые обеспечивают одну возможную последовательность курса. Как всегда, у вас будет возможность организовать содержание курса по своему усмотрению.

Блок	Оценка экзамена (раздел с несколькими вариантами ответов)
Модуль 1: Кинематика	14%–20%
Модуль 2: Законы движения Ньютона	17%–23%
Блок 3: работа, энергия и мощность	14%–17%
Модуль 4: Системы частиц и линейный импульс	14%–17%
Блок 5: Вращение	14%–20%
Модуль 6: Колебания	6%–14%
Блок 7: Гравитация	6%–14%

Научная практика

Структура AP Physics C: Mechanics, включенная в описание курса и экзамена, описывает отдельные навыки, называемые научными практиками, которые учащиеся должны практиковать в течение года, — навыки, которые помогут им научиться думать и действовать как физики.

Навык	Описание	Оценка экзамена (раздел с несколькими вариантами ответов)	Оценка экзамена (раздел свободных ответов)
1. Визуальные представления	Анализировать и/или использовать представления физических ситуаций, за исключением графиков.	14–17%	4–7%
2. Вопрос и метод	Определить научные вопросы и методы.	3–6%	6–11%
3. Представление данных и явлений	Создание визуальных представлений или моделей физических ситуаций.	Не оценивается в разделе множественного выбора	13–20%
4. Анализ данных	Анализировать количественные данные, представленные в виде графиков.	14–17%	8–13%
5. Теоретические отношения	Определить влияние на количество при изменении другого количества или физической ситуации.	25–34%	20–24%
6. Математические процедуры	Решите задачи физических ситуаций, используя математические соотношения.	14–20%	20–24%
7. Аргументация	Разработайте объяснение или научный аргумент.	14–20%	11–18%

AP и высшее образование

Познакомьтесь с комитетом по разработке AP Physics C

Уникальность программы AP заключается в том, что она опирается на комитеты по развитию. Эти комитеты, состоящие из равного числа преподавателей колледжей и опытных преподавателей средней школы AP со всей страны, необходимы для подготовки учебных программ курсов AP и экзаменов.