Алгебра высказываний (булева алгебра) — Информатика, информационные технологии

Основные понятия

Основное понятие булевой алгебры — выказывание. Под простым высказыванием понимается предложение, о котором можно сказать, истинно оно или ложно (третьего не дано). Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (обозначим 0 ) или ИСТИНА (обозначим 3). Например, содержание высказывания А: «дважды два равно четырем» истинно А = 1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ. В дальнейшем нас не будет интересовать содержательная часть высказываний, а только их истинность. Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, записывается А = В.

Логические операции

Сложное высказывание можно построить из простых с помощью логических операций: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций. Рассмотрим их подробней.

Операцией отрицания А называют высказывание (или , говорят не А), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание — унарная (т.е. для одного операнда) логическая операция. Ей соответствует языковая конструкция, использующая частицу НЕ,

Это правило можно записать в виде следующей таблицы:

Такая таблица называется таблицей истинности.

Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается (при этом говорят С равно А и В). Примером такой операции может быть следующая: пусть высказывание А состоит в том, что «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, если ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери», т.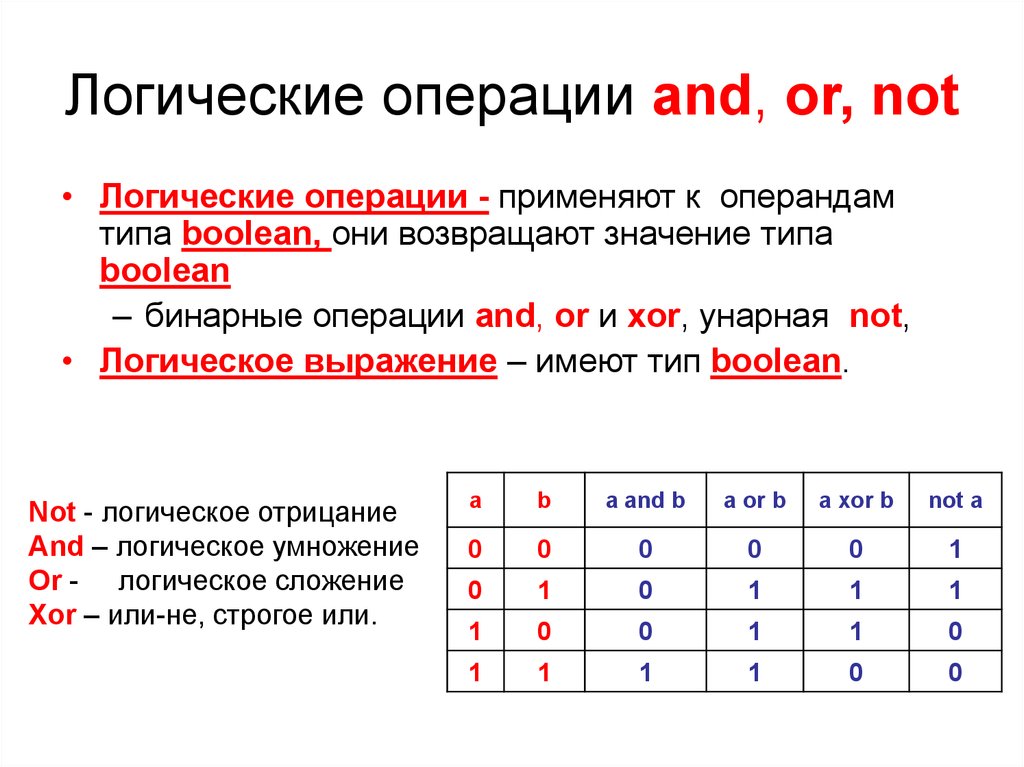 е. данная операция применяется, если два высказывания связываются союзом И.

Таблица истинности этой операции, как следует из определения, имеет вид

Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается (при этом говорят:

С равно А ИЛИ В). Пример такой операции следующий: пусть высказывание А состоит в том, что «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе», т.е. данная операция применяется, если два высказывания связываются союзом ИЛИ.

Таблица истинности такой операции следующая:

Импликацией двух высказываний А (А называется посылкой) и В (В называется заключением) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается (при этом говорят, из А следует В). Примером такой операции может быть любое рассуждение типа: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи».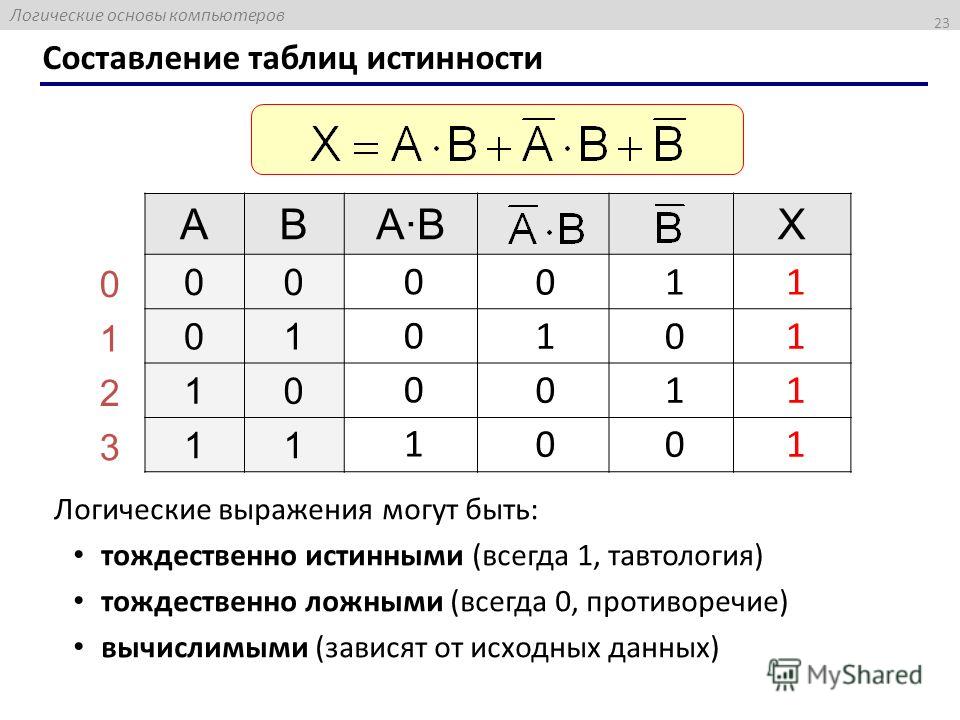 Очевидно, операция не симметрична, т.е. из не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.

Таблица истинности импликации следующая:

Эквиваленцией двух высказываний А и В является новое высказывание С, которое .истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается

Примером такой операции может быть любое высказывание типа: событие А равносильно событию В.

Таблица истинности:

Логические Выражения. Порядок логических операций

С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические выражения, которые также называются булевскими функциями. Например.

Чтобы избежать большого количества скобок в булевских функциях, принято следующее соглашение о старшинстве операций.

Первыми выполняются операции в скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.

Зависимости между логическими операциями

Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истинности следующие равносильности:

Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь возможность приводить формулы с помощью эквивалентных преобразований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований (формул 1—23).

Первая из них — дизъюнктивная нормальная форма (ДНФ), имеет вид , где каждое из составляющих есть конъюнкция простых высказываний и их отрицаний, например:

Вторая- конъюнктивная нормальная форма (КНФ), имеет вид

где каждое из составляющих есть дизъюнкция простых высказываний и их отрицаний, например:

Табличное и алгебраическое задание булевских функций

Задать булевскую функцию можно, определяя ее значения для всех наборов значений аргументов. Каждый аргумент может иметь два значения: 0 и 1, следовательно, n аргументов могут принимать 2n различных наборов. Пусть, например, булевская функция имеет три аргумента: X,, Х2, Х3 Общее число наборов 23 = 8; зададим таблицу истинности функции, указав для каждого набора значение функции.

№	Х1	Х2	Х3	Р
			I

Для составления алгебраической формы по результатам таблицы сделаем следующее. В комбинациях, где функция принимает значение 1, единицу заменим именем функции, а нуль — именем с отрицанием (т.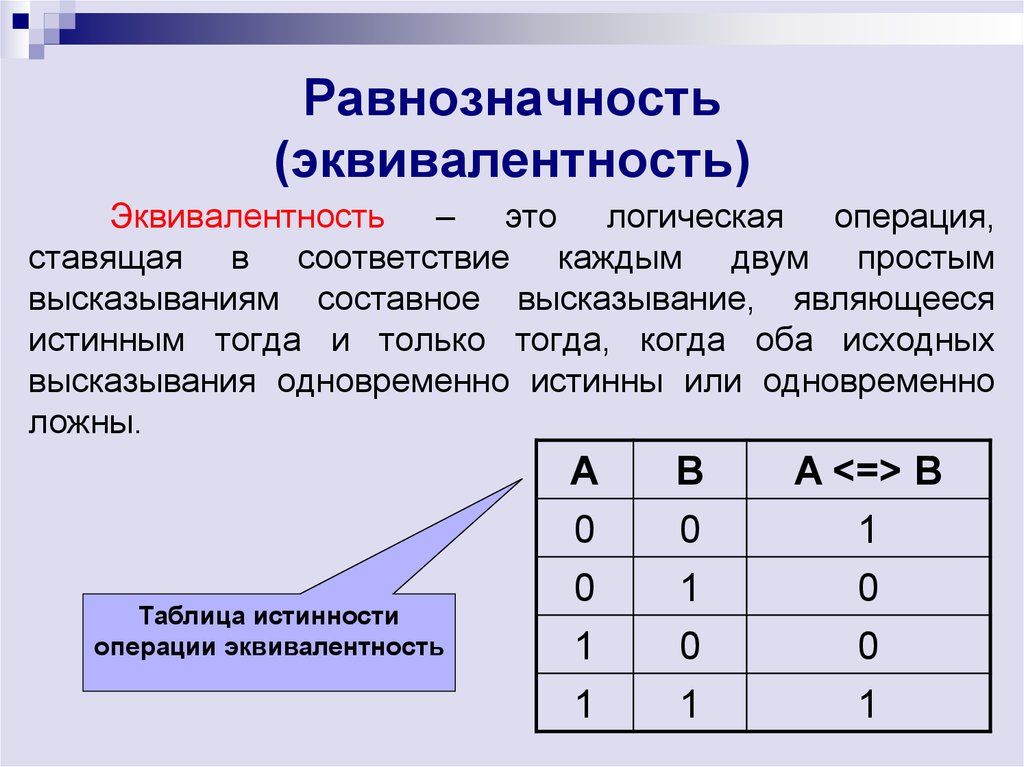 е. комбинации 0 0 1 поставим в соответствие выражение ), все элементы соединим знаками дизъюнкции, для рассматриваемого примера получим

Как нетрудно заметить, построенная функция удовлетворяет заданной таблице истинности. Функция представляет дизъюнктивную нормальную форму. Кроме того, заметим, что в каждую группу дизъюнкций входят все аргументы функции. Такая ДНФ называется совершенной, а каждая группа дизъюнкций называется коституентой единицы.

Аналогично, для комбинаций, где функция принимает значение нуля, можно построить алгебраическую форму

,

которая также удовлетворяет заданной таблице истинности и представляет собой конъюнктивную нормальную форму, в данном случае совершенную. Каждая конъюнкция называется конституентой нуля.

В главе 2 будет показано, как, основываясь на булевой алгебре, создаются цифровые устройства.

1.6.2. Элементы теории множеств

Множеством называется любое объединение определенных вполне различимых объектов; их может и не быть вообще.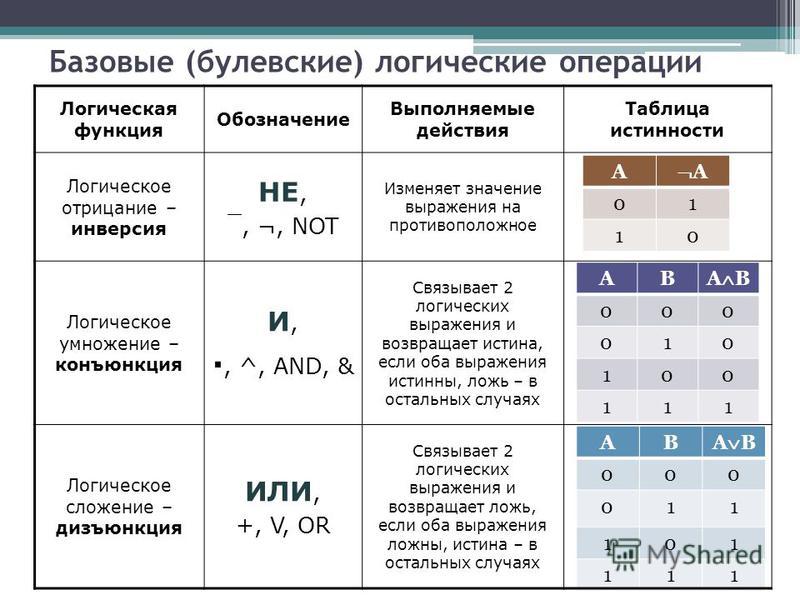 Можно говорить о множестве точек на отрезке [0,1], множестве студентов в группе, множестве снежных дней в июле на экваторе, т.е. множество образуют любые объекты, объединенные по любому признаку. Объекты, составляющие множество, называются элементами множества. Множество, не имеющее ни одного элемента, называется пустым, оно обозначается 0. Множество, состоящее из конечного числа элементов, называется конечным, в противном случае — бесконечным.

Задать множество можно перечислением его элементов. Например, множество образованное из п элементов ар а2, …, ап, обозначается А = {а,, а2, …, ап}; пишется а е А (говорится «элемент а при надлежит множеству А»), если а является элементом множества А, в противном случае

Задать множество можно также, указав общее свойство для всех его и только его элементов. Например, множество точек равноудаленных от концов отрезка.

Два множества считаются равными, если состоят из одних и тех же элементов; записывается этот факт А = В.

Множество А1 называется подмножеством А (записываете ),

если все элементы множества А, являются элементами А,

Для множеств определены следующие операции: объединение, пересечение, дополнение.

Объединением множеств А и В (записывается ) называется

множество, состоящее из элементов как одного, так и второго множества. Например, А и В — множества точек, принадлежащих некоторым двум кругам, имеющим общие точки, тогда объединением будет фигура, состоящая из общих точек.

Пересечением множеств А и В (записывается ) называется

множество, состоящее из элементов, принадлежащих как одному, так и второму множеству одновременно.

Дополнением множества А до В называется множество, состоящее из элементов множества В, не принадлежащих А. Дополнение обозначается (рис. 1.7).

Рис. 1.7. Операции надмножествами

16.3, Элементы теории графов

Основные понятия

Граф задается парой множеств: множества Е, называемого множеством вершин, и множества II, называемого множеством ребер. Ребро есть пара, где ,

указывающая, между какими двумя вершинами проведено ребро. Говорят, что ребро инцидентно вершинам е. , е. Если порядок ребер не имеет значения, т.е. , то ребро называется неориентированным или просто ребром, если же порядок имеет значение, то ребро называется ориентированным ребром или дугой. Вершина еi. — называется началом дуги, еj. — конец дуги. Граф, содержащий хотя бы одну дугу, называется ориентированным графом или орграфом

Граф называется конечным, если множество Е вершин

конечно.

Граф •, у которого любые две вершины соединены ребром,

называется полным. Если хотя бы две вершины соединены несколькими ребрами, то такой граф называется мультиграфом. Две вершины называются смежными, если они соединены ребром. Число ребер, инцидентных данной вершине е., называется локальной степенью этой вершины p(ei) Число ребер r графа G(Е,U) определяется выражением

, где n — количество вершин в графе. Рассмотрим граф,

изображенный на рис. 1.8.

Рис. 1.8. Ориентированный граф

Множество вершин графа состоит из пяти элементов: Е = {1, 2, 3, 4, 5}, а множество ребер U = {(1, 2), (1, 4), (1, 5), (2, 3), (3, 4), {5, 3)}. Ребро (5, 3) — является ориентированным ребром или дугой. Число ребер в графе определяется по значению локальных степеней для каждой вершины:

Важным в теории графов является понятие части графа G(Е,U), который обозначается

Множества вершин и ребер части графа являются подмножествами вершин и ребер исходного графа

Статьи к прочтению:

• Алгоритм эрли (основные принципы)
• Алгоритмы ассиметричного шифрования

Начала Булевой алгебры

Похожие статьи:

• Операции (высказывания) алгебры логики

  Основные понятия алгебры логики. Логические основы ЭВМ Двоичная система счисления — позиционная система счисления с основанием 2. В этой системе…

• Системы функций алгебры логики

  Рассмотрим теорему Жегалкина, которая играет важную роль в алгебре логики. Теорема Жегалкина. Любая булева функция может быть представлена многочленом…

Теория и применение цифровой обработки сигналов

Теория и применение цифровой обработки сигналов

Рабинер Л. , Гоулд Б. Теория и применение цифровой обработки сигналов. М: Мир, 1978. В монографии изложены основы теории дискретных сигналов и почти все современные методы расчета цифровых фильтров. Рассмотрены теория, способы выполнения и применения алгоритмов быстрого преобразования Фурье. Отдельные главы посвящены вопросам проектирования специализированных устройств цифровой обработки и применению цифровых методов для анализа речевых и радиолокационных сигналов. Книга содержит большое количество справочного материала, а также тексты программ для расчета типовых цифровых устройств. Книга представляет большой практический интерес для инженеров-проектировщиков устройств первичной обработки сигналов, использующих для анализа сигналов вычислительные машины, специалистов в области вычислительной математики и программистов. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ 1.2. Обзор основных направлений цифровой обработки сигналов 1. 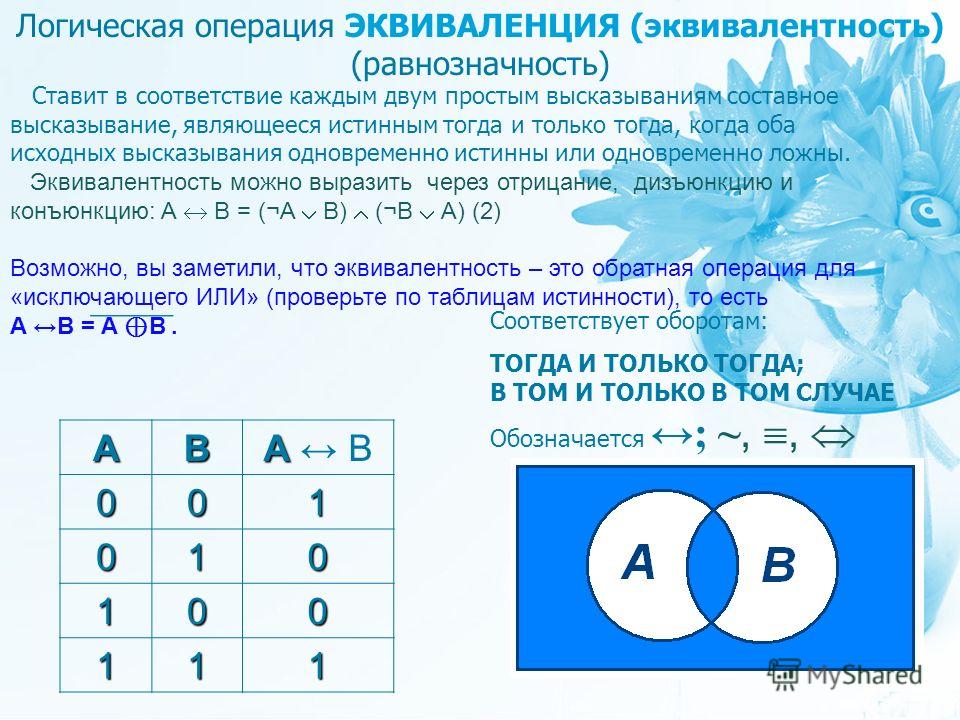3. Построение книги 2.1. Введение 2.2. Последовательности 2.3. Представление произвольных последовательностей 2.4. Линейные системы с постоянными параметрами 2.5. Физическая реализуемость. Устойчивость 2.6. Разностные уравнения 2.7. Частотная характеристика 2.8. Частотная характеристика систем первого порядка 2.9. Частотная характеристика систем второго порядка 2.10. Дискретный ряд Фурье 2.11. Замечания о единицах измерения частоты 2.12. Соотношение между непрерывными и дискретными системами 2.13. z-преобразование 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности 2.15. Обратное z-преобразование 2.16. Свойства z-преобразования 2.17. Решение разностных уравнений с применением одностороннего z-преобразования 2.18. Геометрическая интерпретация преобразования Фурье 2.19. Построение цифровых фильтров (структурные схемы фильтров) 2.20. Структурные схемы фильтров без полюсов 2. 21. Дискретное преобразование Фурье 2.22. Свойства ДПФ 2.23. Свертка последовательностей 2.24. Линейная свертка конечных последовательностей 2.25. Секционированные свертки 2.26. Дискретное преобразование Гильберта 2.27. Преобразование Гильберта действительных сигналов ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ 3.2. Порядок расчета фильтров 3.3. Свойства КИХ-фильтров 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой 3.5. Частотная характеристика КИХ-фильтров с линейной фазой 3.6. Расположение нулей КИХ-фильтров с линейной фазой 3.7. Методы расчета КИХ-фильтров с линейными фазами 3.8. Первый метод расчета — метод взвешивания 3.9. Прямоугольное окно 3.10. «Обобщенное» окно Хэмминга 3.11. Окно Кайзера 3.12. Примеры фильтров нижних частот с различными окнами 3.13. Особенности использования метода взвешивания 3.14. Несколько практических приемов использования окон 3. 15. Дополнительные примеры фильтров рассчитанных методом взвешивания 3.16. Общая характеристика окон 3.17. Второй метод проектирования — метод частотной выборки 3.18. Решение задачи оптимизации 3.19. Линейное программирование 3.20. Фильтры с частотной выборкой вида 1 и 2 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой 3.22. Фильтры вида 2 с частотной выборкой и линейной фазой 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки 3.24. Заключение к описанию метода частотной выборки 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой 3.26. Аппроксимация по Чебышеву со взвешиванием 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой 3.28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций 3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции 3.30. Использование алгоритма замены Ремеза для расчета оптимальных фильтров 3. 31. Расчет оптимальных КИХ-фильтров методами линейного программирования 3.32. Характеристики оптимальных фильтров нижних частот вида 1 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1 3.34. Соотношения между параметрами оптимального фильтра нижних частот 3.35. Свойства оптимальных фильтров нижних частот вида 2 3.36. Характеристики оптимальных дифференциаторов 3.37. Характеристики оптимальных преобразователей Гильберта 3.38. Многополосные оптимальные КИХ-фильтры 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот Приложение Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ 4.2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки 4.3. Методы расчета коэффициентов БИХ-фильтра 4. 4. Расчет цифровых фильтров по фильтрам непрерывного времени 4.5. Метод отображения дифференциалов 4.6. Метод инвариантного преобразования импульсной характеристики 4.7. Билинейное z-преобразование 4.8. Согласованное z-преобразование 4.9. Обзор методов расчета аналоговых фильтров нижних частот 4.10. Расчетные диаграммы фильтров нижних частот 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров 4.12. Частотные преобразования 4.13. Прямые методы расчета цифровых фильтров 4.14. Применение методов оптимизации для расчета БИХ-фильтров 4.15. Обзор методов расчета БИХ-фильтров 4.16. Сравнение КИХ- и БИХ-фильтров 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки Глава 5. ЭФФЕКТЫ КОНЕЧНОЙ РАЗРЯДНОСТИ ЧИСЕЛ В ЦИФРОВЫХ ФИЛЬТРАХ 5.2. Аналого-цифровое преобразование 5.3. Цифро-аналоговое преобразование 5. 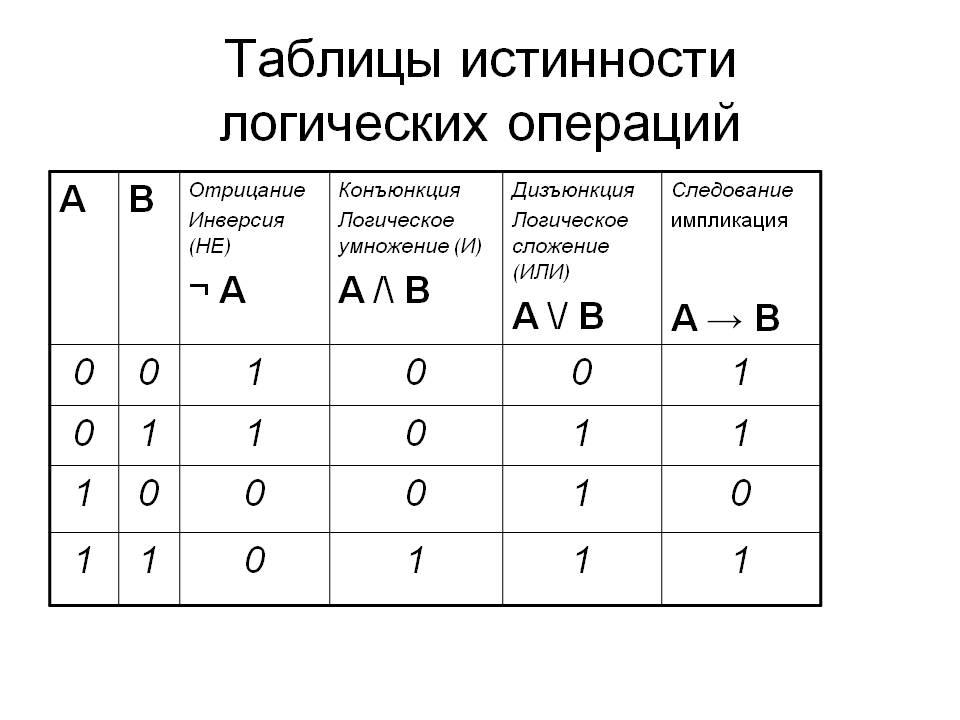4. Системы счисления, применяемые в цифровых устройствах 5.5. Система счисления с фиксированной запятой 5.6. Системы счисления с плавающей запятой 5.7. Система счисления с поблочно плавающей запятой 5.8. Виды квантования в цифровых фильтрах 5.9. Усечение 5.10. Округление 5.11. Шум округления в рекурсивных структурах с фиксированной запятой 5.12. Ограничение динамического диапазона в системах с фиксированной запятой 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме 5.14. Ограничение динамического диапазона при построении фильтров в параллельной форме 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления 5.18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления 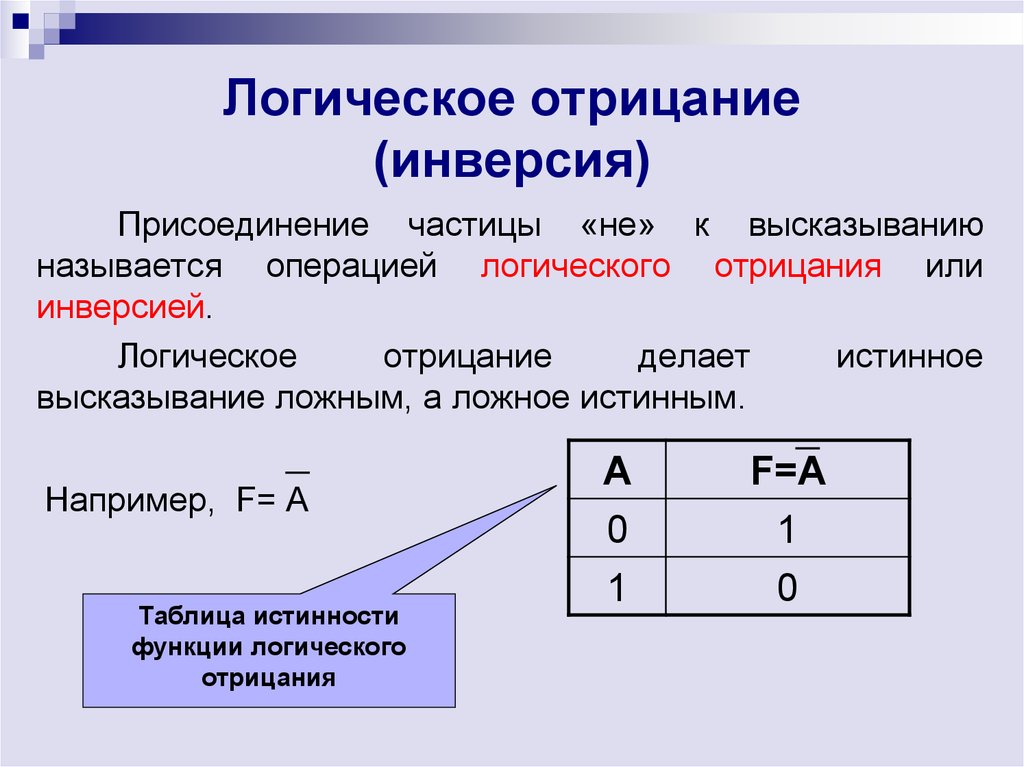5. 19. Шум округления в нерекурсивных структурах с фиксированной запятой 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме 5.21. Шум округления при построении нерекурсивных фильтров в каскадной форме 5.22. Шум округления в рекурсивных структурах с плавающей запятой 5.23. Квантование коэффициентов 5.24. Квантование коэффициентов в рекурсивных структурах 5.25. Квантование коэффициентов при построении фильтров в прямой форме 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов 5.27. Оптимальное квантование коэффициентов 5.28. Квантование коэффициентов в двухполюсном фильтре 5.29. Квантование коэффициентов в нерекурсивных структурах 5.30. Квантование коэффициентов при построении КИХ-фильтров 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме 5.32. Колебания предельного цикла Глава 6. СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ 6.2. Введение в алгоритмы БПФ с основанием 2 6. 3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени 6.4. Перестановка данных и двоичная инверсия 6.5. Программа расчета БПФ на ФОРТРАНе 6.6. Алгоритм БПФ с прореживанием по частоте 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ 6.8. Единый подход к алгоритмам БПФ 6.9. Алгоритмы БПФ с основанием 2 6.10. Спектральный анализ в одной точке z-плоскости 6.11. Спектральный анализ с применением БПФ 6.12. Некоторые характеристики спектрального анализа 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров 6.14. Использование окон при спектральном анализе 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ 6.16. Алгоритм Блюстейна 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации 6.18. Энергетический спектр случайных сигналов 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований ПРИЛОЖЕНИЕ. УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ Глава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ 7.2. Двумерные сигналы 7.3. Двумерные системы 7.4. Физическая реализуемость. Разделимость. Устойчивость 7.5. Двумерные разностные уравнения 7.6. Частотные методы 7.7. Двумерное z-преобразование 7.8. Конечные последовательности 7.9. Свертка последовательностей 7.10. Двумерное ДПФ 7.11. Расчет двумерных фильтров 7.12. БИХ-фильтры 7.13. Устойчивость БИХ-фильтров 7.14. КИХ-фильтры 7.15. Двумерные весовые функции (окна) 7.16. Пример расчета фильтра нижних частот методом взвешивания 7.17. Фильтры с частотной выборкой 7.18. Двумерные фильтры нижних частот с частотной выборкой 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров 7.20. Частотное преобразование одномерных фильтров в двумерные 7.21. Примеры обработки изображений Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов 8.3. Булева алгебра. 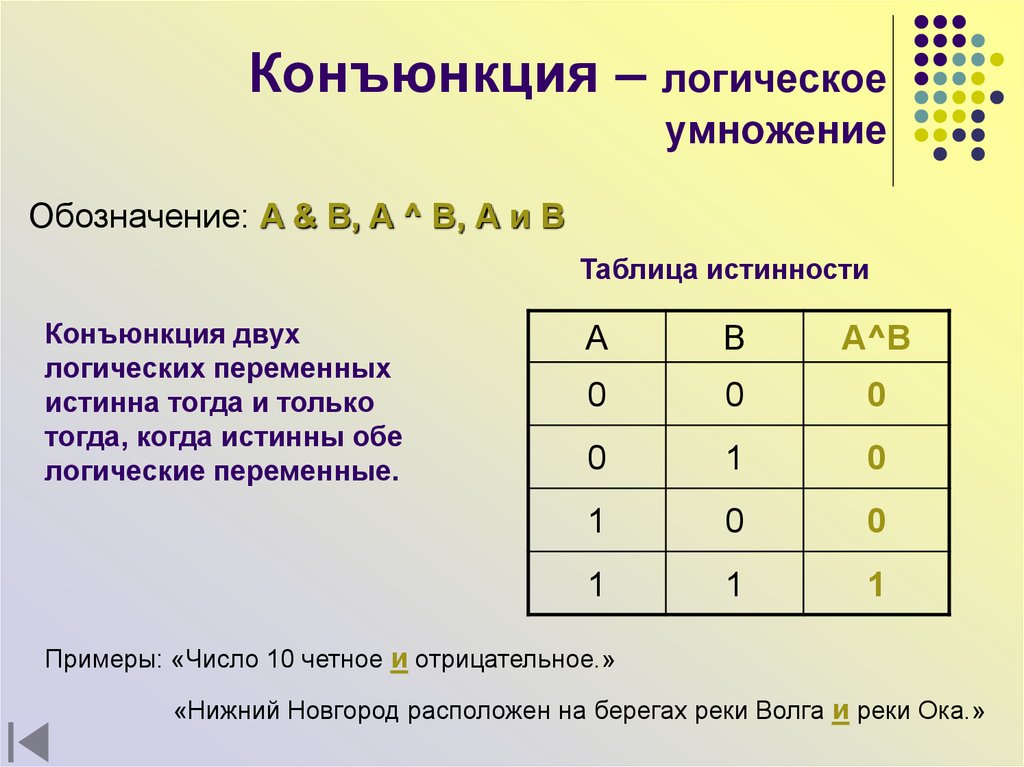Примеры простых логических цепей 8.4. Основные типы интегральных логических схем 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства 8.6. Умножители 8.7. Делители и устройства с плавающей запятой 8.8. Пример: проектирование быстродействующего матричного умножителя 8.9. Заключение ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ 9.2. Аппаратурное построение КИХ-фильтра прямой формы 9.3. Параллелизм при построении КИХ-фильтров прямой формы 9.4. Каскадная форма КИХ-фильтра 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма 9.6. Прямая форма построения БИХ-фильтров 9.7. Каскадная форма БИХ-фильтров 9.8. Мультиплексирование 9.9. Цифровой приемник клавишно-тонального вызова 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах 9. 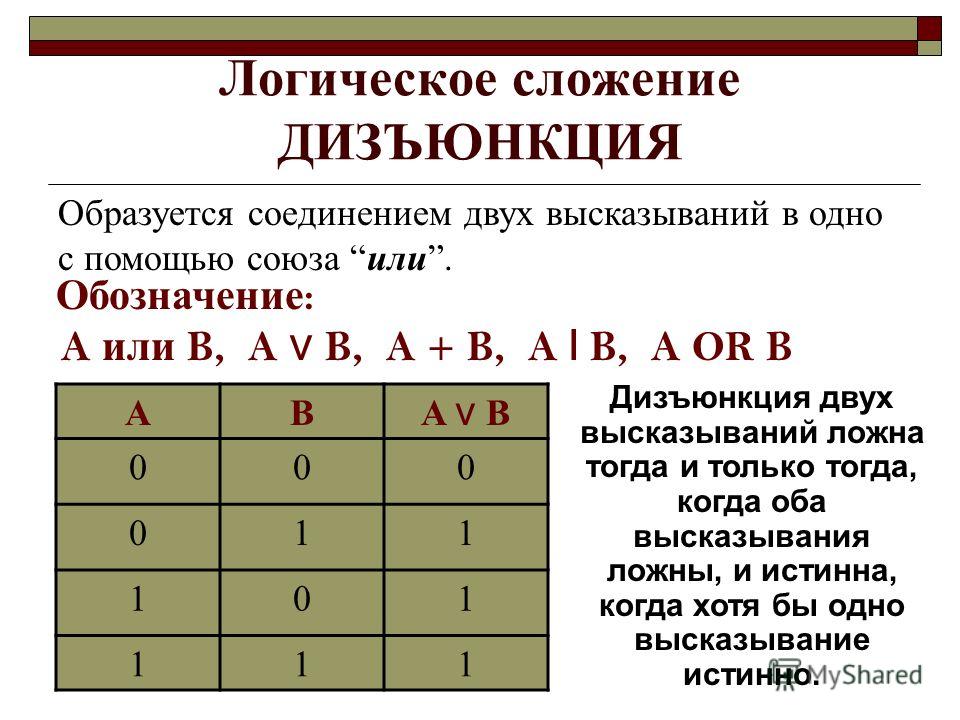12. Специализированный цифровой синтезатор частот 9.13. Методы генерации псевдослучайных чисел 9.14. Методы генерации гауссовых случайных чисел Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ 10.2. Обзор теоретических основ БПФ 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием 10.5. Эффекты квантования в алгоритмах БПФ 10.6. Особенности аппаратурной реализации БПФ с основанием 2 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2 10.9. Выполнение БПФ с использованием сверхоперативной памяти 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом 10.11. Общие вопросы построения поточных схем БПФ 10.12. Поточные схемы БПФ с основанием 2 10.13. Поточная схема БПФ с основанием 4 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4 10.15. Структуры БПФ с повышенным уровнем параллелизма 10. 16. Общие принципы построения специализированных процессоров БПФ 10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом 10.19. Поточный свертыватель с тактовой частотой 10 МГц Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ 11.2. Специализированные и универсальные вычислительные машины 11.3. Способы описания вычислительных машин 11.4. Программа вычисления скользящей суммы 11.5. Особенности ввода — вывода при обработке в реальном времени 11.6. Методы увеличения быстродействия вычислительной машины 11.7. Сверхоперативные ЗУ 11.8. Распараллеливание арифметических операций 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории 11.11. Структурные схемы арифметических устройств 11.12. Синхронизация 11.13. Обзор методов увеличения быстродействия, использованных в FDP 11.14. Выполнение быстрого преобразования Фурье с помощью FDP 11.15. Подпрограммы для действий с плавающей запятой 11.16. Обзор особенностей FDP, связанных с распараллеливанием 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов 11.18. Лабораторная вычислительная система для цифровой обработки сигналов ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ 12.2. Модель образования речи 12.3. Кратковременный спектральный анализ 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе 12.5. Особенности анализа речи 12.6. Система анализа — синтеза 12.7. Полосный вокодер 12.8. Анализаторы вокодеров. Особенности обработки сигналов 12.9. Синтезаторы вокодеров. Особенности обработки сигналов 12.10. Другие схемы вокодеров 12.11. Выделение высоты основного тона и обнаружение тон — шум 12.12. Обнаружитель тон — шум 12. 13. Гомоморфная обработка речи 12.14. Гомоморфный вокодер 12.15. Формантный синтез 12.16. Цепь возбуждения звонких фрикативных звуков 12.17. Генератор случайных чисел 12.18. Цифровая обработка в формантном синтезаторе 12.19. Линейное прогнозирование речи 12.20. Система речевого ответа для вычислительной машины 12.21. Заключение 13.1. Вводные замечания о принципах радиолокации и ее применениях 13.2. Состав и параметры радиолокационной системы 13.3. Выбор сигналов и функция неопределенности 13.4. Цифровые согласованные фильтры для радиолокационных сигналов 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений 13.6. Экспериментальный радиолокатор дальнего действия 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора 13.8. Заключение

Что такое булевская логика и как она используется в программировании

Булева логика является ключевой концепцией любого языка программирования, независимо от того, создаете ли вы видеоигру на C++, разрабатываете следующее лучшее приложение на Swift, выполняете поиск в реляционных базах данных на SQL, или работа с большими данными в Python. В этой статье мы расскажем, что такое логическая логика, как она работает и как создавать собственные логические выражения.

Что такое булева логика?

Булева логика — это тип алгебры, в котором результаты рассчитываются либо как ИСТИНА, либо как ЛОЖЬ (известные как значения истинности или переменные истинности). Вместо использования арифметических операторов, таких как сложение, вычитание и умножение, логическая логика использует три основных логических оператора: И, ИЛИ и НЕ.

ИСТИНА и ЛОЖЬ: их может быть только два

За булевой логикой стоят два очень простых слова: ИСТИНА и ЛОЖЬ.

Обратите внимание, что логическое значение TRUE или FALSE очень отличается от ввода строк «True» и «False» в ваш код. На самом деле языки программирования помещают эти два логических значения в свой собственный тип объекта, отдельный от целых чисел, строк и чисел с плавающей запятой. Но в то время как числовые или строковые значения в программировании могут быть практически бесконечными, есть только два возможных логических значения: ИСТИНА и ЛОЖЬ.

Как это работает? Булева логика рассматривает сообщаемую связь между вещами и определяет, сохраняется ли эта связь. Например, возьмем уравнение:

2 + 2 = 4

Здесь у нас есть две части, 2 + 2 и 4, и мы сообщаем, что эти две части равны друг другу. Это правильно? Да, так что логический результат этого будет ИСТИНА. В этом примере комбинация двух частей 2 + 2 и 4 вместе с отношением (= равно) называется логическим выражением.

Давайте посмотрим на другое логическое выражение:

10 – 4 = 5

Здесь мы сообщаем, что 4, вычитаемое из 10, равно 5. Верно? Конечно, нет, и именно поэтому это логическое выражение вернет значение FALSE.

Логическое выражение	Результат
2 + 2 = 5	ЛОЖЬ
5 – 1 = 4	ИСТИНА
4 * 5 > 10	ИСТИНА
40/10 < 1	ЛОЖЬ

Построение логических выражений

Имейте в виду, что логическая логика работает только тогда, когда выражение может быть ИСТИНА или ЛОЖЬ. Например, выражение 3 + 8 не является логическим выражением, потому что оно не сравнивается и не связано с чем-то другим. Но выражение 3 + 8 = 10 является логическим выражением, потому что теперь мы можем оценить каждую сторону и посмотреть, является ли отношение между ними ИСТИННЫМ или ЛОЖНЫМ (в данном случае ЛОЖНЫМ).

Мы можем строить логические выражения со всеми видами данных, включая переменные. Например, предположим, что мы присвоили эти значения переменным x и y где-то в нашем коде:

x равно 7
y равно 3

Теперь мы можем построить логические выражения, используя наши переменные:

Логическое выражение	Результат
х + у < 11	ЛОЖЬ
х * у = 21	ИСТИНА
х/у > 10	ЛОЖЬ
х + (2 * у) = 13	ИСТИНА

Логические выражения также могут определять, идентичны ли две строки. Просто помните, что большинство языков программирования чувствительны к регистру.

Логическое выражение	Результат
«Я люблю Codecademy» = «Я люблю Codecademy»	ИСТИНА
«Я люблю Codecademy» = «Codecademy»	ЛОЖЬ
«Я люблю Codecademy» = «Я ЛЮБЛЮ Codecademy»	ЛОЖЬ

Существует множество других способов построения логических выражений в зависимости от языка программирования. Например, вы можете использовать логическое выражение, чтобы определить, содержится ли число в списке в Python или текстовая строка находится в таблице базы данных SQL.

Булевы операторы

Теперь, когда вы понимаете основы булевых выражений, давайте рассмотрим еще один ключевой аспект булевой логики: булевы операторы. Есть три основных логических оператора: И, ИЛИ и НЕ.

Чтобы лучше понять, как работают логические операторы, давайте на мгновение представим, что мы находимся в магазине мороженого. Скажем, мы собираемся приготовить мороженое из двух шариков с разными вкусами. Но я немного привередлив в еде, поэтому могу не принимать каждую комбинацию пломбира, которую получаю. Мы можем использовать логические выражения и логические операторы, чтобы выяснить, буду ли я есть мороженое или нет.

AND

Логический оператор AND используется для подтверждения истинности двух или более логических выражений.

Например, в моем мороженом я хочу, чтобы первый вкус был шоколадным, а второй — ванильным. Мы могли бы превратить это в логическое выражение с оператором И, которое выглядит примерно так:

Аромат_1 = Шоколад И Аромат_2 = Ваниль

Это означает, что первый аромат должен быть шоколадным, а второй аромат должен быть ванильным. В противном случае я не буду есть мороженое.

Мы могли бы представить эту ситуацию в виде таблицы возможных вариантов:

Вкус_1	Вкус_2	Ешьте мороженое?
Шоколад	Ваниль	Да
Шоколад	Клубника	№
Манго	Ваниль	№
Манго	Клубника	№

Подобные таблицы постоянно используются в булевой логике. Их называют таблицами истинности, и мы можем составить одну из них для нашего примера с мороженым. Если что-то соответствует моим придирчивым условиям вкуса мороженого, то это ПРАВДА. Если нет, то это ЛОЖЬ.

Вот как таблица выше будет выглядеть в виде таблицы истинности:

Вкус_1	Вкус_2	Результат
ИСТИНА	ИСТИНА	ИСТИНА
ИСТИНА	ЛОЖЬ	ЛОЖЬ
ЛОЖЬ	ИСТИНА	ЛОЖЬ
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ

ИЛИ

Логический оператор ИЛИ проверяет, выполняется ли то или иное условие.

Например, если бы я хотел, чтобы первым ароматом была клубника, а вторым ароматом был манго, то логическое выражение было бы таким:

Аромат_1 = Клубника ИЛИ Аромат_2 = Манго

Возможные варианты можно организовать следующим образом:

Вкус_1	Вкус_2	Ешьте мороженое?
Клубника	Манго	Да
Клубника	Вишня	Да
Вишня	Манго	Да
Ваниль	Малина	№

И таблица истинности будет выглядеть так:

Вкус_1	Вкус_2	Результат
ИСТИНА	ИСТИНА	ИСТИНА
ИСТИНА	ЛОЖЬ	ИСТИНА
ЛОЖЬ	ИСТИНА	ИСТИНА
ЛОЖЬ	ЛОЖЬ	ЛОЖЬ

Обратите внимание, что оператор ИЛИ возвращает ИСТИНА, если одно из двух логических выражений истинно, а также когда оба выражения истинны. По этой причине этот оператор ИЛИ также известен как включающий оператор ИЛИ. В качестве альтернативы есть также оператор XOR (исключающее или), который возвращает ИСТИНА только тогда, когда одно из двух выражений истинно.

NOT

Логический оператор NOT отличается от AND и OR тем, что принимает только один аргумент. Он проверяет, является ли значение FALSE или нет. Иными словами, он меняет значения TRUE на FALSE, а значения FALSE на TRUE. Например, я ненавижу ромовый изюм и абсолютно не буду есть ничего с ромовым изюмом. Как это может выглядеть в виде таблицы?

Вкус	Ешь мороженое?
Шоколад	Да
Ром с изюмом	№

Таблица истинности выглядит так:

Вкус	Результат
ЛОЖЬ	ИСТИНА
ИСТИНА	ЛОЖЬ

Вы можете комбинировать логические выражения, чтобы выразить мое предпочтение мороженого с мороженым, когда речь идет о ромовом изюме, например:

НЕ (Аромат_1 = Ромовый изюм ИЛИ Вкус_2 = Ромовый изюм)

3 29299

3 29299

Вкус_1

Вкус_2	Ешьте мороженое?
Шоколад	Малина	Да
Персик	Ром с изюмом	№
Ром с изюмом	как новый	№
Ром с изюмом	Ром Изюм	№

Предложение OR в круглых скобках вернет TRUE для всего, что содержит ромовый изюм. Применение к нему НЕ изменит значение выражения ИЛИ с ИСТИНА на ЛОЖЬ и наоборот. Подобно операторам в арифметике, логические операторы имеют порядок старшинства: сначала обращаются к элементам в круглых скобках, затем к оператору НЕ, И и, наконец, к ИЛИ. Наша новая таблица истинности выглядит так:

Вкус_1	Вкус_2	Результат
ЛОЖЬ	ЛОЖЬ	ИСТИНА
ЛОЖЬ	ИСТИНА	ЛОЖЬ
ИСТИНА	ЛОЖЬ	ЛОЖЬ
ИСТИНА	ИСТИНА	ЛОЖЬ

Применение вашей булевой логики

Итак, что дальше после изучения основ булевой логики?

Булева логика имеет решающее значение для создания кода, который помогает вашей программе быстро принимать решения относительно данных и входных данных, поэтому попробуйте применить свои логические знания в онлайн-курсе программирования. И если вы не уверены, какой курс выбрать следующим, взгляните на наши карьерные пути разработчиков. Мы поможем вам сосредоточиться на лучших навыках, необходимых для достижения желаемой должности.

---

Курсы и учебные пособия по основам кода | Codecademy

Хотите научиться программировать, но не знаете, с чего начать? Наша область Code Foundations предоставляет обзор основных приложений программирования и учит важным концепциям, которые вы найдете в каждом языке программирования. Этот контент подготовит вас к тому, чтобы наметить курс на более техническое обучение…

Codecademy

Введение в булеву логику — GeeksforGeeks

Булева алгебра — это тип алгебры, который создается путем работы с двоичной системой. В 1854 году Джордж Буль, английский математик, предложил эту алгебру. Это вариант логики высказываний Аристотеля, в которой используются символы 0 и 1, или Истина и Ложь. Булева алгебра связана с бинарными переменными и логическими операциями.

Логическое выражение и переменные

Логическое выражение — это выражение, которое при вычислении дает логическое значение, истинное или ложное, единственный способ выразить логическое значение. Принимая во внимание, что логические переменные — это переменные, которые хранят логические числа. P + Q = R — логическая фраза, в которой P, Q, R — логические переменные, которые могут хранить только два значения: 0 и 1. Компьютер выполняет все операции, используя двоичные 0 и 1, поскольку компьютер понимает машинный язык (0/1 ). Булева логика, названная в честь Джорджа Буля, представляет собой тип алгебры, в которой все значения сводятся к одной из двух возможностей: 1 или 0. Чтобы эффективно понять булеву логику, мы должны сначала понять правила булевой логики, а также истину таблицы и логические вентили.

Таблицы истинности 

Таблица истинности представляет все разнообразие комбинаций входных и выходных значений в виде таблицы. В нем показаны все возможности ввода и вывода и, следовательно, сохраняется таблица истинности имени. В логических задачах, таких как булева алгебра и электронные схемы, обычно используются таблицы истинности. T или 1 означает «Истина», а F или 0 означает «Ложь» в таблице истинности.

Пример:

А	B	X = A.B
T	T	T
T	F	F
F	T	F
F	F	F

Логические элементы 

Логические элементы – это виртуальное или физическое устройство, выполняющее логическую функцию. Они используются для создания логических схем. Логические элементы являются основными компонентами любой цифровой системы. Эта электрическая цепь может иметь только один выход и 1 или более входов. Связь между входом и выходом регулируется определенной логикой. Логические вентили И, ИЛИ, НЕ и т. д. являются примерами логических вентилей.

Типы логических элементов

1. Элемент И (Продукт): Логический элемент с двумя или более входами и одним выходом называется элементом И. Правила логического умножения используются для работы вентиля И. Логический элемент И может иметь любое количество входов, хотя наиболее распространенными являются вентили И с двумя и тремя входами. Если на каком-либо из входов низкий уровень (0), на выходе этого вентиля также низкий уровень. Когда все входы имеют высокий уровень (1), выход также будет высоким.

Логическая схема:

Таблица истинности:

Для вентиля И выход X истинен тогда и только тогда, когда оба входа P и Q истинны. So the truth table of AND gate is as follows:

P	Q	X = P.Q
T	T	T
T	F	F
Ф	Т	Ф
F	F	F

 

2. Элемент ИЛИ (сумма): Логический элемент, выполняющий операцию логического ИЛИ, называется элементом ИЛИ. Если один или оба входа вентиля имеют высокий уровень, логическая операция ИЛИ выдает высокий уровень на выходе (1). (1). Если ни на одном из входов нет высокого уровня, результатом будет низкий уровень на выходе (0). Точно так же, как вентиль И может иметь неограниченное количество входных пробников, вентиль ИЛИ может иметь только один выходной пробник. Логический элемент ИЛИ находит максимум между двумя двоичными цифрами.

Логическая схема:

Таблица истинности:

Для вентиля ИЛИ выход X истинен тогда и только тогда, когда истинен любой из входов P или Q. So the truth table of OR gate is as follows:

P	Q	X = P + Q
T	T	T
T	F	Т
Ф	Т	Т
F	F	F

3. Логические элементы НЕ (дополнение): низким до логического уровня 0, когда их единственный вход находится на логическом уровне 1, или, другими словами, они инвертируют свой входной сигнал. Выход вентиля НЕ возвращает высокий уровень только тогда, когда его вход находится на уровне логического 0. Выход ~ P (~ обозначает «нет») одного входного вентиля НЕ является истинным только тогда, когда вход P ложный или мы можем сказать «неправда». Его также называют обратным вентилем, поскольку он приводит к отрицанию входного логического выражения.

Логическая схема:

Таблица истинности:

Для вентиля НЕ выход X истинен тогда и только тогда, когда вход P ложен. So the truth table of NOT gate is as follows:

P	~P
T	F
F	T

4. NAND Gate: Логический вентиль, известный как вентиль И-НЕ, обеспечивает низкий уровень выходного сигнала (0), только если все его входы истинны, и высокий уровень выходного сигнала (1) в противном случае. В результате вентиль И-НЕ является инверсией вентиля И, и его схема создается путем соединения вентиля И и вентиля НЕ. NAND означает «не И» Gate, и это приводит к ложному результату только тогда, когда оба входа P и Q истинны. Вентиляторы И (вместе с вентилями ИЛИ-НЕ) известны как универсальные вентили, потому что они представляют собой форму логических вентилей, которые могут реализовывать любую логическую функцию без использования вентилей любого другого типа.

Логическая схема:

Таблица истинности:

Для вентиля И-НЕ выход X ложен тогда и только тогда, когда оба входа (т. е. P и Q) истинны. So the truth table of the NAND gate is as follows:

P	Q	~(P.Q)
T	T	F
T	F	Т
Ф	Т	T
F	F	T

5. Nor Gate: 9083 false, и низкий выход (0) в противном случае. В результате вентиль ИЛИ-НЕ является обратным вентилю ИЛИ, и его схема создается путем соединения вентилей ИЛИ и вентилей НЕ. NOR означает «не ИЛИ» Gate, и это приводит к истине только тогда, когда оба входа P и Q ложны.

Логическая схема:

Таблица истинности:

Для вентиля И-НЕ выход X истинен тогда и только тогда, когда оба входа (т. е. P и Q) ложны. So the truth table of NOR gate is as follows:

P	Q	X = ~(P + Q)
T	T	F
T	Ф	Ф
Ф	Т	Ф
F	F	T

и один выход. Только один из входов вентиля XOR должен быть истинным, чтобы выход был истинным. Выход вентиля XOR ложен, если оба его входа ложны, или истинен, если оба его входа истинны. Исключающее ИЛИ означает вентиль «Исключающее ИЛИ», и он приводит к истине только тогда, когда любой из двух входов P и Q истинен, т. е. либо истинно P, либо истинно Q, но не оба одновременно.

Logical circuit:

Truth table:

P	Q	X = P ⊕ Q
T	T	F
T	F	T
F	T	T
F	F	F

7. XNOR Gate: An NOR gate (also known as an Exclusive NOR gate) — это цифровой логический вентиль, который находится прямо напротив вентиля XOR. Он имеет два или более входа и один выход. Когда один из двух его входов истинен, но не оба, он вернет ложь. XNOR означает «Исключающее ИЛИ» Gate, и его результат истинен только тогда, когда оба его входа P и Q либо истинны, либо ложны.

Logical circuit:

Truth table:

.0003

P	Q	X = P XNOR Q
T	T	T
T	F	F
F	T	F
F	F

Закон	или форма	и форма
Закон о личности	P + 1 = P	P.0 = P	P + 1 = P	P.0 = P	P + 1 = P	. P.0 = P	P + 1 = P	P.0 = P	P + 1 = P	P.0 = P	P + 1 = P	P.0 = P	P + 1 = P	P.	P.P = P
Коммутативный закон	P + Q = Q + P	P.Q = Q.P
NULL LAW	1 + P = P	0.P = P	1 + P = P	0,P = P	1 + P = P	0,P = P	1 + P = P	0. P = P	1 + P = P	0.P = P	1 + P = P	0,P = P	1 + P = P	0.P = P	1 + P = P	0.	П + (~П) = 1	P.(~P) = 0
Ассоциативный закон	P + (Q + R) = (P + Q) + R	P.(Q.R) = (P.Q).R
Распределительный закон	P + QR = (P + Q).(P + R)	P.(Q + R) = P.Q + P.R
Закон поглощения	P + PQ = P	P.( P + Q) = P
Закон де Моргана	~(P + Q) = (~P).(~Q)	~(P.Q) = (~P) + (~Q)

Законы де Моргана

Закон Де Моргана гласит:

Утверждение 1: Дополнение произведения (И) двух логических переменных (или выражений) равно сумме (ИЛИ) дополнения каждой логической переменной (или выражения) .

~(P.Q) = (~P) + (~Q) 

Доказательство:

Утверждение: ~(P. Q) = (~P) + (~Q) 

Таблица истинности:

P	Q	(~P)	(~Q)	~(P.Q)	(~P)+(~Q)
T	T	F	F	F	F
T	F	F	T	T	T
F	T	T	F	T	T
F	F	T	T	T	T

Мы можем ясно видеть, что значения истинности для ~(P.Q) равны значениям истинности для (~P) + (~Q), соответствующих тем же входным данным.

Заявление 2: Дополнение суммы (ИЛИ) двух логических переменных (или выражений) равно произведению (И) дополнения каждой логической переменной (или выражения).

~(P + Q) = (~P).(~Q)

Доказательство

Утверждение: ~(P+Q) = (~P). (~Q)

Таблица истинности :

P	Q	(~P)	(~Q)	~(P + Q)	(~P).(~Q)	9
T	T	F	F	F	F
T	F	F	T	F	F
F	T	T	F	F	F
F	F	T	T	T	T
T.	T

T. T.. равные значениям истинности для (~P).(~Q), соответствующие тому же входу.

Логические схемы

Электрическая схема, в которой мы можем подать один или несколько двоичных входов (предполагая два состояния, включено или выключено) и получить один двоичный выход, соответствующий входу, способом, который можно описать как функцию в символическая логика. Элементы И, ИЛИ и НЕ представляют собой базовые логические схемы, выполняющие логические функции — И, ИЛИ и НЕ соответственно. Компьютеры могут выполнять более сложные задачи со схемами, чем с одним вентилем.

Пример: Цепочка из двух логических элементов является наименьшей схемой. Рассмотрим следующую схему:

Эта логическая схема предназначена для логического выражения: (P + Q).R.

Здесь используется первый логический элемент ИЛИ: входы P, Q и выход P + Q.

Затем используется логический элемент И: (P + Q), R является входом в него и (P + Q).R является выходом.

Итак, таблица истинности:

P	Q	R	P + Q	X = (P + Q).R
T	T	T	T	T
T	T	F	T	F
T	F	T	T	T
T	F	F	T	F
F	T	T	T	Т
F	T	F	T	F
F	F	T	F	F
F	F	F	F	F

Примеры вопросов

Вопрос 1. Что такое универсальные ворота?

Решение:

Универсальные вентили — это логические вентили, которые могут реализовывать любую булеву функцию без необходимости использования каких-либо дополнительных вентилей. Универсальных ворот в цифровой электронике всего два: 
1. Ворота НЕ-И и
2. Ворота НЕ-ИЛИ.

Вопрос 2. Разработайте логическую цепь для: A.B + B.C

Решение:

Вопрос 3. Что будет для экспрессии Boolean. Решение:

X = ~(P + Q).R + S

Вопрос 4. Проверьте с помощью таблицы истинности: P + P.Q = P

Решение:

The truth table for P + P.Q = P

P

Q

P.Q

P + P. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника