(21)Булева алгебра (алгебра логики) и ее применение при анализе работы эвм. Понятие о булевых (переключательных) функциях (ппф)
Теоретической основой построения ЭВМ служит специальные математические дисциплины, одной из которых является алгебра логики (булева алгебра). Аппарат булевой алгебры широко используется для описания схем ЭВМ и ЦВМ, а так же для их проектирования и оптимизации. Информация в ЭВМ и цифровых устройствах, так или иначе сводится к ее представлению в 2 СС. На основании зависимости выходных сигналов от входных y=f(x) можно описать любое устройство ЭВМ. Такой зависимостью является булевой функцией, у которой число ее возможных состояний и состояний каждого независимого элемента равно двум (либо 0, либо 1). В технической литературе булевые функции называются логическими или переключательными. Булува алгебра оперирует логическими переменными. Логические переменные может принимать одно из двух значений, да или нет (0;1).
(22)Основные логические операции алгебра логики
На множестве {0;1} в булевой алгебре
определены 3 основных логических
операций: а)И (логическое умножение,
конъюнкция)
.
переменные | НЕ | И | ИЛИ | ||
Х1 | |||||
0 | 0 | 1 | 1 | 0 | 0 |
0 | 1 | 1 | 0 | 0 | |
1 | 0 | 0 | 1 | 0 | 1 |
1 | 1 | 0 | 0 | 1 | 1 |
(23)Область определения пф, наборы аргументов пф, их виды
В общем случае всякая логическая функция
имеет свою область определения,
охватывающую совокупность комбинаций
ее аргументов.
(24)Булевы функции двух аргументов и их характеристика
Т.к. результат любой из логической
операции принимает значение из того же
множества {0;1}, что и аргументы, то можно
составить комбинации логических
операций, когда результат одной операции
используется в качестве операнда в
других операциях. Тогда любая логиче5ская
операция может быть записана как
элементарная логическая функция.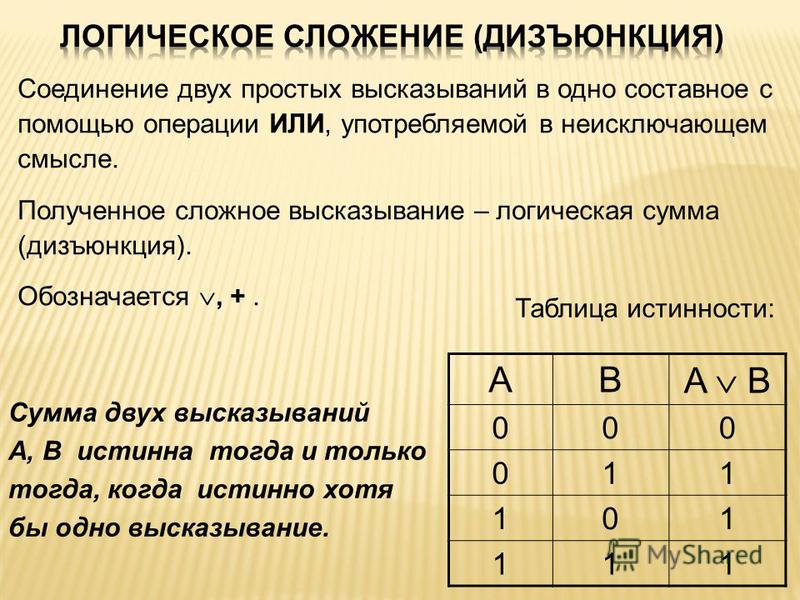
(25)Основные законы алгебры логики
1.Закон одинарных элементов:
2)законы отрицания (противоречия)
3)закон двойного отрицания
4)комбинационные законы
а)тавтология (повторения)
х*х=х
б)коммутативный (переместительный)
х1*х2=х2*х1
в)ассоциативный (сочетательный)
(х1*х2)х3=х1(х2*х3)
г)дистрибутивный (распределительный)
д)поглощение
(х1 поглощает х2)
е)склеивание
ж)обобщенного склеивания
5)законы дуальности (инверсии, двойственности) (теоремы де Моргана)
6)обобщенные законы
дуальности (т. К.Шеннона)
К.Шеннона)
(26)Понятие функциональной полноты системы БФ, основной функционально-полный набор и его смысл
Система булевых функций называется
полной, если на ее основе можно получить
любую логическую функцию, используя
лишь операции суперпозиции. Алгебра
логики дает несколько наборов булевых
функций, обладающих функциональной
полнотой и образующих полный базис
простейших функций, из которых могут
быть построены сколь угодно сложные
функции. В качестве такого набора служит
набор из трех булевых функций, носящих
название основная функция полного
набора. [1] 1)F1(X1,Х2)=(Х1Х2) –
конъюнкция, F7(Х1,Х2)=()-дизъюнкция,
F12(Х1,Х2)=-инверсия.
В общем случае одна из этих функций (F1
или F12) являются излишней, т.к. ее исключение
не приводит к нарушению функциональной
полноты. [2]
[3]
.
Наборы [2] или [3] отсутствующей по одной
операции (функции):
;
.
Однако работа с переключательными
функциями в этих базисах требует от
специалистов специальных навыков.
Эффективная разреженная булева алгебра — то, что нужно алгоритмам анализа графов / Хабр
Создание и практическое использование алгоритмов сильно зависит от возможности эффективно их реализовать. В лаборатории языковых инструментов JetBrains разрабатывают алгоритмы поиска путей в помеченных графах с дополнительными ограничениями. Эти алгоритмы достаточно естественно выражаются в терминах операций над булевыми матрицами, но в современных высокопроизводительных библиотеках линейной алгебры пока нет полного набора необходимых операций над булевым полукольцом. Поэтому мы решили их реализовать.
Всем привет! Меня зовут Мария Карпенко и в этом году я окончила корпоративную магистерскую программу JetBrains в Университете ИТМО по направлению Software Engineering. Я начала интересоваться программированием, обучаясь в СПбГЭУ на направлении «Математические методы в экономике», и на последнем курсе поступила в Computer Science Center (CSC). Именно в CSC я узнала о существовании корпоративной магистратуры и однозначно определилась с выбором программы. Сейчас я стажируюсь в «Яндексе» в команде Трекера.
Я начала интересоваться программированием, обучаясь в СПбГЭУ на направлении «Математические методы в экономике», и на последнем курсе поступила в Computer Science Center (CSC). Именно в CSC я узнала о существовании корпоративной магистратуры и однозначно определилась с выбором программы. Сейчас я стажируюсь в «Яндексе» в команде Трекера.
В первый год магистратуры студенты активно приобретают новые знания, а на втором курсе начинается работа над дипломом. Я старалась выбрать для себя тему, которая позволит погрузиться в новые технологии и алгоритмы, с акцентом на практическую часть. В итоге я остановилась на теме «Реализация операций с разреженными булевыми матрицами на OpenCL». Работу выполняла под руководством Семёна Григорьева, исследователя лаборатории языковых инструментов JetBrains.
Операции над матрицами и графы
Многие алгоритмы для анализа графов можно выразить через операции с их матрицами смежности. Например, транзитивное замыкание, поиск в ширину, прямое произведение графов. Такие базовые матричные операции входят в стандарт GraphBLAS, разработанный для описания алгоритмов обработки графов в терминах линейной алгебры.
Такие базовые матричные операции входят в стандарт GraphBLAS, разработанный для описания алгоритмов обработки графов в терминах линейной алгебры.
В большинстве практических задач графы оказываются сильно разреженными, что приводит к необходимости хранить матрицы и осуществлять операции с ними в сжатых форматах. В лаборатории языковых инструментов JetBrains разрабатывают алгоритмы анализа графов, сводимые к операциям над разреженными булевыми матрицами. Для подтверждения их практической применимости возникла необходимость в эффективной реализации следующих операций с разреженными булевыми матрицами:
матричное умножение;
матричное сложение;
транспонирование матрицы;
извлечение подматрицы;
редуцирование строк матрицы в вектор;
произведение Кронекера.
Специальные реализации этих операций для матриц, определенных над булевым полукольцом, позволяют, во-первых, экономить память: все форматы для хранения разреженных матриц содержат массив со значениями, который в случае булевой матрицы не нужен. Во-вторых, операции с элементами разреженных булевых матриц сводятся к определению отсутствия или наличия значения на конкретной позиции, что значительно быстрее операций с типами float или double.
Во-вторых, операции с элементами разреженных булевых матриц сводятся к определению отсутствия или наличия значения на конкретной позиции, что значительно быстрее операций с типами float или double.
Современные высокопроизводительные библиотеки линейной алгебры содержат лишь некоторые из необходимых операций, чаще всего умножение и сложение без специализации для булевых матриц. На момент начала работы библиотека cuBool, разрабатываемая в той же лаборатории языковых инструментов, содержала полный набор необходимых операций с реализацией на CUDA. На CPU отмечу библиотеку SuiteSparse, в которой полностью реализован стандарт GraphBLAS.
Моей задачей было создать полное решение на OpenCL, которое позволит задействовать видеокарты от AMD и другие устройства, поддерживающие стандарт. От меня не требовалось изобретать новые алгоритмы для операций с матрицами, необходимо было выбрать лучшие и обосновать свой выбор.
Знакомство с технологией и сжатыми форматами
Работа началась с погружения в высокопроизводительные вычисления, в чем мне помог курс от CSC «Вычисления на видеокартах». Помимо доступных и понятных объяснений принципов программирования на видеокартах, курс содержит ряд практических советов и приемов, связанных как с организацией кода, так и с поиском ошибок параллельного программирования. В рамках курса мы реализовывали многие необходимые промежуточные операции, которые пригодились мне в дальнейшем.
Помимо доступных и понятных объяснений принципов программирования на видеокартах, курс содержит ряд практических советов и приемов, связанных как с организацией кода, так и с поиском ошибок параллельного программирования. В рамках курса мы реализовывали многие необходимые промежуточные операции, которые пригодились мне в дальнейшем.
Также в начале работы мы определились с форматом хранения матриц. Так как нам заранее неизвестна структура матрицы, были выбраны наиболее общие и популярные форматы: COO и CSR (CSC). Именно с этими форматами работают большинство библиотек линейной алгебры. Так как в наших задачах матрицы могут быть сверхразреженными, мы сосредоточились на форматах, в которых матрица занимает O(nnz) памяти, где nnz — количество ненулевых элементов. Таким свойством обладают форматы COO и DCSR, полученный из CSR удалением информации о пустых строках.
Представление разреженной матрицы в сжатых форматах. Пример взят из https://www.researchgate.net/figure/CSR-and-DCSR-formats_fig2_325706323Я реализовала операции в разных форматах, выбирая тот или иной формат исходя из особенностей работы с ним. Также были реализованы конвертации между форматами, которые осуществляются достаточно быстро. Некоторые операции по-разному можно реализовать как в COO, так и в DCSR, поэтому основную реализацию я выбирала по результатам замеров.
Также были реализованы конвертации между форматами, которые осуществляются достаточно быстро. Некоторые операции по-разному можно реализовать как в COO, так и в DCSR, поэтому основную реализацию я выбирала по результатам замеров.
Выбранные форматы для операций:
COO:
DCSR:
умножение;
извлечение подматрицы;
редуцирование строк матрицы;
произведение Кронекера.
О реализациях операций
Первыми я реализовала сложение, транспонирование и произведение Кронекера в формате COO. Транспонирование в этом формате получается очень естественно — достаточно переставить массивы строковых и столбцовых индексов и отсортировать результат. Сложение в формате COO — это слияние двух отсортированных массивов с последующим удалением дубликатов.
Произведение Кронекера в COO также достаточно простое, но, как выяснилось позже, реализация через DCSR работает на порядок быстрее.
Для остальных операций однозначно был выбран формат DCSR, так как в них часто требуется индексация строк, которая в COO осуществляется медленнее.
Самая сложная из реализуемых операций — умножение. Алгоритмы умножения матриц развиваются уже несколько десятилетий, и я ознакомилась со многими работами в этой области. Среди всех выделяются работы W. Liu и Y. Nagasaka. Они подтвердили свою практическую применимость в библиотеках, а алгоритм Y. Nagasaka хорошо показал себя в cuBool.
Оба алгоритма опираются на формулировку умножения матриц, основанную на формировании строк матрицы-результата как линейной комбинации строк второй матрицы, то есть если A * B = C, то:
Для булевых матриц задача сводится к формированию строк матрицы C посредством слияния некоторых строк матрицы B и последующего удаления дубликатов. Точно так же складываются матрицы в COO формате.
В алгоритме W. Liu слияние и удаление дубликатов осуществляются различными способами в зависимости от оценки размера строки. Среди них есть пирамидальная сортировка, битоническая сортировка с удалением дубликатов с помощью префиксной суммы, Merge Path. В алгоритме Y. Nagasaka используется один метод удаления дубликатов — хэш-таблицы с открытой адресацией, в которую обращаются несколько потоков одновременно.
В алгоритме Y. Nagasaka используется один метод удаления дубликатов — хэш-таблицы с открытой адресацией, в которую обращаются несколько потоков одновременно.
Я реализовала оба варианта, и в моей реализации алгоритм Y. Nagasaka оказался лучше и по времени, и по памяти.
Отдельно хочется отметить, что алгоритм Y. Nagasaka значительно проще в поддержке и реализации: он состоит из однообразных ядер (программ для видеокарты), которые отличаются только распределением работы потоков, размером и размещением хэш-таблицы.
Извлечение подматрицы и редуцирование строк матрицы в вектор были реализованы последними в формате DCSR.
Эксперименты
В экспериментальной части мы сосредоточились на операциях, которые есть в большинстве библиотек линейной алгебры: сложение и умножение. Сложение мы тестировали на операции M + M2, а умножение — на M2. Для замеров были выбраны десять сильно разреженных матриц из коллекции SuiteSparse, но далее я приведу результаты по трем матрицам, которые можно считать наиболее показательными: две матрицы с равномерно распределенными ненулевыми элементами разных размеров (строки 1 и 3) и матрица с некоторыми плотными строками (строка 2).
Операции выполнялись на трех различных устройствах: две видеокарты (AMD, NVIDIA) и одна FPGA.
Характеристики устройств:
Вендор | NVIDIA | AMD | Intel FPGA |
Имя | GeForce GTX 1070 | Radeon Vega Frontier Edition | Arria 10 |
Глобальная память | 8 Гб | 16 Гб | 8 Гб |
Локальная память | 48 Кб | 64 Кб | 16 Кб |
Макс. | 1024 Б | 256 Б | 2 Гб |
Частота | 1746 MHz | 1600 MHz | 1000 MHz |
Число АЛУ | 1920 | 4096 | 427200 |
Скомпилировать решение на FPGA позволяет технология Intel FPGA SDK for OpenCL. За предоставленный сервер с устройством Arria10 благодарим компанию Selectel.
На FPGA мои реализации сгенерировались в неэффективную архитектуру, и этому есть несколько объяснений. Сами алгоритмы сильно заточены под устройство видеокарт: нагрузка распределяется с учетом организации работы потоков по ворпам и мультипроцессорам.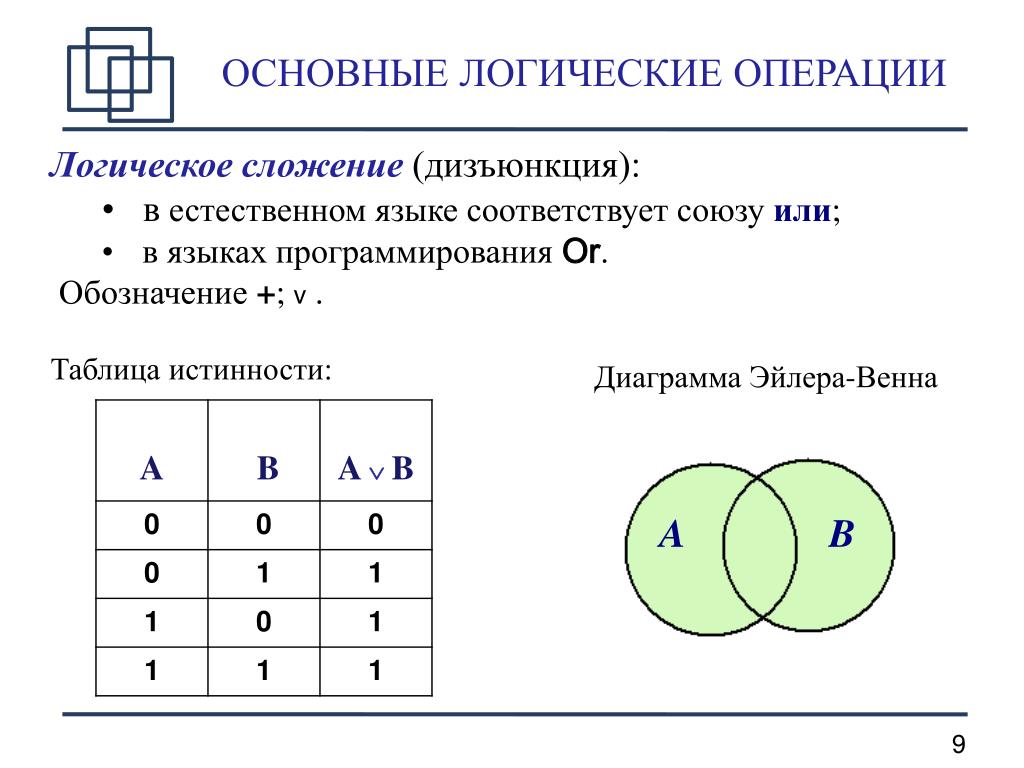 Так как видеокарте не нужно перестраивать свою архитектуру под каждый бинарный файл, мы можем быстро скомпилировать множество ядер, суммарный объем оперативной памяти в которых ничем не ограничен, но в каждом отдельном ядре нужно учитывать ограничения мультипроцессора. С FPGA все иначе: ограничение в 16 КБ затрагивает всю программу, и мне не удалось, например, скомпилировать полный набор ядер для умножения. Пришлось уменьшать число ядер, что привело к неэффективному решению. Время выполнения обеих операций оказалась в сотни раз медленнее CPU-библиотеки SuiteSparse.
Так как видеокарте не нужно перестраивать свою архитектуру под каждый бинарный файл, мы можем быстро скомпилировать множество ядер, суммарный объем оперативной памяти в которых ничем не ограничен, но в каждом отдельном ядре нужно учитывать ограничения мультипроцессора. С FPGA все иначе: ограничение в 16 КБ затрагивает всю программу, и мне не удалось, например, скомпилировать полный набор ядер для умножения. Пришлось уменьшать число ядер, что привело к неэффективному решению. Время выполнения обеих операций оказалась в сотни раз медленнее CPU-библиотеки SuiteSparse.
На операции сложения в моей реализации разница между результатами AMD и NVIDIA объясняется характеристиками видеокарт — AMD почти в 2 раза мощнее.
Сравнение выполнения операции M + M2 на различных устройствах:
№ | Число строк, млн | nnz(M), млн | nnz(M + M2), млн | NVIDIA, мс | AMD, мс | Intel FPGA, мс |
1 | 0,06 | 0,24 | 0,92 | 1,73 ± 3,97 | 1,71 ± 0,30 | 86,51 |
2 | 0,92 | 5,11 | 30,81 | 38,10 ± 0,53 | 19,34 ± 4,68 | 3077,81 |
3 | 2,22 | 4,88 | 13,63 | 15,51 ± 0,48 | 9,27 ± 2,81 | 1248,45 |
В умножении преимущества AMD становится заметно только на матрицах с более плотными строками:
Сравнение выполнения операции M2 на различных устройствах:
№ | Число строк, млн | nnz(M), млн | nnz(M2), млн | NVIDIA (1), мс | NVIDIA (2), мс | AMD (2), мс | Intel FPGA (2), мс |
1 | 0,06 | 0,24 | 0,71 | 2,71 ± 0,11 | 1,88 ± 0,34 | 2,78 ± 1,46 | 5590,79 |
2 | 0,92 | 5,11 | 29,71 | 184,06 ± 0,53 | 126,36 ± 0,34 | 85,97 ± 8,78 | 77601,9 |
3 | 2,22 | 4,88 | 8,76 | 57,27 ± 1,71 | 24,57 ± 0,11 | 29,66 ± 0,85 | — |
(1) — алгоритм W.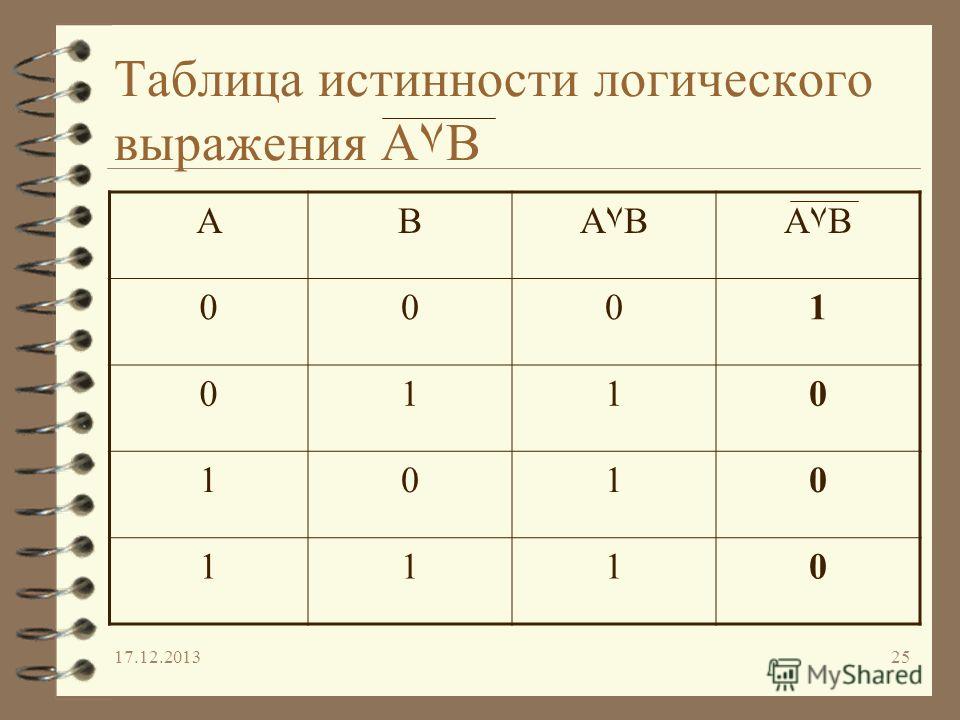 Liu
Liu
(2) — алгоритм Y. Nagasaka
В таблицах ниже представлено сравнение с некоторыми библиотеками линейной алгебры на видеокарте NVIDIA. Как видно из замеров, сложение через перевод матриц в координатный формат реализуют все библиотеки, кроме cuBool. Отмечу, что по потреблению памяти cuBool серьезно выигрывает, так как в используемом алгоритме не выделяется дополнительная память на некоторые промежуточные вычисления.
Сравнение выполнения операции M + M2 среди библиотек линейной алгебры:
№ | nnz(M + M2), млн | cuBool, мс | clBool, мс | Cusp, мс | cuSPARSE, мс | SuiteSpars, мс |
1 | 0,92 | 1,12 ± 0,02 | 1,73 ± 3,97 | 1,54 ± 0,20 | 2,40 ± 0,04 | 3,91 ± 2,06 |
2 | 30,81 | 24,20 ± 0,90 | 38,10 ± 0,53 | 32,08 ± 1,34 | 88,48 ± 0,28 | 77,68 ± 1,66 |
3 | 13,63 | 30,65 ± 1,89 | 15,51 ± 0,48 | 14,75 ± 0,31 | 18,15 ± 0,03 | 50,29 ± 0,93 |
Несмотря на один алгоритм и похожую реализацию, на плотных матрицах cuBool работает заметно быстрее моей реализации clBool. Также cuBool и clBool требуют в среднем на треть меньше памяти, чем другие библиотеки.
Также cuBool и clBool требуют в среднем на треть меньше памяти, чем другие библиотеки.
Сравнение выполнения операции M2 среди библиотек линейной алгебры:
№ | nnz(M2), млн | cuBool, мс | clBool-hash, мс | clSPARSE, мс | cuSPARSE, мс | Cusp, мс | SuiteSparse, мс |
1 | 0,71 | 1,78 ± 0,06 | 1,88 ± 0,34 | 2,02 ± 0,34 | 2,04 ± 0,04 | 5,39 ± 0,12 | 7,92 ± 0,27 |
2 | 29,71 | 42,19 ± 1,26 | 126,36 ± 0,34 | 165,03 ± 8,30 | 4726,33 ± 0,52 | 246,232 ± 9,90 | 712,54 ± 20,07 |
3 | 8,76 | 35,30 ± 0,22 | 24,57 ± 0,11 | 38,51 ± 2,12 | 50,68 ± 0,14 | 51,28 ± 0,35 | 93,47 ± 2,09 |
Заключение
Результат моей работы используется в качестве OpenCL-бэкенда проекта spbla, который был создан для реализации, тестирования и изучения алгоритмов анализа графов, выразимых в терминах операций над булевыми матрицами.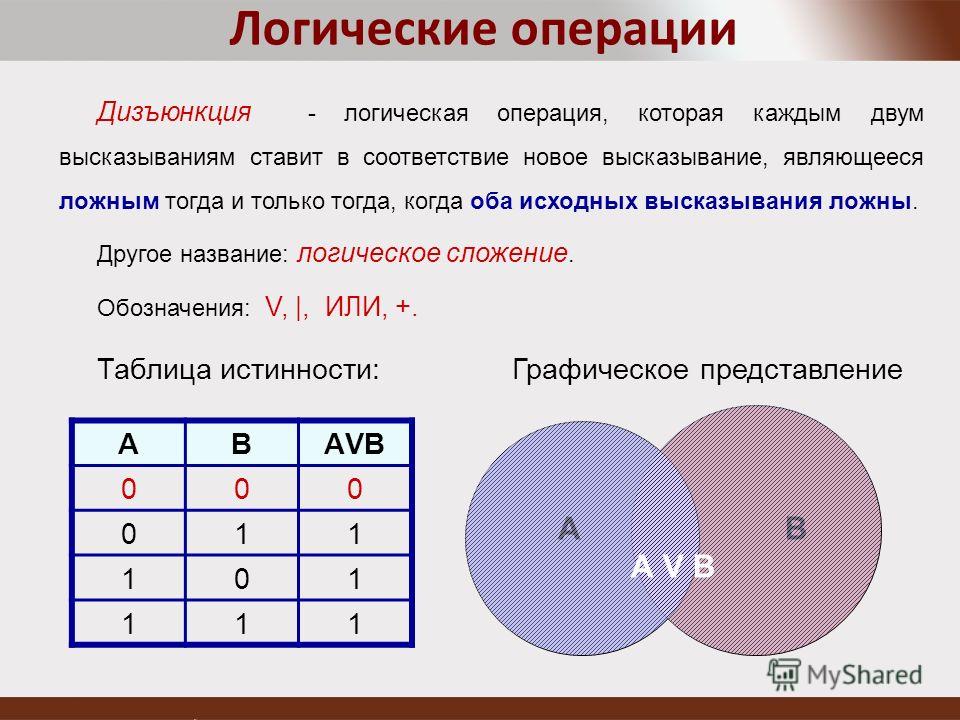
Набор решаемых задач все еще серьезно ограничен по памяти: в ходе итераций алгоритма матрицы становятся плотнее и перестают помещаться в видеопамять. Естественное направление развития проекта — это распределенные алгоритмы для матричных операций и использование виртуальной памяти. Так как библиотеки с подобными решениями появятся нескоро, имеет смысл создавать решения в рамках лаборатории.
Хочется выразить благодарность лаборатории языковых инструментов за предоставление серверов с видеокартами для экспериментов. Отдельно выражаю благодарность научному руководителю Семёну Григорьеву за непрерывное и чуткое руководство, помощь в работе с текстом.
До 9 августа продолжается прием документов на корпоративную магистерскую программу JetBrains «Разработка программного обеспечения». В этом году набор ведется на 30 бюджетных и 5 платных мест. Подробнее о программе можно узнать на сайте или в Telegram-чате для абитуриентов.
Булева алгебра. Алгебра логики. Элементы математической логики
В современном мире мы все чаще используем разнообразные машины и гаджеты. И не только тогда, когда необходимо применить буквально нечеловеческую силу: переместить груз, поднять его на высоту, вырыть длинную и глубокую траншею и т. д. Автомобили сегодня собирают роботы, еду готовят мультиварки, а элементарные арифметические расчеты производят калькуляторы. Все чаще мы слышим выражение «булева алгебра». Пожалуй, пришло время разобраться в роли человека в создании роботов и умении машин решать не только математические, но и логические задачи.
Логика
В переводе с греческого логика – это упорядоченная система мышления, которая создает взаимосвязи между заданными условиями и позволяет делать умозаключения, основываясь на предпосылках и предположениях. Довольно часто мы спрашиваем друг друга: «Логично?» Полученный ответ подтверждает наши предположения либо критикует ход мысли. Но процесс не останавливается: мы продолжаем рассуждать.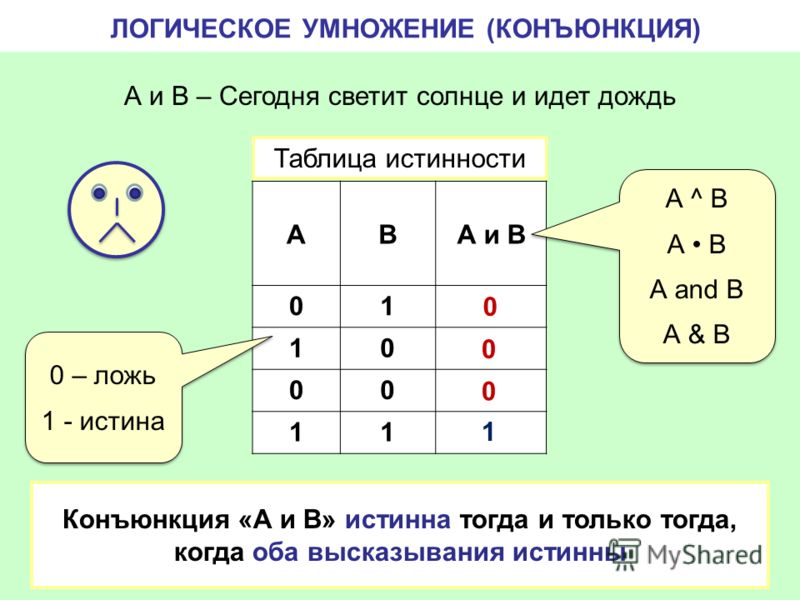
Порой количество условий (вводных) настолько велико, а взаимосвязи между ними столь запутанны и сложны, что человеческий мозг не в состоянии «переварить» все сразу. Может понадобиться не один месяц (неделя, год) для понимания происходящего. Но современная жизнь не дает нам таких временных интервалов на принятие решений. И мы прибегаем к помощи компьютеров. И вот тут-то и появляется алгебра логики, со своими законами и свойствами. Загрузив все исходные данные, мы позволяем компьютеру распознать все взаимосвязи, исключить противоречия и найти удовлетворительное решение.
Математика и логика
Известнейший Готфрид Вильгельм Лейбниц сформулировал понятие «математическая логика», задачи которой были доступны для понимания только узкому кругу ученых. Особого интереса это направление не вызывало, и до середины XIX века о математической логике знали немногие.
Большой интерес в научных сообществах вызвал спор, в котором англичанин Джордж Буль заявил о своем намерении создать раздел математики, не имеющий абсолютно никакого практического применения. Как мы помним из истории, в это время активно развивалось промышленное производство, разрабатывались всевозможные вспомогательные машины и станки, т. е. все научные открытия имели практическую направленность.
Как мы помним из истории, в это время активно развивалось промышленное производство, разрабатывались всевозможные вспомогательные машины и станки, т. е. все научные открытия имели практическую направленность.
Забегая вперед, скажем, что булева алгебра – самая используемая в современном мире часть математики. Так что спор свой Буль проиграл.
Джордж Буль
Сама личность автора заслуживает отдельного внимания. Даже учитывая то, что в прошлом люди взрослели раньше нас, все равно нельзя не отметить, что в 16 лет Дж. Буль преподавал в деревенской школе, а к 20 годам открыл собственную школу в Линкольне. Математик отлично владел пятью иностранными языками, а в свободное время зачитывался работами Ньютона и Лагранжа. И все это — о сыне простого рабочего!
В 1839 году Буль впервые послал свои научные работы в Кембриджский математический журнал. Ученому исполнилось 24 года. Работы Буля настолько заинтересовали членов Королевского научного общества, что в 1844 году он получил медаль за вклад в развитие математического анализа. Еще несколько опубликованных работ, в которых были описаны элементы математической логики, позволили молодому математику занять пост профессора в колледже графства Корк. Напомним, что у самого Буля образования не было.
Еще несколько опубликованных работ, в которых были описаны элементы математической логики, позволили молодому математику занять пост профессора в колледже графства Корк. Напомним, что у самого Буля образования не было.
Идея
В принципе, булева алгебра очень проста. Существуют высказывания (логические выражения), которые, с точки зрения математики, можно определить только двумя словами: «истина» или «ложь». Например, весной деревья расцветают – истина, летом идет снег – ложь. Вся прелесть этой математики заключается в том, что нет строгой необходимости использовать только числа. Для алгебры суждений вполне подходят любые высказывания с однозначным смыслом.
Таким образом, алгебра логики может быть использована буквально везде: в составлении расписаний и написании инструкций, анализе противоречивой информации о событиях и определении последовательности действий. Самое главное — понять, что совершенно неважно, как мы определили истинность или ложность высказывания. От этих «как» и «почему» нужно абстрагироваться. Значение имеет только констатация факта: истина-ложь.
Значение имеет только констатация факта: истина-ложь.
Безусловно, для программирования важны функции алгебры логики, которые записываются соответствующими знаками и символами. И выучить их – это значит освоить новый иностранный язык. Нет ничего невозможного.
Основные понятия и определения
Не вдаваясь в глубины, разберемся с терминологией. Итак, булева алгебра предполагает наличие:
- высказываний;
- логических операций;
- функций и законов.
Высказывания – любые утвердительные выражения, которые не могут быть истолкованы двузначно. Они записываются в виде чисел (5 > 3) или формулируются привычными словами (слон – самое большое млекопитающее). При этом фраза «у жирафа нет шеи» также имеет право на существование, только булева алгебра определит её как «ложь».
Все высказывания должны носить однозначный характер, но они могут быть элементарными и составными. Последние используют логические связки. Т. е. в алгебре суждений составные высказывания образуются сложением элементарных посредством логических операций.
Операции булевой алгебры
Мы уже помним, что операции в алгебре суждений – логические. Подобно тому, как алгебра чисел использует арифметические операции для сложения, вычитания или сравнения чисел, элементы математической логики позволяют составить сложные высказывания, дать отрицание или вычислить конечный результат.
Логические операции для формализации и простоты записываются формулами, привычными для нас в арифметике. Свойства булевой алгебры дают возможность записывать уравнения и вычислять неизвестные. Логические операции обычно записывают с помощью таблицы истинности. Её столбцы определяют элементы вычислений и операцию, которая над ними производится, а строки показывают результат вычислений.
Основные логические действия
Самыми распространенными в булевой алгебре операциями являются отрицание (НЕ) и логические И и ИЛИ. Так можно описать практически все действия в алгебре суждений. Изучим подробнее каждую из трех операций.
Отрицание (не) применяется только к одному элементу (операнду).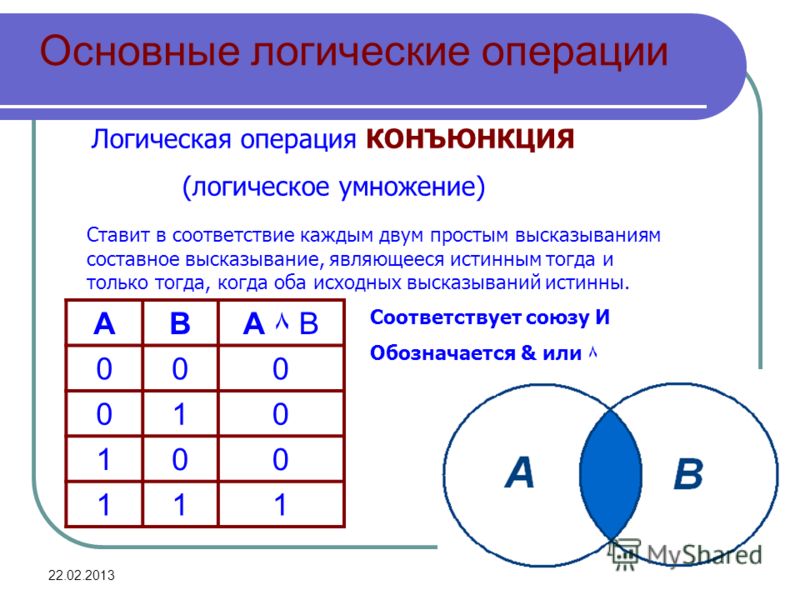 Поэтому операцию отрицания называют унарной. Для записи понятия «не А» используют такие символы: ¬A, A¯¯¯ или !A. В табличной форме это выглядит так:
Поэтому операцию отрицания называют унарной. Для записи понятия «не А» используют такие символы: ¬A, A¯¯¯ или !A. В табличной форме это выглядит так:
Для функции отрицания характерно такое утверждение: если А истинно, то Б – ложно. Например, Луна вращается вокруг Земли – истина; Земля вращается вокруг Луны – ложь.
Логические умножение и сложение
Логическое И называют операцией конъюнкции. Что это значит? Во-первых, что применить ее можно к двум операндам, т. е. И – бинарная операция. Во-вторых, что только в случае истинности обоих операндов (и А, и Б) истинно и само выражение. Пословица «Терпение и труд все перетрут» предполагает, что только оба фактора помогут человеку справиться со сложностями.
Для записи используются символы: A∧Б, A⋅Б или A&&Б.
Конъюнкция аналогична умножению в арифметике. Иногда так и говорят – логическое умножение. Если перемножить элементы таблицы по строкам, мы получим результат, аналогичный логическому размышлению.
Дизъюнкцией называют операцию логического ИЛИ. Она принимает значение истинности тогда, когда хотя бы одно из высказываний истинно (или А, или Б). Записывается это так: A∨Б, A+Б или A||Б. Таблицы истинности для этих операций такие:
Она принимает значение истинности тогда, когда хотя бы одно из высказываний истинно (или А, или Б). Записывается это так: A∨Б, A+Б или A||Б. Таблицы истинности для этих операций такие:
Дизъюнкция подобна арифметическому сложению. Операция логического сложения имеет только одно ограничение: 1+1=1. Но мы же помним, что в цифровом формате математическая логика ограничена 0 и 1 (где 1 – истина, 0 — ложь). Например, утверждение «в музее можно увидеть шедевр или встретить интересного собеседника» означает, что можно посмотреть произведения искусства, а можно познакомиться с интересным человеком. В то же время, не исключен вариант одновременного свершения обоих событий.
Функции и законы
Итак, мы уже знаем, какие логические операции использует булева алгебра. Функции описывают все свойства элементов математической логики и позволяют упрощать сложные составные условия задач. Самым понятным и простым кажется свойство отказа от производных операций. Под производными понимаются исключающее ИЛИ, импликация и эквивалентность. Поскольку мы ознакомились только с основными операциями, то и свойства рассмотрим тоже только их.
Поскольку мы ознакомились только с основными операциями, то и свойства рассмотрим тоже только их.
Ассоциативность означает, что в высказываниях типа «и А, и Б, и В» последовательность перечисления операндов не играет роли. Формулой это запишется так:
(A∧Б)∧В=A∧(Б∧В)=A∧Б∧В,
(A∨Б)∨В=A∨(Б∨В)=A∨Б∨В.
Как видим, это свойственно не только конъюнкции, но и дизъюнкции.
Коммутативность утверждает, что результат конъюнкции или дизъюнкции не зависит от того, какой элемент рассматривался вначале:
A∧Б=Б∧A; A∨Б=Б∨A.
Дистрибутивность позволяет раскрывать скобки в сложных логических выражениях. Правила схожи с раскрытием скобок при умножении и сложении в алгебре:
A∧(Б∨В)=A∧Б∨A∧В; A∨Б∧В=(A∨Б)∧(A∨В).
Свойства единицы и нуля, которые могут быть одним из операндов, также аналогичны алгебраическим умножению на ноль или единицу и сложению с единицей:
A∧0=0,A∧1=A; A∨0=A,A∨1=1.
Идемпотентность говорит нам о том, что если относительно двух равных операндов результат операции оказывается аналогичным, то можно «выбросить» лишние усложняющие ход рассуждений операнды. И конъюнкция, и дизъюнкция являются идемпотентными операциями.
И конъюнкция, и дизъюнкция являются идемпотентными операциями.
Б∧Б=Б; Б∨Б=Б.
Поглощение также позволяет нам упрощать уравнения. Поглощение утверждает, что когда к выражению с одним операндом применяется другая операция с этим же элементом, результатом оказывается операнд из поглощающей операции.
A∧Б∨Б=Б; (A∨Б)∧Б=Б.
Последовательность операций
Последовательность операций имеет немаловажное значение. Собственно, как и для алгебры, существует приоритетность функций, которые использует булева алгебра. Формулы могут упрощаться только при условии соблюдения значимости операций. Ранжируя от самых значимых до незначительных, получим такую последовательность:
1. Отрицание.
2. Конъюнкция.
3. Дизъюнкция, исключающее ИЛИ.
4. Импликация, эквивалентность.
Как видим, только отрицание и конъюнкция не имеют равных приоритетов. А приоритет дизъюнкции и исключающего ИЛИ равны, также как и приоритеты импликации и эквивалентности.
Функции импликации и эквивалентности
Как мы уже говорили, помимо основных логических операций математическая логика и теория алгоритмов использует производные. Чаще всего применяются импликация и эквивалентность.
Чаще всего применяются импликация и эквивалентность.
Импликация, или логическое следование – это высказывание, в котором одно действие является условием, а другое – следствием его выполнения. Иными словами, это предложение с предлогами «если… то». «Любишь кататься, люби и саночки возить». Т. е. для катания необходимо затянуть санки на горку. Если же нет желания съехать с горы, то и санки таскать не приходится. Записывается это так: A→Б или A⇒Б.
Эквивалентность предполагает, что результирующее действие наступает только в том случае, когда истиной являются оба операнда. Например, ночь сменяется днем тогда (и только тогда), когда солнце встает из-за горизонта. На языке математической логики это утверждение записывается так: A≡Б, A⇔Б, A==Б.
Другие законы булевой алгебры
Алгебра суждений развивается, и многие заинтересовавшиеся ученые сформулировали новые законы. Наиболее известными считаются постулаты шотландского математика О. де Моргана. Он заметил и дал определение таким свойствам, как тесное отрицание, дополнение и двойное отрицание.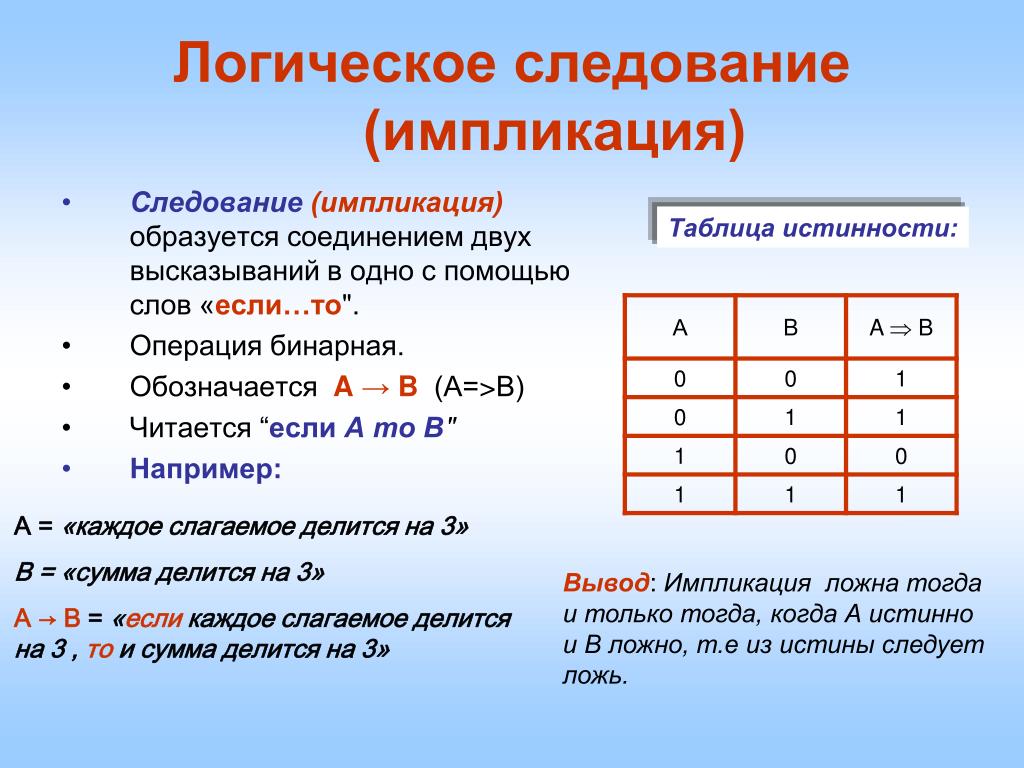
Тесное отрицание предполагает, что перед скобкой нет ни одного отрицания: не (А или Б)= не А или НЕ Б.
Когда операнд отрицается, независимо от своего значения, говорят о дополнении:
Б∧¬Б=0; Б∨¬Б=1.
И, наконец, двойное отрицание само себя компенсирует. Т.е. перед операндом либо исчезает отрицание, либо остается только одно.
Как решать тесты
Математическая логика подразумевает упрощение заданных уравнений. Так же, как и в алгебре, необходимо сначала максимально облегчить условие (избавиться от сложных вводных и операций с ними), а затем приступить к поиску верного ответа.
Что же сделать для упрощения? Преобразовать все производные операции в простые. Затем раскрыть все скобки (или наоборот, вынести за скобки, чтобы сократить этот элемент). Следующим действием должно стать применение свойств булевой алгебры на практике (поглощение, свойства нуля и единицы и т. д).
В конечном итоге уравнение должно состоять из минимального количества неизвестных, объединенных простыми операциями. Легче всего искать решение, если добиться большого количества тесных отрицаний. Тогда ответ всплывет как бы сам собой.
Легче всего искать решение, если добиться большого количества тесных отрицаний. Тогда ответ всплывет как бы сам собой.
Что такое булевская логика и как она используется в программировании
Булева логика является ключевой концепцией любого языка программирования, независимо от того, создаете ли вы видеоигру на C++, разрабатываете следующее лучшее приложение на Swift, выполняете поиск в реляционных базах данных на SQL, или работа с большими данными в Python. В этой статье мы расскажем, что такое логическая логика, как она работает и как создавать собственные логические выражения.
Что такое булева логика?
Булева логика — это тип алгебры, в котором результаты рассчитываются либо как ИСТИНА, либо как ЛОЖЬ (известные как значения истинности или переменные истинности). Вместо использования арифметических операторов, таких как сложение, вычитание и умножение, логическая логика использует три основных логических оператора: И, ИЛИ и НЕ.
ИСТИНА и ЛОЖЬ: их может быть только два
За булевой логикой стоят два очень простых слова: ИСТИНА и ЛОЖЬ.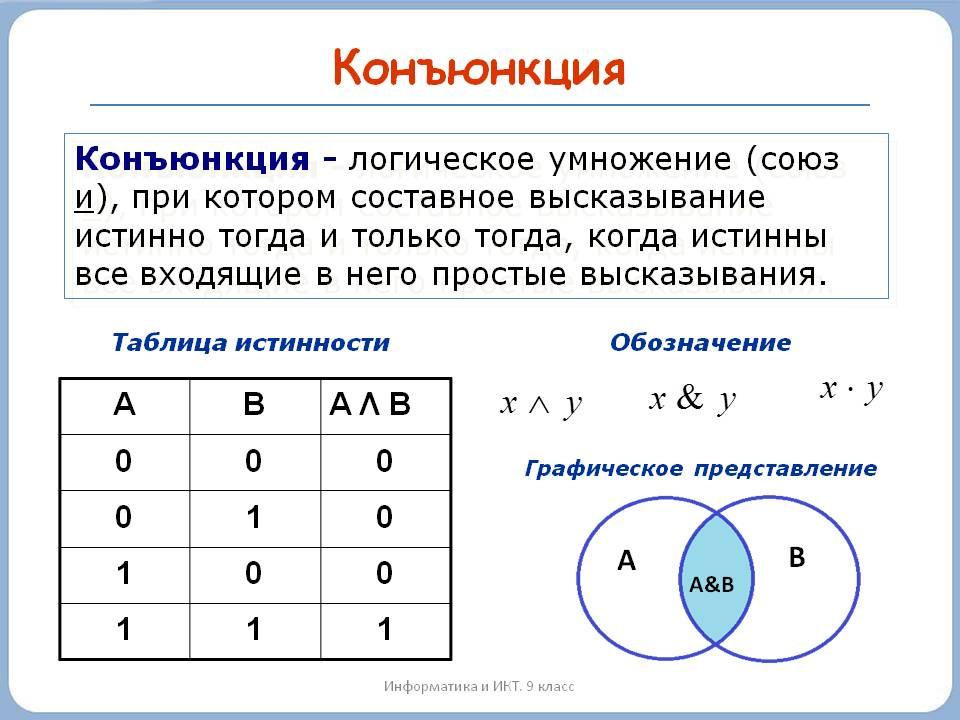
Обратите внимание, что логическое значение TRUE или FALSE очень отличается от ввода строк «True» и «False» в ваш код. На самом деле языки программирования помещают эти два логических значения в свой собственный тип объекта, отдельный от целых чисел, строк и чисел с плавающей запятой. Но в то время как числовые или строковые значения в программировании могут быть практически бесконечными, есть только два возможных логических значения: ИСТИНА и ЛОЖЬ.
Как это работает? Булева логика рассматривает сообщаемую связь между вещами и определяет, сохраняется ли эта связь. Например, возьмем уравнение:
2 + 2 = 4
Здесь у нас есть две части, 2 + 2 и 4, и мы сообщаем, что эти две части равны друг другу. Это правильно? Да, так что логический результат этого будет ИСТИНА. В этом примере комбинация двух частей 2 + 2 и 4 вместе с отношением (= равно) называется логическим выражением.
Давайте посмотрим на другое логическое выражение:
10 – 4 = 5
Здесь мы сообщаем, что 4, вычитаемое из 10, равно 5.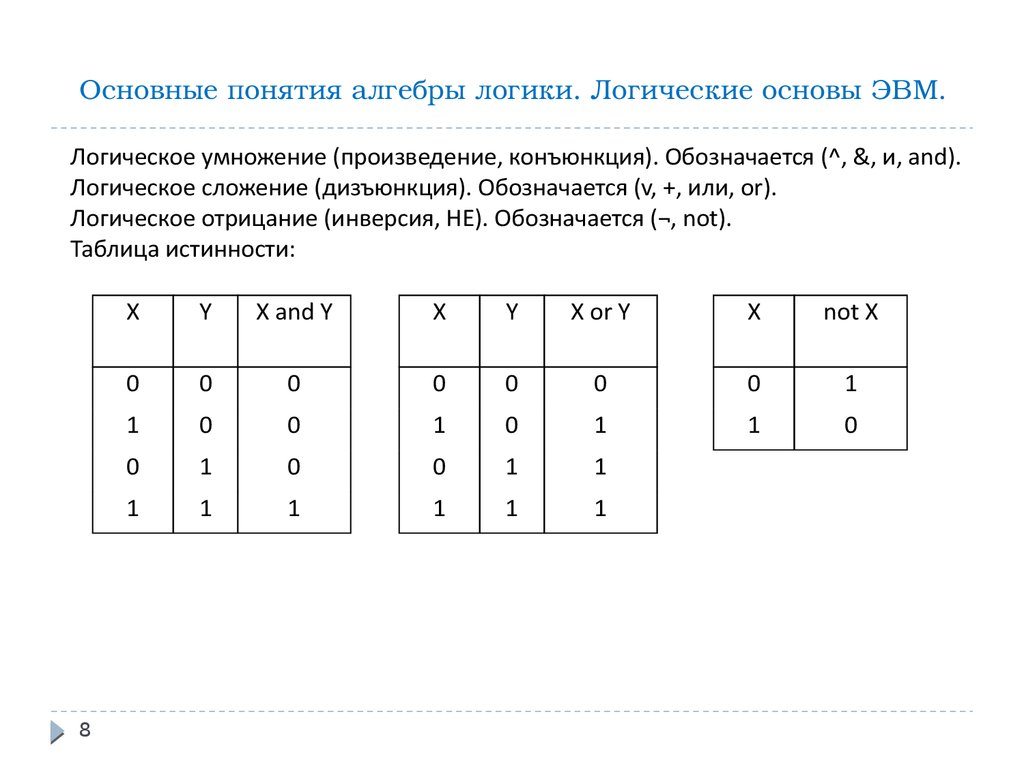 Верно? Конечно, нет, и именно поэтому это логическое выражение вернет значение FALSE.
Верно? Конечно, нет, и именно поэтому это логическое выражение вернет значение FALSE.
Boolean Expression | Result |
2 + 2 = 5 | FALSE |
5 – 1 = 4 | TRUE |
4 * 5 > 10 | TRUE |
40 / 10 < 1 | FALSE |
Building Boolean expressions
Keep in Имейте в виду, что булевская логика работает только тогда, когда выражение может быть ИСТИНА или ЛОЖЬ. Например, выражение 3 + 8 не является логическим выражением, потому что оно не сравнивается и не связано с чем-то другим. Но выражение 3 + 8 = 10 является логическим выражением, потому что теперь мы можем оценить каждую сторону и посмотреть, является ли отношение между ними ИСТИННЫМ или ЛОЖНЫМ (в данном случае ЛОЖНЫМ).
Мы можем строить логические выражения со всеми видами данных, включая переменные. Например, предположим, что мы присвоили эти значения переменным x и y где-то в нашем коде:
x равно 7
y равно 3
Теперь мы можем построить логические выражения, используя наши переменные:
Логическое выражение | Результат |
x + y < 11 | 4 ЛОЖЬ0003 |
x * y = 21 | TRUE |
x / y > 10 | FALSE |
x + (2 * y) = 13 | TRUE |
Логические выражения также могут определять, идентичны ли две строки. Просто помните, что большинство языков программирования чувствительны к регистру.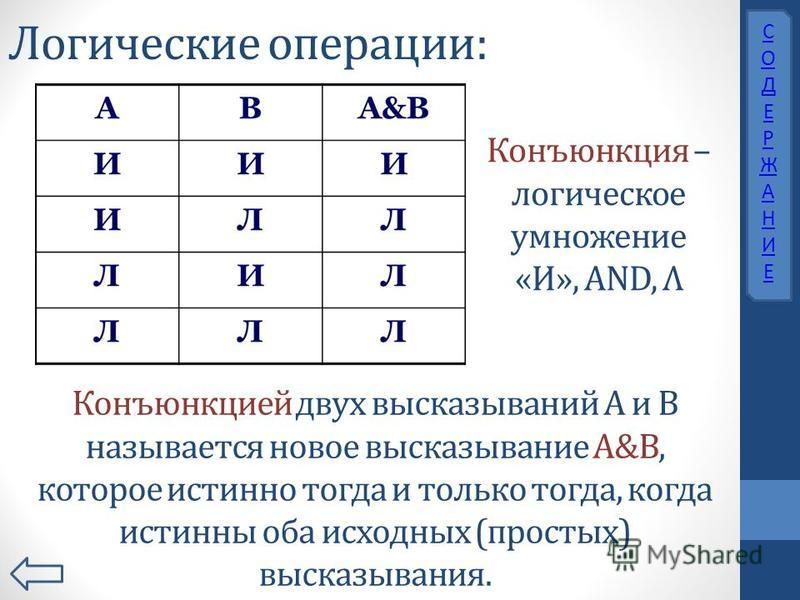
Boolean Expression | Результат |
«I Love Codecademy» = «I Love Codecademy» | True |
«I True | |
« I Love ». | |
«Я люблю Codecademy» = «Я ЛЮБЛЮ Codecademy» | FALSE |
Существует множество других способов построения булевых выражений, в зависимости от языка программирования. Например, вы можете использовать логическое выражение, чтобы определить, содержится ли число в списке в Python или текстовая строка находится в таблице базы данных SQL.
Булевы операторы
Теперь, когда вы понимаете основы булевых выражений, давайте рассмотрим еще один ключевой аспект булевой логики: булевы операторы. Есть три основных логических оператора: И, ИЛИ и НЕ.
Чтобы лучше понять, как работают логические операторы, давайте на мгновение представим, что мы находимся в магазине мороженого. Скажем, мы собираемся приготовить мороженое из двух шариков с разными вкусами. Но я немного привередлив в еде, поэтому могу не принимать каждую комбинацию пломбира, которую получаю. Мы можем использовать логические выражения и логические операторы, чтобы выяснить, буду ли я есть мороженое или нет.
AND
Логический оператор AND используется для подтверждения истинности двух или более логических выражений.
Например, в моем мороженом я хочу, чтобы первый вкус был шоколадным, а второй — ванильным. Мы могли бы превратить это в логическое выражение с оператором И, которое выглядит примерно так:
Аромат_1 = Шоколад И Аромат_2 = Ваниль
Это означает, что первый аромат должен быть шоколадным, а второй аромат должен быть ванильным. В противном случае я не буду есть мороженое.
Мы могли бы организовать эту ситуацию в таблицу таких возможностей, как это:
Flavor_1 | Flavor_2 | ETH SUNDAE? |
Chocolate | Vanilla | Yes |
Chocolate | Strawberry | No |
Mango | Vanilla | No |
Mango | Strawberry | No |
Tables like this are used in Boolean logic all the time. Их называют таблицами истинности, и мы можем составить одну из них для нашего примера с мороженым. Если что-то соответствует моим придирчивым условиям вкуса мороженого, то это ПРАВДА. Если нет, то это ЛОЖЬ.
Их называют таблицами истинности, и мы можем составить одну из них для нашего примера с мороженым. Если что-то соответствует моим придирчивым условиям вкуса мороженого, то это ПРАВДА. Если нет, то это ЛОЖЬ.
Вот как выглядела бы приведенная выше таблица в виде таблицы истинности:
Flavor_1 | Flavor_2 | Result |
TRUE | TRUE | TRUE |
TRUE | ЛОЖЬ | ЛОЖЬ |
ЛОЖЬ | ИСТИНА | 6 3 ЛОЖЬ 60041 |
ЛОЖЬ | ЛОЖЬ | ЛОЖЬ |
ИЛИ
9
Например, если бы я хотел, чтобы первым ароматом была клубника, а вторым ароматом был манго, то логическое выражение было бы таким:
Аромат_1 = Клубника ИЛИ Аромат_2 = Манго
Мы могли бы организовать возможности как:
Аромат_1 | Аромат_2 | Ешьте мороженое? |
Strawberry | Mango | Yes |
Strawberry | Cherry | Yes |
Cherry | Mango | Да |
Vanilla | Raspberry | No |
And the truth table would look like this:
Flavor_1 | Flavor_2 | Результат |
ИСТИНА | ИСТИНА | ИСТИНА | 33UE | 0036 | FALSE | TRUE |
FALSE | TRUE | TRUE |
FALSE | FALSE | FALSE |
Note что оператор ИЛИ возвращает ИСТИНА, если одно из двух логических выражений истинно, а также когда оба выражения истинны. По этой причине этот оператор ИЛИ также известен как включающий оператор ИЛИ. В качестве альтернативы есть также оператор XOR (исключающее или), который возвращает ИСТИНА только тогда, когда одно из двух выражений истинно.
По этой причине этот оператор ИЛИ также известен как включающий оператор ИЛИ. В качестве альтернативы есть также оператор XOR (исключающее или), который возвращает ИСТИНА только тогда, когда одно из двух выражений истинно.
NOT
Логический оператор NOT отличается от AND и OR тем, что принимает только один аргумент. Он проверяет, является ли значение FALSE или нет. Иными словами, он меняет значения TRUE на FALSE, а значения FALSE на TRUE. Например, я ненавижу ромовый изюм и абсолютно не буду есть ничего с ромовым изюмом. Как это может выглядеть в виде таблицы?
Вкус | Ешь мороженое? |
Chocolate | Yes |
Rum Raisin | No |
The truth table looks like this:
Flavor | Результат |
False | True |
True | FALSE | FALSE | 0082 |
Вы можете комбинировать логические выражения, чтобы выразить предпочтения в сфере мороженных синх
Flavor_2
Ешьте мороженое?
Шоколад
Малина
Да
Peach
Rum Raisin
No
Rum Raisin
Mint
No
Rum Raisin
Rum Raisin
No
Предложение ИЛИ в круглых скобках вернет TRUE для всего, что содержит ромовый изюм. Применение к нему НЕ изменит значение выражения ИЛИ с ИСТИНА на ЛОЖЬ и наоборот. Подобно операторам в арифметике, логические операторы имеют порядок старшинства: сначала обращаются к элементам в круглых скобках, затем к оператору НЕ, И и, наконец, к ИЛИ. Наша новая таблица истинности выглядит так:
Применение к нему НЕ изменит значение выражения ИЛИ с ИСТИНА на ЛОЖЬ и наоборот. Подобно операторам в арифметике, логические операторы имеют порядок старшинства: сначала обращаются к элементам в круглых скобках, затем к оператору НЕ, И и, наконец, к ИЛИ. Наша новая таблица истинности выглядит так:
Flavor_1 | Flavor_2 | Result |
FALSE | FALSE | TRUE |
FALSE | ИСТИНА | ЛОЖЬ |
ИСТИНА | ЛОЖЬ | ЛОЖЬ3 30041 |
True | True | False |
Применение своей логики Boolean
Итак, что следующее после изучения базовых знаний логика Boolean??
Булева логика имеет решающее значение для создания кода, который помогает вашей программе быстро принимать решения относительно данных и входных данных, поэтому попробуйте применить свои логические знания в онлайн-курсе программирования.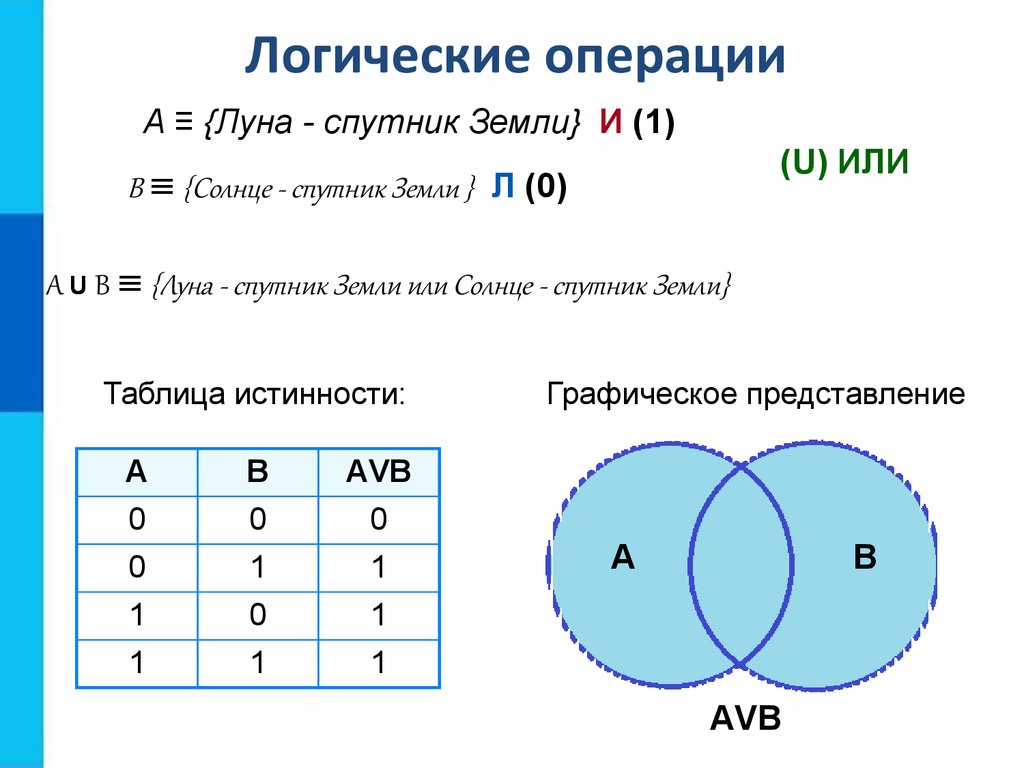
Курсы и учебные пособия по основам кода | Codecademy
Хотите научиться программировать, но не знаете, с чего начать? Наша область Code Foundations предоставляет обзор основных приложений программирования и учит важным концепциям, которые вы найдете в каждом языке программирования. Этот контент подготовит вас к тому, чтобы наметить курс на более техническое обучение…
Codecademy
{{#сравнить сложность «==» «Новичок»}} Подходит для начинающих {{еще}} {{~#сравнить сложность «==» «Продвинутая»~}}{{/compare}} {{сложность}} {{/сравнивать}} {{урокКоличество}} Уроки
Введение в булеву логику
| Указатель статей |
|---|
| Введение в булеву логику |
| Двоичная арифметика и триггеры |
| Вьетнамки — Время входит в логику |
| Больше логики |
Страница 1 из 4
Это может показаться сложной темой, но булеву логику очень легко объяснить и понять. Он представляет собой простейшую из всех логик и саму основу вычислений.
Он представляет собой простейшую из всех логик и саму основу вычислений.
Первый проект Более поздняя версия:
Теперь доступно в мягкой обложке и электронной книге на Amazon.
Содержимое
- Что можно вычислить?
- Конечные автоматы
- Что такое машина Тьюринга?
- Вычислительная сложность
- Невычислимые числа
- Трансфинитное
- Аксиома выбора
- Лямбда-исчисление
- Грамматика и пытки
- Обратная польская запись — RPN
- Введение в булеву логику
- Противостояние недоказуемому — Гёдель и все такое
- Руководство программиста по фракталам
- Руководство программиста по хаосу*
- Простые числа и проверка на простоту
- Клеточные автоматы — как и почему
- Теория информации
- Теория кодирования
- Колмогоров Сложность
*Подлежит пересмотру
Логика, логика везде
Компьютеры и логика неразделимы — верно?
Теперь они есть, но в начале все было гораздо более туманно.
Первые компьютеры были задуманы как автоматические арифметические машины, и хотя их создатели знали, что логика имеет какое-то отношение ко всему этому, они не были на 100% ясны, как и почему.
Даже сегодня мы слишком упрощенно относимся к логике и ее роли в вычислениях и понимании мира, а Джордж Буль, человек, который все это начал, немного переборщил с названиями своих книг на эту тему —
Математический анализ мышления и Исследование законов мышления .
Работа Буля, безусловно, поставила современную логику на правильный путь, но она определенно не имела ничего общего с «законами мысли». Дело в том, что даже сегодня мы не имеем четкого представления о том, какие законы управляют мышлением, а если бы знали, то вся тема искусственного интеллекта была бы закрытой.
Чтобы Джордж Буль был признан отцом современной информационной технологии, он выдвинул идею, одновременно революционную и простую.
Это видео, трейлер к документальному фильму, посвященному двухсотлетию со дня его рождения 2 ноября 1815 года, намекает на то, как его радикальное открытие лежит в основе цифровой эпохи:
youtube.com/embed/aEjzjLv-YjI?rel=0″ frameborder=»0″ allowfullscreen=»true»>
Кем был Джордж Буль?
Современник Чарльза Бэббиджа, с которым он недолго встречался, Буль в наши дни считается «отцом информационного века». Англичанин по происхождению, в 1849 г.он стал первым профессором математики в новом Королевском колледже Ирландии (ныне Университетский колледж) Корка.
Джордж Буль
2 ноября 1815 г. — 8 декабря 1864 г.
Он умер в возрасте 49 лет в 1864 году, и его работа, возможно, никогда не оказала бы влияния на информатику без Клода Шеннона, который 70 лет спустя осознал актуальность символической логики Буля для проектирования. В результате мышление Буля стало практической основой проектирования цифровых схем и теоретической основой цифровой эпохи.
Булева логика
Булева логика очень легко объяснима и понятна.
- Вы начинаете с идеи, что некоторое утверждение P либо истинно, либо ложно, оно не может быть чем-то средним (это называется законом исключенного третьего).

- Затем вы можете составить другие утверждения, истинные или ложные, комбинируя эти исходные утверждения вместе с помощью основных операторов И, ИЛИ и НЕТ.
Вопрос о том, что такое «фундаментальный» оператор, сам по себе представляет собой интересный вопрос, к которому мы вернемся позже, когда спросим, как мало логических операторов нам действительно нужно?
То, как все это работает, более или менее соответствует тому, как мы использовали эти термины в английском языке.
Например, если P истинно, то Not(P) ложно Итак, если «сегодня понедельник» истинно, то «Не (сегодня понедельник)» ложно.
Мы часто переводим это логическое выражение на английский язык как «сегодня не понедельник», и это облегчает понимание того, что оно ложно, если сегодня действительно понедельник.
Вы следите?
Вот в чем проблема такого рода дискуссий. Она очень быстро становится запутанной и трудной для понимания, и в этом заключается часть силы булевой логики.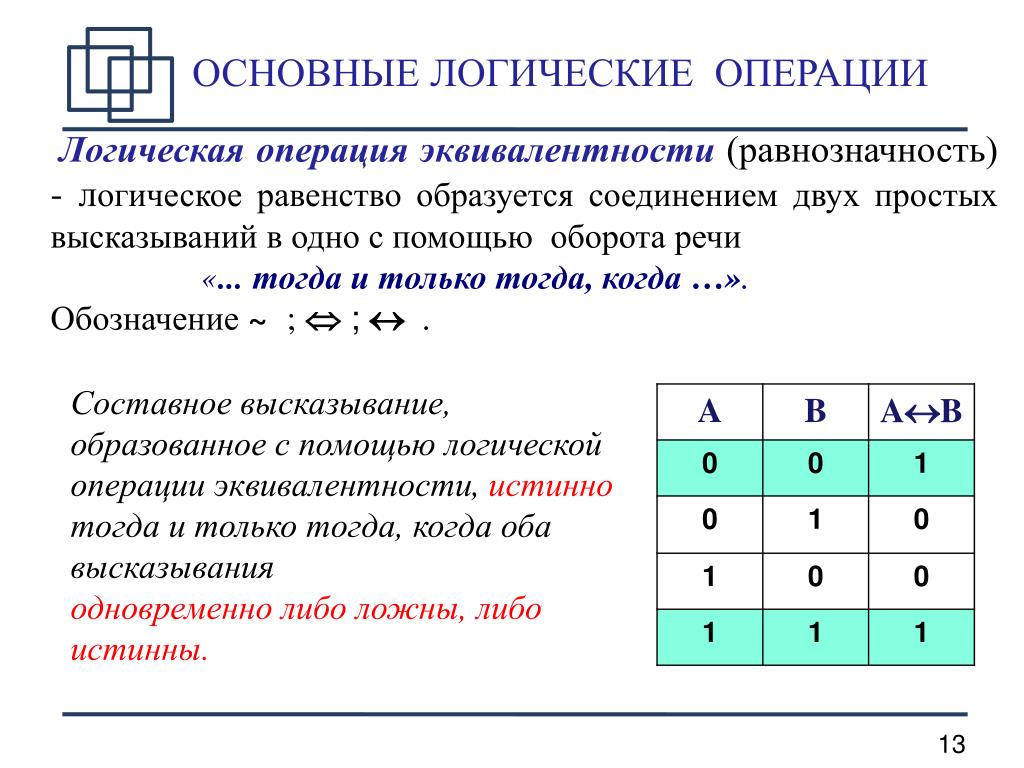 Вы можете четко записывать аргументы в символической форме.
Вы можете четко записывать аргументы в символической форме.
Таблицы истинности
Правила комбинирования выражений обычно записываются в виде таблиц, в которых перечислены все возможные результаты. Они называются таблицами истинности, и для трех основных операторов это:
| П | Q | П И В |
| Ф | Ф | Ф |
| Ф | Т | Ф |
| Т | Ф | Ф |
| Т | Т | Т |
| П | Q | ПОР КВ |
| Ф | Ф | Ф |
| Ф | Т | Т |
| Т | Ф | Т |
| Т | Т | Т |
| П | НЕ П |
| Ф | Т |
| Т | Ф |
Обратите внимание, что хотя логическое значение И совпадает с использованием этого термина в английском языке, логическое значение ИЛИ немного отличается.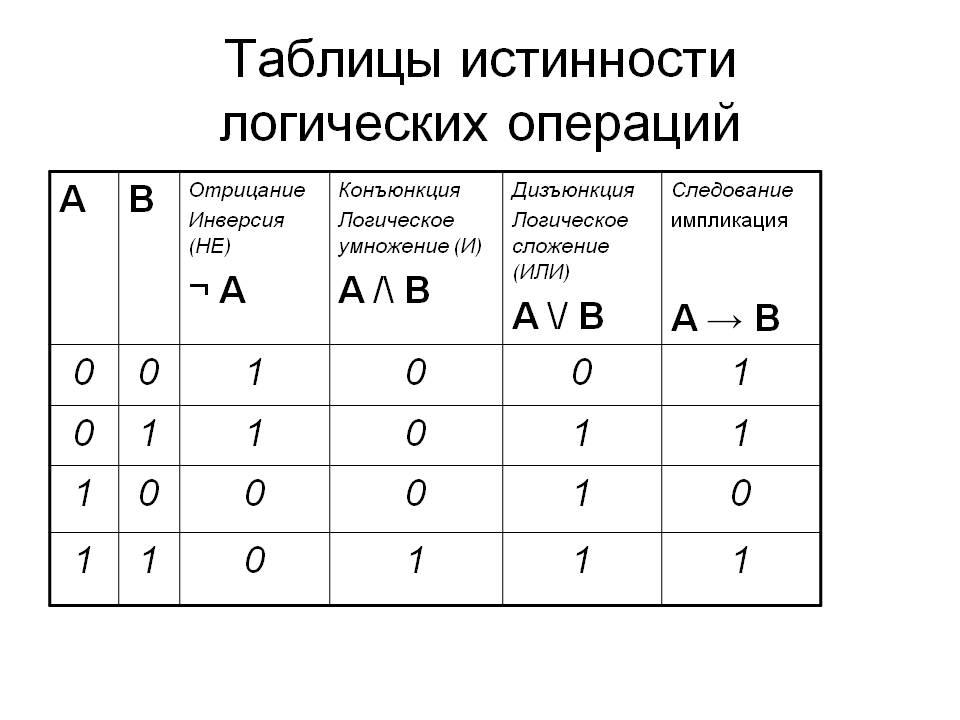
Когда вас спрашивают, хотите ли вы «кофе ИЛИ чай», вы не должны отвечать «да» обоим!
Однако в логическом случае «Или» наверняка включает в себя и то, и другое. Когда истинно P и истинно Q, комбинированное выражение (P или Q) также истинно.
Существует логический оператор, который соответствует использованию термина «или» в английском языке, и он называется «Исключающее или» и записывается как EOR или XOR. Его таблица истинности:
| Р | Q | P Исключающее ИЛИ Q |
| Ф | Ф | Ф |
| Ф | Т | Т |
| Т | Ф | Т |
| Т | Т | Ф |
, и это действительно помешает вам пить чай и кофе одновременно (обратите внимание, что последняя строка — True XOR True = False).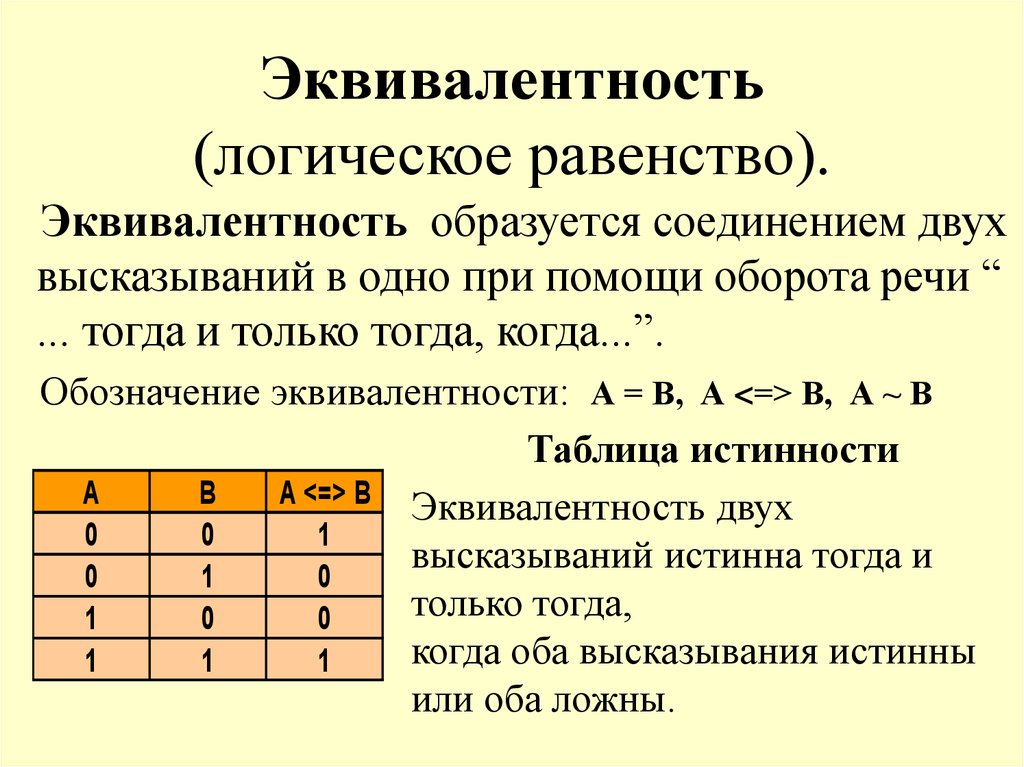
Практические таблицы истинности
Все это кажется очень простым, но какой в этом смысл?
Это определенно не модель для повседневных рассуждений, за исключением самого тривиального уровня «кофе или чай».
Мы используем булеву логику в своем мышлении, ну, политики, вероятно, не используют, но это уже другая история, но только на самом тривиально очевидном уровне.
Однако, если вы начнете проектировать машины, которые должны реагировать на внешний мир даже достаточно сложным образом, вы быстро обнаружите, что булева логика очень помогает.
Например, предположим, что вы хотите создать систему безопасности, которая работает только ночью и реагирует на открытие двери. Если у вас есть датчик освещенности, вы можете рассматривать это как подачу сигнала, указывающего на истинность утверждения:
.P = сейчас день.
Очевидно, что не(P) истинно, когда наступает ночь, и мы впервые применяем булеву логику на практике!
Чего мы действительно хотим, так это чего-то, что подтверждает истинность утверждения:
R= Взлом в процессе
от Р и
Q = Окно открыто
Немного грубого размышления вскоре дает решение, которое
R = Не(P) И Q
То есть истинность «Идет кража со взломом» определяется следующей таблицей истинности:
| П | Q | НЕ(П) | НЕ(П)И Q |
| Ф | Ф | Т | Ф |
| Ф | Т | Т | Т |
| Т | Ф | Ф | Ф |
| Т | Т | Ф | Ф |
Из этого вы должны увидеть, что будильник срабатывает только в ночное время и открывается окно.
Предыдущая — Следующая >>
Булева логика | Цифровые схемы 1: двоичные, логические и логические
Булева логика
Сохранить Подписаться
Пожалуйста, войдите, чтобы подписаться на это руководство.
После входа в систему вы будете перенаправлены обратно к этому руководству и сможете подписаться на него.
Логика
Мы не говорим о философской логике: modus ponens и тому подобное. Мы говорим о булевой логике, также известной как цифровая логика.
Булева логика получила свое название от Джорджа Буля, который сформулировал эту тему в своей книге 1847 года Математический анализ логики . Буль определил алгебру (не шокирующе названную булевой алгеброй) для манипулирования комбинациями значений True и False. True and False (мы будем использовать T и F в качестве сокращения)… звуки, похожие на 1 и 0, или вкл и выкл. Неудивительно, что булева алгебра является основой проектирования цифровых схем.
True and False (мы будем использовать T и F в качестве сокращения)… звуки, похожие на 1 и 0, или вкл и выкл. Неудивительно, что булева алгебра является основой проектирования цифровых схем.
Основные операции
AND
Соединение: результатом является T тогда и только тогда, когда все входы равны T; если любой ввод F, результат F.
OR
Дизъюнкция: результатом является T, если любые (включая все) входы равны T; результат равен F тогда и только тогда, когда все входные данные равны F.
НЕ
Отрицание/инверсия: результат равен T, если вход F, и F, если вход T.
Таблицы истинности
Очень полезным инструментом при работе с булевой логикой является таблица истинности. Для простоты и согласованности мы будем использовать A , B , C и т. д. для входных данных и Q для вывода. В таблицах истинности перечислены все возможные комбинации входных данных. На данный момент мы ограничиваем наши обсуждения двумя входными данными, хотя логических операций может быть сколько угодно. Для каждой комбинации отмечается соответствующий результат. По мере изучения более сложных логических схем мы обнаружим, что выходов тоже может быть несколько.
На данный момент мы ограничиваем наши обсуждения двумя входными данными, хотя логических операций может быть сколько угодно. Для каждой комбинации отмечается соответствующий результат. По мере изучения более сложных логических схем мы обнаружим, что выходов тоже может быть несколько.
Вот таблицы для И , ИЛИ и НЕ .
Комбинации
Эти базовые операции можно комбинировать любым количеством способов для построения буквально всего остального в компьютере.
Одной из наиболее распространенных комбинаций является И-, это просто НЕ И . Точно так же NOR равно NOT OR .
Исключающее ИЛИ/НЕ
Еще одна пара особенно полезных операций (как мы увидим в следующем руководстве) — это исключающее ИЛИ и его отрицание: исключающее ИЛИ.
Исключающее ИЛИ похоже на ИЛИ, за исключением того, что Q равно F, если все входные данные равны T, и T, только если некоторые входные данные равны T.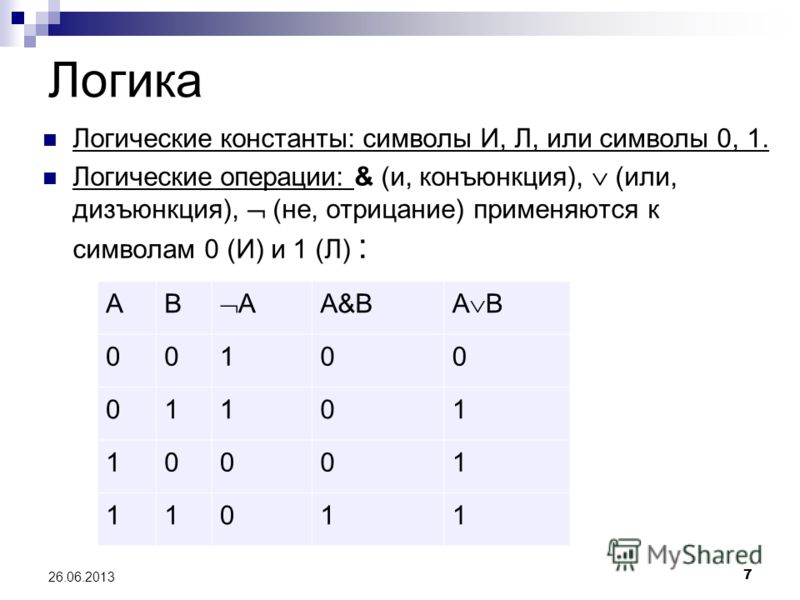 Вы можете описать это как Q, являющийся T, когда не все входные данные одинаковы.
Вы можете описать это как Q, являющийся T, когда не все входные данные одинаковы.
Конечно, XNOR — это противоположное: Q равно T тогда и только тогда, когда все входы одинаковы.
Мы увидим эти ворота позже, когда будем исследовать гадюки.
Magical NAND
NAND особенно интересна. Выше мы обсуждали И , ИЛИ и НЕ как фундаментальные операции. На самом деле NAND — это Фундаментальная операция, поскольку все остальное можно сделать, используя только NAND : мы говорим, что NAND — это функционально завершенный . NOR также функционально завершен, но когда мы рассматриваем схемы реализации, NOR обычно требует больше транзисторов, чем NAND .
Посмотрите таблицу истинности для NAND . Что произойдет, если входные данные будут одинаковыми? И-НЕ действует как , а не . Таким образом, вы можете сделать НЕ из И-НЕ , соединив все его входы вместе.
Таким образом, вы можете сделать НЕ из И-НЕ , соединив все его входы вместе.
NAND просто НЕ И , так что же такое НЕ И-? Это эквивалентно NOT NOT AND . НЕ сокращаются, и у нас остаются И . Таким образом, мы можем сделать AND из 2 NAND , используя один для инвертирования вывода другого.
Как насчет ИЛИ , нашей другой основной операции? Таблицы истинности показывают, что такое A NAND B . Что произойдет, если мы инвертируем A и B (обозначается размещением черточки над А и В )? У нас есть (НЕ А) И-НЕ (НЕ Б) . Напишем для этого таблицу истинности.
Это интересно; это похоже на таблицу истинности для A ИЛИ B .
Это известное явление в булевой алгебре: закон Де Моргана. Первоначально он был сформулирован Августом Де Морганом, математиком XIX века. Он определяет связь между И и ИЛИ . В частности, если вы отрицаете И или ИЛИ , это эквивалентно использованию другой операции с инверсией входных данных:
Первоначально он был сформулирован Августом Де Морганом, математиком XIX века. Он определяет связь между И и ИЛИ . В частности, если вы отрицаете И или ИЛИ , это эквивалентно использованию другой операции с инверсией входных данных:
НЕ (А И В) = (НЕ А) ИЛИ (НЕ В)
и
НЕ (А ИЛИ В) = (НЕ А) И (НЕ В)
Как мы можем это использовать? Ну, НЕ (А И В) то же самое, что и А НЕ И В , поэтому
А НЕ-И В = (НЕ А) ИЛИ (НЕ В)
, если теперь заменить А на (НЕ А) и Б с (НЕ Б) получаем
(НЕ А) И-НЕ (НЕ В) = (НЕ (НЕ А)) ИЛИ (НЕ (НЕ В))
Зная, что пары НЕ сокращаются, у нас остается:
(НЕ А) И-НЕ (НЕ В) = А ИЛИ В
БУМ!
NOT можно получить из NAND , поэтому из 3 NAND можно получить ИЛИ .


 размер блока
размер блока