Теория и применение цифровой обработки сигналов
Теория и применение цифровой обработки сигналов
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ 1.2. Обзор основных направлений цифровой обработки сигналов 1.3. Построение книги 2.1. Введение 2.2. Последовательности 2.3. Представление произвольных последовательностей 2.4. Линейные системы с постоянными параметрами 2.5. Физическая реализуемость. Устойчивость 2.6. Разностные уравнения 2.7. Частотная характеристика 2.8. Частотная характеристика систем первого порядка 2.9. Частотная характеристика систем второго порядка 2.11. Замечания о единицах измерения частоты 2.12. Соотношение между непрерывными и дискретными системами 2.13. z-преобразование 2.14. Соотношение между z-преобразованием и фурье-преобразованием последовательности 2.15. Обратное z-преобразование 2.16. Свойства z-преобразования 2.17. Решение разностных уравнений с применением одностороннего z-преобразования 2.  18. Геометрическая интерпретация преобразования Фурье 18. Геометрическая интерпретация преобразования Фурье2.19. Построение цифровых фильтров (структурные схемы фильтров) 2.20. Структурные схемы фильтров без полюсов 2.21. Дискретное преобразование Фурье 2.23. Свертка последовательностей 2.24. Линейная свертка конечных последовательностей 2.25. Секционированные свертки 2.26. Дискретное преобразование Гильберта 2.27. Преобразование Гильберта действительных сигналов ГЛАВА 3. ТЕОРИЯ И РАСЧЕТ ЦИФРОВЫХ ФИЛЬТРОВ С ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ КОНЕЧНОЙ ДЛИНЫ 3.2. Порядок расчета фильтров 3.3. Свойства КИХ-фильтров 3.4. Характеристики КИХ-фильтров с линейной фазовой характеристикой 3.5. Частотная характеристика КИХ-фильтров с линейной фазой 3.6. Расположение нулей КИХ-фильтров с линейной фазой 3.7. Методы расчета КИХ-фильтров с линейными фазами 3.8. Первый метод расчета — метод взвешивания 3.10. «Обобщенное» окно Хэмминга 3.11.  Окно Кайзера Окно Кайзера3.12. Примеры фильтров нижних частот с различными окнами 3.13. Особенности использования метода взвешивания 3.14. Несколько практических приемов использования окон 3.15. Дополнительные примеры фильтров рассчитанных методом взвешивания 3.16. Общая характеристика окон 3.17. Второй метод проектирования — метод частотной выборки 3.18. Решение задачи оптимизации 3.19. Линейное программирование 3.20. Фильтры с частотной выборкой вида 1 и 2 3.21. Фильтры вида 1 с частотной выборкой и линейной фазой 3.23. Некоторые самые общие результаты расчета фильтров методом частотной выборки 3.24. Заключение к описанию метода частотной выборки 3.25. Третий метод проектирования — проектирование оптимальных фильтров с минимаксной ошибкой 3.26. Аппроксимация по Чебышеву со взвешиванием 3.27. Ограничение на число экстремумов частотной характеристики фильтра с линейной фазой 3.  28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций 28. Решение нелинейных уравнений для КИХ-фильтров с максимумом пульсаций3.29. Расчет КИХ-фильтров с максимумом пульсаций на основе полиномиальной интерполяции 3.31. Расчет оптимальных КИХ-фильтров методами линейного программирования 3.32. Характеристики оптимальных фильтров нижних частот вида 1 3.33. Некоторые дополнительные свойства оптимальных фильтров нижних частот вида 1 3.34. Соотношения между параметрами оптимального фильтра нижних частот 3.35. Свойства оптимальных фильтров нижних частот вида 2 3.36. Характеристики оптимальных дифференциаторов 3.37. Характеристики оптимальных преобразователей Гильберта 3.38. Многополосные оптимальные КИХ-фильтры 3.39. Расчет фильтров при одновременном ограничении и во временной, и в частотной областях 3.40. Непосредственное сравнение различных КИХ-фильтров нижних частот Глава 4. ТЕОРИЯ И АППРОКСИМАЦИЯ ЦИФРОВЫХ ФИЛЬТРОВ С БЕСКОНЕЧНЫМИ ИМПУЛЬСНЫМИ ХАРАКТЕРИСТИКАМИ 4.  2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки 2. Элементарные свойства БИХ-фильтров: квадрат амплитудной характеристики, фазовая характеристика, характеристика групповой задержки4.3. Методы расчета коэффициентов БИХ-фильтра 4.4. Расчет цифровых фильтров по фильтрам непрерывного времени 4.5. Метод отображения дифференциалов 4.6. Метод инвариантного преобразования импульсной характеристики 4.7. Билинейное z-преобразование 4.8. Согласованное z-преобразование 4.10. Расчетные диаграммы фильтров нижних частот 4.11. Сравнение методов инвариантного преобразования импульсной характеристики и билинейного преобразования для эллиптических фильтров 4.12. Частотные преобразования 4.13. Прямые методы расчета цифровых фильтров 4.14. Применение методов оптимизации для расчета БИХ-фильтров 4.15. Обзор методов расчета БИХ-фильтров 4.16. Сравнение КИХ- и БИХ-фильтров 4.17. Сравнение оптимальных КИХ-фильтров и эллиптических фильтров с выравниванием групповой задержки Глава 5.  5.2. Аналого-цифровое преобразование 5.3. Цифро-аналоговое преобразование 5.4. Системы счисления, применяемые в цифровых устройствах 5.5. Система счисления с фиксированной запятой 5.6. Системы счисления с плавающей запятой 5.7. Система счисления с поблочно плавающей запятой 5.8. Виды квантования в цифровых фильтрах 5.9. Усечение 5.10. Округление 5.11. Шум округления в рекурсивных структурах с фиксированной запятой 5.12. Ограничение динамического диапазона в системах с фиксированной запятой 5.13. Ограничение динамического диапазона при построении фильтров в прямой форме 5.15. Ограничение динамического диапазона при построении фильтров в каскадной форме 5.16. Упорядочение размещения блоков и попарный подбор нулей и полюсов блоков при построении фильтра в каскадной форме 5.17. Выводы относительно взаимосвязи между динамическим диапазоном и уровнем шума округления 5.  18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления 18. Дополнительные замечания о взаимосвязи между динамическим диапазоном и уровнем шума округления5.19. Шум округления в нерекурсивных структурах с фиксированной запятой 5.20. Шум округления при построении нерекурсивных фильтров в прямой форме 5.22. Шум округления в рекурсивных структурах с плавающей запятой 5.23. Квантование коэффициентов 5.24. Квантование коэффициентов в рекурсивных структурах 5.25. Квантование коэффициентов при построении фильтров в прямой форме 5.26. Экспериментальная проверка шумовой модели квантования коэффициентов 5.27. Оптимальное квантование коэффициентов 5.28. Квантование коэффициентов в двухполюсном фильтре 5.29. Квантование коэффициентов в нерекурсивных структурах 5.30. Квантование коэффициентов при построении КИХ-фильтров 5.31. Квантование коэффициентов при построении КИХ-фильтров в каскадной форме Глава 6.  СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ СПЕКТРАЛЬНЫЙ АНАЛИЗ И БЫСТРОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ6.2. Введение в алгоритмы БПФ с основанием 2 6.3. Некоторые свойства алгоритма БПФ с основанием 2 и прореживанием по времени 6.4. Перестановка данных и двоичная инверсия 6.5. Программа расчета БПФ на ФОРТРАНе 6.6. Алгоритм БПФ с прореживанием по частоте 6.7. Вычисление обратного ДПФ с помощью алгоритма прямого ДПФ 6.8. Единый подход к алгоритмам БПФ 6.9. Алгоритмы БПФ с основанием 2 6.10. Спектральный анализ в одной точке z-плоскости 6.12. Некоторые характеристики спектрального анализа 6.13. Соотношение между «скачущим» БПФ и гребенкой фильтров 6.14. Использование окон при спектральном анализе 6.15. Измерение спектра в ограниченном секторе z-плоскости с использованием БПФ 6.16. Алгоритм Блюстейна 6.17. Алгоритм z-преобразования с использованием ЛЧМ-фильтрации 6.18. Энергетический спектр случайных сигналов 6.19. Свертка и корреляция с использованием теоретико-числовых преобразований ПРИЛОЖЕНИЕ.  УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ ДЛЯ БПФГлава 7. ВВЕДЕНИЕ В ТЕОРИЮ ДВУМЕРНОЙ ОБРАБОТКИ СИГНАЛОВ 7.2. Двумерные сигналы 7.3. Двумерные системы 7.4. Физическая реализуемость. Разделимость. Устойчивость 7.5. Двумерные разностные уравнения 7.6. Частотные методы 7.7. Двумерное z-преобразование 7.8. Конечные последовательности 7.9. Свертка последовательностей 7.10. Двумерное ДПФ 7.11. Расчет двумерных фильтров 7.12. БИХ-фильтры 7.13. Устойчивость БИХ-фильтров 7.14. КИХ-фильтры 7.15. Двумерные весовые функции (окна) 7.16. Пример расчета фильтра нижних частот методом взвешивания 7.17. Фильтры с частотной выборкой 7.18. Двумерные фильтры нижних частот с частотной выборкой 7.19. Расчет оптимальных (в минимаксном смысле) двумерных фильтров 7.20. Частотное преобразование одномерных фильтров в двумерные 7.21. Примеры обработки изображений Глава 8. ВВЕДЕНИЕ В ЦИФРОВУЮ ТЕХНИКУ 8.2. Некоторые вопросы проектирования аппаратуры цифровой обработки сигналов 8.  3. Булева алгебра. Примеры простых логических цепей 3. Булева алгебра. Примеры простых логических цепей8.4. Основные типы интегральных логических схем 8.5. Серийные логические ИС: вентили, коммутаторы и дешифраторы, триггеры, арифметические и запоминающие устройства 8.6. Умножители 8.7. Делители и устройства с плавающей запятой 8.8. Пример: проектирование быстродействующего матричного умножителя 8.9. Заключение ГЛАВА 9. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ЦИФРОВОЙ ФИЛЬТРАЦИИ И ГЕНЕРАЦИИ СИГНАЛОВ 9.2. Аппаратурное построение КИХ-фильтра прямой формы 9.3. Параллелизм при построении КИХ-фильтров прямой формы 9.4. Каскадная форма КИХ-фильтра 9.5. Прямая форма КИХ-фильтра с высоким уровнем параллелизма 9.6. Прямая форма построения БИХ-фильтров 9.7. Каскадная форма БИХ-фильтров 9.8. Мультиплексирование 9.9. Цифровой приемник клавишно-тонального вызова 9.10. Цифровой преобразователь временного разделения каналов в частотное разделение каналов 9.11. Расчленение цифровых фильтров на составные части при построении их на интегральных микросхемах 9.  12. Специализированный цифровой синтезатор частот 12. Специализированный цифровой синтезатор частот9.13. Методы генерации псевдослучайных чисел 9.14. Методы генерации гауссовых случайных чисел Глава 10. СПЕЦИАЛИЗИРОВАННЫЕ УСТРОЙСТВА ДЛЯ ВЫПОЛНЕНИЯ БПФ 10.2. Обзор теоретических основ БПФ 10.3. Нумерация при БПФ. Двоичная инверсия и разрядная инверсия для алгоритмов БПФ с постоянным основанием 10.5. Эффекты квантования в алгоритмах БПФ 10.6. Особенности аппаратурной реализации БПФ с основанием 2 10.7. Оптимальная аппаратурная реализация алгоритма БПФ с основанием 2 10.9. Выполнение БПФ с использованием сверхоперативной памяти 10.10. Параллельные структуры для алгоритмов БПФ с основаниями 2 и 4, использующие ЗУ с произвольным доступом 10.11. Общие вопросы построения поточных схем БПФ 10.12. Поточные схемы БПФ с основанием 2 10.13. Поточная схема БПФ с основанием 4 10.14. Сравнение поточных схем БПФ с основаниями 2 и 4 10.15. Структуры БПФ с повышенным уровнем параллелизма 10.  16. Общие принципы построения специализированных процессоров БПФ 16. Общие принципы построения специализированных процессоров БПФ10.17. БПФ перекрывающихся массивов на основе ЗУ с произвольным доступом 10.18. Свертка в реальном времени методом БПФ с использованием одного АУ и ЗУ с произвольным доступом 10.19. Поточный свертыватель с тактовой частотой 10 МГц Глава 11. УНИВЕРСАЛЬНЫЕ УСТРОЙСТВА В СИСТЕМАХ ОБРАБОТКИ СИГНАЛОВ 11.2. Специализированные и универсальные вычислительные машины 11.3. Способы описания вычислительных машин 11.4. Программа вычисления скользящей суммы 11.5. Особенности ввода — вывода при обработке в реальном времени 11.6. Методы увеличения быстродействия вычислительной машины 11.7. Сверхоперативные ЗУ 11.8. Распараллеливание арифметических операций 11.9. Параллельная работа ЗУ, АУ, устройств управления и вызова команд 11.10. Быстродействующий цифровой процессор (FDP) Линкольновской лаборатории 11.11. Структурные схемы арифметических устройств 11.12. Синхронизация 11.13.  Обзор методов увеличения быстродействия, использованных в FDP Обзор методов увеличения быстродействия, использованных в FDP11.14. Выполнение быстрого преобразования Фурье с помощью FDP 11.15. Подпрограммы для действий с плавающей запятой 11.16. Обзор особенностей FDP, связанных с распараллеливанием 11.17. Процессор Линкольновской лаборатории LSP (Lincoln Signal Processor 2) для обработки сигналов 11.18. Лабораторная вычислительная система для цифровой обработки сигналов ГЛАВА 12. ЦИФРОВАЯ ОБРАБОТКА РЕЧЕВЫХ СИГНАЛОВ 12.2. Модель образования речи 12.3. Кратковременный спектральный анализ 12.4. Система анализа-синтеза речи, основанная на кратковременном спектральном анализе 12.5. Особенности анализа речи 12.6. Система анализа — синтеза 12.7. Полосный вокодер 12.8. Анализаторы вокодеров. Особенности обработки сигналов 12.9. Синтезаторы вокодеров. Особенности обработки сигналов 12.10. Другие схемы вокодеров 12.11. Выделение высоты основного тона и обнаружение тон — шум 12.12. Обнаружитель тон — шум 12.  13. Гомоморфная обработка речи 13. Гомоморфная обработка речи12.14. Гомоморфный вокодер 12.15. Формантный синтез 12.16. Цепь возбуждения звонких фрикативных звуков 12.17. Генератор случайных чисел 12.18. Цифровая обработка в формантном синтезаторе 12.19. Линейное прогнозирование речи 12.20. Система речевого ответа для вычислительной машины 12.21. Заключение 13.1. Вводные замечания о принципах радиолокации и ее применениях 13.2. Состав и параметры радиолокационной системы 13.3. Выбор сигналов и функция неопределенности 13.4. Цифровые согласованные фильтры для радиолокационных сигналов 13.5. Аэродромный обзорный радиолокатор системы управления полетами. Доплеровская фильтрация как средство подавления мешающих отражений 13.6. Экспериментальный радиолокатор дальнего действия 13.7. Цифровой согласованный фильтр для высококачественного радиолокатора 13.8. Заключение |
10. Применение булевых функций для решения логических задач
В условии задачи выделяются простые высказывания и логические связки между ними.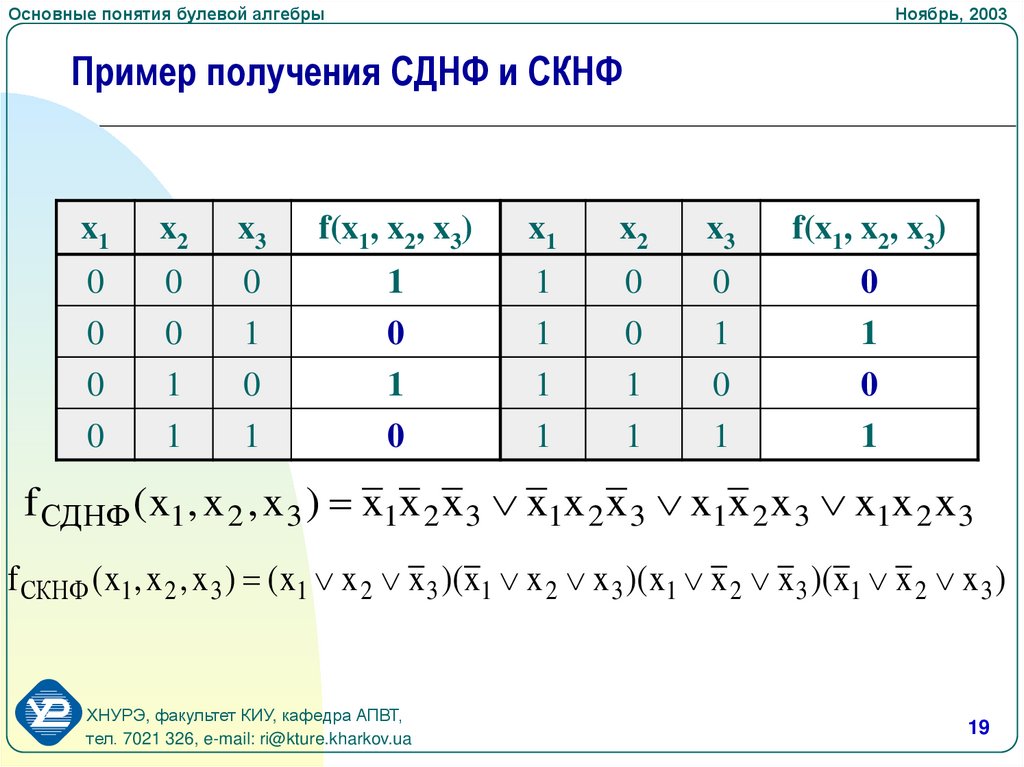 По условию задачи формируются истинные составные высказывания, которые затем соединяются знаком конъюнкции. Полученная истинная формула является символической записью условия задачи. Формула упрощается с помощью равносильных преобразований алгебры высказываний.
По условию задачи формируются истинные составные высказывания, которые затем соединяются знаком конъюнкции. Полученная истинная формула является символической записью условия задачи. Формула упрощается с помощью равносильных преобразований алгебры высказываний.
Пример. Определить, участвовал ли в соревновании Иванов, если известно, что:
1. Если Иванов не участвовал или Петров участвовал, то Сидоров участвовал;
2. Если Иванов не участвовал, то Сидоров не участвовал.
Решение. Выделим в условии задачи простые высказывания: А =
= {Иванов участвовал}, В = {Петров участвовал}, С = {Сидоров участвовал}. Тогда первое условие задачи записывается в виде истинной формулы , второе условие – в виде истинной формулы . Соединим их знаком конъюнкции. Истинная формула является символической записью условия задачи. Упростим полученную формулу с помощью равносильностей алгебры высказываний теоремы 1.1 (см. пункт 1.3):
Так как упрощённая формула принимает значение «истина», то высказывания А и принимают значение «истина». Значит, Иванов участвовал в соревновании. □
Значит, Иванов участвовал в соревновании. □
Задачи и упражнения
1.36. Брауну, Джонсу и Смиту предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что преступники скрылись на синем «Бьюике», Джонс сказал, что это был черный «Крайслер», а Смит утверждает, что это был «Форд Мустанг» и ни в коем случае не синий. Стало известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет. Какого цвета и марки был автомобиль?
1.37. На вопрос, какая завтра будет погода, синоптик ответил:
1) если не будет ветра, то будет пасмурная погода без дождя;
2) если будет дождь, то будет пасмурно и без ветра;
3) если будет пасмурная погода, то будет дождь и не будет ветра.
С помощью алгебры логики определите погоду на завтра.
1.38. Известно, что если математическую логику изучал Василий, то ее изучал и Пётр. Неверно, что если Николай изучал логику, то её изучал и Пётр. Установите, кто из них изучал математическую логику.
Установите, кто из них изучал математическую логику.
1.39. Студенты второго курса Алексей, Борис, Владимир и Глеб сдавали экзамен по дискретной математике. Определите, кто из них сдал экзамен, если известно, что:
1) если Алексей сдал, то Борис тоже сдал;
2) если Борис сдал, то Владимир сдал или Алексей не сдал;
3) если Глеб сдал, то Алексей сдал и Владимир не сдал;
4) если Глеб сдал, то Алексей тоже сдал.
Вопросы для самоконтроля
1. Сформулируйте алгоритм составления формул алгебры высказываний.
2. Сформулируйте алгоритм проверки равносильности формул алгебры высказываний.
3. Укажите сходство и различие понятий «тавтология» и «противоречие».
4. Приведите примеры теорем математического анализа, имеющих конструкцию эквиваленции.
5. Приведите примеры теорем линейной алгебры, имеющих конструкцию импликации.
6. Составьте таблицы истинности для следующих логических операций:
1) Стрелка Пирса: ; 2) Штрих Шеффера: .
7. Сформулируйте определение формулы алгебры предикатов.
8. Образуйте из предикатов задачи 1.16 истинные высказывания.
9. Образуйте из предикатов задачи 1.16 ложные высказывания.
10. С помощью законов де Моргана получите отрицание высказывания, полученного в задаче 1.20.
11. Найдите СДНФ и СКНФ функции с помощью равносильностей алгебры высказываний.
12. Составьте все восемь высказываний, образованных путем применения кванторов к двухместному предикату по обеим переменным.
| < Предыдущая |
|---|
Булева алгебра — законы, правила, теоремы, примеры
Булева алгебра — раздел алгебры, занимающийся логическими операциями над переменными. В булевой алгебре может быть только два возможных значения переменных, то есть либо 1, либо 0. Другими словами, переменные могут обозначать только два варианта: истина или ложь. Три основные логические операции булевой алгебры — это конъюнкция, дизъюнкция и отрицание.
В элементарной алгебре математические выражения используются в основном для обозначения чисел, тогда как в булевой алгебре выражения представляют значения истинности. Значения истинности используют двоичные переменные или биты «1» и «0» для представления состояния входа, а также выхода. Логические операторы И, ИЛИ и НЕ образуют три основных логических оператора. В этой статье мы узнаем больше об определении, законах, операциях и теоремах булевой алгебры.
| 1. | Что такое булева алгебра? |
| 2. | Выражение булевой алгебры |
| 3. | Булевы алгебраические операции |
| 4. | Законы булевой алгебры |
| 5. | Теоремы булевой алгебры |
| 6. | Постулаты булевой алгебры |
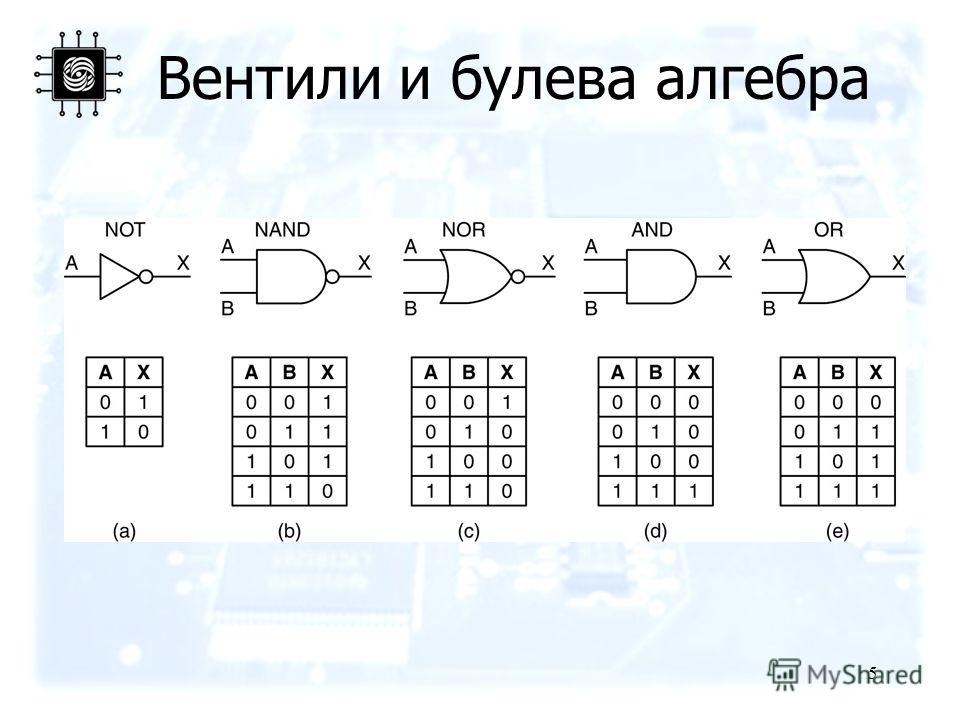
| 7. | Булева алгебра и логические элементы |
8. | Таблица истинности булевой алгебры |
| 9. | Часто задаваемые вопросы по булевой алгебре |
Что такое булева алгебра?
Булева алгебра также известна как бинарная алгебра или логическая алгебра. Основное применение булевой алгебры заключается в том, что она используется для упрощения и анализа различных цифровых логических схем. Диаграммы Венна также можно использовать для визуального представления любой операции булевой алгебры.
Определение булевой алгебры
Булева алгебра может быть определена как тип алгебры, который выполняет логические операции над двоичными переменными. Эти переменные дают истинностные значения, которые могут быть представлены как 0, так и 1. Основными логическими операциями являются конъюнкция, дизъюнкция и отрицание. Логические операторы И, ИЛИ и НЕ используются для представления этих операций соответственно. Более того, эти операции аналогичны пересечению, объединению и дополнению множеств в теории множеств. Вот некоторые из правил булевой алгебры:
Вот некоторые из правил булевой алгебры:
- Любая используемая переменная может иметь только два значения. Двоичный 1 для HIGH и двоичный 0 для LOW.
- Каждая дополнительная переменная представлена чертой сверху, т. е. дополнение переменной B представлено как B¯. Таким образом, если B = 0, то B¯= 1 и B = 1, то B¯= 0,
- Переменные с ИЛИ представлены знаком плюс (+) между ними. Например, OR для A, B, C представляется как A + B + C.
- Две или более переменных с логическим И представлены точкой между ними, например, A.B.C. Иногда точка может быть опущена, как ABC.
Давайте рассмотрим пример,
Предположим, у нас есть две переменные A = 1 и B = 0. Мы должны выполнить операцию И. Логическое выражение может быть представлено как A.B = 1.0 = 0.
Если мы должны выполнить логическую операцию ИЛИ, то логическое выражение задается как A + B = 1 + 0 = 1.
Если мы применим операцию НЕ к обе входные переменные, тогда мы получаем \(\overline{A}\) = 0 и \(\overline{B}\) = 1.
Выражение булевой алгебры
Выражения булевой алгебры — это операторы, в которых используются логические операторы, такие как И, ИЛИ, НЕ, XOR и т. д. Эти логические операторы могут иметь только два выхода: либо истина, либо ложь. В цифровых схемах и логических элементах «1» и «0» используются для обозначения входных и выходных условий. Например, если мы напишем A ИЛИ B, это станет логическим выражением. Существует множество законов и теорем, которые можно использовать для упрощения выражений булевой алгебры, чтобы оптимизировать вычисления, а также улучшить работу цифровых схем.
Булевы алгебраические операции
Существуют три основные операции булевой алгебры. Это конъюнкция, дизъюнкция и отрицание. Логические операторы, эквивалентные этим операциям, приведены ниже.
- Оператор И: Аналогичен конъюнкции. В логическом выражении «•» используется для представления оператора И. Этот оператор возвращает истину тогда и только тогда, когда все входные операнды истинны.

- Оператор ИЛИ: Этот оператор эквивалентен дизъюнкции. В логическом выражении символ «+» используется для обозначения оператора ИЛИ. Оператор возвращает истину тогда и только тогда, когда истинны один или несколько входных операндов.
- Оператор НЕ: Этот логический оператор сравним с отрицанием. Оператор НЕ возвращает значение true, если входная переменная имеет значение false. Точно так же, если входная переменная ложна, она возвращает истину. Надчеркивание переменной используется для представления этого оператора.
Законы булевой алгебры
Булева алгебра в основном используется для упрощения логических схем. Применяя законы булевой алгебры, мы можем упростить логическое выражение и уменьшить количество логических элементов, которые необходимо использовать в цифровой схеме. Некоторые из важных законов булевой алгебры приведены ниже:
Распределительный закон
Распределительный закон гласит, что если мы выполним операцию И над двумя переменными и ИЛИ результата с другой переменной, то это будет равно И для ИЛИ третьей переменной с каждой из первых двух переменных. Логическое выражение задается как
Логическое выражение задается как
A + B.C = (A + B) (A + C)
Таким образом, ИЛИ распределяет по И
Если мы ИЛИ две переменные, то И их результат с другой переменной, то это значение будет равно к ИЛИ И третьей переменной с двумя другими переменными. Это дается:
A .(B+C) = (A.B) + (A.C)
Следовательно, И распределяется по ИЛИ.
Ассоциативный закон
Согласно ассоциативному закону, если более чем две переменные соединены по ИЛИ или по И, то порядок группировки переменных не имеет значения. Результат всегда будет одинаковым. Выражения задаются следующим образом:
A + (B + C) = (A + B) + C
A.(B.C) = (A.B).C
Коммутативный закон
Коммутативный закон утверждает, что если мы поменяем местами порядок операндов (И или ИЛИ) результат логического уравнения не изменится. Это можно представить следующим образом:
A + B = B + A
A.B = B.A
Закон поглощения
Закон поглощения связывает двоичные переменные и помогает сократить сложные выражения за счет поглощения одинаковых переменных. Есть 4 утверждения, подпадающие под действие этого закона:
Есть 4 утверждения, подпадающие под действие этого закона:
- A + A.B = A
- А (А + В) = А
- А + А.В = А + В
- А.(А + В) = А.В
Существуют некоторые свойства и тождества булевой алгебры, которые задаются следующим образом:
- А + 1 = 1
- А + 0 = А
- А . 1 = А
- А . 0 = 0
- А + А = А
- А . А = А
- \(\overline{\overline{A}}\) = А
- А + \(\overline{A}\) = 1
- А . \(\overline{A}\) = 0
Теоремы булевой алгебры
Одной из важнейших теорем булевой алгебры является теорема Де Моргана. Эта теорема состоит из двух утверждений, которые помогают связать операторы И, ИЛИ и НЕ. Два утверждения даны следующим образом:
- Когда две переменные объединяются по И и инвертируются, результат равен ИЛИ каждой инвертированной входной переменной. Логическое выражение: \(\overline{A.B}\) = \(\overline{A}\) + \(\overline{B}\).

- Когда две переменные объединены по ИЛИ и инвертированы, это будет равно И для каждой инвертированной входной переменной. Это определяется как \(\overline{A + B}\) = \(\overline{A}\).\(\overline{B}\)
Постулаты булевой алгебры
Постулаты булевой алгебры — это не законы или теоремы, а истинные утверждения. Этими постулатами являются четыре возможных логических операции ИЛИ и логическое И, а также правила, которым следует оператор НЕ. Ниже приведены постулаты булевой алгебры:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 1
- 0 . 0 = 0
- 0 . 1 = 0
- 1 . 0 = 0
- 1 . 1 = 1
- \(\overline{1}\) = 0
- \(\overline{0}\) = 1
Булева алгебра и логические элементы
Логический элемент является строительным блоком любой цифровой схемы. Эти логические элементы должны принимать решение об объединении различных входных данных в соответствии с некоторой логической операцией и создавать выходные данные.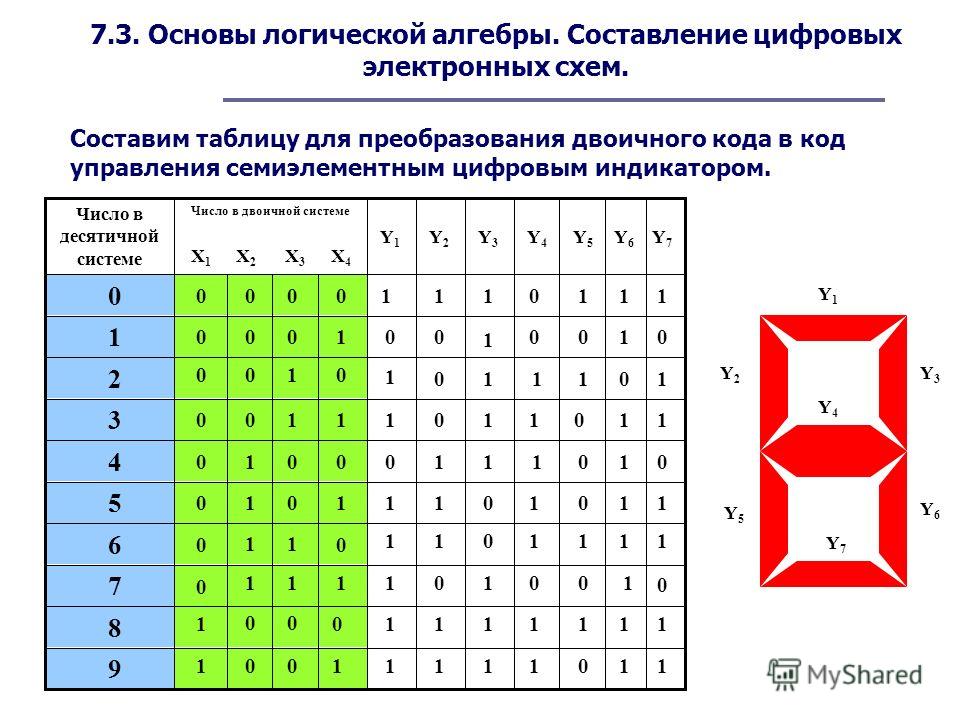 Логические элементы выполняют логические операции на основе булевой алгебры. Предположим, у нас есть два входа A и B. Пусть выход будет R. Тогда ниже приведены различные типы и символы логических элементов.
Логические элементы выполняют логические операции на основе булевой алгебры. Предположим, у нас есть два входа A и B. Пусть выход будет R. Тогда ниже приведены различные типы и символы логических элементов.
И ворота — R = A.B будет логическим выражением. R будет истинным, если оба A и B истинны.
Элемент ИЛИ — логическое уравнение R = A + B. Здесь R будет истинным, если любой из входов A ИЛИ B верен.
вентиль НЕ — также известен как инвертор, а логическое уравнение — R = \(\overline{A}\). Это означает, что вывод истинен только в том случае, если ввод ложен.
вентиль И-НЕ — Это тоже ворота НЕ-И. R = \(\overline{A.B}\) — логическое уравнение. Выход R НЕ будет истинным, если оба A И B верны.
Вентиль ИЛИ — Операция НЕ-ИЛИ приводит к вентилю ИЛИ-НЕ. R = \(\overline{A + B}\) обозначает логическое уравнение и подразумевает, что R истинно, если A и B НЕ истинны.
EX — ворота ИЛИ — Это ворота исключающего ИЛИ. Его можно создать, используя комбинацию вышеупомянутых ворот. R = A ⊕ B — логическое выражение. Это означает, что R истинно, только если истинно либо A, либо B.
EX — вентиль ИЛИ-НЕ — логическое уравнение вентиля исключающее ИЛИ-ИЛИ задается как R = \(\overline{A ⊕ B}\). Это означает, что R истинно, только если оба входа либо истинны, либо ложны.
Таблица истинности булевой алгебры
Таблица истинности булевой алгебры может быть определена как таблица, которая сообщает нам, верно ли логическое выражение для указанных входных переменных. Такая таблица истинности будет состоять только из бинарных входов и выходов. Ниже приведены таблицы истинности для различных логических вентилей.
И ворота
| А | Б | Р = А.Б. |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Ворота ИЛИ
| А | Б | Р = А + В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
НЕ ворота
| А | R = \(\overline{A}\) |
| 1 | 0 |
| 0 | 1 |
вентиль И-НЕ
| А | Б | R = \(\overline{A.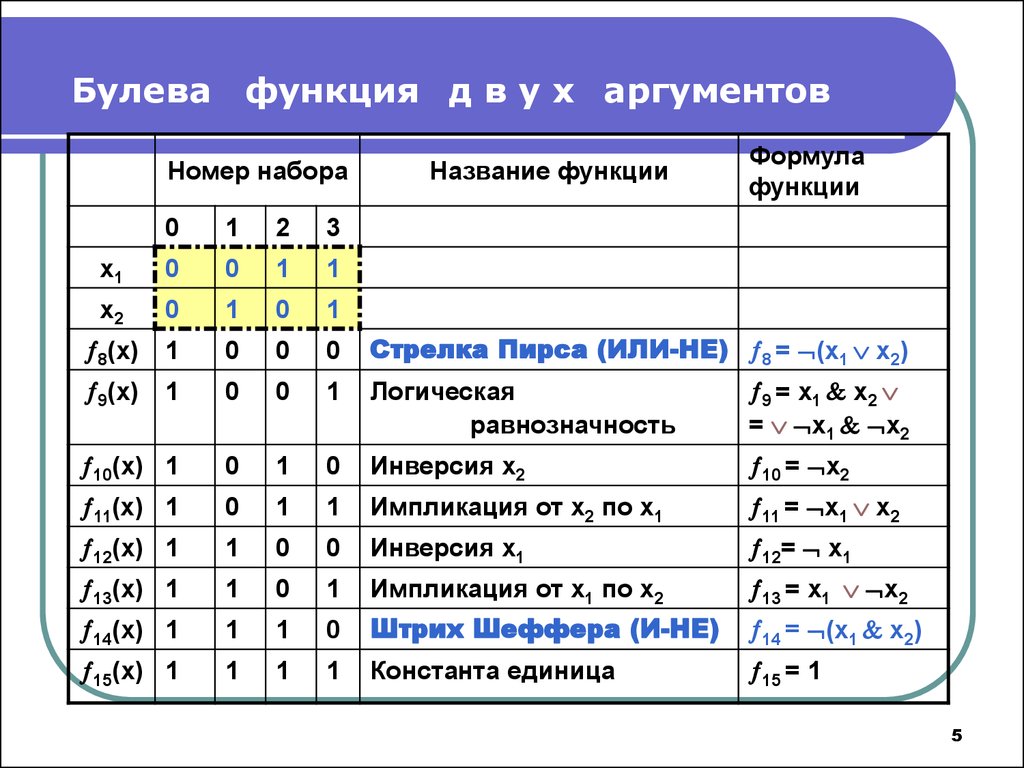 B}\) B}\) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ворота NOR
| A | Б | R = \(\overline{A + B}\) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Ворота EX-OR
| A | Б | Р = А ⊕ В |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Ворота EX — NOR
| A | Б | R = \(\overline{A ⊕ B}\) |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Связанные статьи:
- Наборы
- Калькулятор булевой алгебры
- Дополнение к набору
- Пересечение набора
Часто задаваемые вопросы по булевой алгебре
Что понимается под булевой алгеброй?
Булева алгебра — это тип алгебры, в котором входные и выходные значения могут быть только истинными (1) или ложными (0). Булева алгебра использует логические операторы и используется для построения цифровых схем.
Булева алгебра использует логические операторы и используется для построения цифровых схем.
Что такое правила булевой алгебры?
Основные правила булевой алгебры:
- Любая используемая переменная может иметь только два значения. Двоичный 1 для HIGH и двоичный 0 для LOW.
- Каждая дополнительная переменная представлена чертой сверху, т. е. дополнение переменной B представлено как B¯. Таким образом, если B = 0, то B¯= 1 и B = 1, то B¯= 0,
- Переменные с ИЛИ представлены знаком плюс (+) между ними. Например, OR для A, B, C представляется как A + B + C.
- Две или более переменных с логическим И представлены точкой между ними, например, A.B.C. Иногда точка может быть опущена, как ABC.
Что такое законы булевой алгебры?
Есть четыре основных закона булевой алгебры. Это дистрибутивное право, ассоциативное право, коммутативное право и абсорбционное право. Когда мы упрощаем логическое выражение, эти законы широко используются.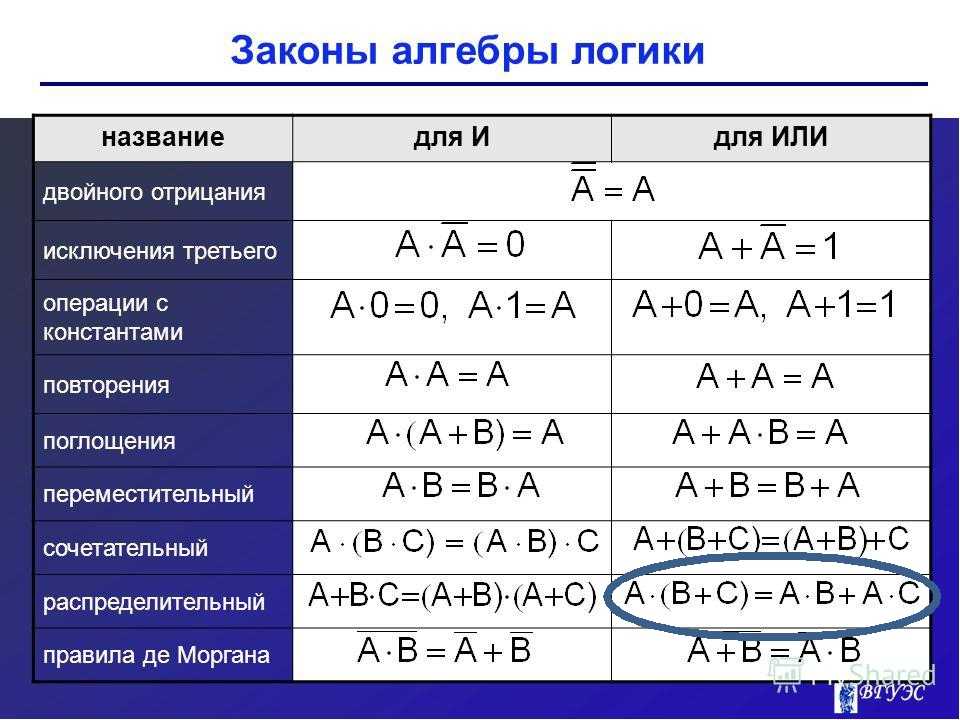
Каковы тождества булевой алгебры?
Важные тождества булевой алгебры приведены ниже:
- A + 1 = 1
- А + 0 = А
- А . 1 = А
- А . 0 = 0
- А + А = А
- А . А = А
- \(\overline{\overline{A}}\) = А
- А + \(\overline{A}\) = 1
- А . \(\overline{A}\) = 0
Как вы занимаетесь булевой алгеброй?
При решении выражения булевой алгебры самое главное помнить законы булевой алгебры, теоремы и связанные с ними тождества. Нам нужно последовательно применять эти правила до тех пор, пока выражение нельзя будет упростить дальше, чтобы получить наш ответ.
Что такое распределительный закон в булевой алгебре?
Закон дистрибутивности в булевой алгебре содержит два утверждения. Два утверждения выглядят следующим образом:
- ИЛИ распределяет по И [A + B.C = (A + B) (A + C)].
- И распределяется по ИЛИ [A .(B+C) = (A.B) + (A.C)]
Что такое закон поглощения в булевой алгебре?
Уравнения булевой алгебры для закона поглощения, которые помогают связать одинаковые переменные, выглядят следующим образом:
- A + A.
 B = A
B = A - А (А + В) = А
- А + А.В = А + В
- А.(А + В) = А.В
Как упростить выражения булевой алгебры?
Мы можем упростить выражения булевой алгебры, используя различные теоремы, законы, постулаты и свойства. В случае цифровых схем мы можем выполнить пошаговый анализ выхода каждого вентиля, а затем применить правила булевой алгебры, чтобы получить максимально упрощенное выражение.
Каковы свойства булевой алгебры?
Булева алгебра имеет три основных свойства, а именно:
- Коммутативное свойство сложения и умножения: порядок переменных может быть изменен на обратный без изменения истинности выражения, т. е. A + B = B + A и AB = BA
- Ассоциативное свойство сложения и умножения: умноженные и добавленные переменные вместе со скобками могут быть изменены без изменения истинности выражения, т. Е. A + (B + C) = (A + B) + C и A (BC) = (AB) C
- Распределительное свойство: выражение, образованное произведением суммы при расширении и переворачивании, показывает, как члены могут быть факторизованы, т.
 е. A(B + C) = AB + BC
е. A(B + C) = AB + BC
Примеры булевой алгебры — Electronics-Lab.com
Примеры булевой алгебры
В предыдущих статьях было показано, что цифровой логический вентиль и цифровая схема могут быть представлены логическим выражением и таблицей истинности . Логическое выражение состоит из ряда переменных, представляющих входные и выходные данные, которые обычно обозначаются буквой «Q». Входы и выходы имеют булев логический тип данных, то есть либо «0», либо «1». В Таблице истинности перечислены выходные данные логического элемента или цифровой схемы для всех возможных комбинаций входных данных. Используя булеву алгебру и законы булевой алгебры, можно сократить сложные цифровые логические схемы.
Идентификация и замена ненужных логических элементов приводит к экономии места, затрат и энергии. Процесс редукции сложной цифровой логической схемы может иметь несколько путей в зависимости от применения законов, теорем и т. Д. Однако пути редукции должны давать аналогичную и простейшую схему, если булева алгебра и законы применяются правильно.
Д. Однако пути редукции должны давать аналогичную и простейшую схему, если булева алгебра и законы применяются правильно.
В этой статье несколько цифровых логических схем уменьшены с использованием булевой алгебры и законов. Процесс редукции был объяснен, а также даны таблицы истинности, чтобы облегчить объяснение и процесс редукции.
Булева алгебра, пример № 1
На следующем рисунке показана цифровая логическая схема. Схема состоит из трех вентилей И и двух вентилей ИЛИ. В общей сложности пять логических элементов необходимы для создания желаемой логической функции. В этом примере желаемая логическая функция сокращается путем применения законов и теорем булевой алгебры.
Рисунок 1: Цифровая логическая схема примера № 1Шаги, связанные с преобразованием логического выражения, следующие:
AB + BC(B+C)
Применение распределительного закона
AB + BBC + BCC
Применение закона тождества (AA=A) ко 2-му и 3-му срокам
AB +
BC Применение закона тождества (A + A = A) ко 2-му и 3-му членамAB + BC
Удаление общего B
B(A+C)
Сокращенное выражение B(A+C) дает тот же логический вывод, что и у исходного выражения. Таблица истинности исходного логического выражения, а также сокращенного выражения (красный) показана ниже:
Таблица истинности исходного логического выражения, а также сокращенного выражения (красный) показана ниже:
Сокращенное выражение требует только двух логических элементов, т. е. элементов И и ИЛИ. Сокращение в три элемента было достигнуто путем применения законов булевой алгебры к сложному выражению. Упрощенная логическая схема показана на следующем рисунке.
Рис. 2: Решение примера № 1Булева алгебра, пример № 2
На следующем рисунке показана еще одна цифровая логическая схема.
Рисунок 3: Цифровая логическая схема из примера № 2 Данная цифровая схема состоит всего из трех логических элементов, т. е. И-НЕ, исключающее ИЛИ и исключающее ИЛИ. Эта цифровая схема сокращается путем построения таблицы истинности. Затем построенная таблица истинности анализируется, чтобы определить единую логику для замены вывода. 2-вход дает четыре комбинации и прост в построении. Для таких типов цифровых схем метод таблицы истинности более осуществим. Следующая таблица легко строится, зная таблицу истинности отдельных вентилей. Выход «C», «D» и «Q» соответствует NAND, XOR и XNOR соответственно. Выходы «C» и «D» становятся входом вентиля XNOR.
Выход «C», «D» и «Q» соответствует NAND, XOR и XNOR соответственно. Выходы «C» и «D» становятся входом вентиля XNOR.
Сгенерированная таблица истинности показана ниже:
Выход цифровой логической схемы имеет значение «ВЫСОКИЙ», когда любой из входов «А» или «В» имеет значение «ВЫСОКИЙ». Это выражение или вывод задается цифровым логическим элементом ИЛИ. Следовательно, данная схема с тремя логическими элементами может быть сведена к одному элементу ИЛИ с входами «А» и «В». Упрощенная логическая схема с тем же выходом, что и исходная цифровая схема, показана ниже:
Рис. 4: Решение примера № 2
Булева алгебра, пример № 3
На следующем рисунке показана другая логическая схема.
Рисунок 5: Цифровая логическая схема из примера № 3 Цифровая логическая схема содержит три логических элемента, т. е. И, ИЛИ-НЕ и ИЛИ. Выход NOR преобразуется в произведение инвертированного индивидуального входа. Конечный результат вентиля ИЛИ, который является функцией всей логической схемы, становится эквивалентным функции логики исключающее ИЛИ. Следовательно, данная цифровая логическая схема с тремя вентилями может быть заменена одним вентилем исключающего ИЛИ-вентиля.
Следовательно, данная цифровая логическая схема с тремя вентилями может быть заменена одним вентилем исключающего ИЛИ-вентиля.
Техника таблицы истинности также была принята для получения эквивалента одного вентиля. Таблица истинности была построена и показана ниже:
Конечный выход схемы «Q» эквивалентен выходу вентиля исключающее ИЛИ-НЕ. Таблица истинности также идентифицирует Exclusive-NOR как одноступенчатый эквивалент данной логической схемы. Вентиль Exclusive-NOR (XNOR) с двумя входами «A» и «B» показан на следующем рисунке.
Рисунок 6: Решение примера № 3Булева алгебра, пример № 4
В последнем примере упрощена более сложная цифровая логическая схема, состоящая из шести логических элементов. Логическая схема, которую нужно уменьшить, показана ниже.
Рисунок 7: Цифровая логическая схема примера № 4 Используя цифровую логическую схему, было получено логическое выражение на каждом этапе, и таблица истинности была построена с использованием этих логических выражений для каждой возможной комбинации входных данных.




 B = A
B = A е. A(B + C) = AB + BC
е. A(B + C) = AB + BC