Шестнадцатеричная система счисления — Студопедия.Нет
Шестнадцатеричная система счисления (позиционная система с основанием 16) широко используется для записи адресов и содержимого ячеек памяти компьютера. Её алфавит содержит 16 цифр, вместе с 10 арабскими цифрами (0..9) используются первые буквы латинского алфавита:
А = 10, В = 11, C = 12, D = 13, Е = 14, F = 15.
Таким образом, старшая цифра в шестнадцатеричной системе — F.
Для перевода чисел из десятичной системы в шестнадцатеричную используют алгоритм деления на 16 и взятия остатков. Важно не забыть, что все остатки, большие 9, нужно заменить на буквы:
Для обратного перехода значение каждой цифры умножают на 16 в степени, равной её разряду, и полученные значения складывают:
Можно также использовать схему Горнера:
1ВС16 = (1 • 16 + 11) • 16 + 12 = 27 • 16 + 12 = 444.
Основания двоичной и шестнадцатеричной систем связаны соотношением 24 = 16, поэтому можно переводить числа из шестнадцатеричной системы в двоичную напрямую.
Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления
1. Перевести значение каждой цифры (отдельно) в двоичную систему. Записать результат в виде тетрады, добавив, если нужно, нули в начало (см. табл. 2.6).
2. Соединить тетрады в одно «длинное» двоичное число.
Например, переведём в двоичную систему число 5Е123
5Е12316 = 101 1110 0001 0010 00112.
Обратите внимание, что для цифр, меньших 8 (кроме первой), результат перевода в двоичную систему нужно дополнить старшими нулями до 4 знаков.
Алгоритм перевода двоичного числа в шестнадцатеричную систему счисления
1.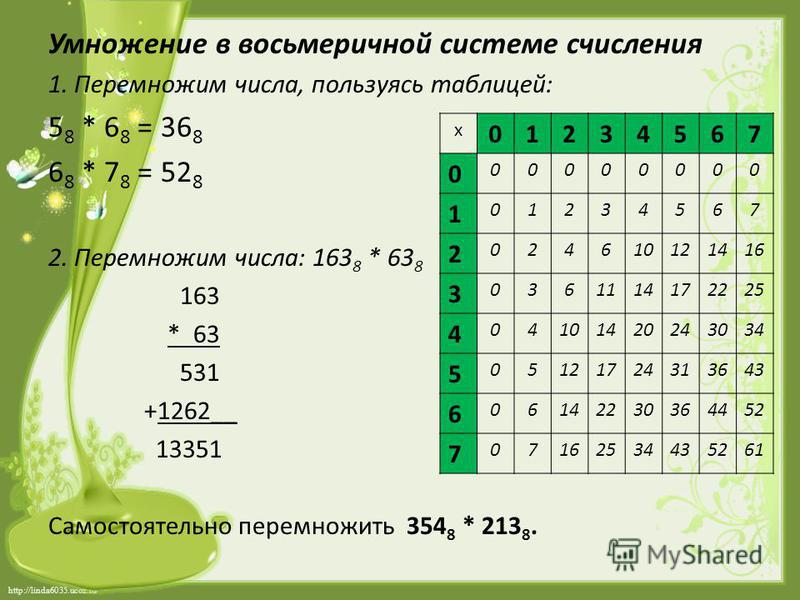 Разбить двоичное число на тетрады, начиная справа.
Разбить двоичное число на тетрады, начиная справа.
В начало самой первой тетрады добавить слева нули, если это необходимо.
2. Перевести каждую тетраду (отдельно) в шестнадцатеричную систему счисления.
3. Соединить полученные цифры в одно «длинное» число.
Например: 10000100001010101111002 = 10 0001 0000 1010 1011 11002 = 210АВС16.
Шестнадцатеричная система оказалась очень удобной для записи значений ячеек памяти. Байт в современных компьютерах представляет собой 8 соседних битов, т. е. две тетрады. Таким образом, значение байтовой ячейки можно записать как две шестнадцатеричные цифры:
Каждый полубайт (4 бита) «упаковывается» в одну шестнадцатеричную цифру. Благодаря этому замечательному свойству, шестнадцатеричная система в сфере компьютерной техники практически полностью вытеснила восьмеричную1.
1 Начиная с 1964 года, когда шестнадцатеричная система стала широко использоваться в документации на новый компьютер IBM/360.
Перевод из шестнадцатеричной системы в восьмеричную (и обратно) удобнее выполнять через двоичную систему. Можно, конечно, использовать и десятичную систему, но в этом случае объём вычислений будет значительно больше.
При выполнении сложения нужно помнить, что в системе с основанием 16 перенос появляется тогда, когда сумма в очередном разряде превышает 15. Удобно сначала переписать исходные числа, заменив все буквы на их численные значения:
При вычитании заём из старшего разряда равен 10
Если нужно работать с числами, записанными в разных системах счисления, их сначала переводят в какую-нибудь одну систему. Например, пусть требуется сложить 538 и 5616 и записать результат в двоичной системе счисления. Здесь можно выполнять сложение в двоичной, восьмеричной, десятичной или шестнадцатеричной системе. Переход к десятичной системе, а потом перевод результата в двоичную трудоёмок. Практика показывает, что больше всего ошибок делается при вычислениях в двоичной системе, поэтому лучше выбирать восьмеричную или шестнадцатеричную систему. Например, переведём число 538 в шестнадцатеричную систему через двоичную:
Практика показывает, что больше всего ошибок делается при вычислениях в двоичной системе, поэтому лучше выбирать восьмеричную или шестнадцатеричную систему. Например, переведём число 538 в шестнадцатеричную систему через двоичную:
538 = 101 0112 = 10 10112 = 2В16.
Теперь сложим числа в 16-ричной системе:
2В16 + 5616 = 8116
и переведём результат в двоичную систему:
8116 = 1000 00012.
Вопросы и задания
1. Какие цифры используются в шестнадцатеричной системе? Сколько их?
2. Почему появилась необходимость использовать латинские буквы?
3. Сформулируйте алгоритмы перевода чисел из шестнадцатеричной системы счисления в двоичную и обратно.
4. Какое минимальное основание должно быть у системы счисления, чтобы в ней могли быть записаны числа 123, 4АВ, 9АЗ и 8455?
Задачи
1. Переведите в двоичную и восьмеричную системы числа 7F1A16, С73В16, 2FE116, А11216.
2. Переведите в двоичную и шестнадцатеричную системы числа 61728, 53418, 77118, 12348.
3. Переведите в восьмеричную и шестнадцатеричную системы числа
а) 11101111010102;
б) 10101011010101102;
в) 1111001101111101012;
4. Переведите числа 29, 43, 54, 120, 206 в шестнадцатеричную, восьмеричную и двоичную системы счисления.
5. Переведите числа 738, 1348, 2458, 3568 и 4678 в шестнадцатеричную, десятичную и двоичную системы счисления.
6. Запишите числа 101101012, 11101002, 10001112, 101111102 в шестнадцатеричной, восьмеричной и десятичной системах счисления.
7. Вычислите значения следующих выражений:
а) 3AF16 + 1СВЕ16;
б) 1ЕА16 + 7D716;
в) А8116 + 37716;
г) 1CFB
д) 22F16 — CFB16;
е) 1АВ16 — 2CD16.
8. Вычислите значения следующих выражений, запишите результат в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления:
а) 4F16 + 1111102;
б) 5А16 + 10101112;
в) 2568 + 2С16;
г) 1101112 + 1358;
д) 1216 + 128 • 112;
е) 358 + 2С16 • 1012.
9. Вычислите значения следующих выражений, запишите результат в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления:
а) 1516 • 1102;
б) 2А16 • 128;
в) 3416 : 328;
г) 7408 : 1816.
*10. Переведите числа 49,6875 и 52,9 в шестнадцатеричную систему счисления.
0x какая система счисления
Шестнадцатеричный код.
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
- * A —10;
- * B —11;
- * C —12;
- * D —13;
- * E — 14;
- * F — 15.
Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн.
Применение. Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код, можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.
Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код, можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
Математический способ записи. В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 303210, в шестнадцатеричной системе данное число будет иметь запись BD816.
В синтаксисе языков программирования. Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код:
* В C, C++ и схожих языках (Java) для этого используется префикс «0x», например: 0x0A0B;
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код;
Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код;
* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Шестнадцатеричные числа
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Содержание
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В математике систему счисления принято писать в подстрочном знаке. Например, десятичное число 1443 можно записать как 144310 или как 5A316.
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа. Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
- Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.

Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·16 2 +10·16 1 +3·16 0
=5·256+10·16+3·1=1280+160+3=144310
Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
101101000112=0101 1010 0011=5A316
Таблица перевода чисел
| 0hex | = | 0dec | = | 0oct | 0 | 0 | 0 | 0 |
| 1hex | = | 1dec | = | 1oct | 0 | 0 | 0 | 1 |
| 2hex | = | 2dec | = | 2oct | 0 | 0 | 1 | 0 |
| 3hex | = | 3dec | = | 3oct | 0 | 0 | 1 | 1 |
| 4hex | = | 4dec | = | 4oct | 0 | 1 | 0 | 0 |
| 5hex | = | 5dec | = | 5oct | 0 | 1 | 0 | 1 |
| 6hex | = | 6dec | = | 6oct | 0 | 1 | 1 | 0 |
| 7hex | = | 7dec | = | 7oct | 0 | 1 | 1 | 1 |
| 8hex | = | 8dec | = | 10oct | 1 | 0 | 0 | 0 |
| 9hex | = | 9dec | = | 11oct | 1 | 0 | 0 | 1 |
| Ahex | = | 10dec | = | 12oct | 1 | 0 | 1 | 0 |
| Bhex | = | 11dec | = | 13oct | 1 | 0 | 1 | 1 |
| Chex | = | 12dec | = | 14oct | 1 | 1 | 0 | 0 |
| Dhex | = | 13dec | = | 15oct | 1 | 1 | 0 | 1 |
| Ehex | = | 14dec | = | 16oct | 1 | 1 | 1 | 0 |
| Fhex | = | 15dec | = | 17oct | 1 | 1 | 1 | 1 |
См.
 также
такжеСсылки
Wikimedia Foundation . 2010 .
Полезное
Смотреть что такое «Шестнадцатеричные числа» в других словарях:
Шестнадцатиричные числа — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Hexspeak — Эта статья содержит незавершённый перевод с иностранного языка. Вы можете помочь проекту, переведя её до конца. Если вы знаете, на каком языке написан фрагмент, укажите его в этом шаблоне … Википедия
Шестнадцатеричная система счисления — Системы счисления в культуре Индо арабская система счисления Арабская Индийские Тамильская Бирманская Кхмерская Лаоская Монгольская Тайская Восточноазиатские системы счисления Китайская Японская Сучжоу Корейская Вьетнамская Счётные палочки… … Википедия
Шестнадцатеричная система — счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.… … Википедия
Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.… … Википедия
Шестнадцатиричная система счисления — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Шестнадцатиричная система исчисления — Шестнадцатеричная система счисления (шестнадцатеричные числа) позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для… … Википедия
Монитор (интерактивная программа) — У этого термина существуют и другие значения, см. Монитор. Монитор компьютера Apple II Монитор интерактивная программа в компьютерах, особенно 1970 х годов, позволяющая осуществлять управление компьютером на низком уровне: просмотр… … Википедия
HIMEM. SYS — HIMEM.SYS драйвер дополнительной (extended memory) и HMA памяти для операционной системы MS DOS, обеспечивающий поддержку дополнительной памяти (extended или expanded). HIMEM.SYS был введён в состав операционной MS DOS 5.0 для возможности… … Википедия
SYS — HIMEM.SYS драйвер дополнительной (extended memory) и HMA памяти для операционной системы MS DOS, обеспечивающий поддержку дополнительной памяти (extended или expanded). HIMEM.SYS был введён в состав операционной MS DOS 5.0 для возможности… … Википедия
Еггогология — Электроника МК 52 с сообщением «ERROR» (из за специфического отображения буквы r зачастую читалось как «ЕГГОГ») Еггогология& … Википедия
ЕГГОГ — Электроника МК 52 с сообщением ERROR (из за специфического отображения буквы r зачастую читалось как «ЕГГОГ» Еггогология изучение скрытых возможностей микрокалькуляторов. Содержание 1 Происхождение … Википедия
Шестнадцатеричная система счисления
Познавательное
Шестнадцатеричная система (англ. — Hexadecimal system ) — это базовая система счисления с снованием 16. Она, наряду с десятичной и двоичной, является одной из наиболее часто встречающихся систем счисления в мире электроники и программирования. Важно понимать, как она работает, потому что во многих случаях имеет смысл представлять число в ней, а не в двоичной или десятичной.
Важно понимать, как она работает, потому что во многих случаях имеет смысл представлять число в ней, а не в двоичной или десятичной.
Шестнадцатеричная система счисления — позиционная система счисления по основанию 16.
Википедия
Существует 16 возможных цифр, которые используют для представления чисел. 10 числовых значений, которые вы привыкли видеть в десятичных числах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9; эти значения по-прежнему представляют то же значение, что и в десятичной системе. Остальные шесть цифр представлены как A, B, C, D, E и F, которые соответствуют числам 10, 11, 12, 13, 14 и 15.
Возможно, Вы столкнетесь с представлением чисел от 10 до 15 в верхнем и нижнем регистрах. Оба варианта считаются верными. Например, A3F — это то же число, что и a3f.
Эта таблица показывает какой шестнадцатеричной цифре эквивалентно значение в десятичном и двоичном формате.
| Десятичный (основание 10) | Двоичный (основание 2) | Шестнадцатеричный (основание 16) |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | Е |
| 15 | 1111 | F |
таблица 16 ричной системы счисления
Перевод из шестнадцатеричной системы и в нее
Преобразование из десятичной в шестнадцатеричную систему и обратно
Чтобы перевести десятичное число в шестнадцатеричное, нужно следовать простому алгоритму преобразования:
- Делим десятичное число на 16.

- Записываем остаток и переводим его в шестнадцатеричный формат.
- Делим результат прошлого действия снова на 16.
- Повторяем, пока в результате мы не получим 0.
- Переписываем записанные остатки в обратном порядке.
- Пример:
Чтобы перевести шестнадцатеричное число в десятичное, нужно каждую цифру с конца этого числа умножить на 16 в степени, соответствующей разряду этой цифры.
Переведем шестнадцатеричное число 5EB в десятеричную систему
5EB = (5 × 16²) + (14 × 16¹) + (11 × 16⁰) = 1515
Преобразование из двоичной в шестнадцатеричную систему и обратно
Чтобы перевести двоичное число в шестнадцатеричное, нужно разделить его на группы по 4 цифры и заменить каждую группу на эквивалент из таблицы
Переведем двоичное число 1010000011111 в шестнадцатеричную систему
Для этого разбиваем число на группу по 4 цифры: 0001 0100 0001 1111
0001 = 1; 0100 = 4; 0001 = 1; 1111 = F
Чтобы сделать обратное преобразование, нужно просто каждую цифру шестнадцатеричного числа заменить на эквивалент по таблице
Переведем шестнадцатеричное число 141F в двоичную систему
1= 0001; 4 = 0100; 1 = 0001; F = 1111
Использование шестнадцатеричной системы
По большей части, шестнадцатеричные коды используются во многих областях вычислительной техники для сокращения двоичного кода до более понятной формы. Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
- Ссылки на цвета в HTML и CSS
- Язык ассемблера
- Сообщения об ошибках
Цвета
Hex система счисления может использоваться для представления цветов на сайтах и в программах редактирования изображений в формате #RRGGBB (# = показатель того, что число было записано в шестнадцатеричном формате, RR = красный, GG = зеленый, BB = синий). Этот система использует две шестнадцатеричных цифры для каждого цвета, например, #AA3300.
Как одна шестнадцатеричная цифра представляет 4 бита, так две шестнадцатеричные цифры вместе составляют 8 бит (1 байт). Значения для каждого цвета находятся в диапазоне от 00 до FF. В двоичной системе, 00 — это 00000000, а FF — это 11111111. Это дает 256 возможных значений для каждого из трех цветов (256 красных х 256 зеленых х 256 синих), а в сумме это больше 16 миллион цветов.
- #FF0000 будет самым чистым красным цветом — Максимум красного, 0 зеленого и 0 синего.

- Черный это #000000 — ни красного, ни зеленого, ни синего.
- Белый — это #FFFFFF — при смешении всех цветов.
Инженер по телевизионному оборудованию Электрика и электроника, это не только моё хобби, но и работа
Шестнадцатеричная система счисления простыми словами. Примеры
Автор Савельев Николай На чтение 4 мин Просмотров 1.9к. Опубликовано Обновлено
Шестнадцатеричная система (англ. — Hexadecimal system ) — это базовая система счисления с снованием 16. Она, наряду с десятичной и двоичной, является одной из наиболее часто встречающихся систем счисления в мире электроники и программирования. Важно понимать, как она работает, потому что во многих случаях имеет смысл представлять число в ней, а не в двоичной или десятичной.
Шестнадцатеричная система счисления — позиционная система счисления по основанию 16.
Википедия
Существует 16 возможных цифр, которые используют для представления чисел. 10 числовых значений, которые вы привыкли видеть в десятичных числах: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9; эти значения по-прежнему представляют то же значение, что и в десятичной системе. Остальные шесть цифр представлены как A, B, C, D, E и F, которые соответствуют числам 10, 11, 12, 13, 14 и 15.
Возможно, Вы столкнетесь с представлением чисел от 10 до 15 в верхнем и нижнем регистрах. Оба варианта считаются верными. Например, A3F — это то же число, что и a3f.
Эта таблица показывает какой шестнадцатеричной цифре эквивалентно значение в десятичном и двоичном формате.
| Десятичный (основание 10) | Двоичный (основание 2) | Шестнадцатеричный (основание 16) |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | А |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | Е |
| 15 | 1111 | F |
Содержание
- Перевод из шестнадцатеричной системы и в нее
- Преобразование из десятичной в шестнадцатеричную систему и обратно
- Преобразование из двоичной в шестнадцатеричную систему и обратно
- Использование шестнадцатеричной системы
- Цвета
Перевод из шестнадцатеричной системы и в нее
Преобразование из десятичной в шестнадцатеричную систему и обратно
Чтобы перевести десятичное число в шестнадцатеричное, нужно следовать простому алгоритму преобразования:
- Делим десятичное число на 16.

- Записываем остаток и переводим его в шестнадцатеричный формат.
- Делим результат прошлого действия снова на 16.
- Повторяем, пока в результате мы не получим 0.
- Переписываем записанные остатки в обратном порядке.
- Пример:
Переведем десятеричное число 1515 в шестнадцатеричную систему
| Деление | Частное | Остаток | Порядок записи (от последнего к первому) |
| 1515/16 | 94 | 11 = B | 3 |
| 94/16 | 5 | 14 = E | 2 |
| 5/16 | 0 | 5 = 5 | 1 |
Ответ: 5EB
Читайте также: Проверяю стратегию Мартингейла на Python и показываю, почему она не работает
Чтобы перевести шестнадцатеричное число в десятичное, нужно каждую цифру с конца этого числа умножить на 16 в степени, соответствующей разряду этой цифры.
Преобразование из двоичной в шестнадцатеричную систему и обратно
Чтобы перевести двоичное число в шестнадцатеричное, нужно разделить его на группы по 4 цифры и заменить каждую группу на эквивалент из таблицы
- Пример:
Переведем двоичное число 1010000011111 в шестнадцатеричную систему
Для этого разбиваем число на группу по 4 цифры: 0001 0100 0001 1111
0001 = 1; 0100 = 4; 0001 = 1; 1111 = F
Ответ: 141F
Чтобы сделать обратное преобразование, нужно просто каждую цифру шестнадцатеричного числа заменить на эквивалент по таблице
- Пример:
Переведем шестнадцатеричное число 141F в двоичную систему
1= 0001; 4 = 0100; 1 = 0001; F = 1111
Ответ: 1010000011111
Использование шестнадцатеричной системы
По большей части, шестнадцатеричные коды используются во многих областях вычислительной техники для сокращения двоичного кода до более понятной формы. Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
Шестнадцатеричный код переводится в двоичный для использования на компьютере. Вот некоторые примеры использования шестнадцатеричного кода:
- Ссылки на цвета в HTML и CSS
- Язык ассемблера
- Сообщения об ошибках
Цвета
Hex система счисления может использоваться для представления цветов на сайтах и в программах редактирования изображений в формате #RRGGBB (# = показатель того, что число было записано в шестнадцатеричном формате, RR = красный, GG = зеленый, BB = синий). Этот система использует две шестнадцатеричных цифры для каждого цвета, например, #AA3300.
Как одна шестнадцатеричная цифра представляет 4 бита, так две шестнадцатеричные цифры вместе составляют 8 бит (1 байт). Значения для каждого цвета находятся в диапазоне от 00 до FF. В двоичной системе, 00 — это 00000000, а FF — это 11111111. Это дает 256 возможных значений для каждого из трех цветов (256 красных х 256 зеленых х 256 синих), а в сумме это больше 16 миллион цветов.
- #FF0000 будет самым чистым красным цветом — Максимум красного, 0 зеленого и 0 синего.

- Черный это #000000 — ни красного, ни зеленого, ни синего.
- Белый — это #FFFFFF — при смешении всех цветов.
Курс Java Multithreading — Лекция: Запись двоичного числа как 1000100В
— Привет, Амиго!
— Привет, Билаабо!
Хочу рассказать тебе немного про различные системы счисления.
Ты уже слышал, что люди пользуются десятичной системой счисления. Вот главные факты этого подхода:
1) Для записи числа используются 10 цифр: 0,1, 2, 3, 4, 5, 6, 7, 8, 9.
Эта равносильно записи 5*100 + 4*10 + 3*1, что можно записать как 5*102+4*101+3*100
Обрати внимание – тысячи, сотни, десятки и единицы – это степени числа 10.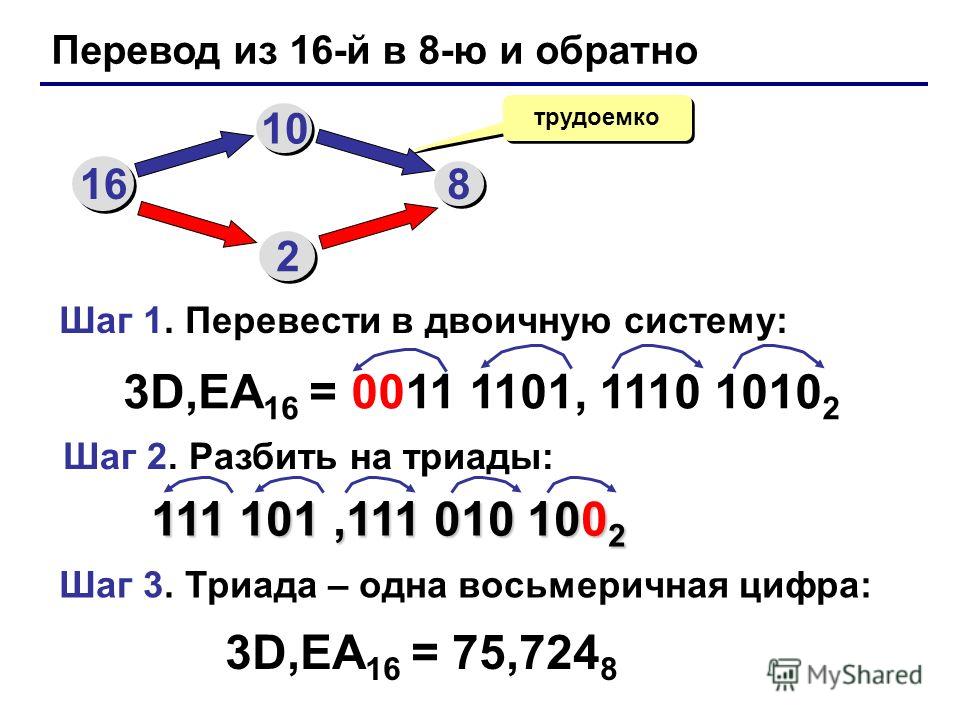
1) Единица – это 10 в нулевой степени.
2) Десять – это 10 в первой степени
3) Сто – это 10 во второй степени
4) Тысяча – это 10 в третьей степени и т.д.
— Ага. Понятно.
— А теперь представь, что цифр всего 8. Тогда у нас есть восьмеричная система счисления и вот ее главные факты:
1) Для записи числа используются 8 цифр: 0,1, 2, 3, 4, 5, 6, 7.
2) Число 5438 значит 5*82+4*81+3*80. Т.е. это 5*64+4*8+3*1 = 320+32+3=35510
Я написал снизу числа знаки 8 и 10, чтобы мы знали, сколько цифр используется для его записи.
— Вроде как и ясно. Я думаю, я бы смог перевести число из восьмеричной системы в десятичную. Но наоборот – вряд ли.
— Все не так уж и сложно. Представь, что тебе нужно перевести кучу песка на нескольких грузовых машинах. У тебя есть карьерные самосвалы, обычные, и совсем маленькие машинки.
Как бы ты возил?
— Сначала я бы насыпал в карьерные самосвалы, они самые большие. Затем, когда понял, что для заполнения машины песка не хватит, то перешел бы на машины поменьше. Затем еще меньше.
— Тут все тоже очень похоже. Давай попробуем перевести число 35510 обратно в восьмеричный формат.
Сначала мы разделим его на 64 (82), получим 5 целых и 35 в остатке. Значит первая цифра нашего числа – 5. Затем разделим остаток на 8(81), получим 4 и 3 в остатке. Так и получится число 5438.
Можно, кстати, пойти и с другой стороны. Ведь 5438 ==5*64+4*8+3 == ((5)*8+4)*8+3. Наши восьмеричные «десятки» и «сотни» обязательно делятся на 8. Значит, остаток от деления на 8 это и будут наши восьмеричные единицы.
Поделим сначала число 355 на 8. Получим 44 и 3 в остатке. Т.е. 355=44*8+3. А 44 можно представить как 5*8+4. Значит 355= (5*8+4)*8+3; Вот наши цифры: 5,4,3. Искомое число 5438
— В общем вроде понятно, но надо немного попрактиковаться, чтобы окончательно во всем разобраться.
— В программировании очень часто используются числа с различным основанием (количеством цифр). Самые популярные – это 2, 8, 10, 16, 64.
— А зачем это нужно. Зачем нужны числа, состоящие из 2, 8, 16 и 64 цифр?
— Дело во внутреннем устройстве процессора. Очень упрощенно — если в проводе есть ток, то говорят, что в нем «единица», если тока нет, то в нем «ноль». Все числа хранятся в памяти в виде ячеек. Устройство таких ячеек очень примитивно. Они тоже могу хранить только 0 или 1.
Зато такое упрощение всего (только 0 или 1) дало возможность сделать элементы внутри процессора и памяти очень маленькими. Современные процессоры и модули памяти включают миллиарды различных элементов. При том, что их площадь зачастую не превышает квадратного сантиметра.
— Ничего себе. Буду знать.
— Теперь перейдем к двоичным числам. Там то же самое, что и с восьмеричными, только еще проще.
1) Для записи числа используются 2 цифры: 0,1
2) Число 1012 значит 1*22+0*21+1*20. Т.е. это 1*4+0*2+1*1 =4+1=510
Т.е. это 1*4+0*2+1*1 =4+1=510
— Да. Я помню. Одна ячейка, которая принимает значение 0 или 1 называется битом. Но т.к. в ней можно сохранить очень мало информации, то их объединяют в группы по 8. И называют такую группу – байтом.
— Именно. Байт – это группа из восьми бит. В нем можно хранить значения: 00000000, 00000001, …, 11111111. Которые соответствуют десятичным 0,1,… 255. Всего 256 значений.
Какое самое большое целое число в Java? Вернее его тип?
— long. long состоит из 8 байт. Т.е. 64 бита и может хранить значения от -263 до 263-1
— Ага. Я не буду касаться темы, как переводить числа из десятичной системы в двоичную или наоборот. Иначе лекция слишком затянется.
Давай лучше еще немного расскажу про 16-ричную систему счисления.
— Да, очень интересно. Для двоичной и восьмеричной систем мы просто выкинули цифры начиная с двойки или восьмерки. А тут как? Мы добавим новые цифры?
— Именно! Смотри:
1) Для записи числа используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
2) Число 54316 значит 5*162+4*161+3*160. Т.е. это 5*256+4*16+3*1 =1280+64+3=134710
Т.е. это 5*256+4*16+3*1 =1280+64+3=134710
— Т.е. мы просто добавили буквы в качестве цифр? О_о
— Ага. А что в этом такого? Зачем придумывать новые цифры, когда с этой ролью отлично справляются буквы. Вот смотри:
| Шестнадцатеричная цифра | Десятичное значение |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 8 | 8 |
| 9 | 9 |
| A | 10 |
| B | 11 |
| C | 12 |
| D | 13 |
| E | 14 |
| F | 15 |
Про перевод из десятичной системы в шестнадцатеричную тоже рассказывать не буду. Зато есть один интересный факт. Шестнадцатеричная цифра – это ровно 4 бита со значениями от 0 до 15. Поэтому один байт можно записать восемью двоичными цифрами (0 или 1) или двумя шестнадцатеричными.
Пример:
| Десятичное число | Двоичное число | Шестнадцатеричное число |
|---|---|---|
| 0 | 0000 0000 | 00 |
| 1 | 0000 0001 | 01 |
| 15 | 0000 1111 | 0f |
| 16 | 0001 0000 | 10 |
| 31 | 0001 1111 | 1f |
| 32 | 0010 0000 | 20 |
| 128 | 1000 0000 | 80 |
| 129 | 1000 0001 | 81 |
| 255 | 1111 1111 | ff |
Шестнадцатеричное представление легко приводится к двоичному (и обратно).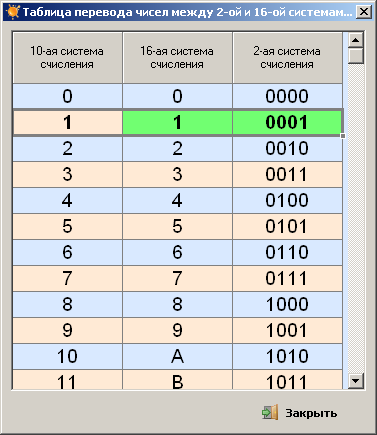 Поэтому, если где-то в программировании нужно показать именно внутреннее байтовое представление числа, то очень редко прибегают к двоичной записи через 0 и 1. Слишком длинно и не понятно. Шестнадцатеричная запись гораздо читабельней и компактней.
Поэтому, если где-то в программировании нужно показать именно внутреннее байтовое представление числа, то очень редко прибегают к двоичной записи через 0 и 1. Слишком длинно и не понятно. Шестнадцатеричная запись гораздо читабельней и компактней.
— Согласен. Даже мне понравилось.
— Кстати, в Java можно прямо в коде записывать числа в различных системах счисления:
| Основание | Отличительный признак | Примеры | Неправильные числа |
|---|---|---|---|
| 2 | 0b в начале числа | 0b00001111 | 0b1111121 |
| 8 | 0 в начале числа | 01234343 | 0128 |
| 10 | нет | 95459 | 909a |
| 16 | 0x в начале числа | 0x10ff | 0x1cgh |
— Отличная лекция. Спасибо, Билаабо.
Тест по теме «системы счисления» | Тест по информатике и икт на тему:
Системы счисления — 1 ВАРИАНТ
- В зависимости от способа изображения чисел системы счисления делятся на.
 ..
..
- арабские и римские
- позиционные и непозиционные
- представление в виде ряда и в виде разрядной сетки
- нет правильного ответа
- Для представления чисел в 16-ричной системе счисления используются…
- цифры 0-9 и буквы A-F
- буквы A-Q
- числа от 0 до 15
- первые 15 букв русского алфавита
- В какой системе счисления может быть записано число 402?
- в двоичной и восьмеричной
- в восьмеричной и десятичной
- в троичной
- в двоичной
- Чему равно число DXXVII в десятичной системе счисления
- 247
- 499
- 1027
- 527
- Когда 2*2 равно 11?
- в троичной системе счисления
- в двоичной системе счисления
- в восьмеричной системе счисления
- в пятеричной системе счисления
- Как записывается максимальное четырехразрядное число в двоичной системе счисления?
- 1000
- 2222
- 1111
- 9999
- Чему равна сумма десятичных чисел 5 и 3 в двоичной системе счисления?
- 1000
- 1111
- 100
- 110
- Как записывается десятичное число 90 в восьмеричной системе счисления
- 132
- 64
- 80
- 100
- Какое минимальное основание должна иметь система счисления, если в ней можно записать числа 423, 767, 563, 210
- 8
- 10
- 9
- 7
- Чему равна сумма десятичного числа 10 и двоичного числа 10 в десятичной системе счисления
- 20
- 12
- 21
- 1010
- Переведите число 243 из десятичной системы счисления в двоичную:
- 11001111
- 1110011
- 110111
- 11110011
- Переведите число 1101 из двоичной системы счисления в десятичную:
- 11
- 13
- 15
- 9
- Младший брат учится в 101 классе.
 Старший на 11 лет старше. В каком классе учится старший брат:
Старший на 11 лет старше. В каком классе учится старший брат:
- 1000
- 1111
- 1010
- 1001
- Вычислить результат сложения двух чисел, записанных римскими цифрами MCM + LXIV:
- 1964
- 2164
- 154
- 2014
- Вычтите числа в двоичной системе счисления 101010 -11011
- 10101
- 111
- 1111
- 1001
Системы счисления — 2 ВАРИАНТ
- Основание системы счисления- это:
А) символы, которые используются для записи чисел
Б) количество символов, которые используются для записи чисел
В) вид системы счисления
Г) нет правильного ответа
- Для представления чисел в 8-ричной системе счисления используются…
А) цифры 0-7или буквы A-Н
Б) буквы A-Н
В) цифры 0-7
Г) первые 8 букв русского алфавита
- В какой системе счисления может быть записано число 202?
А) в двоичной и восьмеричной
Б) в троичной, восьмеричной и десятичной
В) в троичной
Г) в двоичной
- Чему равно число DССXVI в десятичной системе счисления
А)596
Б) 716
В) 714
Г) 316
- Когда 3+3 равно 11?
- в троичной системе счисления
- в двоичной системе счисления
- в восьмеричной системе счисления
- в пятеричной системе счисления
- Как записывается минимальное четырехразрядное число в восьмеричной системе счисления?
- 1000
- 2222
- 1111
- 7777
- Чему равна сумма десятичных чисел 6 и 4 в двоичной системе счисления?
- 1000
- 1010
- 100
- 110
- Как записывается десятичное число 84 в восьмеричной системе счисления
- 26
- 64
- 124
- 100
- Какое минимальное основание должна иметь система счисления, если в ней можно записать числа 423, 769, 563, 2910
- 8
- 10
- 9
- 7
- Чему равна сумма десятичного числа 10 и двоичного числа 101 в десятичной системе счисления
- 15
- 12
- 21
- 1010
- Переведите число 165 из десятичной системы счисления в двоичную:
- 11001111
- 1110011
- 110111
- 11100101
- Переведите число 110110 из двоичной системы счисления в десятичную:
- 56
- 55
- 53
- 54
- Младший брат учится в 100 классе.
 Старший на 10 лет старше. В каком классе учится старший брат:
Старший на 10 лет старше. В каком классе учится старший брат:
- 101
- 110
- 111
- 1001
- Вычислить результат сложения двух чисел, записанных римскими цифрами CML + LXIV:
- 1964
- 2164
- 154
- 1014
- Вычтите числа в двоичной системе счисления 100100 -11111
- 1011
- 101
- 10101
- 1001
Ответы:
1 вариант: 1Б, 2А, 3Б, 4Г, 5А, 6В, 7А, 8А, 9А, 10Б, 11Г, 12Б, 13А, 14А, 15В
2 вариант: 1Б, 2В, 3Б, 4Б, 5Г, 6А, 7Б, 8В, 9Б, 10А, 11Г, 12Г, 13Б, 14Г, 15Б
Кодирование чисел и текста — Информатика, информационные технологии
Кодирование чисел
Бит – наименьшая единица информации, которая выражает логическое «Да» или «Нет» и обозначается 1 или 0. Компьютер преобразует цифровую информацию, представленную в десятичной системе счисления в последовательность 0 и 1, а дальше уже работает с ними.
Системой счисления называют совокупность символов (цифр) и правил их использования для представления чисел.
Пример 1. Число 29 перевести из десятичной системы счисления в двоичную. Перевод осуществляется последовательным делением числа 29 на 2 и записью остатков от деления справа налево, как показано на схеме (рис. 3).
29 : 2 = 14 + 1
14 : 2 = 7 + 0
7 : 2 = 3 + 1
3 : 2 = 1 + 1
1 = 1
Рис. 3. Схема перевода числа из десятичной системы счисления в двоичную
Двоичная система исчисления является позиционной.
Читается: 20 – 1; 21 – 0; 22 – 1; 23 – 1; 24 – 1;
1х20 +0х21 +1х22 + 1х23 +1х24 =1+0+4+8+16=29.
Пример 2. Число 1011, заданное в двоичной системе, перевести в десятичную систему счисления.
1011 a одна единица, одна двойка, нуль четверок и одна восьмерка.
1х20 + 1х21 + 0х22 + 1х23 = 11.
Байт– группа из 8 битов.
Если учесть, что важны не только нули и единицы, но и позиции, в которых они стоят, то с помощью одного байта можно выразить 28 = 256 единиц информации:
0000 0000 = 0
0000 0001 = 1
0000 0010 = 2
0000 0011 = 3
0000 0100 = 4
0000 0101 = 5
………………
1111 1100 = 252
1111 1101 = 253
1111 1110 = 254
11111111 = 255 Писать (или набирать на клавиатуре компьютера) длинные цепочки единиц и нулей при задании чисел в двоичном формате довольно утомительно.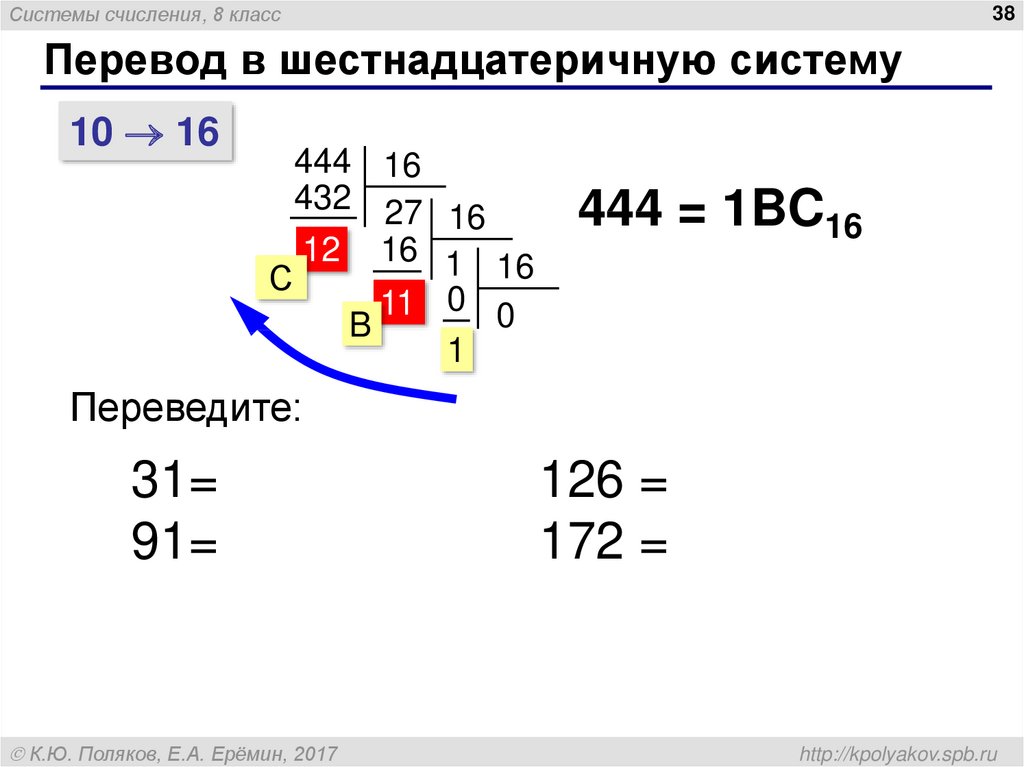 Так же неудобно просматривать содержимое памяти компьютера, представленное в двоичном формате. Поэтому был разработан такой метод представления двоичных данных, когда каждый байт разбивается пополам и каждая 4-битовая его половина записывается в 16-ричной системе счисления. Для ее осуществления цифровой алфавит 10-тичной системы счисления дополнили шестью цифрами, условившись, что: 10 – это A, 11 – это B, 12 – это C, 13 – это D, 14 – это E, 15 – это F. Пример 3. Десятичное число 42936 в двоичном формате имеет вид 1010011110111000. После записи полубайтов 1010 0111 1011 1000 16-ричными цифрами получаем компактную запись представленного числа – A7B8.
Так же неудобно просматривать содержимое памяти компьютера, представленное в двоичном формате. Поэтому был разработан такой метод представления двоичных данных, когда каждый байт разбивается пополам и каждая 4-битовая его половина записывается в 16-ричной системе счисления. Для ее осуществления цифровой алфавит 10-тичной системы счисления дополнили шестью цифрами, условившись, что: 10 – это A, 11 – это B, 12 – это C, 13 – это D, 14 – это E, 15 – это F. Пример 3. Десятичное число 42936 в двоичном формате имеет вид 1010011110111000. После записи полубайтов 1010 0111 1011 1000 16-ричными цифрами получаем компактную запись представленного числа – A7B8.
Кодирование текста
С помощью одного байта, как было показано, можно кодировать 256 значений. Первые 128 кодов (с 0 до 127) – стандартные и обязательные для всех стран. Эту половину таблицы кодов называют таблицей ASCII (стандартный код информационного обмена США) – ввел ее американский институт стандартизации ANSI. В этой части таблицы размещаются прописные и строчные буквы английского алфавита, символы чисел от 0 до 9, все знаки препинания, символы арифметических операций, специальные коды. Коды читают а-эс-цэ-и (аски- коды). Первых 32 кода – управляющие, которые не используются для представления информации (от 0 до 31), а 32 символ – пробел.
В этой части таблицы размещаются прописные и строчные буквы английского алфавита, символы чисел от 0 до 9, все знаки препинания, символы арифметических операций, специальные коды. Коды читают а-эс-цэ-и (аски- коды). Первых 32 кода – управляющие, которые не используются для представления информации (от 0 до 31), а 32 символ – пробел.
33 – 47 – специальные символы, знаки препинания.
48 – 57 – цифры.
58 – 64 – математические символы и знаки препинания.
65 – 90 – прописные буквы английского алфавита.
91 – 96 – специальные символы.
97 – 122 – строчные буквы английского алфавита.
123 – 127 – специальные символы.
Остальные 128 кодов используются для специальных символов и букв национальных алфавитов (в том числе русского). И поскольку общепринятого стандарта для этого не было, возникло много различных кодировок, в том числе, несколько для кириллицы. Для кириллицы используют следующие кодировки: Кириллица (Windows), Кириллица (ISO), Кириллица (KOI8–R).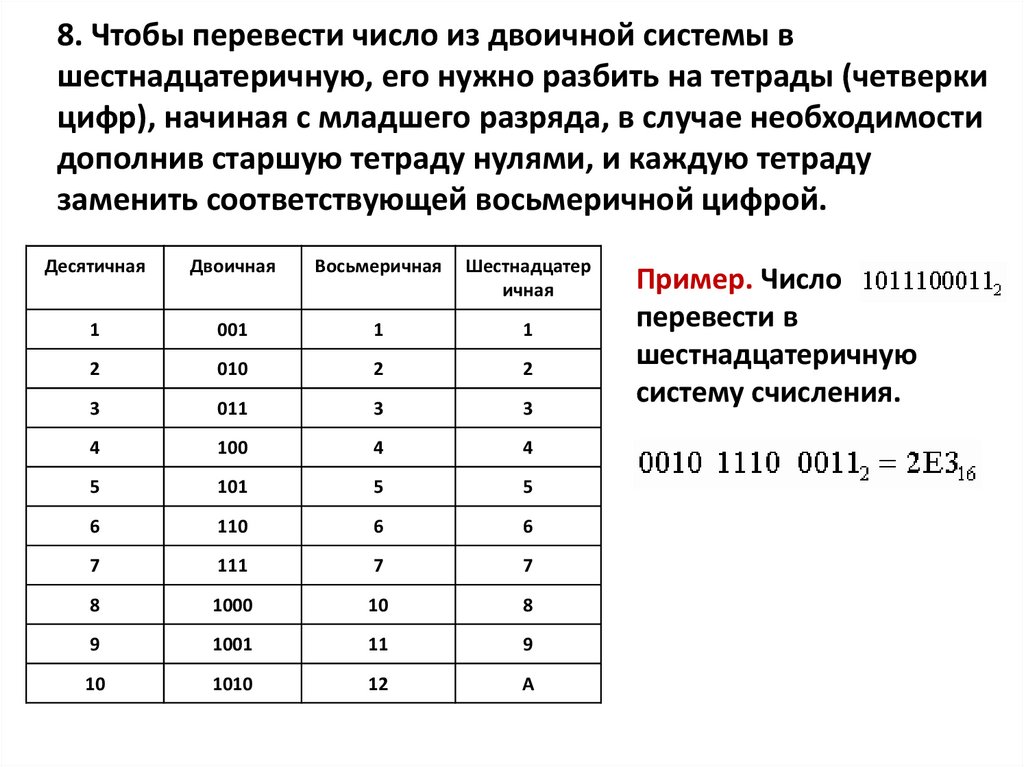 Кириллица (ISO) используется редко. Кириллица (Windows) используется на ПК, работающих на платформе Windows. Де-факто Кириллица(Windows) стала стандартной в российском секторе World Wide Web. Кириллица (KOI8–R) де-факто является стандартной в сообщениях электронной почты и телеконференций.
Кириллица (ISO) используется редко. Кириллица (Windows) используется на ПК, работающих на платформе Windows. Де-факто Кириллица(Windows) стала стандартной в российском секторе World Wide Web. Кириллица (KOI8–R) де-факто является стандартной в сообщениях электронной почты и телеконференций.
В такой ситуации, когда используются различные кодировки кириллицы, на помощь приходят программы – конверторы. Они заменяют двоичный код каждого символа на код, которым такой символ представляется в другой кодировке. Это соответствие определяется таблицей перекодировки. Пользователь должен указать, из какой кодировки в какую идет преобразование, однако есть программы, автоматически определяющие кодировку исходного текста.
Следует отметить, что все рассмотренные кодировки текста ограничены набором кодов (256). Более широкими возможностями обладает система кодировки текста UNICODE, основанная на 16-разрядном кодировании символов. Шестнадцать разрядов обеспечивают кодирование 216 =65536 символов.
Чтобы рисунок буквы был виден на экране, его цвет должен отличаться от цвета фона, на котором он изображается. Поэтому коды символов (порядковые номера в таблице кодирования) необходимо дополнить кодами цвета фона и цвета рисунков. Для этих кодов цветов добавили еще один байт памяти и разделили его пополам – младшую (левую) половину из четырех битов отвели для кодирования цвета рисунка, а старшую для кодирования цвета фона. Этот байт назвали байтом атрибутов символа. Он всегда присутствует вместе с кодом символа в двух байтовых кодах символов, передаваемых в видеопамять для отображения на экране.
Четырьмя байтами можно закодировать 16 цветов, а при необходимости кодирования большего количества цветов применяют многоступенчатую систему кодирования. Содержимое байта атрибутов удобно записывать в 16-ричном формате, у которого первая цифра в этом случае обозначает цвет фона, а вторая – цвет рисунка символа. Например, 16-ричное число 4E кодирует желтые (код желтого цвета Е или 14 в 10-й системе) буквы на красном (код красного цвета равен 4) фоне.
Двухбайтовые кодовые группы каждой буквы текста, содержащие код символа и код атрибутов его изображения для вывода на экран, записываются в память устройства управления, которое называют дисплейным адаптером, а саму память – видеопамятью или видеобуфером.
Последнее название подсказывает, что для постоянного обновления изображения на экране из этого буфера с частотой примерно 25 (или более) раз в секунду считываются коды символов и преобразуются в рисунки букв на экране. Чтобы такое преобразование стало возможным, приходится закодировать и разместить в памяти компьютера и сами рисунки букв. Для изображения символов обычно отводится в зависимости от типа видеосистемы от 8 до 16 строк по 8 пикселов в строке. О каждом пикселе в изображении символа дисплейный адаптер должен знать, относится он к фону или рисунку – то есть достаточно одного бита с двумя состояниями. Если бит содержит 0, то это пиксел фона, а если 1 – то это пиксел рисунка.
256 кодовых групп символов текста хранятся в памяти для рисунков всех изображаемых символов, и вся эта область памяти называется буфером знакогенератора. Адаптер дисплея «узнает» начальный адрес этого буфера (порядковый номер его начального байта, отсчитанный от начала памяти), берет из видеопамяти код символа, означающий порядковый номер его кодовой группы в буфере знакогенератора, умножает на число пиксельных строк в изображении символа и прибавляет полученное число к начальному адресу буфера знакогенератора. Полученное число есть начальный адрес кодовой группы изображения символа. Далее видеоадаптер берет каждый байт кодовой группы изображения и работает уже с отдельными битами байта – для нулевых битов выводит пиксел цветом фона, а для единичных – цветом рисунка (коды цвета фона и рисунка он тоже берет из видеопамяти – из байта атрибутов). Вот так появляются на экране дисплея рисунки букв, как и все в компьютере, закодированные двоичными числами. При выводе изображений символов на печать коды изображений символов и их порядковые номера хранятся в памяти печатающего устройства либо постоянно, либо заносятся туда из памяти компьютера перед началом печати.
Адаптер дисплея «узнает» начальный адрес этого буфера (порядковый номер его начального байта, отсчитанный от начала памяти), берет из видеопамяти код символа, означающий порядковый номер его кодовой группы в буфере знакогенератора, умножает на число пиксельных строк в изображении символа и прибавляет полученное число к начальному адресу буфера знакогенератора. Полученное число есть начальный адрес кодовой группы изображения символа. Далее видеоадаптер берет каждый байт кодовой группы изображения и работает уже с отдельными битами байта – для нулевых битов выводит пиксел цветом фона, а для единичных – цветом рисунка (коды цвета фона и рисунка он тоже берет из видеопамяти – из байта атрибутов). Вот так появляются на экране дисплея рисунки букв, как и все в компьютере, закодированные двоичными числами. При выводе изображений символов на печать коды изображений символов и их порядковые номера хранятся в памяти печатающего устройства либо постоянно, либо заносятся туда из памяти компьютера перед началом печати.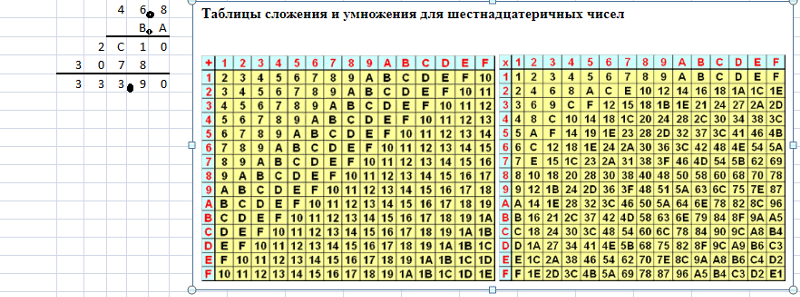
Статьи к прочтению:
- Кодирование и тестирование сверху вниз
- К оформлению семестровой контрольной работы
Кодирование текстовой информации
Похожие статьи:
Отображение чисел и текста с помощью компонентов tlabel, tedit
Простая кнопка. Для этого в панели инструмментов ищем на вкладке Standard компонент Button и щелкаем по нему левой кнопкой мыши. Далее щелкаем той же…
Двоичное кодирование звука
Лабораторная работа №5 Тема: Дискретное (цифровое) представление текстовой, графической, звуковой информации и видеоинформации Цель работы:научиться…
Происхождение английского алфавита (и всех его 26 букв)
Обновлено в 2022 г.
Английский алфавит имеет увлекательную историю, и развитие каждой буквы алфавита имеет свою собственную историю. Хотя английский язык широко распространен, для тех, кто не говорит по-английски, английский язык является одним из самых сложных для изучения. В самом деле, в английском языке много общего, потому что за годы его развития появилось несколько разных языков. Ученые, миссионеры и завоеватели превратили английский язык в то, что мы знаем и на чем говорим сегодня.
Хотя английский язык широко распространен, для тех, кто не говорит по-английски, английский язык является одним из самых сложных для изучения. В самом деле, в английском языке много общего, потому что за годы его развития появилось несколько разных языков. Ученые, миссионеры и завоеватели превратили английский язык в то, что мы знаем и на чем говорим сегодня.
Происхождение алфавитного письма
Раннее алфавитное письмо появилось около четырех тысяч лет назад. По мнению многих ученых, именно в Египте зародилась алфавитная письменность между 1800 и 1900 годами до нашей эры. Происхождением была протосинайская (протоханаанская) форма письма, которая была не очень хорошо известна.
Примерно через 700 лет финикийцы разработали алфавит, основанный на более ранних основах. Он широко использовался в Средиземноморье, включая южную Европу, Северную Африку, Пиренейский полуостров и Левант. Алфавит состоял из 22 букв, все согласные.
В 750 г. до н.э. греки добавили гласные в финикийский алфавит, и эта комбинация считалась первоначальным истинным алфавитом. Это было воспринято латинянами (римлянами) и объединено с некоторыми этрусскими буквами, такими как буквы S и F. Примерно в третьем веке древняя латиница удалила буквы G, J, V/U, W, Y и Z. Когда Римская империя управляла частями мира, они ввели латинский алфавит, полученный из латинской версии, хотя буквы J, U/V и W по-прежнему не использовались.
до н.э. греки добавили гласные в финикийский алфавит, и эта комбинация считалась первоначальным истинным алфавитом. Это было воспринято латинянами (римлянами) и объединено с некоторыми этрусскими буквами, такими как буквы S и F. Примерно в третьем веке древняя латиница удалила буквы G, J, V/U, W, Y и Z. Когда Римская империя управляла частями мира, они ввели латинский алфавит, полученный из латинской версии, хотя буквы J, U/V и W по-прежнему не использовались.
Эволюция английского алфавита
Когда Римская империя достигла Британии, она принесла с собой латинский язык. Британия в то время находилась под контролем англосаксов, германского племени, использовавшего древнеанглийский язык в качестве своего языка. В то время в древнеанглийском языке использовался футорк, более старый алфавит. Его также называли руническим алфавитом.
Древнеанглийский
Сочетание латинского алфавита и рунического алфавита Футорка привело к современному английскому алфавиту. Некоторые из дополнений из рунических алфавитов были «шип» со звуком «т» и «винн» со звуком «у». Помните, что в латинском алфавите не было буквы «w». В Средние века, когда люди в Британии перестали использовать старые руны, буква thorn была заменена буквой th, а руническое wynn стало буквой uu, которая позднее превратилась в букву w.0009
Некоторые из дополнений из рунических алфавитов были «шип» со звуком «т» и «винн» со звуком «у». Помните, что в латинском алфавите не было буквы «w». В Средние века, когда люди в Британии перестали использовать старые руны, буква thorn была заменена буквой th, а руническое wynn стало буквой uu, которая позднее превратилась в букву w.0009
Позже в тот же период были добавлены буквы «j» и «u», и количество букв увеличилось до 26. Однако были включены буквенные комбинации, такие как «æ», «œ» и символ амперсанда (&). в алфавите.
Среднеанглийский
Когда норманны вторглись в Британию в 1066 году нашей эры, низкорожденные использовали древнеанглийский язык. Ученые, духовенство и дворянство писали и говорили на латыни или нормандском языке. После двух столетий норманнского правления письмо на английском языке снова стало популярным, при этом некоторые древнеанглийские буквы были удалены. Джеффри Чосер использовал среднеанглийский язык в «Кентерберийских рассказах» «Купальная жена».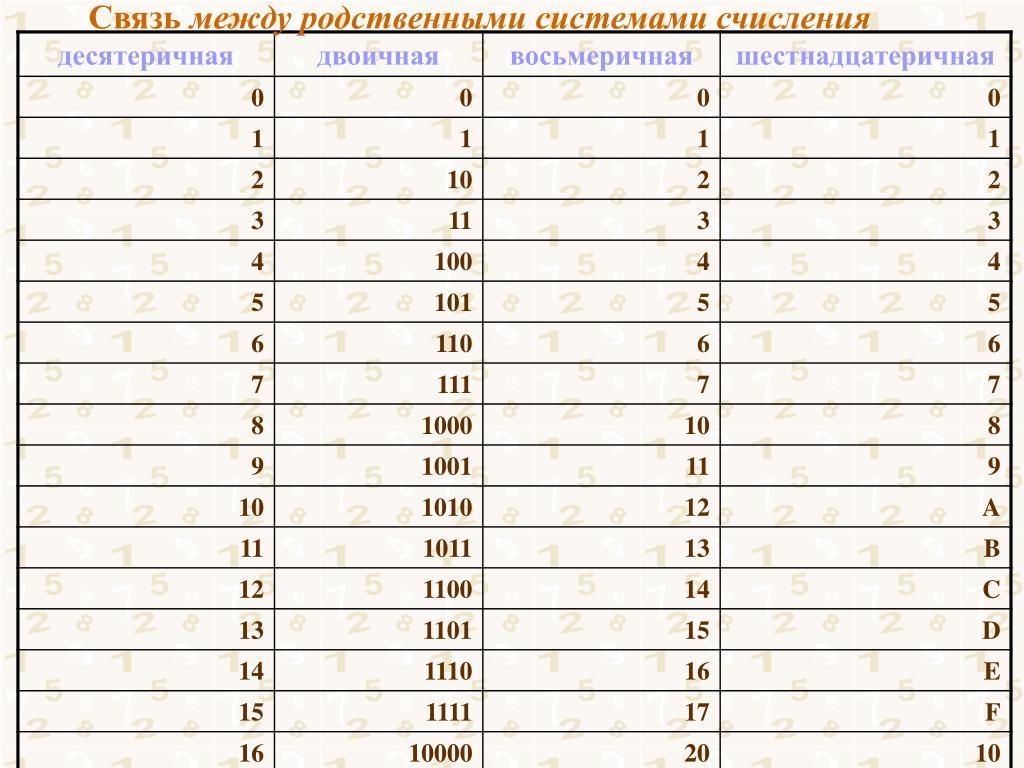
Современный английский
В 15 веке печатный станок был представлен в Великобритании Уильямом Кэкстоном. К этому времени английский язык был стандартизирован. Из-за взаимозаменяемости буквы V и U были разделены, при этом первая стала согласной, а U — гласной.
The Table Alphabeticall, первый словарь на английском языке, опубликованный Робертом Кодри в 1604 году. Буква J также была добавлена в современный английский язык в это время.
Что такое алфавит?
Буквы, используемые языком, в совокупности называются алфавитом. Он имеет фиксированный порядок, основанный на обычаях пользователей. Алфавит используется для письма, а символы, используемые для письма, называются буквами. Каждая буква представляет один звук или родственный звук (также называемый фонемой), используемый в разговорной речи. Алфавит с помощью стандартного направления чтения, пробелов и знаков препинания образует слова, легко читаемые читателями.
Рассказы о буквах английского алфавита
Вероятно, вы один из многих людей, выучивших английский алфавит в очень раннем возрасте. Ваши родители, возможно, научили вас читать алфавит, а также петь «Алфавитную песенку». Но когда вы достигаете дошкольного возраста, вы знаете большинство букв английского алфавита и можете составлять простые слова. Когда вы пошли в школу, вы снова познакомились с английским алфавитом и выучили больше слов, комбинируя буквы.
Поскольку вы начали с изучения английского алфавита, вполне естественно, что вы принимаете его как должное и не проявляете интереса к изучению его истории и истории образования каждой буквы.
Современный алфавит из 26 букв появился в 16 веке. На развитие английского алфавита оказали влияние семитские, финикийские, греческие и римские сценарии. Очень интересно узнать, как образовалась каждая буква.
Буква А
Первоначальная форма буквы А была перевернутой. Он был представлен в 1800-х годах. Будучи перевернутым, он выглядел как голова животного с рогами или оленями. Это было уместно, потому что в древнесемитском языке эта буква переводится как «бык».
Он был представлен в 1800-х годах. Будучи перевернутым, он выглядел как голова животного с рогами или оленями. Это было уместно, потому что в древнесемитском языке эта буква переводится как «бык».
Буква B
В своей первоначальной форме буква B была заимствована из египетских иероглифов, и буква располагалась на животе. В своем первоначальном виде он выглядел как дом с дверью, крышей и комнатой. Символ представлял собой «убежище» около 4000 лет назад.
Письмо C
Письмо пришло от финикийцев. Он имел форму бумеранга или охотничьей палки. Греки называли его «гамма», и вместо того, чтобы писать в другом направлении, он был перевернут в том направлении, в котором он пишется сегодня, а итальянцы придали ему лучшую форму полумесяца.
Буква D
«Далет» — это название, данное букве D финикийцами в 800 г. до н.э. Первоначально он выглядел как грубый треугольник, обращенный влево. Первоначальное значение буквы — «дверь». Когда греки приняли алфавит, они дали ему название «дельта». Позже оно было перевернуто, и римляне придали правой стороне буквы форму полукруга.
Позже оно было перевернуто, и римляне придали правой стороне буквы форму полукруга.
Около 3800 лет назад буква «E» в семитском языке произносилась как «H». Он был похож на фигурку человека с двумя руками и одной ногой. В 700 г. до н.э. гики перевернули его и изменили произношение на звук «и».
Буква FБуква «F» была финикийской и больше походила на «Y». Когда она произносилась в то время, звук был близок к «вау». «дигамма» и придал ей форму, похожую на современную букву «Ф».0009
Буква G
Буква «G» произошла от «зета» греков. Сначала это выглядело как «я», но произношение сделало звук «ззз». Римляне изменили его форму около 250 г. до н.э., придав ему верхнюю и нижнюю части и звук «г». В латыни не было звука «з». В ходе его развития прямые линии стали изогнутыми, закончив его нынешнюю серповидную форму.
Буква H
Буква «H» пришла от египтян и использовалась как символ забора. При произнесении он издавал хриплый звук, поэтому ранние академики считали, что в этом нет необходимости, а британские и латинские ученые в конечном итоге исключили букву H из английского алфавита примерно к 500 году нашей эры.
При произнесении он издавал хриплый звук, поэтому ранние академики считали, что в этом нет необходимости, а британские и латинские ученые в конечном итоге исключили букву H из английского алфавита примерно к 500 году нашей эры.
Буква I
Буква «I» называлась «йод» в 1000 г. до н.э. Это означало руку и руку. Греки назвали его «йота» и сделали вертикальным. В своей эволюции она превратилась в прямую линию около 700 г. до н.э.
Буква J
Буква «I» также использовалась для обозначения звука «J» в древние времена. Он получил свою форму письма в 15 веке как вклад испанского языка. Только около 1640 года письмо регулярно появлялось в печати.
Буква К
Буква «К» — старая буква, так как она произошла от египетских иероглифов. На семитском языке ему дали название «каф», что переводится как «ладонь». В те времена буква была обращена в другую сторону. Когда греки приняли его в 800 г. до н.э., он стал «каппа» и перевернулся вправо.
Буква L
В древнесемитском языке современная буква «L» была перевернутой. Таким образом, это выглядело как крючковатое письмо. Он уже назывался «Эль», что означало «Бог». Финикийцы были ответственны за то, что придали ему перевернутый вид, с крюком, обращенным влево. Они немного поправили крюк и изменили название на «ламед» (произносится «лах-мед»), погонщик для скота. Греки называли его «лямбда» и поворачивали вправо. Окончательный вид буквы «L» с прямой ногой под прямым углом был любезно предоставлен римлянами.
Таким образом, это выглядело как крючковатое письмо. Он уже назывался «Эль», что означало «Бог». Финикийцы были ответственны за то, что придали ему перевернутый вид, с крюком, обращенным влево. Они немного поправили крюк и изменили название на «ламед» (произносится «лах-мед»), погонщик для скота. Греки называли его «лямбда» и поворачивали вправо. Окончательный вид буквы «L» с прямой ногой под прямым углом был любезно предоставлен римлянами.
Буква М
Происхождением буквы «М» были волнистые вертикальные линии с пятью пиками, которые, по мнению египтян, символизировали воду. В 1800 г. до н.э. семиты сократили линии до трех волн, а финикийцы убрали еще одну волну. В 800 г. до н.э. вершины были превращены в зигзаги и перевернуты по горизонтали, образуя букву М, которую мы знаем сегодня.
Буква N
Другим египетским символом была буква «N», которая изначально выглядела как маленькая рябь поверх более крупной ряби, которая обозначала кобру или змею. Древние семиты придали ему звук «н», что символизировало «рыбу». Около 1000 г. до н. э. появилась только одна рябь, и греки назвали ее «ню».0009
Около 1000 г. до н. э. появилась только одна рябь, и греки назвали ее «ню».0009
Буква О
Буква «О» также пришла от египтян. Он назывался «глаз» по-египетски и «айин» по-семитски. Финикийцы еще больше сократили иероглифы, оставив только контур зрачка.
Буква P
В древнем семитском языке сегодняшняя буква «P» выглядела как перевернутая «V». Она произносилась как «pe», что означало «рот». Финикийцы превратили ее вершину в форму диагонального крючка. В 200 г. до н.э. римляне перевернули его вправо и замкнули петлю, образовав букву «П».0009
Буква Q
Первоначальный звук буквы «Q» был похож на «qoph», что переводится как клубок шерсти или обезьяна. Первоначально он был написан как круг, пересекаемый вертикальной линией. В римских надписях около 520 г. до н.э. буква появилась такой, какой мы ее знаем сегодня.
Буква R
Профиль человека, обращенного влево, был оригинальной формой буквы «R», как писали семиты. Оно произносилось как «реш», что означало «голова».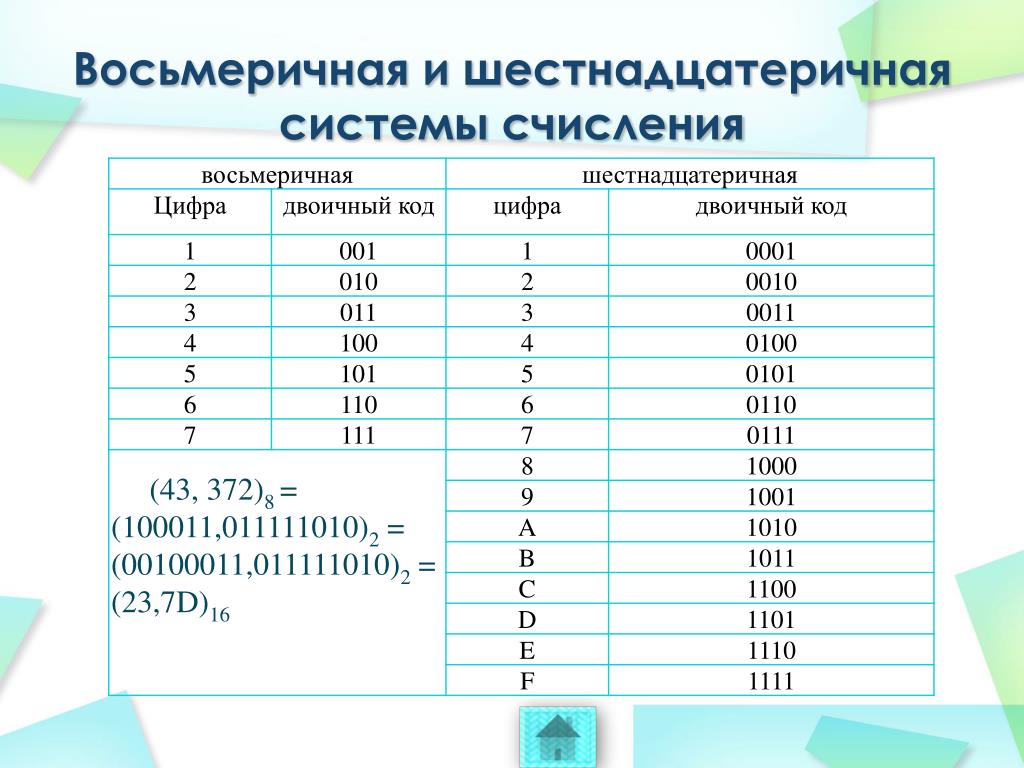 Римляне повернули его вправо и добавили наклонную ногу.
Римляне повернули его вправо и добавили наклонную ногу.
Буква S
Буква «S» раньше выглядела как горизонтальная волнистая буква W, которая использовалась для обозначения лука лучника. Угловатость формы была от финикийцев, которые дали ему название «голень», что переводится как «зуб». Римляне перевернули его в вертикальное положение и назвали «сигма», в то время как римляне перевернули его в положение, которое буква имеет сегодня.
Буква Т
Древние семиты использовали строчную форму буквы «Т», которую мы видим сегодня. Финикийцы называли букву «тау» (знак), которая при произнесении звучала как «ти». Греки называли его «тау». Они также добавили крест в верхней части буквы, чтобы отличить ее от буквы «X»9.0009
Буква U
Буква «U» изначально выглядела как «Y» в 1000 г. до н.э. В то время его называли «вав», что означало «колышек». У греков он назывался «ипсилон». Различие начало появляться примерно в 1400-х годах.
Буква W
Буква «W» появилась в средние века, когда писцы Карла Великого писали две буквы «u» рядом, разделенные пробелом. В то время издаваемый звук был похож на «в». Буква появилась в печати как уникальная буква «W» в 1700 году.
В то время издаваемый звук был похож на «в». Буква появилась в печати как уникальная буква «W» в 1700 году.
Буква Х
Буква «кси» у древних греков звучала как «Х». Строчная форма буквы «Х» встречалась в рукописных рукописях, доступных в средние века. Итальянские печатники конца 15 века также использовали строчные буквы «X».
Буква Y
Начав с «ипсилон», буква Y была добавлена римлянами в 100 г. н.э.
Буква Z
У финикийцев была буква под названием «заин». Она означала «топор». Первоначально она выглядела как буква «I» с засечками вверху и внизу. Примерно в 800 г. до н.э. греки приняли его как «зета» и присвоили ему звук дз. Он не использовался в течение нескольких столетий до прихода нормандских французов и их слов, которые нуждались в звуке буквы «Z».0009
Alphabet Aside…
Компания Day Translations, Inc. занимается письменным и устным переводом на английском и более чем на 100 других языков. Будьте уверены, что наши языковые услуги оказывают опытные и сертифицированные профессионалы. Все наши команды устных и письменных переводчиков являются носителями языка. Они также являются экспертами в предметной области и способны выполнять специальные проекты по письменному и устному переводу. Если вам нужны срочные языковые услуги, вы можете немедленно связаться с Day Translations, позвонив по телефону 1-800-9.69-6853. Вы также можете связаться с нами по электронной почте на странице Свяжитесь с нами.
Будьте уверены, что наши языковые услуги оказывают опытные и сертифицированные профессионалы. Все наши команды устных и письменных переводчиков являются носителями языка. Они также являются экспертами в предметной области и способны выполнять специальные проекты по письменному и устному переводу. Если вам нужны срочные языковые услуги, вы можете немедленно связаться с Day Translations, позвонив по телефону 1-800-9.69-6853. Вы также можете связаться с нами по электронной почте на странице Свяжитесь с нами.
1 и 0 — журнал beanz
Тим Славин / Статьи о концепциях кодирования для детей / Выпуск
за сентябрь 2013 г.Дэвид Дж. Морган на Flickr
Двоичные числа, основанные на единицах и нулях, отражают практическую суть компьютерного оборудования: электричество либо включено, либо выключено. Узнайте, как писать двоичные числа, и (не такой уж секретный) код для преобразования букв английского языка в двоичные числа и обратно.
Когда буква А не буква А? Что ж, компьютеры не используют букву A. Они используют восьмизначное двоичное число 01000001 для представления A. В этом руководстве по двоичным числам описывается, что такое двоичные числа и как их вычислять.
Они используют восьмизначное двоичное число 01000001 для представления A. В этом руководстве по двоичным числам описывается, что такое двоичные числа и как их вычислять.
Компьютеры переносят, вычисляют и преобразуют двоичные числа, потому что аппаратные цепи компьютера имеют только два электрических состояния: включено или выключено. Эти два состояния можно представить как ноль (выключено) или единицу (включено). Все буквы алфавита, цифры и символы преобразуются в восьмизначные двоичные числа, когда вы работаете с ними в программном обеспечении на вашем компьютере.
Создание и преобразование двоичных чисел — хороший способ узнать, как компьютеры обрабатывают данные на самом низком уровне, в своих аппаратных схемах.
Кроме того, я предоставляю бесплатную электронную таблицу Excel, ссылка на которую приведена в конце этой статьи, чтобы помочь вам визуализировать и вычислять двоичные числа.
[Не очень] секретная формула
Чтобы представить букву А как 01000001, компьютеру (и вам, если следовать дальше) потребуются несколько основных инструментов.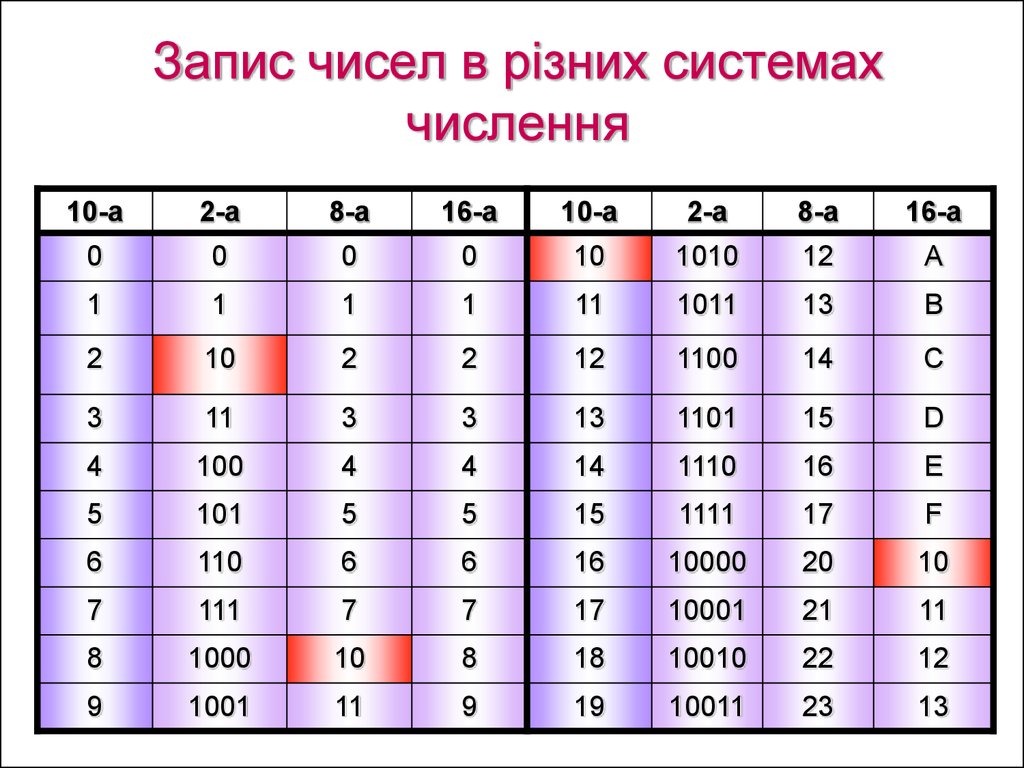 Одним из инструментов является таблица преобразования ASCII. Не вдаваясь в технические подробности, диаграмма ASCII сопоставляет уникальное число от 1 до 255 всем буквам алфавита, заглавным (A-Z) и строчным (az), а также числам (0-9).), пробелы и другие специальные символы. Уникальный номер ASCII, который соответствует каждому символу, например, заглавной букве A, используется для вычисления уникального восьмизначного двоичного числа, комбинации единиц и нулей, например 01000001.
Одним из инструментов является таблица преобразования ASCII. Не вдаваясь в технические подробности, диаграмма ASCII сопоставляет уникальное число от 1 до 255 всем буквам алфавита, заглавным (A-Z) и строчным (az), а также числам (0-9).), пробелы и другие специальные символы. Уникальный номер ASCII, который соответствует каждому символу, например, заглавной букве A, используется для вычисления уникального восьмизначного двоичного числа, комбинации единиц и нулей, например 01000001.
По сути, это двухэтапный секретный код. Первый шаг — получить уникальный номер ASCII для буквы. Второй шаг — создать уникальное восьмизначное двоичное число, представляющее собой комбинацию единиц и нулей для представления числа ASCII.
И, конечно же, переход от восьмизначной комбинации единиц и нулей к букве или символу меняет этот процесс на обратный: сначала преобразуйте двоичное число в число от 1 до 255, а затем используйте это число для поиска буквы в таблице ASCII. .
Как создавать двоичные числа
Двоичные числа состоят из восьми символов, каждый из которых представляет собой либо 1, либо 0.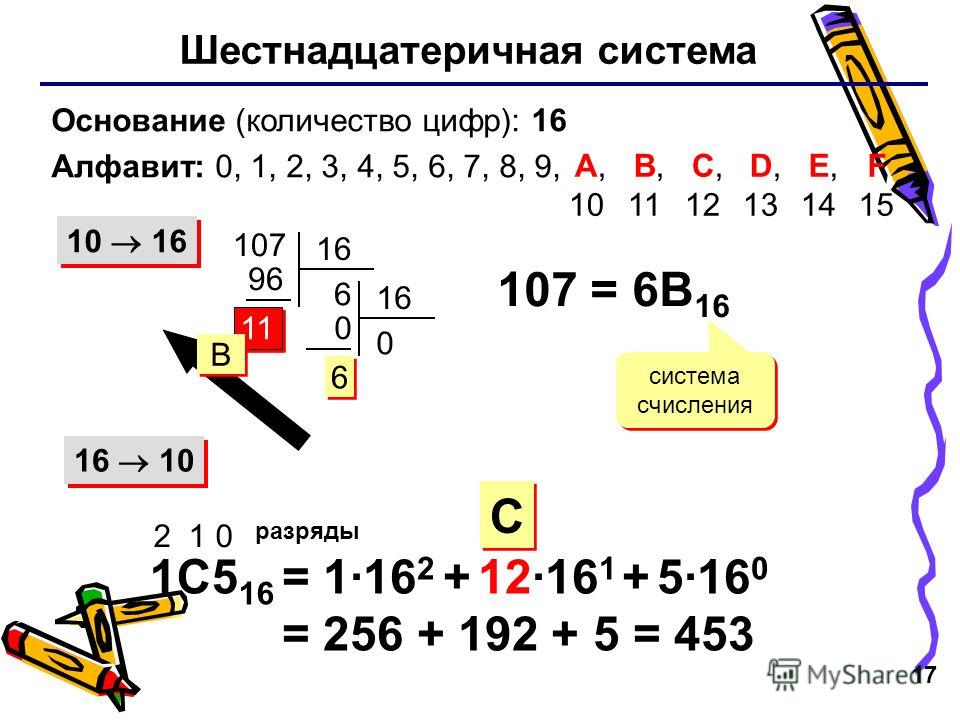 Размещение каждой единицы указывает значение этой позиции, которое используется для вычисления общего значения двоичного числа. Каждая позиция каждого из восьми символов представляет собой фиксированное числовое значение, как показано ниже.
Размещение каждой единицы указывает значение этой позиции, которое используется для вычисления общего значения двоичного числа. Каждая позиция каждого из восьми символов представляет собой фиксированное числовое значение, как показано ниже.
Если вы прочитаете эти значения по умолчанию снизу вверх, сможете ли вы сказать, как вычисляется каждое число, расположенное непосредственно выше? Они удвоены. Таким образом, двоичные числа начинаются снизу с первой позиции, равной 1. Вторая позиция снизу имеет значение 2, третья позиция 4 и так далее.
Если сложить все эти числа (1+2+4+8+16+32+64+128), угадайте, какое число получится? 255, наибольшее число, используемое в таблице ASCII. Существует идеальное соответствие между всеми возможными числами от 1 до 255 в таблице ASCII и вычисленными значениями для всех возможных восьмизначных двоичных чисел.
Чтобы вычислить числовое значение двоичного числа, сложите значения для каждой позиции всех единиц в восьмизначном числе.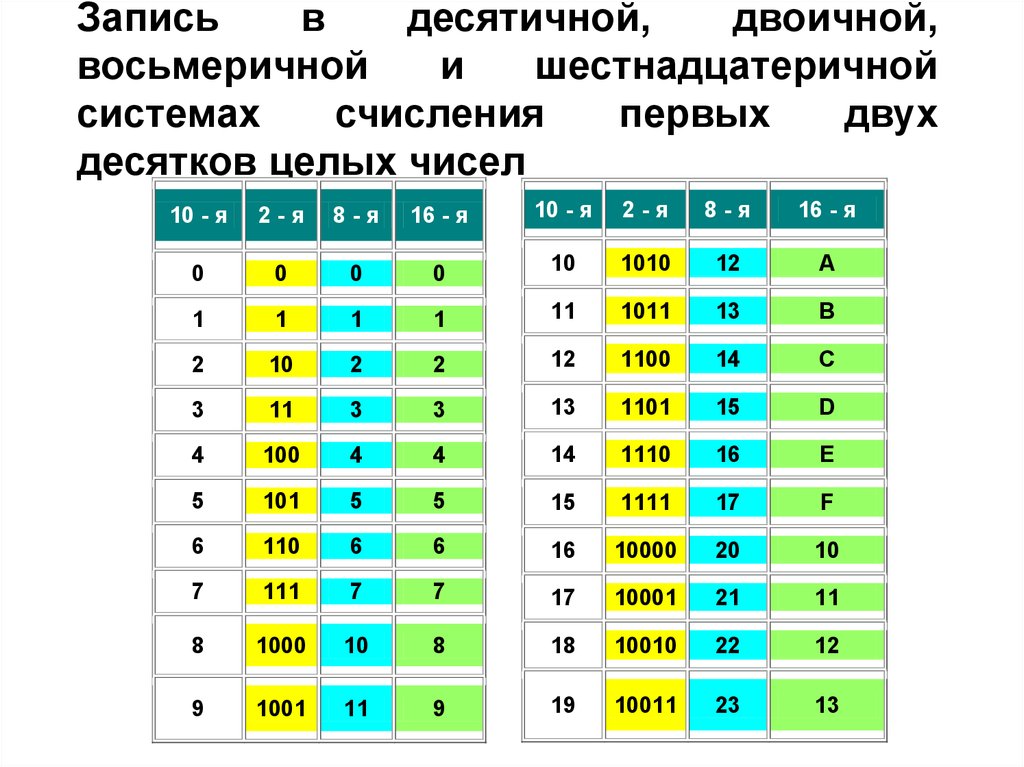 Число 01000001, например, преобразуется в 64 + 1 или 65. Единицы в этом двоичном числе стоят на первой и седьмой позициях, считая снизу вверх или читаясь справа налево. Первой позиции присвоено значение 1, а седьмой позиции присвоено значение 64.
Число 01000001, например, преобразуется в 64 + 1 или 65. Единицы в этом двоичном числе стоят на первой и седьмой позициях, считая снизу вверх или читаясь справа налево. Первой позиции присвоено значение 1, а седьмой позиции присвоено значение 64.
Преобразуем букву в двоичное число
Теперь, когда вы знаете [не очень] секретную формулу для преобразования букв в уникальные числа ASCII в двоичные числа и как создавать двоичные числа, давайте проделаем весь процесс шаг за шагом. Начнем с буквы С.
Во-первых, нам нужно использовать диаграмму ASCII, подобную приведенной ниже, чтобы найти уникальный номер, присвоенный заглавной букве C. Уникальное десятичное число для использования — 67.
| Десятичный | Символ | Десятичный | Символ | Десятичный | Символ | ||
|---|---|---|---|---|---|---|---|
| 32 | Космос | 64 | @ | 96 | ` | ||
| 33 | ! | 65 | А | 97 | и | ||
| 34 | » | 66 | Б | 98 | б | ||
| 35 | # | 67 | С | 99 | в | ||
| 36 | $ | 68 | Д | 100 | д | ||
| 37 | % | 69 | Э | 101 | и | ||
| 38 | и | 70 | Ф | 102 | ф | ||
| 39 | ‘ | 71 | Г | 103 | г | ||
| 40 | ( | 72 | Х | 104 | ч | ||
| 41 | ) | 73 | я | 105 | и | ||
| 42 | * | 74 | Дж | 106 | и | ||
| 43 | + | 75 | К | 107 | к | ||
| 44 | , | 76 | л | 108 | л | ||
| 45 | – | 77 | М | 109 | м | ||
| 46 | .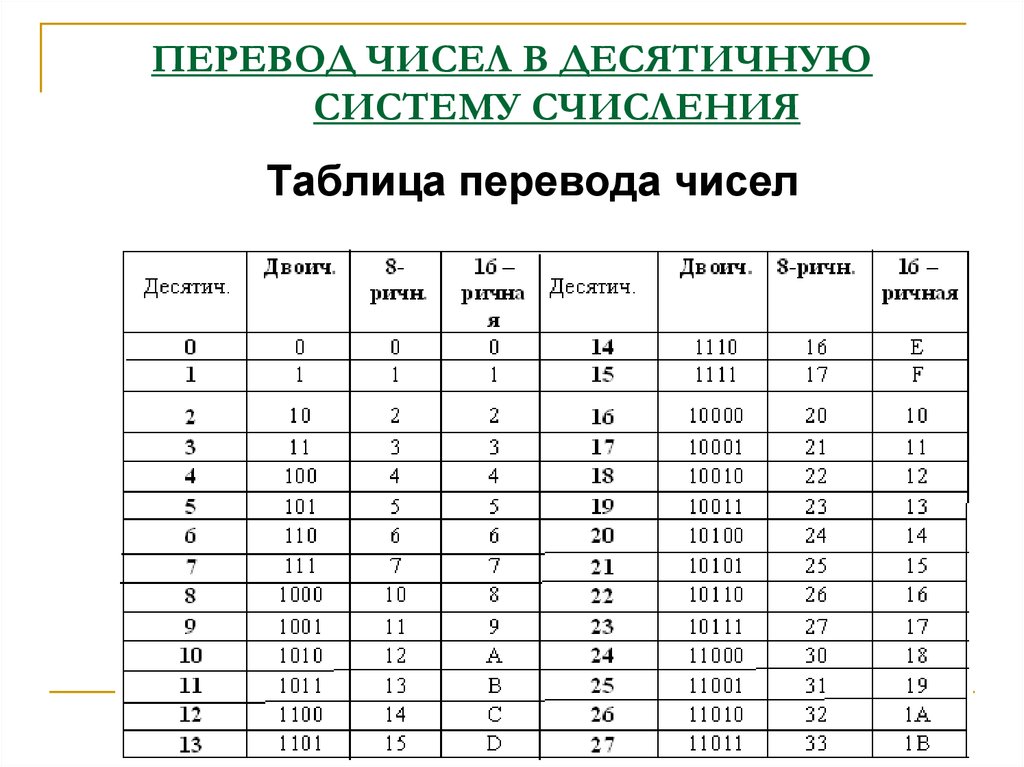 | 78 | Н | 110 | н | ||
| 47 | / | 79 | О | 111 | или | ||
| 48 | 0 | 80 | С | 112 | р | ||
| 49 | 1 | 81 | В | 113 | к | ||
| 50 | 2 | 82 | Р | 114 | р | ||
| 51 | 3 | 83 | С | 115 | с | ||
| 52 | 4 | 84 | Т | 116 | т | ||
| 53 | 5 | 85 | У | 117 | и | ||
| 54 | 6 | 86 | В | 118 | против | ||
| 55 | 7 | 87 | Вт | 119 | с | ||
| 56 | 8 | 88 | х | 120 | х | ||
| 57 | 9 | 89 | Д | 121 | г | ||
| 58 | : | 90 | З | 122 | по | ||
| 59 | ; | 91 | [ | 123 | { | ||
| 60 | 92 | 124 | | | ||||
| 61 | = | 93 | ] | 125 | } | 9126 | ~ |
| 63 | ? | 95 | _ | 127 | ДЕЛ |
Чтобы преобразовать число для C, 67, в двоичное число:
Помните, как двоичные числа читаются снизу вверх, от первой позиции и значения по умолчанию до верхней позиции и значения по умолчанию, причем каждой из восьми позиций символов присваивается уникальное числовое значение? На приведенной ниже диаграмме какая комбинация значений будет равна 67?
Двоичные числа со значениями и позициями Вы правы, если сказали, что значения по умолчанию 1 плюс 2 плюс 64 будут равны 67, числу ASCII для заглавной буквы C.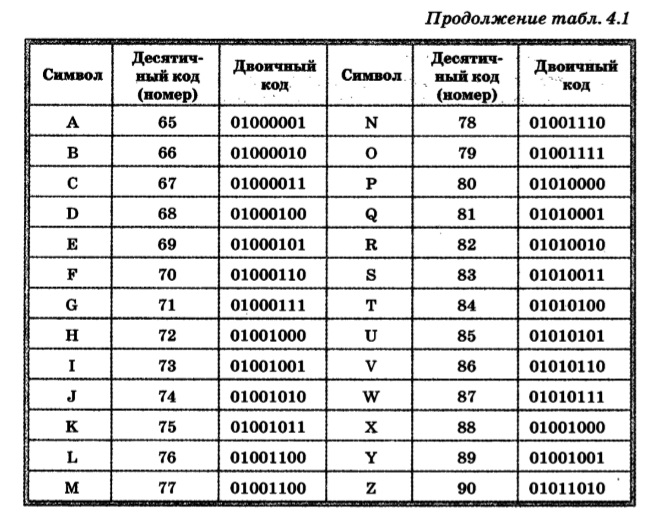 Итак, давайте изменим нули в первой, второй и седьмой позициях на единицы, считается справа налево. Двоичное число для заглавной буквы C:
Итак, давайте изменим нули в первой, второй и седьмой позициях на единицы, считается справа налево. Двоичное число для заглавной буквы C:
Можете ли вы расшифровать это двоичное число? Сложите единицы, чтобы получить 64+16+4 или 84. Найдите десятичное число 84 в таблице ASCII, чтобы найти букву, представленную ниже:
Буква T как двоичное числоЕсли вы преобразовали это двоичное число в заглавную букву T, вы правы. Вот буква A в виде двоичного числа для представления десятичного числа ASCII для A, которое равно 65:
. Буква A как двоичное число. Если мы объединим двоичные числа, которые мы рассмотрели до сих пор, мы можем составить CAT:
.01000011 01000001 01010100
Бонус: псевдокод для разработки преобразователя двоичных чисел
Поняв, как буквы и цифры преобразуются в двоичные числа и обратно, давайте посмотрим, как можно создать программное приложение для выполнения этих преобразований на лету. Приложение не имеет реальной ценности. Но это дает возможность обсудить, как процесс может быть преобразован в программное обеспечение.
Но это дает возможность обсудить, как процесс может быть преобразован в программное обеспечение.
Однако вместо фактического кода мы напишем серию операторов или псевдокод.
Для начала возьмем слово кошка. Какой процесс нам нужен для автоматического преобразования этих букв в двоичные числа? Вот один из возможных наборов шагов, которые мы могли бы закодировать:
.- Разбейте слово на отдельные буквы.
- Для каждой буквы найдите числовое значение ASCII, сопоставленное с буквой.
- Для каждого числового значения ASCII преобразовать в двоичное число.
- : Для каждого двоичного числа сохраните значение двоичного числа. Если это первое двоичное число, создайте начальное значение двоичного числа; если значение двоичного числа существует, добавьте новое двоичное число в конец значения.
Представьте, если бы мы пропустили последний шаг: каков был бы результат этих шагов? У нас было бы только последнее двоичное число для строчной буквы t в cat. Важно, чтобы мы фиксировали каждое двоичное число по мере его создания.
Важно, чтобы мы фиксировали каждое двоичное число по мере его создания.
Другие замечания об этом процессе псевдокода? Нам нужно различать заглавные и строчные буквы, не так ли? В противном случае наше преобразование двоичных чисел может преобразовать двоичные числа в буквы ASCII как CAT, cAT или Cat. Наш поиск для сопоставления букв с таблицей ASCII может привести к неправильному числу.
Бонус-бонус: последняя головоломка
Можете ли вы расшифровать фразу в этом наборе двоичных чисел? Помните, что это восемь блоков символов из 1 и 0.
01000011 01101111 01100100 01100101 01101001 01110011 01010000 01101111 01100101 01110100 01110010 01111001
Вот довольно простой способ преобразовать любую букву в двоичное число. Возьмите калькулятор, найдите десятичное значение ASCII для буквы из приведенной выше таблицы, затем посмотрите на диаграмму двоичных чисел, чтобы найти ближайшее значение к десятичному значению. Вычтите ближайшее число из значения по умолчанию в двоичной диаграмме, чтобы получить значение остатка.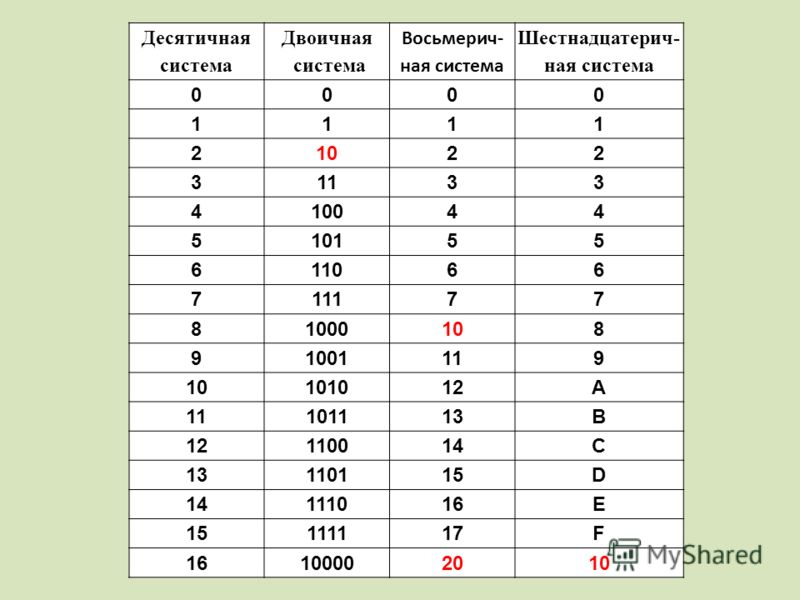 Найдите ближайшее двоичное значение по умолчанию для остатка. Повторяйте, пока не закончатся двоичные значения.
Найдите ближайшее двоичное значение по умолчанию для остатка. Повторяйте, пока не закончатся двоичные значения.
Если вы сообразительны, вы также заметите, что сумма значений под любым из восьми значений по умолчанию равна на единицу меньше, чем значение: поэтому под двоичным значением 4 находятся значения 2 и 1, которые равны 3. Ниже двоичного значения значение 8 равно 4, 2 и 1, что равно 7. Это также может помочь преобразовать буквы в двоичные числа. Например, если ваш остаток равен 7, то вы знаете, что нужно поставить 1 на позиции 4, 2 и 1, чтобы создать эту часть вашего двоичного числа.
Чтобы преобразовать двоичные числа в буквы, просто возьмите лист бумаги, ручку или карандаш и сложите двоичные значения всех единиц. Затем найдите свое общее число в виде десятичного знака ASCII в приведенной выше таблице.
Вот подсказка, которая поможет определить, правильно ли вы решили приведенные выше двоичные числа: в колледже я изучал американскую поэзию, и мне нравится старый слоган, используемый для программного обеспечения для публикации WordPress.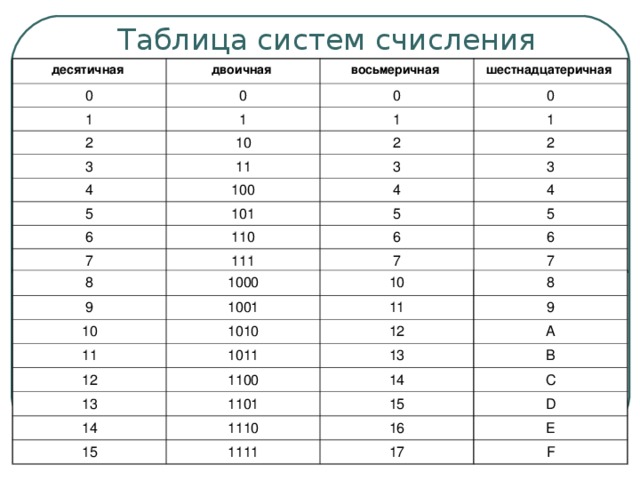
Если вы хотите больше двоичных чисел, ознакомьтесь с нашей статьей о головоломках с двоичными числами Бакуро, которые работают как судоку.
Узнать больше
Рабочий лист двоичных чисел (формат Excel)
https://www.kidscodecs.com/binary-numbers-converter
Рабочий лист«Двоичные числа» (PDF)
https://www.kidscodecs.com/binary-numbers-worksheet
Двоичный преобразователь
http://www.rapidtables.com/convert/number/binary-converter.htm
Учебник по двоичным числам
http://www.math.grin.edu/~rebelsky/Courses/152/97F/Readings/student-binary
Двоичные числа (Википедия)
https://en.wikipedia.org/wiki/Двоичный_номер
Таблица ASCII
http://www.asciitable.com/
Также в выпуске 9 за сентябрь 2013 г.0037
Концепции
1 и 0
Двоичные числа, основанные на единицах и нулях, отражают практическую суть компьютерного оборудования: электричество либо включено, либо выключено. Узнайте, как писать двоичные числа, и (не такой уж секретный) код для преобразования букв английского языка в двоичные числа и обратно.
Узнайте, как писать двоичные числа, и (не такой уж секретный) код для преобразования букв английского языка в двоичные числа и обратно.
Прочитать статью
Люди
Саймон Хотон рассказывает о детях, Python и компьютерных науках
Саймон недавно написал короткую электронную книгу «Руководство для детей по программированию на Python», чтобы научить детей в возрасте 5-8 лет программировать на Python..
Читать статью
Язык месяца
Python
Названный в честь Монти Пайтона, этот язык разработан таким образом, чтобы быть простым, но мощным, простым в кодировании и множеством функций.
Прочитать статью
Фрагменты кода
Переменные
В большинстве или во всех языках программирования переменные работают как контейнеры для хранения чисел, фраз или других важных вещей, используемых в нескольких местах вашего кода. Вот как они работают на нескольких распространенных языках.
Читать статью
Проекты и головоломки
Счастливые числа
Некоторые числа просто имеют положительный настрой.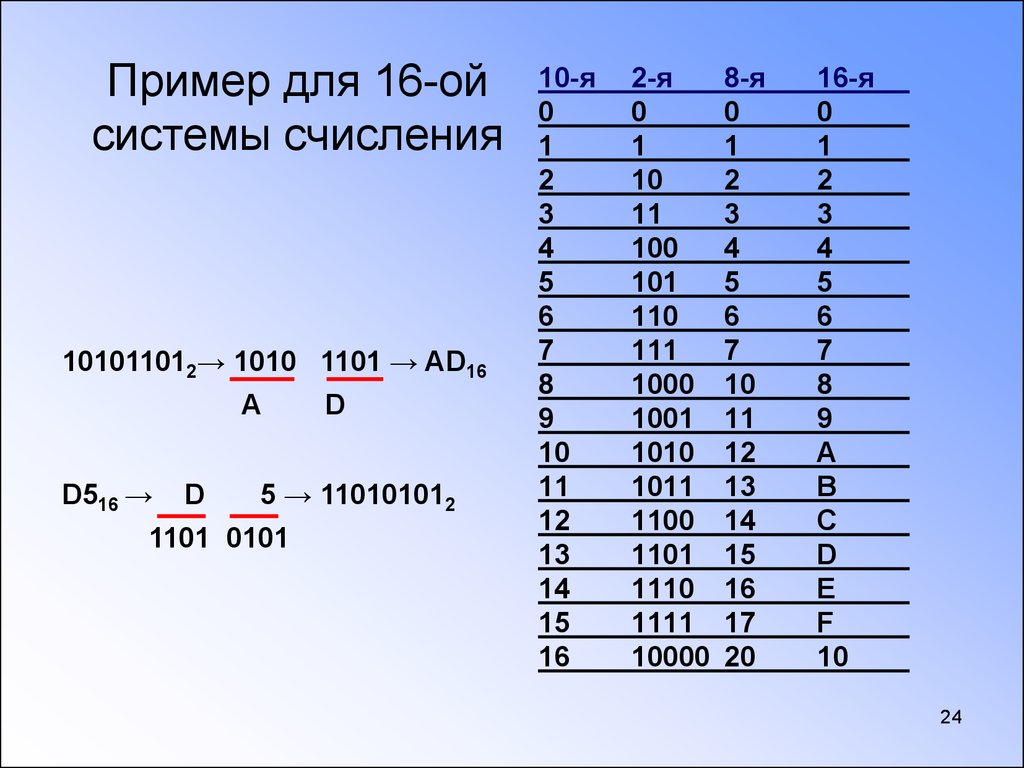 С ними весело играть.
С ними весело играть.
Прочитать статью
Блокнот
Локальные группы кодирования и технологий
Girls Who Code, CoderDojo и другие местные группы — отличные места, где можно научиться программировать, знакомиться с людьми и помогать другим учиться.
Прочитать статью
Проекты и головоломки
Как собрать компьютер
Сборка собственного компьютера — отличный способ не только сэкономить деньги и получить больше вычислительной мощности, но и узнать о менее очевидных аспектах программирования.
Прочитать статью
News Wire
News Wire Сюжеты за сентябрь 2013 г.
Интересные истории о компьютерных науках, программировании и технологиях за август 2013 года.
Прочитать статью
Блокнот
Онлайн-школы программирования
В Интернете есть множество мест, где можно изучить один или несколько языков программирования. Вот краткий список с некоторыми рекомендациями для оценки всех ваших вариантов.
Прочитать статью
Информатика связана с компьютерами не больше, чем астрономия с телескопами, биология с микроскопами или химия с химическими стаканами и пробирками. Наука — это не инструменты. Речь идет о том, как мы их используем, и что мы узнаем, когда мы это делаем.
— Майкл Феллоуз и Ян Парберри
Дополнительные ссылки
Дополнительные ссылки за сентябрь 2013 г.
Ссылки внизу всех статей за сентябрь 2013 г., собранные в одном месте, чтобы вы могли их распечатать, поделиться или добавить в закладки.
Прочитать статью
Люди
Клод Шеннон
Его работа объединяет две темы для этого номера журнала: двоичные числа и проектирование схем. Без Шеннона компьютеры и информатика могли бы быть совсем другими.
Читать статью
писем | КМС
- Поддержка потребителей и информация
- Гранты Программы помощи потребителям
- Внешние апелляции
- Краткое изложение льгот и покрытия и единый глоссарий
- Требования к содержимому для Plan Finder
- План страхования ранее существовавших заболеваний (PCIP)
- Торговые площадки медицинского страхования
- Гранты на планирование и учреждение
- Ранние новаторские гранты 907:25
- Системы информационных технологий
- Государственные инновации
- Реформы рынка медицинского страхования
- Годовые лимиты
- Покрытие для молодых взрослых
- Дедушкины планы
- Коэффициент медицинских потерь
- Обзор страховых тарифов
- Планы медицинского страхования учащихся
- Нефедеральные государственные планы
Поддержка потребителей и информация
Гранты Программы помощи потребителям
Пресс-релизы
- 22 июля 2010 г.

- 19 октября 2010 г.
Новые правила Закона о доступном медицинском обслуживании помогают потребителям лучше понимать и сравнивать льготы и покрытие — открывается в новом окне
Пресс-релизы
- 22 июля 2010 г.
Администрация объявляет о новых мерах Закона о доступном медицинском обслуживании, направленных на защиту потребителей и возложение на пациентов ответственности за их лечение — открывается в новом окне
Краткое изложение льгот и страхового покрытия и унифицированный глоссарий
Пресс-релизы
- 17 августа 2011 г.
Требования к содержимому для Plan Finder
Письма
- 3 мая 2010 г.
Письмо HHS эмитентам рыночного страхования частных лиц и малых групп относительно доступа пользователей и авторизации в системе контроля медицинского страхования - 6 мая 2010 г.
Письмо HHS штатам относительно предоставления данных штатами для системы надзора за медицинским страхованием (PDF – 110 КБ) (PDF) - 9 июля 2010 г.

Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 145 КБ) (PDF) - 10 августа 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 53 КБ) (PDF) - 20 августа 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 149 КБ) (PDF) - 31 августа 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 36 КБ) (PDF) - 2 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений I (PDF – 62 КБ) (PDF)
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений II (PDF – 30 КБ) (PDF)
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений III (PDF – 32 КБ) (PDF) - 8 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 30 КБ) (PDF) - 13 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 204 КБ) (PDF) - 14 сентября 2010 г.

Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 31 КБ) (PDF) - 15 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 75 КБ) (PDF) 907:25 - 16 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 42 КБ) (PDF) - 22 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 30 КБ) (PDF) - 23 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 33 КБ) (PDF) - 24 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 95 КБ) (PDF) - 30 сентября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 58 КБ) (PDF) 907:25 - 28 октября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 266 КБ) (PDF) - 30 ноября 2010 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 122 КБ) (PDF) - 10 декабря 2010 г.

Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 80 КБ) (PDF) - 22 декабря 2010 г.
Письмо HHS организациям, выдающим страховые полисы, относительно ссылок на сети поставщиков услуг (PDF – 32 КБ) (PDF)0933 Письмо HHS организациям, выдающим медицинские страховки, относительно ссылок на формуляры (PDF – 32 КБ) (PDF) - 12 января 2011 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 198 КБ) (PDF) - 19 января 2011 г.
Письмо HHS/OCIIO эмитентам относительно ежемесячных обновлений (PDF – 147 КБ) (PDF) - 15 февраля 2011 г.
Письмо HHS организациям, выдающим страховые полисы, относительно ссылок на сети поставщиков услуг (PDF – 129 КБ) (PDF)0933 Письмо HHS организациям, выдающим медицинские страховки, относительно ссылок на формуляры (PDF — 129 КБ) (PDF) - 12 апреля 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF – 230 КБ) (PDF) - 2 мая 2011 г.

Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF – 65 КБ) (PDF) - 2 июня 2011 г.
Уведомление о предварительном раскрытии информации: Запрос исходных данных по Закону о свободе информации — http://finder.healthcare.gov — Памятка (PDF — 99 КБ) (PDF)
Приложение 1 (PDF — 141 КБ) (PDF)
Приложение 2 (PDF – 157 КБ) (PDF) - 9 июня 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF – 39 КБ) (PDF) - 13 июля 2011 г.
Письмо HHS/CCIIO эмитентам относительно веб-статистики (PDF – 41 КБ) (PDF) - 26 июля 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF – 65 КБ) (PDF) - 11 августа 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 40 КБ) (PDF) - 18 августа 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 39 КБ) (PDF) - 31 августа 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 39 КБ) (PDF) - 16 сентября 2011 г.

Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 86 КБ) (PDF) - 27 сентября 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 65 КБ) (PDF) - 30 сентября 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 51 КБ) (PDF) 907:25 - 12 октября 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 57 КБ) (PDF) - 17 октября 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF — 39 КБ) (PDF) - 21 ноября 2011 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF – 178 КБ) (PDF) - 6 января 2012 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF – 202 КБ) (PDF) - 27 февраля 2012 г.
Изменения шаблона RBIS для индивидуальных/семейных рынков (PDF – 62 КБ) (PDF) 907:25 - 1 марта 2012 г.
Письмо HHS/CCIIO эмитентам относительно ежемесячных обновлений (PDF – 63 КБ) (PDF) - 2 апреля 2012 г.

Изменения в окнах сбора данных HIOS/RBIS (PDF — 40 КБ) (PDF) - 20 апреля 2012 г.
Открытое окно для малых групп HIOS (PDF – 45 КБ) (PDF) - 22 мая 2012 г.
Изменения окна коллекции от 11 июня 2012 г.; Обучение отложено (PDF – 51 КБ) (PDF) - 15 июня 2012 г.
Обучение RBIS по комбинированному окну (PDF – 45 КБ) (PDF) - 26 июня 2012 г.
Краткое изложение преимуществ и ссылки на покрытие (PDF – 35 КБ) (PDF) - 27 июня 2012 г.
Дополнительное окно отправки IFP (PDF – 32 КБ) (PDF) - 19 июля 2012 г.
Индивидуальный/семейный рынок RBIS Open Window Dates (PDF – 51 КБ) (PDF) - 20 августа 2012 г.
27 августа Комбинированное окно HIOB/RBIS (PDF – 46 КБ) (PDF) - 28 сентября 2012 г.
Краткое изложение льгот и покрытия (SBC) без примерных данных покрытия (PDF — 118 КБ) (PDF) - 19 декабря 2012 г.
Истечение срока действия тарифа/тарифного плана и расписание комбинированных окон на 2013 г. (PDF — 80 КБ) (PDF)
(PDF — 80 КБ) (PDF)
Лица, использующие вспомогательные технологии, могут не иметь полного доступа к информации в этом файле. Для получения помощи, пожалуйста, напишите по адресу [email protected].
План страхования ранее существовавших состояний (PCIP)
Письма
- 10 мая 2010 г.
Торговые площадки медицинского страхования
Письма
- 12 ноября 2010 г.
Письмо HHS вождю племени о консультациях с племенем (PDF – 30 КБ) (PDF) - 18 ноября 2010 г.
Письмо HHS губернатору Грегуару, комиссару Клайну и сенатору Муру относительно первоначального руководства бирж медицинского страхования (PDF – 88 КБ) (PDF) - 10 августа 2011 г.
Письмо трех агентств о распределении расходов по программам Medicaid, CHIP, Exchange и другим программам социальных служб (PDF — 189)КБ) (PDF) - 23 января 2012 г.
Письмо трех агентств с дополнительными рекомендациями по распределению затрат на программы Medicaid, CHIP, Exchange и другие программы социальных служб (PDF — 201 КБ) (PDF) - 16 мая 2012 г.

Письмо HHS управляющим о рекомендациях по обмену доступным страхованием (PDF — 31 КБ) (PDF) - 9 ноября 2012 г.
Письмо HHS управляющим о представлении плана биржи (PDF) (PDF — 82 КБ) - 16 ноября 2012 г.
Государственные письма на биржах 907:25 - 10 декабря 2012 г.
Письмо губернатору CO об условном разрешении на создание государственной биржи (PDF — 53 КБ) (PDF)
Письмо губернатору CT об условном разрешении на создание государственной биржи (PDF — 53 КБ) (PDF)
Письмо губернатору Мэриленда об условном разрешении на создание государственной биржи (PDF — 54 КБ) (PDF)
Письмо губернатору Массачусетса об условном разрешении на создание государственной биржи (PDF — 53 КБ) (PDF) )
Письмо губернатору штата Орегон об условном разрешении на создание государственной биржи (PDF – 52 КБ) (PDF)
Письмо губернатору штата Вашингтон об условном разрешении на создание государственной биржи (PDF — 54 КБ) (PDF) - 10 декабря 2012 г.

Письмо управляющим по биржам, рыночным реформам и часто задаваемым вопросам Medicaid (PDF – 72 КБ) (PDF) - 10 декабря 2012 г.
Письмо губернаторам с информацией для территорий относительно Закона о доступном медицинском обслуживании (PDF – 532 КБ) (PDF) - 14 декабря 2012 г.
Письмо DC об условном разрешении на создание государственной биржи (PDF – 55 КБ) (PDF)
Письмо губернатору штата Кентукки об условном разрешении на создание государственной биржи (PDF — 52 КБ) (PDF)
Письмо губернатору штата Нью-Йорк об условном разрешении на создание государственной биржи (PDF — 50 КБ) (PDF) - 20 декабря 2012 г.
Письмо в DE об условном разрешении на создание государственной партнерской биржи (PDF – 53 КБ) (PDF)
Письмо в MN об условном одобрении на создание государственной биржи (PDF – 44 КБ) (PDF)
Письмо в РИ об условном разрешении на создание государственной биржи (PDF – 55 КБ) (PDF) 907:25 - 3 января 2013 г.
Письмо в AR об условном разрешении на создание государственной партнерской биржи (PDF – 71 КБ) (PDF)
Письмо в CA об условном одобрении на создание государственной биржи (PDF – 56 КБ) (PDF)
Письмо в HI об условном разрешении на создание государственной биржи (PDF — 77 КБ) (PDF)
Письмо в ID об условном одобрении на создание государственной биржи (PDF — 69 КБ) (PDF)
Письмо в NV об условном разрешении на создание государственной биржи (PDF – 59KB) (PDF)
Письмо в NM об условном разрешении на создание государственной биржи (PDF – 64 КБ) (PDF)
Письмо в UT об условном одобрении на создание государственной биржи (PDF – 75 КБ) (PDF) )
Письмо VT об условном разрешении на создание государственной биржи (PDF – 69 КБ) (PDF) - 8 февраля 2013 г.

Письмо в штат Миссисипи относительно Marketplace (PDF — 192 КБ) (PDF) - 13 февраля 2013 г.
Письмо в Иллинойс относительно условного одобрения партнерской торговой площадки (PDF — 80 КБ) (PDF) 907:25 - 7 марта 2013 г.
Письмо в Айову относительно условного одобрения партнерской торговой площадки (PDF — 47 КБ) (PDF)
Письмо в Мичиган относительно условного одобрения партнерской торговой площадки (PDF — 58 КБ) (PDF) Утверждение партнерской торговой площадки (PDF — 50 КБ) (PDF)
Письмо в Западную Вирджинию об условном утверждении партнерской торговой площадки (PDF — 50 КБ) (PDF)
Дополнительное письмо в Арканзас об условном одобрении создания государственной партнерской торговой площадки (PDF)
Дополнительное письмо в штат Делавэр об условном разрешении на создание торговой площадки для государственного партнерства (PDF)
Дополнительное письмо в Иллинойс по условному разрешению на создание торговой площадки для государственного партнерства (PDF) - 10 мая 2013 г.

Письмо в Юту относительно программы Health Options для малого бизнеса (PDF) (PDF – 276 КБ) - 13 мая 2013 г.
Письмо основным поставщикам медицинских услуг (PDF) (PDF – 99 КБ) - 14 июня 2013 г.
Письмо в NAIC относительно предлагаемого правила целостности программы (PDF) 907:25 - 1 октября 2013 г.
Письмо в штат Миссисипи относительно программы Health Options для малого бизнеса (PDF — 80 КБ) (PDF)
Письмо в Юту относительно программы Health Options для малого бизнеса (PDF — 85 KB) (PDF) - 31 декабря 2013 г.
Письмо и отчет Конгрессу о проверке дохода домохозяйства и других требований для предоставления Закона о доступном медицинском обслуживании Премиальные налоговые льготы и сокращение доли участия в расходах (PDF) - 15 июня 2015 г.
Письмо губернатору АР об условном разрешении на создание государственной биржи (PDF) (PDF – 53 КБ)
Письмо губернатору Германии об условном разрешении на создание государственной биржи (PDF) (PDF — 53 КБ)
Письмо губернатору Пенсильвании об условном разрешении на создание государственной биржи (PDF) (PDF — 54 КБ) - 4 октября 2016 г.

Письмо губернатору Кентукки об утверждении перехода штата Кентукки от SBM к SBM-FP (PDF)
Примечание. Пользователи вспомогательных технологий могут не иметь полного доступа к информации в этих файлах.
Если вам нужна помощь, отправьте электронное письмо по адресу [email protected].
Гранты на планирование и учреждение
Пресс-релизы
- 29 июля 2010 г.
HHS объявляет о наличии ресурсов на сумму 51 миллион долларов для штатов для создания нового конкурентного рынка медицинского страхования — открывается в новом окне 9077 - 20 января 2011 г.
HHS объявляет о новых ресурсах для помощи штатам в реализации Закона о доступном медицинском обслуживании: штаты продолжают двигаться вперед, получают новую поддержку для внедрения бирж медицинского страхования — открывается в новом окне 907:25 - 11 июля 2011 г.
HHS и штаты предпринимают шаги по созданию бирж доступного страхования, предоставляя американцам те же возможности выбора страхования, что и члены Конгресса — открывается в новом окне - 12 августа 2011 г.

HHS, Казначейство предпринимает новые шаги, чтобы помочь штатам создать биржи доступного страхования — открывается в новом окне
Гранты для первых новаторов
Пресс-релизы
- 29 октября 2010 г.
HHS объявляет о новых конкурсных грантах «Ранним новаторам» для штатов, которые лидируют в гонке за разработку ИТ-систем для государственных бирж – открывается в новом окне 907:25 - 16 февраля 2011 г.
Штаты лидируют в реализации: HHS присуждает гранты «Ранним инноваторам» семи штатам — открывается в новом окне
Системы информационных технологий
Выпуски новостей
- 3 ноября 2010 г.
HHS объявляет о новой федеральной поддержке штатов в разработке и обновлении ИТ-систем Medicaid и систем для регистрации в программах обмена штатов — открывается в новом окне
Государственные инновации
Пресс-релизы
- 10 марта 2011 г.
Администрация Обамы предпринимает новые шаги для поддержки инноваций и расширения прав и возможностей государств – открывается в новом окне
Реформы рынка здравоохранения
Письма
- 14 ноября 2013 г.

Письмо уполномоченным по страхованию о переходной политике рынка (PDF) - 16 июля 2014 г.
Письмо Виргинским островам об определении государства (PDF)
Письмо Северным Марианским островам об определении государства (PDF)
Письмо Гуаму об определении государства (PDF)
Письмо Американскому Самоа об определении государства (PDF)
Письмо Пуэрто-Рико об определении государства (PDF) - 8 марта 2018 г.
Письмо губернатору штата Айдахо и директору Департамента страхования о бюллетене штата Айдахо № 18-01 (PDF) - 27 июня 2022 г.
Письмо эмитентам и планам доступа к покрытию противозачаточными средствами (PDF)
Годовые лимиты
Выпуски новостей
- 9 декабря, 2010 г.
Закон о доступном медицинском обслуживании повышает прозрачность планов «мини-мед» для потребителей — открывается в новом окне
Страхование для молодежи
Письма
- 24 сентября 2010 г.

Письмо Секретаря Себелиуса в Планы медицинского страхования Америки относительно доступа детей к медицинскому страхованию (PDF – 234 КБ) (PDF)
Письмо от Ассоциация Cross and Blue Shield в отношении доступа детей к медицинскому страхованию (PDF – 255 КБ) (PDF) 907:25 - 13 октября 2010 г.
Письмо Секретаря Себелиуса Джейн Л. Клайн относительно политики только для детей (PDF – 214 КБ) (PDF)
Устаревшие планы
Письма
- 12 апреля 2010 г.
Письмо секретаря HHS Себелиуса в Национальную ассоциацию уполномоченных по страхованию (NAIC).
Коэффициент медицинских потерь
Письма
- 12 апреля 2010 г.
Сводное заявление – Секретарская переписка относительно NAIC – открывается в новом окне
Пресс-релизы
- 22 ноября 2010 г.
Новое правило Закона о доступном медицинском обслуживании дает потребителям более выгодную стоимость страховых взносов – открывается в новом окне
Обзор страховых тарифов
Письма
- 7 июня 2010 г.

Секретарь HHS Себелиус Письмо губернаторам и уполномоченным штата по страхованию с объявлением о начале первого раунда грантов на пересмотр страховых премий медицинского страхования (PDF KB23) (PDF) 907:25 - 18 октября 2010 г.
Письмо HHS/OCIIO в Департамент страхования штата Коннектикут о повышении страховой ставки страховой компанией Anthem (PDF – 45 КБ) (PDF) - 21 декабря 2010 г.
Письмо секретаря HHS Себелиуса уполномоченным по страхованию относительно пересмотра ставок премий (PDF) - 21 июля 2015 г.
Письмо HHS/CCIIO уполномоченным по страхованию о пересмотре ставок (PDF)
Пресс-релизы
- 16 августа 2010 г.
Гранты в размере 46 миллионов долларов США для помощи штатам в борьбе с необоснованным повышением страховых взносов – открывается в новом окне 907:25 - 21 декабря 2010 г.
Новые правила Закона о доступном медицинском обслуживании проливают свет на высокие ставки медицинского страхования — открывается в новом окне - 24 февраля 2011 г.

Штаты могут подать заявку на выделение почти 200 миллионов долларов США для борьбы с повышением страховых взносов — открывается в новом окне - 19 мая 2011 г.
Закон о доступном медицинском обслуживании помогает бороться с необоснованным увеличением страховых взносов – открывается в новом окне
Планы медицинского страхования учащихся
Пресс-релизы
- 9 февраля 2011 г.
Новое правило гарантирует, что учащиеся получат медицинскую страховку в соответствии с Законом о доступном медицинском обслуживании — открывается в новом окне
Нефедеральные правительственные планы
Письма
- 5 июня 2020 г.
Письмо спонсорам нефедеральных правительственных планов в отношении руководства по COVID-19 (PDF)
Обновления
- 5 марта 2020 г. Информация, связанная с COVID–19 Страховое покрытие для отдельных лиц и малых групп 907:25
- 12 марта 2020 г.
 Часто задаваемые вопросы о покрытии основных медицинских пособий и коронавирусе (COVID-19)
Часто задаваемые вопросы о покрытии основных медицинских пособий и коронавирусе (COVID-19) - 18 марта 2020 г. Часто задаваемые вопросы о страховом покрытии плана катастроф и коронавирусной болезни 2019 (COVID-19)
- 24 марта 2020 г. Часто задаваемые вопросы о доступности и использовании услуг телемедицины через частное медицинское страхование в ответ на коронавирусную болезнь 2019 г. (COVID-19)
- 24 марта 2020 г. Гибкие условия оплаты и льготного периода, связанные с COVID-19Национальная чрезвычайная ситуация
- 24 марта 2020 г. Часто задаваемые вопросы о лекарствах, отпускаемых по рецепту, и коронавирусной болезни 2019 (COVID-19) для эмитентов, предлагающих медицинское страхование на индивидуальном рынке и рынке малых групп
- 11 апреля 2020 г. Часто задаваемые вопросы о Законе о первом реагировании семей на коронавирус и о реализации Закона о помощи, помощи и экономической безопасности в связи с коронавирусом
* Этот документ был обновлен 15 апреля 2020 г. для исправления ошибки в сноске 10 относительно текущей даты окончания чрезвычайной ситуации в области общественного здравоохранения, связанной с COVID 19.
для исправления ошибки в сноске 10 относительно текущей даты окончания чрезвычайной ситуации в области общественного здравоохранения, связанной с COVID 19. - 13 апреля 2020 г. Отсрочка выплаты пособия за 2019 г. Проверка данных корректировки рисков, осуществляемая HHS (HHS-RADV)
Машинный перевод букв XVI века с латыни на немецкий
Лукас Фишер, Патрисия Шорер, Рафаэль Швиттер, Martin Volk
Abstract
В этом документе описывается наша работа по сбору обучающих данных и разработке системы латино-германского нейронного машинного перевода (NMT) для перевода писем 16-го века. В то время как латынь-немецкий является языковой парой с низким уровнем ресурсов с точки зрения NMT, область эпистолярной латыни 16-го века еще более ограничена в этом отношении. Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и в целом превосходит GoogleTranslate.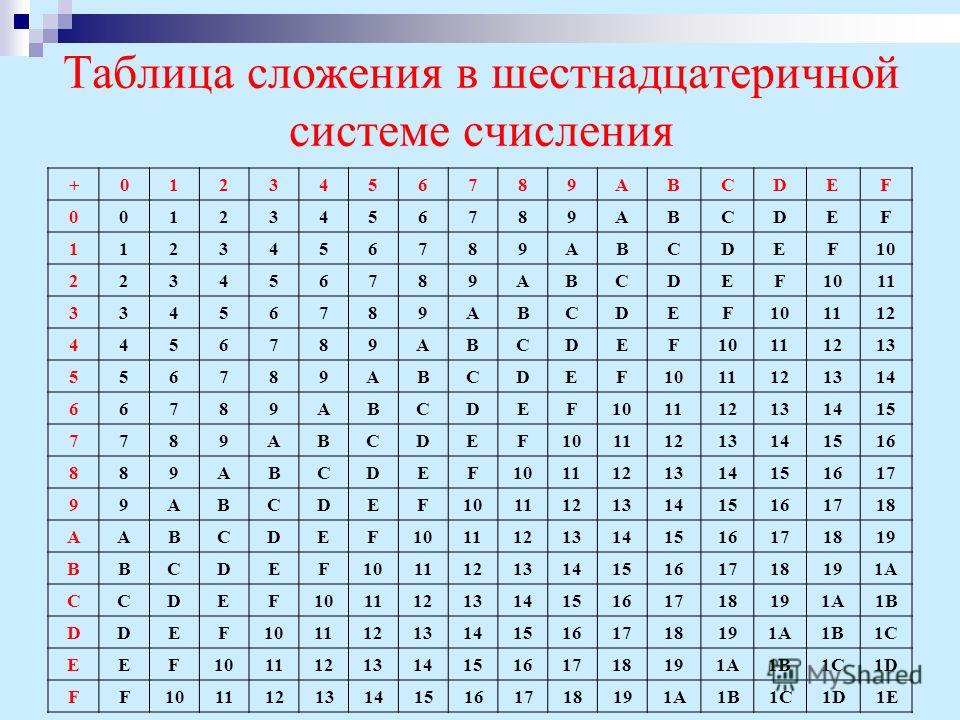 Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.
Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.- ID Антология:
- 2022.LT4HALA-1,7
- Том:
- Слушания второго семинара по языковым технологиям для исторических и древних языков
- Место
- Марсель, Франция
- Места проведения:
- LREC | LT4HALA
- SIG:
- Издатель:
- Европейская ассоциация языковых ресурсов
- Примечание:
- Pages:
- 43–50
- Language:
- URL:
- https://aclanthology.org/2022.lt4hala-1.7
- DOI:
- Bibkey:
- Cite (ACL):
- Лукас Фишер, Патрисия Шойрер, Рафаэль Швиттер и Мартин Фольк. 2022. Машинный перевод букв XVI века с латыни на немецкий. В материалах второго семинара по языковым технологиям для исторических и древних языков , , страницы 43–50, Марсель, Франция.
 Европейская ассоциация языковых ресурсов.
Европейская ассоциация языковых ресурсов. - Процитируйте (неофициально):
- Машинный перевод писем XVI века с латыни на немецкий (Fischer et al., LT4HALA 2022)
- Копия цитирования:
- PDF:
- https://aclanthology.org/2022.lt4hala-1.7.pdf
PDF Процитировать Поиск
- BibTeX
- MODS XML
- Конечная сноска
- Предварительно отформатировано
@inproceedings{fischer-etal-2022-machine,
title = "Машинный перевод писем 16-го века с {L}atin на {G}german",
автор = "Фишер, Лукас и
Шойрер, Патрисия и
Швиттер, Рафаэль и
Волк, Мартин»,
booktitle = "Материалы второго семинара по языковым технологиям для исторических и древних языков",
месяц = июнь,
год = "2022",
address = "Марсель, Франция",
издатель = "Европейская ассоциация языковых ресурсов",
url = "https://aclanthology.org/2022.lt4hala-1.7",
страницы = "43--50",
abstract = "В этом документе описывается наша работа по сбору обучающих данных и разработке системы нейронного машинного перевода с латинского{--}немецкого языка (NMT) для перевода букв 16-го века. В то время как латинский{--}немецкий язык является языковой парой с низким уровнем ресурсов с точки зрения NMT область эпистолярной латыни 16-го века еще более ограничена в этом отношении Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и превосходит GoogleTranslate в целом. Мы ориентируемся на переписку швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.",
}
В то время как латинский{--}немецкий язык является языковой парой с низким уровнем ресурсов с точки зрения NMT область эпистолярной латыни 16-го века еще более ограничена в этом отношении Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и превосходит GoogleTranslate в целом. Мы ориентируемся на переписку швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.",
}
<моды> <информация о заголовке> Машинный перевод букв XVI века с латыни на немецкий <название типа="личное">Лукас Фишер <роль>автор <название типа="личное">Патриция Шёрер <роль>автор <название типа="личное">Рафаэль Швиттер <роль>автор <название типа="личное">Мартин Фолк <роль>автор <информация о происхождении>2022-06 текст <информация о заголовке> Материалы второго семинара по языковым технологиям для исторических и древних языков <информация о происхождении>Европейская ассоциация языковых ресурсов <место>Марсель, Франция публикация конференции В этом документе описывается наша работа по сбору обучающих данных и разработке системы латино-немецкого нейронного машинного перевода (NMT) для перевода писем 16-го века. В то время как латынь-немецкий является языковой парой с низким уровнем ресурсов с точки зрения NMT, область эпистолярной латыни 16-го века еще более ограничена в этом отношении. Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и в целом превосходит GoogleTranslate. Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.
fischer-etal-2022-machine <местоположение>https://aclanthology.org/2022.lt4hala-1.7 <часть> <дата>2022-06 <единица экстента="страница">43 <конец>50
%0 Материалы конференции %T Машинный перевод букв XVI века с латыни на немецкий %A Фишер, Лукас % А Шойер, Патрисия %A Швиттер, Рафаэль %А Волк, Мартин %S Материалы второго семинара по языковым технологиям для исторических и древних языков %D 2022 %8 июня %I Европейская ассоциация языковых ресурсов %C Марсель, Франция %F fischer-etal-2022-машина %X В этом документе описывается наша работа по сбору обучающих данных и разработке системы латино-немецкого нейронного машинного перевода (NMT) для перевода писем 16-го века.В то время как латынь-немецкий является языковой парой с низким уровнем ресурсов с точки зрения NMT, область эпистолярной латыни 16-го века еще более ограничена в этом отношении. Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и в целом превосходит GoogleTranslate. Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени. %U https://aclanthology.org/2022.lt4hala-1.7 %Р 43-50
Markdown (неофициальный)
[Машинный перевод писем XVI века с латыни на немецкий] (https://aclanthology.org/2022.lt4hala-1.7) (Fischer et al., LT4HALA 2022)
- Машинный перевод Письма XVI века с латыни на немецкий (Fischer et al., LT4HALA 2022)
ACL
- Лукас Фишер, Патрисия Шойрер, Рафаэль Швиттер и Мартин Фольк. 2022. Машинный перевод букв XVI века с латыни на немецкий.
 In Материалы второго семинара по языковым технологиям для исторических и древних языков г., страницы 43–50, Марсель, Франция. Европейская ассоциация языковых ресурсов.
In Материалы второго семинара по языковым технологиям для исторических и древних языков г., страницы 43–50, Марсель, Франция. Европейская ассоциация языковых ресурсов.
Чикагское руководство по стилю, 17-е издание // Purdue Writing Lab
Резюме:
В этом разделе содержится информация о Чикагском руководстве по стилю (CMOS) методе форматирования и цитирования документов. Эти ресурсы соответствуют семнадцатому изданию Чикагского руководства по стилю (17-е издание), которое было выпущено в 2017 году.
Обратите внимание, что хотя эти ресурсы отражают самые последние обновления в1546 Чикагское руководство по стилю (17 -е издание ), касающееся методов документирования, вы можете просмотреть полный список обновлений, касающихся использования, технологий, профессиональной практики и т. д., по адресу The Chicago Manual of Style Online .
Введение Чикагское руководство по стилю (CMOS) охватывает множество тем, от подготовки и публикации рукописей до грамматики, использования и документации, и поэтому его с любовью называют «библией редактора».
Материал на этой странице посвящен в основном одному из двух стилей документации CMOS: Системе заметок и библиографии (NB) , которая используется теми, кто работает в области литературы, истории и искусства. Другой стиль документации, система «автор-дата», почти идентичен по содержанию, но немного отличается по форме, и его предпочитают те, кто работает в области социальных наук.
Хотя обе системы передают всю важную информацию о каждом источнике, они различаются не только тем, как они направляют читателей к этим источникам, но и их форматированием (например, положением дат в записях цитирования). ). Примеры того, как эти стили цитирования работают в научных статьях, см. в наших образцах статей:
Образец статьи с датой автора
Образец статьи NB
В дополнение к справке Чикагского руководства по стилю (17-е издание) для получения дополнительной информации учащимся также может быть полезно ознакомиться с Руководством Кейт Л.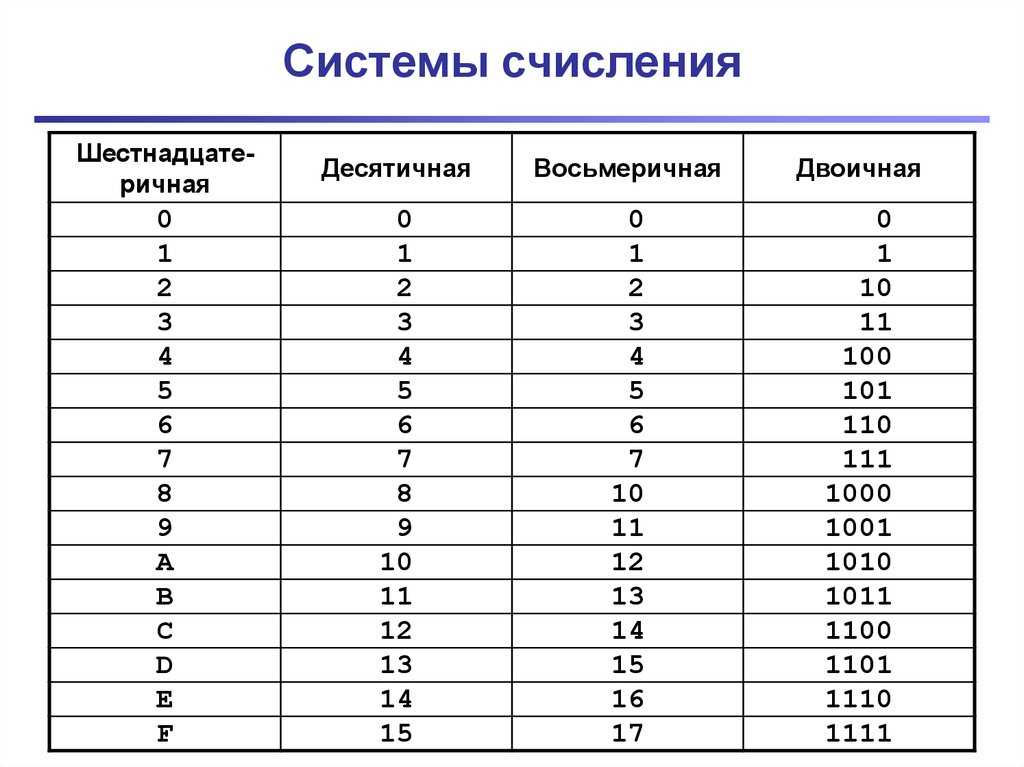 Турабян для писателей Научные статьи, тезисы и диссертации (8-е издание). Это руководство, в котором представлен так называемый стиль цитирования «Турабиан», следует двум шаблонам документации CMOS, но предлагает небольшие модификации, подходящие для студенческих текстов.
Турабян для писателей Научные статьи, тезисы и диссертации (8-е издание). Это руководство, в котором представлен так называемый стиль цитирования «Турабиан», следует двум шаблонам документации CMOS, но предлагает небольшие модификации, подходящие для студенческих текстов.
Система чикагских примечаний и библиографии (NB) часто используется в гуманитарных науках, чтобы предоставить писателям систему для ссылки на свои источники с помощью сносок, концевых сносок, и с помощью библиографии. Это предлагает авторам гибкие возможности для цитирования и дает возможность комментировать эти источники, если это необходимо. Надлежащее использование системы примечаний и библиографии укрепляет доверие к автору, демонстрируя его ответственность перед исходным материалом. Кроме того, это может защитить писателей от обвинений в плагиате, то есть в преднамеренном или случайном использовании исходного материала, созданного другими, без указания в титрах.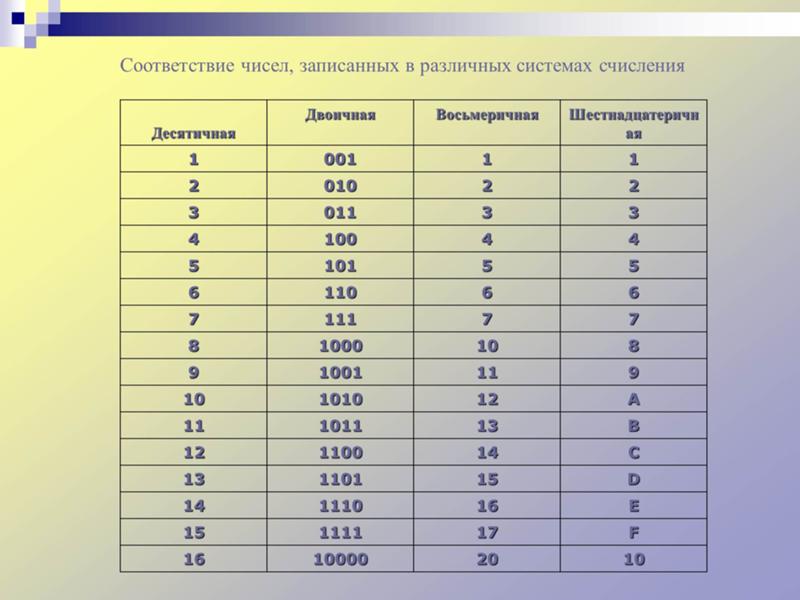
В системе примечаний и библиографии вы должны включать примечание (концевую или сноску) каждый раз, когда используете источник, будь то прямая цитата, парафраз или резюме. Сноски добавляются в конце страницы, на которой есть ссылка на источник, а концевые сноски составляются в конце каждой главы или в конце всего документа.
В любом случае номер надстрочного индекса, соответствующий примечанию, вместе с библиографической информацией об этом источнике должен быть помещен в тексте после конца предложения или пункта, в котором содержится ссылка на источник.
Если работа включает библиографию, что обычно является предпочтительным, то нет необходимости указывать в примечаниях полную информацию о публикации. Однако, если библиография не прилагается к работе, первое примечание для каждого источника должно включать всю необходимую информацию об источнике: полное имя автора, название источника и факты публикации. Если вы снова цитируете тот же источник или если в работу включен библиографический список, в примечании необходимо указать только фамилию автора, сокращенную форму заглавия (если оно состоит более чем из четырех слов) и номер(а) страницы(ов).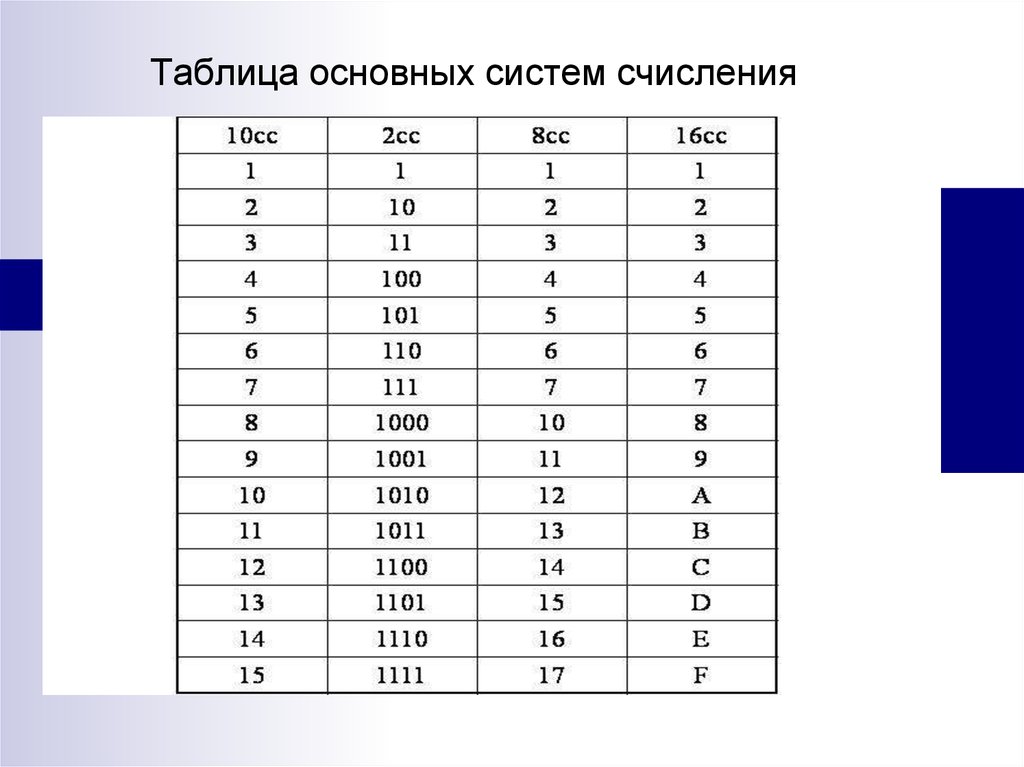 ). Однако в работе, не содержащей библиографии, рекомендуется повторять полную цитату при первом ее использовании в новой главе.
). Однако в работе, не содержащей библиографии, рекомендуется повторять полную цитату при первом ее использовании в новой главе.
В отличие от более ранних выпусков CMOS, если вы цитируете один и тот же источник два или более раз подряд, CMOS рекомендует использовать сокращенные ссылки. В работе с библиографией в первой ссылке следует использовать сокращенную цитату, которая включает имя автора, название источника и номер(а) страницы, а последовательные ссылки на одну и ту же работу могут не указывать название источника и просто включать автора. и номер страницы. Хотя CMOS не рекомендует, но если вы цитируете один и тот же источник и номера страниц из одного источника два или более раз подряд, также можно использовать слово «там же» (от латинского ibidem, что означает «в там же») в качестве соответствующего примечания. Если вы используете тот же источник, но рисуете с другой новой страницы, в соответствующем примечании следует использовать «Там же». запятая и новые номера страниц.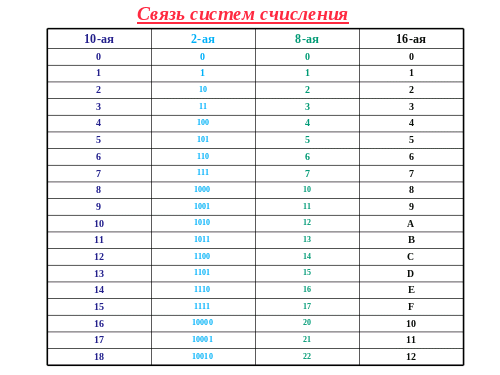
В системе NB сноска или концевая сноска начинается с соответствующего полноразмерного номера, за которым следует точка и затем пробел.
Введение в библиографииВ системе NB библиография представляет собой алфавитный список всех источников, использованных в данной работе. Эта страница, чаще всего озаглавленная «Библиография», обычно помещается в конце работы перед указателем. Он должен включать все источники, цитируемые в работе, и иногда может включать другие соответствующие источники, которые не были процитированы, но содержат дополнительную информацию.
Хотя библиографические записи для разных источников могут иметь различный формат, все включенные источники (книги, статьи, веб-сайты и т. д.) расположены в алфавитном порядке по фамилии автора. Если автор или редактор не указаны, можно использовать название или, в крайнем случае, описательную фразу.
Библиография полезна, но не требуется в работах, которые содержат полную библиографическую информацию в примечаниях.
Общие элементы
Все записи в библиографии будут включать автора (или редактора, составителя, переводчика), название и информацию о публикации.
Имена авторов
Имя автора в библиографии инвертируется, фамилия ставится на первое место, а фамилия и имя разделяются запятой; например, Джон Смит становится Смитом, Джоном.
Названия
Названия книг и журналов выделены курсивом. Названия статей, глав, стихотворений и т.п. заключаются в кавычки.
Информация о публикации
Год публикации указан после названия издателя или журнала.
Пунктуация
В библиографии все основные элементы разделены точками.
Дополнительную информацию и конкретные примеры см. в разделах Книги и Периодические издания.
Обратите внимание, что этот ресурс OWL предоставляет основную информацию о форматировании записей, используемых в библиографии. Для получения дополнительной информации об избранных библиографиях, аннотированных библиографиях и библиографических эссе см. главу 14.61 Чикагского руководства по стилю 9.0005 (17-е издание).
Для получения дополнительной информации об избранных библиографиях, аннотированных библиографиях и библиографических эссе см. главу 14.61 Чикагского руководства по стилю 9.0005 (17-е издание).
Шестнадцатеричные (по основанию 16) числа — катализатор2
Последнее обновление:
В своей статье о числах по основанию 2 (двоичным) я говорил о разнице между десятичными (по основанию 10) числами мы используем в нашей повседневной жизни и числа с основанием 2. В этой статье рассматриваются шестнадцатеричные числа (с основанием 16). Понимание системы base-16 имеет решающее значение для понимания адресов IPv6.
Сводка по основанию 10 и 2
В качестве краткого обзора, десятичная система использует десять цифр: от 0 до 9. Конечно, вы можете считать больше 9. Для этого вы просто используете более одной цифры. Итак, чтобы пройти дальше 9, вы меняете значение на 0 и добавляете 1 слева. Это дает вам число 10.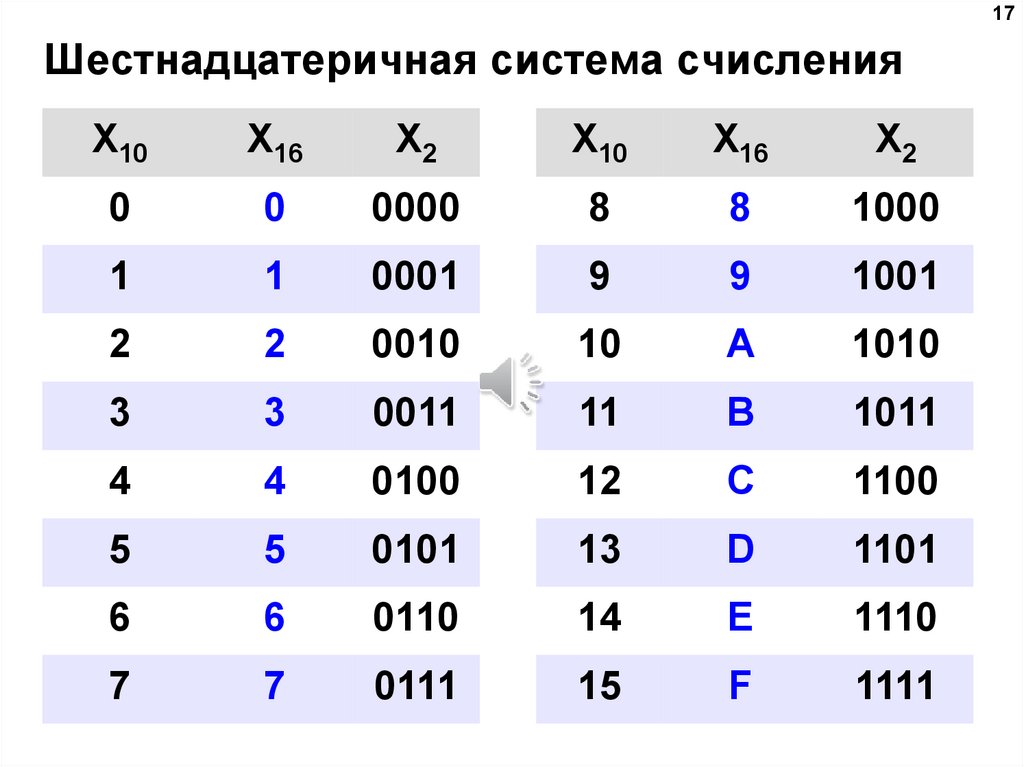
Система с основанием 2 имеет только два значения: 0 и 1. Чтобы представить число больше 1, вы снова используете более одной цифры. Чтобы получить число 2, вы меняете число на 0 и ставите перед ним 1. Итак, в базе 2 число 2 записывается как 10.
База-16
База-16 использует 16 значений: числа от 0 до 9и буквы от A до F. До числа 9 десятичная и шестнадцатеричная системы идентичны: число 9 с основанием 10 также является 9 в основании 16. У нас нет единого числа для десяти, поэтому в базе 16 используются буквы от A до F. Буква A равна 10, B равна 11 и т. д. увеличены. Можете ли вы угадать, какое десятичное число 16 в базе 2 и базе 16?
База-10 | База-2 | База-16 ---------+--------+-------- 0 | 0 | 0 1 | 1 | 1 2 | 10 | 2 3 | 11 | 3 4 | 100 | 4 5 | 101 | 5 6 | 110 | 6 7 | 111 | 7 8 | 1000 | 8 9| 1001 | 9 10 | 1010 | А 11 | 1011 | Б 12 | 1100 | С 13 | 1101 | Д 14 | 1110 | Е 15 | 1111 | Ф
Для обоих вам нужно изменить число на 0 и добавить 1 слева. Представление десятичного числа 15 по основанию 2 равно 1111, поэтому 16 становится 10000. Точно так же буква F является наибольшим значением в основании 16. Таким образом, следующим значением становится 10.
Представление десятичного числа 15 по основанию 2 равно 1111, поэтому 16 становится 10000. Точно так же буква F является наибольшим значением в основании 16. Таким образом, следующим значением становится 10.
Преобразование шестнадцатиричного числа в десятичное
Приведенная выше таблица удобна, но она не поможет вам преобразовать большие числа с основанием 16 в основание 10. Конечно, есть формула для преобразования основания 16 в основание 10. Для каждого шестнадцатеричного символа вам необходимо вычислить десятичное значение, а затем сложить итог. Чтобы вычислить отдельные десятичные значения, вы работаете справа налево. Самое правое шестнадцатеричное значение умножается на 16 0 , следующий по 16 1 и так далее.
Это немного абстрактно, поэтому давайте рассмотрим несколько примеров. Начнем с внесения изменений в приведенную выше таблицу. Все значения base-16 имеют только один символ. Итак, формула представляет собой просто число с основанием 16, умноженное на 16 0 . Поскольку 16 * 0 равно 0, значения не меняются:
Поскольку 16 * 0 равно 0, значения не меняются:
Base-10 | База-16 в базу-10 ---------+------------------------ 0 | 0 х 16 0 = 0 1 | 1 х 16 0 = 1 2 | 2 х 16 0 = 2 3 | 3 х 16 0 = 3 4 | 4 х 16 0 = 4
Стоит отметить, что «нулевая степень» всегда возвращает 1, а не 0, как можно было бы ожидать (почему я рассказываю в своей статье о числах с основанием 2). Таким образом, мы просто умножаем самое правое значение на 1.
Далее, давайте посмотрим на число 10 с основанием 16. Теперь у нас есть два значения: 1 и 0. Чтобы преобразовать шестнадцатеричное число, мы начинаем с правого- наибольшее значение и умножьте его на 16 0 . Это дает нам ноль, так как 0 * 1 ничему не равно. Далее мы берем 1 и умножаем на 16 1 . Это возвращает 16, поэтому шестнадцатеричное число 10 преобразуется в десятичное число 16 (16 + 0 = 16).
Вы можете написать расчет следующим образом:
(1x16 1 ) + (0x16 0 ) = 16
Или вам может показаться более читаемым:
1 x 16 1 16
0 х 16 0 0
----
База-10 16
Если это имеет смысл, то мы можем попробовать что-то более сложное: преобразование ACDC в десятичном виде. Для этого вы выполняете ту же магию. Вы начинаете с самого правого значения ( D , что является десятичным числом 12) и продвигаетесь влево:
Для этого вы выполняете ту же магию. Вы начинаете с самого правого значения ( D , что является десятичным числом 12) и продвигаетесь влево:
10 x 16 3 = 10 x 4096 = 40960
12 х 16 2 = 12 х 256 = 3072
13 х 16 1 = 13 х 16 = 208
12 х 16 0 = 12 х 1 = 12
-----
База-10 44252
Преобразование числа с основанием 10 в число 16
Преобразование числа с основанием 10 в шестнадцатеричное работает так же, как преобразование числа с основанием 10 в двоичное число. Вы делите число на показатель степени (16) и продолжаете делить результат до тех пор, пока частное не станет равным 0. На каждом шаге вы умножаете остаток на 16, чтобы получить шестнадцатеричное значение.
Как всегда, проще всего объяснить это на нескольких примерах. Давайте переработаем десятичное число 44252 и проверим, переводится ли оно в ACDC :
Частное | 16 * Остаток | Шестнадцатеричный
------------------------------+----+ -----
44252/16 = 2765,75 (2765) | 16 * 0,75 = 12 | С
2765/16 = 172,8125 (172) | 16 * 0,8125 = 13 | Д
172 / 16 = 10,75 (10) | 16 * 0,75 = 12 | С
10/16 = 0,625 (0) | 16 * 0,625 = 10 | А
Последним шагом является объединение шестнадцатеричных значений, начиная с последнего значения. Итак, это дает нам ACDC .
Итак, это дает нам ACDC .
Еще один пример: тот же рецепт работает для десятичного числа 16 :
Частное | 16 * Остаток | Шестнадцатеричный
------------------------------+----+ -----
16/16 = 1,0 (1) | 16 * 0 = 0 | 0
1/16 = 0,0625 (0) | 16 * 0,0625 = 1 | 1
Преобразование базы 2 в базу 16
Конечно, вы также можете конвертировать из двоичного в шестнадцатеричный и наоборот. Чтобы преобразовать базу 2 в базу 10, вы разбиваете двоичное значение на блоки из четырех цифр (известные как полубайта ), а затем ищете шестнадцатеричное значение для каждого блока. Чтобы найти шестнадцатеричные значения, вы можете обратиться к слегка измененной таблице base-2, 10 и 16:
Base-10 | База-2 | База-16 ---------+--------+-------- 0 | 0000 | 0 1 | 0001 | 1 2 | 0010 | 2 3 | 0011 | 3 4 | 0100 | 4 5 | 0101 | 5 6 | 0110 | 6 7 | 0111 | 7 8 | 1000 | 8 9| 1001 | 9 10 | 1010 | А 11 | 1011 | Б 12 | 1100 | С 13 | 1101 | Д 14 | 1110 | Е 15 | 1111 | Ф
Единственная разница с таблицей, которую я показал ранее, заключается в том, что все числа с основанием 2 теперь состоят из четырех цифр (т.






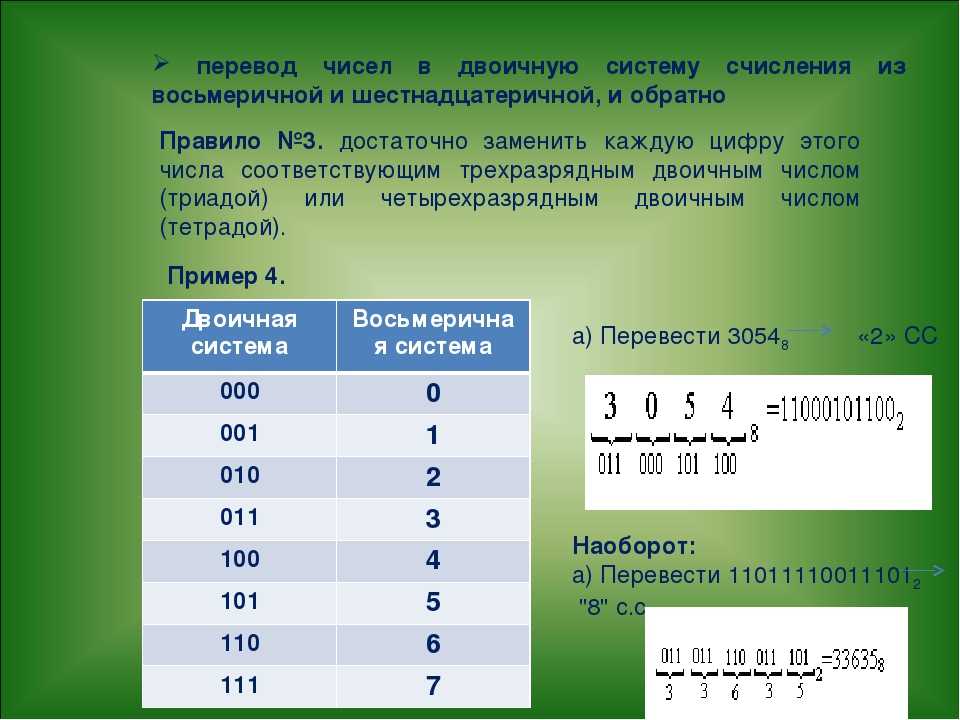
 ..
..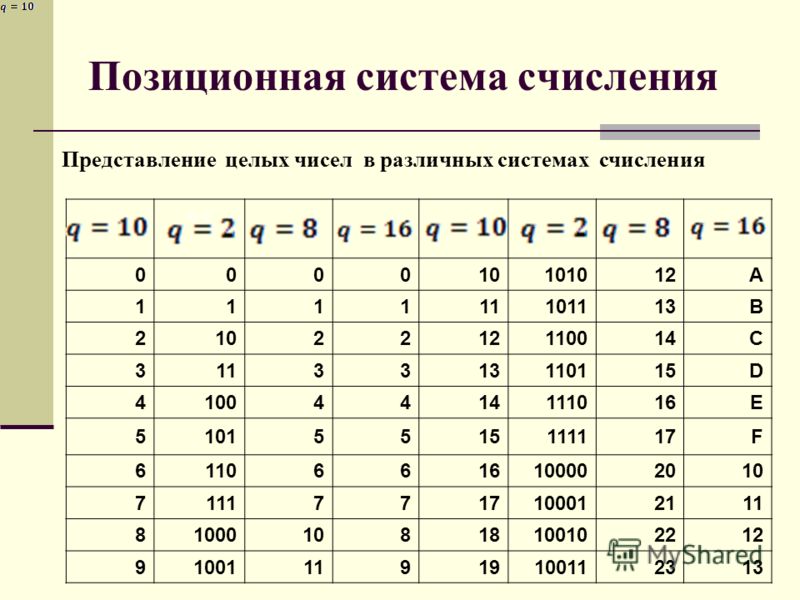 Старший на 11 лет старше. В каком классе учится старший брат:
Старший на 11 лет старше. В каком классе учится старший брат: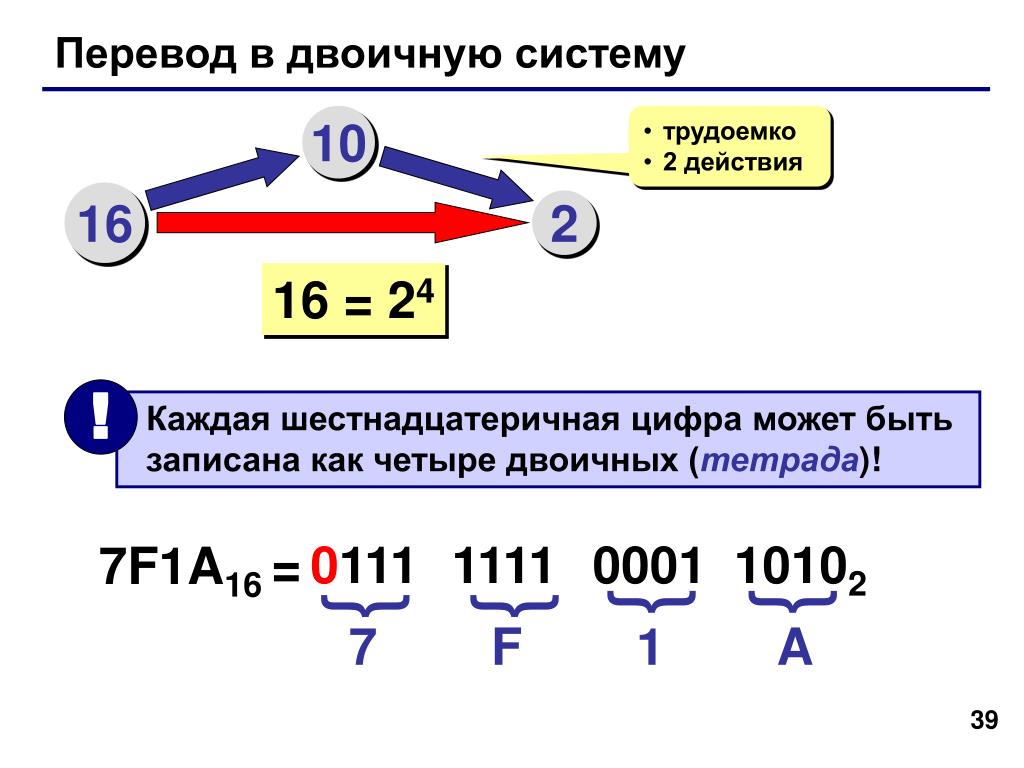 Старший на 10 лет старше. В каком классе учится старший брат:
Старший на 10 лет старше. В каком классе учится старший брат: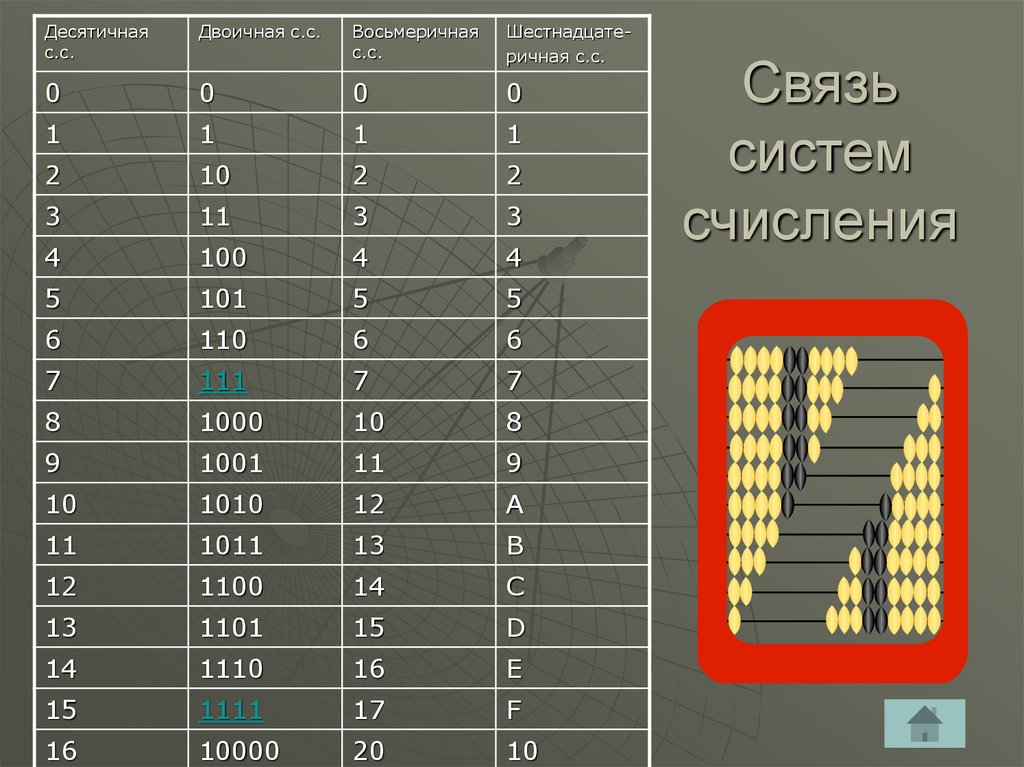

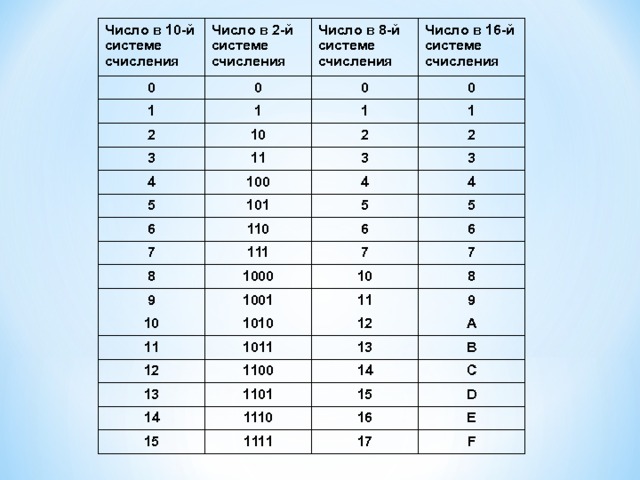
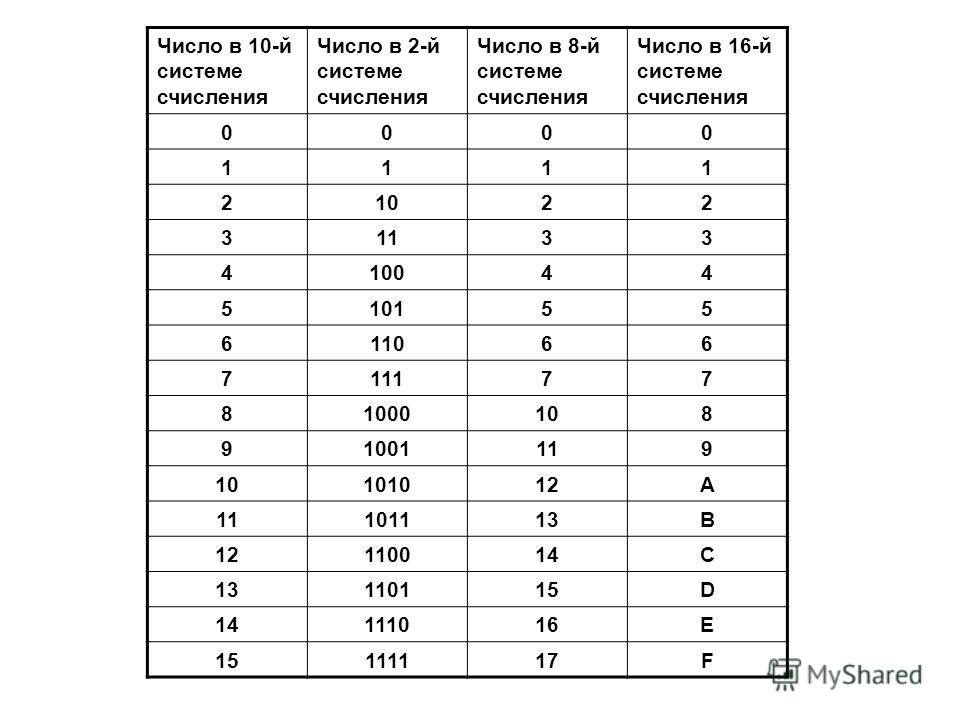
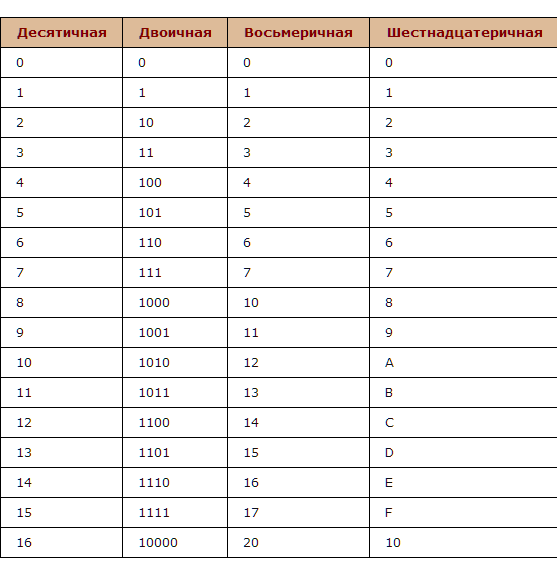

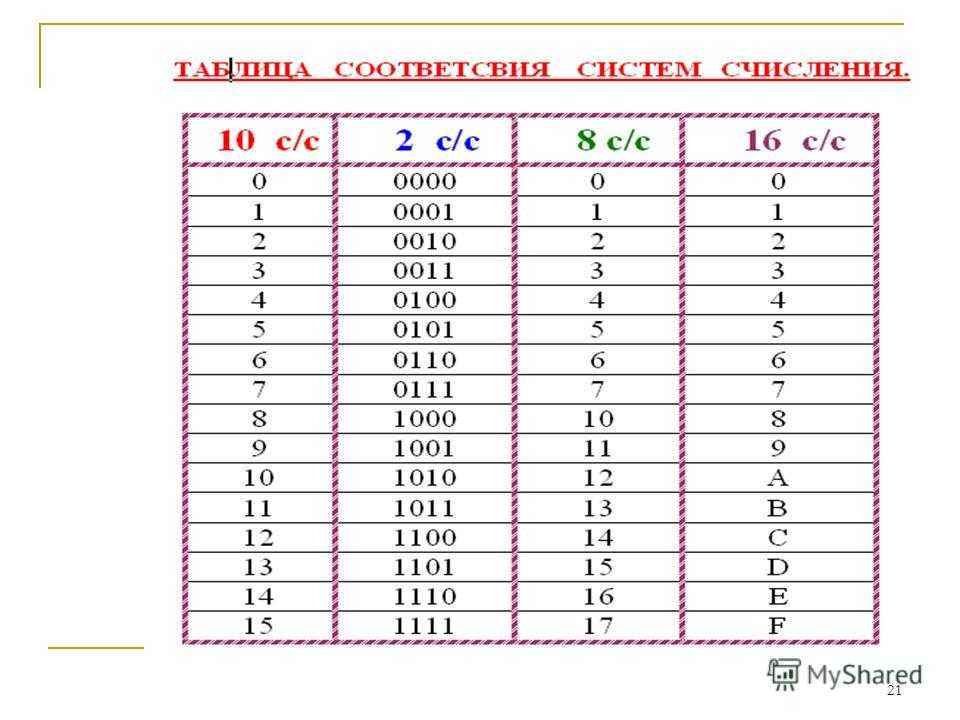
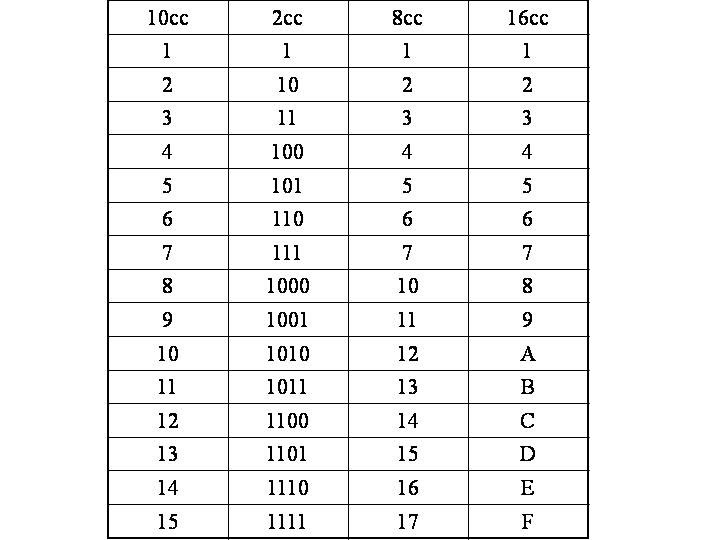 (PDF — 80 КБ) (PDF)
(PDF — 80 КБ) (PDF)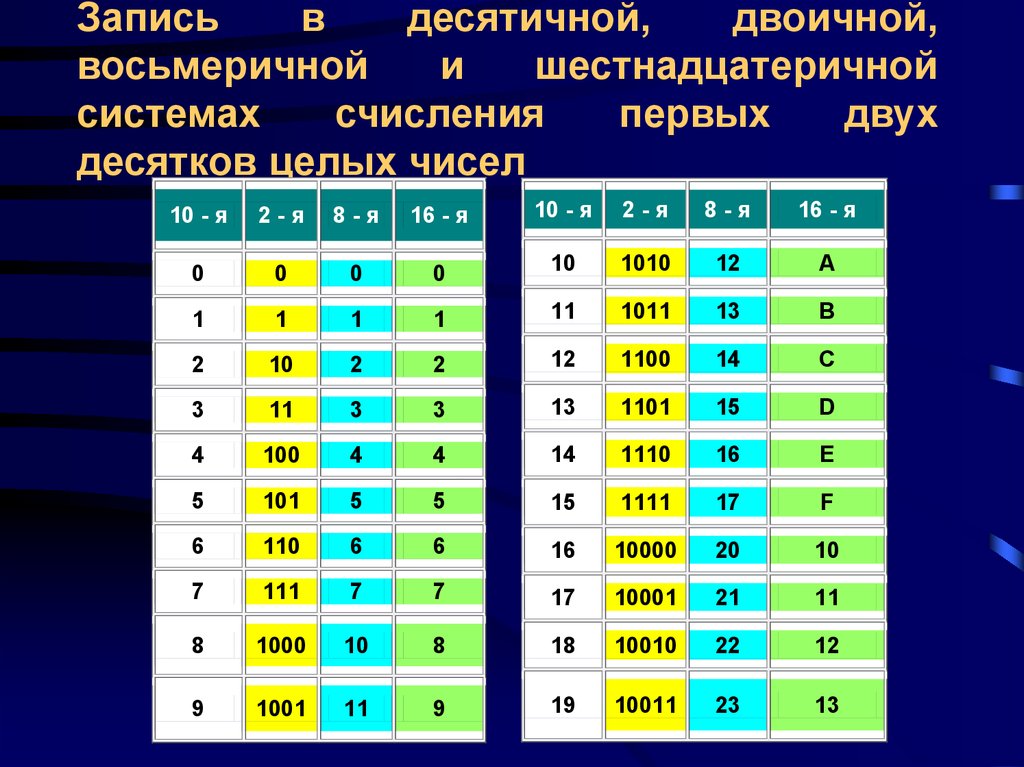
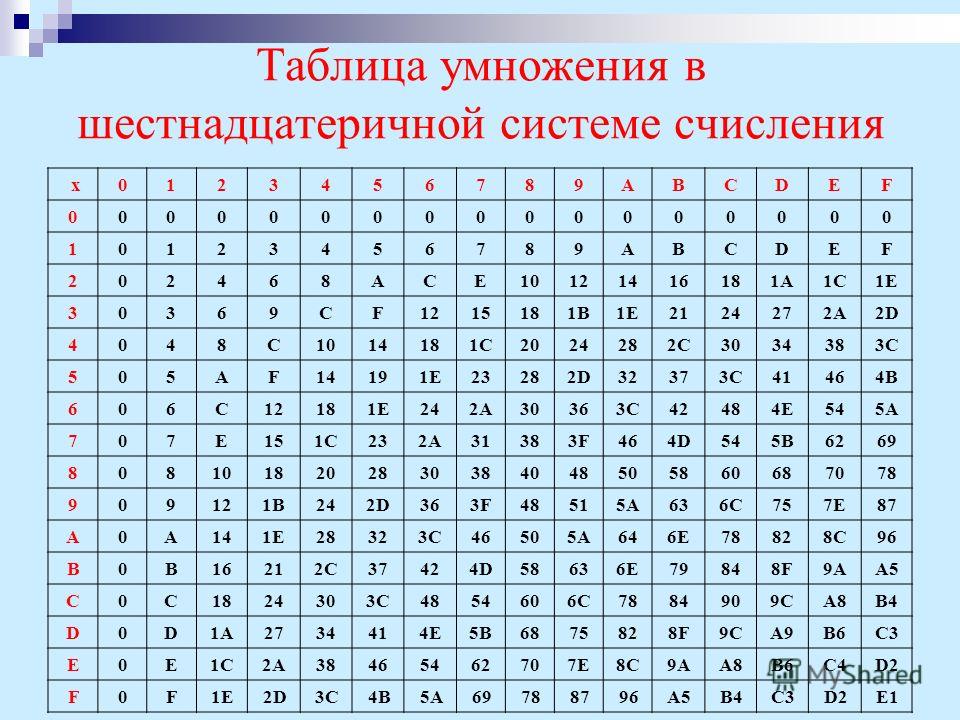

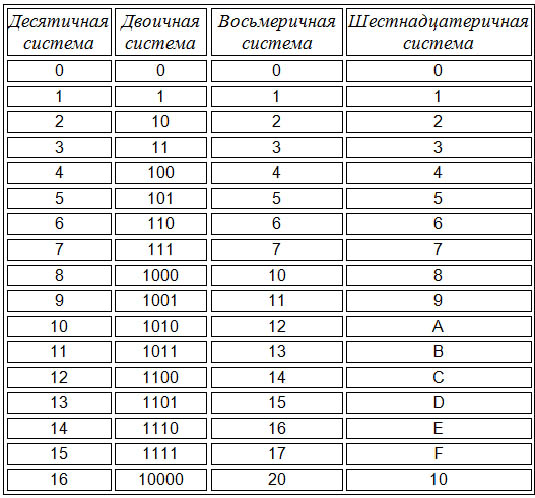


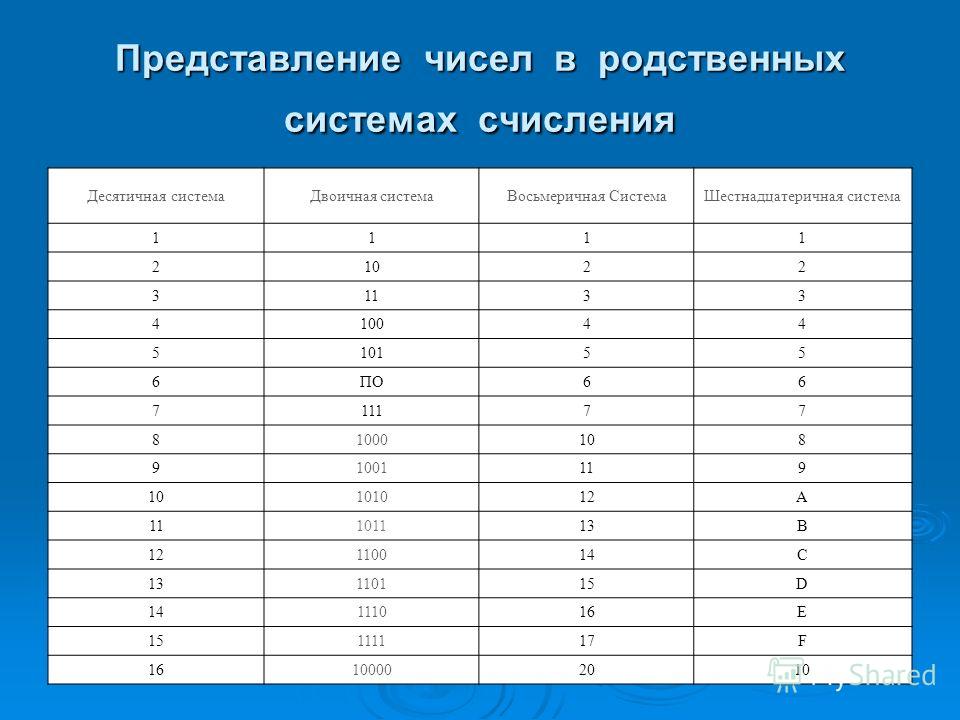

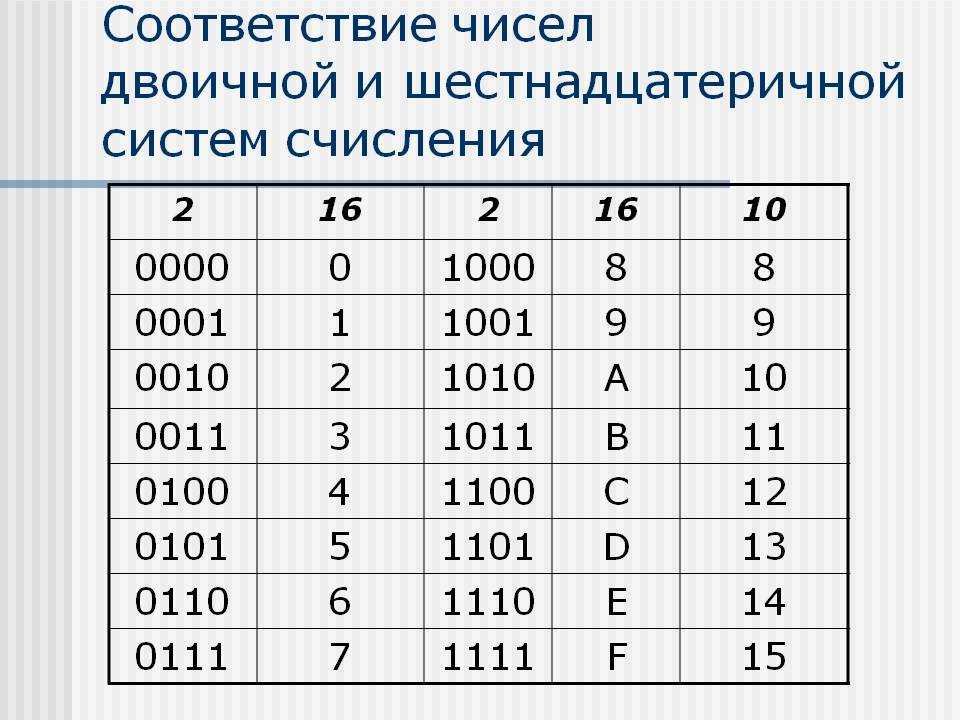
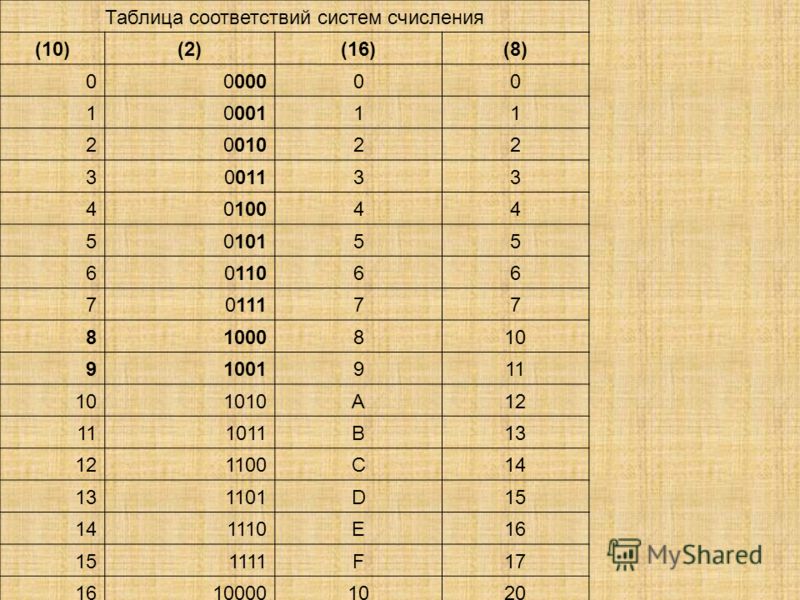
 Часто задаваемые вопросы о покрытии основных медицинских пособий и коронавирусе (COVID-19)
Часто задаваемые вопросы о покрытии основных медицинских пособий и коронавирусе (COVID-19) для исправления ошибки в сноске 10 относительно текущей даты окончания чрезвычайной ситуации в области общественного здравоохранения, связанной с COVID 19.
для исправления ошибки в сноске 10 относительно текущей даты окончания чрезвычайной ситуации в области общественного здравоохранения, связанной с COVID 19.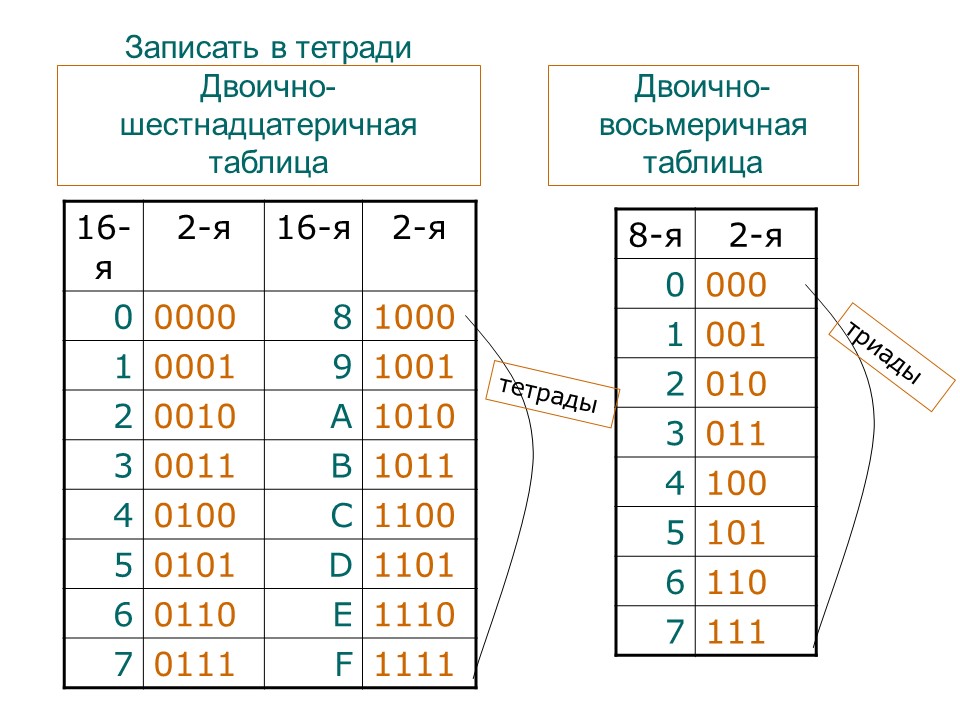 Европейская ассоциация языковых ресурсов.
Европейская ассоциация языковых ресурсов. В то время как латинский{--}немецкий язык является языковой парой с низким уровнем ресурсов с точки зрения NMT область эпистолярной латыни 16-го века еще более ограничена в этом отношении Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и превосходит GoogleTranslate в целом. Мы ориентируемся на переписку швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.",
}
В то время как латинский{--}немецкий язык является языковой парой с низким уровнем ресурсов с точки зрения NMT область эпистолярной латыни 16-го века еще более ограничена в этом отношении Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и превосходит GoogleTranslate в целом. Мы ориентируемся на переписку швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.",
}
 В то время как латынь-немецкий является языковой парой с низким уровнем ресурсов с точки зрения NMT, область эпистолярной латыни 16-го века еще более ограничена в этом отношении. Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и в целом превосходит GoogleTranslate. Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.
В то время как латынь-немецкий является языковой парой с низким уровнем ресурсов с точки зрения NMT, область эпистолярной латыни 16-го века еще более ограничена в этом отношении. Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и в целом превосходит GoogleTranslate. Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени. В то время как латынь-немецкий является языковой парой с низким уровнем ресурсов с точки зрения NMT, область эпистолярной латыни 16-го века еще более ограничена в этом отношении. Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и в целом превосходит GoogleTranslate. Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.
%U https://aclanthology.org/2022.lt4hala-1.7
%Р 43-50
В то время как латынь-немецкий является языковой парой с низким уровнем ресурсов с точки зрения NMT, область эпистолярной латыни 16-го века еще более ограничена в этом отношении. Благодаря нашим усилиям по сбору и генерации данных мы можем обучить модель NMT, которая обеспечивает хорошие переводы для коротких и средних предложений и в целом превосходит GoogleTranslate. Мы сосредоточимся на переписке швейцарского реформатора Генриха Буллингера, но наш параллельный корпус и наша система NMT будут полезны для многих других текстов того времени.
%U https://aclanthology.org/2022.lt4hala-1.7
%Р 43-50
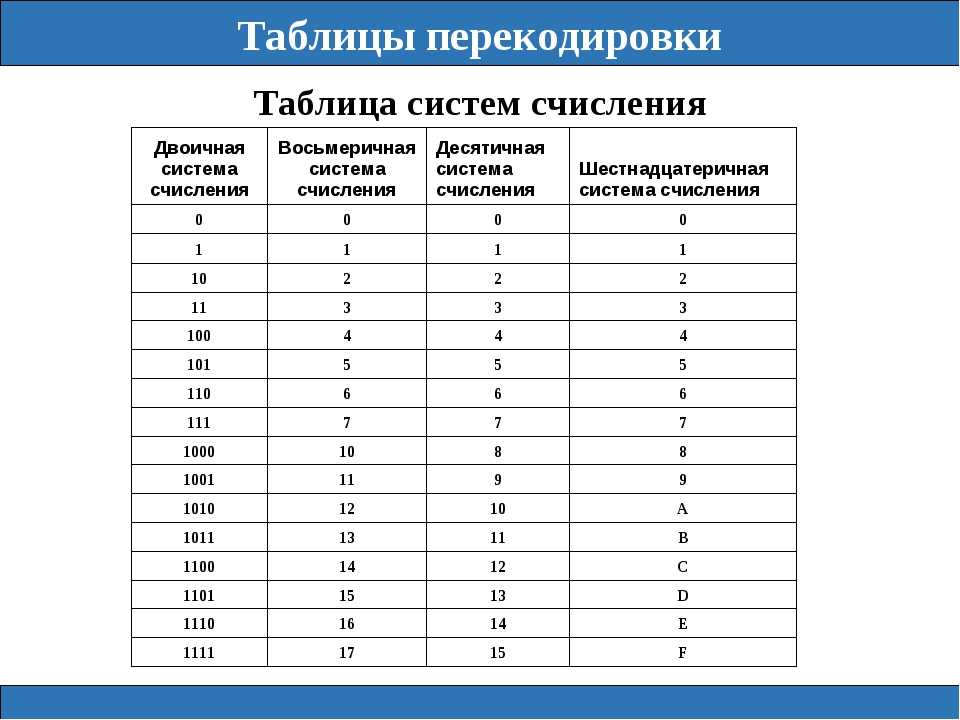 In Материалы второго семинара по языковым технологиям для исторических и древних языков г., страницы 43–50, Марсель, Франция. Европейская ассоциация языковых ресурсов.
In Материалы второго семинара по языковым технологиям для исторических и древних языков г., страницы 43–50, Марсель, Франция. Европейская ассоциация языковых ресурсов.