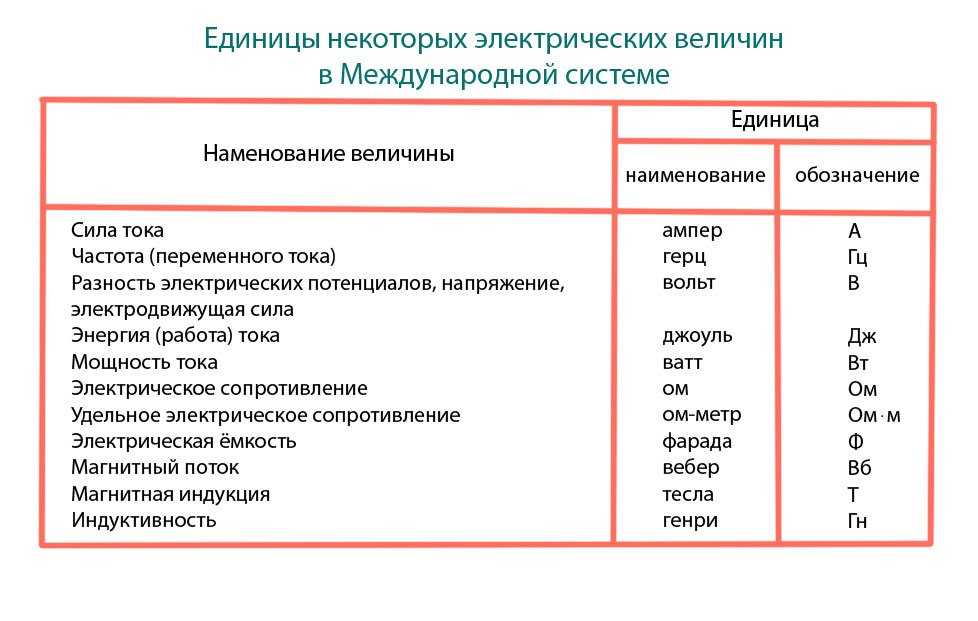
Мощность в физике — обозначение, формулы и примеры
Мощность Это величина, отображающая как быстро выполняется работа или как быстро энергия передается из одного места в другое или преображается из одного типа в другой.
В разных областях физики мощность принято обозначать разными символами, например в механике — N N N, в электротехнике — P P P, а также иногда W W W. Для нахождения величины мощности используют разные формулы:
P = △ E △ t P\;=\;\frac{\triangle E}{\triangle t} P=△t△E,
где P P P мощность, Δ E ΔE ΔE – изменение энергии, Δ t Δt Δt – изменение времени. Или другая интерпретация:
P = F v cos α P\;=\;Fv\cos\alpha P=Fvcosα,
в случае, если на тело, движущееся со скоростью v v v, действует определенная сила F F F, то она совершает работу. Мощность будет равна скалярному произведению силы на скорость, на косинус угла между ними.
Стандартная единица мощности – это ватт, обозначенный Вт (или W W W). Получила название в честь шотландского инженера-механика Джеймса Уатта.
Выходная мощность электрического оборудования, тостера или микроволновой печи, указывается в ваттах. Исходя из понятия мощности один ватт соответсвует одному джоулю работы, выполняемой за одну единицу времени.
Еще одна единица мощности, которая часто используется, особенно, в автомобильной индустрии: лошадиная сила.
Она обозначается сокращением л.с. и берет свое начало в XVII веке. С тех пор метрическая мощность была определена как мощность, необходимая для подъема массы 75 кг на расстояние 1 метр за 1 секунду.
Определение мощности
Допустим, нам необходимо убрать урожай пшеницы с поля площадью 100 га. Это можно сделать вручную или с помощью комбайна. Очевидно, что пока человек обработает 1 га площади, комбайн успеет сделать намного больше. В данном случае разница между человеком и техникой — именно то, что называют мощностью. Отсюда вытекает первое определение.
Мощность в физике — это количество работы, которая совершается за единицу времени. |
Рассмотрим другой пример: между точкой А и точкой Б расстояние 15 км, которое человек проходит за 3 часа, а автомобиль может проехать всего за 10 минут. Понятно, что одно и то же количество работы они сделают за разное время. Что показывает мощность в данном случае? Как быстро или с какой скоростью выполняется некая работа.
В электромеханике данная величина тоже связана со скоростью, а конкретно — с тем, как быстро передается ток по участку цепи. Исходя из этого, мы можем рассмотреть еще одно определение.
| Мощность — это скалярная физическая величина, которая характеризует скорость передачи энергии от системы к системе или скорость преобразования, изменения, потребления энергии. |
Напомним, что скалярными величинами называются те, значение которых выражается только числом (без вектора направления).
Мощность человека в зависимости от деятельности
| Вид деятельности | Мощность, Вт |
| Неспешная ходьба | 60–65 |
| Бег со скоростью 9 км/ч | 750 |
| Плавание со скоростью 50 м/мин | 850 |
| Игра в футбол | 930 |
Подводя итог
Итак, где в реальной жизни Вам могут понадобиться переводы из Вт в киловатты и наоборот:
- Умение применять такие простые расчёты в жизни поможет планировать траты на электричество;
- Знание единиц измерений поможет определить сечение провода для электрической проводки и выбрать подходящие защитные устройства;
- На разных приборах стоят разные значения, поэтому можно подогнать их к единому значению и суммировать.
- Такие знания просты и необходимы каждому человеку, поскольку такие измерения относятся к вычислениям по физике в классах средней школы.
Теперь Вы знаете, как правильно переводы Ватты в Киловатты, как сделать противоположное действие и зачем это нужно. Пусть физические величины не пугают Вас, ведь производить расчёты легко и интересно!
Как обозначается мощность: единицы измерения
В таблице выше вы увидели обозначение в ваттах, и читая инструкции к бытовой технике, можно заметить, что среди характеристик прибора обязательно указано количество ватт. Это единица измерения механической мощности, используемая в международной системе СИ. Она обозначается буквой W или Вт.
Измерение мощности в ваттах было принято в честь шотландского ученого Джеймса Уатта — изобретателя паровой машины. Он стал одним из родоначальников английской промышленной революции.
В физике принято следующее обозначение мощности: 1 Вт = 1 Дж / 1с.
Это значит, что за 1 ватт принята мощность, необходимая для совершения работы в 1 джоуль за 1 секунду.
В каких единицах еще измеряется мощность? Ученые-астрофизики измеряют ее в эргах в секунду (эрг/сек), а в автомобилестроении до сих пор можно услышать о лошадиных силах.
Интересно, что автором этой последней единицы измерения стал все тот же шотландец Джеймс Уатт. На одной из пивоварен, где он проводил свои исследования, хозяин накачивал воду для производства с помощью лошадей. И Уатт выяснил, что 1 лошадь за секунду поднимает около 75 кг воды на высоту 1 метр. Вот так и появилось измерение в лошадиных силах. Правда, сегодня такое обозначение мощности в физике считается устаревшим.
Одна лошадиная сила — это мощность, необходимая для поднятия груза в 75 кг за 1 секунду на 1 метр.
План урока «Работа и мощность электрического тока» | План-конспект по физике по теме:
План урока «Работа и мощность электрического тока»Тема: Работа и мощность электрического тока.
Цели урока:
Обучающая:
организовать деятельность по восприятию первоначального представления о понятии работа, мощность электрического тока
обобщение, систематизация и расширение знаний учащихся о работе и мощности электрического тока;
выявить уровень усвоения темы;
формирование навыков работы с компьютером для получения новых знаний по физике
Развивающая:
развитие логического мышления и аналитических способностей учащихся: сравнивать, сопоставлять, делать выводы по теме;
развитие творческого потенциала учащихся;
проверить уровень самостоятельного мышления обучающегося по применению имеющихся знаний в различных ситуациях.
Воспитывающая:
воспитание информационной культуры учащихся через работу с ЦОРами;
воспитание чувства долга и ответственности за собственные результаты в учебе;
воспитывать умение видеть физику вокруг себя.
Демонстрации: Измерение мощности и работы электрического тока
Тип урока: комбинированный
Вид урока: урок изучения нового материала
ТСО: компьютеры, мультимедиапроектор
ЦОРы: презентация
Ход урока
I этап. Орг. момент.
II этап. Повторение ранее изученного. :
1.Проверь свои знания по теме:
1) Дай определения понятиям: Электрический ток. Электрическое напряжение. Сила тока.
2) Найди правильные формулы.
Формулы электрических законов
Найди правильные формулы
Электрические явления
Выдели в ответе букву
Вопрос | Ответ | № буквы ответа |
Прибор для измерения напряжения | О | 2 буква: ____ |
Единица измерения мощности | Т | 3 буква:____ |
Единица измерения напряжения | Л | 3 буква:____ |
Металл, используемый в аккумуляторах | И | 3 буква: ____ |
Устройство для размыкания и замыкания цепи | Ч | 4 буква:____ |
Величина, характеризующая способность тела совершать работу | Н | 2 буква:____ |
Единица измерения сопротивления | О | 1 буква:____ |
Электрические цепи
Из каких элементов состоит данная электрическая цепь и способы соединения
3) Ответьте на вопросы:
В каких единицах измеряется сила тока?
Как называется прибор для измерения силы тока?
Как включают амперметр для измерения силы тока на участке цепи?
В каких единицах измеряется напряжение?
Как называется прибор для измерения напряжения?
Как включают вольтметр для измерения напряжения на участке цепи?
В каких единицах измеряют время в системе СИ?
Какая величина называется ценой деления прибора?
Как определить цену деления прибора?
III этап.
Изучение нового материала:
Чтобы определить работу электрического тока на каком либо участке цепи, надо напряжение на концах этого участка умножить на электрический заряд, прошедший по нему: A=Uq,
где A – работа, U – напряжение,q – электрический заряд.
Электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q=It.
Работа на участке цепи равна произведению силы тока, напряжения на концах этого участка и времени, в течение которого она совершалась: A=UIt,
где I – сила тока, U – напряжение, t –время.
Если ток проходит по неподвижному проводнику, то вся работа идет на нагревание проводника и, по закону сохранения энергии, Q=A .
Единица измерения работы: Джоуль. 1Дж=1А*с*В.
Мощность численно равна работе, совершенной в единицу времени: P=A/t.
Единица измерения мощности: Вт.
На большинстве приборов указана потребляемая ими мощность.
Мощность тока равна отношению работы за время t к этому интервалу времени: P=UIt/t=U I;
1 Ватт=1Вольт*1 Ампер, 1Вт=1В*А
1гВт=100Вт
1кВт=1000Вт,
1МВт=1000000Вт.
Мощность различных электрических устройств приведена в таблице 9 на стр.120 учебника.
Джеймс Прескотт Джоуль — английский физик.
24 декабря 1818 —11 октября 1889
Джоуль изучал природу тепла, и обнаружил её связь с механической работой. Это привело к теории сохранения энергии, что в свою очередь привело к разработке первого закона термодинамики. В честь Джоуля названа единица измерения энергии — джоуль., Открыл связь между током, текущем через проводник с определённым сопротивлением и выделяющемся при этом теплом, названный законом Джоуля.
IV этап. Закрепление пройденного материала.
1.Ответьте на вопросы:1).Что называют работой тока? 2). Что такое мощность тока? 3). В каких единицах выражается мощность тока? 4). В каких единицах выражается работа тока? 2.
Экспериментальная работа.
Измерение мощности и работы тока в электрической лампе
1)Измерьте вольтметром напряжение на лампе.
2)Измерьте амперметром силу тока.
3)Вычислите мощность тока в лампе.
4)Заметьте время включения и выключения лампы.
По времени его горения и мощности определите работу тока в лампе.
U (В) | I (А) | P = UI (Вт) | t(с) | A=Pt(Дж) |
3. Решение задач.
№1. Какую работу совершает электродвигатель за 1 ч, если сила тока в цепи электродвигателя 5 А, напряжение на его клеммах 220 В? КПД двигателя 80%.
№2.Сколько времени будет нагреваться 1,5 л воды от 20 до 100 градусов Цельсия в электрическом чайнике мощностью 600 Вт, если КПД чайника 80%?
V Этап. Подведение итогов урока.
Подводя итог уроку, предложить ученикам ответить на вопросы:
Два троллейбуса с одинаковыми электродвигателями движутся одновременно один с большей, другой с меньшей скоростью.
У какого из них работа электрического тока больше, если считать, что сопротивление и время движения в обоих случаях одинаковы?
Почему при работе на токарном или сверлильном станке с неправильно заточенным инструментом увеличивается расход электроэнергии?
VI Этап. Рефлексия.
Какую оценку вы бы поставили себе на уроке и почему?
VII Этап. Домашнее задание: Параграфы 50, 51. Упражнение 25.
Использованная литература:1. Перышкин А.В.. Физика. 8 кл.: Учеб. для общеобразоват. учреждений. -5-е изд., стереотип. – М.: Дрофа, 2003. – 192 с.: ил.
2. Марон А.Е. Физика. 8 класс: учебно-методическое пособие /А.Е.Марон, А.А.Марон.-4-е изд., стереотип.-М.:Дрофа,2006.-125 с.:ил.
3. Лукашик В.И. Сборник задач по физике: Учебн. Пособие для учащихся 7-8 кл сред. Шк.-6-е изд., перераб. –М.: Просвещение,1994.-191с.:ил.
IOPscience::.. Страница не найдена
Поиск статей
Выберите журнал (обязательно)
2D Матер. (2014 – настоящее время) Acta Phys.
Грех. (Зарубежный Эдн) (1992 — 1999) Adv. Нац. Науки: наноски. нанотехнологии. (2010 – настоящее время) Заявл. физ. Экспресс (2008 – настоящее время)Biofabrication (2009 – настоящее время)Bioinspir. Биомим. (2006 – настоящее время) Биомед. Матер. (2006 – настоящее время) Биомед. физ. англ. Экспресс (2015 — настоящее время)Br. Дж. Заявл. физ. (1950 — 1967)Чин. Дж. Астрон. Астрофиз. (2001 — 2008)Чин. Дж. Хим. физ. (1987 — 2007)Чин. Дж. Хим. физ. (2008 — 2012)Китайская физ. (2000 — 2007)Китайская физ. B (2008-настоящее время)Chinese Phys. C (2008-настоящее время)Chinese Phys. лат. (1984 — настоящее время)Класс. Квантовая Грав. (1984 — настоящее время) клин. физ. Физиол. Изм. (1980 — 1992)Горючее. Теория Моделирования (1997 — 2004) Общ. Теор. физ. (1982 — настоящее время) Вычисл. науч. Диск. (2008 — 2015)Конверг. науч. физ. Онкол. (2015 — 2018)Распредел. Сист. инж. (1993 — 1999)ECS Adv. (2022 — настоящее время)ЭКС Электрохим. лат. (2012 — 2015)ECS J. Solid State Sci. Технол. (2012 – настоящее время)ECS Sens.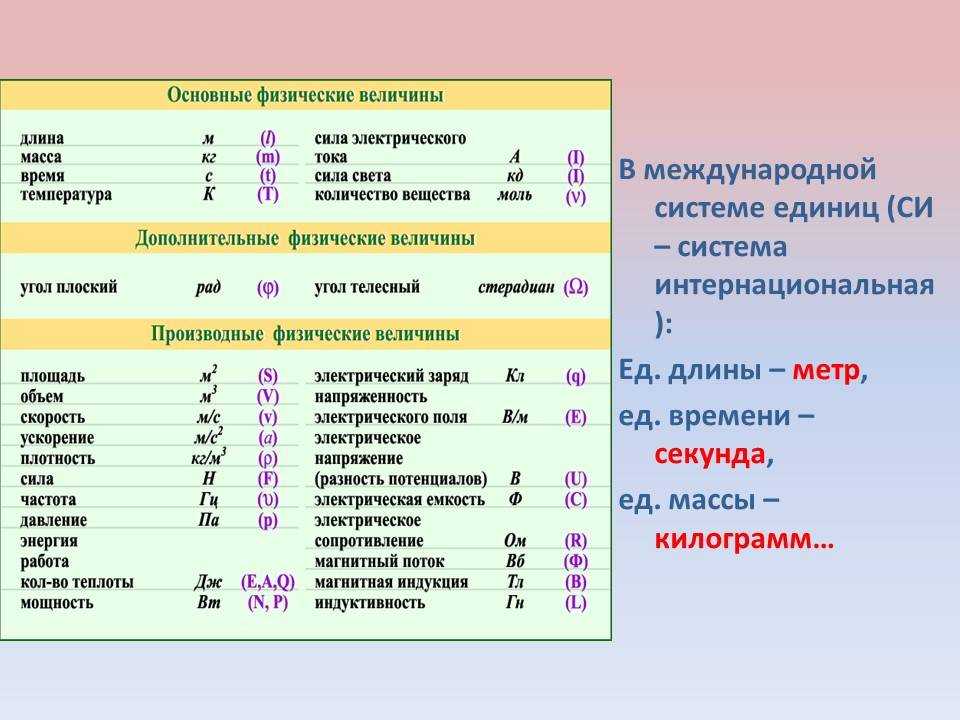
букв PES — IEEE PES
Письма PES
Этот раздел транзакций предлагает средство, которое ускоряет публикацию новых результатов, открытий и разработок. Раздел дает авторам возможность публиковать материалы в течение нескольких месяцев после подачи, чтобы обеспечить быстрое распространение идей и своевременное архивирование разработок в нашей быстро меняющейся области. Приглашаются оригинальные и значительные вклады в приложения, тематические исследования и исследования во всех областях энергетики. Особый интерес представляют материалы, определяющие возникающие проблемы и особые потребности в конкретных областях. Авторам предлагается представить материалы в секцию писем, предлагающие новое понимание устоявшихся методов, концепций и методологий в области электроэнергетики. Такие вклады заметно отличаются от обсуждений статей, недавно опубликованных в Transactions, тем, что первые направлены на расширение масштабов и указывают на потенциальные усовершенствования существующих и устоявшихся технологий.
Объем исходных материалов ограничен 3 отформатированными страницами. Редакции ограничены 3,5 страницами. Письма, превышающие эти ограничения, рассматриваться не будут. Автор отправляет рукопись, загружая PDF-файл письма непосредственно в ScholarOne Manuscripts, где к нему могут получить доступ главный редактор Power Engineering Letters, редакторы и рецензенты. Полные инструкции см. в части 2 набора для авторов https://www.ieee-pes.org/publications/information-for-authors. (Дополнительную информацию см. в разделе «Стоимость обязательных страниц для писем по энергетике».)
Обязательная плата за страниц при отправке. Половина страницы может быть добавлена для ответа на комментарии рецензента. Если в процессе пересмотра и редактирования письмо превысит 3 страницы, с автора будет взиматься плата в размере 200 долларов США за 4-ю страницу. Авторы должны строго следовать формату и шаблону IEEE, чтобы объем принятого письма после доработки и редактирования не превышал 4 страниц.
Любое письмо объемом более 4 страниц (после доработки и форматирования) к публикации не принимается. Если при редактировании/форматировании письмо становится 5 страниц, отдел публикаций и авторы должны работать с главным редактором, чтобы сократить содержание до 4 страниц.
Инструкции по загрузке писем PES
Чтобы письмо можно было отправить и просмотреть, оно должно быть загружено автором в ScholarOne Manuscripts. Процедура загрузки такая же, как и для документов по транзакциям, описанных ранее в разделе «Процедуры подачи документов». Полные инструкции также доступны в ScholarOne Manuscripts. URL-адрес сайта обзора писем: http://mc.manuscriptcentral.com/pesl-pes.
Любые новые материалы, полученные главным редактором Power Engineering Letters, будут возвращены автору для прямой загрузки.
Если письмо будет принято к публикации, автору потребуется загрузить следующие окончательные файлы в ScholarOne Manuscripts (примечание: никакие изменения не могут быть внесены в письмо после принятия):
- исходный файл LaTeX или Microsoft Word letter
- PDF-файл письма
- Отдельные графические файлы в формате Word, eps, ps, tiff, ppt или Excel, если графика не встроена в исходный файл.
