Разбираем кварцевый генератор и его крохотную интегральную схему / Хабр
Кварцевый генератор – важный электронный компонент, обеспечивающий очень точную генерацию тактовой частоты за небольшие деньги. Из-за пьезоэлектрического эффекта его электрические свойства меняются в процессе вибрации. Поскольку можно сделать кристалл, который будет вибрировать с определённой частотой, кварцевые генераторы очень полезны для множества применений. Появились они в 1920-х, и сначала обеспечивали точную генерацию волн для радиостанций. В 1970-м году произошла революция наручных часов, когда в них стали использовать кварцевые генераторы высокой точности. Компьютеры, от ENIAC 1940-х годов и до сей поры используют кварцевые генераторы для генерации тактовой частоты.
В современных ПК всё ещё используются кварцевые генераторы, но для получения многогигагерцовых тактовых частот применяются более сложные технологии. ПК использует кристалл с частотой гораздо меньшей, чем рабочая, и умножает её при помощи фазовой автоподстройки частоты.
Для того, чтобы кристалл вибрировал, его схеме требуются дополнительные компоненты. В 1970-х набрали популярность модульные кварцевые генераторы – в этих компактных и лёгких в использовании микросборках комбинировались сам кристалл, ИС и дискретные компоненты. Мне стало интересно, как работает один из таких модулей, поэтому я вскрыл один из них и провёл реверс-инжиниринг его чипа. В данном посте я расскажу, как он работает, и опишу крохотную КМОП-схему, им управляющую. Оказалось, что внутри модуля происходит больше интересного, чем можно было ожидать.
Модуль генератора
Я изучал модуль от карточки для IBM PC. Модуль находится в прямоугольном металлическом корпусе с 4-мя контактами, защищающем электронику от электрического шума (это Rasco Plus в прямоугольном корпусе справа на фото, а не квадратная ИС от IBM). Модуль генерирует сигнал в 4,7174 МГц, что следует из надписи на его корпусе.
Модуль генерирует сигнал в 4,7174 МГц, что следует из надписи на его корпусе.
Почему же карточка использует кристалл с такой необычной частотой — 4,7174 МГц? В 1970-х IBM 3270 был очень популярным терминалом с ЭЛТ. Терминалы соединялись коаксиальным кабелем и использовали протокол Interface Display System Standard, работавший с тактовой частотой в 2,3587 МГц. В конце 1980-х IBM производила интерфейсные карточки для подсоединения IBM PC к сети 3270. Мой кристалл как раз с одной из таких карточек (тип 56X4927), и частота кристалла равняется 4,7174 МГц – ровно в два раза больше, чем 2,3587 МГц.
Модуль кварцевого генератора находится справа внизу. Надпись на корпусе: Rasco Plus. 4.7174 MHZ, Motorola 1987. Квадратный модуль слева – это ИС от IBM.
Я вскрыл корпус модуля, чтобы посмотреть на его гибридную схему. Я ожидал увидеть там кварцевый кристалл, напоминающий драгоценный камень в шкатулке, однако обнаружил, что кварцевые генераторы используют очень тонкий кварцевый диск.
Внутри корпуса кварцевого генератора – компоненты, закреплённые на керамической подложке. Они подсоединяются к схеме крохотной золотой проволочной разваркой. Конденсатор на 3 нФ и плёночный резистор на 10 Ом, расположенные на подложке методом поверхностного монтажа, отфильтровывают шум, поступающий от контакта питания.
Схема работы ИС
На фото ниже показан крохотный кристалл ИС под микроскопом. Размечены контактные площадки и основные функциональные блоки. Зелёно-коричневые участки – это кремний, формирующий ИС. Жёлтоватый металлический слой соединяет компоненты с ИС. Под металлом находится красноватый слой поликремния, где формируются транзисторы – но он практически полностью закрыт металлическим слоем. По краям чипа расположена проволочная разварка, подсоединённая к контактным площадкам, соединяющим чип с остальными частями модуля. Две площадки (select и disable) не подсоединены. Чип произведён компанией Motorola в 1986. По артикулу SC380003 информации я не нашёл.
По краям чипа расположена проволочная разварка, подсоединённая к контактным площадкам, соединяющим чип с остальными частями модуля. Две площадки (select и disable) не подсоединены. Чип произведён компанией Motorola в 1986. По артикулу SC380003 информации я не нашёл.
Кристалл ИС с разметкой основных блоков. «FF» обозначает триггеры. «sel» – контактные площадки [select pads]. «cap» – площадки, подсоединённые к внутренним конденсаторам.
У ИС есть две задачи. Во-первых, её аналоговые компоненты заставляют кристалл колебаться. Во-вторых, её цифровые компоненты делят частоту на 1, 2, 4 или 8, и выдают сигнал тактовой частоты с большим током (делитель задаётся двумя контактами выбора на ИС).
Кварцевый генератор реализован по приведённой ниже схеме, которая называется «генератор Колпитца». Она сложнее обычной схемы кварцевого генератора. Суть в том, что кристалл и два конденсатора колеблются с заданной частотой. Однако колебания быстро затухли бы, если бы не поддерживающая обратная связь с поддерживающего транзистора.
Типичный кварцевый генератор строится по простой схеме под названием «генератор Пирса», в которой из кристалла и инвертера формируется цепь обратной связи. Два заземлённых конденсатора в середине делают её очень похожей на классический генератор Колпитца.
Не уверен, по какой причине разобранный мною кварцевый генератор использует более сложную схему, которая требует хитрого смещения напряжения.
В 1918 году Эдвин Колпитц, главный исследователь в компании Western Electric, изобрёл кварцевый генератор на катушке индуктивности и конденсаторе. Сегодня эта схема известна, как генератор Колпитца. Идея в том, что катушка индуктивности с конденсатором формируют «резонансный резервуар», колеблющийся с частотой, зависящей от характеристик компонентов. Можно представлять, что электричество в этом резервуаре как бы плещется туда и сюда между катушкой индуктивности и конденсаторами. Сами по себе колебания быстро затухли бы, поэтому для их подпитки используется усилитель. В оригинальном генераторе Колпитца усилителем была электронная лампа.
Упрощённая схема генератора Колпитца с базовыми компонентами.
Ключевая особенность генератора Колпитца заключается в двух конденсаторах, формирующих делитель напряжения. Поскольку они в середине заземлены, на двух концах у них будет напряжение противоположных значений: когда одно повышается, второе понижается. Усилитель берёт сигнал с одного конца, усиливает его, и подаёт на другой. Усилитель инвертирует сигнал, а конденсаторы дают второе инвертирование, так, что обратная связь усиливает оригинальный сигнал (обеспечивая фазовый сдвиг на 360°).
В 1923 году Джордж Вашингтон Пирс, профессор физики в Гарварде, заменил катушку индуктивности в генераторе Колпитца на кристалл. Благодаря этому генератор стал более точным, и его стали широко использовать в радиопередатчиках и других устройствах. Пирс запатентовал своё изобретение и заработал приличные деньги на таких компаниях, как RCA и AT&T. Наличие патентов привело к многолетним судебным тяжбам, дошедшим в итоге до Верховного суда.
Пирс запатентовал своё изобретение и заработал приличные деньги на таких компаниях, как RCA и AT&T. Наличие патентов привело к многолетним судебным тяжбам, дошедшим в итоге до Верховного суда.
Несколько десятилетий генератор Пирса было принято называть генератором Колпитца с кристаллом. В генераторе Пирса часто отсутствовали характерные конденсаторы, вместо которых использовалось паразитная ёмкость электронной лампы. Терминология постепенно менялась, и два разных типа кварцевых генератора начали называть генератором Колпитца (с конденсаторами) и генератором Пирса (без них).
Ещё одно изменение терминологии произошло в связи с тем, что генератор Колпитца, генератор Пирса и генератор Клаппа были топологически идентичными кварцевыми генераторами, отличавшимися только в том, какая часть схемы считалась землёй (коллектор, эмиттер или база соответственно). Все эти генераторы можно называть генераторами Колпитца, только с общим коллектором, общим эмиттером или общей базой.
Этот экскурс в историю я сделал с тем, чтобы показать, что в различных источниках эти генераторы называют по-разному, генераторами Колпитца или Пирса, причём противоречивым образом.
Увеличение напряжения на кристалле включает транзистор, ток идёт в конденсаторы, увеличивая напряжение на них (и на кристалле). Уменьшение напряжения на кристалле выключает транзистор, сток тока (кружок со стрелкой) вытягивает ток из конденсаторов, уменьшая напряжение на кристалле. Таким образом, обратная связь с транзистора усиливает колебания кристалла, поддерживая их.
Цепи напряжения смещения и тока являются важной частью этой схемы. Напряжение смещения устанавливает вентиль транзистора где-то посередине между включённым и выключенным состоянием, поэтому колебания напряжения на кристалле включают его и выключают. Ток смещения находится посередине между значениями токов включённого и выключенного транзистора, поэтому ток, приходящий и уходящий из конденсаторов, сбалансирован (я упрощаю, говоря о включённых и выключенных состояниях – в реальности сигнал будет иметь синусоидальную форму).
Ток смещения находится посередине между значениями токов включённого и выключенного транзистора, поэтому ток, приходящий и уходящий из конденсаторов, сбалансирован (я упрощаю, говоря о включённых и выключенных состояниях – в реальности сигнал будет иметь синусоидальную форму).
Цепи напряжения смещения и тока – это умеренно сложные аналоговые схемы, состоящие из кучки транзисторов и нескольких резисторов. Подробно описывать их не буду, скажу лишь, что они используют цепи обратной связи для генерации нужных фиксированных значений напряжения и тока.
Значительную часть ИС занимают пять конденсаторов. На схеме один расположен сверху, три идут параллельно, формируя нижний конденсатор на схеме, а один стабилизирует цепь напряжения смещения. На фото кристалла ниже показан один из конденсаторов после растворения верхнего металлического слоя. Красные и зелёные участки – это поликремний, формирующий верхнюю пластину конденсатора вместе с металлическим слоем. Расположенный под поликремнием розоватый участок – вероятно, нитрид кремния, формирующий диэлектрический слой. Кремний с добавками, которого на фото не видно, формирует нижнюю пластину конденсатора.
Кремний с добавками, которого на фото не видно, формирует нижнюю пластину конденсатора.
Конденсатор на кристалле. Большой бледный квадрат слева – площадка для подсоединения проволочной разварки к ИС. Сложные структуры слева – фиксирующие диоды контактов. Похожие на клевер структуры справа – это транзисторы.
Интересно, что конденсаторы на чипе не соединяются вместе. Они подсоединены к трём площадкам, связанным между собой проволочной разваркой. Возможно, это придаёт схеме гибкость – ёмкость цепи можно изменить, удалив проводник, ведущий к конденсатору.
Цифровая схема
С правой части чипа находится цифровая схема делителя выходной частоты кристалла на 1, 2, 4 или 8. Благодаря ей один и тот же кристалл может выдавать четыре частоты. Делитель составлен из трёх триггеров, подключённых последовательно. Каждый делит входящий импульс пополам. Мультиплексор 4 к 1 выбирает между оригинальной частотой импульсов или выходом с одного из триггеров.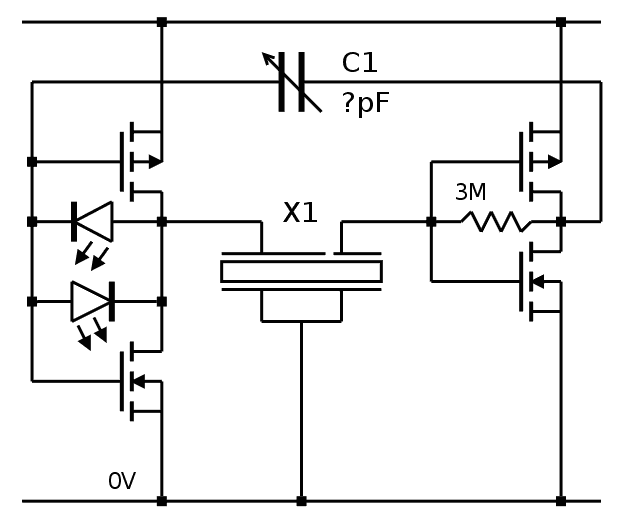 Выбор осуществляется при помощи проводников, подходящих к двум площадкам для выбора с правой части кристалла. Итоговая частота фиксируется на этапе производства. Для декодирования контактов и генерации четырёх управляющих сигналов мультиплексору и триггерам используются четыре вентиля NAND вместе с инверторами.
Выбор осуществляется при помощи проводников, подходящих к двум площадкам для выбора с правой части кристалла. Итоговая частота фиксируется на этапе производства. Для декодирования контактов и генерации четырёх управляющих сигналов мультиплексору и триггерам используются четыре вентиля NAND вместе с инверторами.
Реализация логики КМОП
Кип построен на логике КМОП (комплементарная структура металл-оксид-полупроводник). Она использует совместно работающие транзисторы двух типов, N-МОП и P-МОП. На диаграмме ниже показано устройство N-МОП транзистора. Транзистор можно считать переключателем между истоком и стоком, который контролирует вентиль. Исток и сток (зелёные) состоят из участков кремния с добавками, меняющими его полупроводниковые свойства – из N+ кремния. Вентиль сделан из особого кремния, поликремния, отделённого от кремниевой подложки очень тонким изолирующим слоем оксидным слоем. N-МОП транзистор включается, когда вентиль подтягивается вверх.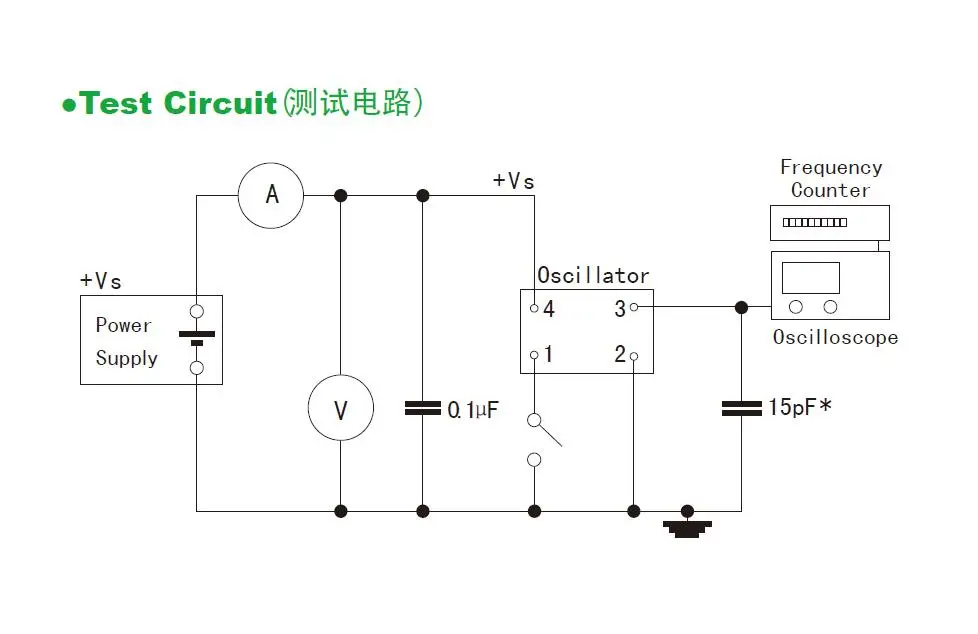
Структура N-МОП транзистора. Структура P-МОП транзистора похожа, однако участки кремния N- и P-типа меняются местами.
Строение P-МОП транзистора противоположно N-МОП: исток и сток состоят из P+ кремния, включённого в N кремний. Работает он тоже противоположно N-МОП транзистору: включается, когда вентиль подтягивается вниз. Обычно P-МОП транзисторы подтягивают сток вверх, а N-МОП – вниз. В КМОП транзисторы работают, дополняя друг друга, подтягивая выходной сигнал вверх или вниз по необходимости.
На диаграмме ниже показано, как в КМОП реализован вентиль NAND. Если на вход подать 0, соответствующий P-МОП транзистор (вверху) включится и притянет выход вверх. Если на оба входа подать 1, N-МОП транзистор (внизу) включится и подтянет выход вниз. Таким образом схема реализует функцию NAND.
На диаграмме ниже показано, как NAND-вентиль выглядит на кристалле. В отличие от изображений в учебниках, у реальных транзисторов бывает сложная, извилистая форма. С левой стороны находятся P-МОП транзистор, а с правой – N-МОП.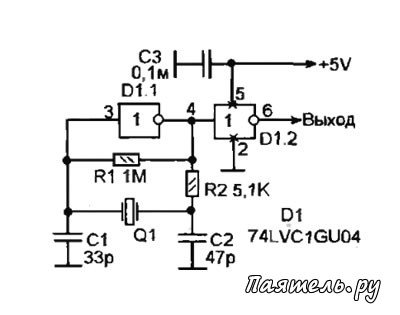 Красноватые дорожки над кремнием – это поликремний, формирующий вентили. Большая часть кремния в подложке благодаря добавкам проводит ток, и выглядит чуть темнее непроводящего кремния без добавок с левого и правого краёв, а также в центре. Для изготовления этого фото металлический слой был вытравлен. Жёлтые линии обозначают места, где раньше были металлические проводники. Кружочки — это связи металлического слоя с нижними слоями, кремния или поликремния.
Красноватые дорожки над кремнием – это поликремний, формирующий вентили. Большая часть кремния в подложке благодаря добавкам проводит ток, и выглядит чуть темнее непроводящего кремния без добавок с левого и правого краёв, а также в центре. Для изготовления этого фото металлический слой был вытравлен. Жёлтые линии обозначают места, где раньше были металлические проводники. Кружочки — это связи металлического слоя с нижними слоями, кремния или поликремния.
Как NAND-вентиль выглядит на кристалле
Транзистор на фото можно сопоставить со схемой NAND-вентиля. Посмотрите на сформированные поликремнием вентили транзистора, и на то, что они разделяют. От участка +5 есть дорожка к выходу через длинный P-МОП транзистор слева. Второй путь идёт через небольшой P-МОП транзистор в центре – это показывает, что транзисторы подключены параллельно. Каждый вентиль контролирует один из входов. Слева дорожка от земли к выходу должна пойти через оба концентрических N-МОП транзистора – они подключены последовательно.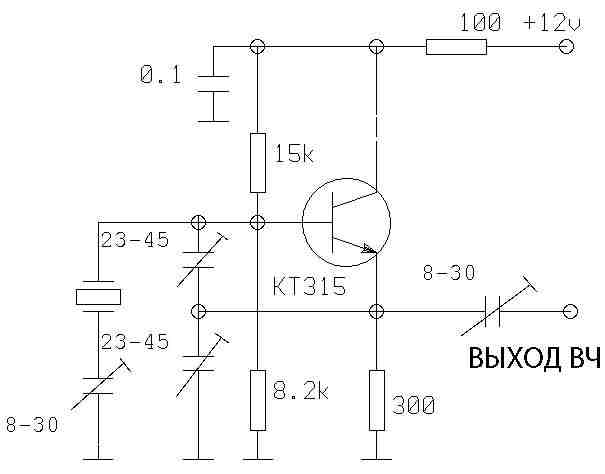
В этой ИС также используется много транзисторов с кольцевыми вентилями. Эта необычная техника расположения элементов позволяет с большой плотностью разместить множество параллельных транзисторов. На фото ниже показано 16 транзисторов с кольцевыми вентилями. Похожие на клевер узоры медного цвета – это сток транзисторов, а снаружи находится исток. Металлический слой (тут он удалён) объединяет соответственно все истоки, вентили и стоки. Параллельные транзисторы работают как один большой. Параллельные транзисторы используются для подачи больших токов на выход. В схеме смещения вместе соединяются различное количество транзисторов (6, 16 или 40), чтобы получать нужное соотношение токов.
Передаточный вентиль
Ещё одна ключевая схема чипа – это передаточный вентиль. Он работает как переключатель, через который сигнал либо проходит, либо нет. На схеме ниже показано, как передаточный вентиль делается из двух транзисторов, N-МОП транзистора и P-МОП транзистора.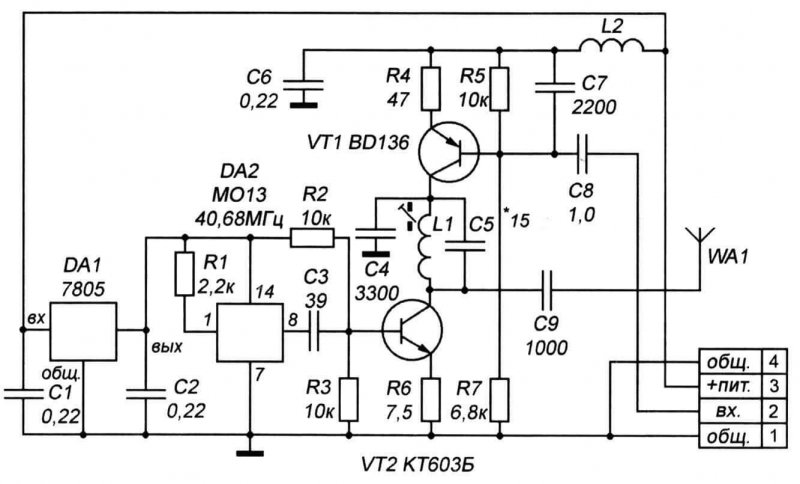 Если по линии enable подаётся большое напряжение, включаются оба транзистора, и входной сигнал проходит на выход. Если напряжение низкое, они выключаются, блокируя сигнал. Справа показано условное обозначение передаточного вентиля на схемах.
Если по линии enable подаётся большое напряжение, включаются оба транзистора, и входной сигнал проходит на выход. Если напряжение низкое, они выключаются, блокируя сигнал. Справа показано условное обозначение передаточного вентиля на схемах.
Мультиплексор
Мультиплексор используется для выбора одного из четырёх тактовых сигналов. На диаграмме ниже показано, как мультиплексор реализован на основе передаточных вентилей. Мультиплексор принимает на вход четыре сигнала: A, B, C и D. Один из входов выбирается через активацию соответствующей линии выбора и её дополнения. Этот вход связывается через передаточный вентиль с выходом, а другие входы блокируются. Хотя мультиплексор можно построить и на стандартных логических вентилях, его реализация на передаточных вентилях получается эффективнее.
Мультиплексор 4 к 1 на основе передаточных вентилей
На схеме ниже показаны транзисторы, из которых состоит мультиплексор. Ко входам B и С подключено по паре транзисторов. Думаю, это сделано потому, что у пары транзисторов сопротивление получается половинным. Поскольку входы В и С предназначены для высокочастотных сигналов, пара транзистора позволяет уменьшить задержки и искажения.
Думаю, это сделано потому, что у пары транзисторов сопротивление получается половинным. Поскольку входы В и С предназначены для высокочастотных сигналов, пара транзистора позволяет уменьшить задержки и искажения.
На фото ниже показано, как мультиплексор реализован на кристалле физически. Лучше всего видно поликремниевые вентили. Металлический слой удалён. Металлические проводники шли вертикально, соединяя соответствующие сегменты транзисторов. Истоки и стоки соседних транзисторов объединены в единые участки, расположенные между вентилями. В верхнем прямоугольнике находятся N-МОП транзисторы, а в нижнем – P-МОП. Поскольку P-МОП транзисторы менее эффективны, нижний прямоугольник должен быть больше.
Триггер
На чипе есть три триггера, делящие тактовую частоту. Кварцевый генератор использует переключаемые триггеры, которые переключаются между 0 и 1 каждый раз, когда получают входящий импульс. Поскольку два входящих импульса дают один исходящий (0→1→0), триггер делит частоту пополам.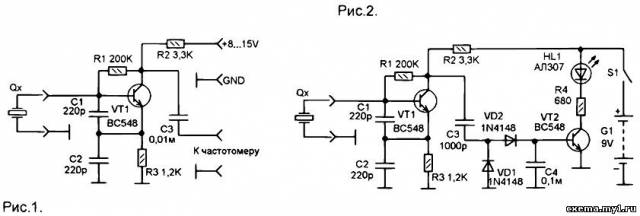
Триггер состоит из передаточных вентилей, инверторов и NAND-вентиля – см. схему ниже. Когда входящий тактовый сигнал равен 1, выход проходит через инвертор и первый передаточный вентиль в точку А. Когда входящий сигнал переключается на 0, открывается первый передаточный вентиль, и в точке А остаётся предыдущее значение. Тем временем закрывается второй передаточный вентиль, поэтому сигнал проходит через второй инвертор и передаточный вентиль в точку В. NAND-вентиль снова его инвертирует, в результате чего значение выхода меняется на противоположное. Второй цикл входящего сигнала тактовой частоты повторяет этот процесс, благодаря чему выход возвращается к изначальному значению. В итоге два цикла входящих сигналов дают один цикл выходящего сигнала, так что триггер делит частоту на 2.
У каждого триггера есть разрешающий вход. Если триггер для выбранного выхода не нужен, он отключается. К примеру, если выбирается режим деления на 2, используется только первый триггер, а два другие отключаются. Полагаю, это делается для уменьшения энергопотребления. Это не зависит от контакта отключения на модуле, который полностью блокирует выходящий сигнал. Это отключаемое свойство опционально; в данном модуле такой функции нет, а контакт отключения не подключен к ИС.
Полагаю, это делается для уменьшения энергопотребления. Это не зависит от контакта отключения на модуле, который полностью блокирует выходящий сигнал. Это отключаемое свойство опционально; в данном модуле такой функции нет, а контакт отключения не подключен к ИС.
На схеме выше инвертеры и передаточные вентили показаны в виде отдельных структур. Однако в триггере используется интересная структура вентилей, комбинирующая инвертер и передаточный вентиль (слева) в единый вентиль (справа). Пара транзисторов, подключенных к data in, работают как инвертер. Однако если сигнал тактовой частоты нулевой, питание и земля блокируются, и вентиль не влияет на выход, сохраняя предыдущее напряжение. Так работает передаточный вентиль.
Комбинированные инвертер и передаточный вентиль
На фото ниже показано, как один из таких вентилей выполнен на кристалле. На фото видно металлический слой сверху. Под ним видно красноватые вентили из поликремния. Слева расположены два P-МОП транзистора в виде концентрических кругов.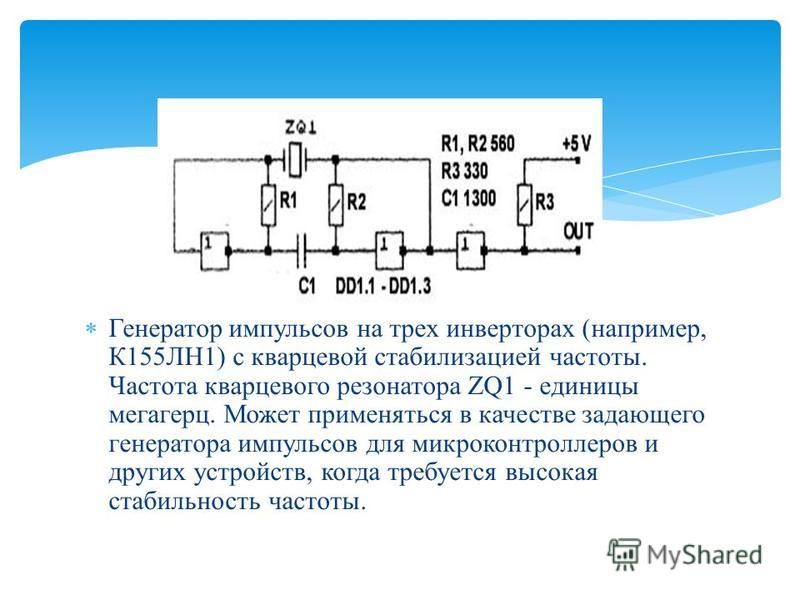 Справа находятся N-МОП транзисторы.
Справа находятся N-МОП транзисторы.
Заключение
Хотя модуль кварцевого генератора снаружи кажется простым, внутри него больше компонентов, чем можно было бы ожидать. Там находится не только кристалл кварца, но и дискретные компоненты, и крохотная ИС. В ИС скомбинированы конденсаторы, аналоговые цепи, обеспечивающие колебания, и цифровые цепи для выбора частоты. Можно выбрать одну из четырёх частот, изменяя проводку ИС на этапе производства.
Больше информации по кварцевым генераторам можно найти на сайтах EEVblog, electronupdate и WizardTim. Про генератор Колпитца можно посмотреть на Hackaday.
Закончу фотографией чипа после удаления слоёв металла и оксида, чтобы было видно кремний и поликремний. Больше всего выделяются крупные розоватые конденсаторы, однако можно рассмотреть и транзисторы.
Кликабельно
КВАРЦЕВЫЙ ГЕНЕРАТОР • Большая российская энциклопедия
Авторы: В. В. Дмитриев
КВА́РЦЕВЫЙ ГЕНЕРА́ТОР, маломощный генератор электрич. колебаний с самовозбуждением, в состав колебательной системы которого входит кварцевый пьезоэлектрический резонатор. Характеризуется высокой стабильностью частоты генерируемых колебаний, что обусловлено высокой добротностью кварцевого резонатора (105–107).
колебаний с самовозбуждением, в состав колебательной системы которого входит кварцевый пьезоэлектрический резонатор. Характеризуется высокой стабильностью частоты генерируемых колебаний, что обусловлено высокой добротностью кварцевого резонатора (105–107).
Схема кварцевого генератора – последовательного резонанса с кварцевым резонатором (КР) в колебательном контуре: C1,2,3 – конденсаторы; R1,2,3,4 – резисторы; L – катушка индукти…
Электрич. схемы К. г. принципиально не отличаются от схем генераторов электрических колебаний с обычными колебательными контурами. Параметры колебательной системы К. г. выбираются так, чтобы бóльшая часть энергии была сосредоточена в кварцевом резонаторе; в этом случае генерируемая частота определяется гл. обр. собственной частотой резонатора. Кварцевый резонатор обладает высокими механич.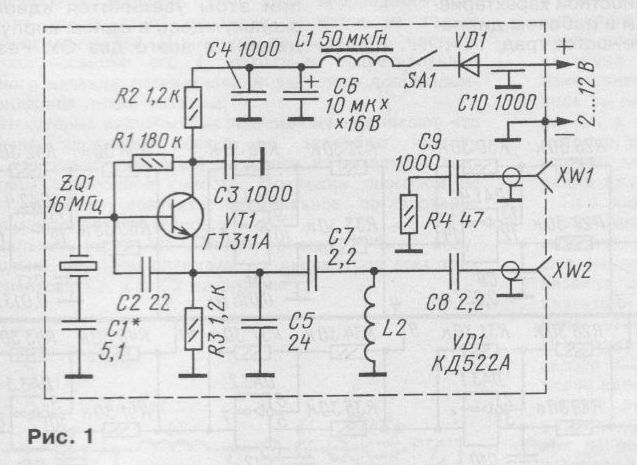 прочностью и химич. стойкостью, нечувствителен к влажности; его собственная частота слабо зависит от темп-ры. Различают схемы К. г. последовательного резонанса, в которых кварцевый резонатор эквивалентен активному сопротивлению (рис.), и осцилляторные – кварцевый резонатор эквивалентен индуктивности. В зависимости от величины нестабильности частоты и/или возможности изменения частоты колебаний К. г. подразделяют на простые, не содержащие дополнит. элементов для улучшения параметров; управляемые, частоту которых можно изменять посредством внешнего воздействия; термокомпенсированные, у которых отклонение (уход) частоты $\Delta f$ от её номинального значения $f$ в заданном интервале темп-р уменьшают с помощью дополнит. электрич. устройств; термостатированные, у которых все или некоторые элементы помещены в термостат.
прочностью и химич. стойкостью, нечувствителен к влажности; его собственная частота слабо зависит от темп-ры. Различают схемы К. г. последовательного резонанса, в которых кварцевый резонатор эквивалентен активному сопротивлению (рис.), и осцилляторные – кварцевый резонатор эквивалентен индуктивности. В зависимости от величины нестабильности частоты и/или возможности изменения частоты колебаний К. г. подразделяют на простые, не содержащие дополнит. элементов для улучшения параметров; управляемые, частоту которых можно изменять посредством внешнего воздействия; термокомпенсированные, у которых отклонение (уход) частоты $\Delta f$ от её номинального значения $f$ в заданном интервале темп-р уменьшают с помощью дополнит. электрич. устройств; термостатированные, у которых все или некоторые элементы помещены в термостат. Существуют также К. г. смешанного типа (напр., управляемый термокомпенсированный К. г.).
Существуют также К. г. смешанного типа (напр., управляемый термокомпенсированный К. г.).
Частота генерируемых колебаний в зависимости от типа К. г. составляет от нескольких кГц до 100 МГц и более. Стабильность частоты, характеризуемая отношением $\Delta f/f$, достигает у простых К. г. ± 5·10–6 в диапазоне темп-р от –60 до 100 °C, у термокомпенсированных 5·10–7 (от –60 до 85 °C), у термостатированных 10–10 (10–40 °C). Мощность К. г. ограничена прочностью кварцевой пластины, её размерами и, как правило, не превышает нескольких десятков Вт. К. г. широко применяются в разл. радиопередающих устройствах (в качестве задающих генераторов), в кварцевых часах, могут служить эталонами времени и стандартов частоты.
ВЧ и СВЧ кварцевые генераторы
Выберите категорию для просмотра продуктов и компаний
Кристаллический осциллятор — это генератор, который использует свойство резонанса кварцевого кристалла для создания электрического сигнала на определенной частоте. Сравните кварцевые генераторы от ведущих производителей по всему RF. Выберите тип, а затем используйте инструмент параметрического поиска, чтобы сузить список продуктов от нескольких производителей. Сравните продукты, загрузите спецификации и получите предложения.
Сравните кварцевые генераторы от ведущих производителей по всему RF. Выберите тип, а затем используйте инструмент параметрического поиска, чтобы сузить список продуктов от нескольких производителей. Сравните продукты, загрузите спецификации и получите предложения.
Подробнее о кварцевых осцилляторах
Кварцевый осциллятор — это генератор, который использует свойство резонанса кварцевого кристалла для создания электрического сигнала на определенной частоте.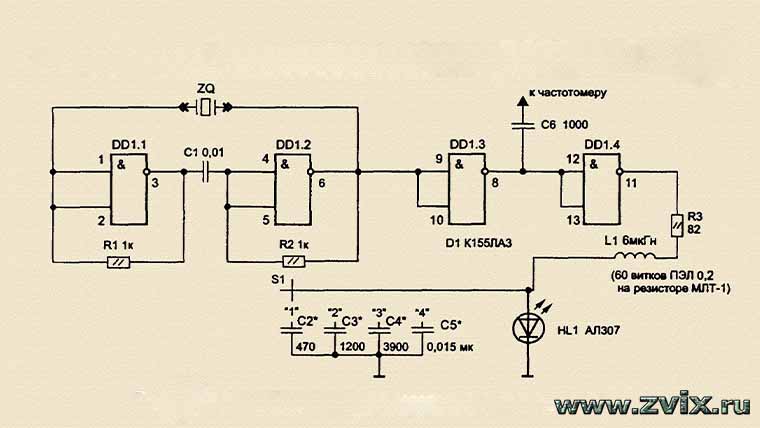 Он основан на обратном пьезоэлектрическом эффекте. Кварцевые генераторы используются для обеспечения стабильного тактового сигнала для цифровых интегральных схем и проектов микроконтроллеров, для отслеживания времени, как в кварцевых наручных часах, и для стабилизации частот для радиопередатчиков и приемников, а также для многих других приложений. Эти устройства можно отсортировать по ряду ключевых параметров, вот некоторые из них:
Он основан на обратном пьезоэлектрическом эффекте. Кварцевые генераторы используются для обеспечения стабильного тактового сигнала для цифровых интегральных схем и проектов микроконтроллеров, для отслеживания времени, как в кварцевых наручных часах, и для стабилизации частот для радиопередатчиков и приемников, а также для многих других приложений. Эти устройства можно отсортировать по ряду ключевых параметров, вот некоторые из них:
Type of Crystal Oscillators:
- VCXO — Voltage Controlled Crystal Oscillators
- TCXO — Temperature Compensated Crystal Oscillators
- OCXO — Oven Controlled Crystal Oscillators
- XO Crystal Oscillators are the main ones
Other types include clock генераторы, кварцевые генераторы с цифровым управлением (DCXO), VCXO с регулируемой температурой, генераторы на ПАВ с регулируемым напряжением (VCSO) и VCTCXO.
Основные характеристики:
Частота (МГц): Это частота, на которой будет работать осциллятор.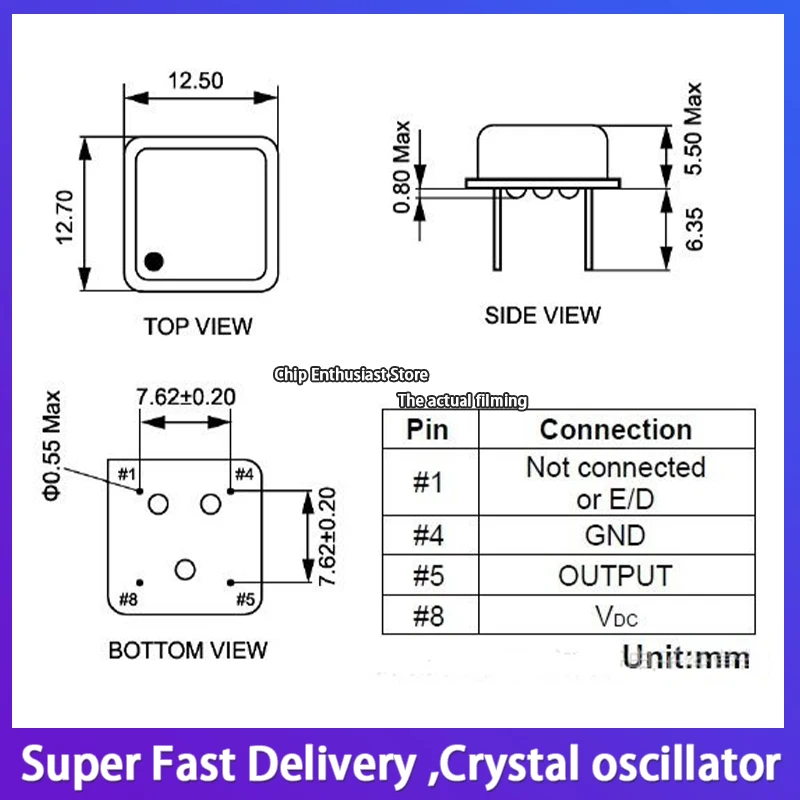
Форма выходного сигнала: Каждый осциллятор обеспечивает определенный тип выходного сигнала — основные типы: синусоида, обрезанная синусоида, LVCMOS, CMOS, HCMOS.
Напряжение питания (В): Это напряжение, которое приводит в действие кварцевый генератор.
Стабильность частоты (ppm): Еще одним важным параметром является стабильность генерируемой частоты. Это говорит нам об отклонении выходной частоты, ожидаемом от кварцевого генератора. Это мера точности, которая определяет приложения, в которых может использоваться кварцевый генератор, поскольку некоторые приложения требуют высокой точности. Щелкните здесь, чтобы узнать больше о стабильности частоты.
Фазовый шум: Фазовый шум — это мера шума, который генерируется вместе с полезным сигналом. Это одна из наиболее важных характеристик кварцевого генератора. Чем ниже фазовый шум, тем лучше. Щелкните здесь, чтобы узнать больше о фазовом шуме.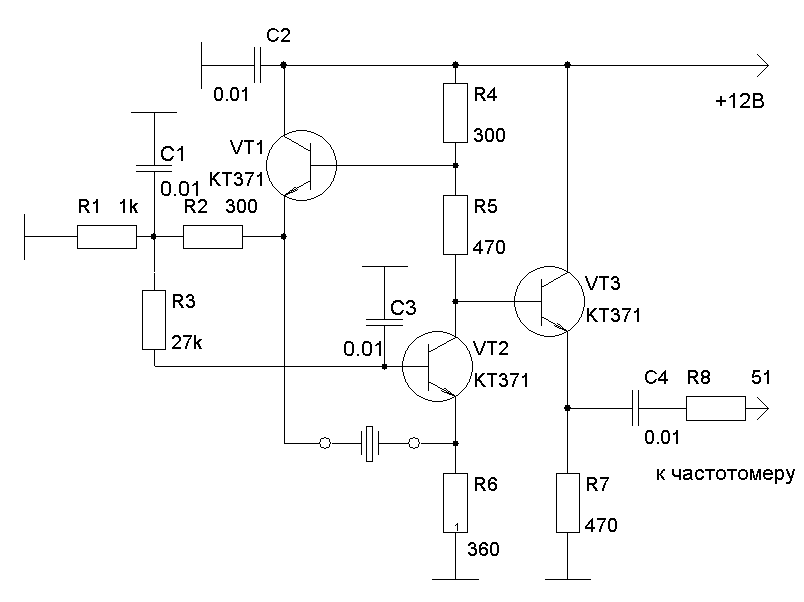
все RF позволяет искать кварцевые генераторы по спецификации в каталогах нескольких производителей. Были перечислены кварцевые генераторы от более чем 100 производителей. Используйте специально разработанные инструменты параметрического поиска, чтобы сузить список продуктов по номинальной частоте, форме выходного сигнала, стабильности частоты, фазовому шуму, напряжению питания и другим параметрам. Вы можете загрузить таблицы данных и запросить расценки через платформу, ваши запросы будут направлены компаниям и их дистрибьюторам в вашем регионе.
Рекомендуемые товары
Объявление
Просматривать
52 Просмотр нет ../
ПросматриватьРазработайте кварцевый осциллятор, соответствующий вашему приложению
Скачать PDF
Abstract
Кристаллы кварца представляют собой механические резонаторы с пьезоэлектрическими свойствами. Пьезоэлектрические свойства (электрический потенциал на кристалле пропорционален механической деформации) позволяют использовать их в качестве элементов электрических цепей. Кристаллы широко используются в качестве резонансных элементов в генераторах из-за их высокого коэффициента добротности (QF), превосходной стабильности частоты, жестких допусков и относительно низкой стоимости. В этом учебном пособии объясняются основные аспекты проектирования, которые необходимо учитывать при проектировании простого кварцевого генератора с использованием кристаллов с AT-срезом. Описаны основные качества кварцевого генератора и факторы, которые могут повлиять на их характеристики в различных приложениях. Темы, обсуждаемые здесь, представляют собой подборку проблем, возникших за десятилетие разработки и применения радиостанций ISM-диапазона. Эти темы включают емкость нагрузки, отрицательное сопротивление, время запуска, стабильность частоты в зависимости от температуры, зависимость от уровня возбуждения, старение кристалла, ошибку частоты и паразитные режимы.
Пьезоэлектрические свойства (электрический потенциал на кристалле пропорционален механической деформации) позволяют использовать их в качестве элементов электрических цепей. Кристаллы широко используются в качестве резонансных элементов в генераторах из-за их высокого коэффициента добротности (QF), превосходной стабильности частоты, жестких допусков и относительно низкой стоимости. В этом учебном пособии объясняются основные аспекты проектирования, которые необходимо учитывать при проектировании простого кварцевого генератора с использованием кристаллов с AT-срезом. Описаны основные качества кварцевого генератора и факторы, которые могут повлиять на их характеристики в различных приложениях. Темы, обсуждаемые здесь, представляют собой подборку проблем, возникших за десятилетие разработки и применения радиостанций ISM-диапазона. Эти темы включают емкость нагрузки, отрицательное сопротивление, время запуска, стабильность частоты в зависимости от температуры, зависимость от уровня возбуждения, старение кристалла, ошибку частоты и паразитные режимы.
Аналогичная версия этой статьи появляется на Electronic Design , 7 сентября 2012 г.
Основы кристалла Модель
Кристаллы кварца электрически моделируются как последовательная ветвь RLC, параллельная шунтирующей емкости (рис. 1). Ответвление серии RLC, часто называемое подвижным плечом, моделирует пьезоэлектрическую связь с механическим кварцевым резонатором. Емкость шунта представляет собой физическую емкость, образованную как емкостью параллельных пластин электродной металлизации, так и паразитной емкостью пакета.
Рис. 1. Простая электрическая модель кварцевого кристалла основной моды.
Модель, показанная на рисунке 1, применима к работе в основном режиме. Подобные модели также применимы для работы обертонов кварцевых резонаторов. Модели обертонов включают в себя дополнительные ветви серии RLC параллельно элементам, показанным на рисунке 1. Дополнительные ветви серии RLC обертонов имеют резонансные частоты, близкие к нечетным кратным резонансной частоте основной серии.
Для кристаллов, работающих в основном режиме с диапазоном частот от 5 МГц до 30 МГц, типичные значения элементов схемы составляют:
C1 от 2 до 20 фФ (движущаяся емкость)
R1 от 10 до 150 Ом (эквивалентное последовательное сопротивление, ESR)
L1 определяется C1 и рабочей частотой (движущаяся индуктивность)
C0 от 0,5 до 5 пФ (шунтирующая емкость)
Где движущиеся элементы являются электрическим аналогом механического резонанса и пьезоэлектрических свойств кристалла. ESR моделирует потери механического резонанса.
Для последовательной цепи RLC без внешнего управляющего напряжения сумма всех напряжений приводит к следующему дифференциальному уравнению:
L × dI/dt + I × R + (1/C) × ∫I × dt = 0
По определению I можно заменить на dQ/dt, что даст:
L × d²Q/dt² + R × dQ/dt + Q/C = 0
Или
d2Q/dt² + (R/L) × dQ/dt + Q/(L × C) = 0
Который имеет форму d2Q/dt² + (ω 0 /QF) × dQ/dt + Q × ω 0 ² = 0.
Это дает хорошо известный результат для цепей RLC: собственная частота, ω 0 , является квадратным корнем, обратным произведению индуктивности и емкости.
Рис. 2. Механическая модель кристалла
Механическая модель кристалла состоит из массы; пружина с соответствующим модулем упругости или жесткостью; и индикатор для моделирования потерь (рис. 2). Силы, приложенные к кристаллу, без учета фиксированной силы и пространственного смещения из-за гравитации, приводят к ускорению массы (второй закон движения Ньютона). В простой линейной модели предполагаются две силы: сила пружины и сила трения. Сила пружины определяется законом Гука, F = K × Y, где K — модуль пружины, а Y — отклонение от положения равновесия. Предполагается, что потери на трение пропорциональны скорости плунжера в демпфере и коэффициенту трения D демпфера. Приравнивание этих сил (без внешних движущих сил) дает:
M × d²Y/dt² + D × dY/dt + K × Y = 0
Или
d²Y/dt² + (D/M) × dY/dt + Y × (K/M) = 0
Который имеет вид d²Y/dt² + (ω 0 /QF) × dY/dt + Y × ω 0 ² = 0.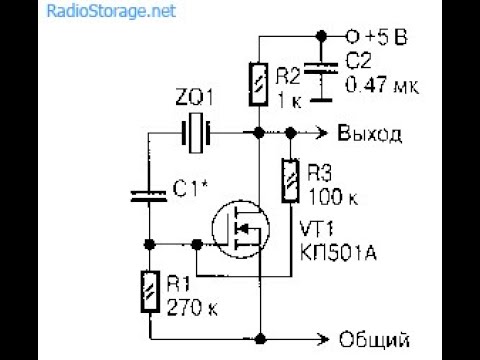
Результирующая собственная частота механической системы должна равняться собственной частоте электрической системы. Это дает:
ω 0 = √(1/(L × C) = √(K/M)
Рис. 3. Кубический кварцевый резонатор. Электроды на верхней и нижней гранях, A = L × W.
Масса кварцевого резонатора кубической или цилиндрической формы с электродной металлизацией на противолежащих гранях самого узкого размера пропорциональна произведению площади электрода на расстояние между электродами (т. е. наименьший размер или толщину), как показано на рис. Рисунок 3.
М ~ А × Т
Где А — площадь электрода, а Т — толщина.
Упругий модуль того же кварцевого резонатора кубической формы пропорционален произведению площади электрода на величину, обратную его толщине.
К ~ А/Т
Отсюда собственная частота механической системы не зависит от площади электрода и обратно пропорциональна толщине:
ω 0 = √(K/M) ~ √(A/(T × A × T) = √(1/T²) = 1/T
Из многих возможных вариантов кристаллов-резонаторов кристаллы AT-среза популярны благодаря своим характеристикам температурного коэффициента и воспроизводимости изготовления. Для кристаллов AT-среза механический резонанс представляет собой режим сдвига, как показано на рисунке 4. В этом режиме работы центр тяжести перемещается как по вертикали, так и по горизонтали. Таким образом, предыдущий анализ представляет собой одномерное приближение, полезное для качественного понимания механического резонанса кристалла с АТ-срезом.
Для кристаллов AT-среза механический резонанс представляет собой режим сдвига, как показано на рисунке 4. В этом режиме работы центр тяжести перемещается как по вертикали, так и по горизонтали. Таким образом, предыдущий анализ представляет собой одномерное приближение, полезное для качественного понимания механического резонанса кристалла с АТ-срезом.
Рис. 4. Толщина АТ-среза, сдвиговый резонанс.
С точки зрения параллельной схемы, общий электрический импеданс кристалла будет обратно пропорционален площади электрода, поскольку большая площадь электрода эквивалентна нескольким параллельным кристаллам с меньшей площадью электрода. Таким образом, последовательное сопротивление и индуктивность движения будут обратно пропорциональны площади электрода; емкость движения и параллельная пластинчатая часть емкости шунта будут пропорциональны площади электрода. Емкость шунта и емкость движения имеют линейную зависимость, поскольку они пропорциональны площади электрода для неупакованного кристалла, обычно известного как заготовка кристалла. Соотношение было бы пропорциональным, если бы паразитной шунтирующей емкостью корпуса можно было пренебречь и если бы поля окантовки параллельных пластин шунтирующей емкости были пренебрежимо малы.
Соотношение было бы пропорциональным, если бы паразитной шунтирующей емкостью корпуса можно было пренебречь и если бы поля окантовки параллельных пластин шунтирующей емкости были пренебрежимо малы.
Ниже приведен список компромиссов дизайна, основанный на предыдущем анализе:
- Меньшие площади кристаллических электродов привлекательны из-за более низкой стоимости и, возможно, меньшего размера упаковки. Однако эта меньшая площадь увеличивает последовательное сопротивление, что замедляет время запуска (см. следующий раздел Startup Time ) и может предотвратить колебания.
- Более крупные площади кристаллических электродов снижают последовательное сопротивление. Однако эта большая площадь увеличивает шунтирующую емкость, которая затем снижает отрицательное сопротивление активной цепи (см. 9).0033 Отрицательное сопротивление ниже), что, в свою очередь, также замедляет время запуска и может предотвратить колебания. Большая площадь кристаллического электрода увеличивает подвижную емкость.
 Чем больше емкость движения, тем выше чувствительность к смещению частоты из-за внешних емкостных нагрузок или «вытягивания» частоты (см. раздел «Нагрузочная емкость » ниже).
Чем больше емкость движения, тем выше чувствительность к смещению частоты из-за внешних емкостных нагрузок или «вытягивания» частоты (см. раздел «Нагрузочная емкость » ниже).
Емкость нагрузки
Многие кварцевые генераторы работают в точке параллельного резонанса кварца и приложенной емкости нагрузки. Емкость нагрузки определяется как эффективная емкость, внешняя по отношению к корпусу кристалла, приложенная между клеммами кристалла, как показано на рис. 5. Производители кристаллов указывают заданную емкость нагрузки вместе с рабочей частотой. Работа с емкостью нагрузки, которая отличается от емкости нагрузки, указанной производителем, приводит к отклонению частоты колебаний от частоты, указанной производителем. Ошибка частоты связана с емкостным «вытягиванием» кристалла. Это можно продемонстрировать, объединив параллельные шунтирующие и нагрузочные емкости, а затем последовательно объединив эту суммарную шунтирующую и нагрузочную емкости с подвижной емкостью, чтобы сформировать общую эффективную емкость.
C EFF = C ДВИЖЕНИЕ × (C НАГРУЗКА + C ШУНТ )/(C НАГРУЗКА + C ШУНТ + C ДВИЖЕНИЕ )
Рис. 5. Емкость нагрузки.
Общее эффективное изменение емкости очень незначительно, потому что емкость движения обычно примерно на три порядка ниже, чем емкости шунта и нагрузки. Следовательно, (C НАГРУЗКА + C ШУНТ )/(C НАГРУЗКА + C SHUNT + C MOTIONAL ) почти равна единице, а эффективная общая емкость очень близка к значению двигательной емкости. Обратите внимание, что по мере увеличения емкости нагрузки (C НАГРУЗКА + C ШУНТ )/(C НАГРУЗКА + C ШУНТ + C ДВИЖЕНИЕ ) приближается к единице, и влияние абсолютных изменений в емкость нагрузки на общую эффективную емкость ослабевает (снижение частоты тянет). Таким же образом, меньшие подвижные емкости также снижают частотное притяжение, поскольку (C НАГРУЗКА + C ШУНТ )/(C НАГРУЗКА + C ШУНТ + C ДВИЖЕНИЕ ) приближается к единице для любой заданной емкости нагрузки. См. рис. 6, где показана зависимость частоты от емкости нагрузки (кривая растяжения) типичного кристалла.
См. рис. 6, где показана зависимость частоты от емкости нагрузки (кривая растяжения) типичного кристалла.
Рисунок 6. Типичная кривая вытягивания для 5fF C MOTIONAL , 3pF C SHUNT , 3pF указан C LOAD , кварц 10MHz.
Отрицательное сопротивление
Генераторы с топологией Пирса или Колпитца обычно используются в сочетании с кварцевым кристаллом для генерации эталонов времени или частоты. Обе топологии называются «трехточечный осциллятор». Общие формы показаны на рисунках 7 и 8. Обратите внимание, что три точки A, B и C идентичны для обеих топологий, за исключением точки AC-земля.
Рис. 7. Генератор Колпитца.
Рис. 8. Генератор Пирса.
Чтобы определить импеданс, подаваемый на кристалл транспроводником (обычно MOSFET или биполярным транзистором, но в некоторых случаях JFET или даже вакуумной лампой) и конденсаторами C3 и C2, мы можем заменить кристалл источником тока, который управляет током. из точки А в точку С эквивалентной схемы генератора Пирса (рис. 9). Из этого:
из точки А в точку С эквивалентной схемы генератора Пирса (рис. 9). Из этого:
В А = -Z3 × I
Где Z3 = 1/(j × ω × C3).
V C = Z2 × I — Z2 × g M × V A = Z2 × I + Z2 × g M × Z3 × I = I × (Z2 + g M × Z3 × Z2)
и g M — малое изменение сигнала тока коллектора на изменение напряжения база-эмиттер для транзистора с биполярным переходом (g M = ΔI C /ΔV BE ), или малое изменение сигнала тока стока на изменение напряжения затвор-исток для полевого МОП-транзистора (g M = ΔI D /ΔV GS ).
Где Z2 = 1/(j × ω × C2).
V CA = V C — V A = I × (Z3 + Z2 + g M × Z3 × Z2)
Z IN = V CA /I = Z3 + Z2 + g M /(C3 × C2 × (j × ω)²) = Z3 + Z2 — g M /(C3 × C2 × ω²)
Рис. 9. Определение входного сопротивления генератора Пирса.
9. Определение входного сопротивления генератора Пирса.
Поскольку Z IN представляет собой импеданс, подаваемый на кристалл двумя конденсаторами и преобразователем, то импеданс, подаваемый на кристалл, фактически является последовательной комбинацией последовательно соединенных С3 и С2 с отрицательным сопротивлением. Обратите внимание, что это позволяет легко установить емкость нагрузки кристалла путем соответствующего выбора C3 и C2, независимо от крутизны.
Этот анализ предполагает, что любое произвольное отрицательное сопротивление для возбуждения кристалла может быть синтезировано с соответствующей крутизной и выбором конденсатора для трехточечного генератора. Это верно при отсутствии какой-либо паразитной емкости между узлами A и C. В действительности, однако, некоторая паразитная емкость всегда будет существовать между узлами A и C. Что еще более важно, шунтирующая емкость кристалла всегда будет уменьшать представленное эффективное отрицательное сопротивление. к подвижной ветви RLC кристалла.
к подвижной ветви RLC кристалла.
Чтобы оценить влияние емкости кварцевого шунта на трехточечный генератор, см. Рисунок 10.
Рис. 10. Эквивалентная схема трехточечного генератора с кварцем.
Возвращаясь к уравнению для входного сопротивления трехточечного генератора:
Z В = Z3 + Z2 + г М × Z3 × Z2
И размещение этого импеданса (Z IN ) параллельно с C SHUNT :
Z ПРИМЕНЯЕТСЯ = [1/Z ШУНТ + 1/(Z3 + Z2 + g M × Z3 × Z2)] -1
Z ПРИМЕНЯЕМЫЙ = [(Z3 + Z2 +Z ШУНТ + g M × Z3 × Z2)/(Z3 × Z ШУНТ + Z2 × Z ШУНТ + g M × Z3 × Z2 × Z ШУНТ )] -1
Z ПРИКЛАДНОЙ = (Z3 × Z ШУНТ + Z2 × Z ШУНТ + g M × Z3 × Z2 × Z ШУНТ )/(Z3 + Z2 +Z ШУНТ + г M × Z3 × Z2)
Заменив общие импедансы емкостными импедансами и взяв действительную часть Z APPLIED , отрицательный импеданс, представленный трехточечным генератором для ветви движения RLC кристалла, равен:
Re{Z ПРИМЕНЯЕМЫЙ } = -(g M × C3 × C2)/[ω² × (C3 × C2 + C3 × C ШУНТ + C2 × C ШУНТ )² + (g M × C ШУНТ )²]
Взяв производную от Re{Z APPLIED } относительно g M и приравняв производную к нулю, получим крутизну g M(MIN)R , при которой возникает минимум (наибольшая величина) отрицательного сопротивления:
g M(MIN)R = ω × [(C3 × C2)/C ШУНТ + C3 +C2]
При g M(MIN)R возникает максимальная величина отрицательного сопротивления, что дает:
Re{Z ПРИМЕНЯЕТСЯ }| МИН = -1/{2 × ω × C ШУНТ × [1 + C ШУНТ × (C3 + C2)/(C3 × C2)]}
Отрицательное сопротивление, Re{Z APPLIED }, имеет следующие характеристики:
- Всегда отрицательное значение.

- Абсолютное значение отрицательного сопротивления падает по мере увеличения C SHUNT . (См. рисунки 11 и 12.)
- Максимально достижимое абсолютное значение отрицательного сопротивления (при g M(MIN)R ) падает по мере увеличения C SHUNT . (См. рисунки 11 и 12.)
- Абсолютное значение отрицательного сопротивления должно быть больше, чем сопротивление движению кристалла, чтобы происходили колебания. Как правило, типичное или номинальное абсолютное значение отрицательного сопротивления должно более чем в четыре раза превышать сопротивление движению.
Рис. 11. Отрицательное сопротивление в зависимости от емкости нагрузки на частоте 10 МГц с крутизной 5 мА/В; Емкость нагрузки обусловлена последовательной комбинацией C3 и C2.
Рис. 12. Отрицательное сопротивление в зависимости от крутизны на частоте 10 МГц с емкостью нагрузки 10 пФ; Емкость нагрузки обусловлена последовательной комбинацией C3 и C2 (каждый по 20 пФ).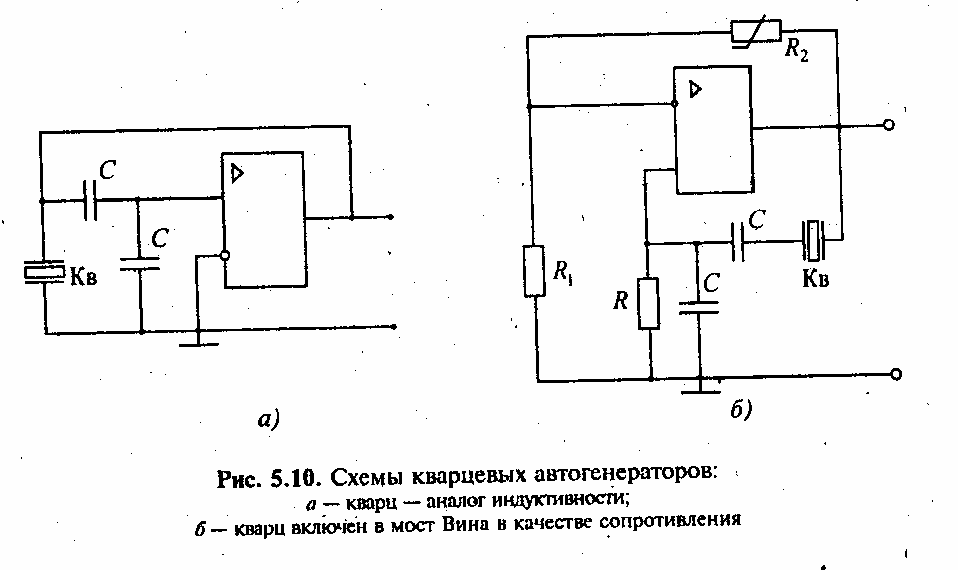
Обратите внимание на сильное влияние C SHUNT на оба графика. Даже небольшое увеличение C SHUNT уменьшает величину отрицательного сопротивления во всех возможных конфигурациях, особенно вблизи пика величины отрицательного сопротивления.
Чтобы применить рекомендуемую емкость нагрузки к кристаллу и поддерживать более высокую величину отрицательного сопротивления, важно поддерживать C ШУНТ маленький и для увеличения С3 и С2 применить необходимую емкость нагрузки. В качестве примера рассмотрим следующие случаи, когда емкость нагрузки кварца составляет 8 пФ, рабочая частота — 10 МГц, кварц C SHUNT — 2 пФ, паразитные значения C3 и C2 — 8 пФ (из-за паразитных емкостей корпуса ИС и печатной платы). ), а крутизна фиксирована (из-за внутреннего смещения ИС и размера устройства) на уровне 1 мА/В.
Дело 1 . Используйте керамические конденсаторы емкостью 8 пФ в положениях C3 и C2 для загрузки кристалла. Эти конденсаторы 8 пФ подключены параллельно с паразитными емкостями 8 пФ для общих значений C3 и C2 16 пФ. Это нагрузит кварц 8 пФ, так как C3 и C2 включены последовательно по отношению к кварцу. В этом случае отрицательное сопротивление, рассчитанное по предыдущему уравнению для Re{Z APPLIED } будет -627 Ом.
Эти конденсаторы 8 пФ подключены параллельно с паразитными емкостями 8 пФ для общих значений C3 и C2 16 пФ. Это нагрузит кварц 8 пФ, так как C3 и C2 включены последовательно по отношению к кварцу. В этом случае отрицательное сопротивление, рассчитанное по предыдущему уравнению для Re{Z APPLIED } будет -627 Ом.
Дело 2 . Используйте керамический конденсатор емкостью 4 пФ параллельно с кристаллом, так как это экономит стоимость одного конденсатора и размещение одного конденсатора поверхностным монтажом по сравнению со случаем 1. Паразитные емкости C3 и C2 по 8 пФ каждая нагружают кристалл по 4 пФ. Дополнительные 4 пФ шунтирующей емкости при параллельном подключении в сумме дают емкость нагрузки 8 пФ. Однако в этом случае отрицательное сопротивление будет всего -466 Ом. из-за нежелательных эффектов увеличения C ШУНТ .
Обратите внимание, что вариант 1 предпочтительнее варианта 2 для конструкции кварцевого генератора из-за более высокого абсолютного значения отрицательного сопротивления.
Время запуска
Время запуска кварцевого генератора может иметь множество различных определений в зависимости от типа системы. Определение времени запуска микропроцессорной системы часто представляет собой время от первоначального включения питания до времени, когда доступен стабильный тактовый сигнал. Определение времени запуска для контура фазовой автоподстройки частоты (ФАПЧ) часто представляет собой время от начальной подачи питания до времени, когда доступен стабильный опорный сигнал, часто устанавливаемый в пределах допустимого смещения частоты от конечной частоты колебаний в установившемся режиме.
Время запуска кварцевого генератора определяется начальным шумом или переходными условиями при включении; расширение огибающей слабого сигнала за счет отрицательного сопротивления; и ограничение конечной амплитуды большого сигнала из-за конечного энергопотребления.
Расширение оболочки является функцией только полного отрицательного сопротивления и динамической индуктивности кристалла. Упрощенная эквивалентная последовательная RLC-цепь будет содержать индуктивность движения, сумму приложенного отрицательного сопротивления трехточечного генератора и сопротивления движения кристалла, а также эффективную последовательную емкость всей сети (в которой преобладает подвижная емкость). Для сети применяется следующее дифференциальное уравнение области Лапласа (без управляющей функции):
Упрощенная эквивалентная последовательная RLC-цепь будет содержать индуктивность движения, сумму приложенного отрицательного сопротивления трехточечного генератора и сопротивления движения кристалла, а также эффективную последовательную емкость всей сети (в которой преобладает подвижная емкость). Для сети применяется следующее дифференциальное уравнение области Лапласа (без управляющей функции):
с × L + R + 1 / (с × С) = 0
Или
s² + s × (R/L) + 1/(L × C) = 0
Корни этого уравнения лежат в:
(½) × {-R/L +/- √[(R/L)² — 4/(L × C)]}
Поскольку в члене R / L внутри квадратного корня полностью преобладает член 1 / (L × C), это сводится к:
-R/(2 × L) +/- j × √[1/(L × C)]
Поскольку значение полного сопротивления R отрицательно, полюса этой системы находятся в правой полуплоскости, и результирующее решение во временной области для этого дифференциального уравнения:
V(t) = K × [e |(R/2 × L)| × t ] × sin{2 × π × √[1/(L × C)] × t + Θ}
Где K — константа, связанная с начальным условием запуска, а Θ — произвольная фаза, связанная с начальным условием запуска.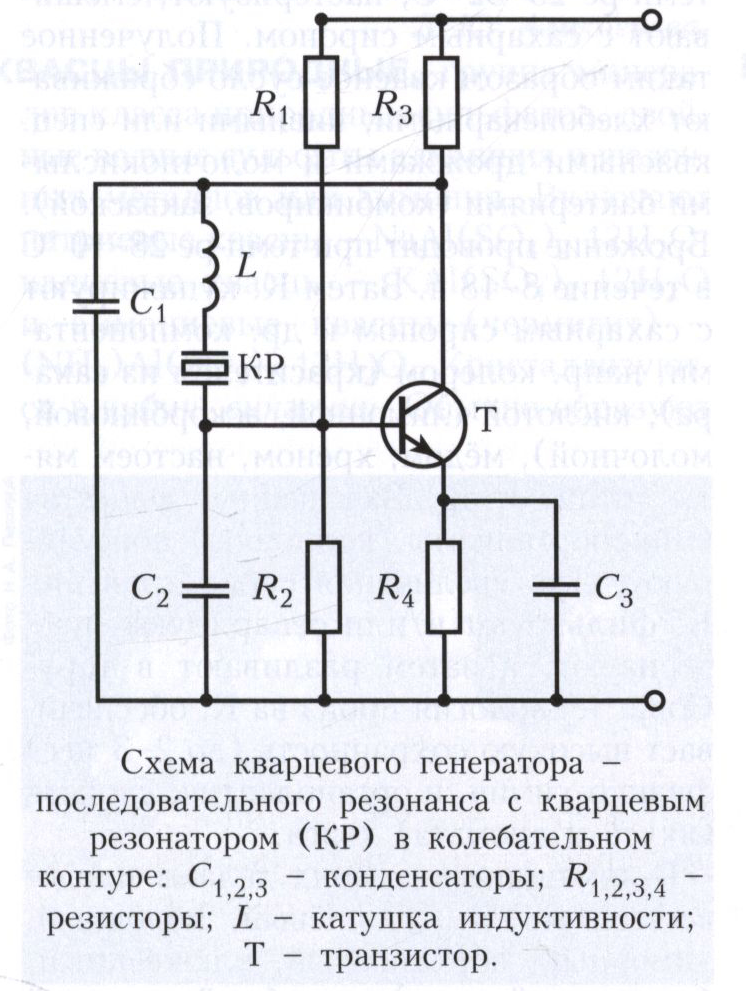 (Обратите внимание, что экспоненциальное расширение будет действительным только для условий слабого сигнала, поскольку мощность, доступная для схемы, ограничена.)
(Обратите внимание, что экспоненциальное расширение будет действительным только для условий слабого сигнала, поскольку мощность, доступная для схемы, ограничена.)
Постоянная времени расширения огибающей положительна и пропорциональна чистому отрицательному сопротивлению трехточечного осциллятора и сопротивлению движению и обратно пропорциональна индуктивности движения. Из-за большой динамической индуктивности кристаллов и ограниченного чистого отрицательного сопротивления кварцевые генераторы имеют очень большое время запуска.
В качестве примера постоянной времени расширения огибающей при запуске кварцевого генератора предположим, что кварц имеет подвижную емкость 5fF и генератор с величиной отрицательного сопротивления 1500 Ом, работающий на частоте 10 МГц. Используя подвижную емкость и рабочую частоту, подвижная индуктивность 50,66 мГн может быть определена как L = 1/(C × ω²). Эта движущая индуктивность дает постоянную времени расширения огибающей колебаний τ = 2 × L/|R| = 67,55 мкс. Обратите внимание, что существует компромисс между меньшей частотой тяги из-за низкой подвижной емкости и более длительным временем запуска из-за высокой подвижной индуктивности, из которых высокая подвижная индуктивность является прямым результатом низкой подвижной емкости. Смягчающим фактором является то, что меньшие подвижные емкости также связаны с меньшими шунтирующими емкостями, что приведет к большим отрицательным сопротивлениям и, таким образом, улучшит время запуска.
Обратите внимание, что существует компромисс между меньшей частотой тяги из-за низкой подвижной емкости и более длительным временем запуска из-за высокой подвижной индуктивности, из которых высокая подвижная индуктивность является прямым результатом низкой подвижной емкости. Смягчающим фактором является то, что меньшие подвижные емкости также связаны с меньшими шунтирующими емкостями, что приведет к большим отрицательным сопротивлениям и, таким образом, улучшит время запуска.
Время запуска является важным конструктивным соображением во многих приложениях с батарейным питанием, где системы находятся в рабочем цикле между выключенным и включенным рабочими состояниями. Более короткое время запуска кварцевого генератора ограничивает потери мощности во время полного прогрева кристалла в маломощных радиосистемах, таких как приемопередатчик MAX7032, передатчик MAX1472 и передатчик MAX7058.
Стабильность частоты в зависимости от температуры
Частотный сдвиг резонансной частоты в зависимости от температуры зависит от угла среза кристалла в зависимости от структуры решетки кварца.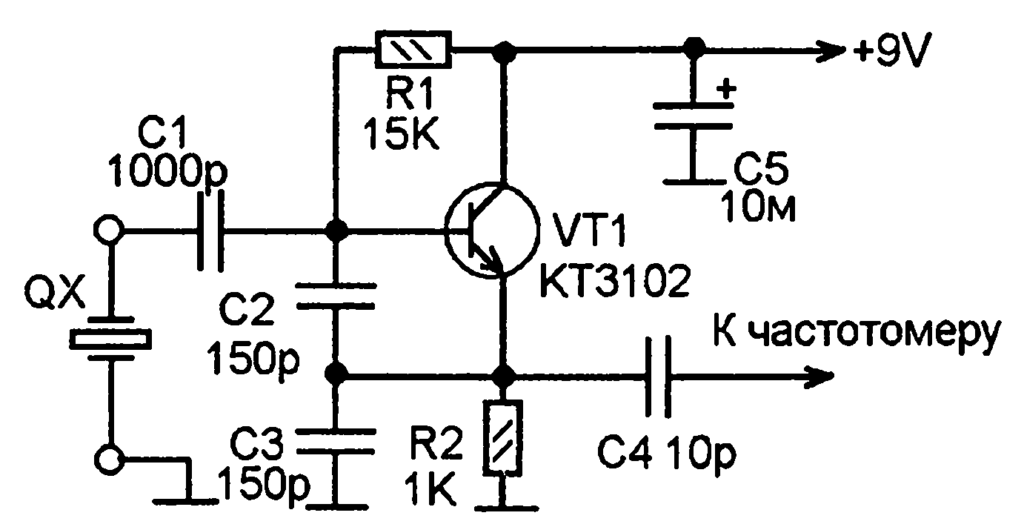 Относительный сдвиг частоты в зависимости от температуры кристаллов кварца АТ-среза можно представить в виде кубического полинома:
Относительный сдвиг частоты в зависимости от температуры кристаллов кварца АТ-среза можно представить в виде кубического полинома:
Δf/f 0 = А 0 + А 1 (Т — Т 0 ) + А 2 (Т — Т 0 )² + А 3 (Т — Т 0 ) )³
Где коэффициенты от А 0 до А 3 являются функциями угла среза кварца.
Стабильность частоты очень важна в радиосистемах с кристаллом в качестве эталона частоты системы. Это особенно верно для узкоканальных приложений на высокой частоте. Примером может служить работа в части полосы пропускания канала 25 кГц диапазона ISM от 863 МГц до 870 МГц в Европе. В этих каналах сдвиг частоты на 5 кГц из 865 МГц (5,78 частей на миллион) может привести к сбою системы или несоблюдению нормативных требований. Как видно на рис. 13, этого невозможно достичь даже с идеальным углом среза, нулевым допуском и нулевым старением кристалла в промышленном диапазоне температур от -40°C до +85°C.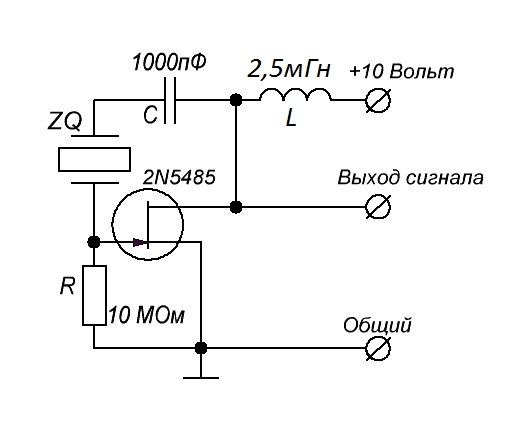 В этом случае радиосистема с внутренним датчиком температуры и синтезатором дробного коэффициента деления с узким шагом частоты, например MAX7049.передатчик, можно использовать для компенсации известных температурных коэффициентов частоты кристалла.
В этом случае радиосистема с внутренним датчиком температуры и синтезатором дробного коэффициента деления с узким шагом частоты, например MAX7049.передатчик, можно использовать для компенсации известных температурных коэффициентов частоты кристалла.
Рис. 13. График зависимости относительного сдвига частоты от температуры для углов кристалла с АТ-срезом в минутах.
Старение
Частота последовательного резонанса кристалла будет медленно меняться с течением времени. Это известно как старение. Обычно изменение частоты на несколько частей на миллион происходит в течение нескольких лет. Большинство изменений обычно происходит в течение первого или двух лет. Старение часто связывают с изменением массы кристаллов во времени. Скорость старения ускоряется при более высоких температурах и более высоких амплитудах колебаний.
Компиляция источников ошибок частоты
Ошибка частоты возникает из-за следующих источников:
- Начальный допуск, который является гарантированным изготовителем допуском по частоте при +25°C и с указанной нагрузочной емкостью, приложенной к кристаллу
- Стабильность частоты в зависимости от температуры
- Тяга из-за изменений емкости нагрузки
- Старение
Зависимость на уровне диска
После некоторого времени бездействия последовательное сопротивление кристалла может подняться до уровня, намного превышающего максимальное значение, указанное в паспорте производителя. Период бездействия может варьироваться от часов до недель. Часто состояние не может повториться. Как только кристалл подвергается вибрации из-за электрического или механического переходного процесса, последовательное сопротивление возвращается к нормальным пределам, указанным в технических характеристиках. Это известно как зависимость от уровня привода или DLD и иногда называется «сонными кристаллами», когда после периода бездействия последовательное сопротивление кристалла является функцией уровня электрического привода переменного тока.
Период бездействия может варьироваться от часов до недель. Часто состояние не может повториться. Как только кристалл подвергается вибрации из-за электрического или механического переходного процесса, последовательное сопротивление возвращается к нормальным пределам, указанным в технических характеристиках. Это известно как зависимость от уровня привода или DLD и иногда называется «сонными кристаллами», когда после периода бездействия последовательное сопротивление кристалла является функцией уровня электрического привода переменного тока.
Считается, что это состояние является результатом дополнительных механических потерь из-за загрязнения внутри корпуса кристалла. Загрязнение может быть жидким или твердым. Жидкость может быть влагой, которая случайным образом конденсируется или замерзает на кристалле при температуре ниже определенной. Состояние нормального последовательного сопротивления возвращается, как только вибрация кристалла удаляет загрязнения с поверхности кварца. Часто загрязнение не оседает снова (или, по крайней мере, не в той же степени) на поверхности кварца, что приводит к непредсказуемому поведению после последующих периодов бездействия.
В других случаях постоянно прикрепленная частица со свойствами, зависящими от времени и/или амплитуды колебаний, плохо прилипшее покрытие электрода, механические царапины или другие дефекты могут привести к DLD.
Никакие изделия из кристаллов не могут быть полностью свободны от DLD, но более качественные продукты демонстрируют гораздо более низкий DLD как по степени увеличения последовательного сопротивления, так и по проценту единиц, демонстрирующих изменения сопротивления.
Чтобы смягчить проблему, связанную с DLD, можно предпринять следующие шаги:
- Работа с большим отрицательным сопротивлением, более чем в четыре раза превышающим максимальное последовательное сопротивление, указанное производителем. Это решит почти все проблемы с DLD.
- Покупка у торговцев кристаллами более высокого качества.
- Оплатить надбавку за тестирование DLD.
Ложные моды
Нежелательные механические резонансы часто существуют вблизи основной частоты. Эти «паразитные моды» могут быть смоделированы как дополнительные последовательные ответвления RLC, параллельные требуемому ответвлению RLC основной частоты, таким же образом, как моделируется работа обертонов. Побочные моды имеют большие потери (меньшие возможности для колебаний), чем желаемая мода; они обычно не вызывают проблем с кварцевым генератором, если только они не имеют очень малых потерь или активная схема очень слабо ограничена.
Эти «паразитные моды» могут быть смоделированы как дополнительные последовательные ответвления RLC, параллельные требуемому ответвлению RLC основной частоты, таким же образом, как моделируется работа обертонов. Побочные моды имеют большие потери (меньшие возможности для колебаний), чем желаемая мода; они обычно не вызывают проблем с кварцевым генератором, если только они не имеют очень малых потерь или активная схема очень слабо ограничена.
Как правило, производители кристаллов проверяют паразитные моды и не будут поставлять устройства с низкими потерями (т. Е. С большей возможностью колебаний) на паразитных резонансных частотах.
Осцилляторы с большим отрицательным сопротивлением обычно ограничивают или обрезают большую часть цикла колебаний. При ограничении эффективное усиление схемы близко к нулю. Следовательно, паразитные моды не имеют необходимого усиления для генерации и эффективно подавляются желаемой генерацией с большим сигналом. В некоторых случаях с более низким отрицательным сопротивлением или схемами с мягким ограничением в течение всего цикла желаемых колебаний существует достаточный коэффициент усиления, чтобы поддерживать вторичные нежелательные колебания.


 Чем больше емкость движения, тем выше чувствительность к смещению частоты из-за внешних емкостных нагрузок или «вытягивания» частоты (см. раздел «Нагрузочная емкость » ниже).
Чем больше емкость движения, тем выше чувствительность к смещению частоты из-за внешних емкостных нагрузок или «вытягивания» частоты (см. раздел «Нагрузочная емкость » ниже).