Действующее напряжение и амплитудное напряжение
Все знают, что действующее напряжение в розетке 220 Вольт (230 по новым нормам, но для данной темы это не имеет особого значения). Это легко проверить при помощи мультиметра, который измерит разность потенциалов между фазой и рабочим нулевым проводником. То есть, при идеальных условиях, потенциал на нулевом проводе 0, а на фазном 220 Вольт. На самом деле все немного не так — переменный ток имеет синусоидальную форму с потенциалом на пиках 310 и -310 Вольт (амплитудное напряжение). Для того чтобы это увидеть, необходимо воспользоваться осциллографом.
Синусоида действующего и амплитудного напряжения
Понятно, что данный материал в большей степени ориентирован на простую аудиторию, у которой не то, что осциллографа нет, даже мультиметр наверняка не у каждого есть. Поэтому все примеры будут браться из среды программы Electronics Workbench, доступной каждому.
И первое, что нам нужно посмотреть — это синусоиду напряжения фазы из розетки. Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:
Для этого в программе отрисуем трехфазную сеть и подключим осциллограф к одной из фаз:
Как видно при показании вольтметра 219,4 Вольт между одной из фаз и PEN проводником, осциллограф показал синусоиду с амплитудой 309,1 Вольт. Это значение напряжения называется максимальным (амплитудным). А 219,4 Вольт, которые показывает вольтметр — это действующее напряжение. Его также называют среднеквадратичным или эффективным. И прежде чем перейти к рассмотрению данной особенности, кратко, простыми словами пройдемся по отрисованной схеме трехфазной сети и разберемся в природе синусоиды.
Начнем со схемы:
- Слева на право — три источника переменного напряжения с фазовыми углами 0, 120, 240 градусов и соединенными звездой.
- Резистор 4 Ом — это заземление нейтрали трансформатора.
- Резисторы по 0,8 Ом — условное сопротивление проводов, зависящее от сечения провода и длины линии.
- Резисторы 15, 10 и 20 Ом — нагрузка потребителей по трем фазам.

- К одной из фаз подключен осциллограф, показывающий амплитуду 309,1 Вольт.
Теперь рассмотрим синусоиду. Переменное напряжение в отличие от постоянного, график которого прямая на осциллографе, непрерывно изменяется как по величине, так и по направлению. Причем изменения эти происходят периодически, то есть точно повторяются через равные промежутки времени.
Переменное напряжение генерируется на электростанциях и посредством повышающих и понижающих распределительных трансформаторов попадает к конечному потребителю. При этом трансформация по пути никак не сказывается на синусоиде напряжения.
Видео — действующее напряжение и амплитудное
С полным и наглядным изложением рассматриваемого вопроса вы можете ознакомиться в следующем видео:
Работа генератора трехфазного переменного тока
Рассмотрим упрощенно работу генератора трехфазного переменного тока. Обмотки статора (фазы А, В и С) генератора расположены под углом 120 градусов относительно друг друга. Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:
Ротор с магнитом вращаясь индуцирует в обмотках статора периодически изменяющиеся ЭДС. Выглядит это следующим образом:
Такое вращение происходит с частотой 50 оборотов в секунду, то есть с частотой 50 Герц. Это значит, что электроны движутся в течение 1 секунды 50 раз в одном направлении (положительный полупериод синусоиды), и 50 — в обратном (отрицательный полупериод), 100 раз проходя чрез нулевое значение. Получается, что к примеру обычная лама накаливания, включенная в сеть с такой частотой, будет затухать и вспыхивать примерно 100 раз за секунду, однако мы этого не замечаем в силу особенностей своего зрения.
Определение действующего напряжения
Теперь непосредственно о том, почему произошел переход от максимального, амплитудного значения напряжения 310 Вольт к действующему 220 Вольт. Ответ можно найти в самом определении.
Действующее (эффективное или среднеквадратичное) значение напряжения — это такое напряжение постоянного тока, которое на такой же резистивной нагрузке выделит такую же мощность, как измеряемое переменное напряжение. Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.
Соответственно, действующее значение силы тока — такое значение силы постоянного тока, при прохождении которого через резистивную нагрузку выделится такая же мощность, что и при прохождении измеряемого тока.
Можно сформулировать и немного иначе. Действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведет такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
Общая формула расчета действующего напряжения произвольной формы следующая:
Объяснение действующего напряжения
Определение и формула — это хорошо. Но лучше все понять на наглядном примере. Объяснить все можно через мощность. Причем есть сложный для восприятия способ и более простой, который мы и рассмотрим далее.
Нам нужно взять один период синусоиды переменного напряжения, на этом промежутке построить синусоиду переменного тока и проанализировать мощность. Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.
Начнем с периода синусоиды переменного напряжения. Здесь же построим синусоиду переменного тока с учетом условной резистивной нагрузки (например, лампочки). По закону Ома сила тока равна напряжению, деленному на сопротивление.
Точные значения в конкретный момент при данном объяснении не принципиальны, поэтому все построения приблизительные. Естественно нужно понимать, что деля напряжение на сопротивление, мы получим синусоиду переменного тока с амплитудой в R раз меньшей, чем у напряжения. R – это значение сопротивления.
Теперь по двум синусоидам строим график мощности по формуле мощность равна силе тока умноженной на напряжение (P = I × U). Так как напряжение и ток имеют общие нулевые точки, то график мощности не будет заходить в отрицательную область. То есть сила тока со знаком «+» и напряжение со знаком «+» дадут мощность со знаком «+», так же как и сила тока со знаком «-» и напряжение со знаком «-» дадут мощность со знаком «+».
Анализируя полученный график можно отметить, что мощность пульсирующая. Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:
Она поднимается до максимального значения и падает до нуля, потом опять поднимается и снова падает. Как на эти колебания мощности реагируют электроприборы? Никак. Поскольку частота переменного тока 50 Герц, то эти колебания происходят очень быстро. Электроприборы откликаются не на максимальные и минимальные значения мощности, а на усредненные. То есть берется максимальное значение мощности и делится на два. Это значение называется действующим и находится по следующей формуле:
Pд = (Imax × Umax) / 2, где Pд — мощность действующая, Imax — сила тока максимальная, Umax — напряжение максимальное.
Двойку можно представить в виде корень из двух умножить на корень из двух. Получаем Действующее значение мощности = сила тока максимальная деленная на корень из двух умноженная на напряжение максимальное деленное на корень из двух (Pд = (Imax/√2) × (Umax/√2)).
Соответственно сила тока максимальная деленная на корень из двух — это действующее значение силы переменного тока, а напряжение максимальное деленное на корень из двух – это действующее значение переменного напряжения.
И действительно, если мы возьмем максимальное напряжение из предыдущего примера 309,1 Вольт и разделим на корень из двух, то получим действующее напряжение (то, которое показывает вольтметр) 219,4 Вольт.
Действующее значение напряжения
В проводниках переменного тока основные электродинамические показатели постоянно изменяются. Вследствие этого возникает вопрос: как можно адекватно оценить напряжение и силу тока в конкретной электроцепи? Так как моментальные и простые усредненные значения недостаточны для полной характеристики электротока, в электродинамике вводят такое понятие, как действующее значение тока.
- Что такое действующее значение напряжения
- Действующее значение тока
- Какие коэффициенты характеризуют переменное напряжение
- Параметры переменного тока
- Формула действующего значение тока
Что такое действующее значение напряжения
Изменение значений переменного тока обычно описывается синусоидальной линией с определенным периодом (Т) и амплитудой напряжения (Um).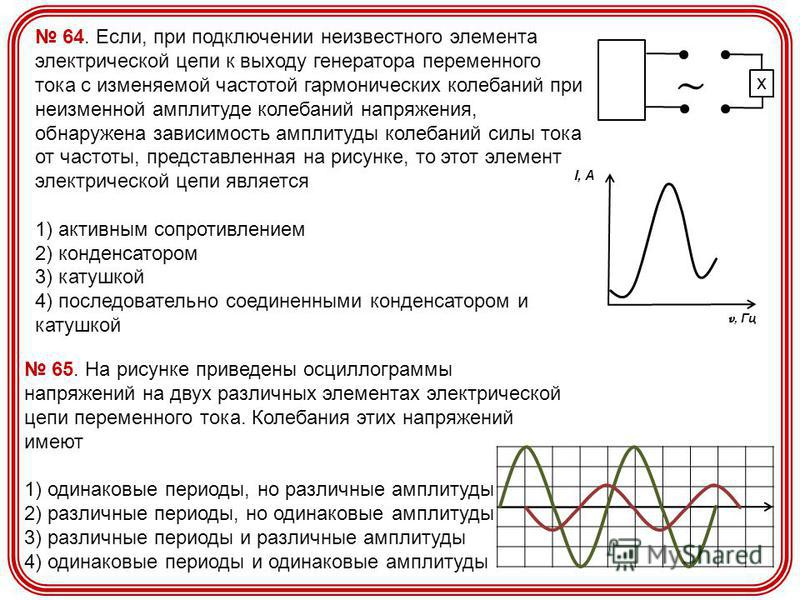 Кроме напряжения, электрический ток также характеризуется силой (I) и мощностью (P). Для постоянного электротока эти параметры складываются в простую формулу:
Кроме напряжения, электрический ток также характеризуется силой (I) и мощностью (P). Для постоянного электротока эти параметры складываются в простую формулу:
P = U × I.
При имеющемся сопротивлении в цепи и с учетом закона Ома (I = U / R) мощность, расходуемую электропотребителем. Можно определить как отношение квадрата напряжения к сопротивлению:
P = U2 / R.
В случае же переменного тока не все так однозначно. С изменением напряжения изменяется и мощность — в каждый момент времени (t) значения отличаются друг от друга. В такой ситуации для оценки электротока удобнее всего использовать его мощностные и тепловые характеристики. Поэтому действующее значение переменного тока приравнивается к работе постоянного тока, производимой за временной промежуток одного периода переменного тока.
При существующей активной нагрузке, независящей от частоты тока и напряжения мгновенная мощность определяется по формуле:
P(t) = U(t) × I(t) = U2 / R
Введя амплитудное значение напряжения, и учитывая период синусоидальной функции, мгновенную мощность можно определить следующим образом:
P(t) = (Um × sin(2π × 1/T))2 / R
Однако этот параметр для переменного тока — не имеет особой важности.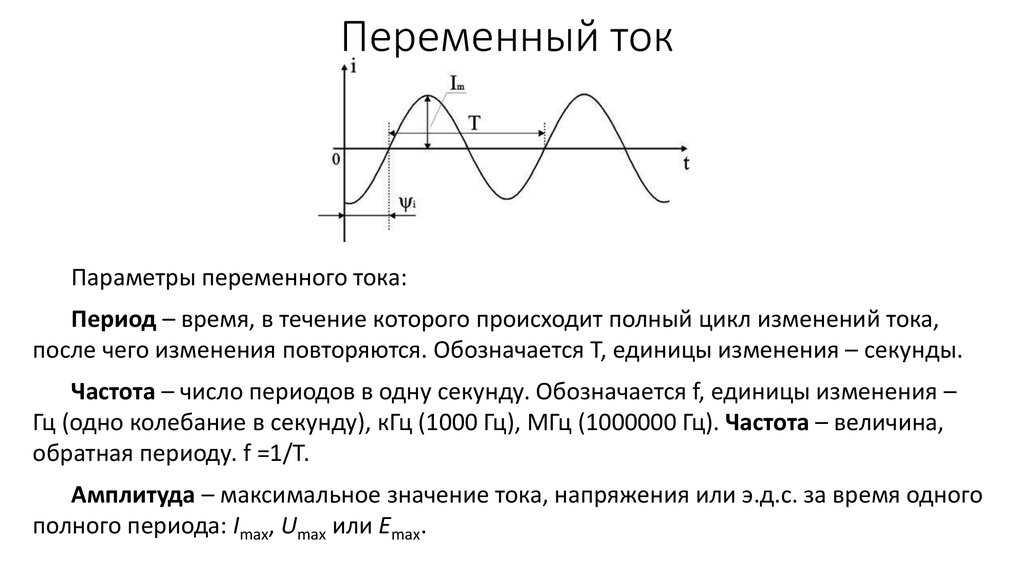 Для практических расчетов обычно берут мощность, усредненную за период. Как раз этот показатель указывается на бытовых электроприборах.
Для практических расчетов обычно берут мощность, усредненную за период. Как раз этот показатель указывается на бытовых электроприборах.
Формула усредненной мощности:
Здесь же представлена формула расчета действующего напряжения.
В вышеприведенной формуле интегрирование квадратной величины с последующим извлечением корня дает понять, почему эффективная величина напряжения также носит название «среднеквадратичной». При этом интегральное выражение под корнем является усредненной мощностью, пропорциональной сопротивлению.
Относительно синусоиды напряжение это интегральное выражение упрощается до формулы:
Именно эти цифры показывают вольтметры, настроенные на измерение проводников переменного тока.
Действующее значение тока
Применив метод интегрирования к квадратам амплитудной силы тока и синусу круговой частоты и выведя среднеквадратичные величины, можно получить действующее значение силы тока:
org/ImageObject»>Сравнивая тепловые эффекты постоянного и переменного электротоков, взятые за одинаковый временной отрезок и при одинаковой активной нагрузке, можно обнаружить, что равенство тепловых характеристик проводников того и другого типа достигается в том случае, если сила линейного тока будет меньше максимальных силовых значений в цепи переменного тока в 1,414 раз.
Какие коэффициенты характеризуют переменное напряжение
Помимо базовых параметров переменного тока, в электротехнике принято производить измерения электросигналов, включая выходные напряжения выпрямителей и импульсы различной формы.
Амплитудное значение напряжения
Под амплитудным или пиковым напряжением подразумевают максимальный показатель U за один период синусоиды:
Um = max(|u(t)|)
Для измерения данного параметра обычно используют вольтметр импульсного типа или осциллограф.
Мгновенное значение тока
Параметр обозначает силу тока или напряжение в конкретный временной момент (u(t), i(t)). В зависимости от динамики электрического сигнала, для определения мгновенных значений могут применяться малоинерционные вольтметры, а также шлейфовые или электронно-лучевые осциллографы.
Среднее значение
Показатель является постоянной составляющей переменного тока. Для напряжения оно рассчитывается по следующей интегральной формуле:
Для синусоидного напряжения с симметричной формой среднее значение равно нулю. Это можно определить с помощью обычного вольтметра. В геометрическом виде это может быть выражено как отношение разности площадей с обеих сторон оси t к периоду. Под названием напряжения смещения величина часто применяется в радиоэлектронике и обозначает напряжение, прилагаемое к электроду для выработки конкретных параметров постоянного электротока.
Среднеквадратичное значение
Среднеквадратичные интегральные величины силы тока и напряжения используются достаточно часто, вследствие их удобства для практического определения электродинамических характеристик в реальных проводниках. Они основываются на сравнении работы постоянного и переменного тока с активной нагрузкой и определенными величинами U и I.
Они основываются на сравнении работы постоянного и переменного тока с активной нагрузкой и определенными величинами U и I.
К примеру, лампочка или обогреватель будут выполнять одинаковую работу по освещению или обогреву как в сети переменного тока со стандартным напряжением 220 В, так и в цепи постоянного тока, если на нее подать такое же напряжение.
Напряжение в электросети обычно выражают в среднеквадратичном исчислении. Большинство приборов, измеряющих силу тока и напряжение, спроектированы под действующие показатели. Отдельные типы амперметров и вольтметров способны показывать верные эффективные значения только для синусоидального тока. В универсальных устройствах, работающих с любыми формами электросигнала, измерение осуществляется с помощью термопреобразователя. При этом фиксируется температура нагревателя, создающего определенное сопротивление.
Кроме того, в измерительных приборах может быть реализован метод возведения в квадрат мгновенного значения, после чего величина усредняется по временному периоду, а затем выводится квадратный корень.
Средневыпрямленное значение
Величина определяется как взятое по модулю среднеарифметическое всех мгновенных значений напряжения. Для одного периода средневыпрямленная величина равна сумме площадей сверху и снизу оси времени. Хотя параметр не находит практического применения, именно он фиксируется по факту большинством измеряющих устройств магнитоэлектрического принципа действия, несмотря на то, что их шкалы имеют градацию для действительных значений. При этом эффективные и средневыпрямленные значения оказываются близки друг к другу только в случае синусоидального напряжения.
Параметры переменного тока
Синусоидальные гармоники являются типичной характеристикой переменного тока. В этом отношении по синусоиде происходит изменение электродвижущей силы и тока при определенной нагруженности цепи. При этом динамика ЭДС может быть описана следующими параметрами:
• Период — время, за которое электродинамические показатели изменяются по полному циклу. Он напрямую связан с частотой вращения роторного механизма генератора электротока.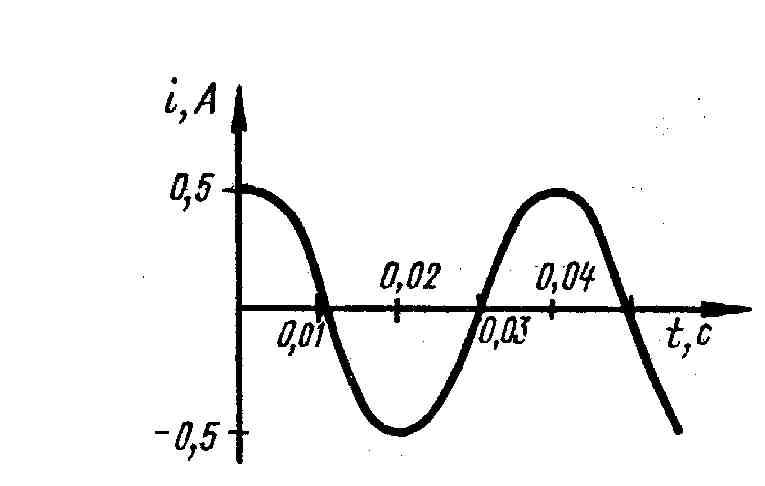
• Частота — определяется как число периодов за одну единицу времени. Современные стандарты для электросетей предписывают частоту переменного тока в 50 герц. Это означает, что за 1 секунду ток меняет направление 50 раз, а один период длится 20 миллисекунд.
• Амплитуда — максимальная величина гармоники переменного тока. В строгом смысле параметр применим исключительно к синусоидальному изменению. С некоторыми допущениями амплитуда может быть определена и для других форм электросигнала. За один период электродвижущая сила дважды доходит до пиковых значений и обозначается как Em+ и Em- соответственно положению полупериодов.
• Угловая частота — скорость колебательного движения, измеряемая в радианах в секунду. При этом один период синусоиды приравнивается к значению 2π. Общая формула угловой частоты: ω = 2π / Т.
• Фаза колебаний — стадия синусоидальной волны, принимаемая как аргумент функции тока, которая отсчитывается от среднего нулевого значения. Величина фазы колебаний, используемая для определения синуса или косинуса фазового угла, описывается формулой φ = ωt.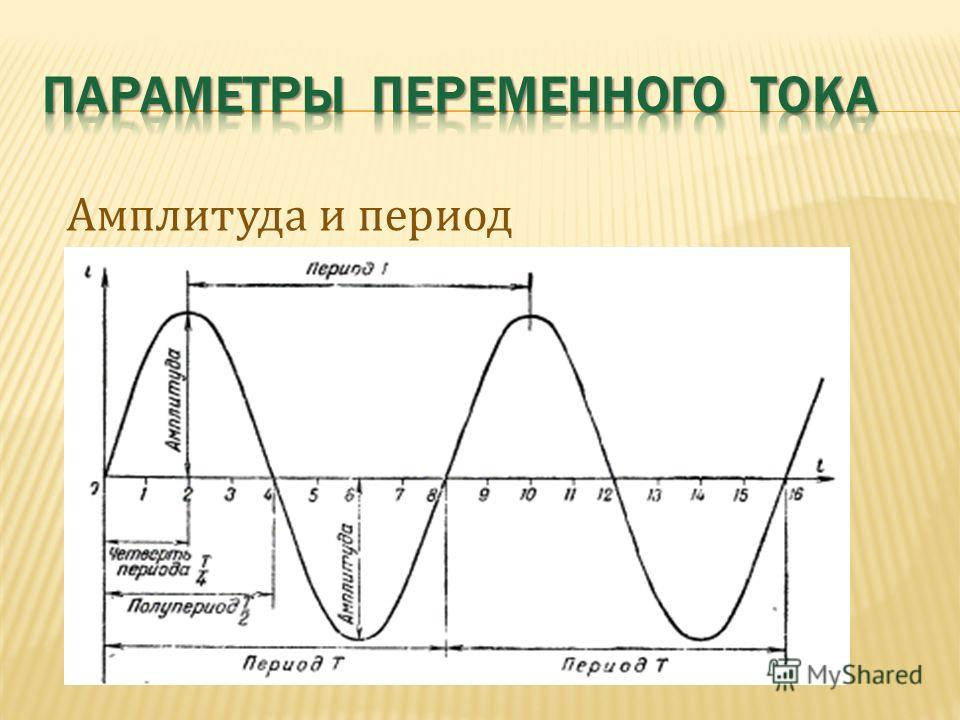
Как в случае со среднеквадратичными значениями тока и напряжения, через основные характеристики определяется и среднее значение ЭДС, которое сводится к следующему выражению:
Формула действующего значение тока
Среднеквадратичные показатели переменного тока определяется как отношение амплитудного значения тока к корню из 2.
Схожим образом обозначаются эффективные значения напряжения и ЭДС.
Действительные значения синусоидального тока помогают производить практическую оценку и описание электроцепей. Несмотря на сложность составляющих понятий, эти величины сводятся к простым выражениям. Номинальное напряжение электрических сетей и приборов представляет собой как раз среднеквадратичное значение. Умножив указанный вольтаж на корень из 2, можно узнать амплитудное значение напряжения электроустройств.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.
Мгновенное амплитудное и действующее значение переменного тока
- Автор: Sereg985
- Прокоментировать
- Рубрика: Строительство
- Ссылка на пост
- https://firmmy.ru/
Содержание
- 0.1 Что ты хочешь узнать?
- 1 Ответ
- 1.1 Проверено экспертом
- 2 Синусоидально изменяющийся ток
- 3 Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
- 4 Векторное изображение синусоидально изменяющихся величин
Речь идём о переменном токе.
Мгновенное значение (ЭДС или напряжения или тока) — значение величины в данный момент времени. обозначается чаще всего маленькими буквами: e, u,i.
обозначается чаще всего маленькими буквами: e, u,i.
Амплитудное значение (ЭДС или напряжения или тока) — максимальное значение. Обозначается :
Действующее значение отличается от максимального тем, что оно меньше максимального в раз, т.е.( на примере тока, для напряжения и ЭДС аналогично):
Обозначается действующее значение или без иднекса или с индексом «д»:
(только русское «д»).
Смысл действующего значения: при переменном токе (i) за период выделиться столько же тепла, сколько выделиться при действующем значении
Имеено действующее значение показывают приборы, подключённые в цепь с переменным током.
Среднее значение величин (-//-) -среднее арифметическое значение величины за полпериода.
Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.
Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины.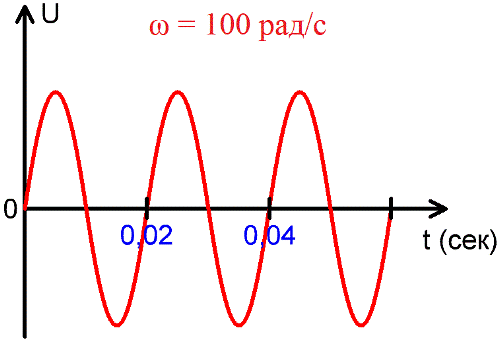 Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.
Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.
Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.
Если ток изменяется по закону синуса, т. е.
,то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:
.Аналогично для действующих значений синусоидальных напряжений:
.Фаза. Сдвиг фаз.
Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды Em, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.
Положение витков задано углами ψ1 и ψ2 для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:
;Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:
;Электрические углы ψ1 и ψ2 характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.
Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.
Дата добавления: 2016-05-25 ; просмотров: 7354 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:
,Аналогично определяются действующие значения ЭДС и напряжения.
Синусоидально изменяющийся ток
Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.
Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат
Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.
Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е1 и е2 соответствуют уравнения:
. Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0): и —начальной фазой ().
Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0): и —начальной фазой ().Величину
, характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.
.Векторное изображение синусоидально изменяющихся величин
На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е1 и е2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.
Пусть, например, в точке разветвления цепи (рис. 5) общий ток
равен сумме токовидвух ветвей:.
Каждый из этих токов синусоидален и может быть представлен уравнением
и.Результирующий ток также будет синусоидален:
.Определение амплитуды
и начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:
.Построение векторной диаграммы в масштабе позволяет определить значения
ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.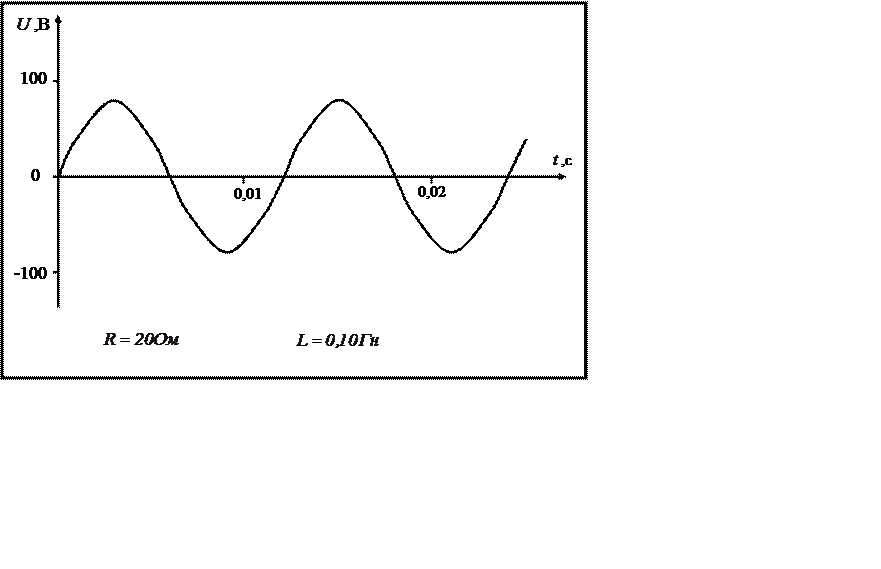
«>
Амплитудное значение — напряжение — Большая Энциклопедия Нефти и Газа, статья, страница 3
Cтраница 3
Необходимость выбора изоляции соответственно амплитудному значению напряжения в V 2 раза большего, чем действующее значение, удорожает установку переменного тока и относится к одному из недостатков его применения. [31]
Прочность динамическая усталостная — амплитудное значение напряжения, при котором материал в данных условиях может обеспечить заданную выносливость. [32]
Необходимо учесть, что амплитудное значение напряжения почти в 1 5 раза превышает действующее, и выбрать конденсаторы на соответствующее номинальное напряжение. [33]
Как известно, отношение амплитудного значения напряжения к среднему различно для разных форм волны напряжения. Кроме того, электрическая прочность электрофильтра зависит от формы волны напряжения. [34]
Изучению вопроса о влиянии амплитудных значений напряжений или деформаций на динамические механические свойства ненаполненных полимеров посвящено небольшое число работ. Так как полимеры характеризуются довольно высокими показателями механических потерь, первый эффект, который наблюдается при увеличении амплитудных значений напряжения или деформации — это повышение температуры образца, особенно при высоких частотах.
[35]
Так как полимеры характеризуются довольно высокими показателями механических потерь, первый эффект, который наблюдается при увеличении амплитудных значений напряжения или деформации — это повышение температуры образца, особенно при высоких частотах.
[35]
| Распределение относительных интенсивностей деформаций Н / е гаах в зависимости от времени выдержки Ат и уровня циклического нагружения. [36] |
Увеличение времени выдержки при амплитудном значении напряжения в полуцикле растяжения интенсифицирует процесс накопления деформаций ползучести. Полученные для сплавов В-95 Т и АК4 — 1 — Т1 данные показывают также, что относительные градиенты R de / emSLX деформаций в упругой области и начальных стадиях упругопластического деформирования примерно равны. [37]
Равенство (6.2) показывает, что амплитудные значения напряжения на сопротивлении и тока в нем связаны законом Ома. Из равенств (6.3) и (6.4) видно, что напряжение иг и ток ir совпадают по фазе.
[38]
Из равенств (6.3) и (6.4) видно, что напряжение иг и ток ir совпадают по фазе.
[38]
С помощью шарового разрядника измеряется амплитудное значение напряжения. Эти таблицы являются результатом тщательной обработки экспериментальных исследований разрядных напряжений шаровых разрядников в ряде лабораторий мира. Разрядное напряжение в газах зависит от давления, температуры и влажности, поэтому стандартные таблицы соответствуют нормальному давлению воздуха 760 мм рт. ст. и нормальной температуре 20 С. Влияние влажности воздуха на разрядное напряжение в однородных полях при обычном ее изменении в лабораториях ничтожно, поэтому таблицы его не учитывают. [39]
Для получения амплитуды приложенного напряжения амплитудные значения напряжений на этих участках необходимо сложить геометрически. Необходимость геометрического сложения амплитудных значений напряжений на отдельных участках цепи обусловлена тем, что напряжения на различных участках при одном и том же токе в них достигают амплитудных значений разновременно. Сдвиг во времени между синусоидально изменяющимися величинами соответствует повороту векторов, отображающих эти синусоидально изменяющиеся величины, на векторной диаграмме одного относительно другого на углы, равные разностям фаз между отображаемыми ими синусоидами.
[40]
Сдвиг во времени между синусоидально изменяющимися величинами соответствует повороту векторов, отображающих эти синусоидально изменяющиеся величины, на векторной диаграмме одного относительно другого на углы, равные разностям фаз между отображаемыми ими синусоидами.
[40]
Под динамической усталостной прочностью понимают амплитудное значение напряжения, при котором в данных условиях материал может обеспечить заданную выносливость. [41]
Максимальное обратное рабочее напряжение представляет собой амплитудное значение напряжения, которое может быть приложено к вентилю в запирающем направлении в течение длительного времени без опасности его пробоя. Величина обратного напряжения з ави-сит от типа вентиля и колеблется в пределах 15 — 200 в для германиевых и 50 — 1000 в для кремниевых вентилей. [42]
| Временная диаграмма измерения. [43] |
Практическое применение находит метод измерения амплитудного значения напряжения с помощью цифровых вольтметров постоянного тока с поразрядным уравновешиванием. [44]
[44]
Для измерения амплитуды импульсов или амплитудного значения напряжения необходимо откалибровать усилитель вертикального отклонения. Для этого, включив тумблер Калибровка амплитуды, устанавливают чувствительность усиления по вертикальному отклонению такой, чтобы изображение калибровочного напряжения на экране приняло размер 70 мм, считая от пика до пика. На шкале осциллографа имеются горизонтальные линии, расположенные симметрично горизонтальной осевой линии и отстоящие от нее вверх и вниз на 35 мм. Затем тумблер Калибровка амплитуды отключают. [45]
Страницы: 1 2 3 4
Амплитудное значение синусоидального напряжения
Содержание:
- 1 Закон Ома.
- 2 Электрические измерения.
- 3 Постоянный и переменный ток.
- 4 Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.
Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой Т .
Количество периодов переменного тока за 1 секунду, есть частота f .
Частота переменного тока f измеряется в герцах .
f = 1 / T.
Например.
Частота в нашей электрической сети 50 Гц . Период этих колебаний будет равен:
T = 1 / f = 1 / 50 = 0,02 сек.
Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.
Umax = Ua и Imax = Ia
За один период напряжение принимает эти значения два раза: + Ua и — Ua .
♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia , и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.
Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.
♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз .
Следовательно действующее (или эффективное) значение переменного тока будет равно:
Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока
Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения
На все эти теоретические размышления можно посмотреть иначе!
♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1 .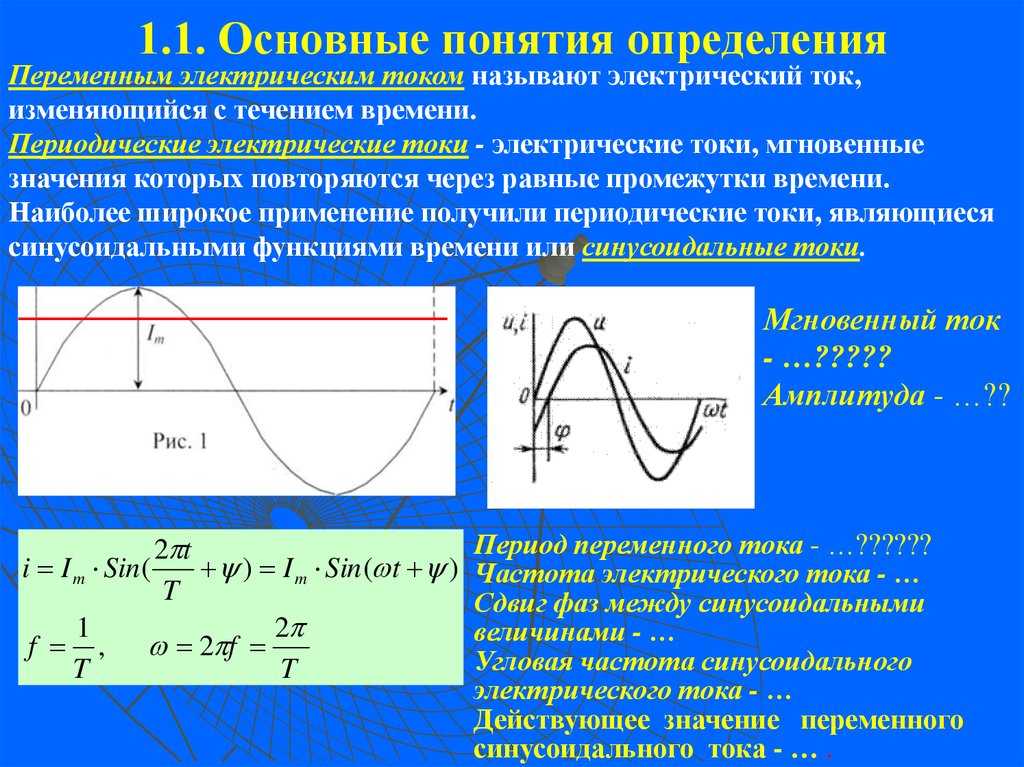
После выпрямительных диодов оно принимает вид как на рисунке 2.
Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.
♦На рисунке приняты обозначения:
Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.
Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I .
Одна и та же электрическая мощность, выраженная в трех видах.
P = Ua х Ia = Uд х Iд = U х I
♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд .
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт .
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.
Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.
Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax . Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой Т .
Количество периодов переменного тока за 1 секунду, есть частота f .
Частота переменного тока f измеряется в герцах .
f = 1 / T.
Например.
Частота в нашей электрической сети 50 Гц . Период этих колебаний будет равен:
T = 1 / f = 1 / 50 = 0,02 сек.
Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.
Umax = Ua и Imax = Ia
За один период напряжение принимает эти значения два раза: + Ua и — Ua .
♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia , и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.
Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.
♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз .
Следовательно действующее (или эффективное) значение переменного тока будет равно:
Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока
Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения
На все эти теоретические размышления можно посмотреть иначе!
♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1 .
После выпрямительных диодов оно принимает вид как на рисунке 2.
Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.
♦На рисунке приняты обозначения:
Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение Ua примем за единицу.
Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I .
Одна и та же электрическая мощность, выраженная в трех видах.
P = Ua х Ia = Uд х Iд = U х I
♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд .
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт .
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.
Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.
Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.
Закон Ома.
Основным законом, которым руководствуются радиолюбители — является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm, 1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.
Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.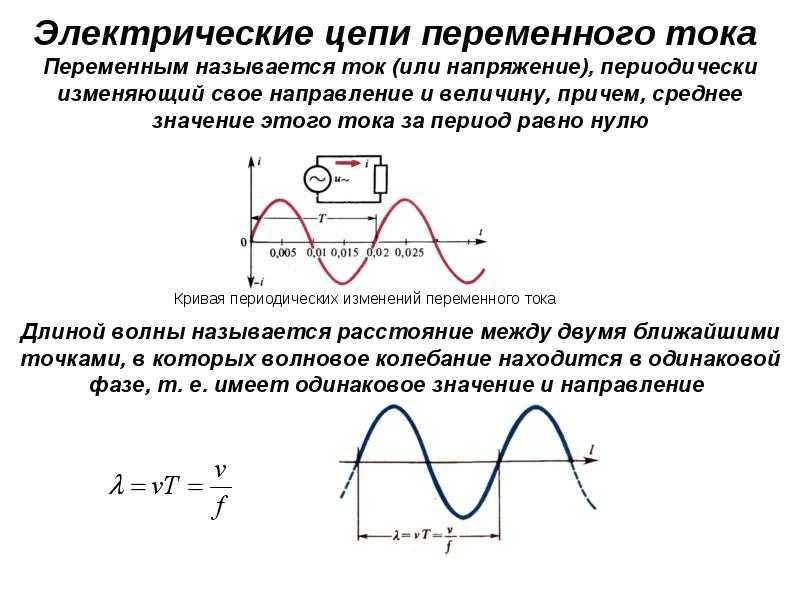
I = U/R, где R — электрическое сопротивление проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.
Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля — Ленца. Звучит так;
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.
Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.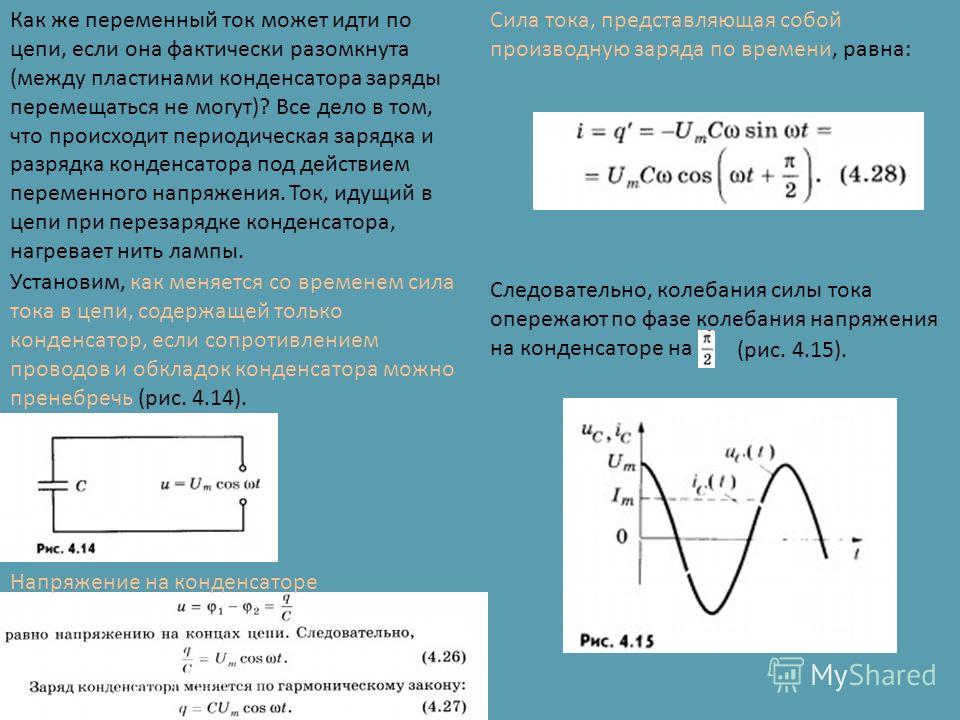
В центре искомые величины, а в секторах с соответствующими цветами — варианты решений в зависимости от известных величин.
Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье — треугольник Ома.
Выглядит она следующим образом:
В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
,
- — ЭДС цепи,
- I — сила тока в цепи,
- R — сопротивление всех элементов цепи,
- r — внутреннее сопротивление источника питания.
Закон Ома для полной цепи звучит так — Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Электрические измерения.
Нарисуем простейшую электрическую цепь, состоящую из батареи «В» и нагрузки «R», и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.
Что бы измерить протекающий в цепи ток, необходимо в разрыв источника питания и нагрузки включить измерительный прибор (амперметр).
Для того, что бы на измеряемую цепь было как можно меньше влияний и для повышения точности измерения, амперметры изготавливают с очень малым внутренним сопротивлением, то есть если включить амперметр в разрыв проверяемой цепи, то он практически не добавит к измеряемой цепи дополнительного сопротивления, и протекающий по цепи ток практически не изменится, или уменьшится на очень незначительную величину не оказывающую значительного влияния на конечный результат измерения.
Поэтому категорически нельзя измерять «ток приходящий на нагрузку» путём подключения амперметра параллельно нагрузке, или непосредственно у источника питания (без нагрузки) и таким образом попытаться замерить выходной ток выдаваемый источником питания или осветительной сетью.
Это равносильно тому, что подключить параллельно нагрузке или источнику питания обычный провод. Попросту сказать — закоротить цепь.
Попросту сказать — закоротить цепь.
Если источник питания обладает хорошей мощностью — будет очень сильный Б А Х . Последствия могут быть самыми разными, от выхода из строя измерительного прибора (амперметра), что обычно и случается, и до выбитых пробок (АЗС) в квартире и обесточивания помещения и возможного поражения током.
Для измерения напряжения на нагрузке необходимо, что бы подключаемый к ней вольтметр не шунтировал нагрузку и не оказывал заметного влияния на результат измерения. Для этого вольтметры изготавливают с очень высоким входным сопротивлением и их наоборот подключают параллельно измеряемой цепи. Благодаря высокому входному сопротивлению вольтметра — сопротивление измеряемой цепи практически не изменяется, или изменяется очень не значительно, не оказывая заметного влияния на результат измерения.
На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.
Постоянный и переменный ток.
Кратко напомню — постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.
Переменный ток (AC) — это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению.
На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.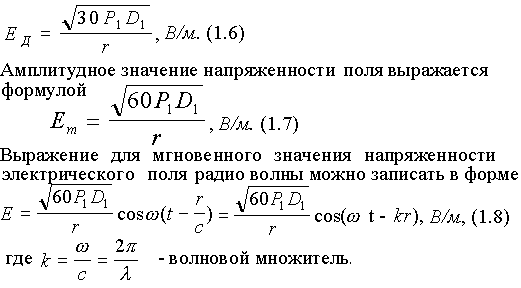
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.
Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Возникает вопрос, как же его измерять? Для его измерения и введено понятие — «Действующее (или эффективное) значение» переменного тока.
Что же такое действующее (или эффективное) и амплитудное значение переменного тока?
Как Вам попроще объяснить, чтобы было понятно.
Действующее (эффективное) значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время, выделяет такое же количество энергии.
То есть если к какой либо активной нагрузке (нагревательный элемент, лампа накаливания, резистор и т.д.) подключить переменный ток, который за определённый промежуток времени (например 10 секунд) выделит на активной нагрузке то-же количество энергии, тепла на нагревательном элементе, резисторе, или разогреет спираль лампы накаливания до точно такой же светоотдачи, что и постоянный ток какой-то определённой величины за тот же промежуток времени (тоже 10 секунд) — то тогда действующее (эффективное) значение такого переменного тока будет равняться величине постоянного тока.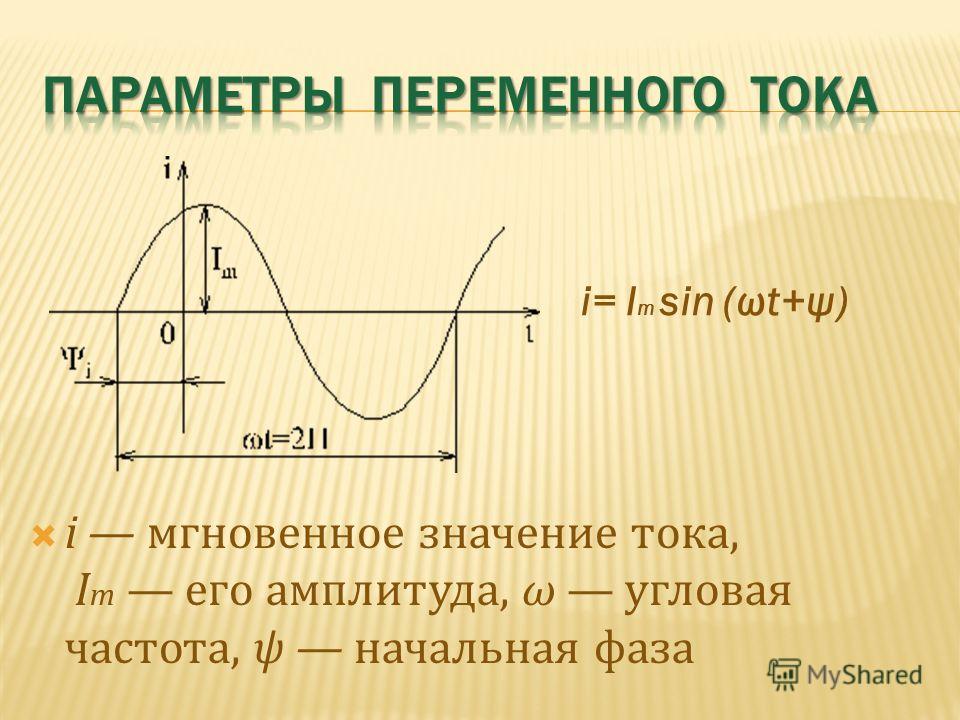
Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.
Что такое «Амплитудное значение» переменного тока?
Если объяснять попроще, то это самое максимальное значение (величина) синусоидального тока на самом пике (максимуме) синусоиды.
Амплитудное значение переменного тока можно измерить электронно — лучевым осциллографом, так как все осциллографы откалиброваны на измерение амплитудных значений.
Поскольку действующее значение переменного синусоидального тока пропорционально квадратному корню из площади, то оно получается в 1,41 раза меньше его амплитудного значения.
Проще говоря — если измерить величину переменного тока (напряжения) электроизмерительными приборами, отградуированными для измерения переменного синусоидального тока (напряжения), то есть например замерить величину переменного напряжения на вторичной обмотке трансформатора, — то амплитудное значение напряжения на этой обмотке будет соответственно в 1,41 раз больше замеренного.
Это справедливо только для переменного синусоидального тока (напряжения).
Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.
Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).
Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.
Для действующего значения переменного синусоидального напряжения (тока) — справедливы формулы для расчётов сопротивлений, мощности, действующих токов и напряжений — приведённые выше в Законе Ома для постоянного тока.
Ответим на вопросы в начале статьи;
Как рассчитать шунт для амперметра?
Большинство отечественных измерительных головок для амперметров, рассчитываются на полное отклонение при подведении к ним напряжения в 75 мВ (0,075 вольта). У них на шкале имеется надпись «НШ — 75 мВ», или «Наружный шунт 75 мв», или что-то подобное.
У них на шкале имеется надпись «НШ — 75 мВ», или «Наружный шунт 75 мв», или что-то подобное.
Нам стало известно две величины, а именно — необходимый нам ток полного отклонения и напряжение полного отклонения измерительной головки.
Например, нам нужно рассчитать шунт на 20 ампер. По Закону Ома 0,075 делим на 20 = 0,00375 Ом.
Изготовить такой шунт можно из медной проволоки, посмотрев её удельное сопротивление по таблице ЗДЕСЬ . Только необходимо брать проволоку, диаметром желательно не менее 1,5 мм, так как шунт при большом токе будет греться, и показания прибора будет изменяться (при нагреве проволоки увеличится её внутреннее сопротивление).
Почему из 12 вольт переменного напряжения, стало около 16 вольт постоянного — надеюсь Вам стало понятно. У переменного напряжения 12 вольт (действующее его значение) — амплитудное значение будет в 1,41 раз больше, то есть 16,92 вольта, минус около вольта падение напряжения на диодах. В итоге получается около 16 вольт — до которых и заряжаются электролитические конденсаторы фильтра.
Как правильно измерить мощность УНЧ?
Давайте для начала вспомним теорию.
Выходная мощность усилителей НЧ измеряется на синусоидальном сигнале. У идеального двухтактного выходного каскада, максимальное амплитудное значение синусоидального сигнала на выходе может приблизиться к величине равной половине напряжения источника питания.
У каскада по мостовой схеме, выходное напряжение может приблизиться к величине напряжения источника питания.
Говоря другими словами, у автомобильной магнитолы при напряжении питания 13,5 вольт, для двухтактного выходного каскада максимальное выходное напряжение (синус) будет 6,5 вольт, а его действующее значение 4,6 вольта, для мостовой схемы соответственно 13 В. и 9,2 вольта.
Возьмём минимальную нагрузку для этих усилителей 2 Ома, соответственно максимальная выходная мощность (исходя из Закона Джоуля — Ленца) для первой магнитолы, которую она выдаст теоретически — будет 10,6 ватта, для второй — 42,3 ватта (это для нагрузки 2 Ома). На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность.
На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность.
В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными «цешками» или бытовыми «цифровиками», так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.
Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт — это развод, рекламный ход и т. д., если только для питания этого усилителя не применяется повышающий преобразователь.
д., если только для питания этого усилителя не применяется повышающий преобразователь.
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.
 2 Термодинамика
2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.
 5 Излучение и спектры
5 Излучение и спектры - 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Что такое пиковое значение, среднее значение и среднеквадратичное значение?
Пиковое значение Синусоидальный сигнал начинается с нуля, достигает пикового значения и снова снижается до нуля за положительный полупериод. В следующем отрицательном полупериоде сигнал проходит через отрицательное пиковое значение и спускается к нулевому значению. Таким образом, за один полный цикл сигнал достигает положительного пикового значения при 90 градусах и отрицательного пикового значения при 270 градусах.
В следующем отрицательном полупериоде сигнал проходит через отрицательное пиковое значение и спускается к нулевому значению. Таким образом, за один полный цикл сигнал достигает положительного пикового значения при 90 градусах и отрицательного пикового значения при 270 градусах.
Максимальное значение, достигаемое переменным сигналом в течение одного цикла, известно как его пиковое значение . Пиковое значение также называется пиковым значением. Пиковое значение симметричного сигнала переменного напряжения и тока также можно определить путем измерения размаха сигнала.
Среднее значениеСинусоидальный сигнал имеет различную величину напряжения или тока в разные моменты времени сигнала. Величина тока или напряжения в конкретный момент времени называется мгновенным значением сигнала. Среднее значение всех мгновенных значений переменного напряжения и тока за один полный цикл называется среднее значение .
Для симметричного синусоидального сигнала положительный полупериод симметричен отрицательному полупериоду. Следовательно, среднее значение одного полного цикла равно нулю. Однако среднее значение рассчитывается без учета знаков. Поэтому для определения среднего значения формы переменного сигнала учитывается только положительный полупериод.
Следовательно, среднее значение одного полного цикла равно нулю. Однако среднее значение рассчитывается без учета знаков. Поэтому для определения среднего значения формы переменного сигнала учитывается только положительный полупериод.
На приведенной выше диаграмме пусть i1, i2, i3…….. in будут средними ординатами.
Среднее значение (Iav) синусоидального сигнала,
= Среднее значение средних ординат
Среднее значение синусоидального сигнала получается путем сложения мгновенных значений напряжения или тока только за половину периода.
Пиковое значение синусоидального напряжения 300 вольт, среднее значение будет;
В ср = 0,637 x 300
В ср = 191,1 В
Среднеквадратичное значение означает среднеквадратичное значение. Среднеквадратичное значение переменного тока определяется постоянным (постоянным) током, который при протекании в течение заданного времени выделяет такое же количество тепла, как и переменный ток при протекании по той же цепи в течение того же времени. Он также известен как действующее значение переменного тока 9.0007
Он также известен как действующее значение переменного тока 9.0007
На приведенной выше диаграмме, если мы рассчитаем количество тепла, выделяемого при протекании электрического тока через ту же цепь за то же время, переменный ток, который производит такое же количество тепла в цепи, поскольку тепло, выделяемое постоянным током, называется среднеквадратичным значением переменного тока. Среднеквадратичное значение равно 240 В переменного тока. Это означает, что напряжение 240 В переменного тока выделяет столько же тепла, сколько выделяется напряжением постоянного тока 240 В для той же цепи.
Среднеквадратичное значение можно определить следующими способами.
Графический метод Графический метод используется для определения среднеквадратичного значения любого несинусоидального сигнала, изменяющегося во времени. Если форма сигнала симметрична относительно оси, для определения среднеквадратичного значения можно использовать аналитический метод. При графическом методе берется ряд средних ординат и записывается их мгновенное значение.
При графическом методе берется ряд средних ординат и записывается их мгновенное значение.
Каждое среднее значение ординаты сигнала умножается само на себя и добавляется к следующему. Квадратное значение делится на количество средних ординат, а затем квадратный корень выражения дает среднеквадратичное значение. Точность измерения зависит от количества средних ординат, взятых для получения мгновенных значений.
Пусть пиковое значение переменного напряжения составляет 25 вольт, а мгновенное значение в середине полупериода переменного тока следующее.
Среднеквадратичное значение напряжения переменного тока рассчитывается следующим образом.
Среднеквадратичное значение волны переменного тока составляет 17,68 вольт.
Аналитический метод расчета среднеквадратичного значенияДля симметричных синусоидальных сигналов напряжения или тока можно использовать аналитический метод для определения среднеквадратичного значения.
Вывод формулы среднеквадратичного значения синусоидального сигналаЕсли пиковое значение напряжения переменного тока составляет 25 вольт, его среднеквадратичное значение будет равно;
V ОБС = 25/1,414 = 17,68 вольт
Уравнения напряжения . значение чистой синусоидальной формы равно 1,11. Если отношение среднеквадратичного значения к среднему значению отличается от 1,11, говорят, что форма сигнала искажена.
значение чистой синусоидальной формы равно 1,11. Если отношение среднеквадратичного значения к среднему значению отличается от 1,11, говорят, что форма сигнала искажена.Related Posts
- Что такое крест-фактор или пик-фактор? Его формула и происхождение
- Что такое форм-фактор? Формула форм-фактора и ее производные
- Определение переменного тока Измерения и преимущества
Похожие посты:
Пожалуйста, подпишитесь на нас и поставьте лайк:
Пиковое значение, среднее значение и среднеквадратичное значение формы волны переменного тока
Как вы знаете, форма волны переменного тока имеет синусоидальный характер. Его величина постоянно меняется со временем, поэтому необходимо найти значение в каждый момент времени и его пиковое значение.
Подобно постоянному току, который имеет постоянную величину, мы находим среднее значение величины переменного тока, который также будет иметь постоянную величину. Для одного полного цикла вы получаете нулевое среднее значение, потому что у него есть как положительные, так и отрицательные циклы.
Для одного полного цикла вы получаете нулевое среднее значение, потому что у него есть как положительные, так и отрицательные циклы.
Следовательно, мы используем среднеквадратичное значение (RMS), которое дает эффективное значение синусоидальной формы волны. В этом разделе вы подробно узнаете о мгновенном значении, пиковом значении, среднем значении и среднеквадратичном значении величины переменного тока.
Мгновенное значение
В любой момент времени ЭДС, индуцируемая в катушке, зависит от скорости, с которой катушка отсекает магнитный поток между полюсами. Это зависит от угла поворота (θ) генерирующего устройства.
Поскольку форма волны переменного тока постоянно меняет свою величину и направление, форма волны в любой момент будет иметь значение, отличное от следующего момента. Например, значение в 1 миллисекунду будет отличаться от значения в 1,2 миллисекунды и так далее. Эти значения известны как мгновенные значения.
Мгновенное значение может быть определено как значение переменной величины в любой конкретный момент времени и обозначается как i и e.
Таким образом, мгновенное значение сигнала переменного тока будет варьироваться в зависимости от положения катушки в магнитном поле, как показано ниже.
Мгновенное значение синусоидального сигнала обобщается формулой.
где E m и I m — максимальные значения напряжения и тока соответственно. θ — угол поворота катушки во времени.
На рисунке ниже показана осциллограмма переменного тока, где мгновенные значения токов i 1 , i 2 , i 3 ,… i n отмечены в разные моменты времени 3 t t t 2 , t 3 ,… t n соответственно. Мгновенное значение будет положительным ( +i ) во время положительного полупериода и отрицательным ( -i ) во время отрицательного полупериода.
Пиковое значение
Это максимальное значение, достигаемое формой сигнала переменного тока либо в положительном полупериоде, либо в отрицательном полупериоде. Он также известен как амплитуда. Обозначается I m (I p ) для тока и E m (E p ) или V m (V p ) на рисунке ниже 6016 p 90 .
Он также известен как амплитуда. Обозначается I m (I p ) для тока и E m (E p ) или V m (V p ) на рисунке ниже 6016 p 90 .
Что такое пиковое значение?
Сумма пиковых значений положительного и отрицательного полупериода называется пиковым значением. Выражается как I pp , как показано на рисунке выше.
Математически это выражается как
Воспользуйтесь калькулятором, чтобы найти размах переменной величины.
Среднее значение
Среднее значение всех мгновенных значений переменной величины за один полный цикл называется средним значением. Это выражается как
Здесь средняя ордината представляет разные моменты формы волны..
Например, рассмотрим синусоидальный сигнал с 10 средними ординатами. Мгновенные значения i 1 , i 2 , i 3 ,… i 10 переменного тока равны 2, 4, 6, 8, 10, 8, 6, 4, 2 соответственно.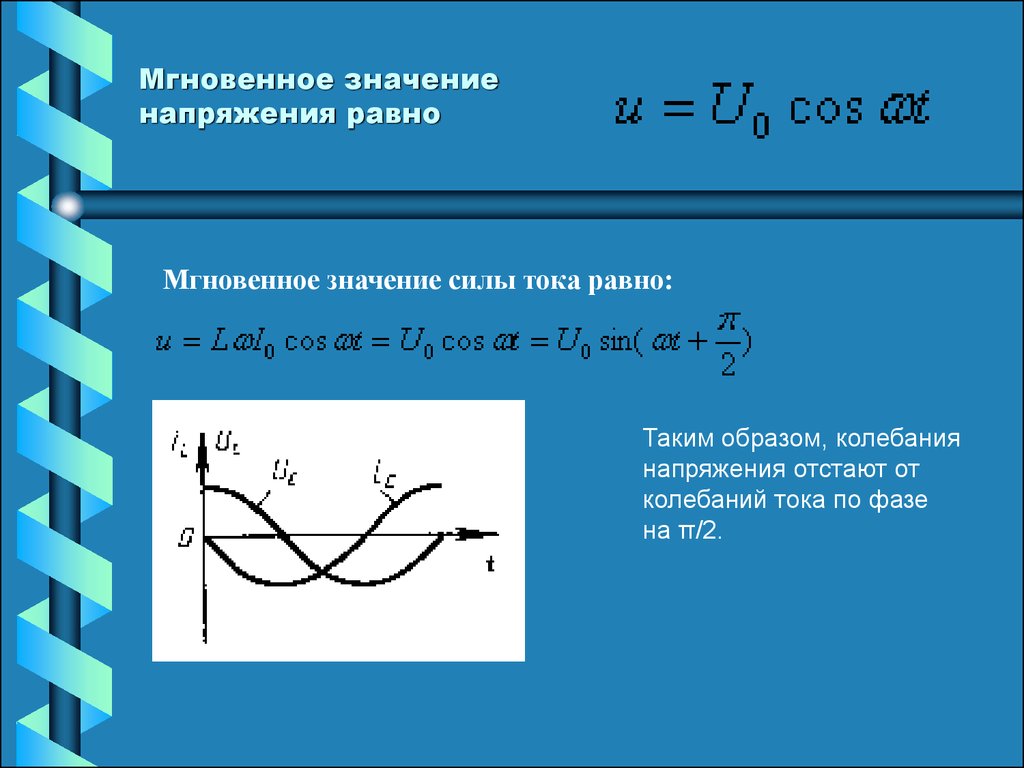
Теперь среднее значение тока рассчитывается как
Среднее значение переменной величины также объясняется как: Когда мы преобразуем переменный ток (AC) в постоянный ток (DC), тогда преобразованное значение постоянного тока будет требуемым средним значением этого переменного тока.
Аналитический метод определения среднего значения
Для одного полного цикла площадь под синусоидальным сигналом может быть определена путем интегрирования следующим образом:
значение тока за один полный цикл. Мгновенное значение переменного тока определяется выражением i = I м sin θ
Теперь среднее значение синусоидальной формы волны получается путем интегрирования синусоидальной величины за полный цикл и деления на общий период времени ( 2π).
Таким образом, мы нашли, что среднее значение синусоидальной формы волны за один полный период равно 0. Оно равно нулю, поскольку один полный период имеет положительный и отрицательный полупериод.
Оно равно нулю, поскольку один полный период имеет положительный и отрицательный полупериод.
Для полупериода, среднее значение синусоиды получается путем интегрирования синусоидальной величины за полупериод (от 0 до π) и деления на половину периода времени (π).
Аналогично, среднее значение напряжения определяется выражением
Таким образом, из этих уравнений, если известно максимальное пиковое значение переменной величины,
Воспользуйтесь калькулятором, чтобы найти среднее значение переменной величины.
Среднеквадратичное значение
Среднеквадратичное значение – это эффективное значение переменной величины. Это означает квадратный корень из среднего (среднего) значения квадрата мгновенных значений. Среднеквадратические значения обозначены как V СКЗ или I СКЗ .
Среднеквадратичное значение переменного тока эквивалентно значению постоянного тока (DC) при протекании по цепи, которая производит такое же количество тепла, что и переменный ток (AC) при протекании по той же цепи для определенного время.
Проще говоря, действующее значение — это эквивалентное значение постоянного тока, которое говорит вам, скольким вольтам или амперам постоянного тока соответствует синусоидальный сигнал с точки зрения его способности производить ту же мощность.
Графически среднеквадратичное значение переменной величины может быть выражено как
Аналитический метод определения среднеквадратичного значения
Аналитически интегрирование выполняется для квадрата функции мгновенного значения синусоидальной величины за полный цикл( от 0 до 2π) и разделите его на общий период времени (2π), чтобы получить среднее значение.
Теперь среднеквадратичное значение получается путем извлечения квадратного корня из всей функции.
Здесь,
Следовательно, среднеквадратичное значение тока становится,
Аналогичным Среднеквадратичное значение переменной величины.
Обобщенная форма сигнала переменного тока, представляющая пиковое значение, среднее значение и среднеквадратичное значение, показана ниже,
Форм-фактор
Отношение между среднеквадратичным значением и средним значением переменной величины называется форм-фактором.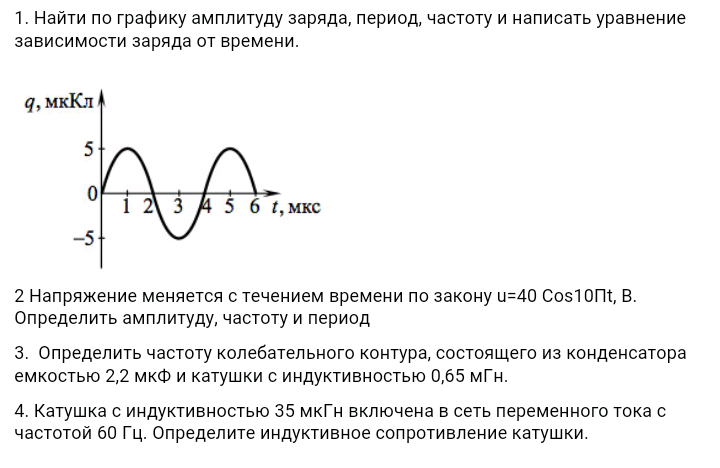 Для чистой синусоидальной формы значение коэффициента формы всегда будет равно 1,11
Для чистой синусоидальной формы значение коэффициента формы всегда будет равно 1,11
Пиковый коэффициент
Пиковый коэффициент определяется как отношение максимального (пикового) значения к среднеквадратичному значению переменной величины. Для чистой синусоидальной формы пиковый коэффициент всегда будет равен 1,414. Пиковый фактор также называют крест-фактором.
- Copy Link
- More
AC Peak Voltage vs. Peak-to-Peak Voltage vs. Среднеквадратичное значение напряжения
Обновлено на 2022 год.
Ключевые выводы
Узнайте, как рассчитать пиковое напряжение переменного тока.
Получите более полное представление о важности пикового напряжения переменного тока для общей схемы.

Узнайте, как различать пиковое напряжение переменного тока, размах напряжения и среднеквадратичное значение напряжения.
Проверка пикового напряжения переменного тока на распределительной подстанции.
Заслуга в открытии электрического заряда принадлежит грекам, и это открытие датируется 2600 лет назад. Электрический заряд также называют статическим электричеством или инертным электричеством. На протяжении нескольких тысячелетий люди обладали неутолимой страстью к молнии и электричеству. От эксперимента Бенджамина Франклина с воздушным змеем в 1752 году до изобретения Вольтой батареи в 1800 году и изобретения электрической лампочки в 1879 году.Томасом Эдисоном, это очарование неоспоримо.
Перенесемся в наши дни, и все еще есть желание понять, использовать и эффективно использовать электричество. Это понятно, поскольку почти каждое устройство, которое мы используем, зависит от той или иной формы питания или электрического заряда. Однако не все источники электроэнергии совместимы с каждой конструкцией устройства. По мере того, как наши знания и понимание электричества увеличивались, росли и наши потребности в электроэнергии.
Однако не все источники электроэнергии совместимы с каждой конструкцией устройства. По мере того, как наши знания и понимание электричества увеличивались, росли и наши потребности в электроэнергии.
Имея это в виду, наши проекты основаны на нашей способности точно оценивать как электрические ограничения, так и требования к мощности. Это включает в себя возможность расчета таких параметров, как пиковое напряжение переменного тока. Среднеквадратичное значение напряжения и среднеквадратичное значение или значение напряжения являются представлениями средней мощности, среднего значения и пикового значения для спектра напряжения переменного тока или формы сигнала переменного тока. Дополнительные элементы напряжения, такие как синусоидальное напряжение, расчет мгновенных значений или эффективного значения для измерения среднеквадратичного значения, а также максимальное значение, могут помочь в понимании истинного среднеквадратичного значения для вашей следующей цепи переменного тока или источника питания переменного тока.
Что такое напряжение?
Напряжение — это электрический потенциал в цепи, обеспечивающий возможность протекания тока. Но само по себе наличие напряжения в цепи не означает, что в цепи присутствует ток. Чтобы ток протекал в цепи, цепь должна быть завершена (замкнутый путь).
Таким образом, напряжение обеспечивает потенциал для присутствия тока в цепи, но ток течет только при наличии завершенного или замкнутого пути. Это связано с тем, что напряжение обеспечивает силу, которая толкает или перемещает электроны внутри цепи, когда путь завершен.
Например, в электрической розетке не течет ток, если к ней не подключено устройство. Однако электрический потенциал или напряжение все еще присутствует. Как только мы подключаем устройство и замыкаем цепь, включив его, напряжение становится активным, и в устройстве протекает ток.
Пиковое напряжение переменного тока
Для каждого электронного устройства требуется источник питания, полностью совместимый с его конструкцией.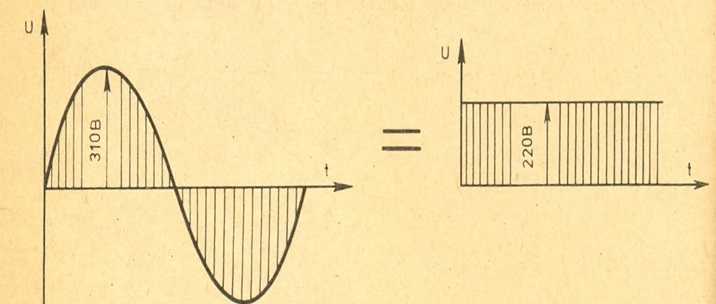 Некоторые устройства используют постоянный ток, тогда как другие устройства используют переменный ток. Существуют также устройства, такие как персональные компьютеры, которые используют постоянный ток, преобразованный из электрических розеток переменного тока. В любом случае существуют параметры, которым должен соответствовать этот источник электроэнергии, чтобы устройство функционировало.
Некоторые устройства используют постоянный ток, тогда как другие устройства используют переменный ток. Существуют также устройства, такие как персональные компьютеры, которые используют постоянный ток, преобразованный из электрических розеток переменного тока. В любом случае существуют параметры, которым должен соответствовать этот источник электроэнергии, чтобы устройство функционировало.
Необходимость различать максимальное или пиковое напряжение и среднеквадратичное (среднеквадратичное) или среднее напряжение имеет первостепенное значение как для конструкции, так и для функциональности. Одним из таких параметров является пиковое напряжение переменного тока. Как вы можете себе представить, использование напряжения, превышающего расчетное устройство, несомненно, приведет к катастрофическому отказу и, возможно, к травмам или смерти. Итак, что такое пиковое напряжение переменного тока?
Как следует из названия, пиковое напряжение переменного тока — это максимальное или пиковое напряжение, которое источник может или будет достигать. Пиковое напряжение, которое мы обозначаем как VP, измеряется от горизонтальной оси (на нулевой опорной высоте) до вершины сигнала или гребня.
Пиковое напряжение, которое мы обозначаем как VP, измеряется от горизонтальной оси (на нулевой опорной высоте) до вершины сигнала или гребня.
Пиковое напряжение переменного тока в сравнении с пиковым напряжением переменного тока
Имейте в виду, что переменный ток означает переменный ток, и это также означает, что напряжение чередуется (меняет полярность) заданное количество раз в заданный период. Возьмем, к примеру, сигнал переменного тока 60 Гц, 120 В:
Обозначение 60 Гц указывает на то, что сигнал будет меняться от отрицательного (пикового) до положительного (пикового) напряжения 60 раз в течение одной секунды. Этот конкретный параметр напряжения называется размахом или VPP, и он не взаимозаменяем с пиковым напряжением.
Понятно, что эти параметры влияют на приложение, с которым совместимо конкретное напряжение, и, таким образом, влияют на общую функциональность. Расчет пикового напряжения переменного тока, размаха напряжения и среднеквадратичного значения напряжения имеет решающее значение.
Расчет пикового напряжения переменного тока
Мы можем рассчитать пиковое напряжение ( V P ), используя размах напряжения ( V PP ), среднеквадратичное значение напряжения или среднее значение напряжения. Формулы расчета В P для синусоидальных сигналов переменного тока:
Если вы получите значение размаха напряжения ( В PP ), вы можете рассчитать пиковое напряжение ( В P ) по следующей формуле:
В P = В PP x 0,5
Если вы получите среднеквадратичное значение напряжения, вы можете рассчитать пиковое напряжение ( В P ), используя следующую формулу :
Если вы получите среднее значение напряжения, вы можете рассчитать пиковое напряжение, используя следующую формулу:
VP = среднее напряжение x (π ÷ 2)
или
VP = среднее напряжение x 1,57
Пиковое напряжение переменного тока, как и множество других параметров, которые мы находим в области электроники, благотворно влияет на общий дизайн и функциональность. Понимание максимального, среднего и минимального потенциала источника электроэнергии значительно повышает точность проектирования, функциональность и производительность устройства.
Понимание максимального, среднего и минимального потенциала источника электроэнергии значительно повышает точность проектирования, функциональность и производительность устройства.
Пиковое напряжение переменного тока, превышающее возможности разветвителей, приведет к катастрофическому отказу.
Как показано на изображении выше, при проектировании электронных схем важно иметь возможность точно определить параметры ваших сигналов переменного тока, чтобы обеспечить адекватную защиту. Это позволяет предотвратить непредвиденные ситуации, которые могут повредить оборудование или создать угрозу для пользователей. Хотя эта статья в основном относится к переменному току, не пренебрегайте схемой постоянного тока, сигналом постоянного тока или схемами питания постоянного тока. Вам по-прежнему необходимо понимать выходную мощность, чтобы обеспечить безопасность, будь то анализ среднеквадратичного значения переменного тока, пикового значения напряжения или любых дополнительных элементов формы переменного сигнала.
Программное обеспечение Cadence для проектирования и анализа печатных плат лидирует в отрасли, предоставляя всесторонние и интегрированные возможности создания схем, компоновки платы, а также возможности моделирования и анализа. Для моделирования, которое включает в себя возможность просмотра различных представлений сигналов переменного тока, стандартом является PSpice.
Если вы хотите узнать больше о том, какое решение может предложить Cadence, обратитесь к нам и нашей команде экспертов.
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостей
Спасибо!
Анализ генерации переменного тока: действующие значения, фазовый угол и частота
Анализ процесса выработки электроэнергии переменного тока и переменного тока, который мы используем почти во всех аспектах нашей жизни, необходим для лучшего понимания того, как энергия переменного тока используется в современных технологиях.
Действующие значения
Выходное напряжение генератора переменного тока можно выразить двумя способами. Один из них — графически с использованием синусоиды (рис. 3). Второй способ — алгебраически с помощью уравнения e = E max sin ωt, которое будет рассмотрено позже в тексте.
Рисунок 3: Синусоида напряжения
Когда напряжение вырабатывается генератором переменного тока, результирующий ток изменяется пропорционально напряжению. Когда катушка генератора вращается на 360°, выходное напряжение проходит один полный цикл. За один цикл напряжение увеличивается от нуля до E в одном направлении, уменьшается до нуля, увеличивается до E max в обратном направлении (отрицательное E max ), а затем снова уменьшается до нуля. Значение E max происходит при 90° и называется пиковым напряжением. Время, за которое генератор совершает один цикл, называется периодом, а количество циклов в секунду называется частотой (измеряется в герцах).
Одним из способов обозначения напряжения или тока переменного тока является пиковое напряжение (E p ) или пиковый ток (I p ). Это максимальное напряжение или ток для синусоидальной волны переменного тока.
Другое значение, значение размаха (E p-p или I p ), представляет собой амплитуду напряжения или диапазон тока, охватываемый синусоидой. Однако значение, наиболее часто используемое для переменного тока, является эффективным значением. Эффективное значение переменного тока — это количество переменного тока, которое производит такой же эффект нагрева, как и равное количество постоянного тока.
Проще говоря, эффективное значение одного ампера переменного тока будет производить такое же количество тепла в проводнике за заданное время, как один ампер постоянного тока. Нагревательный эффект данного переменного тока пропорционален квадрату тока. Эффективное значение переменного тока можно рассчитать, возведя в квадрат все амплитуды синусоиды за один период, взяв среднее значение этих значений, а затем извлекая квадратный корень. Эффективное значение, являющееся корнем среднего (среднего) квадрата токов, известно как среднеквадратичное или среднеквадратичное значение. Чтобы понять значение эффективного тока, приложенного к синусоиде, обратитесь к рисунку 4.9.0007
Эффективное значение, являющееся корнем среднего (среднего) квадрата токов, известно как среднеквадратичное или среднеквадратичное значение. Чтобы понять значение эффективного тока, приложенного к синусоиде, обратитесь к рисунку 4.9.0007
Значения I нанесены на верхнюю кривую, а соответствующие значения I 2 нанесены на нижнюю кривую. Кривая I 2 имеет вдвое большую частоту, чем I, и изменяется выше и ниже новой оси. Новая ось представляет собой среднее значение значений I 2 , а квадратный корень из этого значения представляет собой среднеквадратичное значение или эффективное значение тока. Среднее значение равно ½ I max 2 . Тогда среднеквадратичное значение равно
. Существует шесть основных уравнений, которые используются для преобразования значения переменного напряжения или тока в другое значение, как указано ниже.
- Среднее значение = пиковое значение x 0,637
- Эффективное значение (RMS) = пиковое значение x 0,707
- Пиковое значение = среднее значение x 1,57
- Эффективное значение (RMS) = среднее значение x 1,11
- Пиковое значение = эффективное значение (СКЗ) x 1,414
- Среднее значение = эффективное (СКЗ) x 0,9
Обычно встречающиеся значения тока (I) и напряжения (E) считаются среднеквадратичными; поэтому индекс не используется.
Рисунок 4: Действующее значение тока
Другим полезным значением является среднее значение амплитуды в течение положительной половины цикла.
Уравнение ниже представляет собой математическое соотношение между I av , I max и I.
I av = 0,637 av , E max и E.
E av = 0,637 E max = 0,9 E
Пример 1:
Пиковое значение напряжения в цепи переменного тока составляет 200 В. Каково среднеквадратичное значение напряжения?
E = 0,707E max
E = 0,707 x 200 = 141,4 В
Пример 2:
Чему равно среднее значение силы тока в цепи?
I ср = 0,637 I макс
I ср = 0,637 x 10 = 6,37 ампер
Фазовый угол Фазовый угол — это доля периода в градусах, которая прошла с момента прохождения напряжения или тока через заданное значение. Заданное значение обычно равно нулю. Возвращаясь к рисунку 3, примем точку 1 за начальную точку или нулевую фазу. Фаза в точке 2 составляет 30°, в точке 3 — 60°, в точке 4 — 90° и так далее до точки 13, где фаза равна 360° или нулю. Чаще используется термин «разность фаз».
Заданное значение обычно равно нулю. Возвращаясь к рисунку 3, примем точку 1 за начальную точку или нулевую фазу. Фаза в точке 2 составляет 30°, в точке 3 — 60°, в точке 4 — 90° и так далее до точки 13, где фаза равна 360° или нулю. Чаще используется термин «разность фаз».
Рис. 5: Соотношение фаз
Разность фаз можно использовать для описания двух различных напряжений с одинаковой частотой, которые проходят через нулевые значения в одном и том же направлении в разное время. На рис. 5 углы по оси обозначают фазы напряжений e 1 и e 2 в любой момент времени.
При 120° e 1 проходит через нулевое значение, которое на 60° опережает e 2 ( e 2 равно нулю при 180°). Говорят, что напряжение e 1 ведет e 2 на 60 электрических градусов, или можно сказать, что e 2 отстает от e 1 на 60 электрических градусов.
Разность фаз также используется для сравнения двух разных токов или тока и напряжения.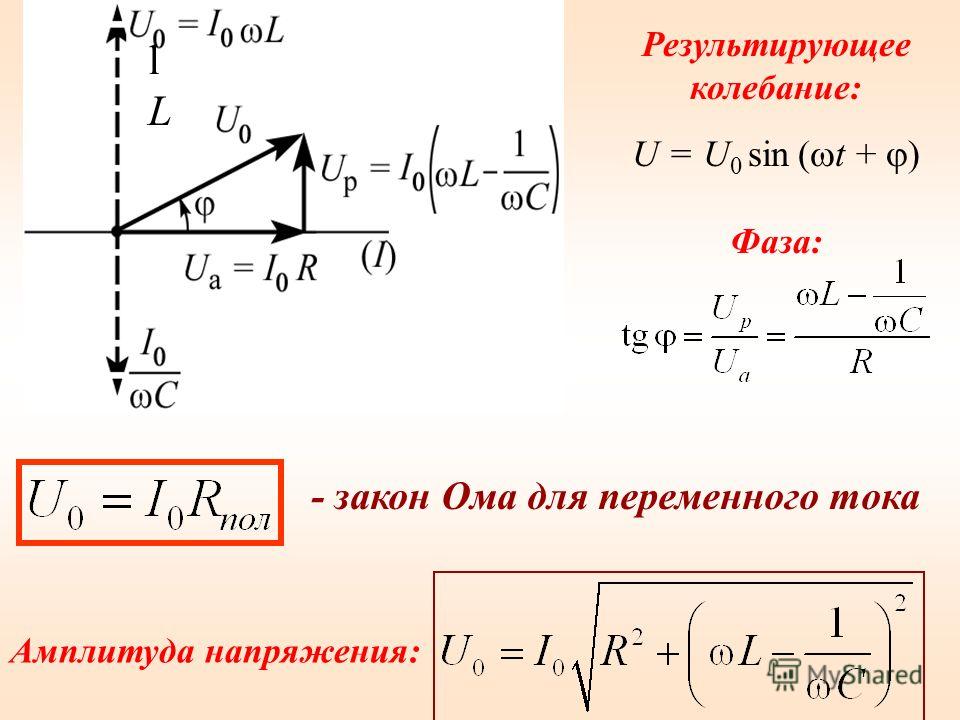 Если разность фаз между двумя токами, двумя напряжениями или напряжением и током составляет ноль градусов, говорят, что они «синфазны». Если разность фаз отличается от нуля, говорят, что они «не совпадают по фазе».
Если разность фаз между двумя токами, двумя напряжениями или напряжением и током составляет ноль градусов, говорят, что они «синфазны». Если разность фаз отличается от нуля, говорят, что они «не совпадают по фазе».
Приведенное ниже уравнение представляет собой математическое представление напряжения, связанного с любой конкретной ориентацией катушки (индуктора).
E = E MAX SINθ
, где
E = индуцированная EMF
E MAX = максимальный индуцированный EMF
θ = Угол от ссылки (градуары или радианы)
Пример 1:
ЭДС индукции в катушке создает максимальную ЭДС 120 В, когда угол от точки отсчета составляет 45 °?e = E max sinθ
e = 120 В Sin (45)
e = 84,84 В
Максимальное индуцированное напряжение также можно назвать пиковым напряжением E p . Если (t) — время, за которое катушка поворачивается на угол (θ), то угловая скорость (ω) катушки равна θ/t и выражается в радианах/сек.
Если (t) — время, за которое катушка поворачивается на угол (θ), то угловая скорость (ω) катушки равна θ/t и выражается в радианах/сек.
Приведенное ниже уравнение является математическим представлением угловой скорости.
θ = ωt
где
ω = угловая скорость (радиан/сек)
t = время поворота на угол от точки отсчета (сек)
θ = угол от точки отсчета (радиан)
Используя законы подстановки, соотношение между наведенным напряжением и максимальным наведенным напряжением , а угловая скорость может быть выражена.
Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между индуцируемым напряжением, максимальным напряжением и угловой скоростью и равно выходной мощности генератора переменного тока.
e = E max sin(ωt)
где
e = ЭДС индукции (вольт)
E max = максимальная ЭДС индукции (вольт)
ω = угловая скорость (радиан/сек) 9002 время поворота на угол от эталона (сек)
Максимальный индуцированный ток рассчитывается аналогичным образом. Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между максимальным индуцированным током и угловой скоростью.
Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между максимальным индуцированным током и угловой скоростью.
i = I max sin(ωt)
где
i = ток индукции (ампер)
I max = максимальный ток индукции (ампер)
ω = угловая скорость (радиан2005/сек) t = время поворота на угол от точки отсчета (сек)
Частота переменного напряжения или тока может быть непосредственно связана с угловой скоростью вращающейся катушки. Единицы угловой скорости — радианы в секунду, а 2π радиан — это полный оборот.
Радиан — это угол, опирающийся на дугу, равную радиусу окружности. Один радиан равен 57,3 градуса. Один цикл синусоидальной волны генерируется, когда катушка вращается на 2π радиан.
Приведенное ниже уравнение представляет собой математическое соотношение между частотой (f) и угловой скоростью (ω) в цепи переменного тока.
ω = 2πf
где
ω = угловая скорость (радиан/с)
f = частота (Гц)
Найдите: 1. Угловую скорость 2. Угол отсчета в 1 мс 3. ЭДС индукции в этой точке
Угловую скорость 2. Угол отсчета в 1 мс 3. ЭДС индукции в этой точке
Решение:
1. ω = 2πf
ω = 2 (3,14) (60 Гц) = 376,8 Радианы/Сек
2. θ = ω
θ = (376.8 Radian/Sec) ( 0,001 сек) = 0,3768 Радианы
3. E = E MAX SINθ
E = (120 В) (SIN 0,3768 Радианы)
E = (120 В) (0,3679)
E = 44,15 V
66666). Будьте первым, кто получит эксклюзивный контент прямо на вашу электронную почту.
Обещаем не спамить. Вы можете отписаться в любое время.
Неверный адрес электронной почты
Принципы генератора (часть вторая)
фары через пятнадцать лет. Google в своей бесконечной мудрости решил удалить Flight-Mechanic из результатов поиска (утверждается, что контент на этом сайте является спамом). Мы обжаловали их решение закрыть нас, но безрезультатно.
К сожалению, поскольку Google имеет монополию на интернет-поиск, это означает, что уровень трафика на сайте упадет до уровня, который сделает его обслуживание нерентабельным. Со временем мы больше не сможем поддерживать пространство на сервере и удалим сайт из Интернета. Спасибо всем, кто поддерживал нас на протяжении многих лет.
Со временем мы больше не сможем поддерживать пространство на сервере и удалим сайт из Интернета. Спасибо всем, кто поддерживал нас на протяжении многих лет.
Чтобы дать отпор монополистической практике таких компаний, как Google, мы рекомендуем использовать конкурирующую поисковую систему, такую как Brave (вы получаете дополнительное преимущество в том, что за вами не следят Big Tech) и отстаивать антимонопольное законодательство от своих представителей.
Рубрики: Основы электричества и электроники
Фазовые отношения
Помимо частотных и циклических характеристик, переменное напряжение и ток также имеют отношение, называемое «фазой». В цепи, питаемой от одного генератора переменного тока, должно быть определенное фазовое соотношение между напряжением и током, чтобы цепь функционировала эффективно. В системе, питаемой от двух или более генераторов переменного тока, должно существовать не только определенное фазовое соотношение между напряжением и током одного генератора переменного тока, но и фазовое соотношение между отдельными напряжениями и отдельными токами.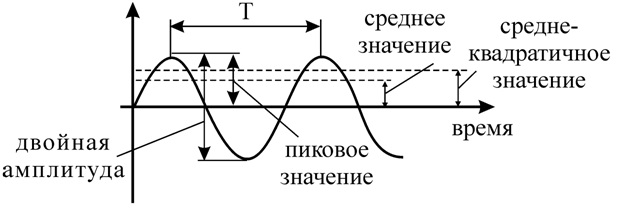 Кроме того, две отдельные цепи можно сравнить, сравнив фазовые характеристики одной с фазовыми характеристиками другой.
Кроме того, две отдельные цепи можно сравнить, сравнив фазовые характеристики одной с фазовыми характеристиками другой.
Синфазное состояние
На рис. 12-112A показаны сигнал напряжения и сигнал тока, наложенные на одну и ту же временную ось. Обратите внимание, что когда напряжение увеличивается в положительном чередовании, ток также увеличивается. Когда напряжение достигает своего пикового значения, то же самое происходит и с током. Обе формы волны затем меняются местами и уменьшаются обратно до нулевой величины, затем продолжаются таким же образом в отрицательном направлении, как и в положительном направлении. Когда две волны, такие как на рис. 12-112А, идут точно в ногу друг с другом, говорят, что они находятся в фазе. Чтобы быть в фазе, два сигнала должны проходить через точки максимума и минимума в одно и то же время и в одном направлении.
Рисунок 12-112. В фазе и в противофазе.Состояние несовпадения фаз
Когда два сигнала проходят через точки максимума и минимума в разное время, между ними существует разность фаз. В этом случае говорят, что две формы волны не совпадают по фазе друг с другом. Термины «опережение» и «запаздывание» часто используются для описания разности фаз между сигналами. Говорят, что сигнал, который первым достигает своего максимального или минимального значения, опережает другой сигнал. На рис. 12-112В показано это соотношение. Первый источник напряжения начинает расти в положении 0°, а второй источник напряжения начинает расти в положении 9°.положение 0°. Поскольку первый источник напряжения начинает свой подъем раньше по времени (на 90°) по отношению ко второму источнику напряжения, говорят, что он опережает второй источник. С другой стороны, говорят, что второй источник отстает от первого источника. Когда сигнал считается опережающим или отстающим, обычно указывается разница в градусах. Если две формы волны отличаются на 360°, говорят, что они находятся в фазе друг с другом. Если разница между двумя сигналами составляет 180°, то они все еще не совпадают по фазе, даже если оба достигают своего минимального и максимального значений одновременно.
В этом случае говорят, что две формы волны не совпадают по фазе друг с другом. Термины «опережение» и «запаздывание» часто используются для описания разности фаз между сигналами. Говорят, что сигнал, который первым достигает своего максимального или минимального значения, опережает другой сигнал. На рис. 12-112В показано это соотношение. Первый источник напряжения начинает расти в положении 0°, а второй источник напряжения начинает расти в положении 9°.положение 0°. Поскольку первый источник напряжения начинает свой подъем раньше по времени (на 90°) по отношению ко второму источнику напряжения, говорят, что он опережает второй источник. С другой стороны, говорят, что второй источник отстает от первого источника. Когда сигнал считается опережающим или отстающим, обычно указывается разница в градусах. Если две формы волны отличаются на 360°, говорят, что они находятся в фазе друг с другом. Если разница между двумя сигналами составляет 180°, то они все еще не совпадают по фазе, даже если оба достигают своего минимального и максимального значений одновременно. [Рис. 12-112]Рис. 12-112. В фазе и в противофазе.
[Рис. 12-112]Рис. 12-112. В фазе и в противофазе.
Практическое замечание: при обнаружении самолета, в котором используются две или более шин переменного тока, возможно, что они могут быть разделены и не синхронизированы, чтобы быть в фазе друг с другом. Когда два сигнала, которые не синхронизированы по фазе, смешиваются, могут быть нанесены серьезные повреждения бортовым системам или бортовому радиоэлектронному оборудованию.
Значения переменного тока
Существуют три значения переменного тока: мгновенное, пиковое и эффективное среднеквадратичное (RMS).
Мгновенное значение
Мгновенное значение напряжения или тока — это индуцированное напряжение или ток, протекающий в любой момент цикла. Синусоида представляет ряд этих значений. Мгновенное значение напряжения изменяется от нуля при 0° до максимума при 90°, обратно до нуля при 180°, до максимума в обратном направлении при 270° и снова до нуля при 360°. Любая точка синусоиды считается мгновенным значением напряжения.
Пиковое значение
Пиковое значение является наибольшим мгновенным значением. Наибольшее единичное положительное значение возникает, когда синусоида напряжения находится под углом 90°, а наибольшее единичное отрицательное значение возникает, когда она составляет 270°. Максимальное значение в 1,41 раза больше эффективного значения. Это так называемые пиковые значения.
Эффективное значение
Эффективное значение также известно как среднеквадратичное значение или среднеквадратичное значение, которое относится к математическому процессу, с помощью которого получено значение. Большинство вольтметров переменного тока при использовании отображают эффективное или среднеквадратичное значение. Эффективное значение меньше максимального значения, равное максимальному значению в 0,707 раза.
Эффективное значение синусоидальной волны на самом деле является мерой теплового эффекта синусоидальной волны. На рис. 12-113 показано, что происходит, когда резистор подключен к источнику переменного напряжения. На рис. 12-113А определенное количество тепла выделяется за счет питания резистора. На рис. 12-113B показан тот же резистор, который теперь подключен к источнику постоянного напряжения. Значение источника постоянного напряжения теперь можно отрегулировать так, чтобы резистор рассеивал такое же количество тепла, как и когда он находился в цепи переменного тока. Среднеквадратичное значение или эффективное значение синусоиды равно напряжению постоянного тока, которое производит такое же количество тепла, как и синусоидальное напряжение.
На рис. 12-113 показано, что происходит, когда резистор подключен к источнику переменного напряжения. На рис. 12-113А определенное количество тепла выделяется за счет питания резистора. На рис. 12-113B показан тот же резистор, который теперь подключен к источнику постоянного напряжения. Значение источника постоянного напряжения теперь можно отрегулировать так, чтобы резистор рассеивал такое же количество тепла, как и когда он находился в цепи переменного тока. Среднеквадратичное значение или эффективное значение синусоиды равно напряжению постоянного тока, которое производит такое же количество тепла, как и синусоидальное напряжение.
Пиковое значение синусоидального сигнала можно преобразовать в соответствующее среднеквадратичное значение с помощью следующего соотношения.
Может применяться как к напряжению, так и к току.
Алгебраическая перестановка формулы и решение для Vp также могут определить пиковое напряжение. Результирующая формула:
Результирующая формула:
Таким образом, значение 110 вольт, данное для переменного тока, подаваемого в дома, составляет всего 0,707 от максимального напряжения этой сети. Максимальное напряжение составляет примерно 155 вольт (110 × 1,41 = максимум 155 вольт).
При изучении переменного тока любые значения тока или напряжения считаются действующими значениями, если не указано иное. На практике используются только действующие значения напряжения и тока. Точно так же вольтметры и амперметры переменного тока измеряют действующее значение.
Противодействие току переменного тока
Есть три фактора, которые могут создать сопротивление потоку электронов (току) в цепи переменного тока. Сопротивление, как и сопротивление цепей постоянного тока, измеряется в омах и оказывает прямое влияние на переменный ток независимо от частоты. С другой стороны, индуктивное реактивное сопротивление и емкостное реактивное сопротивление противодействуют протеканию тока только в цепях переменного тока, а не в цепях постоянного тока. Поскольку переменный ток постоянно меняет направление и интенсивность, катушки индуктивности и конденсаторы также могут препятствовать протеканию тока в цепях переменного тока. Следует также отметить, что индуктивное реактивное сопротивление и емкостное реактивное сопротивление могут создавать фазовый сдвиг между напряжением и током в цепи переменного тока. При анализе цепи переменного тока очень важно учитывать сопротивление, индуктивное сопротивление и емкостное сопротивление. Все три влияют на ток в этой цепи.
Поскольку переменный ток постоянно меняет направление и интенсивность, катушки индуктивности и конденсаторы также могут препятствовать протеканию тока в цепях переменного тока. Следует также отметить, что индуктивное реактивное сопротивление и емкостное реактивное сопротивление могут создавать фазовый сдвиг между напряжением и током в цепи переменного тока. При анализе цепи переменного тока очень важно учитывать сопротивление, индуктивное сопротивление и емкостное сопротивление. Все три влияют на ток в этой цепи.
Рекомендация бортмеханика
Справочник частного пилота Рода Мачадо — Грамотность полетов рекомендует продукты Рода Мачадо, потому что он берет то, что обычно сухо и утомительно, и преображает это с помощью своего характерного юмора, помогая вам оставаться занятым и дольше запоминать информацию. (см. все продукты Рода Мачадо).
Обучение R.M.S. Значения переменного напряжения и тока
Обучение R.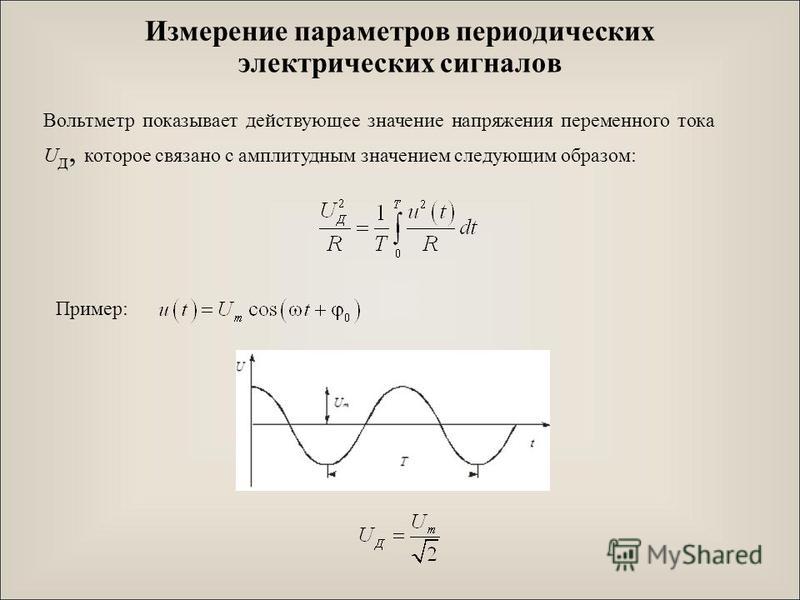 M.S. Значения переменного напряжения и тока
M.S. Значения переменного напряжения и токаЛ. Б. Чебик, W4RNL
Знакомство учащихся с переменными напряжениями и токами неизбежно приводит к обсуждение среднеквадратичных значений ценности. 1 вольт среднеквадратичное значение или 1 ампер среднеквадратичного значения равняется 0,707 от Пиковое напряжение или ток 1 вольт или ампер. Когда студенты спрашивают: «Почему 0,707?» мы обычно делаем то же, что и большинство наших текстов: мы приглашаем ученика к обсуждению среднего квадрата всех бесконечно малых отрезков синуса изгиб. Студент запоминает 1 единицу среднеквадратичного значения. = 0,707 единицы пика отношения, но не связывает четко основные понятия в переменный ток.
Конечно, некоторые ученики довольствуются тем, что запоминают отношения и
пусть дела идут. Тем не менее, некоторые хотят разобраться в отношениях
между пиковым и среднеквадратичным значением значения напряжения и силы тока. Когда я это чувствую,
вот как я поступаю. Я переворачиваю объяснение, начиная с мощности
и никогда не упоминайте среднеквадратичные значения. пока не потребуется назвать единицу измерения.
Задача не так проста, как кажется. Многие студенты радиолюбителей никогда не
освоил основные понятия математики и геометрии. Следовательно, процесс
сбор необходимых идей часто требует нескольких тайм-аутов для
повторение или обучение некоторым важным навыкам.
Я переворачиваю объяснение, начиная с мощности
и никогда не упоминайте среднеквадратичные значения. пока не потребуется назвать единицу измерения.
Задача не так проста, как кажется. Многие студенты радиолюбителей никогда не
освоил основные понятия математики и геометрии. Следовательно, процесс
сбор необходимых идей часто требует нескольких тайм-аутов для
повторение или обучение некоторым важным навыкам.
Однако результаты часто бывают ошеломляющими: упражнение по завязыванию совместные идеи по этой теме часто вызывают повторные выступления со стороны студенты с более продвинутыми идеями в области электроники. Увидев студента самостоятельно закреплять идеи вызывает чувство учителя удовлетворение, которое оправдывает время и энергию, потраченные студентом на подробное путешествие по основным идеям переменного тока.
Следующие примечания отражают то, как я обычно поступаю, в том числе то, как я
постарайтесь обвести учащихся вокруг ловушек и опасностей на этом пути. Хотя в этой пошаговой процедуре нет ничего волшебного, кажется,
Работа. Методы могут быть с пользой адаптированы к другим учебным мероприятиям, как
по базовым предметам и по более сложным темам для обновления лицензии.
Хотя в этой пошаговой процедуре нет ничего волшебного, кажется,
Работа. Методы могут быть с пользой адаптированы к другим учебным мероприятиям, как
по базовым предметам и по более сложным темам для обновления лицензии.
НАЧАТЬ С DC
Первым шагом к хорошему пониманию AC является уверен, что студент полностью понимает как закон Ома, так и степенной закон для постоянного тока. Для наших целей наиболее важной формой закона Ома являетсяЕсли мы позволим R быть некоторым постоянным значением, таким как 1, то отношение E к I должно быть 1:1 или любые другие парные значения, такие как 2:2, 3:3 или 4:4.
Чтобы учащийся понял это, используйте схему или
испытательная установка, сконфигурированная как на рис. 1. Поскольку трудно разработать
испытательное приспособление, позволяющее сравнять E и I без серьезной нагрузки
батареи, схема часто является лучшим учебным пособием, особенно если
дополнен многочисленными примерными расчетами.
Для урока постоянного тока по закону Ома можно использовать цифровые вольтметры и амперметры. помогите понять, что отрицательные значения напряжения и тока также подходят для отношения E к I. Комбинации значений -2:-2, -4:-4, и -6:-6 все дают R 1 Ом, как и положительные числа. разница только в направлении движения электрона через измеритель и резистор.
Также важно подчеркнуть, что значения, считанные со счетчиков — уровни напряжения и тока в момент считывания. Если пренебречь реальными приборными задержками, каждое мгновенное показание представляет собой одинаково мгновенный уровень напряжения и тока.
Мощность, конечно же, скорость использования энергии. При передаче постоянного тока
понимание AC, мы также должны быть уверены, что студент понимает
отношение мощности к работе или общему потреблению энергии. Работа – это скорость
потребление энергии, умноженное на время использования. Измеряем ли мы работу в
ватт-секунды, ватт-часы или киловатт-часы, общая электрическая энергия
используемой нашей схемой на рис. 1, отражает общее количество выделяемого тепла и
рассеивается на резисторе. Чем дольше мы работаем с постоянной скоростью, тем
больше энергии мы используем. Игнорирование фактических средств, используемых для измерения мощности дома
использование, чем дольше мы используем электронагреватель, тем больше мы платим за мощность
компания, которая взимает с нас плату за всю энергию, которую мы используем. Если бы мы запустили то же самое
обогревателя от батарей, мы бы увидели такое же увеличение стоимости, если бы
периодически покупать сменные батареи.
Измеряем ли мы работу в
ватт-секунды, ватт-часы или киловатт-часы, общая электрическая энергия
используемой нашей схемой на рис. 1, отражает общее количество выделяемого тепла и
рассеивается на резисторе. Чем дольше мы работаем с постоянной скоростью, тем
больше энергии мы используем. Игнорирование фактических средств, используемых для измерения мощности дома
использование, чем дольше мы используем электронагреватель, тем больше мы платим за мощность
компания, которая взимает с нас плату за всю энергию, которую мы используем. Если бы мы запустили то же самое
обогревателя от батарей, мы бы увидели такое же увеличение стоимости, если бы
периодически покупать сменные батареи.
Если фактор времени одинаков для всех расчетов, то мощность будет
быть прямо пропорциональна работе. Для постоянного постоянного тока через
резистор постоянного значения с постоянным напряжением, мощность будет пропорциональна
работать. Однако учащийся должен понимать важность
время до приближения к АС.
Во-первых, DC-эквиваленты переменного тока зависят от усреднения
определенные значения в течение как минимум одного цикла. Во-вторых, использование энергии и ее
ставки также являются средними по времени. Формула мощности,
будет иметь решающее значение для преобразования понимания DC в эквивалентное понимание АС. На самом деле, сейчас самое время приступить к маркировке элементы формул, чтобы учащийся мог легко разобраться в идеях. Так давайте преобразуем форму наших формул постоянного тока в следующие:
и
R, конечно, просто все, что преобразует электрическую энергию в тепло. (или другая форма энергии) и, следовательно, не является должным образом ни переменным, ни постоянным током.
Обратите внимание, что в этих формулах я использую символы умножения и
подразделение, наиболее знакомое школьникам-любителям. С калькуляторами и компьютерами,
учащиеся понимают, что «/» означает деление, но при необходимости используют другой
символ деления.
С калькуляторами и компьютерами,
учащиеся понимают, что «/» означает деление, но при необходимости используют другой
символ деления.
ГЕНЕРИРУЮЩАЯ ПЕРЕМЕННОГО ТОКА
Если учащийся хорошо знаком с важными концепциями DC дано на первом шаге, то он или она готовы ко второму шагу: генерация стандартных форм переменного напряжения и тока. Конечно, переменный ток – это любой ток, который периодически меняет направление. В качестве учителям, мы знаем о синусоидальных, прямоугольных, треугольных и составные сигналы, которые невозможно передать одним словом. Тем не менее фундаментальные к понятиям АС есть круговое движение, и ученику будет не комфортно с АС без освоения его основных элементов. Чтобы ввести круговое движение, я обычно использую гипотетический генератор
который проходит через один электрический цикл для каждого механического цикла. Рис. 2
иллюстрирует, как я использую генератор. Когда генератор проходит через
момент времени T0, его положение по вертикали также равно 0. Напряжение и
ток, доступный для нагрузочного резистора, также равен 0. Когда генератор проходит
через Т30, указывающую 30-градусную точку движения по кругу,
его возвышение над 0 является определенной величиной. Здесь мы должны представить
просто количество тригонометрии, необходимое, чтобы узнать, насколько высока рука.
Когда генератор проходит через
момент времени T0, его положение по вертикали также равно 0. Напряжение и
ток, доступный для нагрузочного резистора, также равен 0. Когда генератор проходит
через Т30, указывающую 30-градусную точку движения по кругу,
его возвышение над 0 является определенной величиной. Здесь мы должны представить
просто количество тригонометрии, необходимое, чтобы узнать, насколько высока рука.
Независимо от того, изучал ли студент тригонометрию, несложно
передать идею о том, что отношение стороны, противоположной углу
процент, деленный на гипотенузу, является постоянной величиной для любого заданного угла. затем
мы можем назвать отношение синус угла. Далее мы можем вычислить
значения напряжения для каждого из указанных углов, выбивая
синус угла на недорогом «научном» калькуляторе. Если мы позволим
гипотенуза треугольника равна 1 во всех случаях, тогда
Если гипотенуза имеет значение, отличное от 1, то напряжение или ток стать грехом угла, умноженным на действительное значение гипотенуза.
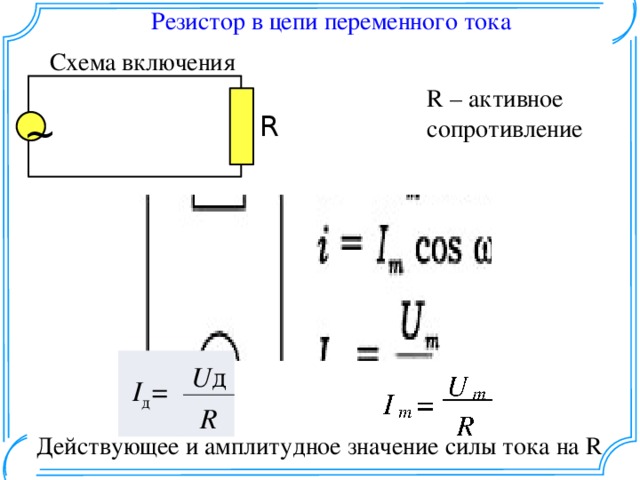
Для этих вводных примеров удобно гипотенуза треугольника равна 1, а сопротивление нагрузки равно 1 Ом. Числа отличных от 1, будет затемнять связь синусов углов с значениям напряжения и тока, а также к значению мощности. Когда урок окончен, вы можете сообщить ученику, что он или она только что закончил или ее первый опыт работы с якобы продвинутой концепцией «нормализованного ценности.»
Вводя понятие мгновенного напряжения или тока, я старайтесь использовать углы в 30 и 60 градусов, избегая 45 градусов как можно чаще. возможный. Цель здесь состоит в том, чтобы убедиться, что учащийся чувствует себя комфортно. круговое движение и синусы без преждевременного включения полуразвитого понятие среднеквадратичного значения в объяснении.
Хотя на рис. 2 показан только первый квадрант движения, я обычно
брать примеры из всех четырех квадрантов. Это показывает, что значения
напряжение и ток (при чисто резистивной нагрузке) принимают как положительные, так и
отрицательные значения, и что они принимают их вместе. Здесь мы можем связать
эти расчеты мгновенных значений напряжения и тока для постоянного тока
измерения, которые мы сделали при изменении направления тока.
Здесь мы можем связать
эти расчеты мгновенных значений напряжения и тока для постоянного тока
измерения, которые мы сделали при изменении направления тока.
На самом деле, теперь мы можем показать, что закон Ома применяется к мгновенным
измеренные или рассчитанные значения переменного тока. В любой точке пути
движение,
Кроме того,
Одним из самых интересных наборов мгновенных значений является
получается, выполняя закон Ома при 90 градусах и снова при 270 градусах. С
пусть гипотенуза будет 1,
и
Аналогично,
и
Поскольку напряжение, ток и мощность никогда не достигают более высоких значений, мы можем переименуйте эти специальные значения в пиковые значения.
 Таким образом, мы определили Epk,
Ипк и Ппк. В этот момент важно вернуть ученика к
диаграмма на рис. 2, чтобы связать значения особых точек в
круговой ход генератора.
Таким образом, мы определили Epk,
Ипк и Ппк. В этот момент важно вернуть ученика к
диаграмма на рис. 2, чтобы связать значения особых точек в
круговой ход генератора.Здесь мы можем открыть некоторые вопросы, на которые еще предстоит ответить. Поскольку пиковое напряжение, ток и мощность возникают только в двух точках на всем протяжении перемещаться внутри генератора, они не сами по себе определяют полную энергию вырабатывается генератором и используется резистором в течение всего цикла. Это значение должно быть меньше пикового значения. Но насколько меньше? Существует ли систематическая связь между пиковым напряжением, током и мощность и общее производство и использование энергии с течением времени? Эти вопросы перейти к шагу 3.
Каждый шаг урока намеренно заканчивается несколькими вопросами
на примере студентов способ обучения себя. Замечая детали
которые приводят к вопросам, а затем, задавая хороший вопрос, студент может
привести себя к хорошим ответам.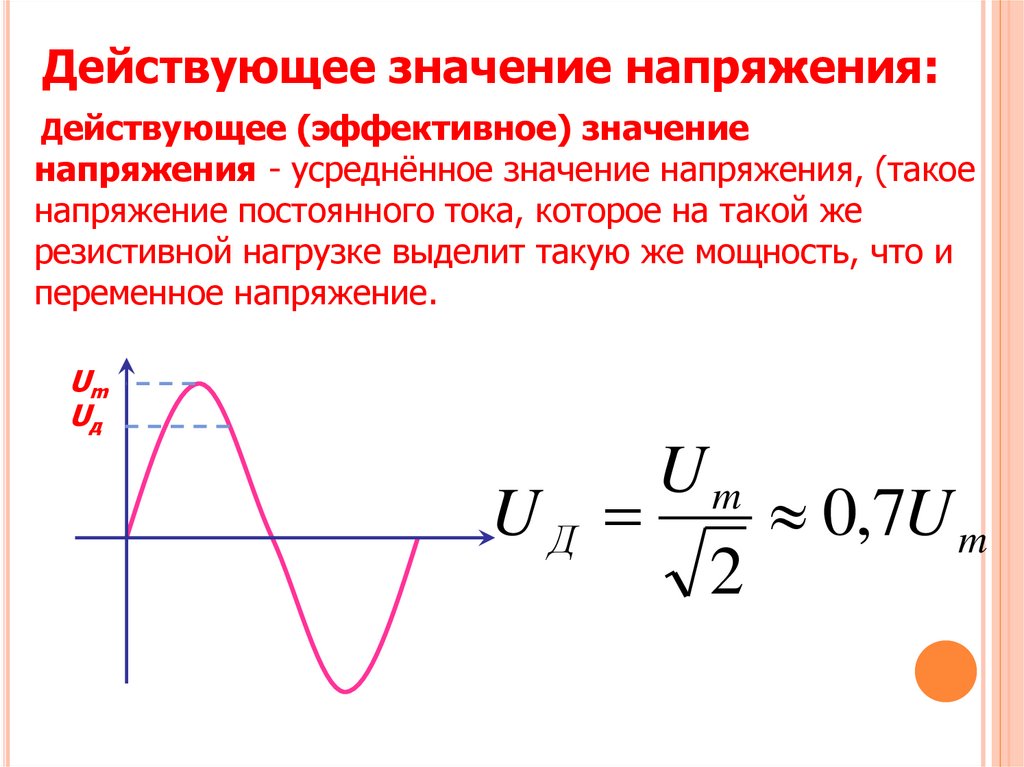 Продолжайте медленно, чтобы метод
тонуть в.
Продолжайте медленно, чтобы метод
тонуть в.
ПИТАНИЕ И РАБОТА ПЕРЕМЕННОГО ТОКА
Одна из трудностей, с которыми я столкнулся при большинстве объяснений Мощность переменного тока — это кривая этой мощности за полный цикл генератора. показывается редко, если вообще когда-либо. Рис. 3 в верхней части этой страницы исправляет ситуация. Некоторые опытные радиолюбители, которых я встречал, никогда не понимали, что кривая был симметричен относительно его пиков и долин. Эта кривая может упростить объяснение средней мощности переменного тока и ее отношение к среднеквадратичным значениям. напряжение и Текущий. Кривая, конечно, представляет собой просто квадрат синусоидальной кривой с максимальным
значение 1. Если у вас есть доступ к программе для работы с электронными таблицами, вы можете создать
кривые на всю страницу, чтобы помочь учащимся в работе со следующим набором идей. Моя процедура началась с настройки столбцов электронной таблицы для каждых 5 градусов.
от 0 до 360 градусов. Следующая строка преобразует их в радианы. (Использовать
Формулу @RAD(X) в столбце A и скопируйте ее для остальных столбцов в виде
блок.) В третьей строке находится синус угла (@sin(X)) (используя
та же процедура «сделай это один раз и заблокируй копирование»). В четвертой строке используется формула «A3 *
A3″ (с блочной копией для остатка), чтобы получить значения для синусоидального
квадратная кривая. График результатов дает точную кривую, помеченную как
вкус. Кривые, показанные здесь, сглажены, чтобы занимать меньше места по вертикали.
но программы для работы с электронными таблицами с отличными графическими способностями (например, Quattro
Используемый здесь Pro 7.0) покажет полные графики 8,5 на 11 дюймов с прекрасным
разрешающая способность.
Моя процедура началась с настройки столбцов электронной таблицы для каждых 5 градусов.
от 0 до 360 градусов. Следующая строка преобразует их в радианы. (Использовать
Формулу @RAD(X) в столбце A и скопируйте ее для остальных столбцов в виде
блок.) В третьей строке находится синус угла (@sin(X)) (используя
та же процедура «сделай это один раз и заблокируй копирование»). В четвертой строке используется формула «A3 *
A3″ (с блочной копией для остатка), чтобы получить значения для синусоидального
квадратная кривая. График результатов дает точную кривую, помеченную как
вкус. Кривые, показанные здесь, сглажены, чтобы занимать меньше места по вертикали.
но программы для работы с электронными таблицами с отличными графическими способностями (например, Quattro
Используемый здесь Pro 7.0) покажет полные графики 8,5 на 11 дюймов с прекрасным
разрешающая способность.
Кривая очень полезна. Во-первых, он показывает различия в
мгновенная мощность во времени. Учащийся теперь может видеть, что фактическое
генерируемая и используемая энергия будет зависеть от времени, как он или она себе представляет. кривая повторяется снова и снова в течение многих циклов. Резистор
будет нагреваться и достигать довольно постоянной температуры с переменным током, так же, как
так было с DC.
кривая повторяется снова и снова в течение многих циклов. Резистор
будет нагреваться и достигать довольно постоянной температуры с переменным током, так же, как
так было с DC.
Чтобы выяснить, сколько энергии используется в единицу времени, потребуется больше
чем мгновенное считывание. Это потребует, чтобы мы усреднили мощность
цикла, что означает период времени в 360 градусов. Думая о степенях как
единицы измерения времени важны для понимания переменного тока, и многие учащиеся никогда не
уловить это фундаментальное понятие. Если это поможет, вы можете преобразовать каждый
градус (или пять градусов) в миллисекунды. Однако, чтобы сохранить
студент от мысли, что эти идеи применимы только к течению американского дома,
использовать несколько частот переменного тока в диапазоне мощностей. При частоте 60 Гц цикл занимает
около 16,7 миллисекунд или около 46 микросекунд на градус. В Европе,
где 50 Гц является довольно стандартным, цикл занимает 20 миллисекунд примерно при 55
микросекунд на градус. Это быстро, но конечно.
Это быстро, но конечно.
Возвращаясь к рис. 3, мы можем только с помощью визуального осмотра увидеть, что Линия 0,5 представляет собой среднее значение всех значений на кривой. учащийся должен провести линию поперек страницы по этой пунктирной линии 0,5, чтобы подчеркнуть это. Площадь внутри пиков над линией 0,5 равна площади вне пиков и ниже линии 0,5: недостающая мощность и нынешняя власть одинакова. Разрезание графика, чтобы показать это, может занять любое время. недоверие к проверке ученика. Конечно, элементарно методы интеграции подтвердят визуальные данные, но мы не будем предположить студента любой математике, которую мы не можем легко преподавать по пути.
Результат этого упражнения является убедительным подтверждением факта
что средняя мощность составляет половину пиковой мощности. Иначе выражается.
Следовательно, если все циклы после первого одинаковы, то общее генерируемая и используемая энергия является функцией средней мощности, умноженной на время создания и использования.

PDC И ПАВЕ
Четвертый шаг в нашем процессе возвращает нас обратно в округ Колумбия. Предположим, мы хотим нагревать резистор как в цепях постоянного, так и переменного тока до одинакового температуры, что указывает на эквивалентное преобразование электрической энергии в тепловая энергия. В этом случае среднее потребление энергии и, следовательно, среднее мощность должна быть одинаковой в обоих случаях. Для постоянного тока эта скорость использования является постоянное, одно и то же в каждое мгновение. Для переменного тока это средняя скорость использования в течение по крайней мере полупериода из множества одинаковых циклов. В противном случае выраженный,Поскольку средняя мощность переменного тока равна постоянной мощности постоянного тока, пиковая мощность переменного тока мощность должна быть в два раза выше мощности постоянного тока, или
Прежде чем оставить позади рис. 3, давайте взглянем на него еще раз. Там
четыре точки на графике, где мгновенная мощность переменного тока равна
средняя мощность переменного тока. Это точки, в которых график мгновенного
мощность пересекает горизонтальную линию 0,5. По времени или от 0 до 360 градусов
оси, эти точки составляют 45, 135, 225 и 315 градусов. Оглядываясь назад на рис.
2, мы видим, что эти точки являются точками на полпути вдоль дуги от
от 0 до 90 градусов, от 90 до 180 градусов и т. д. Смотрим ли мы на
круговую диаграмму или кривую мощности, мы можем сделать вывод, что мощность
ниже точки 45 градусов в половине случаев и выше ее в половине случаев.
3, давайте взглянем на него еще раз. Там
четыре точки на графике, где мгновенная мощность переменного тока равна
средняя мощность переменного тока. Это точки, в которых график мгновенного
мощность пересекает горизонтальную линию 0,5. По времени или от 0 до 360 градусов
оси, эти точки составляют 45, 135, 225 и 315 градусов. Оглядываясь назад на рис.
2, мы видим, что эти точки являются точками на полпути вдоль дуги от
от 0 до 90 градусов, от 90 до 180 градусов и т. д. Смотрим ли мы на
круговую диаграмму или кривую мощности, мы можем сделать вывод, что мощность
ниже точки 45 градусов в половине случаев и выше ее в половине случаев.
Теперь у нас есть достаточно четкое представление о том, как электрическая энергия совершает работу. является ли эта электрическая энергия переменным или постоянным током. Выполнение одной и той же работы указывает эквивалентность двух форм электрической энергии.
Тем не менее, у нас еще остались один или два вопроса. Если мощность постоянного тока
эквивалент мощности переменного тока — это средняя мощность переменного тока или половина пиковой мощности переменного тока,
каковы будут значения переменного напряжения и тока по отношению к пиковому напряжению
и ток, который будет эквивалентен их аналогам постоянного тока?
Если мощность постоянного тока
эквивалент мощности переменного тока — это средняя мощность переменного тока или половина пиковой мощности переменного тока,
каковы будут значения переменного напряжения и тока по отношению к пиковому напряжению
и ток, который будет эквивалентен их аналогам постоянного тока?
EDC-EQUIV И IDC-EQUIV
Наш пятый шаг будет состоять в том, чтобы найти напряжение и ток, которые производят средняя мощность переменного тока, которая составляет половину пиковой мощности. У нас есть несколько пути, по которым это можно сделать. Наилучший эффект на студентов происходит, когда мы используем всех, ибо тогда мы можем показать взаимосвязь многочисленных основных идеи переменного тока. Здесь мы покажем только два. 1. Помните, что пиковая мощность равна 1 ватту, произведенному пиковым
напряжение 1 вольт и пиковый ток 1 ампер, мы можем спросить, какое напряжение и
ток необходим для получения тока, равного половине пиковой мощности. Мы
специально ищут напряжение и ток с одинаковыми числовыми
ценность. Другие значения напряжения и тока, которые производят ту же мощность, могут быть
выводится с одной константой k, такой что
Мы
специально ищут напряжение и ток с одинаковыми числовыми
ценность. Другие значения напряжения и тока, которые производят ту же мощность, могут быть
выводится с одной константой k, такой что
Следовательно, Edc-equiv = Idc-equiv для рассматриваемой задачи. Мы ищем числовое значение, которое при умножении само на себя дает желаемую мощность ценность. Это, конечно, просто квадратный корень из значения мощности. Тем не менее, некоторые учащиеся, возможно, утратили представление о концепции квадрата. корни и требуют объяснения этого порядка.
Эквивалентное постоянному току напряжение и ток представляют собой квадратный корень из
средней или эквивалентной мощности постоянного тока. Мы могли бы формализовать это как
или
Чтобы найти множитель, применимый в равной степени к пиковому напряжению и к пику ток, мы просто извлекаем квадратный корень из 0,5, то есть находим число что при умножении само на себя равно 0,5.
 Результат можно выдавить
любого калькулятора:
Результат можно выдавить
любого калькулятора: или
и
Конечно, из нашего обсуждения базового генератора и резистора цепи, как напряжение, так и ток могут быть отрицательными, но только при одном и том же время.
2. График мгновенных значений напряжения и формы тока
синусоиды, как показано на рис. 4. Этот график можно сравнить с
рис. 3, чтобы получить некоторые ценные данные, но объединение графиков может сделать
сравнение проще. На рис. 5 объединена синусоида напряжение-ток с
график мгновенных значений мощности с использованием отдельных осей, одна на
слева, другой справа. На рис. 6 используется другой подход. Если
студент понимает, что отрицательное напряжение, умноженное на отрицательный ток, дает
положительная мощность, то мы можем построить график абсолютных значений напряжения или
тока для построения графика на рис.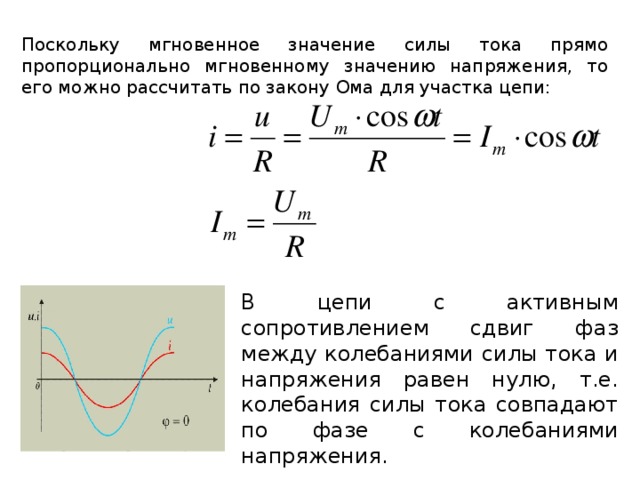 6. Для построения графика абсолютных значений на
электронной таблицы, просто добавьте новую строку в столбец A, используя @ABS(X)
функция. Затем скопируйте новую строку в A для всех столбцов от 0 до 360.
градусов.
6. Для построения графика абсолютных значений на
электронной таблицы, просто добавьте новую строку в столбец A, используя @ABS(X)
функция. Затем скопируйте новую строку в A для всех столбцов от 0 до 360.
градусов.
Какую бы графическую систему вы ни использовали, обратите внимание на количество градусов, при которых мощность пересекает горизонтальную линию 0,5. Тогда спроси, что напряжение и ток находятся в этих градусных точках. Ты можешь читать приблизительные значения из графика для 45, 135, 225 и 315 градусов баллы: чуть более 0,7.
Синус любой из этих точек дает значение 0,707 для
45 и 135 градусов и -0,707 для 225 и 315 градусов. Для мощности 0,5
Ppk, результирующие напряжение и ток составляют 0,707 Epk и 0,707 Ipk,
соответственно.
Для мощности 0,5
Ppk, результирующие напряжение и ток составляют 0,707 Epk и 0,707 Ipk,
соответственно.
На рис. 6 также видно, что кроме точек 0 и 1 на графике, как напряжение, так и ток должны иметь значения больше, чем числовое значение мощности (при равенстве напряжения и тока, перед умножив одно на k, а другое на 1/k).
Наконец, график показывает, что значение напряжения или тока то есть в 0,707 раза больше пикового значения каждого из них представляет одно и то же время линия деления как точка пиковой мощности 0,5. То есть за половину времени каждом цикле значение напряжения, тока или мощности меньше указанное значение и для половины времени каждого цикла значение напряжения, ток или мощность больше указанного значения.
Графические идеи совпадают с прямыми арифметическими идеями
отлично. В этом заключается цель преподавания одного и того же урока из более чем одного
точка зрения. Некоторые учащиеся лучше учатся, видя расчеты; другие
учиться лучше всего из изучения графиков. Некоторые даже объединят идеи из
две перспективы, прежде чем поймать. Не полагайтесь на простое повторение.
Некоторые даже объединят идеи из
две перспективы, прежде чем поймать. Не полагайтесь на простое повторение.
ОБРАТНАЯ ПРОЦЕДУРА
Какой бы маршрут мы ни использовали, результат один и тот же. Мы установили что эквиваленты постоянного тока переменного напряжения и тока составляют 0,707 пикового значения. значения переменного напряжения и тока. Теперь допустим, что 1 переменный вольт постоянного тока-экв = 1 вольт постоянного тока. и 1 экв. переменного тока = 1 ампер постоянного тока. Эта процедура является правильной, поскольку эти значения как в цепях переменного, так и постоянного тока производят одинаковое производство и использование энергии. Каково тогда значение пикового напряжения и тока относительно
Эквивалентные значения постоянного тока. поскольку 1 эквивалентный вольт или ампер постоянного тока = 0,707 пикового значения
напряжения или тока, пиковое напряжение или ток должны равняться постоянному току.
эквивалентное напряжение или ток, деленное на 0,707 или
и
На этом этапе вы можете познакомить ученика с магией
квадратный корень из 2,1 разделить на 0,707 = 1,414 и наоборот. 0,707 равно
половина квадратного корня из 2 или 1,414/2. Если вашим ученикам интересно,
вы можете вернуться к основным идеям тригонометрии и геометрии, чтобы
проследите использование квадратного корня из 2 в связи со сторонами и
гипотенузы прямоугольных треугольников. Знакомство с этими отношениями
выплачивать дивиденды студенту в его или ее последующем изучении электроники.
0,707 равно
половина квадратного корня из 2 или 1,414/2. Если вашим ученикам интересно,
вы можете вернуться к основным идеям тригонометрии и геометрии, чтобы
проследите использование квадратного корня из 2 в связи со сторонами и
гипотенузы прямоугольных треугольников. Знакомство с этими отношениями
выплачивать дивиденды студенту в его или ее последующем изучении электроники.
Или вы можете просто дать для тренировки памяти обычные формулы:
и
ПЕРЕИМЕНОВАНИЕ DC-ЭКВИВАЛЕНТНОСТИ
Вернемся к рис. 4, который до сих пор очень мало работал в одиночку. Используя среднюю или «0,0» линию в качестве ориентира, мы можем спросить, какое значение состоит из всех мгновенных значений напряжения или тока для верхней или нижней части кривой. Так как напряжение и ток равны постоянно меняясь, каждое мгновение бесконечно мало. Мы можем попробовать процесс, взяв значения на каждом 5-градусном интервале, используя калькулятор с триггерными функциями и накопительной памятью. (С использованием
первые 90 градусов кривой сокращает расчет до 19 точек данных.
Тем не менее, компромисс заключается в несколько большем отклонении от правильного
полученное значение.) Результат составляет около 0,629 от пикового значения. Студент
не очень далеко, чтобы узнать, что среднее значение всех
мгновенные значения составляют 0,637 от пикового значения. Это «среднее» переменное напряжение
или текущее значение, конечно, полезно для понимания схем, где
переменный ток был выпрямлен, чтобы обеспечить импульсы только в одном
направление.
(С использованием
первые 90 градусов кривой сокращает расчет до 19 точек данных.
Тем не менее, компромисс заключается в несколько большем отклонении от правильного
полученное значение.) Результат составляет около 0,629 от пикового значения. Студент
не очень далеко, чтобы узнать, что среднее значение всех
мгновенные значения составляют 0,637 от пикового значения. Это «среднее» переменное напряжение
или текущее значение, конечно, полезно для понимания схем, где
переменный ток был выпрямлен, чтобы обеспечить импульсы только в одном
направление.Попробуем другой метод «усреднения». Сначала возьмем квадрат каждое мгновенное значение. Затем сложите все квадраты. В-третьих, возьмите среднее (или среднее) всех квадратов путем деления суммы квадратов по количеству мгновенных значений. Наконец, возьмите квадрат корень результата.
Этот метод «среднеквадратичного» (среднеквадратического) извлечения квадратного корня из
среднее квадратов всех значений напряжения или тока при
кривая в диапазоне от 0 до 1 дает значение, идентичное DC
эквивалентное значение напряжения и тока. Мы можем аппроксимировать процесс
проверка всех значений с интервалом в 5 градусов. Результат, используя 19данные
точек (как результат использования всех возможных мгновенных значений), является
0,707 от пикового значения. Полное среднеквадратичное значение расчет просто расширяет наши
более ранний арифметический вывод эквивалентных значений постоянного тока.
Мы можем аппроксимировать процесс
проверка всех значений с интервалом в 5 градусов. Результат, используя 19данные
точек (как результат использования всех возможных мгновенных значений), является
0,707 от пикового значения. Полное среднеквадратичное значение расчет просто расширяет наши
более ранний арифметический вывод эквивалентных значений постоянного тока.
Исходя из этого, Edc-equiv и Idc-equiv получили свои общие названия: Erms и
Irms, где «среднеквадратичное значение» означает «среднеквадратичное значение». Следовательно, мы можем принять окончательный
шаг перемаркировки более ранних формул:
И наоборот,
Теперь учащийся имеет в своем распоряжении именно отношения требуется на экзаменах. Кроме того, он или она также имеет представление о взаимосвязь многих фундаментальных идей, касающихся переменного и постоянного тока напряжение, ток и мощность.





 2 Термодинамика
2 Термодинамика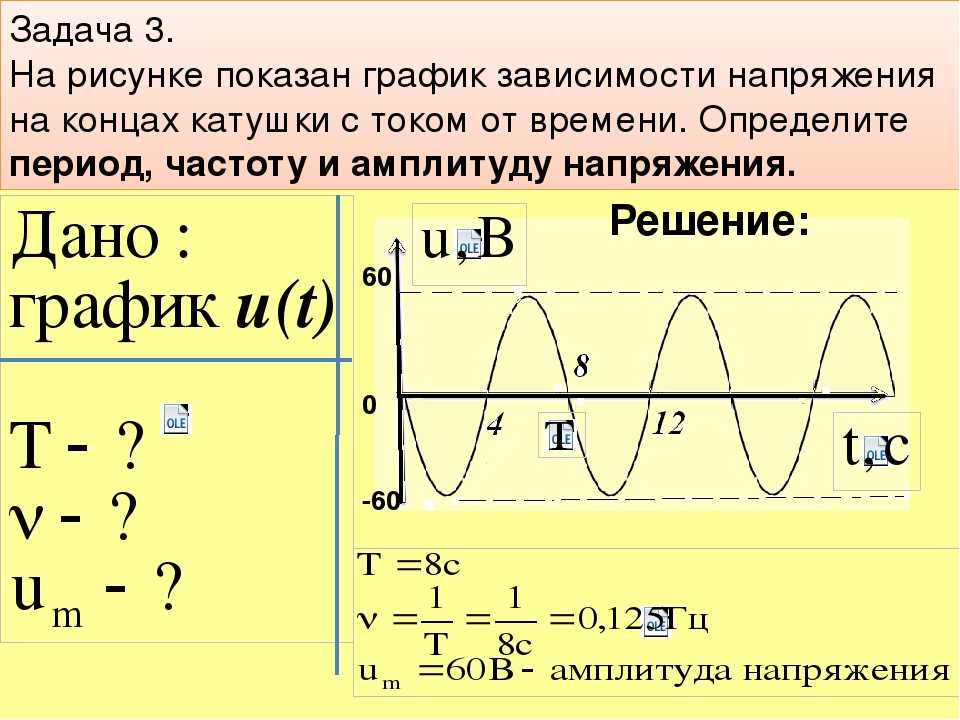 5 Излучение и спектры
5 Излучение и спектры
