Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Физика
| Похожие вопросы |
Котелок ёмкостью 3 литра3 литра плотно набили снегом и поставили на примус. Когда снег растаял, котелок оказался на 1/41/4 своего объёма наполнен
Когда снег растаял, котелок оказался на 1/41/4 своего объёма наполнен
Решено
Масса оболочки воздушного шара составляет 210 кг.Надутый гелием, он может поднять груз массой 1010 кг.При этом плотность гелия в шаре 0,18 кг/м3 , а…
Решено
проезжая по выпуклому мосту со скоростью, модуль которой u=18м/c,автомобиль в верхней точке давит на мост с силой,модуль которой на 20% меньше модуля…
мензурке, наполненной водой, плавает тело, привязанное нитью к её дну. Нить перерезали, в результате чего уровень воды в мензурке понизился так, как
Пользуйтесь нашим приложением
5. Электромагнитные колебания 5. 5.1.1. Найти отношения амплитудных значений сил тока Im, напряжений Um , электрических WBm и магнитных WEm мощностей, если начальный заряд qm на конденсаторе, включенном в идеальный колебательный контур, увеличился в 10 раз. Решение 1. Предположим, что электрический заряд в колебательном контуре изменяется по закону , (1) в этом случае уравнение силы тока представится следующим образом , (2) где 0 циклическая частота собственных колебаний в электрическом контуре. 2. Образуем систему уравнений для амплитудных значений сил токов, из которых найдём их отношение . (3) 3. Взаимосвязь между зарядом и напряжением установим из следующих соображений . (4) 4. Ввиду идеальности колебательного контура для энергии можно записать следующие соотношения . (5) 5.1.2. В идеальном колебательном контуре амплитудное значение напряжения на конденсаторе увеличивается на Um= 10 В, при этом максимальная сила тока через индуктивность возросла в 3 раза. Решение 1. Для идеального колебательного контура закон сохранения энергии можно записать следующим образом (1) 2. Поделим уравнения (1) друг на друга почленно , (2) . (3) 3. Из уравнения (3) следует, что . (4) 4. Изменение напряжения можно записать следующим образом , (5) откуда , (6) . (7) 5.1.3. В идеальном колебательном контуре амплитудное значение напряжения на конденсаторе равно Um = 100 В, а максимальная сила тока через индуктивность Im = 100 мА. Определить силу тока через индуктивность и напряжение на конденсаторе, когда электрическая энергия, запасаемая в конденсаторе, совпадает по величине с магнитной энергией, присутствующей в индуктивности. Решение 1. Равенство двух видов энергии, электрической и магнитной и закон сохранения энергии дают основание записать следующие соотношения , (1) , (2) . 2. Аналогичные соотношения можно записать и для силы тока через индуктивность , (4) . (5) 5.1.4. В идеальном контуре наблюдаются электромагнитные колебания с периодом Т = 100 мкс. Какой промежуток времени пройдёт с момента возникновения колебаний до состояния равенства электрической и магнитной составляющих энергии? Решение 1. В соответствие с уравнением (1) предыдущей задачи . (1) 2. С другой стороны . (2) 3. При нулевой начальной фазе = 0, . (3) 4. Совместим уравнения (2) и (3) , (4) . (5) 5.1.5. Определить, через какой промежуток времени после начала колебаний в идеальном LC контуре заряд на конденсаторе с периодом колебаний Т = 100 мкс достигнет впервые, величины равной половине амплитудного значения. Решение 1. Запишем уравнение, характеризующее изменение во времени заряда конденсатора . (1) 2. Подставим в уравнение заданное условие , (2) . 5.1.6. В идеальном колебательном RC контуре ёмкость конденсатора увеличилась в 100 раз, а индуктивность катушки уменьшилась в 25 раз. Как при этом поменялась частота собственных колебаний? Решение 1. Уравнение периодов и частот собственных колебаний , (1) . (2) 2. Отношение частот при заданном изменении ёмкости и индуктивности . (3) Частота, таким образом, уменьшилась в два раза. 5.1.7. В некоторый момент времени при возникновении колебаний в идеальном контуре энергия, накопленная в конденсаторе, становится в три раза больше энергии, запасаемой индуктивностью. В каком отношении будет находиться мгновенное значение напряжения на обкладках конденсатора с амплитудным значением. Определить в единицах периода промежуток времени от начала колебаний до наступления заданного режима. Решение 1. По условию задачи магнитная составляющая энергии WB в три раза меньше магнитной составляющей WE, т. , (1) В соответствие с законом сохранения энергии , (2) 2. Разрешим последнее уравнение относительно действующего напряжения . (3) 3. Уравнение колебаний напряжения на обкладках конденсатора позволяет определить искомый промежуток времени , (4) . (5) 5.1.8. В колебательном контуре без затухания при увеличении ёмкости на С = 0,2 мкФ, частота колебаний уменьшилась в 1,2 раза. Определить начальную и конечную ёмкость контура. Решение 1. Частота собственных колебаний контура без затухания связана с его параметрами, следующими соотношениями , (1) откуда . (2) 2. Уравнение (2) позволяет записать изменение ёмкости и найти искомые величины С1 и С2 . (3) . (4) 5.1.9. Идеальный колебательный контур, включённый в антенный блок радиоприёмника содержит конденсатор ёмкостью С = 9 пФ и катушку с индуктивностью L =1 мГн. На какую длину волны настроен колебательный контур? Решение 1. , (1) . (2) 5.1.10. Плоский конденсатор с площадью обкладок s = 10 3 м2 и расстоянием между пластинами d= 10 3 м, включён в идеальный колебательный контур радиоприёмника, содержащий катушку с индуктивностью L = 50 мкГн. Определить диэлектрическую проницаемость материала, помещённого между обкладками конденсатора, если радиоприёмник настроен на длину волны = 250 м. Решение 1. Запишем уравнение ёмкости плоского конденсатора с заполнением пространства между пластинами диэлектриком с проницаемостью . (1) 2. Длину волны, на которую настроен контур, определим уравнением (2) предыдущей задачи . (2) 3. Подставим в последнее уравнение значение ёмкости . (3) 4. Разрешим уравнение (3) относительно диэлектрической проницаемости . 5.1.11. В некоторый момент времени сила тока в проводниках, подключенных к квадратным пластинам со стороной а = 1 м плоского конденсатора с диэлектрическом из титаната бария ( = 1000), составила i = 10 А. С какой скоростью изменяется напряжённость электрического поля в конденсаторе? Решение 1. Выразим силу тока через скорость изменения заряда, а электрическую ёмкость через напряжение на обкладках , (2) . (3) 2. Напряжённость электрического поля между пластинами конденсатора определится как . (4) 5.1.12. Частица массой m и зарядом q влетает в однородное электрическое поле, напряжённость которого изменяется со временем по закону E=E0sint. Начальная скорость частицы v0 направлена перпендикулярно вектору напряжённости. Определите уравнение движения частицы.
1. Запишем уравнение второго закона Ньютона для заряженной частицы, на которую действует сила Кулона, изменяющаяся по закону синуса , (1) . 2. Проинтегрируем уравнение (2) дважды , (3) . (4) 3. Постоянные интегрирования определим из начальных условий . (5) 5.1.13. Напряжение на обкладках конденсатора ёмкостью С = 10 мкФ, включенного в идеальный колебательный контур изменяется в соответствие с законом u(t) = 100 cos103t. Определить индуктивность катушки, период колебаний и закон изменения силы тока через индуктивность. Решение 1. В данном случае циклическая частота собственных колебаний контура 0 = 103 рад/с, поэтому период колебаний . (1) 2. Индуктивность катушки определим, воспользовавшись уравнением Томсона 5 мГн. (2) 3. Закон изменения силы тока определится уравнением , (3) . (4) 5.1.14. Сила тока через индуктивность изменяется в соответствие с законом i(t) = 10 2sin62,8t. Определить амплитудные значения электрической и магнитной составляющих энергии, запасаемой в идеальном контуре, обладающем индуктивностью L = 1 Гн. Решение 1. Заданное уравнение силы тока позволяет определить период колебаний . (1) 2. Ёмкость конденсатора определим из формулы Томсона . (2) 3. Амплитудное значение магнитной составляющей энергии . (3) 5.1.15. После того, как конденсатору, входящему в состав колебательного контура, сообщили заряд qmax = 1 мКл, возникли электромагнитные колебания, которые через некоторое время исчезли. Определить количество выделившегося при этом тепла, если цилиндрический конденсатор длиной l = 5 см с внешним радиусом r1 = 1 см и внутренним r2 = 0,5 см снабжён фторопластовым диэлектриком с проницаемостью = 150. Решение 1. Найдём ёмкость цилиндрического конденсатора с заданными параметрами . (1) 2. Согласно закону сохранения, вся первоначальная энергия, сообщённая колебательной системе, в конечном счете, перейдёт в тепло . (2)
Решение 1. Определим ёмкость конденсатора , (1) 2. Найдём индукцию катушки , (2) . 3. Период колебаний контура . (3) 4. Количество колебаний за время . (4) 5.1.17. В идеальном колебательном контуре с ёмкостью С1 = 2 мкФ резонансные колебания устанавливаются на частоте 1 = 500 Гц. При подключении параллельно первому конденсатору ёмкости С2, резонансная частота понизилась до 2 = 250 Гц. Определить ёмкость конденсатора С2. Решение 1. Запишем условия резонанса . (1) 2. Поделим уравнения (1) почленно , (2) откуда . 5.1.18. Конденсатор ёмкостью С = 1 мкФ включен в идеальный контур с двумя параллельными катушками L1 = 0,1 Гн, L2 = 0,2 Гн. Найти амплитудное значение силы кока в контуре, если максимальное напряжение на обкладках конденсатора составляет um = 10 В. Решение 1. Запишем закон сохранения энергии применительно к контуру
2. При возникновении электромагнитных колебаний обе катушки пересекаются один и тем же магнитным потоком, т.е. . (2) 3. Суммарный ток в этом случае можно представить следующим образом . (3) 4. Выразим из уравнения (4) значения токов через катушки , (4) 5. Подставим значения токов im1 и im2 в исходное уравнение (1) , (5) откуда . (6)
Решение 1. Так как ёмкости всех конденсаторов одинаковы, то будут одинаковыми и потенциалы точек 1 и 2, т.е. 1 = 2, четыре конденсатора соединены параллельно, что даёт возможность частоту контура записать так . (1) 5.2. Затухающие электромагнитные колебания
Решение 1. Найдём ёмкостное и индуктивное сопротивление контура . (1) 2. Определим амплитудное значение силы тока, протекающего через катушку и активное сопротивление , (2) . (3) где u* эффективное значение напряжения, Z импеданс (суммарное сопротивление), RL индуктивное сопротивление, RC ёмкостное сопротивление. 3. Амплитудное падение напряжения на элементах схемы , (4) . (5) 4. Сдвиг фаз между колебаниями силы тока в цепи и колебания сетевого напряжения , (6) . (7) 5. Уравнения колебаний силы тока и напряжения . (8) . (9) 5.2.2. В RLC контуре в течение N = 10 полных колебаний амплитуда напряжения на конденсаторе уменьшилась в 1,5 раза. Определить добротность контура. Решение 1. Запишем уравнения для добротности Q и логарифмического декремента контура . (1) 2. Выразим амплитуду напряжения через указанный в условии задачи промежуток времени . (2) 3. Преобразуем уравнение (2) к виду . (3) 4. Сопоставляя уравнения(1) и (3), получим . (4) 5.2.3. Колебательный RLC контур имеет следующие параметры: R = 100 Ом, С = 1 мкФ, L = 1 Гн. Определить число полных колебаний N в течение которых амплитуда уменьшится в е раз. Решение 1. . (1) 2. Выразим коэффициент затухания через параметры контура и подставим его значение в уравнение (1) . (2) 3. Найдём период затухающих колебаний . (3) 4. Циклическая частота собственных незатухающих колебаний . (4) 5. Подставим в уравнение (3) значения 0 и . (5) 6. Определим искомое число колебаний . (6) 5.2.4. Имеется последовательное соединение активного сопротивления R = 1 кОм, индуктивности L = 10 –2 Гн и ёмкости С =0,2 нФ. Определите сопротивление цепи при подаче на неё напряжения с частотой 1 МГц и падение напряжения на каждом элементе, если амплитуда внешнего напряжения составляет um = 100 В. Решение 1. Определим полное сопротивление заданной цепи, с учётом того, что , (1) . (2) 2. Определим амплитудное im и эффективное i* значение силы тока . 3. Определим падение напряжения на активном сопротивлении R, конденсаторе С и индуктивности L . (4) 5.2.5. Внешняя цепь переменного тока с частотой = 1000 Гц состоит из активного сопротивления R = 10 Ом и катушки индуктивностью L = 10 –2 Гн. Определите падение напряжения на индуктивности, когда максимальное напряжение на активном сопротивлении составляет uR(m) = 8,82 В? Решение 1. Определим циклическую частоту колебаний . (1) 2. Найдём полное сопротивление заданной цепи . (2) 3. Амплитудное и эффективное значение силы тока в цепи . (3) 4. Падение напряжения на активном сопротивлении uR и индуктивности uL . (4) 5.2.6. Катушка индуктивностью L = 1 Гн, конденсатор ёмкостью С = 1 мкФ и активное сопротивление R = 10 Ом образуют колебательный контур. Конденсатору первоначально сообщают заряд qm = 1 нКл. Решение 1. Определим циклическую частоту собственных незатухающих колебаний в контуре . (1) 2. Коэффициент затухания прямо пропорционален величине активного сопротивления и обратно пропорционален удвоенной индуктивности контура . (2) 3. Определим циклическую частоту затухающих колебаний через параметры контура . (3) 4. Найдём период затухающих колебаний . (4) 5. Логарифмический декремент колебаний . (5) 6. Амплитудное значение напряжения на обкладках конденсатора определим, воспользовавшись зависимостью заряда, ёмкости и разности потенциалов . (6) 7. Если предположить, что напряжение изменяется по закону косинуса без начальной фазы, то уравнение можно записать следующим образом , . (7) 5.2.7. Энергия колебательного контура в течение N = 100 полных колебаний уменьшилась в z = 225 раз. Решение 1. В соответствие с законом сохранения энергии, амплитудное значение электрической составляющей энергии должно быть равным магнитной составляющей, запасаемой в индуктивности . (1) 2. Отношение энергий z можно представить через величины соответствующих сил токов , (2) с другой стороны, декремент затухания определяется через период Т и коэффициент затухания , откуда следует, что . (3) 3. Уравнение (3) позволяет найти величину логарифмического декремента . (4) 5.2.8. В колебательном контуре с добротностью Q = 103 происходят колебания с циклической частотой =103 с1. За какой промежуток времени амплитудное значение силы тока через индуктивность уменьшится в 23 раза? Решение 1. Запишем уравнение изменение силы тока в контуре с затуханием , (1) откуда . (2) 2. Выразим из уравнения (2) время , в течение которого происходит заданное затухание . 3. Коэффициент затухания связан с добротностью контура следующими соотношениями . (4) 4. Подставим значение коэффициента затухания из уравнения (4) в уравнение (3) . (5) 2.5.9. На последовательно соединённые: активное сопротивление R = 800 Ом, катушку с индуктивностью L = 1,27 Гн и конденсатор ёмкостью С = 1,59 мкФ подаётся действующее напряжение u* = 127 В промышленной частоты = 50 Гц. Определить действующее значение силы тока в цепи, сдвиг фаз между током и напряжением, а так же действующие значения падения напряжения на элементах схемы, мощность выделяемую в цепи. Решение 1. Найдём величину циклической частоты колебаний и амплитудное значение напряжения . (1) 2. Определим далее импеданс цепи . (2) 3. Амплитудное значение силы тока в цепи . (3) 4. Действующее значение силы тока , (4) . (5) 4. Разность фаз между током и напряжением определяется отношением активной составляющей сопротивления к реактивной составляющей . 5. Падение напряжения на элементах схемы . (7) 6. Мощность, выделяемая в цепи . (8) 2.5.10. К бытовой сети с действующим напряжением u* = 220 В и частотой = 50 Гц подключена схема, состоящая из последовательно включенного активного сопротивления R = 10 Ом и катушки индуктивностью 30 мГн. Какое количество тепла выделится в активном сопротивлении за время = 1 с? Решение 1. Запишем уравнение полного сопротивления цепи . (1) 2. Действующая сила тока, потребляемая цепью = 3,95 А. (2) 3. Количество тепла, выделяющееся на активном сопротивлении . (3) 2.5.11. Колебательный R,L,C контур обладает собственной частотой колебаний 0 = 1 кГц, резонанс контура проявляется на частоте r = 800 Гц. Найти частоту затухающих колебаний контура. Решение 1. Циклическая частота затухающих колебаний контура . (1) 2. Циклическая частота резонансных колебаний . 3. Объединим уравнения (2) и (1) . (3) 4. Подставим значение коэффициента затухания из уравнения (3) в уравнение (1) , (4) . (5) 2.5.12. В RLC контуре наблюдаются затухающие колебания с периодом Т = 100 мс. В течение 10 периодов колебаний амплитудное значение силы тока в цепи уменьшилось в 20 раз. Найти величину резонансной частоту колебательного контура. Решение 1. Амплитудное значение силы тока при затухающих колебаниях можно представить следующим образом , (1) 2. Определим отношение амплитудных значений силы тока при первом и десятом колебании . (2) 3. Выразим из последнего уравнения величину коэффициента затухания . (3) 4. Запишем уравнение для циклической частоты затухающих колебаний в контуре . (4) 5. Определим далее циклическую резонансную частоту , (5) . (6)
Решение 1. Определим амплитудное значение напряжения на обкладках конденсатора в момент времени t =0 . (1) 2. Найдём величину коэффициента затухания цепи . (2) 3. Период затухающих колебаний . (3) 4. Запишем уравнение изменения напряжения на обкладках конденсатора , (4) . (5) 5. Как видно из уравнения (5), амплитудное значение напряжения на обкладках конденсатора будет изменяться по экспоненциальному закону . (6)
5.2.14. Цепь состоит из конденсатора ёмкостью С = 1 мкФ и катушки индуктивностью L = 1 Гн и активного сопротивления R. За время = 1 с напряжение на обкладках конденсатора уменьшилось в n = 10 раз. Определить логарифмический декремент колебаний и величину сопротивления R. Решение 1.Определим период колебаний, воспользовавшись формулой Томсона . (1) которая справедлива при , (2) в рассматриваемом случае (1/LC) = 106. 2. Запишем закон изменения напряжения на обкладках конденсатора и определим логарифмический декремент . (3) 3. Величину сопротивления определим из уравнения взаимосвязи логарифмического декремента и коэффициента затухания . (4) 5.2.15. Цилиндрическая катушка индуктивности длиной l = 1 м и площадью поперечного сечения s = 110 4 м2 включена в бортовую сеть судна с частотой изменения силы тока = 400 Гц. Решение 1. Определим циклическую частоту колебаний . (1) 2. Заданные по условию задачи данные позволяют определить индуктивность катушки . (2) 3. Разность фаз между силой тока и напряжением в общем случае R,LC цепи определяется уравнением , (3) отсутствие в цепи конденсатора, позволяет формулу упростить . (4) 4. Подставим уравнение индуктивности (2) в уравнение сдвига фаз . (5) 5. Разрешим уравнение (5) относительно активного сопротивления катушки R . (6) 5.2.15. RLC контур включён в сеть переменного тока. Максимальная разность потенциалов на обкладках конденсатора равна um = 10 В. Найти среднюю величину мощности, потребляемой контуром при незатухающих колебаниях, если L = 1 Гн, C = 1 мкФ, R = 100 Ом. Решение 1. Определим амплитудное значение заряда на конденсаторе . 2. Найдём амплитудное значение силы тока в цепи из следующих соображений ; (2) . (3) 3. Средняя мощность, потребляемая цепью , (4) . (5) |
Ч. 15 задач — University Physics Volume 2
Проблемы
15.1 Источники переменного тока
14.
15.2 Простые цепи переменного тока
15.
Рассчитайте реактивное сопротивление конденсатора емкостью 5,0 мкФ5,0 мкФ при (а) 60 Гц, (б) 600 Гц и (в) 6000 Гц.
16.
Какова емкость конденсатора с реактивным сопротивлением 10 Ом 10 Ом при частоте 60 Гц?
17.
Рассчитайте реактивное сопротивление катушки индуктивности 5,0 мГн при (а) 60 Гц, (б) 600 Гц и (в) 6000 Гц.
18.
Какова собственная индуктивность катушки с реактивным сопротивлением 10 Ом 10 Ом при частоте 60 Гц?
19.
При какой частоте реактивное сопротивление конденсатора 20 мкФ20 мкФ равно реактивному сопротивлению катушки индуктивности 10 мГн?
20.
При частоте 1000 Гц реактивное сопротивление катушки индуктивности 5,0 мГн равно реактивному сопротивлению конкретного конденсатора. Какова емкость конденсатора?
21.
Резистор 50 Ом 50 Ом подключен параллельно ЭДС v(t)=(160В)sin(120πt)v(t)=(160В)sin(120πt). Запишите выражение для тока через резистор.
22.
Конденсатор емкостью 25 мкФ25 мкФ подключен к ЭДС, определяемой выражением v(t)=(160 В)sin(120πt)v(t)=(160 В)sin(120πt). а) Чему равно реактивное сопротивление конденсатора? (b) Напишите выражение для текущего выхода источника.
23.
Катушка индуктивности 100 мГн подключена к ЭДС предыдущей задачи. а) Чему равно реактивное сопротивление катушки индуктивности? б) Напишите выражение для тока через катушку индуктивности.
15,3 Цепи серии RLC с переменным током
24.
Каково сопротивление последовательной комбинации резистора 50 Ом 50 Ом, конденсатора 5,0 мкФ 5,0 мкФ и конденсатора 10 мкФ 10 мкФ на частоте 2,0 кГц?
25.
Резистор и конденсатор соединены последовательно через генератор переменного тока. ЭДС генератора определяется как v(t)=V0cosωt,v(t)=V0cosωt, где V0=120В,V0=120В,ω=120πрад/с,ω=120πрад/с, R=400ΩR=400Ω, и C=4,0 мкФ=4,0 мкФ. а) Чему равно сопротивление цепи? б) Какова амплитуда тока через резистор? в) Напишите выражение для тока через резистор. г) Напишите выражения, представляющие напряжения на резисторе и на конденсаторе.
26.
Резистор и катушка индуктивности соединены последовательно через генератор переменного тока. ЭДС генератора определяется выражением v(t)=V0cosωt,v(t)=V0cosωt, где V0=120VV0=120В и ω=120πрад/с; ω=120πрад/с; также R=400ΩR=400Ω и L=1,5H.L=1,5H. а) Чему равно сопротивление цепи? б) Какова амплитуда тока через резистор? в) Напишите выражение для тока через резистор. (d) Напишите выражения, представляющие напряжения на резисторе и на катушке индуктивности.
В цепи серии RLC амплитуда напряжения и частота источника составляют 100 В и 500 Гц соответственно, R = 500 Ом, R = 500 Ом, L = 0,20 Гн, L = 0,20 Гн и C = 2,0 мкФ.С=2,0 мкФ. а) Чему равно сопротивление цепи? б) Какова амплитуда тока от источника? (c) Если ЭДС источника определяется выражением v(t)=(100В)sin1000πtv(t)=(100В)sin1000πt, как изменяется ток со временем? (d) Повторите расчеты с C , измененным на 0,20 мкФ. 0,20 мкФ.
0,20 мкФ.
28.
Цепь серии RLC с R = 600 Ом R = 600 Ом, L = 30 мГн, L = 30 мГн и C = 0,050 мкФС = 0,050 мкФ питается от источника переменного тока, частота и амплитуда напряжения которого составляют 500 Гц и 50 В соответственно. . а) Чему равно сопротивление цепи? б) Какова амплитуда тока в цепи? в) Чему равен фазовый угол между ЭДС источника и тока?
29.
Для схемы, показанной ниже, каковы (а) полное сопротивление и (б) фазовый угол между током и ЭДС? (c) Напишите выражение для i(t).i(t).
15,4 Мощность в цепи переменного тока
30.
ЭДС источника переменного тока определяется выражением v(t)=V0sinωt,v(t)=V0sinωt, где V0=100VV0=100В и ω=200πрад/с.ω=200πрад/с. Рассчитайте среднюю выходную мощность источника, если он подключен через (а) конденсатор 20 мкФ20 мкФ, (б) катушку индуктивности 20 мГн и (в) резистор 50 Ом 50 Ом.
31.
Расчет среднеквадратичного значения тока для источника переменного тока определяется выражением v(t)=V0sinωt,v(t)=V0sinωt, где V0=100VV0=100В и ω=200πрад/sω=200πрад/с при подключении через (a) a конденсатор 20 мкФ20 мкФ, (б) катушка индуктивности 20 мГн и (в) резистор 50 Ом 50 Ом.
32.
Катушка индуктивности 40 мГн подключена к источнику переменного тока частотой 60 Гц, амплитуда напряжения которого составляет 50 В. Если к катушке индуктивности приложить вольтметр переменного тока, что он покажет?
33.
Для цепи RLC серии амплитуда напряжения и частота источника 100 В и 500 Гц соответственно; R=500 Ом R=500 Ом; и L=0,20HL=0,20H. Найдите среднюю мощность, рассеиваемую на резисторе, при следующих значениях емкости: (a) C=2,0 мкФ=2,0 мкФ и (б) C=0,20 мкФ.C=0,20 мкФ.
34.
Источник переменного тока с амплитудой напряжения 10 В отдает электрическую энергию мощностью 0,80 Вт при выходном токе 2,5 А. Каков фазовый угол ϕϕ между ЭДС и током?
35.
Цепь серии RLC имеет импеданс 60 Ом 60 Ом и коэффициент мощности 0,50, при этом напряжение отстает от тока. а) Следует ли последовательно с элементами включить конденсатор или катушку индуктивности, чтобы повысить коэффициент мощности цепи? б) При каком реактивном сопротивлении катушки индуктивности коэффициент мощности увеличится до единицы?
15,5 Резонанс в цепи переменного тока
36.
(a) Рассчитайте резонансную угловую частоту цепи серии RLC , для которой R=20 Ом R=20 Ом, L=75 мHL=75 мГн и C=4,0 мкФ.C=4,0 мкФ. (b) Если R изменить на 300 Ом, 300 Ом, что произойдет с резонансной угловой частотой?
37.
Резонансная частота цепи серии RLC составляет 2,0×103 Гц.2,0×103 Гц. Если собственная индуктивность в цепи равна 5,0 мГн, какова емкость в цепи?
38.
(a) Какова резонансная частота цепи серии RLC с R=20 Ом, R=20 Ом, L=2,0 мHL=2,0 мГн и C=4,0 мкФС=4,0 мкФ? б) Каково сопротивление цепи в резонансе?
39.
Для схемы серии RLC : R=100 Ом R=100 Ом, L=150 мHL=150 мГн и C=0,25 мкФ.C=0,25 мкФ. а) Если к цепи подключен источник переменного тока переменной частоты, при какой частоте на резисторе будет рассеиваться максимальная мощность? б) Какова добротность цепи?
40.
Источник переменного тока с амплитудой напряжения 100 В и переменной частотой f управляет последовательной цепью RLC с R = 10 Ом R = 10 Ом, L = 2,0 мHL = 2,0 мГн и C = 25 мкФ.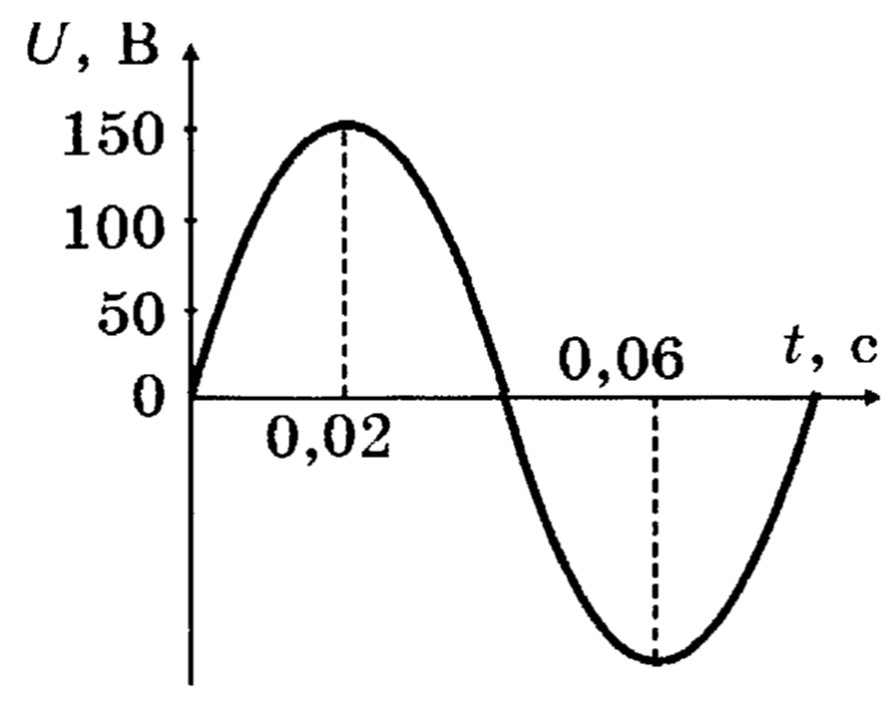 C = 25 мкФ. (a) Постройте ток через резистор как функцию частоты f . (b) Используйте график для определения резонансной частоты цепи.
C = 25 мкФ. (a) Постройте ток через резистор как функцию частоты f . (b) Используйте график для определения резонансной частоты цепи.
41.
(a) Какова резонансная частота резистора, конденсатора и катушки индуктивности, соединенных последовательно, если R=100 Ом, R=100 Ом, L=2,0HL=2,0Гн и C=5,0 мкФС=5,0 мкФ? (b) Если эта комбинация подключена к источнику 100 В, работающему на резонансной частоте, какова выходная мощность источника? (c) Что такое Q цепи? г) Какова пропускная способность цепи?
42.
Предположим, катушка имеет собственную индуктивность 20,0 Гн и сопротивление 200 Ом 200 Ом. Какая (а) емкость и (б) сопротивление должны быть соединены последовательно с катушкой, чтобы получить контур с резонансной частотой 100 Гц и Q 10?
43.
Генератор переменного тока подключен к устройству, внутренние цепи которого неизвестны. Мы знаем только ток и напряжение вне устройства, как показано ниже. Основываясь на предоставленной информации, какой вывод вы можете сделать об электрической природе устройства и его энергопотреблении?
Мы знаем только ток и напряжение вне устройства, как показано ниже. Основываясь на предоставленной информации, какой вывод вы можете сделать об электрической природе устройства и его энергопотреблении?
15,6 Трансформеры
44.
Повышающий трансформатор сконструирован так, что выходное напряжение его вторичной обмотки составляет 2000 В (среднеквадратичное значение) при подключении первичной обмотки к линейному напряжению 110 В (среднеквадратичное значение). а) Если в первичной обмотке 100 витков, то сколько витков во вторичной обмотке? б) Если резистор, подключенный к вторичной обмотке, потребляет среднеквадратичное значение тока 0,75 А, какова сила тока в первичной обмотке?
45.
Повышающий трансформатор, подключенный к линии 110 В, используется для питания газоразрядной трубки водорода напряжением 5,0 кВ (среднеквадратичное значение). Лампа рассеивает 75 Вт мощности. а) Каково отношение числа витков вторичной обмотки к числу витков первичной обмотки? б) Каковы среднеквадратичные значения тока в первичной и вторичной обмотках? в) Каково эффективное сопротивление источника 110 В?
а) Каково отношение числа витков вторичной обмотки к числу витков первичной обмотки? б) Каковы среднеквадратичные значения тока в первичной и вторичной обмотках? в) Каково эффективное сопротивление источника 110 В?
46.
Источник ЭДС переменного тока обеспечивает мощность 5,0 мВт при среднеквадратичном токе 2,0 мА, когда он подключен к первичной обмотке трансформатора. Среднеквадратичное значение напряжения на вторичной обмотке равно 20 В. а) Чему равны напряжение на первичной обмотке и сила тока во вторичной обмотке? б) Каково соотношение вторичных и первичных витков трансформатора?
47.
Трансформатор используется для понижения напряжения 110 В от настенной розетки до 9,0 В для радиоприемника. а) Если в первичной обмотке 500 витков, то сколько витков во вторичной обмотке? б) Если радиоприемник работает при токе 500 мА, каков ток через первичную обмотку?
48.
Трансформатор используется для питания модели поезда на 12 В питанием от настенной розетки на 110 В. Поезд работает с мощностью 50 Вт. а) Чему равно среднеквадратичное значение тока во вторичной обмотке трансформатора? б) Чему равно среднеквадратичное значение тока в первичной обмотке? в) Каково отношение числа первичных и вторичных витков? г) Чему равно сопротивление поезда? д) Каково сопротивление источника 110 В?
OpenStax College Physics Solution, глава 23, задача 101 (задачи и упражнения)
Вопрос
Цепь серии RLC имеет резистор $2,50 \textrm{ }\Omega$, $100 \textrm{ }\mu \textrm{H} $ индуктор и конденсатор $80,0 \textrm{ }\mu \textrm{F}$. (a) Найдите полное сопротивление цепи на частоте 120 Гц. (b) Найдите полное сопротивление цепи на частоте 5,00 кГц. (c) Если источник напряжения имеет $V_{\textrm{rms}} = 5,60 \textrm{V}$, что $I_{\textrm{rms}}$ на каждой частоте? г) Какова резонансная частота цепи? (e) Что такое $I_{\textrm{rms}}$ в резонансе?
Стенограмма видео
Это ответы по физике в колледже с Шоном Дычко. Имеем схему R L C , сопротивлением два с половиной Ома, индуктивностью 100 мкГн и емкостью 80 мкФ. А в части А нам нужно найти импеданс цепи при частоте 120 герц. И тогда в части Б частота будет пять килогерц. Итак, давайте разберемся, как использовать эти индуктивность и емкость в нашей формуле импеданса. Таким образом, импеданс равен квадратному корню из квадрата сопротивления плюс индуктивные реактивы минус емкостное реактивное сопротивление в квадрате. Таким образом, индуктивный реагент равен двум пи, умноженным на частоту, умноженной на индуктивность, а емкостной реагент равен одному на два пи, умноженным на частоту, умноженной на емкость. Итак, мы можем заменить каждый из них в нашей формуле импеданса. Итак, имеем, что импеданс равен квадратному корню из 9.0195 R в квадрате плюс два числа пи, умноженные на частоту, умноженную на индуктивность, минус единица на два числа пи, умноженная на частоту, умноженная на емкость, а затем возведите эту разницу в квадрат.
Имеем схему R L C , сопротивлением два с половиной Ома, индуктивностью 100 мкГн и емкостью 80 мкФ. А в части А нам нужно найти импеданс цепи при частоте 120 герц. И тогда в части Б частота будет пять килогерц. Итак, давайте разберемся, как использовать эти индуктивность и емкость в нашей формуле импеданса. Таким образом, импеданс равен квадратному корню из квадрата сопротивления плюс индуктивные реактивы минус емкостное реактивное сопротивление в квадрате. Таким образом, индуктивный реагент равен двум пи, умноженным на частоту, умноженной на индуктивность, а емкостной реагент равен одному на два пи, умноженным на частоту, умноженной на емкость. Итак, мы можем заменить каждый из них в нашей формуле импеданса. Итак, имеем, что импеданс равен квадратному корню из 9.0195 R в квадрате плюс два числа пи, умноженные на частоту, умноженную на индуктивность, минус единица на два числа пи, умноженная на частоту, умноженная на емкость, а затем возведите эту разницу в квадрат. Таким образом, для части А мы имеем квадратный корень из двух с половиной омов в квадрате плюс два пи, умноженные на 120 герц, умноженные на 100 микрогенри, то есть умноженные на десять до минус шесть генри, минус единица на два пи, умноженная на 120 герц, умноженная на 80, умноженная на десять. минус шесть фарад. И эта разница возводится в квадрат. И тогда мы получаем 16,7 Ом — это наше сопротивление. Теперь для части B все то же самое, за исключением того, что вместо частоты 120 герц у нас есть пять раз десять до трех герц. И это работает до 3,71 Ом. И часть C просит нас выяснить, что такое RMS Ток, проходящий через цепь на каждой частоте. Итак, это будет напряжение, деленное на импеданс. Таким образом, при пяти килогерцах ток будет равен 5,6 вольт, деленных на импеданс, который мы рассчитали при пяти килогерцах, что составляет 3,71186 Ом, для тока 1,51 ампера. При частоте 120 герц сила тока будет 5,6 вольта, деленная на импеданс, который мы рассчитали в части А, 16,692 Ом, что составляет 0,335 ампер.
Таким образом, для части А мы имеем квадратный корень из двух с половиной омов в квадрате плюс два пи, умноженные на 120 герц, умноженные на 100 микрогенри, то есть умноженные на десять до минус шесть генри, минус единица на два пи, умноженная на 120 герц, умноженная на 80, умноженная на десять. минус шесть фарад. И эта разница возводится в квадрат. И тогда мы получаем 16,7 Ом — это наше сопротивление. Теперь для части B все то же самое, за исключением того, что вместо частоты 120 герц у нас есть пять раз десять до трех герц. И это работает до 3,71 Ом. И часть C просит нас выяснить, что такое RMS Ток, проходящий через цепь на каждой частоте. Итак, это будет напряжение, деленное на импеданс. Таким образом, при пяти килогерцах ток будет равен 5,6 вольт, деленных на импеданс, который мы рассчитали при пяти килогерцах, что составляет 3,71186 Ом, для тока 1,51 ампера. При частоте 120 герц сила тока будет 5,6 вольта, деленная на импеданс, который мы рассчитали в части А, 16,692 Ом, что составляет 0,335 ампер.


 03.16
03.16 1. Свободные электромагнитные колебания
1. Свободные электромагнитные колебания Определить амплитуду напряжения до увеличения напряжения и начальное напряжение на конденсаторе.
Определить амплитуду напряжения до увеличения напряжения и начальное напряжение на конденсаторе.  (3)
(3) (3)
(3)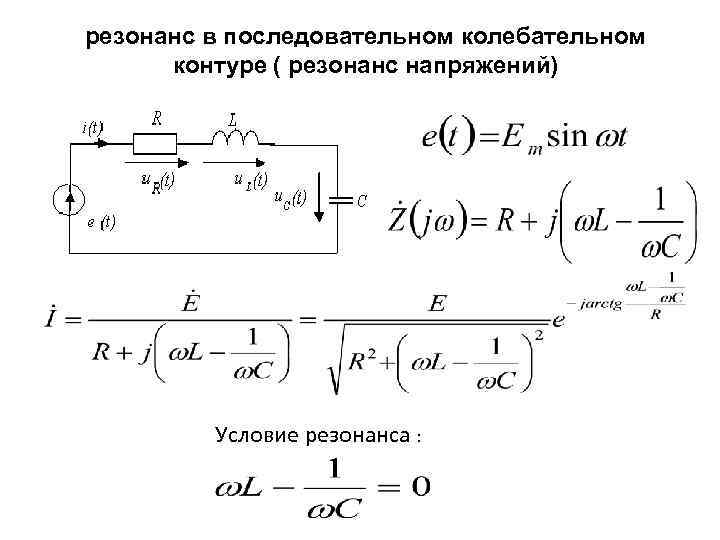 е.
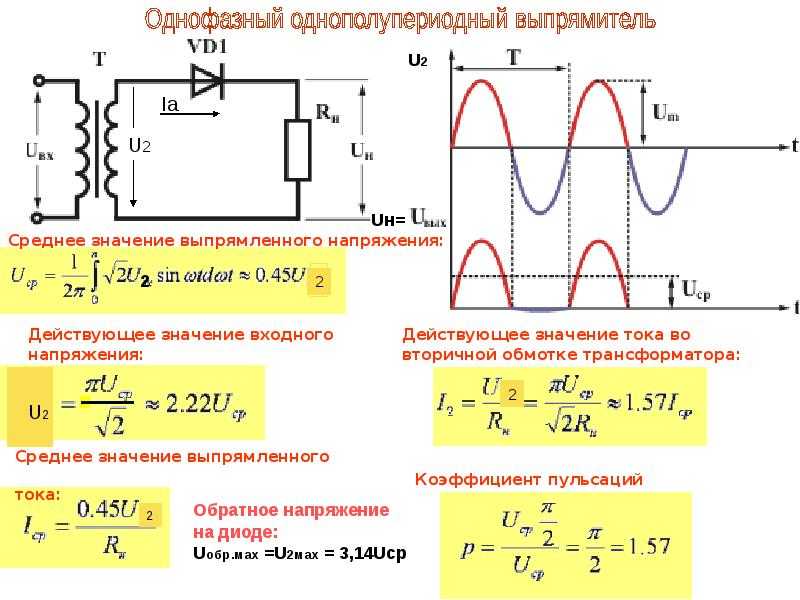
е. Используя формулу Томсона и соотношение между длиной волны и периодом электромагнитных колебаний, получим
Используя формулу Томсона и соотношение между длиной волны и периодом электромагнитных колебаний, получим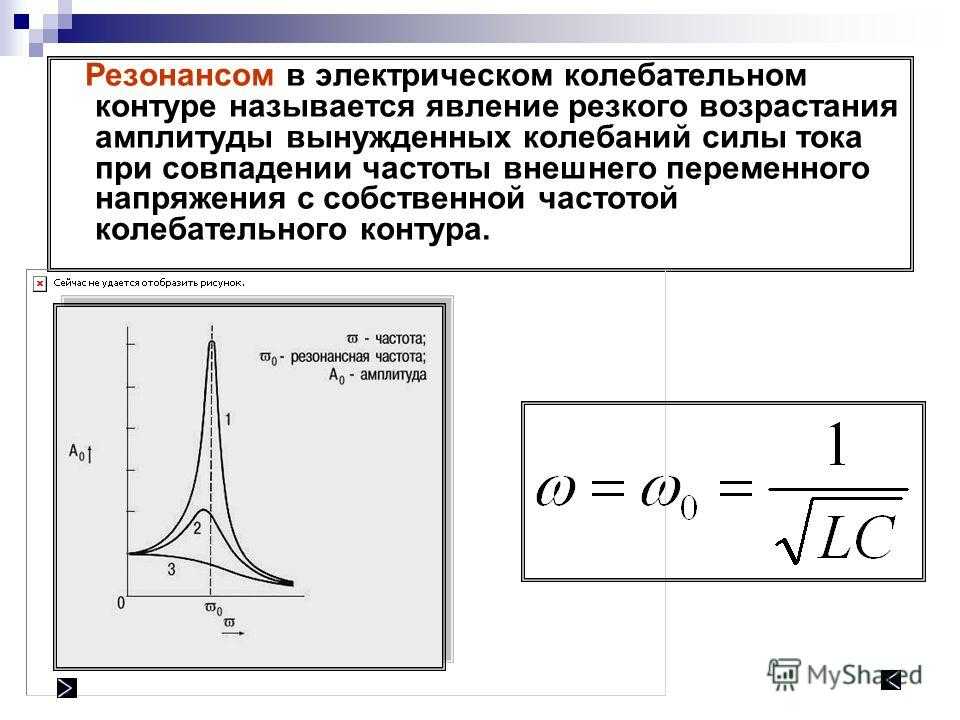 (4)
(4) (2)
(2)
 Внутрь цилиндрического каркаса помещён стальной сердечник с магнитной проницаемостью = 200. Плоский конденсатор, состоящий из n = 10 параллельно включенных квадратных металлических пластин со стороной а = 1 см, между которыми помещена слюда, толщиной 100 мкм. Определить число полных колебаний N в контуре за время = 1,2 с.
Внутрь цилиндрического каркаса помещён стальной сердечник с магнитной проницаемостью = 200. Плоский конденсатор, состоящий из n = 10 параллельно включенных квадратных металлических пластин со стороной а = 1 см, между которыми помещена слюда, толщиной 100 мкм. Определить число полных колебаний N в контуре за время = 1,2 с. (3)
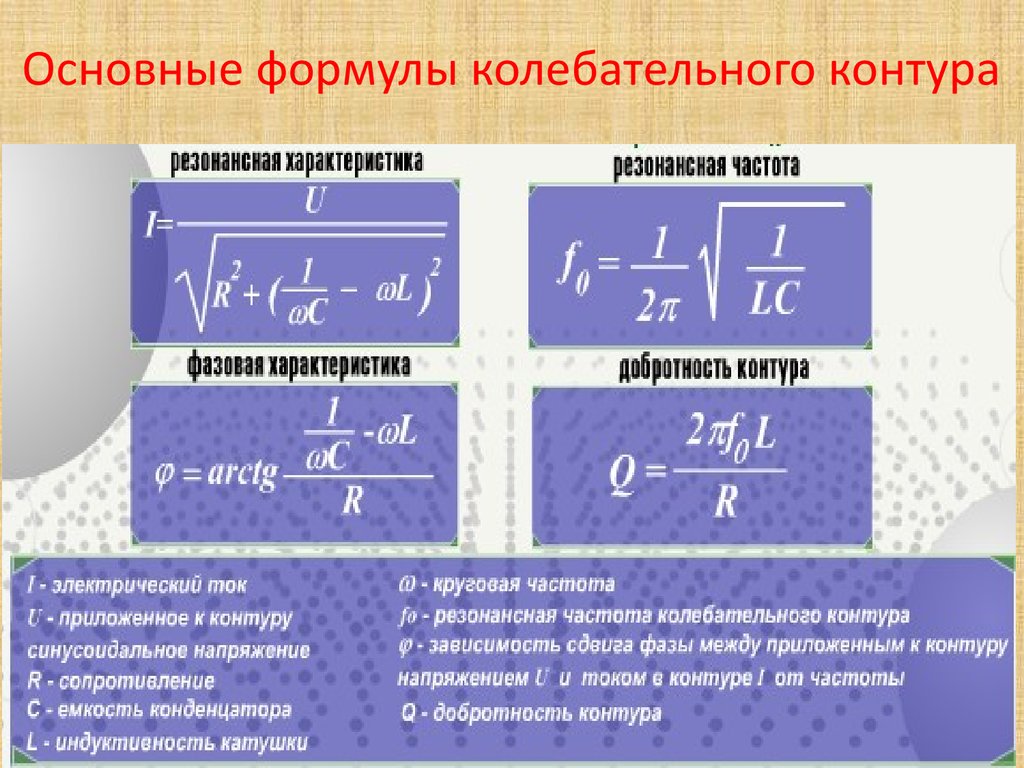
(3)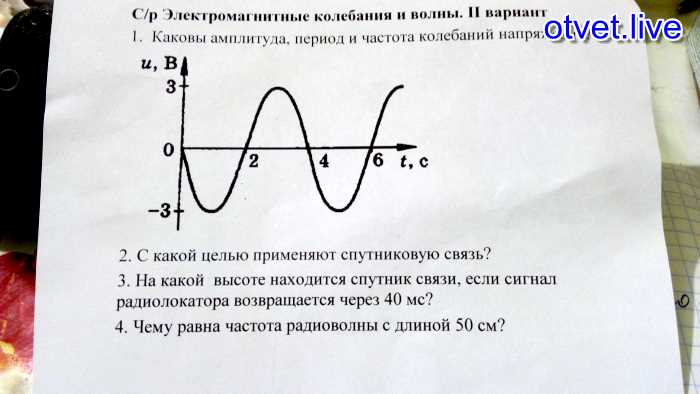 определить частоту собственных колебаний контура.
определить частоту собственных колебаний контура.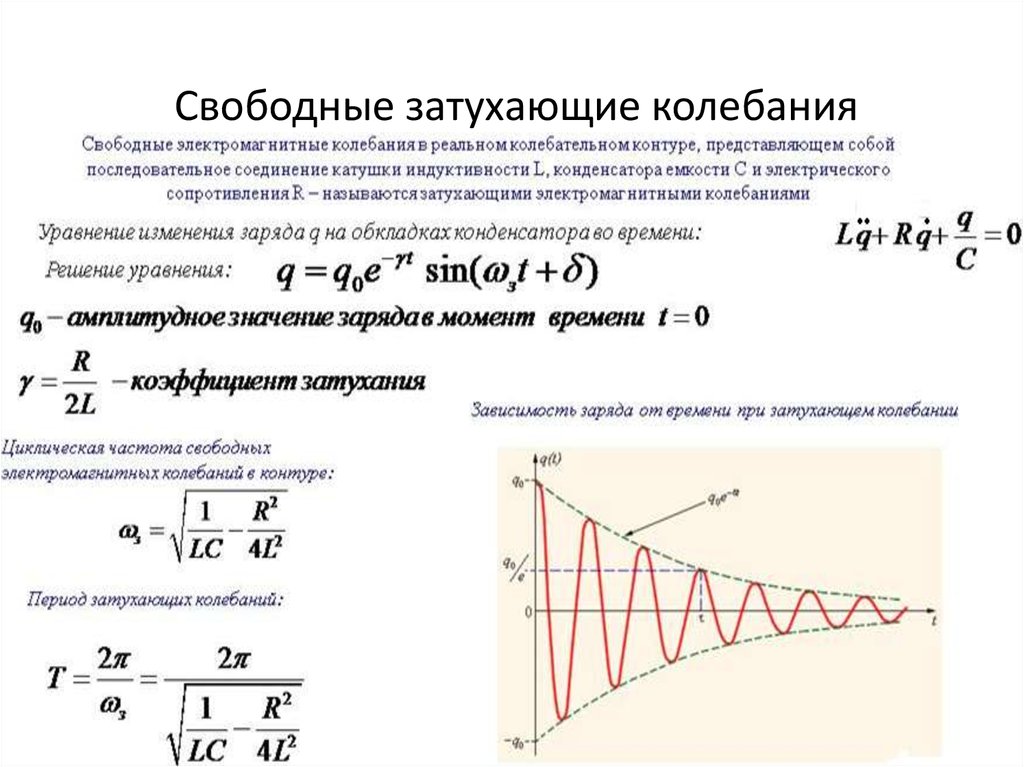
 Запишем соотношение амплитудных значений силы тока для колебательной системы с затуханием
Запишем соотношение амплитудных значений силы тока для колебательной системы с затуханием (3)
(3)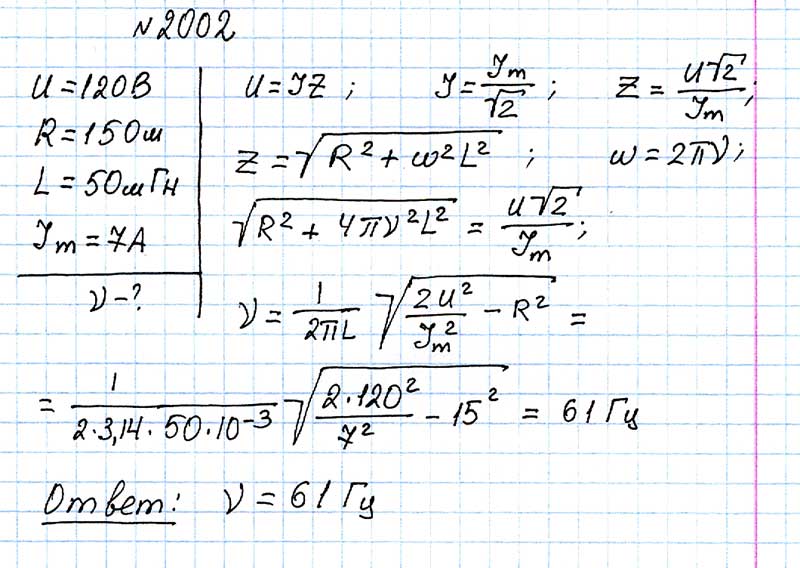 Найти логарифмический декремент затухания колебаний, период колебаний и записать уравнение изменения напряжения на обкладках конденсатора.
Найти логарифмический декремент затухания колебаний, период колебаний и записать уравнение изменения напряжения на обкладках конденсатора. Найти величину логарифмического декремента.
Найти величину логарифмического декремента.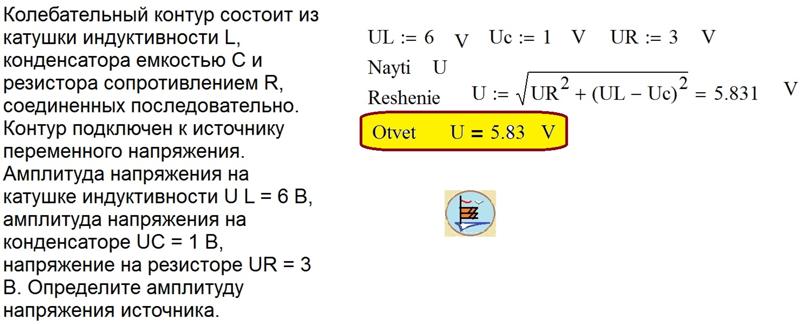 (3)
(3)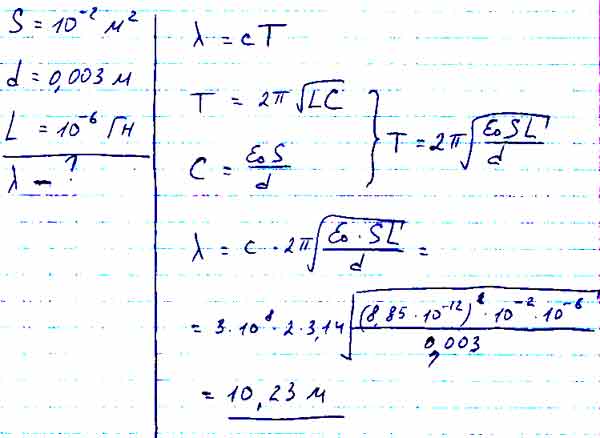 (6)
(6) (2)
(2) Определить период колебаний контура и логарифмический декремент . Как во времени будет изменяться напряжение на обкладках конденсатора? Получить аналитическую и графическую зависимость uC = f(t).
Определить период колебаний контура и логарифмический декремент . Как во времени будет изменяться напряжение на обкладках конденсатора? Получить аналитическую и графическую зависимость uC = f(t).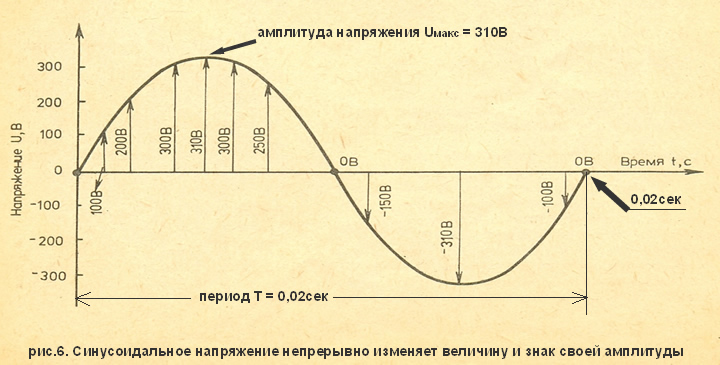 0135
0135 Найти активное сопротивление катушки, если она содержит N = 6000 витков при разности фаз между током и напряжением = 600.
Найти активное сопротивление катушки, если она содержит N = 6000 витков при разности фаз между током и напряжением = 600. (1)
(1)