что это, их виды, какие алгоритмы есть у поисковиков Яндекс и Гугл 

Хотим мы этого или не хотим, но уже сегодня человечество живет наполовину в цифровом мире. Математика – Богиня нашего цифрового мира и Алгоритм – пророк ее.

Впрочем, алгоритмы властвуют над человеком практически с того момента, когда двуногое существо начало мыслить и планировать свои действия на шаг вперед, что и дало людям критическое преимущество в борьбе за существование перед животными, живущими инстинктами.

Однако, инстинкт тоже в своем роде является алгоритмом, а в чем же тогда преимущество человека?

• Инстинкты властвуют над животными.
• Человек же создает алгоритмы сам.

Именно способность самостоятельно создавать подобные действия и является кардинальным отличием мыслящего человека от подвластного природным инстинктам животного.

Что называется алгоритмом

В математике и информатике под алгоритмом понимается порядок операций или набор инструкций, предназначенных для описания последовательности действий исполнителя в процессе выполнения практической задачи, приводящей к заранее известному результату.

• Исполнителем может быть как человек, так и механизм или цифровая вычислительная машина.

Многие люди не догадываются, но с алгоритмами люди сталкиваются буквально на каждом шагу в своей обычной жизни. И даже более того, без них человек не смог бы и шагу ступить.

Наиболее знакомые людям алгоритмы – это бытовые привычки. По сути, личность человека – это набор привычек, то есть, постоянно повторяющихся действий привычного поведения.

• Проснулся, встал, умылся, побрился, выпил чашечку кофе, оделся, поехал на работу.
• В офисе снял пальто, включил комп, запустил MS Word, продолжил работу над документами.

Думаю вам такой порядок действий хорошо знаком.

В глобальном смысле вся жизнь человека подчинена пролонгированному решению – родился, получил образование, устроился на работу, женился, родил детей, воспитал, вышел на пенсию.

Аналогичным образом функционируют и компьютерные программы, только для вычислительной машины порядок операция кодируется в виде последовательности цифр, букв и символов.

Виды

Понятно, что, чем сложнее порядок операций, приводящих к определенному результату, тем длиннее программа. Причем, алгоритм, то есть, порядок действий, не обязательно выглядит как линейна последовательность.

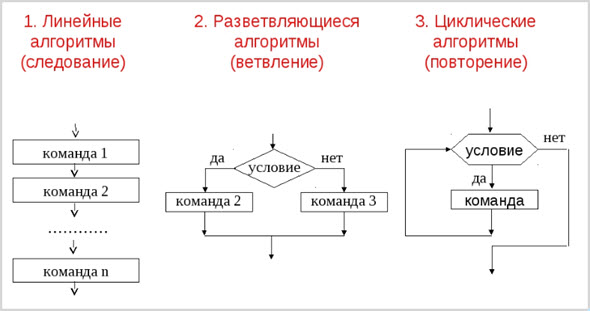
В зависимости от практической задачи структура алгоритма может изменяться.

• Линейный алгоритм. Все операции идут одна за другой.
• Разветвляющийся алгоритм. Применяется в случаях, когда в процессе исполнения программы обстоятельства (отсюда и задачи) могут существенно поменяться.

Например, программа управления буром на нефтяной вышке. Пока грунт однообразный, бурение происходит в одном режиме. Если сверло натыкается на более твердую породу, происходит изменение режима бурения, для чего переключается программный алгоритм.

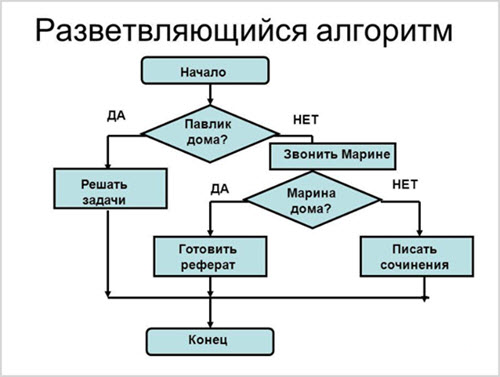
Говоря простыми словами, разветвляющийся «algorithm» еще можно описать словами из американского боевика: «Что-то пошло не так. Переходим к плану «Б». Планы А и Б – это и есть ветви решения поведения боевой группы на задании, в условиях непредсказуемо меняющейся обстановки.

Жизнь человека – это тоже сложный разветвляющийся алгоритм. Пока мужчина холост – он живет по одному порядку, а когда женится – алгоритм (порядок жизни) мужчины кардинально меняется.

• Циклический алгоритм. Подразумевается повторяющаяся последовательность операций, приводящая к одинаковым результатам раз за разом. Массовое производство одинаковых изделий.

Здесь можно привести в пример работу повара в ресторане быстрого питания. Посетителе все как один заказывают гамбургеры. Повар, чтобы приготовить сотни гамбургеров, в течение рабочего дня повторяет одну и ту же последовательность операций. Открыл холодильник – вытащил полуфабрикат – поджарил котлету – разрезал булку – вложил котлету – добавил соус– закрыл булку.

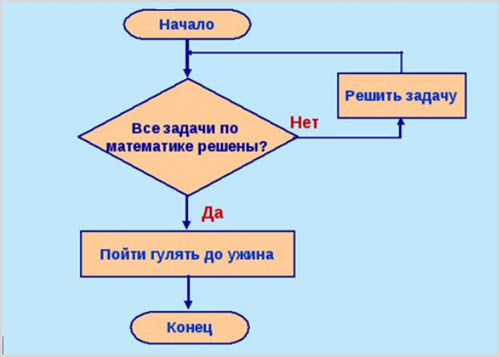
Циклические действия мы видим в человеческом обществе. В некотором смысле, большинство людей повторяют один и тот же цикл жизни на протяжении столетий. Кажется, в буддизме это называется «карма».

• Карма – это глобальный алгоритм жизни обычного человека, еще не достигшего «просветления».

В практике программирования, в жизни, на производстве алгоритмы могут быть любой сложности, в сочетании всех трех описанных типов.

Мы начали наше исследование с того, что цифровизация изменила человеческую цивилизацию. А когда начали углубленно разбираться в математических решениях, неожиданно выяснилось – ничего не изменилось от начала времен. Люди всегда жили по строгим правилам. Даже те люди полностью во власти алгоритмов, которые и считать-то не умеют.

В каких сферах их применяют

Алгоритмы буквально пронизывают всю Вселенную. Сам термин «algorithm», как принято считать, происходит от имени средневекового арабского математика Аль-Хорезми.

В новой истории данное понятие стало известно широкой публике в середине 20-го века, когда в моду вошла кибернетика. Основные принципы компьютерной алгоритмики как раз и были разработаны где-то в 50-х – 60-х годах прошлого века, в том числе советскими учеными.

Это интересно: Что такое Апгрейд, Стрим, Мемы, Франшиза

В каких сферах деятельности применяются алгоритмы? Проще назвать – где они не применяются. В практическом смысле их массовое применение есть в промышленном производстве и сфере обслуживания позволило сделать колоссальный рывок в благосостоянии человеческого общества.

• На заводах и фабриках алгоритмам починены все рабочие процессы, во время которых изготавливаются товары народного потребления в количестве, достаточном, чтобы обеспечить всех. Наибольший прорыв в промышленности произошел, когда в производство начали внедряться станки с числовым программным управлением, изготавливающим детали по заранее подготовленным и закодированным в компьютерных решениях.
• Школьная программа – это алгоритм массового донесения знаний до миллионов детей и подростков.
• Специальный алгоритм боевой подготовки превращает молодых людей в защитников Родины.

Возьмите лист бумаги и последовательно запишите все действия, которые вы совершаете каждый день. Составьте такие списки действий на всю неделю. Скорее всего окажется, что с понедельника по пятницу у вас вполне такой циклический алгоритм, а в субботу происходит небольшое ответвление.

В течение дня вы выполняете ряд линейных алгоритмов, приводящих к заранее известным результатам (приготовление и прием пищи, стирка одежды, исполнение своих профессиональных обязанностей в офисе или цеху).

Кстати, автоматическая стиральная машинка тоже использует ряд циклических алгоритмов в зависимости от типа белья.

По каким алгоритмам работает поиск от Google и Яндекс

Яркий пример – работа поисковых сервисов. Как же Яндекс и Google могут так быстро находить на миллионах сайтов в интернете ответы практически на любой вопрос пользователя?

Как известно из инсайдерских кругов, поисковые системы используют порядка 1500 алгоритмов для того, чтобы пользователи могли быстро находить в интернете любую информацию.

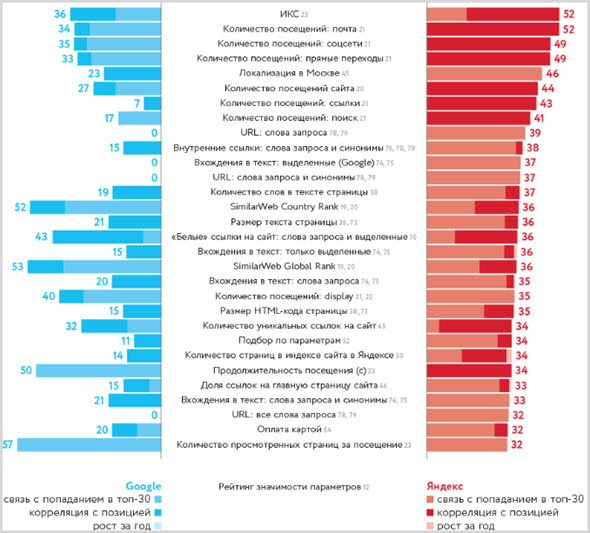
На самом общем уровне можно выделить три глобальных алгоритма поисковых машин.

• Индексация – сбор данных, опубликованных на всех сайтах в интернете.
• Определение релевантности. Информация на веб-страницах сортируется по тематикам поисковых запросов.
• Ранжирование. По каждой теме производится оценка качества и полезности ответов. Затем на странице результатов поиска ответы размещаются «по ранжиру», в порядке убывания качества и соответствия.

Многие пользователи полагают, что после запуска поиска по фразе Google со всех ног мечется по всему интернету и там ищет относящуюся к делу (релевантную) информацию.

Прочитай это:

 Что такое ранжирование сайта и какие факторы на это влияют

Ничего подобного. Весь контент со всех веб-страниц заранее собирается специальными программами (которые тоже есть алгоритмы) – так называемыми поисковыми роботами.

Собранная информация хранится в Индексе поисковой машины – базе данных. Слово Index по-английски означает «каталог». Это примерно, как в обычной библиотеке все книги разделены по полкам, а в Каталоге лежат карточки с краткими описаниями. Индекс Яндекса – это и есть такой цифровой каталог всего интернет-контента.

Когда пользователь запускает поиск по определенному вопросу, в работу вступает алгоритм определения релевантности. Соответствие контента на сайте вопрос пользователя определяется до смешного просто – если в тексте присутствуют фразы, соответствующего поисковому запросу – такой контент признается релевантным и подготавливается к выдаче.

Фразы в тексте, соответствующие поисковому запросу принято называть «ключевыми словами» или «ключевиками».

Чтобы поисковой машине было легче найти контент на сайте, веб-мастера специально добавляют в текстовый контент соответствующие ключевые слова. Это называется «поисковая оптимизация».

После того, как алгоритм релевантности нашел в базе данных (индексе) весь контент, подходящий по теме поискового запроса, в работу включаются все те сотни и тысячи алгоритмов, предназначенные для определения качества и полезности контента.

• Оценка уникальности.
• Проверка достоверности и актуальности сведений.
• Объем и профессиональный уровень контента (информационная ценность).
• Авторитетность автора, репутация публикатора.
• Цитируемость – кто и как ссылается на данный контент на сторонних сайтах.
• И еще проверка контента и сайта в целом по нескольким сотням разных алгоритмов.

Некоторые алгоритмы поисковых систем известны и имеют названия.

• Алгоритм Яндекса ИКС определяет качество контента на сайте.
• Алгоритм Google «Колибри» предназначен для улучшенного поиска и ранжирования контента, написанного естественным разговорным языком.

Зная, что некоторые недобросовестные веб-мастера порой идут на манипуляции, чтобы получить преимущества в поисковой выдаче, программисты Google и Яндекс разработали фильтры. С помощью фильтров поисковый компьютер выявляет «серые», недобросовестные способы оптимизации сайтов и «пессимизирует», понижает такие ресурсы в результатах поиска по запросу.

• Фильтр Яндекса «Минусинск» выявляет и понижает в выдаче сайты, использующие покупные SEO-ссылки.
• Фильтр Гугл «Пингвин» предназначен для определения неестественных, искусственных ссылок.

Чтобы не допустить недобросовестной оптимизации и манипуляций, поисковые компании сохраняют свои истинные алгоритмы в строжайшем секрете.

Так то, всё, что известно относительно алгоритмов Яндекса и Google веб-мастерам и специалистам по поисковому продвижению, найдено и выявлено чисто эмпирическим путем или относится к области гипотетических предположений.

АЛГОРИТМ, — это… Что такое АЛГОРИТМ,?

алгорифм, Ч точное предписание, к-рое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного исходного данного (из нек-рой совокупности возможных для данного А. исходных данных) и направленный на получение полностью определяемого этим исходным данным результата. А. являются, напр., известные из начальной школы правила сложения, вычитания, умножения и деления столбиком; в этих А. возможными результатами служат натуральные числа, записанные в десятичной системе, а возможными исходными данными — упорядоченные пары таких чисел.

 

Вообще говоря, не предполагается, что результат будет обязательно получен: процесс применения А. к конкретному возможному исходному данному (т. е. алгоритмич. процесс, развертывающийся начиная с этого данного) может также оборваться безрезультатно (в этом случае говорят, что произошла безрезультатная остановка) или не закончиться вовсе. В случае, если процесс заканчивается (соответственно не заканчивается) получением результата, говорят, что А. применим (соответственно неприменим) к рассматриваемому возможному исходному данному. (Можно построить такой А. , для к-рого не существует А., распознающего по произвольному возможному для исходному данному, применим к нему или нет; такой А. 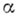можно, в частности, построить так, чтобы совокупностью его возможных исходных данных служил натуральный ряд.)

Понятие А. занимает одно из центральных мест в современной математике, прежде всего вычислительной. Так, проблема численного решения уравнений данного типа заключается в отыскании А., к-рый всякую пару, составленную из произвольного уравнения этого типа и произвольного положительного рационального числа , перерабатывает в число (или набор чисел), отличающееся (отличающихся) от корня (корней) этого уравнения меньше, чем на 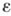. Усовершенствование цифровых вычислительных машин дает возможность реализовать на них все более сложные А. Однако встретившийся в описывающей понятие А. формулировке термин «вычислительный процесс» не следует понимать в узком смысле только цифровых вычислений: уже в школьном курсе алгебры говорят о буквенных вычислениях, да и в арифметич. вычислениях появляются отличные от цифр символы (скобки, знак равенства, знаки арифметич. действий). Целесообразно, таким образом, рассматривать А., оперирующие с произвольными символами и их комбинациями. Простейшим случаем такой комбинации является линейная последовательность символов, образующая слово, однако можно рассматривать и «нелинейные» комбинации — такие, как алгебраич. матрицы, знакосочетания в смысле Н. Бурбаки (N. Bour-baki), фразы того или иного языка с расставленными стрелками синтаксич. управления и, вообще, размеченные тем или иным способом графы. Наиболее общее интуитивное понимание состоит в том, что исходными данными и результатами А. могут служить самые разнообразные конструктивные объекты. Это открывает возможность широкого применения понятия А. Можно говорить об А. перевода с одного языка на другой, об А. работы поездного диспетчера (перерабатывающего информацию о движении поездов в приказы) и др. примерах алгоритмич. описания процессов управления; именно поэтому понятие А. является одним из центральных понятий кибернетики.

Пример алгоритма. Пусть возможными исходными данными и возможными результатами служат всевозможные слова в алфавите . Условимся называть переход от слова Xк слову Y»допустимым» в следующих двух случаях (ниже Робозначает произвольное слово): 1) X имеет вид аР, а Y имеет вид Рb;2) Xимеет вид bаР, a Y имеет вид Раbа. Формулируется предписание: «взяв к.-л. слово в качестве исходного, делай допустимые переходы до тех пор, пока не получится слово вида ааР;тогда остановись, слово Ри есть результат». Это предписание образует А., к-рый обозначим 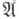. Возьмем в качестве исходного данного слово bаbаа. После одного перехода получим bаааbа, после второго ааbааbа. В силу предписания мы должны остановиться, результат есть bааbа. Возьмем в качестве исходного данного слово bааbа. Получим последовательно аbааbа, bааbаb, аbаbаbа, bаbаbаb, bаbаbаbа,…. Можно доказать, что процесс никогда не кончится (т. е. никогда не возникает слово, начинающееся с аа, и для каждого из получающихся слов можно будет совершить допустимый переход). Возьмем теперь в качестве исходного данного слово аbааb. Получим bааbb, аbbаbа, bbаbаb. Далее мы не можем совершить допустимый переход, и в то же время нет сигнала остановки. Произошла безрезультатная остановка. Итак, применим к слову bаbаа и неприменим к словам bааbа и аbааb.

Значение алгоритмов. А. встречаются в науке на каждом шагу: умение решать задачу «в общем виде» всегда означает, по существу, владение нек-рым А. Говоря, напр., об умении человека складывать числа, имеют в виду не то, что он для любых чисел рано или поздно сумеет найти их сумму, а то, что он владеет нек-рым единообразным приемом сложения, применимым к любым двум конкретным записям чисел, т. е., иными словами, А. сложения (примером такого А. и является известное правило сложения чисел столбиком). Понятие задачи «в общем виде» уточняется при помощи понятия массовая алгоритмическая проблема (м. а. п.). М. а. п. задается серией отдельных, единичных проблем и состоит в требовании найти единый А. их решения (когда такого А. не существует, говорят, что рассматриваемая м. а. п. неразрешима). Так, проблема численного решения уравнений данного типа и проблема автоматического перевода суть м. а. п.: образующими их единичными проблемами являются в 1-м случае проблемы численного решения отдельных уравнений данного типа, а во 2-м случае — проблемы перевода отдельных фраз. Ролью м. а. сфера приложения понятия А.: напр., а алгебре возникают м. а. п. проверки алгебраич. равенств различных типов, в математич. логике — м. а. п. распознавания выводимости предложений из заданных аксиом и т. п. (для математич. логики понятие А. существенно еще и потому, что на него опирается центральное для математич. логики понятие исчисления, служащее обобщением и уточнением интуитивных понятий «вывода», и «доказательства»). Установление неразрешимости к.-л. м. а. п. (напр., проблемы распознавания истинности или доказуемости для к.-л. логнко-математич. языка) является важным познавательным актом, показывающим, что для решения конкретных единичных проблем данной серии принципиально необходимы специфические для каждой отдельной проблемы методы.

Содержательные явления, к-рые легли в основу образования понятия «А.», издавна занимали важное место в науке. С древнейших времен многие задачи математики заключались в поисках тех или иных конструктивных методов. Эти поиски, особенно усилившиеся в связи с созданием удобной символики, а также осмысления принципиального отсутствия искомых методов в ряде случаев (задача о квадратуре круга и подобные ей) — все это было мощным фактором развития научных знаний. Осознание невозможности решить задачу прямым вычислением привело к созданию в 19 в. теоретико-множественной концепции. Лишь после периода бурного развития этой концепции (в рамках к-рой вопрос о конструктивных методах в современном их понимании вообще не возникает) оказалось возможным в сер. 20 в. вновь вернуться к вопросам конструктивности, но уже на новом уровне, обогащенном выкристаллизовавшимся понятием А. Это понятие легло в основу конструктивного направления в математике.

Само слово «А.» происходит от algoritmi, являющегося, в свою очередь, латинской транслитерацией арабского имени хорезмийского математика 9 в. аль-Хорезми.

В средневековой Европе А. назывались десятичная позиционная система счисления и искусство счета в ней, поскольку именно благодаря латинскому переводу (12 в.) трактата аль-Хорезми Европа познакомилась с позиционной системой.

Строение алгоритмического процесса. Алгоритмич. процесс есть процесс последовательного преобразования конструктивных объектов (к. о.), происходящий дискретными «шагами»; каждый шаг состоит в смене одного к. о. другим. Так, при применении А. 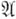к слову baaba возникают последовательно baaba, abaaba, bааbаb и т. д. А при применении, скажем, А. вычитания столбиком к паре (307, 49) последовательно возникнут такие к. о.:

При этом в ряду сменяющих друг друга к. о. каждый последующий полностью определяется (в рамках данного А.) непосредственно предшествующим. При более строгом подходе предполагается также, что переход от каждого к. о. к непосредственно следующему достаточно «элементарен» — в том смысле, что происходящее за один шаг преобразование предыдущего к. о: в следующий носит локальный характер (преобразованию подвергается не весь к. о., а лишь нек-рая, заранее ограниченная для данного А. его часть, и само это преобразование определяется не всем предыдущим к. о., а лишь этой ограниченной частью).

Таким образом, наряду с совокупностями возможных исходных данных и возможных результатов для каждого А. имеется еще совокупность возможных промежуточных результатов, представляющая собой ту рабочую среду, в к-рой развивается алгорит-мич. процесс. Для А. все три совокупности совпадают, а для А. вычитания столбиком — нет: возможными исходными данными служат пары чисел, возможными результатами — числа (все в десятичной системе), а возможные промежуточные результаты суть «трехэтажные» записи вида 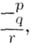где — запись числа в десятичной системе, 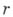— такая же запись или пустое слово, а р — запись числа в десятичной системе с допущением точек над нек-рыми цифрами. Как правило, для данного А. можно выделить 7 характеризующих его (не независимых) параметров: 1) совокупность возможных исходных данных, 2) совокупность возможных результатов, 3) совокупность возможных промежуточных результатов, 4) правило начала, 5) правило непосредственной переработки, 6) правило окончания, 7) правило извлечения результата.

«Уточнения» понятия алгоритма. Понятие А. в его общем виде принадлежит к числу основных первоначальных понятий математики, не допускающих определения в терминах более простых понятий. Возможные уточнения понятия А. приводят, строго говоря, к известному сужению этого понятия. Каждое такое уточнение состоит в -том, что для каждого из указанных 7 параметров А. точно описывается нек-рый класс, в пределах к-рого этот параметр может меняться. Выбор таких классов и отличает одно уточнение от другого. Поскольку 7 параметров однозначно определяют нек-рый А., то выбор 7 классов изменения этих параметров определяет нек-рый класс А. Однако такой выбор может претендовать на название «уточнения», лишь если имеется убеждение, что для произвольного А., имеющего допускаемые данным выбором совокупности возможных исходных данных и возможных результатов, может быть указан равносильный ему А. из определенного данным выбором класса А. Это убеждение формулируется для каждого уточнения в виде основной гипотезы, к-рая — при современном уровне наших представлений — не может быть предметом математич-доказательства.

Первые уточнения описанного типа предложили в 1936 Э. Л. Пост (Е. L. Post, см. [5]) и А. М. Тьюринг (А. М. Turing, см. [3], [4]), их конструкции во многом предвосхитили идеи, заложенные в основу современных цифровых вычислительных машин. Известны также уточнения, сформулированные А. А. Марковым (см. [10], [11], Нормальный алгорифм).и А. Н. Колмогоровым (см. [ 12], [ 13]; последний предложил трактовать конструктивные объекты как топологич. комплексы определенного вида, что дало возможность уточнить свойство «локальности» преобразования). Для каждого из предложенных уточнений соответствующая основная гипотеза хорошо согласуется с практикой. В пользу этой гипотезы говорит и то, что, как можно доказать, все предложенные уточнения в нек-ром естественном смысле эквивалентны друг другу.

В качестве примера рассмотрим уточнение, предложенное А. М. Тьюрингом. В своем оригинальном виде это уточнение заключалось в описании нек-рой абстрактной вычислительной машины, состоящей из: 1) бесконечной ленты, разбитой на следующие друг за другом в линейном порядке ячейки, причем в каждой ячейке записан к.-л. символ из так наз. «внешнего алфавита» машины, и 2) каретки, находящейся в каждый момент в нек-ром «состоянии» (из заданного конечного списка состояний), способной перемещаться вдоль ленты и изменять содержимое ячеек; А. вычислений на такой машине («тыорингов А.») задается в виде программы, управляющей действиями каретки. Более подробное и точное описание см. в статье Тьюринга машина;здесь приводится модернизированное изложение конструкции Тьюринга в терминах, указанных выше 7 параметров. Чтобы задать тыорингов А., надо указать: а) попарно непересекающиеся алфавиты Б, Д, Ч с выделенной в Дбуквой 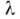и выделенными в Чбуквами и , б) набор пар вида , где 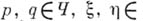, а Тесть один из трех знаков — , 0, +, причем предполагается, что в этом наборе (наз. программой) нет 2 пар с одинаковыми первыми членами. Параметры А. задаются так: возможными исходными данными и возможными результатами служат слова в Б, а возможными промежуточными результатами — слова в алфавите содержащие не более одной буквы из Ч. Правило начала: исходное слово Рпереводится в слово . Правило окончания: заключительным является промежуточный результат, содержащий со. Правило извлечения результата: результатом объявляется цепочка всех тех букв заключительного промежуточного результата, к-рая идет вслед за w и предшествует первой букве, не принадлежащей Б. Правило непосредственной переработки, переводящее , состоит в следующем. Приписываем к Аслева и справа букву ; затем в образовавшемся слове часть вида , где , , 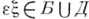заменяем на слово Qпо следующему правилу: в программе ищется пара с первым членом ; пусть второй член этой пары есть ; если 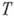есть -, то 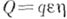; если Тесть 0, то ; если Тесть +, то 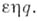Возникающее после этой замены слово и есть А’.

Лит. см. [3]-[5], [10]-[13] при СТ. Алгоритмов теория, В. А. Успенский.

Математическая энциклопедия. — М.: Советская энциклопедия. И. М. Виноградов. 1977—1985.

алгоритм — это… Что такое алгоритм?

        АЛГОРИТМ (алгорифм; от лат. формы имени ученого 9 в. аль-Хорезми — Algorithmi) — точное предписание о порядке выполнения некоторой системы операций над исходными данными для получения желаемого результата, которое исполняется вычислителем (человеком, вычислительной машиной). Примерами А. являются «школьные» правила обращения с целыми числами, записанными в десятичной системе счисления: сложение, вычитание и умножение «столбиком», деление с остатком «уголком». А. является одним из основных неопределяемых понятий математики и близких наук, напр. кибернетики, информатики. К основным параметрам А. относят: 1) совокупность возможных исходных данных; 2) совокупность возможных результатов; 3) совокупность возможных промежуточных данных; 4) совокупность возможных инструкций (команд) для преобразования данных; 5) условия начала и завершения работы А. Совокупности из пп. 1—3 предполагаются состоящими из конструктивных объектов, т.е. из конечных слов, возможно, устроенных нелинейно (пример: столбики в действиях над числами), в фиксированных конечных алфавитах. Совокупность из п. 4 конечна. При заданных исходных данных А. задает вычислительный (алгоритмический) процесс: последовательность, начинающаяся исходными данными; т.е. каждый член этой последовательности, кроме первого, получается из предыдущего в результате применения инструкции в соответствии с предписанием, с указанием этой инструкции. Если эта последовательность конечна и последний ее член удовлетворяет условию завершения работы (в частности, последний член последовательности принадлежит совокупности возможных результатов), то считается, что А. завершил свою работу результативно (А. применим к заданным исходным данным) и ее результатом является последний член последовательности; в противном случае (т.е. когда вычислительный процесс бесконечен или конечен, но не удовлетворяет описанному условию) считается, что А. не применим к заданным исходным данным. К основным свойствам А. относят: дискретность — отчетливость каждого шага всякого вычислительного процесса; детерминированность — каждые конкретные исходные данные А. определяют ровно один вычислительный процесс; массовость — совокупность возможных исходных данных бесконечна; элементарность шагов вычислительного процесса — на каждом шаге процесса вычислитель в состоянии выполнить соответствующую инструкцию.

        Иногда к А. относят процедуры, имеющие дело с объектами, не являющимися конструктивными. Таковы, напр., геометрические процедуры нахождения середины отрезка с помощью циркуля и линейки, нахождения наибольшей общей меры двух отрезков и т.п. Возможны и другие ослабления требований, напр., отказ от детерминированности.

        Каждый А. определяет вычислимую функцию (функцию, вычислимую данным А.): аргумент функции принимает значения из совокупности возможных исходных данных, а значениями являются соответствующие результаты работы А. Одна вычислимая функция может определяться разными А.

        Начиная с 30-х гг. 20 в. математики выработали многочисленные формальные аналоги понятия А. и вычислимой функции: машина Поста; машина Тьюринга; нормальный алгорифм Маркова; частично рекурсивная функция; А.-определимая функция и др. В дальнейшем были предложены и другие формализации; в частности, программы, написанные на любом языке программирования из применяемых на практике, задают А. Все предложенные до сих пор формализации понятия А. оказались эквивалентными: классы определяемых ими функций совпадают. Это подтверждает так называемый тезис Черча: класс вычислимых функций, задаваемых (неформальными) А., совпадает с вычислимыми функциями, задаваемыми А., описанными в одной (любой) из указанных формализации. Поскольку А., заданный в фиксированной формализации, является точно описанным математическим объектом, тезис Черча позволил создать математическую теорию алгоритмов.

        А.В. Чагров

        Лит.: Катленд Н. Вычислимость: Введение в теорию рек у р с и в н ы х функций. М., 1983; Мальцев А.И. Алгоритмы и рекурсивные функции. М., 1986; Марков А.А., Нагорный Н.М. Теория алгорифмов. М., 1996; Роджерс X. Теория рекурсивных функций и эффективная вычислимость. М., 1972.

Энциклопедия эпистемологии и философии науки. М.: «Канон+», РООИ «Реабилитация». И.Т. Касавин. 2009.

Алгоритмы – Все об алгоритмах / Хабр

США, Техас, Остин, клуб Continental
Воскресенье, 5 января 1987 г.

— Спасибо за приглашение, мистер Ломуто. Скоро я возвращаюсь в Англию, так что это было очень вовремя.

— Спасибо, что согласились со мной встретиться, мистер… сэр… Чарльз… Энтони Ричард… Хоар. Это большая честь для меня. Я даже не знаю, как к вам обращаться. У вас есть рыцарский титул?

— Зовите меня Тони, и, если вы позволите, я буду называть вас Нико.

На первый взгляд — обычная картина: два человека наслаждаются виски. Однако внимательному наблюдателю открываются интригующие подробности. Прежде всего — напряжение, которое можно было резать ножом.

Одетый в безупречно подогнанный костюм-тройку с нарочитой небрежностью, на какую способен только англичанин, Тони Хоар был таким же воплощением Британии, как и чашка чая. Смиренное выражение лица, с которым он попивал из своего стакана, без всяких слов выражало его мнение в споре между бурбоном и скотчем. Сидевший напротив Нико Ломуто представлял полную ему противоположность: одетый в джинсы программист, мешавший виски с колой (что для Тони было настолько возмутительно, что он сразу решил подчёркнуто это игнорировать — как резкий запах пота или оскорбительную татуировку), в состоянии некого расслабленного трепета перед гигантом информатики, с которым он только что познакомился лично.

— Послушайте, Тони, — сказал Нико после того, как иссякли темы для обычной лёгкой беседы. — По поводу того алгоритма разбиения. Я даже не собирался его публиковать…

— Что? Ах да, алгоритм разбиения, — Тони поднял брови в притворном изумлении, словно забыв, что каждая статья или книга о быстрой сортировке за последние пять лет упоминала их имена вместе. Очевидно, что именно это связывало этих двух людей и было причиной этой встречи, но Тони, как безупречный джентльмен, мог бы часами говорить о погоде, если бы собеседник не упомянул о стоящем в комнате розовом слоне.

Введение в алгоритм A* / Хабр

При разработке игр нам часто нужно находить пути из одной точки в другую. Мы не просто стремимся найти кратчайшее расстояние, нам также нужно учесть и длительность движения. Передвигайте звёздочку (начальную точку) и крестик (конечную точку), чтобы увидеть кратчайший путь. [Прим. пер.: в статьях этого автора всегда много интерактивных вставок, рекомендую сходить в оригинал статьи.]
Для поиска этого пути можно использовать алгоритм поиска по графу, который применим, если карта представляет собой граф. A* часто используется в качестве алгоритма поиска по графу. Поиск в ширину — это простейший из алгоритмов поиска по графу, поэтому давайте начнём с него и постепенно перейдём к A*.

Представление карты

Первое, что нужно при изучении алгоритма — понять данные. Что подаётся на вход? Что мы получаем на выходе?

Вход: алгоритмы поиска по графу, в том числе и A*, получают в качестве входных данных граф. Граф — это набор точек («узлов») и соединений («рёбер») между ними. Вот граф, который я передал A*:

A* не видит ничего другого. Он видит только граф. Он не знает, находится ли что-то в помещении или за его пределами, дверь это или комната, насколько велика область. Он видит только граф! Он не понимает никакой разницы между картой сверху и вот этой:

Выход: определяемый A* путь состоит из узлов и рёбер. Рёбра — это абстрактное математическое понятие. A* сообщает нам, что нужно перемещаться из одной точки в другую, но не сообщает, как это нужно делать. Помните, что он ничего не знает о комнатах или дверях, он видит только граф. Вы сами должны решить, чем будет являться ребро графа, возвращённое A* — перемещением с тайла на тайл, движением по прямой линии, открытием двери, бегом по кривому пути.

Компромиссы: для каждой игровой карты есть множество разных способов передачи графа поиска пути алгоритму A*. Карта на рисунке выше превращает двери в узлы.

А что, если мы превратим двери в рёбра?

А если мы применим сетку для поиска пути?

Граф поиска пути не обязательно должен быть тем же, что используется в вашей игровой карте. В карте на основе сеток можно использовать граф поиска пути без сеток, и наоборот. A* выполняется быстрее с наименьшим количеством узлов графа. С сетками часто проще работать, но в них получается множество узлов. В этой статье рассматривается сам алгоритм A*, а не дизайн графов. Подробнее о графах можно прочитать на моей другой странице. Для объяснений я в дальнейшем буду использовать сетки, потому что так проще визуализировать концепции.

Алгоритмы

Существует множество алгоритмов, работающих с графами. Я рассмотрю следующие:

Поиск в ширину выполняет исследование равномерно во всех направлениях. Это невероятно полезный алгоритм, не только для обычного поиска пути, но и для процедурной генерации карт, поиска путей течения, карт расстояний и других типов анализа карт.

Алгоритм Дейкстры (также называемый поиском с равномерной стоимостью) позволяет нам задавать приоритеты исследования путей. Вместо равномерного исследования всех возможных путей он отдаёт предпочтение путям с низкой стоимостью. Мы можем задать уменьшенные затраты, чтобы алгоритм двигался по дорогам, повышенную стоимость, чтобы избегать лесов и врагов, и многое другое. Когда стоимость движения может быть разной, мы используем его вместо поиска в ширину.

A* — это модификация алгоритма Дейкстры, оптимизированная для единственной конечной точки. Алгоритм Дейкстры может находить пути ко всем точкам, A* находит путь к одной точке. Он отдаёт приоритет путям, которые ведут ближе к цели.

Я начну с самого простого — поиска в ширину, и буду добавлять функции, постепенно превращая его в A*.

Поиск в ширину

Ключевая идея всех этих алгоритмов заключается в том, что мы отслеживаем состояние расширяющегося кольца, которое называется границей. В сетке этот процесс иногда называется заливкой (flood fill), но та же техника применима и для карт без сеток. Посмотрите анимацию расширения границы:

Как это реализовать? Повторяем эти шаги, пока граница не окажется пустой:

1. Выбираем и удаляем точку из границы.
2. Помечаем точку как посещённую, чтобы знать, что не нужно обрабатывать её повторно.
3. Расширяем границу, глядя на её соседей. Всех соседей, которых мы ещё не видели, добавляем к границе.

Давайте рассмотрим это подробнее. Тайлы нумеруются в порядке их посещения:

Алгоритм описывается всего в десяти строках кода на Python:

frontier = Queue()
frontier.put(start )
visited = {}
visited[start] = True

while not frontier.empty():
   current = frontier.get()
   for next in graph.neighbors(current):
      if next not in visited:
         frontier.put(next)
         visited[next] = True

В этом цикле заключается вся сущность алгоритмов поиска по графу этой статьи, в том числе и A*. Но как нам найти кратчайший путь? Цикл на самом деле не создаёт путей, он просто говорит нам, как посетить все точки на карте. Так получилось потому, что поиск в ширину можно использовать для гораздо большего, чем просто поиск путей. В этой статье я показываю, как он применяется в играх tower defense, но его также можно использовать в картах расстояний, в процедурной генерации карт и многом другом. Однако здесь мы хотим использовать его для поиска путей, поэтому давайте изменим цикл так, чтобы отслеживать, откуда мы пришли для каждой посещённой точки, и переименуем visited в came_from:

frontier = Queue()
frontier.put(start )
came_from = {}
came_from[start] = None

while not frontier.empty():
   current = frontier.get()
   for next in graph.neighbors(current):
      if next not in came_from:
         frontier.put(next)
         came_from[next] = current

Теперь came_from для каждой точки указывает на место, из которого мы пришли. Это похоже на «хлебные крошки» из сказки. Нам этого достаточно для воссоздания целого пути. Посмотрите, как стрелки показывают обратный путь к начальной позиции.

Код воссоздания путей прост: следуем по стрелкам обратно от цели к началу. Путь — это последовательность рёбер, но иногда проще хранить только узлы:

current = goal 
path = [current]
while current != start: 
   current = came_from[current]
   path.append(current)
path.append(start) # optional
path.reverse() # optional

Таков простейший алгоритм поиска путей. Он работает не только в сетках, как показано выше, но и в любой структуре графов. В подземелье точки графа могут быть комнатами, а рёбра — дверями между ними. В платформере узлы графа могут быть локациями, а рёбра — возможными действиями: переместиться влево, вправо, подпрыгнуть, спрыгнуть вниз. В целом можно воспринимать граф как состояния и действия, изменяющие состояние. Подробнее о представлении карт я написал здесь. В оставшейся части статьи я продолжу использовать примеры с сетками, и расскажу о том, для чего можно применять разновидности поиска в ширину.

Ранний выход

Мы нашли пути из одной точки во все другие точки. Часто нам не нужны все пути, нам просто нужен путь между двумя точками. Мы можем прекратить расширять границу, как только найдём нашу цель. Посмотрите, как граница перестаёт расширятся после нахождения цели.

Код достаточно прямолинеен:

frontier = Queue()
frontier.put(start )
came_from = {}
came_from[start] = None

while not frontier.empty():
   current = frontier.get()

   if current == goal: 
      break           

   for next in graph.neighbors(current):
      if next not in came_from:
         frontier.put(next)
         came_from[next] = current

Стоимость перемещения

Пока мы делали шаги с одинаковой стоимостью. В некоторых случаях поиска путей у разных типов движения есть разная стоимость. Например, в Civilization движение через равнины или пустыню может стоить 1 очко движения, а движение через лес — 5 очков движения. На карте в самом начале статьи прохождение через воду стоит в 10 раз дороже, чем движение по траве. Ещё одним примером является диагональное движение в сетке, которое стоит больше, чем движение по осям. Нам нужно, чтобы поиск пути учитывал эту стоимость. Давайте сравним количество шагов от начала с расстоянием от начала:

Для этого нам нужен алгоритм Дейкстры (также называемый поиском с равномерной стоимостью). Чем он отличается от поиска в ширину? Нам нужно отслеживать стоимость движения, поэтому добавим новую переменную cost_so_far, чтобы следить за общей стоимостью движения с начальной точки. При оценке точек нам нужно учитывать стоимость передвижения. Давайте превратим нашу очередь в очередь с приоритетами. Менее очевидно то, что у нас может получиться так, что одна точка посещается несколько раз с разной стоимостью, поэтому нужно немного поменять логику. Вместо добавления точки к границе в случае, когда точку ни разу не посещали, мы добавляем её, если новый путь к точке лучше, чем наилучший предыдущий путь.

frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0

while not frontier.empty():
   current = frontier.get()

   if current == goal:
      break
   
   for next in graph.neighbors(current):
      new_cost = cost_so_far[current] + graph.cost(current, next)
      if next not in cost_so_far or new_cost < cost_so_far[next]:
         cost_so_far[next] = new_cost
         priority = new_cost
         frontier.put(next, priority)
         came_from[next] = current

Использование очереди с приоритетами вместо обычной очереди изменяет способ расширения границы. Контурные линии позволяют это увидеть. Посмотрите видео, чтобы понаблюдать, как граница расширяется медленнее через леса, и поиск кратчайшего пути выполняется вокруг центрального леса, а не сквозь него:

Стоимость движения, отличающаяся от 1, позволяет нам исследовать более интересные графы, а не только сетки. На карте в начале статьи стоимость движения основана на расстоянии между комнатами. Стоимость движения можно также использовать, чтобы избегать или предпочитать области на основании близости врагов или союзников. Интересная деталь реализации: обычная очередь с приоритетами поддерживает операции вставки и удаления, но в некоторых версиях алгоритма Дейкстры используется и третья операция, изменяющая приоритет элемента, уже находящегося в очереди с приоритетами. Я не использую эту операцию, и объясняю это на странице реализации алгоритма.

Эвристический поиск

В поиске в ширину и алгоритме Дейкстры граница расширяется во всех направлениях. Это логичный выбор, если вы ищете путь ко всем точкам или ко множеству точек. Однако обычно поиск выполняется только для одной точки. Давайте сделаем так, чтобы граница расширялась к цели больше, чем в других направлениях. Во-первых, определим эвристическую функцию, сообщающую нам, насколько мы близки к цели:

def heuristic(a, b):
   # Manhattan distance on a square grid
   return abs(a.x - b.x) + abs(a.y - b.y)

В алгоритме Дейкстры для порядка очереди с приоритетами мы использовали расстояние от начала. В жадном поиске по первому наилучшему совпадению для порядка очереди с приоритетами мы вместо этого используем оцененное расстояние до цели. Точка, ближайшая к цели, будет исследована первой. В коде используется очередь с приоритетами из поиска в ширину, но не применяется cost_so_far из алгоритма Дейкстры:

frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
came_from[start] = None

while not frontier.empty():
   current = frontier.get()

   if current == goal:
      break
   
   for next in graph.neighbors(current):
      if next not in came_from:
         priority = heuristic(goal, next)
         frontier.put(next, priority)
         came_from[next] = current

Давайте посмотрим, как это работает:

Ого! Потрясающе, правда? Но что случится на более сложной карте?

Эти пути не являются кратчайшими. Итак, этот алгоритм работает быстрее, когда препятствий не очень много, но пути не слишком оптимальны. Можно ли это исправить? Конечно.

Алгоритм A*

Алгоритм Дейкстры хорош в поиске кратчайшего пути, но он тратит время на исследование всех направлений, даже бесперспективных. Жадный поиск исследует перспективные направления, но может не найти кратчайший путь. Алгоритм A* использует и подлинное расстояние от начала, и оцененное расстояние до цели.

Код очень похож на алгоритм Дейкстры:

frontier = PriorityQueue()
frontier.put(start, 0)
came_from = {}
cost_so_far = {}
came_from[start] = None
cost_so_far[start] = 0

while not frontier.empty():
   current = frontier.get()

   if current == goal:
      break
   
   for next in graph.neighbors(current):
      new_cost = cost_so_far[current] + graph.cost(current, next)
      if next not in cost_so_far or new_cost < cost_so_far[next]:
         cost_so_far[next] = new_cost
         priority = new_cost + heuristic(goal, next)
         frontier.put(next, priority)
         came_from[next] = current

Сравните алгоритмы: алгоритм Дейкстры вычисляет расстояние от начальной точки. Жадный поиск по первому наилучшему совпадению оценивает расстояние до точки цели. A* использует сумму этих двух расстояний.

Попробуйте в оригинале статьи делать отверстия в разных местах стены. Вы обнаружите, что жадный поиск находит правильный ответ, A* тоже его находит, исследуя ту же область. Когда жадный поиск по первому наилучшему находит неверный ответ (более длинный путь), A* находит правильный, как и алгоритм Дейкстры, но всё равно исследует меньше, чем алгоритм Дейкстры.

A* берёт лучшее от двух алгоритмов. Поскольку эвристика не оценивает расстояния повторно, A* не использует эвристику для поиска подходящего ответа. Он находит оптимальный путь, как и алгоритм Дейкстры. A* использует эвристику для изменения порядка узлов, чтобы повысить вероятность более раннего нахождения узла цели.

И… на этом всё! В этом и заключается алгоритм A*.

Дополнительное чтение

Вы готовы реализовать его? Попробуйте использовать готовую библиотеку. Если вы хотите реализовать его самостоятельно, то у меня есть инструкция по пошаговой реализации графов, очередей и алгоритмов поиска пути на Python, C++ и C#.

Какой алгоритм стоит использовать для поиска путей на игровой карте?

• Если вам нужно найти пути из или ко всем точкам, используйте поиск в ширину или алгоритм Дейкстры. Используйте поиск в ширину, если стоимость движения одинакова. Используйте алгоритм Дейкстры, если стоимость движения изменяется.
• Если нужно найти пути к одной точке, используйте жадный поиск по наилучшему первому или A*. В большинстве случаев стоит отдать предпочтение A*. Когда есть искушение использовать жадный поиск, то подумайте над применением A* с «недопустимой» эвристикой.

А что насчёт оптимальных путей? Поиск в ширину и алгоритм Дейкстры гарантированно найдут кратчайший путь по графу. Жадный поиск не обязательно его найдёт. A* гарантированно найдёт кратчайший путь, если эвристика никогда не больше истинного расстояния. Когда эвристика становится меньше, A* превращается в алгоритм Дейкстры. Когда эвристика становится больше, A* превращается в жадный поиск по наилучшему первому совпадению.

А как насчёт производительности? Лучше всего устранить ненужные точки графа. Если вы используете сетку, то прочитайте это. Уменьшение размера графа помогает всем алгоритмам поиска по графам. После этого используйте простейший из возможных алгоритмов. Простые очереди выполняются быстрее. Жадный поиск обычно выполняется быстрее, чем алгоритм Дейкстры, но не обеспечивает оптимальных путей. Для большинства задач по поиску путей оптимальным выбором является A*.

А что насчёт использования не на картах? Я использовал в статье карты, потому что думаю, что на них проще объяснить работу алгоритма. Однако эти алгоритмы поиска по графам можно использовать на любых графах, не только на игровых картах, и я пытался представить код алгоритма в виде, не зависящем от двухмерных сеток. Стоимость движения на картах превращается в произвольные веса рёбер графа. Эвристики перенести на произвольные карты не так просто, необходимо создавать эвристику для каждого типа графа. Для плоских карт хорошим выбором будут расстояния, поэтому здесь мы использовали их.

Я написал ещё много всего о поиске путей здесь. Не забывайте, что поиск по графам — это только одна часть того, что вам нужно. Сам по себе A* не обрабатывает такие аспекты, как совместное движение, перемещение препятствий, изменение карты, оценку опасных областей, формации, радиусы поворота, размеры объектов, анимацию, сглаживание путей и многое другое.

Компьютеры и Интернет

Алгоритм – это пошаговое решение определенной проблемы. В большинстве своём в общем смысле алгоритм – это любой набор подробных инструкций, которые могут предоставить прогнозируемость конечного результата с известным началом. Алгоритмы хороши только в инструкции, но, и результат будет неправильным, если алгоритм не определен надлежащим образом.

Примеры алгоритмов

Типичный пример алгоритма будет инструкция по сборке модели самолета. Учитывая стартовый набор и число отмеченных частей, можно следовать инструкциям, приведенным в результате с прогнозируемым конечным результатом: собранный самолет. Опечатки в инструкции, или неспособность должным образом следовать шагам, приведёт в неисправность конечный продукт.

Компьютерная программа – это ещё один широко распространенный пример. Каждая компьютерная программа – это просто последовательность инструкций, которые могут различаться по сложности, и перечислены в определённом порядке, предназначенные для выполнения конкретной задачи. Математика также использует алгоритмы для решения уравнений вручную, без использования калькулятора. Последний пример – человеческий мозг: большинство концепций человеческого мозга определяют всё его поведение — от приобретения продуктов питания до влюблённости — как результат сложного алгоритма.

Классы алгоритмов

Пока нет общепризнанных классов для различных типов алгоритмов, но есть общие классы,которым  алгоритмы часто могут принадлежать. Среди них:

Алгоритм динамического программирования: этот класс помнит старые результаты и пытается использовать их, чтобы ускорить процесс поиска новых результатов.

Жадные алгоритмы: жадные алгоритмы предпринимают попытку не только найти решение, но и найти идеальное решение для любой проблемы.

Алгоритм переборов: такой подход начинается в какой-то случайной точке и перебирает все варианты, пока не найдёт решение.

Рандомизированные алгоритмы: этот класс включает любой алгоритм, который в ходе процесса в любой момент использует случайное число.

Алгоритмы  ветвей и границ: образуют дерево подзадач основной задачи, после каждой ветки, пока она либо не будет решена, либо будет сосредоточена в другой ветке.

Простые рекурсивные алгоритмы: этот тип идёт на прямое решение то сразу, то отступает, чтобы найти более простое решение.

Алгоритмы обратного слежения: такие алгоритмы проводят тест для решения; если решение нашло алгоритм и задача решена, если нет, то он повторяется не один раз, и тесты проходят снова, и продолжаются до тех пор, пока решение не будет найдено.

Алгоритмы разделяй и властвуй: этот алгоритм, похожи на алгоритмы ветвей и границ, за исключением что они используют поиск метода алгоритмов обратного слежения повторяющихся во время разделения задачи на подзадачи.

Последовательные и параллельные алгоритмы

Помимо этих общих классов, алгоритмы также могут быть разделены на две основные группы: последовательные алгоритмы, которые предназначены для последовательного выполнения, в котором каждая операция является принятой в линейном порядке; и параллельные алгоритмы, используемые на компьютерах под управлением параллельных процессоров, в котором имеется ряд операций который выполняются параллельно друг другу. Параллельные алгоритмы существуют в природном мире в случае, например, генетические мутации различных видов.

Алгоритм Википедия

Алгори́тм (лат. al­go­rithmi — от арабского имени математика Аль-Хорезми^[1]) — конечная совокупность точно заданных правил решения произвольного класса задач или набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.

Ранее в русском языке писали «алгорифм», сейчас такое написание используется редко, но тем не менее имеет место исключение (нормальный алгорифм Маркова).

Часто в качестве исполнителя выступает компьютер, но понятие алгоритма необязательно относится к компьютерным программам, так, например, чётко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек (а может быть и некоторый механизм, ткацкий станок, и пр.).

Можно выделить алгоритмы вычислительные (далее речь в основном идёт о них), и управляющие. Вычислительные по сути преобразуют некоторые начальные данные в выходные, реализуя вычисление некоторой функции. Семантика управляющих алгоритмов существенным образом может отличаться и сводиться к выдаче необходимых управляющих воздействий либо в заданные моменты времени, либо в качестве реакции на внешние события (в этом случае, в отличие от вычислительного алгоритма, управляющий может оставаться корректным при бесконечном выполнении).

Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако в явном виде понятие алгоритма сформировалось лишь в начале XX века.

Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений^[2] или «эффективного метода»^[3]; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Чёрча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга.