Для любых векторов 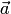 ,
, 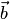 ,
, 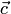 и любого действительного числа
и любого действительного числа 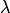 :
:
1. 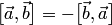 ;
;
2. ;
3. 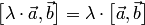 .
.
Первое свойство определяет антисимметричность векторного произведения, второе и третье — аддитивность и однородность по первому множителю. Эти свойства аналогичны свойствам произведения чисел: первое свойство «противоположно» закону коммутативности умножения чисел (закон антикоммутативности), второе свойство соответствует закону дистрибутивности умножения чисел по отношению к сложению, третье — закону ассоциативности умножения. Поэтому рассматриваемая операция и называется произведением векторов. Поскольку ее результатом является вектор, то такое произведение векторов называется векторным.

Докажем первое свойство, предполагая, что векторы 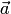 и
и 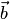 не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы
не коллинеарны (в противном случае обе части доказываемого равенства равны нулевому вектору). По определению векторы 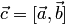
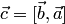 имеют равные длины
имеют равные длины 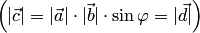 и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов
и коллинеарны (так как оба вектора перпендикулярны одной плоскости). По определению тройки векторов  и
и 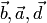 — правые, т.е. вектор
— правые, т.е. вектор 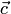
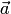 к
к 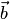 происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора
происходит в положительном направлении (против часовой стрелки), если смотреть из конца вектора 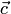 , а вектор
, а вектор 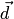 направлен так, что кратчайший поворот от
направлен так, что кратчайший поворот от 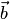
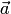 происходит в положительном направлении, если смотреть из конца вектора
происходит в положительном направлении, если смотреть из конца вектора 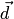 (рис. 1.43). Это означает, что векторы
(рис. 1.43). Это означает, что векторы 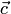 и
и 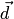 противоположно направлены. Следовательно,
противоположно направлены. Следовательно, 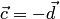 , что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13).
, что и требовалось доказать. Доказательство остальных свойств приведено ниже (см. пункт 1 замечаний 1.13). 1. 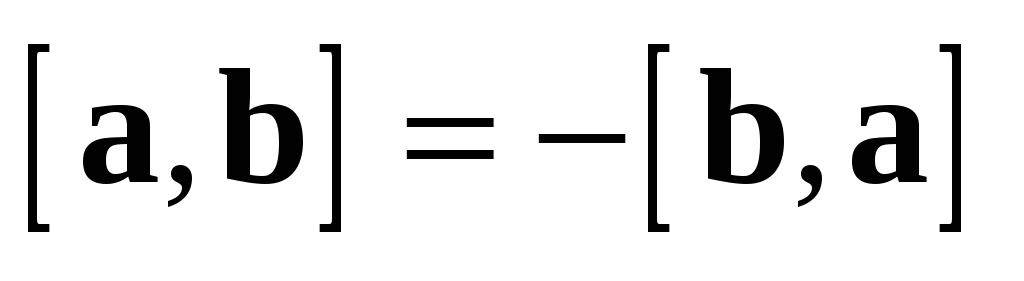 ;
;
2. 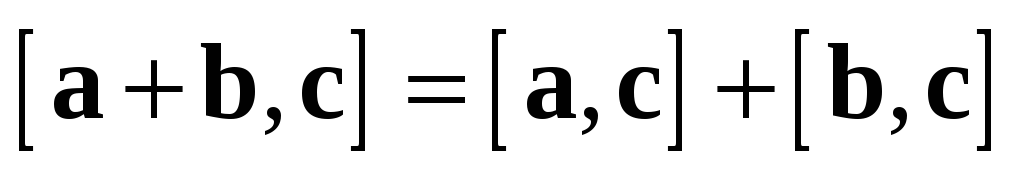 ;
;
3. 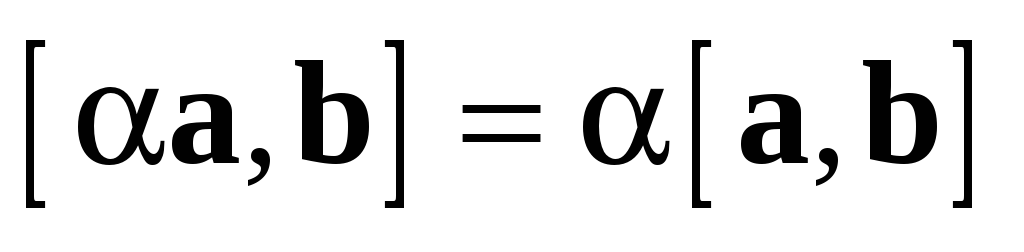 ;
;
4. Для любого 
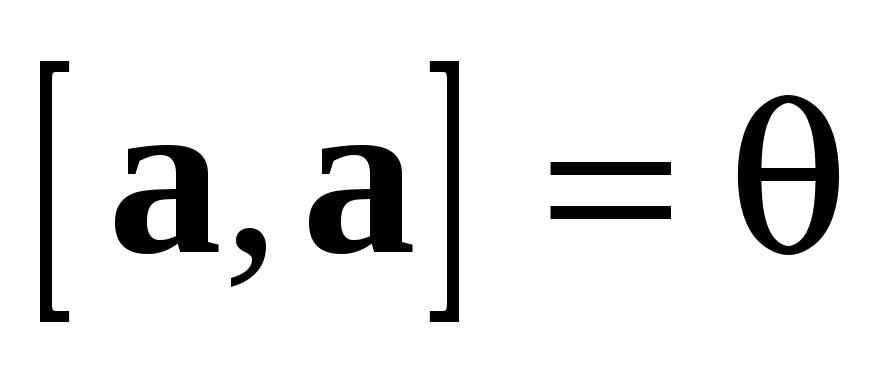
Доказательство свойства 1.
Обозначим 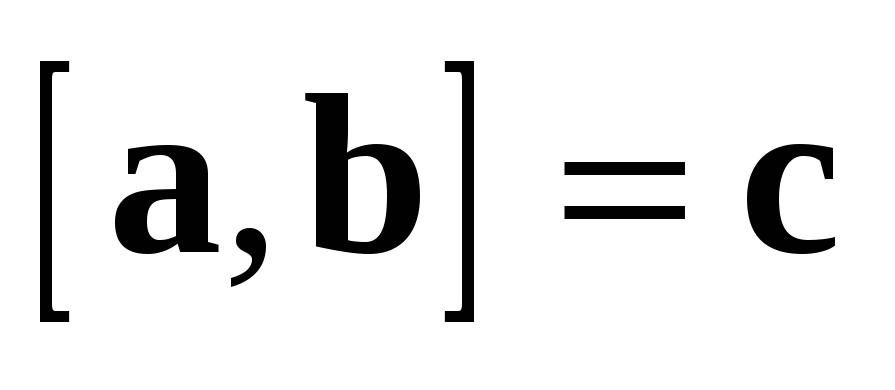 ,
, 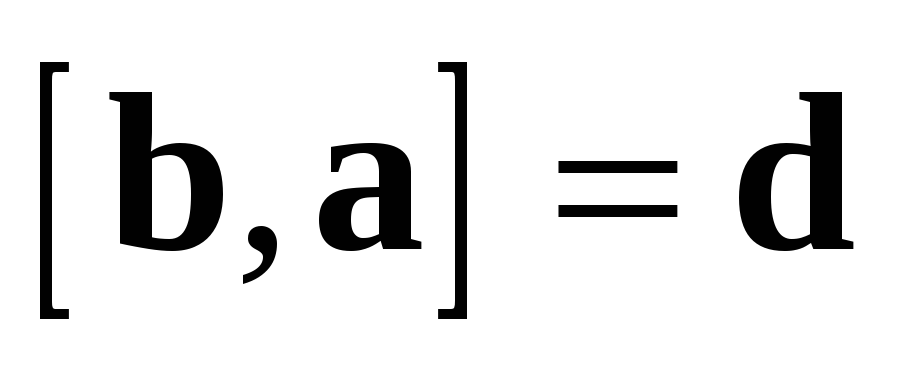 .
Нам нужно доказать, что справедливо
равенство между векторами:
.
Нам нужно доказать, что справедливо
равенство между векторами: 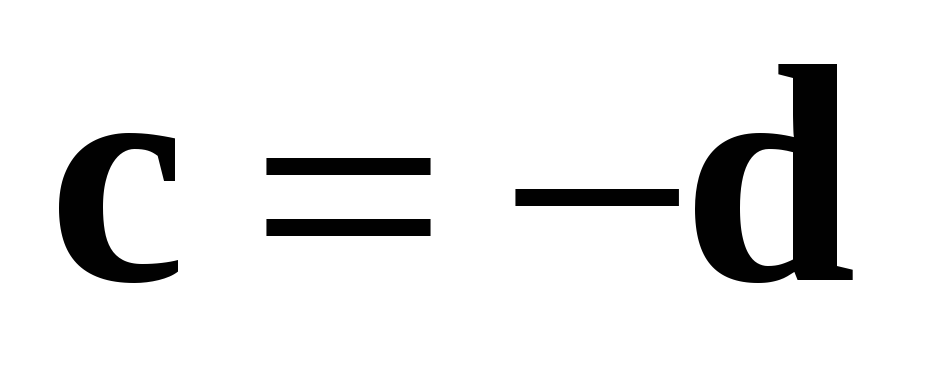
В соответствии с определением, данным
в лекции 1, нужно убедиться, что  и направления
и направления 
 совпадают.
совпадают.Из определения 5 получаем
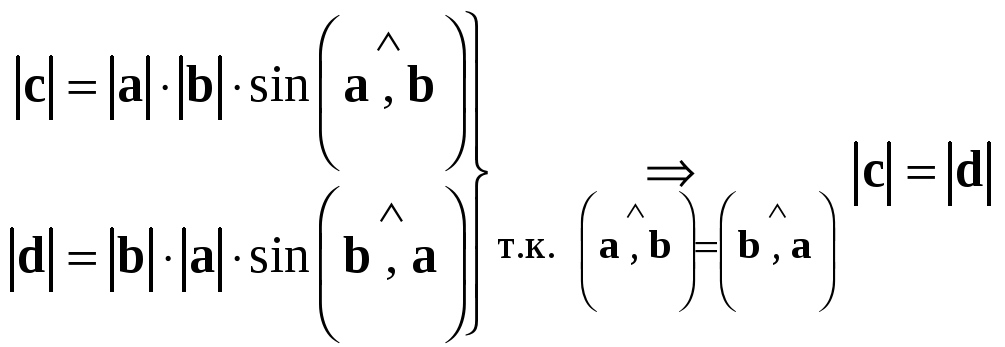 .
.
По определению 5
,  и
и  ,
,  ,
следовательно,
,
следовательно, 
 оба перпендикулярны плоскости
оба перпендикулярны плоскости  ,
определяемой векторами
,
определяемой векторами  и
и  ,
следовательно,
,
следовательно,  и
и 
Пусть  ,
,  и
и  приведены к одному началу. Так как они
составляют правую тройку, в соответствии
с определением 3 с конца вектора
приведены к одному началу. Так как они
составляют правую тройку, в соответствии
с определением 3 с конца вектора  кратчайший поворот от
кратчайший поворот от  к
к 
 ,
что и вектор
,
что и вектор  ,
кратчайший поворот от
,
кратчайший поворот от  к
к  кажется совершающимся по
ходу часовой стрелки, следовательно,
вектор
кажется совершающимся по
ходу часовой стрелки, следовательно,
вектор 
 .
Учитывая уже установленную коллинеарность
.
Учитывая уже установленную коллинеарность  и
и  ,
получаем
,
получаем  .
.Свойство 2 примем без доказательства.
Доказательство свойства 3.
Обозначим 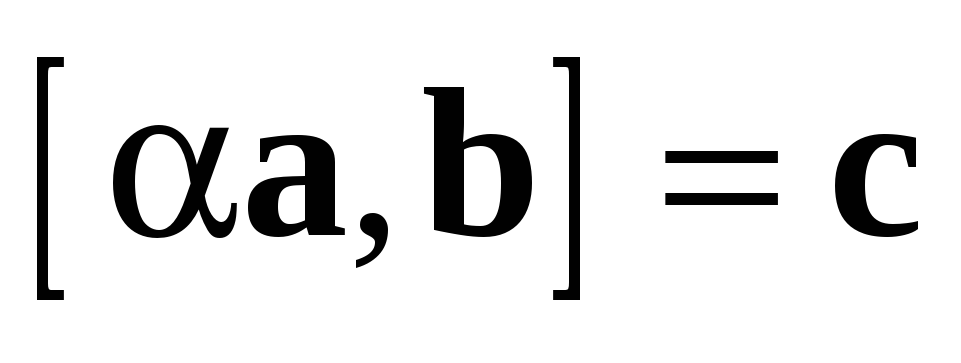 ,
, 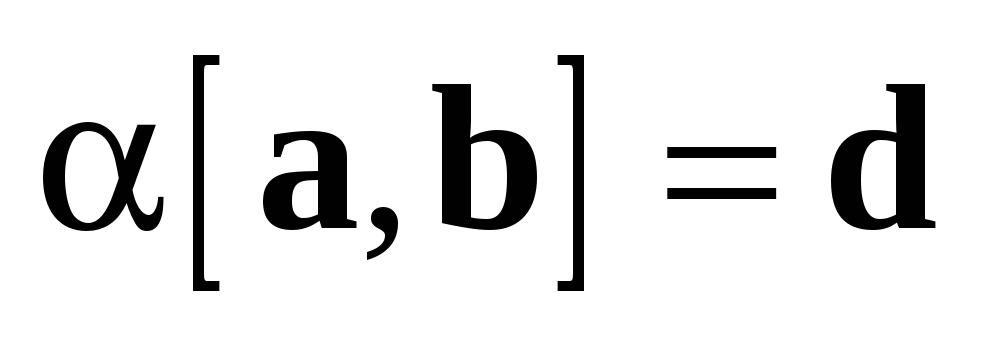
Случай 1. 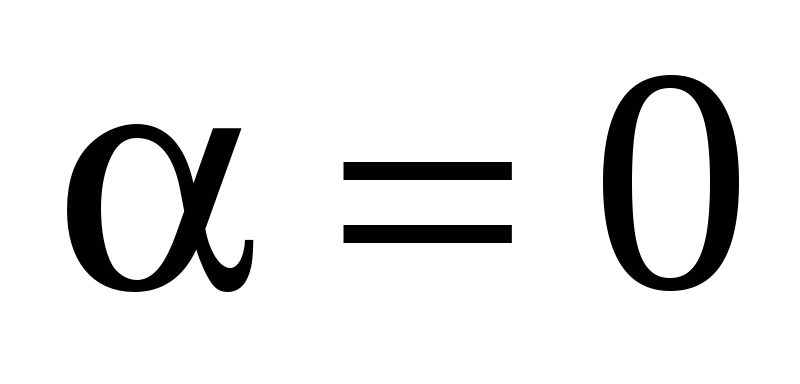 .
Тогда
.
Тогда 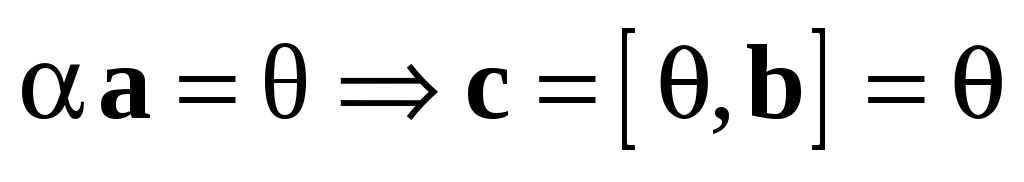 (так как
(так как 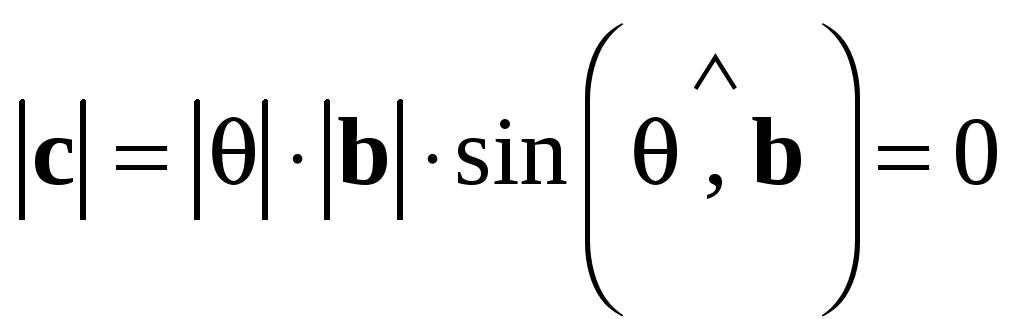 ),
при этом
),
при этом 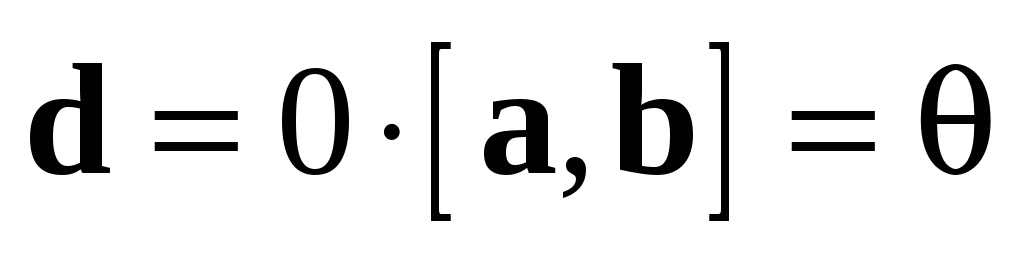 ,
следовательно,
,
следовательно, 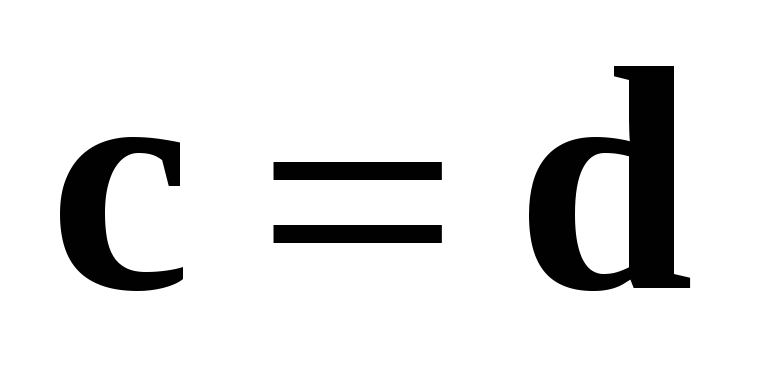 .
.
Случай 2. 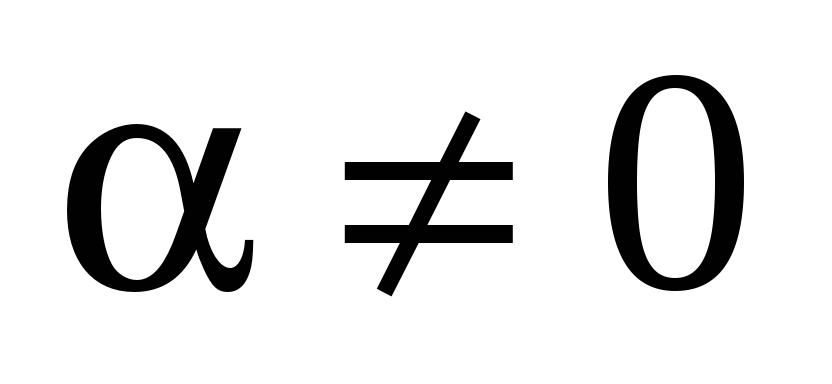
а) Векторы  и
и  коллинеарны. Тогда по теореме 4
коллинеарны. Тогда по теореме 4 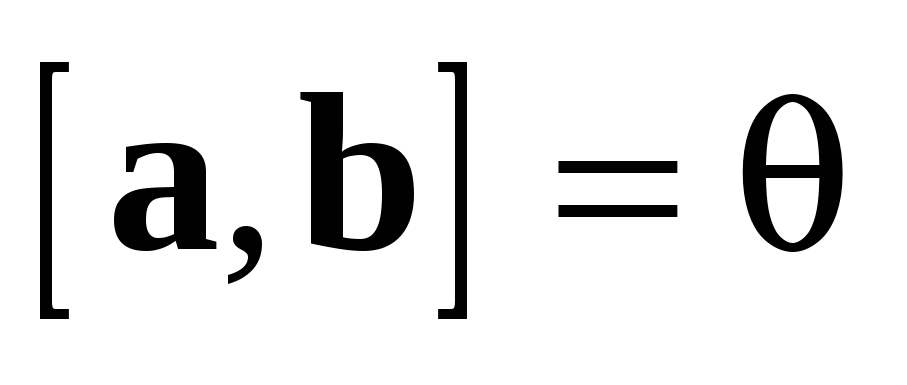 и
и 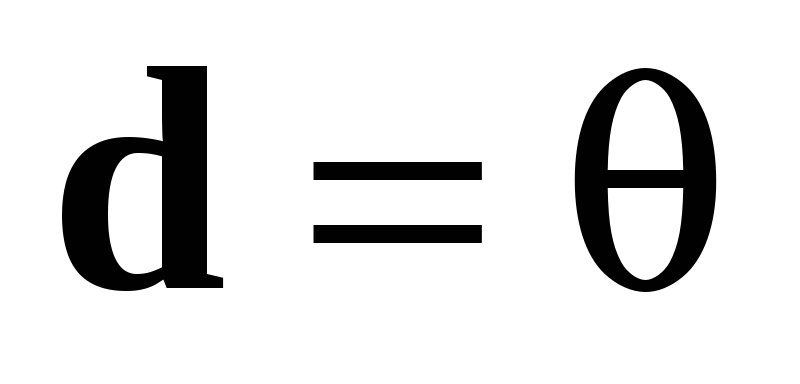 ;
;  коллинеарен
коллинеарен  (как произведение вектора
(как произведение вектора  на число), следовательно,
на число), следовательно,  коллинеарен
коллинеарен  ,
и по теореме 4
,
и по теореме 4  ,
значит,
,
значит,  .
.
б) Векторы  и
и  не коллинеарны. Пусть
не коллинеарны. Пусть  .
Тогда
.
Тогда
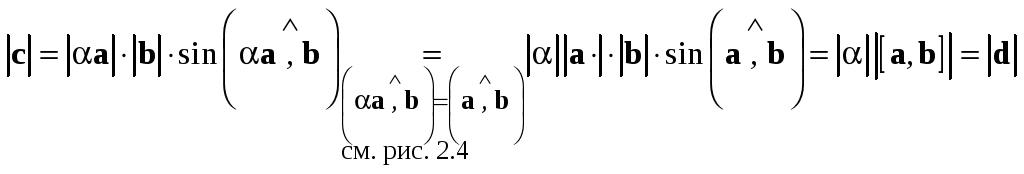
 .
.
Имеем  ,
следовательно,
,
следовательно,  коллинеарен
коллинеарен 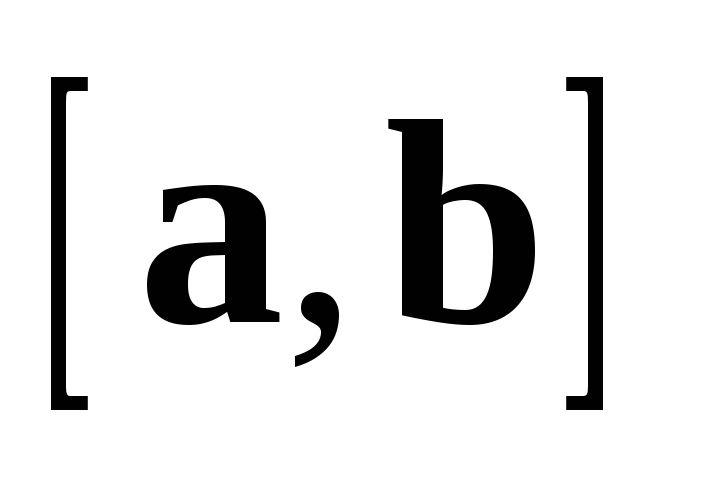 .
С другой стороны,
,
поэтому
.
С другой стороны,
,
поэтому  коллинеарен
коллинеарен 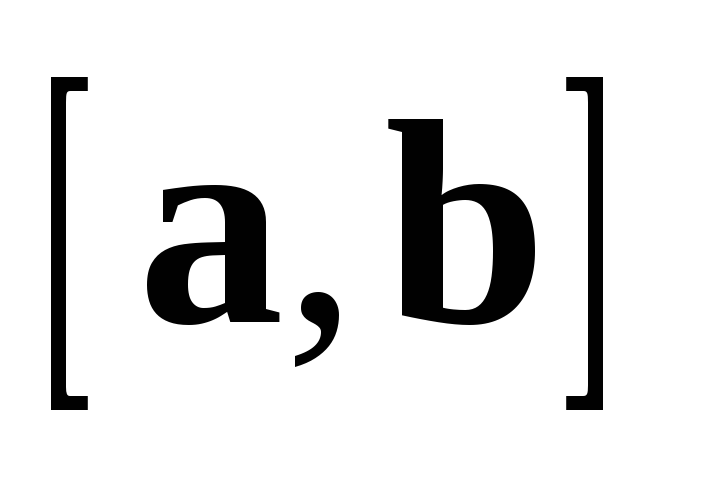 .
Таким образом, и
.
Таким образом, и  коллинеарны.
коллинеарны.
Так как 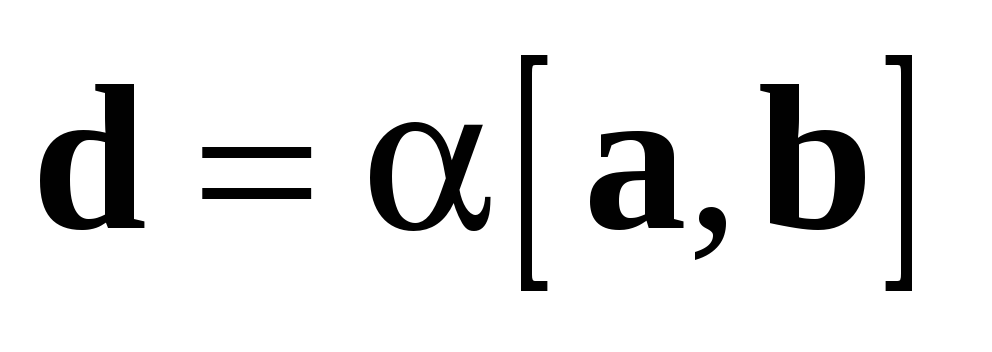 ,
а
,
а 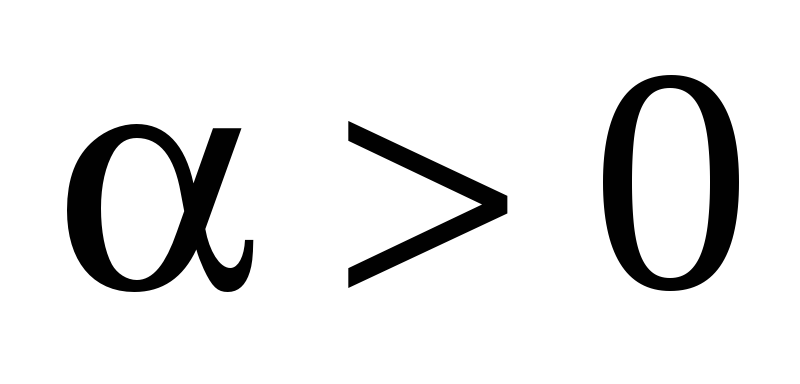 ,
то направление
,
то направление  совпадает с направлением вектора
совпадает с направлением вектора 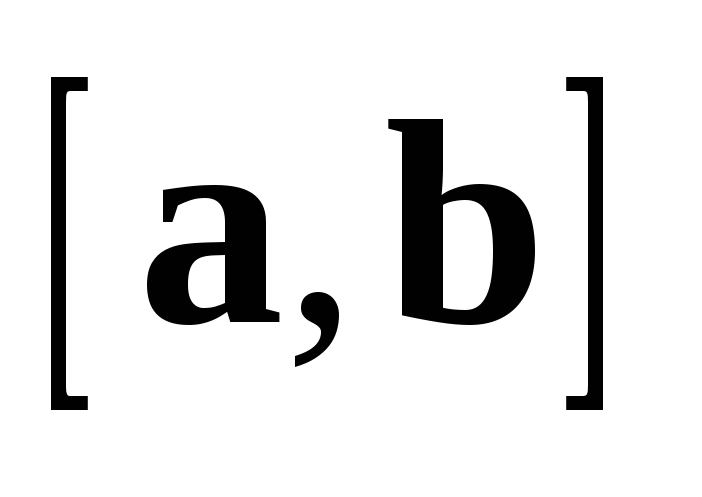 .
.
Направление 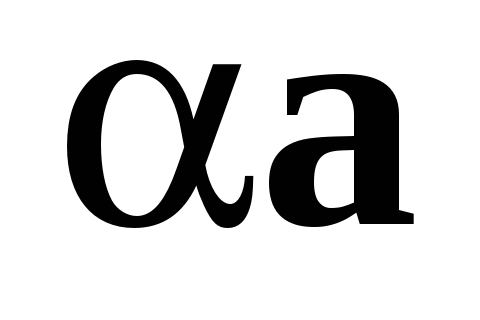 совпадает с направлением
совпадает с направлением  ,
а
,
а 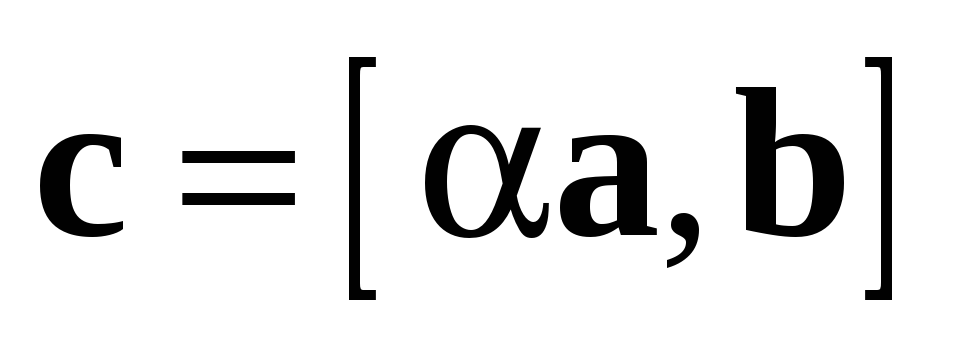 ,
следовательно, направление
,
следовательно, направление  совпадает с направлением
совпадает с направлением 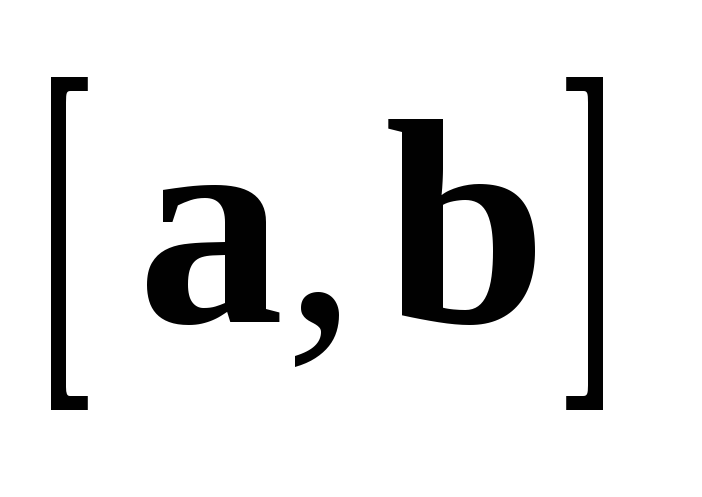 .
.
Итак,  и
и  коллинеарны и направления их совпадают,
т.е.
коллинеарны и направления их совпадают,
т.е. 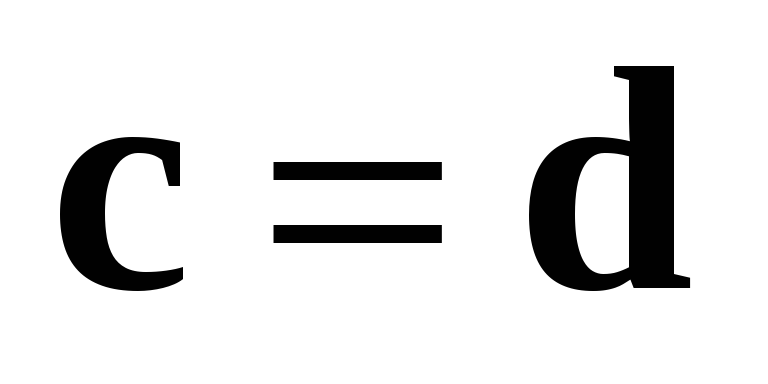 и свойство 3 в этом случае справедливо.
и свойство 3 в этом случае справедливо.
Пусть 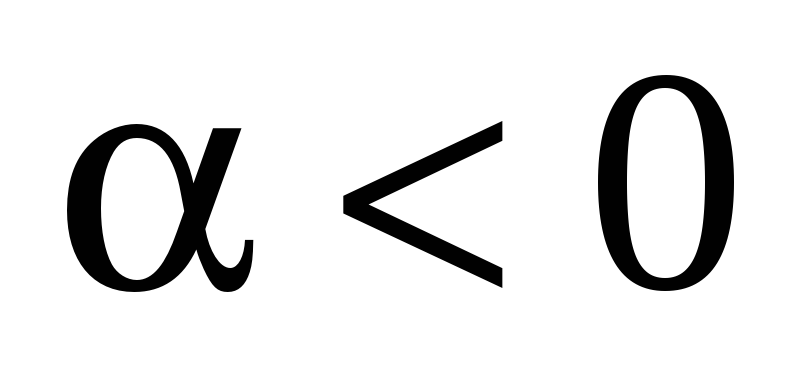 .
Тогда
.
Тогда
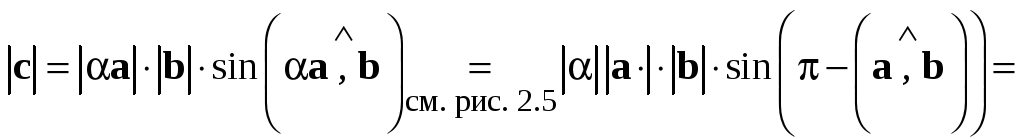
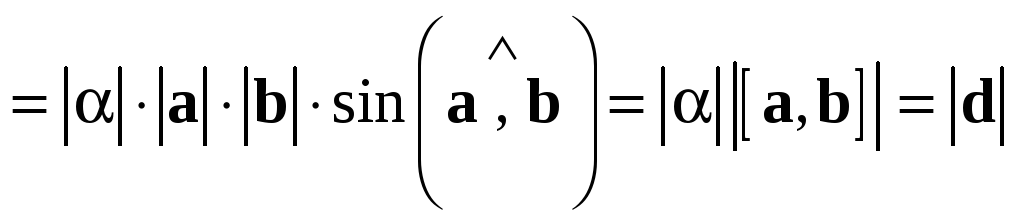 .
.
И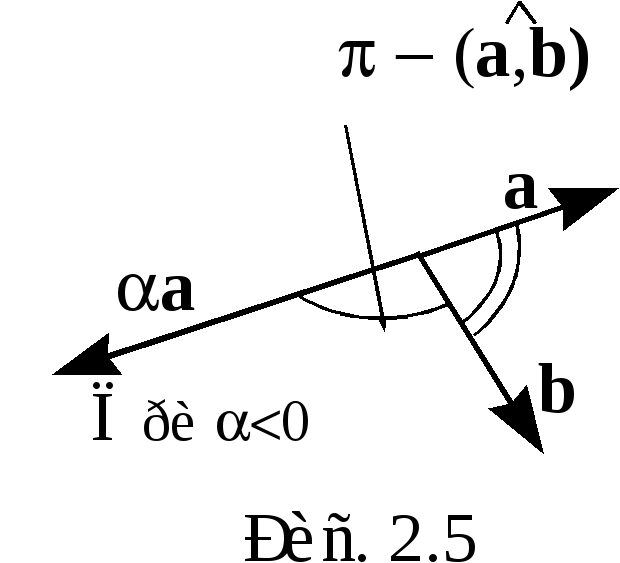 меем
меем 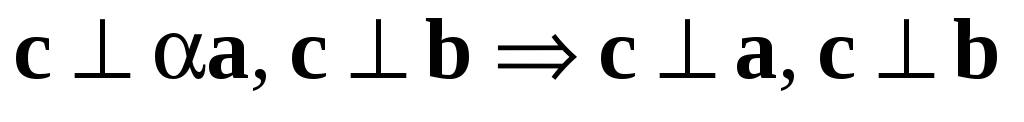 и
и  коллинеарен
коллинеарен 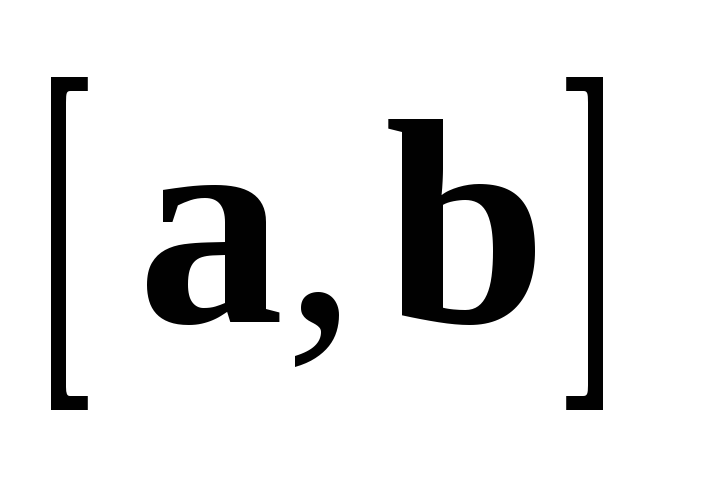 .
С другой стороны
.
С другой стороны 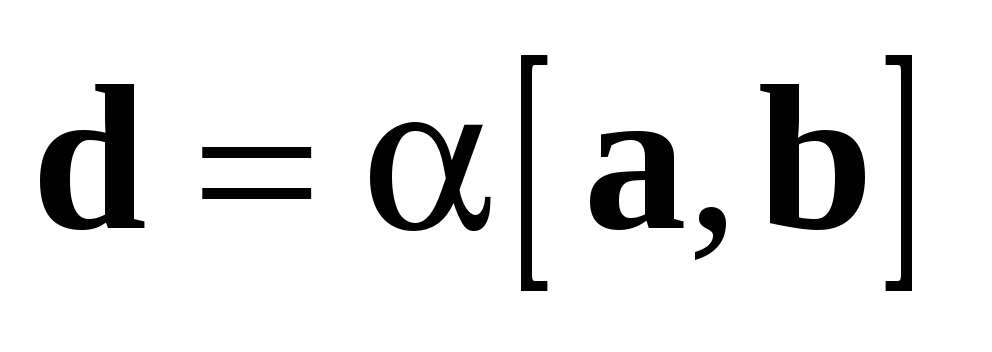 и
и  коллинеарен вектору
коллинеарен вектору 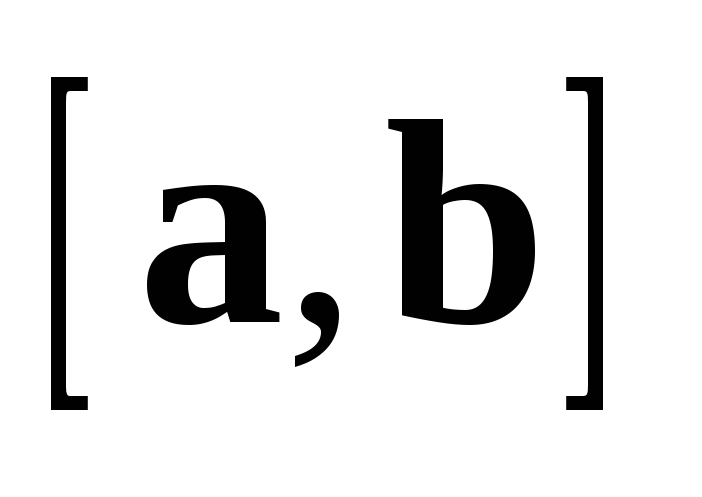 .
Таким образом,
.
Таким образом,  и
и  коллинеарны (и коллинеарны вектору
коллинеарны (и коллинеарны вектору 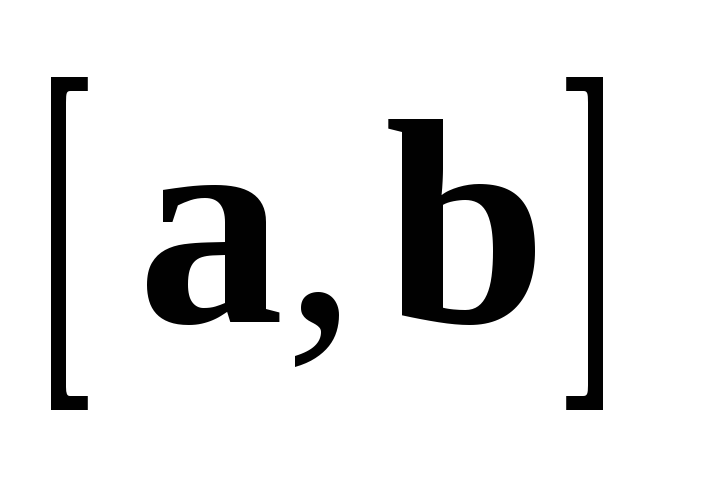 ).
).
Вектор 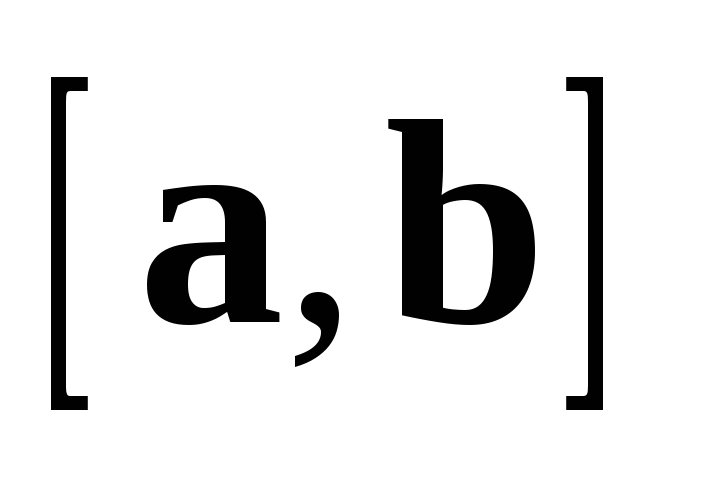 в соответствии с определениями 5 и 3
направлен таким образом, что с конца
в соответствии с определениями 5 и 3
направлен таким образом, что с конца 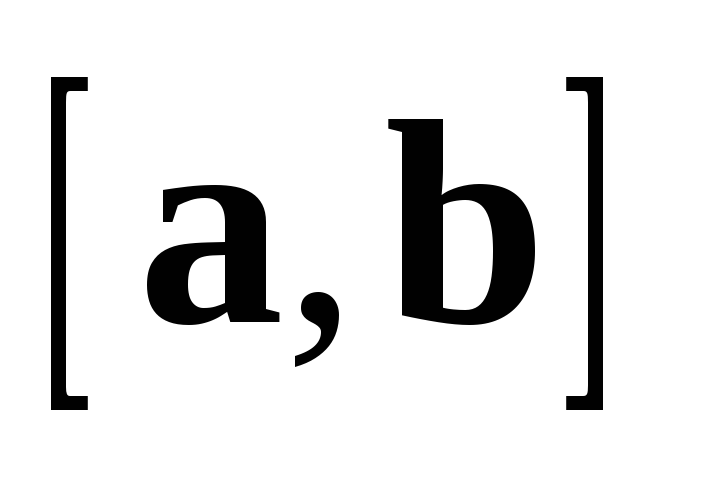 кратчайший поворот от
кратчайший поворот от  к
к  кажется совершающимся против хода
часовой стрелки, тогда (
кажется совершающимся против хода
часовой стрелки, тогда (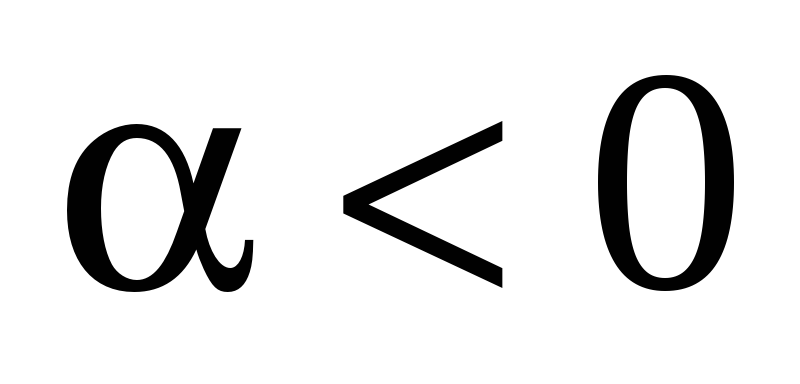 ),
с конца
),
с конца  кратчайший поворот от
кратчайший поворот от  к
к  кажется совершающимся по ходу часовой
стрелки, следовательно, векторы
кажется совершающимся по ходу часовой
стрелки, следовательно, векторы  и
и 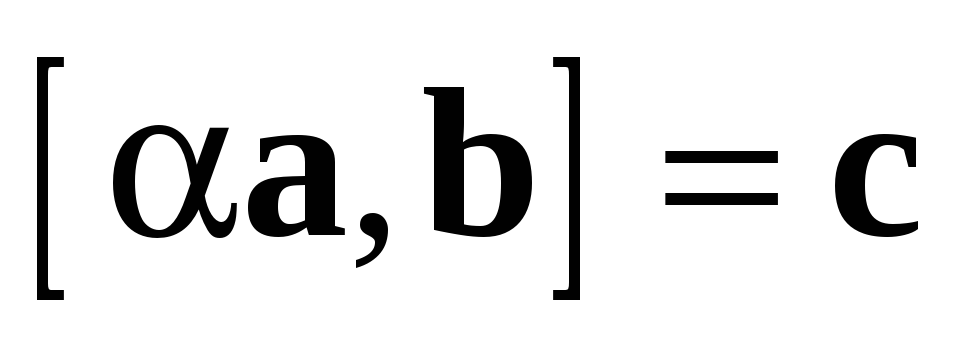 имеют противоположное направление.
имеют противоположное направление.
Вектор  ,
равный
,
равный 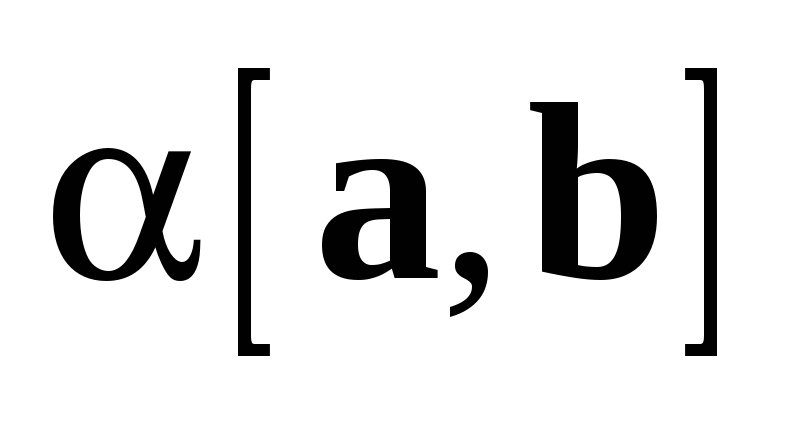 ,
тоже имеет направление, противоположное
направлению
,
тоже имеет направление, противоположное
направлению 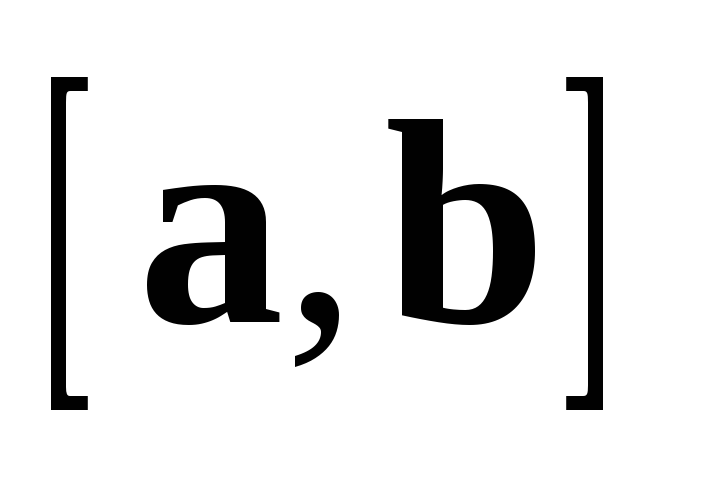 ,
таким образом,
,
таким образом,  и
и  направлены одинаково.
направлены одинаково.
Учитывая доказанное ранее равенство 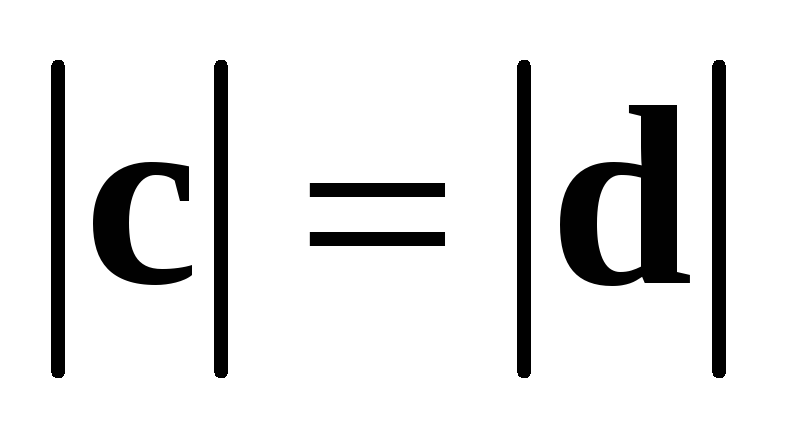 и коллинеарность
и коллинеарность  и
и  ,
заключаем, что
,
заключаем, что 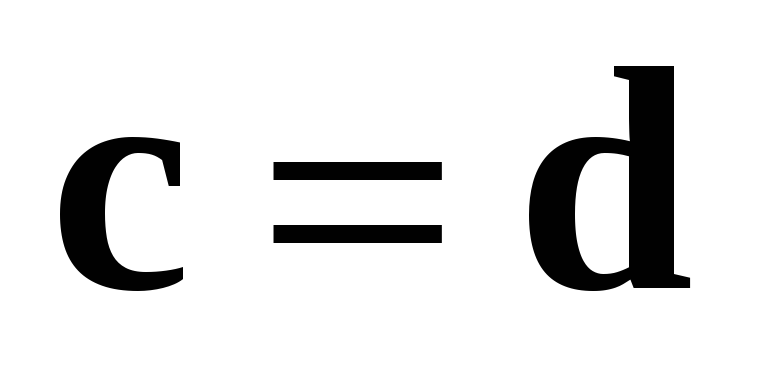 ,
– свойство 3 справедливо и в этом случае.
,
– свойство 3 справедливо и в этом случае.
Доказательство свойства 4.
Так как любой вектор  коллинеарен сам себе, то свойство 4, т.е.
равенство
коллинеарен сам себе, то свойство 4, т.е.
равенство 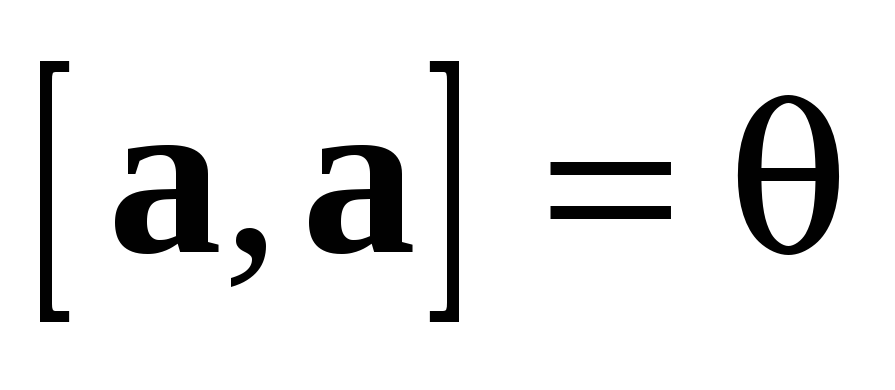 ,
следует из теоремы 4.
,
следует из теоремы 4.
Замечание. Свойства 2 и 3 справедливы также в форме:
 ).
). 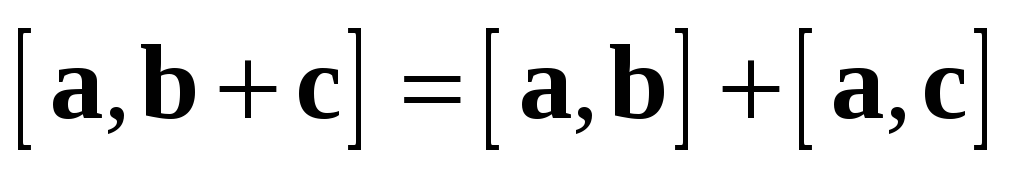 ;
;
 ).
). 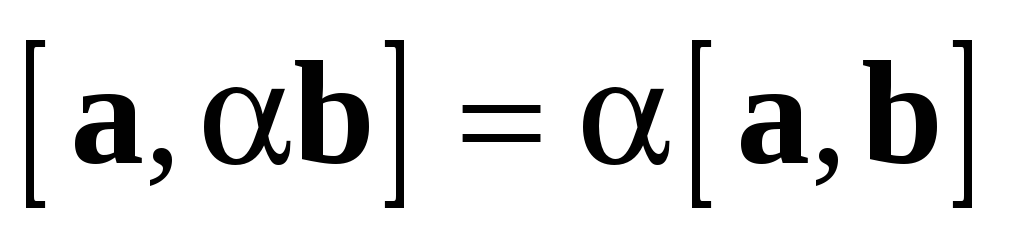 .
.
В самом деле, докажем, например,  :
:
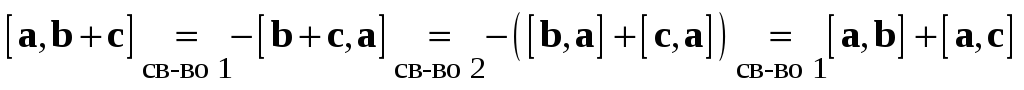 .
.
Аналогично обосновывается  .
.
Доказанные алгебраические свойства дают возможность, перемножая векторно линейные комбинации векторов, группировать коэффициенты, как при перемножении многочленов.
Теорема 5. Пусть  ,
, ,
, – декартов базис,
– декартов базис, 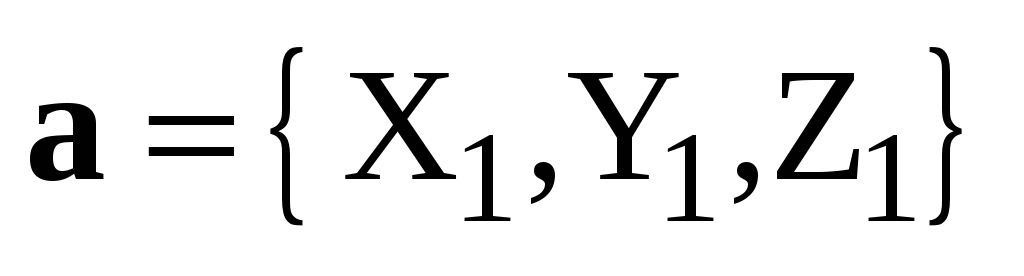 ,
, 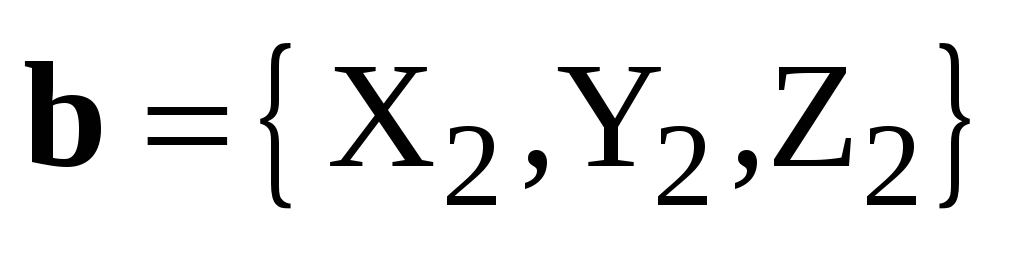 .
Тогда
.
Тогда 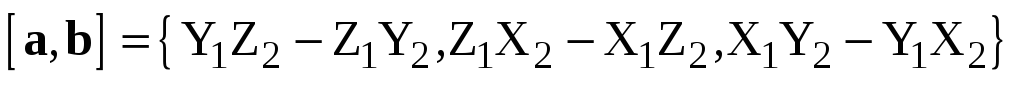 .
.
Доказательство. Имеем
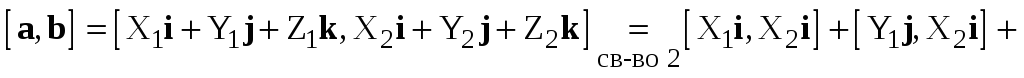
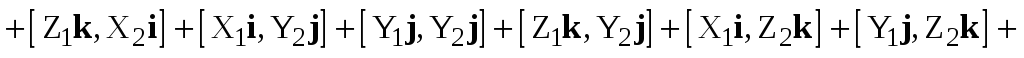
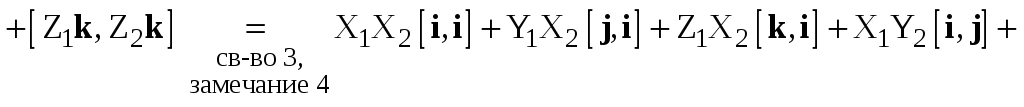
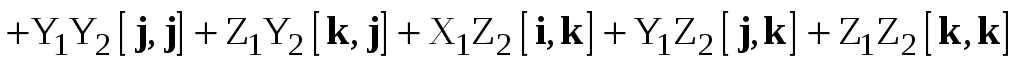 .
(2.6)
.
(2.6)
Найдем всевозможные векторные произведения базисных векторов.
В силу свойства 4 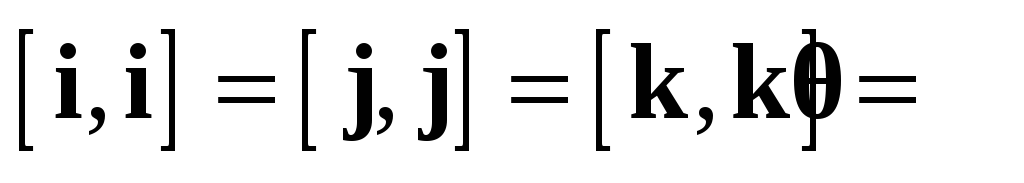 .
.
Так как базис  ,
, ,
, декартов и длина каждого базисного
вектора равна единице, каждое из
оставшихся шести векторных произведений
либо вектор базиса, либо противоположный
ему. Векторы базиса образуют правую
тройку, поэтому
декартов и длина каждого базисного
вектора равна единице, каждое из
оставшихся шести векторных произведений
либо вектор базиса, либо противоположный
ему. Векторы базиса образуют правую
тройку, поэтому
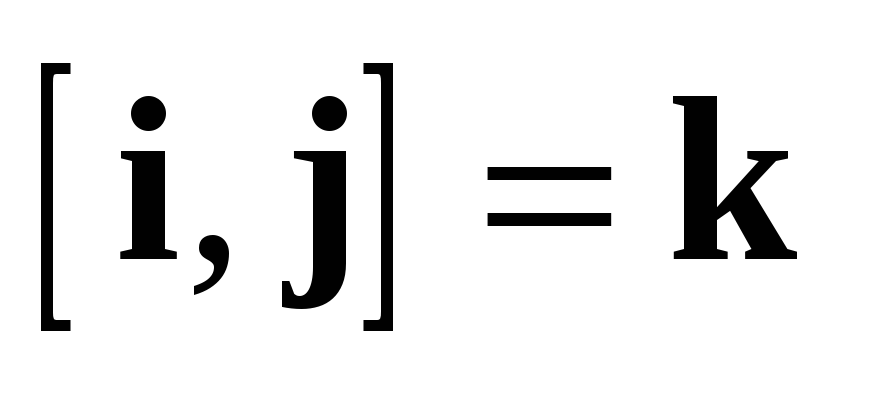 ,
, 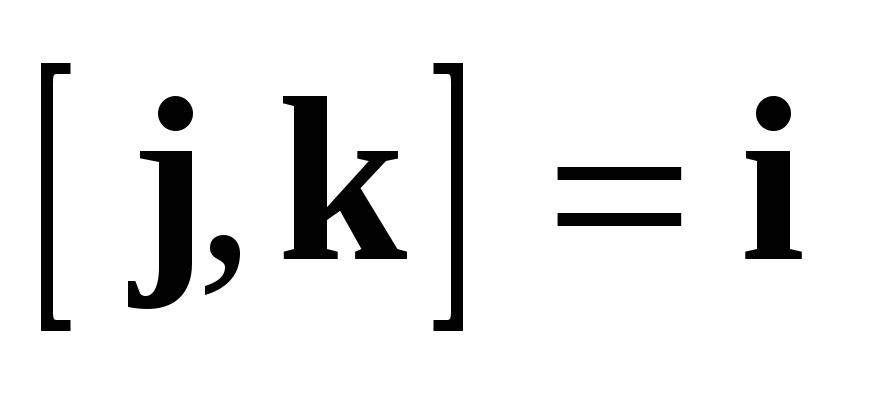 ,
, 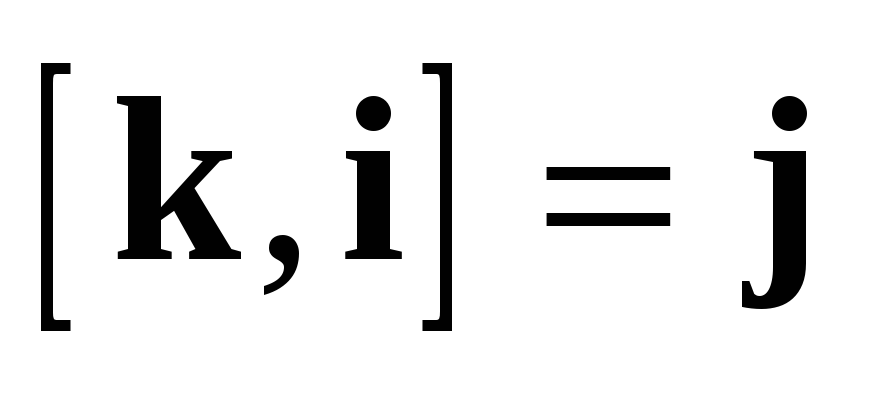 ,
(2.7)
,
(2.7)
а, привлекая свойство 1 и используя (2.7), получаем
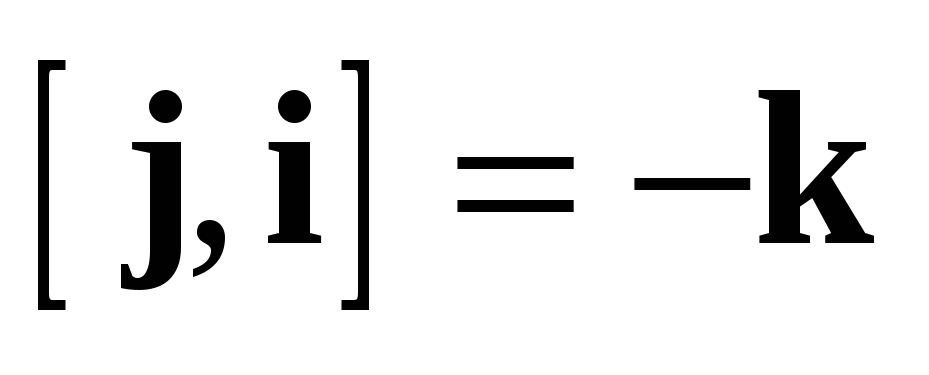 ,
, 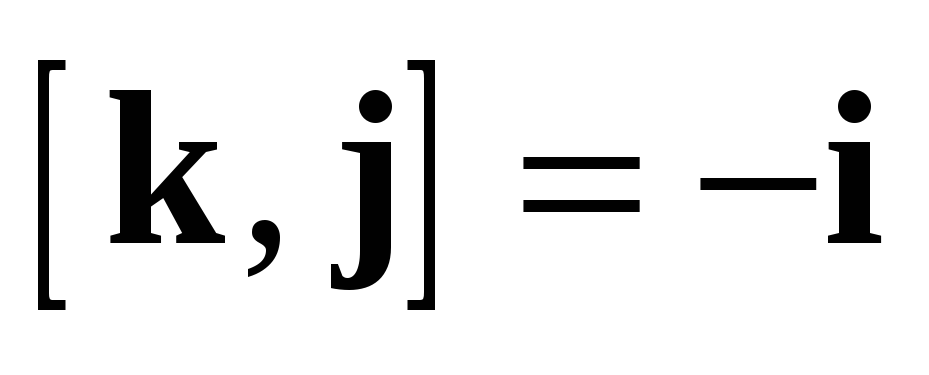 ,
, 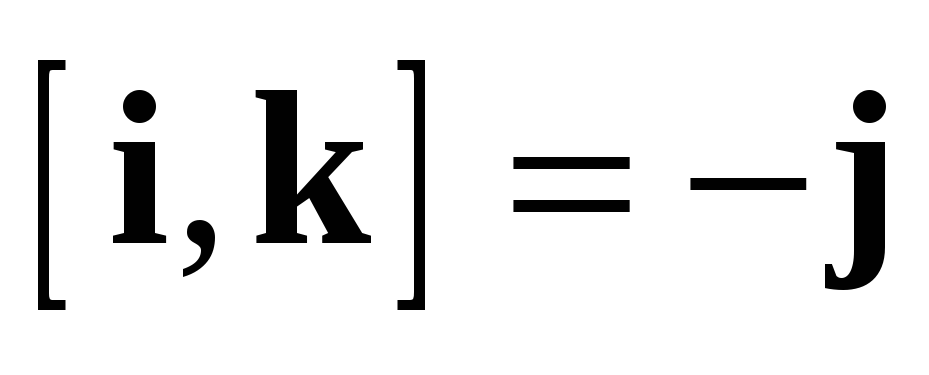 ,
,
Подставляя эти соотношения в (2.6), приходим к равенству
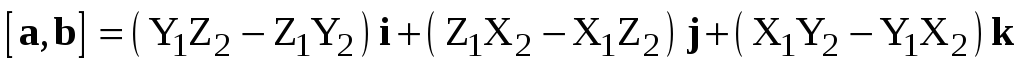
или
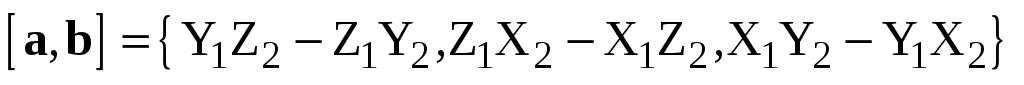 .
(2.8)
.
(2.8)
Следствие. Пусть  ,
, ,
, – декартов базис,
– декартов базис, 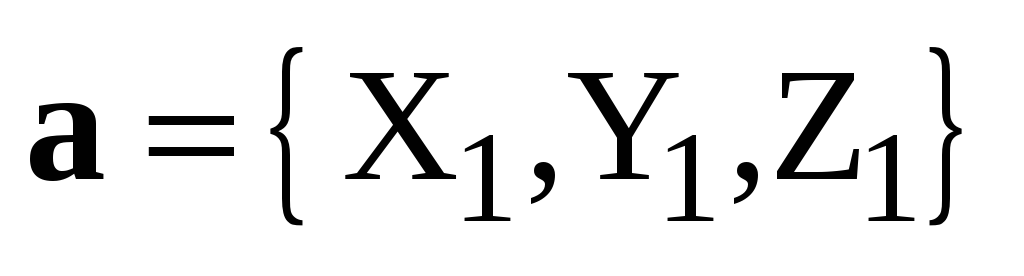 ,
, 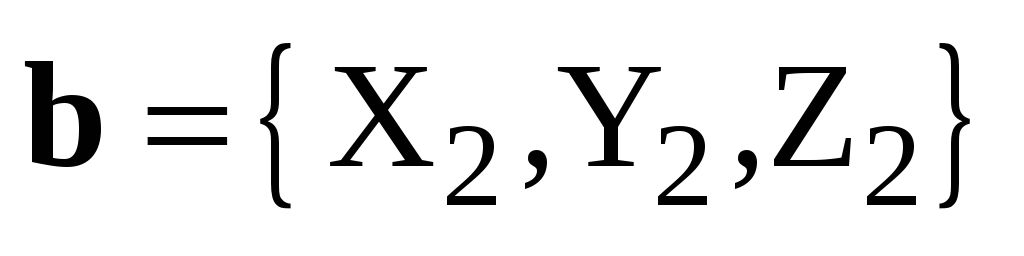 .
Векторы
.
Векторы  и
и  коллинеарны в том и только том случае,
когда
коллинеарны в том и только том случае,
когда 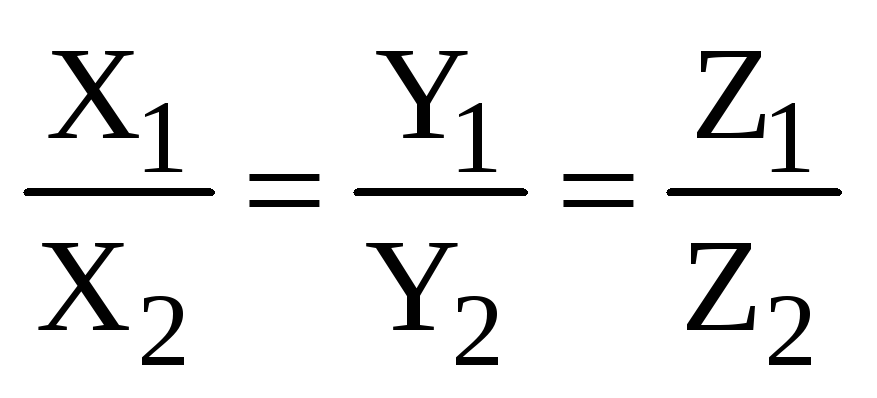 .
.
Действительно,  и
и  коллинеарны в том и только том случае
(см. теорему 4), когда
коллинеарны в том и только том случае
(см. теорему 4), когда 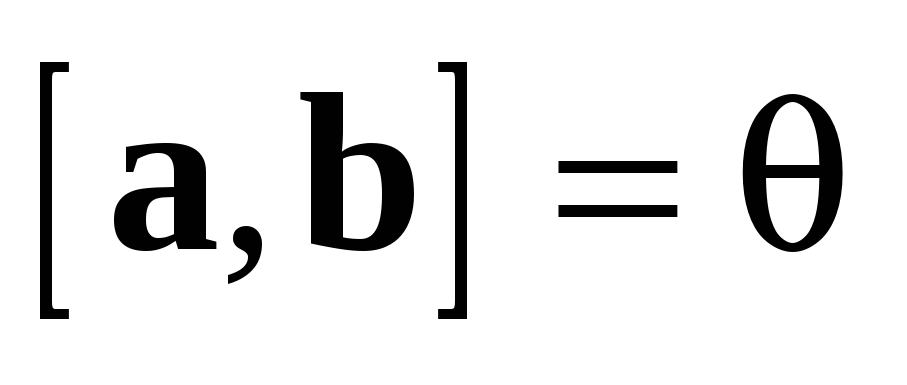 .
Учитывая теорему 5, получаем:
.
Учитывая теорему 5, получаем:  и
и  коллинеарны в том и только том случае,
когда
коллинеарны в том и только том случае,
когда
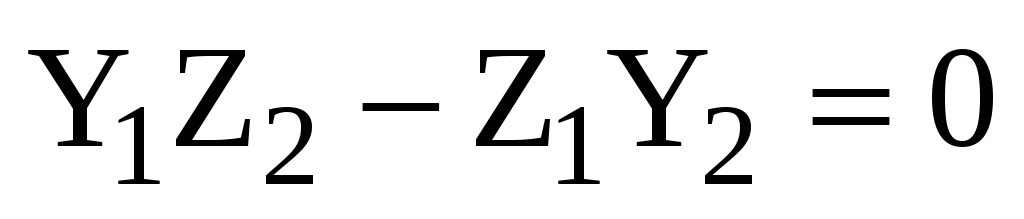 ,
, 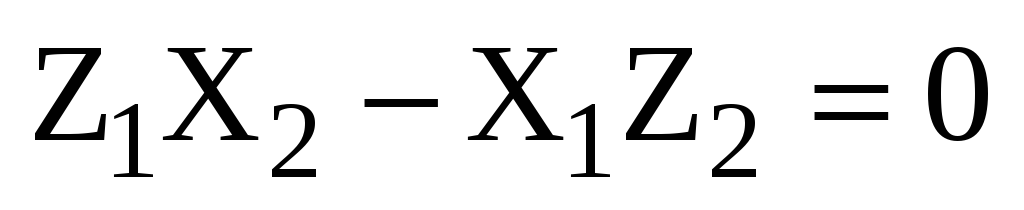 ,
, 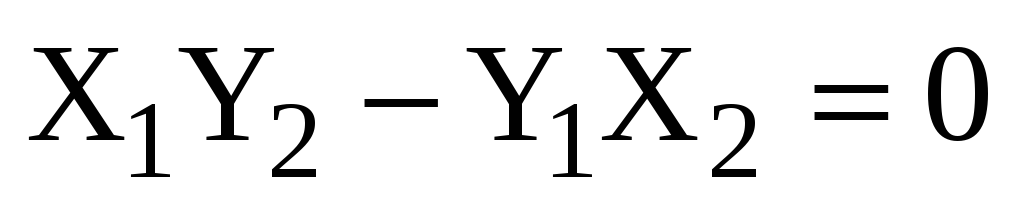 ,
,
или
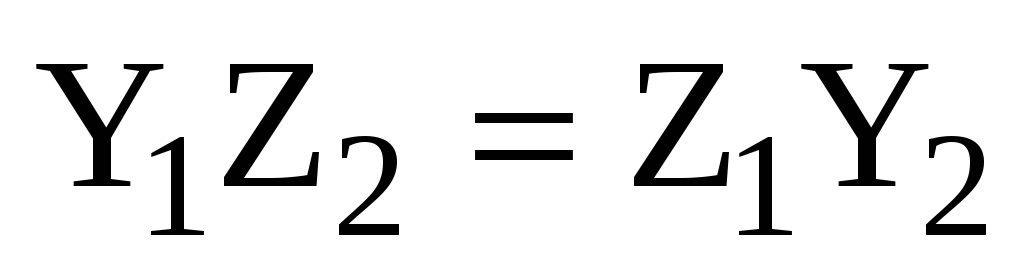 ,
, 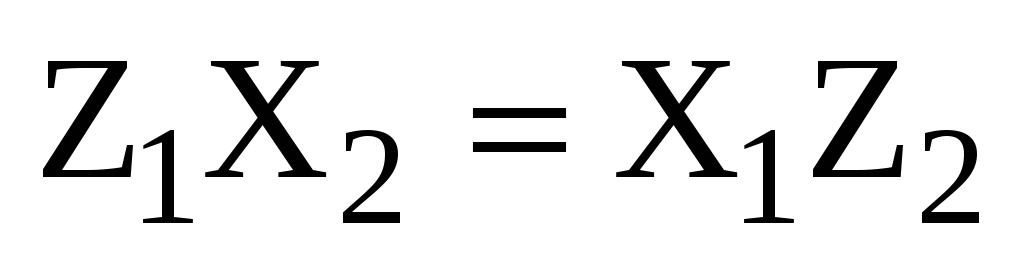 ,
, 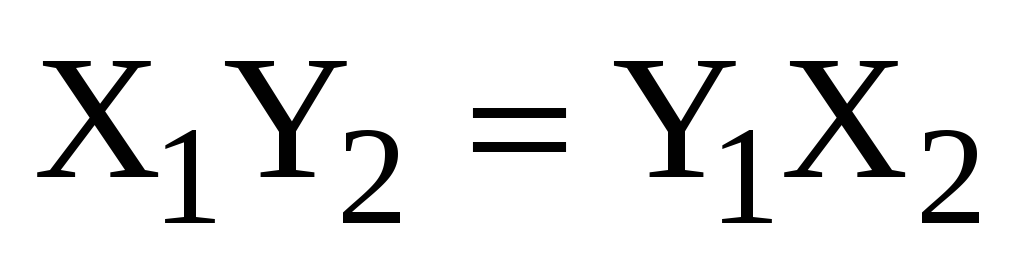 ,
(2.9)
,
(2.9)
или
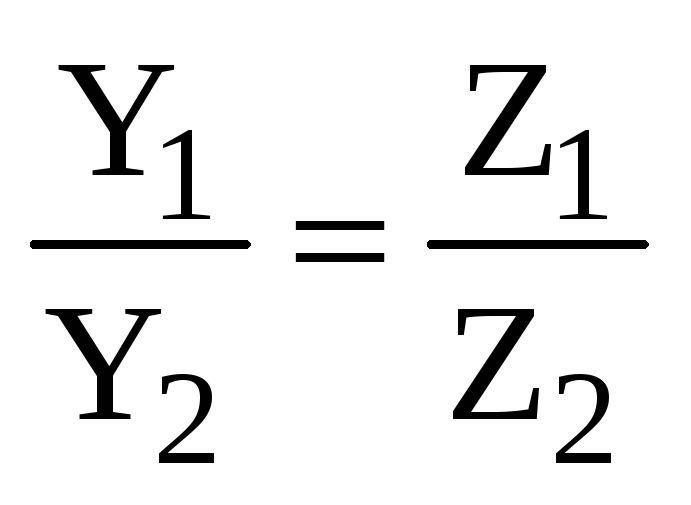 ,
, 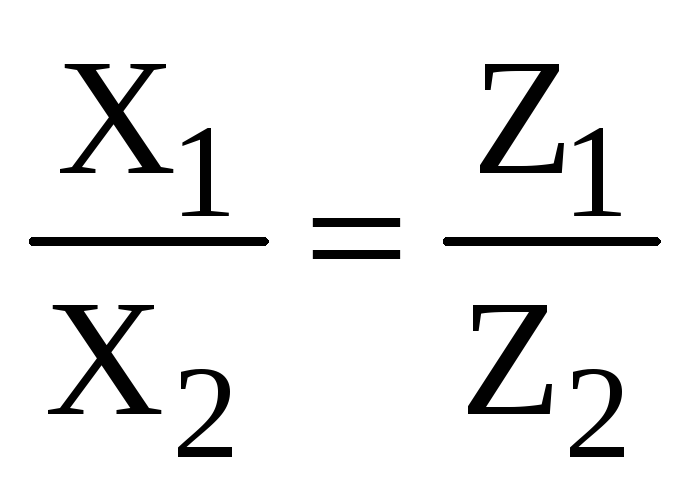 ,
, 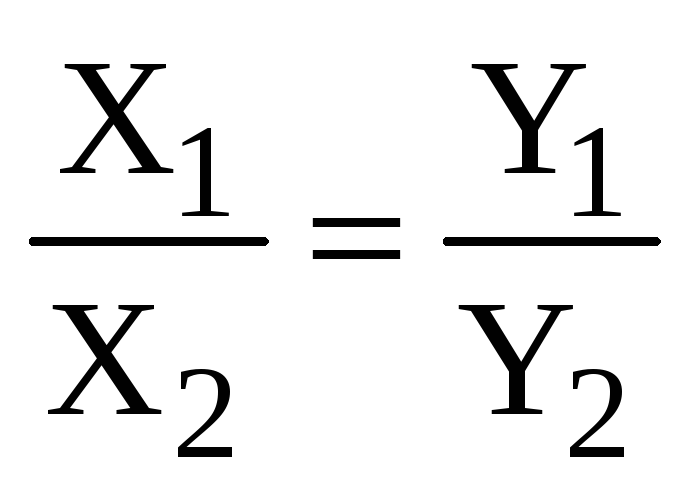 ,
,
или
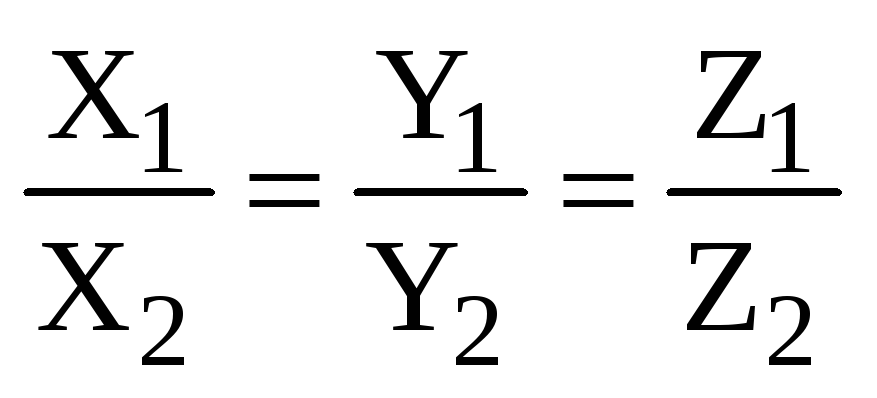 .
(2.10)
.
(2.10)
Замечание. Чтобы обойти трудность с равенством
нулю знаменателя в (2.10), договоримся в
том случае, когда  – координаты некоторых векторов
– координаты некоторых векторов  и
и  ,
понимать равенство (2.10) как три равенства
(2.9).
,
понимать равенство (2.10) как три равенства
(2.9).
1. 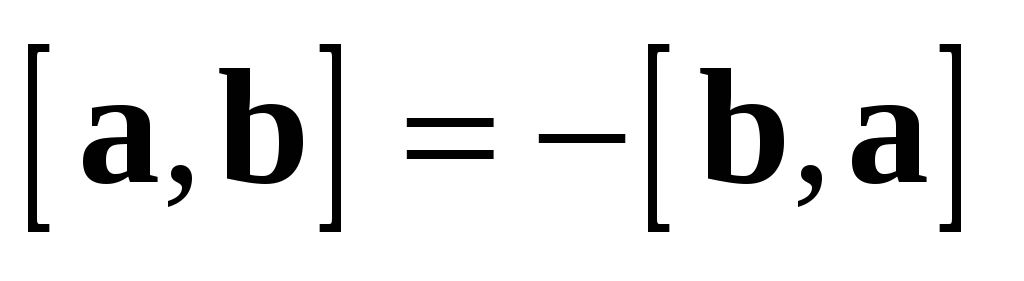 ;
;
2. 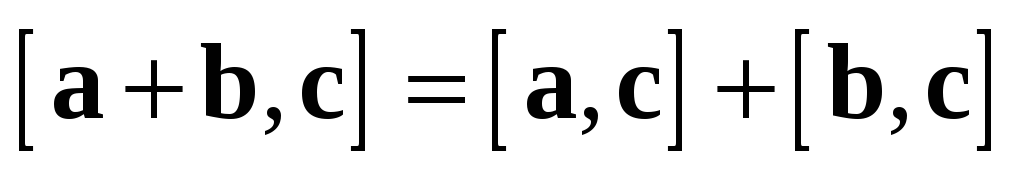 ;
;
3. 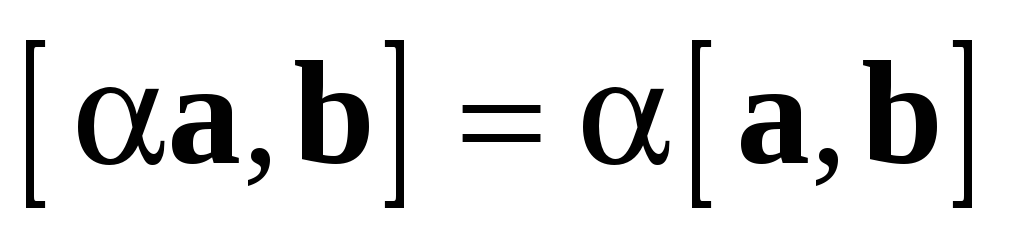 ;
;
4. Для любого 
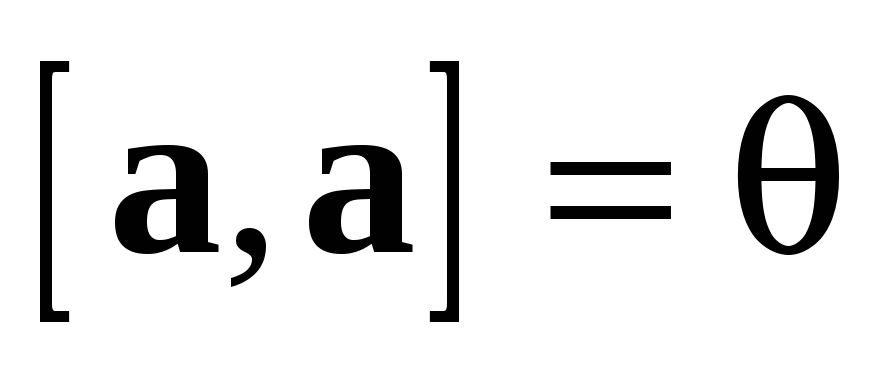 .
.
Доказательство свойства 1.
Обозначим 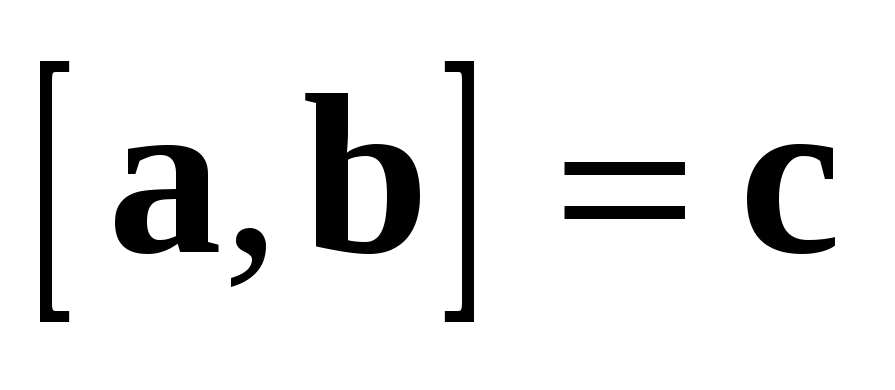 ,
, 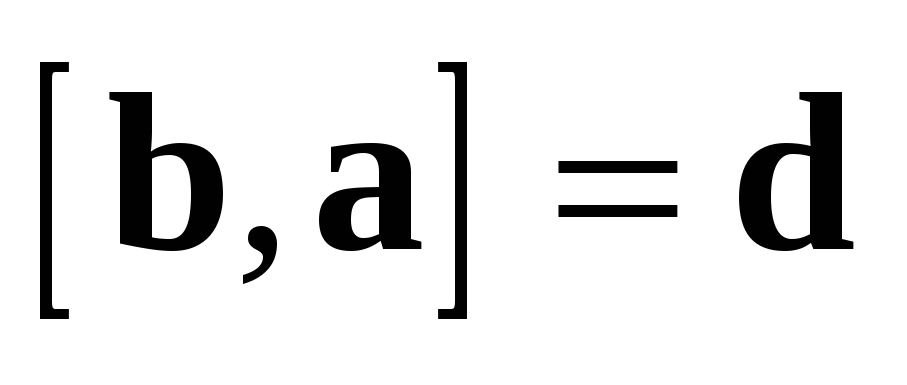 .
Нам нужно доказать, что справедливо
равенство между векторами:
.
Нам нужно доказать, что справедливо
равенство между векторами: 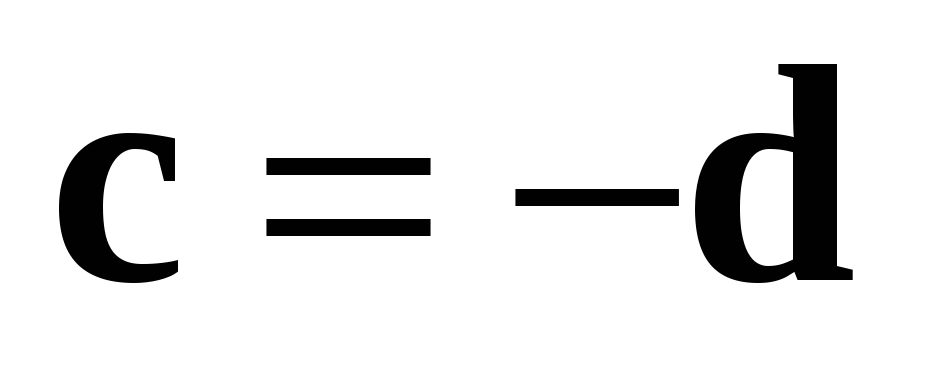
В соответствии с определением, данным
в лекции 1, нужно убедиться, что 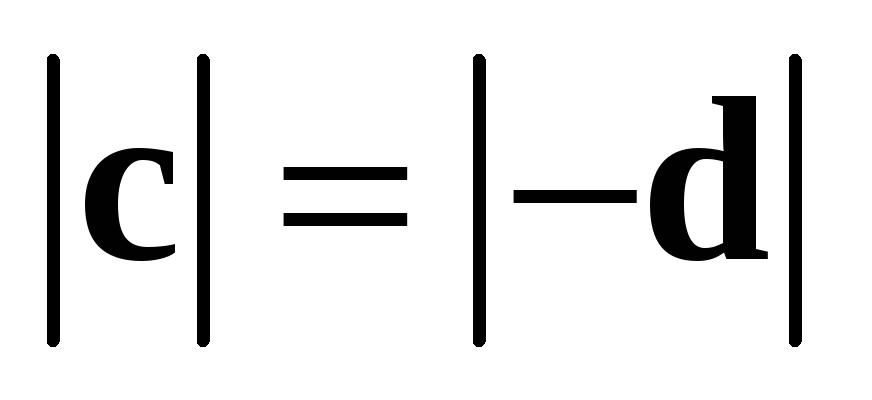 и направления
и направления  и
и 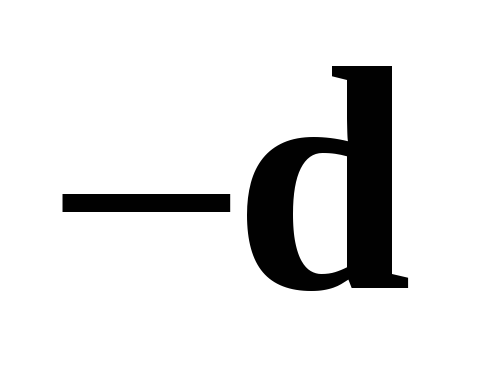 совпадают.
совпадают.
Из определения 5 получаем
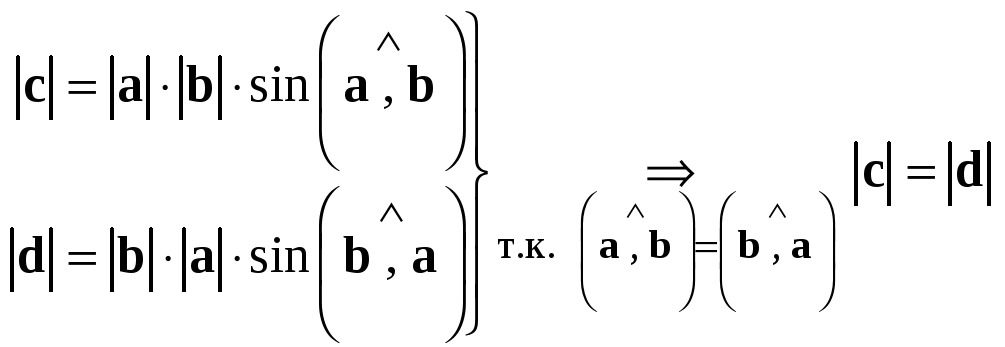 .
.
По определению 5  ,
,  и
и 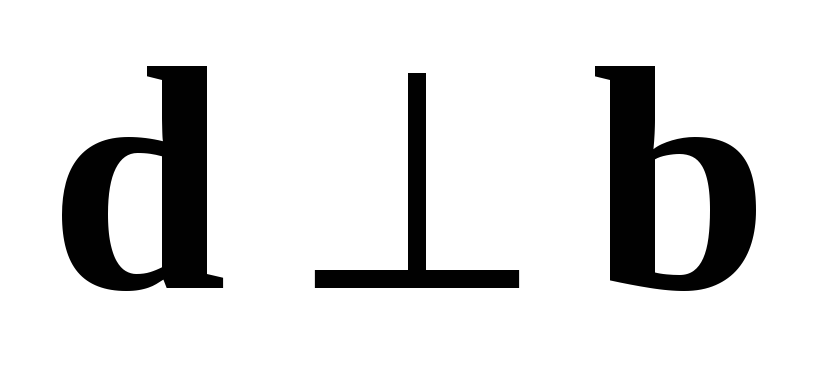 ,
, 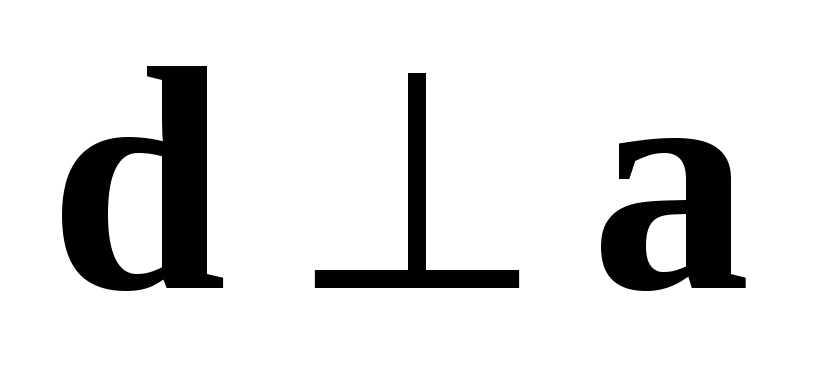 ,
следовательно,
,
следовательно,  и
и  оба перпендикулярны плоскости
оба перпендикулярны плоскости  ,
определяемой векторами
,
определяемой векторами  и
и  ,
следовательно,
,
следовательно,  и
и  коллинеарны.
коллинеарны.
Пусть  ,
,  и
и  приведены к одному началу. Так как они
составляют правую тройку, в соответствии
с определением 3 с конца вектора
приведены к одному началу. Так как они
составляют правую тройку, в соответствии
с определением 3 с конца вектора  кратчайший поворот от
кратчайший поворот от  к
к  кажется совершающимся против хода
часовой стрелки. Тогда для любого
вектора, расположенного по ту же сторону
от
кажется совершающимся против хода
часовой стрелки. Тогда для любого
вектора, расположенного по ту же сторону
от  ,
что и вектор
,
что и вектор  ,
кратчайший поворот от
,
кратчайший поворот от  к
к  кажется совершающимся по
ходу часовой стрелки, следовательно,
вектор
кажется совершающимся по
ходу часовой стрелки, следовательно,
вектор  расположен по другую сторону от плоскости
расположен по другую сторону от плоскости  .
Учитывая уже установленную коллинеарность
.
Учитывая уже установленную коллинеарность  и
и  ,
получаем
,
получаем 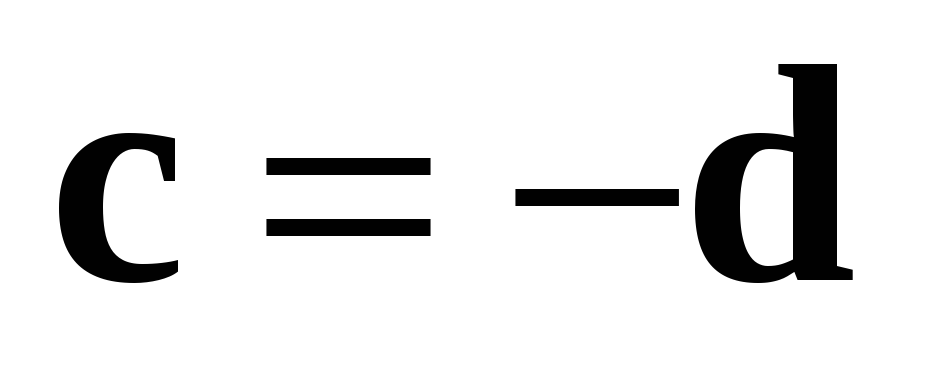 .
.
Свойство 2 примем без доказательства.
Доказательство свойства 3.
Обозначим 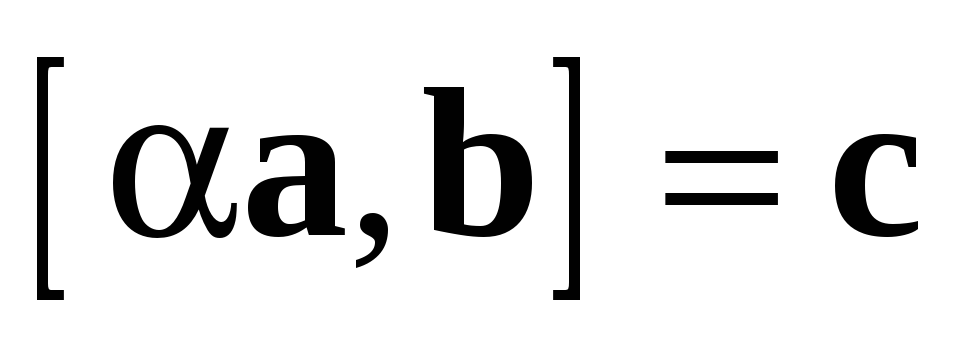 ,
, 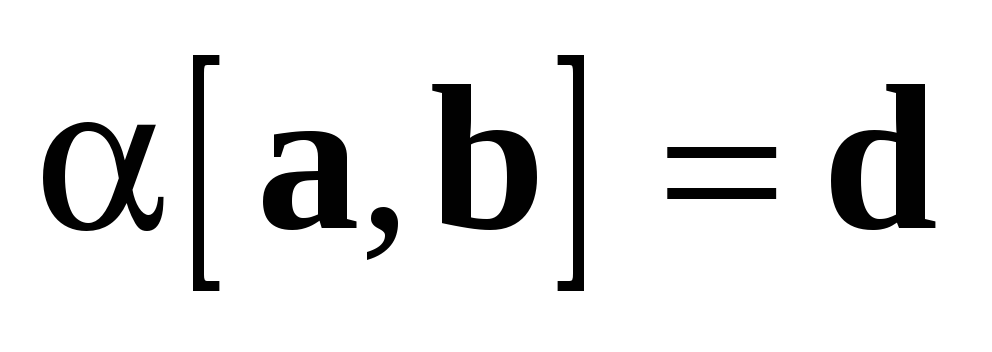 .
.
Случай 1. 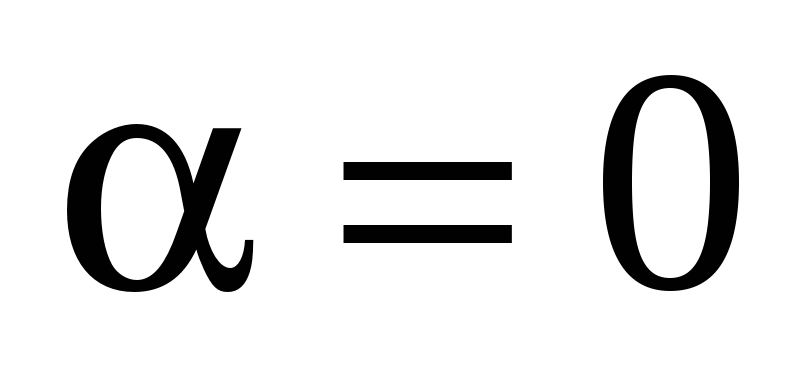 .
Тогда
.
Тогда 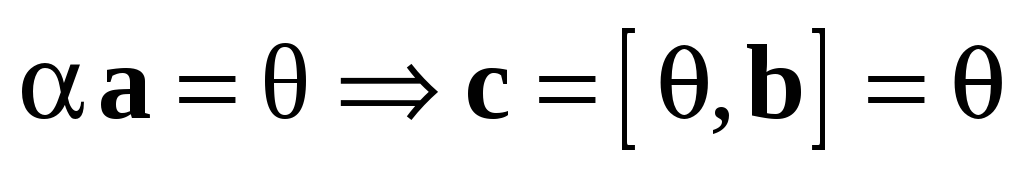 (так как
(так как 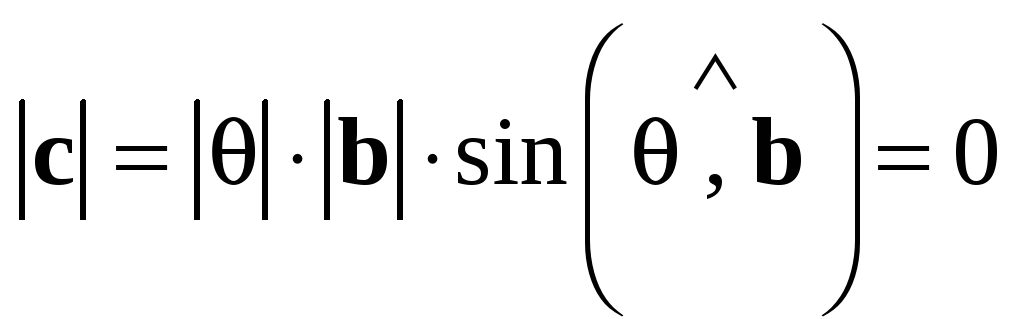 ),
при этом
),
при этом 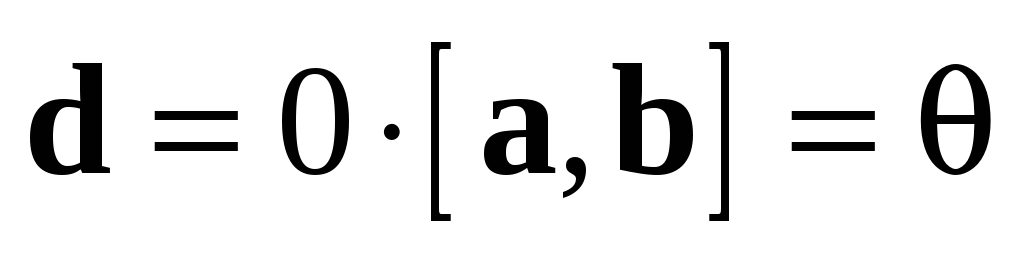 ,
следовательно,
,
следовательно, 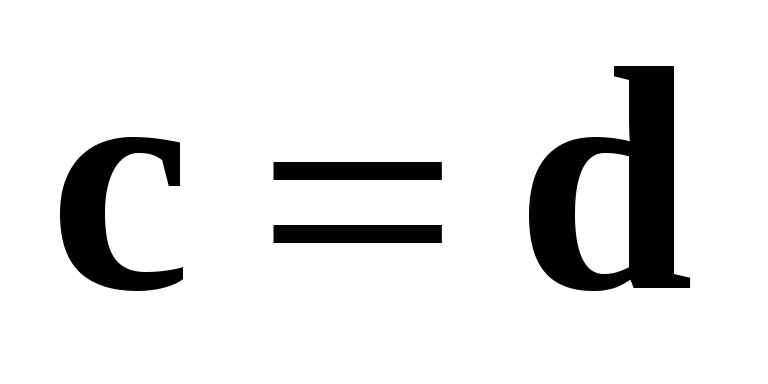 .
.
Случай 2. 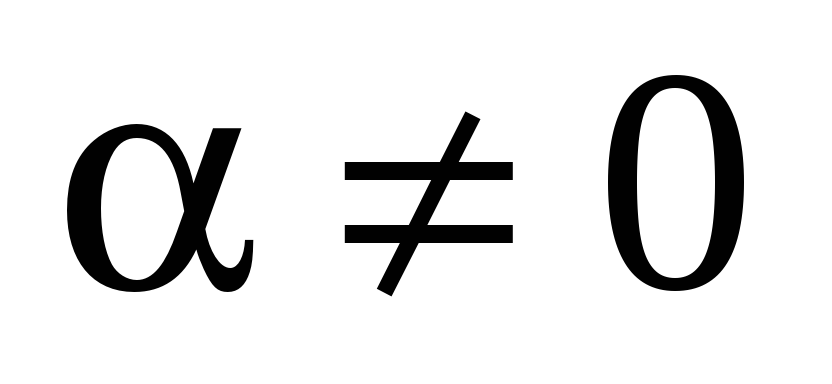 .
.
а) Векторы  и
и  коллинеарны. Тогда по теореме 4
коллинеарны. Тогда по теореме 4 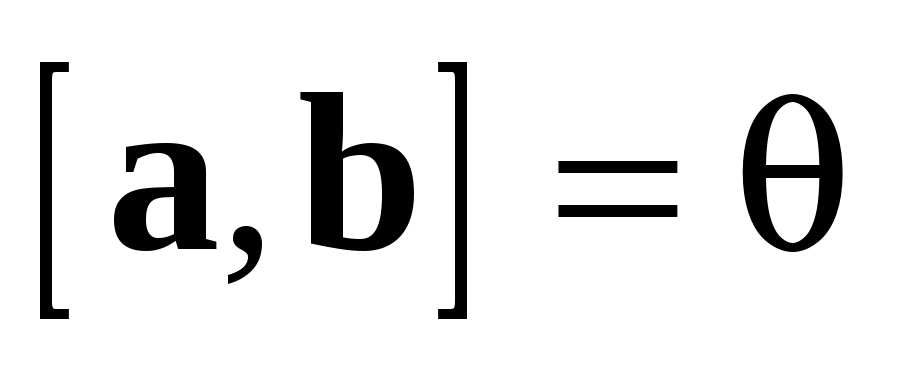 и
и 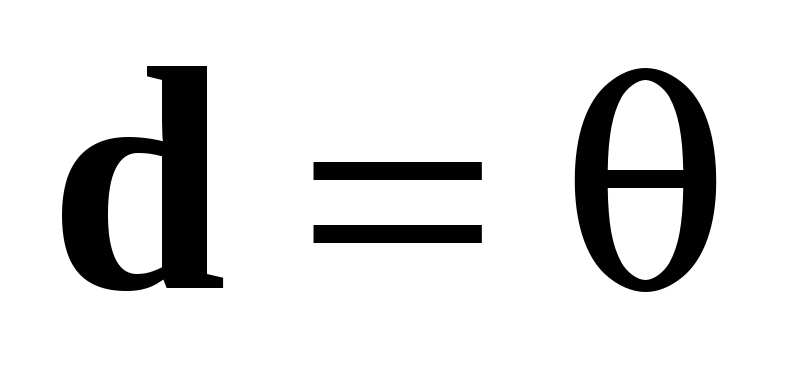 ;
;  коллинеарен
коллинеарен  (как произведение вектора
(как произведение вектора  на число), следовательно,
на число), следовательно,  коллинеарен
коллинеарен  ,
и по теореме 4
,
и по теореме 4 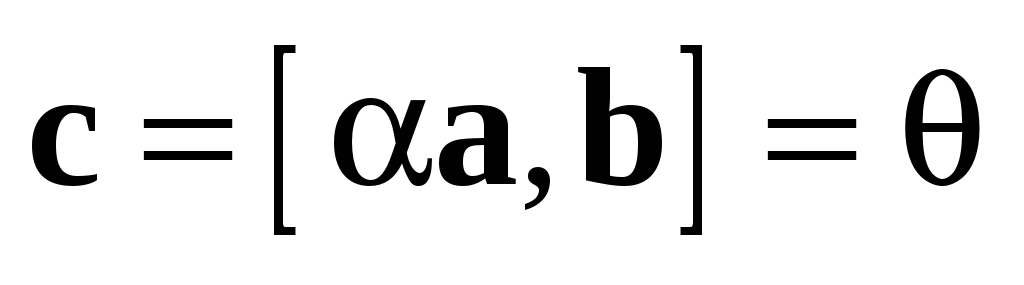 ,
значит,
,
значит,  .
.
б) Векторы  и
и  не коллинеарны. Пусть
не коллинеарны. Пусть  .
Тогда
.
Тогда
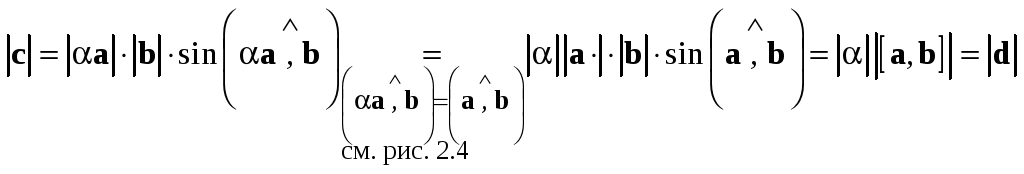
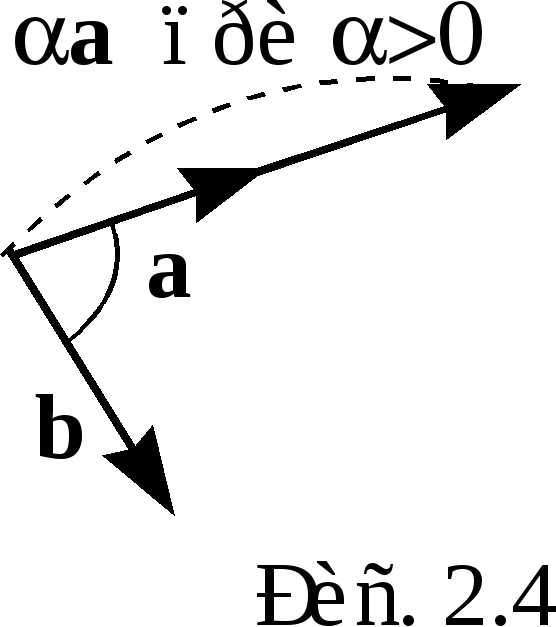 .
.
Имеем 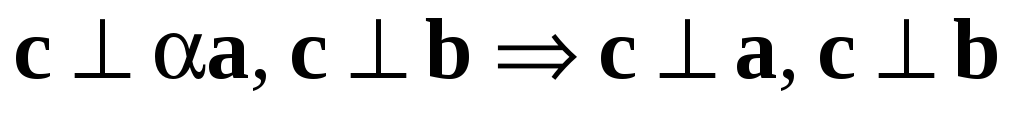 ,
следовательно,
,
следовательно,  коллинеарен
коллинеарен 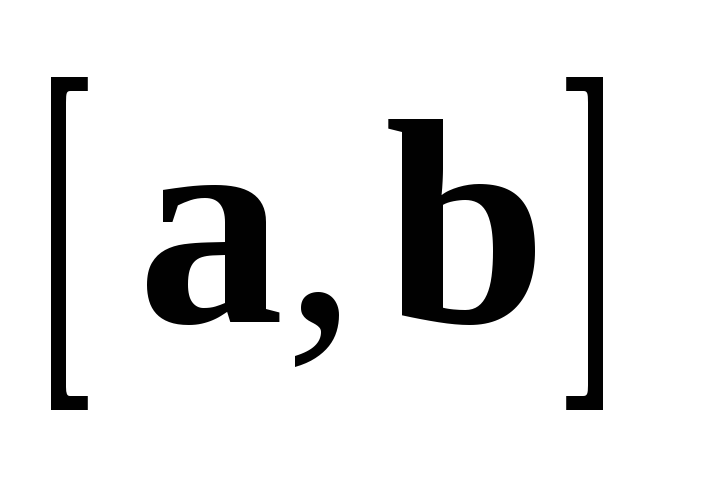 .
С другой стороны,
.
С другой стороны, 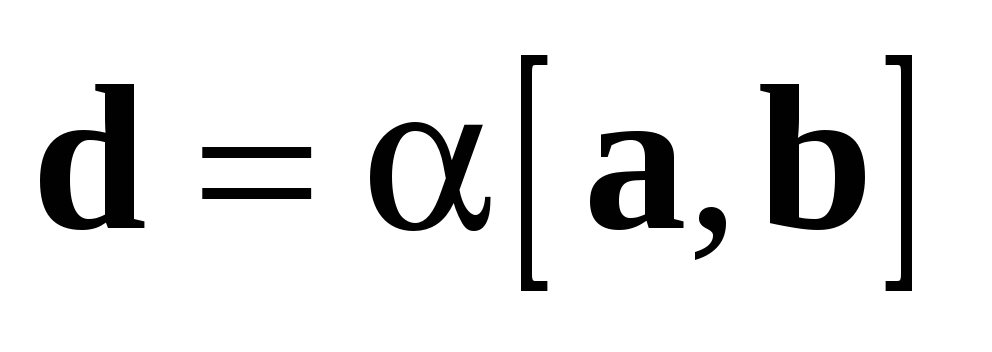 ,
поэтому
,
поэтому  коллинеарен
коллинеарен 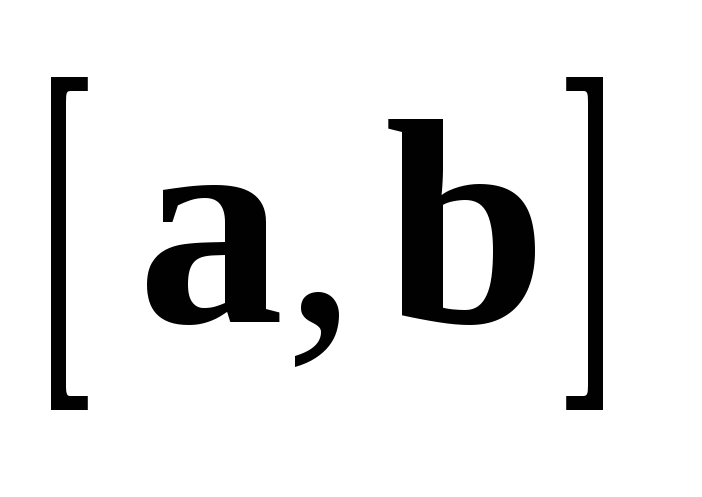 .
Таким образом,
.
Таким образом,  и
и  коллинеарны.
коллинеарны.
Так как 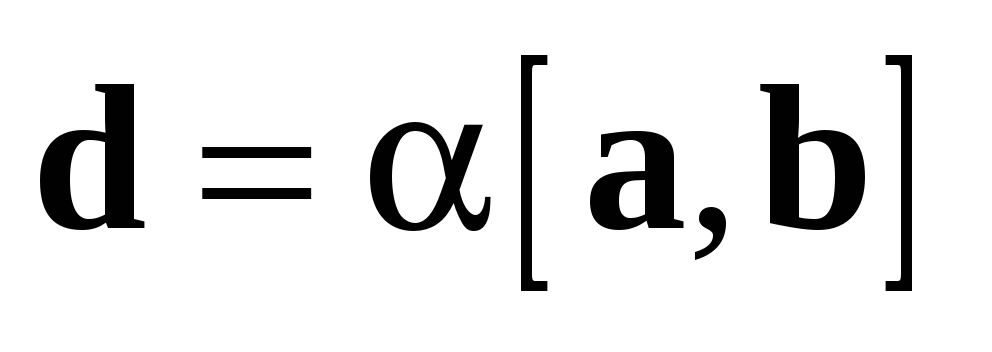 ,
а
,
а  ,
то направление
,
то направление  совпадает с направлением вектора
совпадает с направлением вектора  .
.
Направление 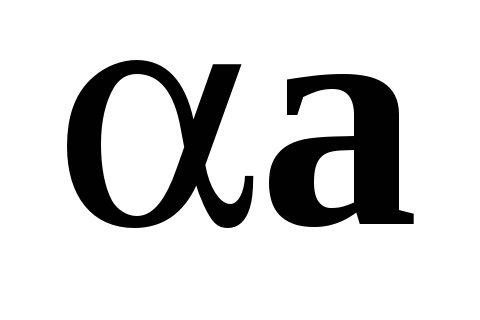 совпадает с направлением
совпадает с направлением  ,
а
,
а 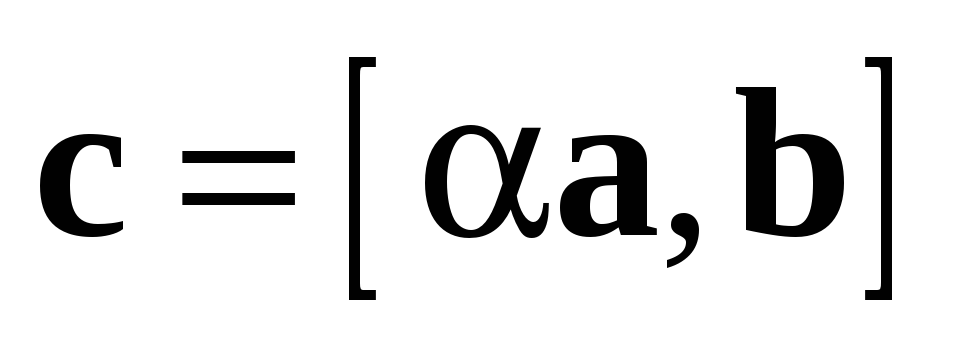 ,
следовательно, направление
,
следовательно, направление  совпадает с направлением
совпадает с направлением  .
.
Итак,  и
и  коллинеарны и направления их совпадают,
т.е.
коллинеарны и направления их совпадают,
т.е.  и свойство 3 в этом случае справедливо.
и свойство 3 в этом случае справедливо.
Пусть 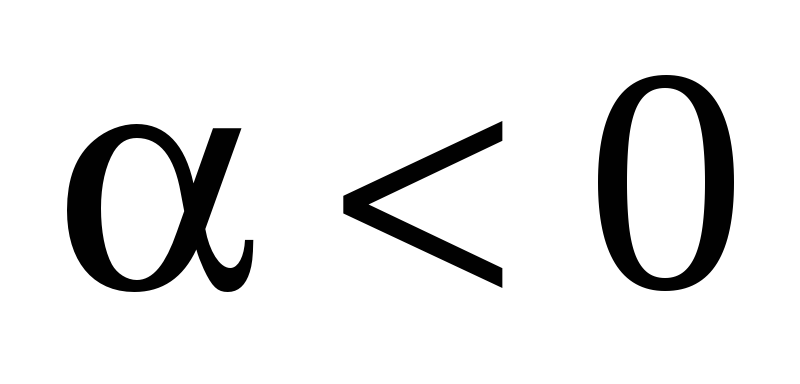 .
Тогда
.
Тогда
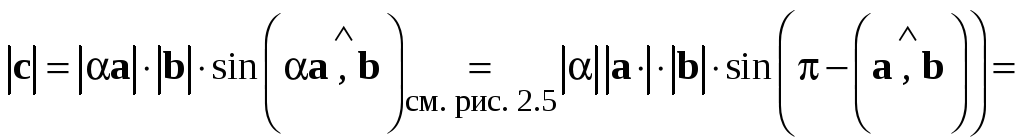
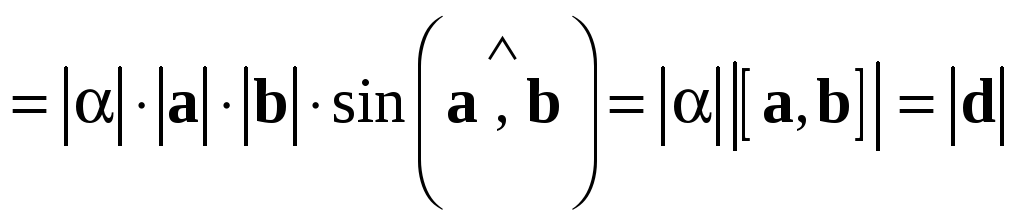 .
.
И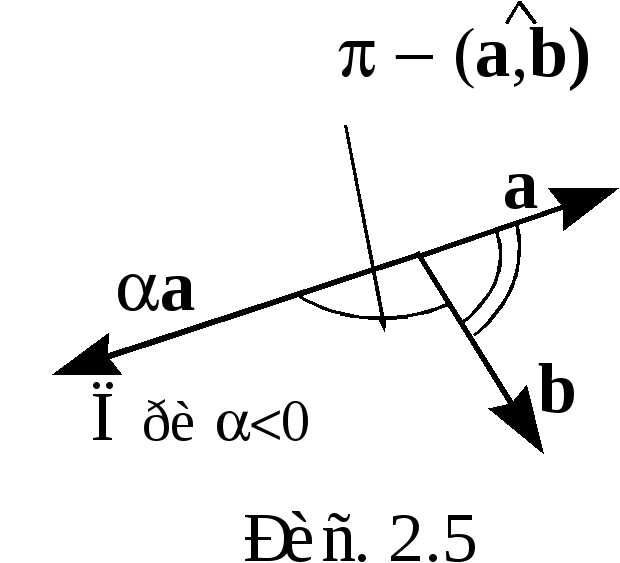 меем
меем  и
и  коллинеарен
коллинеарен 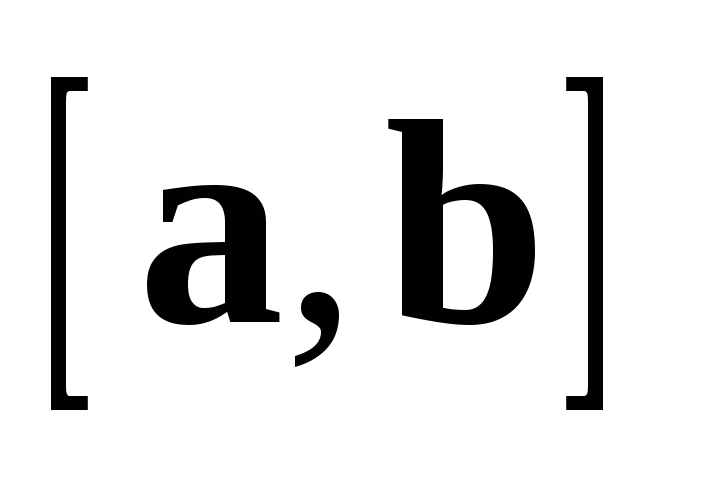 .
С другой стороны
.
С другой стороны 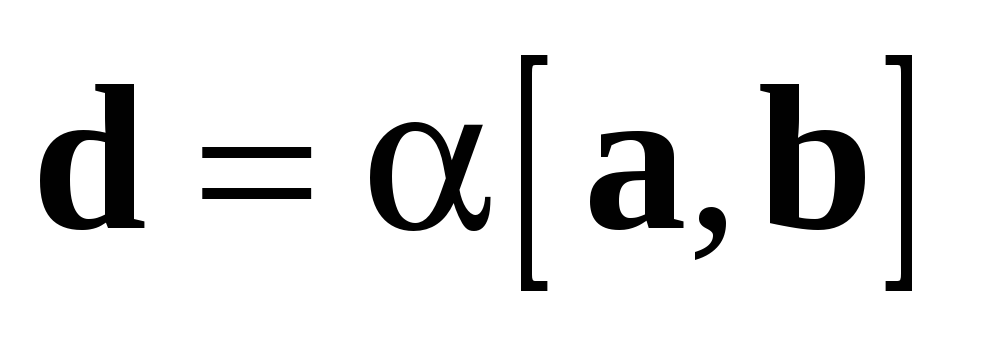 и
и  коллинеарен вектору
коллинеарен вектору 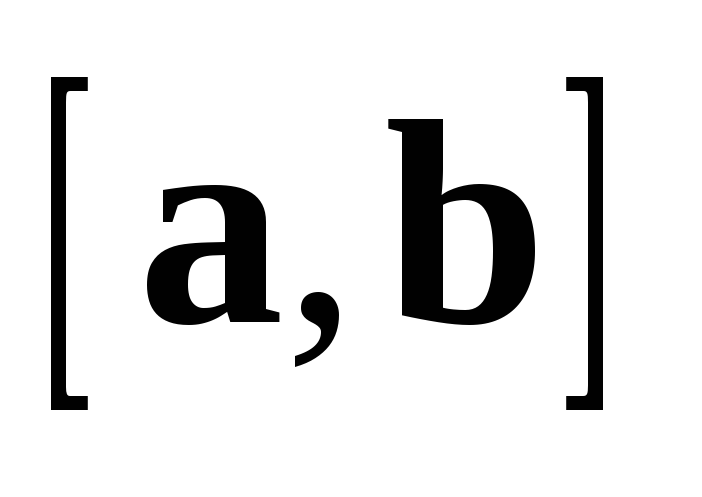 .
Таким образом,
.
Таким образом,  и
и  коллинеарны (и коллинеарны вектору
коллинеарны (и коллинеарны вектору 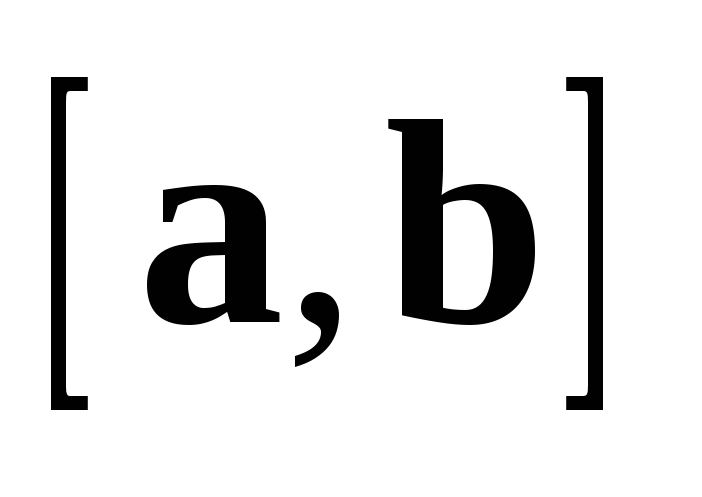 ).
).
Вектор 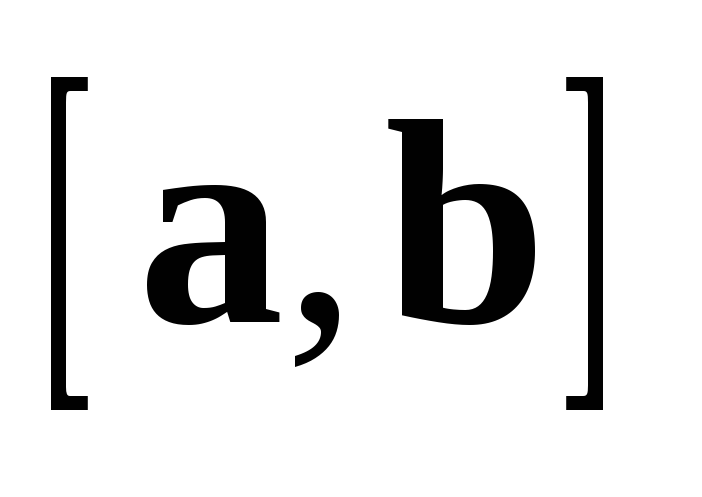 в соответствии с определениями 5 и 3
направлен таким образом, что с конца
в соответствии с определениями 5 и 3
направлен таким образом, что с конца 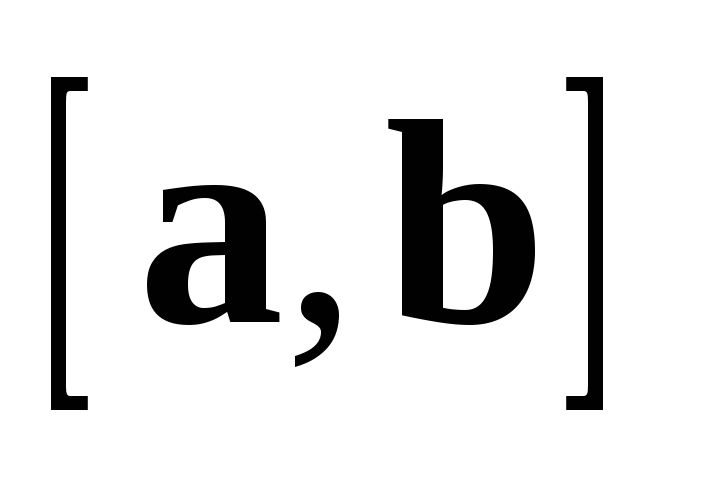 кратчайший поворот от
кратчайший поворот от  к
к  кажется совершающимся против хода
часовой стрелки, тогда (
кажется совершающимся против хода
часовой стрелки, тогда (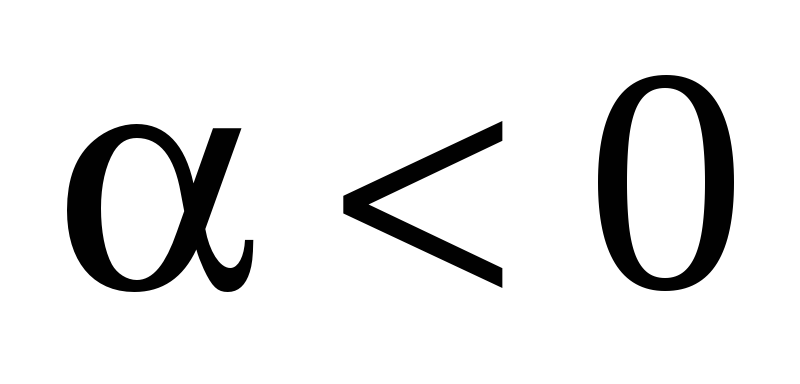 ),
с конца
),
с конца 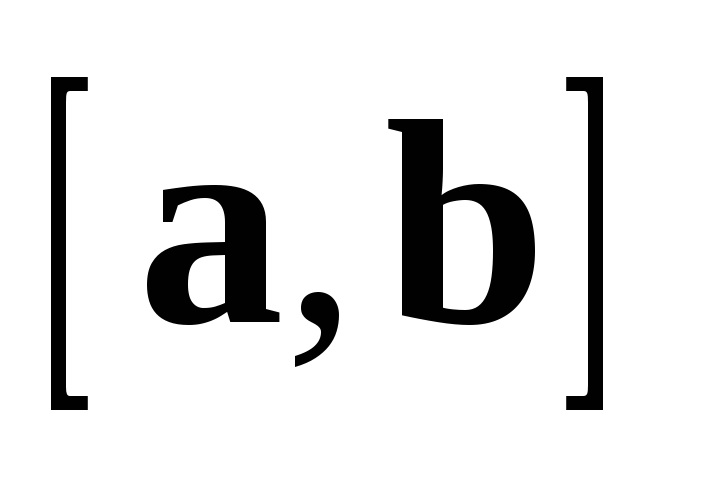 кратчайший поворот от
кратчайший поворот от 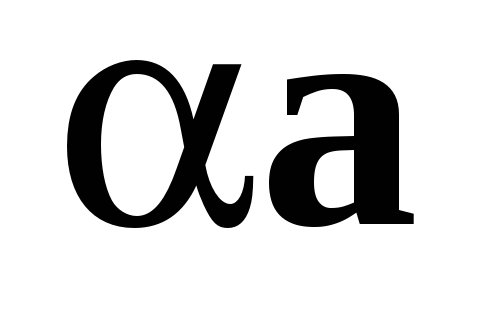 к
к  кажется совершающимся по ходу часовой
стрелки, следовательно, векторы
кажется совершающимся по ходу часовой
стрелки, следовательно, векторы  и
и 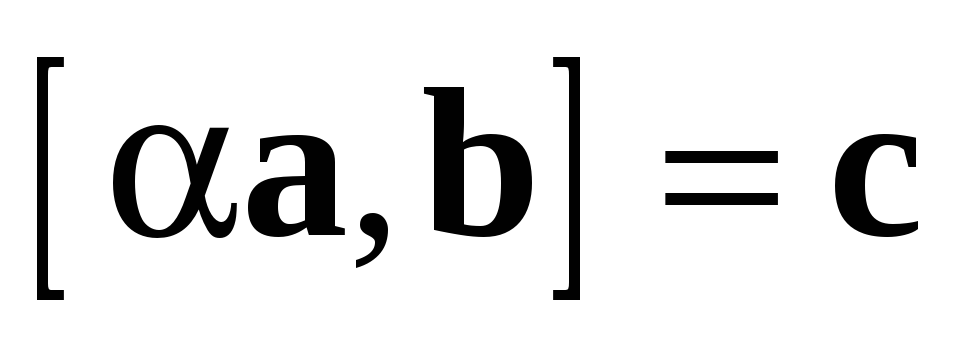 имеют противоположное направление.
имеют противоположное направление.
Вектор  ,
равный
,
равный  ,
тоже имеет направление, противоположное
направлению
,
тоже имеет направление, противоположное
направлению 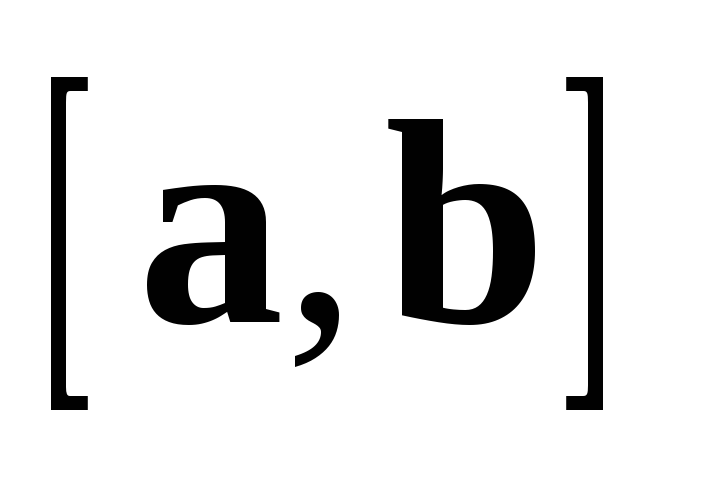 ,
таким образом,
,
таким образом,  и
и  направлены одинаково.
направлены одинаково.
Учитывая доказанное ранее равенство 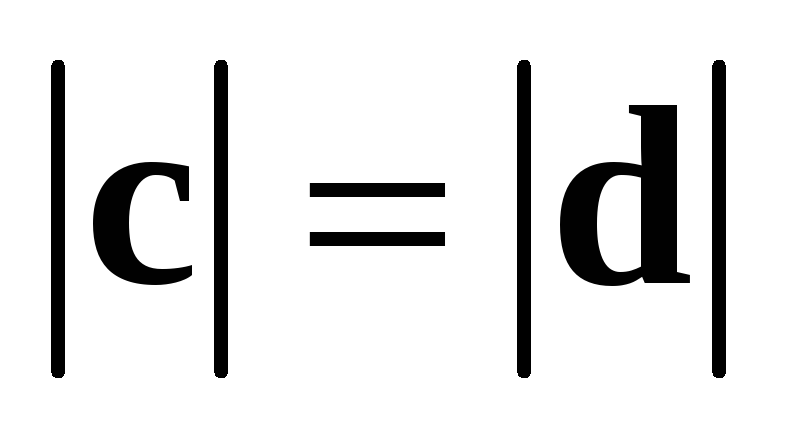 и коллинеарность
и коллинеарность  и
и  ,
заключаем, что
,
заключаем, что 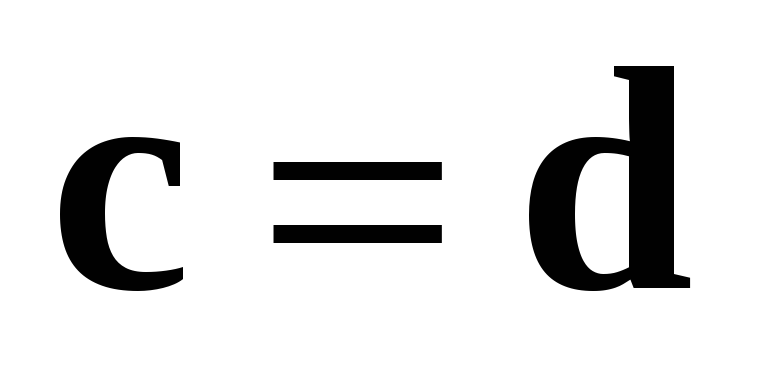 ,
– свойство 3 справедливо и в этом случае.
,
– свойство 3 справедливо и в этом случае.
Доказательство свойства 4.
Так как любой вектор  коллинеарен сам себе, то свойство 4, т.е.
равенство
коллинеарен сам себе, то свойство 4, т.е.
равенство 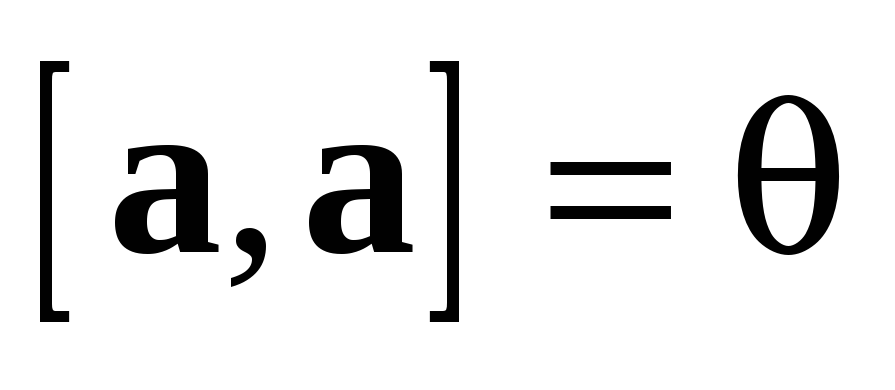 ,
следует из теоремы 4.
,
следует из теоремы 4.
Замечание. Свойства 2 и 3 справедливы также в форме:
 ).
). 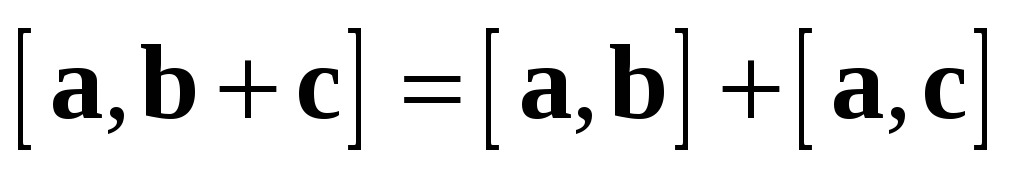 ;
;
 ).
). 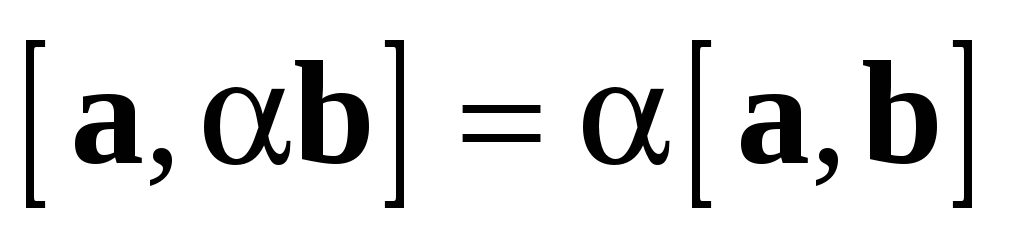 .
.
В самом деле, докажем, например,  :
:
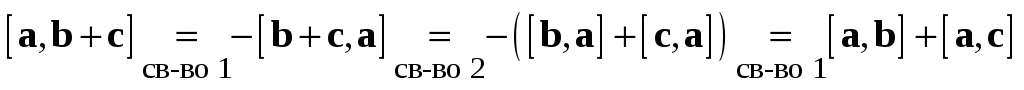 .
.
Аналогично обосновывается  .
.
Доказанные алгебраические свойства дают возможность, перемножая векторно линейные комбинации векторов, группировать коэффициенты, как при перемножении многочленов.
Теорема 5. Пусть , ,
, – декартов базис,
– декартов базис, 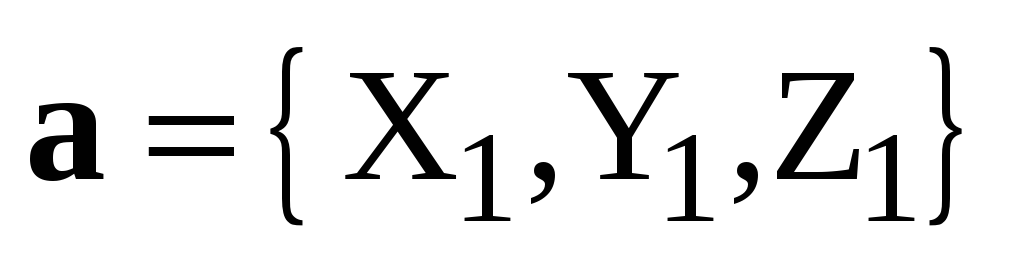 ,
, 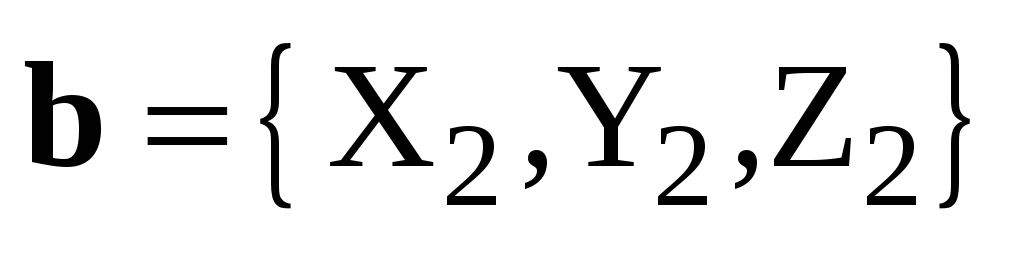 .
Тогда
.
Тогда 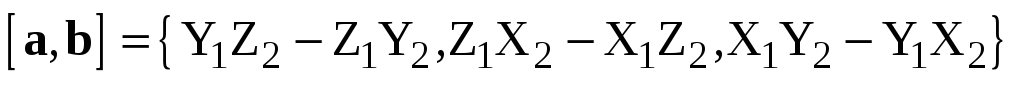 .
.
Доказательство. Имеем
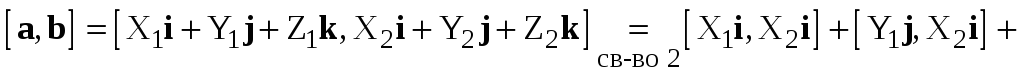
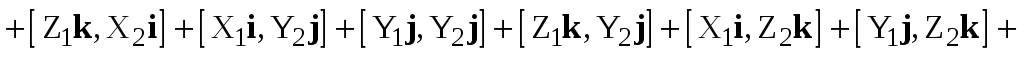
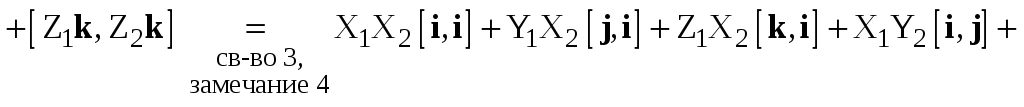
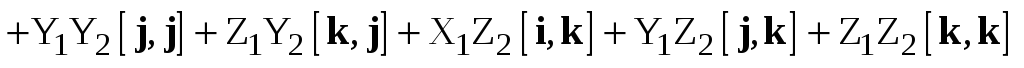 .
(2.6)
.
(2.6)
Найдем всевозможные векторные произведения базисных векторов.
В силу свойства 4 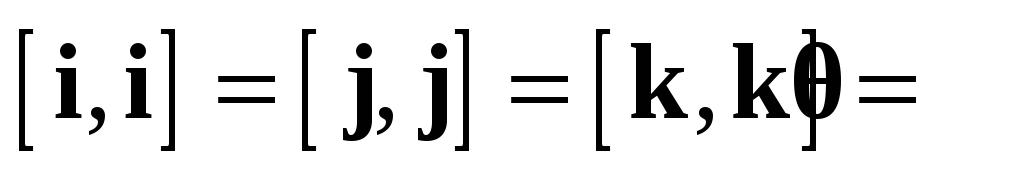 .
.
Так как базис  ,
, ,
, декартов и длина каждого базисного
вектора равна единице, каждое из
оставшихся шести векторных произведений
либо вектор базиса, либо противоположный
ему. Векторы базиса образуют правую
тройку, поэтому
декартов и длина каждого базисного
вектора равна единице, каждое из
оставшихся шести векторных произведений
либо вектор базиса, либо противоположный
ему. Векторы базиса образуют правую
тройку, поэтому
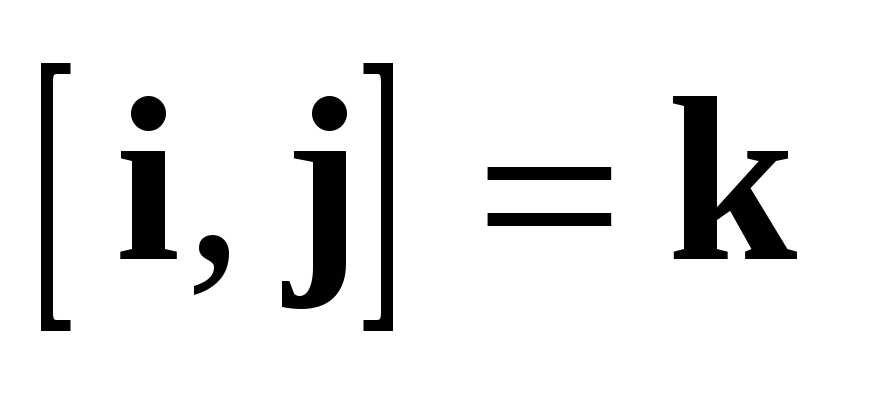 ,
, 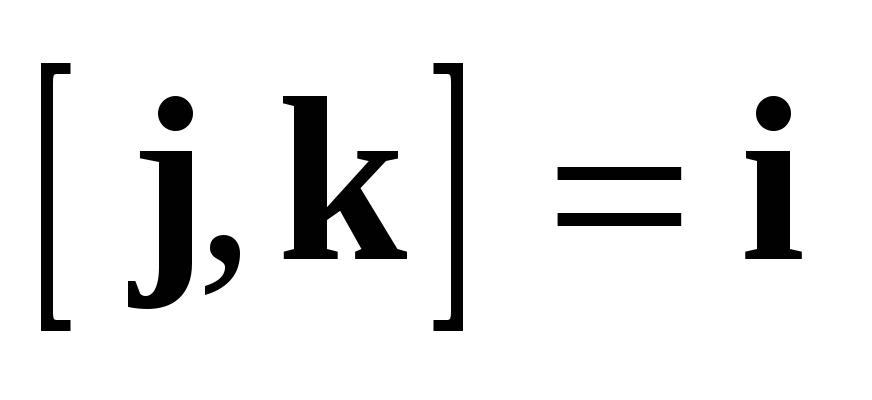 ,
, 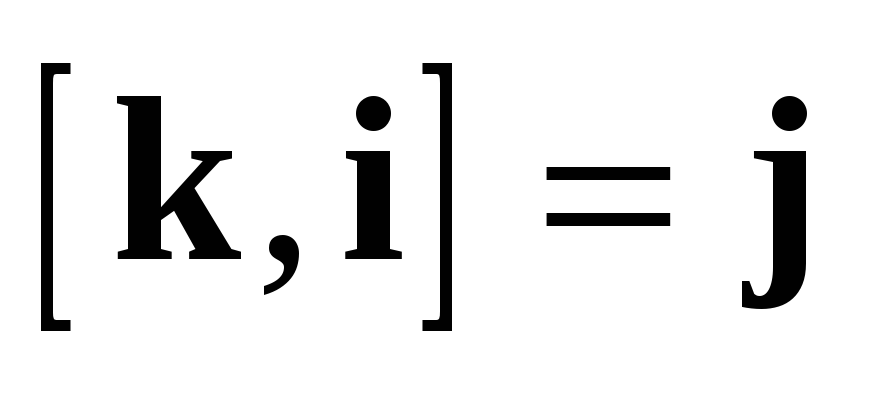 ,
(2.7)
,
(2.7)
а, привлекая свойство 1 и используя (2.7), получаем
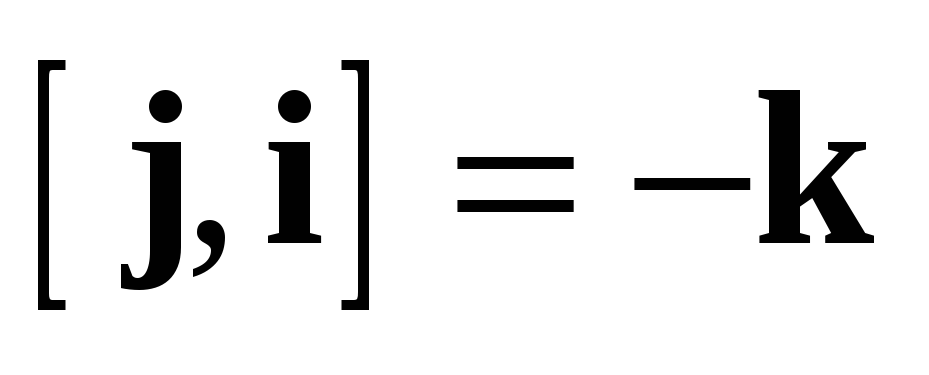 ,
, 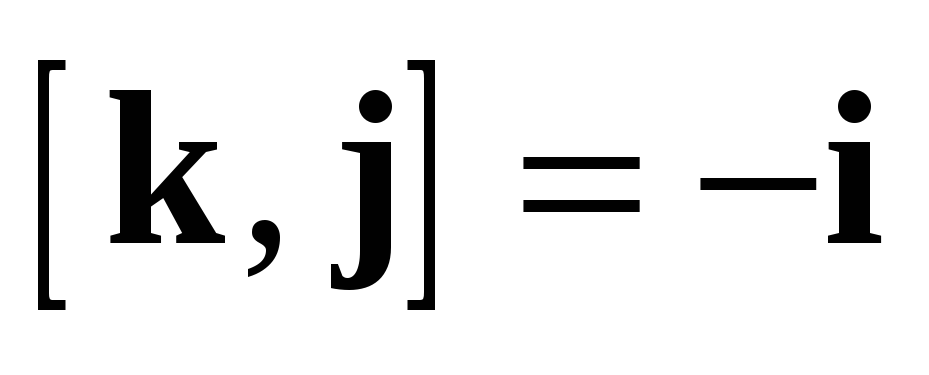 ,
, 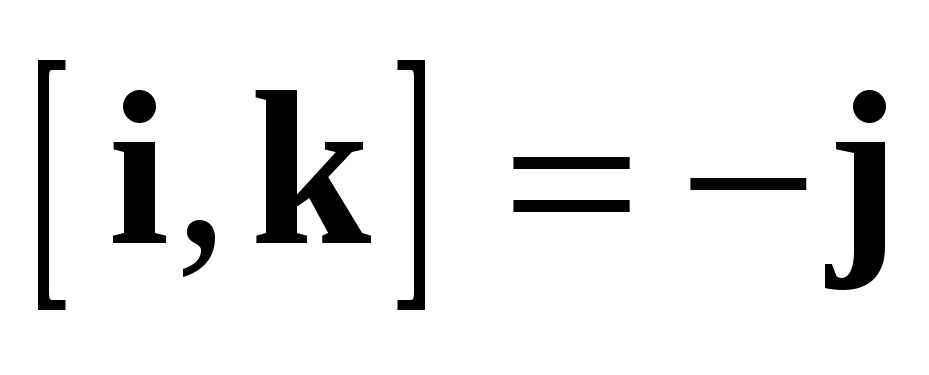 ,
,
Подставляя эти соотношения в (2.6), приходим к равенству
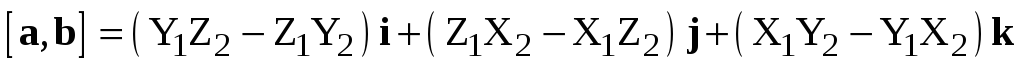
или
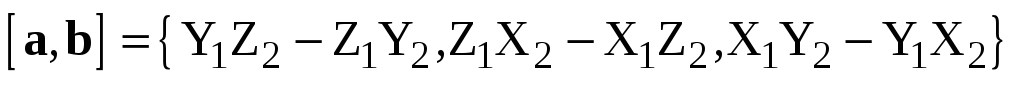 .
(2.8)
.
(2.8)
Следствие. Пусть  ,
, ,
, – декартов базис,
– декартов базис, 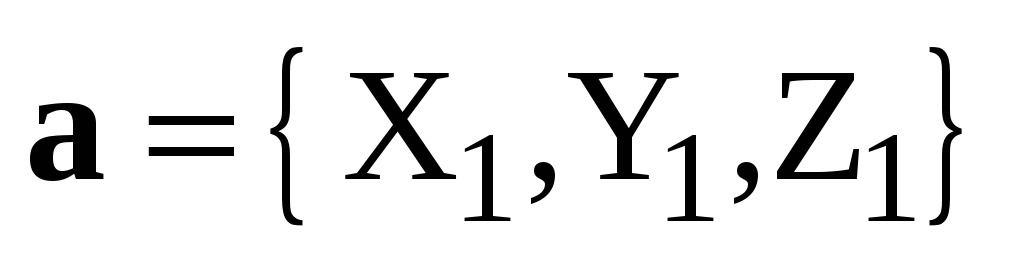 ,
, 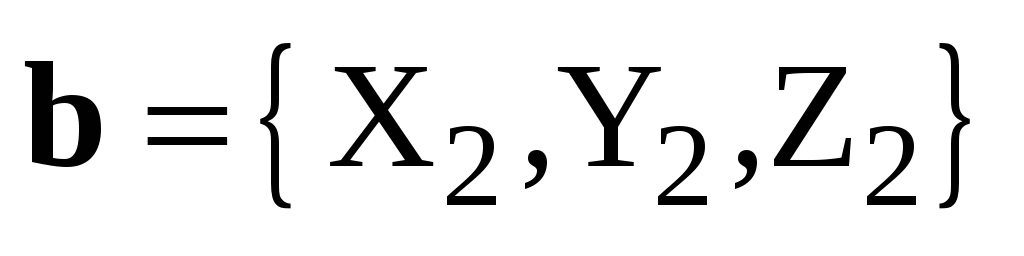 .
Векторы
.
Векторы  и
и  коллинеарны в том и только том случае,
когда
коллинеарны в том и только том случае,
когда 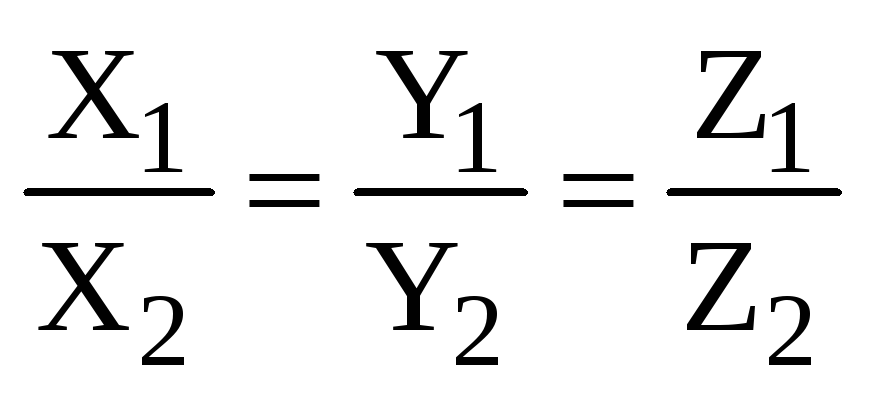 .
.
Действительно,  и
и  коллинеарны в том и только том случае
(см. теорему 4), когда
коллинеарны в том и только том случае
(см. теорему 4), когда 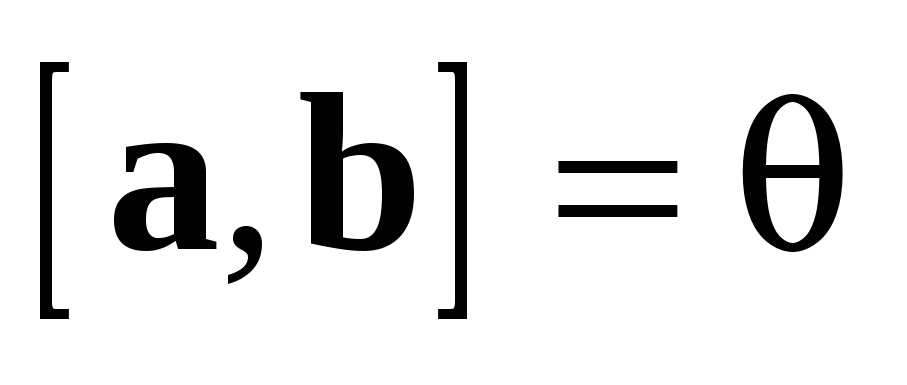 .
Учитывая теорему 5, получаем:
.
Учитывая теорему 5, получаем:  и
и  коллинеарны в том и только том случае,
когда
коллинеарны в том и только том случае,
когда
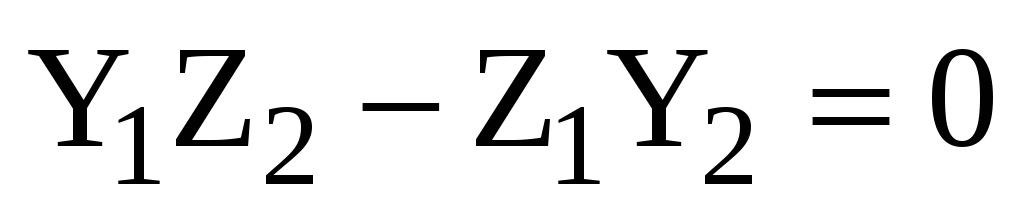 ,
, 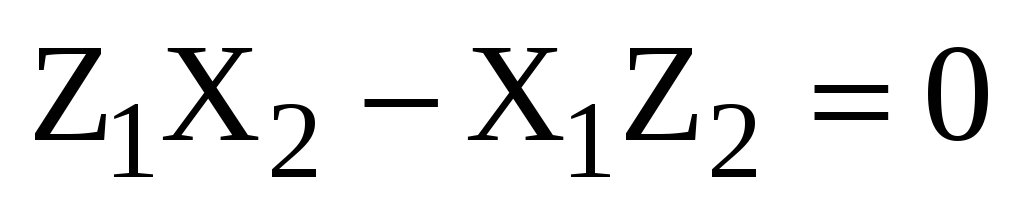 ,
, 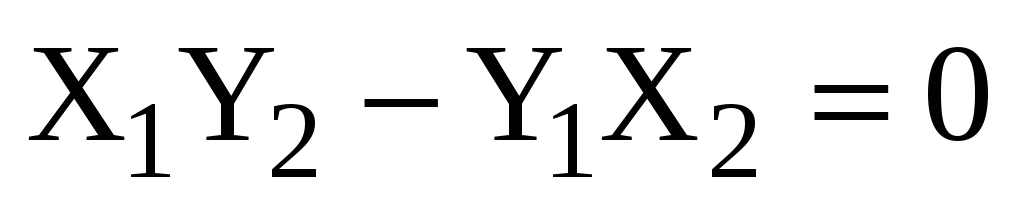 ,
,
или
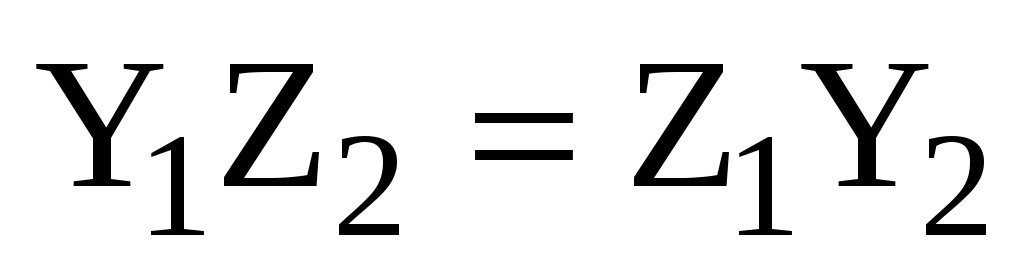 ,
, 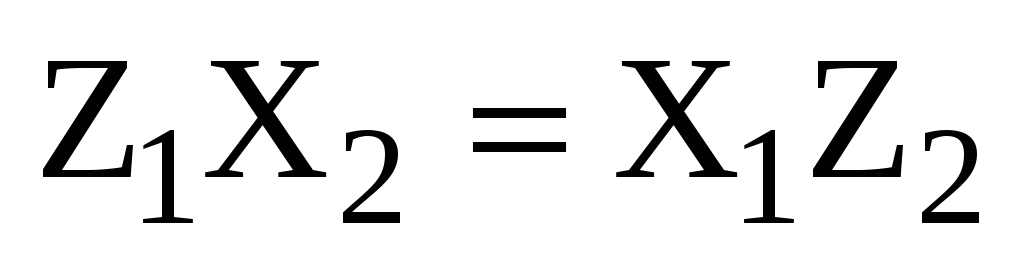 ,
, 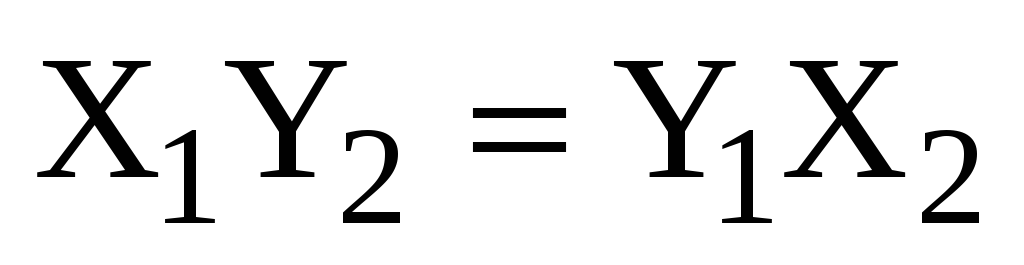 ,
(2.9)
,
(2.9)
или
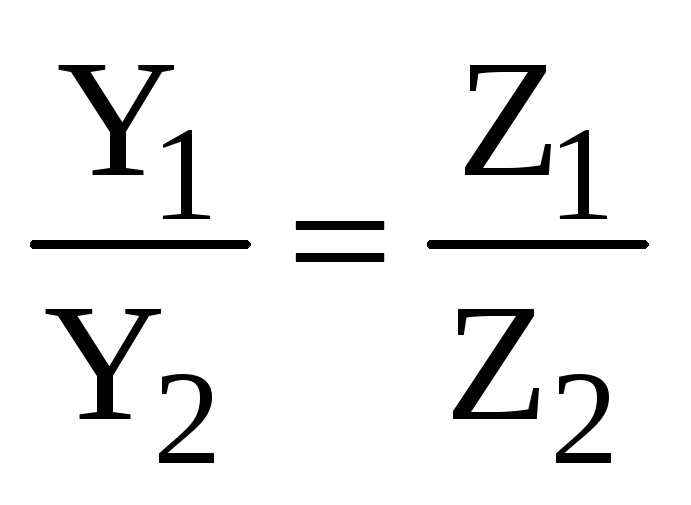 ,
, 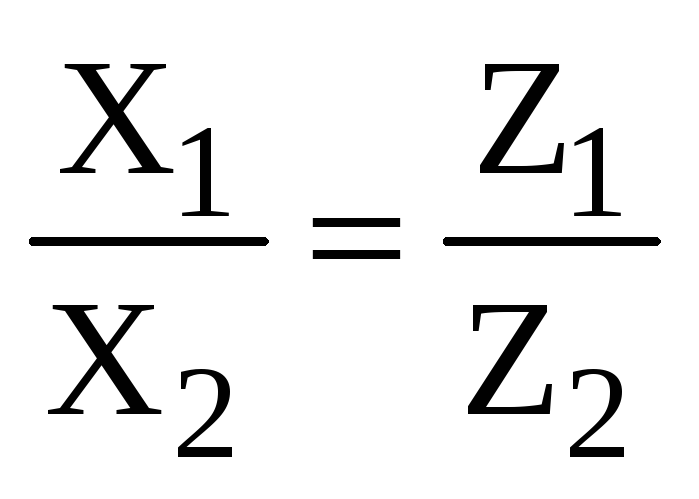 ,
, 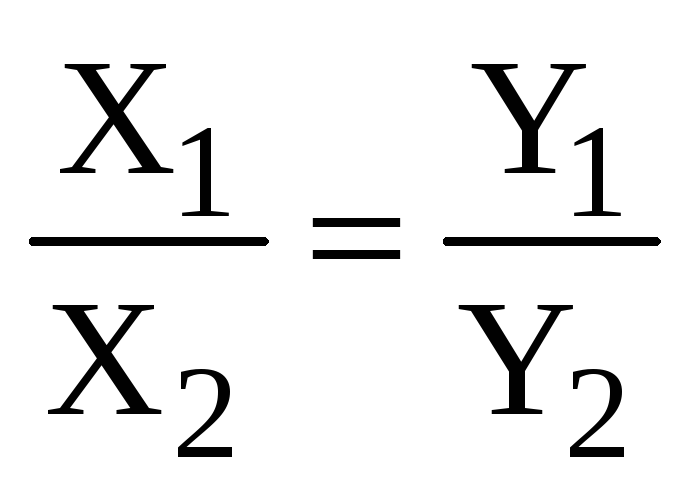 ,
,
или
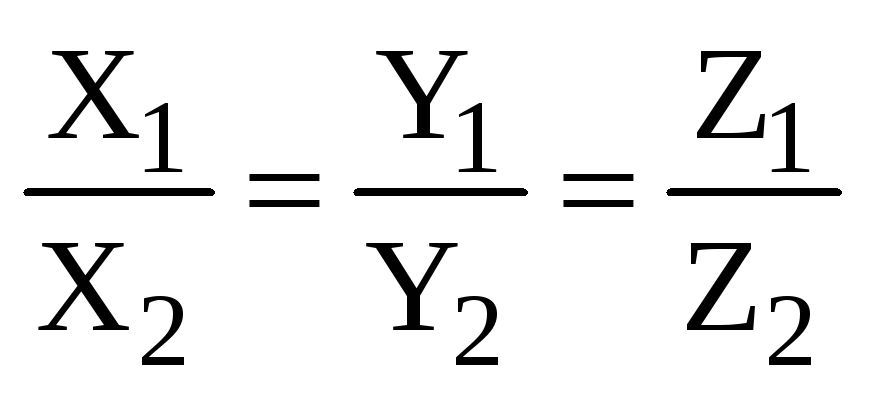 .
(2.10)
.
(2.10)
Замечание. Чтобы обойти трудность с равенством
нулю знаменателя в (2.10), договоримся в
том случае, когда 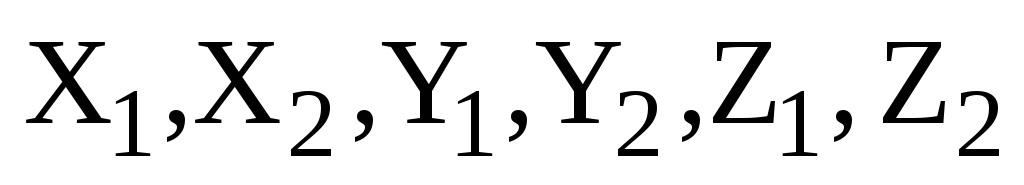 – координаты некоторых векторов
– координаты некоторых векторов  и
и  ,
понимать равенство (2.10) как три равенства
(2.9).
,
понимать равенство (2.10) как три равенства
(2.9).
1. Модуль векторного произведения численно равен площади параллелограмма, построенного на множителях (рис. 1.42,6).
2. Векторное произведение равняется нулевому вектору тогда и только тогда, когда множители коллинеарны, т.е.
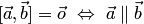 , в частности,
, в частности, 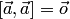 .
.
Первое свойство следует из определения. Докажем второе свойство. Равенство 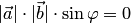 возможно в трех случаях:
возможно в трех случаях:  , или
, или 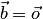 , или
, или 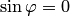 . В каждом из этих случаев векторы
. В каждом из этих случаев векторы 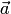 и
и 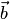 коллинеарны (см. разд. 1.1).
коллинеарны (см. разд. 1.1).

Пример 1.19. Вычислить площади параллелограмма и треугольника, построенных на векторах 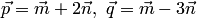 , где
, где 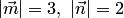 , угол между векторами
, угол между векторами 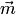 и
и 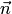 равен
равен 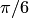 (рис. 1.44).
(рис. 1.44).
Решение. Используя алгебраические свойства, найдем сначала векторное произведение
а затем его модуль .
По первому геометрическому свойству векторного произведения искомая площадь параллелограмма равна 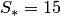 , а площадь треугольника в 2 раза меньше:
, а площадь треугольника в 2 раза меньше: 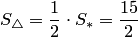 .
.
Векторное произведение векторов Википедия
 Векторное произведение в трёхмерном евклидовом пространстве
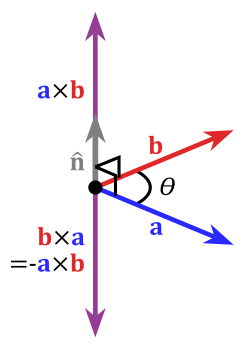
Векторное произведение в трёхмерном евклидовом пространствеВекторное произведение двух векторов в трёхмерном евклидовом пространстве — вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами, а выбор из двух направлений определяется так, чтобы тройка из по порядку стоящих в произведении векторов и получившегося вектора была правой[⇨]. Векторное произведение коллинеарных векторов (в частности, если хотя бы один из множителей — нулевой вектор) считается равным нулевому вектору.
Таким образом, для определения векторного произведения двух векторов необходимо задать ориентацию пространства, то есть сказать, какая тройка векторов является правой, а какая — левой. При этом не является обязательным задание в рассматриваемом пространстве какой-либо системы координат. В частности, при заданной ориентации пространства результат векторного произведения не зависит от того, является ли рассматриваемая система координат правой или левой. При этом формулы выражения координат векторного произведения через координаты исходных векторов в правой и левой ортонормированной прямоугольной системе координат отличаются знаком.
Векторное произведение не обладает свойствами коммутативности и ассоциативности. Оно является антикоммутативным и, в отличие от скалярного произведения векторов, результат является опять вектором.
Полезно для «измерения» перпендикулярности векторов — модуль векторного произведения двух векторов равен произведению их модулей, если они перпендикулярны, и уменьшается до нуля, если векторы коллинеарны.
Широко используется во многих технических и физических приложениях. Например, момент импульса и сила Лоренца математически записываются в виде векторного произведения.
1. 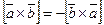 (антиперестановочность).
(антиперестановочность).
2. 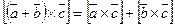 (линейность).
(линейность).
3. 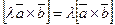 .
.
4. 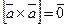 .
.
Векторное произведение через координаты.
Теорема. Если в правой системе координат 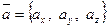 ,
, 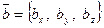 , то
, то
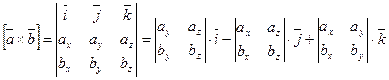 .
.
Доказательство.
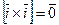 ,
, 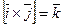 ,
, 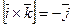 ,
, 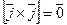 ,
, 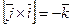 ,
, 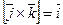 ,
, 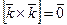 ,
, 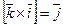 ,
, 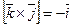 .
.
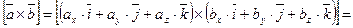
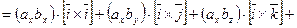
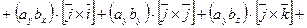
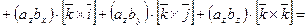
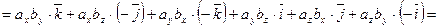
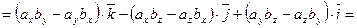
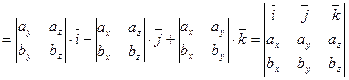 . □
. □
Смешанное произведение.
Определение. Смешанным произведением трёх векторов 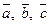 называется число:
называется число:
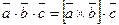 ,
,
т.е. скалярное произведение векторов 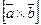 и
и 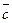 .
.
Векторное произведение
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
САМАРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра математики и бизнес-информатики
РЕФЕРАТ
Дисциплина: Линейная алгебра
На тему: «Векторное произведение»
Выполнила
студентка 1 курса, группы 23101.50
Богачева Е.С.
Преподаватель:
Сахабиева Г.А.
Самара
2014
План
Введение
1. Определение
2. Правые и левые тройки векторов в трёхмерном пространстве
3. Свойства
3.1 Основные геометрические свойства векторного произведения
3.2 Основные алгебраические свойства векторного произведения
4. Выражение для векторного произведения в декартовых координатах
5. Алгебра Ли векторов
Источники, литература
Введение
Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны.
Определить векторное произведение можно по-разному, и теоретически, в пространстве любой размерности n можно вычислить произведение n-1 векторов, получив при этом единственный вектор, перпендикулярный к ним всем. Но если произведение ограничить нетривиальными бинарными произведениями с векторным результатами, то традиционное векторное произведение определено только в трёхмерном и семимерном пространствах. Результат векторного произведения, как и скалярного, зависит от метрики Евклидова пространства.
В отличие от формулы для вычисления по координатам векторов скалярного произведения в трёхмерной прямоугольной системе координат, формула для векторного произведения зависит от ориентации прямоугольной системы координат или, иначе, её «хиральности».
1. Определение
Векторным произведением вектора a на вектор b назовем вектор c, удовлетворяющий условию
1) 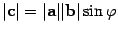 , где
, где 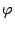 — угол между a и b и, если
— угол между a и b и, если 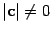 , то еще двум условиям:
, то еще двум условиям:
вектор c ортогонален векторам a и b;
из конца вектора c кратчайший поворот от вектора a (первого сомножителя) к вектору b (второму сомножителю) виден против часовой стрелки. (Начала векторов предполагаются совмещенными).
Обозначение:
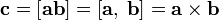
2. Правые и левые тройки векторов в трехмерном пространстве
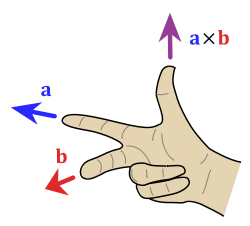
Нахождение направления векторного произведения с помощью правила правой руки
Рассмотрим
упорядоченную тройку некомпланарных
векторов 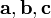 в
трёхмерном пространстве. Совместим
начала этих векторов в точке
в
трёхмерном пространстве. Совместим
начала этих векторов в точке 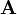 (то
есть выберем произвольно в пространстве
точку
(то
есть выберем произвольно в пространстве
точку 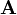 и
параллельно перенесём каждый вектор
так, чтобы его начало совпало с точкой
и
параллельно перенесём каждый вектор
так, чтобы его начало совпало с точкой 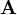 ).
Концы векторов, совмещённых началами
в точке
).
Концы векторов, совмещённых началами
в точке  ,
не лежат на одной прямой, так как векторы
некомпланарны. Рассмотрим плоскость
,
не лежат на одной прямой, так как векторы
некомпланарны. Рассмотрим плоскость  —
единственную плоскость, проходящую
через концы векторов, совмещённых
началами в точке
—
единственную плоскость, проходящую
через концы векторов, совмещённых
началами в точке  .
Тогда можно в плоскости
.
Тогда можно в плоскости  провести
через концы векторов
провести
через концы векторов 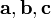 ,
совмещённых началами в точке
,
совмещённых началами в точке  ,
единственную окружность и выяснить
направление обхода трёх точек на
окружности, смотря на неё с одной из
сторон от плоскости.
,
единственную окружность и выяснить
направление обхода трёх точек на
окружности, смотря на неё с одной из
сторон от плоскости.
Упорядоченная
тройка некомпланарных векторов 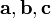 в
трёхмерном пространстве называется правой,
если наблюдателю, находящемуся по одну
сторону с точкой
в
трёхмерном пространстве называется правой,
если наблюдателю, находящемуся по одну
сторону с точкой  от
плоскости
от
плоскости  ,
обход концов приведённых в общее начало
,
обход концов приведённых в общее начало  векторов
векторов  в
указанном порядке кажется совершающимся
в плоскости
в
указанном порядке кажется совершающимся
в плоскости  по
часовой стрелке. В этом случае наблюдателю,
находящийся с другой стороны от плоскости
по
часовой стрелке. В этом случае наблюдателю,
находящийся с другой стороны от плоскости 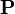 ,
обход концов таких векторов будет
казаться совершающимся против часовой
стрелки.
,
обход концов таких векторов будет
казаться совершающимся против часовой
стрелки.
B
противном случае 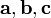 — левая тройка.
— левая тройка.
Другое определение связано с правой рукой человека (см. рисунок), откуда и берётся название.
Все правые между собой (и левые между собой) тройки векторов называются одинаково ориентированными.
Заметим, что для двух данных векторов рассматриваемого пространства определения «правой» и «левой» тройки векторов не зависят от хиральности рассматриваемой системы координат; более того, они вообще не требуют задания в рассматриваемом пространстве какой-либо системы координат, как и не требует этого само векторное произведение.
3. Свойства
3.1 Основные геометрические свойства векторного произведения
3.1.1 Векторное
произведение 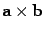 равно
нулю тогда и только тогда, когда векторы a и b — коллинеарные.
равно
нулю тогда и только тогда, когда векторы a и b — коллинеарные.
Доказательство: Из
определения векторного произведения
получим, что 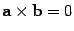 тогда
и только тогда, когда
тогда
и только тогда, когда 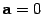 ,
или
,
или 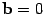 ,
или
,
или 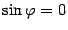 .
Из последнего равенства получим, что
.
Из последнего равенства получим, что 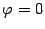 или
или 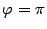 ,
в этом случае векторы a и b коллинеарны.
Вспомнив, что нулевой вектор считается
коллинеарным любому другому вектору,
получим, что предложение верно и при a или b,
равных нулю.
векторный
произведение геометрический алгебраический
,
в этом случае векторы a и b коллинеарны.
Вспомнив, что нулевой вектор считается
коллинеарным любому другому вектору,
получим, что предложение верно и при a или b,
равных нулю.
векторный
произведение геометрический алгебраический
3.1.2 Площадь параллелограмма, сторонами которого служат векторы a и b, равна модулю их векторного произведения,
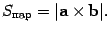
Доказательство естественным образом вытекает из условия 1 в определении векторного произведения.
3.1.3 Если 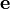 — единичный вектор, ортогональный
векторам
— единичный вектор, ортогональный
векторам 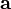 и
и 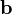 и выбранный так, что тройка — правая, а
и выбранный так, что тройка — правая, а 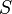 — площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:
— площадь параллелограмма, построенного
на них (приведённых к общему началу), то
для векторного произведения справедлива
формула:
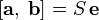
3.1.4 Если 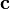 — какой-нибудь вектор,
— какой-нибудь вектор, 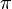 — любая плоскость, содержащая этот
вектор,
— любая плоскость, содержащая этот
вектор, 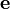 — единичный вектор, лежащий в плоскости
— единичный вектор, лежащий в плоскости 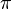 и ортогональный к
и ортогональный к 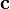 ,
, 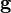 — единичный вектор, ортогональный к
плоскости
— единичный вектор, ортогональный к
плоскости 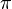 и направленный так, что тройка векторов
и направленный так, что тройка векторов 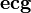 является правой, то для любого лежащего
в плоскости
является правой, то для любого лежащего
в плоскости  вектора
вектора 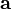 справедлива
формула:
справедлива
формула:
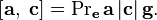
3.1.5 При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c. Такое произведение трех векторов называется смешанным.
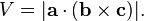
3.2. Основные алгебраические свойства векторного произведения
3.2.1 Векторное
произведение антикоммутативно, то есть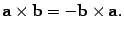 (в другой формулировке: если
изменить порядок сомножителей, то
векторное произведение меняет направление
на противоположное; антикоммутативность).
(в другой формулировке: если
изменить порядок сомножителей, то
векторное произведение меняет направление
на противоположное; антикоммутативность).
Доказательство: Пусть 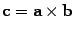 ,
, 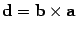 .
Нужно показать, что
.
Нужно показать, что 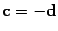 .
Из условия 1 следует, что
.
Из условия 1 следует, что 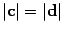 . Если
. Если 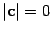 ,
то очевидно, что
,
то очевидно, что 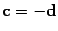 .
Если
.
Если 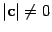 , то векторы c и d — коллинеарны, так как
оба лежат на прямой, ортогональной
плоскости векторов a и b. Таким образом,
остаются только две возможности:
, то векторы c и d — коллинеарны, так как
оба лежат на прямой, ортогональной
плоскости векторов a и b. Таким образом,
остаются только две возможности: 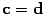 или
или 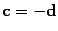 .
Пусть вектор
.
Пусть вектор 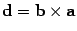 совпадает с вектором
совпадает с вектором 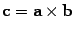 .
Тогда в силу условия 3 из конца одного
и того же вектора и поворот от a к b, и
поворот от b к a по кратчайшему направлению
виден против часовой стрелки, что
невозможно. Следовательно,
.
Тогда в силу условия 3 из конца одного
и того же вектора и поворот от a к b, и
поворот от b к a по кратчайшему направлению
виден против часовой стрелки, что
невозможно. Следовательно, 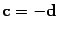 .
.
3.2.2 Для
любых векторов a и b и любого числа 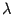 выполняется равенство
выполняется равенство 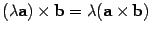 (свойство
ассоциативности
относительно
умножения на скаляр).
(свойство
ассоциативности
относительно
умножения на скаляр).
Доказательство: Если 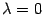 , то утверждение очевидно. Если векторы
a и b — коллинеарные, то векторы
, то утверждение очевидно. Если векторы
a и b — коллинеарные, то векторы 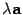 и b — тоже коллинеарные, и поэтому обе
части доказываемого равенства равны
нулю.
и b — тоже коллинеарные, и поэтому обе
части доказываемого равенства равны
нулю.
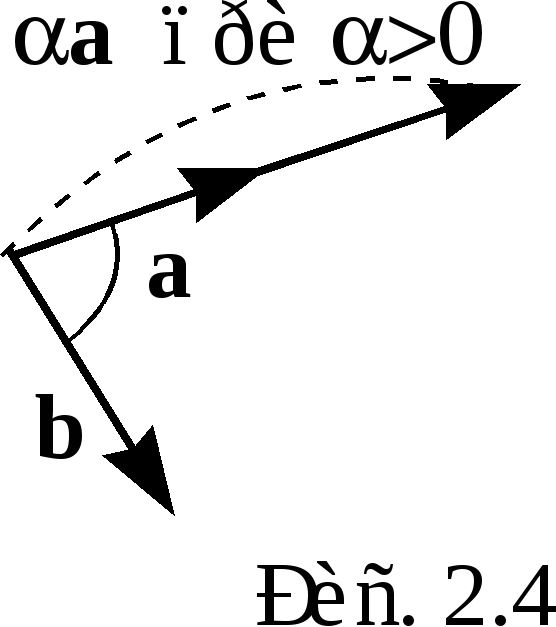
Пусть 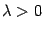 , a, b – неколлинеарные,
, a, b – неколлинеарные, 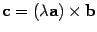 ,
, 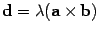 . Тогда углы, образованные векторами a
и b и векторами
. Тогда углы, образованные векторами a
и b и векторами 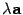 и b, равны. Следовательно,
и b, равны. Следовательно,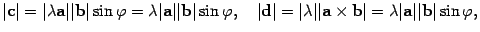
то
есть 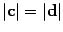 . Оба вектора c и d перпендикулярны
плоскости векторов a и b и направлены
одинаково, так как равны углы между
сомножителями. Следовательно,
. Оба вектора c и d перпендикулярны
плоскости векторов a и b и направлены
одинаково, так как равны углы между
сомножителями. Следовательно, 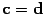 .
.
Пусть 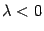 . Тогда векторы
. Тогда векторы 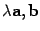 образуют угол
образуют угол 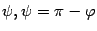 (см. рисунок).
(см. рисунок).
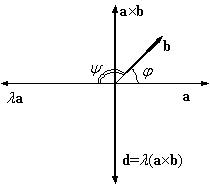
Вычисляем модули:
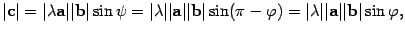
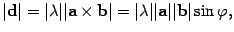
то
есть 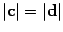 . Векторы
. Векторы 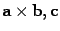 и d перпендикулярны плоскости векторов
a и b. Векторы
и d перпендикулярны плоскости векторов
a и b. Векторы 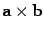 и c имеют противоположные направления,
так как поворот от a и
и c имеют противоположные направления,
так как поворот от a и
от 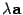 к вектору b происходят в противоположных
направлениях. Но вектор d имеет направление,
противоположное вектору
к вектору b происходят в противоположных
направлениях. Но вектор d имеет направление,
противоположное вектору 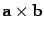 (см. рисунок) и, следовательно, одинаковое
с вектором c. Получили, что
(см. рисунок) и, следовательно, одинаковое
с вектором c. Получили, что 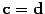 .
.
3.2.3 Векторное
произведение обладает свойством
дистрибутивности по сложению, то есть
выполняется равенство 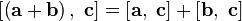 .
.
4. Выражение для векторного произведения в декартовых координатах
Если
два вектора 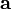 и
и 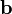 определены своими прямоугольными
декартовыми координатами, а говоря
точнее — представлены в ортонормированном
базисе
определены своими прямоугольными
декартовыми координатами, а говоря
точнее — представлены в ортонормированном
базисе
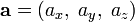
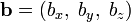
а система координат правая, то их векторное произведение имеет вид
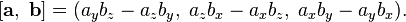
Теорема. Пусть 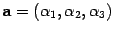 ,
, 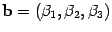 .
Тогда
.
Тогда
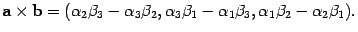
Доказательство: По
условию 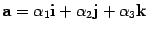 ,
, 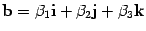 . По свойству ассоциативности векторного
произведения получим
. По свойству ассоциативности векторного
произведения получим
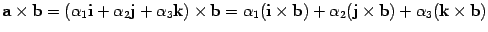
По тем же правилам
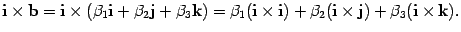
По
таблице умножения 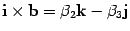 . Аналогично находим
. Аналогично находим 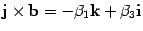 ,
, 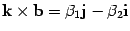 . Подставив полученные результаты в
формулу, получим
. Подставив полученные результаты в
формулу, получим
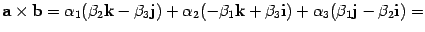
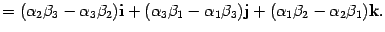
Запомнить полученную формулу тяжело. Чтобы облегчить этот процесс, вводят еще два дополнительных объекта — матрицу и определитель.
Матрицей
второго порядка называют таблицу из
четырех чисел, которая обозначается 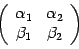 ,
матрицей третьего порядка называется
таблица из 9 чисел —
,
матрицей третьего порядка называется
таблица из 9 чисел — 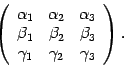
Определителем
матрицы второго порядка будем называть
число 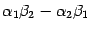 . Определитель второго порядка обозначается
. Определитель второго порядка обозначается 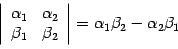 .
.
Определителем матрицы третьего порядка будем называть число
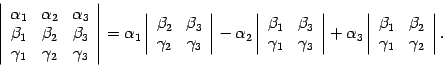
5. Алгебра Ли векторов
Векторное
произведение вводит на 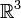 структуру
алгебры Ли (поскольку оно удовлетворяет
обеим аксиомам — антисимметричности
и тождеству Якоби). Эта структура
соответствует отождествлению
структуру
алгебры Ли (поскольку оно удовлетворяет
обеим аксиомам — антисимметричности
и тождеству Якоби). Эта структура
соответствует отождествлению 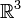 с
касательной алгеброй Ли so(3)
к
группе Ли SO(3)
ортогональных
линейных преобразований трёхмерного
пространства.
с
касательной алгеброй Ли so(3)
к
группе Ли SO(3)
ортогональных
линейных преобразований трёхмерного
пространства.
Источники, литература
https://ru.wikipedia.org
http://webmath.exponenta.ru
Ильин В. А., Позняк Э.Г. Линейная алгебра: Учеб.: Для вузов. — 5-е изд. – М.: ФИЗМАЛИТ, 2001.
Коллинеарные векторы. Копланарные векторы. Равенство векторов. Параллельная передача
векторов. Добавление векторов. Вычитание векторов.
Законы сложения векторов. Законы умножения вектора на число
. Скалярное произведение векторов. Угол между ненулевыми векторами. Скалярная площадь
Свойства скалярного произведения.Единичные ортогональные векторы.
Координаты вектора. Алгебраические операции с векторами. Вектор
произведение векторов. Свойства векторного произведения. Необходимое и
достаточное условие коллинеарности векторов. Необходимое и достаточное
условие компланарности векторов.
Вектор — это направленный отрезок, соединяющий две точки в пространстве (на плоскости). Векторы обычно подписываются либо маленькими буквами, либо начальными и конечными точками. Например, вектор, направленный из точки A в точку B , может быть подписан как a ,
__
Нулевой вектор 0 или 0 равен вектор, для которого начальная и конечная точки совпадают, т.е.е. А = В . Отсюда следует: 0 = 0 .
Длина (модуль) вектора a , подписанный как | а | , — длина его сегмента изображения AB . В частности, | 0 | = 0
Векторы называются коллинеарными векторами, если их направленные сегменты принадлежат параллельным линиям. Коллинеарные векторы a и b подписаны как a || б .
Три или более векторов называются копланарными , если они лежат в одной плоскости.
Равенство векторов. Два вектора a и b равны , если они коллинеарны и их длины равны , то есть a || б и | а | = | b | , Следовательно, вектора не изменяются при параллельной передаче.
Добавление векторов. Поскольку векторы направляются в сегментов , то их сложение может быть выполнено геометрически. (алгебраическое сложение векторов см. Ниже, в пункте Единицы ортогональных векторов).
Предположим, что __ __
a = AB и b = CD,
затем __ __
a + b = AB + CD
— вектор, полученный после выполнения двух операций:
a — параллельный перенос одного из векторов, пока его начальная точка не совпадет с
,— конечной точкой другого вектора;
b ) геометрическое сложение путем рисования результирующего вектора из начальной точки
неподвижного вектора в конечную точку перенесенного вектора.
Вычитание векторов. Эта операция сокращается до предыдущей путем замены вычитаемого вектора на противоположный:
a b = a + ( b ).
Законы сложения. I. a + b = b + a (C m m u t a t i v i t y).
II. ( a + b ) + c = a + ( b + c ) (A s s o c i a t i v i t y).
III. a + 0 = a.
IV. a + ( a ) = 0 .
Законы умножения вектора на число.
I. 1 a = a , 0 a = 0, м 0 = 0 , ( 1) a = a .
II. м а = а м , | м а | = | м | | а | .
III. m (n a ) = (m n) a . (умножение на
умножение на число).
IV. ( m + n ) a = m a + n a , (D — распределение
м ( a + b ) = м a + м b . умножение на число).
__ __
Скалярное произведение векторов. Угол между ненулевыми векторами AB и CD — это угол, образованный при параллельной передаче одного из векторов до совпадения точек A и C.Скалярное произведение векторов , и b называется числом, равным , как произведение длин (модулей) этих векторов на косинус угла между ними:
If один из векторов является нулевым вектором, тогда скалярное произведение этих векторов равно нулю по определению:
( a, 0 ) = ( 0 , b ) = 0.
Если оба вектора ненулевые, то косинус угла между ними можно найти по формуле:
Скалярное произведение ( a, ), равное | а | ², называется скалярным квадратом.
Длина вектора a и его скалярный квадрат связаны соотношением:
Скалярное произведение двух векторов равно:
— положительных , если угол между векторами острый ;
— отрицательно, , если угол между векторами равен , тупо .
Скалярное произведение двух ненулевых векторов равно , равному нулю , , если и только если угол между векторами прямой, то есть эти векторы перпендикулярны (ортогонально):
Свойства скалярного произведения. Для любых векторов a, b, c и любого числа м действительны следующие соотношения:
I. ( a, b ) = ( б, ) . (по т. Ч.)
II. ( м а, б ) = м ( а, б ) .
III. ( a + b, c ) = ( a, c ) + ( b, c ) . (в режиме реального времени)
Единичные ортогональные векторы. В любую прямоугольную систему координат можно ввести единичных двух-двух ортогональных векторов i , j и
.свойств векторов | Wyzant Resources
Векторы следуют большинству тех же правил арифметики, что и скалярные числа. Последующий различные свойства, которые применяются к векторам в двухмерном и трехмерном пространство и важно иметь в виду
Добавление векторов
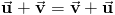
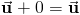
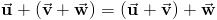
Скалярные и векторные свойства
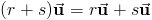
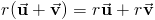
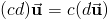
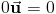
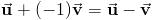
Точка Свойства продукта
Точечный продукт определен как
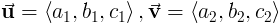
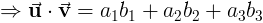
так же как
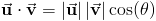
Следующие свойства содержат
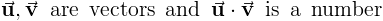
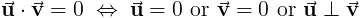
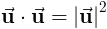
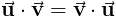
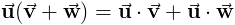
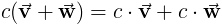
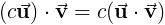
Свойства перекрестного продукта
Совокупный продукт определяется как
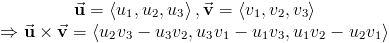
Как и
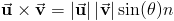
Следующие свойства содержат
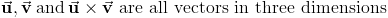
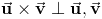
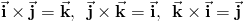
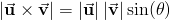

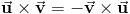
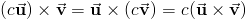
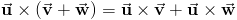
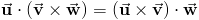
Точечное произведение двух векторов
Алгебраическая интерпретация. Точечное произведение двух векторов a и b является скалярной величиной, равной сумме попарных произведений координатных векторов a и b.
Точечный продукт также называется скалярным продуктом или внутренним продуктом .
Точечный продукт — формулы
Формула точечного произведения для плоских задач
В случае плоской задачи скалярное произведение векторов a = {a x ; а х } и б = {б х ; b y } можно найти по следующей формуле:
a · b = a x · b x + a y · b y
Формула точечного произведения для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {a x ; и ; а z } и b = {b x ; b и ; b z } можно найти по следующей формуле:
a · b = a x · b x + a y · b y + a z · b z
Формула точечного произведения для задач с n-мерным пространством
В случае проблемы n-мерного пространства скалярное произведение векторов a = {a 1 ; 2 ; ,..; a n } и b = {b 1 ; b 2 ; …; b n } можно найти по следующей формуле:
a · b = a 1 · b 1 + a 2 · b 2 + … + a n · b n
Примеры вычисления точечного произведения векторов для плоских задач
Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Пример 2. Найти произведение точек векторов a и b, если их величины равны | a | = 3, | b | = 6, а угол между векторами равен 60˚.Решение: a · b = | a | · | Б | cos α = 3 · 6 · cos 60˚ = 9.
Пример 3. Найти произведение точек векторов p = a + 3b и q = 5a — 3 b, если их величины равны | a | = 3, | b | = 2, а угол между векторами a и b равен 60˚.Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b == 5 | a | 2 + 12 a · b — 9 | b | 2 = 5 · 3 2 + 12 · 3 · 2 · cos 60˚ — 9 · 2 2 = 45 +36 -36 = 45.
,{n} \ times X $ на $ X $, так что склейка сохраняет линейную структуру векторного пространства. Здесь $ E $ называется волоконным пространством ( пучка ), $ X $ является базой , а $ n $ является ранга или измерения пучка. Морфизмы алгебраического векторного расслоения определяются так же, как и в топологии. Более общее определение, которое подходит для любой схемы, включает в себя понятие пучка. Пусть $ \ mathcal {E} $ — локально свободный пучок $ \ mathcal {O} _ {X} $ -модулей конечного (постоянного) ранга; тогда аффинный морфизм $ V (\ mathcal {E}): \ operatorname {Spec} (\ operatorname {Sym} \ mathcal {E}) \ to X $, где $ \ operatorname {Sym} \ mathcal {E} $ равен пучок симметричных алгебр из $ \ mathcal {E} $ называется векторным расслоением , связанным с $ \ mathcal {E} $.Эта терминология иногда также сохраняется, когда $ \ mathcal {E} $ является произвольным квазикогерентным пучком. Пучок $ \ mathcal {E} $ может быть однозначно восстановлен из алгебраического векторного расслоения $ V (\ mathcal {E}) $, а категория алгебраических векторных расслоений на $ X $ двойственна категории локально свободных пучков $ \ mathcal {O} _ {X} $ -модули. Более того, для $ X $ -схемы $ Y $ множество $ X $ -морфизмов $ Y \ to V (\ mathcal {E}) $ биективно соответствует множеству $ \ mathcal {O} _ {X} $ -модульные гомоморфизмы $ \ mathcal {E} \ to {f ^ {*}} (\ mathcal {O} _ {Y}) $, где $ f $ — структурный морфизм $ X $ -схемы $ Y $ ,Говорят, что {n} $ очень вполне достаточно .Другие примеры алгебраических векторных расслоений включают касательное расслоение $ T (X) $ на гладком многообразии $ X $ и расслоения, построенные из него различными операциями (см. Касательное расслоение; канонический класс; нормальное расслоение).
Алгебраическое векторное расслоение на многообразии, определенном над полем комплексных чисел $ \ mathbb {C} $, может рассматриваться как аналитическое и как топологическое (в комплексной топологии) алгебраическое векторное расслоение. Аналитические и алгебраические векторные расслоения эквивалентны на полном алгебраическом многообразии (см. Теорему сравнения в алгебраической геометрии).Топологические векторные расслоения не всегда допускают алгебраическую структуру, и даже когда они это делают, такая структура обычно не уникальна. Если алгебраическое векторное расслоение рассматривается как топологическое, то могут использоваться топологические методы; в частности, могут быть введены классы Черна алгебраических векторных расслоений. Также существует абстрактное определение классов Черна, которое включает $ K $ -функционер или один из вариантов этальных когомологий.
Свойства алгебраического векторного расслоения будут зависеть от того, является ли его база полной или аффинной схемой.Если база аффинна, т. Е. $ X = \ operatorname {Spec} (A) $, то алгебраические векторные расслоения соответствуют проективным модулям конечного типа над кольцом $ A $. Если ранг алгебраического векторного расслоения $ E $ выше размерности базы $ X $, то $ E $ можно представить в виде $ E = E ‘\ oplus 1 $, где $ 1 $ — одномерный тривиальный комплект. Обратите внимание, что $ E ‘$ обычно не определяется однозначно. Более того, если ранг $ E $ выше размерности базы и $ E \ oplus 1 \ cong F \ oplus 1 $, то $ E \ cong F $ ([4]).Если $ X $ — неособая одномерная схема (т.е. $ A $ — кольцо Дедекинда), то любое алгебраическое векторное расслоение является прямой суммой тривиального и линейного расслоения. Это также относится к алгебраическим векторным расслоениям на неособой аффинной поверхности над алгебраически замкнутым полем, бирационально эквивалентным линейчатой поверхности.
Случай проективной базы.
Изучение линейных расслоений на проективных многообразиях является классической проблемой алгебраической геометрии (см. Группу Пикара; схема Пикара).Изучение алгебраических векторных расслоений высших рангов началось в 1957 году, когда А. Гротендик показал, что алгебраические векторные расслоения на проективной прямой являются прямыми суммами линейных расслоений. М. Атия классифицировал алгебраические векторные расслоения на эллиптической кривой $ X $: если $ \ mathcal {E} (r, d) $ обозначает множество алгебраических векторных расслоений неразложимых (в прямую сумму) алгебраических векторных расслоений ранга $ r $ и степень $ d $ («степень» следует понимать как степень определителя расслоения), тогда $ \ mathcal {E} (r, d) $ совпадает с точками кривой $ X сам $ ([3]).
Концепция стабильных алгебраических векторных расслоений оказалась полезной при изучении алгебраических векторных расслоений на кривых. Для данного алгебраического векторного расслоения $ E $, пусть
.
