Электротехника ТОЭ: 1.5.2. Законы Кирхгофа
Теория / 1.5. Основные законы, действующие в электрических цепях / 1.5.2. Законы Кирхгофа
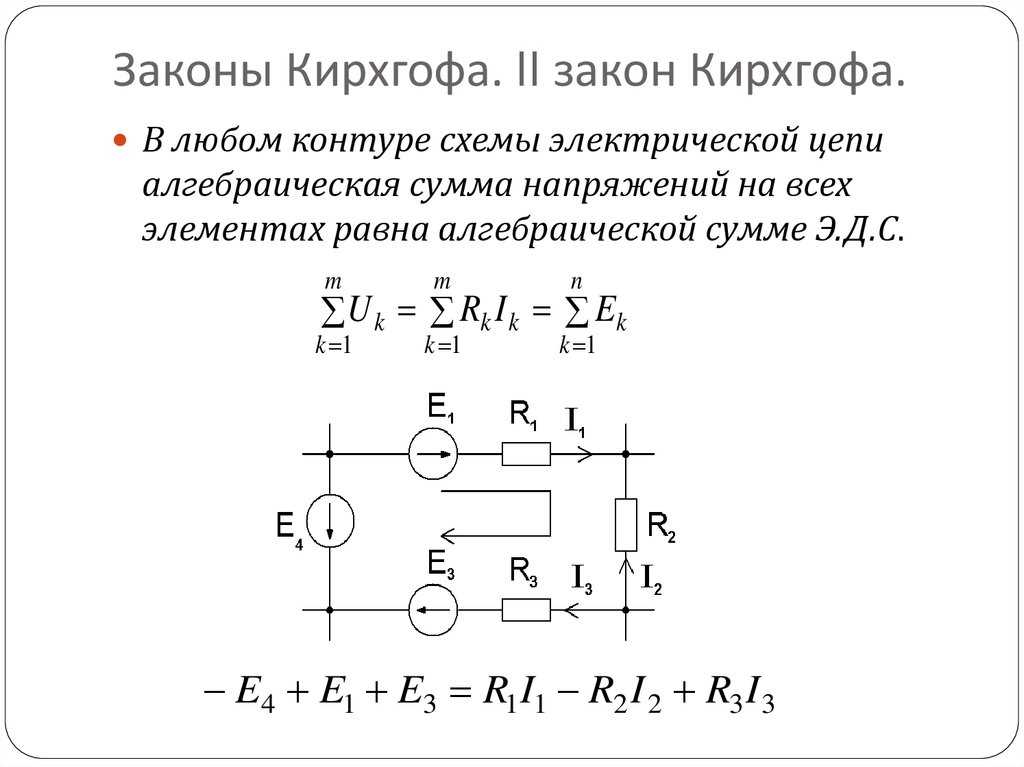
Для расчета электрических цепей используют два закона Кирхгофа.
Первый закон Кирхгофа применяется к узлам электрической цепи и выражает баланс токов в них.
Первый закон Кирхгофа состоит в том, что алгебраическая сумма токов в узле равна нулю. В общем виде формулировку этого закона можно записать как
Возьмем произвольный узел, в котором протекают токи, указанные стрелками (рис. 1.21).
Токи, направленные к узлу берутся с одним знаком, токи, направленные от узла – с противоположным. Будем считать положительными токи, направленные от узла, тогда первый закон Кирхгофа запишется
Это выражение можно преобразовать, перенеся отрицательные токи в правую часть,
Отсюда следует другая формулировка первого закона Кирхгофа: сумма токов, подходящих к узлу, равна сумме токов, отходящих от узла. Это говорит о том, что в узле заряд не накапливается.
Это говорит о том, что в узле заряд не накапливается.
Второй закон Кирхгофа применяется к контурам электрической цепи и выражает баланс напряжений в них: алгебраическая сумма ЭДС в замкнутом контуре равна алгебраической сумме падений напряжения на элементах этого контура. При составлении уравнений действует следующее правило знаков: электродвижущая сила берется со знаком плюс, если ее действие совпадает с направлением обхода контура, падение напряжения берется со знаком плюс, если направление тока в элементе совпадает с направлением обхода контура, в противном случае знак – минус. Для доказательства рассмотрим разветвленную электрическую цепь, представленную на рис. 1.22.
Выберем направление обхода контура по часовой стрелке и определим потенциалы точек 1, 2, 3, 4, 5, 6, 1. Начнем с точки 1, считая потенциал этой точки φ1 известным. ЭДС, направленная вдоль контура, повышает потенциал, тогда потенциал точки 2 определится выражением
На участке 2 – 3 ток течет вдоль обхода контура от точки 2 к точке 3, следовательно, потенциал точки 3 ниже потенциала точки 2 на величину падения напряжения на сопротивлении R2 . В этом случае потенциал третьей точки выразится через потенциал второй в соответствии с формулой
В этом случае потенциал третьей точки выразится через потенциал второй в соответствии с формулой
На участках с сопротивлениями R4 и R5 ток направлен против обхода контура, следовательно, вдоль обхода потенциалы повышаются:
Аналогично определим потенциалы остальных точек:
Изменение потенциала вдоль замкнутого контура равно нулю, так как мы вышли из точки с потенциалом φ1 и возвращаемся в эту же точку:
Подставляя в эту формулу выведенные выше выражения для потенциалов, получим
Поскольку сумма потенциалов равна нулю, то получим
Линейные электрические цепи постоянного тока
1.2 Законы Ома, Кирхгофа
Основные законы электротехники справедливы для линейных и нелинейных электрических цепей с постоянными
и переменными токами. Рассмотрим эти законы применительно к линейным цепям с постоянным током.
Рассмотрим эти законы применительно к линейным цепям с постоянным током.
На постоянном токе сопротивление ветви с индуктивностью равно нулю, а с конденсатором – бесконечности. Таким образом, при рассмотрении электрической цепи постоянного тока в установившемся режиме пассивными элементами схемы будут являться резистивные элементы, а активными – постоянные источники ЭДС и/или источники тока. Индуктивности и конденсаторы учитываются в схемах цепей переменного тока и при переходных процессах, возникающих в электрических цепях при переходе от одного режима к другому.
Закон Ома
а) для участка цепи: в любом сопротивлении ток прямо пропорционален напряжению и обратно пропорционален сопротивлению
б) для цепи с одним источником ЭДС (рисунок 1): ток через ЭДС прямо пропорционален величине ЭДС и
обратно пропорционален эквивалентному сопротивлению цепи.
в) для цепи с одним источником тока (рисунок 2):
напряжение на источнике тока прямо пропорционально произведению величины тока источника на эквивалентное сопротивление цепи.
Первый закон Кирхгофа: Алгебраическая сумма токов в узле равна нулю
Этот закон применяется к узлам электрической цепи. Векторная диаграмма токов в узле представлена на рисунке 3.
Рисунок 3
Алгебраически суммируют токи в ветвях, сходящихся в рассматриваемом узле. Знаки токов при этом соответствуют выбранным положительным направлениям. Bсе токи, направленные к узлу, в формуле (1.1) берутся со знаком «+», а токи, направленные от узла, со знаком «-»
Так для узла, представленном на рисунке 3, имеем формулу
Первый закон Кирхгофа отражает тот факт, что в узле цепи электрический заряд не накапливается и не
расходуется.
Второй закон Кирхгофа: Алгебраическая сумма ЭДС в любом замкнутом контуре цепи равна алгебраической сумме падений напряжений на резисторах (сопротивлениях) этого контура.
Так, для цепи с резистивным элементами имеем уравнение
Направление обхода контура выбирают произвольно. При обходе контура соблюдают правило знаков. ЭДС и падения напряжения, совпадающие по направлению с обходом включают в уравнение равновесия (1.2) со знаком «+», противоположные обходу включают со знаком «-». Тогда для контура рисунка 4 получаем
Энергетический баланс в электрических цепях: При наличии токов в резисторах цепи выделяется Джоулево
тепло. Суммарная энергия, выделяющаяся в единицу времени (называемая мощность потерь) должна быть
равна суммарной энергии отдаваемой источниками за то же время (мощности источников) – закон
сохранения энергии применительно к электрическим цепям.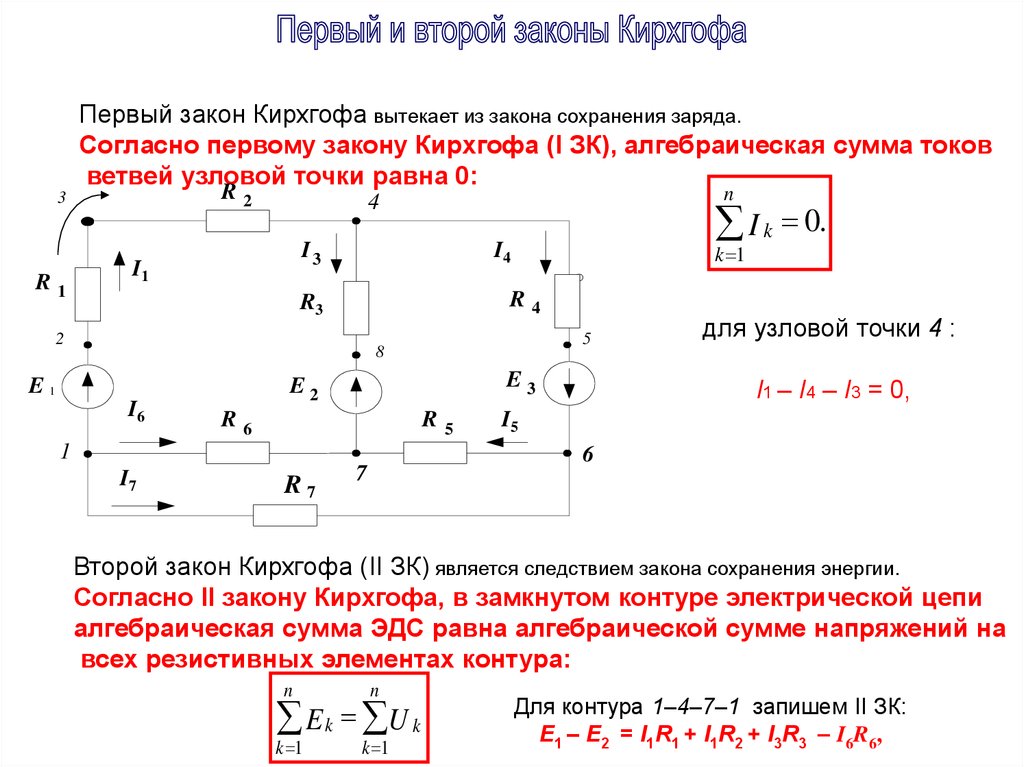
Закон Джоуля – Ленца: В любом сопротивлении мощность тепловой энергии равна произведению квадрата тока на величину этого сопротивления
Баланс мощности − это равенство мощностей источников электрической энергии мощностям приемников энергии
Произведения величины источника ЭДС в k-ой ветви Е к на ток k-ой ветви I к
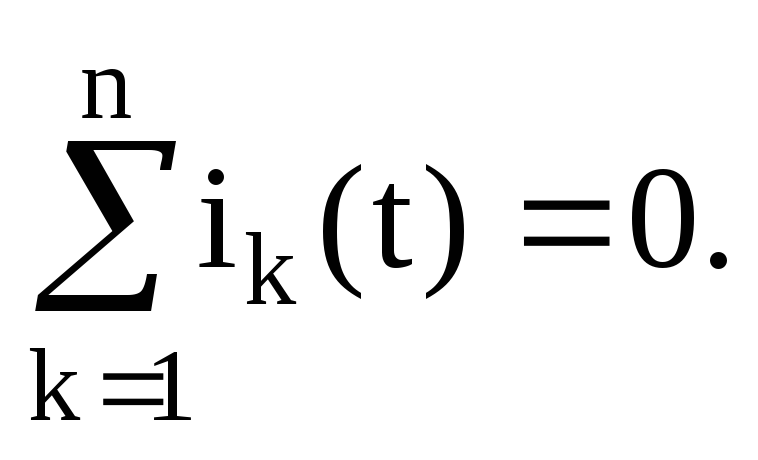 Отрицательная вырабатываемая мощность источника ЭДС или тока
свидетельствует о том, что источник не вырабатывает мощность, а потребляет ее.
Отрицательная вырабатываемая мощность источника ЭДС или тока
свидетельствует о том, что источник не вырабатывает мощность, а потребляет ее.
Для проверки правильности расчета токов и напряжений производится сравнение вырабатываемой (мощности источников) и потребляемой (мощности приемников) мощности
Для схемы, представленной на рисунке 5, баланс мощности запишется в виде
1.2 Метод контурных токов
Метод контурных токов является одним из основных расчетных методов и пригоден для линейных цепей постоянного и переменного тока.
Сущность метода заключается в том, что в качестве искомых неизвестных рассматривают не действительные
токи в ветвях цепи, а условные, так называемые контурные токи. Число контурных токов, равное числу
независимых контуров цепи, всегда меньше числа токов ветвей.
Вывод основных расчетных соотношений сделаем на примере цепи постоянного тока с источниками ЭДС в ветвях (рисунок 5), которая имеет ветвей – 3, узлов – 2.
Число независимых контуров данной цепи равно 2. Направления контурных токов I11 и I22 показаны стрелками. Для каждого из контуров запишем уравнения равновесия напряжений по 2-ку закону Кирхгофа. При этом учтем, что ток (I11 — I22) в смежной ветви (сопротивление R2) имеет направление сверху вниз, то есть направлен по контурному току I11
 В ветвях R1 и R3 имеют место контурные токи I11 и
I22 .
В ветвях R1 и R3 имеют место контурные токи I11 и
I22 .Определив из системы (3) контурные токи (расчетные величины), рассчитываем токи ветвей по следующим формулам:
I1 = I11; I2 = I11 – I22; I3 = I22.
Когда в цепи присутствуют идеальные источники тока, эти токи целесообразно принять за контурные, тогда число контурных токов и, соответственно, число уравнений сократится.
1.3 Методы узловых потенциалов (напряжений) и двух узлов.
Метод узловых потенциалов (напряжений)
Этот метод расчета линейных цепей основан на первом законе Кирхгофа и законе Ома. Метод узловых
потенциалов целесообразно применять для расчета цепей, число узлов в которых меньше числа ветвей,
кроме того, этот метод расчета удобен при определении токов в схемах, имеющих ветвь (ветви) только с
идеальным источником ЭДС (рисунок 6). В этой схеме 4 узла (y = 4), 7 ветвей (b = 7).
Метод узловых
потенциалов целесообразно применять для расчета цепей, число узлов в которых меньше числа ветвей,
кроме того, этот метод расчета удобен при определении токов в схемах, имеющих ветвь (ветви) только с
идеальным источником ЭДС (рисунок 6). В этой схеме 4 узла (y = 4), 7 ветвей (b = 7).
При расчете схемы этим методом потенциал одного из узлов схемы принимают равным нулю; этот узел называется базисным. При этом токораспределение в цепи не меняется, так как не образуется дополнительная ветвь. Искомые потенциалы других узлов схемы – это напряжения их относительно базисного узла, поэтому этот метод называют также методом узловых напряжений (напряжение – это разность потенциалов).
Если в схеме есть ветвь, содержащая только ЭДС, то принимают равным нулю потенциал одного из узлов, к
которым присоединена эта ветвь.
Например, потенциал первого узла φ 1 примем равным нулю,
φ 1 = 0 – базисный (опорный) узел, то потенциал второго узла φ 2 = Е 2 .
Неизвестными остаются потенциалы третьего φ 3 , четвертого φ 4 узлов. Уравнения для их определения составляются по следующему алгоритму:
1) потенциал рассматриваемого узла (φ К ) умножается на сумму проводимостей ветвей, подходящих к данному узлу;
2) к этому произведению дописываются со знаком минус произведения потенциалов всех соседних узлов на проводимости ветвей, соединяющих эти узлы с рассматриваемым;
3) в правой части уравнения записывается алгебраическая сумма произведений ЭДС ветвей на их
проводимости и алгебраическая сумма токов источников тока, подходящих к рассматриваемому узлу, при
этом ЭДС и токи источников тока, направленные к этому узлу входят со знаком “плюс”, а от
узла – со знаком “минус”.
Из системы (5) определяются неизвестные потенциалы узлов φ3 и φ4. По закону Ома рассчитываются токи ветвей по найденным потенциалам узлов
В формулы расчета токов (6) со знаком “плюс” входят потенциалы узлов, от которых направлены токи, а со знаком “минус” – потенциалы узлов, к которым направлены токи ветвей. ЭДС Е имеет знак “плюс”, если ее направление совпадает с направлением тока ветви. Обычно в расчетах положительные направления токов выбираются произвольно. Отрицательное значение тока, полученное в результате расчетов, указывает на то, что действительное направление противоположно выбранному.
Напряжение на зажимах источника тока
Метод двух узлов
При параллельном соединении между двумя узлами находятся несколько ветвей, при этом напряжение на всех ветвях одинаково (рисунок 7)
Примем, что φb = 0 – базисный узел, при этом неизвестным является потенциал узла
«а» φа. Уравнение для определения φа имеет вид
Уравнение для определения φа имеет вид
Напряжение между двумя узлами схемы определяется по формуле
Основы схем — Законы Кирхгофа — NightShade Electronics
перейти к содержаниюСоздано
Последнее обновление
Byaaron Liebold
Печать
- Основные
- Учебные пособия по электронике .
< Все темы
Густав Кирхгоф был физиком, который определил два закона, которые имеют первостепенное значение для понимания поведения электрических цепей.
Текущий закон Кирхгофа (KCL)
Первый закон Кирхгофа касается узлов в цепи. В нем говорится, что алгебраическая сумма всех токов, поступающих в узел цепи, равна нулю . Мы должны указать, что это алгебраическая сумма, потому что мы должны обратить внимание на знак (положительный или отрицательный) протекающего тока. Ток, втекающий в узел, положителен, а ток, вытекающий из узла, отрицателен. Этот закон очень силен
Ток, втекающий в узел, положителен, а ток, вытекающий из узла, отрицателен. Этот закон очень силен
Теперь мы должны ответить на очевидный вопрос: «Что такое узел?» Узел — это любая точка схемы, где компоненты соединяются проводами. Это может быть земля, источник напряжения или любой другой клубок проводов, соединяющих компоненты друг с другом. Однако мы можем применить KCL в более широком смысле, нарисовав круг вокруг любой части нашей схемы, с компонентами или без них, и сумма токов в этом круге и вне его будет равна нулю. 9N I_{out\_N}\)
\(\large I_{in\_1} + I_{in\_2} + \ . \ . \ . \ + I_{in\_N} = I_{out\_1} + I_ {out\_2} + \ . значение тока Z.
Это очень легко сделать с текущим законом Кирхгофа. Во-первых, мы определяем всю мешанину резисторов как один узел (рисуем круг). Теперь мы определяем положительное направление потока на каждом проводе, соединяющемся с узлом. Это указано стрелками. Теперь мы знаем, что сумма всех токов, входящих и исходящих из нашего узла, равна нулю. Запишем текущий баланс следующим образом:
Запишем текущий баланс следующим образом:
\(\large I_X + I_Y + I_Z = 25 мА + (-10 мА) + (-I_Z) = 0\)
Ток X положительный, потому что он втекает в узел, а ток Y и ток Z отрицательны потому что они вытекают из узла. Теперь решим уравнение для тока Z.
\(\большой I_Z = -(I_X) — (I_Y) = -(25 мА) — (-10 мА) = -15 мА\)
Как только мы решим для тока Z, находим, что он равен -15мА. Отрицательное значение подтверждает, что ток Z вытекает из узла.
Использование альтернативной формы KCL
Вот еще одна схема, в которой мы хотим сделать то же самое, но на этот раз мы будем использовать альтернативную форму закона тока Кирхгофа, где сумма всех токов в узле равна сумма всех токов, выходящих из узла.
Первым шагом является определение направления потока в каждом проводе, подключенном к контуру, который мы будем называть положительным направлением. Наше определение протекания положительного тока будет следовать стрелкам на проводах.
Теперь складываем все токи, втекающие в узел слева от знака равенства. В данном случае это только ток A. А токи, выходящие из узла, суммируются справа от знака равенства. это уравновешивает текущий вход и выход узла.
\(\большой I_A = I_B + I_C, \счетчик 6,64 мА = I_B + 12,8 мА\)
Еще раз, решим для тока B:
\(\большой I_B = I_A — I_C = 6,64 мА — 12,8 мА = -6,16 мА\)
В этом случае мы нашли, что ток B равен -6,16 мА. Отрицательное значение просто означает, что наше определение тока для этого провода является обратным. Ток B фактически течет в цепь.
Закон Кирхгофа о напряжении (KVL)
Второй закон Кирхгофа — это закон напряжения. В нем говорится, что алгебраическая сумма всех напряжений вокруг любого контура в цепи равна нулю. Это говорит о том, что если вы начинаете с точки в цепи и суммируете увеличение или уменьшение напряжения каждого компонента по мере прохождения петли в цепи, сумма будет равна нулю, когда вы вернетесь в исходную точку. .
.
Этот закон показан на картинке выше. Начиная с точки А, у нас есть 0В. Когда мы движемся от A к B, есть источник напряжения, который добавляет 15 В. Над ним находится амперметр, который не мешает цепи. Он сообщает только ток, поэтому мы не будем добавлять или вычитать напряжение для амперметра. Теперь, в точке B, мы на 15В. Двигаясь от B к C, мы проходим через резистор. Напряжение уменьшается пропорционально току через резистор. Снижение напряжения регулируется законом Ома. Зная силу тока и сопротивление, можно рассчитать падение напряжения.
\(\large V = I \cdot R = (9,93 мА)(560 \Омега) = 5,56 В\)
Закон Ома говорит нам, что на резисторе 560 Ом возникает падение напряжения 5,56 В, через которое протекает ток 9,93 мА. . Теперь, потеряв 5,56 В на резисторе, напряжение в точке С равно 9,44 В. При переходе от C к D и от D к A ток проходит еще через два резистора. Оба этих падения напряжения также рассчитываются по закону Ома.
\(\большой V = I \cdot R = (9,93 мА)(680 \Омега) = 6,67 В\)
\(\большой V = I \cdot R = (90,93 мА)(270 \Омега) = 2,68 В\)
Используя все эти вычисления, мы можем записать сумму для всего контура.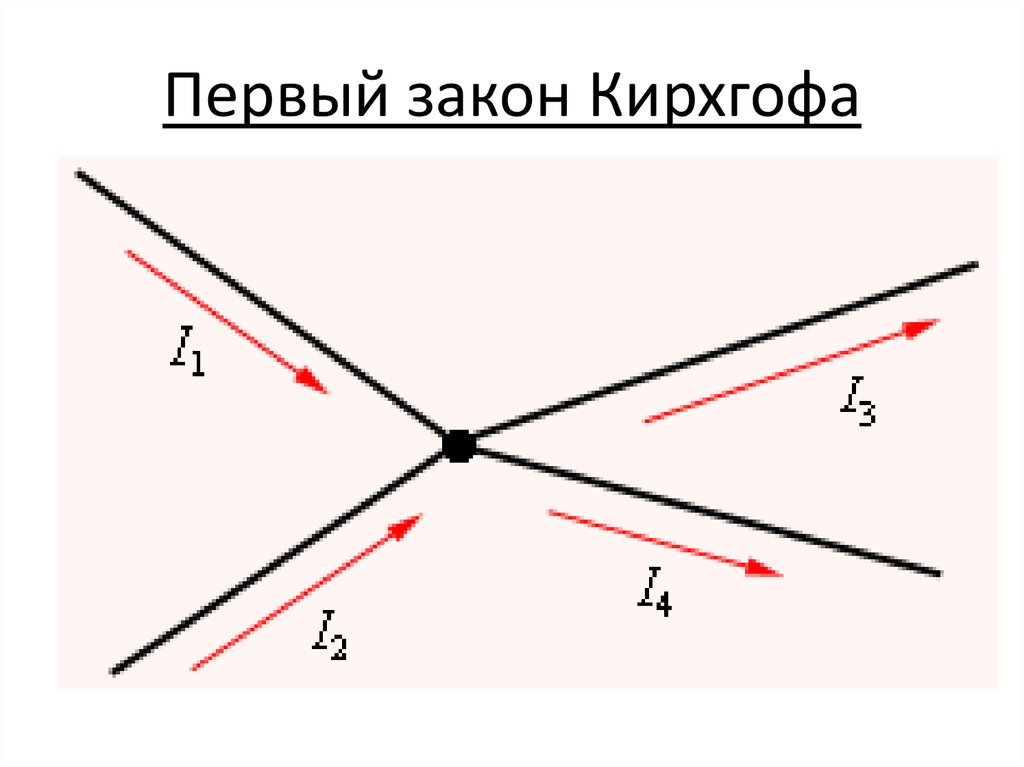 Повышение напряжения (как у источника) положительное, а падение напряжения (как у резисторов) отрицательное.
Повышение напряжения (как у источника) положительное, а падение напряжения (как у резисторов) отрицательное.
\(\большой 15В – (9,93мА)(560) – (9,93мА)(680) – (9,93мА)(270) = 0\)
Мы можем видеть, что это соотношение верно, но используя его как это не очень полезно. Что мы можем сделать, так это использовать его для нахождения напряжения в любой точке цепи относительно другой точки цепи. Даже если бы мы ничего не знали о напряжениях в этой цепи, мы могли бы произвольно назвать точку А землей (0 В). Затем мы можем найти напряжение в каждой другой точке цепи относительно точки А, суммируя все скачки и падения напряжения на этом пути. Все эти уравнения начинаются с напряжения в точке A (0 В), а затем добавляют увеличение или уменьшение напряжения каждого компонента в точке пути A и интересующей точке (B, C или D).
\(\большое V_{B} = 0В + 15В = 15В\)
\(\большое V_{C} = 0В + 15В — (9,93мА)(560\Омега) = 9,44В\)
\ (\large V_{D} = 0 В + 15 В – (9,93 мА)(560\Омега) – (9,93 мА)(680) = 2,68 В\)
Использование KCL и KVL для анализа цепи
В этом примере , у нас есть схема с некоторыми пропущенными значениями.
Используя KCL и KVL, мы можем найти эти пропущенные значения.
Я начал с определения узлов в цепи. Для нашего анализа мы начнем с предположения, что напряжение узла A (Va) равно 0 В. Теперь мы можем начать вычислять напряжение в других узлах. Во-первых, мы будем решать для Vb. Если мы начнем с узла A, мы сможем добраться до узла B, только пройдя через источник 5 В. Итак, начинаем с 0в и через источник напряжение увеличивается на 5В, делаем Vb равным 5В.
\(\большое Vb = 0В + 5В = 5В\)
Далее мы можем определить напряжение узла C (Vc). Начиная с узла A, мы поднимаемся к узлу B и получаем 5 В, затем ток проходит через резистор 680 Ом, чтобы добраться до узла C. Мы можем видеть по амперметру, что между узлами B и C течет ток 22,06 мА, поэтому мы можем использовать закон Ома для расчета падения напряжения на резисторе.
\(\большое Vc = 0 В + 5 В – (0,02206 А)(680 \Омега) = -10 В\)
Это показывает нам, что напряжение в узле C составляет -10 В. Это означает, что напряжение в узле C на 10 В меньше, чем напряжение в узле A (0 В).
Теперь мы рассчитаем напряжение в узле D. Похоже, это будет сложно, так как мы не знаем, какой ток протекает через узел D, но падение напряжения на диоде (практически) не зависит от величины тока, протекающего через него. Это делает наш расчет очень простым. Начиная с узла A и переходя к узлу B, мы получаем 5 В. Затем при переходе от узла B к узлу D напряжение падает на 0,6 В, когда оно проходит через диод. Это делает Vd равным 4,4 В.
\(\большой Vd = 0В + 5В – 0,6В = 4,4В\)
Теперь мы знаем напряжение в каждом узле, но не знаем ток, протекающий через узел D (Ib). На самом деле мы можем вычислить Ib двумя разными способами. Первый заключался в использовании KCL. Зная значения Ia и Ic, мы можем легко сбалансировать токи в узле B и из узла B, чтобы найти Ib. Мы знаем, что ток на входе (Ia) равен выходному току (Ib и Ic).
\(\большой Ia = Ib + Ic\)
\(\большой Ib = Ia – Ic = 32 мА – 22 мА = 10 мА\)
Мы также можем рассчитать это, используя закон Ома с напряжением узла D и сопротивление между узлом D и узлом A.
Мы знаем, что ток, протекающий через резистор от узла D к узлу A, равен напряжению, отличному от узла D и узла A, деленному на сопротивление.
\(\large I = \frac{V}{R} = \frac{4,4V – 0V}{440 \Omega} = 10mA\)
Предыдущий Основы схем – законы Ома и Джоуля
Содержание
Что такое закон Кирхгофа | Определение, примеры, схемы: Электронаправляющая
от Er. викаш
В этой статье мы прочитаем о Что такое Законы Кирхгофа в главе по физике. Это правило очень важно. Что такое закон Кирхгофа? Вопросы задаются в 10 и 12 классах, а также на других конкурсных экзаменах.
Что такое закон Кирхгофа, первый закон относится к току, а второй к напряжению, и когда ему дается соединение или соединение, петля, ветвь или ветвь. Чтобы понять первый закон Кирхгофа, сначала нужно понять три вещи: соединение и ответвление. Вы можете прочитать определение всех из них ниже.
Чтобы понять первый закон Кирхгофа, сначала нужно понять три вещи: соединение и ответвление. Вы можете прочитать определение всех из них ниже.
Кирхгоф был немецким физиком, который в 1842 году ученый Кирхгоф проводил некоторые электрические эксперименты. Ученый Кирхгоф дал два правила анализа электрических цепей, которые применимы во всех типах электрических сетей, эти законы показывают сохранение заряда и энергии, с помощью которых мы можем строить электрические сети любой конфигурации. На самом деле первый и второй законы Кирхгофа основаны на законе Ома, или можно сказать, что это приложение закона Ома, предназначенное для решения сложных схем. .
Что такое ветвь, по закону Кирхгофа понимать ту часть электрической цепи, где значение тока остается постоянным, эта часть называется ветвью, точка электрической цепи, где сходятся три или более ветвей, называется соединением, его называют узлом. А еще называется развязкой.
Что такое законы Кирхгофа
В электрических цепях иногда много резисторов и элементов соединены сложным образом. Выведенные нами ранее формулы для последовательного и бокового соединения не всегда достаточны для всех электрических токов и разностей потенциалов в цепи. Два закона, которые называются законами Киркгофа. Различные типы постоянного тока Ученый по имени Кирхгоф установил два правила для электрических цепей, а именно:
Выведенные нами ранее формулы для последовательного и бокового соединения не всегда достаточны для всех электрических токов и разностей потенциалов в цепи. Два закона, которые называются законами Киркгофа. Различные типы постоянного тока Ученый по имени Кирхгоф установил два правила для электрических цепей, а именно:
Первый действующий закон Кирхгофа
(i) Действующий закон: «Сумма токов, идущих к стыку проводников, равна сумме токов, идущих от соединения». Если токи, ведущие к слиянию, равны i1, i2, а токи, выходящие из слияния, равны i₃, i₄, i₅, то
i₁ + I₂ = i₃ + i₄ + i₅
входящие токи в любой точке (узле) цепи равны сумме выходных токов. То есть алгебраическая сумма токов в любом узле равна нулю.
∑ i = 0(ноль) ……(1)
i₁ + i₂ – i₃ – i₄ – i₅ = 0 ……(2)
Или + i₃ i₄ +
Первый закон Кирхгофа можно также записать как – «Сумма всех электрических токов, входящих в узел электрической цепи, равна сумме всех электрических токов, выходящих из этого соединения».
Таким образом, из уравнения видно, что сумма всех токов, приходящих к узлу, равна сумме всех токов, уходящих от этого узла. Другими словами, при протекании постоянного тока по цепи заряд не накапливается и не снимается ни с одного соединения цепи, т.е. в основе закона Кирхгофа лежит принцип сохранения заряда, он называется током Кирхгофа. говорят. Также называется правилом.
Второй закон напряжения Кирхгофа
(ii) Закон напряжения: Алгебраическая сумма обратных сил, действующих в замкнутой цепи, равна алгебраической сумме произведений токов, протекающих в ее ветвях, и сопротивлений этих ветвей. . Другими словами,
∑IR = ∑E ……(4)
Другими словами, потенциальный закон Кирхгофа применяется внутри контура, в котором несущая сила, приложенная в любой замкнутой цепи, равна алгебраической сумме потенциалы компонентов, присутствующих в цепи, то есть алгебраическая сумма разностей потенциалов компонентов в замкнутой цепи равна нулю. Закон Кирхгофа используется для определения величины тока в цепях смешанного типа. Второй закон Кирхгофа основан на сохранении энергии, его также называют Закон напряжения Кирхгофа.
Закон Кирхгофа используется для определения величины тока в цепях смешанного типа. Второй закон Кирхгофа основан на сохранении энергии, его также называют Закон напряжения Кирхгофа.
При расчетах следует учитывать следующие правила:
- Когда мы движемся в направлении тока, мы принимаем произведение тока и его соответствующего сопротивления положительным, а когда мы движемся в противоположном направлении ток, мы принимаем произведение тока и его соответствующего сопротивления отрицательным.
- В электролите элемента электродвижущая сила считается отрицательной при движении от отрицательного электрода к положительному электроду и считается положительной при движении от положительного к отрицательному электроду.
Разберем это на примере, предположим, что на данном рисунке есть электрическая цепь, в которой ток протекает через внешнее сопротивление R путем параллельного соединения ячеек, имеющих Е₁ или Е₂ соответственно, а внутреннее сопротивление этих ячеек равно р₁В.
соответственно. r₂ Теперь, если ток, отбираемый от этих ячеек, равен I₁ или I₂ соответственно и если ток через внешнее сопротивление R равен I₃, то по первому закону Кирхгофа на переходе D
i₃ = i₁ + i₂ …… (5)
теперь в цепи ADCBA в соответствии со вторым законом Кирхгофа,
I₁R₁ в цепи CDEFC,
I₂r₂ + (I₁ + I₂)R − E₂ = 0 ……(7)
По второму закону Кирхгофа в цепи AEFBA,
(I₁ + I₂)R E₁ = 0 ……(8)
При решении приведенного выше уравнения (6) или (7)
получаются значения I₁ или I₂.
Подробнее-
- Что такое сопротивление? | Формула, Комбинация, Закон
- Зачем нужно заземление?
- Что такое закон Ома
Вопросы- Найдите значение i3 в данной схеме –
SOL. Применить закон Кирхгофа для тока в данном узле.
i1 + i2 = i3 + i4 замените известное значение
2 + 9 = i3 + 4 Найдите i3 i3 = 7 A
Часто задаваемые вопросы
Вопрос-1 На какой величине основан второй закон Кирхгофа для электрической цепи?
Ответ: Закон сохранения энергии
Вопрос-2 Что такое закон сохранения заряда? / Что такое закон сохранения зарядов на хинди?
Ответ- Вы не можете ни создать, ни уничтожить заряд, этот заряд по своей сути бесплатный и может быть перенесен из одного места в другое.


 Теперь складываем все токи, втекающие в узел слева от знака равенства. В данном случае это только ток A. А токи, выходящие из узла, суммируются справа от знака равенства. это уравновешивает текущий вход и выход узла.
Теперь складываем все токи, втекающие в узел слева от знака равенства. В данном случае это только ток A. А токи, выходящие из узла, суммируются справа от знака равенства. это уравновешивает текущий вход и выход узла.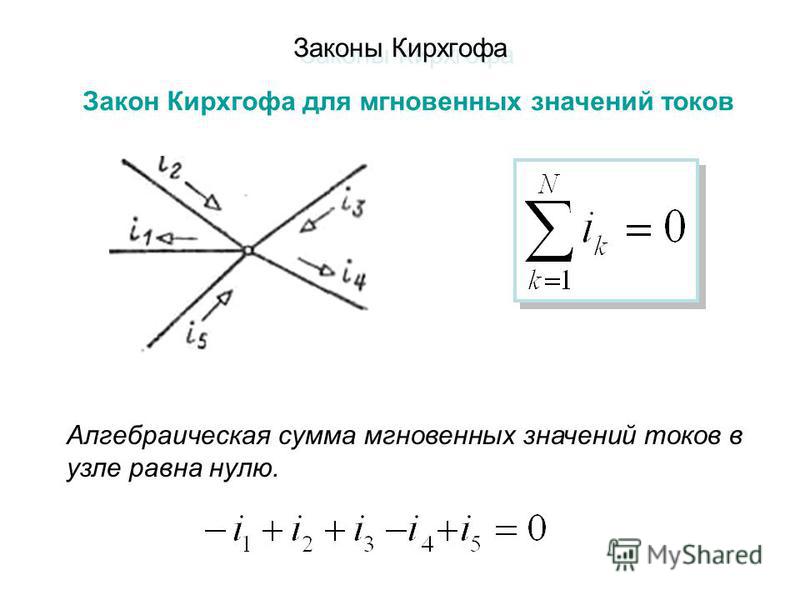 Используя KCL и KVL, мы можем найти эти пропущенные значения.
Используя KCL и KVL, мы можем найти эти пропущенные значения.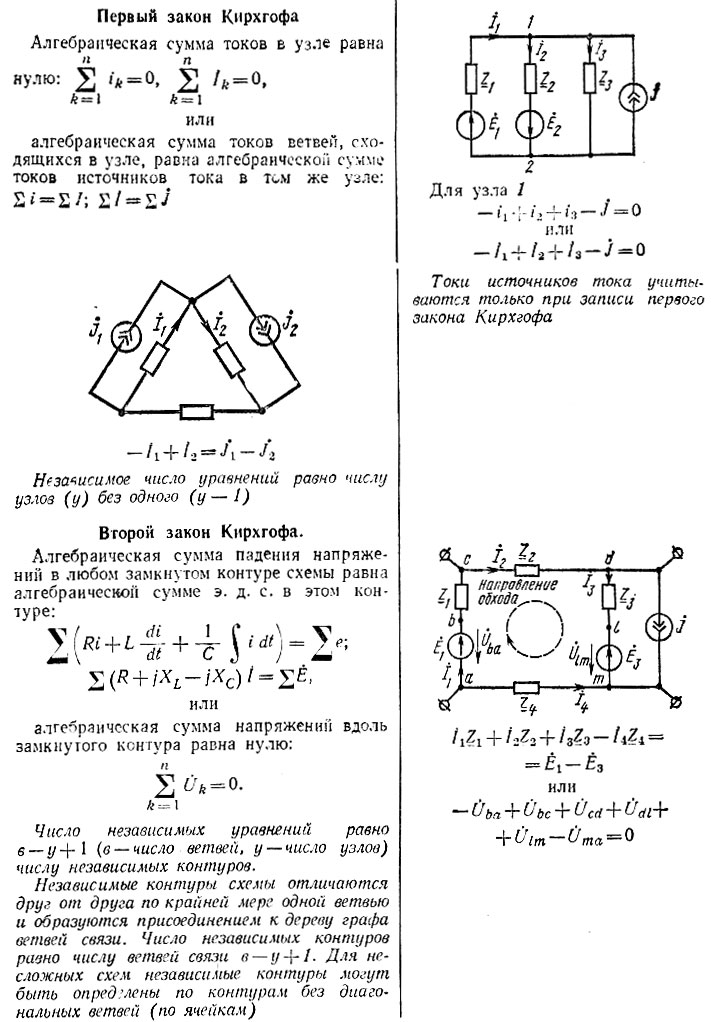
 Мы знаем, что ток, протекающий через резистор от узла D к узлу A, равен напряжению, отличному от узла D и узла A, деленному на сопротивление.
Мы знаем, что ток, протекающий через резистор от узла D к узлу A, равен напряжению, отличному от узла D и узла A, деленному на сопротивление.