План-конспект урока по информатике и икт (11 класс) на тему: Алгебра высказываний. Таблицы истинности основных логических операций
Урок по теме «Алгебра высказываний. Таблицы истинности основных логических операций»
Цели урока:
- Обучающая — познакомиться с логическими операциями, с помощью которых можно составлять сложные высказывания и научиться определять их истинность.
- Развивающая — развивать мышление учащихся посредством анализа, сравнения и обобщения изучаемого материала, самостоятельность, развитие речи;
- Воспитательная – аккуратность, усидчивость, стремление к достижению результата своей деятельности.
Тип урока: урок новых знаний.
Возраст учащихся: 11 класс.
Ход урока
- Оргмомент.
- Подготовка к восприятию нового материала, мотивация;
Учитель: На прошлых уроках мы с Вами познакомились с логикой как наукой, выяснили, какие формы мышления существуют. Сегодня на уроке мы остановимся на одной из этих форм – суждении (или высказывании). Запишем заголовок: Алгебра высказываний.
Учитель: Вспомним, что такое высказывание?
Ученик: Высказывание — это форма мышления, в котором что-то утверждается или отрицается об объектах или явлениях реальной действительности.
Учитель: Какие классификации высказываний вы знаете?
Ученик: Высказывания бывают простые и сложные, истинные и ложные
Учитель: Хорошо. На доске представлено два высказывания(слайд 1)
«Два умножить на 2 равно 4» и «Два умножить на два равно 5»
Что вы можете о них сказать?
Ученик: Первое высказывание истинно, а второе ложно.
Учитель: Давайте обозначим наши высказывания латинскими буквами A и B т.е.
А= «Два умножить на 2 равно 4»
В= «Два умножить на два равно 5»
И попробуем как бы перевести их на «математический язык», не рассматривая конкретное содержание (слушаем ответы учащихся и в итоге получаем)
А=1 (истина)
В=0 (ложь)
Вывод (в тетрадь): Все высказывания мы будем обозначать именами логических переменных – A, B, C, D и т. д., которые могут принимать только два значения – 1 и 0.
Учитель: А как же быть со сложными высказываниями? С помощью каких союзов в русском языке они образованы?
Ученик: С помощью союзов и, или, но, а, если…то, тогда и т. д.
Учитель: Получается, что эти союзы вы как бы тоже должны перевести на «язык математики». Для их обозначения используются логические операции, с которыми нам предстоит сегодня познакомится. А изучением этих логических операций занимается раздел логики – алгебра высказываний.
(В тетрадь) Алгебра высказываний была разработана для того, чтобы можно было определить истинность или ложность составных высказываний, не вникая в их содержание.
Учитель: Давай те приступим к изучению логических операций
- Изложение нового материала
(В тетрадь) Для образования сложных высказываний используются логические операции:
- Конъюнкция (и, ^, &)-
Рассмотрим следующие высказывания:
2*2=5 | 3*3=10 | |
2*2=5 | 3*3=9 | |
2*2=4 | 3*3=10 | |
2*2=4 | 3*3=9 |
Соединим их союзом и
2*2=5 | и | 3*3=10 |
2*2=5 | и | 3*3=9 |
2*2=4 | и | 3*3=10 |
2*2=4 | и | 3*3=9 |
и сделаем вывод об их истинности, обозначив высказывания первого столбца –А, второго – В, и придав им значение истинности с помощью 0 и 1 т.е.
Определим теперь истинность высказывания А& В (дети, рассуждая приходят к таблице)
Учитель: Итак, что же такое конъюнкция, и когда она истинна?
(В тетради) Конъюнкция (и, ^, &) – логическая операция, которая истинна тогда и только тогда, когда истинны оба высказывания.
Учитель: Перенесите таблицу с доски в тетрадь
Конъюнкцию называют логическим умножением, объясните почему?
Таким же образом доводим учащихся до определений остальных логических операций, т.е.
- Дизъюнкция(или, |, ∨) –
Рассмотрим следующие высказывания:
2*2=5 | или | 3*3=10 |
2*2=5 | или | 3*3=9 |
2*2=4 | или | 3*3=10 |
2*2=4 | или | 3*3=9 |
И приходим к выводу
(В тетради) Дизъюнкция(или, |, ∨) – логическая операция, которая ложна тогда и только тогда, когда ложны оба высказывания.
Учитель: Перенесите таблицу с доски в тетрадь
Дизъюнкцию называют логическим сложением, объясните почему?
- Отрицание(не,⎤) –
Рассмотрим следующие высказывания:
Число 5 — чётное |
Число 5 -нечётное |
(В тетради) Отрицание(не,⎤) – логическая операция, которая делает истинное высказывание ложным, а ложное – истинным.
Учитель: Перенесите таблицу с доски в тетрадь
- Импликация (Если…то, →,⇒) –
Рассмотрим следующие высказывания:
А= «Число делится на 10»
В= «Число делится на 5»
(Рассмотреть примеры – 22, 45, 50, 60)
(В тетради) Импликация (Если…то, →,⇒) – логическая операция, которая ложна тогда и только тогда, когда из истинности первого высказывания следует ложь второго.
Учитель: Перенесите таблицу с доски в тетрадь
А | В | А → В |
0 | 0 | 1 |
0 | 1 | 1 |
1 | 0 | 0 |
1 | 1 | 1 |
- Эквивалентность (Тогда и только тогда….В том, и только в том случае..↔,⇔) –
Рассмотрим следующие высказывания:
А= «Компьютер может производить вычисления»
В= «Компьютер включен»
(рассмотреть все варианты)
(В тетради) Эквивалентность (Тогда и только тогда….В том, и только в том случае..↔,⇔) – логическая операция, которая ложна тогда и только тогда, когда одновременно истинны или ложны оба высказывания.
Учитель: Перенесите таблицу с доски в тетрадь
А | В | А ⇔ В |
0 | 0 | 1 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
- Закрепление полученных знаний на практике
1 задание. Выделите в составных высказываниях простые. Обозначьте каждое из них буквой и запишите с помощью логических операций каждое составное высказывание
- Число 456 четное и трехзначное.
- Неверно, что Солнце движется вокруг Земли.
- Неверно, что принтер — устройство ввода информации и сканер — устройство вывода информации.
- Если на Новый год будет много снега, то мы пойдем на лыжах в лес или уедем кататься в горы.
2 задание. Найдите значение логических выражений:
- (1 \/ 1) & (1 \/ 0)
- (0& 1) \/ (1 \/ 0)
- 1 & (⎤1 \/ 1) & 1
- ((1 → 0) \/ (1 ↔ 0)) & 1
- Итог урока и постановка домашнего задания
Учитель: Сегодня мы с вами рассмотрели логические высказывания и логические операции. С какими операциями мы познакомились? Как нам проще запомнить ТИ этих операций? Вопросы по данной теме? Запишите домашнее задание – выучить таблицы значений основных логических операций + карточки
- (1 & 0) → (1 \/ 0)
- (0& ⎤1) \/ (0&1)
- 0 & (1 ↔0) \/ 1
- ((1 ↔ 0) \/ (0 → 1)) \/ 1
Конспект урока по информатике «Понятие высказывания и логические операции над высказываниями. Составление таблиц истинности»
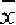
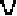
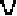
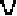
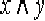
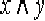 Подготовила: Гунченко Яна Александровна,
Подготовила: Гунченко Яна Александровна,учитель математики и информатики
МОУ «Казинская СОШ»
Валуйского района Белгородской области
Тема: «Понятие высказывания и логические операции над высказываниями. Составление таблиц истинности»
Цели и задачи занятия: (слайд 2)
Образовательные: познакомить обучающихся с краткой историей возникновения булевой алгебры, логическими операциями над высказываниями; научить составлять таблицы истинности; способствовать развитию у учащихся логического мышления.
Развивающие: развивать внимание, память, речь, мыслительную деятельность учащихся, умения анализировать, обобщать и наблюдать, сравнивать, выделять главное, делать выводы.
Воспитательные:
Ход занятия:
Организационный момент
Изложение нового материала
Историческая справка
В XVII веке великий немецкий учёный Лейбниц задумал создать свою новую логику, которая была бы «искусством исчисления». Он считал, что основные понятия должны быть обозначены символами, которые соединяются по определённым правилам, и это позволяет всякие рассуждения заменить вычислением.
Первая реализация идеи Лейбница принадлежит математику Джорджу Болю.
Джордж Буль родился в Англии 2 ноября 1815 года. Всю свою жизнь он работал учителем математики и физики в школе. Из воспоминаний его учеников известно, какое огромное значение придавал Буль развитию творческих способностей учащихся. При изложении нового материала он стремился к тому, чтобы его ученики сами заново «открывали» некоторые формулы и законы.
Рассказывая ученикам о трудностях, с которыми ученые неизбежно сталкивались в поиске истины, учитель любил повторять одну восточную мудрость: даже персидский трон не может принести человеку столько наслаждений, как самое маленькое научное открытие. Буль никогда не терял надежды, что когда-нибудь и его ученики сделают настоящее открытие.
Диапазон научных интересов Буля был очень широк: в равной степени его интересовали математика и логика — наука о законах и формах мышления. В те времена логика считалась гуманитарной наукой, и многих, кто знал Джорджа Буля, удивляло, как в одном человеке могли уживаться точные методы познания, присущие математике, и чисто описательные методы логики.
Но ученому захотелось сделать науку о законах и формах мышления такой же строгой, как и любая из естественных наук, скажем математика и физика. Для этого Буль стал обозначать буквами не числа, как это делается в обычной алгебре, а высказывания и показал, что такими уравнениями, очень схожими с алгебраическими, можно решать вопросы об истинности и ложности высказываний, сделанных человеком. Так возникла алгебра Буля.
В наши дни алгебра логики стала важнейшей составной частью математики. Одна из ее задач — это решение всевозможных уравнений, числовые соотношения в которых заменены буквенными. Каждый из вас, наверное, на всю свою жизнь запомнил, как решать уравнения второй и третьей степени с буквенными коэффициентами. Так вот, Буль в своей новой алгебре воспользовался всеми этими формулами и правилами.
Новым в алгебре Буля является то, что элементы множества, которые в ней изучаются, являются не числами, а высказываниями. Если при решении обычных алгебраических уравнений определяется, какому числу равняется неизвестное X, школьная алгебра ищет ответ на вопрос: «Сколько?»
Алгебра логики ищет ответ на вопрос: «Верно ли то или другое высказывание, обозначенное буквой X?»
Смысл и содержание высказывания здесь не играют никакой роли. Каждое высказывание может быть только или истинным, или ложным. Оно не может быть наполовину истинным и наполовину ложным. В качестве примера можно вспомнить метание жребия при помощи монеты.
Там рассматриваются только два состояния монеты — орел или решка. По договоренности сторон орел это ДА, а решка это НЕТ. Никакие другие промежуточные положения в теории вероятностей не учитываются, хотя они и возможны. Подброшенная монета может упасть на ребро, докатиться по полу до ножки стула или стола и так и остаться в вертикальном положении, а то и вообще провалиться в широкую щель в полу. (По аналогии с электрическими схемами две последних ситуации можно рассматривать как неисправность в виде обгоревшего контакта). Но в те далекие времена булева алгебра, увы, широкого распространения не получила.
Вновь «открыл» алгебру Буля Клод Шеннон. (слайд 4) В 1938 году, будучи еще студентом Массачусетского технологического института и Америке, молодой Клод доказал, что алгебра Буля полностью подходит для анализа и синтеза релейных и переключательных схем. С помощью алгебры Буля можно очень просто составить электрическую схему автомата, работающего на реле.
Для этого, оказывается, нужно только точно знать, что должен делать автомат, то есть нужно иметь алгоритм его работы. Так была заложена основа теории цифровых машин, действующих по принципу ДА или НЕТ.
Понятие высказывания (суждения)
Высказывание (суждение) — связное повествовательное предложение, о котором можно сказать, истинно оно или ложно. (слайд 5)
Примеры:
«5 > 3» – истинное высказывание.
«Сочи – столица России» — ложное высказывание.
«Астрономия – интересный предмет». Данное предложение не является высказыванием, так как не имеет единого мнения о том, истинно это предложение или ложно.
« y > 7, y Є Z». Предложение не является высказыванием из-за присутствия в нем переменной.
Выделяют общие и частные суждения.
Общие суждения выражают свойства групп объектов или явлений, а частные – конкретные (частные) факты.
Примеры:
«Некоторые ученики — двоечники» — частное, истинное;
«Любой квадрат является прямоугольником»- общее, истинное;
Логические операции и таблицы истинности
Логические операции — мыслительные действия, результатом которых является изменение содержания или объема понятий, а также образование новых понятий.
1) Логическое умножение или конъюнкция: (слайд 6)
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Таблица истинности для конъюнкции
х
у
1
1
1
0
0
0
1
0
0
0
0
Пример.
x – «6 делится на 2», y – «6 делится на 3». Тогда – «6 делится на 2»«6 делится на 3» истинно.
2) Логическое сложение или дизъюнкция: (слайд 7)
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
х
у
xy
1
1
1
1
0
1
0
1
1
0
0
0
Пример.
x – «5>3», y – «2>4». Тогда xy – «5>3»«2>4» истинно, так как истинно высказывание x.
3) Логическое отрицание или инверсия: (слайд 8)
Инверсия — это сложное логическое выражение, если исходное логическое выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное логическое выражение ложно, то результат отрицания будет истинным. Другими простыми слова, данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Таблица истинности для инверсии
х
1
0
0
1
4) Логическое следование или импликация: (слайд 9)
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (х), а второе (у) является следствием.
Таблица истинности для импликации
х
у
x→y
1
1
1
1
0
0
0
1
1
0
0
1
Пример.
1) x – «12 делится на 6», y – «12 делится на 3». Тогда импликация x→y – «если 12 делится на 6, то оно делится на 3» истинна, так как истинна посылка x, и истинно заключение y.
2) x – «12 делится на 2 и 3», y – «12 делится на 7». Тогда импликация x→y – «если 12 делится на 2 и 3, то оно делится на 7» ложна, так как условие истинно, а заключение ложно.
5) Логическая равнозначность или эквивалентность: (слайд 10)
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Таблица истинности для эквивалентности
х
у
x↔y
1
1
1
1
0
0
0
1
0
0
0
1
Пример.
x – «Треугольник ABC с вершиной A и основанием BC равнобедренный», y – «B=C». Эквиваленция x↔y – «Треугольник ABC с вершиной A и основанием BC равнобедренный тогда и только тогда, когда B=C.» Эквиваленция x↔y истинна, так как высказывания x и y либо одновременно истинны, либо одновременно ложны.
Порядок выполнения логических операций в сложном логическом выражении (слайд 11)
1.Инверсия;
2.Конъюнкция;
3.Дизъюнкция;
4.Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Закрепление изученного
1. Определите, какие из перечисленных предложений являются суждениями и каково их значение истинности: (слайд 12)
«Зеленая доска» — не суждение;
«В настоящий момент все ученики 9 «А» присутствуют на уроке информатики и внимательно слушают» — суждение, ложное;
«Вы сегодня готовы к уроку?» — не суждение;
«Учиться хорошо может не каждый» — суждение, истинное;
«Посмотрите на доску» — не суждение;
«В конце любого урока звенит звонок» — суждение, истинное;
«3+5=9» — суждение, ложное.
2. Определите, какие из суждений являются частными, а какие общими и каково их значение истинности: (слайд 13)
1)«Владивосток – столица Албании» — частное, ложное;
2) «У всех уличных люков крышка круглая, а не квадратная потому, что она не может соскользнуть в люк, если поставить ее на ребро» — общее, истинное;
3)« Для любого х, х2> 0» — общее, ложное;
4)«Все компьютеры в этом кабинете рабочие» — общее, ложное.
3.Построим таблицу истинности логического выражения: 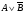 . (слайд 14)
. (слайд 14)
1)Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2)Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум и количество логических операции двум, то есть количество столбцов таблицы истинности равно четырём.
3)Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
A
B
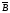
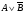
0
0
1
1
0
1
0
0
1
0
1
1
1
1
0
1
4. Построить таблицу истинности для высказывания: (слайд 15)
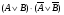
1)Определим количество строк в таблице. Для этого: считаем количество переменных, в нашем случае логическая функция содержит 2 переменные: А и В.
Количество строк в таблице истинности должно быть равно 22=4.
2)Определяем количество столбцов. Это количество логических переменных плюс количество логических операций.
В нашем случае количество переменных равно двум, а количество логических операции — пяти, то есть количество столбцов таблицы истинности равно семи.
3)Строим таблицу с указанным количеством строк и столбцов, обозначаем столбцы и вносим в таблицу возможные наборы значений исходных логических переменных и заполняем таблицу истинности по столбцам.
Можно сначала выполнить логическое отрицание или найти значение сначала в первой скобке, затем инверсию и значение во второй скобке, затем значение между этими скобками.
A
B
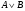
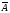
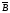
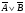
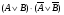
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
4.Подведение итогов занятия.
Обобщить пройденный материал, оценить работу активных учеников.
Домашнее задание. (слайд 16)
Построить таблицу истинности для формулы: 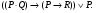
Использованный источники:
Д.А. Беликов, Е.В. Каминская «Информатика. Основы алгебры высказываний: Учебно-методический комплекс» / Томск: ТГУ, 2011
Электрик инфо [Электронный ресурс]. – Режим доступа: http://electrik.info/main/fakty/229-buleva-algebra-chast-1-nemnogo-istorii.html (Дата обращения: 13.06.2015).
С.В. Костенко, Т.А. Маничева, А.П. Филимонова «Элементы математической логики с приложением: Учебно-методическое пособие» / Благовещенск: Амурский гос. ун-т, 2002.
Информационно-образовательная среда СГЭУ [Электронный ресурс]. – Режим доступа: http://ios.sseu.ru/public/eresmat/metod/met6/parmet6_2.htm (Дата обращения: 14.06.2015).
Webmath.ru Образовательные онлайн сервисы [Электронный ресурс]. – Режим доступа: http://www.webmath.ru/poleznoe/tables_istinnosti.php (Дата обращения: 14.06.2015).
Логические операции и таблицы истинности
Логические операции над высказываниями
1. Отрицание.
Эта логическая операция соответствует в обыденной жизни частице «не».
Определение. Отрицанием высказывания x называется новое высказывание, которое является истинным, если высказывание 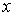 ложно, и ложным, если высказывание x истинно.
ложно, и ложным, если высказывание x истинно.
Отрицание высказывания x обозначается 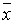 и читается не x. Логические значения высказывания
и читается не x. Логические значения высказывания 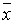 модно описать с помощью таблицы, которая называется таблицей истинности:
модно описать с помощью таблицы, которая называется таблицей истинности:
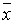
1
0
0
1
Пусть x высказывание. Так как 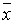 тоже высказывание, то можно образовать отрицание высказывания
тоже высказывание, то можно образовать отрицание высказывания 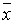 , то есть высказывание
, то есть высказывание 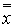 , которое является двойным отрицанием высказывания x. Логические значения высказываний
, которое является двойным отрицанием высказывания x. Логические значения высказываний 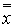 и xсовпадают.
и xсовпадают.
2. Дизъюнкция (логическое сложение).
Эта логическая операция соответствует союзу «или».
Определение. Дизъюнкцией двух высказываний x, y называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний x или y истинно и ложным, если они оба ложны.
Дизъюнкция высказываний x, y обозначается x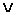 y и читается «x или y». Логические значения дизъюнкции описываются таблицей истинности:
y и читается «x или y». Логические значения дизъюнкции описываются таблицей истинности:
y
x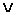 y
y
1
1
1
1
0
1
0
1
1
0
0
0
Высказывания x, y называются членами дизъюнкции.
Пример.
x – «5>3», y – «2>4». Тогда x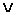 y – «5>3»
y – «5>3»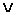 «2>4» истинно, так как истинно высказывание x.
«2>4» истинно, так как истинно высказывание x.
В алгебре логики союз «или» всегда употребляется в неисключающем смысле. Из определения дизъюнкции и отрицания следует, что высказывание x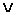
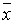 всегда истинно.
всегда истинно.
3. Конъюнкция.
Эта логическая операция соответствует союзу «и».
Определение. Конъюнкцией двух высказываний x, y называется новое высказывание, которое считается истинным, если оба высказывания x, y истинны, и ложным, если хотя бы одно из них ложно.
Конъюнкция высказываний x, y обозначается 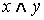 и читается «x и y». Высказывания x, y называются членами конъюнкции. Логические значения конъюнкции описываются следующей таблицей истинности:
и читается «x и y». Высказывания x, y называются членами конъюнкции. Логические значения конъюнкции описываются следующей таблицей истинности:
y
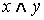
1
1
1
1
0
0
0
1
0
0
0
0
Пример.
x – «6 делится на 2», y – «6 делится на 3». Тогда 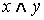 – «6 делится на 2»
– «6 делится на 2»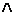 «6 делится на 3» истинно.
«6 делится на 3» истинно.
Из определения операции конъюнкции видно, что союз «и» в алгебре логики употребляется в том же смысле, что и в повседневной речи. Но в обычной речи не принято соединять союзом «и» два высказывания, далеких друг от друга по содержанию, а в алгебре логики рассматривается конъюнкция двух любых высказываний.
Из определения операций конъюнкции и отрицания следует, что высказывание 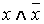 всегда ложно.
всегда ложно.
4. Импликация.
Эта логическая операция соответствует словам «если…,то…».
Определение. Импликацией двух высказываний x, y называется новое высказывание, которое считается ложным, если x истинно, а y ложно, и истинным во всех остальных случаях.
Импликация высказываний обозначается x→y и читается «если x, то y» или «из x следует y». Высказывание x называется условием или посылкой, а высказывание y – следствием или заключением. Высказывание x→y называется следованием или импликацией. Логические значения операции импликации описываются следующей таблицей истинности:
xy
x→y
1
1
1
1
0
0
0
1
1
0
0
1
Пример.
1) x – «12 делится на 6», y – «12 делится на 3». Тогда импликация x→y – «если 12 делится на 6, то оно делится на 3» истинна, так как истинна посылка x, и истинно заключение y.
2) x – «12 делится на 2 и 3», y – «12 делится на 7». Тогда импликация x→y – «если 12 делится на 2 и 3, то оно делится на 7» ложна, так как условие истинно, а заключение ложно.
Употребление слов «если…,то…» в алгебре логики отличается от употребления их в обыденной речи, когда, как правило, считается, что если высказывание x ложно, то высказывание «если x, то y» вообще не имеет смысла. Кроме того, строя предложение «если x, то y» в обыденной речи всегда подразумевается, что предложение y вытекает из предложения x. Употребление слов «если…, то…» в математической логике не требует этого, так как в ней смысл высказываний не рассматривается.
Импликация играет важную роль в математических доказательствах, так как многие теоремы формулируются в условной форме «если x, то y». Если при этом известно, что x истинно и доказана истинность импликации x→y то истинно и заключение y. В этом случае пишут x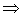 y и говорят, что из x следует y. Это классическое правило вывода постоянно используется в математике.
y и говорят, что из x следует y. Это классическое правило вывода постоянно используется в математике.
1. Эквиваленция.
Эта логическая операция соответствует словам «тогда и только тогда, когда».
Определение. Эквиваленцией или эквивалентностью двух высказываний x, y называется новое высказывание, которое считается истинным, если оба высказывания x, y либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях.
Эквиваленция высказываний x, y обозначается символом x↔y и читается «для того чтобы x, необходимо и достаточно, чтобы y» или «x тогда и только тогда, когда y». Логические значения операции эквиваленции описываютсяследующей таблицей истинности:
xy
x↔y
1
1
1
1
0
0
0
1
0
0
0
1
Высказывания x, y называются членами эквиваленции.
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
2. определить число строк в таблице по формуле m=2n, где n — количество переменных;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
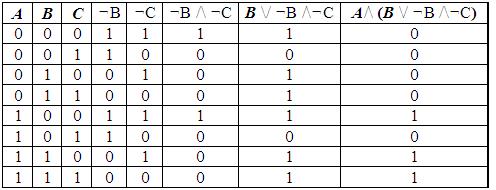
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 23 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
Пример 2. Определите истинность логического выражения F(А, В) = (А\/ В)/\(¬А\/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
А
В
А\/ В
¬А
¬В
¬А\/¬В
F
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Пример 3. Построёте таблицу истинности для логического выражения
F = (A\/ B) /\ ¬С
В данной функции три логические переменные – А, В, С
количество строк таблицы = 23 =8
В формуле 3 логические операции.
Расставляем порядок действий
1) А\/ В; 2) ¬С; 3) (AVB) /\ ¬С .
количество столбцов таблицы = 3 + 3 = 6
В
С
A\/B
¬С
(A\/B) /\ ¬С
0
0
0
0
1
0
0
0
1
0
0
0
0
1
0
1
1
1
0
1
1
1
0
0
1
0
0
1
1
1
1
0
1
1
0
0
1
1
0
1
1
1
1
1
1
1
0
0
Пример 4. Определите истинность формулы: F = ((С \/В) В) /\ (А /\ В) => В.
Построим таблицу истинности этой формулы.
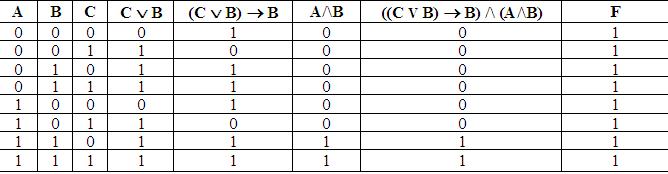
Ответ: формула является тождественно истинной.
Пример 5. Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.
Дан фрагмент таблицы истинности выражения F:
X
Y
Z
F
0
0
0
1
0
0
1
0
0
1
0
1
Какое выражение соответствует F?
1) ¬X/\¬Y/\Z 2) ¬X\/¬Y\/Z 3) X\/Y\/¬Z 4) X\/Y\/Z
Решение (вариант 1, через таблицы истинности):
Чтобы решить данную задачу можно построить часть таблицы истинности для каждой из четырех функций, заданных в ответе для заданных наборов входных переменных, и сравнить полученные таблицы с исходной:
XY
Z
F
¬X
¬Y
¬Z
¬X/\¬Y/\Z
¬X\/¬Y\/Z
X\/Y\/¬Z
X\/Y\/Z
0
0
0
1
1
1
1
0
1
1
0
0
0
1
0
1
1
0
1
1
0
1
0
1
0
1
1
0
1
0
1
1
1
Очевидно, что значения заданной функции F совпадают со значениями выражения X\/Y\/¬Z. Следовательно, правильный ответ – 3.
Ответ: 3
Решение (Вариант 2):
Чтобы не строить таблицу истинности для каждого выражения, можно просто перепроверить предложенные ответы по заданной таблице истинности. Т.е. в каждую из четырех предложенных функций последовательно подставлять значения переменных X, Y и Z, из заданной таблицы истинности и вычислять значения логического выражения. Если значения вычисляемого выражения совпадут со значением F во всех трех строчках заданной таблицы, то это и есть искомое выражение.
Рассмотрим данный конкретный пример:
1) первое заданное выражение ¬X/\¬Y/\Z = 0 при X=0, Y=0, Z=0, что не соответствует первой строке таблицы;
2) второе заданное выражение ¬X\/¬Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы;
3) третье выражение X\/Y\/¬Z соответствует F при всех предложенных комбинациях X,Y и Z;
4) четвертое выражение X\/Y\/Z = 1 при X=0, Y=0, Z=1, что не соответствует второй строке таблицы.
Ответ: 3
Для самостоятельного выполнения
Построить таблицу истинности для выражения
F= (AVB) & (¬AV¬B)
XVY& ¬Z.

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X,Y,Z. Дан фрагмент таблицы истинности выражения F:
Y
Z
F
0
0
0
1
0
0
1
0
0
1
0
1
Какое выражение соответствует F
¬X /\ ¬Y /\ Z
¬X V ¬Y V Z
X V Y V¬Z
X V Y V Z
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X,Y,Z. Дан фрагмент таблицы истинности выражения F:
Y
Z
F
1
0
0
1
0
0
0
1
1
1
1
0
Какое выражение соответствует F?
¬X /\¬Y /\¬Z
X /\ Y /\ Z
X V Y V Z
¬ X V¬Y V¬Z
Урок информатики «Таблицы истинности логических выражений»
Конспект урока по информатике в 8 классе
Тема: Сложные высказывания. Таблицы истинности
Тип урока: урок закрепления.
Цели:
Сформировать у учащихся навыки построения таблиц истинности и работы со сложными логическими выражениями.
Воспитание целостного представления о естественно-математических дисциплинах, установление межпредметных связей.
Развитие навыков обобщения и анализа.
Оборудование: презентация PowerPoint, памятки по логическими операциям, программа тестирования.
Ход урока
А
 ктуализация опорных знаний (3 мин.). Сегодня мы продолжим знакомство с алгеброй логики, научимся составлять сложные логические выражения и их таблицы истинности. (Записываем в тетрадях тему).
ктуализация опорных знаний (3 мин.). Сегодня мы продолжим знакомство с алгеброй логики, научимся составлять сложные логические выражения и их таблицы истинности. (Записываем в тетрадях тему).
Что изучает алгебра логики и какие есть логические операции мы вспомним, выполнив задание (на слайде). Установите соответствие между пунктами первого и второго столбцов:
Работа со сложных высказываниями. (20 мин)
Алгебра логики изучает высказывания, которые или истинны или ложны. С помощью логических операций из простых высказываний можно построить составные.
На прошлом уроке мы познакомились с таблицами истинности логических операций. Повторим их по памяткам и с помощью слайда.
Логические операции имеют определённый приоритет:
действия в скобках, инверсия, &, Ú , Þ , Û (записываем в тетрадях).
Вспомним, как с помощью логических союзов формулируются сложные высказывания и определим их истинность (устно по слайдам).
Письменное задание (в тетрадях и у доски).
Найдите значения логических выражений:
(1Ú1)&(1 Ú 0)
(1&0 Ú 0&0) Þ1
(
 (1&1) Ú 0)Û(0Ú1)
(1&1) Ú 0)Û(0Ú1)
Решение логических задач с помощью составления таблиц истинности.(10 мин)
Задача. В классе оказалось разбито стекло. Учитель объясняет директору: это сделал Коля или Саша. Но Саша этого не делал, т.к. в это время сдавал мне зачет. Следовательно, это сделал Коля. Логично ли рассуждает учитель?
Решение: Для того, чтобы ответить на вопрос формализуем данное сложное высказывание. Обозначим высказывание
К – это сделал Коля
С – это сделал Саша
Составим сложное высказывание (К C ) & С К. Всегда ли верно это высказывание? Как это узнать? Надо перебрать все возможные значения переменных. Будем делать это в таблице, называемой таблицей истинности (записываем на доске и в тетрадях).
Составим логическое выражение ответа мамы и предполагаемые действия Васи:
( А В) = А В (Закон де Моргана)
Проверим правильность этого закона с помощью таблицы истинности.
В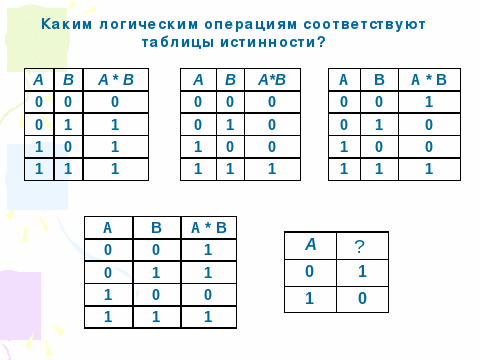 ыполняем по вариантам (1 вариант составляет таблицу истинности для первого выражения, 2 вариант – для второго). Результаты сравниваем.
ыполняем по вариантам (1 вариант составляет таблицу истинности для первого выражения, 2 вариант – для второго). Результаты сравниваем.
Закрепление перед тестированием по слайду:
Компьютерное тестирование(7 мин).
Подведение итогов и выставление оценок (2 мин).
Д/з: с.129-132, №3.2 (письм.)
План-конспект урока по информатике и икт (9 класс) на тему: Основные понятия алгебры логики. Логические выражения и логические операции
Тема урока: «Основные понятия алгебры логики. Логические выражения и логические операции»
Тип урока: открытия новых знаний.
УУД:
личностные — понимание роли фундаментальных знаний как основы современных информационных технологий;
метапредметные – навыки формализации и анализа логической структуры высказываний; способность видеть инвариантную сущность во внешне различных объектах;
предметные – представление об основных логических операций, правила определения их истинности
Задачи урока:
- Знакомство с логическими операциями и приоритетом их выполнения;
- Отработка умений составления логических выражений, соответствующих сложным высказываниям.
- Умение определять истинность сложных высказываний, связанных логическим умножением, сложением и отрицанием
Ход урока
1. Организационный момент
Приветствие учителем учащихся, выявление отсутствующих, проверка подготовленности к уроку, организация внимания.
2.Мотивация (самоопределения) к учебной деятельности.
3.Открытие нового знания.
Запишите, пожалуйста, тему урока «Основные понятия алгебры логики. Логические выражения и логические операции». Но обратите внимание слово ЛОГИКА в сочетание со словом АЛГЕБРА. (Слайд 1)
Алгебра – это раздел математики, предназначенный для описания действий над переменными величинами, которые принято обозначать строчными латинскими буквами, например a, b, x, y и т.д.
Что же изучает алгебра? (числа, числовые величины, числовые выражения, а также правила выполнения действий над ними).
Что же изучает логика? Логика – (от древнегреч. — слово, мысль, понятие, рассуждение, закон) — наука о законах и формах мышления (понятие, высказывание, умозаключение).
Давайте попробуем понять, чем же занимается алгебра логики!? Алгебра логики изучает общие операции над высказываниями. Основы данной алгебры были положены английским математиком Джорджем Булем в 19 веке, также её называли булевой алгеброй. (Слайд 2)
Давайте вспомним, что же такое высказывание?
Высказывание (суждение) — это повествовательное предложение, в котором что-либо утверждается или отрицается. По поводу любого высказывания можно сказать истинно оно или ложно.(Слайд 3)
Пример 1.
Давайте определим с вами, какое предложение мы можем назвать логическим высказывание.
«Москва – столица РФ». Можно ли в отношении этого высказывания однозначно сказать «истинно» оно или «ложно»? Да, можно. Данное высказывание «истинно», поэтому его можно назвать логическим высказывание.
«Информатика – интересный предмет». В отношении этого высказывания нельзя однозначно сказать «ложно» оно или «истинно». Кому-то информатика нравится, кто-то к ней равнодушен, кто-то вообще не любит.
Пример 2.
Определите истинность высказываний.
- Треугольник – геометрическая фигура.
- У каждой лошади есть хвост.
- Париж — столица Китая.
- Лед – твердое состояние воды.
- Все люди космонавты.
Основные понятия логики.
В алгебре логики высказывания обозначаются именами логических переменных (А, В, С), которые могут принимать значения истина (1) или ложь (0).
Истина, ложь – логические константы. (Слайд 4)
Логическое выражение – простое или сложное высказывание. Сложное высказывание строится из простых с помощью связок «И», «ИЛИ», «НЕ», которые в алгебре логики заменяются на логические операции.(Слайд 5, 6)
Логические операции.
Рассмотрим три основные (базовые) логические операции.
1. Отрицание или инверсия – добавляется частица НЕ или слова НЕВЕРНО,ЧТО, обозначается символом ¬ , ¯.
Пусть A – Сейчас на дворе лето.
Вывод: если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот, если исходное выражение ложно, то оно будет истинным. (Слайд 7).
2. Конъюнкция( логическое умножение) – соединение двух логических выражений (высказываний ) с помощью союза И. Эта операция обозначается символами & и .
Правила выполнения логической операции отражаются в таблице, которая называется таблицей истинности:
Вывод: логическая операция «конъюнкция» истинна тогда и только тогда, когда оба логических выражения истинны. (Слайд 8, 9)
3. Дизъюнкция (логическое сложение) – соединение двух логических высказываний с помощью союза ИЛИ. Эта операция обозначается значком V.
Рассмотрим таблицу истинности для данной логической операции.
Обозначим через A — летом я поеду в лагерь, B – летом я поеду в к бабушке.
AVB — Летом я поеду в лагерь или поеду к бабушке.
Вывод: Логическая операция «конъюнкция» ложна тогда и только тогда, когда оба простых высказывания ложны, в противном случае она истинна.
Методическая разработка по информатике и икт (9 класс) по теме: Логические выражения и базовые логические операции. Таблицы истинности.
По теме: методические разработки, презентации и конспекты
 Элементы математической логики. Логические операции. Конструирование логических выражений с использованием отношений и логических операций
Элементы математической логики. Логические операции. Конструирование логических выражений с использованием отношений и логических операций При обучении в школе важное значение имеет предмет «Информатика и ИКТ». Один из разделов теоретического курса – логика – рассматривает законы и правила логического мышления, которые являют…
Самостоятельная работа по теме «Логичесие операции. Таблицы истинности»Самостоятельная работа состоит из четырех вариантов, расчитана на 15 минут. Использованы задания для подготовки к ЕГЭ (А3) из материалов К. Полякова (http://kpolyakov.narod.ru/school/ege.htm, дата обр…
 Презентация к уроку информатики «Логические операции и таблицы истинности. Решение задач.»
Презентация к уроку информатики «Логические операции и таблицы истинности. Решение задач.»Презентация к уроку информатики «Логические операции и таблицы истинности»Данная презентация состоит из разделов:Логические операции, примеры;Порядок выполнения логических операций;Примеры решен…
 Алгебра высказываний. Таблицы истинности основных логических операций
Алгебра высказываний. Таблицы истинности основных логических операцийКласс: 9-11 классТема: Алгебра высказываний. Таблицы истинности основных логических операцийТип урока: урок изучения нового материалаПродолжительность занятия: 45 минут…
 Презентация к уроку по теме: «Логические операции. Составление таблиц истинности».
Презентация к уроку по теме: «Логические операции. Составление таблиц истинности».Составления таблиц истинности с примениний знаний логических операций….
 Логические операции. Построение таблиц истинности.
Логические операции. Построение таблиц истинности.Разработка урока по теме «Алгебра логики». Таблицы истинности….
 Проверочная работа по упрощению логических выражений и по логическим схемам
Проверочная работа по упрощению логических выражений и по логическим схемамРабота проверяет знания учащихся на упрощение логических выражений по основным логическим законам и построению и распознованию логических схем….


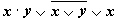
 ктуализация опорных знаний (3 мин.). Сегодня мы продолжим знакомство с алгеброй логики, научимся составлять сложные логические выражения и их таблицы истинности. (Записываем в тетрадях тему).
ктуализация опорных знаний (3 мин.). Сегодня мы продолжим знакомство с алгеброй логики, научимся составлять сложные логические выражения и их таблицы истинности. (Записываем в тетрадях тему). (1&1) Ú 0)Û(0Ú1)
(1&1) Ú 0)Û(0Ú1)