Список логических символов — Википедия

Символ	Название	Объяснение	Примеры	Значение Unicode	Название в HTML	Символ LaTeX
	Читается как
	Категория
	Импликация	A ⇒ B верно, только когда либо A ложно, либо B истинно. → может означать то же самое, что и ⇒ (символ может также указывать область определения и область значений функции, см. таблицу математических символов). ⊃ может означать то же самое, что и ⇒ (символ может также обозначать надмножество).	x = 2  ⇒  x2 = 4 истинно, но x2 = 4   ⇒  x = 2, в общем случае, ложно (поскольку x может быть равен −2).	U+21D2 U+2192 U+2283	⇒ → ⊃	⇒{\displaystyle \Rightarrow }\Rightarrow →{\displaystyle \to }\to ⊃{\displaystyle \supset }\supset ⟹{\displaystyle \implies }\implies
	из .. следует; если .. то
	логика высказываний, алгебра Гейтинга[en]
	Тогда и только тогда	A ⇔ B истинно, только если оба значения A и B ложны, либо оба истинны.	x + 5 = y + 2  ⇔  x + 3 = y	U+21D4 U+2261 U+2194	⇔ ≡ ↔	⇔{\displaystyle \Leftrightarrow }\Leftrightarrow ≡{\displaystyle \equiv }\equiv ↔{\displaystyle \leftrightarrow }\leftrightarrow ⟺{\displaystyle \iff }\iff
	тогда и только тогда
	логика высказываний
	отрицание	Утверждение ¬A истинно тогда и только тогда, когда A ложно. Знак /, расположенный поверх другого оператора, означает то же самое, что «¬», помещённое перед выражением.	¬(¬A) ⇔ A x ≠ y  ⇔  ¬(x = y)	U+00AC U+02DC	¬ ˜ ~	¬{\displaystyle \neg }\lnot или \neg ∼{\displaystyle \sim }\sim
	not (не)
	логика высказываний
	конъюнкция	Утверждение A ∧ B истинно, если и A, и B истинны, и ложно в противном случае.	n < 4  ∧  n >2  ⇔  n = 3, если n  — натуральное число.	U+2227 U+0026	&and; &amp;	∧{\displaystyle \wedge }\wedge или \land \&[2]
	and (и)
	логика высказываний, Булева алгебра
	логическая дизъюнкция	Утверждение A ∨ B верно, если A или B (или оба) верны. Если оба не верны, утверждение неверно.	n ≥ 4  ∨  n ≤ 2  ⇔ n ≠ 3 когда n является натуральным числом.	U+2228	&or;	∨{\displaystyle \lor }\lor или \vee
	or (или)
	логика высказываний, Булева алгебра
	исключающее или	Утверждение A ⊕ B верно, когда либо A, либо B верно, но не оба. A ⊻ B означает то же самое.	(¬A) ⊕ A всегда верно, A ⊕ A всегда неверно.	U+2295 U+22BB	&oplus;	⊕{\displaystyle \oplus }\oplus ⊻{\displaystyle \veebar }\veebar
	xor
	логика высказываний, Булева алгебра
	Тавтология	Утверждение ⊤ безусловно верно.	A ⇒ ⊤ всегда верно.	U+22A4	T	⊤{\displaystyle \top }\top
	верх
	логика высказываний, Булева алгебра
	Противоречие	Утверждение ⊥ безусловно неверно.	⊥ ⇒ A всегда верно.	U+22A5	&perp; F	⊥{\displaystyle \bot }\bot
	ложь, неверно, ошибочно
	логика высказываний, Булева алгебра
	Квантор всеобщности	∀ x: P(x) или (x) P(x) означает P(x) верно для всех x.	∀ n ∈ ℕ: n2 ≥ n.	U+2200	&forall;	∀{\displaystyle \forall }\forall
	для любого; для всех
	Логика первого порядка
∃	Квантор существования	∃ x: P(x) означает, что существует по меньшей мере один x, такой, что P(x) верно.	∃ n ∈ ℕ: n чётно.	U+2203	&exist;	∃{\displaystyle \exists }\exists
	существует
	логика первого порядка
∃!	Единственность	∃! x: P(x) означает, что существует ровно один x, такой, что P( x) верно.	∃! n ∈ ℕ: n + 5 = 2n.	U+2203 U+0021	&exist; !	∃!{\displaystyle \exists !}\exists !
	существует в точности один
	логика первого порядка
	Определение	x := y илиx ≡ y означает, что x является другим обозначением для y (но заметьте, что ≡ может означать и другое, как, например, конгруэнтность). P :⇔ Q означает, что P логически эквивалентно Q.	cosh x := (1/2)(exp x + exp (−x)) A XOR B :⇔ (A ∨ B) ∧ ¬(A ∧ B)	U+2254 (U+003A U+003D) U+2261 U+003A U+229C	:= : &equiv; &hArr;	:={\displaystyle :=}:= ≡{\displaystyle \equiv }\equiv ⇔{\displaystyle \Leftrightarrow }\Leftrightarrow
	определяется как
	везде
()	приоритетная группировка	Операции внутри скобок выполняются первыми.	(8 ÷ 4) ÷ 2 = 2 ÷ 2 = 1, но 8 ÷ (4 ÷ 2) = 8 ÷ 2 = 4.	U+0028 U+0029	()	( ){\displaystyle (~)} ()
	скобки
	везде
⊢	Выводимо[en]	x ⊢ y означает, что y выводимо из x (в некоторых формальных системах).	A → B ⊢ ¬B → ¬A	U+22A2	&#8866;	⊢{\displaystyle \vdash }\vdash
	выводимо
	логика высказываний, логика первого порядка
⊨	Модель[en]	x ⊨ y означает, что x семантически влечёт за собой y	A → B ⊨ ¬B → ¬A	U+22A8	&#8872;	⊨{\displaystyle \vDash }\vDash
	влечёт
	логика высказываний, логика первого порядка

Конъюнкция — Википедия

Конъю́нкция (от лат. conjunctio — «союз, связь») — логическая операция, по смыслу максимально приближенная к союзу «и». Синонимы: логи́ческое «И», логи́ческое умноже́ние

, иногда просто «И»^[1].

Конъюнкция может быть бинарной операцией (т. e. иметь два операнда), тернарной операцией (т. e. иметь три операнда), или n-арной операцией (т. e. иметь n операндов).

Наиболее часто встречаются следующие обозначения для операции конъюнкции:

a∧b,a&&b,a&b,a⋅b,aANDb,min(a,b){\displaystyle a\land b,\quad a\And \And b,\quad a\And b,\quad a\cdot b,\quad a\,\,\mathrm {AND} \,\,b,\quad \min(a,b)}

(в случае использования точки, как знака логического умножения, этот знак, как и при обычном умножении в алгебре, может быть опущен: ab{\displaystyle ab}^[1]).

При этом обозначение a∧b{\displaystyle a\land b}, рекомендованное стандартом ISO 31-11, наиболее широко распространено в современной математике и математической логике, где оно, впрочем, конкурирует со знаком амперсанда &^[1]; последний, появившись ещё в I веке до н. э. как графическое сокращение (лигатура) латинского союза et ‘и’, уже Якобом и Иоганном Бернулли в 1685 году использовался в качестве логической связки (у них он, однако, связывал не высказывания, а понятия)^[2][3]. Джордж Буль (а за ним — и другие пионеры систематического применения символического метода к логике: У. С. Джевонс, Э. Шрёдер, П. С. Порецкий) обозначал конъюнкцию знаком ⋅{\displaystyle \cdot } — как обычное умножение^[4]. Символ ⋀ (перевёрнутый знак дизъюнкции) в качестве обозначения конъюнкции был предложен Арендом Гейтингом (1930)^[5].

Обозначение ⋀ для конъюнкции было использовано и в раннем языке программирования Алгол 60^[6]. Однако из-за отсутствия соответствующего символа в стандартных наборах символов (например, в ASCII или EBCDIC), применявшихся на большинстве компьютеров, в получивших наибольшее распространение языках программирования были предусмотрены иные обозначения для конъюнкции. Так, в Фортране IV и PL/I применялись соответственно обозначения .AND. и & (с возможностью замены последнего на ключевое слово AND)^[7]; в языках Паскаль и Ада используется зарезервированное слово and^[8][9]; в языках C и C++ применяются обозначения & для побитовой конъюнкции и && для логической конъюнкции^[10]).

Наконец, при естественном упорядочении значений истинности двузначной логики (когда полагают, что 0<1{\displaystyle 0<1}), оказывается, что (a∧b)=min(a,b).{\displaystyle (a\land b)\,=\,\min(a,b).} Таким образом, конъюнкция оказывается частным случаем операции вычисления минимума; это открывает наиболее естественный способ определить операцию конъюнкции в системах многозначной логики (хотя иногда рассматривают и другие способы обобщения конъюнкции — например, такой: (a∧b)=ab(mod⁡k){\displaystyle (a\land b)\,=\,ab\;(\operatorname {mod} k)} в случае k-значной логики, в которой множество значений истинности представлено начальным отрезком {0,…,k−1}{\displaystyle \{0,\dots ,k-1\}} полугруппы N{\displaystyle \mathbb {N} } натуральных чисел)^[11][12].

Определение.
Логическая функция MIN в двухзначной (двоичной) логике называется конъюнкция (логи́ческое «И», логи́ческое умноже́ние или просто «И»).

Правило: результат равен наименьшему операнду.

Описание.
В булевой алгебре конъюнкция — это функция двух, трёх или более переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle false,true} или F,T{\displaystyle F,T} или «ложь», «истина», но при таком обозначении необходимо дополнительно доопределять старшинство, например, true>false{\displaystyle true>false}, при цифровом обозначении старшинство естественно 1>0{\displaystyle 1>0}.
Правило: результат равен 1{\displaystyle 1}, если все операнды равны 1{\displaystyle 1}; во всех остальных случаях результат равен 0{\displaystyle 0}.

Таблицы истинности:
для бинарной конъюнкции

для тернарной конъюнкции

a{\displaystyle a}	b{\displaystyle b}	c{\displaystyle c}	a∧b∧c{\displaystyle a\land b\land c}
0	0	0	0
1	0	0	0
0	1	0	0
1	1	0	0
0	0	1	0
1	0	1	0
0	1	1	0
1	1	1	1

Конъюнкция коммутативна, ассоциативна и дистрибутивна по отношению к слабой дизъюнкции^[13].

Операции, называемой в двоичной логике конъюнкция, в многозначных логиках обычно сопоставляется операция минимум: min(a,b){\displaystyle min(a,b)}, где a,b∈{0,…,k−1},{\displaystyle a,b\in \{0,\dots ,k-1\},} а k{\displaystyle k} — значность логики; впрочем, возможны и другие варианты обобщения обычной конъюнкции на многозначный случай. Как правило, стараются сохранить совместимость с булевой алгеброй для значений операндов 0{\displaystyle 0} и k−1{\displaystyle k-1}.

Следует отметить, что название этой операции минимум имеет смысл в логиках с любой значностью, в том числе и в двоичной логике, а названия конъюнкция, логи́ческое «И», логическое умноже́ние и просто «И» характерны для двоичной логики, а при переходе к многозначным логикам используются реже.

В классическом исчислении высказываний свойства конъюнкции определяются с помощью аксиом. Классическое исчисление высказываний может быть задано разными системами аксиом, и некоторые из них будут описывать свойства конъюнкции. Один из самых распространённых вариантов включает 3 аксиомы для конъюнкции:
a∧b→a{\displaystyle a\land b\to a}
a∧b→b{\displaystyle a\land b\to b}
a→(b→(a∧b)){\displaystyle a\to (b\to (a\land b))}

С помощью этих аксиом можно доказать другие формулы, содержащие операцию конъюнкции. Обратите внимание, что в классическом исчислении высказываний не происходит вычисления результата по значениям операндов (как в булевой алгебре), а требуется доказать формулу как единое целое на основе аксиом и правил вывода.

Логический элемент «И»

Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения^[13]. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах есть «1»,
• «0» тогда и только тогда, когда хотя бы на одном входе есть «0»

С точки зрения теории множеств, конъюнкция аналогична операции пересечения.

В компьютерных языках используется два основных варианта конъюнкции: логическое «И» и побитовое (поразрядное) «И». Например, в языках C/C++ логическое «И» обозначается символом «&&», а побитовое — символом «&». В терминологии, используемой в C#, операцию «&» принято называть логическим «И», а операцию «&&» — условным «И», поскольку значения операндов являются условиями для продолжения вычисления. В языках Pascal/Delphi оба вида конъюнкции обозначаются с использованием ключевого слова «and», а результат действия определяется типом операндов. Если операнды имеют логический тип (например, Boolean) — выполняется логическая операция, если целочисленный (например, Byte) — поразрядная.

Логическое «И» применяется в операторах условного перехода или в аналогичных случаях, когда требуется получение результата false{\displaystyle false} или true{\displaystyle true}. Например:

if (a & b & c) 
{
    /* какие-то действия */
};

Сравнение в данном случае будет продолжаться до конца выражения, независимо от промежуточных результатов. Принцип работы условного «И» в аналогичной ситуации:

a = false; b = true; c = true;
if (a && b && c) 
{
    /* какие-то действия */ 
};

Проверка истинности выражения в данном случае остановится после проверки переменной a, так как дальнейшее сравнение не имеет смысла.

Результат будет равен true{\displaystyle true}, если оба операнда равны true{\displaystyle true} (для числовых типов не равны 0{\displaystyle 0}). В любом другом случае результат будет равен false{\displaystyle false}.

При этом применяется стандартное соглашение: если значение левого операнда равно false{\displaystyle false}, то значение правого операнда не вычисляется (вместо b{\displaystyle b} может стоять сложная формула). Такое соглашение ускоряет исполнение программы и служит полезным приёмом в некоторых случаях. Компилятор Delphi поддерживает специальную директиву, включающую

или выключающую

подобное поведение. Например, если левый операнд проверяет возможность вычисления правого операнда:

if (a != 0 && b / a > 3) 
{
    /* какие-то действия */
};

В этом примере, благодаря проверке в левом операнде, в правом операнде никогда не произойдет деления на ноль.

Побитовое «И» выполняет обычную операцию булевой алгебры для всех битов левого и правого операнда попарно. Например,

если
a =	011001012{\displaystyle 01100101_{2}}
b =	001010012{\displaystyle 00101001_{2}}
то
a И b =	001000012{\displaystyle 00100001_{2}}

Часто указывают на сходство между конъюнкцией и союзом «и» в естественном языке. Составное утверждение «A и B» считается истинным, когда истинны оба утверждения A и B, в противном случае составное утверждение ложно. Это в точности соответствует определению конъюнкции в булевой алгебре, если «истину» обозначать как 1{\displaystyle 1}, а «ложь» как 0{\displaystyle 0}. При этом часто делают стандартную оговорку о неоднозначности естественного языка. Например, в зависимости от контекста союз «и» может нести дополнительный оттенок «и тогда», «и поэтому», «и потом». Отличие логики естественного языка от математической остроумно выразил американский математик Стивен Клини, заметив, что в естественном языке «Мэри вышла замуж и родила ребенка» — не то же самое, что «Мэри родила ребенка и вышла замуж».

1. ↑ ^{1 2 3} Кондаков, 1975, с. 264—266, 534—536.
2. ↑ Ampersand (неопр.). // Website Online Etymology Dictionary. Дата обращения 7 февраля 2016.
3. ↑ Кондаков, 1975, с. 67.
4. ↑ Стяжкин Н. И. . Формирование математической логики. — М.: Наука, 1967. — 508 с. — С. 321, 348, 352, 368.
5. ↑ Earliest Uses of Symbols of Set Theory and Logic (неопр.). // Website Jeff Miller Web Pages. Дата обращения 7 февраля 2016.
6. ↑ Кондаков, 1975, с. 30.
7. ↑ Пратт Т. . Языки программирования: разработка и реализация. — М.: Мир, 1979. — 574 с. — С. 352, 439.
8. ↑ Грогоно П. . Программирование на языке Паскаль. — М.: Мир, 1982. — 384 с. — С. 51.
9. ↑ Вегнер П. . Программирование на языке Ада. — М.: Мир, 1983. — 240 с. — С. 68.
10. ↑ Эллис М.^[en], Строуструп Б. . Справочное руководство по языку программирования C++ с комментариями. — М.: Мир, 1992. — 445 с. — ISBN 5-03-002868-4. — С. 65, 86—87.
11. ↑ Яблонский С. В. . Введение в дискретную математику. — М.: Наука, 1979. — 272 с. — С. 9—10, 37.
12. ↑ Рвачёв В. Л. . Теория R-функций и некоторые её приложения. — Киев: Наукова думка, 1982. — 552 с. — С. 38, 66.
13. ↑ ^{1 2} Словарь по кибернетике. 2-е изд / Под ред. В. С. Михалевича. — Киев: Украинская советская энциклопедия, 1989. — 751 с. — ISBN 5-88500-008-5.

Формальная
Математическая (теоретическая, символическая)	Высказывание — построение над множеством {B,¬,∧,∨,0,1}{\displaystyle \{B,\neg ,\land ,\lor ,0,1\}} 2 константы 0 1
См. также

Таблица математических символов — Википедия

Символ (TeX) (Команда (TeX))	Символ (Юникод)	Название	Значение	Пример
		Произношение
		Раздел математики
⇒{\displaystyle \Rightarrow } (\Rightarrow) →{\displaystyle \rightarrow } (\rightarrow) ⊃{\displaystyle \supset } (\supset)	⇒ → ⊃	Импликация, следование	A⇒B{\displaystyle A\Rightarrow B} означает «если A{\displaystyle A} верно, то B{\displaystyle B} также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒ или для обозначения надмножества, см. ниже.).	x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4} верно, но x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2} неверно (так как x=−2{\displaystyle x=-2} также является решением).
		«влечёт» или «если…, то» или «отсюда следует»
		везде
⇔{\displaystyle \Leftrightarrow } (\Leftrightarrow)	⇔	Равносильность	A⇔B{\displaystyle A\Leftrightarrow B} означает «A{\displaystyle A} верно тогда и только тогда, когда B{\displaystyle B} верно».	x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y}
		«если и только если» или «равносильно»
		везде
∧{\displaystyle \wedge } (\wedge)	∧	Конъюнкция	A∧B{\displaystyle A\wedge B} истинно тогда и только тогда, когда A{\displaystyle A} и B{\displaystyle B} оба истинны.	(n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, если n{\displaystyle n} — натуральное число.
		«и»
		Математическая логика
∨{\displaystyle \vee } (\vee)	∨	Дизъюнкция	A∨B{\displaystyle A\vee B} истинно, когда хотя бы одно из условий A{\displaystyle A} и B{\displaystyle B} истинно.	(n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, если n{\displaystyle n} — натуральное число.
		«или»
		Математическая логика
¬{\displaystyle \neg } (\neg)	¬	Отрицание	¬A{\displaystyle \neg A} истинно тогда и только тогда, когда ложно A{\displaystyle A}.	¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)}
		«не»
		Математическая логика
∀{\displaystyle \forall } (\forall)	∀	Квантор всеобщности	∀x,P(x){\displaystyle \forall x,P\left(x\right)} обозначает «P(x){\displaystyle P\left(x\right)} верно для всех x{\displaystyle x}».	∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n}
		«Для любых», «Для всех», «Для всякого»
		Математическая логика
∃{\displaystyle \exists } (\exists)	∃	Квантор существования	∃x,P(x){\displaystyle \exists x,\;P\left(x\right)} означает «существует хотя бы один x{\displaystyle x} такой, что верно P(x){\displaystyle P\left(x\right)}»	∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (подходит число 5)
		«существует»
		Математическая логика
={\displaystyle =}	=	Равенство	x=y{\displaystyle x=y} обозначает «x{\displaystyle x} и y{\displaystyle y} обозначают одно и то же значение».	1 + 2 = 6 − 3
		«равно»
		везде
:={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } (:\Leftrightarrow) =def{\displaystyle {\stackrel {\rm {def}}{=}}} (\stackrel{\rm{def}}{=})	:= :⇔	Определение	x:=y{\displaystyle x:=y} означает «x{\displaystyle x} по определению равен y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означает «P{\displaystyle P} по определению равносильно Q{\displaystyle Q}»	ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}\left(x\right):={1 \over 2}\left(e^{x}+e^{-x}\right)} (определение гиперболического косинуса) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (определение исключающего «ИЛИ»)
		«равно/равносильно по определению»
		везде
{,}{\displaystyle \{,\}}	{ }	Множество элементов	{a,b,c}{\displaystyle \{a,\;b,\;c\}} означает множество, элементами которого являются a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}.	N={1,2,…}{\displaystyle \mathbb {N} =\{1,\;2,\;\ldots \}} (множество натуральных чисел)
		«Множество…»
		Теория множеств
{|}{\displaystyle \{|\}}	{|}	Множество элементов, удовлетворяющих условию	{x|P(x)}{\displaystyle \{x\,|\,P\left(x\right)\}} означает множество всех x{\displaystyle x} таких, что верно P(x){\displaystyle P\left(x\right)}.	{n∈N|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}}
		«Множество всех… таких, что верно…»
		Теория множеств
∅{\displaystyle \varnothing } (\varnothing) {}{\displaystyle \{\}}	∅ {}	Пустое множество	{}{\displaystyle \{\}} и ∅{\displaystyle \varnothing } означают множество, не содержащее ни одного элемента.	{n∈N|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,|\,1<n^{2}<4\}=\varnothing }
		«Пустое множество»
		Теория множеств
∈{\displaystyle \in } (\in) ∉{\displaystyle \notin } (\notin)	∈ ∉	Принадлежность/непринадлежность к множеству	a∈S{\displaystyle a\in S} означает «a{\displaystyle a} является элементом множества S{\displaystyle S}» a∉S{\displaystyle a\notin S} означает «a{\displaystyle a} не является элементом множества S{\displaystyle S}»	2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} }
		«принадлежит», «из» «не принадлежит»
		Теория множеств
⊆{\displaystyle \subseteq } (\subseteq) ⊂{\displaystyle \subset } (\subset)	⊆ ⊂	Подмножество	A⊆B{\displaystyle A\subseteq B} означает «каждый элемент из A{\displaystyle A} также является элементом из B{\displaystyle B}». A⊂B{\displaystyle A\subset B} обычно означает то же, что и A⊆B{\displaystyle A\subseteq B}. Однако некоторые авторы используют ⊂{\displaystyle \subset }, чтобы показать строгое включение (то есть ⊊{\displaystyle \subsetneq }).	(A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} }
		«является подмножеством», «включено в»
		Теория множеств
⊇{\displaystyle \supseteq } (\supseteq) ⊃{\displaystyle \supset } (\supset)	⊇ ⊃	Надмножество	A⊇B{\displaystyle A\supseteq B} означает «каждый элемент из B{\displaystyle B} также является элементом из A{\displaystyle A}». A⊃B{\displaystyle A\supset B} обычно означает то же, что и A⊇B{\displaystyle A\supseteq B}. Однако некоторые авторы используют ⊃{\displaystyle \supset }, чтобы показать строгое включение (то есть ⊋{\displaystyle \supsetneq }).	(A∪B)⊇A{\displaystyle (A\cup B)\supseteq A} R⊇Q{\displaystyle \mathbb {R} \supseteq \mathbb {Q} }
		«является надмножеством», «включает в себя»
		Теория множеств
⊊{\displaystyle \subsetneq } (\subsetneq)	⊊	Собственное подмножество	A⊊B{\displaystyle A\subsetneq B} означает A⊆B{\displaystyle A\subseteq B} и A≠B{\displaystyle A\neq B}.	N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} }
		«является собственным подмножеством», «строго включается в»
		Теория множеств
⊋{\displaystyle \supsetneq } (\supsetneq)	⊋	Собственное надмножество	A⊋B{\displaystyle A\supsetneq B} означает A⊇B{\displaystyle A\supseteq B} и A≠B{\displaystyle A\neq B}.	Q⊋N{\displaystyle \mathbb {Q} \supsetneq \mathbb {N} }
		«является собственным надмножеством», «строго включает в себя»
		Теория множеств
∪{\displaystyle \cup } (\cup)	∪	Объединение	A∪B{\displaystyle A\cup B} означает множество, содержащее все элементы из A{\displaystyle A} и B{\displaystyle B}	A⊆B⇔A∪B=B{\displaystyle A\subseteq B\Leftrightarrow A\cup B=B}
		«Объединение … и …», «…, объединённое с …»
		Теория множеств
∩{\displaystyle \cap } (\cap)	⋂	Пересечение	A∩B{\displaystyle A\cap B} означает множество одинаковых элементов, принадлежащих и A{\displaystyle A}, и B{\displaystyle B}.	{x∈R|x2=1}∩N={1}{\displaystyle \{x\in \mathbb {R} \,|\,x^{2}=1\}\cap \mathbb {N} =\{1\}}
		«Пересечение … и … «, «…, пересечённое с …»
		Теория множеств
∖{\displaystyle \setminus } (\setminus)	\	Разность множеств	A∖B{\displaystyle A\setminus B} означает множество элементов, принадлежащих A{\displaystyle A}, но не принадлежащих B{\displaystyle B}.	{1,2,3,4}∖{3,4,5,6}={1,2}{\displaystyle \{1,\;2,\;3,\;4\}\setminus \{3,\;4,\;5,\;6\}=\{1,\;2\}}
		«разность … и …», «минус», «… без …»
		Теория множеств
→{\displaystyle \to } (\to)	→	Функция (отображение)	f:X→Y{\displaystyle f\colon X\to Y} означает функцию f{\displaystyle f} с областью определения X{\displaystyle X} и областью значений Y{\displaystyle Y}.	Функция f:Z→N∪{0}{\displaystyle f\colon \mathbb {Z} \to \mathbb {N} \cup \{0\}}, определённая как f(x)=x2{\displaystyle f\left(x\right)=x^{2}}
		«из … в …»,
		везде
↦{\displaystyle \mapsto } (\mapsto)	↦	Отображение	f:x↦f(x){\displaystyle f\colon x\mapsto f\left(x\right)} означает, что образом x{\displaystyle x} после применения функции f{\displaystyle f} будет f(x){\displaystyle f\left(x\right)}.	Функцию, определённую как f(x)=x2{\displaystyle f\left(x\right)=x^{2}}, можно записать так: f:x↦x2{\displaystyle f\colon x\mapsto x^{2}}
		«отображается в»
		везде
N{\displaystyle \mathbb {N} } (\mathbb N)	N или ℕ	Натуральные числа	N{\displaystyle \mathbb {N} } означает множество {1,2,3,…}{\displaystyle \{1,\;2,\;3,\;\ldots \}} или реже {0,1,2,3,…}{\displaystyle \{0,\;1,\;2,\;3,\;\ldots \}} (в зависимости от ситуации).	{|a||a∈Z}=N{\displaystyle \{\left|a\right|\,|\,a\in \mathbb {Z} \}=\mathbb {N} }
		«Эн»
		Числа
Z{\displaystyle \mathbb {Z} } (\mathbb Z)	Z или ℤ	Целые числа	Z{\displaystyle \mathbb {Z} } означает множество {…,−3,−2,−1,0,1,2,3,…}{\displaystyle \{\ldots ,\;-3,\;-2,\;-1,\;0,\;1,\;2,\;3,\;\ldots \}}	{a,−a|a∈N}∪{0}=Z{\displaystyle \{a,\;-a\,|\,a\in \mathbb {N} \}\cup \{0\}=\mathbb {Z} }
		«Зед»
		Числа
Q{\displaystyle \mathbb {Q} } (\mathbb Q)	Q или ℚ	Рациональные числа	Q{\displaystyle \mathbb {Q} } означает {pq|

Конспект «Логические значения, операции, выражения»

Логические значения, операции, выражения

Код ОГЭ: 1.3.3. Логические значения, операции, выражения

Алгебра логики, логические высказывания

Наука, изучающая формы, методы и законы правильного мышления, называется логикой. Она интересуется не содержанием мышления, а его формой, поэтому ее часто называют еще формальной логикой.

Форма мышления — это способ выражения мыслей или форма, по которой они строятся.

Форма, обозначающая какой–либо объект или отличающий его признак, называется понятием. Примеры понятий: «компьютер», «планета», «длина», «профессия».

Форма, утверждающая или отрицающая что–либо о свойствах понятий и отношений между ними, называется утверждением (высказыванием, суждением). Примеры логических утверждений: «Декодирование — процесс восстановления информации из закодированного представления»; «В двоичной системе используются две цифры: 0 и 1»; «Париж — столица Франции». Утверждения могут быть истинными или ложными. Так, высказывание «Шанхай — столица Франции» является ложным утверждением.

Форма, в которой из двух или нескольких высказываний получают новое утверждение, называется умозаключением. Пример умозаключения: «Периферийные устройства компьютера — это устройства для ввода или вывода информации. Сканер — устройство для переноса текста и изображений с бумаги в компьютер. Следовательно, сканер — периферийное устройство».

Правила, которые должны соблюдаться, чтобы на основании истинных суждений получить истинные выводы, — это законы мышления. Логика изучает эти законы и способы получения новых утверждений на основании уже имеющихся.

Математическая логика использует для установления истинности или ложности высказываний математические методы. Она пользуется специальным символьным языком, подобным языку математики, поэтому ее часто называют символьной логикой.

Алгебра логики — раздел математической логики, в котором методы алгебры используются в логических преобразованиях. Она изучает логические высказывания и методы установления их истинности или ложности с помощью алгебраических методов.

Логическое высказывание — это любое повествовательное предложение, в отношении которого можно однозначно утверждать, что его содержание истинно или ложно. Вопросительные и повелительные предложения не являются логическими высказываниями. Но и не каждое повествовательное предложение является логическим высказыванием. Например, суждение «Лето было очень дождливым» не является однозначным, для утверждения «Существует несколько Вселенных» нельзя однозначно определить истинность; поэтому такие предложения не являются логическими высказываниями (утверждениями).

Таким образом, отличительной особенностью логических высказываний является возможность принимать одно из двух значений — истина и ложь. Истинность или ложность высказывания определяется вне алгебры логики — с помощью наблюдений, научных исследований, практических опытов и т. п.

В алгебре логики различают простые высказывания и сложные (составные), составленные из нескольких простых. Если в высказывании нельзя выделить некую часть, которая не совпадает по смыслу с исходным высказыванием и сама является высказыванием, то оно называется простым высказыванием. Простые высказывания обычно обозначаются латинскими буквами A, B, C и т. д.

Сложные высказывания представляют собой объединение простых высказываний с помощью логических связок. В качестве логических связок используются слова «не», «и», «или», «тогда и только тогда», «если … то». Истинность или ложность получаемых таким образом сложных высказываний определяется значением простых высказываний. Например, из простых высказываний «Офис фирмы находится в Мадриде» и «Офис фирмы находится в Берлине» можно составить сложные: «Офис фирмы находится в Мадриде или Берлине», «Офис фирмы находится в Мадриде и Берлине», «Если офис фирмы находится в Мадриде, то он находится в Берлине». Истинность первого из них означает, что офис фирмы находится в одном из названных городов или же имеются офисы в обоих городах. Ложность его означает, что ни в одном из этих городов офиса нет. Второе составное утверждение истинно тогда, когда в обоих городах имеется офис фирмы. Если же офис существует только в Берлине или только в Мадриде, — второе составное высказывание ложно.

В классической, двузначной алгебре логики логических значений всего два: истина (True) и ложь (False). Им соответствует цифровое представление — 1 и 0. Иногда эти значения записывают как «да» и «нет». Факт истинности или ложности некоторого высказывания А записывают соответственно как А = 1 или А = 0.

Логические операции

В алгебре логики логические связки рассматриваются как логические операции. Они имеют свои названия и обозначения. Результаты применения каждой операции к логическим высказываниям (истинным или ложным) можно представить в виде таблицы. В ней указывают все возможные сочетания значений исходных логических высказываний и истинность или ложность результата. Такие таблицы называют таблицами истинности операции. Обычно в них используют обозначения логических значений 0 и 1 или ложь и истина.

Основные логические операции — отрицание, конъюнкция, дизъюнкция, исключающая дизъюнкция, следование, эквивалентность.

Логическое отрицание (инверсия) — логическая операция, в результате которой из данного высказывания получается новое высказывание — отрицание исходного. Обозначается символически чертой сверху (Ā) или условными обозначениями ¬А, not А, не А (читается «отрицание А», «не А», «А ложно», «неверно, что А»).

Высказывание ¬А ложно, когда А истинно, и истинно, когда А ложно.

Таблица истинности операции отрицания

Если обозначить через А высказывание «Арбуз является ягодой», то ¬А соответствует высказыванию «Арбуз не является ягодой» («Неверно, что арбуз — ягода»).

Отрицание является унарной операцией. Унарная (одноместная) операция — это операция, которая применяется к одному операнду.

Остальные логические операции являются двуместными (бинарными). Бинарная (двуместная) операция — это операция, которая выполняется над двумя операндами.

Логическое умножение (конъюнкция) — операция, соединяющая два или более высказываний при помощи связки «и». Эта связка символически обозначается с помощью знака ∧ и читается «А и В». Для обозначения конъюнкции также применяются знаки: А • В, А & В, А и В, А and В, а иногда между высказываниями не ставится никакого знака: АВ.

Высказывание А ∧ В истинно только тогда, когда оба высказывания А и В истинны. Высказывание А ∧ В ложно только тогда, когда ложно хотя бы одно из высказываний А или В.

Таблица истинности операции конъюнкции

Например, высказывания «Лондон расположен севернее Лиссабона» и «Лондон расположен восточнее Лиссабона» истинны. Тогда истинным будет и составное логическое высказывание «Лондон расположен севернее и восточнее Лиссабона». Высказывания «Лондон расположен не севернее и восточнее Лиссабона», «Лондон расположен севернее и не восточнее Лиссабона», «Лондон расположен не севернее и не восточнее Лиссабона» — ложны.

Логическое сложение (дизъюнкция) — операция, соединяющая два или более высказываний при помощи связки « или». Эта связка символически обозначается с помощью знака v и читается «А или В». Для обозначения дизъюнкции также применяются знаки: А + В, А или В, А or В, А | B.

Высказывание А v В истинно только тогда, когда хотя бы одно из высказываний А или В истинно. Высказывание А v В ложно только тогда, когда оба высказывания А и В ложны.

Таблица истинности операции дизъюнкции

Например, высказывания «Виктор старше Ольги» и «Виктор — однофамилец Ольги» истинны. Тогда истинными будут и составные логические высказывания «Виктор старше Ольги или Виктор — однофамилец Ольги», «Виктор младше Ольги или Виктор — однофамилец Ольги», «Виктор старше Ольги или Виктор — не однофамилец Ольги». Высказывание «Виктор младше Ольги или Виктор — не однофамилец Ольги» — ложно, поскольку ложны оба составляющие его простые высказывания.

Исключающее сложение (исключающая дизъюнкция, строгая дизъюнкция, сложение по модулю два, дизъюнкция строго–разделительная) — логическая операция, соединяющая два высказывания при помощи связки «или», употребленной в исключающем смысле (называется также исключающее «или»). Операция символически обозначается с помощью знака ⊕ и читается «либо А, либо В».

Высказывание А ⊕ В истинно только тогда, когда высказывания А и В имеют различные значения.

Таблица истинности операции строгой дизъюнкции

Например, результат исключающей дизъюнкции двух высказываний «Виктор не старше Ольги» и «Виктор младше Ольги» всегда будет истиной, кто бы из них не был старше.

Логическое следование (импликация) — логическая операция, соединяющая два высказывания при помощи связки «если… то» в сложное высказывание. Операция символически обозначается с помощью знака → и читается «Если А, то В», «А влечет В», «из А следует В», «А имплицирует В». Для обозначения импликации применяются также знаки ⊃ или ⇒. Первое логическое высказывание является условием (посылкой), а второе — следствием (заключением).

Для операции импликации справедливо утверждение, что из лжи может следовать все что угодно, а из истины — только истина. Таким образом, импликация А → В ложна только тогда, когда А истинно, а В ложно (из истинного высказывания следует ложное). Во всех остальных случаях импликация истинна.

Таблица истинности операции импликации

Для высказываний «Луна — спутник Земли» и «Сумма углов треугольника не равна 180°» (первое истинно, второе ложно) составное высказывание «Если Луна — спутник Земли, то сумма углов треугольника не равна 180°» будет ложным. Однако истинными будут высказывания «Если Луна — спутник Земли, то сумма углов треугольника равна 180°», «Если Луна — не спутник Земли, то сумма углов треугольника не равна 180°» и «Если Луна — не спутник Земли, то сумма углов треугольника равна 180°». Этот пример наглядно демонстрирует, что в алгебре логики смысл высказываний не учитывается, а рассматриваются только их истинность или ложность.

Логическое равенство (эквивалентность, следование, двойная импликация, равнозначность) — логическая операция, позволяющая из двух высказываний А и В получить новое высказывание А ≡ В (читается «А эквивалентно B»). Эта операция может быть выражена связками «тогда и только тогда», «необходимо и достаточно», «равносильно». Для обозначения эквивалентности применяются знаки ~, ⇔.

Если оба высказывания имеют различные логические значения, результатом операции эквивалентности всегда будет ложь. Если же оба простые высказывания ложны или оба истинны, то составное логическое высказывание всегда будет истинно.

Таблица истинности операции эквивалентности

Для высказываний «Линейное уравнение всегда имеет решение» и «Кит — млекопитающее» их эквивалентность всегда будет истиной, так как оба простые утверждения истинны.

Таким образом, сводная таблица истинности для всех основных логических операций имеет вид:

Логические выражения

Логические высказывания могут быть записаны в виде формул (логических выражений). Логические выражения включают логические переменные, знаки логических операций, логические константы (истина и ложь) и скобки. Логические выражения принимают значения истина или ложь.

Правила построения логических выражений:

• любая логическая переменная или константа (истина и ложь) являются логическим выражением;
• если А — , то ¬А — тоже логическое выражение;
• если А и В — логические выражения, то А ∧ В; А v В ; А ⊕ В; А → В; А ~ В — тоже логические выражения.

Например, A ⊕ истина v В v ложь — логическое выражение; А v ⊕ В v ложь не является логическим выражением.

Логическое выражение, принимающее значение истина при любых значениях входящих в него переменных, называется тождественно–истинным выражением (тавтологией). Например, А v В v ¬А; (А ∧ ¬А) → В.

Логическое выражение, принимающее значение ложь при любых значениях входящих в него переменных, называется тождественно–ложным выражением (противоречием). Например, А ∧ ¬А; В ~ ¬В.

Логическое выражение, принимающее как значение ложь, так и значение истина при разных значениях входящих в него переменных, называется выполнимым выражением.

ПРИОРИТЕТ ЛОГИЧЕСКИХ ОПЕРАЦИЙ

Для сложных логических выражений, содержащих несколько логических операций, определен порядок выполнения действий (приоритет): сначала операции отрицания, затем операции логического умножения, потом операции логического сложения и исключающего сложения, последними выполняются операции импликации и эквивалентности. Операции выполняются слева направо. Порядок выполнения может быть изменен с помощью скобок.

Приоритет выполнения логических операций в логических выражениях

Пример 1
Определить порядок выполнения логических операций в выражении.
Вычислить его значение, если А = 1, В = 0, С = 1.
¬А ∧ С v (A ⊕ В) ∧ В

Решение. Первыми вычисляются значения в скобках. Затем выполняются операции по приоритетам: самый высокий приоритет имеет операция отрицания, после нее, как в математике, следуют операции умножения, а затем сложения. Таким образом, порядок будет следующий: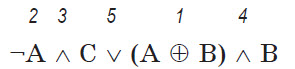

Тогда значение выражения ¬1 ∧ 1 v (1 ⊕ 0) ∧ 0 после вычисления отрицания и выражения в скобках: 0 ∧ 1 v 1 ∧ 0, после операций умножения: 0 v 0. Итог: 0.
Ответ: логическое выражение ложно.

Пример 2
Для каких из приведенных слов истинно следующее высказывание?
(Вторая буква гласная) ИЛИ (Первая буква гласная) И НЕ (Длина имени не больше 5 букв)

1) Олег   2) Марианна  3) Светлана   4) Ольга.

Решение.

1.  В соответствии с приоритетом выполнения операций сначала нужно вычислить результат операции отрицания: «Длина имени больше 5 букв». Такие имена — Марианна, Светлана.
2. Затем необходимо рассчитать результат конъюнкции (связка И) второго и третьего высказываний. Конъюнкция истинна только тогда, когда истинны оба высказывания. Следовательно, нужно выбрать имена, в которых и первая буква гласная, и длина имени больше 5 букв — таких имен среди вариантов нет.
3. Результат дизъюнкции (связка ИЛИ) истинен только тогда, когда истинно или одно, или второе, или одновременно оба простые высказывания. Первое простое высказывание истинно для имени Марианна, второе ложно для указанных имен. Таким образом, верный вариант ответа — 2.

Ответ: 2) Марианна.

СВЯЗЬ МЕЖДУ ЛОГИЧЕСКИМИ ОПЕРАЦИЯМИ

Между логическими операциями существует взаимосвязь. Операции исключающего «или», следования и эквивалентности можно выразить через операции отрицания, логического сложения и умножения, что отражено в следующей таблице.

Связь между логическими операциями

Поэтому операции отрицания, логического сложения и логического умножения называют основными логическими операциями: их достаточно, чтобы построить любое логическое выражение.

Если логическое выражение содержит только операции отрицания, логического сложения и логического умножения, говорят, что выражение находится в нормальной форме.

РАВНОСИЛЬНЫЕ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ

Логические выражения, значения которых совпадают для всех наборов входящих в них переменных, называются равносильными, или эквивалентными.

Чтобы убедиться, что два выражения равносильны, можно построить для них таблицы истинности. Если в таблицах совпадут все значения, значит, выражения равносильны.

Пример 3
Проверить равносильность выражений А ~ E и (Ā ∧ Ē) v (A ∧ E).

Решение. Для проверки следует создать таблицу истинности, содержащую столько строк, сколько возможно наборов значений переменных, входящих в выражение. Для двух переменных (А и E) количество наборов равно четырем. К двум столбцам для значений переменных (А и E) нужно присовокупить количество столбцов, равное количеству операций в выражении. Таким образом, необходимо создать таблицу, содержащую 4 строки и 7 столбцов.

Заполним первые 2 столбца (А и E) всеми сочетаниями значений переменных. Запишем в качестве заголовков столбцов все операции выражения в порядке их выполнения (в соответствии с приоритетами и скобками). Рассчитаем значения этих операций: сначала выражения в скобках, затем результат их сложения.

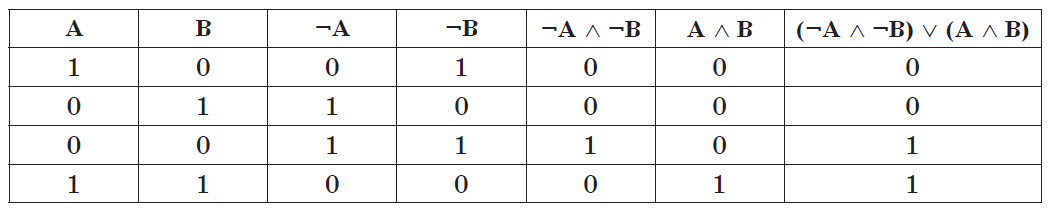
Последний столбец содержит результирующее значение выражения. Он совпадает с таблицей истинности для операции эквивалентности. Следовательно, выражения равносильны.

Основные законы алгебры логики

Для сложных логических выражений с большим числом переменных определение их истинности путем построения таблиц истинности становится громоздким. В таких случаях применяют способы упрощения выражений. Под упрощением понимают равносильное преобразование выражения к его нормальной форме.

Нормальная форма выражения содержит только операции отрицания, конъюнкции и дизъюнкции и не содержит отрицания выражений и двойных отрицаний.

Для упрощения используют равносильные преобразования, которые иначе называют основными законами алгебры логики.

Тождественные преобразования логических выражений

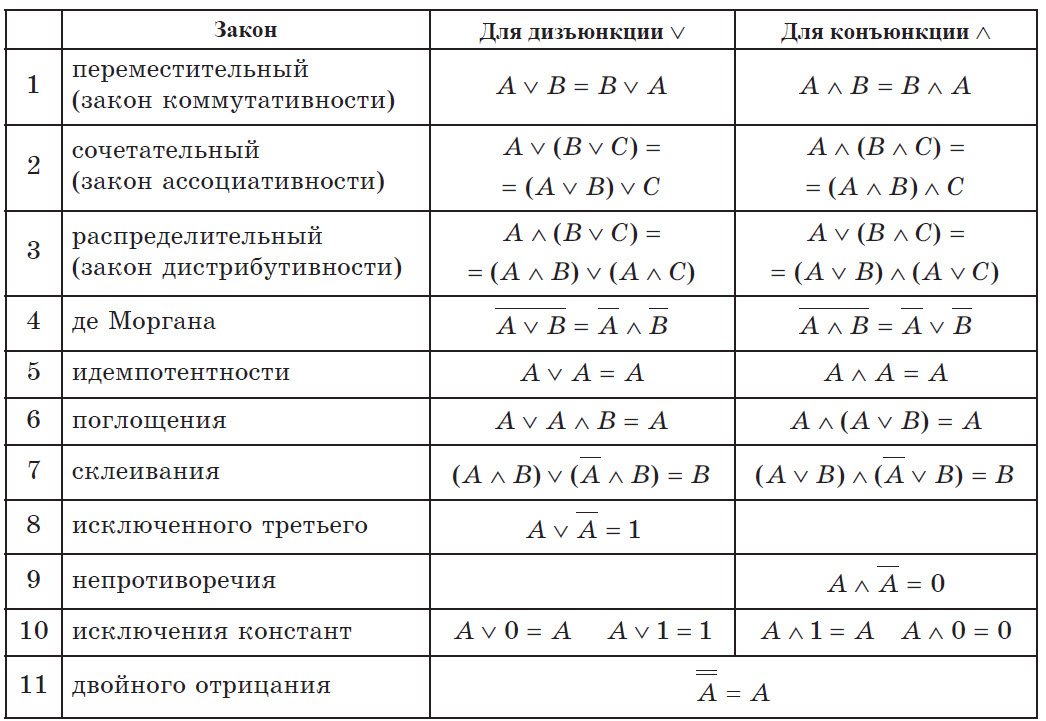
Для всех тождественных преобразований выполняется закон двойственности: если в формуле преобразования заменить конъюнкцию на дизъюнкцию, дизъюнкцию — на конъюнкцию, значения 1 — на 0, 0 — на 1, то закон, сформулированный для конъюнкции, примет форму аналогичного закона для дизъюнкции, и наоборот.

Прежде всего при равносильных преобразованиях избавляются от отрицания выражений, потом — от логических операций исключающей дизъюнкции, следования и эквивалентности. Затем используют законы алгебры логики для уменьшения количества переменных в выражении.

Пример 4
Выбрать выражение, которое равносильно выражению (A ∧ B) v (Ā ∧ B).

1) A         2) A ∧ B          3) Ā ∧ B           4) B

Решение. В соответствии с законом склеивания (A ∧ B) v (Ā ∧ B) = B, следовательно, исходное выражение равносильно выражению В.
Ответ: 4) В.

ОПРЕДЕЛЕНИЕ ЗНАЧЕНИЙ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ

Выражения, которые принимают логические значения (истина или ложь) в результате выполнения операций сравнения (больше >, меньше <, больше или равно ≥, меньше или равно ≤, равно =, не равно ≠), также являются логическими выражениями. Кроме операций сравнения и логических операций такие выражения могут включать функции и алгебраические операции. Приоритет выполнения этих операций таков:

1. Вычисление значений функций.
2. Выполнение алгебраических операций (вначале возведение в степень, затем умножение и деление, после чего вычитание и сложение).
3. Выполнение операций сравнения (в порядке записи).
4. Выполнение логических операций (сначала операции отрицания, затем операции логического умножения, потом операции логического сложения, последними выполняются операции импликации и эквивалентности).

Если в логическом выражении используются скобки, то сначала выполняются заключенные в них операции.

Пример 5
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1          2) 2         3) 3        4) 4

Решение. В соответствии с приоритетами операций сначала следует выполнить операции сравнения, затем отрицания, а потом — конъюнкцию. Отрицанием высказывания М ≥ 10 является высказывание М < 10. Получим выражение М < 10 ∧ M > 3. Для того чтобы это выражение (конъюнкция) было истинным, должны выполняться (т. е. быть истинными) оба неравенства. Следовательно, значение М должно быть больше 3, но меньше 10. Среди предложенных значений этому условию удовлетворяет только одно — число 4.
Ответ: 4) 4.

Задачи, подобные предыдущему примеру, можно решать и с помощью таблиц истинности.

Пример 6.
Для какого из приведенных ниже значений числа М истинно следующее выражение?
¬М ≥ 10 ∧ M > 3

1) 1           2) 2         3) 3        4) 4

Решение. Составим таблицу истинности: все операции выражения укажем в столбцах таблицы, все предложенные значения М укажем в ее строках. Рассчитаем значения таблицы:

Последний столбец содержит результат всего выражения. Истинным оно будет только для значения числа М, равного 4.
Ответ: 4) 4.

Пример 7.
В табличной форме представлены ежемесячные данные о продаже групп товаров за полгода. Сколько групп товаров демонстрировали рост продаж в весенние месяцы или вышли на уровень свыше 80 % в июне?

Решение. Переформулируем условие задачи: необходимо найти группы товаров, для которых (Март < Апрель) ∧ (Апрель < Май) v (Июнь > 80).

Введем обозначения:
А = (Март < Апрель)
В = (Апрель < Май)
С = (Июнь > 80)

Тогда выражение можно записать как А ∧ В v С.

Логическое выражение состоит из одной конъюнкции и одной дизъюнкции. Значение выражения конъюнкции истинно только тогда, когда истинны оба составляющие его простых выражения ((Март < Апрель) и (Апрель < Май)). Значение выражения дизъюнкции будет истинным, если хотя бы одно из составляющих его простых высказываний будет истинным.

Составим таблицу истинности для исходных данных.

Логическому выражению удовлетворяют 3 записи — 4–я, 6–я и 7–я.
Ответ: 3.

 

---

Конспект урока по информатике «Логические значения, операции, выражения».

Вернуться к Списку конспектов по информатике.

 

Импликация — Википедия

Импликация (от лат. implicatio — «связь») — бинарная логическая связка, по своему применению приближенная к союзам «если…, то…».

Импликация записывается как посылка ⇒{\displaystyle \Rightarrow } следствие; применяются также стрелки другой формы и направленные в другую сторону, но всегда указывающие на следствие.

Суждение, выражаемое импликацией, выражается также следующими способами^[1][2]:

Импликация играет очень важную роль в умозаключениях. С её помощью формулируются определения различных понятий, теоремы, научные законы^[3].

При учёте смыслового содержания высказываний импликация подразумевает причинную связь между посылкой и заключением^[4].

В булевой логике импликация — это функция двух переменных (они же — операнды операции, они же — аргументы функции). Переменные могут принимать значения из множества {0,1}{\displaystyle \{0,1\}}. Результат также принадлежит множеству {0,1}{\displaystyle \{0,1\}}. Вычисление результата производится по простому правилу, либо по таблице истинности. Вместо значений 0,1{\displaystyle 0,1} может использоваться любая другая пара подходящих символов, например false,true{\displaystyle \operatorname {false} ,\operatorname {true} } или F,T{\displaystyle F,T} или «ложь», «истина».

Правило:

Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Иными словами, импликация A→B{\displaystyle A\to B} это сокращённая запись для выражения ¬A∨B{\displaystyle \neg A\lor B}.

Таблицы истинности:

прямая импликация (от a к b) (материальная импликация (англ.)русск., материальный кондиционал (англ.)русск.)

• если первый операнд не больше второго операнда, то 1,
• если a⩽b{\displaystyle a\leqslant b}, то истинно (1).

«Житейский» смысл импликации. Для более лёгкого понимания смысла прямой импликации и запоминания её таблицы истинности может пригодиться житейская модель:

А — начальник. Он может приказать «работай» (1) или сказать «делай что хочешь» (0).

В — подчиненный. Он может работать (1) или бездельничать (0).

В таком случае импликация — не что иное, как послушание подчиненного начальнику. По таблице истинности легко проверить, что послушания нет только тогда, когда начальник приказывает работать, а подчиненный бездельничает.

обратная импликация (англ.)русск. (от b к a, A∨(¬B){\displaystyle A\lor (\neg B)})

• если первый операнд не меньше второго операнда, то 1,
• если a⩾b{\displaystyle a\geqslant b}, то истинно (1).

Обратная импликация — отрицание (негация, инверсия) обнаружения увеличения (перехода от 0 к 1, инкремента).

отрицание (инверсия, негация) прямой импликации

• если первый операнд больше второго операнда, то 1,
• если a>b{\displaystyle a>b}, то истинно (1).

отрицание (инверсия, негация) обратной импликации (англ.)русск. (¬A∧B{\displaystyle \lnot A\land B}), разряд займа в двоичном полувычитателе.

• если первый операнд меньше второго операнда, то 1,
• если a<b{\displaystyle a<b}, то истинно (1).

Другими словами, две импликации (прямая и обратная) и две их инверсии — это четыре оператора отношений. Результат операций зависит от перемены мест операндов.

Синонимические импликации выражения в русском языке[править | править код]

• Если А, то Б
• Б в том случае, если А
• При А будет Б
• Из А следует Б
• В случае А произойдет Б
• Б, так как А
• Б, потому что А
• А — достаточное условие для Б
• Б — необходимое условие для А

Импликация высказываний означает, что одно из них следует из другого. Импликация обозначается символом ⇒{\displaystyle \Rightarrow }, и ей соответствует вложение множеств: пусть A⊂B{\displaystyle A\subset B}, тогда

x∈A⇒x∈B.{\displaystyle x\in A\Rightarrow x\in B.}

Например, если A{\displaystyle A} — множество всех квадратов, а B{\displaystyle B} — множество прямоугольников, то, конечно, A⊂B{\displaystyle A\subset B} и

(a — квадрат) ⇒{\displaystyle \Rightarrow } (a — прямоугольник).

(если a является квадратом, то a является прямоугольником).

В классическом исчислении высказываний свойства импликации определяются с помощью аксиом.

Можно доказать эквивалентность импликации A→B{\displaystyle A\rightarrow B} формуле ¬A∨B{\displaystyle \neg A\lor B} (с первого взгляда более очевидна её эквивалентность формуле ¬(A∧¬B){\displaystyle \neg (A\land \neg B)}, которая принимает значение «ложь» в случае, если выполняется A (посылка), но не выполняется B (следствие)). Поэтому любое высказывание можно заменить на эквивалентное ему без знаков импликации.

В интуиционистской логике импликация никоим образом не сводится к отрицаниям. Скорее напротив, отрицание ¬A можно представить в виде A→⊭{\displaystyle A\rightarrow \nvDash }, где ⊭{\displaystyle \nvDash } — пропозициональная константа «ложь». Впрочем, такое представление отрицания возможно и в классической логике.

В интуиционистской теории типов импликации соответствует множество (тип) отображений из A в B.

В учении о силлогизмах импликации отвечает «общеутвердительное атрибутивное высказывание».

В языках программирования импликация используется, как правило, неявно. Например, конструкция, предполагающая истинность условий B в данном участке программы:

 if (!(выражение A) || выражение B) {
    сделать_что-то_полезное
 } else {
    сбой
 }

будет успешно выполняться тогда и только тогда, когда верна импликация A → B. В то же время эти условия можно спокойно написать в одной строке, объединив их оператором конъюнкции.

 if (выражение A) and (выражение B) {
    сделать_что-то_полезное
 }

При стандартных опциях компилятора (Delphi, C++ Builder)^{[прояснить]} проверка идёт до тех пор, пока результат не станет очевидным, и если А ложно, то (А и В) ложно вне зависимости от В, и не нужно ставить ещё один условный оператор.

 //выражение A - ложно
 if (выражение A) {
    // Дальше проверка не идёт
    ... if (выражение B) {
       сделать_что-то_полезное
    } ...
 }

В функциональных языках импликация может быть не только правилом вычислений, но и видом отношения между данными, то есть обрабатываться (в том числе и выполняться) и создаваться по ходу выполнения программы.

• Эдельман С.Л. Математическая логика. — М.: Высшая школа, 1975. — 176 с.
• Игошин В.И. Задачник-практикум по математической логике. — М.: Просвещение, 1986. — 158 с.
• Гиндикин С.Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.
• Барабанов О.О. Импликация / Труды XI международных Колмогоровских чтений: сборник статей. – Ярославль: Изд-во ЯГПУ, 2013. С.49-53.

16.Алгебра логики. Понятие высказывания. Логические константы, переменные, функции. Логические выражения.

Алгебра логики (высказываний) — раздел математической логики, изучающий высказывания и логические операции над ними.

Высказывание(суждение) – любое повествовательное предложение в отношении которого можно однозначно сказать, истинно оно или ложно.

Примеры высказываний:

1) Земля — планета Солнечной системы.

2) 2+8<5

3) 5×5=25

4) Всякий квадрат есть параллелограмм

5) Каждый параллелограмм есть квадрат

6) 2×2=5

Высказываниями не являются:

«он сероглаз»

«x2-4x+3=0»

Алгебра логики (высказываний) работает с высказываниями.

Различают:

Истина: Аристотель — основоположник логики.

Ложь: На яблонях растут бананы.

• Логические переменные (предикаты)– логические высказывания, значения которых меняются в зависимости от входящих в них переменных, обозначаются заглавными латинскими буквами А, В, С,D,F,…

А = {Аристотель — основоположник логики} – истина.

В = {На яблонях растут бананы} – ложь.

Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А = 1, В = 0.

• Логические функции (логические формулы) – сложные логические выражения, образованные из простых и связанные логическими операциямиИ, ИЛИ, НЕи др.)

Высказывание «Все мышки и кошки с хвостами» является сложным и состоит из двух простых высказываний.

А=«Все мышки с хвостами» и В=«Все кошки с хвостами»

Его можно записать в виде логической функции, значение которой истинно: F(A,B)=AиB.

В математической логике не рассматривается конкретное содержание высказывания, важно только, истинно оно или ложно.

Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть только ложь (0)илиистина (1).

Истина,ложь–логические константы.

В алгебре логики высказывания принято обозначать прописными латинскими буквами: A, B, X, Y.

Логические высказывания:

Логические выражения бывают простымиилисоставными (сложными).

Простое логическое выражение состоит из одного высказывания и не содержит логических операций. В нём возможно только два результата – либо «истина», либо «ложь».

17.Операции алгебры логики. Таблицы истинности логических операций. Вычисление логических выражений.

Сложное логическое высказывание строится из простых с помощью логических связок (таких как «И», «ИЛИ», «НЕ»), которые называютсялогическими операциями.

• На улице светит солнце и на улице идет дождь. (А и В)

• На улице светит солнце или на улице идет дождь. (А или В)

Основные логические операции:

• НЕ(логическое отрицание,инверсия)

• ИЛИ(логическое сложение,дизъюнкция)

• И(логическое умножение,конъюнкция)

Операция НЕ (отрицание, инверсия)

Отрицание (инверсия) – операция логического отрицания.

Добавляется частица НЕили словаНЕВЕРНО, ЧТО…

Обозначение: не, not, ¬ , ¯.

Если исходное выражение истинно, то результат его отрицания будет ложным, и наоборот, если исходное выражение ложно, то оно будет истинным.

А – Земля вращается вокруг Солнца – истинно

¬А – Земля не вращается вокруг Солнца – ложно

Операция И (логическое умножение, конъюнкция)

Конъюнкция (логическое умножение) – соединение двух логических выражений (высказываний) с помощью союзаИ.

Обозначение: и, and, ×, & ,Ù

Логическая операция конъюнкция истинна только в том случае, если оба простых высказывания истинны, в противном случае она ложна.

А – У меня есть знания для сдачи зачета.

В – У меня есть желание для сдачи зачета.

У меня есть знания И желание для сдачи зачета.

AÙB

Операция ИЛИ (логическое сложение, дизъюнкция)

Дизъюнкция (логическое сложение) – соединение двух логических высказываний с помощью союза ИЛИ.

Обозначение: или, or, +,V

Логическая операция дизъюнкция ложна, если оба простых высказывания ложны. В остальных случаях она истинна.

A – Летом я поеду в лагерь

B – Летом я поеду к бабушке

Летом я поеду в лагерь или поеду к бабушке

AVB

Другие логические операции:

Импликация («если …, то …»)

Импликация (логическое следование)– связывает два логических выражения, из которых первое является условием, а второе – следствием из этого условия. Операция обозначается словами: «Если…, то…» (Если А, то В).

Результат операции импликацииложен только тогда, когда предпосылка А истинна, а заключение В (следствие) ложно.

А – идёт дождь

В – на улице сыро

Если идёт дождь, то на улице сыро.

А → В

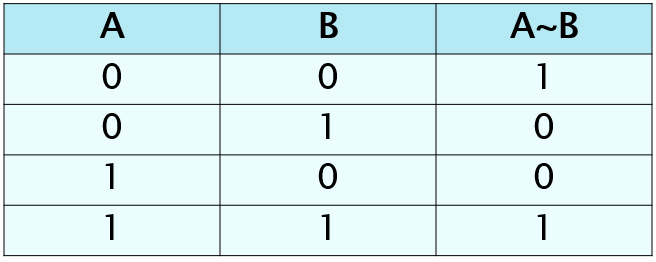
Эквивалентность («тогда и только тогда, …»)

Эквивалентность (логическое тождество, равнозначность) – определяет результат сравнения двух логических выражений. Операция обозначается словами: «…тогда и только тогда, когда…» (А т. и т. т. когда В)

Обозначение: «,Û,º, ~

Результат операции эквивалентностьистинен только тогда, когда А и В одновременно истинны или одновременно ложны.

А – день сменяет ночь

В – солнце скрывается за горизонтом

День сменяет ночь тогда и только тогда, когда солнце скрывается за горизонтом.

А ~ В

Таблицы истинности:

Таблица истинности отрицания (Операция НЕ (отрицание, инверсия):

Таблица истинности конъюнкции (Операция И (логическое умножение, конъюнкция):

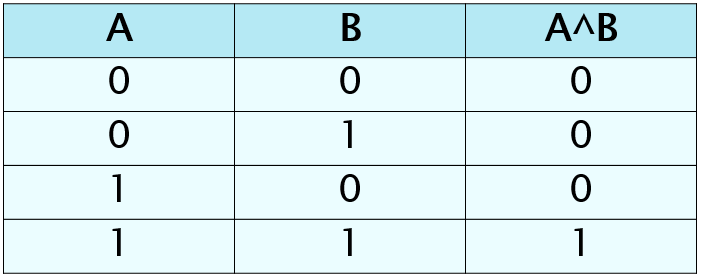
Таблица истинности дизъюнкции (Операция ИЛИ (логическое сложение, дизъюнкция):

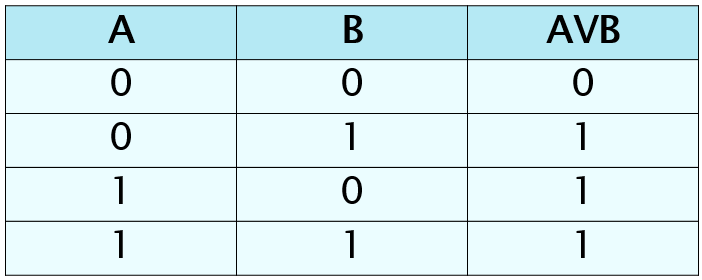
Таблица истинности импликации(Импликация («если …, то …»):

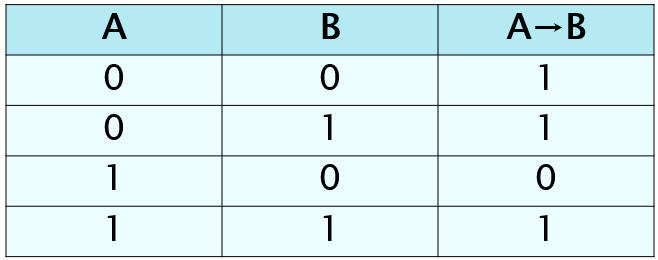
Таблица истинности эквивалентности (Эквивалентность («тогда и только тогда, …»):

Эквиваленция — Википедия

Эквиваленция
Исключающее ИЛИ-НЕ, EQ, XNOR
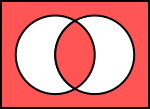Диаграмма Венна
Определение	x=y{\displaystyle x=y}
Таблица истинности	(1001){\displaystyle (1001)}
Логический вентиль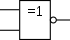
Нормальные формы
Дизъюнктивная	x⋅y+x¯⋅y¯{\displaystyle x\cdot y+{\overline {x}}\cdot {\overline {y}}}
Конъюнктивная	(x¯+y)⋅(x+y¯){\displaystyle ({\overline {x}}+y)\cdot (x+{\overline {y}})}
Полином Жегалкина	1⊕x⊕y{\displaystyle 1\oplus x\oplus y}
Принадлежность предполным классам
Сохраняет 0	Нет
Сохраняет 1	Да
Монотонна	Нет
Линейна	Да
Самодвойственна	Нет

Не следует путать с отношением эквивалентности.

Логическая равнозначность или эквивале́нция (или эквивале́нтность^[1]) — это логическое выражение, которое является истинным тогда, когда оба простых логических выражения имеют одинаковую истинность. Двуместная логическая операция обычно обозначается символом ≡ или ↔.

Эквиваленция A⟺B{\displaystyle A\iff B} — это сокращённая запись для выражения (¬A∧¬B)∨(A∧B){\displaystyle (\neg A\land \neg B)\lor (A\land B)}

Задаётся следующей таблицей истинности:

a{\displaystyle a}	b{\displaystyle b}	a≡b{\displaystyle a\equiv b}
0	0	1
1	0	0
0	1	0
1	1	1

Таким образом, высказывание A ≡ B означает «A то же самое, что B», «A эквивалентно B», «A тогда и только тогда, когда B».

Не надо путать эквиваленцию — логическую операцию с логической эквивалентностью^[en] высказываний — бинарным отношением. Связь между ними следующая:

Логические выражения A{\displaystyle A} и B{\displaystyle B} эквивалентны в том и только в том случае, когда эквиваленция A⟺B{\displaystyle A\iff B} истинна при всех значениях логических переменных.

Содержание

• 1 Примечания
• 2 См. также
• 3 Ссылки
• 4 Литература

1. ↑ Алгебра логики — статья из Большой советской энциклопедии. 

• Элемент XNOR (англ.) — физическая реализация эквиваленции.

• Математические основы информатики. Журнал 1 сентября

• Мендельсон Э. «Введение в математическую логику». — М. Наука, 1971.

Логические операции
Дизъюнкция Импликация Конъюнкция Отрицание (унарная) Сложение по модулю 2 Стрелка Пирса Условная дизъюнкция (тернарная) Штрих Шеффера Эквиваленция

Это заготовка статьи по логике. Вы можете помочь проекту, дополнив её.