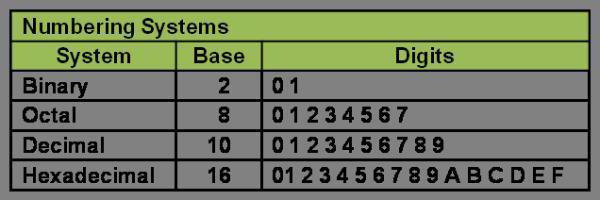
Алфавиты различных систем счисления

Система счисления	Основание	Алфавит цифр
Десятичная	10	0 1 2 3 4 5 6 7 8 9
Двоичная	2	0 1
Восьмеричная	8	0 1 2 3 4 5 6 7
Шестнадцатеричная	16	0 1 2 3 4 5 6 7 8 9 A B C D E F

Запись числа в какой-либо системе исчисления с основанием pозначает сокращенную запись выражения.

a_n-1·p^n-1+a_n-2·p^n-2+…+a₁·p¹+a₀·p⁰+a_-1·p^-1+…+a_-m·p^-m (1)

где a_i– цифра системы счисления;nиm– число целых и дробных разрядов соответственно.

Перевод целых чисел из любой системы счисления в десятичную

Полная запись в виде выражения (1) позволяет перевести число в любой системе счисления в десятичное, например,

273₈=2·8²+7·8¹+3·8⁰=187₁₀

Перевод целых чисел из десятичной системы счисления

Для перевода целого десятичного числа Nв систему счисления с основаниемpнеобходимо последовательно разделитьNнаpс остатком. Первое неполное частное опять следует поделить наpс остатком и так далее, пока не будет получено неполное частное меньше, чем основание. Первый остаток будет соответствовать разряду единиц числа с основаниемp, второй остаток – следующему разряду и т.п. Последнее неполное частное будет соответствовать старшему разряду числа с основаниемp.

Например, переведем число 187 в восьмеричную систему.

187 : 8 = 23 (3 в остатке)

23 : 8 = 2 (7 в остатке)

2 : 8 =0 (2 в остатке, так как 2 < 8)

Получаем число в восьмеричной системе 273

8

Системы счисления с основанием 2ⁿ

Такие системы счисления легко переводятся в двоичную систему счисления и обратно. Через двоичную систему счисления их можно связать друг с другом.

В табл. 2.14 представлены целые числа от 0 до 7 для десятичной, двоичной и восьмеричной систем.

Таблица 2.14

Связь двоичной и восьмеричной систем

p=10	0	1	2	3	4	5	6	7
p=2	000	001	010	011	100	101	110	111
p=8	0	1	2	3	4	5	6	7

Первые незначащие нули для двоичных чисел от 000 до 011 приведены здесь для удобства пересчета чисел из восьмеричной системы в двоичную. Например, для перевода числа 213₈в двоичную систему счисления следует заменить каждый разряд восьмеричного числа триадой (тройкой) двоичных чисел. Получим:

213₈ = 010001011₂

Первый незначащий ноль результата можно отбросить, то есть

213₈ = 10001011₂

В табл. 2.15 представлены целые числа от 0 до 15 для десятичной, двоичной, шестнадцатеричной систем.

Первые незначащие нули для двоичных чисел от 0000 до 0111 приведены здесь для удобства пересчета чисел из шестнадцатеричной системы в двоичную.

Таблица 2.15

Связь двоичной и шестнадцатеричной систем

p=10	0	1	2	3	4	5	6	7
p=2	0000	0001	0010	0011	0100	0101	0110	0111
p=16	0	1	2	3	4	5	6	7

p=10	8	9	10	11	12	13	14	15
p=2	1000	1001	1010	1011	1100	1101	1110	1111
p=16	8	9	A	B	C	D	E	F

Например, для перевода числа 72A₁₆или 72Ah(гдеhотhexadecimal– шестнадцатеричная) в двоичную систему счисления следует заменить каждый разряд шестнадцатеричного числа тетрадой (четверкой) двоичных чисел. Получим:

72A₁₆ = 011100101010₂

Первый незначащий ноль слева можно отбросить, то есть

72A₁₆ = 11100101010₂

Для перевода шестнадцатеричного числа в восьмеричное число целесообразно в качестве промежуточной использовать двоичную систему. Например, для перевода числа

72A₁₆ = 11100101010₂

используемего двоичное представление, в котором выделим триады двоичных чисел, начиная с младшего разряда единиц

11’100’101’010₂

и заменим их восьмеричными числами (табл. 2) 3452₈

Таким образом, 72A₁₆ = 3452₈

Системы записи чисел — Википедия

Системы счисления в культуре
Индо-арабская
Арабская Тамильская Бирманская	Кхмерская Лаосская Монгольская Тайская
Восточноазиатские
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные
Абджадия Армянская Ариабхата Кириллическая Греческая	Грузинская Эфиопская Еврейская Акшара-санкхья
Другие
Вавилонская Египетская Этрусская Римская Дунайская	Аттическая Кипу Майяская Эгейская Символы КППУ
Позиционные
2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60
Нега-позиционная
Симметричная
Смешанные системы
Фибоначчиева
Непозиционные
Единичная (унарная)

Система записи чисел — способ представления чисел в письменном виде.

По-видимому, хронологически первая система записи чисел каждого народа, овладевшего счётом. Натуральное число изображается путём повторения одного и того же знака (чёрточки или точки). Например, чтобы изобразить число 26, нужно провести 26 чёрточек (или сделать 26 засечек на кости, камне и т. д.). Впоследствии, ради удобства восприятия больших чисел, эти знаки группируются по три или по пять. Затем равнообъёмные группы знаков начинают заменяться каким-либо новым знаком — так возникают прообразы будущих цифр.

Древнеегипетская система записи[править | править код]

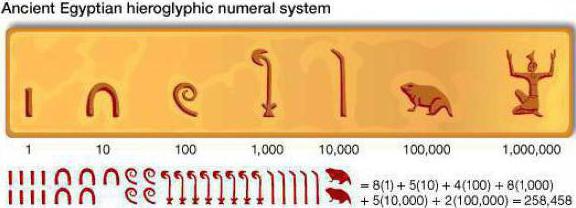
Древнеегипетская десятичная непозиционная система счисления возникла во второй половине третьего тысячелетия до н. э. Для обозначения чисел 1, 10, 10², 10³, 10⁴, 10⁵, 10⁶, 10⁷ использовались специальные цифры. Числа в египетской системе записи записывались как комбинации этих цифр, в которых каждая из цифр повторялась не более девяти раз. Значение числа равно простой сумме значений цифр, участвующих в его записи.^[1]

Вавилонская система записи[править | править код]

Алфавитные системы записи[править | править код]

Алфавитными системами записи пользовались древние армяне, грузины, греки (ионическая система записи), арабы (абджадия), евреи (см. гематрия), индийцы (акшара-санкхья) и другие народы Ближнего Востока. В славянских богослужебных книгах греческая алфавитная система была переведена на буквы кириллицы.^[1]

Еврейская система записи[править | править код]

Еврейская система записи в качестве цифр использует 22 буквы еврейского алфавита. Каждая буква имеет своё числовое значение от 1 до 400 (см. также Гематрия). Ноль отсутствует. Цифры, записанные таким образом, наиболее часто можно встретить в нумерации лет по иудейскому календарю.

Греческая система записи[править | править код]

Греческая система записи, также известная как ионийская или новогреческая — непозиционная система записи. Алфавитная запись чисел, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита, а также некоторые буквы доклассической эпохи, такие как ϛ (стигма), ϟ (коппа) и ϡ (сампи).

Римская система записи[править | править код]

Каноническим примером почти непозиционной системы записи является римская, в которой в качестве цифр используются латинские буквы:

I обозначает 1,

V — 5,

X — 10,

L — 50,

C — 100,

D — 500,

M — 1000

Например, II = 1 + 1 = 2

здесь символ I обозначает 1 независимо от места в числе.

На самом деле, римская система не является полностью непозиционной, так как меньшая цифра, идущая перед большей, вычитается из неё, например:

IV = 4, в то время как:

VI = 6

Система счисления майя[править | править код]

Майя использовали 20-ичную систему счисления за одним исключением: во втором разряде было не 20, а 18 ступеней, то есть за числом (17)(19) сразу следовало число (1)(0)(0). Это было сделано для облегчения расчётов календарного цикла, поскольку (1)(0)(0) = 360 примерно равно числу дней в солнечном году.

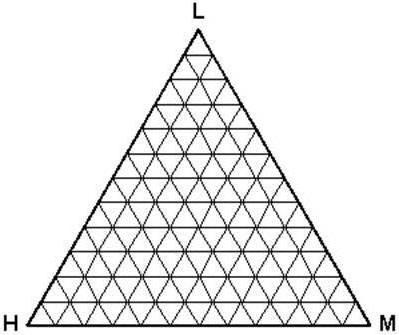
Для записи основными знаками были точки (единицы) и отрезки (пятёрки).

Кипу инков[править | править код]

Прообразом баз данных, широко использовавшихся в Центральных Андах (Перу, Боливия) в государственных и общественных целях в I—II тысячелетии н. э., была узелковая письменность Инков — кипу, состоявшая как из числовых записей десятичной системы^[2], так и не числовых записей в двоичной системе кодирования^[3]. В кипу применялись первичные и дополнительные ключи, позиционные числа, кодирование цветом и образование серий повторяющихся данных^[4]. Кипу впервые в истории человечества использовалось для применения такого способа ведения бухгалтерского учёта как двойная запись^[5].

определение, свойства, примеры :: SYL.ru

Основой многих расчетов, как простых бытовых, так и сложнейших математических, является десятичная система счисления. Троичная же известна гораздо меньшему кругу людей, ведь применяется она весьма редко.

Всего три цифры

Некоторые из нас редко сталкиваются с иными системами счисления, поэтому вначале может быть трудно отстраниться от привычных понятий — десятков, сотен, тысяч и так далее. Существует несколько параметров, которыми обладает любая из систем: основание, алфавит, разрядные цифры и разрядные слагаемые.

По основанию мы можем понять, как называется система счисления: троичная система имеет основание три, а десятичная — десять (работает и обратное правило — по названию сразу видно основание).

Алфавитом в системах счисления называется набор символов, которые в данном случае используются для записи чисел. Например, в десятичной системе используется десять цифр (считая ноль), а вот в двоичной их всего две, ноль и единица. В троичной же могут применяться 0, 1 и 2. К тому, почему основанием является тройка, а символов в алфавите — четыре, вернемся позже.

Разрядной цифрой называется наименьшее число, которое можно добавить в разряде, а разрядным слагаемым является цифра, записанная в каком-либо определенном разряде с добавлением нужного количества нолей. Максимально возможное значение разрядного слагаемого всегда зависит от системы счисления. Восьмеричная система счисления во втором разряде имеет разрядное слагаемое 70, в двоичной оно будет равно 10, в троичной — 20, а в десятичной — 90.

К примеру, если разложить десятичное число 158 на разрядные слагаемые, получится такой пример: 100+50+8 (третий разряд). А второразрядное число 98 предстанет в виде 90+8.

Алфавит

Числа в троичной системе счисления могут обозначаться как всем привычными цифрами 0, 1 и 2. Тогда это несимметричная троичная система. В симметричной же используются знаки «минус» и «плюс», таким образом, в записях используется число «-1». Оно так же может обозначаться как единица с чертой вверху или внизу, как латинская буква i.

Троичные цифры можно закодировать тремя любыми знаками, например «А,Б,В», однако предварительно необходимо указывать их старшинство (к примеру, А меньше Б, Б меньше В).

Простая формула

Чтобы перевести число из десятичной в троичную систему счисления, нужно воспользоваться общей формулой. Необходимо делить десятичное число на основание необходимой системы и записывать остатки справа налево. Возьмем для примера число 30. Первым действием делим его на 3. Получаем 10 без остатка, поэтому записываем 0. Десять делится на 3 с остатком 1, поэтому записываем 1. В третьем действии 3 делим на основание системы и записываем сначала остаток, затем результат деления. В итоге получаем троичное число 1010.

Арифметические действия

Если, например, компьютеры легко проводят математические операции в своей «родной» бинарной системе, то людям бывает трудно перестроить мышление, ведь для нас основной является десятичная система счисления. Троичная система обладает большей емкостью по сравнению с бинарной, и вычисления в ней несколько сложнее, однако во всех позиционных системах применяется таблица сложения.

Пожалуй, все помнят, по какому принципу составляется сетка в игре «Морской бой»: в левом вертикальном столбце записываются цифры, а в верхнем горизонтальном — буквы. Сетку сложения можно составить по тому же принципу. Например, в несимметричной троичной системе всего три символа, таким образом столбцов будет четыре, в каждый из них следует вписать последовательную цепочку цифр. На примере: нижний горизонтальный столбец будет таков: 0, 00, 01, 02. Второй столбец: 1, 01, 02, 10. Третий: 2, 02, 10, 11. Можно расширить таблицу, если требуются числа из других разрядов (например, 001 и т. д.).

Умножение

В троичной системе счисления таблица умножения выглядит короче и лаконичнее, нежели в десятичной, и само действие — не намного сложнее, ведь перемножать придется числа не больше двойки. Чтобы умножить в столбик, необходимо записать два троичных числа друг над другом, затем последовательно умножать первый множитель на разрядные числа второго, пропуская ноль. Таким образом, умножение цифры 102 на 101 будет выглядеть так: 2*1=2, 0*1=0, 1*1=1. Записываем 102. Далее пропускаем ноль и умножаем на единицу (старшее число второго множителя).

Однако сложение в троичной системе счисления можно произвести и без всякой таблицы. Для этого нужно вспомнить простое правило, гласящее: если результат сложения превышает разряд, следует разделить второе число пополам. Разберем пример: допустим, необходимо сложить 6 и 8. Результатом сложения превышает данную разрядность, поэтому делим 8 на 2, получаем 4. Окончательный пример выглядит так: 6+8=(6+4)+4=10+4=14.

Немного истории

Даже для бытовых расчетов не всегда использовалась десятичная система счисления. Троичная система частично использовалась еще у древних шумеров: их меры денег и весов были кратны трем. С древних времен и до наших дней на рычажных весах используется подобие троичной системы. Знаменитым Фибоначчи, итальянский ученым и математиком (настоящее имя — Леонардо Пизанский) была предложена целочисленная симметричная троичная система счисления. Таблица умножения в ней, как заметил французский математик О.Л. Коши, почти в четыре раза короче, по сравнению с десятичной.

Нечетная система счисления

Троичная система имеет нечетное основание, поэтому реализуется симметричное расположение цифр относительно нуля (-1, 0, 1), с чем связано несколько свойств.
Отрицательные числа представляются в троичной системе более естественно, а также отсутствует проблема округления, ведь младшие цифры, отбрасываемые при округлении, в троичной системе никогда не превосходят по абсолютной величине часть числа, соответствующей младшей значащей цифре младшего разряда. То есть в троичной системе следует только отбросить младшие цифры, и получится наиболее точное приближение.

Отрицательные числа

Довольно интересно представление отрицательных цифр в симметричной троичной системе счисления. Так как одним из знаков в алфавите является «-1» или единица с чертой сверху, то отпадает надобность в отдельном разряде знака, а выполнение арифметических операций не нуждаются в использовании обратного кода, так как любые действия с симметричным троичным числом выполняются по обычному правилу, но с учетом знака числа. Положительность или отрицательность числа определяется по тому, какой знак имеет старшее число в последовательности. Чтобы сменить знак числа, нужно инвертировать знаки всех присутствующих в коде чисел.

Взаимодействие с другими системами

Некоторые системы счисления стали знаменитыми благодаря использованию их в компьютерных технологиях. Например двоичная система, или бинарный код — эти слова часто используются в СМИ и кинематографе, так что знакомы они практически всем. А вот восьмеричная система счисления мало у кого на слуху, хотя используется в сфере IT-технологий из-за того, что легко переводится в двоичную и наоборот, но гораздо более емкая.

Для троичной системы таким емким аналогом является девятеричная.

Замена двоичной логики

Основой всех электронно-вычислительных машин нашего времени является двоичная логика, хотя троичная считается более перспективной. Удивительно, но еще в пятидесятые годы прошлого века в компьютере «Сетунь», построенном в МГУ, уже использовался симметричный троичный код. С 2008 года же в калифорнийском университете повторили опыт более чем полувековой давности, построив компьютерную систему ТСА2, также основанную на троичной логике.

Ее преимущества перед бинарной в том, что используется меньше разрядов. Например, число 10 десятичной системы в двоичной системе предстает как 1010, а в троичной несимметричной — как 101, или как +0+ в симметричной. Емкость также играет роль в том случае, если должна быть выбрана определенная система счисления. Троичная логика экономична и может вместить больший диапазон чисел при том же количестве знаков.

У тех, кто не знаком с бинарным кодом, может возникнуть вопрос: а зачем тогда вообще использовать такие системы счисления, если десятичная — емкая и понятная? Дело в том, что понимание компьютером двоичного кода основано на простой логике: есть сигнал, нет сигнала. Наличие сигнала означает единицу, а его отсутствие — ноль, только и всего. Машина не воспринимает код как цифры. При использовании десятичного кода специалистам пришлось бы придумать, какой вариант будет соответствовать каждой из цифр, но это только усложнило бы задачу, а вот понимание троичного кода реализовывается достаточно просто: отсутствие сигнала, слабый сигнал, сильный сигнал.

Квантовая механика может показаться чем-то фантастическим. Ее законы продолжают удивлять всех, кто впервые с ней сталкивается, однако люди уже давно задумались об использовании ее для создания компьютера нового поколения, более мощного и очень быстрого. Однако это потребует и новых алгоритмов защиты. Например, чтобы получить доступ к кредитной карте, необходимо разложить на простые множители огромное число, имеющее сотни знаков. Самый быстрый современный компьютер сможет сделать это за время, равно возрасту нашей Вселенной, однако квантовый компьютер, основанный на троичной логике, вполне справится с этой задачей.

Кубит — квантовый бит — основан на неопределенности спина электрона. Он может вращаться как по часовой стрелке (примем это за единицу), так и против (ноль), однако есть и третий вариант — неопределенность, что вполне может быть третьим «символом» в алфавите, и тогда троичная логика отлично укладывается.

Комплексная работа

Да, использование троичного кода в среднем ускоряет работу компьютера на 50 %, но если «перевод» в троичную систему счисления всех устройств все же произойдет, то как же будут работать старые приложения и программы? Неужели придется менять все и сразу? Нет. Троичная логика как стоящая на разряд выше включает в себя все возможности двоичного кода, и, сверх этого, еще и целый ряд преимуществ. Однако программы должны быть оптимизированы под троичный код, иначе будут работать по-старому.

Греческая система счисления — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 мая 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 мая 2019; проверки требует 1 правка.

Системы счисления в культуре
Индо-арабская
Арабская Тамильская Бирманская	Кхмерская Лаосская Монгольская Тайская
Восточноазиатские
Китайская Японская Сучжоу Корейская	Вьетнамская Счётные палочки
Алфавитные
Абджадия Армянская Ариабхата Кириллическая Греческая	Грузинская Эфиопская Еврейская Акшара-санкхья
Другие
Вавилонская Египетская Этрусская Римская Дунайская	Аттическая Кипу Майяская Эгейская Символы КППУ
Позиционные
2, 3, 4, 5, 6, 8, 10, 12, 16, 20, 60
Нега-позиционная
Симметричная
Смешанные системы
Фибоначчиева
Непозиционные
Единичная (унарная)

Гре́ческая систе́ма счисле́ния, также известная как иони́йская или новогре́ческая — непозиционная система счисления. Алфавитная запись чисел, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита, а также некоторые буквы доклассической эпохи, такие как ϝ (дигамма), ϟ (коппа) и ϡ (сампи). Одно из начертаний дигаммы внешне похоже на распространившуюся в византийскую эпоху лигатуру ϛ (ϲτ), поэтому распространилось заблуждение, что для записи числа 6 использовалась стигма.^[1]

Эта система пришла на смену аттической, или старогреческой, системе, которая господствовала в Греции в III веке до н. э.

Необходимость сохранять порядок букв ради сохранения их числовых значений привела к относительно ранней (IV век до н. э.) стабилизации греческого алфавита.

Данные символы позволяют записать лишь целые числа от 1 до 999, например:

• 45 — με͵,
• 632 — χλβ͵,
• 314 — τιΔ͵,
• 999 — ϡϙθ͵.

Символы Юникода для обозначения счёта: U+0374 ʹ greek numeral sign и U+0375 ͵ greek lower numeral sign^[2].

• J. J. O’Connor, E. F. Robertson. Greek number systems (неопр.). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland (январь 2001).
• Титло — программа для перевода греческих ионических чисел

система счисления. Виды систем счисления

В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления. Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.

Что это значит?

Начнем с определения основного понятия. Как отмечает учебник «Информатика», система счисления — это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.

В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.

В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.

В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.

Непозиционные системы

К непозиционным системам счисления относятся:

1. Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
2. Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.
3. Буквенные, в которых числа обозначались с помощью алфавита того или иного языка. Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
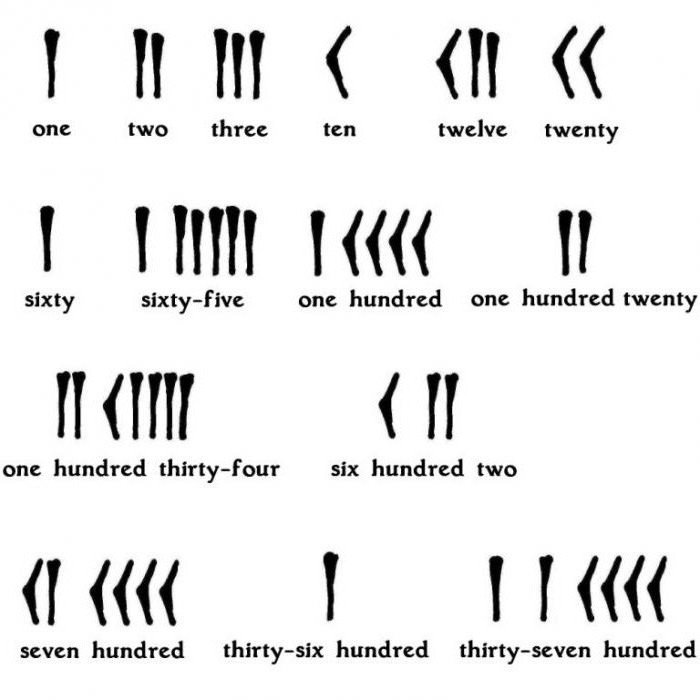
4. Вавилонская система счисления, в которой использовалось всего два обозначения для записи – клинья и стрелочки.
5. В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.

Позиционные системы

Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:

• двоичная;
• восьмеричная;
• десятичная;
• шестнадцатеричная;
• шестидесятеричная, используемая при счете времени (к примеру, в минуте — 60 секунд, в часе — 60 минут).

Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.

Десятичная система

Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.

Двоичная система

Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.

Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.

Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.

Восьмеричная система

Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.

Двоично-десятичная система

Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.

Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.

Шестнадцатеричная система

В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная. В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.

При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.

Перевод чисел: из десятичной в двоичную

Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.

Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.

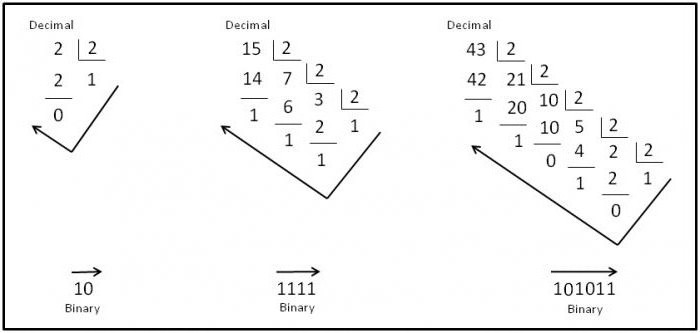
Например, переведем число 9 в двоичную систему:

Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.

После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.

Проводим ту же операцию с 2. В остатке получаем 0.

В итоге деления у нас получается 1.

Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.

Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.

Перевод чисел: из двоичной в десятичную

Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.

Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.

Для школьников этот алгоритм можно объяснить проще:

Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.

Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.

Выглядеть это будет следующим образом:

1*2³ + 0*2²+0*2¹+1*2⁰= 8+0+0+1 =9.

При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.

Другие варианты перевода

В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».

Арифметические операции

Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.

Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.

Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.

Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.