Активное сопротивление — проводник — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Активное сопротивление проводника зависит от его размеров и формы. [1]
Активное сопротивление проводника для токов высокой частоты определяется удельным сопротивлением его поверхностного слоя. Для уменьшения этого сопротивления поверхность проводников, работающих в цепях высокой частоты, часто покрывают слоем серебра. [2]
Активное сопротивление проводника зависит от его размеров и формы. [3]
Активное сопротивление проводника различно при постоянном и переменном токе из-за поверхностного эффекта и эффекта близости. [4]
| Возникновение поверхностного эффекта. [5] |
Активное сопротивление проводника увеличивается с увеличением частоты протекающего по нему переменного тока. Для частоты 50 гц, применяющейся в промышленной электротехнике, это увеличение незначительно, а для частот более высоких активное сопротивление проводника может весьма заметно превышать омическое. Кроме того, неравномерное распределение тока обусловливает уменьшение магнитного потока внутри самого провода, вследствие чего уменьшается его индуктивность тем резче, чем выше частота переменного тока, передаваемого по проводу.
[6]
Для частоты 50 гц, применяющейся в промышленной электротехнике, это увеличение незначительно, а для частот более высоких активное сопротивление проводника может весьма заметно превышать омическое. Кроме того, неравномерное распределение тока обусловливает уменьшение магнитного потока внутри самого провода, вследствие чего уменьшается его индуктивность тем резче, чем выше частота переменного тока, передаваемого по проводу.
[6]
Активное сопротивление проводника увеличивается по мере возрастания частоты переменного тока. Например, стальной провод диаметром 5 мм и длиной 1 км имеет при постоянном токе сопротивление, равное 20 омам, а при переменном токе с частотой 20 000 герц — 75 омам. Для частоты переменного тока в 50 герц, применяемого обычно в электрических установках, увеличение сопротивления незначительно. [7]
Активное сопротивление проводников тока определяют измерительными мостами или методом амперметра-вольтметра. Когда нужно знать действительное значение сопротивления проводников, пользуются мостами постоянного тока или методом амперметра-вольтметра. Чтобы установить, находится ли измеряемое сопротивление в допустимых пределах, используют одинарные или двойные автоматические мосты. Для определения процента отклонения измеряемого сопротивления от номинального его значения применяют одинарные или двойные процентные измерительные мосты.
[8]
Когда нужно знать действительное значение сопротивления проводников, пользуются мостами постоянного тока или методом амперметра-вольтметра. Чтобы установить, находится ли измеряемое сопротивление в допустимых пределах, используют одинарные или двойные автоматические мосты. Для определения процента отклонения измеряемого сопротивления от номинального его значения применяют одинарные или двойные процентные измерительные мосты.
[8]
Активное сопротивление проводников токопроводящих частей измеряют методом сопротивления. [9]
Зная активное сопротивление проводника, нетрудно определить и мощность, которая в нем выделяется. [10]
Поскольку активное сопротивление проводника зависит от величины поперечного сечения того поверхностного слоя проводника, в котором течет ток, то для токов СВЧ активное сопротивление тонкостенной трубки не отличается от активного сопротивления проводника в виде сплошного стержня, сделанного из того же металла и имеющего тот же диаметр, что и сплошная трубка.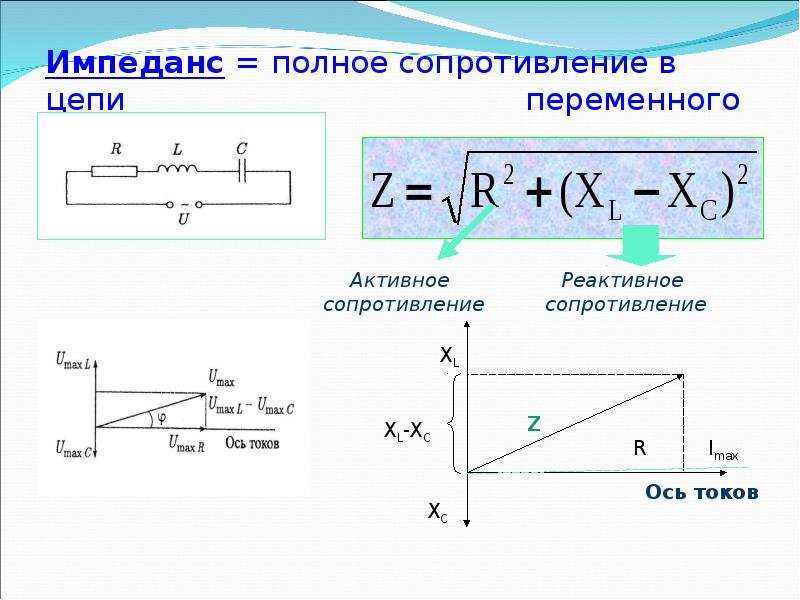
Поскольку активное сопротивление проводника зависит от величины поперечного сечения того поверхностного слоя проводника, в котором течет ток, то для токов сверхвысокой частоты активное сопротивление тонкостенной трубки не отличается от активного сопротивления проводника в виде сплошного стержня, сделанного из того же металла и имеющего тот же диаметр, что и сплошная трубка. [12]
Увеличение активного сопротивления проводников тока якоря и катушек полюсов происходит из-за надрыва и трещин в проводниках или повреждения контактных соединений — распайки концов обмотки в петушках коллектора якоря, ослабления крепления или распайки наконечников. [13]
Под активным сопротивлением проводника понимают такое сопротивление, в котором энергия выделяется в виде теплоты. Электрическая цепь обладает активным сопротивлением К, индуктивностью L и емкостью С, которые являются ее параметрами.
[14]
Электрическая цепь обладает активным сопротивлением К, индуктивностью L и емкостью С, которые являются ее параметрами.
[14]
Яэ — активное сопротивление проводника
Страницы: 1 2 3 4
формула, от чего зависит, в чем измеряется активное сопротивление
Содержание:
Что такое сопротивление
Ток, протекая через провода и различные радиодетали, тратит свою энергию. Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
Это явление количественно выражается величиной сопротивления. В электротехнике его разделяют на активное и реактивное сопротивление. В первом случае при прохождении тока часть его энергии превращается в тепловой вид, а иногда и в другие (например, проявляется в химических реакциях). Величина активного сопротивления зависит от частоты переменного электротока и возрастает с ее увеличением.
Второй тип сопротивления имеет более сложную природу и возникает в момент включения или выключения потребителя электроэнергии в сеть переменного или постоянного тока. В цепи с реактивным сопротивлением энергия электрического тока частично превращается в другую форму, а затем переходит обратно, то есть, наблюдается периодический колебательный процесс. Полное сопротивление цепи включает в себя активный и реактивный типы, которые учитываются по особым правилам.
Виды сопротивления
В электротехнике рассматривается активное электрическое сопротивление, а также две разновидности реактивного: индуктивное и ёмкостное.
Какое сопротивление называется реактивным, какое активным
Активное электросопротивление — это важный параметр электрической сети, который обуславливает превращение электрической энергии, поступающей в участок электроцепи или в отдельный элетроэлемент в любой другой тип энергии: химическую, механическую, тепловую, электромагнитную. Процесс превращения при этом считаю необратимым.
Типы рассматриваемой величины и формулы ее расчета
Реактивное сопротивление по-другому называется реактансом и представляет собой сопротивляемость элементов электроцепи, которые вызывается измерением силы электротока или напряжения из-за имеющейся емкости или индуктивности этого элемента. При реактансе происходит обменный процесс между отдельным компонентом сети и источником энергии. Часто это понятие относят к простому электрическому сопротивлению, однако оно отличается некоторыми моментами.
Течение переменного электротока не зависит от типа сопротивляемости элементов и всей сети
Какие отличия
Отличия этих типов электросопротивления в том, что «внутри» активностного типа энергия не накапливается, так как она попадает в активностый элемент и отдается окружающей среде в виде другого ее типа. Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.
Это может быть тепло или механическое поднятие груза, свечение, химическая реакция, задание чему-либо скорости.
Индуктивная величина и ее формулы
Важно! Преданная электроэлементу с активностным электросопротивлением энергия преображается и конвертируется, но не возвращается в сеть.
Сопротивляемость же реактивная, наоборот, копит энергию внутри себя за ¼ всего периода синусоидального электротока, а за следующую четверть возвращает ее обратно в сеть. То есть, в окружающую среду полученная энергия не передается.
Комплексная сопротивляемость отдельного элетроэлемента сети R
В активностном типе фазы электрических токов и напряжения совпадают, следовательно, выделяется некоторое количество электроэнергии. В реактивном виде фазы электротока и напряжения расходятся, поэтому энергия передается обратно. Это во многом объясняет то, что активностные электроэлементы нагреваются, а реактивные — нет.
Активная сопротивляемость в цепи переменного синусоидального тока
Области проявления
Реактанс электросопротивления проявляется в емкости и индукции. Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.
Первое обуславливается наличием емкости проводниках и обмотках или включением в электрическую цепь переменного тока различных конденсаторов. Чем выше емкость потребителя и угловой частоты сигнала электротока, тем меньше емкостная характеристика.
Вам это будет интересно Особенности активно-емкостной нагрузки
Сопротивляемость, которую оказывает проводник переменному току и электродвижущей силе самоиндукции, называется индуктивным. Оно зависит от индуктивности потребителя. Чем выше его индуктивность и выше частота переменного электротока, тем выше индуктивное электросопротивление. Выражается оно формулой: xl = ωL, где xl — это электросопротивление индукции, L — индуктивность, а ω — угловая частота тока.
Емкостный реактанс электросопротивление проявляется, например, в конденсаторе, который накапливает электроэнергию в виде электромагнитного поля между своими обкладками. Индуктивное электросопротивление можно наблюдать в дросселе, который накапливает энергию в виде магнитного поля внутри своей обмотки.
Активностным же электросопротивлением может обладать любой резистор, линии электропередач, обмотки трансформатора или электрического двигателя.
Индукция ЭДС может наблюдаться в дросселе
Таким образом, активный резист и реактанс во многом отличаются друг от друга не только разницей по названию, но и по физическим свойствам. Первый вид превращает электроэнергию в другой вид и отдает ее в окружающую среду. Второй же — возвращает ее обратно в электросеть.
Переменный ток
Для того чтобы понять, что такое активное сопротивление, необходимо разобраться в самом явлении переменного тока. Переменным является такой тип тока, который непрерывно изменяет направление своего протекания. Во время протекания потенциалы переменного тока постоянно изменяются. Это происходит благодаря работе генератора, а точнее за счет взаимодействия магнитного поля с медной обмоткой. Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.
Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.
Роль переменного тока сложно переоценить. Главное его достоинство заключается в простоте передачи от источника к потребителю, возможность занижать или увеличивать напряжение при помощи трансформаторов. Также, переменные электрические токи можно доставлять потребителю с гораздо меньшими затратами.
Активное сопротивление
Переменный ток доставляется потребителю с целью его преобразования в иные виды энергии, например, тепло и свет. В бытовых сетях преобладает использование однофазного переменного тока. При подключении потребителя создается активное сопротивление.
Простые цепи переменного тока с активным сопротивлением включает в себя генератор тока и идеальный резистор. При этом должны соблюдаться необходимые условия для идеальной цепи:
- Активное сопротивление не должно равняться нулю, обязательное условие.
- Емкость и индуктивность цепи должны быть равны нулю.

Также, для идеального активного сопротивления должны соблюдаться следующие условия:
- Соблюдаются закон Ома для мгновенных, среднеквадратичных и амплитудных параметров цепи.
- Значение полностью независимо от амплитудных колебаний.
- Между током и напряжением отсутствует сдвиг фаз.
- Элемент, находящийся под напряжением, выделяет долю тепловой энергии, то есть нагревается.
Все эти условия позволяют электрическим приборам работать в пределах точно установленных параметров с максимальным КПД. Любое изменение может быть причиной отсутствия надежного контактного соединения или неисправностью самого потребителя.
Для того чтобы рассчитать величину активного сопротивления в цепи, необходимо знать величину напряжения и силы тока. Для расчета используется формула: R=U/I. Формула состоит из следующих значений:
- «R» — сопротивление, Ом;
- «U» — величина напряжения, вольт;
- «I» — величина силы тока, ампер.
Далее можно сделать простой расчет. В качестве потребителя выступает электрическая печь, включенная в цепь однофазного переменного тока:
В качестве потребителя выступает электрическая печь, включенная в цепь однофазного переменного тока:
- Напряжение цепи 240 вольт.
- При замере силы тока получено значение 4 ампера.
- R= 240/4=60 Ом.
Расчетная величина активного сопротивления — это не окончательное значение. На нее влияет прежде всего сечение проводов включенных в цепь, схема взаимодействия между цепями емкостных и полупроводниковых элементов.
Активное значение цепи также вызывает безвозвратную потерю первоначальной электрической энергии, а так же приводит к снижению мощности.
Зависимость
Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.
Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.
Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.
Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.
Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2,то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р= UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
В чем измеряется реактивное сопротивление
Само по себе, явление реактанса характерно только для цепей с электрическим током переменного типа. Обозначается оно латинской буквой «X» и измеряется в Омах. В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения. Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.
Обозначается оно латинской буквой «X» и измеряется в Омах. В отличие от активностного варианта, реактанс может иметь как положительное, так и отрицательное значение. Знак «+» или «-» соответствует знаку, по которому сдвигается фаза электротока и напряжения. Знак положительный, когда ток отстает от напряжения и отрицателен, когда кот опережает напряжение.
Важно! Абсолютно чистое реактивное электросопротивление имеет сдвиг фазы на ± 180/2. То есть, фаза «двигается» на π/2.
Как правильно измерять сопротивление
При работе с радиоаппаратурой иногда требуется измерять не только активностное, но и реактивное электросопротивление (индуктивность и емкость). Для измерений применяют косвенный метод использования мультиметра, а более точные значения получают при мостовом методе.
Косвенный метод наиболее прост в своей реализации, так как не требует дополнительных схем включения. Одна требуется наличие трех отдельных приборов: амперметра, вольтметра и ваттметра. Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².
Если измерить напряжение и силу электротока в цепи, то можно получить полное электросопротивление: Z=U*I После измерения активностной мощности P, можно получить величину активного сопротивления отдельного элемента: R= P/I².
Катушка
Катушка индуктивности представляет собой металлический или ферритный сердечник, на который намотано несколько витков медного провода. Элемент обладает следующими свойствами:
- За счет индуктивности ограничивается скорость изменения токов.
- С увеличением частоты тока катушка способна увеличить свое сопротивление (скин-эффект).
- Создает магнитное поле.
- Увеличивает и накапливает напряжение.
- Создает сдвиг фаз переменного тока.
- Пропорционально скорости движения тока создает ЭДС самоиндукции.
Все эти свойства находят применение при разработке радиоприемных устройств, генераторов частоты, тестеров, магнитометров и других видов сложного оборудования.
Конструкция и разновидности
Все типы катушек индуктивности имеют одинаковую конструкцию, независимо от области их использования. Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
Особенности, внесенные для получения индивидуальных параметров, влияют на тип детали.
- Соленоид. Компонент с увеличенной общей длиной обмоточного провода. Обмотка больше диаметра детали.
- Тороидальная. В такой катушке соленоид выполнен в форме «тора».
- Многослойный тип, имеет несколько рядов обмотки.
- Секционированная. Обмотка имеет несколько разделенных секций, иногда из провода разного сечения. Наиболее известной катушкой этого типа является трансформатор или дроссель.
- Универсальная, может совмещать сразу несколько вариантов обмотки.
Независимо от конструкции, все катушки работают по одному и тому же принципу.
Замер сопротивления и формула расчета
Замерить активное сопротивление катушки индуктивности можно только в обесточенном виде. Делается это при помощи мультиметра.
- Мультиметр надо перевести в режим омметра.
- Красный измерительный щуп соединить с первым выходом катушки.
- Черный измерительный щуп соединить со вторым выходом.

- Прибор покажет только активное сопротивление обмотки.
При помощи тестера можно определить только целостность витков. Если элемент включен в цепь под напряжением, то величину сопротивления находят за счет простого вычисления по формуле: Z=U/I.
Для расчета по этой формуле, при помощи тестера определяют сначала величину тока (I) и напряжения (U). Активное сопротивление измеряется в Омах.
Зная формулу расчета активного и индуктивного сопротивления, полное сопротивление элемента может быть найдено с помощью формулы:
Z= 2×(R×R+XL×XL)
В этом выражении R является активным сопротивлением, а XL — индуктивным.
Активное сопротивление катушки
Активное сопротивление обуславливается омической характеристикой проводов обмотки. При работе на низких частотах, омическое сопротивление не зависит от частоты. В мощных устройствах необходимо учитывать эффект близости, который заключается в том, что токи и образуемое ими магнитное поле вызывают вытеснение тока в проводах соседних витков. В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.
В результате, снижается эффективное используемое сечение провода и растет его омическое сопротивление.
Обратите внимание! На высоких частотах проявляется скин-эффект, который заключается в том, что ток вытесняется в поверхностные слои провода. В результате этого снижается используемое сечение кабеля. Для снижения скин-эффекта вместо одного проводника используют жгут из нескольких более тонких – литцендрат, либо поверхность провода покрывают слоем серебра, поскольку оно обладает наименьшим удельным сопротивлением.
Скин-эффект
В мощных электромагнитных системах (ускорители частиц) для снижения активного сопротивления, используется свойство сверхпроводимости – полное исчезновение сопротивления при охлаждении некоторых материалов ниже критической температуры.
Провод литцендрат
Во многих случаях применения катушек индуктивности следует учитывать влияние активного сопротивления обмоток. Данный параметр может отрицательно влиять не только путем снижения добротности, но и вызывать повышенный нагрев проводников обмоток в том случае, когда устройство работает с большими токами.
Определение активного сопротивления проводов
Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.
Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
- l – длина линии, м;
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см.
 таблицу 1.14 [Л2. с.30].
таблицу 1.14 [Л2. с.30].
Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуляПростой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
| На главную § 53. Активное сопротивление в цепи переменного тока Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением . К активным сопротивлениям при промышленной частоте (50 Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и направление тока. Это значит, что ток и напряжение совпадают по фазе. Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отложим в выбранном масштабе по горизонтали вектор напряжения . Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (φ = 0), откладываем вектор тока I по направлению вектора напряжения. Сила тока в такой цепи определяется по закону Ома: В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения. Пример. К цепи переменного тока с активным сопротивлением Показание амперметра, измеряющего действующее значение тока, Среднее значение активной мощности, потребляемой сопротивлением, Р = I U = 220 · 4 = 880
|
Активное сопротивление в цепи переменного тока — Студопедия
Поделись
КОНТРОЛЬНАЯ РАБОТА
вариант №13
по дисциплине: Электроника и электротехника
тема: Активное сопротивление в цепи переменного тока
Выполнил:
Студент 3 курса заочной
формы обучения
Направление подготовки/специальность ТБ 31-16 «Техносферная безопасность»
__________/ И. Х. Мухамадьянов
Х. Мухамадьянов
Преподаватель: Доцент кафедры
_______________ Альмухаметов Р.Ф.
УФА 2018
Содержание
1. Введение……………………………………………………………..3
2. Активное сопротивление в цепи переменного тока………………5
3. Список использованной литературы………………………………16
2
Введение
Любое тело, по которому протекает электрический ток, оказывает ему определенное сопротивление. Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.
Электронная теория так объясняет сущность электрического сопротивления металлических проводников. Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Свободные электроны при движении по проводнику бесчисленное количество раз встречают на своем пути атомы и другие электроны и, взаимодействуя с ними, неизбежно теряют часть своей энергии. Электроны испытывают как бы сопротивление своему движению. Различные металлические проводники, имеющие различное атомное строение, оказывают различное сопротивление электрическому току.
Точно тем же объясняется сопротивление жидких проводников и газов прохождению электрического тока. Однако не следует забывать, что в этих веществах не электроны, а заряженные частицы молекул встречают сопротивление при своем движении.
Сопротивление обозначается латинскими буквами R или r.
За единицу электрического сопротивления принят ом.
Ом есть сопротивление столба ртути высотой 106,3 см с поперечным сечением 1 мм2 при температуре 0° С.
Если, например, электрическое сопротивление проводника составляет 4 ом, то записывается это так: R = 4 ом или r = 4ом.
Для измерения сопротивлений большой величины принята единица, называемая мегомом.
Чем больше сопротивление проводника, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем легче электрическому току пройти через этот проводник.
Следовательно, для характеристики проводника (с точки зрения прохождения через него электрического тока) можно рассматривать не
3
только его сопротивление, но и величину, обратную сопротивлению и называемую, проводимостью.
Электрической проводимостью называется способность материала пропускать через себя электрический ток.
Так как проводимость есть величина, обратная сопротивлению, то и выражается она как 1/R, обозначается проводимость латинской буквой g.
Сопротивление различных проводников зависит от материала, из которого они изготовлены. Для характеристики электрического сопротивления различных материалов введено понятие так называемого удельного сопротивления.
Удельным сопротивлением называется сопротивление проводника длиной 1 м и площадью поперечного сечения 1 мм2. Удельное сопротивление обозначается буквой греческого алфавитар. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Удельное сопротивление обозначается буквой греческого алфавитар. Каждый материал, из которого изготовляется проводник, обладает своим удельным сопротивлением.
Например, удельное сопротивление меди равно 0,017, т. е. медный проводник длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,017 ом. Удельное сопротивление алюминия равно 0,03, удельное сопротивление железа — 0,12, удельное сопротивление константана — 0,48, удельное сопротивление нихрома — 1-1,1.
Сопротивление проводника прямо пропорционально его длине, т. е. чем длиннее проводник, тем больше его электрическое сопротивление.
Сопротивление проводника обратно пропорционально площади его поперечного сечения, т. е. чем толще проводник, тем его сопротивление меньше, и, наоборот, чем тоньше проводник, тем его сопротивление больше.
4
Активное сопротивление в цепи переменного тока
Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную работу или в тепловую энергию, называется активным сопротивлением.
К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электронагревательные устройства.
Рассмотрим цепь переменного тока (рис. 56), в которую включено активное сопротивление. В такой цепи под действием переменного напряжения протекает переменный ток. Изменение тока в цепи, согласно закону Ома, зависит только от изменения напряжения, подключенного к ее зажимам. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
5
Из сказанного следует, что в цепи переменного тока с активным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и направление тока. Это значит, что ток и напряжение совпадают по фазе.
Построим векторную диаграмму действующих величин тока и напряжения для цепи с активным сопротивлением. Для этого отложим в выбранном масштабе по горизонтали вектор напряжения . Чтобы на векторной диаграмме показать, что напряжение и ток в цепи совпадают по фазе (φ = 0), откладываем вектор тока I по направлению вектора напряжения.
Сила тока в такой цепи определяется по закону Ома:
В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.
Пример. К цепи переменного тока с активным сопротивлением r = 55 ом подключен генератор, максимальное значение напряжения которого
Um = 310,2 в.
Определить:
1) показание вольтметра, подключенного к зажимам генератора;
2) показание амперметра, включенного в цепь;
3) среднее значение мощности, потребляемой сопротивлением.
Решение. Известно, что электроизмерительные приборы, включенные в цепь переменного тока, измеряют действующие значения. Поэтому показание вольтметра, измеряющего напряжение,
Поэтому показание вольтметра, измеряющего напряжение,
6
Показание амперметра, измеряющего действующее значение тока,
Среднее значение активной мощности, потребляемой сопротивлением, Р = I U = 220 · 4 = 880 вт или Р = I2 r = 42 · 55 = 16 · 55 = 880 вт.
7
Когда в электрическую цепь переменного тока подключается активное сопротивление R, то под воздействием разницы потенциалов источника в цепи начинает течь ток I. В тех случаях, когда изменение напряжения происходит по синусоидальному закону, который выражается, как
u = Um sin ωt, то изменение тока i также идет по синусоиде:
i = Im sin ωt
При этом Im = Um/R
Так что получается, что изменение напряжения и тока происходят по одинаковым законам. При этом через нулевое значение они проходят одновременно и своих максимальных значений также достигают одновременно. Из этого следует, что когда в электрическую цепь переменного тока подключается активное сопротивление R, то напряжение и ток совпадают по фазе.
8
Если взять равенство Im = Um / R и каждую из его частей разделить на √2, то в итоге получится ни что иное, как закон Ома, применимый для той цепи, которая рассматривается: I = U/R.
Таким образом, получается, что это основополагающий закон для той цепи, которая имеет в своем составе только активное сопротивление, с точки зрения математики имеет такую же форму, что и для цепи тока постоянного.
Электрическая мощность
Такой показатель, как электрическая мощность P для цепи, имеющей в своем составе активное сопротивление, равняется произведению мгновенного значения напряжения U на мгновенное значение силы тока i в любой момент времени. Из этого следует, что в цепях переменного тока, в отличие от цепей тока постоянного, мгновенная мощность P – величина непостоянная, а ее изменение происходит по кривой. Для того чтобы получить ее графическое представление, необходимо ординаты кривых напряжения U и силы тока i перемножить при разных углах ωt. Мощность изменяется по отношению к изменению тока с двойной частотой ωt.
9
Это означает, что половине периода изменения напряжения и тока соответствует один период изменения мощности. Следует заметить, что абсолютно все значения, которые может принимать мощность, являются положительными величинами. С точки зрения физики это означает, что от источника к приемнику передается энергия. Своих максимальных значений мощность достигает тогда, когда ωt = 270° и ωt = 90°.
В практическом отношении о той энергии W, которую создает электрический ток, принято судить по средней мощности, выражаемой формулой Рср = Р, а не по мощности максимальной. Ее можно определить, перемножив на время протекания тока среднее значение мощности W = Pt.
Относительно линии АБ, соответствующей среднему значению мощности P, кривая мгновенной мощности симметрична. По этой причине
P = Pmax / 2 = UI
Если использовать закон Ома, то можно выразить активную мощность в следующем виде:
P = I2R или P = U2/R.
Специалисты в области электротехники ту среднюю мощность, которую потребляет активное сопротивление, чаще всего именуют или просто мощностью, или активной мощностью, а для ее обозначения используется буква P.
10
Поверхностный эффект
Необходимо особо отметить такую особенность проводников, включенных в сеть переменного тока: их активное сопротивление во всех случаях оказывается больше, чем если бы они были включены в сеть тока постоянного. Причина этого состоит в том, что переменный ток не протекает равномерно распределяясь по всему поперечному сечению проводника, как ведёт себя постоянный ток, а выводится на его поверхность. Таким образом, получается, что при включении проводника в цепь переменного тока его полезное сечение оказывается значительно меньшим, чем при включении в цепь тока постоянного. Именно поэтому его сопротивление возрастает. В физике и электротехнике это явление называется поверхностным эффектом.
То, что переменный ток распределяется по сечению проводника неравномерно, объясняется действием электродвижущей силы самоиндукции. Она индуцируется в проводнике тем магнитным полем, которое создается током, проходящим по нему. Необходимо заметить, что действие этого магнитного поля распространяется не только на окружающее проводник пространство, но и на внутреннюю его часть. По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.
По этой простой причине те слои проводника, которые располагаются ближе к его центру, находятся под воздействием большего магнитного потока, чем те слои, что располагаются ближе к его поверхности. Соответственно, электродвижущая сила самоиндукции, которая возникает во внутренних слоях, существенно больше, чем та, что образуется в слоях внешних.
Электродвижущая сила самоиндукции является существенным препятствием для изменения тока, и поэтому он будет следовать преимущественно по поверхностным слоям проводника. Необходимо также отметить, что сопротивление активных проводников в цепях переменного тока существенно зависит от частоты: чем она больше, тем выше ЭДС самоиндукции, и поэтому ток в большей степени подвергается вытеснению на поверхность.
11
Активным или ваттным сопротивлением называется всякое сопротивление, поглощающее электрическую энергию или вернее превращающее ее в другой вид энергии, например в тепловую, световую или химическую.
Потери энергии, а, следовательно, и активное сопротивление в электрической цепи при переменном токе всегда больше потерь энергии в этой же цепи при постоянном токе. Причина этого заключается в том, что в цепях переменного тока потери энергии обусловлены не только обычным омическим сопротивлением проводников, но и многими другими причинами.
Причина этого заключается в том, что в цепях переменного тока потери энергии обусловлены не только обычным омическим сопротивлением проводников, но и многими другими причинами.
Рассмотрим некоторые из этих.
Так, например, наличие конденсатора в цепи переменного тока связано с дополнительными потерями энергии в результате периодического (с частотой переменного тока) изменения поляризации диэлектрика или, попросту говоря, в результате непрерывного переворачивания взад и вперед молекулярных парных зарядов. При этом происходит нагревание диэлектрика, т. е. электрическая энергия превращается в тепловую. Эти потери энергии называются диэлектрическими потерями.
Кроме диэлектрических потерь, как уже говорилось раньше, происходят потери энергии из-за утечки тока вследствие несовершенства изоляции между пластинами конденсаторов. Эти потери называются потерями утечки.
Вокруг всякого переменного тока существует переменное магнитное поле. Следовательно, во всех окружающих железных предметах происходит непрерывное переворачивание молекулярных магнитиков в такт с частотой переменного тока. В результате железные предметы, находящиеся в поле переменного тока, нагреваются, т. е электрическая энергия превращается в тепловую. Эти потери называются потерями на гистерезис.
В результате железные предметы, находящиеся в поле переменного тока, нагреваются, т. е электрическая энергия превращается в тепловую. Эти потери называются потерями на гистерезис.
Благодаря электромагнитной индукции переменный электрический ток наводит в близлежащих замкнутых электрических цепях индукционные токи, что связано с нагреванием этих цепей, т. е. с дополнительными потерями энергии.
12
Кроме того, такие же индукционные круговые токи возникают не только в замкнутых электрических цепях, но и в близлежащих металлических предметах и нагревают их. Эти токи называются токами Фуко. Возникновение токов Фуко также сопряжено с потерями электрической энергии.
Токи Фуко не всегда являются вредными. Например, на принципе токов Фуко основана защита радиоприборов медными или алюминиевыми экранами от переменных магнитных полей высокой частоты.
Наконец, при очень высоких частотах цепь переменного тока может излучать электромагнитные волны (радиоволны), что связано с потерями на излучение.
Наличие всех этих потерь увеличивает активное сопротивление цепи переменному току.
Опыт показывает, что при высоких частотах и омическое сопротивление проводника оказывается значительно большим, чем при постоянном токе.
Для объяснения этого явления увеличим мысленно сечение проводника (и посмотрим, что происходит в нем при прохождении по нему переменного тока. Вдоль проводника взад и вперед с частотой переменного тока движется огромное количество электронов.
Активное сопротивление цепи переменного тока
Поверхностный эффект, как фактор увеличения активного сопротивления в цепи переменного тока. Ток вытесняется магнитным полем на поверхность проводника (а), поэтому у поверхности проводника плотность тока больше, чем внутри проводника (б).
До сих пор нам было известно, что движущийся по проводнику переменный поток электронов создает вокруг него переменное магнитное поле. Теперь же, когда мы заглянем внутрь проводника, мы увидим, что магнитное поле имеется и внутри проводника. Это вызвано тем, что каждый
Это вызвано тем, что каждый
13
1электрон при движении создает вокруг себя магнитное поле, а так как часть электронов движется вблизи оси проводника, то они создают магнитное поле не только во вне, но и внутри проводника.
Продолжая присматриваться к происходящему внутри проводника, мы заметим, что наиболее быстро движутся электроны, находящиеся у поверхности проводника, а по мере приближения к середине проводника амплитуда (размах) колебаний электронов становится все меньше и меньше.
Почему же электроны колеблются с различными амплитудами в разных точках сечения проводника?
Это явление также имеет свое объяснение. Вспомним, что при всяком изменении скорости движения электрона на него действует ЭДС самоиндукции, противодействующая этому изменению. Вспомним также, что ЭДС самоиндукции зависит от числа магнитных силовых линий вокруг движущегося электрона. Чем большим числом магнитных силовых линий охватывается электрон, тем труднее ему совершать колебательное движение.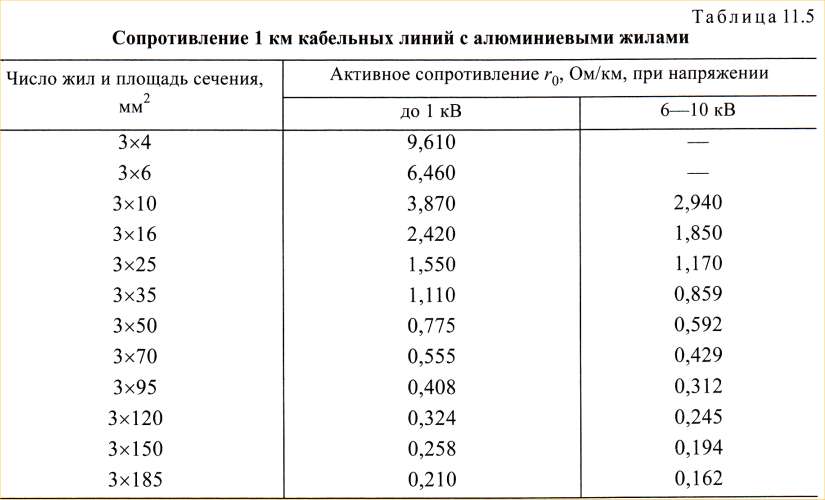
Теперь становится ясным, почему электроны, находящиеся у поверхности проводника, колеблются с большой амплитудой, а электроны, находящиеся глубоко внутри проводника, — с малой. Ведь первые охватываются только теми магнитными силовыми линиями, которые расположены вне проводника, а вторые охватываются и внешними и внутренними магнитными силовыми линиями.
Таким образом, плотность переменного тока получается большей у поверхности проводника и меньшей внутри его.
При очень высоких частотах противодействие ЭДС самоиндукции внутри проводника становится настолько сильным, что все электроны движутся только по поверхности проводника. Это явление и называется поверхностным эффектом. Так как активное сопротивление проводника зависит от его сечения, а полезным сечением при токе высокой частоты оказывается только тонкий наружный слой проводника, то вполне понятно, что его активное сопротивление увеличивается с повышением частоты
14
переменного тока.
Для уменьшения поверхностного эффекта проводники, по которым протекают токи высокой частоты, делают трубчатыми и покрывают их слоем хорошо проводящего металла, например серебра.
В целях борьбы с явлением поверхностного эффекта применяют также провода специальной конструкции, так называемый литцендрат.
литцендрат
Такой проводник свивают из отдельных тонких медных жилок, имеющих эмалевую изоляцию, причем скрутка жилок производится таким образом, чтобы каждая из них проходила поочередно то внутри проводника, то снаружи его.
Явление поверхностного эффекта особенно сильно сказывается в железных проводах, в которых вследствие большой магнитной проницаемости железа внутренний магнитный поток оказывается особенно большим и поэтому явление поверхностного эффекта становится очень заметным даже при сравнительно низких (звуковых) частотах.
15
Формула расчета реактивного сопротивления проводника: калькулятор расчетов
Содержание
- Сопротивления цепи
- Формула расчета реактивного сопротивления
- Импеданс элемента
- Понятие тока и напряжения
- Измерители LCR 816, LCR 817, LCR 827, LCR 819 и LCR 829
- Треугольник сопротивлений
- Физика
- § 2.
 9. Закон Ома для электрической цепи переменного тока
9. Закон Ома для электрической цепи переменного тока - От каких факторов зависит сопротивление
Сопротивления цепи
Уравнение (5-30) можно переписать в следующем виде
U = √(Ir)2 + (IxL)2 = I√r2 + x2L = Iᴢ
откуда ток в цепи
I = U/z = U / √(r2 + x2L)
Величина
z = √(r2 + x2L) = √(r2 + ωL)2
называется полным сопротивлением цепи.
Сопротивления r, xL и z графически можно изобразить сторонами прямоугольного треугольника — треугольника сопротивлении (рис. 5-20),который можно получить из треугольника напряжений, уменьшив каждую из его сторон в I раз.
Так как треугольники сопротивлений и напряжений подобны, то угол сдвига φ между напряжением и током, равный углу между сторонами треугольника z и r, можно определить через
cos φ = Ua /U
Рис 5-20. Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью
Треугольник сопротивлений цепи с активным сопротивлением и индуктивностью
Формула расчета реактивного сопротивления
В общем случае для деталей катушечного типа применяются выражения:
X = L*w = 2* π*f*L.
Для конденсаторов применяют формулы:
X = 1/(w*C)= 1/(2* π*f*C).
Для конкретного элемента, нужные параметры которого известны, величина может быть вычислена с использованием онлайн калькулятора. В форму потребуется ввести нужные данные и нажать на кнопку, инициирующую расчеты.
Умение рассчитывать данную составляющую сопротивляемости поможет узнать величину тепловых потерь на используемых нагрузках. При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
Из всех трёх величин наиболее значимой является ёмкостное сопротивление конденсатора, но при определённых обстоятельствах индуктивное тоже оказывает влияние. Часто при расчётах паразитные значения вроде индуктивности или активного сопротивления принимаются ничтожно малыми, а конденсатор в этом случае называется идеальным.
Полное сопротивление элемента выражается в формуле Z = (R2 + (Xl-Xc) 2 ) ½, где
- Xl — индуктивность;
- Xс — ёмкость;
- R — активная составляющая.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
- X > 0, в элементе проявляются индуктивные свойства;
- X = 0, в ёмкости присутствует только активная величина;
- X < 0, в элементе проявляется ёмкостное сопротивление.
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Импеданс элемента.
Понятие тока и напряжения
Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.
Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.
В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.
Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.
То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.
Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.
Другими словами, сопротивление — это величина, препятствующая прохождению тока.
Измерители LCR 816, LCR 817, LCR 827, LCR 819 и LCR 829
Это стационарные, лабораторные, высокопрецизионные измерители RLC. Предназначенные, прежде всего, для фундаментальных лабораторных исследований или высокоточных измерение на производственной линии. Отличия между моделями составляет:
- Различные частоты тест-сигнала. Для измерителя LCR 816 верхняя частота составляет 2 кГц, для измерителей LCR 817 и LCR 827 верхняя частота составляет 10кГц , LCR 819 и LCR 829 верхняя частота составляет 100 кГц. Нижние частоты измерения для всех приборов одинаковы и составляют 12 Гц.
- Измерители LCR 827 и LCR 829 модифицированы для использования в промышленности.
 Модификация заключается в уменьшении времени измерения, что позволило ускорить процесс обработки измерения компонентов на конвейере, но в то же время увеличило погрешность измерения (но позволило ей остаться в пределах 0,1%). Второе изменение касается возможности применения механического манипулятора для сортировки радио компонентов при производстве или входном контроле. Сортировки осуществляется загрузкой соответствующего программного обеспечения как в измеритель RLC, так и в манипулятор. Сортировка может производиться по различным критериям — по абсолютному отклонению, по относительному отклонению и т.д.
Модификация заключается в уменьшении времени измерения, что позволило ускорить процесс обработки измерения компонентов на конвейере, но в то же время увеличило погрешность измерения (но позволило ей остаться в пределах 0,1%). Второе изменение касается возможности применения механического манипулятора для сортировки радио компонентов при производстве или входном контроле. Сортировки осуществляется загрузкой соответствующего программного обеспечения как в измеритель RLC, так и в манипулятор. Сортировка может производиться по различным критериям — по абсолютному отклонению, по относительному отклонению и т.д.
Общими особенностями измерителей RLC компании GOOD WILL являются:
- Базовая погрешность измерения 0,05%.
- 503 частоты тест-сигнала, что позволяет проводить измерения не только на стандартных частотах (110Гц, 1 кГц, 10 кГц и 100 кГц) как было раньше, но и формировать практически непрерывную сетку частот измерительного сигнала.
- Регулировка уровня тест-сигнала от 5 мВ до 1,275 В с шагом 5 мВ, что так же позволяет формировать практически непрерывную сетку уровней.
 Это особенно актуально при измерении параметров нелинейных компонентов реактивные значения, которых зависят от уровня сигнала. Причем измеритель RLC обеспечивает как режим стабилизации уровня тест- сигнала, т.е его стабилизацию при изменении сопротивления реактивного элемента которое неизбежно зависит от частоты тест сигнала, так и отключение его стабилизации.
Это особенно актуально при измерении параметров нелинейных компонентов реактивные значения, которых зависят от уровня сигнала. Причем измеритель RLC обеспечивает как режим стабилизации уровня тест- сигнала, т.е его стабилизацию при изменении сопротивления реактивного элемента которое неизбежно зависит от частоты тест сигнала, так и отключение его стабилизации. - Ветренее смещение измерительного сигнала постоянным напряжением в пределах от 0 В до 2В, или внешнее смещении до 30 В. Как уже ранее упоминалось, это необходимо при измерении таких компонентов как варикапов, ёмкость которых зависит от приложенного постоянного напряжения или трансформаторов, параметры которых зависят от степени намагничивания постоянным напряжением.
- Отображение относительного или абсолютного результата измерения.
- Память на 100 профилей условий измерения.
- Усреднение результатов измерения для повышения точности измерения.
- Программная компенсация режимов коротко замыкания (КЗ) и холостого хода (ХХ).

- Интерфейс RS-232 для связи с компьютером.
- Закрытая программная калибровка для обеспечения требуемой погрешности измерения в межповерочном интервале.
- Большой высококонтрастный дисплей, на котором отображаются не только результаты измерения основных и дополнительных параметров, но и условия измерения.
- Комплект дополнительных аксессуаров включает множество устройств и приспособлений для подключения различных радио- электронных компонентов и радио устройств с различной конструкцией выводов.
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза. Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.
Величина и начальная фаза переменного тока, создаваемого переменным напряжением, зависят не только от величины сопротивлений, образующих электрическую цепь, но и от индуктивности и емкости этой цепи.Активное сопротивление в цепи переменного тока.Строго говоря, любая электрическая цепь обладает, кроме сопротивления, также индуктивностью и емкостью. Если по проводнику проходит ток, то вокруг него возбуждается магнитное поле, т.
е. имеют место явления индуктивности. Ток возникает под действием электрического поля на заряды, следовательно, проводник должен обладать емкостью, так как в диэлектрической среде вокруг него возникает поток смещения.Однако в ряде случаев относительная роль двух из трех параметров R, L, С в электрической цепи практически незначительна.
Это позволяет рассматривать подобную цепь как обладающую только сопротивлением, или только индуктивностью, или только емкостью.Мы рассмотрим поочередно условия в трех таких простейших цепях переменного тока.В цепи, содержащей только сопротивление г, синусоидальное напряжени u = Um sin ?t источника электроэнергии создает ток:i = u : r = (Um: r ) sin ?tТак как сопротивление r от времени не зависит, то в этой цепи ток совпадает по фазе с напряжением (рис. 1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
1) и изменяется также синусоидально:i = Imsin ?tздесь:Im= Um: rРисунок 1 Кривые мгновенных значений напряжения и тока в цепи,содержащей только сопротивление r.Разделив последнее выражение на , получим формулу закона Омадля действующих значений напряжения и тока:I = U : rКак видно из формулы, этот закон для цепей переменного тока, содержащих только сопротивление r, имеет такой же вид, как и закон Ома для цепи постоянного тока.В цепи переменного тока сопротивление r называется активным сопротивлением. Это сопротивление, в котором электроэнергия преобразуется в другую форму (в теплоту и др.).Оно может существенно отличаться от сопротивления rпри постоянном токе.
Сопротивление для постоянного тока называют омическим, чтобы отличить его от активного сопротивления для переменного тока.Различие между активным и омическим сопротивлениями обуславливается рядом причин. Одна из них – поверхностный эффект, частичное вытеснение переменного тока в поверхностные слои проводника.Чем больше частота переменного тока, тем это вытеснение значительнее. Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?
Из-за поверхностного эффекта сопротивлениеrоказывается уже существенно большим, чем вычисленное по формуле:r = ?
(l : S)Поверхностный эффект создается тем, что переменное магнитное поле индуктирует во внешних слоях проводника меньшую ЭДС самоиндукции, чем во внутренней его части.Особенно сильно поверхностный эффект увеличивает активное сопротивление стальных проводов. На активное сопротивление медных и алюминиевых проводов при промышленной частоте поверхностный эффект существенно влияет только при больших сечениях проводов (свыше 25 кв. мм).Кроме поверхностного эффекта, большое увеличение активного сопротивления электрической цепи могут вызывать потери энергии в переменном электромагнитном поле цепи от гистерезиса и вихревых токов.Поделитесь полезной статьей:
https://youtube.com/watch?v=NSxgxMNG2fwrel%3D0%26amp%3Bcontrols%3D0%26amp%3Bshowinfo%3D0
- electrosam.ru
- electrono.ru
- electroandi.ru
- fazaa.ru
Физика
§ 2.9. Закон Ома для электрической цепи переменного тока
Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).
2.20).
Рис. 2.20
Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?
Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:
В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.
Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.
Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).
Векторная диаграмма электрической цепи
Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.
Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор mR должен совпадать по направлению с вектором m. Его модуль равен UmR = ImR.
Рис. 2.21
Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и mL должен быть повернут относительно вектора m на π/2. Его модуль равен UmL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)
Вектор напряжения на конденсаторе mC отстает по фазе от вектора m на π/2 и поэтому повернут на этот угол относительно вектора m направо. Его модуль равен .
Его модуль равен .
Для нахождения вектора суммарного напряжения m нужно сложить три вектора: mR, mL и mC. Вначале удобнее сложить два вектора mL и mC (рис. 2.22).
Рис. 2.22
Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор mL + mC с вектором mR, получим вектор m, характеризующий колебания напряжения в сети.
По теореме Пифагора (из треугольника АОВ):
или
Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:
Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.
Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:
От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2. 9.3):
9.3):
Мгновенное значение силы тока меняется со временем гармонически:
где φc, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.
Сдвиг фаз между током и напряжением
Сдвиг фаз φc, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами m и m (см. рис. 2.22). Как следует из этого рисунка,
Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φc = -φ и
В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.
От каких факторов зависит сопротивление
Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.
Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.
Цепь, в которой возникает индукция
В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.
Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.
Вам это будет интересно Особенности свободной энергии
Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.
Принцип действия электродвижущей силы
Tags: ампер, амплитуда, бра, вид, гистерезис, диаграмма, дом, е, емкость, измерение, как, компьютер, конденсатор, контур, кт, лс, магнит, нагрузка, напряжение, потенциал, провод, р, расчет, резистор, резонанс, ряд, сопротивление, тен, тип, ток, трансформатор, треугольник, ук, фаза, эффект
Тест «Активное сопротивление в цепи переменного тока.
 Действующие значение силы тока и напряжения». Вариант 1.
Действующие значение силы тока и напряжения». Вариант 1.
Получите готовые материалы учителя на весь учебный год для работы в классе и удалённо! Подробнее…
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Выбрать материалы
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Состоит из 6 тестовых вопросов. Время выполнения — 4 минут.
Вопрос 1
Электрическое сопротивление проводника называют активным, потому что энергия источника тока (генератора) превращается . ..
..
Варианты ответов
- во внутреннюю энергию проводника
- в энергию электрического поля внутри проводника
- в энергию магнитного поля, возникающего в проводнике
- в энергию электромагнитного поля
Вопрос 2
В цепь переменного тока включен проводник с активным сопротивлением R = 24 Ом (см.рисунок). Если напряжение u на зажимах цепи меняется по гармоническому закону u = 48 sin(4t), то закон изменения силы тока в цепи имеет вид:
Варианты ответов
- i = 2 cos (2t)
- i = 2 sin (2t)
- i = 2 sin (4t)
- i = 2 cos (4t)
Вопрос 3
Амплитудное значение силы переменного тока Im в цепи, содержащей только проводник с активным сопротивлением R = 2 Ом, равно 3 А. Какова средняя мощность \(<p>\) переменного тока в цепи?
Какова средняя мощность \(<p>\) переменного тока в цепи?
Варианты ответов
- 18 Вт
- 12 Вт
- 9 Вт
- 6 Вт
Вопрос 4
Амплитудное значение силы переменного тока в цепи Im = 2,8 А. Чему равно действующее значение силы тока I?
Варианты ответов
- 1,4 А
- 2 А
- 3,9 А
- 5,6 А
Вопрос 5
Амперметры и вольтметры переменного тока регистрируют . ..
..
Варианты ответов
- только амплитудные значения силы тока и напряжения
- только действующие значения силы тока и напряжения
- как действующие, так и амплитудные значения силы тока и напряжения
- действующие значения силы тока и амплитудные значения напряжения
Вопрос 6
Мощность переменного тока на участке цепи, содержащей только активное сопротивление, равна 50 Вт. Если действующее значение силы тока в цепи 5 А, то действующее значение напряжения на этом участке равно …
Варианты ответов
- 20 В
- 15 В
- 10 В
- 5 В
Пройти тест
Сохранить у себя:
© 2020, Никифорова Наталья Владиленовна 1442
myCableEngineering.
 com > Сопротивление проводника
com > Сопротивление проводникаСопротивление постоянному току
CENELEC CLC/TR 50480
сопротивление кабелей можно оценить в соответствии с техническим отчетом CENELC CLC/TR 50480 «Определение площади поперечного сечения проводников и выбор защитных устройств» от февраля 2011 г.
Для проводника:
R=ρ20S
R = постоянный ток сопротивление кабеля Ом.м -1
ρ 20 = удельное электрическое сопротивление материала проводника при 20 °С, Ом·м
S = площадь поперечного сечения проводника, м 2 [или 1e -6 мм 7 Ан 2 9000] альтернатива расчету постоянного тока сопротивление указано в IEC 60228 «Проводники изолированных кабелей». В стандарте есть таблицы максимально допустимого сопротивления для различных медных и алюминиевых кабелей. Для получения более подробной информации см. IEC 60228 Сопротивление постоянному току
Типовые удельные сопротивления можно найти в разделе «Полезные таблицы» базы знаний.
IEC 60228 и IEC 60909-2
Стандарт IEC 60228 «Проводники изолированных кабелей» определяет максимально допустимое сопротивление проводников. Значения, указанные в стандарте IEC 60228, используются на сайте myCableEngineering.com. Для ситуаций и кабелей, не предусмотренных IEC 60228, значения сопротивления рассчитываются по формулам CENELEC.
Рассчитанное выше сопротивление действительно для неэкранированных кабелей. Для экранированных кабелей (или любого типа с магнитным экраном) с металлическим экраном, заземленным с обоих концов, сопротивление увеличивается, как показано в IEC 609.09-9 «Токи короткого замыкания в трехфазной сети переменного тока». системы — Часть 2: Данные электрооборудования для расчетов тока короткого замыкания, таблица 7. См. Импеданс для получения более подробной информации.
Сопротивление переменному току
Сопротивление проводника переменному току всегда больше сопротивления постоянному току. Основными причинами этого являются «скин-эффект» и «эффект близости», которые более подробно обсуждаются ниже. Расчет переменного тока сопротивление выводится из уравнений, приведенных в IEC 60287 «Электрические кабели. Расчет номинального тока».
Расчет переменного тока сопротивление выводится из уравнений, приведенных в IEC 60287 «Электрические кабели. Расчет номинального тока».
Скин-эффект и эффект близости учитываются по следующим формулам:
Rac=R[1+γs+γp]
где
R ac = сопротивление проводника переменному току
R проводника
y s = коэффициент скин-эффекта
y p = коэффициент эффекта близости
Хотя вышеприведенные формулы довольно просты, вычисление факторов скин-эффекта и эффекта близости немного больше. участие, но все же не слишком сложно.
Скин-Эффект
По мере увеличения частоты тока поток электричества становится более сконцентрированным вокруг внешней части проводника. На очень высоких частотах в первую очередь по этой причине часто используются полые проводники. На частотах мощности (обычно 50 или 60 Гц), хотя и менее выраженных, изменение сопротивления из-за скин-эффекта все же заметно.
Коэффициент скин-эффекта y s определяется по формуле:
γs=XS4192+0,8XS4 с Xs2=8πfR10−7ks
Где:
F = частота подачи, HZ
K S = коэффициент эффекта кожи из таблицы ниже
R = Сопротивление DC с помощью эффекта связи
. магнитные поля проводников, расположенных близко друг к другу. Распределение магнитного поля неравномерно, а зависит от физического расположения проводников. Поскольку флюс режет проводники неравномерно, это приводит к неравномерному распределению тока по кабелепроводу и изменению сопротивления.
Формулы для коэффициента эффекта близости различаются в зависимости от того, говорим ли мы о двух или трех ядрах.
γp=Xp4192+0.8Xp4dcS2×2.9
— two core cables or two single-core cables
γp=Xp4192+0.8Xp4dcs2×0.312dcs2+1.18Xp4192+0.8Xp4+0.27
— for three core cables or three одножильные кабели
где (для обоих случаев):
Xp2=8πfR10−7kp
d c = диаметр жилы (мм)
s = расстояние между осями проводника (мм)
k p = коэффициент эффекта близости из таблицы ниже
Примечание:
1. для трех одиночных жил с неравным шагом, s = √(s 1 x s 2 )
для трех одиночных жил с неравным шагом, s = √(s 1 x s 2 )
2. для фасонных проводников y p составляет две трети значения, рассчитанного выше, с
d c = d x = диаметр эквивалентного круглого провода той же площади поперечного сечения (мм)
s = (d x + t), где t — толщина изоляции между проводниками (мм)
* для s , мы можем получить некоторое преимущество, используя геометрическое расстояние. См. Среднее геометрическое расстояние .
Коэффициент k
s и k p| к с | к р | ||
|---|---|---|---|
| Медь | Круглый многожильный или сплошной | 1 | 1 |
| Круглый сегментный | 0,435 | 0,37 | |
| Секторная | 1 | 1 | |
| Алюминий | Круглый многожильный или сплошной | 1 | 1 |
| Круглый 4 сегмент | 0,28 | 0,37 | |
| Круглый 5 сегмент | 0,19 | 0,37 | |
| Круглый сегмент 6 | 0,12 | 0,37 | |
Регулировка температуры
Регулятор постоянного тока сопротивление проводника зависит от температуры:
Rt=R20[1+α20(t−20)]
где R t = сопротивление проводника при t °C
R 20 = сопротивление проводника при 20 °С
t = температура проводника, °С
α 20 = температурный коэффициент сопротивления материала при температуре 20 °С в разделе «Полезные таблицы» базы знаний.
РАБОЧАЯ ТЕМПЕРАТУРА КАБЕЛЯ
При нулевом токе температура проводника кабеля будет такой же, как температура окружающей среды. При максимальном номинальном длительном токе кабель будет иметь предельную температуру изоляции (обычно 70 °C для изоляции из термопласта и 9 °C).0 °C для термореактивной изоляции). При номинальном токе между этими крайними значениями температура кабеля будет иметь значение между температурой окружающей среды и предельной температурой.
Рабочую температуру кабеля можно найти из:
t=(IbIz)2×(Tc−Ta)+Ta
где I b = расчетный ток кабеля, А
I z = номинальный длительный ток кабеля, А
T a = температура окружающей среды, °C
T c = предельная температура проводника [изоляции], °C
Основы сопротивления проводников при высоких частотах
С появлением систем на частотах выше 60 Гц мы наблюдаем повышенный интерес к рейтингу кабелей в этих приложениях.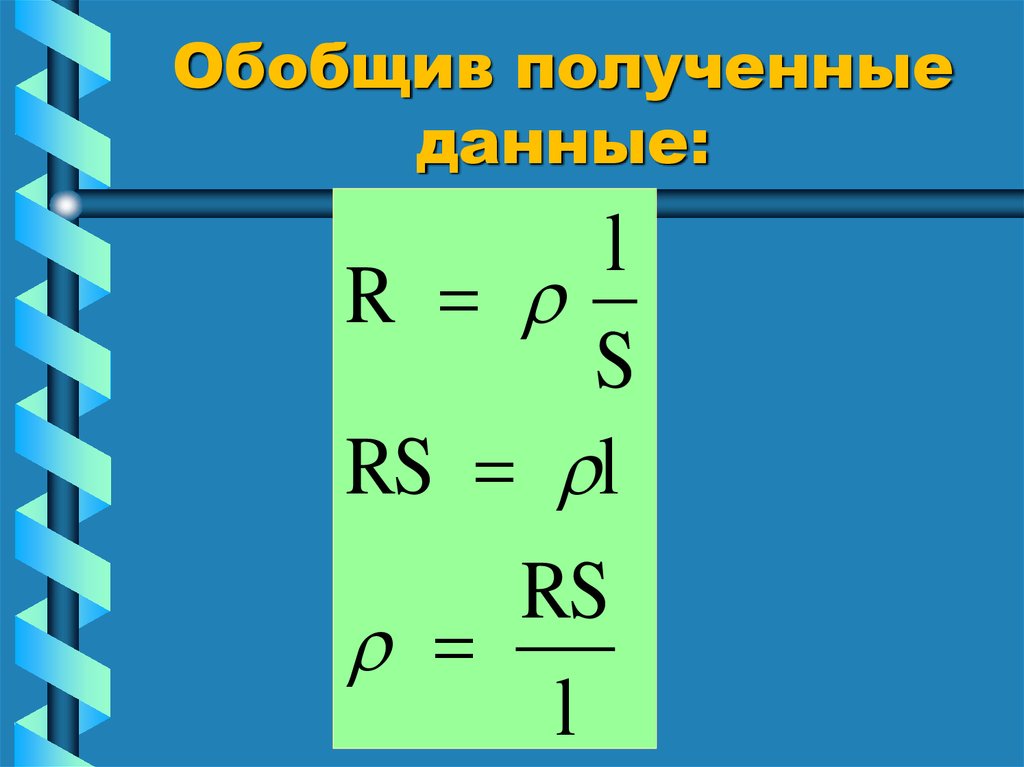 Конечно, здесь на ум приходят компьютерные системы мейнфреймов, работающие на частоте 400 Гц.
Конечно, здесь на ум приходят компьютерные системы мейнфреймов, работающие на частоте 400 Гц.
Есть несколько факторов, которые существенно влияют на сопротивление проводника при увеличении частоты. Поговорим о каждом подробно и предложим предлагаемый метод определения силы тока проводника на частоте 400 Гц по сравнению с таковой на частоте 60 Гц.
Ключевые факторы
В общем, вы должны проектировать 3-фазные энергосистемы с частотой 400 Гц так же, как и системы с частотой 60 Гц, но вы должны понимать, что более высокая частота увеличивает поверхностный эффект и эффекты близости в проводнике. Это, в свою очередь, увеличит эффективное сопротивление проводника. Повышенная частота также увеличит реактивное сопротивление цепи, что в сочетании с сопротивлением увеличит падение напряжения.
Более высокая частота также увеличивает влияние магнитных материалов на реактивное сопротивление и нагрев кабеля. Именно по этой причине не следует прокладывать проводники частотой 400 Гц в магнитопроводе или слишком близко к магнитным конструкциям в здании.
Потери из-за частоты пропорциональны квадрату линейного тока. Так что для очень малых токов этими потерями можно пренебречь. Однако для больших токов они могут быть значительными.
Кабели в воздушной и немагнитной трубе
Мы ограничим наше обсуждение здесь одножильным 600-вольтовым кабелем. Для частот примерно до 1000 Гц можно предположить, что реактивное сопротивление прямо пропорционально частоте. Уменьшением индуктивности из-за частот до этой величины можно пренебречь, потому что оно минимально — и намеренно вносимая погрешность ничтожна. Однако для частот выше 1000 Гц следует включить поправку на индуктивность. В этих случаях индуктивность определяется следующим уравнением:
L = ([0,1404 × log 10 2S/D C ] + [0,0153 × L/L O ]) × 10 -3 Генри на 1000 футов
Где,
L = индуктивность относительно нейтрали
L/L O = поправочный коэффициент из таблицы 1 (нажмите здесь, чтобы увидеть таблицу 1 )
S = осевое расстояние между проводниками (дюймы)
D C = Диаметр проводника (дюймы)
Расчет коэффициентов сопротивления
Из оригинальной статьи Неера Макграта под названием «Расчет повышения температуры и нагрузочной способности кабельных систем» мы знаем, что для любой кабельной системы отношение сопротивления проводника переменному/постоянному току (R AC /R DC ) равно выражается следующим уравнением:
R AC /R DC = 1 + Y C + Y S + Y P (уравнение 1)
Где Y C , Y S и Y P — это эффекты проводника, оболочки и кабелепровода соответственно. Поскольку мы рассматриваем только неметаллические оболочки в воздухе или в неметаллическом трубопроводе, нас должно интересовать только Y C в нашем обсуждении.
Поскольку мы рассматриваем только неметаллические оболочки в воздухе или в неметаллическом трубопроводе, нас должно интересовать только Y C в нашем обсуждении.
Статья Неера Макграта также показывает, что вы можете выразить Y C следующим образом:
Y C = Y CS + Y CP
Где Y CS — проводящий компонент из-за скин-эффекта , а Y CP — проводящий компонент из-за эффекта близости .
Таким образом, принимая во внимание приведенные выше комментарии, уравнение 1 принимает следующий вид:
R AC /R DC = 1 + Y CS + Y CP (уравнение 2)
Как скин-эффект, так и эффект близости являются функцией F (x) , которая для сплошных и концентрических круглых проводников приведена в таблице 1. Таким образом, для Y CS и Y CP мы имеем следующие уравнения:
Y CS = F (x) (уравнение 3)
Y CP = F (x) K 2 × [ (1,18/F (X) + 0,27) + 0,312K 2 ] (уравнение 4)
Где,
К = Д С /С,
x = 0,0276 × √f/R DC
f = частота в Гц
R DC = сопротивление проводника постоянному току при рабочей температуре (Ом на 1000 футов)
D C = диаметр проводника (дюймы)
S = осевое расстояние между проводниками (дюймы)
F (х) = функция x из таблицы 1
Таблица 2 (нажмите здесь, чтобы увидеть Таблица 2 ) перечислены отношения сопротивления переменному/постоянному току, рассчитанные по уравнениям 3 и 4. С
С
Вы можете определить допустимую нагрузку проводника данного сечения при частоте 400 Гц, умножив номинал для 60 Гц на соответствующий коэффициент ухудшения характеристик. Для больших размеров снижение номинальных характеристик является консервативным, поскольку они фактически основаны на номинальных значениях постоянного тока проводников. Вы можете считать маленькую погрешность из соображений безопасности незначительной ввиду возможных изменений толщины изоляции и т. д.
Кроме того, приведенные здесь коэффициенты сопротивления не включают потерь в какой-либо металлической оболочке, броне или кабелепроводе. Потери в тонкой алюминиевой броневой ленте могут быть небольшими, но потери в металлическом трубопроводе могут быть достаточно большими, чтобы вызвать проблемы при больших токах.
Сопротивление в проводнике: Физическая зона
Сопротивление в проводнике: Физическая зонаИмя пользователя:
Пароль:
Я забыл свое имя пользователя или пароль.

В поддержку всех учеников, которые вынуждены покинуть школу из-за коронавируса. вирус. Доступ к урокам зоны физики и зоны химии теперь доступен бесплатно плата . Это будет сохраняться как минимум до 1 августа 2020 года. Учитесь и будьте здоровы.
| Дом | Рабочие тетради по физике | Физическая зона | Химическая зона | О | Помощь | Присоединиться к |
| Уроки физики | Обзор | Ссылки | Решения | Магазин физики |
На сопротивление проводника влияют три внешних фактора.
Толщина (площадь поперечного сечения провода), длина и температура имеют некоторые значения.
влияние на величину сопротивления, создаваемого в проводнике. Четвертый фактор – это
проводимость материала, который мы используем. Некоторые металлы просто более электрически
проводящий, чем другие. Это, однако, считается внутренним фактором, а не
внешний.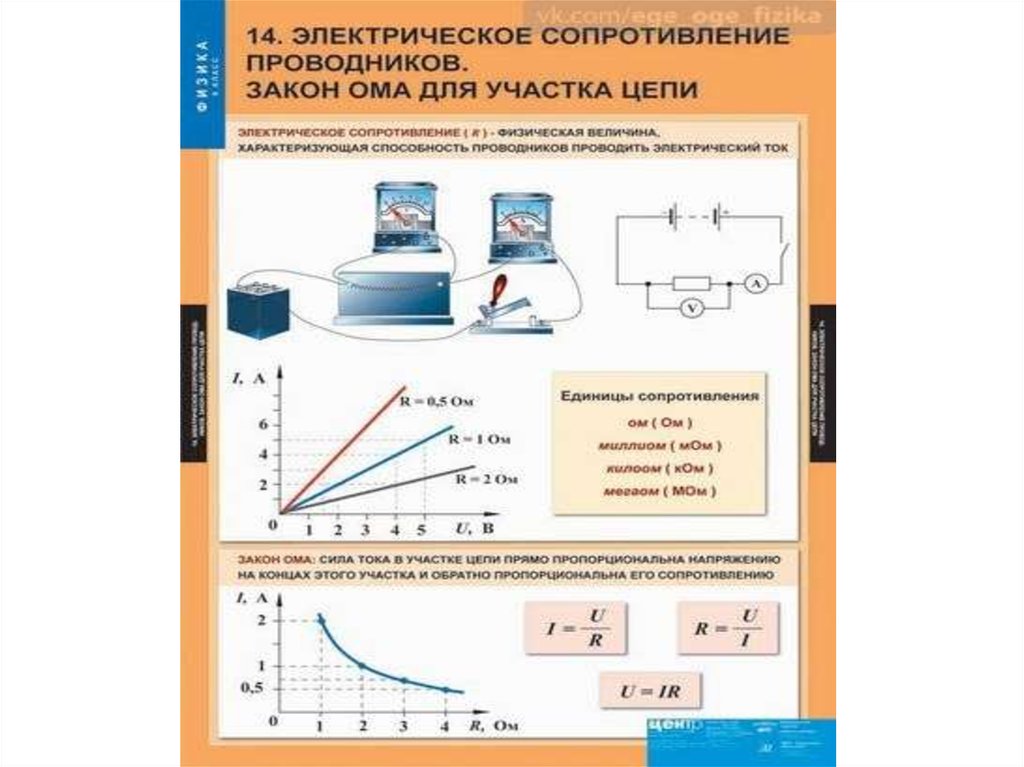
- Площадь поперечного сечения
- Площадь поперечного сечения проводника (толщина) аналогична поперечному сечению
прихожей. Если зал очень широкий, через него будет проходить большой ток,
в то время как через узкий зал было бы трудно пройти из-за ограничения высокой скорости потока. Анимация на
слева демонстрируется сравнение между проводом с малой площадью поперечного сечения ( A ) и большим
один ( А ). Обратите внимание, что электроны кажутся
движутся с одинаковой скоростью в каждом из них, но в большей проволоке гораздо больше электронов.
Это приводит к большему току, что позволяет нам сказать, что сопротивление меньше
в проводе с большей площадью поперечного сечения.
- Длина проводника
- Длина проводника аналогична длине коридора. короче
Коридор позволит людям проходить с большей скоростью, чем более длинный коридор.

- Температура
Температура проводника менее заметно влияет на сопротивление
проводник. Было бы так же трудно применить аналогию с коридором, как трудно сказать
будет ли горячий коридор заставлять нас двигаться быстрее или медленнее, чем холодный коридор. К
по-настоящему понять эффект, вы должны представить, что происходит в проводнике, когда он нагревается.
Помните, что тепло в атомном или молекулярном масштабе является прямым представлением
колебания атомов или молекул. Более высокая температура означает больше вибраций.
Представьте коридор, полный людей. Половина людей (электроны)
пытаясь двигаться в том же направлении, что и вы, а другая половина (протоны) равномерно
разнесены, но неподвижны в коридоре. Это будет означать холодную проволоку. С
провод холодный, протоны мало колеблются, поэтому между ними могут бегать электроны
довольно быстро. 905:35 Когда проводник (коридор) нагревается, протоны начинают вибрировать и
немного сместившись с места. По мере того как их движение становится более неустойчивым, они более
может мешать и нарушать поток электронов. В результате
чем выше температура, тем выше сопротивление. Ярким примером этого является, когда
ты включаешь лампочку. В первый момент проволока (нить накала) холодная и имеет
низкое сопротивление, но по мере того, как провод нагревается и испускает свет, его сопротивление увеличивается.
В результате мы можем сказать, что закон Ома выполняется до тех пор, пока температура не изменится.
По мере того как их движение становится более неустойчивым, они более
может мешать и нарушать поток электронов. В результате
чем выше температура, тем выше сопротивление. Ярким примером этого является, когда
ты включаешь лампочку. В первый момент проволока (нить накала) холодная и имеет
низкое сопротивление, но по мере того, как провод нагревается и испускает свет, его сопротивление увеличивается.
В результате мы можем сказать, что закон Ома выполняется до тех пор, пока температура не изменится.
При экстремально низких температурах некоторые материалы не имеют измеримых
сопротивление. Это называется сверхпроводимостью. Материалы известны как
сверхпроводники. Постепенно мы создаем материалы, которые становятся сверхпроводниками при
более высоких температурах, и начинается гонка за поиском или созданием материалов, обладающих сверхпроводимостью при
комнатная температура. Мы болезненно далеки от финиша.
В заключение можно сказать, что короткая толстая холодная проволока делает
лучший проводник.
Если бы вы создали формулу, связывающую площадь поперечного сечения, длину и электропроводность (удельное сопротивление) к сопротивлению провода это будет выглядеть так это:
| Ом — сопротивление проводника в
Ом A – площадь поперечного сечения, м 2 – длина провода в метрах это Удельное сопротивление материала в Ом (метры) |
Удельное сопротивление — это значение, которое зависит только от используемого материала. За Например, золото будет иметь более низкую ценность, чем свинец или цинк, потому что оно является лучшим проводником. чем они есть.
В целом важно понимать, что:
- если вы удвоите длину провода, вы удвоите сопротивление провода.
- если удвоить площадь поперечного сечения провода, то его сопротивление снизится на половина.
электрических цепей — Почему сопротивление проводника увеличивается с длиной?
спросил
Изменено 1 год, 4 месяца назад
Просмотрено 206 раз
$\begingroup$
Наиболее распространенное объяснение состоит в том, что чем длиннее провод, тем больше столкновений электронов происходит при переходе от одного конца провода к другому. Хотя я согласен с этим, я не понимаю, что для постоянного тока ток — это количество заряда, которое проходит через ЛЮБОЕ поперечное сечение проводника в единицу времени. Какое отношение имеет длина проводника к тому, сколько зарядов пройдет через любое поперечное сечение проводника в единицу времени? Если я возьму поперечное сечение, близкое к началу проводника, заряды, которые начинают двигаться с одного конца, не испытывают столько столкновений, когда они достигают этого поперечного сечения, близкого к началу, как они будут, когда они подходят к другому концу проводника. . Кажется, что сопротивление должно увеличиваться от одного конца проводника к другому. о чем ты думаешь?
Хотя я согласен с этим, я не понимаю, что для постоянного тока ток — это количество заряда, которое проходит через ЛЮБОЕ поперечное сечение проводника в единицу времени. Какое отношение имеет длина проводника к тому, сколько зарядов пройдет через любое поперечное сечение проводника в единицу времени? Если я возьму поперечное сечение, близкое к началу проводника, заряды, которые начинают двигаться с одного конца, не испытывают столько столкновений, когда они достигают этого поперечного сечения, близкого к началу, как они будут, когда они подходят к другому концу проводника. . Кажется, что сопротивление должно увеличиваться от одного конца проводника к другому. о чем ты думаешь?
- электрические цепи
- электрические токовые
- электрические сопротивления
- проводники
$\endgroup$
1
$\begingroup$
Если я возьму поперечное сечение, близкое к началу проводника, заряды, которые начинают двигаться с одного конца, не будут испытывать столько столкновений, когда они доберутся до этого поперечного сечения, близкого к началу, как они будут, когда они доберутся до другого конца проводника.
проводник. Кажется, что сопротивление должно увеличиваться от одного конца проводника к другому.
Кажется, вы сами ответили на свой вопрос. Вы описываете учитывая меньшую длину, и правильно делаете вывод, что сопротивление было бы меньше.
Какое отношение имеет длина проводника к тому, сколько зарядов пройдет через любое поперечное сечение проводника в единицу времени?
Нет. Ты прав; для постоянного тока более длинный резистор будет иметь такое же количество зарядов, протекающих через него в единицу времени (как видно из определения тока). Однако вам потребуется больше мощности (большая разность потенциалов), чтобы поддерживать постоянный ток по мере увеличения длины резистора. Таким образом, сопротивление более длинного резистора больше.
$\endgroup$
1
$\begingroup$
Наиболее распространенное объяснение состоит в том, что чем длиннее провод, тем больше электронов столкновения при переходе от одного конца провода к другому.
Да, и из-за этого требуется больше работы на единицу заряда (большее напряжение $V$), чтобы переместить такое же количество заряда в единицу времени (тот же ток $I$) с одного конца провода на другой конец провод тем длиннее этот провод. Тогда по закону Ома
$$I=\frac{V}{R}$$
Отсюда следует, что если напряжение $V$ должно быть больше, чтобы получить такой же ток $I$ в более длинном проводе, сопротивление $R$ более длинный провод должен быть выше.
Надеюсь, это поможет.
$\endgroup$
$\begingroup$
Давайте упростим визуализацию. Рассмотрим трубу, и ваша задача — пропустить через нее воду. Вы применяете какую-то энергию, чтобы доставить воду с одной стороны к другому концу. Эта энергия представляет собой разность потенциалов или то, что мы называем вольтами. Если труба длиннее, для того же количества воды вам потребуется больше энергии, а это означает, что сопротивление, оказываемое трубой в целом потоку воды, больше. Отсюда большее сопротивление. Если длина трубы мала, то для транспортировки такого же количества воды требуется меньше энергии. Отсюда и меньшее сопротивление. Здесь количество воды, протекающей в единицу времени, аналогично текущему.
Отсюда большее сопротивление. Если длина трубы мала, то для транспортировки такого же количества воды требуется меньше энергии. Отсюда и меньшее сопротивление. Здесь количество воды, протекающей в единицу времени, аналогично текущему.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. 9Монитор сопротивления с двумя проводниками 0000 Ом для двух операторов
9Монитор сопротивления с двумя проводниками 0000 Ом для двух операторовПокупатель #:
Доставить: {{vm.session.shipTo.lastName}} {{vm.session.shipTo.firstName}},
| Количество | Цена | Сохранить |
|---|---|---|
| {{pricebreak.breakQty}} | {{pricebreak.breakPriceDisplay}} | {{pricebreak.savingsMessage}} |
Цена недоступна
0″> {{vm.product.inventoryDetail.poQty}} Поступление от производителя: {{vm.product.inventoryDetail.poArrivalDate != null ? vm.product.inventoryDetail.poArrivalDate : vm.product.inventoryDetail.leadDate | дата: «ММ/дд/гггг» }}
Время выполнения заказа производителем при отсутствии на складе: {{vm.product.inventoryDetail.leadTime}} дней
Этот товар снят с производства.
Вы можете приобрести не более {{vm.product.qtyOnHand}} на складе.
Доступна рекомендуемая замена {{vm.product.inventoryDetail.secondaryProductUrlText}}. Доступен возможный вариант {{vm.product.inventoryDetail.secondaryProductUrlText}}. Нажмите ЗДЕСЬ, чтобы найти возможную замену.
Вес продукта: {{vm.product.shippingWeight}} фунтов на {{vm.product.unitOfMeasureDisplay}}
Страна происхождения: {{vm.product. countryOfOfOrigin}}
countryOfOfOrigin}}
Единица измерения:
Количество
недоступно для этого варианта.
Минимальное количество заказа: {{vm.product.minimumOrderQty}} Количество товара должно быть кратно {{vm.product.minimumOrderQty}}.
Настроить
Расписание доставки
Добавить в список
{{section.sectionName}}
Выберите {{section. sectionName}}
sectionName}}
{{styleTrait.nameDisplay}} {{styleTrait.unselectedValue ? «» : «Выбрать»}} {{styleTrait.unselectedValue ? styleTrait.unselectedValue : styleTrait.nameDisplay}}
- Информация о продукте
- Техническая информация
- {{спецификация.имяДисплей}}
- Запчасти и аксессуары
- Сопутствующие товары
Информация о продукте
Техническая информация
length > 0″> Видео о продуктахЗапчасти и аксессуары
Сопутствующие товары
Твое сообщение *
Электронное письмо было успешно отправлено. Электронная почта не была успешно отправлена, пожалуйста, проверьте ввод формы.
×
{{::crossSellProduct.shortDescription}}
Сопротивление проводника в зависимости от роялти бесплатно векторное изображение
Сопротивление проводника в зависимости от роялти бесплатно векторное изображение- лицензионные векторы org/ListItem»> Векторы сопротивления
ЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатная/Редакционная | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменять | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по запросу |
Способы покупкиСравнить
Плата за изображение € 14,99 Кредиты € 1,00 Подписка € 0,69 Оплатить стандартные лицензии можно тремя способами. Цены евро евро .
Цены евро евро .
| Оплата с | Цена изображения |
|---|---|
| Плата за изображение € 14,99 Одноразовый платеж | |
| Предоплаченные кредиты € 1 Загружайте изображения по запросу (1 кредит = 1 евро). Минимальная покупка 30р. | |
| План подписки От 0,69 € Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение € 39,99 Кредиты € 30,00Существует два способа оплаты расширенных лицензий. Цены евро евро .
| Оплата с | Стоимость изображения |
|---|---|
Плата за изображение € 39,99 Оплата разовая, регистрация не требуется.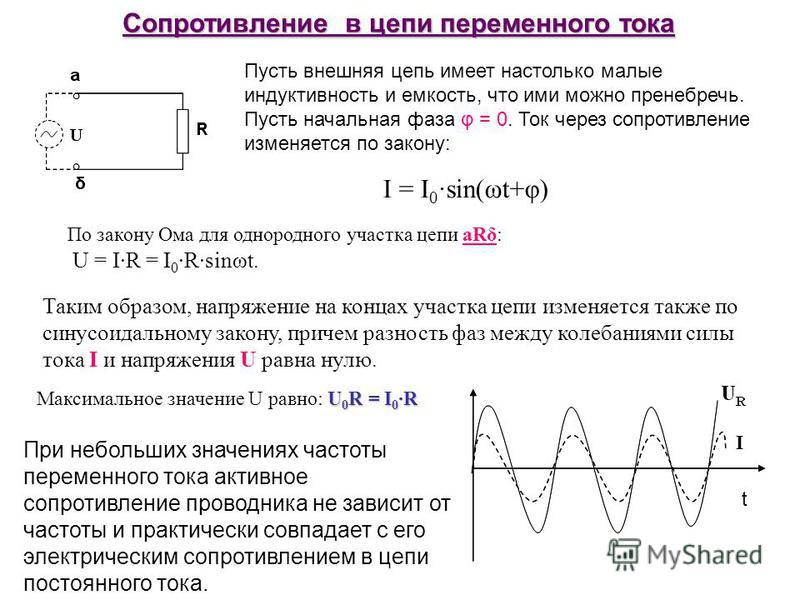 | |



 таблицу 1.14 [Л2. с.30].
таблицу 1.14 [Л2. с.30]. При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода. Отсюда выразим синусоидальный ток .
Отсюда выразим синусоидальный ток . Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.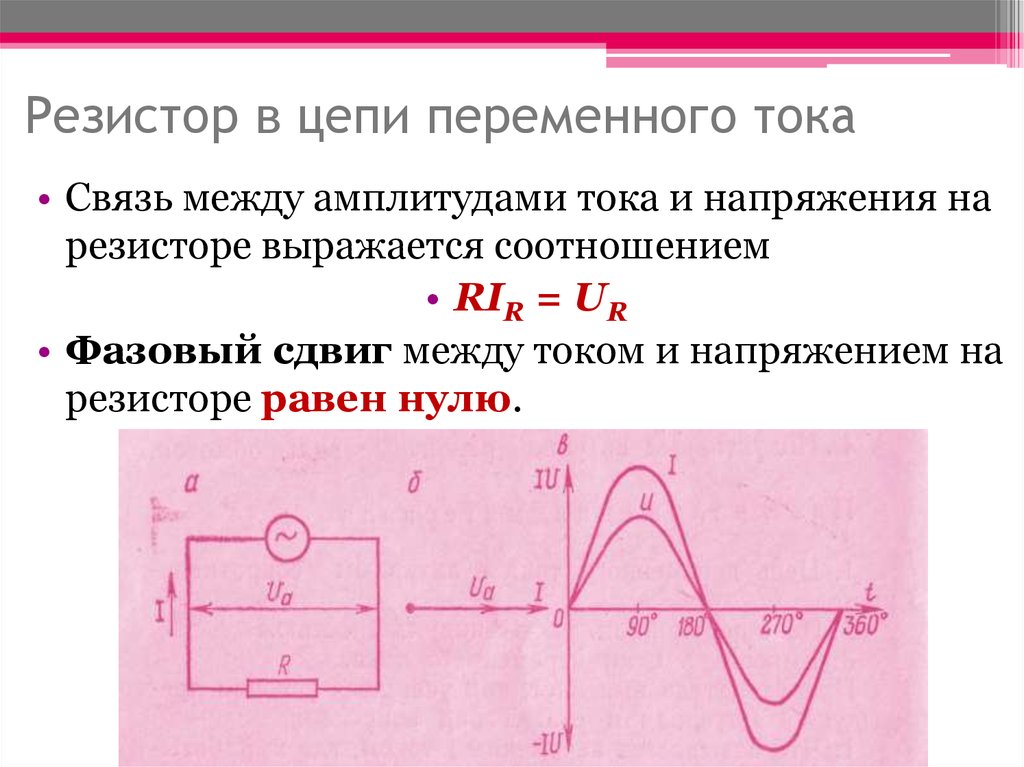 При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
При параллельном подсоединении конденсатора с подходящей емкостью можно решить проблему энергетических потерь на индуктивных нагрузках.
 Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Хl, где Х является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.
Однако довольно часто требуется определить индуктивное сопротивление Х кабельной линии с определенной протяженностью. Для этого применяется простая первоначальная формула Х = Хl, где Х является индуктивным сопротивлением 1 км проводника, а l – длина этого проводника. Полученный результат измеряется в единицах Ом/км.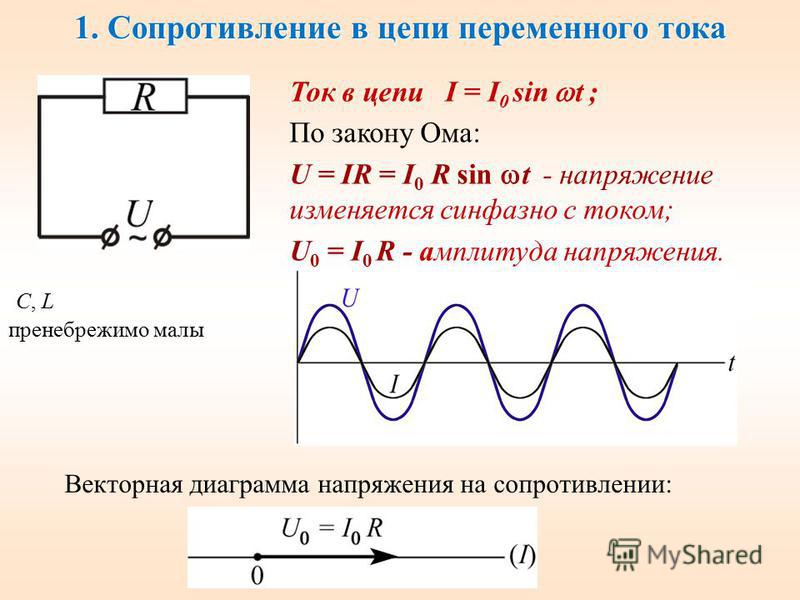
 Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.
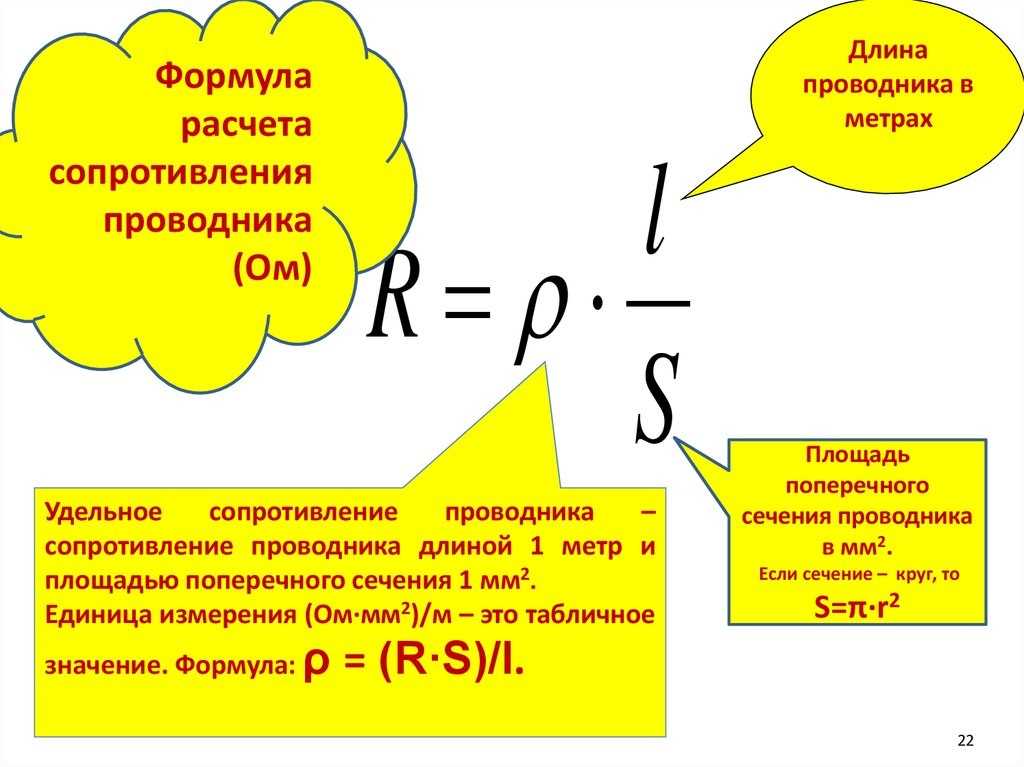 Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.
Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.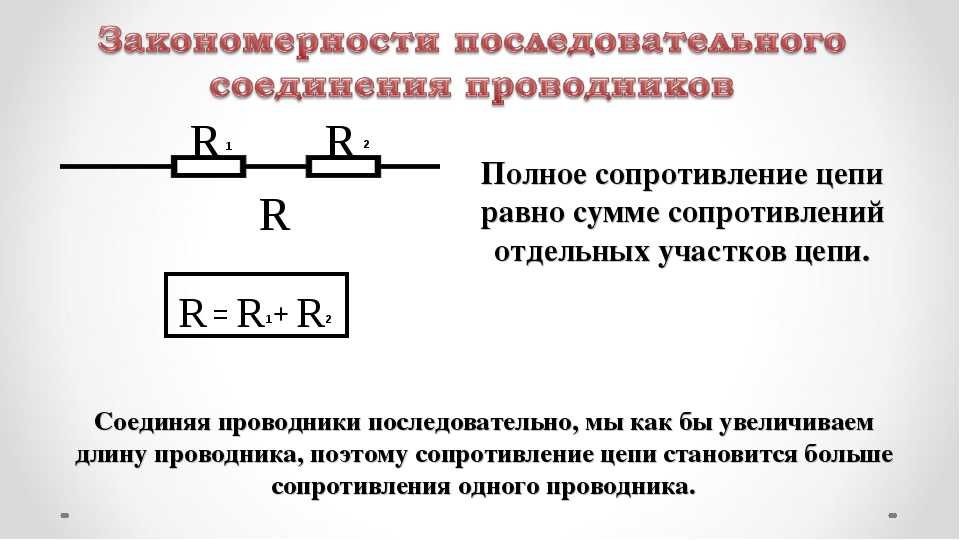
 То же самое происходит с резистором, в котором тепло выделяется, но обратно в электроэнергию не превращается.
То же самое происходит с резистором, в котором тепло выделяется, но обратно в электроэнергию не превращается. В зависимости от частоты тока, при ее возрастании, наблюдается и одновременный рост сопротивления, что отражается в формуле xl = wL.
В зависимости от частоты тока, при ее возрастании, наблюдается и одновременный рост сопротивления, что отражается в формуле xl = wL.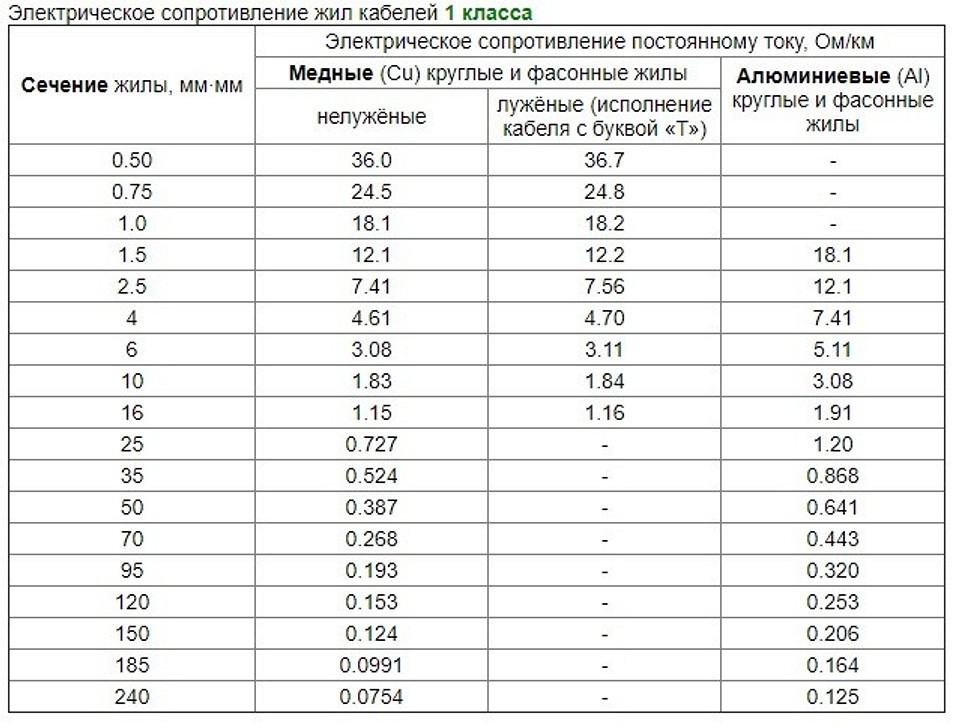

 Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле: Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока.
Ёмкостное сопротивление (X C ). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°: В этом случае электрическая энергия называется активной.
В этом случае электрическая энергия называется активной.

 Элементы, характеризующие преобразование электромагнитной энергии в тепло, называются активными сопротивлениями (обозначаются R). Элементы, связанные с наличием только магнитного поля, называются индуктивностями. Элементы, связанные с наличием электрического поля, называются емкостями. Типичными представителями активных сопротивлений являются резисторы, лампы накаливания, электрические печи и т.д. Индуктивностью обладают катушки реле, обмотки электродвигателей и транс-форматоров. Индуктивное сопротивление подчитывается по формуле:
Элементы, характеризующие преобразование электромагнитной энергии в тепло, называются активными сопротивлениями (обозначаются R). Элементы, связанные с наличием только магнитного поля, называются индуктивностями. Элементы, связанные с наличием электрического поля, называются емкостями. Типичными представителями активных сопротивлений являются резисторы, лампы накаливания, электрические печи и т.д. Индуктивностью обладают катушки реле, обмотки электродвигателей и транс-форматоров. Индуктивное сопротивление подчитывается по формуле: Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота. Образованию данной величины способствуют изменения электроэнергии и ее переход в другие виды энергетических состояний.
Образованию данной величины способствуют изменения электроэнергии и ее переход в другие виды энергетических состояний.
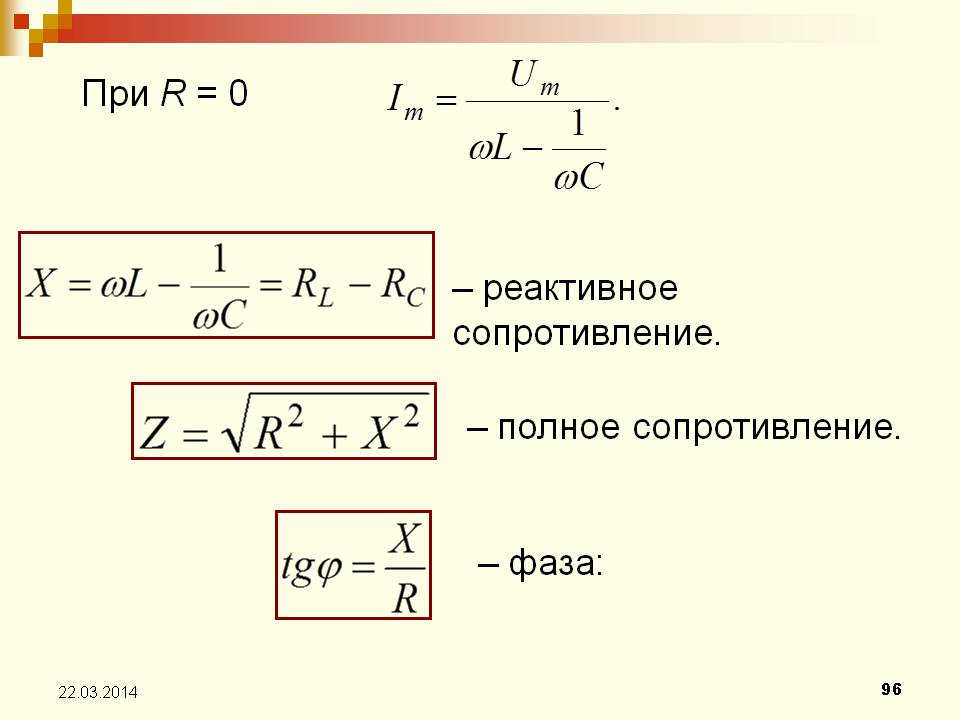 Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.
Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным. Двигаясь или колеблясь, заряды совершают работу, которая выделяется на сопротивлении нагрузки.
Двигаясь или колеблясь, заряды совершают работу, которая выделяется на сопротивлении нагрузки.
 Низкоомными материалами принято считать:
Низкоомными материалами принято считать:
 Мощностные потери, характерные для активных сопротивлений, связаны с характеристиками проводниковых компонентов и качествами изоляционного покрытия
Мощностные потери, характерные для активных сопротивлений, связаны с характеристиками проводниковых компонентов и качествами изоляционного покрытия 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т
13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т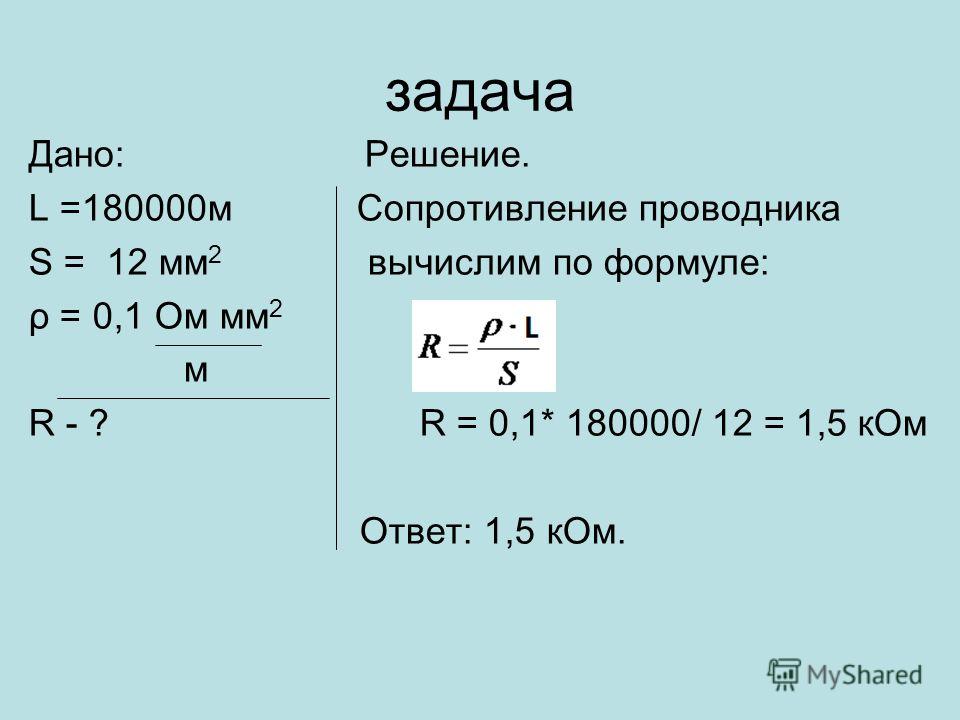
 О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи. Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.
Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает. Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.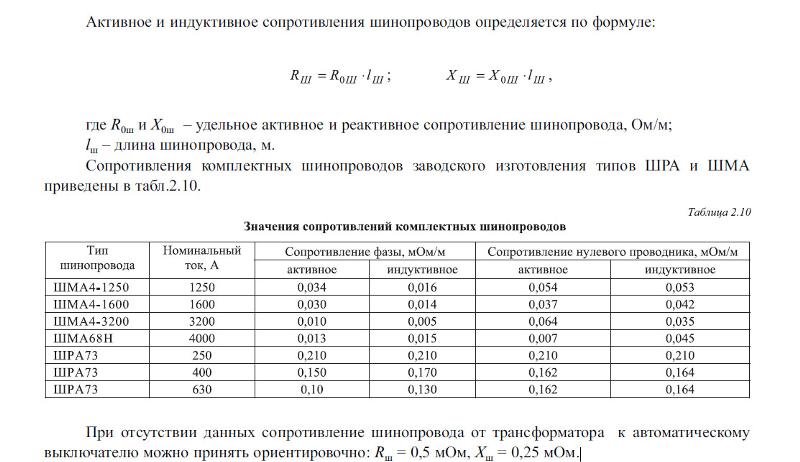
 Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу. Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру. Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.
Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз. 2Rt$$
2Rt$$ 9. Закон Ома для электрической цепи переменного тока
9. Закон Ома для электрической цепи переменного тока Модификация заключается в уменьшении времени измерения, что позволило ускорить процесс обработки измерения компонентов на конвейере, но в то же время увеличило погрешность измерения (но позволило ей остаться в пределах 0,1%). Второе изменение касается возможности применения механического манипулятора для сортировки радио компонентов при производстве или входном контроле. Сортировки осуществляется загрузкой соответствующего программного обеспечения как в измеритель RLC, так и в манипулятор. Сортировка может производиться по различным критериям — по абсолютному отклонению, по относительному отклонению и т.д.
Модификация заключается в уменьшении времени измерения, что позволило ускорить процесс обработки измерения компонентов на конвейере, но в то же время увеличило погрешность измерения (но позволило ей остаться в пределах 0,1%). Второе изменение касается возможности применения механического манипулятора для сортировки радио компонентов при производстве или входном контроле. Сортировки осуществляется загрузкой соответствующего программного обеспечения как в измеритель RLC, так и в манипулятор. Сортировка может производиться по различным критериям — по абсолютному отклонению, по относительному отклонению и т.д. Это особенно актуально при измерении параметров нелинейных компонентов реактивные значения, которых зависят от уровня сигнала. Причем измеритель RLC обеспечивает как режим стабилизации уровня тест- сигнала, т.е его стабилизацию при изменении сопротивления реактивного элемента которое неизбежно зависит от частоты тест сигнала, так и отключение его стабилизации.
Это особенно актуально при измерении параметров нелинейных компонентов реактивные значения, которых зависят от уровня сигнала. Причем измеритель RLC обеспечивает как режим стабилизации уровня тест- сигнала, т.е его стабилизацию при изменении сопротивления реактивного элемента которое неизбежно зависит от частоты тест сигнала, так и отключение его стабилизации.

 проводник. Кажется, что сопротивление должно увеличиваться от одного конца проводника к другому.
проводник. Кажется, что сопротивление должно увеличиваться от одного конца проводника к другому.