Определение активных и индуктивных сопротивлений проводов
Доброго времени суток. В данной статье речь пойдет о расчете активных и индуктивных сопротивлений для воздушных и кабельных линий из цветных металлов, таких как медь и алюминий. Данные расчеты обычно приходится выполнять, когда нужно выполнить расчет токов короткого замыкания в распределительных сетях.
Определение активного сопротивления проводов
Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.
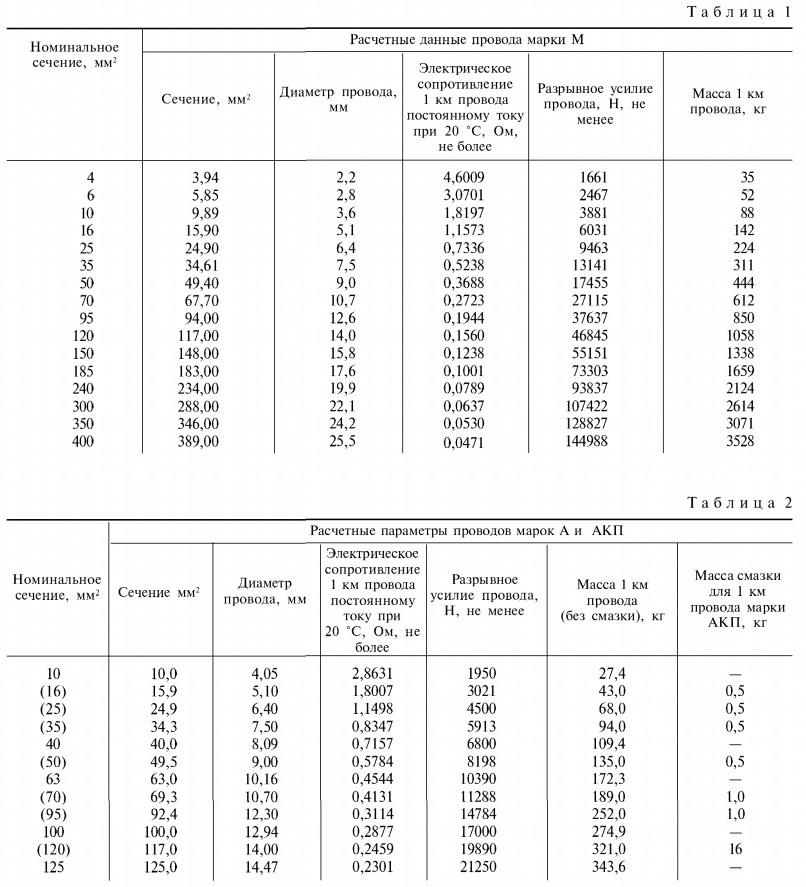
Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:
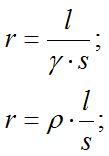
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
- l – длина линии, м;
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см. таблицу 1.14 [Л2. с.30].
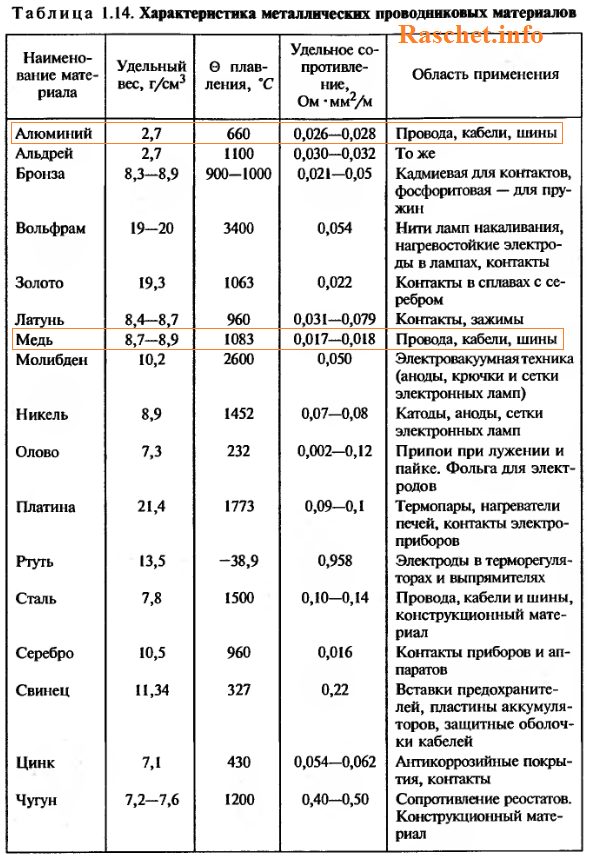
Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].
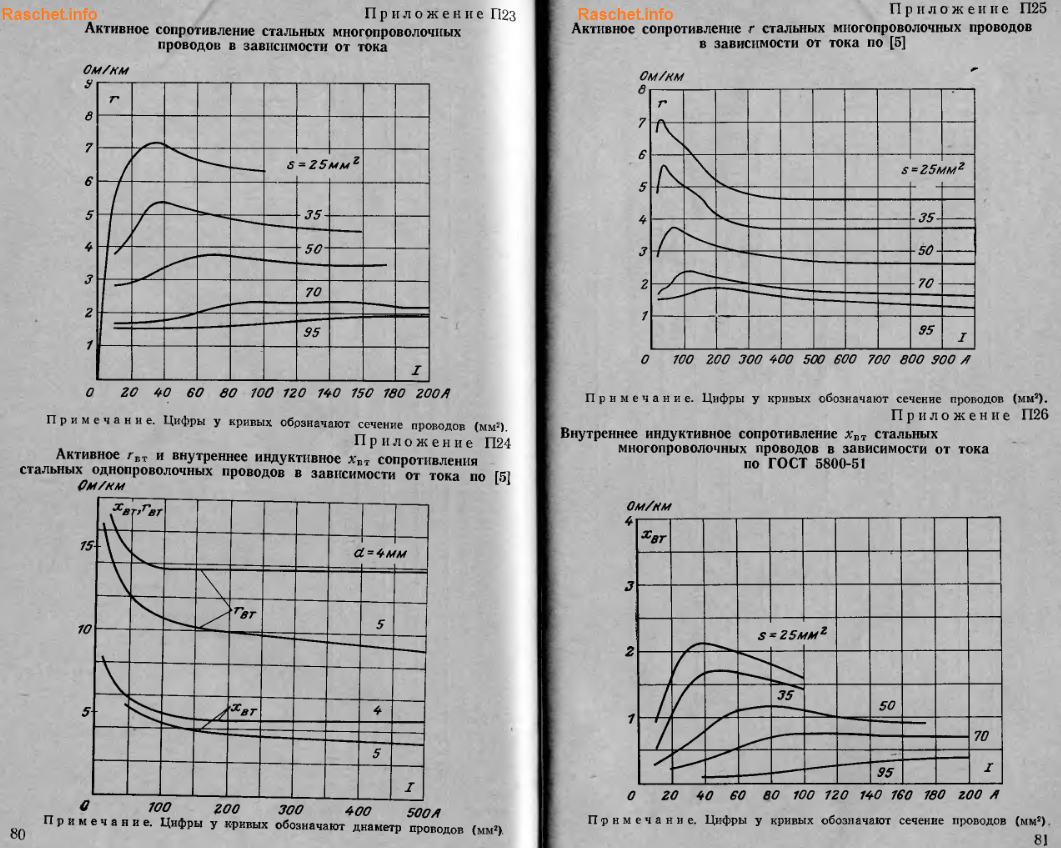
Определение индуктивного сопротивления проводов
Индуктивное сопротивление воздушных линий для стандартной частоты f = 50 Гц и относительной магнитной проницаемости для цветных металлов µ = 1, определяется по известной всем формуле [Л1.с.19]:
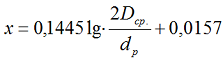
где:
- Dср. – среднее геометрическое расстояние между проводами, мм;
- dр – расчетный диаметр провода (мм2), определяется по ГОСТ 839-80, таблицы 1 -4;
Среднее геометрическое расстояние между проводами определяется по формуле [Л1.с.19]:
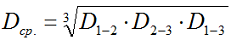
где:
- D1-2 — расстояние между проводами первой и второй фазы;
- D2-3 — расстояние между проводами второй и третей фазой;
- D1-3 — расстояние между первой и третей фазой.
Данные значения определяются по чертежам опор линий электропередачи.
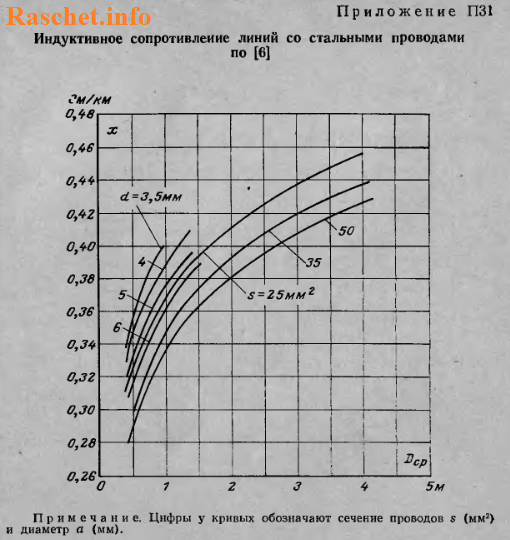
Для упрощения расчетов индуктивного сопротивления проводов рекомендуется использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.
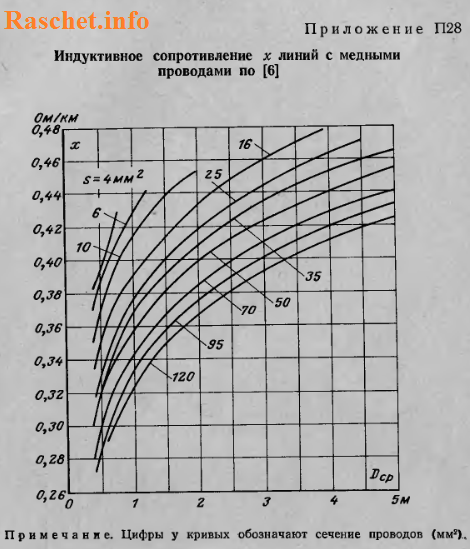
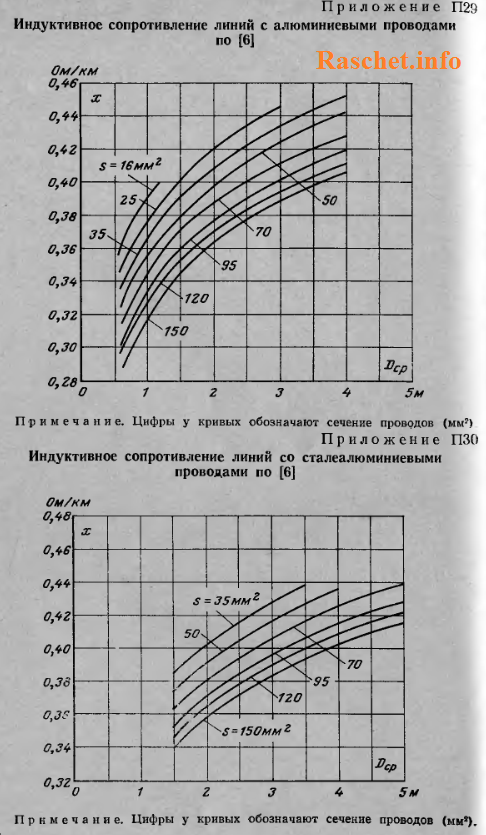
Если же нужно выполнить приближенный расчет, то можно использовать в расчетах средние значения сопротивлений:
- для линий 0,4 – 10 кВ х = 0,3 Ом/км;
- для линий 35 кВ х = 0,4 Ом/км;
- для стальных проводов использовать приложение П6 [Л1.с.70];
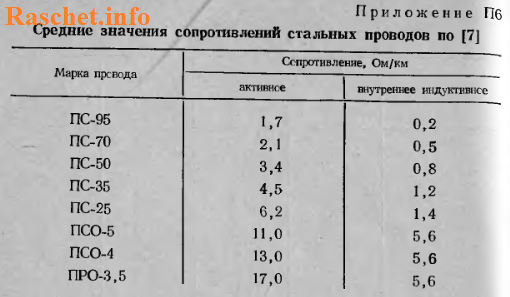
Индуктивное сопротивление кабелей рассчитать довольно сложно, из-за различной их конструкции. Поэтому активные и индуктивные сопротивления кабелей рекомендуется принимать по справочникам, приложение П7 [Л1.с.70].
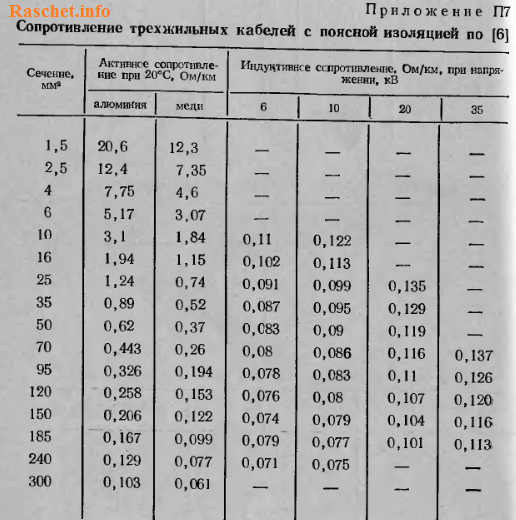
Если же нужно выполнить приближенный расчет, можно принять индуктивные сопротивления:
- для кабелей сечением 16 – 240 мм2 х = 0,06 Ом/км для напряжения до 1000 В;
- для кабелей сечением 16 – 240 мм2 х = 0,08 Ом/км для напряжения 6 – 10 кВ;
- для проводов проложенных на роликах х = 0,20 Ом/км;
- для проводов проложенных на изоляторах х = 0,25 Ом/км;
Литература:
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.
Поделиться в социальных сетях
8.Активное и Индуктивное сопротивление линий
Активное сопротивление линии – сопротивление проводника переменному току.
По своей величине активное сопротивление больше сопротивления постоянного тока, это вызвано частотой, и как следствие появление поверхностного эффекта. Это приводит к тому, что ток как бы перемещается от центра к поверхности. Это возникает благодаря противо ЭДС, которое создается переменным током, в результате ток в центральной части значительно меньше, чем у поверхности. Сечение провода используется не полностью. Поэтому сопротивление по отношению к омическому выше. Этот эффект резко проявляется при токах большой частоты, а также в стальных проводах.
Для линий выполненных из цветных металлов появление поверхностного эффекта незначительно, при расчетах активное сопротивление приравнивается омическому. Также не учитывается сопротивление проводников в зависимости от температуры. Считаем сопротивление при +20С.
Активное сопротивление, как правило, определяется через значение погонных 1 км провода R=r0l, r0 – сопротивление одного км провода, l-длина. Эти данные даются в справочниках.
Активное сопротивление стального провода значительно больше омического сопротивления. Стоит учитывать потери на вихревые токи и перемагничивание в стали, которые зависят от сечения. Для практических расчетов можно использовать справочные данные, однако это необходимо учитывать при больших токах нагрузки. Эти явления проявляются меньше в многопроволочных проводниках
Индуктивное сопротивление линий.
При передачи энергии переменным током вокруг провода создается переменное магнитное поле, которое является источником возникновения реактивного индуктивного сопротивления. Это сопротивление зависит от расстояния между проводами, от диаметра провода и от тока проходящему по этому проводу. Величина индуктивного сопротивления одного провода (фазы) выражается сложной формулой, в которой учитывается расстояние между проводами, диаметр провода, материал, фактический средний геометрический диаметр провода. Все эти данные при заданной частоте находятся также по справочникам. При расчетах с увеличением расстояния между проводами (увеличивается с увеличением напряжения) индуктивное сопротивление носит нелинейный характер. Эти данные для конкретных линий с учетом сечения провода, частоты, приводятся в справочниках. Транспозиция выравнивает условия для всех фаз.
В местных сетях при незначительной протяженности к транспозиции не прибегают. Это допустимо при погрешности 1-2 %.
Реактивное сопротивление иногда разделяют на внешнее (зависит от геометрических параметров линии) и внутреннее (зависит от материала, тока). Внешнее индуктивное сопротивление является постоянной для данного провода и не зависит от тока. Для практического применения можно пользоваться справочными данными. В этих таблицах индуктивность зависит от диаметра провода и геометрических размеров.
В КЛ индуктивное сопротивление значительно ниже, чем в ВЛ.
Данные по индуктивному сопротивлению даются в каталогах завода изготовителя.
Общее выражение для определения реактивного индуктивного сопротивления: X=x0l
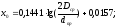 Из-за емкости
проводов ток в линии непрерывно изменяется
вдоль нее. Однако в любой схеме замещения
линии электропередачи всегда можно
выделить участок с сопротивлениями R
и X,
ограниченный проводимостями, на
протяжении которого ток остается
неизменным по величине и по фазе. Такой
участок схемы замещения называют звеном
(рис. 9-1).
Из-за емкости
проводов ток в линии непрерывно изменяется
вдоль нее. Однако в любой схеме замещения
линии электропередачи всегда можно
выделить участок с сопротивлениями R
и X,
ограниченный проводимостями, на
протяжении которого ток остается
неизменным по величине и по фазе. Такой
участок схемы замещения называют звеном
(рис. 9-1).
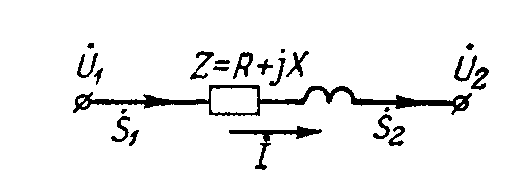
Падение напряжения в линии, состоящей из одного или нескольких последовательно включенных звеньев, полностью сосредоточено в них. Поэтому электрический расчет линий электропередачи на падение напряжения производят по звеньям, предварительно определяя расчетом мощность начала или конца каждого звена, исходя из заданной мощности и учитывая потери мощности в сопротивлениях и проводимостях схемы замещения. Очевидно, что при расчете линии, состоящей только из одною звена, напряжения по концам звена являются одновременно и напряжениями по концам линии.
Рис. 9-1. Схема замещения звена линии.
Расчет линий электропередачи по схемам замещения с сосредоточенными сопротивлениями и проводимостями без введения поправочных коэффициентов дает достаточную для практических целей точность при длинах воздушных линий до 300 км и кабельных — до 50 км. Нагрузки, учитываемые при расчете, должны быть выражены в комплексной форме.
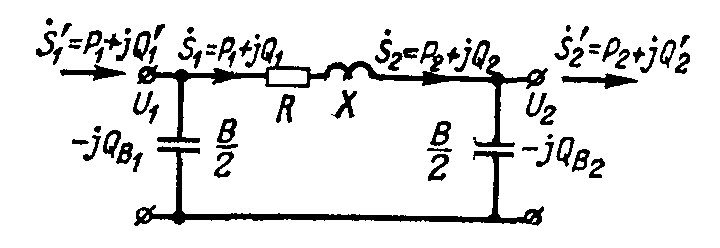
Рис. 9-2. Расчетная П-образная схема замещения линии.
На рис. 9-2 представлена П-образная расчетная схема замещения линии электропередачи, состоящая из одного звена; там же указаны нагрузки, приходящиеся на отдельные участки схемы.
9 провода и тросы воздушный линий
На воздушных линиях электропередачинапряжением выше 1000 В применяют голые провода и тросы. Находясь на открытом воздухе, они подвергаются воздействиям атмосферы (ветер, гололед, изменение температуры) и вредных примесей окружающего воздуха (сернистые газы химических заводов, морская соль) и поэтому должны обладать достаточной механической прочностью и быть устойчивыми против коррозии (ржавления). Раньше на воздушных линиях применялись медные провода, а теперь используют алюминиевые, сталеалюминевые и стальные, а в отдельных случаях и провода из специальных сплавов алюминия – альдрея и др. Грозозащитные тросы выполняются, как правило, из сталиГрозозащитные тросы подвешивают выше проводов для защиты их от атмосферных перенапряжений. На линиях напряжением ниже 220 кВ тросы подвешивают только на подходах к подстанциям. При этом снижается вероятность перекрытия проводов линии вблизи подстанции. На линиях напряжением 220 кВ и выше тросы подвешиваются вдоль всей линии. Обычно используются тросы из стальных проволок. Ранее тросы на линиях всех номинальных напряжений заземлялись наглухо на каждой опоре. Опыт эксплуатации показал, что в замкнутых контурах заземляющей системы – тросы – опоры появились токи. Они возникли вследствие действия ЭДС, наводимых в тросах путем электромагнитной индукции. При этом в ряде случаев в многократно заземленных тросах получились значительные потери электроэнергии, особенно в линиях сверхвысоких напряжений. Исследования показали, что при подвеске тросов повышенной проводимости (сталеалюминиевых) на изоляторах тросы могут быть использованы в качестве проводов связи и в качестве токонесущих проводов для электроснабжения потребителей малой мощности.
Для обеспечения соответствующего уровня грозозащиты линий тросы при этом должны присоединяться к заземленным через искровые промежутки.
Активное и индуктивное сопротивление кабелей и проводов. Емкостная проводимость линий электропередач
Для того, чтобы произвести расчет электрической сети на потерю напряжения необходимо знать параметры линий, а именно их сопротивления и проводимости. Если производятся расчеты цепей постоянного тока, то вполне достаточно знать только омическое сопротивление линии. А вот при расчете линии переменного тока одного омического сопротивления бывает недостаточно, и помимо активных сопротивлений, необходимо знать еще индуктивные сопротивления и емкостные проводимости проводов и кабелей.
Активное сопротивление проводов и кабелей
Из электротехники известно, что полное сопротивление при равных условиях переменному и постоянному току будут отличаться. Касается это также проводов и кабелей. Это вызвано тем, что переменный ток распределяется по сечению неравномерно (поверхностный эффект). Однако для проводов из цветных металлов и с частотой переменного напряжения 50 Гц этот эффект не оказывает слишком большого влияния и им можно пренебречь. Таким образом, при расчете проводников из цветных металлов, их сопротивления переменному и постоянному току принимаются равными.
На практике активное сопротивление медных и алюминиевых проводников рассчитывают по формуле:

Где: l – длина в км, γ – удельная проводимость материала провода м/ом∙мм2, r0 – активное сопротивление 1 км провода на фазу Ом/км, s – площадь поперечного сечения, мм2.
Величина r0, как правило, берется из таблиц справочников.
На активное сопротивление провода влияет и температура окружающей среды. Величину r0 при температуре Θ можно определить по формуле:

Где: α – температурный коэффициент сопротивления; r20 – активное сопротивление при температуре 20 0С, γ20 – удельная проводимость при температуре в 20 0С.
Стальные провода обладают значительно большими активными сопротивлениями, чем аналогичные провода из цветных металлов. Его увеличение обусловлено значительно меньшей величиной удельной проводимости и поверхностным эффектом, который у стальных проводов выражен гораздо более ярко, чем у алюминиевых или медных. Более того, в стальных проводах присутствуют потери активной энергии на вихревые токи и перемагничивание, что в схемах замещения линий учитывают дополнительной составляющей активного сопротивления.
Активное сопротивление стальных проводов (в отличии от проводов из цветных металлов) сильно зависит от величины протекаемого тока, поэтому использовать постоянное значение удельной проводимости при расчетах нельзя.
Активное сопротивление стальных проводов в зависимости от протекающего тока аналитически выразить весьма трудно, поэтому для его определения используют специальные таблицы.
Индуктивное сопротивление проводов и кабелей
Для определения индуктивного сопротивления (обозначается Х) кабельной или воздушной линии определенной протяженности в километрах удобно пользоваться выражением:

Где: Х0 – индуктивное сопротивление одного километра провода или кабеля на фазу, Ом/км.
Х одного километра воздушной или кабельной линии можно определить по формуле:

Где: Dср – расстояние среднее между проводами или центрами жил кабелей, мм; d – диаметр токоведущей жилы кабеля или диаметр провода, мм; μт – относительная магнитная проницаемость материала провода;
Первый член правой части уравнения обусловлен внешним магнитным полем и называется внешним индуктивным сопротивлением Х0/. Из этого выражения видно, что Х0/ зависит только от расстояния между проводами и их диаметра, а так как расстояние между проводами выбирается исходя из номинального напряжения линии, соответственно Х0/ будет расти с ростом номинального напряжения линии. Х0/ воздушных линий больше, чем кабельных. Это связано с тем, что токоведущие жилы кабеля располагаются друг к другу значительно ближе, чем провода воздушных линий.
Для одной фазы:

Где: D1:2 расстояние между проводами.
Для одинарной трехфазной линии при расположении проводов по треугольнику:

При горизонтальном или вертикальном расположении проводов трехфазной линии в одной плоскости:

Увеличение сечения проводов линии ведет к незначительному уменьшению Х0/.
Второй член уравнения для определения X0 обусловлен магнитным полем внутри проводника. Он выражает внутреннее индуктивное сопротивление Х0//.
Таким образом выражение для Х0 можно представить в виде:

Для линий из немагнитными материалов μ = 1 внутреннее индуктивное сопротивление Х0// по сравнению с внешним Х0/ составляет ничтожную величину, поэтому им очень часто пренебрегают.
В таком случае формула для определения Х0 примет вид:

Для практических расчетов индуктивные сопротивления кабелей и проводов определяют по соответствующим таблицам.
В случае приближенных расчетов можно считать для воздушных линий напряжением 6-10 кВ Х0 = 0,3 – 0,4 Ом/км, а для кабельных Х0 = 0,08 Ом/км.
Внутренне индуктивное сопротивление стальных проводов сильно отличается от Х0// проводов из цветных металлов. Это вызвано тем, что Х0// пропорционально магнитной проницаемости μr, которая сильно зависит от величины тока в проводе. Если для проводов из цветных металлов μr = 1, то для стальных проводов μr может достигать величины в 103 и даже выше.
Х0// для линий прокладываемых стальными проводами пренебрегать нельзя. Как правило, данную величину берут из таблиц, составленных на основе экспериментальных данных.
Сопротивления r0 и Х0// при некоторых значениях тока могут достигать максимальных значений, а затем с увеличением тока уменьшатся. Это явление объясняется магнитным насыщением стали.
Емкостная проводимость линий
Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.
Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:

Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.
Емкостная проводимость одноцепной воздушной линии определяется по формуле:

Определение рабочей емкости кабельной линии по формулам, в которые входят диэлектрическая проницаемость изоляции кабеля, геометрические размеры и другие конструктивные особенности, задача не из легких, поэтому значения рабочей емкости определяют по специальным таблицам, составленным заводом изготовителем для различных марок кабелей, в зависимости от их номинального напряжения.
Емкостной ток вначале линии при холостом ходе (при отключенных электроприемниках) можно определить из формулы:

Где: U – линейное напряжение сети, В; l – длина линии, км;
Емкостные токи имеют серьезное значение в воздушных линиях с рабочим напряжением 110 кВ и выше и в кабельных линиях с напряжением выше 10 кВ. При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.
В сети с изолированной нейтралью величину емкостного тока однофазного замыкания на землю приближенно можно определить по формулам:
- Для воздушной линии:

- Для кабельной линии:

Примечания: Емкостная проводимость трехфазных воздушных линий, Ф/км, подсчитывается по рабочей емкости линии:
| |||||||||||||||
Силовые кабели 1-10 КВ с пластмассовой изоляцией. Расчёт активного и индуктивного сопротивлений
«Подскажите, где можно найти таблицы с удельными сопротивлениями силовых кабелей с пластмассовой изоляцией?».
Подобные вопросы в последнее время всё чаще появляются в редакционной почте. Их задают специалисты проектных и электроснабжающих организаций, которым необходимы эти данные для правильного расчёта токов коротких замыканий. Нормативно-техническая документация с точными параметрами отсутствует. Мы обратились во Всероссийский НИИ кабельной промышленности (ВНИИКП), специалисты которого Михаил Кузьмич Каменский и Станислав Дмитриевич Холодный сегодня рассказывают о методике расчёта удельных сопротивлений силовых кабелей.

Михаил Каменский, к.т.н., заведующий лабораторией силовых кабелей

Станислав Холодный, д.т.н., старший научный сотрудник ОАО «ВНИИКП», г. Москва
При расчёте токов коротких замыканий в электрических сетях в соответствии с ГОСТ 28249-93 [1] необходимо знать величины активного и индуктивного сопротивлений прямой, обратной и нулевой последовательностей силовых кабелей. В настоящее время промышленность освоила выпуск нового поколения кабелей с пластмассовой изоляцией на напряжение 1–10 кВ. В связи с этим назрела необходимость уточнения параметров таких кабелей и внесения их в нормативную документацию. Во ВНИИКП разработан инженерный метод расчёта сопротивлений прямой, обратной и нулевой последовательностей многожильных силовых кабелей на напряжение 0,6/1 кВ и одножильных кабелей на напряжение 6/10 кВ с изоляцией из сшитого полиэтилена как наиболее востребованной группы кабелей для распределительных сетей.
Основа методики расчёта
В основу метода расчёта положено представление несимметричных напряжений (токов) в трёхфазной симметричной сети в виде суммы трёх симметричных составляющих: прямой, обратной и нулевой последовательностей, различающихся чередованием фаз. В этом случае значения фазных напряжений  будут определены в виде комплексных величин:
будут определены в виде комплексных величин:
 (1)
(1)
где  , – единичные векторы. Решая систему уравнений (1) относительно трёх неизвестных U1, U2 и U0, получим:
, – единичные векторы. Решая систему уравнений (1) относительно трёх неизвестных U1, U2 и U0, получим:
 (2)
(2)
где  – симметричные составляющие фазных напряжений прямой, обратной и нулевой последовательностей соответственно.
– симметричные составляющие фазных напряжений прямой, обратной и нулевой последовательностей соответственно.
Если к симметричной цепи приложена симметричная система фазных напряжений прямой, обратной и нулевой последовательностей, то в ней возникает симметричная система токов прямой, обратной и нулевой последовательностей. Отношения симметричных составляющих фазных напряжений к соответствующим симметричным составляющим токов являются комплексными сопротивлениями прямой (z1), обратной (z2) и нулевой (z0) последовательностей. Для симметричной трёхфазной цепи сопротивления прямой и обратной последовательностей одинаковы и равны [2]:
z1 = z2 = R – jwL (3)
где R – активное сопротивление жилы кабеля, Ом/м;
L – индуктивность жилы кабеля, Гн/м.
Понятие средней индуктивности
Следует иметь в виду, что сопротивление некоторых конструкций кабелей не является симметричным, например, четырёхжильных кабелей или одножильных кабелей, расположенных в одной плоскости. В этом случае при расчётах вводят понятие средней индуктивности Lср. В этой связи средняя индуктивность четырёхжильного кабеля или одножильных кабелей, расположенных в плоскости, будет равна
 (4)
(4)
где  – среднее расстояние между центрами жил кабеля, мм; d0 – диаметр токопроводящей жилы, мм;
– среднее расстояние между центрами жил кабеля, мм; d0 – диаметр токопроводящей жилы, мм;
m0 = 4p • 10–7 Гн/м – относительная магнитная проницаемость.
Для четырёхжильных кабелей (рис. 1) среднее расстояние между центрами жил в соответствии с [2] может быть рассчитано по формуле:
 (5)
(5)
где  — расстояние между центрами жил кабеля, мм
— расстояние между центрами жил кабеля, мм
Рис. 1. Схема четырёхжильного кабеля

Рис. 2. Схема прокладки одножильных кабелей

При прокладке одножильных кабелей в одной плоскости среднее расстояние между центрами жил будет равно:
 (6)
(6)
где  – расстояние между центрами кабелей (рис. 2).
– расстояние между центрами кабелей (рис. 2).
Эффект близости
При расчёте индуктивности следует учитывать и влияние поверхностного эффекта и эффекта близости. Индуктивность симметричной цепи из двух изолированных жил можно рассчитать по формуле [3]:
 (7)
(7)
где L1-2 – индуктивность цепи, Гн/км;
d0 – диаметр токопроводящей жилы, мм;
 – расстояние между центрами жил, мм;
– расстояние между центрами жил, мм;
Q (Х) – коэффициент, учитывающий внутреннюю индуктивность токопроводящей жилы.
Значения Q (Х) в зависимости от параметра Х принимаем по данным [3]. Параметр Х рассчитываем по формулам:
 – для медных жил;
– для медных жил;
 – для алюминиевых жил, где f – частота, Гц.
– для алюминиевых жил, где f – частота, Гц.
При расчётах индуктивности кабелей с секторными жилами следует принимать значение эквивалентного диаметра жилы, который равен диаметру круглой жилы, имеющей ту же площадь поперечного сечения, что и секторная жила. Для четырёхжильных кабелей среднее расстояние между центрами основных жил:

Тогда индуктивность в пересчёте на одну жилу получим по формуле:
 (8)
(8)
где L – индуктивность в пересчёте на 1 жилу четырёхжильного кабеля, мГн/км;
k – коэффициент формы. Для трёхжильных кабелей k = 1, для четырёхжильного кабеля k = 1,12.
Значение коэффициента Q(Х) в зависимости от сечения токопроводящей жилы принимают от 0,5 до 1. Как правило, для большинства типов силовых кабелей значение Q(Х) принимают равным 0,5 или 0,75 [5, 6]. Результаты расчёта параметров четырёхжильных кабелей типа АПвПГ (АПвВГ) на 0,6/1 кВ (производство по ТУ 16.К71-277-98) – в табл. 1.
Особенности расчёта одножильных кабелей
При расчёте сопротивлений одножильных кабелей с пластмассовой изоляцией среднего напряжения надо учитывать, что токи в металлических экранах приводят к увеличению эффективного активного сопротивления и снижению индуктивного сопротивления. В этом случае полное сопротивление одножильного кабеля в трёхфазной системе (z) можно рассчитать вместо формулы (3) по формуле:
z = R1(1 + y) + jw(L – wMЭ • m2), (9)
где у – коэффициент потерь энергии в металлическом экране,
 (10)
(10)
 (11)
(11)
где RЭ – активное сопротивление металлического экрана, Ом/км;
R1 – активное сопротивление токопроводящей жилы, Ом/км;
МЭ – коэффициент взаимной индуктивности для экранов, мГн/км,
 (12)
(12)
где dЭ – диаметр металлического экрана, мм.
При расположении одножильных кабелей в плоскости с расстоянием между кабелями, равным диаметру кабеля, значение взаимной индуктивности (МЭ) примерно равно МЭ = 0,322 мГн/км, wМЭ = 0,1 Ом/км. Значение m2МЭ при сечениях экрана до 35 мм2 не более 2% от общей индуктивности кабеля, поэтому его влиянием можно пренебречь. Однако увеличение сопротивления жилы за счёт потерь в экране кабеля при сечении токопроводящих жил более 300 мм2 достигает 22,6%, поэтому оно должно учитываться при расчётах полного сопротивления одножильного кабеля.
Результаты расчёта параметров одножильного кабеля марки АПвП 6/10 кВ (производство по ТУ 16.К71-335-2004) – в табл. 2.
Таблица 1. Расчётные значения параметров прямой последовательности кабелей марки АПвПГ (АПвВГ) 0,6/1 кВ

Таблица 2. Расчётные значения параметров кабеля марки АПвП (АПвВ) 6/10 кВ

Таблица 3. Расчётные значения параметров нулевой последовательности кабеля марки АПвПГ (АПвВГ) 0,6/1 кВ

Рис. 3. Схема токов нулевой последовательности в 4-жильном кабеле

Рис. 4. Схема замещения цепи «фаза – нулевая жила»

О сопротивлении нулевой последовательности
Для расчёта сопротивлений нулевой последовательности рассмотрим схему токов нулевой последовательности в четырёхжильном кабеле, приведенную на рис. 3. Падение напряжения в цепи нулевой последовательности (фаза – нулевая жила) рассмотрим по схеме замещения цепи, приведенной на рис. 4, которая аналогична схеме замещения в [2]:
U0 = I0z0, (13)
где U0 – падение напряжения нулевой последовательности;
I0 – ток нулевой последовательности;
z0 – сопротивление нулевой последовательности.
Сопротивление нулевой последовательности будет равно:
z0 = R1 + 3jx0,3 + 3z0,3 , (14)
где R1 – активное сопротивление прямой последовательности жилы кабеля, Ом/км;
х0,З – индуктивное сопротивление прямой последовательности: три жилы – нулевой проводник;
z0,З – суммарное сопротивление нулевого проводника (R0) и реактивного сопротивления земли (хЗ).
Значение z0,З можно рассчитать по формуле:
 (15)
(15)
где R0 — активное сопротивление нулевого проводника, Ом/км. Активную (Rez0) и реактивную (Imz0) составляющие z0 получим по формулам:
 (16)
(16)
 (17)
(17)
Значение реактивного сопротивления х0,З для четырёхжильного кабеля можно определить по формуле:
x0,З = jwL0,З , (18)
где L0,З – индуктивность прямой последовательности: три жилы – нулевой проводник, которую можно рассчитать по формуле (8).
В расчётах хЗ в соответствии с рекомендациями [4, 5] принимают равным 0,6 Ом/км.
Результаты расчёта параметров четырёхжильных кабелей марки АПвВГ (АПвПГ) приведены в табл. 3. Приведенные в таблицах 1–3 параметры силовых кабелей могут быть использованы для практических целей при проектировании кабельных линий.
Нужно обратить внимание на то обстоятельство, что индуктивное сопротивление одножильных кабелей с полиэтиленовой изоляцией в трёхфазной сети в значительной мере зависит от взаимного расположения кабелей. Эта зависимость особенно проявляется в случае параллельной прокладки в плоскости двух и более кабелей на одну фазу.
В этом случае при расчёте индуктивности по выражению (4) необходимо в качестве среднего расстояния между осями кабелей (ср) использовать среднее геометрическое значение расстояния между осями проложенных совместно кабелей.
Руководствуясь предложенным методом расчёта, можно определить сопротивления прямой, обратной и нулевой последовательностей для кабелей с пластмассовой изоляцией любого конструктивного исполнения.
При этом дополнительно необходимо учитывать увеличение индуктивности, если кабель содержит металлическую оболочку или броню из стальных лент или других ферромагнитных материалов.
Литература
1. ГОСТ 28249-93. Короткие замыкания в электропроводках. Методы расчёта в электроустановках переменного тока напряжения до 1 кВ.
2. Ульянов С.А. Короткие замыкания в электрических системах. – М.: Госэнергоиздат, 1949.
3. Основы кабельной техники. Уч. пособие для вузов / Под редакцией В.А. Привезенцева. – М.: Энергия, 1975.
4. Холодный С.Д., Филиппов М.М., Кричко В.А., Миронов И.А. Расчёт токов в оболочках и экранах и их термической стойкости при однофазном двойном замыкании в разветвлённой кабельной сети // Электричество. – 2001. – № 8.
5. Платонов В.В., Быкадоров В.Ф. Определение мест повреждения на трассе кабельной линии. – М.: Энергоатомиздат, 1993.
6. Электротехнический справочник / Под редакцией профессоров МЭИ. Том 2. – М.: Энергоатомиздат, 1986.
Пример определения индуктивного сопротивления ВЛ 10 кВ
В данной статье будет рассматриваться пример определения индуктивного сопротивления воздушной линии 10 кВ.
Пример
Требуется определить индуктивное сопротивление воздушной линии 10 кВ со сталеалюминиевыми проводами марки АС-50/8,0, длина линии составляет 5 км, используется промежуточная опора П10-16.
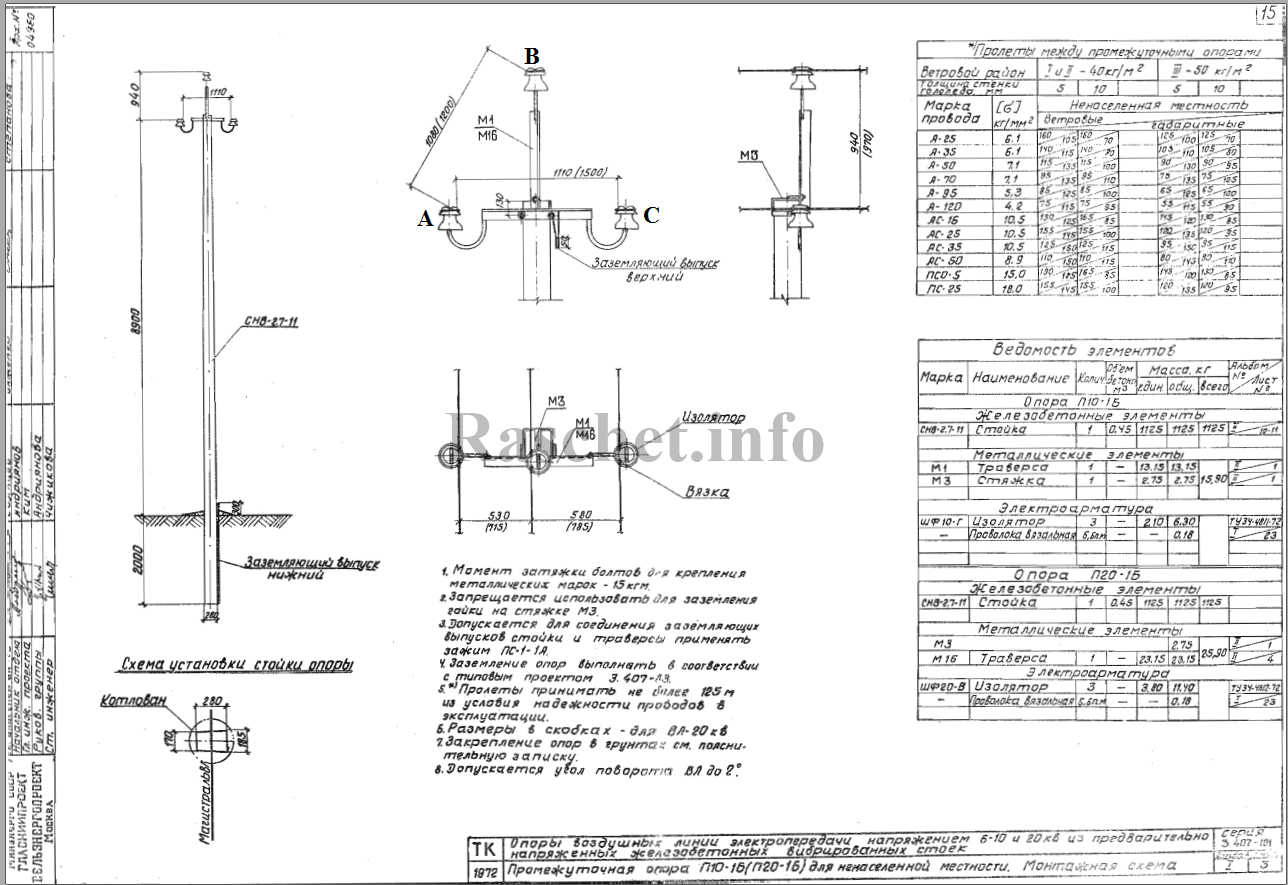
Рис.1 — Габаритный чертеж опоры П10-16
Решение
Определять индуктивное сопротивление проводов будем по формулам представленным в статье: «Определение активных и индуктивных сопротивлений проводов».
1. Определяем среднее геометрическое расстояние между проводами по формуле [Л1. с19], зная расстояния между фазами по габаритному чертежу на опору П10-16 (см. рис.1):
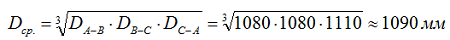
где:
- DА-В = 1080 мм — расстояние между проводами фаз А и В;
- DВ-С = 1080 мм — расстояние между проводами фаз В и С;
- DС-А = 1110 мм — расстояние между проводами фаз С и А.
2. Определяем индуктивное сопротивление для проводов марки АС-50/8,0 по формуле [Л1.с.19]:
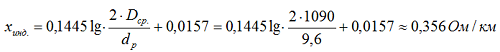
где:
- Dср. = 1090 мм – среднее геометрическое расстояние между проводами;
- dр = 9,6 мм – расчетный диаметр провода, определяется по ГОСТ 839-80, таблица 4;
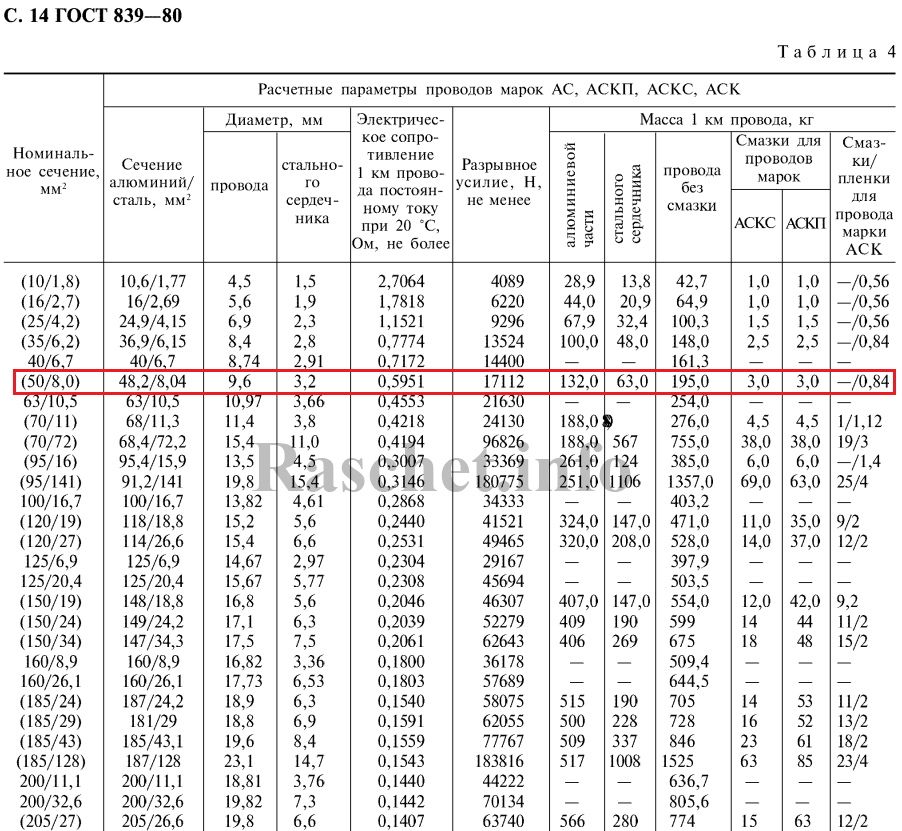
С не большой погрешностью, такой же результат можно получить по приложению П30 [Л1.с. 84], если кривую для провода сечением 50 мм2 продлить до Dср = 1,09 м, то индуктивное сопротивление будет равно 0,358 Ом/км. Принимаю хинд. = 0,356 Ом/км, так как считаю это более точное значение.
3. Определяем индуктивное сопротивление для всей линии:
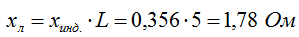
где: L = 5 км – длина воздушной линии 10 кВ.
Для упрощения расчетов индуктивного сопротивления проводов рекомендую использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.
Литература:
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Поделиться в социальных сетях
Благодарность:
Если вы нашли ответ на свой вопрос и у вас есть желание отблагодарить автора статьи за его труд, можете воспользоваться платформой для перевода средств «WebMoney Funding».
Данный проект поддерживается и развивается исключительно на средства от добровольных пожертвований.
Проявив лояльность к сайту, Вы можете перечислить любую сумму денег, тем самым вы поможете улучшить данный сайт, повысить регулярность появления новых интересных статей и оплатить регулярные расходы, такие как: оплата хостинга, доменного имени, SSL-сертификата, зарплата нашим авторам.
Активное сопротивление, индуктивность, емкость
а) Активное сопротивление R, r – это идеализированный элемент цепи, в котором происходят необратимые превращения электрической энергии в тепловую:
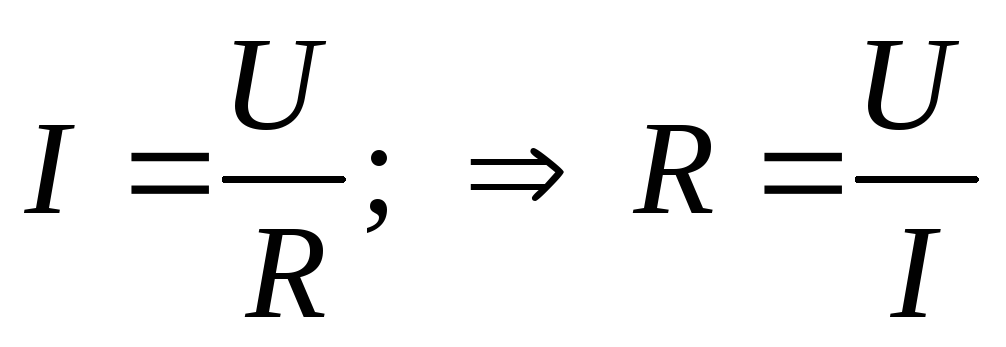 ,
(3.5)
,
(3.5)
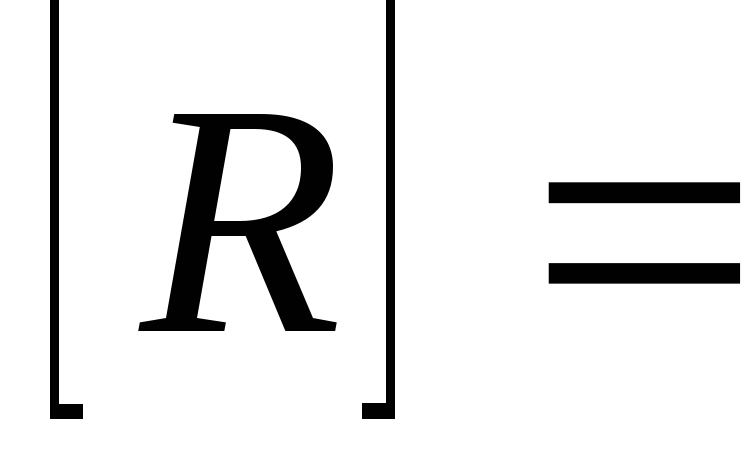 А.
А.
б) Индуктивность L – идеализированный элемент цепи, который характеризуется способностью накапливать энергию магнитного поля. Индуктивность численно равна отношению потокосцепления к току, которым это потокосцепление обусловлено:
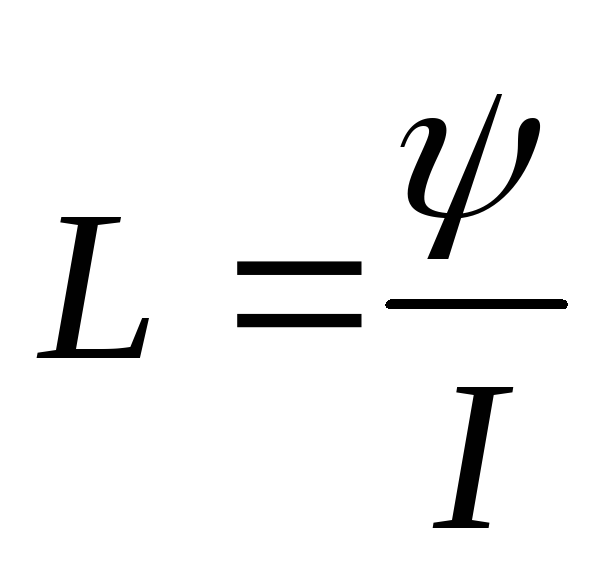 ,
(3.6)
,
(3.6)
где 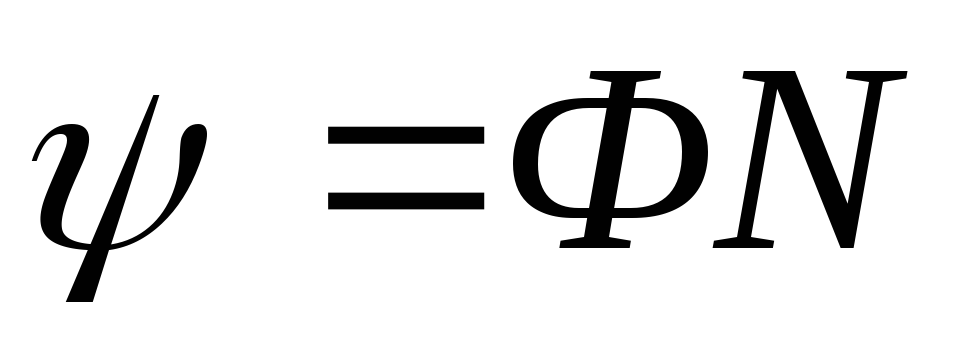 — поток сцепления катушки индуктивности,
— поток сцепления катушки индуктивности,
N –число витков катушки,
Ф– магнитныйпоток.
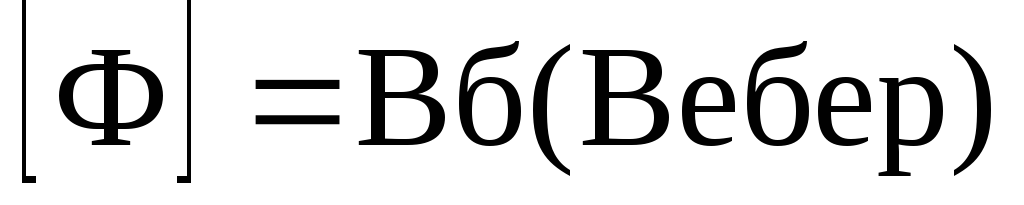 .
.
в) Емкость C– идеализированный элемент электрической цепи, который характеризуетсяспособностью накапливать энергию электрического поля.
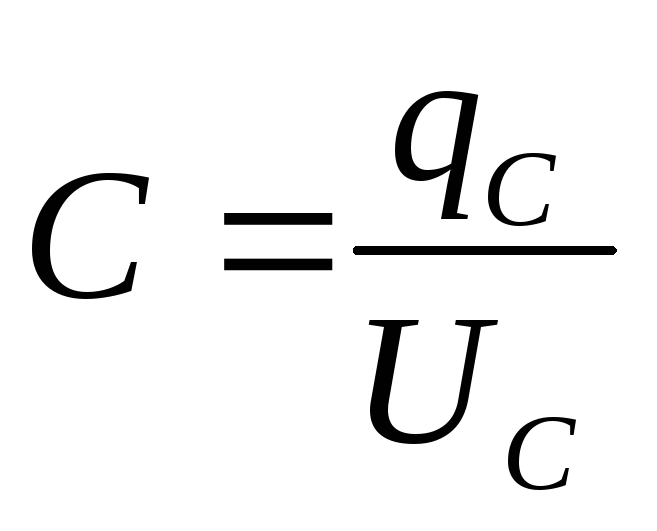 ,
(3.7)
,
(3.7)
где 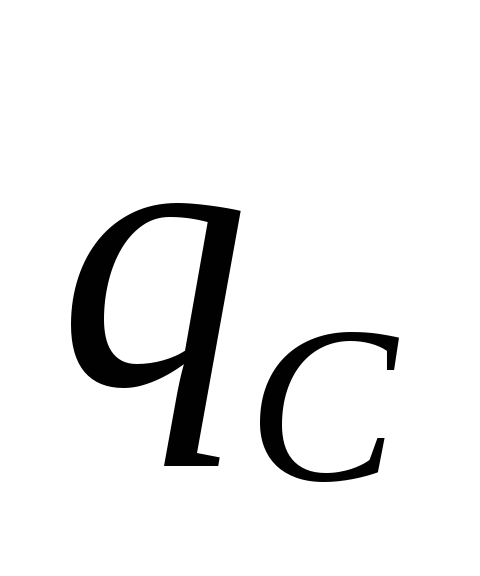 –
заряд на обкладках или пластинах
конденсатора,
–
заряд на обкладках или пластинах
конденсатора,
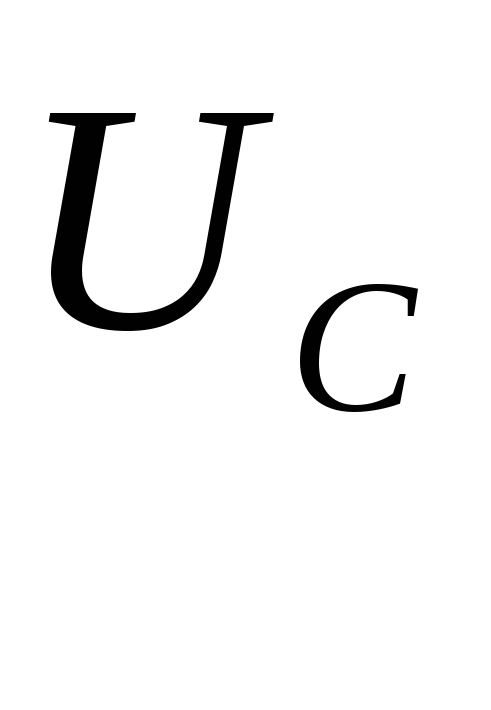 – разность потенциалов между пластинами
конденсатора.
– разность потенциалов между пластинами
конденсатора.
Емкость
С – не зависит от 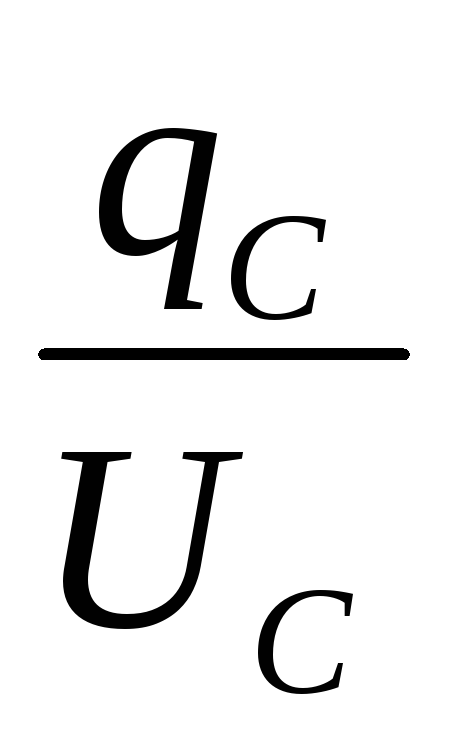 ,
а определяется размерами, формой
конденсатора, а также диэлектрическими
свойствами среды, находящейся между
обкладками конденсатора.
,
а определяется размерами, формой
конденсатора, а также диэлектрическими
свойствами среды, находящейся между
обкладками конденсатора.
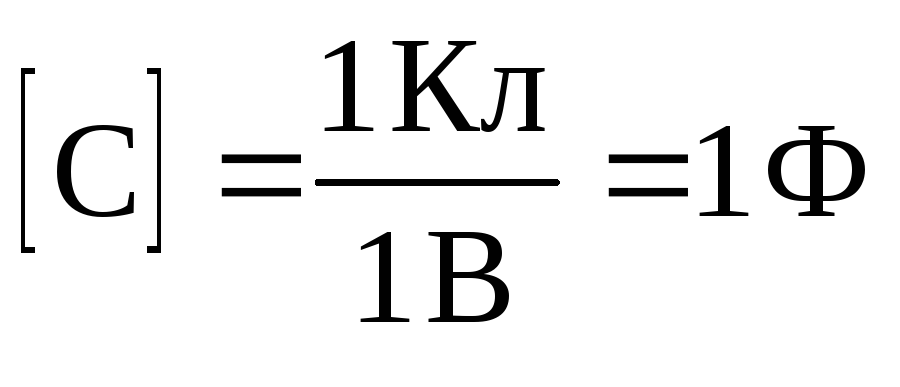 .
.
Действующее значение переменного тока
Колебания, возникающие под воздействием внешней периодически изменяющейся ЭДС, называются вынужденными электромагнитными колебаниями. Установившиеся вынужденные электромагнитные колебания можно рассматривать как протекание переменного тока в цепи, содержащей резистор, катушку индуктивности и конденсатор.
На рис. 3.5 представлен график переменного синусоидального тока.
Рис. 3.5. График переменного тока
Действующее значение переменного тока равно такому значению постоянного тока, которое за время, равное периоду переменного тока, выделяет в том же сопротивлении такое же количество теплоты, что и данный ток. Определяется по формуле 3.8.
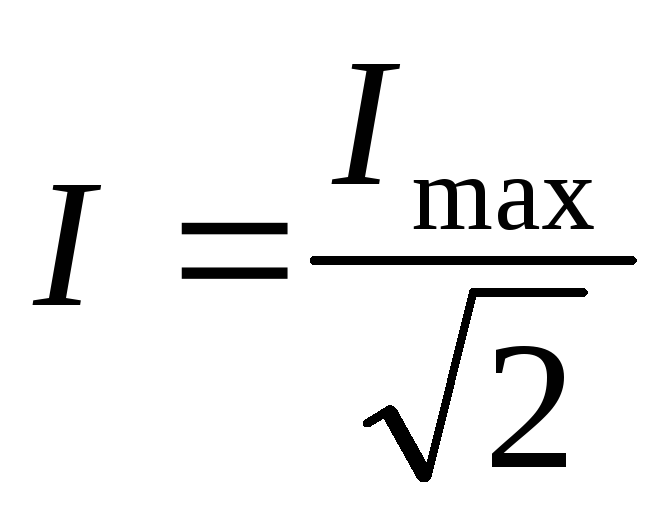 . (3.8)
. (3.8)
Активное, реактивное и полное сопротивление в цепях переменного тока
Ток в активном сопротивлении
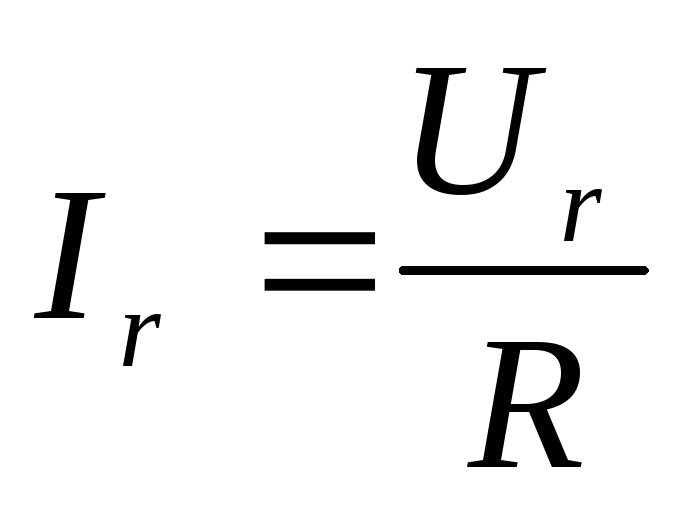 ,
(3.9)
,
(3.9)
где Ir, Ur — действующие значения тока и напряжения на активном сопротивлении R.
Сдвиг фаз между током и напряжением на резисторе равен нулю (см. рис. 3.6).
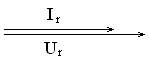
Рис. 3.6. Векторная диаграмма тока и напряжения на резисторе
Ток в индуктивности
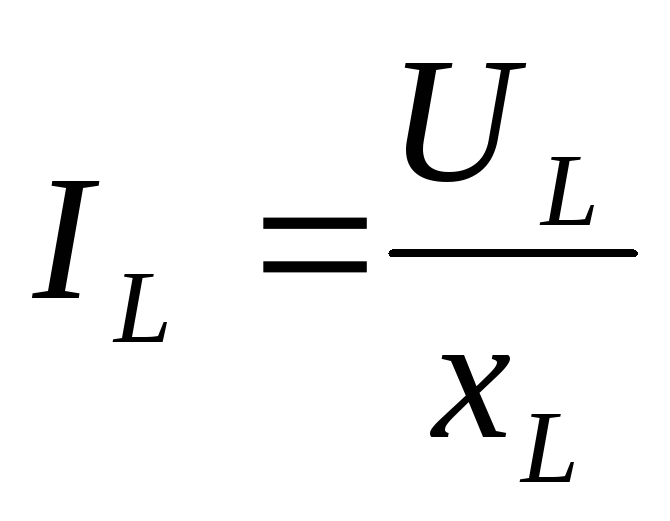 ,
(3.10)
,
(3.10)
где IL, UL — действующие значения тока и напряжения на индуктивном сопротивлении хL.
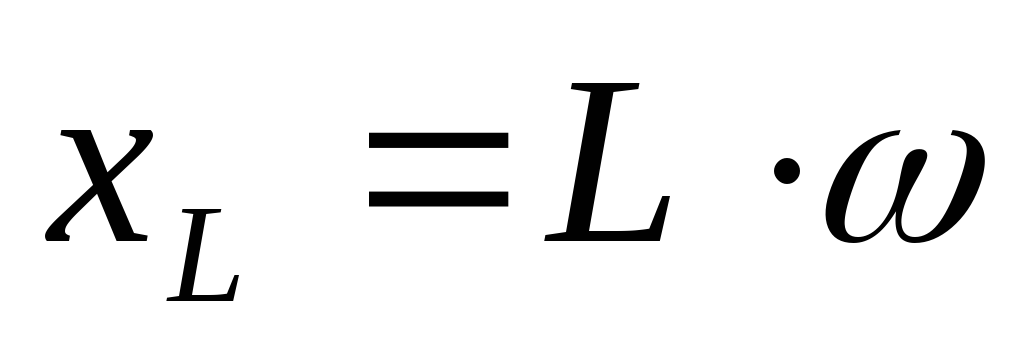 ,
(3.11)
,
(3.11)
где ω – циклическая частота, равна нуль, поэтому при постоянном токе катушка индуктивности не имеет сопротивления.
В индуктивном сопротивлении ток отстает от напряжения на угол 90° (рис. 3.7).
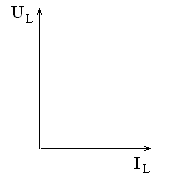
Рис. 3.7. Векторная диаграмма тока и напряжения на индуктивности
Величина хC называется реактивным емкостным сопротивлением.
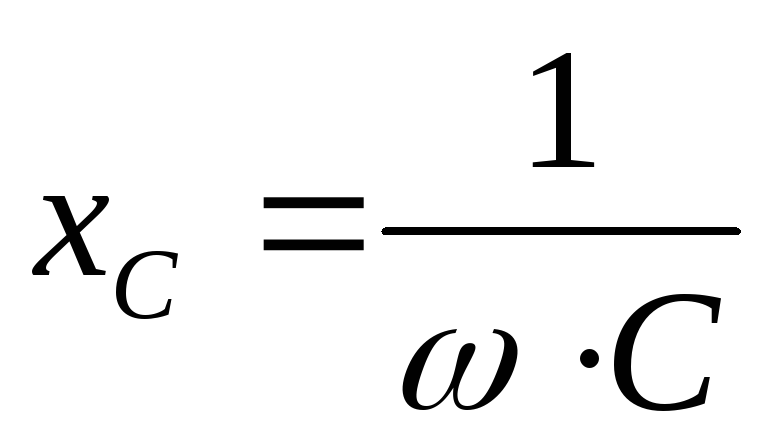 .
(3.12)
.
(3.12)
При емкостном сопротивлении напряжение отстает от тока на угол 90° (рис. 3.8).
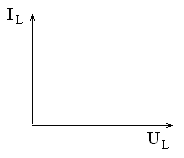
Рис. 3.8. Векторная диаграмма тока и напряжения на емкости
Для постоянного тока ω равна нулю и хC=∞, т.е. постоянный ток через конденсатор течь не может.
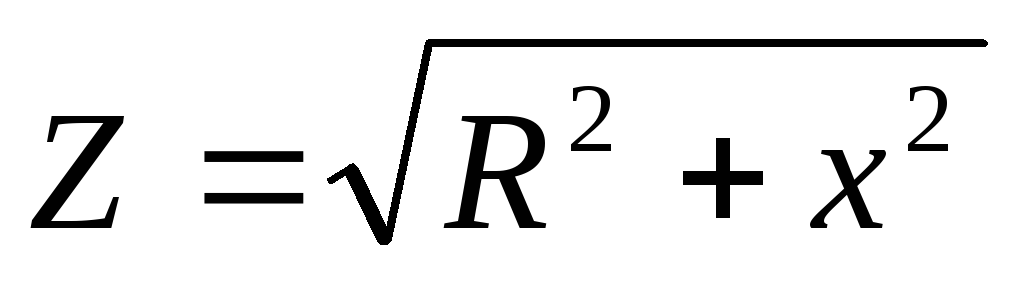 ,
(3.13)
,
(3.13)
где Z – полное сопротивление цепи,
х – реактивное сопротивление: 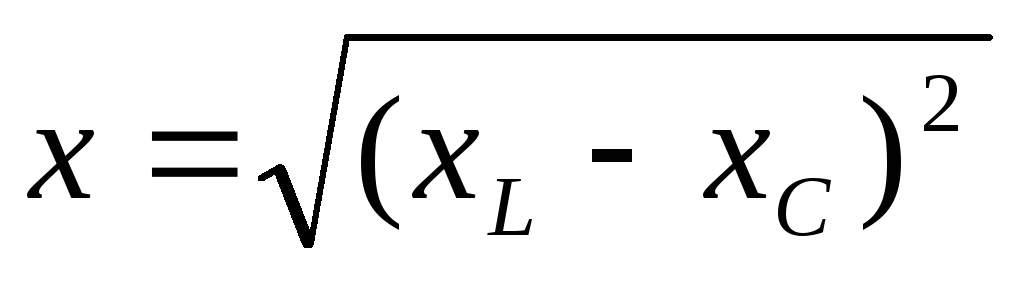 .
.


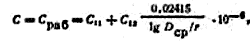 где
С11 — Со — частичная емкость фазы на
землю; C12 — частичная емкость между
фазами; D ср— среднегеометрическое
расстояние между проводами; r — внешний
радиус провода.
где
С11 — Со — частичная емкость фазы на
землю; C12 — частичная емкость между
фазами; D ср— среднегеометрическое
расстояние между проводами; r — внешний
радиус провода.