Активное, ёмкостное и индуктивное сопротивления
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Активное, ёмкостное и
индуктивное
сопротивления
Изучите тему. В тетради выполните конспект,
подготовьтесь к практической работе по решению задач
(разберите примеры решения задач)
Активное сопротивление
Активное сопротивление –R: обычное
электрическое сопротивление проводника, в
котором происходит превращение
электрической энергии во внутреннюю.
l
R
s
-активное сопротивление
проводника
сечения, ρ-удельное сопротивление.
Рассмотрим электрическую
цепь переменного тока с
активным сопротивлением.
Закон колебания напряжения
на резисторе: u U m sin t
Мгновенное значение силы
тока можно найти из закона
R
i
Um
Im 0
u
Ома:
T
t
i
U sin t
u
m
I m sin t
R
R
Выводы
Колебания силы тока и напряжения на
активном сопротивлении совпадают по
фазе.
Амплитудные и действующие значения
U .
связаны формулой:
Um и
I
Im
R
R
При низких частотах активное
сопротивление не зависит от частоты.
На активном сопротивлении происходят
электрической энергии во внутреннюю.
Емкостное сопротивление –XC
Закон колебания напряжения
на емкости:
u U m sin t
C
Im
i
Um
0
Мгновенное значение силы тока
можно найти через первую
производную заряда по
времени: i q . Из формулы
емкости:
u
1/4 т
T
t
q
C q Cu CU m sin t
u
Получаем:
В цепи переменного тока
конденсатор периодически
заряжается и разряжается,
поэтому переменный ток
проходит через конденсатор.
i CU m sin t CU m cos t
2
Из выражения
I m CU m
Um Um
Im
1
XC
C
1
XC
C
Выводы
Колебания силы тока опережают колебания
напряжения на емкости по фазе /2 или на ¼ T.
Емкостное сопротивление обратно пропорционально
емкости и частоте переменного тока.
1
XC
C
Амплитудные и действующие значения связаны
U
формулой: I U m и
.
I
m
XC
XC
Потребляемая энергия за период равна нулю:
половину периода конденсатор запасает энергию,
вторую половину периода отдает энергию в цепь.
Индуктивное сопротивление- XL
L
ω
Um
i
Im 0
X L L
u
¼T
T
t
сопротивление
В цепи переменного
тока в катушке
возникает ЭДС
самоиндукции, которая
противодействует
изменениям силы тока.
Это приводит к
появлению
дополнительного
сопротивления –
индуктивного.
Рассмотрим электрическую цепь
переменного тока с индуктивностью L.
Закон колебания силы тока в цепи:
i I m sin t
u e iR
Из закона Ома для участка цепи с ЭДС получаем:
Рассмотрим идеальную катушку, для которой R=0.
Из закона э-м индукции : L I -среднее значение ЭДС
is
t самоиндукции
, что мгновенное значение ЭДС самоиндукции пропорционально
u e 0 u e Li
u L I m sin t I m L cos t U m sin t
2
U
U
Из выражения U I L I m m
m
m
m
XL
L X L
L
Выводы
Колебания силы тока отстают от колебаний
напряжения по фазе на или на ¼ периода.
2
Индуктивное сопротивление пропорционально
круговой частоте ω и индуктивности L.
Амплитудные и действующие значения связаны
формулами:
Um и I U .
Im
XL
XL
Потребляемая энергия за период равна нулю:
половину периода энергия накапливается в
магнитном поле катушки, вторую половину периода
катушка отдает энергию в цепь.
Характеристики сопротивлений
Задача 1.
В цепи переменного тока с частотой50 Гц при напряжении 220 В возникает сила тока
4 А. Известно, что в эту цепь включена катушка с
ничтожно малым активным сопротивлением.
Какова индуктивность катушки?
ДАНО: РЕШЕНИЕ
Индуктивное сопротивление определяется по
формуле
Циклическую частоту можно рассчитать по
выражению
Запишем закон Ома для участка цепи
Приравняем две последних формулы для
расчёта индуктивного сопротивления и
выразим индуктивность катушки
Ответ: 175 мГн.
Задача 2. . При увеличении частоты от 50 Гц до 60 Гц,
ёмкостью уменьшилось на 10 Ом. Найдите электроёмкость
конденсатора.
РЕШЕНИЕ
Ёмкостное сопротивление определяется по формуле
Циклическую частоту можно определить по
выражению
Тогда ёмкостное сопротивление
Применим данную формулу для двух значений
частоты
Изменение ёмкостного сопротивления конденсатора
определяется по формуле
Тогда электроёмкость конденсатора
Ответ: 53 мкФ.
English Русский Правила
Элементарный учебник физики Т2
Элементарный учебник физики Т2
ОглавлениеИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮГлава I. Электрические заряды § 1. Электрическое взаимодействие. § 2. Проводники и диэлектрики. § 3. Разделение тел на проводники и диэлектрики § 4. Положительные и отрицательные заряды § 5. Что происходит при электризации? § 7. Электризация трением. § 8. Электризация через влияние. § 9. Электризация под действием света. § 10. Закон Кулона. § 11. Единица заряда. Глава II. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ § 12. Действие электрического заряда на окружающие тела. § 13. Понятие об электрическом поле. § 14. Напряженность электрического поля. § 15. Сложение полей. § 16. Электрическое поле в диэлектриках и в проводниках. § 17. Графическое изображение полей. § 18. Основные особенности электрических карт. § 19. Применение метода линий поля к задачам электростатики. § 20. Работа при перемещении заряда в электрическом поле.  § 21. Разность потенциалов (электрическое напряжение). § 22. Эквипотенциальные поверхности. § 23. В чем смысл введения разности потенциалов? § 24. Условия равновесия зарядов в проводниках. § 25. Электрометр. § 26. В чем различие между электрометром и электроскопом? § 27. Соединение с Землей. § 28. Измерение разности потенциалов в воздухе. Электрический зонд. § 29. Электрическое поле Земли. § 30. Простейшие электрические поля. § 31. Распределение зарядов в проводнике. Клетка Фарадея. § 32. Поверхностная плотность заряда. § 33. Конденсаторы. § 34. Различные типы конденсаторов. § 35. Параллельное и последовательное соединение конденсаторов. § 37. Почему электрическое поле ослабляется внутри диэлектрика? § 38. Энергия заряженных тел. Энергия электрического поля. Глава III. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК § 39. Электрический ток и электродвижущая сила. § 40. Признаки электрического тока.  § 41. Направление тока. § 42. Сила тока. § 43. «Скорость электрического тока» и скорость движения носителей заряда. § 44. Гальванометр. § 45. Распределение напряжения в проводнике с током. § 46. Закон Ома. § 47. Сопротивление проводов. § 49. Сверхпроводимость. § 50. Последовательное и параллельное соединение проводников. § 51. Реостаты. § 52. Распределение напряжения в цепи. § 53. Вольтметр. § 54. Каким должно быть сопротивление вольтметра и амперметра? § 55. Шунтирование измерительных приборов. Глава IV. ТЕПЛОВОЕ ДЕЙСТВИЕ ТОКА § 56. Нагревание током. Закон Джоуля-Ленца. § 57. Работа, совершаемая электрическим током. § 58. Мощность электрического тока. § 59. Контактная сварка. § 60. Электрические нагревательные приборы. Электрические печи. § 61. Понятие о расчете нагревательных приборов. § 62. Лампы накаливания. § 63. Короткое замыкание. § 64.  Электрическая проводка.Глава V. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ЭЛЕКТРОЛИТЫ § 65. Первый закон Фарадея. § 66. Второй закон Фарадея. § 67. Ионная проводимость электролитов. § 68. Движение ионов в электролитах. § 69. Элементарный электрический заряд. § 70. Первичные и вторичные процессы при электролизе. § 71. Электролитическая диссоциация. § 72. Градуировка амперметров при помощи электролиза. § 73. Технические применения электролиза. Глава VI. ХИМИЧЕСКИЕ И ТЕПЛОВЫЕ ГЕНЕРАТОРЫ ТОКА § 74. Введение. Открытие Вольты. § 75. Правило Вольты. Гальванический элемент. § 76. Как возникают э. д. с. и ток в гальваническом элементе? § 77. Поляризация электродов. § 78. Деполяризация в гальванических элементах. § 79. Аккумуляторы. § 80. Закон Ома для замкнутой цепи. § 81. Напряжение на зажимах источника тока и э. д. с. § 82. Соединение источников тока. § 83. Термоэлементы. § 84. Термоэлементы в качестве генераторов.  § 85. Измерение температуры с помощью термоэлементов. Глава VII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ МЕТАЛЛЫ § 86. Электронная проводимость металлов. § 87. Строение металлов. § 88. Причина электрического сопротивления. § 89. Работа выхода. § 90. Испускание электронов накаленными телами. Глава VIII. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ГАЗЫ § 91. Самостоятельная и несамостоятельная проводимость газов. § 92. Несамостоятельная проводимость газа. § 93. Искровой разряд. § 94. Молния. § 95. Коронный разряд. § 96. Применения коронного разряда. § 97. Громоотвод. § 98. Электрическая дуга. § 99. Применения дугового разряда. § 100. Тлеющий разряд. § 101. Что происходит при тлеющем разряде? § 102. Катодные лучи. § 103. Природа катодных лучей. § 104. Каналовые лучи. § 105. Электронная проводимость в высоком вакууме. § 106. Электронные лампы. § 107. Электроннолучевая трубка. Глава IX. ПРОХОЖДЕНИЕ ЭЛЕКТРИЧЕСКОГО ТОКА ЧЕРЕЗ ПОЛУПРОВОДНИКИ § 108. 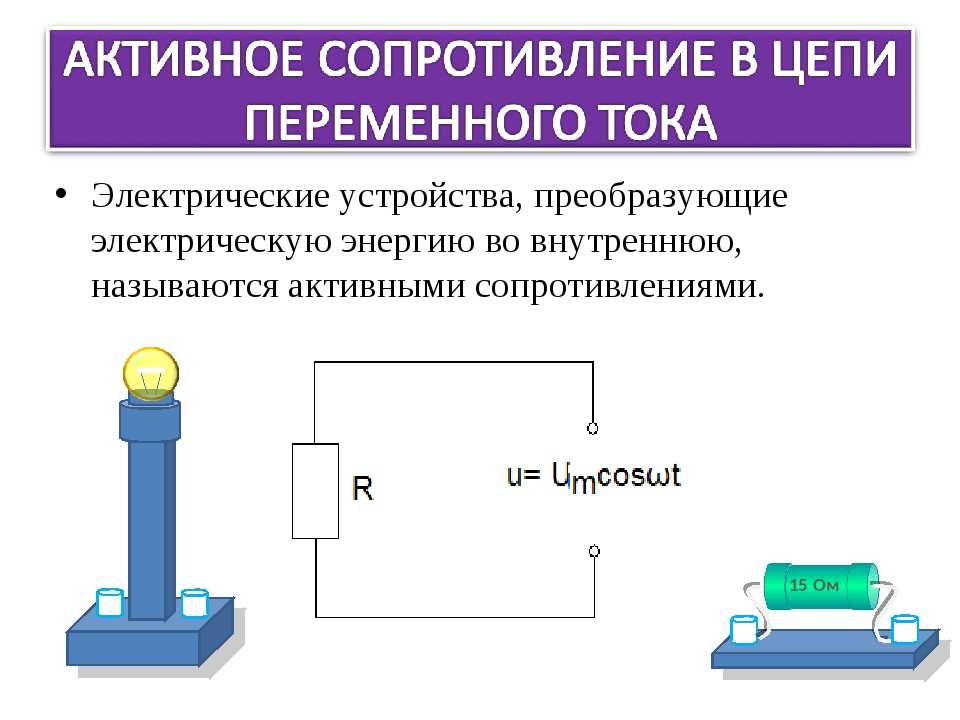 Природа электрического тока в полупроводниках.§ 109. Движение электронов в полупроводниках. § 110. Полупроводниковые выпрямители. § 111. Полупроводниковые фотоэлементы. Глава X. ОСНОВНЫЕ МАГНИТНЫЕ ЯВЛЕНИЯ § 112. Естественные и искусственные магниты. § 113. Полюсы магнита и его нейтральная зона. § 114. Магнитное действие электрического тока. § 115. Магнитные действия токов и постоянных магнитов. § 116. Происхождение магнитного поля постоянных магнитов. § 117. Гипотеза Ампера об элементарных электрических токах. Глава XI. МАГНИТНОЕ ПОЛЕ § 118. Магнитное поле и его проявления. Магнитная индукция. § 119. Магнитный момент. Единица магнитной индукции. § 120. Измерение магнитной индукции поля с помощью магнитной стрелки. § 121. Сложение магнитных полей. § 122. Линии магнитного поля. § 123. Приборы для измерения магнитной индукции. Глава XII. МАГНИТНЫЕ ПОЛЯ ЭЛЕКТРИЧЕСКИХ ТОКОВ § 124. Магнитное поле прямолинейного проводника и кругового витка с током.  § 125. Магнитное поле соленоида. Эквивалентность соленоида и полосового магнита. § 126. Магнитное поле внутри соленоида. Напряженность магнитного поля. § 127. Магнитное поле движущихся зарядов. Глава XIII. МАГНИТНОЕ ПОЛЕ ЗЕМЛИ § 128. Магнитное поле Земли. § 129. Элементы земного магнетизма. § 130. Магнитные аномалии и магнитная разведка полезных ископаемых. § 131. Изменение элементов земного магнетизма с течением времени. Магнитные бури. Глава XIV. СИЛЫ, ДЕЙСТВУЮЩИЕ В МАГНИТНОМ ПОЛЕ НА ПРОВОДНИКИ С ТОКОМ § 132. Введение. § 133. Действие магнитного поля на прямолинейный проводник с током. Правило левой руки. § 134. Действие магнитного поля на виток или соленоид с током. § 135. Гальванометр, основанный на взаимодействии магнитного поля и тока. § 136. Сила Лоренца. § 137. Сила Лоренца и полярные сияния. Глава XV. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ § 138. Условия возникновения индукционного тока. § 139. Направление индукционного тока.  Правило Ленца.§ 140. Основной закон электромагнитной индукции. § 141. Электродвижущая сила индукции. § 142. Электромагнитная индукция и сила Лоренца. § 143. Индукционные токи в массивных проводниках. Токи Фуко. Глава XVI. МАГНИТНЫЕ СВОЙСТВА ТЕЛ § 144. Магнитная проницаемость железа. § 145. Магнитная проницаемость различных веществ. Вещества парамагнитные и диамагнитные. § 146. Движение парамагнитных и диамагнитных тел в магнитном поле. Опыты Фарадея. § 147. Молекулярная теория магнетизма. § 148. Магнитная защита. § 149. Особенности ферромагнитных тел. § 150. Основы теории ферромагнетизма. Глава XVII. ПЕРЕМЕННЫЙ ТОК § 151. Постоянная и переменная электродвижущая сила. § 152. Опытное исследование формы переменного тока. Осциллограф. § 153. Амплитуда, частота и фаза синусоидального переменного тока и напряжения. § 154. Сила переменного тока. § 155. Амперметры и вольтметры переменного тока. § 156. Самоиндукция. § 157. 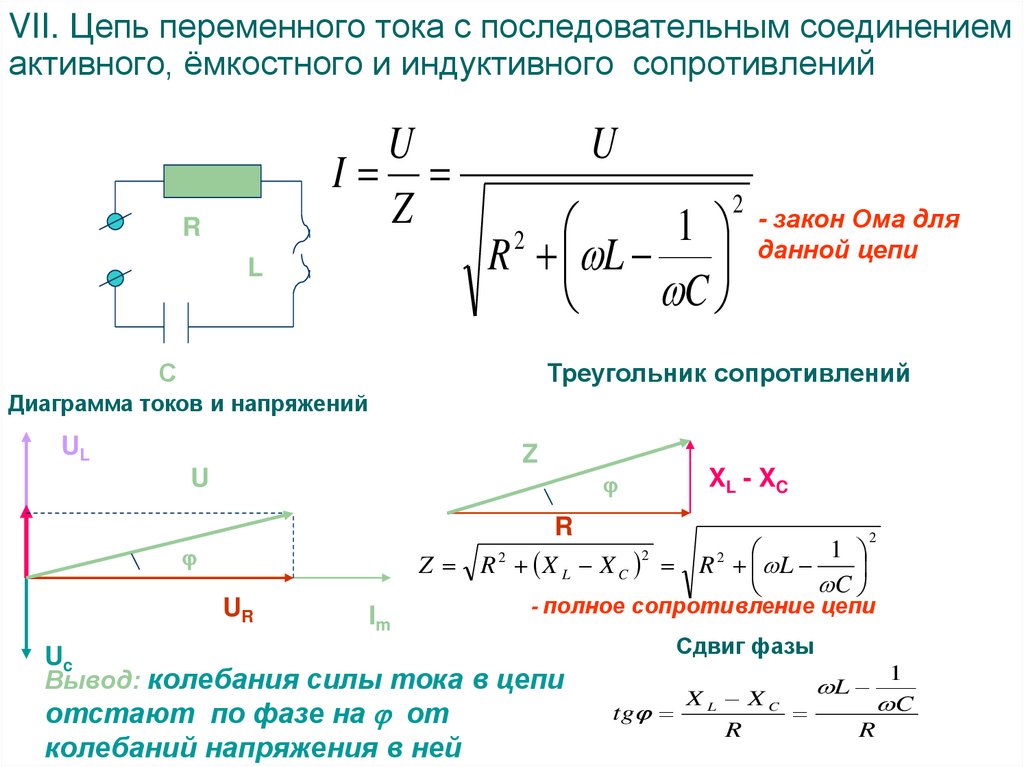 Индуктивность катушки.§ 158. Прохождение переменного тока через конденсатор и катушку с большой индуктивностью. § 159. Закон Ома для переменного тока. Емкостное и индуктивное сопротивления. § 160. Сложение токов при параллельном включении сопротивлений в цепь переменного тока. § 161. Сложение напряжений при последовательном соединении сопротивлений в цепи переменного тока. § 162. Сдвиг фаз между током и напряжением. § 163. Мощность переменного тока. § 164. Трансформаторы. § 165. Централизованное производство и распределение электрической энергии. § 166. Выпрямление переменного тока. Глава XVIII. ЭЛЕКТРИЧЕСКИЕ МАШИНЫ: ГЕНЕРАТОРЫ, ДВИГАТЕЛИ, ЭЛЕКТРОМАГНИТЫ § 167. Генераторы переменного тока. § 168. Генераторы постоянного тока. § 169. Генераторы с независимым возбуждением и с самовозбуждением. § 170. Трехфазный ток. § 171. Трехфазный электродвигатель. § 172. Электродвигатели постоянного тока. § 173. Основные рабочие характеристики и особенности двигателей постоянного тока с параллельным и последовательным возбуждением.  § 174. Коэффициент полезного действия генератора и двигателя. § 175. Обратимость электрических генераторов постоянного тока. § 176. Электромагниты. § 177. Применение электромагнитов. § 178. Реле и их применения в технике и автоматике. Ответы и решения к упражнениям Приложения Предметный указатель Таблицы |
Почему мощность в чисто индуктивной и чисто емкостной цепи равна нулю?
Почему мощность равна нулю (0) в чисто индуктивной, чисто емкостной цепи или в цепи, в которой ток и напряжение не совпадают по фазе на 90°?
Вопросы такого типа задают на собеседованиях по электротехнике или электронике. Итак, давайте вернемся к основам, чтобы прояснить основные и важные понятия электротехники.
1. Почему мощность в цепи равна нулю (0), в которой ток и напряжение равны 90° не по фазе?
Если ток и напряжение не совпадают по фазе на 90 градусов, то мощность (P) будет равна нулю.
Причина следующая:
Мы знаем, что мощность в однофазных цепях переменного тока:
P= V I Cos θ
Где;
- P = мощность в ваттах
- В = напряжение в вольтах
- I = ток в амперах
- Cos θ = коэффициент мощности цепи, т. е. разность фаз между волнами тока и напряжения.
Если угол между током и напряжением равен 90° (θ = 90), то
Мощность = P = V I Cos (90°) = 0 ….. → [Cos (90°) = 0]
Итак, если положить Cos 90° = 0, тогда общая мощность цепи будет равна нулю (т.е. в чистой индуктивной цепи или емкостной цепи, где напряжение опережает ток на 90°, а ток опережает на 90° напряжение соответственно).
- Связанный пост: Почему потоки в первичной и вторичной обмотках всегда равны?
2. Почему мощность в чистой индуктивной цепи равна нулю (0).
Мы знаем, что в чисто индуктивной цепи ток отстает от напряжения на 90 градусов (другими словами, напряжение опережает ток на 90 градусов), т.
е. разность фаз между током и напряжением составляет 90 градусов.
Как объяснялось выше, если ток и напряжение сдвинуты по фазе на 90° друг относительно друга, как в чисто индуктивной цепи, общая мощность цепи будет равна 0, как показано ниже.
P= V I Cos θ
, если угол между током и напряжением равен 90° (θ = 90), тогда
Мощность P = V I Cos (90°) = 0
[Обратите внимание, что Cos (90°) = 0]
Это показывает, что в случае чисто индуктивной цепи общая мощность цепи будет равна нулю , поскольку Cos 90° = 0.
3. Почему мощность в чисто емкостной цепи равна нулю (0)?
Мы знаем, что в чисто емкостной цепи ток опережает напряжение на 90° (другими словами, напряжение отстает на 90° от тока), т. е. разность фаз между током и напряжением составляет 90°.
Как упоминалось выше, если ток и напряжение сдвинуты по фазе на 90° друг от друга, как в чисто емкостной цепи, общая мощность цепи будет равна нулю, как показано ниже.
Мощность в цепи переменного тока
P= V I Cos θ
, если угол между током и напряжением равен 90 ( θ = 90) Градус. затем
Мощность P = V I Cos (90°) = 0
[Обратите внимание, что Cos (90°) = 0]
Это показывает то же самое, что и чисто индуктивная цепь, т.е. в случае чисто емкостной цепи, общая мощность , поскольку Cos 90° = 0.
Короче говоря, в цепи, где напряжение или ток опережают или отстают на 90° (разность фаз = 90°) друг от друга, положительный цикл отменяет отрицательный что приводит к нулевой средней мощности цепи, т. е. общий коэффициент мощности цепи переменного тока равен нулю, что приводит к нулевой средней мощности.
Похожие сообщения:
- Можно ли использовать трансформатор 50 Гц на частоте 5 Гц или 500 Гц?
- Какой трансформатор более эффективен при работе на частоте 50 Гц или 60 Гц?
- Почему трансформатор не работает от источника постоянного тока вместо переменного?
- Какой трансформатор более эффективен при работе на частоте 50 Гц или 60 Гц?
- Почему мы не можем хранить переменный ток в батареях вместо постоянного?
- Почему в емкостной цепи увеличивается ток при увеличении частоты?
- Почему ток в индуктивной цепи увеличивается при уменьшении частоты?
- Почему коэффициент мощности уменьшается при увеличении индуктивности или индуктивного реактивного сопротивления?
- Почему коэффициент мощности уменьшается, когда емкостное реактивное сопротивление увеличивается или емкость уменьшается?
URL-адрес скопирован
Показать полную статью
Связанные статьи
Кнопка «Вернуться к началу»
Улучшение коэффициента мощности, расчет коэффициента мощности Индуктивные и емкостные нагрузки
Содержание
1
Коэффициент мощности: Коэффициент мощности представляет собой отношение фактической мощности к полной или полной мощности.
Сначала мы поймем, что такое истинная мощность:
Мы используем истинную мощность через подстанцию, используя распределительные линии, и мы используем эту мощность для питания наших приборов. Теперь эта истинная мощность является фактической мощностью, которая используется для выполнения какой-либо полезной работы устройством. В случае электрического вентилятора истинная мощность — это мощность, которая используется для работы этого вентилятора, или, говоря иначе, это мощность, необходимая для вращения крыльев этого вентилятора. Истинная мощность — это трение от общей мощности, подводимой к этому устройству. Таким образом, помимо истинной мощности, у нас есть еще и реактивная мощность.
Реактивная мощность: Таким образом, как следует из названия, реактивная мощность используется в качестве реактивного элемента нагрузки. В случае этого вентилятора эта реактивная мощность используется для создания магнитного поля внутри двигателя этого вентилятора.
Таким образом, эта реактивная мощность не способствует созданию какой-либо полезной работы, но все же требуется для создания магнитного потока, чтобы двигатель вентилятора мог вращаться. Таким образом, у нас есть всего две составляющие: активная мощность и реактивная мощность. Векторная сумма этой истинной мощности и реактивной мощности называется полной мощностью.
Обычно реальная мощность обозначается символом P, а реактивная мощность обозначается символом Q, а кажущаяся мощность обозначается символом S. Итак, теперь давайте рассмотрим эти разные мощности и коэффициент мощности на примере одной схемы. .
Рассмотрим однофазный источник переменного тока 230 В, к которому подключена резисторная нагрузка только 60 Ом, чтобы найти ток, протекающий через эту систему.
Разделим напряжение на сопротивление:
В=IR
I=V/R
I=230/60
I=3,83 А
Поскольку это резистивная цепь, ток и напряжение будут синфазны друг с другом. В фазе означает, что ток и напряжение достигают своего нулевого значения и своего пикового значения в одно и то же время.
Теперь, если мы нарисуем форму сигнала мощности этой схемы, она будет выглядеть как
Мощность всегда будет положительной, что означает, что любая мощность, потребляемая системой, используется, и мощность не тратится впустую.
P=VI
P=230×3,83
P=880,9 ватт
Мощность 880,9 ватт вырабатывается исходным генератором, который потребляет только механическую энергию, и мы можем сказать, что мощность, потребляемая этой схемой, является активной мощностью.
Случай 2:
Теперь мы заменим резистор 60 Ом катушкой Генри 160 миллиметров, чтобы рассчитать ток, протекающий через эту цепь.
Сначала нам нужно рассчитать реактивное сопротивление катушки индуктивности, и мы можем сделать это, используя формулу:
X L =2πfL
X L =2π×50×0,16
X L =50,24 Ом
Теперь мы можем рассчитать ток в цепи: /R
I=230/50,24
I=4,57A
Поскольку ток чисто индуктивной цепи не совпадает по фазе с напряжением на 90 градусов, чтобы получить мощность этой цепи, мы будем умножать напряжение и ток в каждом случае и результирующая форма волны мощности в такой цепи будет чередовать положительное и отрицательное значение мощности.
Это означает, что некоторое количество мощности потребляется схемой и такое же количество возвращается, и эта мощность называется реактивной мощностью.
P=VI
P=230×4,571
P=1051,1 ВАР
Случай 3:
Теперь, если мы добавим катушку индуктивности с резистором. Предположим, что сопротивление резистора равно 40 Ом, а значение реактивного сопротивления катушки индуктивности равно j40 Ом.
Таким образом, ток «I», получаемый из источника, будет равен:
I= 240/(j40+40)
I= 4,2426<-45 напряжение и ток. Напряжение опережает ток на 45 градусов, и когда мы умножаем эти две формы волны; это покажет нам, что в течение большей части времени мощность поглощается из источника, но в течение небольшого промежутка времени мощность возвращается к источнику, и это из-за реактивного элемента в нашей цепи. Итак, сначала мы найдем истинную мощность, а также реактивную мощность. Значит истинная мощность будет равна:
P=I 2 R
P=(4,2426) 2 ×40
P=720 Вт
Теперь реактивную мощность можно найти по формуле: 55
LIX Q=
P=(4,2426) 2 ×40
P=720 ватт
Таким образом, мы можем получить как активную, так и реактивную мощность.
Теперь мы найдем общую мощность или полную мощность, просто перемножив напряжение и ток:
S=4,2426×240
S=1018 ВА
Теперь мы представим эти мощности на векторной диаграмме, затем используем мощность 92 этот треугольник импеданса будет преобразован в треугольник мощности. Таким образом, соотношение истинной мощности и кажущейся мощности даст нам коэффициент мощности.
cosΦ = (I 2 R)/(I 2 Z)
cosΦ = P/S
Коэффициент мощности также может быть представлен как cosΦ . Реактивный элемент чисто индуктивный, но если у нас есть емкостное реактивное сопротивление, то треугольник мощности будет выглядеть так:
Таким образом, в любом случае коэффициент мощности будет равен cosΦ, независимо от того, является ли нагрузка индуктивной или емкостной, значение мощности коэффициент будет находиться в диапазоне от -1 до 1,
Индуктивная нагрузка:
Таким образом, всякий раз, когда у нас есть индуктивная нагрузка, значение коэффициента мощности будет между 0 и 1.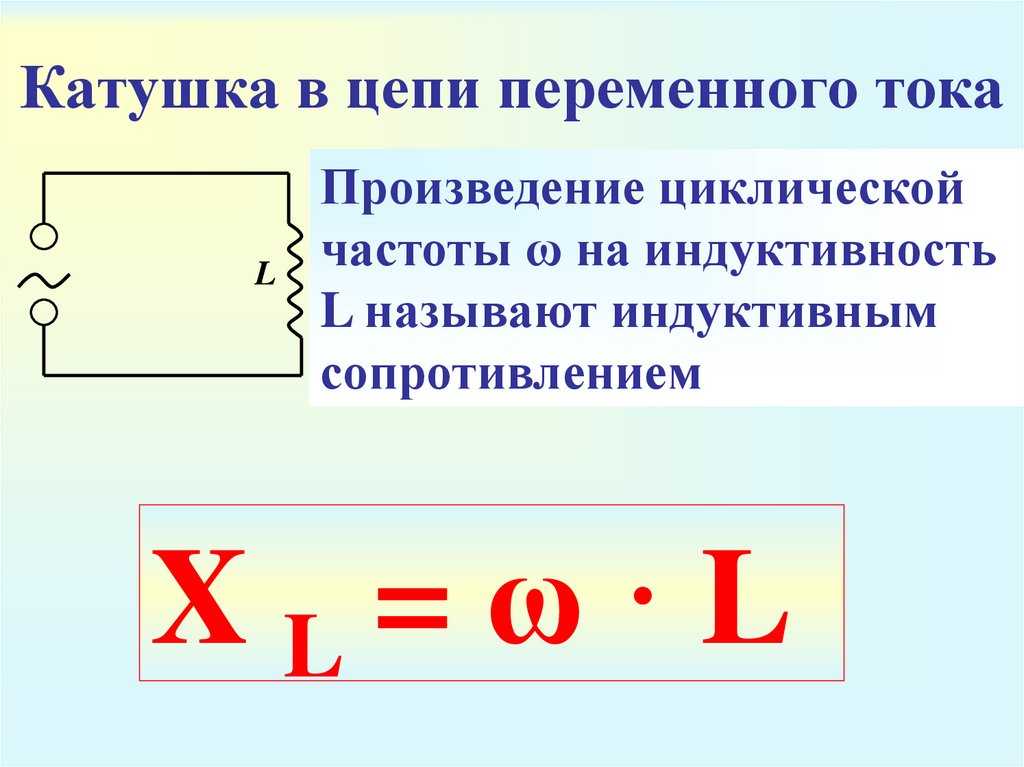
При индуктивной нагрузке коэффициент мощности известен как отстающий коэффициент мощности, поскольку при индуктивной нагрузке ток отстает от напряжения.
Емкостная нагрузка:
При наличии емкостной нагрузки значение коэффициента мощности находится в диапазоне от -1 до 0. При емкостной нагрузке коэффициент мощности известен как опережающий коэффициент мощности
, поскольку при емкостной нагрузке ток опережает напряжение.
Коэффициент мощности цепи резистивной и индуктивной нагрузки можно рассчитать по формуле:
Как мы рассчитали выше, фактическая мощность равна 720 Вт, а полная мощность равна 1018 ВА.
Коэффициент мощности = P/S
Коэффициент мощности = 720/1018
Коэффициент мощности = 0,707
Значение коэффициента мощности должно быть близким к единице. Таким образом, когда у нас плохой коэффициент мощности, это означает, что мы потребляем дополнительную мощность для реактивного элемента через нагрузку, и эта дополнительная мощность означает, что мы потребляем дополнительную величину тока, который приведет к падению напряжения на кабелях, что означает, что мы получим меньшее количество напряжения в наших домах и офисах.
Так что все это в основном является дополнительной нагрузкой на поставщика электроэнергии. Поэтому всякий раз, когда у нас плохой коэффициент мощности, эти поставщики электроэнергии взимают плату за плохой коэффициент мощности, что известно как штраф за коэффициент мощности. Поэтому, когда у нас плохой коэффициент мощности, счет за электроэнергию нашей системы также увеличится. Вот почему в промышленности наибольшее значение придается коэффициенту мощности.
Коэффициент мощности Улучшение:
Теперь давайте рассмотрим, что у нас есть индуктивная нагрузка, состоящая из резистора и катушки индуктивности, и мы считаем, что коэффициент мощности для этой системы равен cosΦ 1 . Таким образом, чтобы улучшить коэффициент мощности, мы уменьшим угол, и когда этот угол равен нулю, мы получим коэффициент мощности, равный единице. Поэтому уменьшить угол нам нужно, чтобы уменьшить значение реактивного сопротивления, поэтому, когда мы вводим конденсатор в цепь. Емкостное реактивное сопротивление будет вычтено из индуктивного реактивного сопротивления, поэтому эффективное реактивное сопротивление будет уменьшено, а коэффициент мощности будет улучшен.
Будем считать, что при введении конденсатора наш множитель будет cosΦ 2 и новое реактивное сопротивление будет X. Где X равно:
X= X L -X c
X c = X X 9094 L
X c =R[tanΦ 1 -tanΦ 2 ]
Итак, если мы знаем значение начального коэффициента мощности и улучшенного коэффициента мощности, то мы можно рассчитать значение этого емкостного сопротивления из приведенной выше схемы, мы знаем, что значение коэффициента мощности равно 0,707, и мы хотим улучшить этот коэффициент мощности до единицы, тогда значение реактивного сопротивления должно быть равно нулю, что означает, что емкостное сопротивление должно быть к этому индуктивному сопротивлению. Теперь мы знаем, что реактивная мощность будет равна:
Q = V 2 /x L = V 2 /x C
x C = V 2 /Q
x C 2 /Q
x C . Таким образом, из этих вычислений мы получаем значение X c Теперь, чтобы найти емкость конденсатора, мы будем использовать формулу: C=80/(2π×50) C=40 мкФ Таким образом, просто установив конденсатор емкостью 40 мкФ, мы можем добиться единичного коэффициента мощности в нашей схеме. При введении этого конденсатора общая мощность также будет уменьшена. Итак, для этого нам нужно найти полное сопротивление цепи, которое равно: Z=X c || Z L Полное сопротивление конденсатора равно –j80 Z=(-j80×(40+j40))/(40-j40) При вычислении значения мы получаем значение Z: Z =80 Ом Теперь для расчета величины тока, который может быть получен от источника: I=240/80 I=3A Теперь мы можем видеть, что раньше схема потребляла ток 4,2426 ампер, а сейчас он может потреблять ток 3А. Коэффициент мощности цепи будет равен единице. Всякий раз, когда у нас есть линейные нагрузки, коэффициент мощности известен как коэффициент мощности смещения, поскольку ухудшение коэффициента мощности будет происходить из-за реактивного элемента, присутствующего в цепи. Поскольку этот реактивный элемент вносит разность фаз между напряжением и током, этот тип коэффициента мощности известен как коэффициент мощности смещения. Когда у нас есть нелинейная нагрузка, то в таком случае мы также использовали гармоники тока, которые являются искажением формы волны. Общий коэффициент мощности = смещение PF × искажение PF Таким образом, в практической системе, когда у нас есть нелинейные нагрузки, в таком случае, просто применяя конденсатор, мы не можем улучшить коэффициент мощности, потому что это ухудшение коэффициента мощности происходит из-за гармонические искажения. Поэтому для этого мы в первую очередь удаляем эти гармоники тока, чего можно добиться, применяя пассивные или активные фильтры подавления гармоник. Таким образом, когда у нас есть нелинейная нагрузка, то, применяя пассивный или активный фильтр подавления гармоник, мы можем улучшить коэффициент мощности системы. Предположим, что мы строим сталелитейный завод, для которого мы привезли трансформатор мощностью 200 кВА, способный передавать мощность 170 кВт.
Эти расчеты относятся к линейным нагрузкам, включающим конденсатор, резистор и катушку индуктивности.
Но в реальной системе, если мы видим, что у нас есть нелинейные нагрузки, как в случае частотно-регулируемого привода или сервоприводов, мы используем выпрямительный мост или схемы выпрямителя внутри этих приводов, поэтому из-за этих нелинейных элементов у нас есть гармоники текущий. Это означает, что помимо основной частоты тока у нас также были гармоники, и из-за этих гармоник происходят искажения тока, и мы имеем ухудшение коэффициента мощности. Коэффициент мощности смещения:
Коэффициент мощности искажения:
Из-за этого любое ухудшение, которое мы использовали для получения коэффициента мощности, известно как коэффициент мощности искажения. В реальной системе у нас есть оба типа коэффициентов мощности. Зачем повышать коэффициент мощности?
