Реактивная мощность, расчет и измерение, формулы

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, называется реактивной мощностью (Q).

Содержание

Активная, реактивная и кажущаяся мощность

Другими словами, активную мощность можно назвать: реальная мощность, действительная мощность, полезная мощность, реальная мощность. В цепи постоянного тока мощность, отдаваемая в нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, т.е.

потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет коэффициента мощности.

Однако для синусоидальных сигналов, т.е. в цепях переменного тока, ситуация сложнее из-за разницы фаз между током и напряжением. Таким образом, среднее значение мощности (активная мощность), которая фактически питает нагрузку, определяется как:

В цепи переменного тока, если она является чисто активной (резистивной), формула для мощности такая же, как и для постоянного тока: P = U I.

Формулы для активной мощности

P = U I – в цепях постоянного тока

P = U I cosθ в однофазных цепях переменного тока

P = √3 U_L I_L cosθ – в трехфазных цепях переменного тока

P = √ (S 2 – Q 2 ) или

P = √ (VA 2 – Var 2 ) или

Активная мощность = √ (кажущаяся мощность 2 – реактивная мощность 2 ) или

кВт = √ (кВА 2 – квар 2 )

Реактивная мощность (Q)

Назвать ее бесполезной или бессмысленной силой тоже было бы сильно.

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, называется реактивной мощностью (Q).

Реактивная мощность – это мощность, которая отбирается и затем возвращается в нагрузку благодаря своим реактивным свойствам. Единицей измерения активной мощности является ватт, 1 Вт = 1 В x 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного или электрического поля в случае индуктора или конденсатора соответственно.

Реактивная мощность определяется как

и может быть положительным (+Ue) для индуктивных нагрузок и отрицательным (-Ue) для емкостных нагрузок.

Единицей измерения реактивной мощности является реактивный вольт-ампер (вар): 1 вар = 1 В x 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, создаваемого 1 В х 1 А.

Полная мощность – это величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителей необходимым количеством электроэнергии и поддерживает их работу. Для его расчета используется формула: S = .

Формулы для активной мощности, реактивной мощности и кажущейся мощности

Активная мощность считается основным компонентом. Это величина, характеризующая процесс преобразования электрической энергии в другие формы энергии. Другими словами, это скорость, с которой потребляется электроэнергия. Это значение, которое отображается на счетчике электроэнергии и за которое платят потребители. Активная мощность рассчитывается по формулеP = U x I x cosf.

В отличие от активной мощности, которая представляет собой энергию, принимаемую непосредственно приборами и преобразуемую в другие формы энергии – тепло, свет, механическую энергию и т.д., – реактивная мощность является своего рода невидимым помощником. Он вносит свой вклад в электромагнитные поля, которые потребляются электродвигателями. Прежде всего, он определяет характер нагрузки и может не только генерироваться, но и потребляться. Реактивная мощность рассчитывается по формуле: Q = U x I x sinf.

Полная мощность – это величина, состоящая из активной и реактивной составляющих. Это то, что обеспечивает потребителей необходимым количеством электроэнергии и поддерживает их жизнедеятельность. Для его расчета используется формула: S = .

S = √P2 + Q2, все равны U*I .

Активная мощность: формула, как определить – Asutpp

Характеристики мощности установки или сети являются базовыми для большинства известного электрооборудования. Активная мощность (передаваемая, потребляемая) описывает долю общей мощности, которая передается за определенный период с частотой переменного тока.

Определение

Активная и реактивная мощности могут быть найдены только в переменном токе, поскольку характеристики сети (ток и напряжение) в постоянном токе всегда равны.

Единицей измерения активной мощности является ватт, а реактивной мощности – реактивный вольтамперметр и килоВАР (кВАр).

Стоит отметить, что как суммарные, так и активные характеристики могут измеряться в кВт и кВА, это зависит от параметров оборудования и сети. В промышленных цепях он обычно измеряется в киловаттах.

В электротехнике активный компонент используется как мера передачи энергии через отдельные электрические устройства. Давайте посмотрим, сколько энергии потребляют некоторые из них:

Прибор	Мощность бытовых приборов, ватт/час
Зарядное устройство	2
Люминесцентная лампа CRL	От 50
Звуковая система	30
Электрический чайник	1500
Стиральная машина	2500
Полуавтоматический инвертор	3500
Очиститель высокого давления	3500

Соответственно, активная мощность является положительной характеристикой данной электрической цепи и является одним из основных параметров для выбора электрооборудования и контроля потребления электроэнергии.

Выработка активного ингредиента

Обозначение реактивного компонента:

Это номинальное значение, которое характеризует нагрузки в электрооборудовании через колебания ЭДС и потери во время работы оборудования. Другими словами, передаваемая энергия переходит в конкретный преобразователь реактивности (это конденсатор, диодный мост и т. д.) и видна только в том случае, если схема содержит этот компонент.

Расчет

Для определения активной мощности необходимо знать полную мощность, а для ее расчета используется следующая формула:

S = U I, где U – напряжение сети, а I – сила тока в сети.

Такой же расчет производится при вычислении передачи энергии катушки в симметричном соединении. Расположение следующее:

Симметричная диаграмма нагрузки

При расчете активной мощности учитывается фазовый угол или коэффициент (cos φ), таким образом:

Очень важным фактором является то, что эта электрическая величина может быть положительной или отрицательной. Это зависит от того, какую характеристику имеет cos φ.

Если синусоидальный ток имеет фазовый угол от 0 до 90 градусов, то активная мощность положительна, если от 0 до -90, то отрицательна.

Это правило применимо только к синхронному (синусоидальному) току (используется для питания асинхронных двигателей, станков).

Также характерно, что в трехфазной системе (напр. трансформатор или генератор) активная громкость полностью создается на выходе.

Расчет трехфазной сети

Максимальная активная мощность равна P, а максимальная реактивная мощность равна Q.

Поскольку реактивная мощность определяется движением и энергией магнитного поля, ее формула (включая фазовый угол) выглядит следующим образом:

Для несинусоидального тока очень трудно определить размеры сети стандартным способом. Чтобы определить правильные характеристики для расчета активной и реактивной мощности, используются различные измерительные приборы. К ним относятся вольтметр, амперметр и другие. Исходя из уровня нагрузки, выбирается подходящая формула.

Поскольку реактивные и активные характеристики связаны с кажущейся мощностью, их соотношение (баланс) выглядит следующим образом:

S = √P2 + Q2, все равны U*I .

Но если ток протекает непосредственно через реактивное сопротивление. Потери в сети отсутствуют. Это связано с индуктивной составляющей, C, и сопротивлением, L. Они рассчитываются по формулам:

Индуктивное сопротивление: xL = ωL = 2πfL,

Емкостное сопротивление: xc = 1/(ωC) = 1/(2πfC).

Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, который можно использовать для определения того, сколько энергии используется не по назначению или “теряется” при работе оборудования.

Если в сети присутствует реактивная активная составляющая, всегда необходимо рассчитывать коэффициент мощности.

Эта величина не имеет единицы измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные компоненты.

С помощью этого значения становится ясно, в каком направлении и как смещается энергия по отношению к напряжению сети. Для этого вам понадобится диаграмма треугольника напряжения:

Диаграмма треугольника напряжения

При наличии конденсатора, например, формула для коэффициента выглядит следующим образом:

Для получения наиболее точных результатов рекомендуется не округлять полученные данные.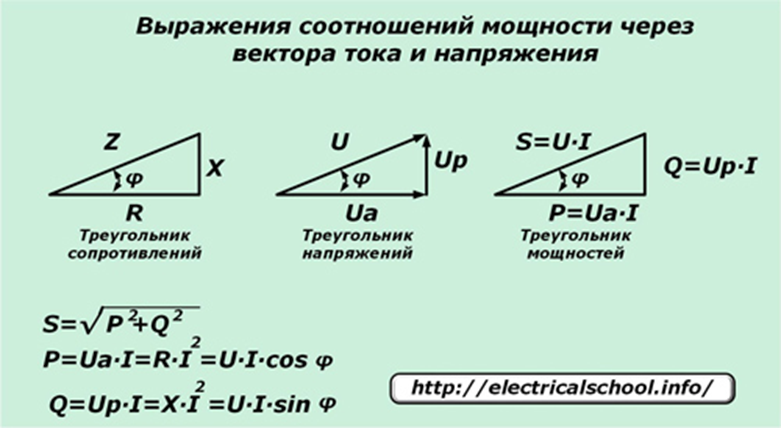

Компенсация

Учитывая, что при данном резонансе реактивная мощность равна 0:

Q = QL – QC = ULI – UCI

Для повышения эффективности работы данного устройства используются специальные устройства, позволяющие минимизировать влияние потерь на сеть. В частности, это устройства ИБП. Электрические потребители со встроенным аккумулятором (например, ноутбуки или портативные устройства) не нуждаются в этом устройстве, но для большинства других людей источник бесперебойного питания необходим.

Установив такой источник, вы сможете не только свести на нет негативные последствия потерь, но и снизить стоимость ваших счетов за электроэнергию. Эксперты доказали, что источник бесперебойного питания экономит в среднем от 20 до 50 % электроэнергии. Почему это происходит:

1. Нагрузка на силовые трансформаторы значительно снижается;
2. Кабели меньше нагреваются, что не только положительно сказывается на их работе, но и повышает безопасность;
3. Уменьшаются помехи для сигнального и радиооборудования;
4. Гармоники в электрической сети снижаются на порядок.

В некоторых случаях специалисты используют не полноценные ИБП, а специальные компенсирующие конденсаторы. Они подходят для бытового использования и продаются во всех магазинах электротоваров. Все приведенные выше формулы могут быть использованы для расчета запланированной и достигнутой экономии.

– Активная мощность (P) – выполняет полезную работу (полезная мощность) и преобразуется в другие формы энергии (тепловая энергия: водонагреватель, утюг и т.д. являются активными нагрузками)

Как найти полную мощность

Полная мощность ( S ) состоит из двух компонентов:

– Активная мощность (P) – выполняет полезную работу (полезная мощность) и преобразуется в другие формы энергии (тепловая энергия: водонагреватель, утюг и т.д. являются активными нагрузками)

– Реактивная мощность (Q) является либо индуктивной, либо емкостной, в зависимости от нагрузки в сети. Чаще всего мы используем индуктивную энергию дома, любой электроприбор, имеющий катушку, обмотку, является реактивной нагрузкой (электродрель, блендер, холодильник). Энергия не рассеивается реактивными элементами, она накапливается на них в течение половины периода и возвращается в сеть. Хотя многие электроприборы не могли бы функционировать без реактивного компонента, его присутствие вызывает ряд негативных последствий:

– нагрев проводников;

– Воздействие на сеть – добавление реактивного компонента в сеть, который затем оказывает негативное воздействие на потребителей.

Конечно, между вышеперечисленными параметрами существуют корреляции. Расчет кажущейся мощности производится по следующей формуле:

Активная и реактивная мощность находятся в прямой зависимости от коэффициента мощности (cosφ):

Видимая мощность обеспечивает потребителей всеми необходимыми компонентами и рассчитывается:

На следующей диаграмме (треугольник власти) показана зависимость полной мощности и ее составляющих от угла cosφ, т. е. угла смещения между напряжением и током.

Единицы измерения немного отличаются, хотя смысл тот же: полная мощность измеряется в ВА (вольт-амперах), активная мощность – в Вт (ваттах), а реактивная мощность – в ВАР (вольт-амперах реактивной мощности).

Единицей измерения реактивной мощности является реактивный ампер-вольт (Вар): 1 Вар = 1 В x 1 А. Проще говоря, единица реактивной мощности описывает величину магнитного или электрического поля, создаваемого 1 В x 1 А.

Активная, реактивная и кажущаяся мощность

Другими словами, активную мощность можно назвать: реальная мощность, действительная мощность, полезная мощность, реальная мощность. В цепи постоянного тока мощность, подводимая к нагрузке постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, т.е.

потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет коэффициента мощности.

Однако для синусоидальных сигналов, т. е. в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активной мощности), которая фактически питает нагрузку, определяется как:

В цепи переменного тока, если она является чисто активной (резистивной), формула для мощности такая же, как и для постоянного тока: P = V I.

Формула для активной мощности

P = V I – в цепях постоянного тока

P = V I cosθ – в однофазных цепях переменного тока

P = √3 V_L I_L cosθ – в трехфазных цепях переменного тока

P = √ (S 2 – Q 2 ) или

P = √ (VA 2 – Var 2 ) или

активная мощность = √ (кажущаяся мощность 2 – реактивная мощность 2 ) или

кВт = √ (кВА 2 – квар 2 )

Реактивная мощность (Q)

Назвать ее бесполезной или бессмысленной силой тоже было бы сильно.

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, называется реактивной мощностью (Q).

Реактивная мощность – это мощность, которая забирается и затем возвращается нагрузкой благодаря своим реактивным свойствам. Единицей измерения активной мощности является ватт, 1 Вт = 1 В x 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного или электрического поля в случае индуктора или конденсатора соответственно.

Реактивная мощность определяется как

и может быть положительным (+Ve) для индуктивных нагрузок и отрицательным (-Ve) для емкостных нагрузок.

Единицей измерения реактивной мощности является реактивный вольт-ампер (вар): 1 вар = 1 В x 1 А. Проще говоря, единица реактивной мощности описывает величину магнитного или электрического поля, создаваемого 1 В x 1 А.

Формулы для реактивной мощности следующие

Реактивная мощность = √ (Полная мощность 2 – Активная мощность 2 )

квар = √ (кВА 2 – кВт 2 )

Общая мощность (S)

Полная мощность – это произведение напряжения и тока, без учета фазового угла между ними. Вся мощность в сети переменного тока (рассеянная и поглощенная/возвращенная) является полной мощностью.

Комбинация реактивной и активной мощности называется кажущейся мощностью. Произведение среднеквадратичного значения напряжения и среднеквадратичного значения тока в цепи переменного тока называется кажущейся мощностью.

Это произведение напряжения и тока без учета фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. В чисто активной цепи кажущаяся мощность равна активной мощности, в то время как в индуктивной или емкостной цепи, где есть реактивное сопротивление, кажущаяся мощность больше активной мощности.

Формула кажущейся мощности

Полная мощность = √ (активная мощность 2 + реактивная мощность 2 )

кВА = √(кВт 2 + кВАр 2 )

Обратите внимание, что

• Резистор принимает активную энергию и отдает ее в виде тепла и света.
• Индуктивность принимает реактивную мощность и отдает ее обратно в виде магнитного поля.
• Конденсатор принимает реактивную мощность и отдает ее обратно в виде электрического поля.

Все эти величины связаны друг с другом тригонометрически, как показано на рисунке:

Если в трехфазной цепи нет нейтрального провода, для измерения полной мощности достаточно двух ваттметров, даже если нагрузка несимметрична.

Мощность трехфазной сети: активная, реактивная, полная

Значения полной активной мощности и полной реактивной мощности в трехфазной цепи равны суммам активной и реактивной мощностей, соответственно, в каждой из трех фаз A, B и C. Следующие формулы иллюстрируют это утверждение:

Здесь Ua, Ub, Uc, Ia, Ib, Ic – фазные напряжения и токи, а φ – фазовый сдвиг.

Если нагрузка симметрична, то есть активная и реактивная мощности каждой фазы равны, достаточно умножить значение фазной мощности на количество фаз, чтобы найти полную мощность многофазной цепи. Затем из рассчитанных активной и реактивной мощностей вычисляется полная мощность:

В приведенных выше формулах можно выразить фазовые значения через их линейные величины, которые будут отличаться для цепей типа “звезда” или “треугольник”, но формулы мощности в конечном итоге будут одинаковыми:

Из приведенных выше выражений видно, что независимо от схемы подключения потребителей электроэнергии, будь то треугольник или звезда, если нагрузка симметрична, формулы для нахождения мощности будут одинаковы как для треугольника, так и для звезды:

Эти формулы представляют собой линейные значения напряжения и тока и записываются без подписей. Это обычный способ обозначения напряжения и тока без индексов, т.е. если индексов нет, то это означает линейные значения.

Для измерения активной мощности в электрической цепи используется специальный измерительный прибор, называемый ваттметром. Показания определяются по формуле:

В приведенной формуле Uw и Iw – это векторы напряжения, приложенного к нагрузке, и тока, протекающего через нее.

Характер активной нагрузки и подключение фаз могут быть разными, поэтому ваттметры будут отличаться в зависимости от конкретных обстоятельств и схемы подключения.

Для симметрично нагруженных трехфазных цепей достаточно одного ваттметра, подключенного только к одной из фаз, для приблизительного измерения полной активной мощности, если не требуется высокая точность. Затем умножьте показания ваттметра на количество фаз, чтобы получить полную активную мощность цепи:

Для четырехпроводной цепи с нейтральным проводом для точного измерения активной мощности требуется три ваттметра, показания каждого из которых считываются, а затем суммируются, чтобы получить полную мощность цепи:

Если в трехфазной цепи отсутствует нейтральный проводник, для измерения полной мощности достаточно двух ваттметров, даже если нагрузка несимметрична.

Если нейтральный проводник отсутствует, то фазные токи связаны между собой согласно первому закону Кирхгофа:

Тогда сумма показаний пары ваттметров будет равна:

Таким образом, если сложить показания пары ваттметров, мы получим полную активную мощность в тестируемой трехфазной цепи, причем показания ваттметра зависят как от размера нагрузки, так и от ее характера.

Глядя на векторную диаграмму токов и напряжений для симметричной нагрузки, можно сделать вывод, что показания ваттметра определяются следующими формулами:

Анализируя эти выражения, мы видим, что при чисто активной нагрузке, когда φ = 0, показания обоих ваттметров будут равны, т.е. W1 = W2.

При активной индуктивной нагрузке, когда 0 ≤ φ ≤ 90°, показания ваттметра 1 будут меньше показаний ваттметра 2, т.е. W1 60° показания ваттметра 1 будут отрицательными, т.е. W1

При активной емкостной нагрузке, когда 0 ≥ φ ≥ -90°, ваттметр 2 будет показывать меньше, чем ваттметр 1, т. е. W1 > W2. При φ

Если вам понравилась эта статья, пожалуйста, не стесняйтесь поделиться ею в социальных сетях. Это очень поможет в развитии нашего сайта!

Читайте далее:

• Ваттметр в розетке: какую мощность он измеряет, как его подключить.
• Трехфазные электрические цепи; Студопедия.
• Что такое реактивная мощность и как с ней бороться; Сайт для электриков – статьи, советы, примеры, диаграммы.
• Полное сопротивление цепи переменного тока – Основы электроники.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Почему необходима компенсация реактивной мощности; Школа инженеров-электриков: электротехника и электроника.
• Измерительный инструмент – это инструмент для измерения. Что такое измерительный инструмент?.

Активная, реактивная и полная мощность

Мгновенная мощность p, потребляемая на данном участке цепи, определяется как произведение мгновенных значений тока i и напряжения u:

. (11)

Из соотношения (11) видно, что мгновенная мощность p, в зависимости от значения синусов, может быть как положительной, так и отрицательной.

Физический смысл положительного значения мгновенной мощности в том, что это мощность, поступающая в цепь от источника (генератора). Под отрицательной мощностью понимают мощность, отдаваемую в цепь и генератору в процессе разрядки конденсатора, а также обусловленную током самоиндукции.

Практический интерес представляет не мгновенная мощность, а так называемая активная мощность, которая определяется как среднее значение мгновенной мощности, потребляемой на данном участке цепи за достаточно большой промежуток времени. Поскольку мгновенная мощность изменяется периодически, то усреднение достаточно провести за один период T = 2/:

. (12)

После преобразования произведения синусов и выполнения интегрирования выражения (12) получим выражение для активной мощности:

. (13)

Для контроля за параметрами электрической цепи используются измерительные приборы, амперметры и вольтметры. Механическое перемещение стрелок, «световых зайчиков» и других элементов, позволяющих регистрировать показание прибора, обусловлено работой тока в течение определенного промежутка времени на участке цепи, где включен прибор. Поэтому измерительные приборы не могут показать мгновенные значения силы тока и напряжения, в том числе и амплитудные их значения.

Показания амперметров и вольтметров в цепи переменного тока соответствуют, так называемым, действующим (эффективным) значениям силы тока I и напряжения U.

Действующим значением силы переменного тока называется сила такого постоянного тока, при протекании которого в том же сопротивлении R за одинаковое время, равное целому числу периодов T, выделяется такая же энергия, как и при протекании переменного тока. Из этого определения следует, что

. (14)

Если сила тока изменяется по гармоническому закону (1), то после подстановки этого выражения в соотношение (14) и интегрирования следует, что

. (15)

Аналогично определяется и действующее значение переменного напряжения

. (16)

Поскольку действующие значения отличаются от амплитудных только постоянным коэффициентом, то для них, на основании, рассмотренной на рисунке 3 векторной диаграммы, можно построить треугольник напряжений (рисунок 5).

К роме того, использование действующих значений позволяет несколько упростить математические соотношения. Так выражение (13) с учетом соотношений (15) и (16) можно записать в виде

. (17)

Из соотношений (13) и (17) следует, что активная мощность P зависит не только от амплитудных или действующих значений силы тока и напряжения, но и от сдвига фаз  между током и напряжением. Максимальное значение мощности, потребляемое данной цепью P_max = IU, характеризует мощность, поступающую в цепь от источника (генератора), называется полной мощностью, обозначается S, и достигается при  = 0, т.е. в случае, когда, согласно соотношению (10), реактивное сопротивление цепи равно нулю.

Следовательно, величина

(18)

показывает, какую часть активная мощность в цепи составляет от полной мощности. Величина cos называется коэффициентом мощности.

Рассмотрим физические процессы, определяющие то, что, в общем случае, коэффициент мощности всегда меньше единицы, т.е.

активная мощность всегда меньше полной мощности, поступающей в цепь.

Энергия, поступающая в цепь от источника, расходуется на выделение тепла и энергию магнитного и электрического полей, которые возникают в катушке индуктивности и конденсаторе. Следовательно, полная мощность, поступающая в цепь от источника, может быть представлена следующим образом:

, (19)

где P_R — тепловая мощность, выделяющаяся в резисторе, P_C — скорость изменения энергии электрического поля в конденсаторе, P_L— скорость изменения магнитного поля в катушке индуктивности. Последние две величины можно также рассматривать, как мощности, потребляемые емкостной и индуктивной нагрузками.

Получим в явном виде зависимость введенных мощностей от времени:

, (20)

, (21)

. (22)

С оотношение (20) для мощности, выделяющейся на активном сопротивлении, показывает, что эта величина изменяется во времени с циклической частотой в два раза большей, чем ток и напряжение. График зависимости этой величины от времени представлен на рисунке 6 и показывает, что мощность, потребляемая активной нагрузкой, всегда положительная величина.

Среднее значение этой мощности за период, с учетом связи между напряжениями на рисунке 4 и формул (15) и (16):

.

Следовательно, по физическому смыслу, введенная ранее, активная мощность P представляет собой энергию, которая в виде тепла выделяется в единицу времени на сопротивлении R , т.е. уходит из цепи (поэтому это сопротивление и называется активным). Активная мощность измеряется в ваттах (Вт).

Мощность, потребляемая емкостной и индуктивной нагрузкой, также изменяется в зависимости от времени с циклической частотой в два раза большей, чем ток и напряжение. Но, в отличие от активной мощности, эти величины могут иметь положительные и отрицательные значения, что наглядно представляют графики на рисунке 6.

Рассчитаем средние значения этих мощностей за период:

,

.

Физический смысл равенства нулю среднего значения мощности, потребляемой емкостной нагрузкой за период в том, что, сколько энергии забирается конденсатором из цепи в те доли периода, когда конденсатор заряжается, столько же энергии отдается в цепь при его разрядке.

Аналогичные процессы происходят на участке цепи с соленоидом. Следовательно, в емкостной и индуктивной нагрузках, энергия не уходит из цепи. Дважды за период изменения тока энергия в этих нагрузках забирается и дважды за период отдается обратно в цепь и генератору. Поэтому емкостная и индуктивная нагрузки называются реактивными, и соответственно общее емкостное и индуктивное сопротивление называется реактивным.

Общая мощность, потребляемая реактивной нагрузкой

.

Рассчитаем энергию, потребляемую за четверть периода в емкостной и реактивной нагрузках:

. (23)

Для характеристики меры обменной энергии между реактивной нагрузкой и цепью с генератором вводят понятие реактивной мощности

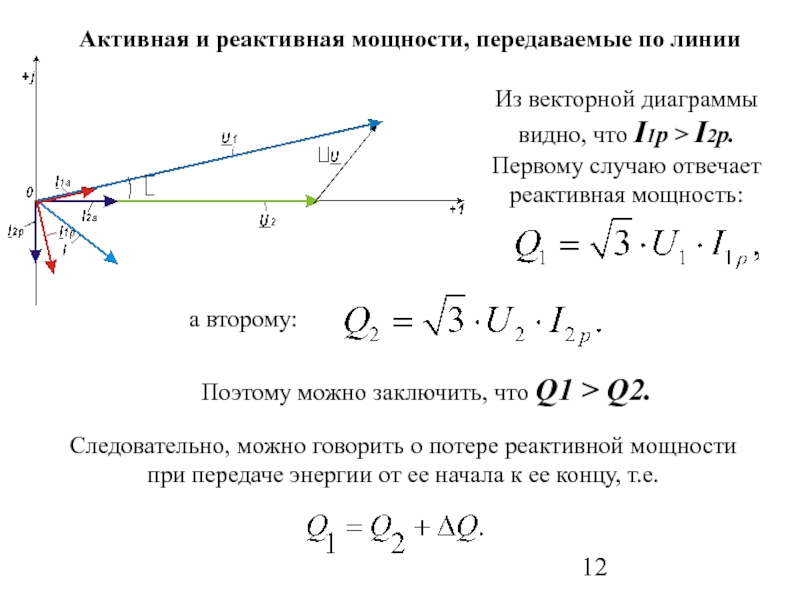. (24)

В качестве единицы измерения реактивной мощности используется вольт-ампер реактивный (ВАр).

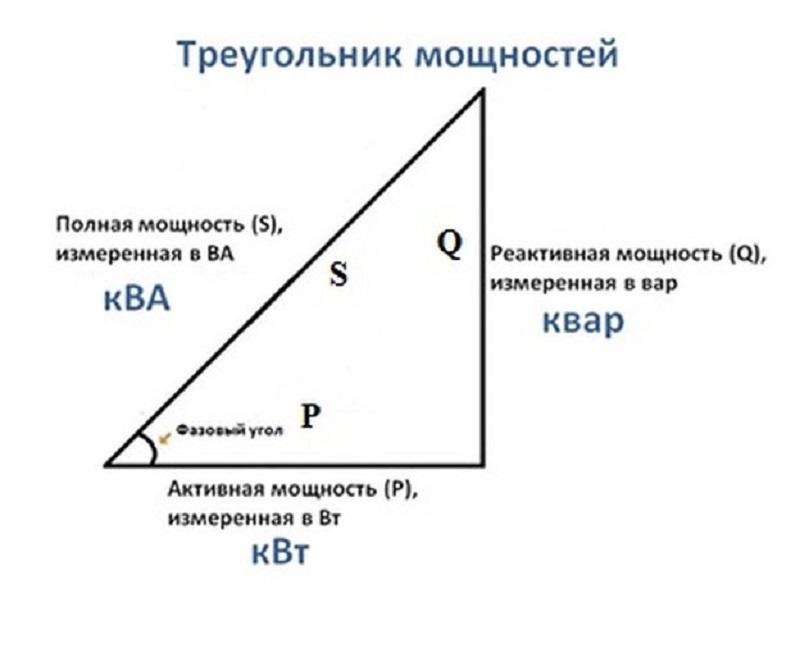
Соотношение между полной, активной и реактивной мощностями можно также получить из так называемого «треугольника мощностей». Треугольник мощностей, представленный на рисунке 7, получается из треугольника напряжений при умножении всех сторон последнего (рисунок 4) на величину, равную действующему значению силы тока в цепи.

Из треугольника мощностей следует, что

. (25)

Н а практике конструкция, габариты и, следовательно, стоимость различных приборов и устройств определяются не активной или реактивной мощностями, которые зависят от режима работы цепи, а полной мощностью, т.е. действующими значениями тока и напряжения, на которые рассчитано устройство.

Поэтому на корпусах реальных устройств указывается значение полной мощности. Чтобы отличить при расчетах полную мощность от активной и реактивной мощностей, за единицу измерения полной мощности принят Вольт-Ампер (ВА). Распределение полной мощности в цепи, как следует из выше изложенного, зависит от вида нагрузки. Как уже обсуждалось, долю, которую составляет активная мощность от полной мощности, поступающей в сеть, определяет коэффициент мощности, значение которого можно также выразить из треугольника напряжений на рисунке 4:

.

Если в участке цепи имеются только емкостное и индуктивное сопротивления (L  1/(C)  0, R  0), то сдвиг фаз  =  2. Тогда cos = 0 и, несмотря на наличие напряжения и тока в цепи (U  0, I  0), активная мощность P = 0. Поэтому, как обсуждалось выше, сопротивление X_L-X_C= L  1/(C) называется неактивным, или реактивным.

Если нагрузка «чисто индуктивная» (R  0, 1/(C)  0, L  0, tg = + ,  = + /2), то напряжение опережает ток на /2 или по времени на 1/4 периода T. В этом случае коэффициент мощности также равен нулю cos=0. Но проволочные обмотки реальных индуктивных катушек, если они не находятся в сверхпроводящем состоянии, всегда обладают определенным активным сопротивлением R и поэтому сдвиг фаз  в них меньше, чем /2.

Для «чисто емкостной нагрузки» (R  0, L  0, 1/(C)  0, tg = — ,  = — /2) напряжение отстает от тока на /2 и коэффициент мощности также равен нулю.

Если индуктивное и емкостное сопротивления участка цепи одинаковы (L = 1/(C)) или рассматриваемый участок цепи содержит только активное сопротивление (L  0, 1/(C)  0, R  0, tg = 0,  = 0), то напряжение и ток совпадают по фазе, а коэффициент мощности равен cos=1.

Следовательно, коэффициент мощности определяет долю потребляемой мощности в данной цепи.

Остальная часть полной мощности, в виде мощности тока самоиндукции, генерируемого в цепи потребителя, и мощности тока разряда конденсатора, возвращается обратно в цепь и к генератору. Эта мощность теряется, идя на нагревание проводов в линии передач.

Активная, реактивная и кажущаяся мощность

Различные формы электрической мощности-

Активная мощность, реактивная мощность и кажущаяся мощность представляют собой различные формы электрической мощности, и они проявляются, когда электрическая мощность подается на индуктивную нагрузку. Происходит это из-за коэффициента мощности .

Сначала давайте разберемся в значении этих различных мощностей –

Активная мощность – Активная мощность – это мощность, которая фактически используется нагрузкой. Обозначается цифрой Вт или кВт.

Реактивная мощность – Реактивная мощность – это мощность, которая не используется (или теряется) нагрузкой, но добавляется к мощности, потребляемой нагрузкой. Обозначается ВАр или КВАр.

Полная мощность – Полная мощность – это мощность, подаваемая на нагрузку, которая включает как активную, так и реактивную мощность. Обозначается ВА или кВА.

На картинке выше изображен стакан жидкости с пеной (это может быть любой холодный напиток), где жидкость является основным напитком, который следует употреблять, а пена не является фактическим напитком, но она занимает место и образует стакан полный. Теперь, если мы сравним это с мощностью, подаваемой на индуктивную нагрузку, где жидкость представляет собой активную мощность, пена представляет собой реактивную мощность, а полное стекло (жидкость + пена) представляет собой полную мощность.

Следовательно, с точки зрения электрической мощности, мы можем сказать, что реактивная мощность – это потеря мощности, которая не используется нагрузкой, но является частью полной мощности (полной мощности), подаваемой на нагрузку. Поэтому очень важно избегать реактивной мощности в системе. Но при индуктивных нагрузках это практически невозможно, поэтому можно было бы избежать реактивной мощности, улучшив коэффициент мощности.

Технически это можно объяснить с помощью векторной диаграммы, приведенной ниже. Существует соотношение между активной, реактивной и полной мощностью, которое приведено ниже –

Примечание – Для опережающего тока треугольник мощности становится обратным. Эта характеристика тока помогает улучшить коэффициент мощности. Когда устройство с опережающим коэффициентом мощности подключается параллельно с нагрузкой, отстающий коэффициент мощности частично нейтрализуется, таким образом, коэффициент мощности улучшается.

Активная, реактивная и полная мощность в цепях переменного и постоянного тока –

Мощность в цепи постоянного тока –

В цепи постоянного тока существует только один тип мощности, используемой нагрузкой, поскольку существует нет понятия коэффициента мощности (или разности фаз между напряжением и током). Мощность в цепи постоянного тока указана ниже-

P = V * I (где P = активная/реальная мощность, V = напряжение, I = ток). Мощность измеряется в ваттах (или Вт)

Мощность в цепи переменного тока –

В цепи переменного тока из-за коэффициента мощности – учитываются активная мощность, реактивная мощность, полная мощность.

Active Power —

P = V * I COS Ø …… однофазная мощность

P = g3 * V * I COS Ø …0005

(где P = активная/реальная мощность, V = линейное напряжение, I = линейный ток, CosØ = коэффициент мощности). Мощность измеряется в ваттах (или W)

Реактивная мощность —

Q = V * I SIN Ø …… мощность однофазного

Q = G3 * В * I SIN Ø ……Трехфазная мощность

(где Q = реактивная мощность, V = линейное напряжение, I = линейный ток, SineØ = разность фаз между напряжением и током). Мощность измеряется в ВАр (или реактивных вольт-амперах)

Полная мощность –

Полная мощность (включая активную и реактивную мощность), формула которой приведена ниже –

S = V * I …………. . Однофазная мощность

S =   Г3 * В * I  ………. Трехфазная мощность

(где S = полная мощность, V = линейное напряжение, I = линейный ток. Мощность измеряется в ВА (или вольтамперах).

Часто задаваемые вопросы (FAQ) по активной мощности, реактивной мощности и полная мощность –

В1) В чем разница между активной и реактивной мощностью?

Ответ) Активная мощность — это мощность, которая фактически используется нагрузкой, а реактивная мощность — это мощность, которая не используется нагрузкой (не используется нагрузкой из-за индуктивной нагрузки).

Q2) Какие альтернативные слова используются для реактивной мощности?

Ответ) Альтернативные слова реактивной мощности: безваттная мощность, отработанная мощность, бесполезная мощность.

Q3) Какие альтернативные слова используются для активной мощности?

Ответ) Альтернативные слова реактивной мощности: Реальная мощность, Реальная мощность, Полная мощность в ваттах, Полная мощность.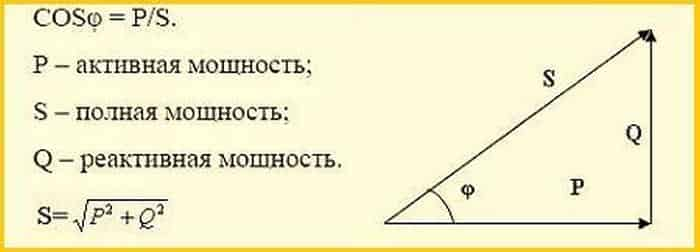

Активная, реактивная и полная мощность

Активная, реактивная и полная мощность

2023-03-10

• Основные понятия электротехники
• Активная, реактивная и полная мощность
  • Активная мощность
  • Реактивная мощность
  • Полная мощность
• Компенсация реактивной мощности

Основные понятия энергетики

Электротехника — важнейшая отрасль физики, непосредственно связанная с производством, обработкой, передачей и использованием электроэнергии. В нем описываются основные концепции науки об электричестве и связанные с ними отношения, основанные на физике, а также вводится ряд математических формул для понимания процессов, упомянутых выше. Чтобы плавно погрузиться в электротехнику, нужно полностью понимать основные термины и понятия: напряжение, сила тока, сопротивление, частота и мощность. Этот текст посвящен последнему.

Активная, реактивная и полная мощность

Наверное, все мы слышали об электроэнергии. Когда мы выбираем электрические бытовые приборы, т.е. холодильников, духовок и чайников мы смотрим на многие параметры, включая мощность, выраженную в ваттах или киловаттах.

Мощность измеряет работу, которую физическая система может выполнить в единицу времени. Следующая формула описывает это отношение:

Ключ:
W – рабочий [J];
t – время [с]

Мы различаем три вида мощности, объединенные в так называемый «треугольник мощности»:

• Активная мощность;
• Реактивная мощность;
• Полная мощность.

Согласно математической интерпретации, векторная сумма активной мощности (P) и реактивной мощности (Q) равна полной мощности (S).

Активная мощность

Активная мощность, также известная как «истинная или реальная мощность» или «полезная мощность», генерируется при преобразовании работы устройств в тепловую, механическую или световую энергию. Единицей активной мощности является ватт, а его математическая интерпретация следующая:

Ключ: P – активная мощность [Вт];
U – напряжение [В];
I – сила тока [А];
cosϕ – фазовый коэффициент – это отношение активной мощности к полной мощности (и связанное со сдвигом фаз между током и напряжением).

Активная мощность определяется как среднее значение мгновенной мощности.

Измеряется ваттметром. Упомянем также схему Арона, измеряющую активную мощность в трехпроводной трехфазной системе.

Реактивная мощность

Также называется «бесполезной» или «бесваттной» мощностью и не участвует в использовании электроэнергии для обеспечения приемника энергией. Однако он участвует в хранении энергии магнитных и электрических полей. Реактивная мощность является необходимой составляющей мощности для правильной работы электрооборудования, такого как трансформаторы или электродвигатели.

Реактивная мощность выражается как произведение действующего напряжения и действующего тока и синуса фазового сдвига между током и напряжением.

Ключ:
Q – Активная мощность [ВАР];
U – напряжение [В];
I – сила тока (ток) [А];
sinϕ– синус фазового сдвига между действующим током и напряжением.

Существует два типа реактивной мощности:

• Емкостная реактивная мощность Q _c , которая характеризует конденсаторы или длинные электрические провода;
• Индуктивная реактивная мощность Q _L , которая характеризует все устройства с проволочными катушками, т.е. электродвигатели или трансформаторы.

Полная мощность

Как и активная и реактивная мощность, полная мощность является произведением напряжения и силы тока. Поскольку это векторная сумма двух составляющих мощности, мы иногда называем ее «полной мощностью».

Обозначение:
S – полная мощность [ВА];
U – напряжение [В];
I – сила тока [А]

Компенсация реактивной мощности

Доставка электроэнергии от электростанции к конечным потребителям предполагает ее передачу на очень большие расстояния. Как уже упоминалось, это генерирует емкостную реактивную мощность. Необходимо уменьшить принимаемую реактивную мощность, так как она вызывает значительные потери энергии при передаче, а это требует использования электрических шнуров с проводами большего диаметра. Другая проблема заключается в том, что реактивная мощность снижает напряжение в трансформаторах и линиях электропередач. Чтобы противодействовать этим неблагоприятным последствиям реактивной мощности, конечные пользователи (особенно те, которые потребляют много энергии) компенсируют реактивную мощность, чтобы снизить свои счета за электроэнергию. Для уменьшения индуктивной реактивной мощности можно, например, подключить батареи конденсаторов, а для уменьшения емкостной реактивной мощности — батареи катушек индуктивности.

Снижение реактивной мощности выгодно как для собственника объекта, так как он платит меньше за электроэнергию, так и для энергораспределителя, для которого снижение потерь при передаче означает экономию на дорогостоящей замене линий электропередачи и наладке трансформаторных сетей.