Понятие о реактивных и активных мощностях и нагрузках
Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Батареи статических конденсаторов
Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.
Понятие о реактивной мощности
Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.
На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:
P = U x I.
Измеряется в ваттах (Вт).
В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.
Реактивная нагрузка бывает двух видов:
- Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
- Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.
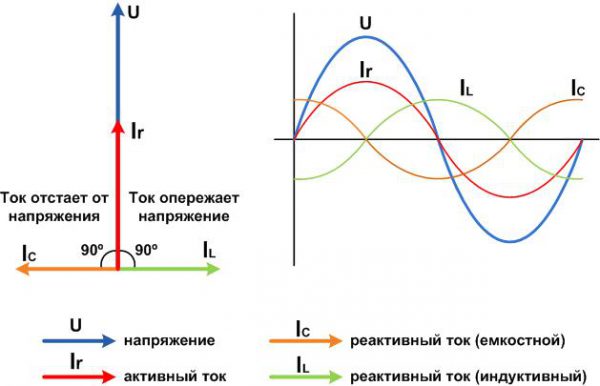
Емкостная и индуктивная нагрузка
Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.
Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ». Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой. Одновременно по цепи протекает реактивный ток, не выполняющий никакую эффективную работу. Следовательно, потребляется реактивная мощность.
Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.
Расчет реактивной мощности ведется по формуле:
Q = U x I x sin φ.
В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).
Выражение для активной мощности:
P = U x I x cos φ.
Треугольник мощностей
Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей. Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную. Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).
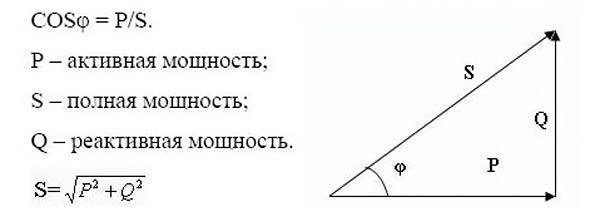
Треугольник мощностей
Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.
Полная мощность не находится как алгебраическая сумма активного и реактивного мощностного значения, это векторная сумма P и Q. Ее количественное значение вычисляется извлечением квадратного корня из суммы квадратов мощностных показателей: активного и реактивного. Измеряться полная мощность может в ВА (вольтампер) или производных от него: кВА, мВА.
Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.
Коэффициент мощности
Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:
cos φ = P/S.
Данный коэффициент находит эффективность работы сети.
Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.
Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.
Если, к примеру, имеется катушка, для которой:
- Р = 80 Вт;
- Q = 130 ВАр;
- тогда S = 152,6 BA как среднеквадратичный показатель;
- cos φ = P/S = 0,52 или 52%
Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.
Коррекция cos φ
Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.
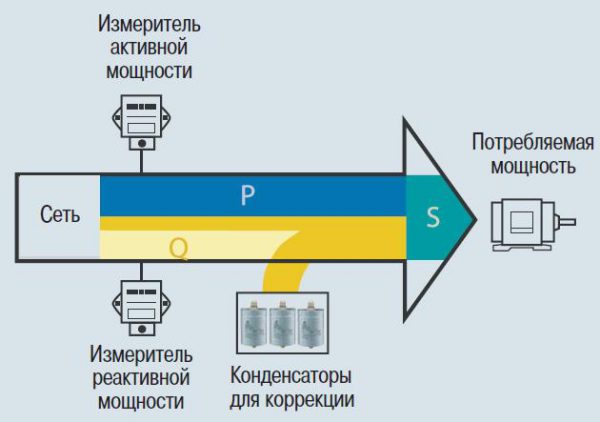
Принцип компенсации реактивной мощности
Главные потребители реактивной энергии:
- Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
- Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
- Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
- Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.
Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней. Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения. Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.
Как и где измеряют cos φ
Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

Фазометр
Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.
- Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
- При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
- Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Синхронный компенсатор
Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.
Видео
Оцените статью:Реактивная мощность — это… Что такое Реактивная мощность?
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность
Мгновенная электрическая мощность P (t), выделяющаяся на элементе электрической цепи — произведение мгновенных значений напряжения U (t) и силы тока I (t) на этом элементе:
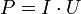 |
Если элемент цепи — резистор c электрическим сопротивлением R, то
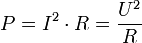 |
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то среднюю мощность можно вычислить по формулам:
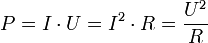 |
Мощность переменного тока
Активная мощность
Среднее за период Т значение мгновенной мощности называется активной мощностью: 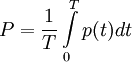 . В цепях однофазного синусоидального тока
. В цепях однофазного синусоидального тока 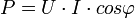 , где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле
, где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле 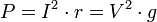 . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
. В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением 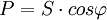 . Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
. Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
Реактивная мощность
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ. Единица реактивной мощности — вольт-ампер реактивный (
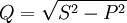 . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
. Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Полная мощность
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I; связана с активной и реактивной мощностями соотношением: 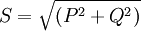
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой: 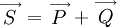
Измерения
Литература
- Бессонов Л. А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа, 1978
Ссылки
См. также
Wikimedia Foundation. 2010.
Активная и реактивная мощность 2020
Питание — это комбинация напряжения и тока в электрических цепях. С технической точки зрения, это скорость передачи электрической энергии электрическими цепями, что означает скорость передачи энергии. Аббревиатуры AC и DC часто используются в системах электропитания в качестве переменного тока и постоянного тока соответственно. Оба представляют собой разные типы тока, используемые для передачи электрической энергии. Активная мощность и реактивная мощность являются двумя наиболее распространенными терминами, используемыми для описания потока энергии в электроэнергетических системах. Активная мощность — это реальная мощность, тогда как реактивная мощность используется для передачи реальной мощности. В этой статье освещаются некоторые ключевые различия между ними.
Что такое активная сила?
В простых цепях переменного тока напряжение и ток являются синусоидальными, что означает, что форма волны имеет близкое сходство с идеальной синусоидальной волной. В случае чисто резистивной нагрузки напряжение и ток изменяют свою полярность в одно и то же время и в каждый момент времени, это значение положительно означает, что направление тока не меняется в обратном направлении. В этом случае передается только активная мощность. Активная мощность или реальная мощность — это мощность, которая фактически потребляется в цепи переменного тока. Проще говоря, рассеиваемая мощность называется активной силой. Он обозначается заглавной буквой «P» и измеряется в ваттах (W) в основном киловатт (KW) и мегаватт (МВт).
Что такое реактивная сила?
В случае чисто реактивной нагрузки напряжение не соответствует фазе тока. Произведение напряжения и тока положительно для половины каждого цикла, тогда как для другой половины цикла значение отрицательно, так как мощность непрерывно протекает между источником и нагрузкой. Это приводит к тому, что реактивная мощность передается на нагрузку. Проще говоря, реактивная мощность — это неиспользуемая мощность или мнимая мощность, которая не используется для какой-либо полезной работы, и существует, когда напряжение и ток не соответствуют фазе. Он обозначается заглавной буквой «Q» и измеряется вольтамперной реактивной (var) в отличие от единицы мощности СИ, которая является ваттом.
Разница между активной и реактивной мощностью
Определение
В электрических системах переменного тока величина мощности, используемой для создания эффективной работы, означающая количество мощности, которое фактически передается нагрузке, такой как трансформатор, называется «активной мощностью» или «реальной мощностью» или «истинной мощностью». Это полезная сила, которая фактически натягивается нагрузкой в результате рассеивания энергии в виде тепла. С другой стороны, реактивная мощность — это мощность, которая непрерывно отскакивает назад и вперед между источником и нагрузкой, что означает мощность, которая не может использоваться для эффективной работы в цепи переменного тока или в системе.
Единица измерения
Ватт является общей единицей для всех видов мощности, которая символизируется как «W», но блок обычно зарезервирован для активной мощности. Он практически измеряется в киловаттах (кВт) и мегаваттах (МВт) в электроэнергетических системах. Реактивная мощность — это форма мощности, но она не выражается в ваттах. Вместо этого он выражается реактивным вольт-амперным реактивным (var) в электроэнергетически
12. Активная реактивная, полная мощность.
Р = Ur*I = I^2*r — активная мощность цепи, Вт, кВт; QL = UL*I = I^2*XL —реактивная индуктивная мощность цепи, обусловленная энергией магнитного поля, вар.
QС = UС*I = I^2*XС — реактивная емкостная мощность цепи, обусловленная энергией электрического поля, вар.
Q = QL — QС = I^2x — реактивная мощность цепи, вар, это та мощность, которой приемник обменивается с сетью;
S = U*I = I^2*Z— полная мощность цепи. В • А;
cos φ = r/z = P/S—коэффициент мощности
Реактивные мощности, обусловленные соответственно энергией магнитного поля индуктивности и электрического поля емкости, не совершают никакой полезной paботы, они оказывают существенное влияние на режим работы электрической цепи. Коэффициент мощности показывает, какая часть полной мощности является активной мощностью. Полная мощность и коэффициент мощности наряду с другими параметрами являются расчетными величинами и в конечном счете определяют габаритные размеры трансформаторов и других устройств. Ваттметр измеряет активную мощность Р цепи.
14. Закон Ома для цепи синусоидального тока.
Если ток является синусоидальным с циклической частотой , а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается; величины, входящие в него, становятся комплексными: I=U/Z;
U = U0eiωt — напряжение или разность потенциалов,
I — сила тока,
Z = Re−iδ — комплексное сопротивление (импеданс),
R = (Ra^2 + Rr^2)^1/2 — полное сопротивление,
Rr = ωL − 1/(ωC) — реактивное сопротивление (разность индуктивного и емкостного),
Rа — активное (омическое) сопротивление, не зависящее от частоты,
δ = − arctg (Rr/Ra) — сдвиг фаз между напряжением и силой тока.
15. Треугольник сопротивлений и проводимостей.
Из выражения Z=R+jX, вытекает, что модуль комплексного сопротивления равен z=(r^2+x^2)^0.5, следовательно z, можно представить, как гипотенузу прямоугольного треугольника, в котором один из катетов= r, а другой =x, а tg(ФИ)=x/r. Аналогично представляется треугольник проводимости, y=(g^2+b^2)^0.5, только в нем tg(ФИ)= b/g.
Треугольник сопротивлений и проводимостей дает графическую интерпретацию связи между полным сопротивление и активного и реактивного сопротивления, а также полной проводимость, и активной и реактивной проводимостью.
№ 16. Законы Кирхгофа в символической форме записи
Первый закон:
Алгебраическая сумма значений токов, сходящихся в любом узле схемы, равна нулю:
Σ Ik= 0
Второй закон:
Алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура:
Σ Ik*Zk=ΣEk
(Величины в уравнениях являются комплексными (с точками сверху))
№ 12, 17. Активная, реактивная и полная мощности. Коэффициент мощности
Активная мощность P– среднее значение мгновенной мощностиpза период Т:
P= 1 /T*0∫Tpdt, [P] = Вт
Реактивная мощность Q– произведение напряженияUна участке цепи на токIпо этому участку на синус угла φ междуUиI:
Q=U*I*sin(φ), [Q] = ВАр (вольт-амперы реактивные)
Полная мощность: S=U*I, [S] = ВА
P^2 +Q^2 =S^2 – т.е. графически можно представить в виде прямоугольноготреугольника мощности
Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения:
cos(φ) =P/S
№ 18. Мгновенная мощность и колебание энергии в цепи синусоидального тока
Мгновенная мощность– произведение мгновенного значения напряженияuна участке цепи на мгновенное значение токаi, протекающего по этому участку:
p=u*i
Энергия магнитного поля катушки: Wм =L*i^2 / 2
Энергия электрического поля конденсатора: Wэ =C*uC^2 / 2
№ 19. Эквивалентные преобразования в электрических цепях
Теорема компенсации: в любой электрической цепи без изменения токораспределения сопротивление можно заменить ЭДС, численно равной падению напряжения на заменяемом сопротивлении и направленной встречно току в этом сопротивлении.
Несколько параллельно включённых ветвей, содержащих источники ЭДС и тока и сопротивления можно заменить одной эквивалентной ветвью со следующими параметрами:
gэ = Σgk
Eэ = (ΣEk*gk+ ΣIk) / Σgk
№ 20. Метод законов Кирхгофа
1. Произвольно выбрать положительные направления токов в ветвях и направления обхода контуров
2. Составить уравнения по первому закону Кирхгофа для всех узлов, кроме одного
3. Составить уравнения по второму закону Кирхгофа так, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, которая ещё не входила ни в одно из уравнений
№ 21. Метод контурных токов
Применяется для уменьшения числа уравнений в системе и теоретическом анализе схемы. За искомые токи принимают контурные токи и составляется система уравнений по второму закону Кирхгофа, число уравнений равно числу независимых контуров:
I11 * R11 + I22 * R12 + … = E11
I11 * R21 + I22 * R22 + … = E22
…
где I11,I22 – контурные токи;R11,R22 – суммы сопротивлений в контуре;R12,R21 – взаимные сопротивления контуров, взятых с минусом;E11,E22 – сумма ЭДС в контуре. После нахождения контурных токов вычисляют исходные токи
№ 22. Принцип наложения и метод наложения
Принцип наложения: ток вk-цепи равен алгебраической сумме токов, вызываемых каждой из ЭДС:
Ik = E1 * gk1 + E2 * gk2 + … + En * gkn
По методу наложения поочерёдно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя из схемы остальные, затем находят исходные токи в ветвях
№ 23. Входные и взаимные проводимости ветвей
Коэффициенты g(из предыдущего вопроса) имеют размерность проводимости. Коэффициенты с одинаковыми индексами (gmm) называют входными проводимостями ветвей (ветвиm), коэффициенты с разными индексами (gkm) – взаимными проводимостями ветвей (ветвейkиm) (k– ветвь с ЭДС,m– текущая ветвь)
№ 24. Метод узловых потенциалов
За неизвестные принимают потенциалы узлов схемы и составляется система уравнений по первому закону Кирхгофа, число уравнений равно числу узлов минус 1:
φ1 * g11 + φ2 * g12 + … = I11
φ1 * g21 + φ2 * g22 + … = I22
…
где φ1,φ2 – потенциалы узлов;g11,g22 – суммы проводимостей всех ветвей, сходящихся в узле;g12,g21 – сумма проводимостей ветвей между узлами, взятых с минусом;I11,I22 – узловые токи, равные сумме токов, полученных от деления ЭДС, подходящих к узлу, на сопротивление данных ветвей. После решения системы определяют токи в ветвях по закону Ома для участка цепи, содержащего ЭДС
№ 25. Метод эквивалентного генератора
По отношению к выделенной цепи всю остальную часть схемы можно заменить эквивалентным генератором, состоящим из ЭДС E=Uxxи сопротивленияRвх
1. Ветвь, ток в которой необходимо определить, размыкают и находят напряжение на её зажимах
2. Определяют входное сопротивление Rвх всей схемы относительно зажимов при закороченных источниках ЭДС
3. Рассчитывают ток: I=Uxx/ (R+Rвх)
Реактивная мощность | Домашний электрик
Электрическая мощность — это сейчас для нас все. Мы живем на электричестве, мы его пьем, едим, им греемся, на нем ездим. Через него смотрим на целый мир, им общаемся, и уж как-то им начинаем и думать. Но мощность электрическая имеет некоторое лукавое измерение, с помощью которого способна от нас утекать.
Мощность бывает активная, а бывает полная. Спрашивается, полная чем? А вот, мол, тем, что нам служит на пользу, что делает нам полезную работу, но и… оказывается, это еще не все. Еще есть вторая составляющая, которая получается этаким довеском, и она просто сжигает энергию. Греет то что не надо, а нам от этого ни жарко, ни холодно.
Такая мощность называется реактивной. Но виноваты, как это ни странно, мы сами. Вернее, наша система выработки, передачи и потребления электроэнергии.
Мощность активная, реактивная и полная
Мы пользуемся электричеством с помощью сетей переменного тока. Напряжение у нас в сетях каждую секунду колеблется 50 раз от минимального значения до максимального. Это так получилось. Когда изобретали электрический генератор, который механическое движение преобразует в электричество, то оказалось, что perpetuum mobile, или, переведя с латинского, вечное движение, легче всего устроить по кругу. Изобрели когда-то колесо, и с тех пор знаем, что если его подвесить на оси, то можно вращать долго-долго, а оно будет оставаться все на том же месте — на оси.
Почему у нас в сети напряжение переменное
И электрический генератор имеет ось и нечто, на ней вращающееся. А в результате и получается электрическое напряжение. Только генератор состоит из двух частей: вращающейся, ротора, и неподвижной, статора. И обе они участвуют в выработке электроэнергии. А когда одна часть крутится около другой, то неизбежно точки поверхности вращающейся части то приближаются к точкам поверхности неподвижной, то от них отдаляются. И это совместное их положение с неизбежностью описывается только одной математической функцией — синусоидой. Синусоида есть проекция вращения по кругу на одну из геометрических осей. Но осей таких можно построить много. Обычно наши координаты друг другу перпендикулярны. И тогда при вращении по кругу некоторой точки на одной оси проекцией вращения будет синусоида, а по другой — косинусоида, или та же синусоида, только смещенная относительно первой на четверть поворота, или на 90°.
Вот нечто такое и представляет собой напряжение, которое доводит до нашей квартиры электрическая сеть.

угол поворота здесь разбит не на 360 градусов,
а на 24 деления. То есть одно деление соответствует 15°
6 делений = 90°
Итак, напряжение в нашей сети синусоидальное с частотой 50 герц и амплитудой 220 вольт, потому что удобнее было делать генераторы, которые вырабатывают напряжение именно переменное.
Выгода от переменного напряжения — выгода системы
А чтобы сделать напряжение постоянным, надо специально его выпрямить. И это можно делать либо прямо в генераторе (специально сконструированном — тогда он станет генератором постоянного тока), либо когда-нибудь потом. Вот это «когда-нибудь» и получилось снова очень кстати, потому что переменное напряжение можно преобразовывать трансформатором — повышать или понижать. Это оказалось вторым удобством переменного напряжения. А повысив его трансформаторами до напряжений буквально ЗАПРЕДЕЛЬНЫХ (полмиллиона вольт и больше), можно передавать на гигантские расстояния по проводам без гигантских при этом потерь. И это тоже пришлось вполне кстати в нашей большой стране.
Вот, доведя, все-таки, напряжение до нашей квартиры, понизив его до хоть сколько-то мыслимой (хотя все еще и опасной) величины в 220 вольт, преобразовать его в постоянное опять забыли. Да и зачем? Лампочки горят, холодильник работает, телевизор показывает. Хотя в телевизоре этих постоянных/переменных напряжений… но, не будем тут еще и об этом.
Убытки от переменного напряжения
И вот мы пользуемся сетью переменного напряжения.
А в ней присутствует «плата за забывчивость» — реактивное сопротивление наших потребляющих сетей и их реактивная мощность. Реактивное сопротивление — это сопротивление переменному току. И мощность, которая просто-напросто уходит мимо наших потребляющих электроприборов.
Ток, идя по проводам, создает вокруг них электрическое поле. Электростатическое поле притягивает к себе заряды со всего, что источник поля, то есть ток, окружает. А изменение тока создает еще и поле электромагнитное, которое начинает бесконтактно наводить во всех проводниках вокруг электрические токи. Так, наша токовая синусоида, как только мы что-то у себя включаем, есть не просто ток, а непрерывное его изменение. Проводников вокруг хватает, начиная от металлических корпусов тех же электроприборов, металлических труб водоснабжения, отопления, канализации и кончая прутами арматуры в железобетонных стенах и перекрытиях. Вот во всем этом и наводится электричество. Даже вода в бачке унитаза, и та участвует во всеобщем веселье — в ней тоже индуцируются токи наводки. Такое электричество нам совсем не нужно, мы его «не заказывали». Но оно эти проводники пытается разогреть, а значит, уносит из нашей квартирной сети электроэнергию.
Получается, наша пространственная система прохождения тока у нас в квартире работает как большой трансформатор, и уходящая «в стены» энергия как раз и характеризуется реактивной частью этой мощности (индуктивная составляющая). А еще «мегасеть» работает и как большой конденсатор — вспомним электростатическую составляющую, — при этом статические заряды, наводимые во всем окружающем, заставляют заряды нашей электрической сети (а ток — это движение зарядов) реагировать на наведенные заряды вокруг — паразитную емкость. Это уже емкостная составляющая. «Конструкция» этой самой, охватившей нас со всех сторон паразитной невидимой сети просто неописуема. Мы же сами в ней участвуем — в наших телах и заряды накапливаются, и токи наводятся. Следовательно, вся эта паразитная реактивная нагрузка, ее сопротивление, мощность не могут поддаваться никакому расчету. Но вот мощность измеряется. А именно, как соотношение полезной мощности и полной.
Рассчитать или измерить мощность: полную, активную и реактивную
Чтобы охарактеризовать соотношение мощностей в сети нашего переменного тока, рисуют треугольник.
 Треугольник мощностей в цепи переменного тока
Треугольник мощностей в цепи переменного токаP – активная мощность, она же полезная активная нагрузка,
Q – мощность реактивная.
Мощность полную можно замерить ваттметром, а активная мощность получается расчетом нашей сети, в которой мы учитываем только полезные для нас нагрузки. Естественно, сопротивлением проводов мы пренебрегаем, считая их малыми относительно полезных сопротивлений электроприборов.
Полная мощность
S = U x I = Ua x If
А вот мощность паразитную, реактивную можно получить из данного треугольника по теореме Пифагора.

То есть, чем «тупее» этот острый угол, тем хуже у нас работает внутренняя квартирная потребляющая сеть — много энергии уходит в потери.
Что такое активная, реактивная и полная мощности
Угол j можно еще назвать углом фазового сдвига между током и напряжением в нашей сети. Ток является результатом приложения к нашей сети исходного напряжения в 220 вольт частотой в 50 герц. Когда нагрузка активна, то фаза тока совпадает с фазой напряжения в ней. А реактивные нагрузки эту фазу сдвигают на этот угол.
 Диаграмма тока и напряжения в сети переменного тока
Диаграмма тока и напряжения в сети переменного токаСобственно говоря, угол и характеризует степень эффективности нашего потребления энергии. И надо стараться его уменьшить. Тогда S будет приближаться к P.
Только удобнее оперировать не с углом, а с косинусом угла. Это как раз и есть соотношение двух мощностей:
 Формула
ФормулаКосинус угла приближается к единице, когда угол приближается к нулю. То есть, чем острее угол j, тем лучше, эффективнее работает электрическая потребляющая сеть. На практике, если добиться величины косинуса фи (а его можно выразить в процентах) порядка 70–90%, то это уже считается неплохо.
Часто используется другое отношение, связывающее активную мощность и реактивную:
 Еще формула
Еще формулаИз диаграммы тока и напряжения можно найти выражения для мощностей: активной, реактивной и полной.
 Диаграммы тока
Диаграммы токаЧто такое реактивная мощность
Реактивная мощность бывает индуктивная и емкостная. Они ведут себя в электрической цепи по-разному. На постоянном токе индуктивность — это просто кусок провода, имеющий какое-то очень малое сопротивление. А конденсатор на постоянном напряжении — просто разрыв в цепи.
И когда мы их включаем в цепь, подводим к ним напряжение, во время переходного процесса они ведут себя тоже прямо противоположно. Конденсатор заряжается, при этом возникающий ток сначала большой, потом, по мере зарядки, маленький, уменьшающийся до нуля.
В индуктивности, катушке с проводом, возникающее магнитное поле после включения в самом начале сильно препятствует прохождению тока, и он сначала маленький, потом увеличивается до своего стационарного значения, определяемого активными элементами схемы.
Конденсаторы, таким образом, способствуют изменению тока в цепи, а индуктивности препятствуют изменению тока.
Индуктивная и емкостная составляющие сопротивления сети
Таким образом, реактивные элементы имеют свои разновидности сопротивления — емкостное и индуктивное. С полным сопротивлением, включающим активную и реактивную составляющие, это связывается следующей формулой:
Z = R + jX
Z – полное сопротивление,
R – активное сопротивление,
X – реактивное сопротивление.
В свою очередь, реактивное сопротивление состоит из двух частей:
X = XL — XC
XL – индуктивной и XC – емкостной.
Отсюда мы видим, что вклад в реактивную составляющую у них разный.
Все, что в сети индуктивно, увеличивает реактивное сопротивление сети, все, что в сети имеет емкостной характер, уменьшает реактивное сопротивление.
На этом и строится возможность уменьшения паразитного, реактивного сопротивления.
Электроприборы, влияющие на качество потребления
Если бы все приборы у нас в сети были, как лампочки, то есть являлись чисто активной нагрузкой, проблем бы не было. Была бы активная потребляющая сеть, одна сплошная активная нагрузка, и, как говорится, в чистом поле — вокруг ничего, то все легко бы подсчитывалось по законам Ома и Кирхгофа, и было справедливо — сколько потребил, за столько и заплатил. Но вот имея и вокруг себя загадочную токопроводящую «инфраструктуру», и в самой сети множество неучтенных емкостей и индуктивностей, мы и получаем, кроме полезной нам, еще и реактивную, ненужную нам нагрузку.
Как от нее избавиться? Когда электрическая потребляющая сеть уже создана, то можно проводить мероприятия по уменьшению реактивной составляющей. Компенсация и строится на «антагонизме» индуктивностей и емкостей.
То есть, в сложившейся сети следует измерить ее составляющие, а потом придумать компенсацию.
Особенно хороший эффект от таких мероприятий достигается в больших потребляющих сетях. Например, на уровне заводского цеха, имеющего большое количество постоянно работающего оборудования.
Для компенсации реактивной составляющей используются специальные компенсаторы реактивной мощности (КРМ), содержащие в своей конструкции конденсаторы, меняющие суммарный сдвиг фаз в сети в лучшую сторону.
 Компенсатор реактивной мощности
Компенсатор реактивной мощности Еще один КРМ
Еще один КРМ Один из видов КРМ
Один из видов КРМ Есть и такие КРМ
Есть и такие КРМЕще приветствуется использование в сетях синхронных двигателей переменного тока, так как они способны компенсировать реактивную мощность. Принцип простой: в сети они способны работать в режиме двигателя, а когда при сдвиге фаз наблюдается «завал» электроэнергии (других слов язык уже не находит), они способны компенсировать это, «подрабатывая» в сети в режиме генератора.
Похожие статьи:Реактивная мощность. Расчёт
Реактивная мощность обусловлена способностью реактивных элементов накапливать и отдавать электрическую или магнитную энергию.
Eмкостная нагрузка в цепи переменного тока за время половины периода накапливает заряд в обкладках конденсаторов и отдаёт его обратно в источник.
Индуктивная нагрузка накапливает магнитную энергию в катушках и возвращает её в источник питания в виде электрической энергии.
Напряжение на выводах реактивного элемента будет достигать максимального значения во время смены направления тока, следовательно, расхождение во времени между напряжением и током в пределах элемента составит четверть периода (сдвиг фаз 90°).
Угол сдвига фаз φ в цепи нагрузки определяется соотношением активного и реактивного сопротивлений нагрузки.
Реактивная мощность характеризует потери, созданные реактивными элементами в цепи переменного тока, и выражается формулой Q = UIsinφ.
Природу потерь в цепи с реактивными элементами можно рассмотреть с помощью графиков на рисунках.

φ = 90° sin90° = 1 cos90° = 0
При отсутствии активной составляющей в нагрузке, сдвиг фаз между напряжением и током составит 90°.
В начале периода, когда напряжение максимально – ток будет равен нулю, следовательно, мгновенное значение мощности UI в это время будет равно нулю.
В течении первой четверти периода, мощность можно видеть на графике, как произведение UI,
которое станет равным нулю при максимуме тока и нулевом значении напряжения.
В следующую четверть периода на графике UI принимает отрицательное значение, следовательно, мощность возвращается обратно в источник питания. То же самое произойдёт и в отрицательном полупериоде тока. В результате средняя (активная) потребляемая мощность P avg за период будет равна нулю.
В таком случае:
Реактивная мощность Q = UIsin90° = UI
Потребляемая мощность P = UIcos90° = 0
Полная мощность S = UI = √(P² + Q²) будет равна реактивной мощности
Коэффициент мощности P/S = 0
При отсутствии реактивных элементов и сдвига фаз в нагрузках, мгновенная мощность в полупериоде Umax*Imax будет максимальной, и в следующем полупериоде произведение отрицательного напряжения с отрицательным током дадут положительный результат – полезную мощность в нагрузке.

φ = 0° sin90° = 0 cos90° = 1
В этом случае:
Реактивная мощность Q = UIsin0 = 0
Потребляемая мощность P = UIcos0 = UI
Полная мощность S = UI = √(P² + Q²) будет равна потребляемой мощности
Коэффициент мощности P/S = 1
Ниже представлен рисунок графиков со сдвигом фаз 45°, для случая равенства активного и реактивного сопротивлений в нагрузке.

φ = 45° sin45° = cos45° = √2/2 ≈ 0.71
Здесь:
Реактивная мощность Q = UIsin45° = 0.71UI
Потребляемая мощность P = UIcos45° = 0.71UI
Полная мощность S = √(P² + Q²) = UI
Коэффициент мощности P/S = 0.71
В примерах рассмотрены случаи с индуктивной нагрузкой, когда ток отстаёт от напряжения (положительный сдвиг фаз).
В случаях с ёмкостной нагрузкой, процессы и расчёты аналогичны,
только напряжение будет отставать от тока (отрицательный сдвиг фаз).
Угол сдвига фаз в сети определится соотношением активного и реактивного сопротивлений нагрузок в
параллельном соединении следующим образом:

XL и XС соответственно индуктивное и ёмкостное сопротивление нагрузок.
Преобладание индуктивных нагрузок будет уменьшать общее индуктивное сопротивление.
Из выражения видно, что угол в этом случае будет принимать положительный знак,
а преобладание ёмкостных нагрузок будет уменьшать ёмкостное сопротивление и вызывать отрицательный сдвиг.
При равенстве индуктивного и ёмкостного сопротивлений, угол сдвига будет равен нулю.
В бытовых и производственных потребителях индуктивное сопротивление обычно существенно преобладает над ёмкостным.
Подробнее о вычислениях общего угла сдвига φ для вариантов соединений активного и реактивного сопротивлений в нагрузках можно ознакомиться на страничке электрический импеданс.
Компенсация реактивной мощности
Огромное количество индуктивных нагрузок в сети суммарно обладает колоссальной реактивной мощностью, которая возвращается в генераторы и не совершает никакой полезной работы, расходуя энергию на нагрев кабелей и проводов ЛЭП, перегружает трансформаторы, снижая их КПД, тем самым уменьшая пропускную способность активных токов.
Если параллельно индуктивной нагрузке подключить конденсатор,
фаза тока в цепи источника будет смещаться в противоположную сторону, компенсируя угол, созданный индуктивностью нагрузки.
При определённом соотношении номиналов,
можно добиться отсутствия сдвига фаз, следовательно, и отсутствия реактивных токов в цепи источника питания.
Ёмкость конденсатора определяется реактивным (индуктивным) сопротивлением нагрузки, которое необходимо компенсировать:
C = 1/(2πƒX),
X = U²/Q — реактивное сопротивление нагрузки,
Q — реактивная мощность нагрузки.
Компенсация реактивных токов в сети позволяет значительно уменьшить потери на активном сопротивлении проводов ЛЭП, кабелей и обмоток трансформаторов питающей сети.
В целях компенсации реактивной мощности на производственных предприятиях, где основными потребителями энергии являются асинхронные электродвигатели,
индукционные печи, люминесцентное освещение, которые обладают индуктивным сопротивлением, часто применяют специальные конденсаторные
установки, способные в ручном или автоматическом режиме поддерживать нулевой сдвиг фаз, тем самым минимизировать реактивные потери.
В масштабах энергосистемы компенсация происходит непосредственно на электростанциях путём контроля сдвига фаз и обеспечения соответствующего тока подмагничивания роторных обмоток синхронных генераторов станций.
Компенсация реактивной мощности — одна из составляющих комплекса мер по Коррекции Коэффициента Мощности (ККМ) в электросети (Power Factor Correction — PFC в англоязычной литературе). Применяется в целях уменьшения потерь электроэнергии, как на паразитную реактивную, так и нелинейную составляющую искажений тока в энергосистеме. Более подробно с материалом о ККМ (PFC) можно ознакомиться на странице — коэффициент мощности.
Онлайн-калькулятор расчёта реактивной мощности и её компенсации.
Достаточно вписать значения и кликнуть мышкой в таблице.
Реактивная мощность Q = √((UI)²-P²)  |
Похожие страницы с расчётами:
Рассчитать импеданс.
Рассчитать частоту резонанса колебательного контура LC.
Рассчитать реактивное сопротивление катушки индуктивности L и конденсатора C.
Альтернативные статьи: Дизель-генератор
Реактивная мощность — это… Что такое Реактивная мощность?
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
Мгновенная электрическая мощность
Мгновенная электрическая мощность P (t), выделяющаяся на элементе электрической цепи — произведение мгновенных значений напряжения U (t) и силы тока I (t) на этом элементе:
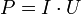 |
Если элемент цепи — резистор c электрическим сопротивлением R, то
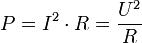 |
Мощность постоянного тока
Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то среднюю мощность можно вычислить по формулам:
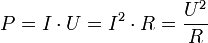 |
Мощность переменного тока
Активная мощность
Среднее за период Т значение мгновенной мощности называется активной мощностью: 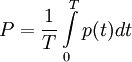 . В цепях однофазного синусоидального тока
. В цепях однофазного синусоидального тока 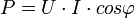 , где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле
, где U и I — действующие значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле 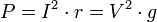 . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением
. В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением 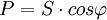 . Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
. Единица активной мощности — ватт (W, Вт). Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом активной мощности является мощность, поглощаемая нагрузкой.
Реактивная мощность
Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи переменного тока, равна произведению действующих значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: Q = UI sin φ. Единица реактивной мощности — вольт-ампер реактивный (var, вар). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: 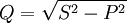 . Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
. Реактивная мощность в электрических сетях вызывает дополнительные активные потери (на покрытие которых расходуется энергия на электростанциях) и потери напряжения (ухудшающие условия регулирования напряжения). В некоторых электрических установках реактивная мощность может быть значительно больше активной. Это приводит к появлению больших реактивных токов и вызывает перегрузку источников тока. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности. Для СВЧ электромагнитного сигнала, в линиях передачи, аналогом реактивной мощности является мощность, отраженная от нагрузки.
Необходимо отметить, что величина sinφ для значений φ от 0 до плюс 90 ° является положительной величиной. Величина sinφ для значений φ от 0 до минус 90 ° является отрицательной величиной. В соответствии с формулой Q = UI sinφ реактивная мощность может быть отрицательной величиной. Но отрицательное значение мощности нагрузки характеризует нагрузку как генератор энергии. Активное, индуктивное, емкостное сопротивление не могут быть источниками постоянной энергии. Модуль величины Q = UI sinφ приблизительно описывает реальные процессы преобразования энергии в магнитных полях индуктивностей и в электрических полях емкостей. Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения. Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sinφ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.
Полная мощность
Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S = U×I; связана с активной и реактивной мощностями соотношением: 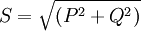 , где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (VA, ВА).
, где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0). Единица полной электрической мощности — вольт-ампер (VA, ВА).
Векторная зависимость между полной, активной и реактивной мощностью выражается формулой: 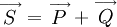
Измерения
Литература
- Бессонов Л. А. — Теоретические основы электротехники: Электрические цепи — М.: Высш. школа, 1978
Ссылки
См. также
Wikimedia Foundation. 2010.

