Site Loader
Posted on 26.03.2023

Вся элементарная математика — Средняя математическая интернет-школа

Вектор – это направленный отрезок, соединяющий две точки в пространстве или в плоскости. Векторы обычно  обозначаются либо маленькими буквами, либо начальной и конечной точками. Сверху обычно ставят чёрточку.

Например, вектор, направленный из точки A к точке B , можно обозначить a ,

__

Нулевой вектор 0 или 0 — это вектор, у которого начальная и конечная точки совпадают, т. e . A = B . Отсюда, 0 = – 0 .

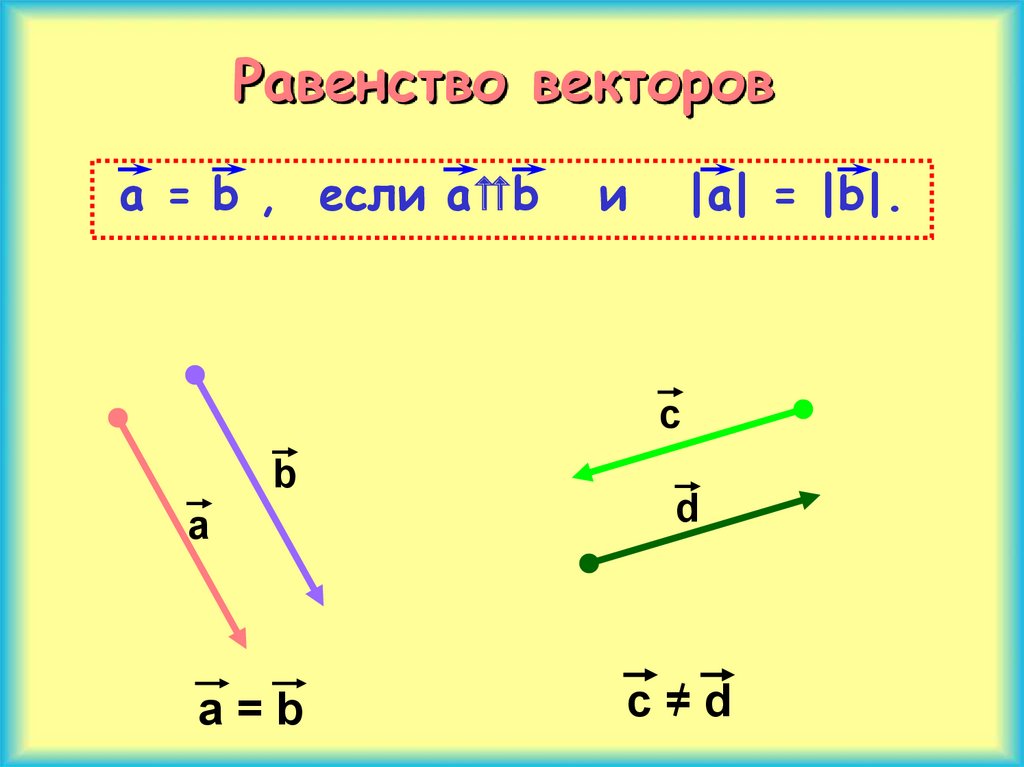
Длина (модуль) вектора a — это длина отображающего его отрезка AB , обозначается | a | . В частности,  | 0 | = 0.

Векторы называются коллинеарными , если их направленные отрезки лежат на параллельных прямых. Коллинеарные векторы a и b обозначаются a || b .

Три и более векторов называются компланарными

, если они лежат в одной плоскости .

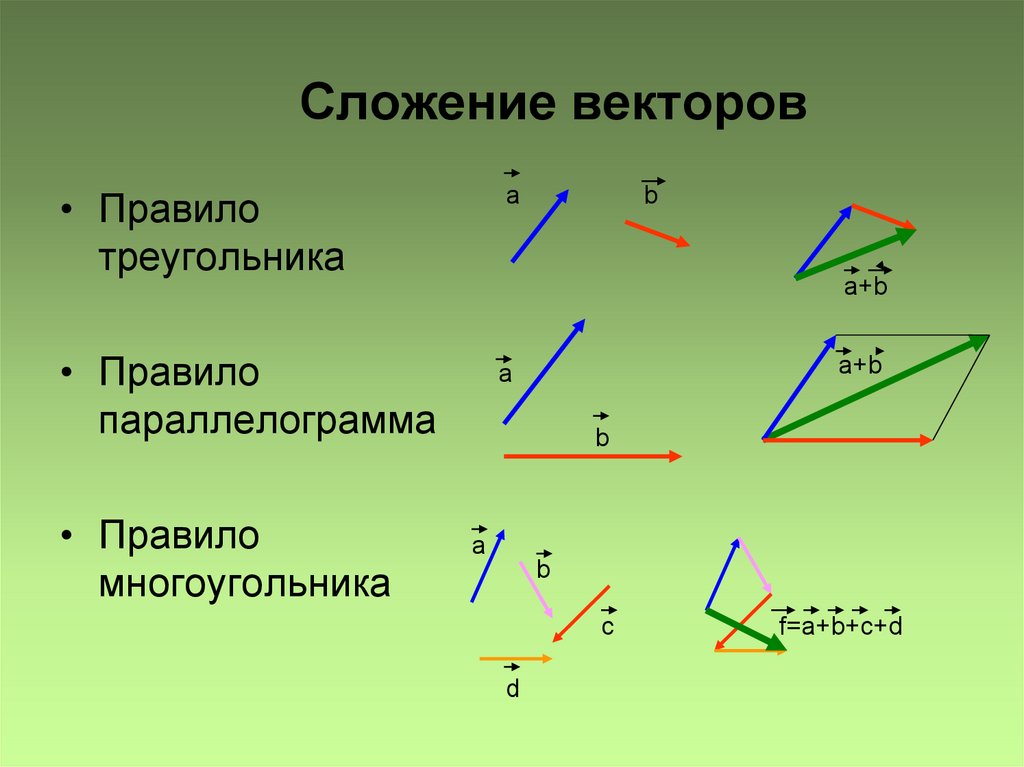
Сложение векторов. Так как векторы — это направленные отрезки, то их сложение может быть выполнено геометрически .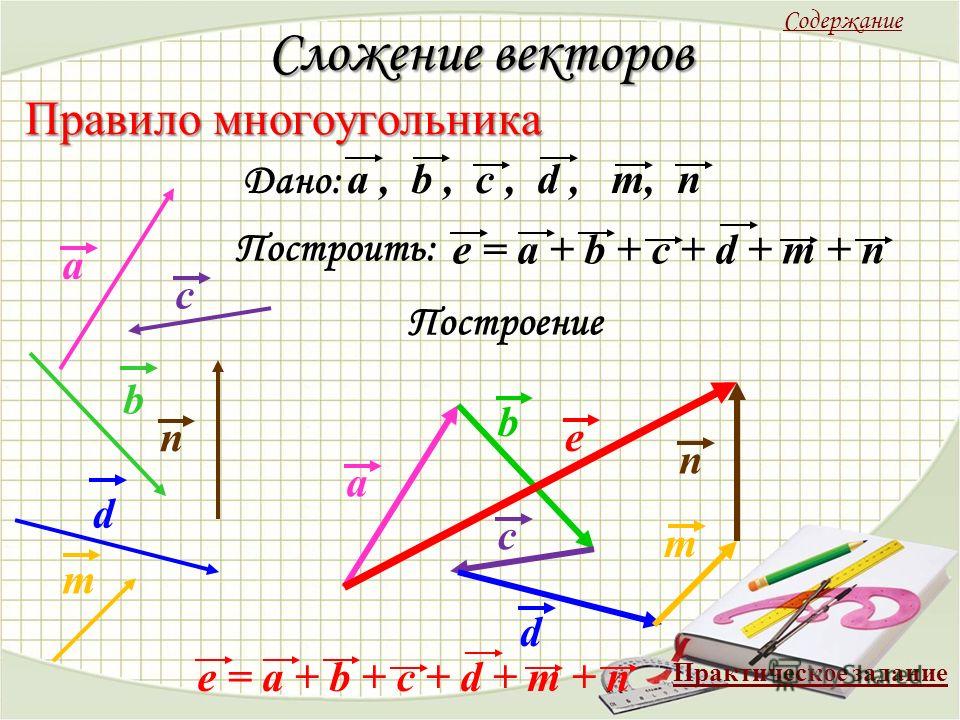 (Алгебраическое сложение векторов изложено ниже, в пункте «Единичные ортогональные векторы»). Предположим , что

__                  __

a = AB and b =

CD ,

тогда вектор __ __

a + b = AB + CD

есть результат выполнения двух операций:

a ) параллельного переноса одногоиз векторов таким образом, чтобы его начальная точка совпала с конечной точкой второго вектора;

б ) геометрического сложения , т.е. построения результирующего вектора, идущего от начальной точки неподвижного вектора к конечной точке перенесённого вектора .

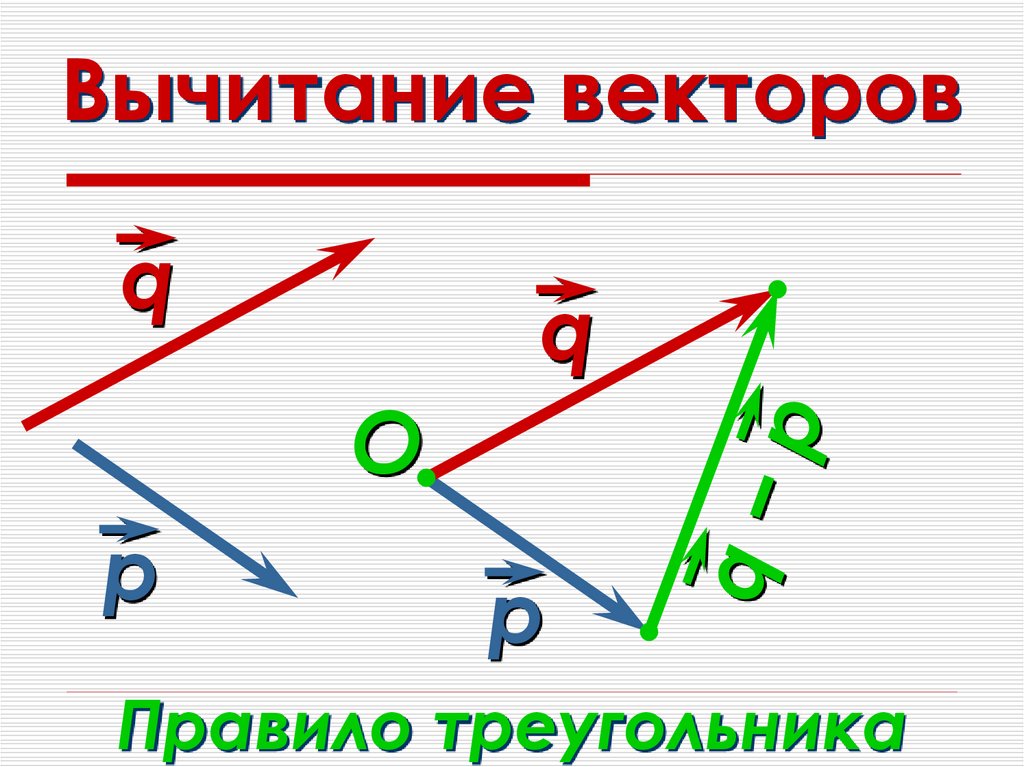
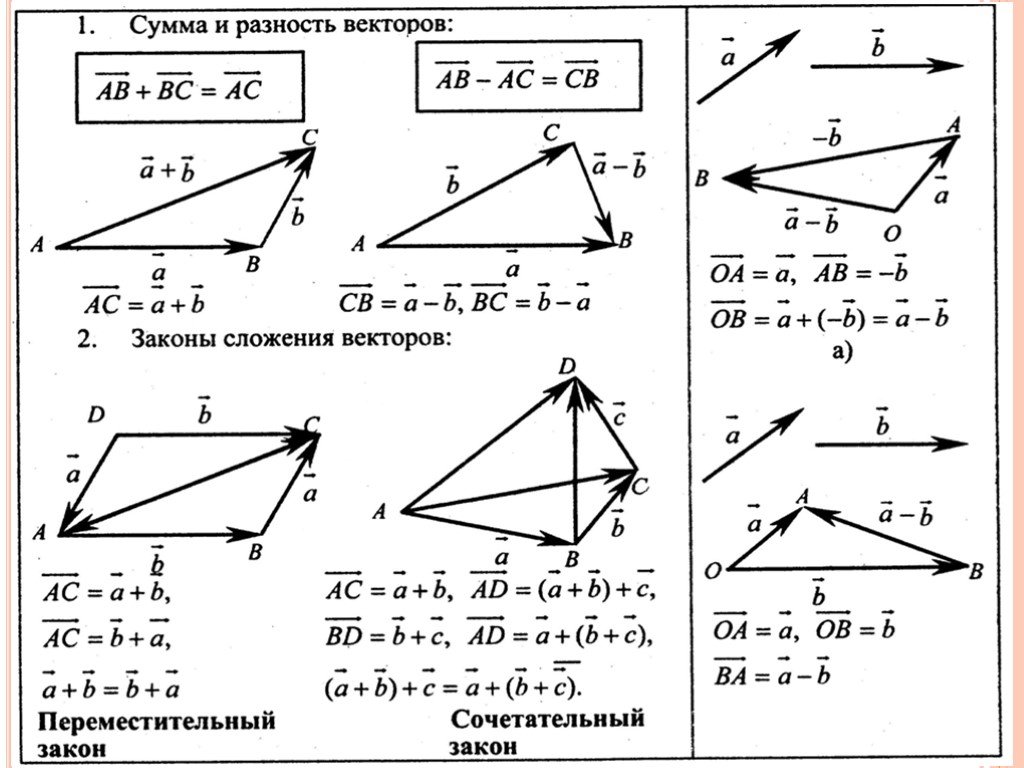
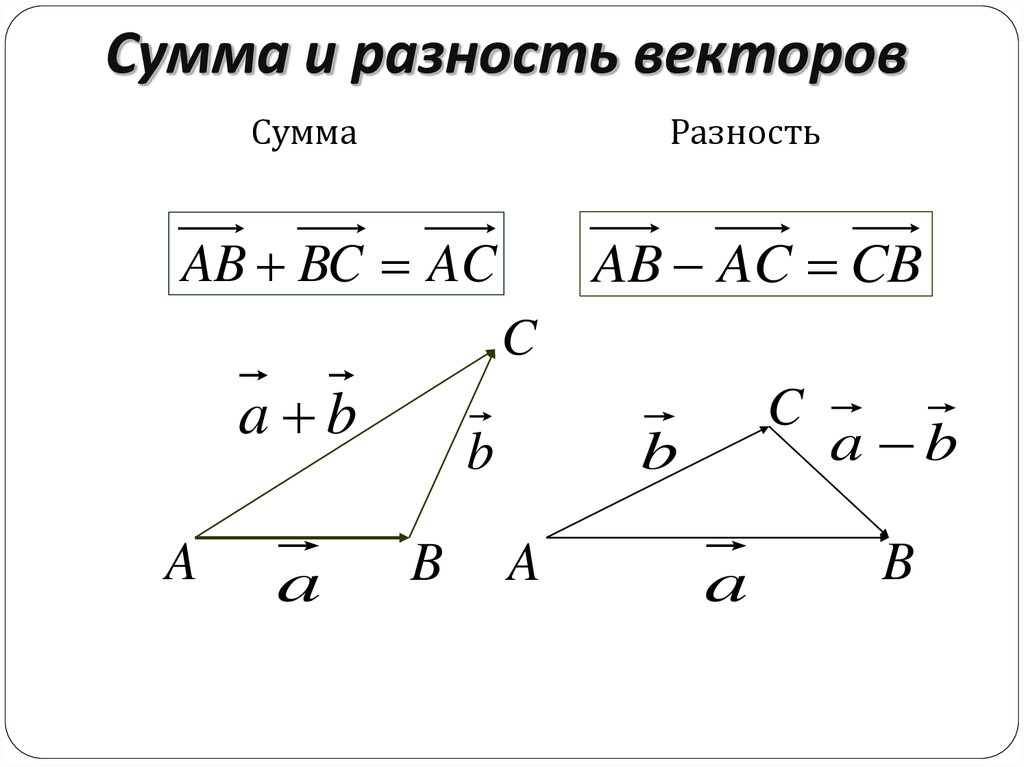
Вычитание векторов. Эта операция сводится к предыдущей путём замены вычитаемого вектора на противоположный: a – b = a + ( – b ) .

Законы сложения .

I .

a + b = b + a ( П е р е м е с т и т е л ь н ы й   закон ).

II . ( a + b ) + c = a + ( b + c )  ( С о ч е т а т е л ь н ы й   закон ).

III . a + 0 = a .

IV. a + ( – a ) = 0 .

Законы умножения вектора на число.

I. 1 · a = a ,

0 · a = 0 , m · 0 = 0 ,  ( – 1 ) · a = – a .

II.     m a = a m , | m a | = | m

| · | a | .

III . m ( n a ) = ( m n ) a . ( С о ч е т а т е л ь н ы й

закон умножения на число ).

IV . ( m + n ) a = m a + n a

, ( Р а с п р е д е л и т е л ь н ы й

m ( a + b ) = m a + m b . закон умножения на число ).

Скалярное произведение векторов . __     __

Угол между ненулевыми векторами AB и CD – это угол, образованный векторами при их параллельном переносе до совмещения точек A и C . Скалярным произведением векторов a и b называется число, равное произведению их длин на косинус угла между ними:

Если один из векторов нулевой, то их скалярное произведение в соответствии с определением равно нулю:

( a ,

0 ) = ( 0 , b ) = 0 .

Если оба вектора ненулевые, то косинус угла между ними вычисляется по формуле :

Скалярное произведение ( a , a ), равное | a | 2 , называется скалярным квадратом. Длина вектора a

и его скалярный квадрат связаны соотно шением:

Скалярное произведение двух векторов:

— положительно , если угол между векторами острый ;

— отрицательно, если угол между векторами тупой .

Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда угол между ними прямой, т.е.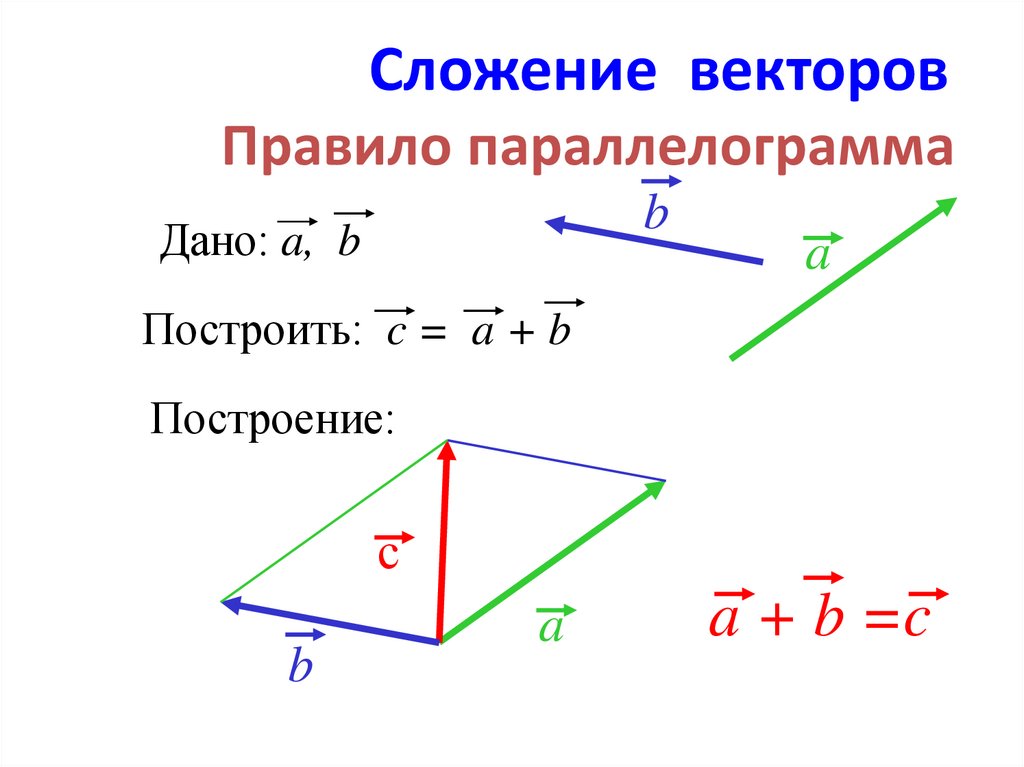 когда эти векторы перпендикулярны (ортогональны):

Свойства скалярного произведения. Для любых векторов a , b , c и любого числа m справедливы следующие соотношения:

I . ( a , b ) = ( b , a ) . ( П е р е м е с т и т е л ь н ы й   закон )

II . ( m a , b ) = m ( a , b ) .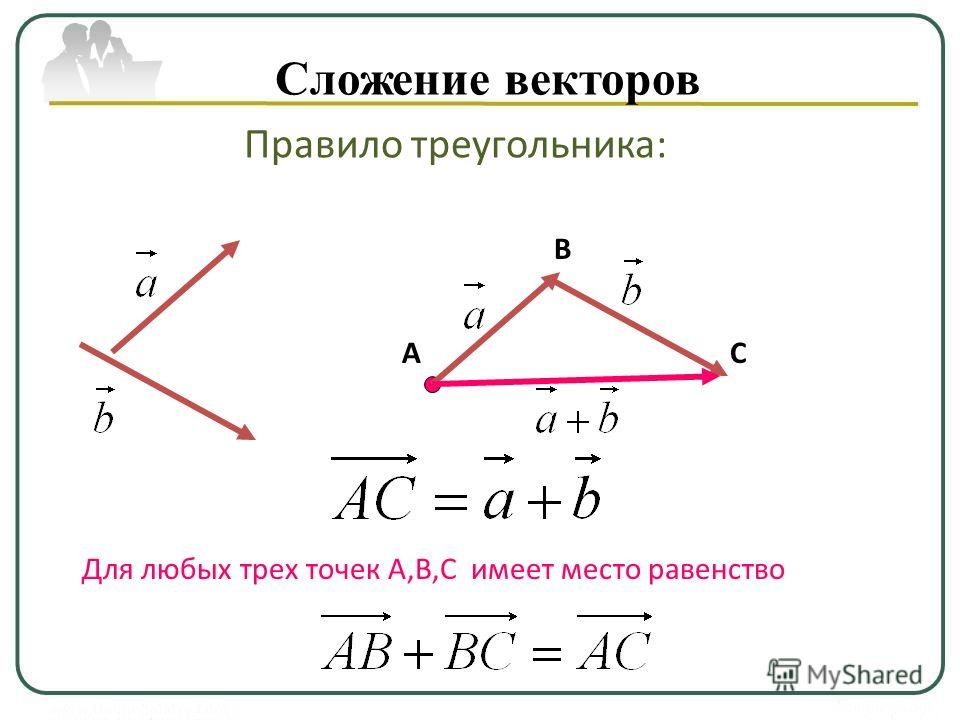

III . ( a + b , c ) = ( a , c ) + ( b , c ) . ( Р а с п р е д е л и т е л ь н ы й   закон )

Единичные ортогональные векторы. В любой прямоугольной системе координат можно ввести единичные попарно ортогональные векторы i , j и k ,  связанные с координатными осями: i – с осью Х , j – с осью Y и k – с осью Z .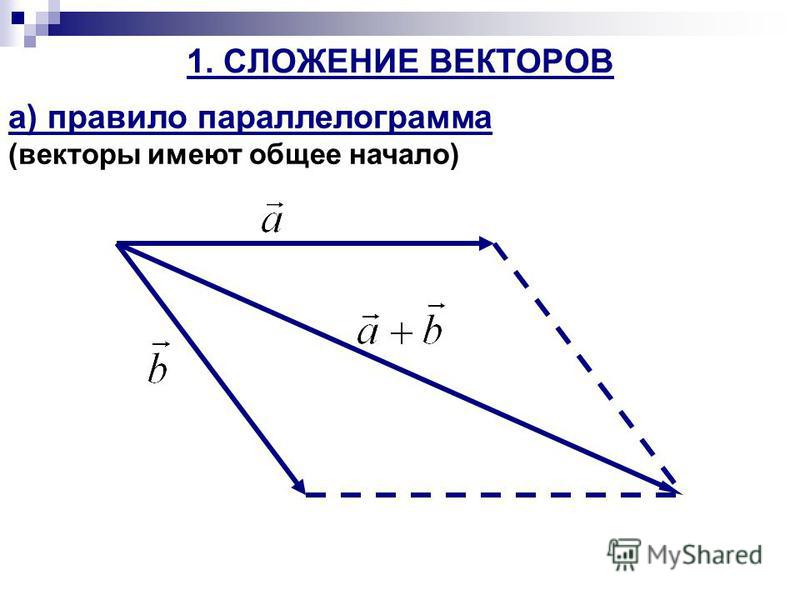 В соответствии с этим определением:

( i , j ) = ( i , k ) = ( j , k ) = 0,

| i | = | j | = | k | = 1.

Любой вектор a может быть выражен через эти векторы единственным образом: a = x i + y j + z k . Другая форма записи : a = ( x, y, z ). Здесь x , y , z — координаты вектора a в этой системе координат. В соответствии с последним соотношением и свойствами единичных ортогональных векторов i , j , k скалярное произведение двух векторов можно выразить иначе.

Пусть a = ( x , y , z ) ; b = ( u , v , w ) . Тогда ( a , b ) = xu + yv + zw .

Скалярное произведение двух векторов равно сумме произведений соответствующих координат.

Длина (модуль) вектора a = ( x , y , z ) равна:


Кроме того, теперь мы получаем возможность проведения алгебраических операций над векторами, а именно, сложение и вычитание векторов может выполняться по координатам :

a + b = ( x + u , y + v , z + w ) ;

a – b = ( x – u , y – v , z – w ) .

Векторное произведение векторов. Векторным произведением [ a ,

b ] векторов a и b ( в указанном порядке )  называется вектор:


Существует другая формула длины вектора [ a, b ] :

/\

| [ a, b ] | = | a | | b |  sin ( a, b ) ,

т. e . длина ( модуль )  векторного произведения векторов a и b равна произведению длин ( модулей ) этих векторов на синус угла между ними. Иначе говоря: длина ( модуль ) вектора [ a , b ] численно равна площади параллелограмма, построенного на векторах a и b .

Свойства векторного произведения .

I . Вектор [ a , b ] перпендикулярен (ортогонален) обоим векторам a и b .

( Докажите это , пожалуйста ! ) .

II. [ a , b ] = – [ b , a ] .

III. [ m a , b ] = m [ a , b ] .

IV. [ a + b , c ] =  [ a , c ] + [ b , c ] .

V. [ a , [ b , c ] ] = b ( a , c ) – c ( a , b ) .

VI.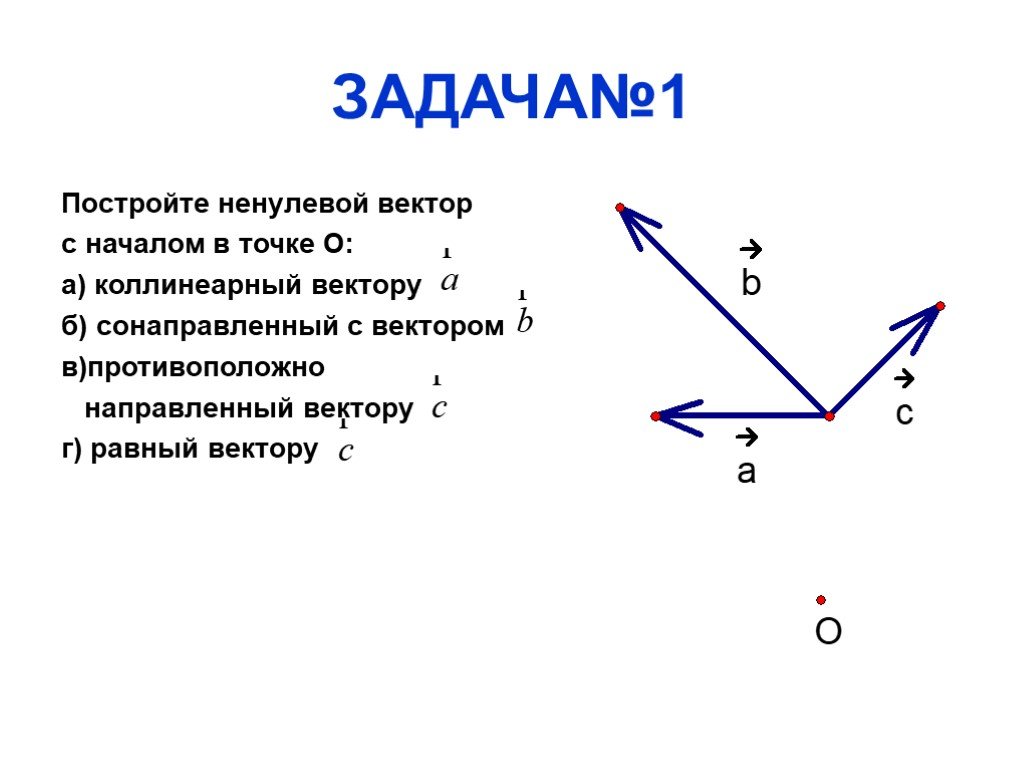 [ [ a , b ] , c ] = b ( a , c ) – a ( b , c ) .

Необходимое и достаточное условие коллинеарности векторов

a = ( x , y , z )  и b = ( u, v, w ) :

Необходимое и достаточное условие компланарности векторов a = ( x, y, z ), b = ( u, v, w ) и c = ( p, q, r ) :


П р и м е р . Даны векторы: a = ( 1, 2, 3 ) и b = ( – 2 , 0 ,4 ).

Вычислить их скалярное и векторное произведения и угол

между этими векторами.

Р е ш е н и е . Используя соответствующие формулы (см. выше), получим:

a ). скалярное произведение:

( a , b ) = 1 · ( – 2 ) + 2 · 0 + 3 · 4 = 10 ;

б). векторное произведение:

Назад

ВЕКТОР А

  • Состав: 93% Мета-арамид 5% Пара-арамид 2% Антистатика
  • Поверхн. плотность: 210 г/м2
  • Ширина: 150 см
  • Переплетение: саржа

ВЕКТОР – группа термостойких арамидных тканей с огнезащитными, антиэлектростатическими и НМВО свойствами для производства спецодежды работающих в нефтяных компаниях. Торговый Дом Текстиль — разработчик и владелец технического задания на изготовление термостойких тканей ВЕКТОР А, ВЕКТОР AL. Компания ООО «Торговый Дом Текстиль» выступает гарантом защитных, эксплуатационных, гигиенических и экологических свойств тканей группы ВЕКТОР в промышленных партиях.

ВЕКТОР А:

Организована и успешно функционирует многоуровневая система контроля качества термостойких тканей группы ВЕКТОР: 

  1. на производстве, на каждой стадии производственного процесса; 
  2. аккредитованными российскими лабораториями; 
  3. службой входного контроля ООО «Торговый Дом Текстиль».

Для защиты от контрафакта запланировано в конце III квартала 2018 года введение технологического процесса нанесения принтерной печати на изнаночную сторону материалов: названия тканей ВЕКТОР А, ВЕКТОР AL и логотипа компании ООО «Торговый Дом Текстиль».

Термостойкие арамидные ткани ВЕКТОР А сертифицированы и поставляются в промышленных масштабах для изготовления летней и зимней огнестойкой спецодежды.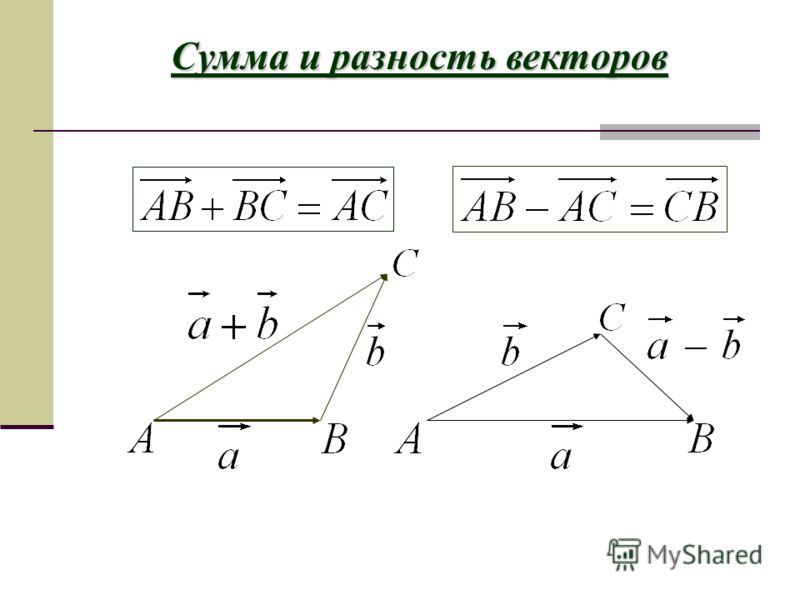

  • ГОСТ 11209-2014
  • ГОСТ 12.4.310-2016
  • ГОСТ 12.4.124-83
  • ГОСТ Р ЕН 1149-5-2008
  • ГОСТ ISO 11612-2014
  • ГОСТ ISO 14116-2016
  • Технический регламент таможенного союза 019/2011

    Карта цветов

    Рекомендации по уходу

    В этой же группе

    • ВЕКТОР АL
    • Плотность: 180 г/м2

    Создание, изменение и доступ к векторным элементам

    В этой статье вы узнаете о векторах в программировании на R. Вы научитесь создавать их, получать доступ к их элементам с помощью различных методов и изменять их в своей программе.

    Вектор — это базовая структура данных в R. Она содержит элементы того же типа. Типы данных могут быть логическими, целочисленными, двойными, символьными, сложными или необработанными.

    Тип вектора можно проверить с помощью функции typeof() .

    Еще одним важным свойством вектора является его длина. Это количество элементов в векторе, и его можно проверить с помощью функции 9.0007 длина() .

    Как создать вектор в R?

    Векторы обычно создаются с помощью функции c() .

    Так как вектор должен иметь элементы одного типа, эта функция попытается привести элементы к одному типу, если они разные.

    Приведение от младших к более высоким типам от логического к целому к двойному к символьному.

     > х <- с(1, 5, 4, 9, 0)
> тип(х)
[1] «двойной»
> длина (х)
[1] 5
> x <- c(1, 5. 4, ИСТИНА, "привет")
> х
[1] «1» «5.4» «ИСТИНА» «привет»
> тип(х)
[1] "персонаж"

    Если мы хотим создать вектор последовательных чисел, очень полезен оператор : .

    Пример 1: Создание вектора с помощью: оператора 
     > х <- 1:7; Икс
[1] 1 2 3 4 5 6 7
> у <- 2:-2; у
[1] 2 1 0 -1 -2

    Более сложные последовательности могут быть созданы с помощью функции seq() , например определения количества точек в интервале или размера шага.

    Пример 2. Создание вектора с помощью функции seq() 
     > seq(1, 3, by=0.2) # указать размер шага
[1] 1,0 1,2 1,4 1,6 1,8 2,0 2,2 2,4 2,6 2,8 3,0
> seq(1, 5, length.out=4) # указать длину вектора
[1] 1,000000 2,333333 3,666667 5,000000

    Как получить доступ к элементам вектора?

    Доступ к элементам вектора можно получить с помощью векторной индексации. Вектор, используемый для индексации, может быть логическим, целочисленным или вектором символов.

    Использование целочисленного вектора в качестве индекса

    Индекс вектора в R начинается с 1, в отличие от большинства языков программирования, где индекс начинается с 0.

    Мы можем использовать вектор целых чисел в качестве индекса для доступа к определенным элементам.

    Мы также можем использовать отрицательные целые числа, чтобы вернуть все элементы, кроме указанных.

    Но мы не можем смешивать положительные и отрицательные целые числа, в то время как индексация и действительные числа, если они используются, усекаются до целых чисел.

     > х
[1] 0 2 4 6 8 10
> x[3] # доступ к третьему элементу
[1] 4
> x[c(2, 4)] # доступ ко 2-му и 4-му элементам
[1] 2 6
> x[-1] # доступ ко всем элементам, кроме 1-го
[1] 2 4 6 8 10
> x[c(2, -4)] # нельзя смешивать положительные и отрицательные целые числа
Ошибка в x[c(2, -4)]: только 0 могут быть смешаны с отрицательными нижними индексами
> x[c(2.4, 3.54)] # действительные числа усекаются до целых
[1] 2 4

    Использование логического вектора в качестве индекса

    Когда мы используем логический вектор для индексации, возвращается позиция, где логический вектор равен TRUE .

    Эта полезная функция помогает нам фильтровать вектор, как показано ниже.

     > х[с(ИСТИНА, ЛОЖЬ, ЛОЖЬ, ИСТИНА)]
[1] -3 3
> x[x < 0] # фильтрация векторов по условиям
[1] -3 -1
> х [х > 0]
[1] 3

    В приведенном выше примере выражение x>0 даст логический вектор (ЛОЖЬ, ЛОЖЬ, ЛОЖЬ, ИСТИНА) , который затем используется для индексации.

    Использование вектора символов в качестве индекса

    Этот тип индексации полезен при работе с именованными векторами. Мы можем назвать каждый элемент вектора.

     > x <- c("первый"=3, "второй"=0, "третий"=9)
> имена(х)
[1] "первый" "второй" "третий"
> х["секунда"]
второй
0
> х[с("первый", "третий")]
первая треть
3 9

    Как изменить вектор в R?

    Мы можем изменить вектор с помощью оператора присваивания.

    Мы можем использовать методы, описанные выше, для доступа к определенным элементам и их модификации.

    Если мы хотим обрезать элементы, мы можем использовать переназначения.

     > х
[1] -3 -2 -1 0 1 2
> х[2] <- 0; x # изменить 2-й элемент
[1] -3 0 -1 0 1 2
> х[х<0] <- 5; x # изменить элементы меньше 0
[1] 5 0 5 0 1 2
> х <- х[1:4]; x # обрезать x до первых 4 элементов
[1] 5 0 5 0

    Как удалить вектор?

    Мы можем удалить вектор, просто назначив NULL к нему.

     > х
[1] -3 -2 -1 0 1 2
> х <- NULL
> х
НУЛЕВОЙ
> х[4]
НУЛЕВОЙ
    • ПРЕДЫДУЩАЯ
      Функция R switch()
    • СЛЕДУЮЩИЙ
      R Матрица

    Легкий, сверхбыстрый инструмент для создания конвейеров для наблюдения

    Vector | Легкий, сверхбыстрый инструмент для построения пайплайнов наблюдаемости. Версия Vector 0.28.1

    Легкий и сверхбыстрый инструмент для построения конвейеров наблюдаемости

    Быстрый старт

    Язык векторного преобразования

    Компоненты

    Собирайте, преобразовывайте и маршрутизируйте все ваши журналы и показатели с помощью одного простого инструмента.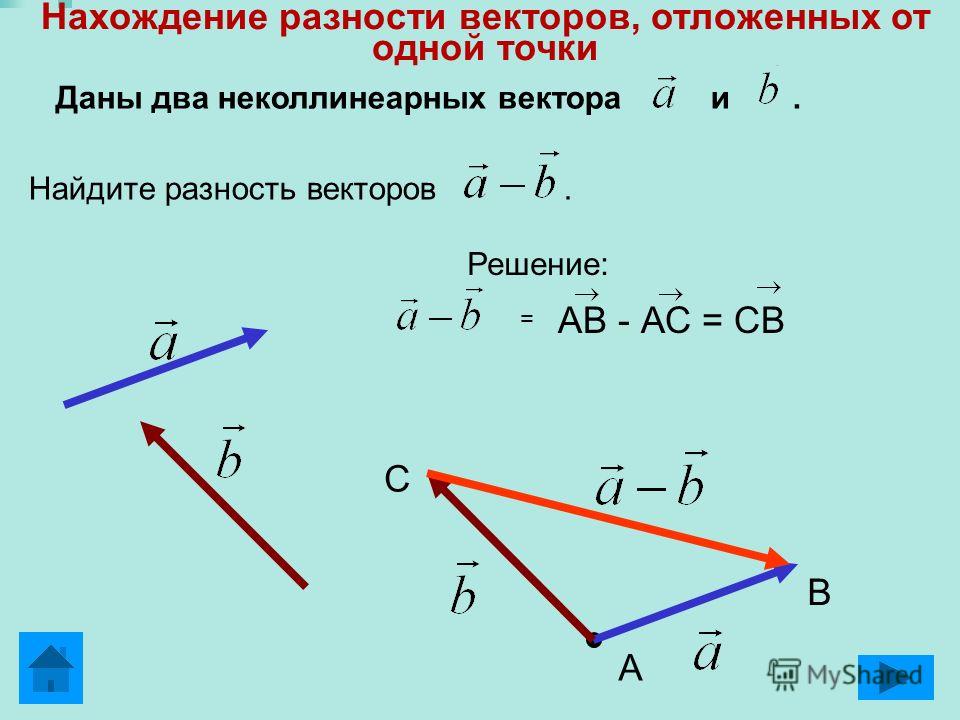

    Сверхбыстрый и надежный

    Построенный на Rust, Vector невероятно быстр, эффективно использует память и предназначен для обработки самых ресурсоемких рабочих нагрузок.

    От начала до конца

    Vector стремится быть единственным инструментом, который вам нужен для получения данных о наблюдаемости от A до B, развертывая его в качестве демона, вспомогательной машины или агрегатора.

    Unified

    Vector поддерживает журналы и метрики, упрощая сбор и обработку всех ваших данных для наблюдения.

    Нейтральный поставщик

    Компания Vector не отдает предпочтение платформам каких-либо конкретных поставщиков и создает честную и открытую экосистему с учетом ваших интересов. Блокировка бесплатно и будущее.

    Программируемые преобразования

    Гибко настраиваемые преобразования Vector предоставляют вам всю мощь программируемых сред выполнения. Обрабатывайте сложные варианты использования без ограничений.

    Четкие гарантии

    Гарантии имеют значение, и компания Vector четко указывает, какие гарантии она предоставляет, помогая вам сделать правильный выбор для вашего варианта использования.

    Разверните Vector в различных ролях в соответствии с вашим вариантом использования.
    Перемещение данных из точки А в точку Б без объединения инструментов.

    Узнайте больше о топологии распределенного развертывания для Vector

    Узнайте больше о топологии централизованного развертывания для Vector

    Узнайте больше о топологии развертывания на основе потоков для Vector

    Простой компонуемый формат позволяет создавать гибкие конвейеры

    /etc/vector/vector.toml

    Примеры конфигурации представлены в формате TOML, но Vector также поддерживает YAML и JSON

    Упакован в виде одного двоичного файла. Никаких зависимостей, времени выполнения и безопасности памяти.

    Одиночный двоичный файл

    X86_64, ARM64/v7

    Без среды выполнения

    Сейф для памяти

    Установка в одну строку:

    • Для людей
    • Для машин
     curl --proto '=https' --tlsv1.2 -sSf https://sh.vector.dev | bash 
     curl --proto '=https' --tlsv1.2 -sSf https://sh.vector.dev | bash -s -- -y

    Или выберите предпочтительный метод:

    Платформы

    Менеджеры пакетов

    Операционные системы

    Руководство

    Широкий выбор источников, преобразований и приемников

    4 источники

    AMQP Метрики Apache Показатели AWS ECS AWS Kinesis Firehose АВС S3 АМС SQS Агент Datadog Демонстрационные журналы днстап Журналы докера

    13 преобразовывает

    Remap с VRL Совокупность Метаданные AWS EC2 Дедупликация Фильтр Войти в метрику Луа Метрика для регистрации Уменьшать Маршрут

    48 раковины

    AMQP Журналы AWS Cloudwatch Показатели AWS Cloudwatch Журналы AWS Kinesis Data Firehose Журналы AWS Kinesis Streams АВС S3 АМС SQS Аксиома Хранилище BLOB-объектов Azure Журналы Azure Monitor

    7,4 тыс.

    alexxlab

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *