Обратный и дополнительный коды числа
Назначение сервиса. Онлайн-калькулятор предназначен для представления чисел в обратном и дополнительном коде.- Решение онлайн
- Видеоинструкция
- Также решают
Число
Найти: прямой код обратный код дополнительный код
Вместе с этим калькулятором также используют следующие:
Операции с двоичными числами (сложение и вычитание)
Умножение двоичных чисел
Формат представления чисел с плавающей запятой
Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1.3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M

Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp103
Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
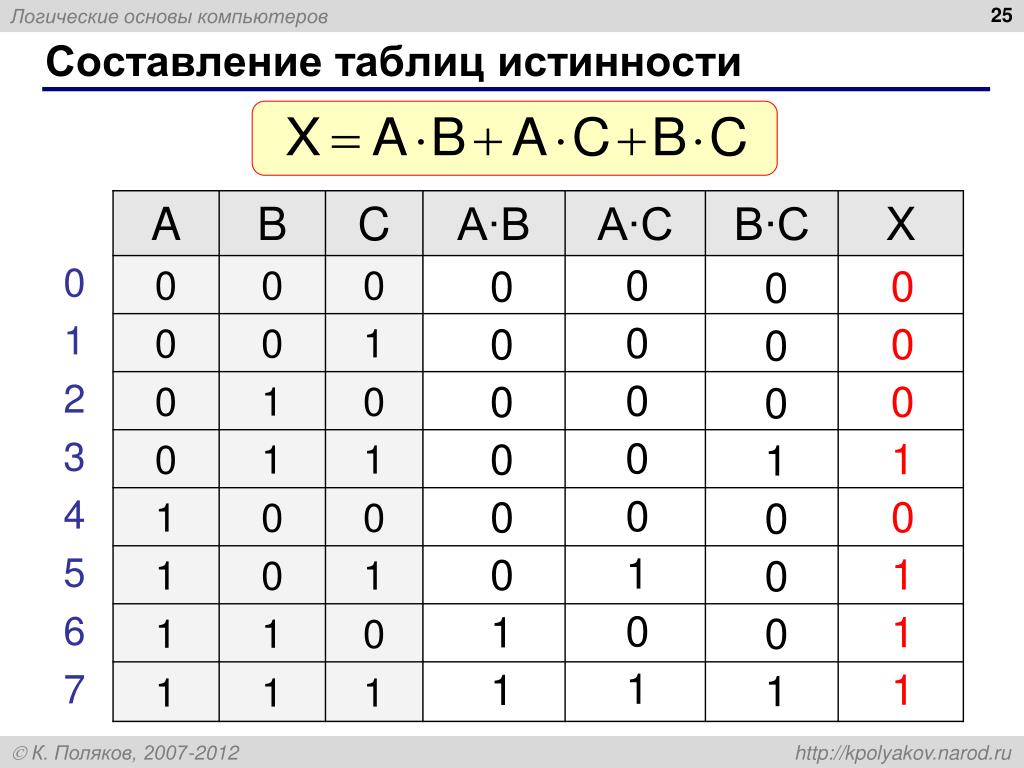
Таблица истинности
Алгебра и геометрия
Целые числа в ЭВМ могут быть представлены в виде:- прямого кода. Прямой код двоичного числа совпадает по изображению с записью самого числа.
- обратного кода
- дополнительного кода. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.

Прямой код числа кодирует только знаковую информацию и используется для хранения положительных и отрицательных чисел в ЭВМ. Прямой код двоичного числа совпадает по изображению с записью самого числа, но в знаковом разряде ставится 0, если число положительное и, 1 если число отрицательное.
Следует помнить, что положительные числа в обратном и дополнительном коде совпадают с прямым кодом.
1) Прямой код числа (кодируется только знаковая информация), “+”=0; ”-”=1.
Для прямого кода возможны два представления нуля, машинный положительный ноль, т.е. +0,110=0,110, машинный отрицательный ноль, т.е. -0,111=1,111.
Пример перевода
x1=10101-[x1
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение.
 Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
Пример перевода
x2=-11101-[x2]обр=100010
x3=0,101-[x3]обр=0,101
x4=-0,111-[x4]обр=1,000
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x1
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т.

Как определить, положительное или отрицательное число? Знак числа определяет старший бит: 0 — положительное число, 1 — отрицательное число. Например, для числа 1,001 сразу можно определить, что оно отрицательное (меньше нуля).
Пример. Представить в дополнительном коде десятичные числа: -4.
Решение. Представим число в двоичном коде.
4 = 00001002
Инвертируем все разряды числа, а в знаковый разряд заносим 1
.
Добавляем к младшему разряду
1.
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 |

| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 |
| 7 | | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Число -4 представляется в двоичном дополнительном коде как
11111100
Алгебра логики и таблицы истинности.
 (лекция 4)
(лекция 4)Похожие презентации:
Основы логики. Таблица истинности. Равносильные логические выражения
Алгебра логики
Основные понятия алгебры логики
Логические операции и таблицы истинности
Логика высказываний. Таблицы истинности
Алгебра логики
Построение таблиц истинности для логических выражений
Логические основы компьютера. Формы человеческого мышления. Формальная логика
Логика высказываний
Элементы алгебры логики. Математические основы информатики. Таблицы истинности
1. Алгебра логики и таблицы истинности
Лекция № 42. Основные понятия
Логика — это наука о формах и способах мышления. Этоучение о способах их рассуждений и доказательств.
Понятие — это форма мышления, которая выделяет
существенные признаки предмета или класса предметов,
позволяющие отличать их от других.
Высказывание — это формулировка своего понимания
окружающего
мира.

Высказывание
является
повествовательным предложением, в котором что-либо
утверждается или отрицается.
Умозаключение — это форма мышления, с помощью которой
из одного или нескольких суждений может быть получено
новое суждение (знание или вывод).
Логическая переменная — это простое высказывание,
содержащее только одну мысль.
Ее символическое обозначение — латинская буква (например,
A,B,X,Y и т.д.).
Значением логической переменной могут быть только
константы ИСТИНА и ЛОЖЬ (1 и 0).
Составное высказывание — логическая функция, которая
содержит несколько простых мыслей, соединенных между
собой с помощью логических операций.
Ее символическое обозначение — F(A, B…)
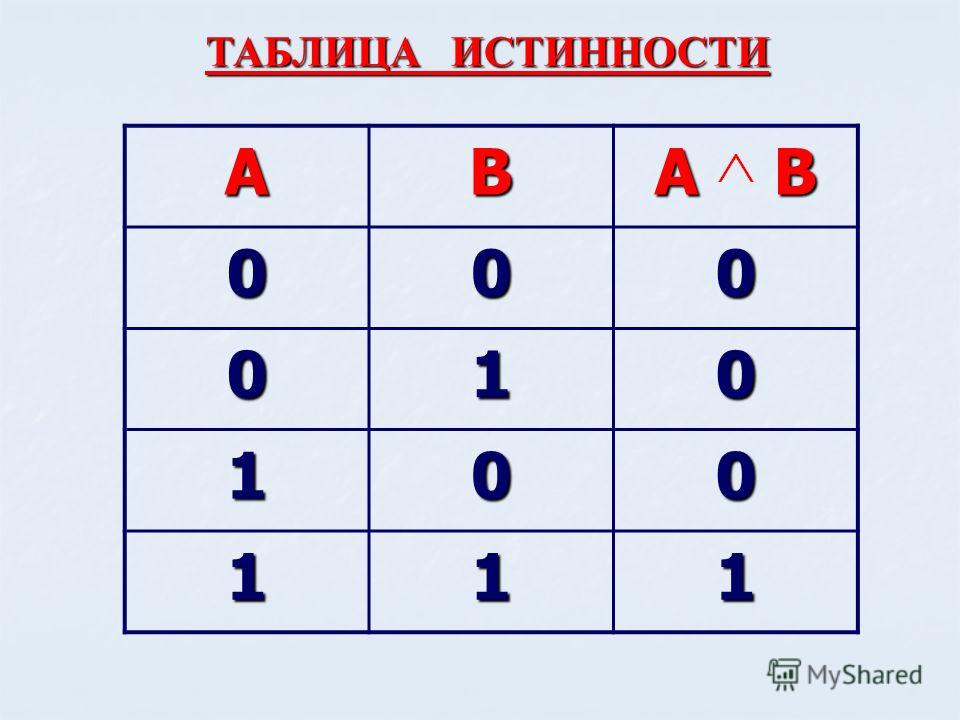
5. Логические связки
A№ Логическая
связка
Название
Обозначение
Высказывание
Математическая
запись
1
и
конъюнкция
логическое умножение
,
*, And
AиВ
A B,
A * B,
2
или
дизъюнкция
логическое сложение
+, Or
A или В
A B
A + B,
A Or B
3
не
инверсия,
логическое отрицание
¬,
Not
не А
¬А,
Not A
4
Если…то
импликация,
логическое следование
→,
Если A, то В
A→B
A B
5
тогда и
только
тогда
эквивалентность,
равносильность,
логическое тождество
,
,
А тогда и
только
тогда, когда
В
А В,
А В,
A B
A And B
А В
А В
6.
 В
ВДизъюнкция
А
В
AvB
Инверсия
А
¬А
Импликация
Эквивалентность
А
В А→В
А
В
А≡В
0
0
0
0
0
0
0
0
1
0
0
1
0
1
0
0
1
1
0
1
0
1
1
0
1
0
1
0
0
1
0
1
1
0
0
1
0
0
1
1
1
1
1
1
1
0
1
1
1
1
1
1
Вывод:
резу- Вывод: результат Вывод: результат Вывод: результат Вывод:
результат
льтат будет ис- будет ложным тог- будет
ложным, будет ложным тог- будет истинным тогтинным тогда и да и только тогда, если исходное
да и только тогда, да и только тогда,
только
тогда, когда оба исход- выражение
ис- когда из истинного когда оба высказыкогда оба исхо- ных высказывания тинно, и наоборот основания (А) сле- вания одновременно
дных высказы- ложны, и истиндует ложное след- либо ложны, либо
вания истинны ным в остальных
ствие (В)
истинны
случаях
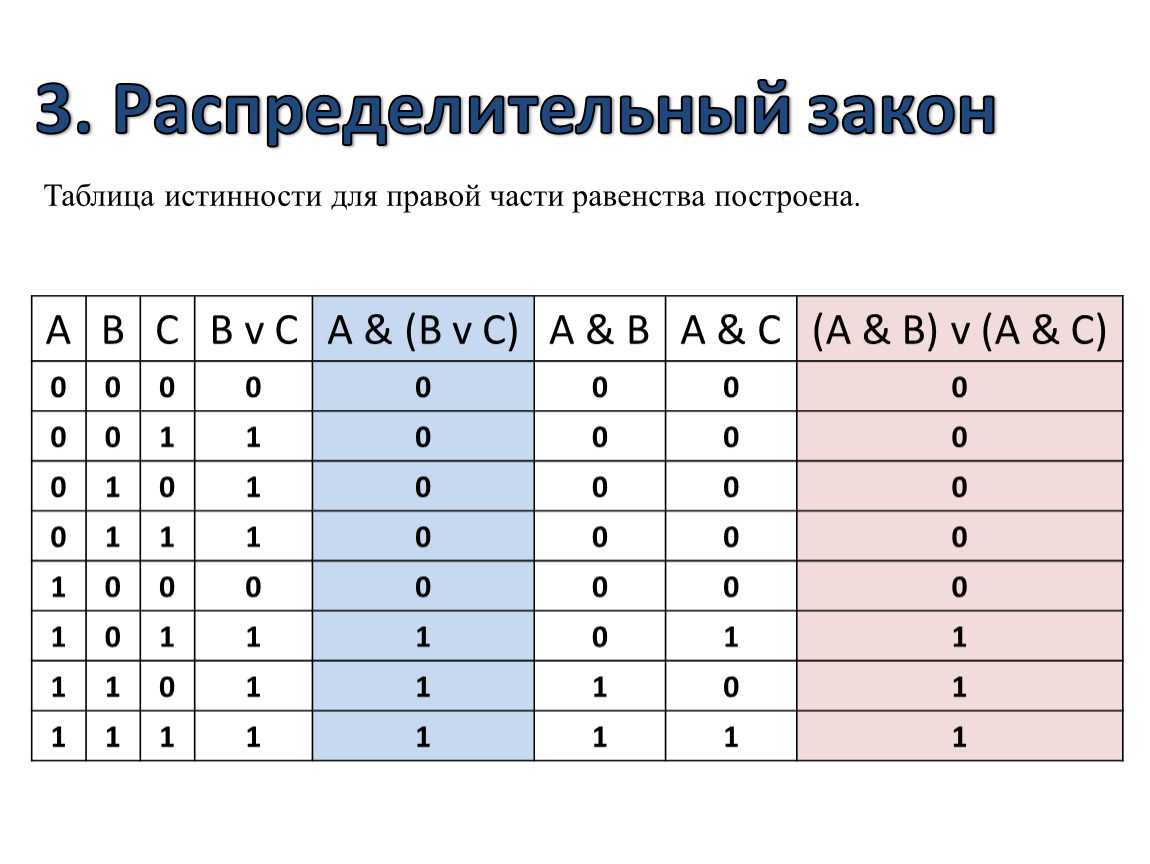
Если составное высказывание (логическую функцию)
выразить в виде формулы, в которую войдут логические
переменные и знаки логических операций, то получится
логическое выражение, значение которого можно
вычислить.
 ), дизъюнкция (v),
), дизъюнкция (v),импликация (→), эквивалентность (≡).
9. Для составления таблицы необходимо:
1.2.
3.
4.
5.
Выяснить количество строк в таблице (вычисляется как
2n+1, где n — количество переменных).
Выяснить количество столбцов = количество переменных
+ количество логических операций.
Установить последовательность выполнения логических
операций.
Построить таблицу, указывая названия столбцов и
возможные наборы значений исходных логических
переменных.
Заполнить таблицу истинности по столбцам.
10. Пример 1
Построим таблицу истинности для выражения F = (AvB)&(¬Av¬B).Количество строк = 22 (2 переменных) + 1(заголовки столбцов) = 5.
Количество столбцов = 2 логические переменные (А, В) + 5 логических
операций (v, &, ¬, v, ¬) = 7.
Расставим порядок выполнения операций: 1 5 2 4 3
(AvB)&(¬Av¬B)
А
В
AvB
¬А
¬В
¬Av¬B
(AvB)&(¬Av¬B)
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
11.
 Логические схемыЭлементы, реализующие базовые логические операции,
Логические схемыЭлементы, реализующие базовые логические операции,назвали
базовыми
логическими
элементами
или
вентилями и характеризуются они не состоянием
контактов, а наличием сигналов на входе и выходе
элемента.
Их
названия
и
условные
обозначения
являются
стандартными и используются при составлении и
описании логических схем компьютера.
13. Правило построение логических схем
1) Определить число логических переменных.2) Определить количество базовых логических
операций и их порядок.
3) Изобразить для каждой логической операции
соответствующий ей вентиль.
4)Соединить вентили в порядке выполнения
логических операций.
14. Пример 2
Пусть X = истина, Y = ложь. Составитьлогическую схему для следующего
логического выражения: F = XvY&X.
Две переменные — X и Y.
2 1
Две логические операции: XvY&X.
15. Задание 1.
Составьте таблицы истинности дляследующих логических
выражений:
1.
 F = (X&¬Y)vZ.
F = (X&¬Y)vZ.2. F = X&YvX.
3. F = ¬(XvY)&(YvX).
4. F = ¬((XvY)&(ZvX))&(ZvY).
5. F = A&B&C&¬D.
6. F = (AvB)&(¬BvAvB)
18. Задание 2.
19. Задание 3.
Постройте логическую схему,соответствующую логическому выражению, и
найдите значение логического выражения:
1. F=AvB&¬C, если А=1, В=1, С=1.
2. F=¬(AvB&C), если А=0, В=1, С=1.
3. F= ¬AvB&C, если А=1, В=0, С=1.
4. F=(AvB)&(CvB), если А=0, В=1, С=0.
5. F=¬(A&B&C), если А=0, В=0, С=1.
6. F=(A&B&C)v(B&Cv¬A), если А=1, В=1, С=0.
7. F=B&¬Av¬B&A, если А=0, В=0.
20. Задание 4.
Постройте логические выражения клогическим схемам:
English Русский Правила
[Решено] Таблица истинности для данной логической схемы:
Таблица истинности для данной логической схемы:
A Б С 0 0 0 0 1 1 1 0 0 1 1 1 А Б С 0 0 0 0 1 1 1 0 1 1 1 0 А Б С 0 0 1 0 1 0 1 0 0 1 1 1 А Б С 0 0 1 0 1 0 1 0 1 1 1 0
Опция 4:
| А | Б | С |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Бесплатно
RPMT Тест оптики 1
17,9 тыс. пользователей
пользователей
10 вопросов
40 баллов
10 минут
Понятие:
Здесь мы использовали понятия И и НЕ-И вентилей. (1)
входы A и b, то выход: Y = \(\overline{A.B}\) —— (2)
Вычисление:
Дано:
В этой схеме мы обозначили ее как 1,2,3 часть схемы, имеющую выходы Y1, Y2, 1, Y2, и C 900. из первых двух входных элементов И-НЕ, Y2 = решение для вторых двух входных элементов И-НЕ
C = решение для третьего элемента И, соединяющего оба элемента И-НЕ как два входа
Из принципиальной схемы видно, что Y1 = \(\overline{ А.Б}\) —— (3)
и, Y2 = \(\overline{\overline{A}.B}\) —— (4)
Здесь выведите C = Y2.Y1 = \(\overline{A.B}\).\( \overline{\overline{A}.B}\) = \(\overline{\overline{A}.B + AB}\) (по теореме Де Моргана)
Это можно записать как: \(\overline{ (\overline{A} + A)B}\) = \(\overline{1} + \overline{B} = \overline{B}\) (где \(A+ \overline{A} = 1\))
Итак, мы можем записать таблицу истинности как C = \(\overline{B}\) —— (4)
когда B = 0, то C = 1, B = 1, затем C = 0, так что решение совершенно не зависит от A.
Итак, таблица истинности:
| A | Б | С |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
H вариант 4) правильный.
Скачать решение PDFПоделиться в WhatsApp
Последние обновления NEET
Последнее обновление: 28 марта 2023 г.
15 декабря 2022 г. Национальное агентство по тестированию опубликовало уведомление о дате экзамена NEET 2023. Экзамен будет проведен 7 мая 2023 года. Расписание консультаций по национальному вступительному экзамену (NEET) было опубликовано для округов Махараштры, Ассама и Карнатаки. Ознакомьтесь с подробным графиком консультирования NEET на связанной странице.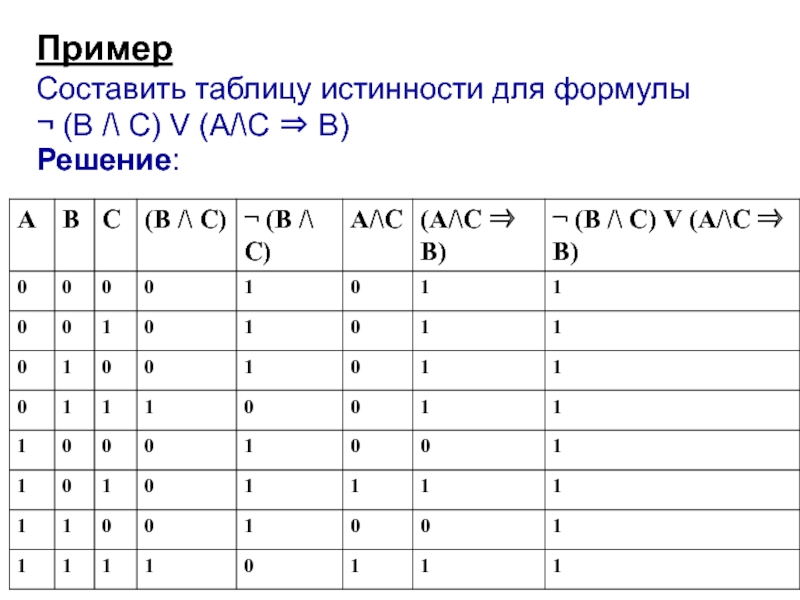 Национальное агентство тестирования (NTA) ежегодно проводит экзамен NEET для поступления в медицинские колледжи. Кандидаты могут проверить свои результаты NEET на официальном сайте NTA. Для официального ключа ответов NEET кандидаты должны пройти шаги, упомянутые здесь.
Национальное агентство тестирования (NTA) ежегодно проводит экзамен NEET для поступления в медицинские колледжи. Кандидаты могут проверить свои результаты NEET на официальном сайте NTA. Для официального ключа ответов NEET кандидаты должны пройти шаги, упомянутые здесь.
Предлагаемые экзамены
Булева алгебра с использованием справочных таблиц (LUT)
Перейти к содержимому Урок 4: Что такое справочная таблица (LUT)?В предыдущей статье мы обсудили основы булевой алгебры, а именно, как работают вентили И, ИЛИ, НЕ, исключающее ИЛИ и И-НЕ. Обсуждалась концепция таблиц истинности . На этой странице мы расширим тему работы таблиц истинности и обсудим более сложные уравнения булевой алгебры.
Во-первых, следует отметить, что все те дискретные логические элементы, которые мы обсуждали ранее (И, ИЛИ и т. д.), на самом деле , а не физически существуют внутри ПЛИС! Однако эти функции можно выполнять. Способ, которым FPGA могут выполнять булевую алгебру, заключается в использовании справочных таблиц (LUT) . Справочная таблица — это отдельный блок функций, который может быть запрограммирован в программе Digital Designer. LUT используют ту же концепцию таблицы истинности, чтобы связать выходные данные с входными данными. Давайте попробуем пример. 9= XOR
д.), на самом деле , а не физически существуют внутри ПЛИС! Однако эти функции можно выполнять. Способ, которым FPGA могут выполнять булевую алгебру, заключается в использовании справочных таблиц (LUT) . Справочная таблица — это отдельный блок функций, который может быть запрограммирован в программе Digital Designer. LUT используют ту же концепцию таблицы истинности, чтобы связать выходные данные с входными данными. Давайте попробуем пример. 9= XOR
Таким образом, логическое уравнение Q = A*B + A’ можно прочитать так: «На выходе Q получается A и B или не A». Давайте посмотрим на таблицу истинности и схему, созданную этим уравнением. Как видно из изображения ниже, для создания этой схемы требуется три вентиля.
| Таблица истинности – A*B + A’ | ||
|---|---|---|
| Вход А | Вход Б | Выход Q |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Таблица истинности в приведенном выше примере имеет два входа (A и B), что означает, что есть четыре возможных выхода. (количество входов). Давайте теперь рассмотрим еще один пример с тремя входами. Вот уравнение, для которого мы собираемся создать таблицу истинности: Q = A + (C*B’). Обратите внимание, что круглые скобки указывают на то, что операция C AND NOT B выполняется до операции ИЛИ.
(количество входов). Давайте теперь рассмотрим еще один пример с тремя входами. Вот уравнение, для которого мы собираемся создать таблицу истинности: Q = A + (C*B’). Обратите внимание, что круглые скобки указывают на то, что операция C AND NOT B выполняется до операции ИЛИ.
| Таблица истинности – A + (C*B’) | |||
|---|---|---|---|
| Вход А | Вход Б | Вход С | Выход Q |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Как упоминалось в начале этой статьи, внутри FPGA фактически не существует дискретных логических элементов. Вместо этого в FPGA используются справочные таблицы или LUT. Цифровой дизайнер запрограммировал LUT для выполнения уравнения булевой алгебры, подобного двум, которые мы видели выше. Как и следовало ожидать, все возможные комбинации логических выражений должны быть запрограммированы в справочной таблице. Я скажу это снова по-другому: Один LUT с 3 входами может составить любое уравнение булевой алгебры, которое вы можете придумать, используя 3 входных сигнала. Удивительно!
Вместо этого в FPGA используются справочные таблицы или LUT. Цифровой дизайнер запрограммировал LUT для выполнения уравнения булевой алгебры, подобного двум, которые мы видели выше. Как и следовало ожидать, все возможные комбинации логических выражений должны быть запрограммированы в справочной таблице. Я скажу это снова по-другому: Один LUT с 3 входами может составить любое уравнение булевой алгебры, которое вы можете придумать, используя 3 входных сигнала. Удивительно!
LUT могут быть разных размеров в зависимости от используемой FPGA, но все они ведут себя одинаково. Не так давно 3-входовые LUT были нормой, но сегодня распространены 4-входовые и даже 5-входовые LUT. Если вам нужно составить более сложное выражение, вы можете просто использовать больше справочных таблиц. LUT являются одним из двух наиболее фундаментальных компонентов FPGA. Одна ПЛИС содержит тысячи таких компонентов. Теперь, когда вы лучше знакомы с этими удивительно универсальными компонентами, пришло время обсудить другой наиболее важный элемент внутри FPGA:
The Flip-Flop (AKA Register)
Примечание для читателя: во многих учебниках и классах будет уделено значительное количество времени обсуждению того, как можно подключить LUT для создания оптимального решения логического выражения.