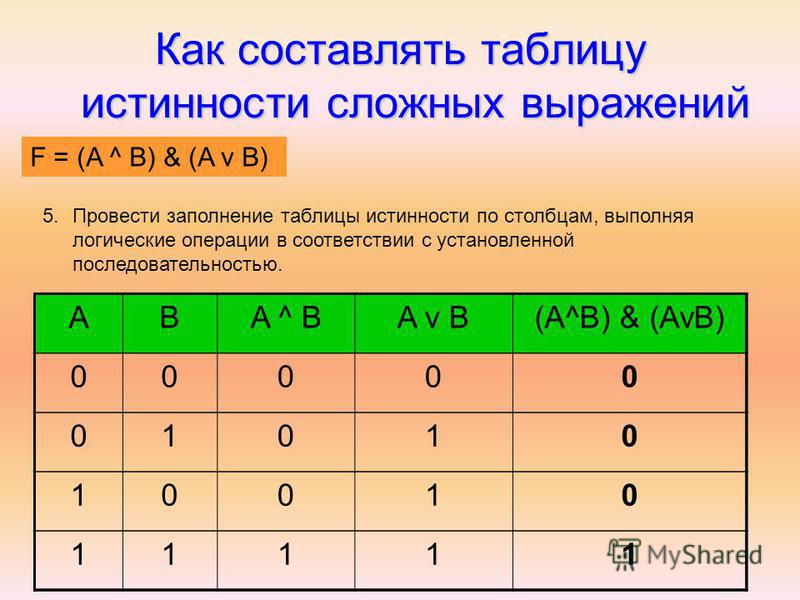
Свойства логических операций. Законы алгебры логики

Похожие презентации:

Пиксельная картинка

Информационная безопасность. Методы защиты информации

Электронная цифровая подпись (ЭЦП)

Этапы доказательной медицины в работе с Pico. Первый этап

История развития компьютерной техники

От печатной книги до интернет-книги

Краткая инструкция по CIS – 10 шагов

Информационные технологии в медицине

Информационные войны

Моя будущая профессия. Программист

1. Переместительный закон
2. Сочетательный закон
3. Распределительный закон
4. Закон двойного отрицания
5. Закон исключенного третьего
6. Закон повторения
7. Законы операций с 0 и 1
8. Законы общей инверсии (законы де Моргана)
• Для логического умножения:
A&B=B&A
• Для логического сложения:
AvB=BvA
• Для логического умножения:
(A & B) & C = A & (B & C)
• Для логического сложения:
(A v B) v C = A v (B v C)
Вывод: при одинаковых знаках операций скобки

можно ставить произвольно или вообще опускать.
• Для логического умножения:
A & (B v C) = (A & B) v (A & C)
• Для логического сложения:
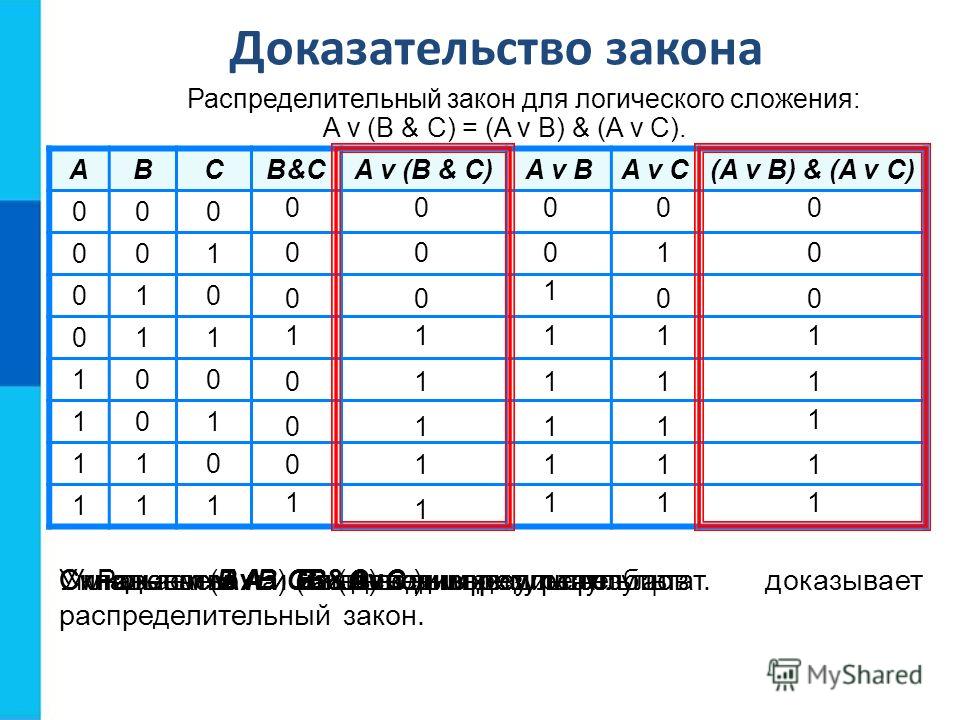
A v (B & C) = (A v B) & (A v C)
Докажем распределительный закон для логического умножения.
Для этого построим таблицу истинности:
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
Заполним столбец B v C. Для этого выполним дизъюнкцию
(сложение) значений столбцов B и С:
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)

0
0
0
0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
Теперь заполним столбец A & (B v C). Для этого выполним
конъюнкцию (умножение) значений столбцов A и (B v С):
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
1
0
1
0
0
0
0
1
0
1
1
1
1
1
0
1
1
1
1
1
1
1
Таблица истинности для левой части равенства построена. Теперь построим
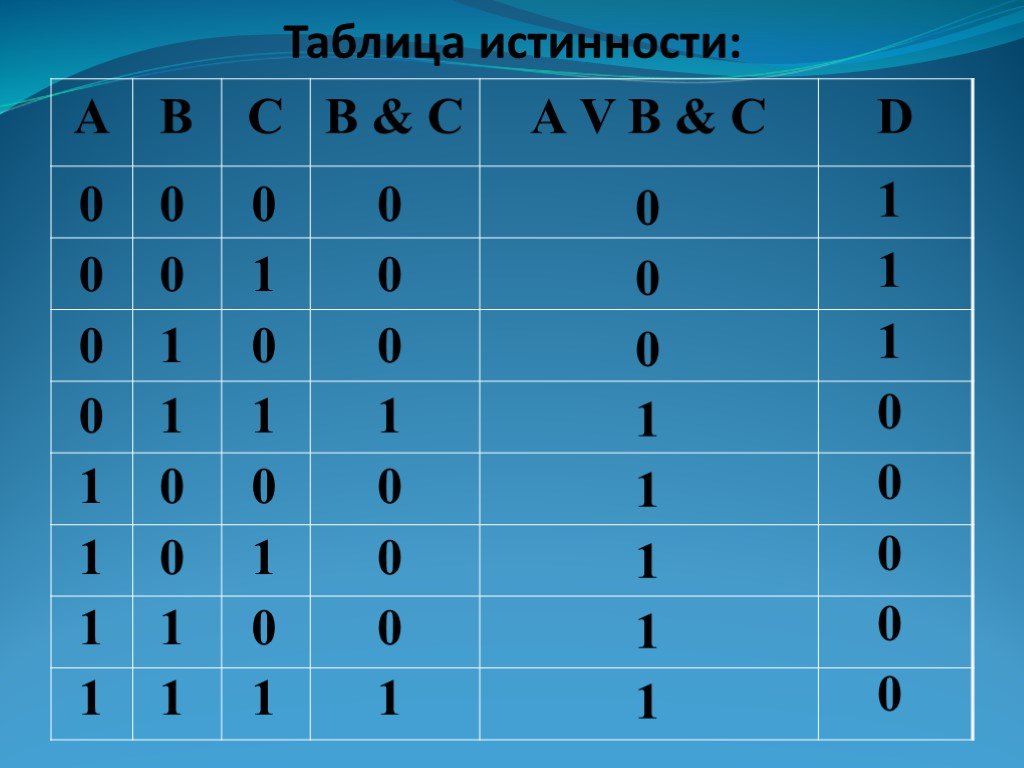
таблицу истинности для правой части и сравним значения.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
1
1
0
0
1
0
1
0
0
1
1
1
0
1
0
0
0
0
1
0
1
1
1
1
1
0
1
1
1
1
1
1
1
Вычислим значения столбца A & B. Для этого выполним конъюнкцию
(умножение) значений столбцов A и B.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
1
1
0
0
0
1
0
1
0
0
0
1
1
1
0
0
1
0
0
0
0
0
1
0
1
1
1
0
1
1
0
1
1
1
1
1
1
1
1
1
Вычислим значения столбца A & C. Для этого выполним конъюнкцию
(умножение) значений столбцов A и C.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
1
0
1
0
0
0
0
1
1
1
0
0
0
1
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
Вычислим значения столбца (A & B) v (A & C). 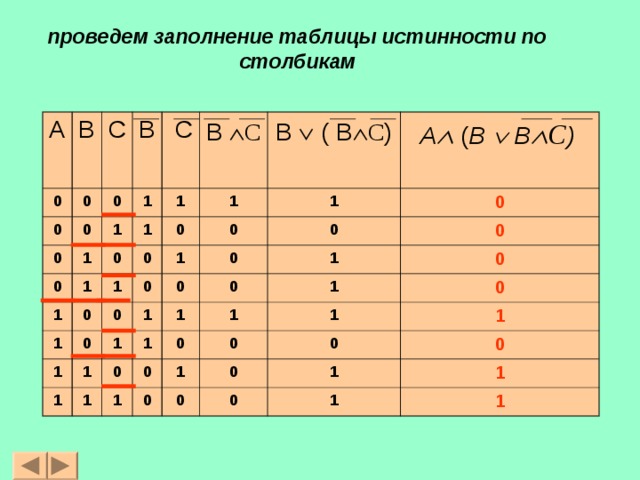Для этого выполним
дизъюнкцию (сложение) значений столбцов A & B и A & C.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
Таблица истинности для правой части равенства построена.
A B C B v C A & (B v C) A & B A & C (A & B) v (A & C)
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
Сравним значения. 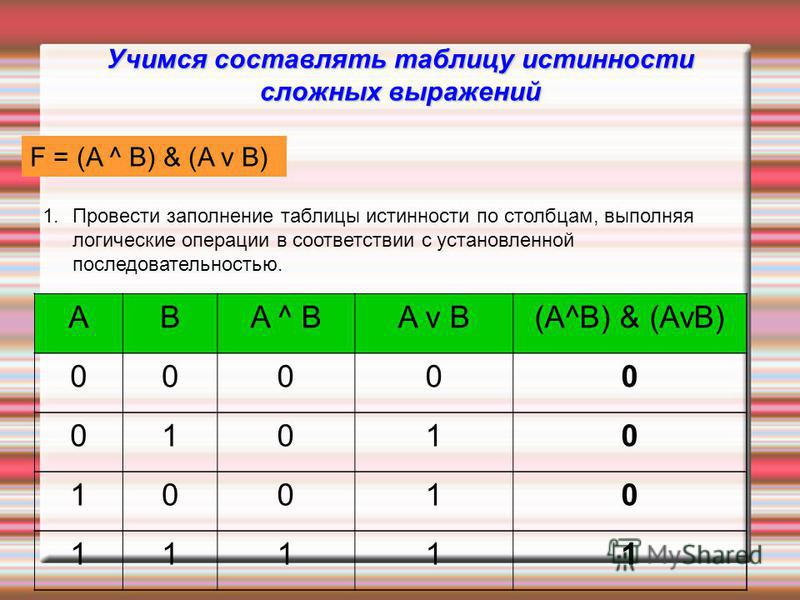Значения одинаковы, значит выражение

A & (B v C) = (A & B) v (A & C)
справедливо. Что и требовалось доказать.
A & (B v C)
(A & B) v (A & C)
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
ഥ

English     Русский Правила

Презентация на тему: Алгебра высказываний Лекция 3

Цель: ознакомить с понятиями ДНФ, СДНФ, сформировать навыки приведения высказываний к ДНФ и СДНФ, показать возможности применения алгебры высказываний при решении логических задач, упрощении переключательных схем

Дизъюнктивные нормальные формы (ДНФ)

Определение 1

F,если a = 1
F a
F ,если a = 0.
			Утверждение 2
A 1 A
			Доказательство
		A	a	Aa
0			0	1
0			1	0
1			0	0
1			1	1

Определение 3

Конъюнкция логических переменных или их отрицаний называется

элементарной конъюнкцией (ЭК).

Общий вид элементарной конъюнкции: A1a1 A2a2 … Anan

Пример

AC, AB, A C , BC, ABC, B C , A

Определение 4

Высказывание называется дизъюнктивной нормальной формой (ДНФ), если оно представляет собою дизъюнкцию элементарных конъюнкций.

Общий вид ДНФ: K1 K2 … Km

Примеры

AB C

A B C

A

A B

A C

A C

ABC BC A

Теорема

Любое высказывание приводимо к ДНФ.

Схема приведения высказывания к ДНФ

1)Избавиться от импликации и эквивалентности, используя законы 16), 17)

2)Донести отрицания до переменных, используя законы Моргана.

3)Раскрыть скобки, используя дистрибутивные законы.

4)Упростить полученное высказывание.

Пример

Привести высказывание к ДНФ

F AC B A CBAC B A CB

AC B A CB AC B A CB

A C B A CB ACB ACB

A CB(C B) ACB A(C B)

A CBC C BB ABCC ABCB

A CB ABC

A CB BC

A C(B B)

A C

Построение высказываний по таблице истинности. Совершенные дизъюнктивные нормальные формы (СДНФ)

Определение 1

Пусть X A1 , A2 ,…, An – некоторое множество логических переменных. Элементарная конъюнкция, в которую входят все

логические переменные, называется полной элементарной конъюнкцией относительно множества X .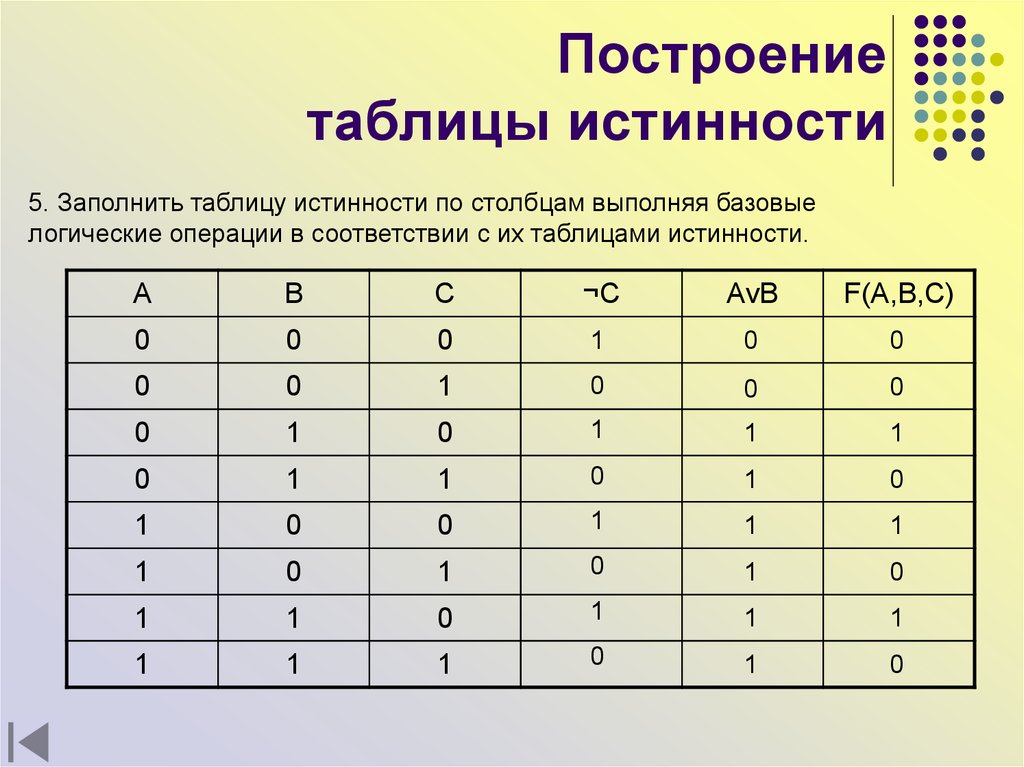

Пример

X A, B,C

A, AC, ABC, B AC, B AC, ABC

СДНФ

Определение 2

•Дизъюнктивная нормальная форма называется совершенной (СДНФ), если все составляющие ее элементарные конъюнкции являются полными.

X A, B,C

Примеры

AB BCA B

ABC

ABC

ABC

AB

ABC

ABC

ABC

ABC ABC ABC

Приведение высказывания к СДНФ

Теорема

Высказывание, не являющееся тождественно ложным, приводимо к СДНФ.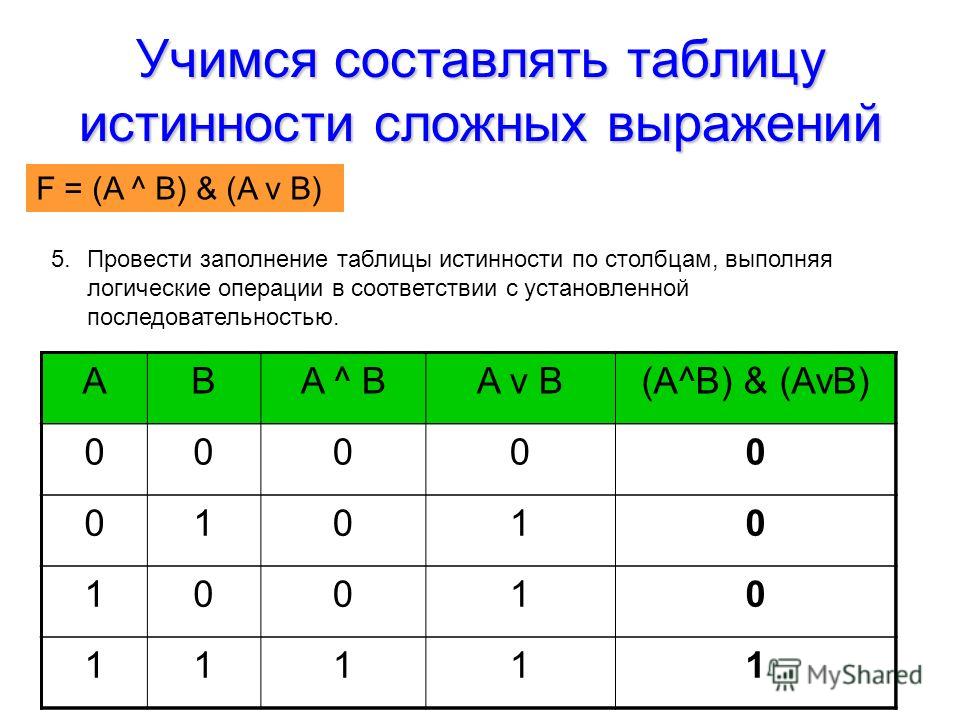

Правило приведения высказывания к СДНФ

•СДНФ содержит столько полных элементарных конъюнкций, сколько единиц в последнем столбце таблице истинности.

•Вид каждой полной элементарной конъюнкции определяется соответствующим набором значений переменных, а именно, если переменная принимает значение 0, то над ней в полной элементарной конъюнкцией ставится отрицание, иначе – отрицание не ставится.

Пример

• Построить по таблице истинности СДНФ

A B C F

0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

F ABC ABC ABC ABC

[Решено] Таблица истинности функции f(ABCD) = m(0, 1, 3, 4, 8,

Таблица истинности функции f(ABCD) = m(0, 1, 3, 4, 8, 9)

А	Б	С	ф
0	0	0	Вт
0	0	1	х
0	1	0	Д
0	1	1	0
1	0	0	З
1	0	1	0
1	1	0	0
1	1	1	0

 

где W, X, Y, Z определяются как (d — дополнение D)

1. D, d, 1, 1
2. 1, d, D, 1
3. 1, 1, D , d
4. 1, D, d, 1

Вариант 4 : 1, D, d, 1

Бесплатно

ST 1: Сопротивление материалов

2,9 тыс. пользователей

15 вопросов

30 баллов

15 минут

Данная функция, f(ABCD) = m (0, 1, 3, 4, 8, 9)

Представление K-карты для приведенной выше булевой функции: 9

Из данной таблицы истинности ), f = W ⇒ W = 1

(2) для (A = 0 = B, C = 1), f = X ⇒ X = D

(3) для (A = 0 = C , B = 1), f = Y ⇒ Y = D̅ = d

(4) для (A = 1, B = C = 0, f = Z ⇒ Z = 1

Скачать решение PDF

Поделиться в WhatsApp

Последние обновления RCFL

Последнее обновление: 22 сентября 2022 г.

Компания Rashtriya Chemicals & Fertilizers Limited (RCFL) опубликовала официальное уведомление о вакансиях стажера-оператора и младшего пожарного 14 марта 2022 года. Всего было объявлено о наборе 137 вакансий в RCFL в 2022 году. Начало подачи онлайн-заявки 14 марта 2022 г. и заканчивается 28 марта 2022 г. RFCL является ведущей коммерческой компанией в области производства и сбыта удобрений и промышленных химикатов. Таким образом, это отличная возможность трудоустройства для тех, кто ищет работу в правительстве. Кандидаты должны ознакомиться с учебным планом RCFL и шаблоном экзамена, чтобы лучше понять суть экзамена.

Предлагаемые экзамены

Truthtable — Таблица истинности для доказательства истинности/ложности аргумента

спросил 11 лет, 11 месяцев назад

Изменено 11 лет, 11 месяцев назад

Просмотрено 725 раз

Может ли кто-нибудь помочь мне с таблицами истинности? Я хотел бы создать таблицу истинности, чтобы доказать, правда это или нет.

• правдивость

1

 A B C B∧C A∨(B∧C) A ∨ B A ∧ C (A ∨ B) ∨ (A ∧ C)
0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0
0 1 0 0 0 1 0 1
0 1 1 1 1 1 0 1
1 0 0 0 1 1 0 1
1 0 1 0 1 1 1 1
1 1 0 0 1 1 0 1
1 1 1 1 1 1 1 1
 

Когда A=0, B=1 и C=0

 A ∨ (B ∧ C) = 0
(А ∨ В) ∨ (А ∧ С) = 1 ∨ 0 = 1
 

Итак, A ∨ (B ∧ C) = A ∨ B) ∨ (A ∧ C) ложно.

1

А = 0, В = 0, С = 0
А ∨ (В ∧ С) = 0 ∨ (0 ∧ 0) = 0 ∨ 0 = 0
(А ∨ В) ∨ (А ∧ С) = 0
 

Сделайте то же самое для еще 7 комбинаций A, B и C.

А = 0, В = 0, С = 1
А = 0, В = 1, С = 0
//// и т. д.
 

Если вы обнаружите, что оба конца одинаковы для всех восьми, то это доказано. В противном случае это не то же самое. 93=8 записей таблицы истинности будет достаточно. Я предлагаю разбить столбцы в вашей таблице, чтобы получить один логический результат за раз. Если два столбца двух сторон вашего логического уравнения совпадают, вы доказали, что они одинаковы, в противном случае у вас будет один или несколько контрпримеров.