Презентация «Основы логики Алгебра высказываний»

Cлайд 1

Основы логики Алгебра высказываний Автор: Сергеев Евгений Викторович МОУ СОШ №4 г. Миньяра Челябинской области [email protected] http://shk4-minyar.ucoz.ru

Cлайд 2

Алгебра высказываний Алгебра высказываний была разработана для того, чтобы определять истинность или ложность составных высказываний, не вникая в их содержание

Cлайд 3

Логические переменные Логические переменные – простые высказывания, содержащие только одну мысль. Обозначаются буквами латинского алфавита: A, B, C… Логические переменные могут принимать лишь два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0)

Cлайд 4

Логические переменные Например, два простых высказывания: А = «2 2 = 4» истина (1) В = «2 2 = 5» ложь (0) являются логическими переменными А и В

Cлайд 5

В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «ИСТИНА» (1) или «ЛОЖЬ» (0)

Cлайд 6

В алгебре высказываний над логическими переменными (над высказываниями) можно производить определенные логические операции, в результате которых получаются новые высказывания

Cлайд 7

Составные высказывания Высказывания, состоящие из нескольких простых суждений и содержащие в себе более, чем одну простую мысль, называются логическими функциями Обозначаются F(A,B,C…) Также могут принимать значения «ИСТИНА» или «ЛОЖЬ» в зависимости от того, какие значения имеют входящие в их состав логические переменные и от действий над ними

Cлайд 8

Логические операции Конъюнкция (логическое умножение, «И») Дизъюнкция (логическое сложение, «ИЛИ») Инверсия (логическое отрицание, «НЕ») Импликация (логическое следование, «Если А, то В») Эквивалентность (логическое равенство, «А тогда и только тогда, когда В»)

Cлайд 9

Объединение двух или нескольких высказываний в одно с помощью союза «И» называется операцией логического умножения, или конъюнкцией

Cлайд 10

Логическая функция, полученная в результате конъюнкции, истинна тогда и только тогда, когда истинны все входящие в него логические переменные

Cлайд 11

Конъюнкция. Определите истинность логической функции «2 2 = 5» И «3 3 = 10» «2 2 = 5» И «3 3 = 9» «2 2 = 4» И «3 3 = 10» «2 2 = 4» И «3 3 = 9» Истинна только функция (4)

Cлайд 12

Запись конъюнкции на формальном языке алгебры высказываний F(A,B) = A & B или F(A,B) = A B Также может встретиться запись, типа: F(A,B) = A * B или F(A,B) = A and B

Cлайд 13

Значение логической функции определяется по ее таблице истинности Таблица истинности показывает какие значения принимает логическая функция при всех возможных значениях логических переменных

Cлайд 14

Таблица истинности для конъюнкции A B A B 2 2 = 5 3 3 = 10 ЛОЖЬ 2 2 = 5 3 3 = 9 ЛОЖЬ 2 2 = 4 3 3 = 10 ЛОЖЬ 2 2 = 4 3 3 = 9 ИСТИНА

Cлайд 15

Таблица истинности для конъюнкции A B A B 0 0 0 0 1 0 1 0 0 1 1 1

Cлайд 16

Объединение двух или нескольких высказываний в одно с помощью союза «ИЛИ» называется операцией логического сложения, или дизъюнкцией

Cлайд 17

Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна хотя бы одна из входящих в него логических переменных

Cлайд 18

Дизъюнкция. Определите истинность логической функции «2 2 = 5» ИЛИ «3 3 = 10» «2 2 = 5» ИЛИ «3 3 = 9» «2 2 = 4» ИЛИ «3 3 = 10» «2 2 = 4» ИЛИ «3 3 = 9» Ложна только функция (1), остальные истинны

Cлайд 19

Запись дизъюнкции на формальном языке алгебры высказываний F(A,B) = A B Также может встретиться запись, типа: F(A,B) = A + B или F(A,B) = A or B

Cлайд 20

Таблица истинности для дизъюнкции A B A B 2 2 = 5 3 3 = 10 ЛОЖЬ 2 2 = 5 3 3 = 9 ИСТИНА 2 2 = 4 3 3 = 10 ИСТИНА 2 2 = 4 3 3 = 9 ИСТИНА

Cлайд 21

Таблица истинности для дизъюнкции A B A B 0 0 0 0 1 1 1 0 1 1 1 1

Cлайд 22

Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или инверсией

Cлайд 23

Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным [логическая отрицательная единица, перевертыш]

Cлайд 24

Инверсия Пусть A = «2 2 = 4» – истинное высказывание, тогда F(A) = «2 2 ≠ 4» – ложное высказывание

Cлайд 25

Запись инверсии на формальном языке алгебры высказываний F(A) = ¬A или F(A) = Ā Также может встретиться запись, типа: F(A) = not А

Cлайд 26

Таблица истинности для инверсии А ¬А 0 1 1 0

Cлайд 27

Таблицы истинности основных логических функций Логическое умножение A 0 0 1 1 B 0 1 0 1 A B 0 0 0 1 Логическое сложение Логическое отрицание A 0 1 ¬A 1 0 A 0 0 1 1 B 0 1 0 1 А В 0 1 1 1

Cлайд 28

Дополнительные логические функции Импликацию и эквивалентность можно выразить через конъюнкцию, дизъюнкцию и отрицание, поэтому их называют дополнительными логическими функциями: Импликация: А → В = ¬A В или А В = ¬A В или А В = ¬A В Эквивалентность: А ↔ В = (¬A В) (¬B A) или А В = (¬A В) (¬B A) или А ≡ В = (¬A В) (¬B A)

Cлайд 29

Импликация Объединение двух высказываний, из которых первое является условием, а второе – следствием из него, называется импликацией (логическим следованием)

Cлайд 30

Импликация Импликация ложна тогда и только тогда, когда условие истинно, а следствие ложно Пример: Если выучишь материал, то сдашь зачет Это высказывание ложно только тогда, когда материал выучен, а зачет не сдан, т.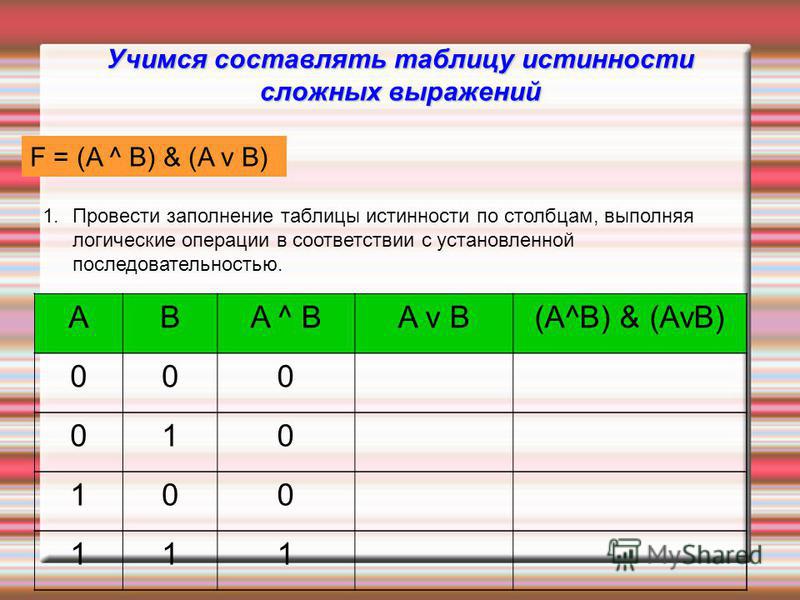

к. сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой

Cлайд 31

Таблица истинности для импликации A B A → B 0 0 1 0 1 1 1 0 0 1 1 1

Cлайд 32

Эквивалентность Эквивалентность – это логическая операция, объединяющая два простых высказывания в одно составное и которое является истинным тогда и только тогда, когда оба исходных высказывания одновременно либо истинны, либо ложны.

Cлайд 33

Таблица истинности для эквивалентности A B A B 0 0 1 0 1 0 1 0 0 1 1 1

Cлайд 34

Переместительный Дизъюнкция: X Y ≡ Y X Конъюнкция: X Y ≡ Y X Основные законы алгебры высказываний

Cлайд 35

Сочетательный Дизъюнкция: X (Y Z) ≡ (X Y) Z Конъюнкция: X (Y Z) ≡ (X Y) Z Основные законы алгебры высказываний

Cлайд 36

Распределительный Дизъюнкция: X (Y Z) ≡ X Y X Z Конъюнкция: X (Y Z) ≡ (X Y) (X Z) Основные законы алгебры высказываний

Cлайд 37

Правила де Моргана Дизъюнкция: ¬(X Y) ≡ ¬X ¬Y Конъюнкция: ¬(X Y) ≡ ¬X ¬Y Основные законы алгебры высказываний

Cлайд 38

Идемпотенции Дизъюнкция: X X ≡ X Конъюнкция: X X ≡ X Основные законы алгебры высказываний

Cлайд 39

Поглощения Дизъюнкция: X (X Y) ≡ X Конъюнкция: X (X Y) ≡ X Основные законы алгебры высказываний

Cлайд 40

Склеивания Дизъюнкция: (X Y) (¬X Y) ≡ Y Конъюнкция: (X Y) (¬X Y) ≡ Y Основные законы алгебры высказываний

Cлайд 41

Переменная со своей инверсией Дизъюнкция: X ¬X ≡ 1 Конъюнкция: X ¬X ≡ 0 Основные законы алгебры высказываний

Cлайд 42

Операция с константами Дизъюнкция: X 0 ≡ X, X 1 ≡ 1 Конъюнкция: X 0 ≡ 0, X 1 ≡ X Основные законы алгебры высказываний

Cлайд 43

Двойного отрицания ¬(¬X) ≡ X Основные законы алгебры высказываний

Cлайд 44

Порядок действий Действия в скобках Отрицание Конъюнкция Дизъюнкция Импликация Эквивалентность

Вопрос 2

Логические выражения и их преобразования. Таблицы истинности.

Логические выражения. Каждое составное высказывание можно выразить в виде формул (логического выражения), в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.

Для записи составных высказываний в виде логических выражений на формальном языке (языке алгебры логики0 в составном высказывании нужно выделить простые высказывания и логические связи между ними.

Запишем в форме логического выражения составное высказывание «2*2=5 или 2*2=4 или 2*24»проанализируем составное высказывание. Оно состоит из двух простых высказываний,

А= «2*2=5»- ложно (0)

В= «2*2-4» -истинно (1).

Тогда составное высказывание можно записать в следующей форме,

«А или В и Ā или В».

теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполнения логических операций. При выполнении логических операций определен следующий порядок их выполнения, инверсия , конъюнкция, дизъюнкция. Для изменения указанного порядка могут использоваться сковки.

F=(AuB)&(ĀuB).

Истинности или ложности составных высказываний можно определить чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.

П одставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции.

Таблицы истинности. Для каждого составного высказывания (логического выражения) можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний (логических переменных).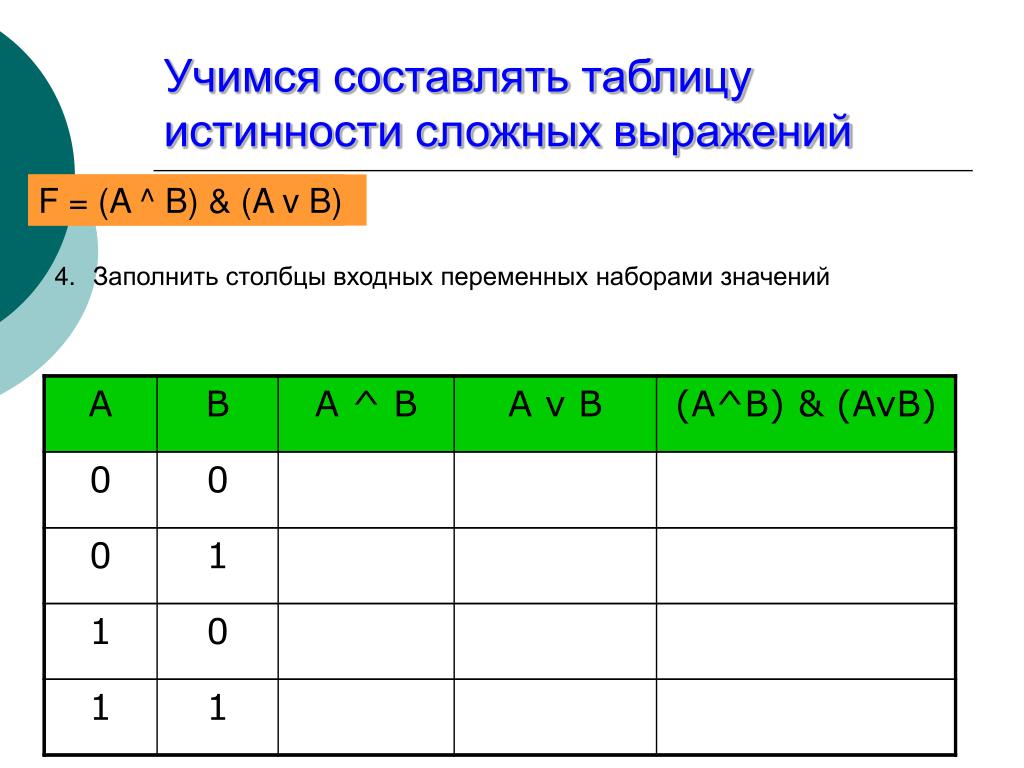

При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.

Во-первых, необходимо определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных n, то количество строк =2^{n .}

В нашем случае логическая функция F=(AB)&(Ā¯B) имеет две переменное и, следовательно, количество строк в таблице истинности должно быть равно 4.

Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций равно пяти, т.е. количество столбцов таблицы истинности равно семи.

В-третьих, необходимо построить таблицу истинности с указанным количеством строк и столбцов, обозначить столбцы и внести возможные наборы значений исходных логических переменных .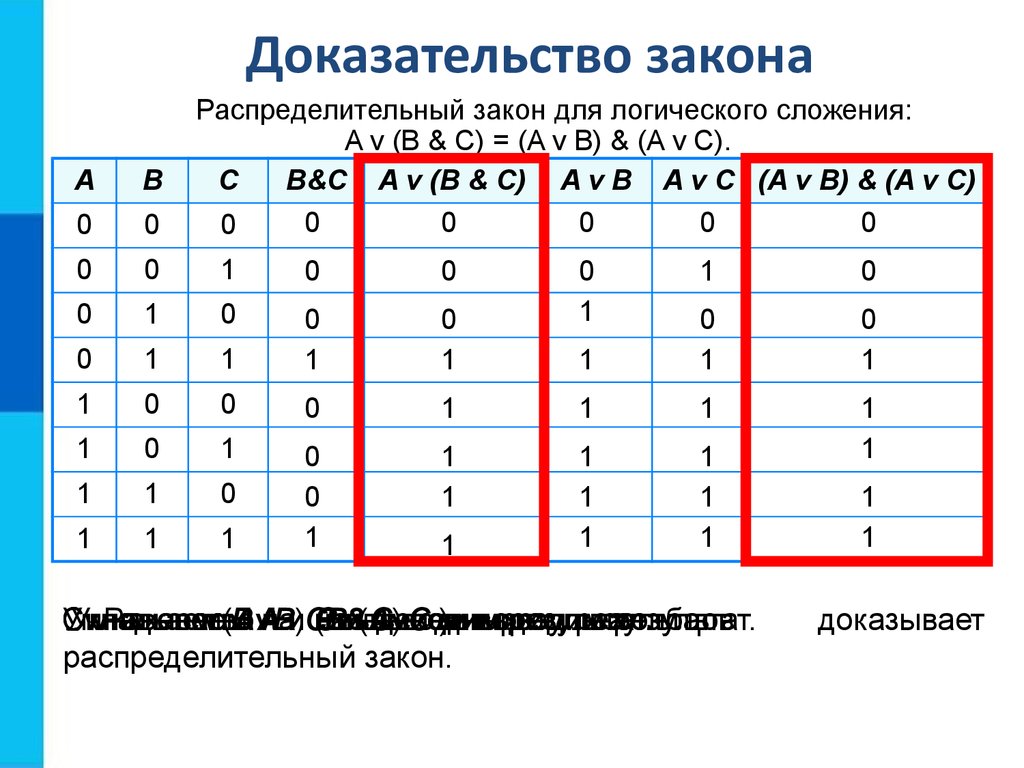

A B AB Ā ¯B

0 0 0 1 1 1 0

0 1 1 1 0 1 1

1 0 1 0 1 1 1

1 1 1 0 0 0 0

В-четвертых, необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности. Теперь мы можем определить значение логической функции для любого набора значений логических переменных.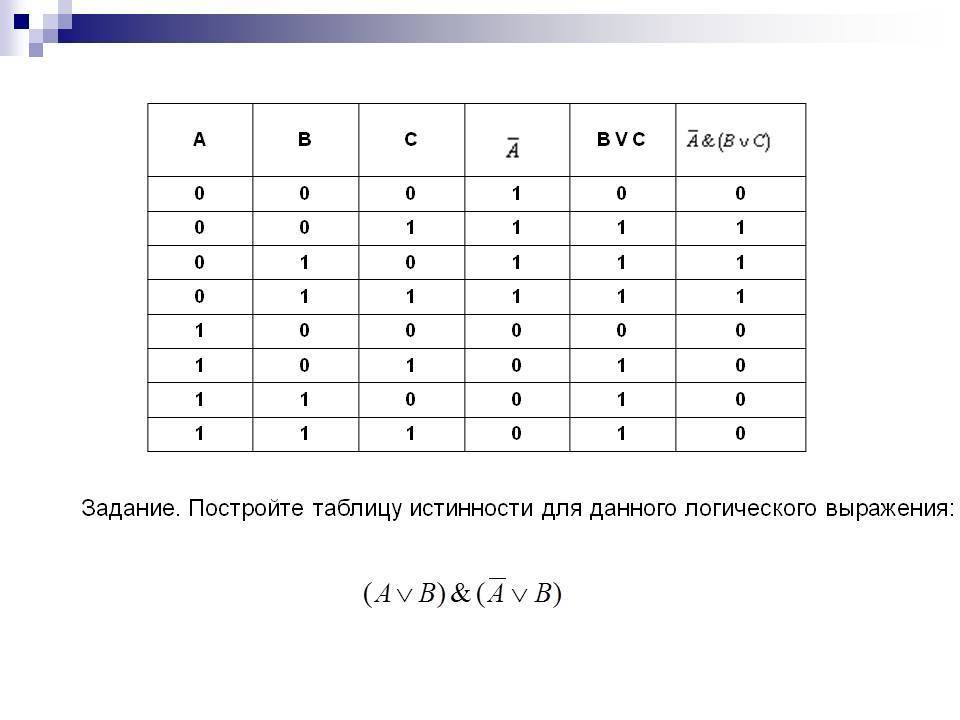

Равносильные логические ворожения. Логические выражения, у которых таблицы истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».

Д окажем, что логические ворожения равносильны.

П остроим сначала таблицу истинности для логического выражения.

А В Ā

0 0 1 1 1

0 1 1 0 0

1 0 0 1 0

1 1 0 0 0

Таблица истинности

А В

0 0 0 1

0 1 1 0

1 0 1 0

1 1 1 0

Таблицы истинности совпадают, следовательно, логические выражения равносильны.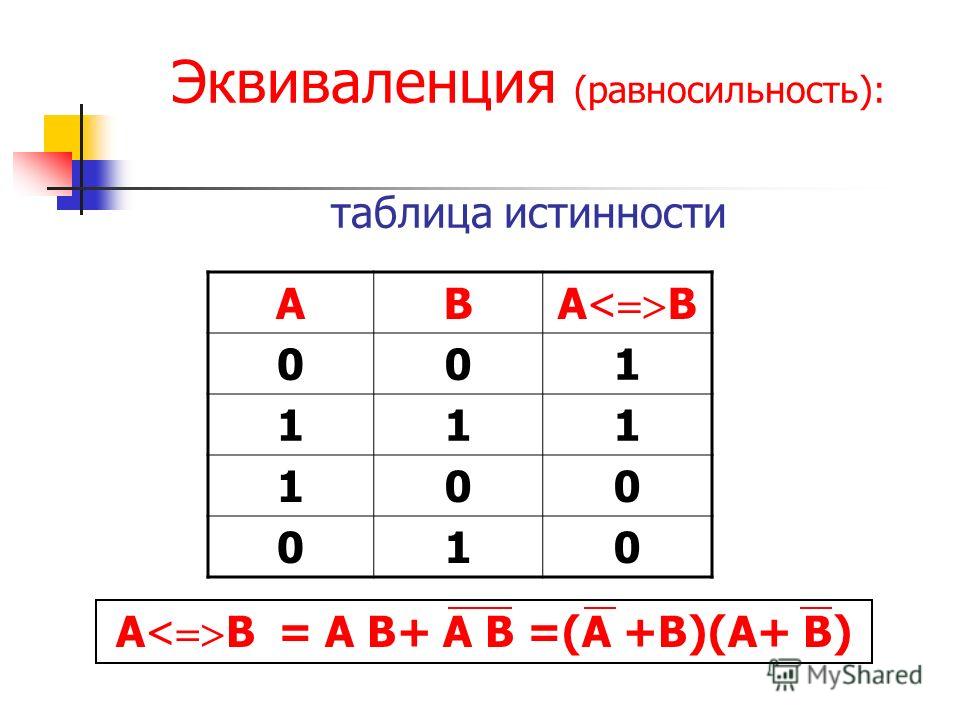

Логические функции.

Любое составное высказывание можно рассматривать как логическую функцию F(Х₁,Х₂…Х_n), аргументами которой являются логические переменные X₁,X₂….X_n (простые высказывания). Сама функция и аргументы могут принимать только два различных значения «истина» (1) и «ложь» (0).

Выше были рассмотрены функции двух аргументов, логическое умножение F=(A,B)=A&B, логическое сложение F=(A,B)=AB, а также логическое отрицание F(A)=Ā, в котором значение второго аргумента можно считать равным нулю.

Каждая логическая функция двух аргументов четыре возможных набора значений аргументов. По формуле можем определить какое количество различных логических функций двух аргументов, может существовать,

Т аким образом, существует 16 различных логических функций двух аргументов, каждая из которых задается собственной таблицей истинности.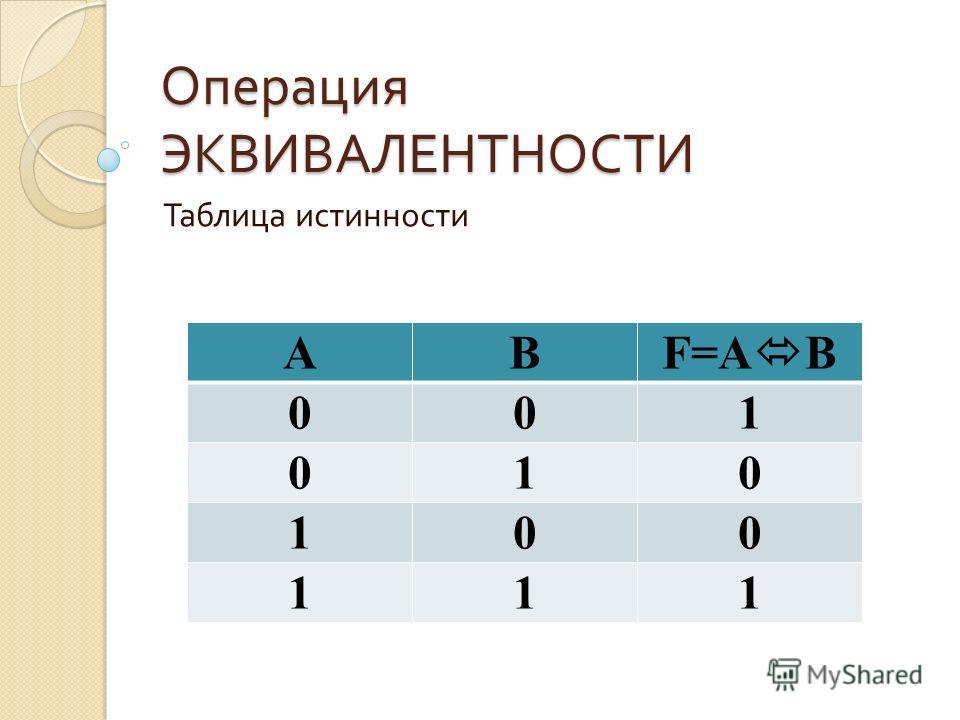

В обыденной и научной речи кроме базовых логических связок «и», «или», «не», используется и некоторые другие, «если…то», «тогда…и только тогда, когда…» и др. некоторые из них имеют свое название и свой символ и им соответствует определенные логические функции.

Логическое следование (импликация). Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».

Составное высказывание, образованное с помощью операции логического следования (импликации), ложна тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).

Логическая операция импликация «если А то В», обозначается А→В и выражается с помощью логической функции F₁₄ ,которая задается соответствующей таблицей истинности.

А В F₁₄=A→B

0 0 1

0 1 1

1 0 0

1 1 1

Например, высказывание «если число делится на 10, то оно делится на 5» истинно, т.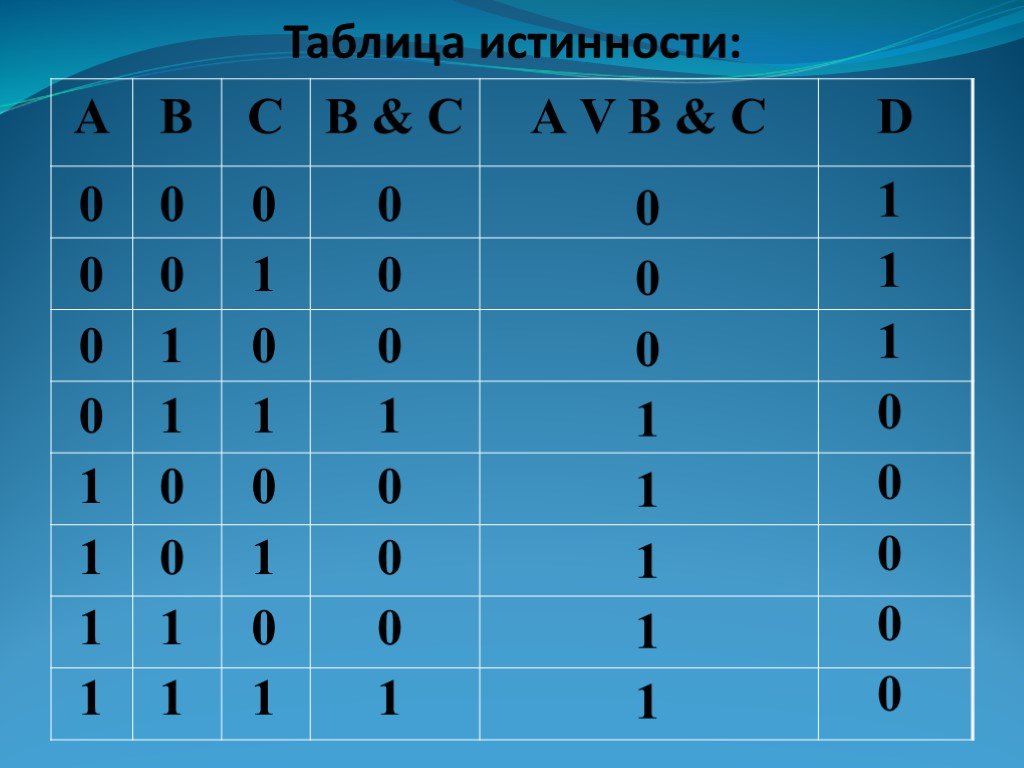 к. истинны и первое высказывание (предпосылка), и второе высказывание (вывод).

Высказывание №если число делится на 10, то оно делится на 3» ложно, т.к. из истинной предпосылки делится ложный вывод.

Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание (предпосылка)ложно, то вне зависимости от истинности или ложности второго высказывания (вывода) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно.

В алгебре высказываний все логические функции могут быть сведены путем логических преобразований к трем базовым, логическому умножению, логическому сложению и логическому отрицанию. Докажем методы сравнения таблиц истинности, что операция импликация А→В равносильна логическому выражению ĀB.

А В Ā ĀB

0 0 1 1

0 1 1 1

1 0 0 0

1 1 0 1

Таблицы истинности совпадают, что и требовалось доказать.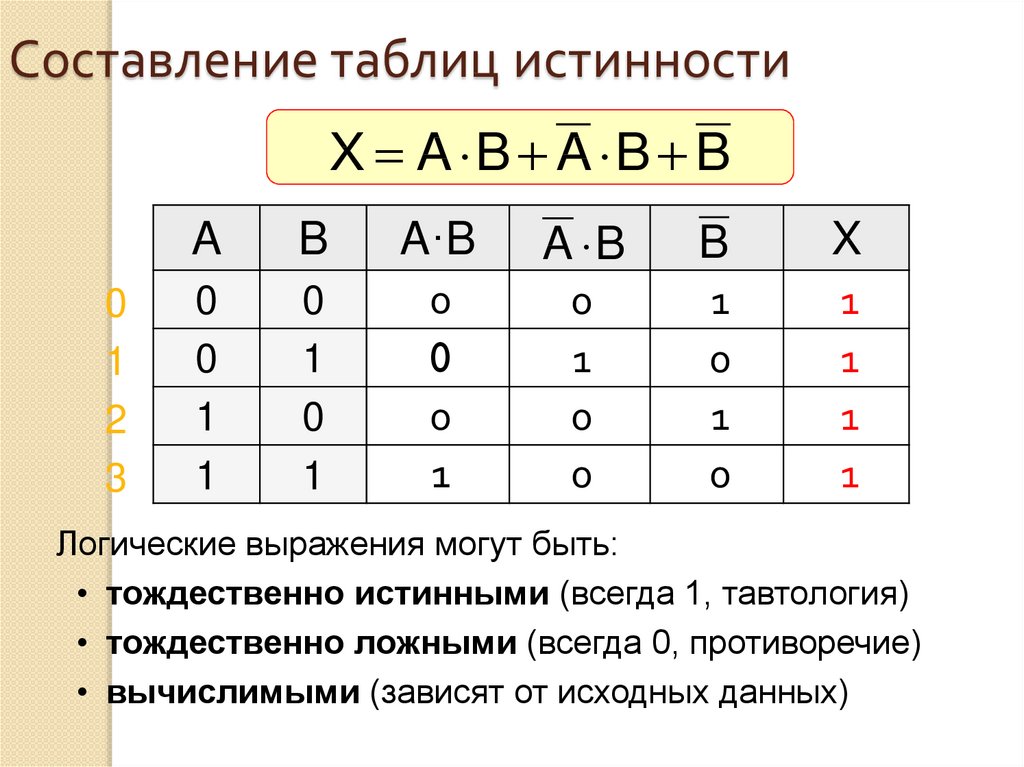

Логическое равенство (эквивалентность). Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда…».

Логическая операция эквивалентности «А эквивалентно В» обозначается АВ и выражается с помощью логической функции F₁₀, которая задается соответствующей таблицей истинности.

А В F₁₀

0 0 1

0 1 0

1 0 0

1 1 1

[Решено] Вопрос 1: Основные таблицы истинности (4 балла) A B A . B A +B A ~A NN A 0…

Получите больше от подписки*

• Доступ к более чем 100 миллионам учебных ресурсов по конкретным курсам
• Круглосуточная помощь опытных наставников по более чем 140 предметам
• Полный доступ к более чем 1 миллиону решений для учебников

*Вы можете изменить, приостановить или отменить в любое время

Вопрос задан kharvey101

Текст транскрипции изображения

Вопрос 1: Основные таблицы истинности (4 балла) Заполните таблицы истинности для И, ИЛИ, НЕ и двойного отрицания.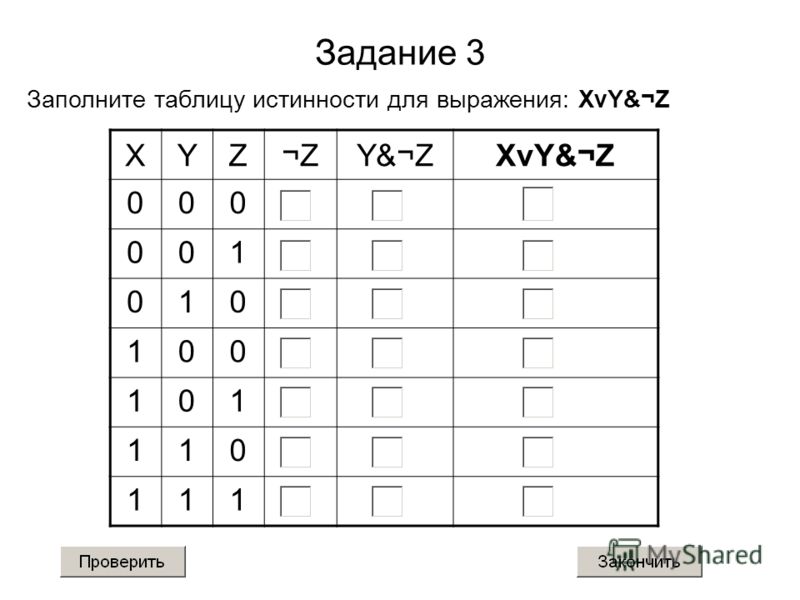

… Показать больше

Информатика Инженерная технология Программирование на Питоне СРТ 101

Ответ и объяснение

Решено проверенным экспертом

Рейтинг Helpful

Answered by SargentLlama1068

inia pulvinar tort

l	i	sus	cong
0	0	0	0
0	x	0	x
x	0	0	x
x	x	x	x

trices ac magna. Fu

l	f	ic
0	x	0
x	0	x

Unlock full access to Course Hero

Изучите более 16 миллионов пошаговых ответов из нашей библиотеки

Подпишитесь, чтобы посмотреть ответ

Пошаговое объяснение

s an Fu ur laoreet.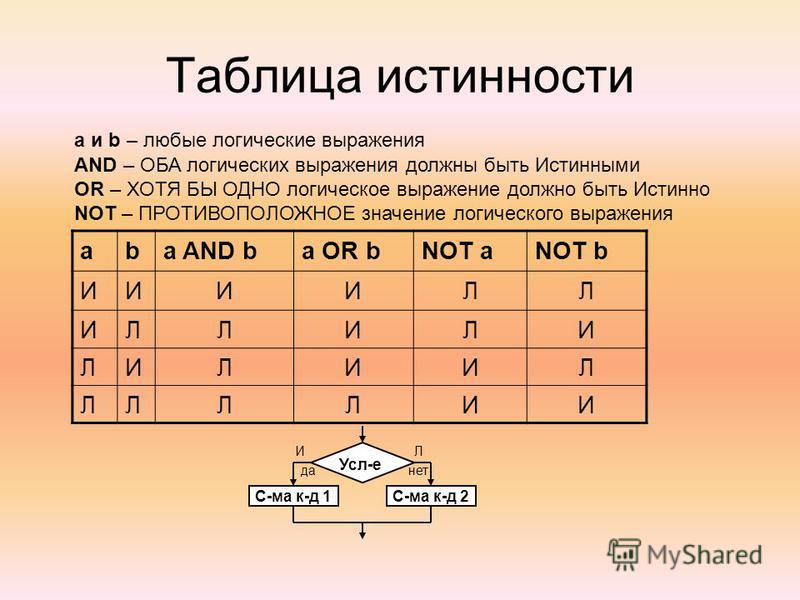 Nam risus ante s ante, dapibus cing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, dapibus a molest

gue

ris Do trices ac magna. Fusce dui m risus ante, dapibus iscing elit. Nam lacinia pulvinar tortor nec facilisis. Pellentesque dapibus efficitur laoreet. Nam risus ante, да

gue

m ri Fu risus ante, dapibus a molestie consequat, ultrices ac magna.

gue

icitur l ctum vitae odio molestie consequat, ultrices ac magna. Fusce dui lectus, congue vel laoreet ac, dictum vitae odio. Донец Аликет. Lorem ipsum dolor sit amet

sum dolor sit amet, consectetur adipiscing elit

gue

molestie consequat, ultrices ac magna. Fusce d

gue

ac, dictum vit

gue

dictum vitae odio.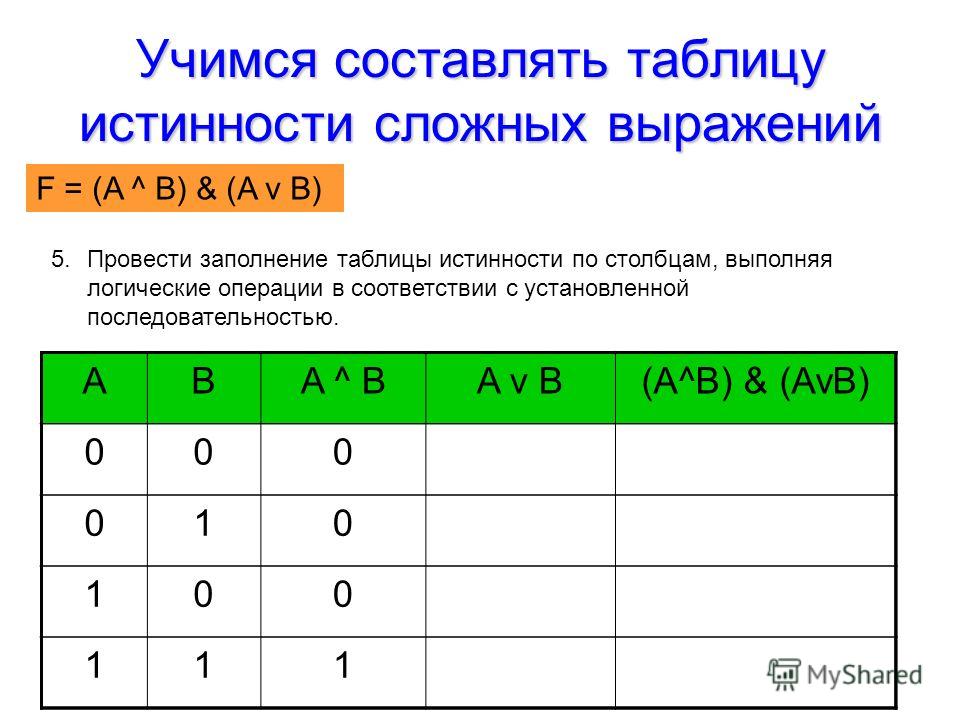 Донец Аликет. Lorem ip

Отзывы студентов

100% (2 оценки)

Подробное объяснение

Легко понять

Четкое форматирование

CS101 — Булева логика

В 1840-х годах английский математик Джордж Буль разработал алгебру (набор операторов и законов) для переменных, которые могут иметь только два состояния – истинно, и ложно. Таким образом, логическое значение эквивалентно одному биту:

 Ложь = 0 = выкл.
   True = 1 = on 

Операторы, определенные Булем, распространены во всех вычислениях. Вы могли столкнуться с ними при поиске в библиотеке или других базах данных. Мы рассмотрим следующие:

Таблица иллюстрирует как алгебраическую нотацию, так и нотацию на принципиальной схеме . Элементы принципиальных схем называются вентилями , , как в «И-вентиль» или «Исключающее-ИЛИ».

Поведение этих операторов может быть определено таблиц истинности:

 A B A·B A+B A' A⊕B
    0 0 0 0 1 0
    0 1 0 1 1 1
    1 0 0 1 0 1
    1 1 1 1 0 0 

Мы объединяем вентили в комбинационных схем для достижения различных эффектов.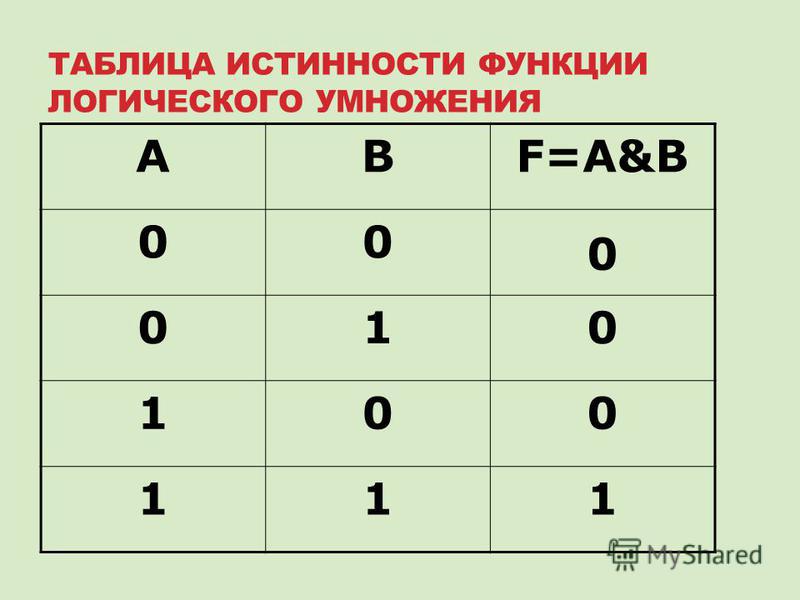 Например, алгебраическое выражение X = A·B + A·C точно соответствует следующей принципиальной схеме:

, и мы можем обнаружить его действие, заполнив таблицу истинности:

 А В С D=A·B E=A·C X=D+E
    0 0 0 0 0 0
    0 0 1 0 0 0
    0 1 0 0 0 0
    0 1 1 0 0 0
    1 0 0 0 0 0
    1 0 1 0 1 1
    1 1 0 1 0 1
    1 1 1 1 1 1 

Упражнение: Попробуйте нарисовать схемы и таблицы истинности для X=(A·B)' и для X=A'+B' . Они должны давать одинаковый результат для входных данных А и В . Это один из законов ДеМоргана.

@secboffin в Твиттере

Мы просто посмотрим на защелку S-R (NAND).

• Шлепанцы, защелки и детали памяти [8:53] от Computerphile

Этот раздел относится к программе Logisim, которая должна работать на любой платформе с Java Runtime Environment. Если вы получаете сообщение об ошибке «неизвестный разработчик» на Mac, перейдите в Системные настройки »Безопасность и найдите кнопку с надписью Все равно открыть.