513 в шестнадцатеричной системе счисления: Перевод 513 из десятичной в шестнадцатеричную систему счисления — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Задания для самостоятельного выполнения — Студопедия

Поделись

1. Переведите целые числа из десятичной системы счисления в двоичную:

а)513; в)600; д)602; ж)1000;

б)2304; г)5001; е)7000; з)8192.

2. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками):

а)0,4622; в)0,5198; д)0,5803; ж)0,6124;

б)0,7351; г)0,7982; е)0,8544; з)0,9321.

3. Переведите смешанные десятичные числа в двоичную систему счисления:

а)40,5; б)31,75; в)124,25; г)125,125.

4. Переведите целые числа из десятичной в восьмеричную систему счисления:

а) 8700; б)8888; в)8900; г)9300.

5. Переведите целые числа из десятичной в шестнадцатеричную систему счисления:

а)266; б)1023; в)1280; г)2041.

6. Переведите числа из десятичной системы счисления в восьмеричную:

а) 0,43; б) 37,41; в) 2936; г)481,625.

7. Переведите числа из десятичной системы счисления в шестнадцатеричную:

а) 0,17; б)43,78; в)25,25; г)18,5.

8. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основанием 2, 8, 10 и 16.

Основание 2	Основание 8	Основание 10	Основание 16



			2А

9. Переведите двоичные числа в восьмеричную систему счисления:

а)1010001001011; в)1011001101111; д)110001000100;

б)1010,00100101; г)1110,01010001; е)1000,1111001.

10. Переведите двоичные числа в шестнадцатеричную систему счисления:

а)1010001001011; в)1011001101111; д)110001000100;

б)1010,00100101; г)1110,01010001; е)100,1111001.

11. Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:

а)266₈; в)1270₈; д)10,23₈;

б)266₁₆; г)2а19₁₆; е)10,23₁₆.

12. Осуществите перевод чисел по схеме А₁₀»А₁₆»А₂» А₈:

а) 16547; б) 21589;

в) 8512; г) 7756;

д) 5043; е) 2323.

13. Перевести числа из восьмеричной системы счисления в шестнадцатеричную:

а) 12754;

б) 1515;

в) 7403.

14. Перевести числа из шестнадцатеричной системы счисления в восьмеричную:

а) 1АЕ2;

б) 1С1С;

в) 34Е.

15. Сколько разрядов будет в числе, если записать его в восьмеричной системе счисления:

а) 10111010₂; б) 11001111000111₂;

в) А18С₁₆; г) 1375ВЕ₁₆.

16. Сколько разрядов будет в числе, если записать его в шестнадцатеричной системе счисления:

а) 10111010₂; б) 11001111000111₂;

в) 77731₈; г) 101154₈.

17. Сравните числа:

а) 125₁₆ и 111100010101₂; б) 757₈ и 1110010101₂; в) А23₁₆ и 1232₈;

г) 12,25₁₆ и 111,100010101₂; д) 63,5751₈ и 11100,10101₂; е) В,А₁₆ и 11,3₈.

12 в 16 системе счисления. Микросхемы и их функционирование

Шестнадцатеричная система счисления. аша первая программа.

Для написания программ на Ассемблере, необходимо разобраться с шестнадцатеричной системой счисления. Ничего сложного в ней нет.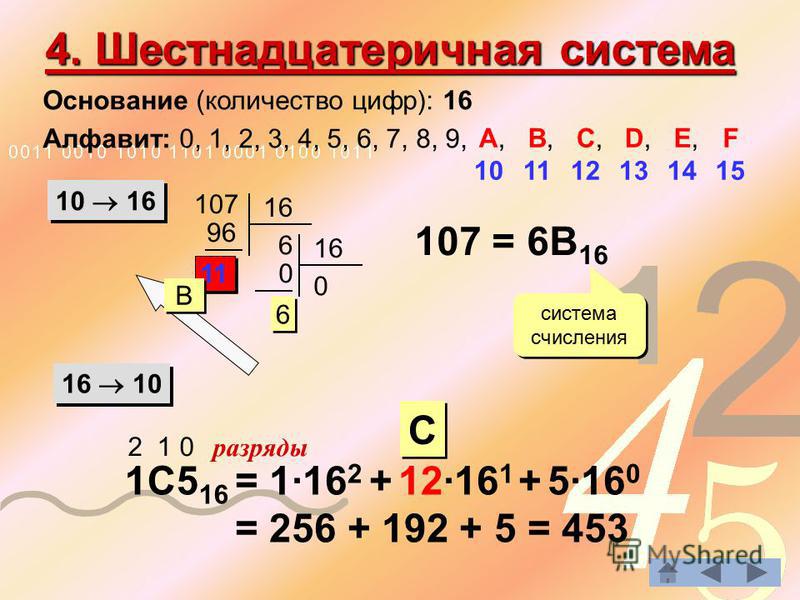 Мы используем в жизни десятичную систему. Уверен, что вы все ее знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя аналогию с десятичной.

Итак, в десятичной системе если мы к какому-нибудь числу справа добавим нуль, то это число увеличится в 10 раз. Например: 1 х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В этой системе мы используем цифры от 0 до 9, т.е. десять разных цифр (собственно, поэтому она и называется десятичная).

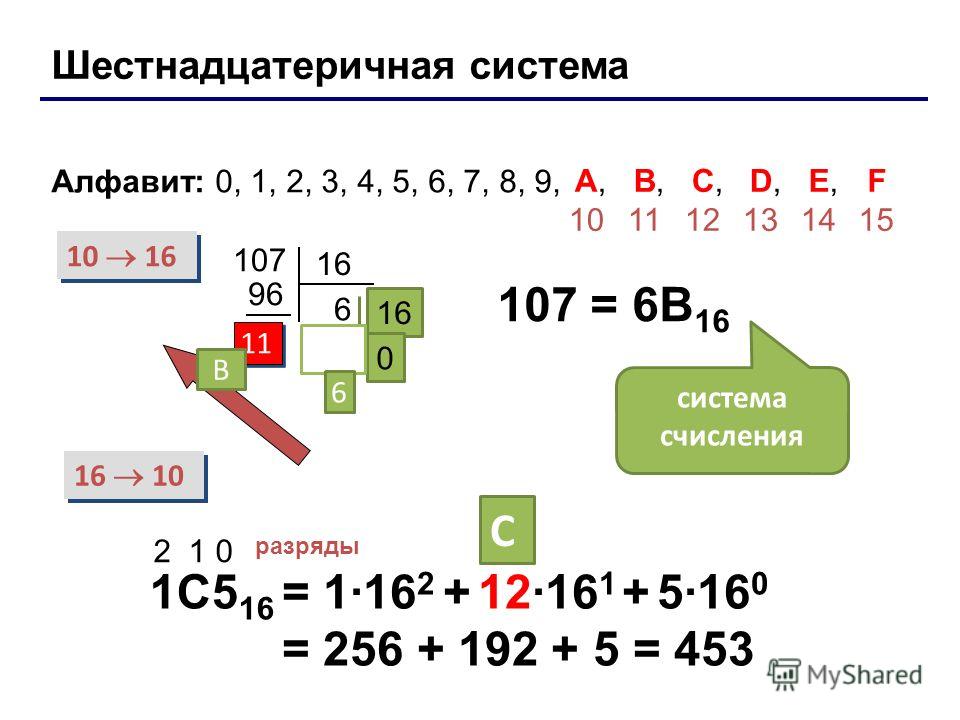
В шестнадцатеричной системе мы используем, соответственно, шестнадцать «цифр». Я специально написал слово «цифр» в кавычках, т.к. в ней используются не только цифры. Да и в самом деле как так? Объясняю: от 0 до 9 мы считаем так же, как и в десятичной, а вот дальше будет так: A, B, C, D, E, F. Число F, как не трудно посчитать, будет равно 15 в десятичной системе (см. табл. 1).

Десятичное число	Шестнадцатеричное число

Таблица 1. Десятичная и шестнадцатеричная системы.

Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в

16 раз.

Пример 1: 1 х 16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т.д.

Вы смогли отличить в Примере 1 шестнадцатеричные числа от десятичных? А из этого ряда: 10, 12, 45, 64, 12, 8, 19? Это могут быть как шестнадцатеричные, так и десятичные. Для того, чтобы не было путаницы, и компьютер смог бы однозначно отличить одни числа от других, в Ассемблере принято после шестнадцатеричного числа ставить символ h или H (H это сокращение от англ. hexadecimal (шестнадцатеричное). Для краткости его иногда называют просто Hex ) . А после десятичного ничего не ставить. Т.к. числа от 0 до 9 в обоих системах имеют одинаковые значения, то числа, записанные как 5 и 5h одно и тоже.

Т.о. Пример 1 (см. выше) правильнее будет записать так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h.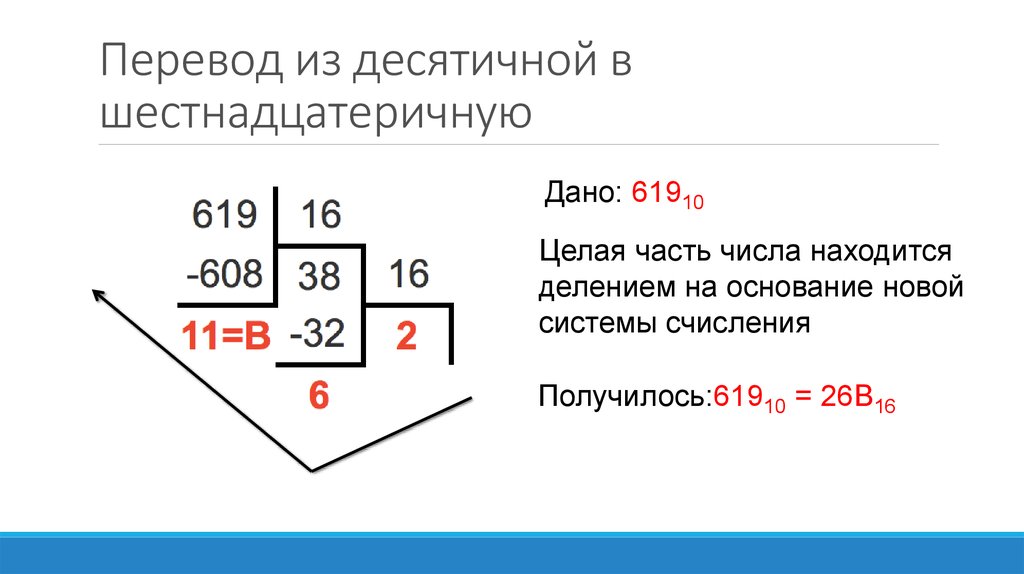 Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h = 1000h.

Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.

Итак, подведем итог. Шестнадцатеричная система счисления состоит из 10 цифр (от 0 до 9) и 6 букв латинского алфавита (A, B, C, D, E, F). Если к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в

16 раз. Очень важно уяснить данную тему , так как мы будем постоянно использовать ее при написании программ.

Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.

Примерно так:

строк	Код программы
(1)	mov ah,9

Объяснения:

В строке (1) мы делаем то-то, а в строке (15) то-то.

Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.

И еще. Строчные и ПРОПИСНЫЕ буквы в Ассемблере не различаются. Записи вида:

Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.

Итак, переходим к нашей первой программе:

(1) CSEG segment

(2) org 100h

(4) Begin:

(6) mov ah,9

(7) mov dx,offset Message

(8) int 21h

(10) int 20h

(11)

(12) Message db «Hello, world!$»

(13) CSEG ends

(14) end Begin

Для того, чтобы объяснить все операторы данного примера, нам потребуется несколько выпусков.

Поэтому описание некоторых команд мы просто опустим на данном этапе. Просто считайте, что так должно быть. В самое ближайшее время мы рассмотрим эти операторы подробно. Итак, строки с номерами (1), (2) и (13) вы просто игнорируете.

Строки (3), (5), (9) и (11) остаются пустыми. Это делается для наглядности. Ассемблер их будет просто опускать.

Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin ( Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).

Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).

Регистр процессора это специально отведенная память для хранения какого-нибудь числа.

Например:

Если мы хотим сложить два числа, то в математике запишем так:

A, B и C это своего рода регистры (если говорить о компьютере), в которых могут хранится некоторые данные. А=5 можно прочитать как: Присваиваем А число 5 .

Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.

В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).

Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.

Прерывание MS-DOS это своего рода подпрограмма (часть MS-DOS) , которая находится постоянно в памяти и может вызываться в любое время из любой программы.

Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):

Программа сложения двух чисел

НачалоПрограммы

A=5 в переменную A заносим значение 5

B=8 в переменную B значение 8

ВызовПодпрограммы Сложение

теперь С равно 13

A=10 тоже самое, только другие числа

B=25

ВызовПодпрограммы Сложение

теперь С равно 35

КонецПрограммы

Подпрограмма Сложение

C=A+B

ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали

КонецПодпрограммы

В данном примере мы дважды вызвали подпрограмму Сложение , которая сложила два числа, переданные ей в переменных A и B.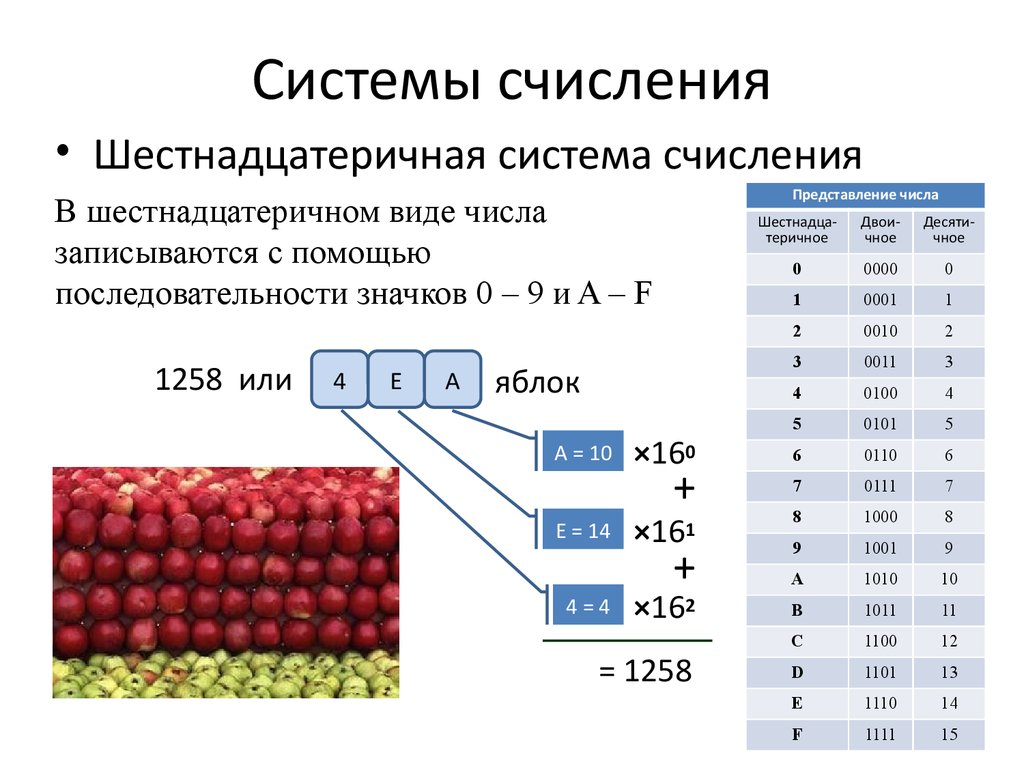 Результат помещается в переменную С. Когда вызывается подпрограмма, компьютер запоминает с какого места она была вызвана, а затем, когда закончила работу подпрограмма, компьютер возвращается в то место, откуда она вызывалась. Т.о. можно вызывать подпрограммы неопределенное количество раз с любого места.

При выполнении строки (8) программы на Ассемблере мы вызываем подпрограмму (в данном случае это называется прерывание), которая выводит на экран строку. Для этого мы, собственно, и помещаем необходимые значения в регистры. Всю необходимую работу (вывод строки, перемещение курсора) берет на себя подпрограмма. Эту строку можно прочитать так: вызываем двадцать первое прерывание ( int от англ. interrupt прерывание). Обратите внимание, что после числа 21 стоит буква h. Это, как мы уже знаем, шестнадцатеричное число (33 в десятичной системе). Конечно, нам ничего не мешает заменить строку int 21h на int 33. Программа будет работать корректно. Просто в Ассемблере принято указывать номер прерывания в шестнадцатеричной системе.

В строке (10) мы, как вы уже догадались, вызываем прерывание 20 h. Для вызова данного прерывания не нужно указывать какие-либо значения в регистрах. Оно выполняет только одну задачу: выход из программы (выход в DOS). В результате выполнения прерывания 20h, программа вернется туда, откуда ее запускали (загружали, вызывали). Например, в Norton Commander или DOS Navigator.

Строка (12) содержит сообщение для вывода. Первое слово ( message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.

Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:

(10) mov dx,offset Mess2

(13) Message db «Hello, world!$»

(14) Mess2 db «Это Я! $»

и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет

Обратите внимание на последний символ в строках Message и Mess2 — $. Он указывает на конец строки. Если мы его уберем, то 21 h прерывание продолжит вывод до тех пор, пока не встретится где-нибудь в памяти символ $. На экране мы увидим мусор .

Если у вас есть отладчик, то можно посмотреть как будет работать наша программа.

Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.

Возникла в древнем Вавилоне. В Индии система работает в виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали называть арабской.

Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.

Примеры , стандартная десятичная система счисления — это позиционная система. Допустим, дано число 453 . Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50 , а 3 — единицы и значению 3 . Легко заметить, что с увеличением разряда увеличивается значение. Таким образом, заданное число запишем в виде суммы 400+50+3=453.

Шестнадцатеричная система счисления.

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления. Основанием шестнадцатеричной системы счисления является число 16.

Записывая числа в восьмеричной системе счисления мы получаем довольно компактные выражения, однако в шестнадцатеричной системе мы получаем выражения более компактными.

Первыми десятью цифрами из шестнадцати шестнадцатеричных цифрах является стандартный интервал 0 — 9 , последующие шесть цифр выражают при помощи первых букв латинского алфавита: A , B , C , D , E , F . Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.

Применение шестнадцатеричной системы счисления.

Шестнадцатеричную систему счисления довольно хорошо используют в современных компьютерах, например с ее помощью указывают цвет: #FFFFFF — белый цвет.

Перевод чисел из одной системы счисления в другую.

Перевод чисел из шестнадцатеричной системы в десятичную.

Что бы перевести шестнадцатеричное число в десятичное , нужно заданное число привести к виду суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например , переведем шестнадцатеричное число 5A3 в десятичное. Здесь 3 цифры. Исходя их выше сказанного правила, приведем его к виду суммы степеней с основанием 16:

5A3 16 = 3·16 0 +10·16 1 +5·16 2 = 3·1+10·16+5·256 = 3+160+1280 = 1443 10

Перевод чисел из двоичной системы в шестнадцатеричную и наоборот.

Для перевода многозначного двоичного числа в шестнадцатеричную систему необходимо разделить его на тетрады справа налево и поменять все тетрады соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную необходимо поменять каждую все цифры на соответствующие тетрады из таблицы перевода, которую вы найдете ниже.

Например :

010110100011 2 = 0101 1010 0011 = 5A3 16

Таблица перевода чисел.

Алгоритм перевода чисел из одной системы счисления в другую.

1. Из десятичной системы счисления:

делим число на основание переводимой системы счисления;
находим остаток от деления целой части числа;
записываем все остатки от деления в обратном порядке;

2. Из двоичной системы счисления:

для перевода в десятичную систему счисления находим сумму произведений основания 2 на соответствующую степень разряда;
для перевода числа в восьмеричную разбиваем число на триады.

Например, 1000110 = 1 000 110 = 1068

для перевода числа из двоичной системы счисления в шестнадцатеричную разбиваем число на группы по 4 разряда.

Например, 1000110 = 100 0110 = 4616.

Таблицы для перевода:

Двоичная СС	Шестнадцатеричная СС
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

Двоичная СС

Шестнадцатеричная запись («Hex») — удобный способ представления двоичных значений. Так же, как десятичная система счисления имеет основание десять, а двоичная — два, шестнадцатеричная система имеет основание шестнадцать.

Система счисления с основанием 16 использует числа от 0 до 9 и буквы от A до F. Рисунок показывает эквивалентные десятичные, двоичные и шестнадцатеричные значения для двоичных чисел от 0000 до 1111. Для нас легче выражать значение в виде одной шестнадцатеричной цифры, чем в виде четырех битов.

Понимание Байтов

Учитывая, что 8 битов (байт) являются стандартной двоичной группировкой, двоичные числа от 00000000 до 11111111 могут быть представлены в шестнадцатеричной записи как числа от 00 до FF. Начальные нули всегда отображаются, чтобы завершить 8-разрядное представление. Например, двоичное значение 0000 1010 в шестнадцатеричном виде будет 0A.

Представление Шестнадцатеричных Значений

Отметьте: Важно отличать шестнадцатеричные значения от десятичных значений для символов от 0 до 9, как показано на рисунке.

Шестнадцатеричные значения обычно представляются в тексте значением, которому предшествует 0x (например 0x73), или с помощью нижнего индекса 16. Реже, они могут сопровождаться буквой H, например 73H. Однако, поскольку текст нижнего индекса не распознается ни в командной строке, ни в средах программирования, в техническом представлении шестнадцатеричных чисел им предшествует «0x» (нуль X). Поэтому, примеры выше были бы показаны в виде 0x0A и 0x73 соответственно.

Шестнадцатеричная запись используется, чтобы представлять MAC-адреса Ethernet и адреса IP Версии 6.

Шестнадцатеричные Преобразования

Преобразования чисел между десятичными и шестнадцатеричными значениями являются простыми, но быстрое деление или умножение на 16 не всегда удобно. Если такие преобразования необходимы, обычно легче преобразовать десятичное или шестнадцатеричное значение в двоичное, а затем преобразовать двоичное значение в десятичное или шестнадцатеричное, в зависимости от того, что требуется получить.

С практикой возможно распознать двоичные шаблоны битов, которые соответствуют десятичным и шестнадцатеричным значениям. Рисунок показывает эти шаблоны для некоторых 8-разрядных значений.

Многие пользователи компьютеров понимают, что компьютер работает в двоичной системе счисления. Традиционно состояния двоичной системы представляются цифрами 0 и 1, хотя, если говорить более точнее, каждое состояние обозначает наличие или отсутствие сигнала, т. е. правильнее будет назвать состояния «выключено» и «включено», либо «нет» и «да». Состоянию «выключено» или «нет» соответствует цифра 0, а состоянию «включено» или «да» цифра 1. Простым пользователям обычно нет необходимости полностью понимать устройство компьютера, однако двоичная система счисления дает о себе знать в виде различных ограничений основанных на степени двойки. Более компактный вариант двоичной системы называют шестнадцатеричной. Число шестнадцать является четвертой степенью числа два. Из этого следует, что можно достаточно просто переводить длинных двоичные последовательностей из нулей и единиц в короткие шестнадцатеричные. Для этого достаточно разбить двоичную последовательность на группы по четыре разряда (цифры) начиная с младшего разряда (справа) и заменить каждую группу на соответствующее шестнадцатеричное значение.

Шестнадцатеричную систему принято использовать для удобства восприятия двоичных данных, так как переводы из шестнадцатеричной системы в двоичную и обратно осуществляются простой заменой строк. Компьютер работает исключительно с двоичными последовательностями, а шестнадцатеричная запись этой последовательности в четыре раза компактнее, так как у этой системы основание 16 (2 16), а двоичной 2. Двоичная последовательность может быть достаточно громоздкой. Например, запись числа 513 требует десять двоичных разрядов (1000000001), а в шестнадцатеричной только три (201). Тем не менее, для представления любых шестнадцатеричных чисел требуется шестнадцать разных символов, а не десять, которые используются в привычной нам десятичной системе счисления. Первые десять символов это символы в интервале от 0 по 9, остальные это буквы латинского алфавита в интервале от A по F. Буквы обычно (но не всегда) пишут в верхнем регистре (заглавные) в шестнадцатеричной записи числа. Первые десять символов (от 0 по 9) записываются аналогично цифрам в десятичной системе счисления и соответствуют им.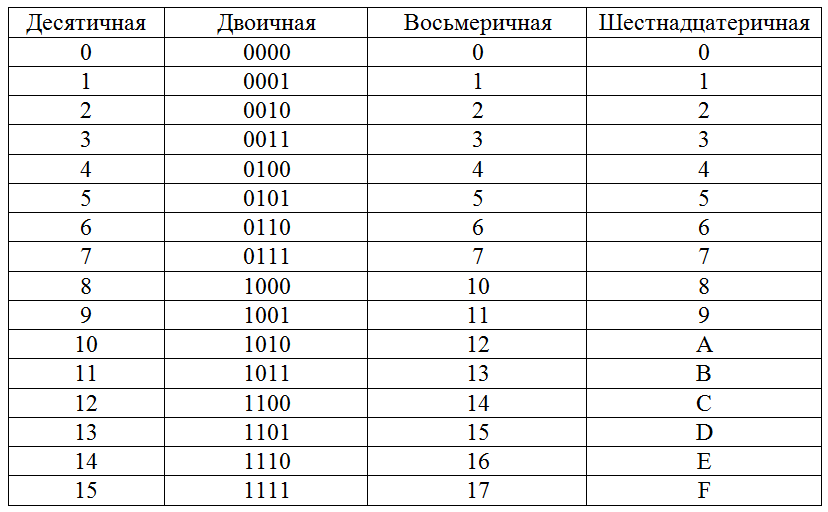 Буквы в интервале от A по F соответствуют значениям в интервале от 10 до 15.

Рассмотрим соответствие чисел от 0 по 15 шестнадцатеричной и двоичной системам счисления.

Десятичная запись	Шестнадцатеричная запись	Двоичная запись
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Записи 10, 11 и т. д. в десятичной, двоичной и шестнадцатеричной системах не соответствуют друг другу. Рассмотрим небольшой пример. Пусть у нас имеется шестнадцатеричное число число 1A5E. для перевода в двоичную запись достаточно просто заменить шестнадцатеричные разряды на соответствующие двоичные группы. Получится 0001 1010 0101 1110. Если убрать незначащие нули перед числом и записать его без разделителей получим 1101001011110. Для обратного перевода разделим число на группы по четыре разряда начиная с младшего (с правой стороны), а также для удобства добавим незначащие нули в старшей группе до 4 разрядов. Получим 0001 1010 0101 1110. Заменим группы на соответствующие шестнадцатеричные значения, получим 1A5E.

Для перевода шестнадцатеричного числа в десятичное представление можно воспользоваться схемой по которой мы записываем десятичные числа. В десятичном числе каждый разряд обозначает соответствующую степень числа десять начиная с нулевой с возрастанием справа налево. Например, десятичное число 123 обозначает 1*10 2 + 2*10 1 + 3*10 0 .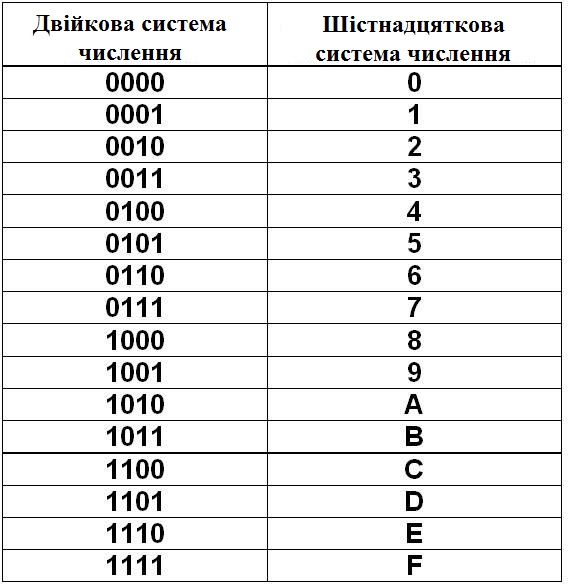 Аналогичным методом переведем число 1A5E в десятичную систему счисления. В шестнадцатеричной системе счисления, также как и в десятичной каждый разряд обозначает соответствующую степень числа шестнадцать начиная с нулевой с возрастанием справа налево. Символы 1 и 5 в шестнадцатеричной системе счисления соответствуют значениям 1 и 5 в десятичной, а символы A и E — 10 и 14. Тогда 1A5E можно представить в десятичной системе счисления как 1*16 3 + 10*16 2 + 5*16 1 + 14*16 0 = 6750. Однако для оценки шестнадцатеричных чисел вовсе не обязательно переводить их в десятичные. Правила сравнения, сложения и умножения в этой системе такие же как и в десятичной, главное не забывать, что каждый разряд может содержать значения от 0 до 15. Для более быстрого перевода числе между система счисления можно воспользоваться стандартным калькулятором в Windows, для этого достаточно в расширенном режиме калькулятора выбрать систему счисления, ввести в ней число и выбрать нужную систему счисления, в которой следует отобразить результат.

Так как шестнадцатеричные числа, состоящие только из чисел, легко спутать с десятичными, их обычно помечают так, чтобы было ясно, что используется именно шестнадцатеричная запись. Шестнадцатеричные записи обычно помечают либо добавлением в конец строчной буквы „h”, либо приставки „0x” перед записью числа. Таким образом шестнадцатеричное число 1A5E может быть записано как 1A5Eh или 0x1A5E, где „h” на конце или „0x” в начале обозначают, что используется шестнадцатеричная запись.

Шестнадцатеричная система счисления , на сегодняшний день является наиболее популярным средством компактной записи двоичных чисел. Очень широко используется при разработке и проектировании цифровой техники.

Как следует из названия, основанием данной системы является число шестнадцать 16 или в шестнадцатеричной системе 10 16 . Чтобы не было путаницы, при записи чисел в системах счисления отличных от десятичных, справа внизу от основной записи числа будем указывать основание системы счисления. Раз основанием системы является число шестнадцать, значит, для изображения чисел нам потребуется шестнадцать цифр. Первые десять цифр берутся из, привычной нам, десятичной системы (0,1,..,8,9) и еще добавляются шесть букв латинского алфавита (a,b,c,d,e,f) . Например в шестнадцатеричном числе 3f7c2 буквы «f» и «c» являются шестнадцатеричными цифрами.

Счет в шестнадцатеричной системе происходит аналогично счету в десятичной. Давайте попробуем считать и записывать числа конструируя их из имеющихся шестнадцати цифр:

Ноль — 0 ;
Один — 1 ;
Два — 2 ;
…
и так далее…
…
Восемь — 8 ;
Девять — 9 ;
Десять — a ;
Одиннадцать — b ;
Двенадцать — c ;
Тринадцать — d ;
Четырнадцать — e ;
Пятнадцать — f ;

А что делать дальше? Все цифры кончились. Как же изобразить число Шестнадцать? Поступим аналогично тому как мы поступали в десятичной системе. Там мы вводили понятие десятка, здесь же введем понятие «шестнадцать» и скажем, что шестнадцать — это одина «шестнадцать» и ноль единиц. А это уже можно и записать — «10 16 «.

Итак, Шестнадцать — 10 16 (одна «шестнадцать», ноль единиц)
Семнадцать — 11 16 (одна «шестнадцать», одна единица)
…
и так далее…
…
Двадцать пять — 19 16 (одна «шестнадцать», девять единиц)
Двадцать шесть — 1a 16 (одна «шестнадцать», десять единиц)
Двадцать семь — 1b 16 (одна «шестнадцать», одинадцать единиц)
…
и так далее…
…
Тридцать — 1e 16 (одна «шестнадцать», четырнадцать единиц)
Тридцать один — 1f 16 (одна «шестнадцать», пятнадцать единиц)
Тридцать два — 20 16 (две «шестнадцать», ноль единиц)
Тридцать три — 21 16 (две «шестнадцать», одна единица)
…
и так далее…
…
Двести пятьдесят пять — ff 16 (пятнадцать по «шестнадцать», пятнадцать единиц)

Двести пятьдесят шесть — 100 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», ноль единиц)
Двести пятьдесят семь — 101 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», одна единица)
Двести пятьдесят восемь — 102 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», две единицы)
. ..
и так далее…
…

Всегда, когда у нас исчерпался набор цифр для отображения следующего числа, мы вводим более крупные единицы счета (т.е. считаем по «шестнадцать», по «Двести пятьдесят шесть» и т.д.) и записываем число с удлинением на один разряд.

Рассмотрим число 3e2c 16 записанное в шестнадцатиричной системе счисления. Про него можно сказать, что оно содержит: три по четыре тысячи девяносто шесть, «e» (четырнадцать) по двести пятьдесят шесть, два по шестнадцать и «c» (двенадцать) единиц. И получить его значение через входящие в него цифры можно следующим образом.

3e2c 16 = 3 *4096+14 *256+2 *16+12 *1, здесь и далее знак * (звездочка) означает умножение.

Но ряд чисел 4096, 256, 16, 1 есть не что иное, как целые степени числа шестнадцать (основания системы счисления) и поэтому можно записать:

3e2c 16 = 3 *16 3 +14 *16 2 +2 *16 1 +12 *16 0

Подобным образом для шестнадцатиричной дроби (дробного числа) например: 0. 5a2 16 про него можно сказать, что оно содержит: пять шестнадцатых, «a» (десять) двести пятьдесят шестых и две четыретысячи девяносто шестых долей. И его значение можно вычислить следующим образом:

0.5a2 16 = 5 *(1/16) + 10 *(1/256) + 2 *(1/4096)

И здесь ряд чисел 1/16; 1/256 и 1/4096 есть не что иное, как целые степени числа шестнадцать и мы также можем записать:

0.5a2 16 = 5 *16 -1 + 10 *16 -2 + 2 *16 -3

Для смешанного числа 7b2.1f9 аналогичным образом можем записать:

7b2.1f9 = 7 *16 2 +11 *16 1 +2 *16 0 +1 *16 -1 +15 *16 -2 +9 *16 -3

Пронумеруем разряды целой части некоторого шестнадцатиричного числа, справа налево, как 0,1,2…n (нумерация начинается с нуля!). А разряды дробной части, слева направо, как -1,-2,-3…-m, то значение некоторого шестнадцатиричного числа может быть вычислено по формуле:

N = d n 16 n +d n-1 16 n-1 +…+d 1 16 1 +d 0 16 0 +d -1 16 -1 +d -2 16 -2 +…+d -(m-1) 16 -(m-1) +d -m 16 -m

Где: n — количество разрядов в целой части числа минус единица;
m — количество разрядов в дробной части числа
d i — цифра стоящая в i -м разряде

Эта формула называется формулой поразрядного разложения шестнадцатиричного числа, т.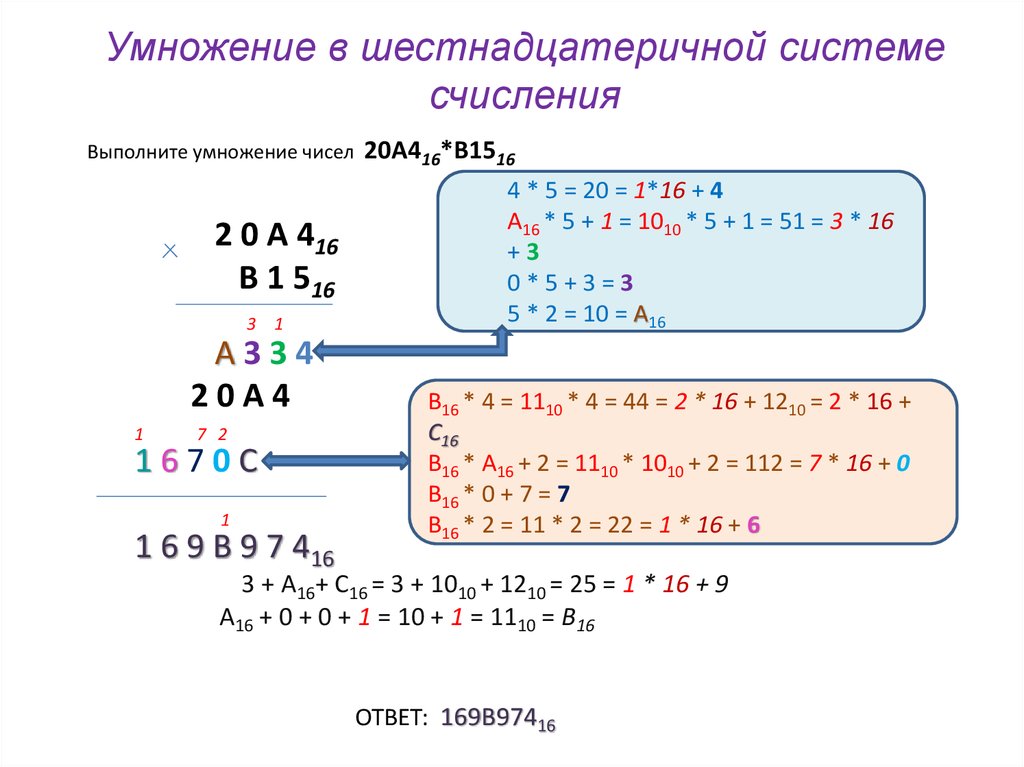 е. числа записанного в шестнадцатиричной системе счисления. Если мы в этой формуле заменим число шестнадцать на некоторое произвольное число q , то получим формулу разложения для числа записанного в q-й системе счисления, т.е. с основанием q :

N = d n q n +d n-1 q n-1 +…+d 1 q 1 +d 0 q 0 +d -1 q -1 +d -2 q -2 +…+d -(m-1) q -(m-1) +d -m q -m

По этой формуле всегда можно вычислить значение числа записанного в любой позиционной системе счисления с основанием q .

С другими системами счисления можно познакомиться на нашем сайте по следующим ссылкам.

513 в шестнадцатеричном формате: (513)10 = (?)16

Дом
Цифровые числа
Десятичный калькулятор
(513)10 в шестнадцатеричном формате

(513)10 = (?)16. Десятичное число 513 в шестнадцатеричном преобразовании содержит подробную информацию о том, что является шестнадцатеричным эквивалентом (513)10, и пошаговую работу по преобразованию десятичного числа 513 в его эквивалентное шестнадцатеричное число (с основанием 16) вручную.

(513)10 в шестнадцатеричном эквиваленте:
513 ₁₀ = 201 ₁₆

Следовательно,
(201)16 является шестнадцатеричным эквивалентом (513)10

, где
513 ₁₀ представляет данное десятичное число, 109 10-10-10 представляет основание 10 в 513 или десятичной системе счисления,
201 ₁₆ является шестнадцатеричным эквивалентом десятичной системы счисления 513,
16 в 201 ₁₆ представляет собой основание-16 или шестнадцатеричную систему счисления.

Важные примечания: (513)10 в шестнадцатеричном формате
Ниже приведены некоторые важные примечания, которые следует помнить при преобразовании десятичного числа 513 (с основанием 10) в шестнадцатеричный эквивалент (с основанием 16).

Начальный или первый остаток при выполнении операции 513 MOD-16 является наименее значащим битом (LSB).
Последним остатком при выполнении операции 513 MOD-16 является старший бит (MSB).
Найдите эквивалентное шестнадцатеричное число для каждого остатка операции 513 MOD-16, прежде чем упорядочивать числа от MSB до LSB, чтобы найти шестнадцатеричный эквивалент.
Остатки операции 513 MOD-16 в шестнадцатеричных эквивалентах должны быть записаны от MSB до LSB, чтобы сформировать шестнадцатеричный эквивалент для данного десятичного числа (513)10.

Для десятичных значений, отличных от 513, используйте следующий инструмент:

В приведенном ниже пошаговом решении показано, как преобразовать (513)10 в эквивалентное ему шестнадцатеричное число. Представьте каждый остаток операции 513 MOD-16 в шестнадцатеричном эквиваленте и упорядочив их от MSB к LSB, получится шестнадцатеричный эквивалент 513.

Решенный Пример:
Что такое шестнадцатеричный эквивалент 513?

шаг 1 Обратите внимание на входные параметры, значения и то, что нужно найти:

Входные значения:
Десятичное число = (513) ₁₀

Что нужно найти:
Каково шестнадцатеричное значение десятичного числа 513?
(513)10 = (?)16

Шаг 2 Выполните последовательную операцию MOD-16 для десятичного числа 513, пока частное не станет равным 0, и отметьте начальный остаток как младший бит, а конечный остаток как старший бит, как показано ниже:

Последовательная операция MOD-16 для 513

513 MOD-16	513 / 16 = 32	Remainder is 1 → LSB
32 MOD-16	32 / 16 = 2	Remainder is 0
2 MOD-16	2 / 16 = 0	Остаток равен 2 → MSB

шаг 3 Используйте приведенную ниже таблицу, чтобы найти эквивалентное шестнадцатеричное представление для каждого остатка последовательной операции 513 MOD-16:

Decimal:	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
HEX:	1	2	3	4	5	6	7	8	0		8	0		8		0	8		00100	B	C	D	E	F

Десятичная 1 в шестнадцатеричном формате равна 1 → LSB
Десятичная 0 в шестнадцатеричном формате равна 0
Десятичная 2 в шестнадцатеричном формате равна 2 → MSB

шаг 4 эквивалентное шестнадцатеричное число (с основанием 16) для десятичного числа (с основанием 10) 513:
= 201
(513) ₁₀ = (201) ₁₆

Следовательно,
шестнадцатеричный эквивалент 513 равен (201)16.

Десятичный 513 в шестнадцатеричном формате | работа, решение

Как написать 513 в шестнадцатеричном формате?

513 записывается как 201 в шестнадцатеричном формате

Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Десятичное число 513 в шестнадцатеричном формате | работа, решение или преобразование десятичного в шестнадцатеричное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.

Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.

С помощью этого конвертера вы можете получить ответы на такие вопросы, как:

Что такое 513 в двоичном формате?
Что такое 513 в шестнадцатеричном формате?
Что такое 513 в восьмеричной системе?
Как преобразовать 513 в двоичный код?
Как преобразовать 513 в двоичный код? И так далее.

Десятичная в двоичную диаграмму, включая шестнадцатеричную и восьмеричную0100

0 0 1 1 1 1 2 2 2 10 3 3 3 11 4 4 4 100 5 5 5 101 6 6 6 110 7 7 7 111 8 8 10 1000 9 9 11 1001 10 A 12 1010 11 B 13 1011 12 C 14 1100 13 D 15 1101 14 E 16 1110 15 F 17 1111

Dec	Hex	Oct	Bin
16	10	20	10000
17	11	21	10001
18	12	22	10010
19	13	23	10011
20	14	24	10100
21	15	25	10101
22	16	26	10110
23	17	27	10111
24	18	30	11000
25	19	31	11001
26	1A	32	11010
27	1B	33	11011
28	1C	34	11100
29	1D	35	11101
30	1E	36	11110
31	1F	37	11111

Dec	Hex	Oct	Bin
32	20	40	100000
33	21	41	100001
34	22	42	100010
35	23	43	100011
36	24	44	100100
37	25	45	100101
38	26	46	100110
39	27	47	100111
40	28	50	101000
41	29	51	101001
42	2A	52	101010
43	2B	53	101011
44	2C	54	101100
45	2D	55	101101
46	2E	56	101110
47	2F	57	101111

Dec	Hex	Oct	Bin
48	30	60	110000
49	31	61	110001
50	32	62	110010
51	33	63	110011
52	34	64	110100
53	35	65	110101
54	36	66	110110
55	37	67	110111
56	38	70	111000
57	39	71	111001
58	3A	72	111010
59	3B	73	111011
60	3C	74	111100
61	3D	75	111101
62	3E	76	111110
63	3F	77	111111

Образцы базовых переводов

300000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Frail.