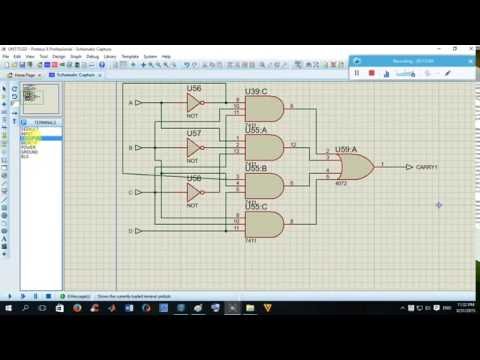
Изучение работы 4-х разрядного полного сумматора с ускоренным переносом (к555им6, 74283).
Он строится на основе 4-х разрядного полного сумматора и схемы ускоренного переноса. Такое включение обеспечивает одновременное появление выходного сигнала даже при увеличении разрядности сумматора.
Рис. 4 Условно-графическое обозначение сумматора К555ИМ6.
Таблица 3. Таблица истинности одноразрядного полного сумматора.
Рис. 5 Схема исследования сумматора К555ИМ6.
Рис. 6 Временные диаграммы, поясняющие сумматора К555ИМ6.
Таблица 4. Таблица задержек сумматора К555ИМ6.
С0 | А1 | А2 | А4 | В1 | В2 | В3 | В4 | ||
С4 | |||||||||
S1 | |||||||||
S2 | |||||||||
S3 | |||||||||
S4 |
Справочные данные: время задержки
распространения сигнала не более 24 нс.
Вывод: смоделированная схема работает согласно таблице истинности данного сумматора. Полученные в результате моделирования времена задержки распространения сигнала соответствуют типовым значениям для использованных при моделировании схем.
3.Изучение работы 4-х разрядного вычитателя, построенного на одноразрядном полном сумматоре (к155им5,74ls183).
Данное устройство выполняет операцию вычитания двоичных чисел: S = A – B. Если число B > A, то на выходе Cn+1 субтрактора появляется сигнал высокого уровня.
Одноразрядный вычитатель можно построить на основе одноразрядного полного сумматора, подключив ко входу А и к выходу S инверторы. Действительно, подставив в таблицу одноразрядного полного сумматора значение A , получим, что S = S’, Сn+1 = Cn+1‘
Рис. 7 Условно-графическое обозначение сумматора К155ИМ5.
Таблица 5.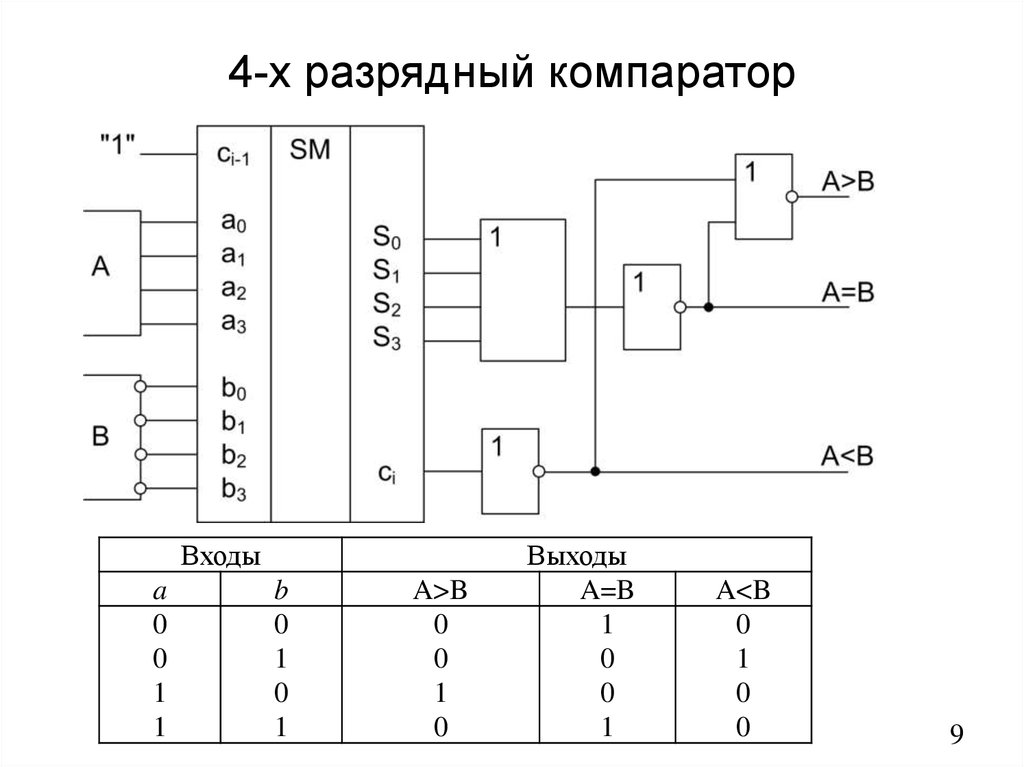
Таблица истинности
одноразрядного вычитателя
Рис.8 Схема исследования четырехразрядного вычитателя
Рис. 9 Временные диаграммы, поясняющие работу четырёхразрядного вычитателя
Таблица 6. Таблица задержек четырёхразрядного вычитателя.
С0 | А1 | А2 | А3 | А4 | В1 | В2 | В3 | В4 | |
Р | |||||||||
S1 | — | — | — | — | — | — | |||
S2 | — | — | — | — | |||||
S3 | — | — | |||||||
S4 |
Справочные данные(74LS183):
среднее время задержки распространения
сигнала 15 нс.
Вывод: смоделированная схема работает согласно таблице истинности данного четырехразрядного вычитателя. Полученные в результате моделирования времена задержки распространения сигнала соответствуют типовым значениям для использованных при моделировании схем.
НОУ ИНТУИТ | Лекция | Комбинационные микросхемы. Часть 2
< Лекция 5 || Лекция 6: 1234 || Лекция 7 >
Аннотация: В лекции рассказывается о комбинационных микросхемах: сумматорах, преобразователях кодов, одновибраторах и генераторах, об их алгоритмах работы, параметрах, типовых схемах включения, а также о реализации на их основе некоторых часто встречающихся функций.
Ключевые слова: сумматор, adder, входной, SM, функция, единица, таблица истинности, разность, выход, быстродействие, Z-резистор, одновибраторы, monostable multivibrator, логический уровень, память, информация, инверсный выход, логический, прямой, вывод, запуск, интервал, погрешность, генератор, диапазон, значение
Сумматоры
intuit.ru/2010/edi»>Микросхемы сумматоров (английское Adder), как следует из их названия, предназначены для суммирования двух входных
двоичных кодов, то есть выходной код будет равен арифметической сумме двух входных кодов. Например, если один входной
код — 7 (0111), а второй — 5 (0101), то суммарный код на выходе будет 12 (1100). Сумма двух двоичных чисел с числом
разрядов N может иметь число разрядов (N + 1). Например, при суммировании чисел 13 (1101) и 6 (0110) получается
число 19 (10011). Поэтому количество выходов сумматора на единицу больше количества разрядов входных кодов. Этот
дополнительный (старший) разряд называется выходом переноса.На схемах сумматоры обозначаются буквами SM. В отечественных сериях код, обозначающий микросхему сумматора, — ИМ.
Сумматоры бывают одноразрядные (для суммирования двух одноразрядных чисел), 2-х разрядные (суммируют 2-х разрядные
числа) и 4-х разрядные (суммируют 4-х разрядные числа).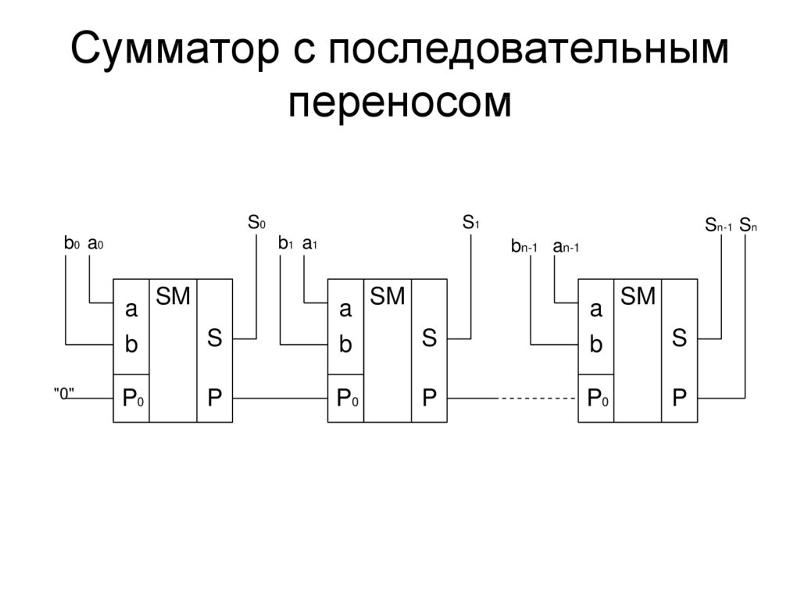
Рис. 6.1. Примеры микросхем сумматоров
Помимо выходных разрядов суммы и выхода переноса, сумматоры имеют вход расширения (другое название — вход переноса) С для объединения нескольких сумматоров с целью увеличения разрядности. Если на этот вход приходит единица, то выходная сумма увеличивается на единицу, если же приходит нуль, то выходная сумма не увеличивается. Если используется одна микросхема сумматора, то на ее вход расширения С необходимо подать нуль.
Для примера в табл. 6.1 приведена полная таблица истинности 2-разрядного сумматора ИМ2.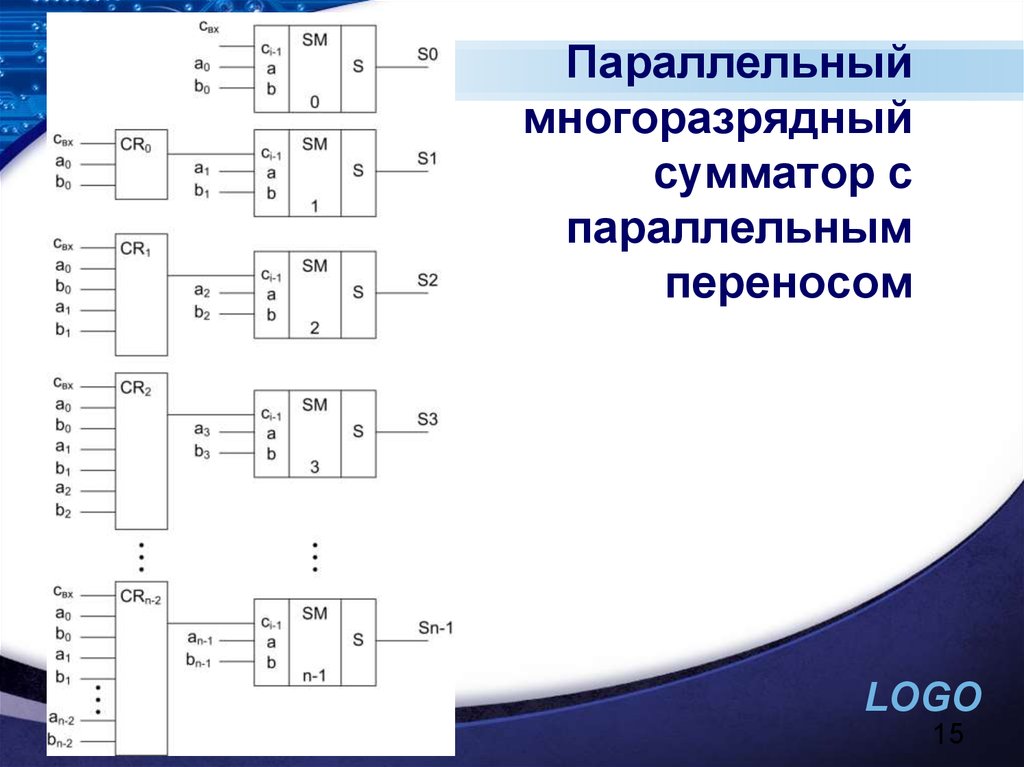
Как видно из таблицы,
выходной 3-разрядный код (Р, S1, S0) равен сумме входных 2-разрядных кодов (А1, А0) и (В1, В0), а также сигнала С.
Нулевые разряды — младшие, первые разряды — старшие. Полная таблица истинности 4-разрядного сумматора будет
чрезмерно большой, поэтому она не приводится. Но суть работы остается точно такой же, как и в случае 2-разрядного
сумматора.
Сумматоры могут использоваться также для суммирования чисел в отрицательной логике (когда логической единице
соответствует электрический нуль, и наоборот, логическому нулю соответствует электрическая единица). Но в этом
случае входной сигнал переноса С также становится инверсным, поэтому при использовании одной микросхемы сумматора
на вход С надо подать электрическую единицу (высокий уровень напряжения). Инверсным становится и выходной сигнал
переноса Р, низкий уровень напряжения на нем (электрический нуль) соответствует наличию переноса. То есть получается,
что сумматор абсолютно одинаково работает как с положительной, так и с отрицательной логикой.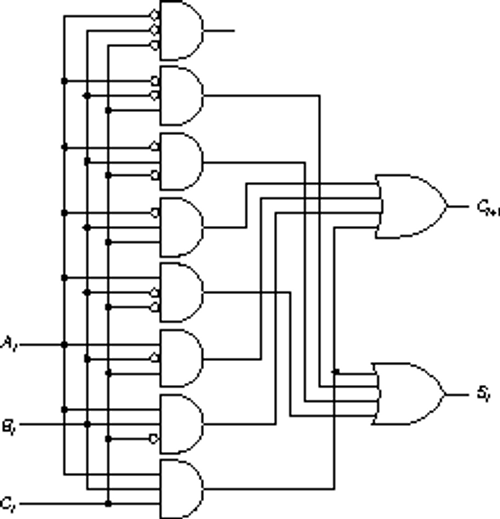
| Входы | Выходы | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| C=0 | C=1 | ||||||||
| A1 | A0 | B1 | B0 | P | S1 | S0 | P | S1 | S0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 |
intuit.ru/2010/edi»>Рассмотрим пример. Пусть нам надо сложить два числа 5 и 7 в отрицательной логике. Числу 5 в положительной
логике соответствует двоичный код 0101, а в отрицательной — код 1010. Числу 7 в положительной логике соответствует
двоичный код 0111, а в отрицательной — код 1000. При подаче на вход сумматора кодов 1010 (десятичное число 10 в
положительной логике) и 1000 (десятичное число 8 в положительной логике) получаем сумму 10 + 8 = 18, то есть код
10010 в положительной логике. С учетом входного сигнала переноса С=1 (отсутствие входного переноса в отрицательной
логике) выходной код сумматора получится на единицу больше: 18 + 1 = 19, то есть 10011. При отрицательной логике
это будет соответствовать числу 01100, то есть 12 при отсутствии выходного переноса. В результате получили 5+7=12.Сумматор может вычислять не только сумму, но и разность входных кодов, то есть работать вычитателем. Для
этого вычитаемое число надо просто поразрядно проинвертировать, а на вход переноса С подать единичный сигнал
(рис.
6.2).
Рис. 6.2. 4-х разрядный вычитатель на сумматоре ИМ6 и инверторах ЛН1
Например, пусть нам надо вычислить разность между числом 11 (1011) и числом 5 (0101). Инвертируем поразрядно число 5 и получаем 1010, то есть десятичное 10. Сумматор при суммировании 11 и 10 даст 21, то есть двоичное число 10101. Если сигнал С равен 1, то результат будет 10110. Отбрасываем старший разряд (выходной сигнал Р) и получаем разность 0110, то есть 6.
Еще пример. Пусть надо вычислить разность между числом 12 (1100) и числом 9 (1001). Инвертируем поразрядно 9, получаем 0110, то есть десятичное 6. Находим сумму 12 и 6, получаем 18, а с учетом С = 1 получаем 19, то есть двоичное 10011. В четырех младших разрядах имеем 0011, то есть десятичное 3.
Каскадировать сумматоры для увеличения разрядности очень просто.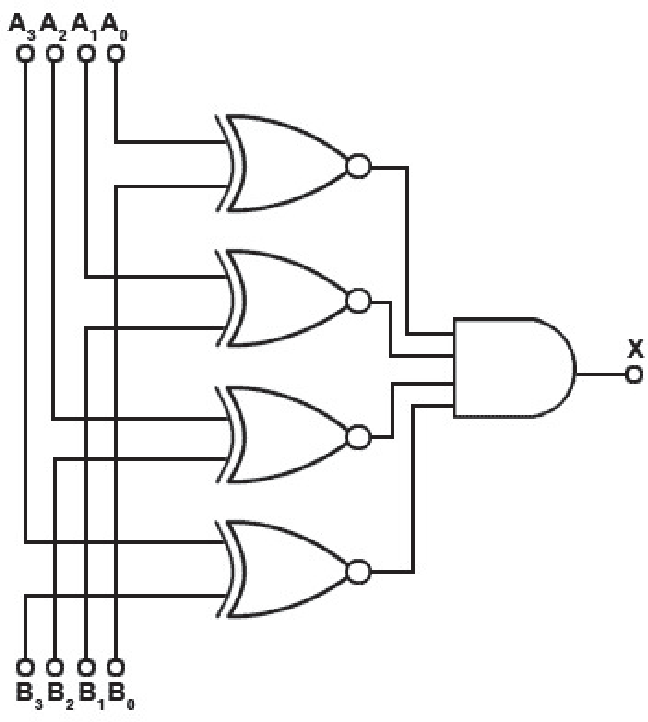
Надо сигнал с выхода переноса сумматора,
обрабатывающего младшие разряды, подать на вход переноса сумматора, обрабатывающего старшие разряды
(рис. 6.3).
При объединении трех 4-разрядных сумматоров получается 12-разрядный сумматор, имеющий дополнительный 13-й разряд
(выход переноса Р).
Рис. 6.3. Каскадирование сумматоров ИМ6 для увеличения разрядности
Неопределенные состояния на выходах сумматора могут возникать при любом изменении любого из входных кодов
(рис. 6.4). Выходной код суммы может принимать в течение короткого времени значения, никак не связанные с
входными кодами, а на выходе переноса могут появляться короткие паразитные импульсы. Это связано прежде всего
с неодновременным изменением разрядов входных кодов. Чтобы избежать влияния этих неопределенных состояний на
дальнейшую схему, необходимо предусматривать синхронизацию или стробирование выходных сигналов.
Но для этого
надо располагать информацией о моментах изменения входных кодов, которая имеется далеко не всегда.
Рис. 6.4. Неопределенные состояния на выходах сумматора при изменении входных кодов
Задержки сумматора ИМ6 от входов до выходов суммы примерно вдвое превышает задержку логического элемента, а от входов до выхода переноса — примерно в полтора раза. Задержки сумматора ИМ3 больше задержек ИМ6 почти вдвое. Поэтому в схемах, где важно быстродействие, лучше использовать ИМ6. Особенно это существенно при каскадировании для увеличения разрядности, так как там задержки отдельных микросхем суммируются. Точные величины задержек надо смотреть в справочниках.
Дальше >>
< Лекция 5 || Лекция 6: 1234 || Лекция 7 >
4-значное сложение — с перегруппировкой
LearnPracticeDownload
4-значное сложение относится к сложению чисел, в которых одно или оба слагаемых состоят из 4 цифр.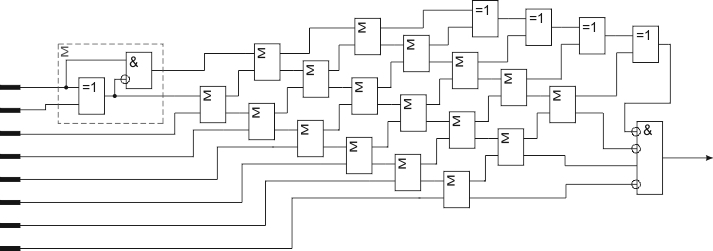
Процедура сложения 4-х цифр такая же, как и сложения 3-х цифр, только с увеличением количества цифр в слагаемых. Давайте узнаем больше о 4-значном сложении с перегруппировкой и без перегруппировки вместе с решенными примерами.
| 1. | Что такое 4-значное сложение? |
| 2. | 4-значное сложение без перегруппировки |
| 3. | Добавление 4 цифр с перегруппировкой |
| 4. | Сложение 4 цифр с использованием 3 цифр |
| 5. | Часто задаваемые вопросы о 4-значном дополнении |
Что такое 4-значное сложение?
4-значное сложение требует правильного размещения чисел в столбцах с использованием соответствующих разрядов, таких как единицы, десятки, сотни, тысячи и т. д. Сложение 4-значных чисел выполняется так же, как сложение 2- или 3-значных чисел с переносом и без переноса.
В арифметическом сложении складываемые числа называются слагаемыми, а конечный результат, который мы получаем после сложения этих чисел, называется суммой.
При сложении 4-х цифр мы в основном используем метод сложения столбцов. Давайте разберемся с 4-значным сложением, выполнив следующие шаги:
- Шаг 1: Разместите числа (сложения), которые нужно сложить, таким образом, чтобы они располагались в столбцах в соответствии с их разрядностью. Например, цифра единиц должна быть в столбце единиц, цифра десятков должна быть в столбце десятков и так далее.
- Шаг 2: Затем числа можно добавлять столбец за столбцом справа налево, начиная с столбца единиц.
- Шаг 3: После завершения сложения соответствующие суммы записываются внизу.
- Шаг 4: Ту же процедуру необходимо повторить для всех разрядных значений, пока мы не достигнем разряда тысяч.
4-значное сложение без перегруппировки
При выполнении 4-значного сложения, если сумма цифр слагаемых меньше или равна 9, такое сложение называется 4-значным сложением без перегруппировки или без переноса.
Давайте разберемся с 4-значным сложением на примере. Давайте добавим 4-значные числа: 6134 и 2423, используя следующие шаги.
- Шаг 1: Добавьте числа в столбце единиц. 4 + 3 = 7. Напишите 7 в столбце единиц.
- Шаг 2: Добавьте числа в столбце десятков. 3 + 2 = 5. Запишите 5 в столбце десятков.
- Шаг 3: Добавьте числа в столбец сотен. 1 + 4 = 5. Запишите 5 в столбце сотен.
- Шаг 4: Добавьте числа под столбцом тысяч. 6 + 2 = 8. Запишите 8 в столбце тысяч.
Следует отметить, что сумма каждого столбца меньше 9так что никакой перегруппировки. Таким образом, сложение четырехзначных чисел 6134 и 2423 дает сумму 8557.
4-значное сложение с перегруппировкой
Сложение, при котором сумма цифр слагаемых в любом из столбцов больше 9, называется сложением с перегруппировкой или сложением с переносом. Чтобы сложить два числа с перегруппировкой, мы находим сумму цифр, а затем пишем только единицы, ставя цифру суммы в соответствующий столбец.
Затем мы переносим разряд десятков в столбец слева и продолжаем сложение. Давайте разберемся с 4-значным сложением с перегруппировкой на примере.
Пример: Сложите 4-значные числа: 3195 и 6237.
Решение: Выполним сложение 4-значных чисел с перегруппировкой, используя следующие шаги.
- Шаг 1: Добавьте числа в столбце единиц. 5 + 7 = 12. Напишите 2 в столбце единиц и перенесите 1 в столбец десятков. (Перегруппировка)
- Шаг 2: Добавьте числа в столбце десятков. 9 + 3 + 1 (перенос) = 13. Запишите 3 в столбце десятков и перенесите 1 в столбец сотен. (Перегруппировка)
- Шаг 3: Добавьте числа в столбец сотен. 1 + 2 + 1 (перенос) = 4. Запишите 4 в столбце сотен.
- Шаг 4: Добавьте числа в столбец тысяч. 3 + 6 = 9 тысяч. Напишите 9 в колонке тысяч.
Таким образом, сложение четырехзначных чисел 3195 и 6237 дает в сумме 9432.
4-значное сложение с использованием 3 чисел
4-значное сложение также можно выполнить с помощью 3 слагаемых.
Давайте разберемся в этом с помощью примера.
Пример: Сложите 4-значные числа: 4013, 1223 и 9903.
Решение: Давайте выполним шаги, описанные ниже, для сложения 4-значных чисел.
- Шаг 1: Добавьте числа в столбце единиц. 3 + 3 + 3 = 9. Напишите 9 в столбце единиц.
- Шаг 2: Добавьте числа в столбце десятков. 1 + 2 + 0 = 3. Запишите 3 в столбце десятков.
- Шаг 3: Добавьте числа в столбец сотен. 0 + 2 + 9 = 11. Напишите 1 в столбце сотен и перенесите 1 в столбец тысяч.
- Шаг 4: Добавьте числа в столбец тысяч. 4 + 1 + 9 + 1 (перенос) = 15. Запишите 5 в столбце тысяч и 1 в качестве переноса в столбце десяти тысяч. Поскольку в столбце с десятью тысячами нет числа, мы уменьшим перенос 1 в столбце с десятью тысячами.
Таким образом, сложение четырехзначных чисел 4013, 1223 и 9903 дает сумму 15139.
0056 Пример 1: Сложите заданные четырехзначные числа: 4472 и 5227. Решение: Выполним четырехзначное сложение данных чисел, используя следующие шаги. Таким образом, сложение четырехзначных чисел 4472 и 5227 дает в сумме 9699. Пример 2: Сложите заданные четырехзначные числа, 7963 и 3278. Решение: Выполним сложение четырехзначных чисел, используя следующие шаги. Таким образом, сложение четырехзначных чисел 7963 и 3278 дает сумму 11241. Пример 3: Сумма 4010 и 3111 равна ____. Решение: При сложении 4-значного числа мы начинаем сложение со столбца единиц, затем столбца десятков, затем столбца сотен и, наконец, столбца тысяч. Следовательно, сумма 4010 и 3111 равна 7121. перейти к слайдуперейти к слайдуперейти к слайду Разбивайте сложные концепции с помощью простых визуальных средств. Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций. Записаться на бесплатный пробный урок перейти к слайдуперейти к слайду Примеры 4-значного сложения
Запишите 4 в столбце десятков и перенесите 1 в столбец сотен.
4 + 3 = 7. Напишите 7 в столбце тысяч. Практические вопросы по сложению четырехзначных чисел
Часто задаваемые вопросы о 4-значном дополнении
Что такое 4-значное сложение в математике?
4-значное сложение — это сложение, когда одно или оба сложения состоят из 4 цифр. При выполнении 4-значного сложения мы добавляем каждую цифру одну за другой, начиная со столбца единиц, за которым следует столбец десятков, столбец сотен и затем столбец тысяч.
Какое правило сложения четырехзначных чисел?
Правила сложения 4-значных чисел такие же, как и для сложения 2-значных или 3-значных чисел.
Ниже приведены основные правила сложения четырехзначных чисел:
- Мы начинаем складывать числа по столбцам справа налево, добавляя числа в каждом столбце. Это означает, что мы начинаем со столбца единиц, затем переходим к столбцу десятков, затем к столбцу сотен и так далее.
- После завершения сложения соответствующие суммы записываются внизу.
- Ту же самую процедуру нужно повторить для всех разрядных значений, пока мы не достигнем разряда тысяч.
Приведите пример сложения 4-х цифр с перегруппировкой.
Вот пример 4-значного сложения с перегруппировкой. Давайте добавим 3195 и 6237.
- Шаг 1: Добавьте числа в столбце единиц. 5 + 7 = 12. Напишите 2 в столбце единиц и перенесите 1 в столбец десятков.
- Шаг 2: Добавьте числа в столбце десятков. 9 + 3 + 1 (перенос) = 13. Запишите 3 в столбце десятков и перенесите 1 в столбец сотен.
- Шаг 3: Добавьте числа в столбец сотен. 1 + 2 + 1 (перенос) = 4. Запишите 4 в столбце сотен.
- Шаг 4: Добавьте числа в столбец тысяч. 3 + 6 = 9. Запишем 9 в столбце тысяч.
Таким образом, сумма 3195 и 6237 равна 9432.
Как сложить 4 цифры без перегруппировки?
4-значное сложение без перегруппировки означает сложение чисел по столбцам, начиная со столбца единиц, за которым следует столбец десятков, затем столбец сотен и затем столбец тысяч. При этом сумма чисел всегда меньше или равна 9поэтому нет переноса, следовательно, нет перегруппировки чисел.
Что такое сложение и вычитание четырехзначных чисел?
4-значное сложение и вычитание аналогичны 3-значному сложению и вычитанию, за исключением того факта, что количество цифр в числах должно быть 4. 4-значное сложение означает сложение, в котором одно или оба слагаемых равны 4- цифры числа. Точно так же 4-значное вычитание означает вычитание, состоящее из 4-значных чисел.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочий лист для сложения 4 цифр
Рабочие листы по математике и
наглядный учебный план
Изучение определений, фактов и примеров
Сложение является одной из основных математических операций , которая представляет собой процесс сложения двух или более двух величин или чисел вместе, чтобы получить общее количество.
Числа, которые складываются друг с другом, называются слагаемыми, а результат суммы, которую мы получаем после выполнения операции, называется суммой. Самый простой способ получить сумму 4-значных чисел состоит в том, чтобы сначала расположить их в соответствии с их разрядными значениями: единицы числа в разряде единиц, десятки в разряде десятков, сотни в разряде сотен и тысячи в разряде тысяч.
Шаги для решения 4-значного сложения
После того, как вы расположили свои числа в соответствии с их разрядами, затем нужно сложить все числа, которые лежат на их единицах, десятках, сотнях и тысячах. Имейте в виду, что всегда важно сначала добавить те, а затем остальные.
Когда мы делаем сложение чисел , всегда начинайте складывать числа с правой стороны на левую.
Короче говоря, правила такие же, как и для чисел, содержащих менее 4 цифр или около того.
Например: (i) 6437 + 3241
Шаг 1: Складываем числа, которые выпадают до своего номинала единиц => 7+1=8
Шаг 2: Складываем числа, которые выпадают до своего номинала десятков => 3+4=7
Шаг 3: Сложение чисел, которые выпадают на сотни номинала => 4+2=6
Шаг 4: Сложение чисел, выпадающих на тысячный номинал => 6+3=9
Расположение чисел в соответствии с их номиналами для сложения
Пример: (ii) 2488 + 9927
4-значный Пример сложения чисел
Сложение единиц 8+7=15, перенос 1 вперед и запись 5 в столбце единиц
Сложение десятков 1+8+2= 11, перенос вперед и запись 1 в столбце десятков
Сложение сотен 1+3+9=13, перенос 1 вперед и запись 3 в столбец сотен
Сложение тысяч 1+2+9= 12, запишите 12 как есть.
Сумма 2388 + 9927 равна 12315.
ПРИМЕЧАНИЕ. Если сумма чисел имеет двузначное число, то вы переносите ее на следующую цифру, за исключением последней цифры, потому что вы можете прямо записать ее вместо ответа. . Не надо возить.
Решенные примеры
Q 1. 7001 + 6999
Решенный пример 4-значного сложения Вопрос
Ответ: Сложение единиц 1+9=10, перенос 1 вперед и запись 0 в столбце единиц
Сложение десятков 1+0+9= 10, перенос вперед и запись 0 в столбце десятков
Сложение сотен 1+0+9=10, перенос 1 и запись 0 в столбце сотен
Сложение тысячи 1 + 7 + 6 = 14, запишите 14 как есть.
Сумма 7001 + 6999 равна 14000.
Вопрос 2. 2224 + 9347
Решенный пример 4-значного сложения Вопрос
Ответ: Сложение единиц 4+7=11, перенос 1 вперед и запись 1 в столбце единиц
Сложение десятков 1+2+4= 7,
Сложение сотен 2+3=5,
Сложение тысяч 2+9= 11, запишите 11 как есть.
The sum of 2224 + 9347 is 11571.
Practice Questions
Q 1. 4994 + 3445
Ans: 8439
Q 2. 9543 + 3543
Ans: 13086
Q 3. 2998 + 6758
ANS: 9756
Q 4. 5379 + 3909
ANS: 9288
Q 5. 1209 + 6480
ANS: 7689
Q 6. 7645 + 6598
534.243434343434 3S: 140325 Q 6. 7645 + 6598
5.0003
Q 7. 5347 + 4650
Ответ: 9,997
Q 8. 8905 + 5321
Ответ: 14,226
Резюме
Выполняется операция сложения двух и более чисел. попытался научить самый простой способ сложить 4-значных чисел . Вы ознакомились с пошаговой процедурой сложения четырехзначных чисел, и в статье также было показано несколько решенных примеров для лучшего понимания.
