1.2 Перевод целых чисел из одной системы счисления в другую
Возможен перевод чисел из десятичной системы счисления в двоичную. Для этого надо число, заданное в десятичной системе счисления, разделить на основание двоичной системы счисления 2. Причем деление производить до тех пор, пока частное не станет меньше делителя, а получившиеся остатки записать в обратном порядке.
При обратном переводе используется метод, базирующийся на умножении цифр переводимого числа на основание двоичной системы счисления в степени q, где q – порядковый номер разряда.
Контрольный пример. Перевести число 614 из десятичной системы счисления в двоичную.
Для
этого число 61410 делим на
основание двоичной системы счисления
– цифру 2. Полученное частное делим до
тех пор, пока оно не станет меньше
делителя (основания двоичной системы
счисления – 2). Первой цифрой искомого
числа является последнее частное, а
остальные цифры – это остатки, полученные
от деления, т.
Контрольный пример. Перевести двоичное число 10011012 в десятичную систему счисления.
Применим следующий метод:
160504131201102 = 1 * 20 + 0 * 21 + 1 * 22 + 1 * 23 +0 * 24 +0 * 25 +1 * 26 =
= 1 + 4 + 8 +64 = 7710.
Перевод
из десятичной системы счисления в
восьмеричную аналогичен переводу из
десятичной системы счисления в двоичную.
А перевод из восьмеричной системы
счисления в десятичную производится
по тому же правилу, что и перевод из
двоичной системы счисления в десятичную.
Так при переводе числа 614
Перевод
из десятичной системы счисления в
шестнадцатеричную и наоборот выполняется
по тем же правилам, описанным выше. При
переводе числа 61410 получаем число 26616.
При
переводе числа 61410 получаем число 26616.
Перевести число 25310 в двоичную систему счисления. Выполнить обратный перевод полученного числа.
Перевести число 25310 в шестнадцатеричную систему счисления. Выполнить обратный перевод полученного числа.
3 Вопросы к практическому занятию
1. Что называется системой счисления?
2. Какие Вы знаете позиционные системы счисления?
3. Сформулируйте общее правило перевода целого числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.
4. Сформулируйте общее правило перевода двоичных (восьмеричных, шестнадцатеричных) целых чисел в десятичную систему счисления.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3
ТАБЛИЦЫ
ПЕРЕВОДА ЧИСЕЛ. ПЕРЕВОД СМЕШАННЫХ ЧИСЕЛ
ПЕРЕВОД СМЕШАННЫХ ЧИСЕЛ
1 Теоретическая часть
1.1 Перевод чисел из одной системы счисления в другую, используя таблицы перевода
Возможен
перевод чисел из восьмеричной системы
счисления в двоичную и наоборот,
используя таблицу 1, и из шестнадцатеричной
системы счисления в двоичную и, наоборот,
используя таблицу 2. Каждая восьмеричная
цифра записывается с помощью трех
двоичных цифр (триады), т. к. 8 = 2
Контрольный пример. Перевести число 25, заданное в восьмеричной системе счисления, в двоичную.
Перевод будем осуществлять, используя таблицу 1.
Учитывая, что цифра 28 = 10, а цифра 58 = 101, получим 258 = 10 1012.
Контрольный
пример.
Перевести двоичное число 1010 в восьмеричную
систему счисления.
Разобьем число 1010 на триады, начиная справа, и добавим недостающие слева нули: 001 010. Далее воспользуемся таблицей 1.
Учитывая, что 0012 = 18, а 0102 = 28, получим 1 0102 = 128
Таблица 1 – Соответствие цифр восьмеричной системы счисления и двоичной
Восьмеричная система счисления | Двоичная система счисления |
0 | 000 |
1 | 001 |
010 | |
3 | 011 |
4 | 100 |
5 | 101 |
6 | 110 |
7 | 111 |
Контрольный
пример. Перевести
число 147, заданное в шестнадцатеричной
системе счисления, в двоичную.
Перевести
число 147, заданное в шестнадцатеричной
системе счисления, в двоичную.
Используя таблицу 2, получим 14716 0001 0100 01112.
Таблица 2 – Соответствие цифр шестнадцатеричной системы счисления и двоичной
Шестнадцатеричная система счисления | Двоичная система счисления |
0 | 0000 |
1 | 0001 |
0010 | |
3 | 0011 |
4 | 0100 |
5 | 0101 |
6 | 0110 |
7 | 0111 |
8 | 1000 |
9 | |
A | 1010 |
B | 1011 |
C | 1100 |
D | 1101 |
E | 1110 |
F | 1111 |
Контрольный
пример.
Разобьем число 10111 на тетрады, начиная справа, и добавим недостающие слева нули: 0001 0111. Для перевода воспользуемся таблицей 2 и получим 01 01112 1716.
Функция ОСНОВАНИЕ в Excel переводит число в систему счисления
Функция ОСНОВАНИЕ выполняет преобразование числового значение в указанную систему счисления (двоичная, восьмеричная, шестнадцатеричная и т. д.) и возвращает соответствующий результат в виде текстовой строки.
Примеры использования функции ОСНОВАНИЕ в Excel
Пример 1. Для хранения чисел в БД удобно использовать их представление в двоичной системе счисления. Выполнить преобразование представленных значений.
Исходная таблица:
Для преобразования используем формулу:
Описание аргументов:
- B2 – число, которое требуется преобразовать;
- 2 – указатель вида системы счисления.
Выполним преобразование для всех чисел.
Ошибка #ЧИСЛО! Возникла потому, что -56 находится вне диапазона допустимых значений (отрицательное число). Результат вычисления формулы =ОСНОВАНИЕ(0,9;2) эквивалентен результату =ОСНОВАНИЕ(0;2), поскольку рассматриваемая функция усекает дробные значения аргумента число до целых значений.
Перевод числа из одной системы счисления в другую в Excel
Пример 2. Преобразовать числа, записанные в шестнадцатеричной системе счисления в двоичную систему с длиной полученной строки не менее 20 символов.
Таблица значений:
В Excel предусмотрена формула ШЕСТН.В.ДВ, однако она поддерживает значения из диапазона от FFFFFFFE00 до 1FF. Поэтому выполним промежуточное преобразование в десятичную систему и воспользуемся функцией ОСНОВАНИЕ для перевода в двоичную:
Описание аргументов:
- ШЕСТН.В.ДЕС(A2) – исходное число, преобразованное в десятичную систему счисления;
- 2 – указание на вид системы счисления;
- 20 – минимальное количество символов в возвращаемой строке.

Результаты расчетов:
Сложение чисел в разных системах счисления в Excel
Пример 3. Отобразить результаты сложения двух чисел, записанных в двоичной системе, в виде чисел в десяти- и тридцатидвухричных системах счисления.
Исходная таблица:
В ячейке A6 запишем следующую формулу:
Функция ДВ.В.ДЕС преобразует числа из двоичной в десятеричную систему.
В ячейке B6 запишем формулу:
В данном способе выполняется преобразование в понятную многим десятичную систему счисления, в которой и выполняется операция сложения чисел (вместо, например, алгоритма сложения в столбик в двоичной системе, где необходимо учитывать правила: 0+0=0, 1+1=10 и т. д.). Функцией ОСНОВАНИЕ выполняется преобразование результата в требуемые системы исчисления. Пример расчета:
Особенности использования функции ОСНОВАНИЕ в Excel
Функция имеет следующую синтаксическую запись:
=ОСНОВАНИЕ(число;основание;[минимальная_длина])
Описание аргументов:
- число – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 0 до 253, которое требуется преобразовать к указанной системе счисления.

- основание – обязательный аргумент, характеризующий числовое значение из диапазона целых чисел от 2 до 36, которое является основанием требуемой системы исчисления.
- [минимальная_длина] – необязательный аргумент, характеризующий числовое значение из диапазона от 0 до 255, определяющее минимальную длину в символах возвращаемой текстовой строки.
Примечания:
- Функция возвращает код ошибки #ЧИСЛО!, если любой из ее аргументов является числовым значением, выходящим за пределы допустимых для данного аргумента значений.
- Если один или несколько аргументов являются текстовой строкой, рассматриваемая функция вернет код ошибки #ЗНАЧ!.
- Функция доступна только в новых версиях программы (Excel 2013 и более поздних).
- В отличие, например, от функции ДЕС.В.ДВ, которая выполняет преобразование чисел из диапазона от -512 до 511, функция ОСНОВАНИЕ выполняет преобразование чисел от 0 до 253.
- При явном указании аргумента [минимальная_длина] возможны следующие ситуации:
- длина полученного значения меньше, чем регламентируется аргументом [минимальная_длина].
 В этом случае в начале возвращаемой строки слева будет добавлено определенное количество нулей для достижения требуемой длины;
В этом случае в начале возвращаемой строки слева будет добавлено определенное количество нулей для достижения требуемой длины; - длина рассчитанного значения больше, чем регламентируемая. Функция ОСНОВАНИЕ вернет полученный результат, не урезая его. Например, функция с аргументами (12345;2;20) вернет значение «00000011000000111001», а функция с аргументами (12345;2;2) вернет «11000000111001».
преобразовать десятичное число 253 в восьмеричное
Как записать число 253 в восьмеричном формате (с основанием 8)?
253 равно 375 в восьмеричной форме
| ||||||||||||||||
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа.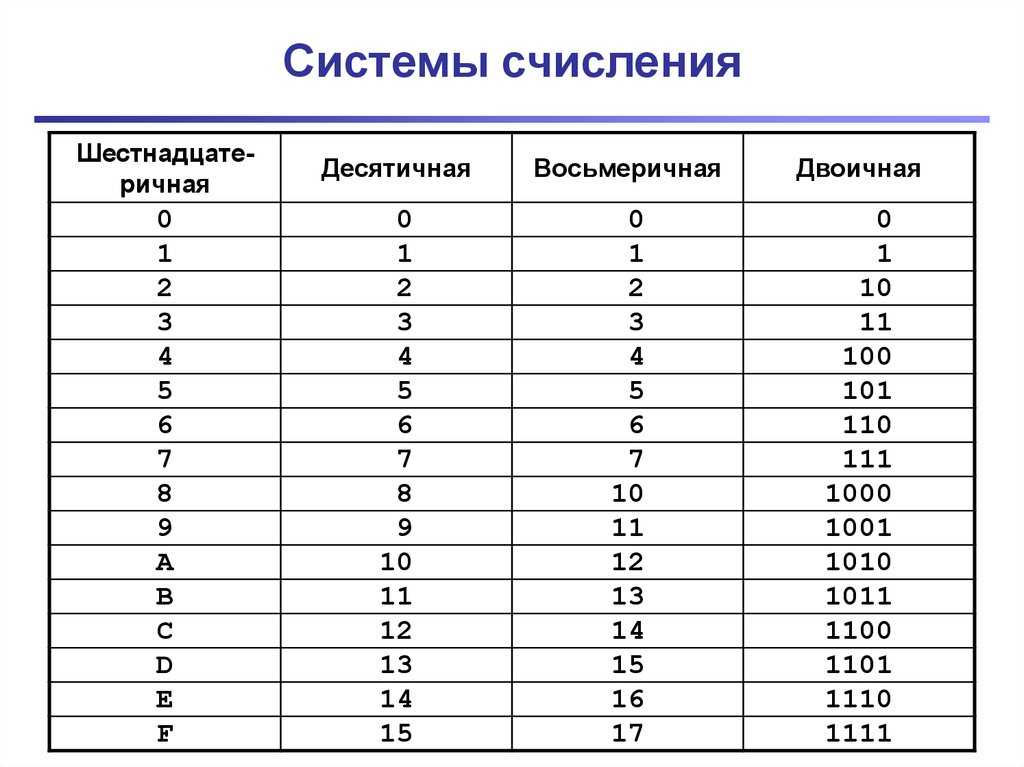 Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать десятичное число 253 в восьмеричное или преобразовать десятичное число в восьмеричное.
Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответ на такие вопросы, как: преобразовать десятичное число 253 в восьмеричное или преобразовать десятичное число в восьмеричное.
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 110999 | 110999 | 110999 | 110 | 110 | 110999 | 110999 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| 10 | A | 12 | 1010 |
| 11 | B | 13 | 1011 |
| 12 | C | 14 | 9009 |
| 13 | D | 9 | |
| 13 | D | 9 9007 | 0008 1101 |
| 14 | E | 16 | 1110 |
| 15 | F | 17 | 1111 |
| Dec | Hex | Oct | Bin | |||||
|---|---|---|---|---|---|---|---|---|
| 16 | 10 | 20 | 10000 | |||||
| 17 | 11 | 21 | 10001 | |||||
| 18 | 12 | 22 | ||||||
| 18 | 12 | 22 | ||||||
| 10010 | ||||||||
| 19 | 13 | 23 | 10011 | |||||
| 20 | 14 | 24 | 10100 | |||||
| 21 | 15 | 25 | 10101 | |||||
| 22 | 16 | 26 | 10110 | |||||
| 23 | 17 | 27 | 10111 | |||||
| 24 | 18 | 30 | 18 | 30 | 9000 | 0009 | ||
| 25 | 19 | 31 | 11001 | |||||
| 26 | 1A | 32 | 11010 | |||||
| 27 | 1B | 33 | 11011 | |||||
| 28 | 1C | 34 | 11100 | |||||
| 29 | 1d | 35 | 11101 | |||||
| 30 | 36 | 11110 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | |
| 33 | 21 | 41 | 100001 | |
| 34 | 22 | 42 | 100010 | |
| 35 | 23 | 43 | 100011 | |
| 36 | 24 | 44 | 100100 | |
| 37 | 25 | 45 | 100101 | |
| 38 | 26 | 46 | 100110 | |
| 39 | 27 | 47 | 100111 | |
| 40 | 28 | 50 | 101000 | |
| 41 | 29 | 51 | 101001 | 51 | 101001 | 0007 | 42 | 2A | 52 | 101010 |
| 43 | 2B | 53 | 101011 | |
| 44 | 2C | 54 | 101100 | |
| 45 | 2D | 55 | 101101 | |
| 46 | 2E | 56 | 101110 | |
| 47 | 2F | 8 57101111 |
| Dec | Hex | Oct | Bin | ||||
|---|---|---|---|---|---|---|---|
| 48 | 30 | 60 | 110000 | ||||
| 49 | 31 | 61 | 110001 | ||||
| 50 | 32 | 62 | 110010 | ||||
| 51 | 33 | 63 | 110011 | ||||
| 52 | 34 | 64 | 110100 | 64 | 110100 | 64 | 1101009 | 9000
| 53 | 35 | 65 | 110101 | ||||
| 54 | 36 | 66 | 110110 | ||||
| 55 | 37 | 67 | 110111 | ||||
| 56 | 38 | 70 | 111000 | ||||
| 57 | 39 | 71 | 111001 | ||||
| 58 | 3A | 72 | 111010999 | ||||
| 111010999 | |||||||
| 111010 | |||||||
| 1110109 | |||||||
| 111010 | |||||||
| 3B | 73 | 111011 | |||||
| 60 | 3C | 74 | 111100 | ||||
| 61 | 3D | 75 | 111101 | ||||
| 62 | 3E | 76 | 111110 | ||||
| 63 | 3F | 77 | 111111 |
| DEC | HEX | октября | Bin | октября | октября | октября | октября0007 | 64 | 40 | 100 | 1000000 |
|---|---|---|---|
| 65 | 41 | 101 | 1000001 |
| 66 | 42 | 102 | 1000010 |
| 67 | 43 | 103 | 1000011 |
| 68 | 44 | 104 | 1000100 |
| 69 | 45 | 100009 | 1000101 | 100009 | 1000101 | 9000
| 70 | 46 | 106 | 1000110 |
| 71 | 47 | 107 | 1000111 |
| 72 | 48 | 110 | 1001000 |
| 73 | 49 | 111 | 1001001 |
| 74 | 4A | 112 | 1001010 |
| 4B | 113 | 1001011 | 0007 | 76 | 4C | 114 | 1001100 |
| 77 | 4D | 115 | 1001101 |
| 78 | 4E | 116 | 1001110 |
| 79 | 4F | 117 | 1001111 |
| DEC | HEX | OCT | BIN | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 80 | 50 | 120 | 80 | 50 | 120 | ||||
| 81 | 51 | 121 | 1010001 | ||||||
| 82 | 52 | 122 | 1010010 | ||||||
| 83 | 53 | 123 | 1010011 | ||||||
| 84 | 54 | 124 | 1010100 | ||||||
| 85 | 55 | 125 | 1010101 | ||||||
| 56 | 126 | 86 | 56 | 126 | 956 | 126 | 1010110 | ||
| 87 | 57 | 127 | 1010111 | ||||||
| 88 | 58 | 130 | 1011000 | ||||||
| 89 | 59 | 131 | 1011001 | ||||||
| 90 | 5A | 132 | 1011010 | ||||||
| 91 | 5B | 133 | 1011011 | ||||||
| 5C | 134 | 995C | 134 | 91011100 | |||||
| 93 | 5D | 135 | 1011101 | ||||||
| 94 | 5E | 136 | 1011110 | ||||||
| 95 | 5F | 137 | 1011111 |
| Dec | HEX | OCT | BIN | |
|---|---|---|---|---|
| 96 | 60 | 140 | ||
| 97 | 619 | 999|||
| 97 | 61 | 0009 | 141 | 1100001 |
| 98 | 62 | 142 | 1100010 | |
| 99 | 63 | 143 | 1100011 | |
| 100 | 64 | 144 | 1100100 | |
| 101 | 65 | 145 | 1100101 | |
| 102 | 66 | 146 | 1100110 | |
| 103 | 67 | |||
| 100009 | 67 | |||
| 100009 | 67 | |||
| 100009 | 67 | |||
| 147 | 1100111 | |||
| 104 | 68 | 150 | 1101000 | |
| 105 | 69 | 151 | 1101001 | |
| 106 | 6A | 152 | 1101010 | |
| 107 | 6B | 153 | 1101011 | |
| 108 | 6C | 154 | 1101100 | |
| 109 | 0008 6D | 155 | 1101101 | |
| 110 | 6E | 156 | 1101110 | |
| 111 | 6F | 157 | 1101111 |
| Dec | Hex | Октябрь | BIN | |||
|---|---|---|---|---|---|---|
| 112 | 70 | 160 | 1110000 | |||
| 113 | 71 | 161 | 1110001 | 161 | 110001 | |
| 114 | 72 | 162 | 1110010 | |||
| 115 | 73 | 163 | 1110011 | |||
| 116 | 74 | 164 | 1110100 | |||
| 117 | 75 | 165 | 1110101 | |||
| 118 | 76 | 166 | 1110110 | |||
| 119 | 167 | 11101119 | 9000167999 | 11101119 | 0009||
| 120 | 78 | 170 | 1111000 | |||
| 121 | 79 | 171 | 1111001 | |||
| 122 | 7A | 172 | 1111010 | |||
| 123 | 7B | 173 | 1111011 | |||
| 124 | 7C | 174 | 1111100 | |||
| 125 | 7D | 175999 | 11111111119 | 7D | 175999 | 1111101 | 0009
| 126 | 7E | 176 | 1111110 | |||
| 127 | 7F | 177 | 1111111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 128 | 80 | 200 | 10000000 |
| 129 | 81 | 201 | 10000001 |
| 130 | 82 | 202 | 10000010 |
| 131 | 83 | 203 | 10000011 |
| 132 | 84 | 204 | 10000100 |
| 133 | 85 | 205 | 10000101 |
| 134 | 86 | 206 | 10000110 |
| 135 | 87 | 207 | 10000111 |
| 136 | |||
| 0008 88 | 210 | 10001000 | |
| 137 | 89 | 211 | 10001001 |
| 138 | 8A | 212 | 10001010 |
| 139 | 8B | 213 | 10001011 |
| 140 | 8C | 214 | 10001100 |
| 141 | 215 | 10001101 | |
| 142 | 10001101 | ||
| 142 | 00098E | 216 | 10001110 |
| 143 | 8F | 217 | 10001111 |
| Dec | Hex | Oct | Bin | |||
|---|---|---|---|---|---|---|
| 144 | 90 | 220 | 10010000 | |||
| 145 | 91 | 221 | 10010001 | |||
| 146 | 9000222 | 10010010 | 92222 | 10010010 | 0009||
| 147 | 93 | 223 | 10010011 | |||
| 148 | 94 | 224 | 10010100 | |||
| 149 | 95 | 225 | 10010101 | |||
| 150 | 96 | 226 | 10010110 | |||
| 151 | 97 | 227 | 10010111 | |||
| 152 | 98 | 230 | 152 | 230 | 900010011000 | |
| 153 | 99 | 231 | 10011001 | |||
| 154 | 9A | 232 | 10011010 | |||
| 155 | 9B | 233 | 10011011 | |||
| 156 | 9C | 234 | 10011100 | |||
| 157 | 9D | 235 | 10011101 | |||
| 158 | 236 | 158 | 2360009 | 10011110 | ||
| 159 | 9F | 237 | 10011111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 160 | A0 | 240 | 10100000 | |
| 161 | A1 | 241 | 10100001 | |
| 162 | A2 | 242 | 10100010 | |
| 163 | 10100010 | |||
163009 | A3 | 243 | 10100011 | |
| 164 | A4 | 244 | 10100100 | |
| 165 | A5 | 245 | 10100101 | |
| 166 | A6 | 246 | 10100110 | |
| 167 | A7 | 247 | 10100111 | |
| 168 | A8 | 10101000 | ||
| 10101000 | ||||
| 169 | A9 | 251 | 10101001 | |
| 170 | AA | 252 | 10101010 | |
| 171 | AB | 253 | 10101011 | |
| 172 | AC | 254 | 10101100 | |
| 173 | г. н.э. н.э. | 255 | 10101101 | |
| 174 | AE | 256 | 10101110 | 0010 |
| 175 | AF | 257 | 10101111 |
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 176 | B0 | 260 | 10110000 |
| 177 | B1 | 261 | 10110001 |
| 178 | B2 | 262 | 10110010 |
| 179 | B3 | 10110011 | |
| 180 | B4 | 264 | 10110100 |
| 181 | B5 | 265 | 10110101 |
| 182 | B6 | 266 | 10110110 |
| 183 | B7 | 267 | 101101119 |
| 184 | B8 | 270 | 10111000 |
| 185 | B 00 | ||
| 185 | B | 0||
| 185 | B | 0||
| 185 | B9 | 271 | 10111001 |
| 186 | BA | 272 | 10111010 |
| 187 | BB | 273 | 10111011 |
| 188 | BC | 274 | 10111100 |
| 189 | BD | 275 | 10111101 |
| 190 | BE | 276 | 101110 |
| 191 | 10111110 | ||
| 191 | 0009BF | 277 | 10111111 |
| Dec | Hex | Oct | Bin | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 192 | C0 | 300 | 11000000 | |||||||||
| 193 | C1 | 301 | 11000001 | |||||||||
| 194 | C2 | 302 | 11000010 | |||||||||
| 195 | C3 | 303 | 11000011 | 303 | 11000011 | 11000011 | 11000011 | |||||
| 196 | C4 | 304 | 11000100 | |||||||||
| 197 | C5 | 305 | 11000101 | |||||||||
| 198 | C6 | 306 | 11000110 | |||||||||
| 199 | C7 | 307 | 11000111 | |||||||||
| 200 | C8 | 310 | 11001000 | |||||||||
| 201 | C9 | 311 | C9 | 311 | ||||||||
| 202 | CA | 312 | 11001010 | |||||||||
| 203 | CB | 313 | 11001011 | |||||||||
| 204 | CC | 314 | 11001100 | |||||||||
| 205 | CD | 315 | 11001101 | |||||||||
| 206 | CE | 316 | 11001110 | |||||||||
| 207 | CF | 317009 | 11001111 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 208 | D0 | 320 | 11010000 | |
| 209 | D1 | 321 | 11010001 | |
| 210 | D2 | 322 | 11010010 | |
| 211 | D3 | 323 | 11010011 | |
| 212 | 11010011 | |||
| 212 | 0009 | D4 | 324 | 11010100 |
| 213 | D5 | 325 | 11010101 | |
| 214 | D6 | 326 | 11010110 | |
| 215 | D7 | 327 | 110101119 | |
| 216 | D8 | 330 | 11011000 | |
| 217 | D9 | 331 | 11011001 | |
| 331 | 11011001 | |||
| 0008 218 | DA | 332 | 11011010 | |
| 219 | DB | 333 | 11011011 | |
| 220 | DC | 334 | 11011100 | |
| 221 | DD | 335 | 11011101 | |
| 222 | DE | 336 | 11011110 | |
| 223 | DF | 337 | 110111119 | 0010 |
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 224 | E0 | 340 | 11100000 | |
| 225 | E1 | 341 | 11100001 | |
| 226 | E2 | 342 | 11100010 | |
| 227 | E3 | 343 | 11100011 | |
| 228 | E4 | |||
| 228 | 9000 | 344 | 11100100 | |
| 229 | E5 | 345 | 11100101 | |
| 230 | E6 | 346 | 11100110 | |
| 231 | E7 | 347 | 11100111 | |
| 232 | E8 | 350 | 11101000 | |
| 233 | E9 | 351 | 11101001 | |
| 234 | EA | 01|||
| 234 | 0009 | 352 | 11101010 | |
| 235 | EB | 353 | 11101011 | |
| 236 | EC | 354 | 11101100 | |
| 237 | ED | 355 | 11101101 | |
| 238 | EE | 356 | 11101110 | |
| 239 | EF | 357 | 111011 |
9000
| Dec | Hex | Oct | Bin | |
|---|---|---|---|---|
| 240 | F0 | 360 | 11110000 | |
| 241 | F1 | 361 | 11110001 | |
| 242 | F2 | 362 | 11110010 | |
| 243 | F3 | 363 | 11110011 | |
| 244 | F4 | 364 | 11101009 | 0009 |
| 245 | F5 | 365 | 11110101 | |
| 246 | F6 | 366 | 11110110 | |
| 247 | F7 | 367 | 11110111 | |
| 248 | F8 | 370 | 11111000 | |
| 249 | F9 | 371 | 11111001 | |
| 250 | FA | 372 | 0008 11111010 | |
| 251 | FB | 373 | 11111011 | |
| 252 | FC | 374 | 11111100 | |
| 253 | FD | 375 | 11111101 | |
| 254 | FE | 376 | 11111110 | |
| 255 | FF | 377 | 111111111999910 |
Номерная базовая конвертер
Пожалуйста, перейдите на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
- 1100 hexadecimal to binary
- 1E0 hexadecimal to decimal
- 174000 octal to hexadecimal
- 312 octal to hexadecimal
- 3712 decimal to octal
- 166 decimal to hexadecimal
- 100110 binary to hexadecimal
- 1100110000000000 двоичный в шестнадцатеричный
- 7B0 шестнадцатеричный код в восьмеричный
Десятичный 253 в восьмеричном | работа, решение
Как записать восьмеричное число 253?
253 записывается как 375 в восьмеричном формате
Преобразование из/в десятичное в двоичное. Преобразование десятичных чисел. Возможно, вы обратились к нам в поисках ответов на такие вопросы, как: Десятичное число 253 в восьмеричном | работа, решение или преобразование из десятичного в восьмеричное. Используйте калькулятор ниже, чтобы преобразовать в / из основных базовых систем.
Чтобы использовать этот калькулятор, просто введите значение в любом поле слева.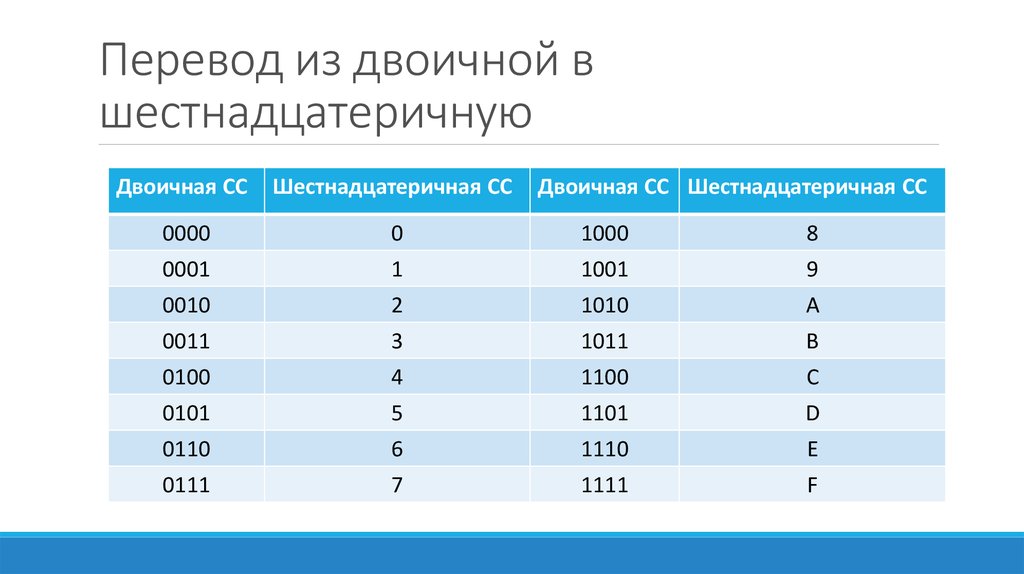
С помощью этого конвертера вы можете получить ответы на такие вопросы, как:
- Что такое 253 в двоичном формате?
- Что такое 253 в шестнадцатеричном формате?
- Что такое 253 в восьмеричной системе?
- Как преобразовать 253 в двоичный код?
- Как преобразовать 253 в двоичный код? И так далее.
Десятичная в двоичную диаграмму, включая шестнадцатеричную и восьмеричную0009
| Dec | Hex | Oct | Bin |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 0008 2210010 | |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 17 | 27 | 10111 |
| 24 | 18 | 30 | |
| 0008 11000 | |||
| 25 | 19 | 31 | 11001 |
| 26 | 1A | 32 | 11010 |
| 27 | 1B | 33 | 11011 |
| 28 | 1C | 34 | 11100 |
| 29 | 1D | 35 | 11101 |
| 30 | 1E | 36 | 111110 |
| 31 | 1F | 37 | 11111 |
| Dec | Hex | Oct | Bin | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 32 | 20 | 40 | 100000 | ||||||
| 33 | 21 | 41 | 100001 | ||||||
| 34 | 22 | 42 | 100010 | ||||||
| 35 | 23 | 43 | |||||||
| 100011 | |||||||||
| 36 | 24 | 44 | 100100 | ||||||
| 37 | 25 | 45 | 100101 | ||||||
| 38 | 26 | 46 | 100110 | ||||||
| 39 | 27 | 47 | 100111 | ||||||
| 40 | 28 | 50 | 101000 | ||||||
| 41 | 2951 | 101001 | 29 | 51 | 101001 | 51 | 101001 | 0009||
| 42 | 2A | 52 | 101010 | ||||||
| 43 | 2B | 53 | 101011 | ||||||
| 44 | 2C | 54 | 101100 | ||||||
| 45 | 2D | 55 | 101101 | ||||||
| 46 | 2E | 56 | 101110 | ||||||
| 47 | 2F | 57 | 101111 | 2F | 57 | 101111 | 0060
Образцы конверсии. |




 В этом случае в начале возвращаемой строки слева будет добавлено определенное количество нулей для достижения требуемой длины;
В этом случае в начале возвращаемой строки слева будет добавлено определенное количество нулей для достижения требуемой длины; 0008 31
0008 31