формулы, определение, задачи / Блог :: Бингоскул

Кратко о 2 законе Ньютона: формулы, определение, задачи

Ньютон установил связь между ускорением и силой, где F – сила, действующая на тело массой m, вызывает ускорение тела равное – a.

 

Помни!!!

• 2 закон Ньютона называют еще основным законом динамики.
• Под телом подразумевают материальную точку, движение которой рассматривают в инерциальной системе отсчета.

---

1. Формулировка

«В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки»

2. Определение

Сила, действующая на тело, равна произведению массы тела на сообщаемое этой силой ускорение, причем направления силы и ускорения совпадают.

Если на тело действует сила, то оно приобретает ускорение.

3. Формула

Математически второй закон Ньютона записать в виде:

m\overrightarrow { a } =\overrightarrow { F }

• m — масса материальной точки
• \overrightarrow { F } — сила действующая на тело/ускорение материальной точки
• \overrightarrow { a } — ускорение тела

Второй закон Ньютона в импульсной форме:

\frac { d \overrightarrow { p } } { dt } =\overrightarrow { F }

• \overrightarrow { p } — импульс точки,

\overrightarrow { p } = m\overrightarrow { v }

• \overrightarrow { v } — скорость точки.
• \frac { d \overrightarrow { p } } { dt } — производная импульса по времени.

 

Единица измерения — единица силы — 1 Н (1 ньютон) — сила, которая телу массой 1 кг сообщает ускорение 1 м/с².

1 Н = 1 кг · 1 м/с² = 1 кг · м/с².

 

Ускорение, приобретаемое материальной точкой в ИСО:

• Прямо пропорционально действующей на точку силе;
• Обратно пропорционально массе точки;
• Направлено в сторону действия силы.

Если на тело одновременно действуют несколько сил — F1,F2 и F3, то под силой в формуле, выражающей второй закон Ньютона, нужно понимать равнодействующую всех сил:

F=F1+F2+F3

Задачи с ответами смотри в задании 2 по физике.

---

Смотри также:

формула и определение / Блог :: Бингоскул

Кратко о 1 законе Ньютона: формула, определение и формулировка

Помни!!!

• В основе динамики материальной точки лежат три закона Ньютона.
• Первый закон Ньютона — закон инерции
• Под телом подразумевают материальную точку, движение которой рассматривают в инерциальной системе отсчета.

---

1. Формулировка

«Существуют такие инерциальные системы отсчёта, относительно которых тело, если на него не действуют другие силы (либо действие других сил компенсируется), находится в покое либо движется равномерно и прямолинейно».

2. Определение

Первый закон Ньютона — всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит её изменить это состояние.

Первый закон Ньютона — закон инерции (Галилей вывел закон инерции)

Закон инерции: Если на тело нет внешних воздействий, то данное тело сохраняет состояние покоя или равномерного прямолинейного движения относительно Земли.

Инерциальная система отсчёта (ИСО) – система, которая либо покоится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Т.е. система отсчета, в которой выполняется 1-й закон Ньютона.

• Масса тела – количественная мера его инертности. В СИ она измеряется в килограммах.
• Сила – количественная мера взаимодействия тел. Сила – векторная величина и измеряется в ньютонах (Н). Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.

3. Формула

Формулы нет. Формула первого закона Ньютона не существует.

Первый закон Ньютона содержится 2 важных утверждения:

1. все тела обладают свойством инерции;
2. инерциальные системы отсчета существуют.

---

Это интересно:

Конспект «Второй закон Ньютона. Третий закон Ньютона»

«Второй закон Ньютона. Третий закон Ньютона»

Коды ОГЭ 1.9 — 1.10. Второй закон Ньютона. Сонаправленность вектора ускорения тела и вектора силы, действующей на тело. Взаимодействие тел. Третий закон Ньютона.

---

---

Второй закон Ньютона: Равнодействующая сил, приложенных к телу, равна произведению массы этого тела на сообщаемое ему ускорение:  .

Второй закон Ньютона справедлив для сил любой природы. При этом следует помнить, что сила (равнодействующая сил) определяет только ускорение тела. Величины скорости и перемещения могут быть любыми в зависимости от начальных условий.

Внимание! Направление ускорения всегда совпадает с направлением равнодействующей силы R !
Внимание! Под действием постоянной силы тело движется равноускоренно: 

Внимание! Основная модель при решении динамических задач с помощью второго закона Ньютона – материальная точка. Все силы считаются приложенными к одной точке – центру масс.

Третий закон Ньютона: Любые два тела взаимодействуют силами одной природы, направленными вдоль одной прямой, равными по величине и противоположными по направлению:  , где F₁₂ – сила, с которой первое тело действует на второе, a F₂₁ – сила, с которой второе тело действует на первое.

Внимание! Две силы, возникающие при взаимодействии, приложены к разным телам, поэтому их нельзя складывать! Они не могут уравновешивать друг друга!

Третий закон Ньютона часто используется для расчёта сил, действующих на одно из двух взаимодействующих тел, если известны силы, действующие на другое тело.

---

 

---

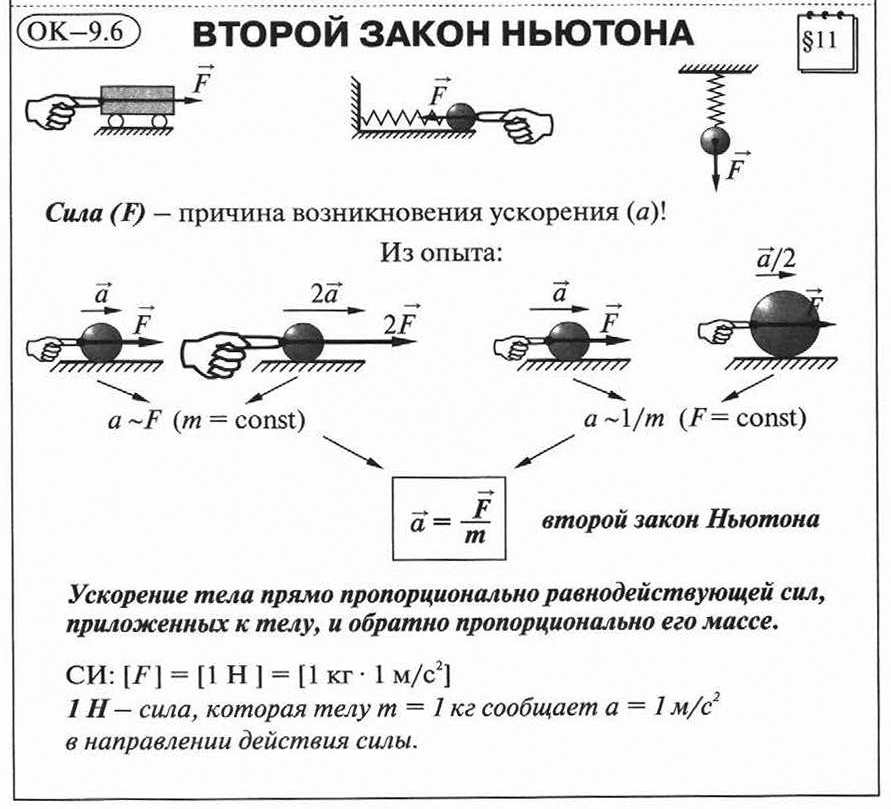
Конспект урока по физике в 9 классе «Второй закон Ньютона. Третий закон Ньютона».

Следующая тема: «Трение покоя и трение скольжения» (код ОГЭ 1.11)

Смотрите также конспект «ЗАДАЧИ на законы Ньютона с решениями»

 

Второй закон Ньютона — это… Что такое Второй закон Ньютона?

Второй закон Ньютона — дифференциальный закон движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил. Один из трёх законов Ньютона.

Второй закон Ньютона в его наиболее распространённой формулировке утверждает: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

В приведённой формулировке второй закон Ньютона справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта.

Формулировки

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

• «Школьная формулировка»: в инерциальных системах ускорение, приобретаемое материальной точкой (телом), прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки (тела).

Обычно этот закон записывается в виде формулы:

,

где  — ускорение тела,  — сила, приложенная к телу, а  — масса тела, причём  — константа.

Или, в ином виде:

• Формулировка второго закона Ньютона с использованием понятия импульса:

В инерциальной системе отсчета производная импульса материальной точки по времени равна действующей на него силе^[2].

где  — импульс (количество движения) тела,  — время, а  — производная по времени.

Уравнения, соответствующие данному закону, называются уравнениями движения материальной точки.

Применимость различных формулировок

Второй закон Ньютона в виде приближённо справедлив только для скоростей, много меньших скорости света и в инерциальных системах отсчёта. В виде второй закон Ньютона точно справедлив также в инерциальных системах отсчёта специальной теории относительности и в локально инерциальных системах отсчёта общей теории относительности.

Примечания

1. ↑ Исаак Ньютон. Математические начала натуральной философии. — М.: Наука, 1989. — С. 40. — 690 с. — («Классики науки»). — 5 000 экз. — ISBN 5-02-000747-1
2. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7

См. также

для материальной точки в ИСО

Видеоурок: Второй закон Ньютона

Лекция: Второй закон Ньютона: для материальной точки в ИСО

Второй закон Ньютона

Для того, чтобы придать любому телу ускорения, необходимо взаимодействовать с ним. Чем больше масса тела, тем большую силу следует приложить для получения большего ускорения.

В ИСО ускорение, которое имеет тело, напрямую зависит от силы, которую применяют к телу и обратно пропорционально его массе. Чтобы определить ускорение тела, следует определить, в какую сторону направлена равнодействующая сила.

Второй закон Ньютона через импульс:

Более того, из этого следует, что если к телам приложить одинаковую силу так, что масса одного тела меньше, чем масса другого, то первое тело будет приобретать большее ускорение.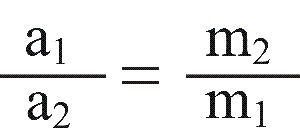

Основные принципы решения задач на 2 закон Ньютона

1. Если две величины из формулы Второго закона Ньютона известны, то следует преобразовать её так, чтобы можно было определить неизвестную величину. После этого следует подставить все значения, выраженные в СИ.

2. Если известна только одна ФВ из закона, но даны дополнительные кинематические величины, то для определения неизвестной величины следует воспользоваться дополнительными кинематическими формулами.

3. Если даны силы, действующие на тело, то прежде, чем найти неизвестную, следует найти равнодействующую по принципу суперпозиции.

Третий закон Ньютона — Википедия

Третий закон Ньютона или закон равенства действия и противодействия

— один из трёх основных законов ньютоновской механики.

Закон был впервые сформулирован И. Ньютоном в книге «Математические начала натуральной философии» (1687):

Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны^[1].

Более точно, под телами нужно понимать материальные точки; современная формулировка закона такова:

Силы взаимодействия двух материальных точек равны по величине, противоположно направлены, и действуют вдоль прямой, соединяющей эти материальные точки^[2].

В виде формулы:

F→12=−F→21{\displaystyle {\vec {F}}_{12}=-{\vec {F}}_{21}},

где F→12{\displaystyle {\vec {F}}_{12}} — сила, с которой первое тело действует на второе («действие»), а F→21{\displaystyle {\vec {F}}_{21}} — сила, с которой второе тело действует на первое («противодействие»).

• Кирпич, неподвижно лежащий на столе, давит на него с силой P=mg{\displaystyle P=mg}, направленной вниз (и называемой весом). Согласно третьему закону Ньютона, со стороны стола на кирпич действует сила той же величины, направленная вверх (она называется реакцией опоры).
• Яблоко падает на землю, поскольку Земля притягивает его с силой F=mg{\displaystyle F=mg}. При этом, с точно такой же по величине силой яблоко притягивает Землю. Однако, поскольку масса Земли чрезвычайно велика, её перемещение под действием этой силы пренебрежимо мало.

Краткая формулировка закона в виде «действие равно противодействию» может вызывать недоразумения, например такой парадокс:

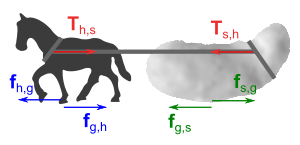
Пусть лошадь запряжена в телегу, и тянет её с некоторой силой вперёд. Но согласно 3-му закону Ньютона, существует сила противодействия, равная ей по величине и направленная назад. Поскольку в сумме обе силы дают ноль, телега никогда не сможет сдвинуться с места.

Ошибка здесь в том, что силы действия и противодействия приложены к разным телам (в этом примере: к телеге и к лошади), поэтому их бессмысленно складывать. Кроме этих сил, и на лошадь и на телегу действует сила трения, которая, собственно, и приводит лошадь в движение (именно, сила трения копыт лошади об землю направлена вперёд и преодолевает силу противодействия телеги, в то время как сила тяги лошади преодолевает силу трения телеги об землю, направленную назад)^[3].

Рассмотрим два тела, которые взаимодействуют только друг с другом (замкнутая система). Тогда, согласно второму закону Ньютона, их ускорения a→1{\displaystyle {\vec {a}}_{1}} и a→2{\displaystyle {\vec {a}}_{2}} определяются из уравнений

F→21=m1a→1,F→12=m2a→2.{\displaystyle {\vec {F}}_{21}=m_{1}{\vec {a}}_{1},\quad {\vec {F}}_{12}=m_{2}{\vec {a}}_{2}.}

С учётом третьего закона Ньютона отсюда получается

m1a→1+m2a→2=0,{\displaystyle m_{1}{\vec {a}}_{1}+m_{2}{\vec {a}}_{2}=0,}

или же

ddt(m1v→1+m2v→2)=0,{\displaystyle {\frac {d}{dt}}(m_{1}{\vec {v}}_{1}+m_{2}{\vec {v}}_{2})=0,}

m1v→1+m2v→2=const,{\displaystyle m_{1}{\vec {v}}_{1}+m_{2}{\vec {v}}_{2}={\text{const}},}

где v→1{\displaystyle {\vec {v}}_{1}} и v→2{\displaystyle {\vec {v}}_{2}} — скорости тел. Величина p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}} называется импульсом тела, а последнее соотношение есть закон сохранения импульса. Дополнив 3-й закон Ньютона принципом независимости действия сил, можно вывести закон сохранения импульса для замкнутой системы, состоящей из произвольного числа тел. Хотя в рамках ньютоновской механики закон сохранения импульса является следствием законов Ньютона, опыт показывает, что это один из наиболее общих законов физики, который выполняется даже тогда, когда сама ньютоновская механика неприменима^[2].

Как 3-й закон Ньютона, так и более общий закон сохранения импульса являются следствиями фундаментальной симметрии природы — однородности пространства. Однородность пространства означает, что все его точки равноправны, то есть, закон движения замкнутой системы не изменится, если систему переместить в пространстве как целое.

Связь 3-го закона Ньютона с однородностью пространства хорошо видна в рамках лагранжева формализма. Если пространство однородно, то потенциальная энергия может зависеть только от разностей координат тел: U=U(r→1−r→2){\displaystyle U=U({\vec {r}}_{1}-{\vec {r}}_{2})}, поэтому

F→21=−dUdr→1=−∇→U(r→1−r→2),{\displaystyle {\vec {F}}_{21}=-{\frac {dU}{d{\vec {r}}_{1}}}=-{\vec {\nabla }}U({\vec {r}}_{1}-{\vec {r}}_{2}),}

F→12=−dUdr→2=∇→U(r→1−r→2),{\displaystyle {\vec {F}}_{12}=-{\frac {dU}{d{\vec {r}}_{2}}}={\vec {\nabla }}U({\vec {r}}_{1}-{\vec {r}}_{2}),}

откуда следует F→21=−F→12{\displaystyle {\vec {F}}_{21}=-{\vec {F}}_{12}}^[4].

Третий закон Ньютона, как и вообще вся ньютоновская механика, связан с идеей действия на расстоянии, согласно которой сила, действующая со стороны одного тела на другое в некоторый момент времени, определяется их положением в тот же момент времени. Другими словами, это означает бесконечную скорость передачи взаимодействий. Согласно современным представлениям, взаимодействия передаются посредством полей, и, как следует из опыта, имеют конечную скорость, не превышающую скорости света. Поэтому при движении со скоростями, близкими к скорости света, или же когда расстояния между телами слишком велики, третий закон Ньютона неприменим. Однако закон сохранения импульса по-прежнему выполняется, если кроме импульса тел, учесть также импульс поля (например электромагнитного, гравитационного), посредством которого они взаимодействуют^[2].

Пример: на тело, поглощающее свет, действует сила давления света. Но никакой «силы противодействия» здесь нет, как нет и никакого тела, к которому она была бы приложена. С точки зрения закона сохранения импульса, давление света возникает потому, что импульс электромагнитного поля передаётся телу^[2].

Физический закон — Википедия

Материал из Википедии — свободной энциклопедии

Физи́ческий зако́н — устойчивые повторяющиеся объективные закономерности, существующие в природе^[1]. Открытые человечеством физические законы представляют из себя эмпирически установленные и выраженные в строгой словесной и/или математической формулировке устойчивые, повторяющиеся в эксперименте связи между физическими величинами в явлениях, процессах и состояниях тел и других материальных объектов в окружающем мире^[2].

Выявление физических закономерностей составляет основную задачу физической науки.

Для того, чтобы некая связь могла быть названа физическим законом, она должна удовлетворять следующим требованиям:

• Эмпирическая подтверждённость: физический закон считается установленным, если имеет экспериментальное подтверждение.
• Универсальность: математическое выражение частного закона, определяющего связи между параметрами одной конкретной системы, может иногда описывать самые разнообразные явления. Кроме того, в соответствии с принципом единства законов природы, частные законы применимы, в пределах существующих ограничений параметров объекта и среды, в любой точке Вселенной, а всеобщие законы одинаково действуют на всех уровнях организации материи в пространстве и времени, а также определяют природу Вселенной.^[3][4]
• Устойчивость: свойства Вселенной определяют неизменность физических законов^[5].

Хотя физические законы, как правило, выражаются в виде строгого словесного утверждения и/или математической формулы, по выражению нобелевского лауреата Поля Дирака, «физический закон должен обладать математической красотой»^[6]. Кроме того интересен следующий факт: было отмечено, что из 35 законов элементарной физики лишь 17 формулируются при помощи математических уравнений и из более чем 300 понятий лишь около 50 вводятся при помощи формул, остальные формулируются и вводятся лишь словесно^[7].

Одними из самых известных физических законов являются^[8]:

Некоторые физические законы не могут быть доказаны и являются основными, то есть носят универсальный характер в рамках области применения и по своей сути являются определениями. Такие законы часто называют принципами.^[9] Они являются обобщением экспериментальных фактов. К ним относятся, например, второй закон Ньютона (определение силы), закон сохранения энергии^[10] (определение энергии), принцип наименьшего действия (определение действия) и др.

Также существует ряд физических принципов, являющихся самыми широкими, всеохватывающим обобщениями частных законов физики.^[9] В их число входят: принцип неопределённости, принцип причинности, принцип дополнительности, принцип эквивалентности, принцип релятивистской инвариантности и т. д.^[11]. Они формулируются как идеи, обобщающие экспериментальные данные и позволяющие единообразно объяснить всю совокупность рассматриваемых данной теорией явлений.^[9]

Некоторые физические теории: классическая механика, термодинамика, теория относительности, строятся на основе небольшого числа исходных физических принципов, из которых в качестве следствия выводятся все частные законы^[12]. Такой подход к изучению явлений природы получил название метода принципов. Его основоположником являются Ньютон и Эйнштейн.^[9][13]

Часть физических законов являются простыми следствиями некоторых симметрий, существующих в системе. Так, законы сохранения согласно теореме Нётер являются следствиями симметрии пространства и времени. А принцип Паули, например, является следствием идентичности электронов (антисимметричность их волновой функции относительно перестановки частиц).

Все физические законы являются следствием эмпирических наблюдений и верны с той точностью, с которой верны экспериментальные наблюдения. Это ограничение не позволяет утверждать, что какой-либо из законов носит абсолютный характер. Известно, что часть законов заведомо не являются абсолютно точными, а представляют собой приближения к более точным. Так, законы Ньютона справедливы только для достаточно массивных тел, двигающихся со скоростями, значительно меньшими скорости света. Более точными являются законы квантовой механики и специальной теории относительности. Однако, и они в свою очередь являются приближениями более точных уравнений квантовой теории поля.

1. ↑ Трофимова Т. И. Курс физики: учеб. пособие для вузов. — 11. — Москва: Издательский центр «Академия», 2006. — С. 5. — 560 с. — ISBN 5-7695-2629-7.
2. ↑ Селезнев Ю. А. Основы элементарной физики. — М., Наука, 1966. — С. 11 — 408 с.
3. ↑ Ханнанов Н. К., Чижов Г. А. Физика. Учебник для классов с углубленным изучением физики. 10 класс. — 1. — ДРОФА, 2013. — С. 350-390. — 481 с. — ISBN 978-5-358-12648-0.
4. ↑ Малов И. Ф. Универсальность законов природы (Жизнь на Земле, во Вселенной). (неопр.). Мир Культуры (22 октября 2014 года). Дата обращения 6 октября 2019.
5. ↑ Розенталь И. Л. Физические закономерности и численные значения фундаментальных постоянных. Успехи физических наук (1980 г. ).— Том 131, вып. 2. — Дата обращения 06 октября 2019 года.
6. ↑ Медведев Б В, Ширков Д В. П. А. М. Дирак и становление основных представлений квантовой теории поля (рус.) // Успехи физических наук. — 1987-09-01. — Т. 153, вып. 9. — С. 59–104. — ISSN 0042-1294.
7. ↑ Селезнев Ю. А. Основы элементарной физики. — М., Наука, 1966. — Тираж 100 000 экз. — с. 401
8. ↑ 100 великих научных открытий / Д. К. Самин. — М.: Вече, 2002. — 480 с. — 25 000 экз. — ISBN 5-7838-1085-1.
9. ↑ ^{1 2 3 4} Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 11
10. ↑ Сивухин Д. В. Общий курс физики. Механика. — М., Наука, 1979. — Тираж 50 000 экз. — с. 149
11. ↑ Селезнев Ю. А. Основы элементарной физики. — М., Наука, 1966. — Тираж 100 000 экз. — с. 11
12. ↑ Мощанский В. Н. Формирование мировоззрения учащихся при изучении физики. — М., Просвещение, 1976. — Тираж 80 000 экз. — с. 114
13. ↑ Эйнштейн А. Физика и реальность. — М., Наука, 1965. — 359 c.

• Pичард Фейнман. Характер физических законов. — Издание второе, исправленное. (1-е изд.— М., «Мир» 1968 г.). — М.: Наука, 1987. — 160 с. — 163 000 экз.
• Claus Kiefer. On the Concept of Law in Physics (англ.) // Proceedings of the conference «The concept of law in science», Heidelberg, 4-5 June 2012. — arXiv:1301.5110.