1.2. Законы ома
Министерство образования и науки РТ |
КАЗАНСКИЙ ЭНЕРГЕТИЧЕСКИЙ ТЕХНИКУМ
Лабораторная работа №2
Законы Ома и Кирхгофа в цепях
постоянного тока
Методические указания к лабораторной работе по дисциплине “Электротехника”
Казань 2009
Цель работы — опытная проверка законов Ома и Кирхгофа и применение их для расчета электрических цепей постоянного тока.
1. КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
1.1. ОБЩИЕ СВЕДЕНИЯ
Электрической цепью называют совокупность устройств и объектов, соединенных определенным образом и образующих путь для протекания электрического тока.
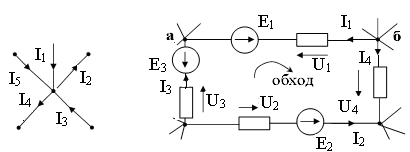
Для наглядности электрические цепи изображают рисунком, на котором в виде условно графических обозначений (УГО) показывают все элементы, входящие в цепь и способы их соединения между собой. Такой рисунок называют электрической схемой. Пример схемы электрической цепи приведен на рис.1.1. Это цепь постоянного тока, она содержит: Е1, Е2, Е3 – источники ЭДС, стрелка в их условном обозначении означает направление возрастания потенциала;

Рис. 1.1. Схема электрической цепи
С точки зрения расположения и соединения элементов электрические цепи описываются следующими понятиями.
Ветвь — участок цепи, состоящий из одного или нескольких элементов, соединенных между собой последовательно. При последовательном соединении элементов через все элементы рассматриваемой ветви проходит один и тот же ток. Примерами ветвей на схеме являются участки цепи:
Узел — место (точка) соединения трех или большего числа ветвей. На схеме узлами являются точки
При изображении на схеме узел показывают либо совмещенным способом — одной точкой (рис.1.2а), либо разнесенным способом — несколькими точками с перемычкой между ними, не обладающей электрическим сопротивлением (рис.1.2б). Смысл узла в обоих случаях один и тот же — это точки с одинаковым потенциалом.
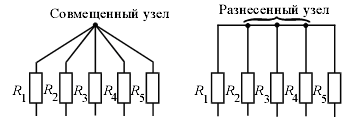
а) б)
Рис.1.2 Узлы электрической цепи
Соединение, при котором все ветви (участки) цепи присоединены к одной паре узлов, называют параллельным. При параллельном способе соединения каждая из ветвей находится под одним и тем же напряжением.
Цепи, в которых элементы или ветви соединены последовательно и параллельно называют цепями со смешанным соединением элементов.
Контур — образован ветвями и узлами, которые образуют замкнутый путь для протекания электрического тока. Примеры контуров: abca, bdcb, acda, abdca, acbda, abcda.
Схема с последовательным соединением элементов образует один контур и называется
Схема со смешанным соединением элементов, в общем случае образует несколько контуров и называется многоконтурной схемой,
Под расчетом (анализом) электрической цепи понимают нахождение токов во всех ветвях схемы. Все расчеты электрических цепей основываются на физических законах, к числу которых относятся законы Ома, Кирхгофа и Джоуля-Ленца.
Закон Ома устанавливает связь между током, напряжением и параметрами элементов в неразветвленной электрической цепи и позволяет рассчитывать в них токи. В электротехнике рассматривают три формулировки закона Ома.
Немецкий физик Г. Ом (1787-1854) экспериментально установил, что ток на пассивном участке цепи с полным сопротивлением R (рис.1.3а) определяется соотношением:
| (1.1) |
где  и
и 
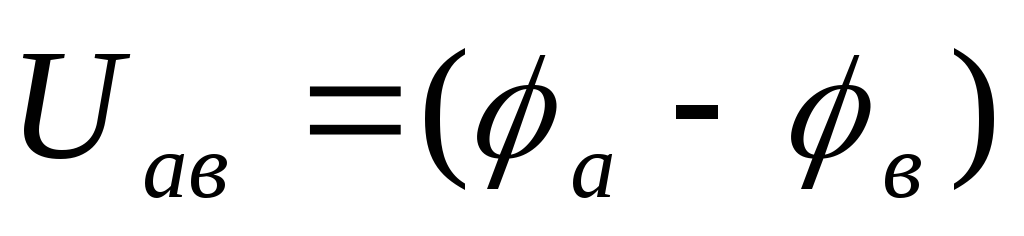 —
падение напряжения на этом участке
цепи.
—
падение напряжения на этом участке
цепи.
За положительное направление напряжения принимается направление в сторону меньшего потенциала. На пассивном участке положительное направление тока и напряжения совпадают.
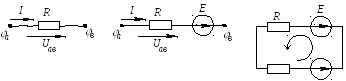
а) б) в)
Рис. 1.3. К определению законов Ома
Например, для нахождения тока (рис.1.1) на пассивном участке цепи dc с сопротивлением R4, необходимо найти φd и φc, а затем рассчитать ток:
| (1.2) |
Обобщенный закон Ома для участка цепи, содержащего источники ЭДС (рис.1.3б), выражается уравнением
| (1.3) |
Для
записи закона Ома выбирают положительное
направление тока, после чего ЭДС Е и напряжение 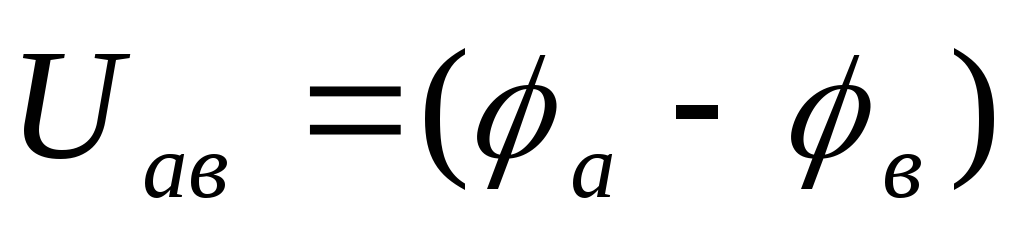 в выражении (1.3) со знаком плюс, если их
направления совпадают с направлением
тока, и со знаком минус, когда их
направления противоположны направлению
тока. Если при расчете ток окажется с
отрицательным знаком, то действительные
направления тока противоположно
первоначально выбранному направлению.
в выражении (1.3) со знаком плюс, если их
направления совпадают с направлением
тока, и со знаком минус, когда их
направления противоположны направлению
тока. Если при расчете ток окажется с
отрицательным знаком, то действительные
направления тока противоположно
первоначально выбранному направлению.
Закон Ома для полной цепи (рис.1.3в), т.е. для замкнутой цепи (для контура): ток в простой одноконтурной цепи выражается уравнением
| (1.4) |
где 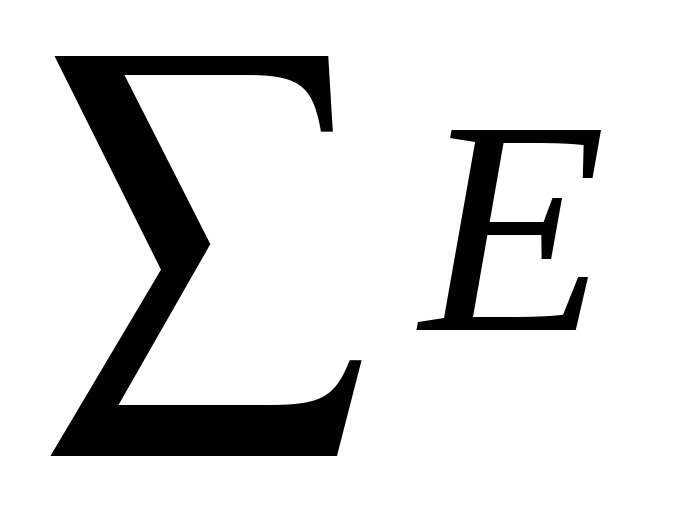 —
алгебраическая сумма ЭДС источников
ЭДС в контуре.
—
алгебраическая сумма ЭДС источников
ЭДС в контуре.
ЭДС
в выражении (1.4) берутся со знаком «плюс»
если выбранное направление тока и ЭДС
совпадают и со знаком «минус» если
не совпадают; 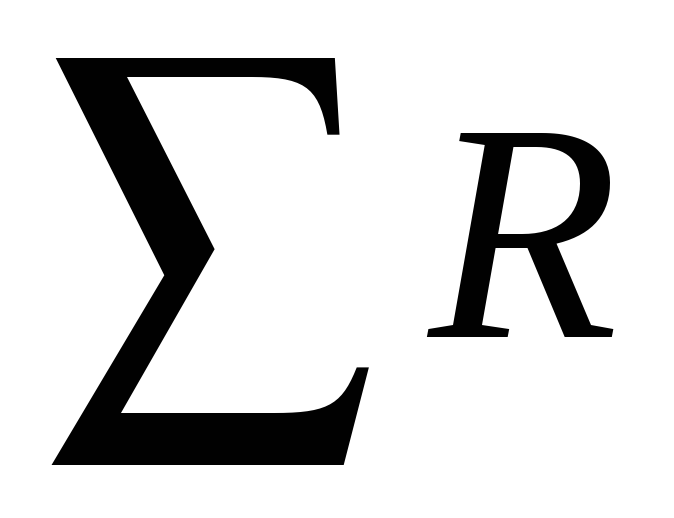
1.3. Законы кирхгофа
Первый закон Кирхгофа устанавливает связь между токами, сходящимися в узле (рис.1.4а) электрической цепи: алгебраическая сумма токов, сходящихся в узле, равна нулю:
| (1.5) |
При
записи уравнений по первому закону
Кирхгофа токи, направленные к узлу,
берут с одним знаком, обычно со знаком
«плюс»,
а токи, направленные от узла, — со знаком
«минус»
или наоборот. Например, для узла в (рис.1.1) первый закон Кирхгофа записывается
так: 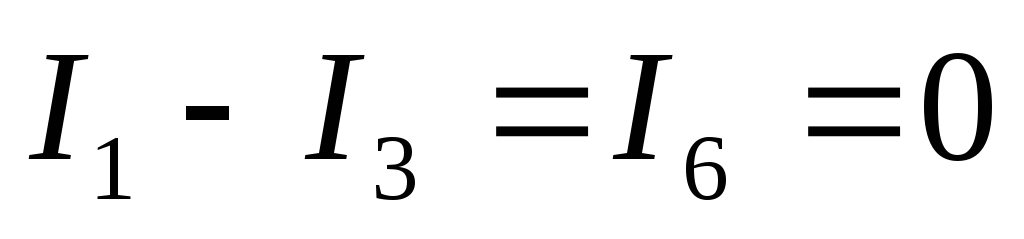 ,
а для узла на рис.1.4а:
,
а для узла на рис.1.4а: 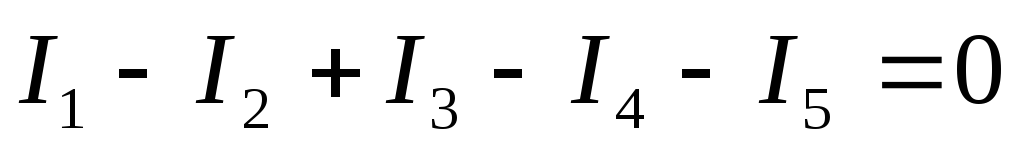 .
.
а) б)
Рис. 1.4. Участки схем, поясняющие применение а) первого б) второго законов Кирхгофа
Второй закон Кирхгофа устанавливает связь между напряжениями на элементах контура электрической цепи (рис.1.4б). Он имеет две формулировки.
Формулировка 1: алгебраическая сумма ЭДС в любом замкнутом контуре электрической цепи равна алгебраической сумме падений напряжения на всех участках контура:
| (1.6) |
где n — число источников ЭДС в контуре,
m — число элементов с сопротивлением Rk в контуре,
— напряжение или падение напряжения на k-м элементе контура.
Формулировка 2: алгебраическая сумма напряжений на всех элементах контура, включая источники ЭДС, равна нулю, т. е.
| (1.7) |
При записи уравнений по второму закону Кирхгофа необходимо:
задать условные положительные направления ЭДС, токов и напряжений;
выбрать положительное направление обхода контура, для которого записывается уравнение, обычно по часовой стрелки, его показывают дугой в контуре;
записать уравнение, пользуясь одной из формулировок, причем слагаемые, входящие в уравнение, берут со знаком «плюс», если их условные положительные направления совпадают с направлением обхода контура, и со знаком «минус», если они противоположны.
Например, для контура (рис.1.4б) при указанном направлении обхода уравнения имеют вид
-U1-U2 + U3 + U4 = E1 – E2 – E3 — (формулировка 1)
—U1—U2 + U3 + U4 — E1 + E2 + E3 =0 — (формулировка 2)
Вторым законом Кирхгофа можно пользоваться и для определения напряжения между двумя произвольными точками схемы. Для этого в уравнения (1.6) необходимо ввести напряжение между этими точками, которое как бы дополняет незамкнутый контур до замкнутого. Например, для определения напряжения Uaв (рис.1.4б) можно написать уравнение, откуда Uab = E1 – U1.
2.4. Источники тока. Закон Ома для полной цепи
Для того чтобы поддерживать разность потенциалов на концах проводника и, следовательно, существование постоянного электрического тока в проводнике и постоянное тепловыделение, необходимы источники электрической энергии (электрического тока). В источниках такого рода происходит разделение зарядов разных знаков и на выходных клеммах появляется разность потенциалов.
Подключим какую-нибудь нагрузку (сопротивление) к источнику электрической энергии. Получим замкнутую цепь. Каким образом движутся заряды вне и внутри источника тока? Прежде всего, еще раз напомним, что мы рассматриваем только стационарные токи, т.е. заряды нигде не накапливаются, а просто циркулируют по замкнутой цепи. Вне источника (во внешней цепи) ток идет от «плюса» к «минусу» (клемма «плюс» – клемма с большим потенциалом, клемма «минус» – клемма с меньшим потенциалом). Таким образом, во внешней цепи заряды движутся в направлении, в котором на них действует электрическое поле внутри проводника: положительные по полю, отрицательные против поля. Внутри источника электрической энергии (во внутренней цепи) ток идет от «минуса» к «плюсу», т.е. заряды движутся в направлении, противоположном тому, в котором на них действует электрическое поле. Значит, внутри источника перемещение зарядов вызывается не электрическим полем, а какими-то иными причинами. Эти причины (химические, механические, световые, магнитные и т. д.) зависят от природы источника тока.
Силы, действующие внутри источника электрической энергии, заставляющие заряды двигаться против действия электрического поля, называются сторонними силами. При этом часто при решении каких-то задач природа этих сил значения не имеет и не конкретизируется. Сторонние силы при упорядоченном движении зарядов совершают работу, за счет которой, например, нагреваются сопротивления. Очевидно, что полный запас энергии источника тока равен работе, которую могут совершить сторонние силы.
К идее о необходимости действия в замкнутой цепи сторонних сил полезно прийти и иным образом. Представим себе, что на свободные заряды в замкнутой цепи действовали бы одни электрические силы. Известно, что цепь при прохождении по ней тока нагревается. Выделившееся тепло тогда можно было бы рассматривать только как результат работы электрических сил (электрического поля). Но работа электрического поля по перемещению зарядов по замкнутой траектории (в данном случае замкнутой цепи) равна нулю (этот факт подробно обсуждался в п.1.12). А значит, не могла бы нагреваться и цепь, что явно противоречит опыту. Следовательно, где-то в замкнутой цепи обязательно должны действовать силы не электростатического происхождения, работа которых отлична от нуля, т.е. сторонние силы. Место действия сторонних сил в замкнутой цепи и можно назвать источником электрической энергии или источником тока.
Важнейшей характеристикой источника тока является электродвижущая сила (ЭДС). Можно дать два эквивалентных определения ЭДС.
1) ЭДС – разность потенциалов на выходных клеммах источника тока при разомкнутой внешней цепи (или когда ток через источник не идет). Далее мы покажем, что в случае разрядки или зарядки источника тока разность потенциалов на его выходных клеммах соответственно меньше ЭДС и больше ЭДС.
2) ЭДС – работа сторонних сил (источника) по разделению единичного заряда (или просто при прохождении через источник единичного заряда):
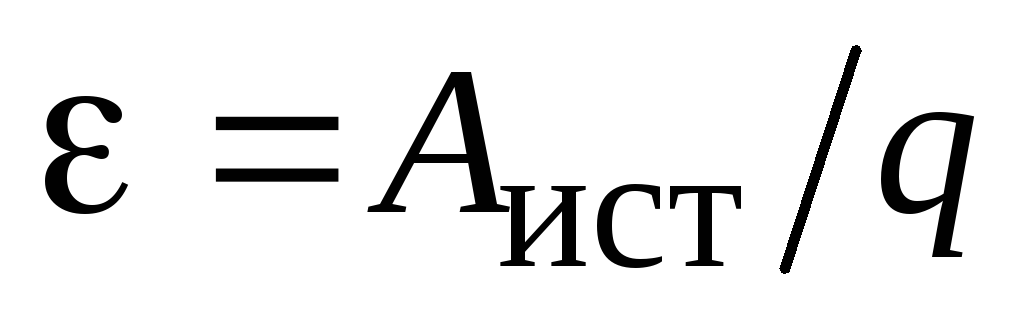 .
(2.12)
.
(2.12)
Из (2.12) следует, что, зная ЭДС источника, силу тока и время его протекания, можно определить работу, совершенную сторонними силами:
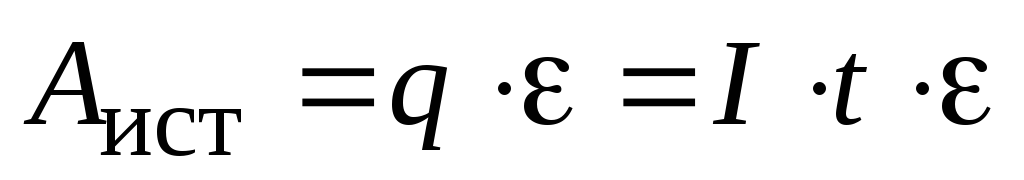 .
(2.13)
.
(2.13)
Обсудим
вторую характеристику источника –
внутреннее сопротивление. Представим
себе, что мы замкнули клеммы источника
проводником с исчезающе малым
сопротивлением  ,
другими словами, сделали короткое
замыкание источника. Тогда, если бы
источник был идеальным, т.е. на его
выходных клеммах разность потенциалов
была бы всегда равна ЭДС, то по закону
Ома мы получили бы
,
другими словами, сделали короткое
замыкание источника. Тогда, если бы
источник был идеальным, т.е. на его
выходных клеммах разность потенциалов
была бы всегда равна ЭДС, то по закону
Ома мы получили бы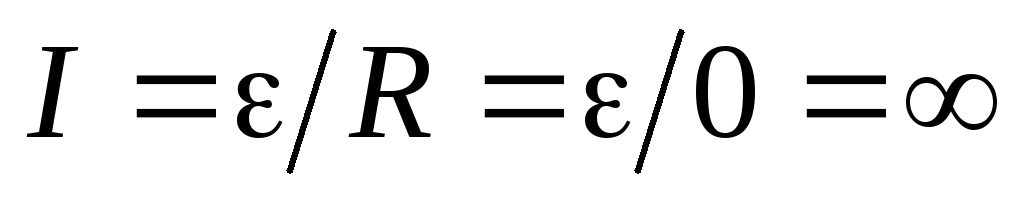 ,
т.е. источник давал бы бесконечный ток
и в единицу времени совершал бы бесконечно
большую работу (см. (2.13)), что невозможно.
Таким образом, при работе любого источника
обязательно должны существовать
какие-либо внутренние механизмы
ограничения максимального тока. Эти
механизмы могут быть различными в
зависимости от природы источника тока.
Однако все они могут быть смоделированы,
если ввести вторую характеристику
источника – внутреннее сопротивление
,
т.е. источник давал бы бесконечный ток
и в единицу времени совершал бы бесконечно
большую работу (см. (2.13)), что невозможно.
Таким образом, при работе любого источника
обязательно должны существовать
какие-либо внутренние механизмы
ограничения максимального тока. Эти
механизмы могут быть различными в
зависимости от природы источника тока.
Однако все они могут быть смоделированы,
если ввести вторую характеристику
источника – внутреннее сопротивление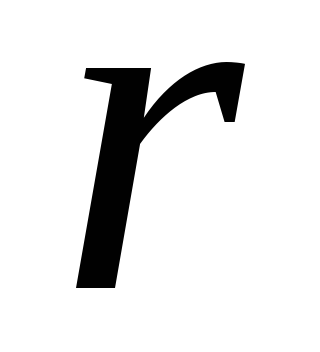 .
В этом случае при коротком замыкании
за счет конечного внутреннего сопротивления
источника мы получим конечный ток в
цепи, называемый током короткого
замыкания:
.
В этом случае при коротком замыкании
за счет конечного внутреннего сопротивления
источника мы получим конечный ток в
цепи, называемый током короткого
замыкания: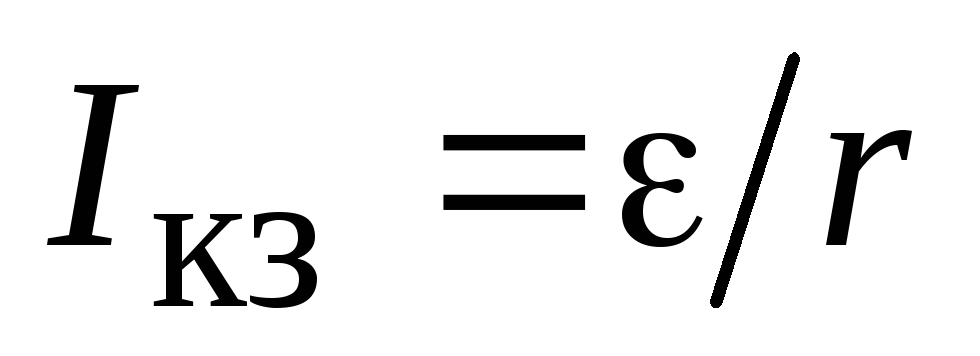 .
Это максимальный ток, который может
давать источник. Итак, внутреннее
сопротивление источника
.
Это максимальный ток, который может
давать источник. Итак, внутреннее
сопротивление источника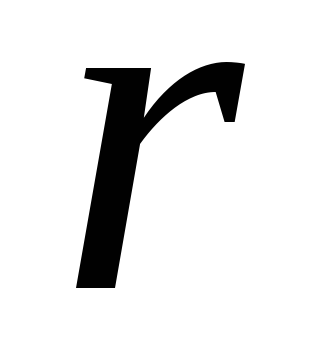 – это характеристика, определяющая
ток короткого замыкания или максимальные
ток и мощность, которые может давать
источник.
– это характеристика, определяющая
ток короткого замыкания или максимальные
ток и мощность, которые может давать
источник.
 ,
разность потенциалов на клеммах которого
всегда равна
,
разность потенциалов на клеммах которого
всегда равна ,
и последовательно соединенного
с ним сопротивленияr,
которое называется внутренним
сопротивлением источника тока.
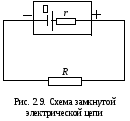
Такая модель источника тока показана
на рис. 2.9.
,
и последовательно соединенного
с ним сопротивленияr,
которое называется внутренним
сопротивлением источника тока.
Такая модель источника тока показана
на рис. 2.9. На
этом же рис. 2.9 к клеммам источника
подключено некоторое, отличное от нуля
сопротивление R.
Поскольку внутреннее и внешнее
сопротивления соединены последовательно,
полное сопротивление цепи будет 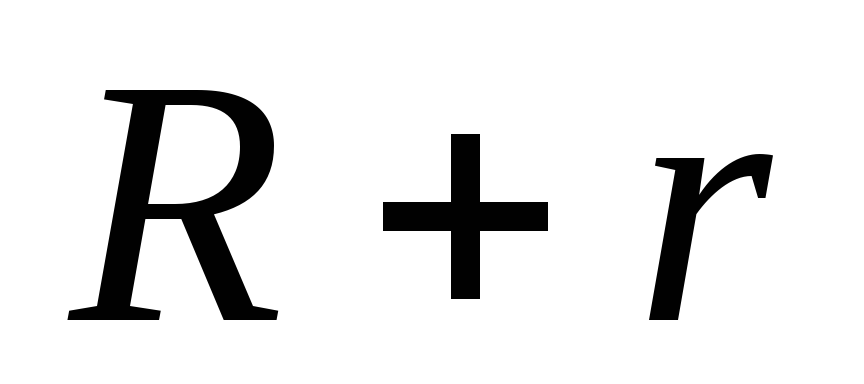 ,
и по цепи потечет ток:
,
и по цепи потечет ток:
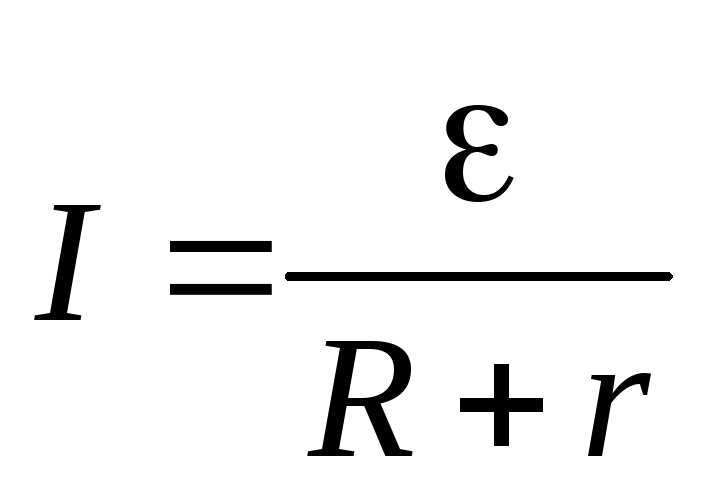 . (2.14)
. (2.14)
Последнее равенство называется законом Ома для полной цепи.
Уравнение
(2.14) легко преобразуется к виду: 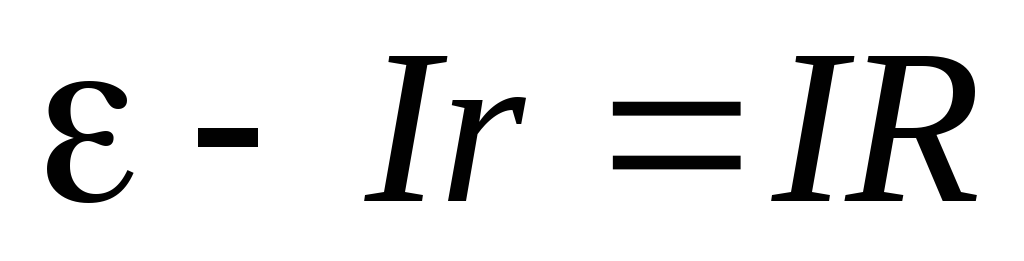 .
Правая часть этого равенства (а значит
и левая) есть напряжение на внешнем
сопротивленииR.
Это напряжение суть напряжение на
выходных клеммах источника тока, так
как сопротивление R непосредственно к этим клеммам подключено.
Таким образом, при разрядке источника
током I напряжение на его клеммах:
.
Правая часть этого равенства (а значит
и левая) есть напряжение на внешнем
сопротивленииR.
Это напряжение суть напряжение на
выходных клеммах источника тока, так
как сопротивление R непосредственно к этим клеммам подключено.
Таким образом, при разрядке источника
током I напряжение на его клеммах:
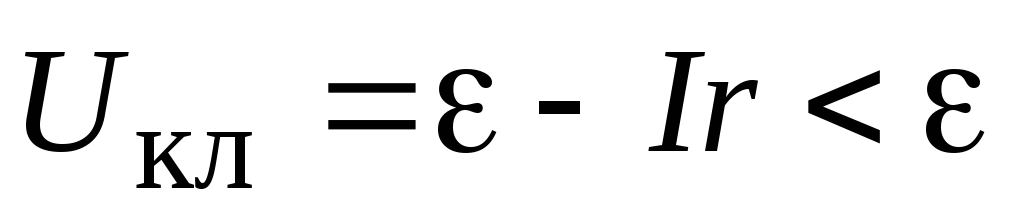 .
(2.15)
.
(2.15)
Это
напряжение тем ближе к ЭДС, чем меньше
внутреннее сопротивление и ток разрядки.
При 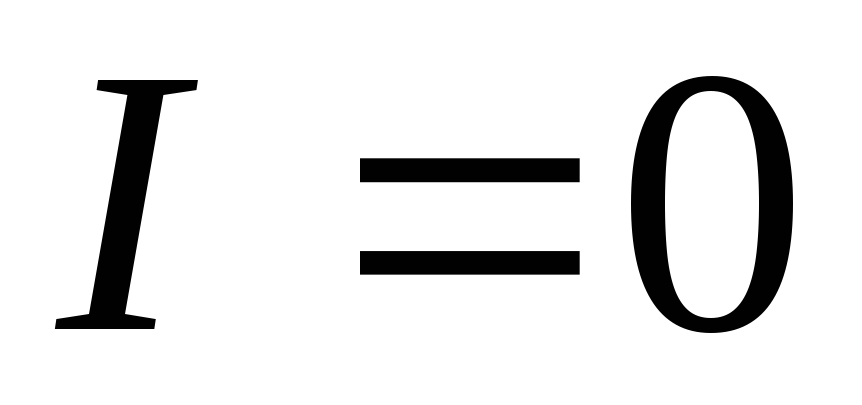 в соответствии с данным выше первым
определением ЭДС из (2.15) получим
в соответствии с данным выше первым
определением ЭДС из (2.15) получим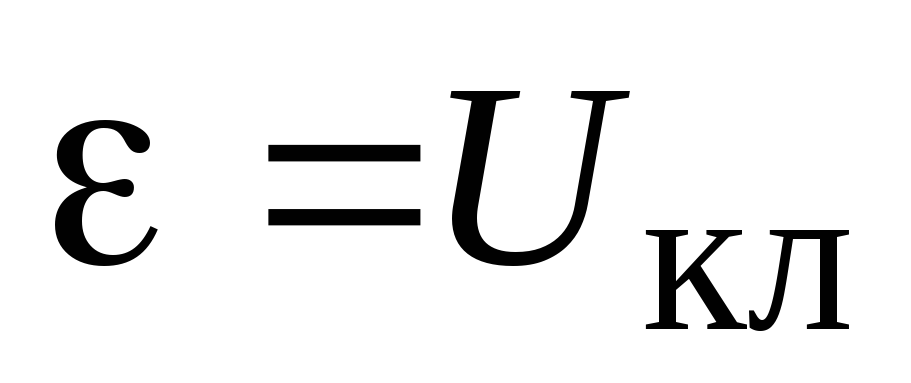 .
.
Пример
2.7. В схеме
на рис. 2.9 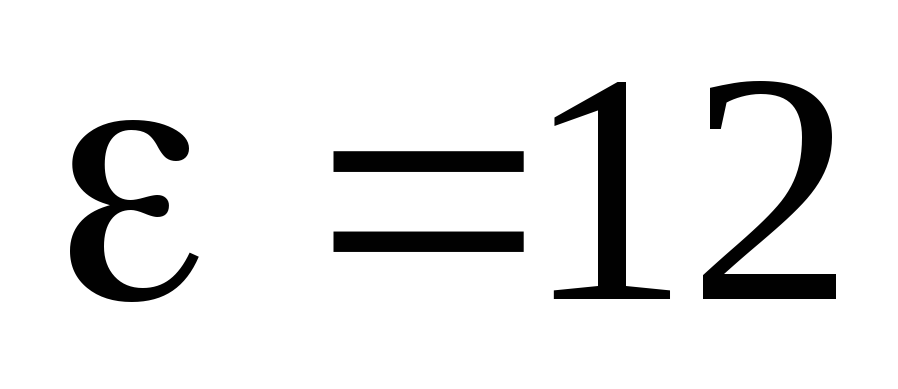 В,
В,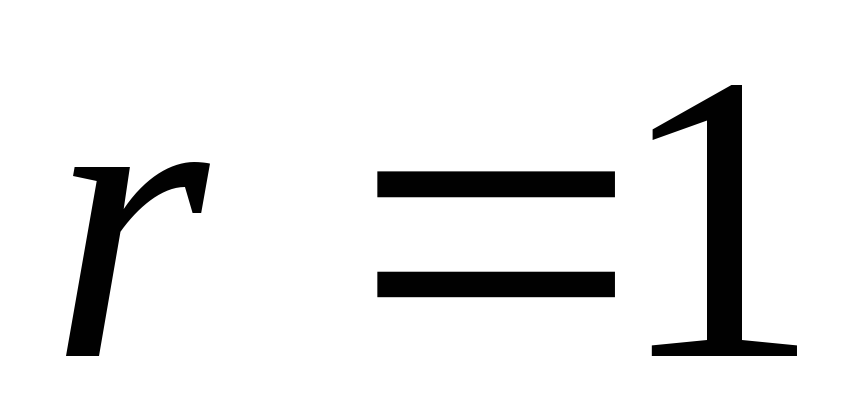 Ом,
Ом,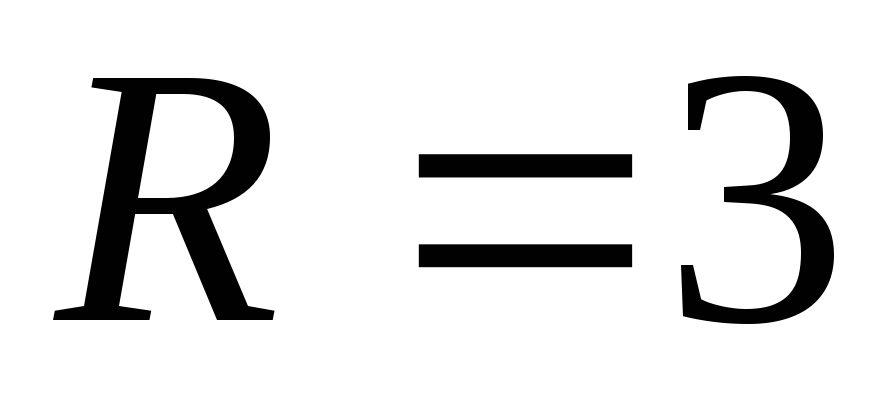 Ом.
Ом.
Определить силу тока в цепи. По закону Ома для полной цепи (2.14) получим:
 А.
А.Определить напряжение на клеммах источника тока. Напряжение на клеммах источника суть напряжение на нагрузке R:
 В. Естественно то же самое получается
и по формуле (2.15).
В. Естественно то же самое получается
и по формуле (2.15).Определить мощность, выделяющуюся во внешней цепи. Мощность, выделяющаяся во внешней цепи, есть мощность, выделяющаяся на нагрузке R, поэтому:
 Вт.
Вт.Определить мощность, выделяющуюся во внутренней цепи. Конечно, при работе источника тока нагревается не только внешняя нагрузка, но и сам источник, поскольку он обладает внутренним сопротивлением. Мощность, выделяющаяся во внутренней цепи, есть мощность, выделяющаяся на сопротивлении r:
 Вт.
Вт.Определить мощность источника тока (мощность, развиваемую сторонними силами). Работа источника тока расходуется на нагревание как внешней нагрузки, так и самого источника тока, поэтому:
 Вт. Можно рассуждать и по-другому,
опираясь на уравнение (2.13):
Вт. Можно рассуждать и по-другому,
опираясь на уравнение (2.13): Вт.
Вт.Определить КПД схемы. Полезной следует считать часть мощности источника, которая выделяется на внешнем сопротивлении, поэтому:
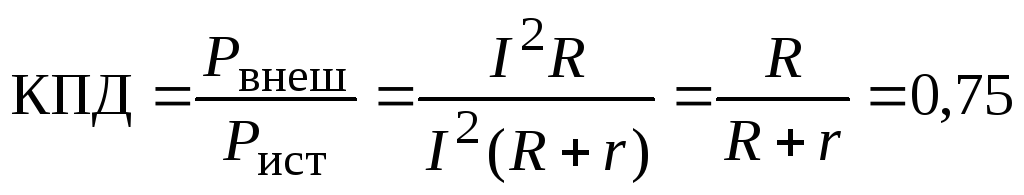 (или
75%).
(или
75%).
Определить максимальный ток, который может давать заданный источник. Ток будет максимален при коротком замыкании источника (т.е. при
 ):
):
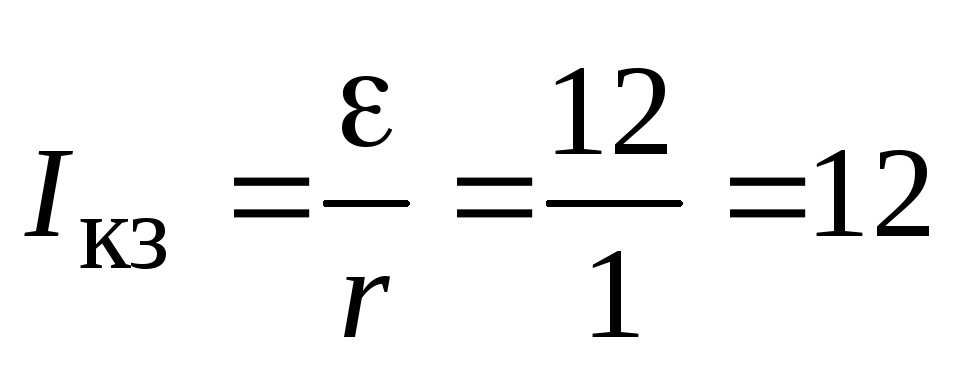 (А).
(А).
Пример
2.8. Каким
должно быть сопротивление 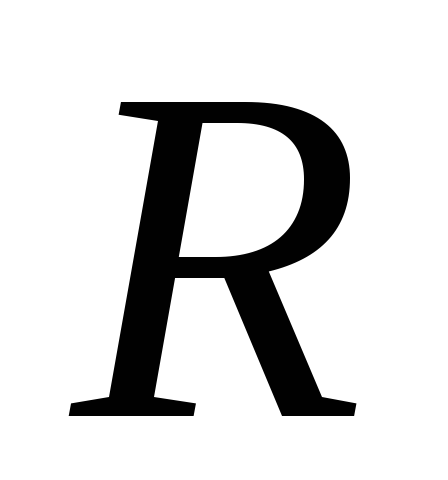 при заданных параметрах источника тока
и r для того, чтобы во внешней цепи выделялась
максимальная мощность? Чему равна эта
максимальная мощность?
при заданных параметрах источника тока
и r для того, чтобы во внешней цепи выделялась
максимальная мощность? Чему равна эта
максимальная мощность?
Решение. Пользуясь законом Ома для полной цепи (2.14) для мощности, выделяемой во внешней цепи, можно записать:
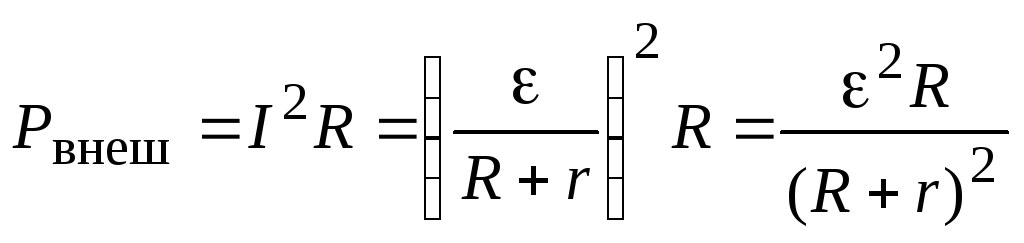 (2.16)
(2.16)
Рвнеш
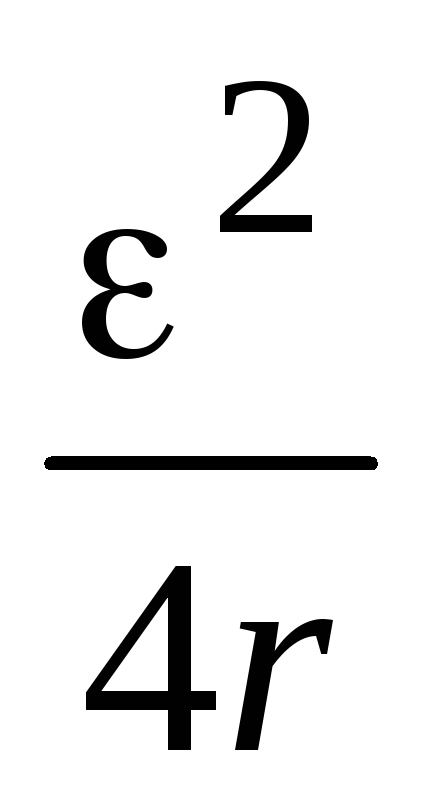
R1R=r R2R

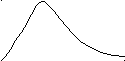












Рис. 2.10. Зависимость мощности, выделяемой во внешней цепи от сопротивления
График
зависимости функции  показан на рис. 2.10. Ясно, что эта функция
должна иметь точку максимума (т.е.
значение
показан на рис. 2.10. Ясно, что эта функция
должна иметь точку максимума (т.е.
значение 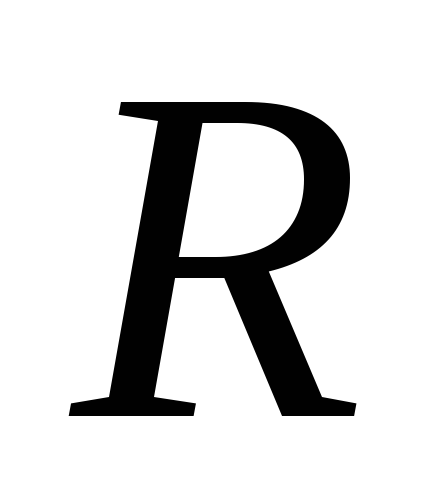 ,
при котором мощность во внешней цепи
максимальна), поскольку из (2.16) следует,
что
,
при котором мощность во внешней цепи
максимальна), поскольку из (2.16) следует,
что 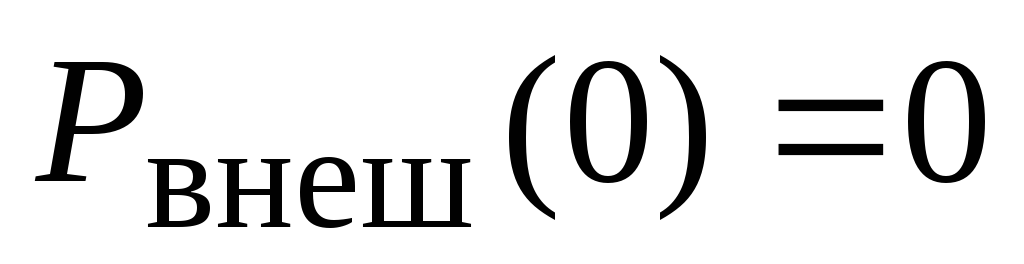 и
и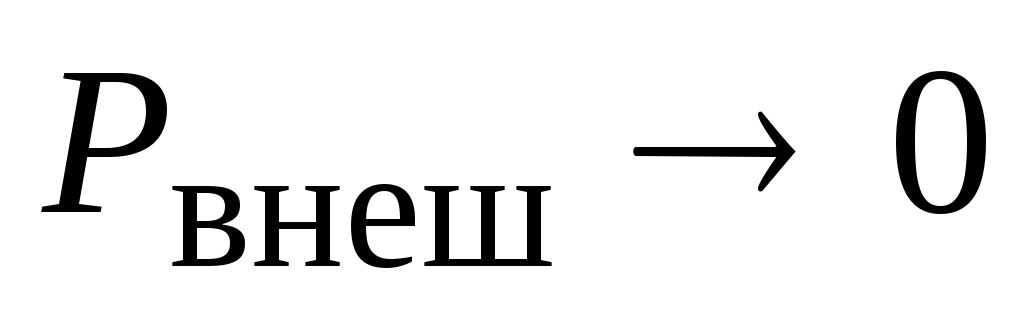 при
при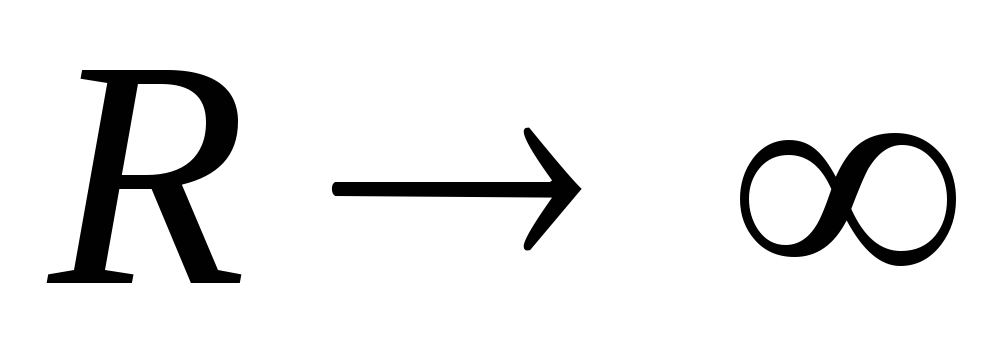 .
Найдем точку максимума функции
.
Найдем точку максимума функции .
Для этого продифференцируем
.
Для этого продифференцируем по сопротивлению
по сопротивлению и приравняем производную к нулю:
и приравняем производную к нулю:
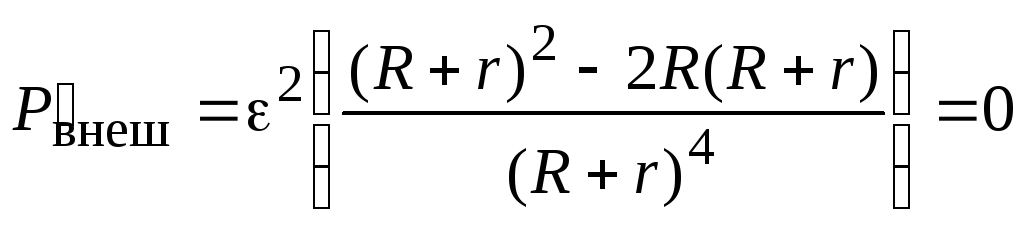 ,
,
откуда
получаем: 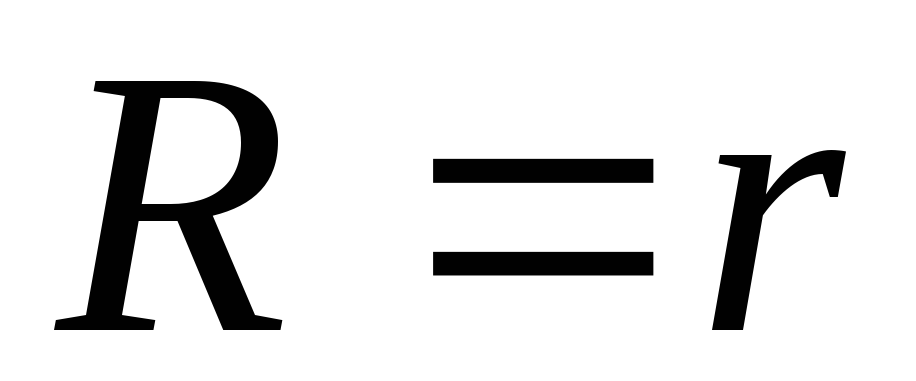 .
Таким образом, мощность, выделяемая во
внешней цепи максимальна, когда внешнее
сопротивление равно внутреннему
сопротивлению источника (рис. 37).
.
Таким образом, мощность, выделяемая во
внешней цепи максимальна, когда внешнее
сопротивление равно внутреннему
сопротивлению источника (рис. 37).
По формуле (2.16) рассчитаем максимальное значение мощности, выделяемой во внешней цепи:
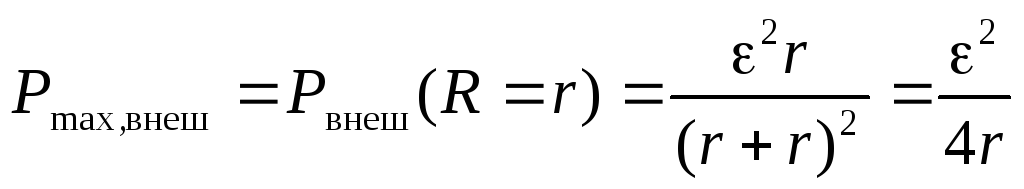 .
.
Отметим, что КПД схемы при этом равен всего на всего 50%, т.е. половина мощности выделяется во внешней цепи и половина – во внутренней:
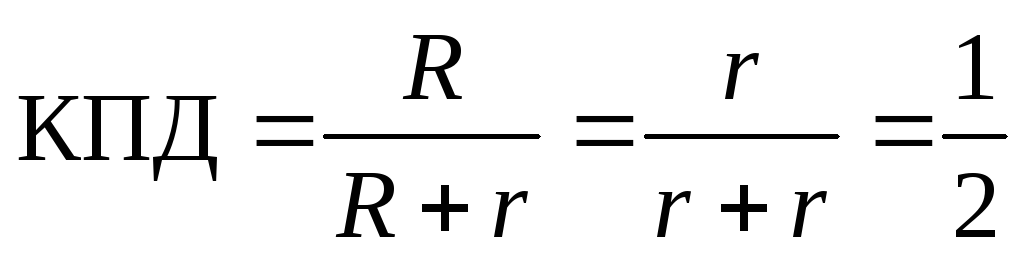 .
.
Анализируя
график на рис. 2.10, можно сделать вывод,
что какое-то требуемое значение мощности,
выделяемой во внешней цепи, можно
получить двумя способами: подключая к
источнику тока некоторые сопротивления  и
и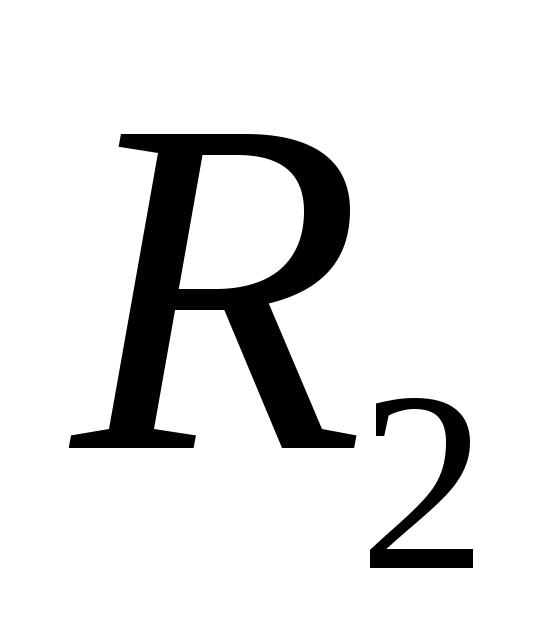 ,
причем
,
причем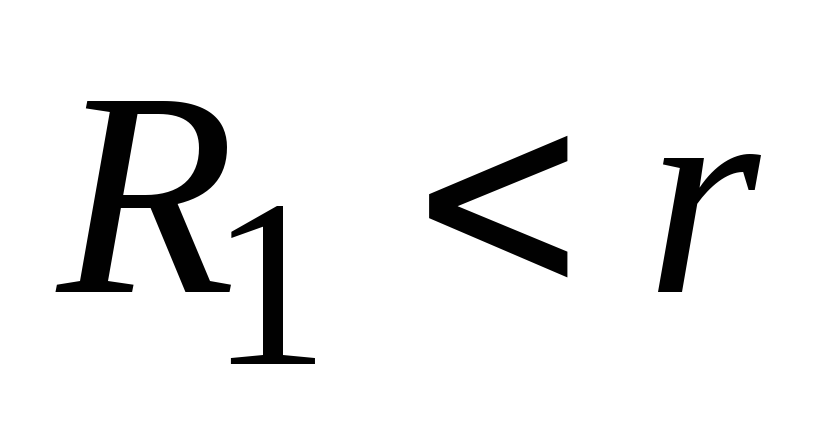 ,
а
,
а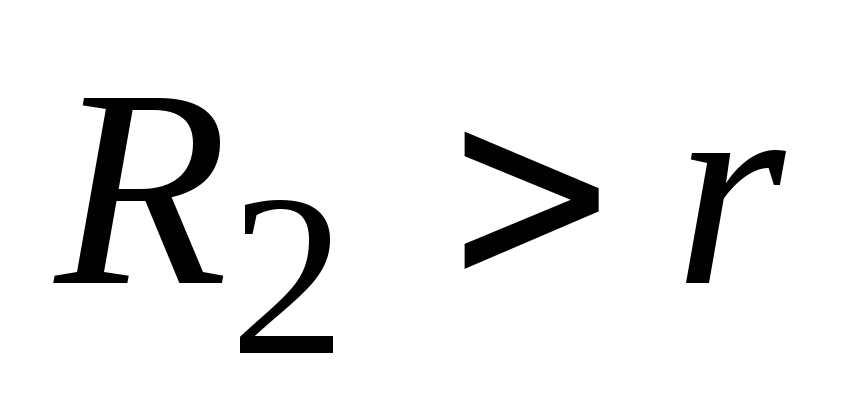 .
Какой вариант следует выбрать? Конечно,
предпочтение следует отдать второму
варианту (т.е. включить большее
сопротивление
.
Какой вариант следует выбрать? Конечно,
предпочтение следует отдать второму
варианту (т.е. включить большее
сопротивление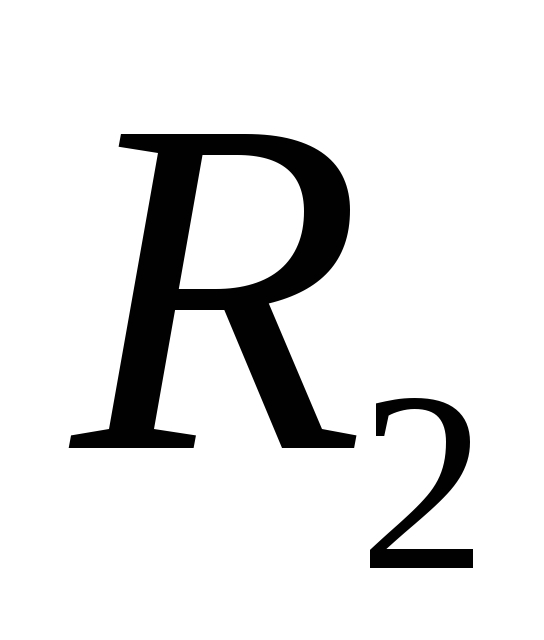 ),
поскольку КПД схемы в этом случае будет
больше (см. вопрос 6 примера 2.5). При
подключении же сопротивления
),
поскольку КПД схемы в этом случае будет
больше (см. вопрос 6 примера 2.5). При
подключении же сопротивления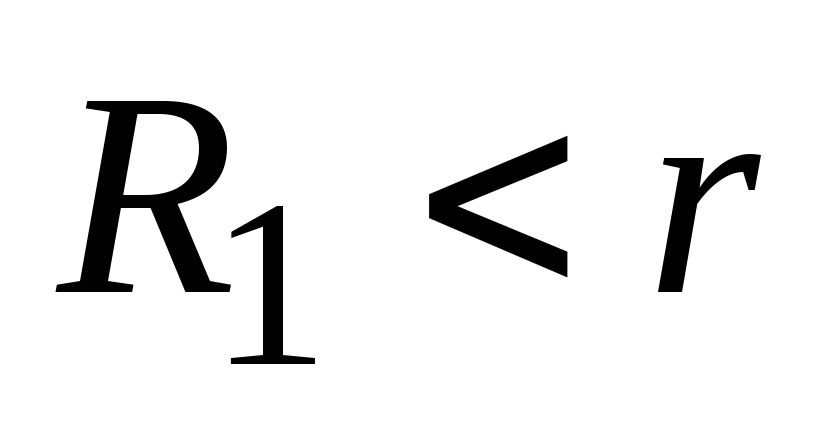 КПД будет меньше 50%. Во внешней цепи мы
тоже получим требуемую мощность, но при
этом еще большая мощность будет бесполезно
выделяться во внутренней цепи, т.е.
расходоваться на нагрев самого источника.
В результате источник быстрее израсходует
свой ресурс.
КПД будет меньше 50%. Во внешней цепи мы
тоже получим требуемую мощность, но при
этом еще большая мощность будет бесполезно
выделяться во внутренней цепи, т.е.
расходоваться на нагрев самого источника.
В результате источник быстрее израсходует
свой ресурс.
Закон Ома
Закон Ома для участка цепи, не содержащего источника ЭДС (рис. 1.4), устанавливает связь между напряжением и током этого участка и может быть записан в виде:
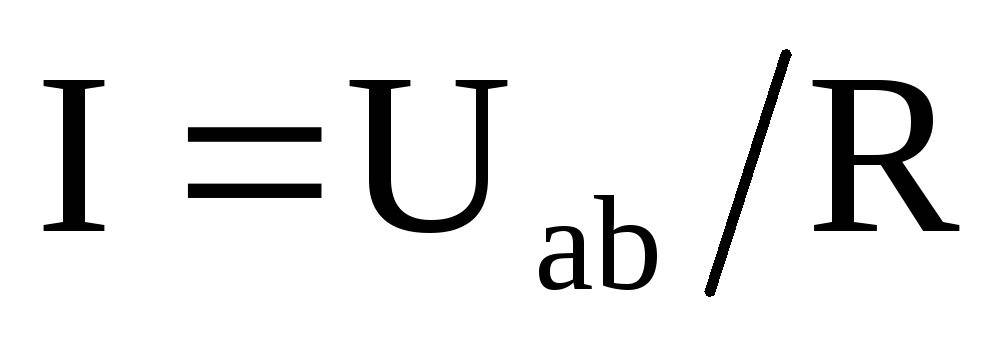 или
или 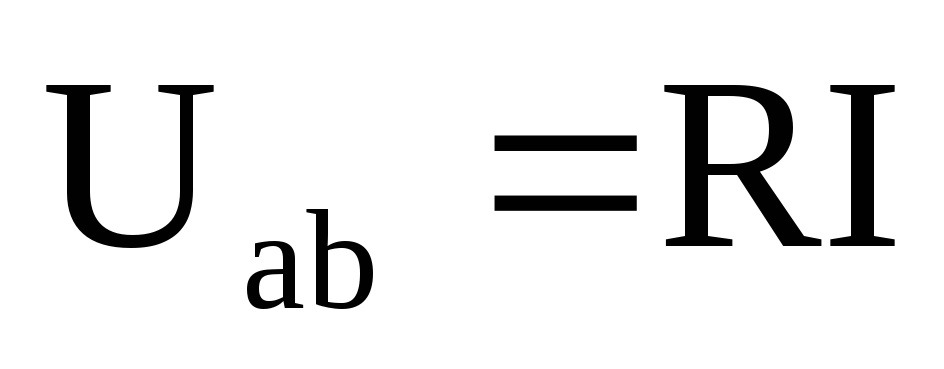 ,
,
г деR-
коэффициент пропорциональности между
напряжением и током на участке ab.
деR-
коэффициент пропорциональности между
напряжением и током на участке ab.
Ток в сопротивлении направлен от точки с большим потенциалом к точке с меньшим потенциалом. Положительное направление напряжения на сопротивлении всегда совпадает по направлению с током.
Напряжение
Uab между двумя точками равно разности
потенциалов этих точек: 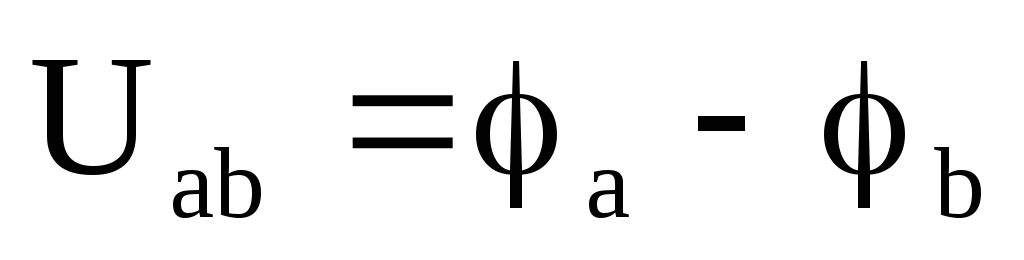 .
.
Тогда
на основании закона Ома можно сделать
следующие записи: 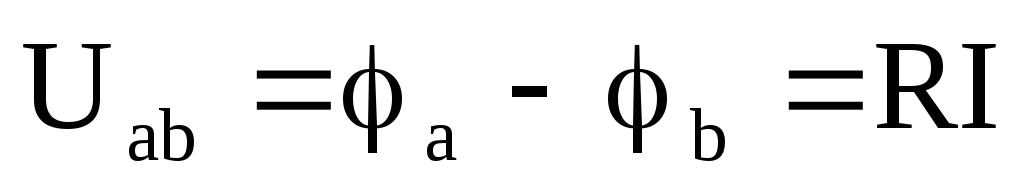 ;
;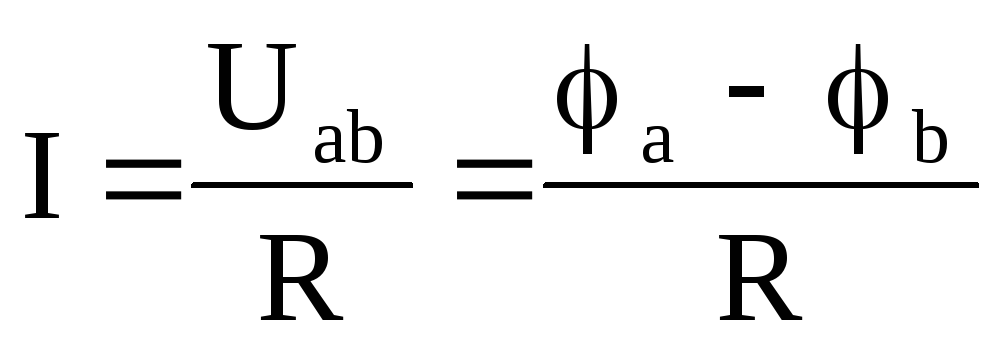 ;
;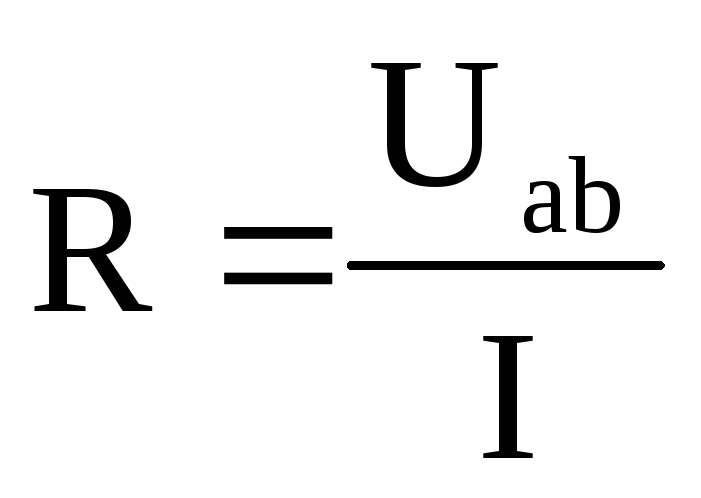 .
.
Определим ток на участке цепи, содержащей несколько элементов (рис. 1.5). Для этого выразим значение потенциала точки а относительно потенциала точки b. Примем потенциал точки b равным нулю и последовательно определим потенциалы всех остальных точек участка.
При
переходе от точки b к точке d через сопротивление rвн потенциал увеличивается на величину
напряжения на этом участке, так как ток
течет от точки с большим потенциалом к
точке с меньшим потенциалом: 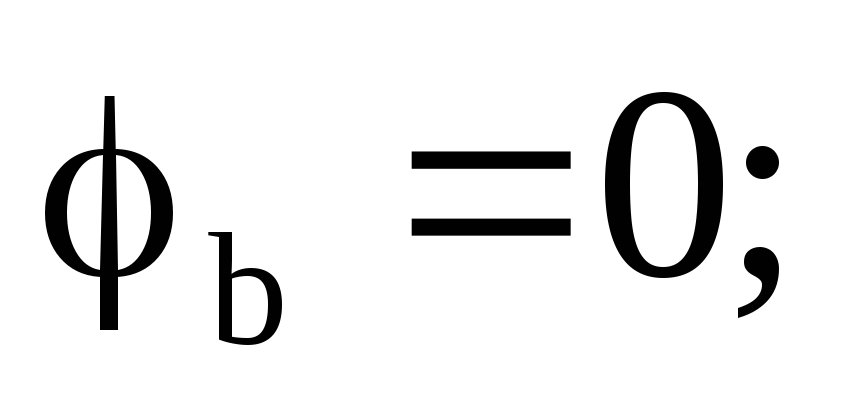
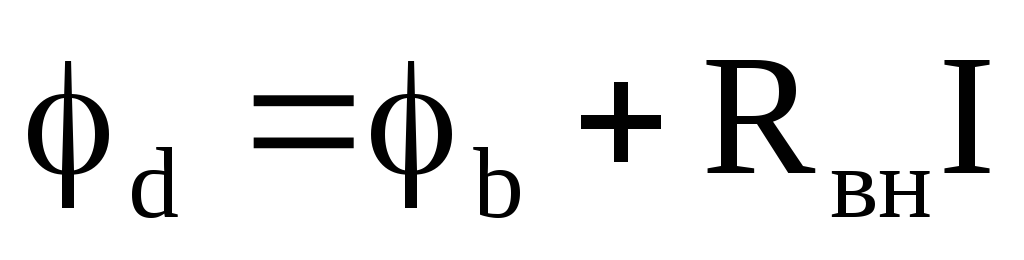 .
.
Потенциал
точки с меньше потенциала точки d на величину ЭДС Е, так как ЭДС всегда
направлена в сторону высокого потенциала
независимо от направления тока: 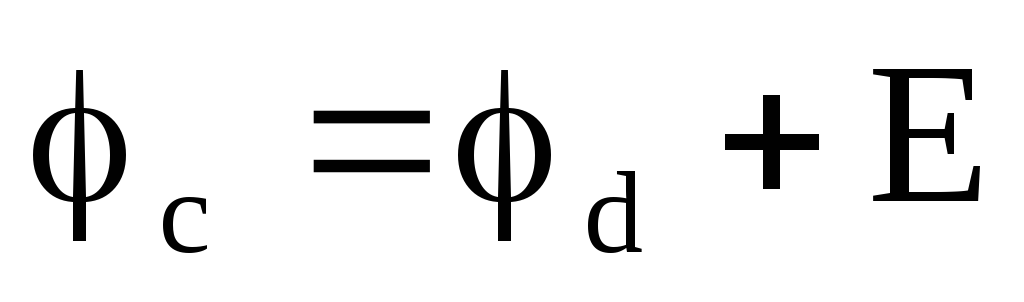 .
.
При
переходе от точки с к точке а через
сопротивление R
потенциал увеличивается на величину
напряжения на этом сопротивлении, так
как мы движемся против тока: 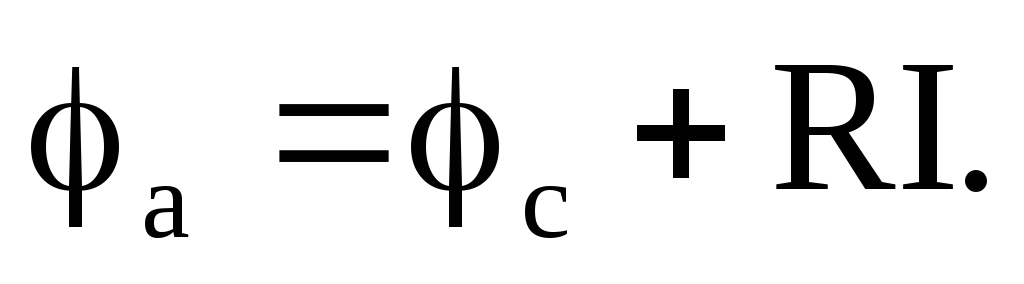
Определим
значение потенциала точка а через потенциал точки b:  .
.
Выразив из этого уравнения ток, получим выражение для закона Ома:
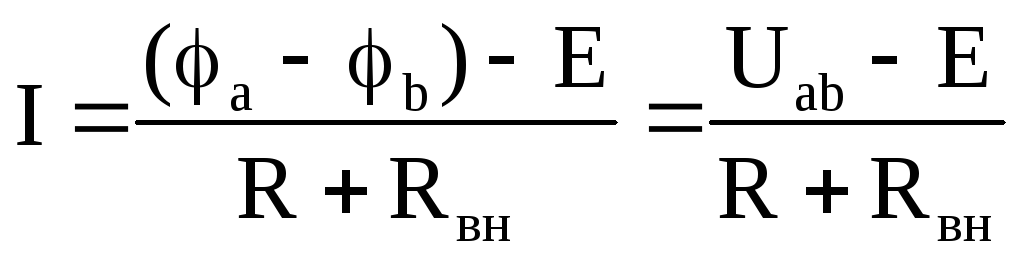 ,
или в обобщенном виде
,
или в обобщенном виде
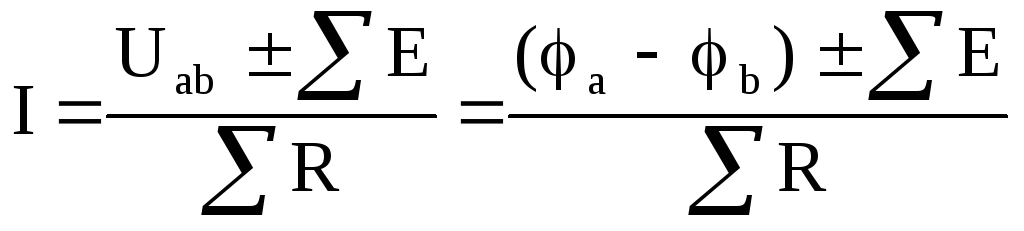 ,
,
где
Uab=(φa-φb)
— напряжение на зажимах всего участка
цепи направленное по току; ΣЕ
–алгебраическая сумма ЭДС участка
цепи, в которой ЭДС берется со знаком
«+», если ее направление совпадает с
направлением тока, или со знаком «-»,
если не совпадает; 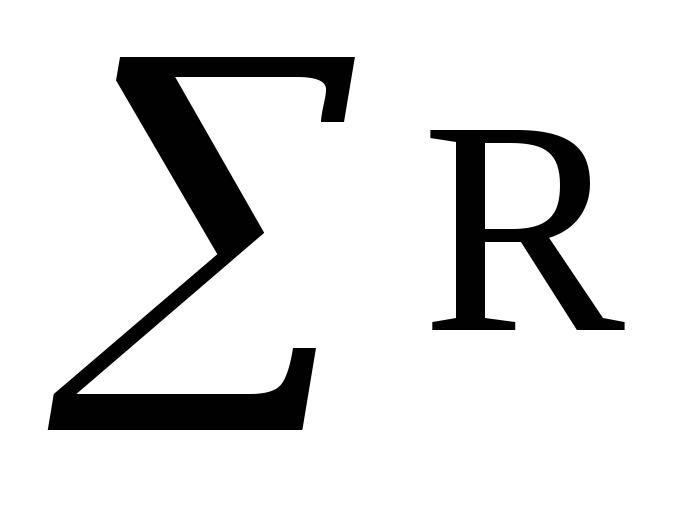 — сумма сопротивлений данного участка
цепи.
— сумма сопротивлений данного участка
цепи.
В случае, если полученное в результате расчета значение тока отрицательно, это значит, что его действительное направление противоположно ранее принятому за положительное.
Законы Кирхгофа
Режим работы цепи любой конфигурации полностью определяется первым и вторым законами Кирхгофа.
Первый закон Кирхгофа применяется к
узлам схемы и формулируется следующим
образом: алгебраическая сумма токов в
узле равна нулю: 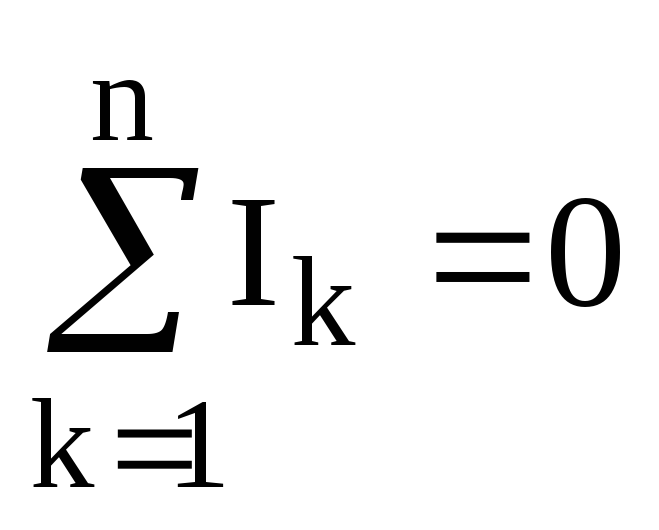 .
.
В этом уравнении токи входящие в узел записываются со знаком «плюс», а выходящие из узла – со знаком «минус».
Второй закон Кирхгофа применяется к
контурам схемы электрической цепи и
формулируется следующим образом: в
любом замкнутом контуре алгебраическая
сумма напряжений на приемниках, входящих
в контур, равна алгебраической сумме
ЭДС: 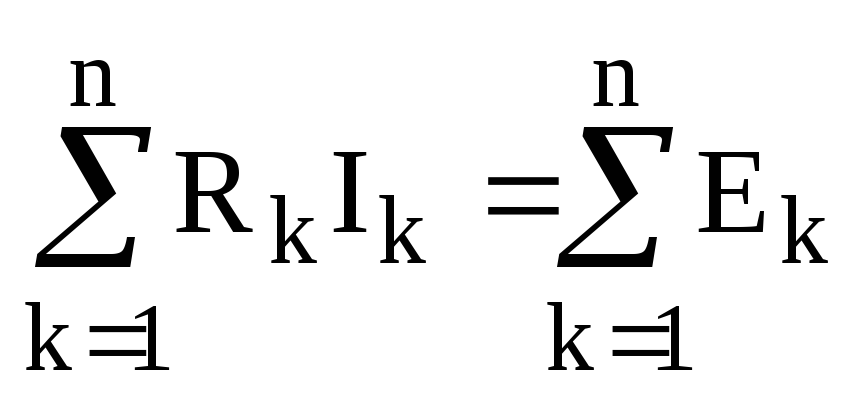 .
.
В этом уравнении положительные знаки принимаются для токов и ЭДС, направления которых совпадают с произвольно выбранным направлением обхода рассматриваемого контура.
Эквивалентные преобразования в электрических цепях
С целью упрощения расчета электрической цепи часто оказывается целесообразным осуществить эквивалентное преобразование некоторой части цепи. Часть цепи до преобразования эквивалентна этой же части после преобразования при условии, что режим в остальной непреобразованной части схемы остается неизменным. То есть разность потенциалов между зажимов преобразованной части схемы остается такой же, как и напряжение на зажимах непреобразованной части схемы, а так же входной ток преобразованной части схемы остается неизменным.
Ветвь может содержать любое число последовательно соединенных элементов цепи. При этом последовательным соединением участков электрической цепи называют соединение, при котором через все участки цепи проходит один и тот же ток. При этом напряжение на зажимах этого участка цепи равно сумме напряжений на каждом из ее элементов (рис. 1.6):
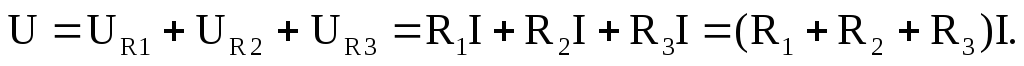
Если мы хотим заменить участок цепи,
состоящий из нескольких последовательно
соединенных элементов, одним эквивалентным,
то напряжение на нем будет равно: 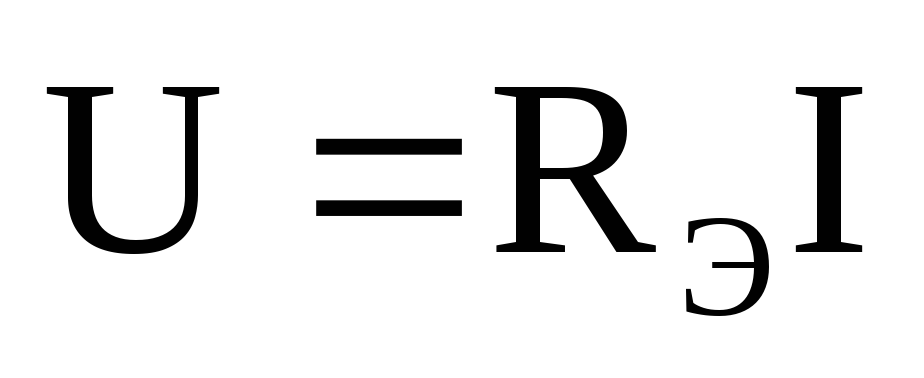 .
.
Учитывая условия эквивалентного преобразования, получаем:
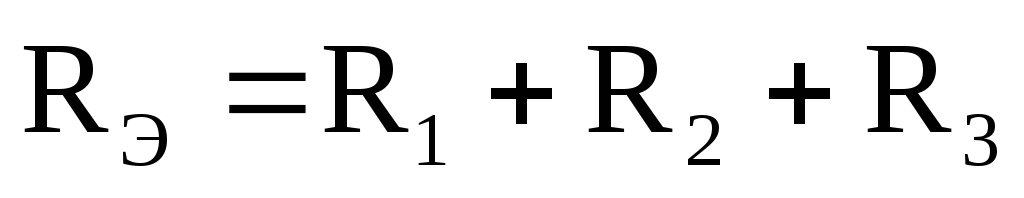 .
.
То есть при последовательном соединении элементов сопротивление цепи равно сумме сопротивлений составляющих ее элементов.
П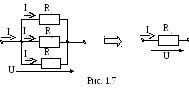 араллельнымсоединением участков (ветвей) электрической
цепи называют соединение, при котором
все участки цепи присоединены к одной
паре узлов (рис. 1.7), и на всех этих участках
одно и то же напряжение.
араллельнымсоединением участков (ветвей) электрической
цепи называют соединение, при котором
все участки цепи присоединены к одной
паре узлов (рис. 1.7), и на всех этих участках
одно и то же напряжение.
При этом ток на входе цепи равен сумме токов параллельных ветвей:
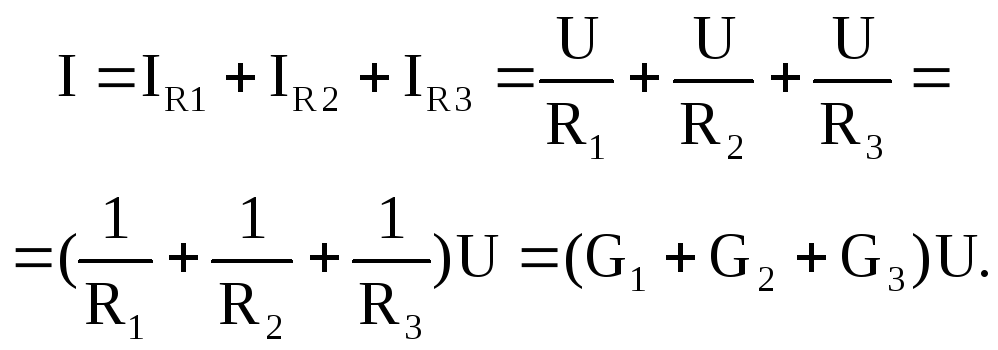
В том случае, если необходимо заменить
участок электрической цепи, состоящий
их нескольких параллельно соединенных
элементов, одним эквивалентным, то ток
такого эквивалентного элемента будет
определяться: 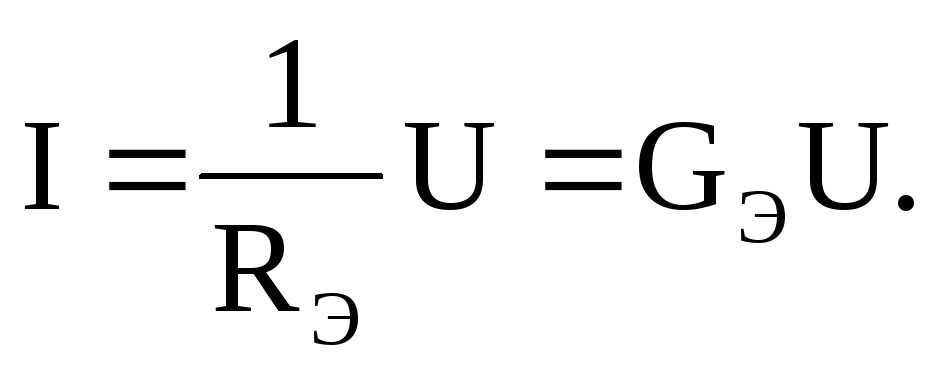
Учитывая условия эквивалентного
преобразования, можно записать: 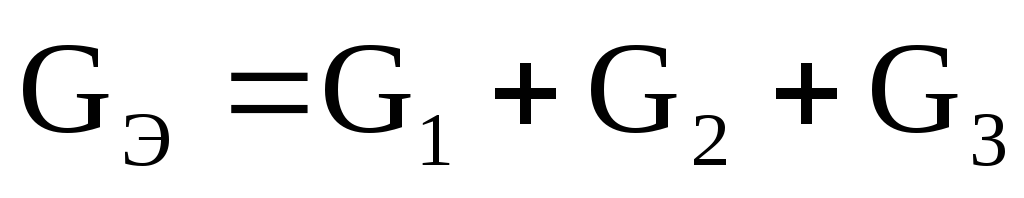 или
или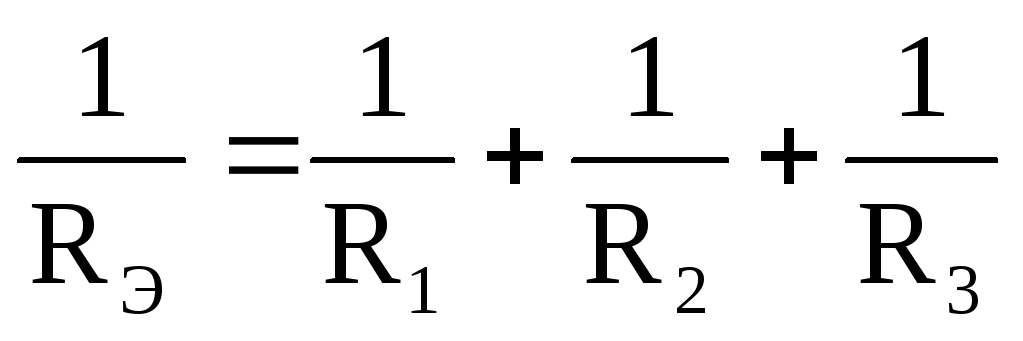 ,
то есть при параллельном соединении
приемников для получения эквивалентной
проводимости, складывают проводимости
параллельных ветвей.
,
то есть при параллельном соединении
приемников для получения эквивалентной
проводимости, складывают проводимости
параллельных ветвей.
Отсюда можно получит формулу для определения эквивалентного сопротивления:
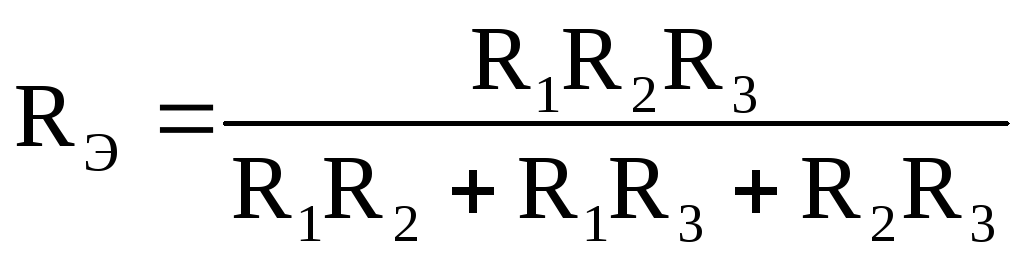 .
.
Для случая параллельного соединения
двух ветвей это выражение буде иметь
вид: 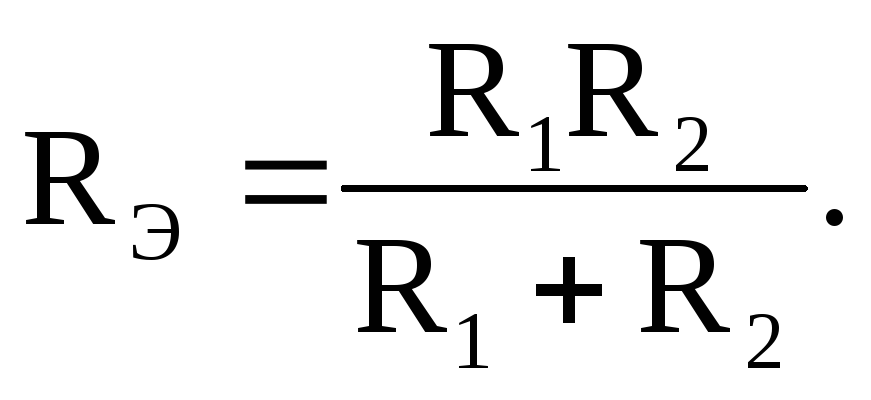
При расчете электрических цепей возникает необходимость эквивалентных преобразований звезды сопротивлений (рис. 1.8, а) в треугольник сопротивлений (рис. 1.8, б). Соединения звездой и треугольником эквивалентны друг другу при условии, что при одинаковых в обоих случаях напряжениях U12,U23,U31между точками 1, 2 и 3 и токиI1,I2,I3, подходящие к этим точкам от остальной части цепи, одинаковы в обоих случаях.
Р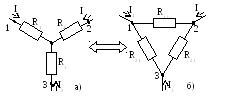 ис.
1.8
ис.
1.8
Формулы для определения сопротивлений лучей звезды через сопротивления сторон треугольника имеют вид:
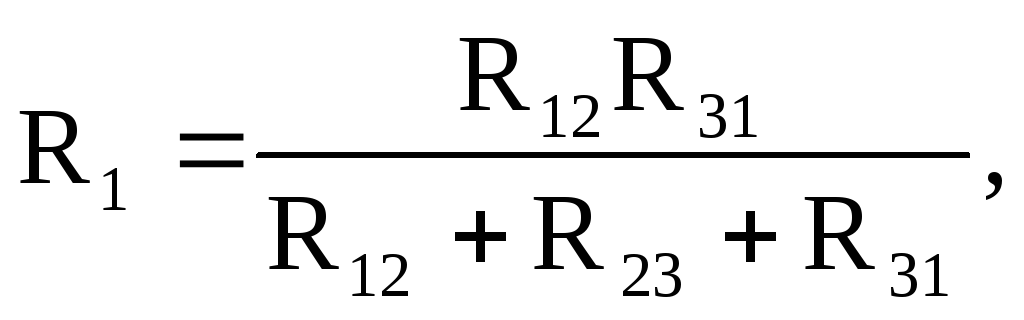
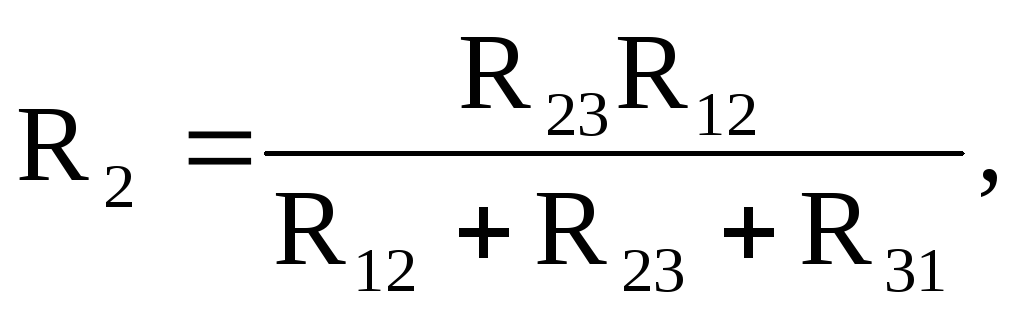
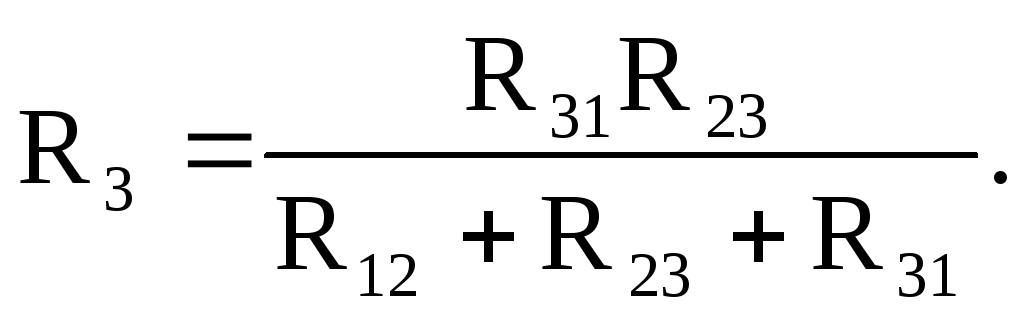
Формулы для расчета сопротивлений сторон треугольника через сопротивления лучей звезды имеют вид:
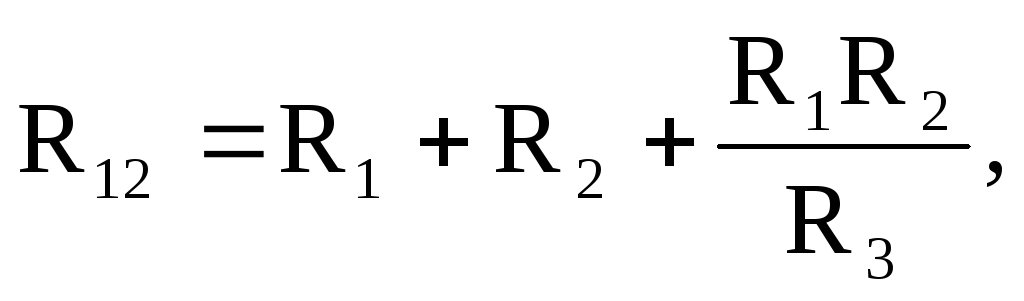
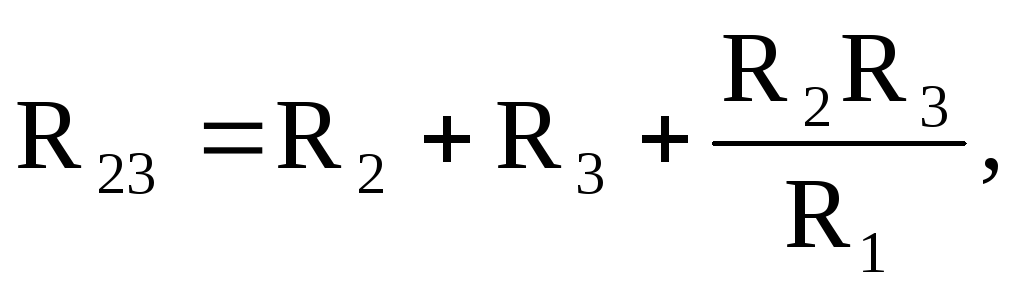
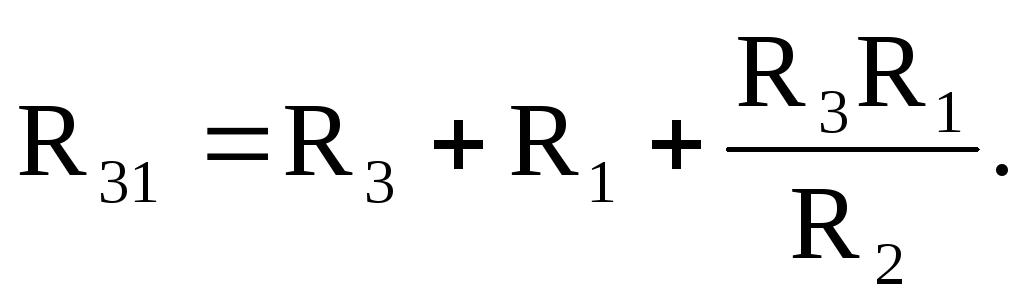
3.2. Закон Ома в дифференциальной форме
Найдем
связь между векторами 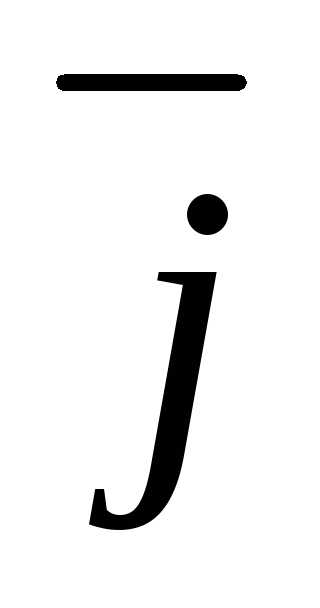 и
и  . Для этого мысленно выделим в
окрестности некоторой точки проводника
элементарный цилиндрический объем
с образующими, параллельными векторам
. Для этого мысленно выделим в
окрестности некоторой точки проводника
элементарный цилиндрический объем
с образующими, параллельными векторам 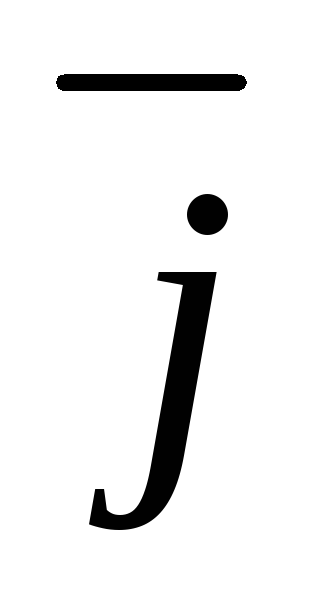 и
и  ,
(см.
рис.
4 ).
,
(см.
рис.
4 ).
Между
концами проводника длиной dl напряжение U = Edl, под действием которого через его
поперечное сечение площадью dS
течет ток I = jdS. Сопротивление цилиндрического
проводника, в нашем случае, равно R = 
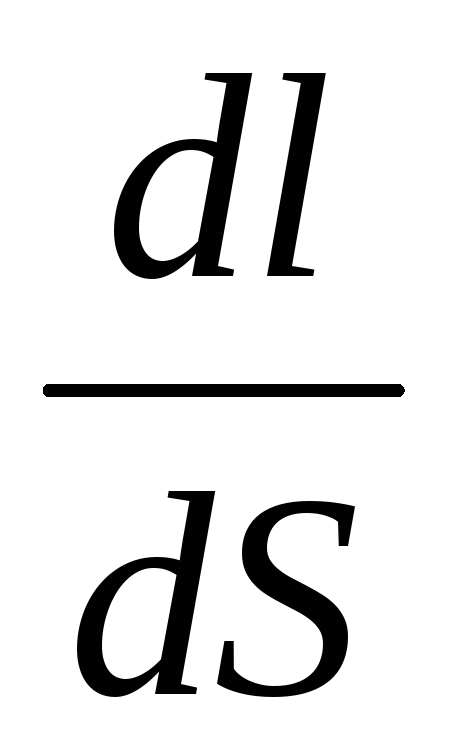 .Используя закон Ома для участка цепи
I
=
.Используя закон Ома для участка цепи
I
= 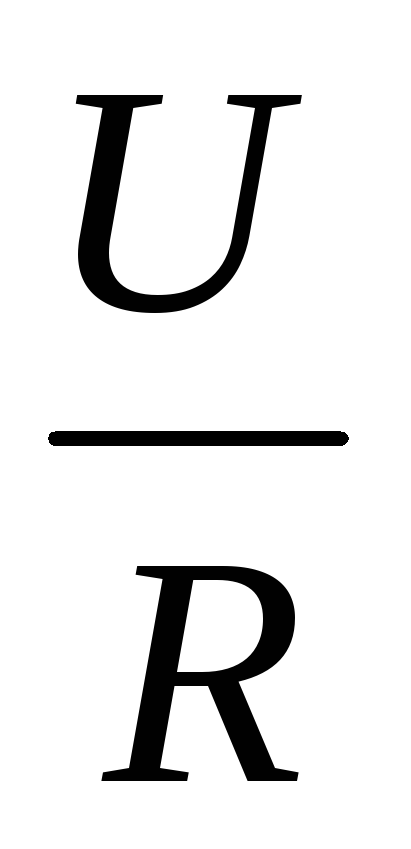 ,
находим: jdS =
,
находим: jdS = 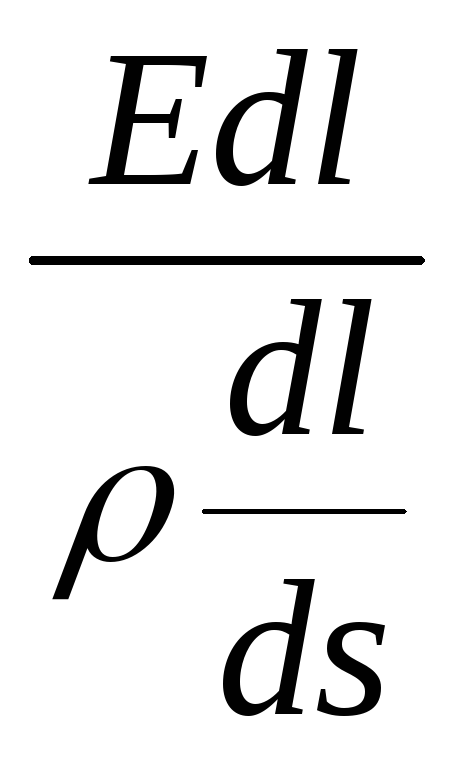 , откуда
и получаем закон Ома в дифференциальной
форме
, откуда
и получаем закон Ома в дифференциальной
форме  =
= 
 =
=  , (16)
, (16)
где  =
=  удельная электропроводность;
[
удельная электропроводность;
[ ]
= 1 /
(Ом м)
= 1
См
/
м, где
1
См
= 1 /
Ом
–
это единица измерения электропроводности
в СИ, называемая сименс (См). Для металлов
согласно классической теории
электропроводности
]
= 1 /
(Ом м)
= 1
См
/
м, где
1
См
= 1 /
Ом
–
это единица измерения электропроводности
в СИ, называемая сименс (См). Для металлов
согласно классической теории
электропроводности  =
,
(17)
=
,
(17)
где
n
—
концентрация свободных электронов,
она может достигать 10
 10
10 электрон / м
электрон / м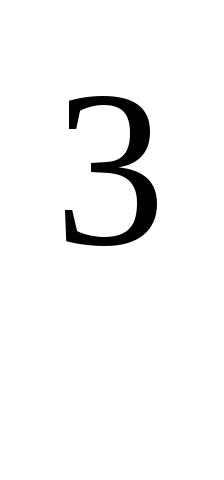 ; e—заряд
электрона, m — его масса;
<
; e—заряд
электрона, m — его масса;
<
 > — средняя длина свободного пробега
электрона; < v
> =
> — средняя длина свободного пробега
электрона; < v
> = 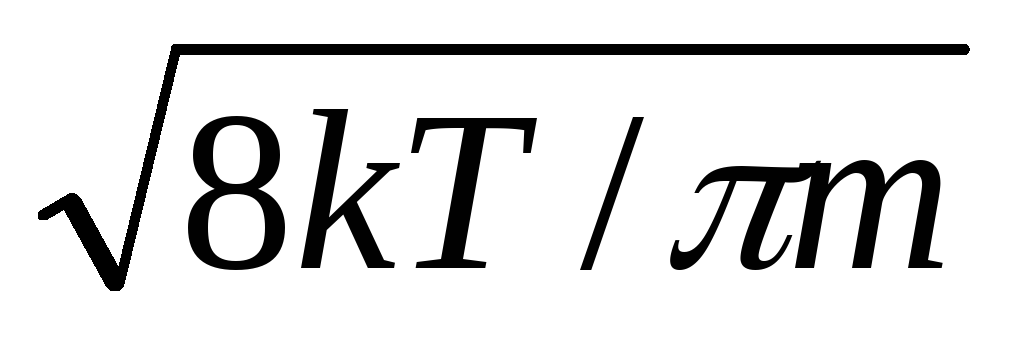 (18)
(18)
<
v
> —
средняя скорость теплового движения
электрона, k = 1,38 10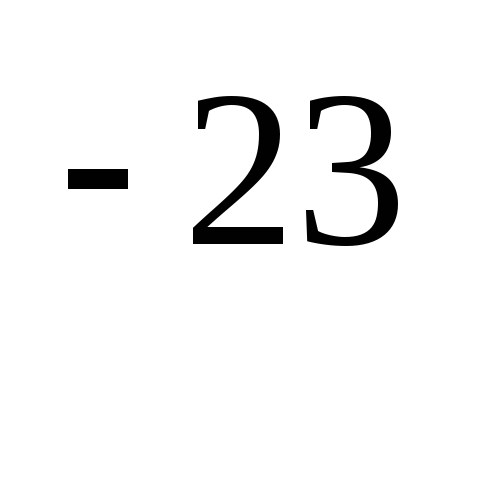 Дж/К
—
постоянная Больцмана.
Дж/К
—
постоянная Больцмана.
С
учетом
(18)
из
(17)
следует, что
~ 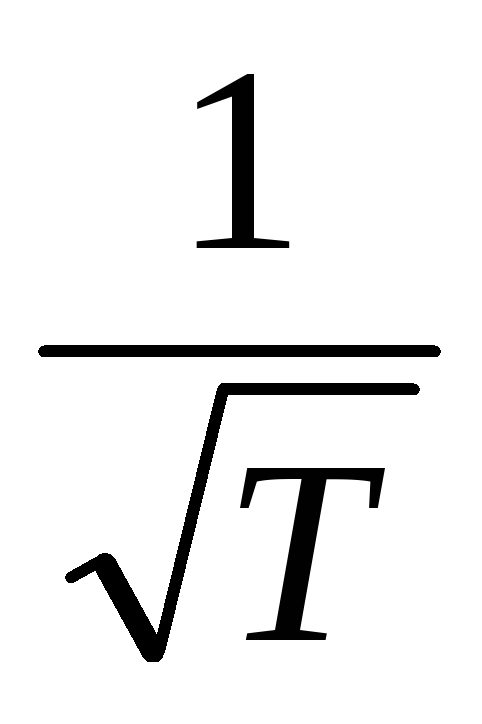 ,
а
,
а 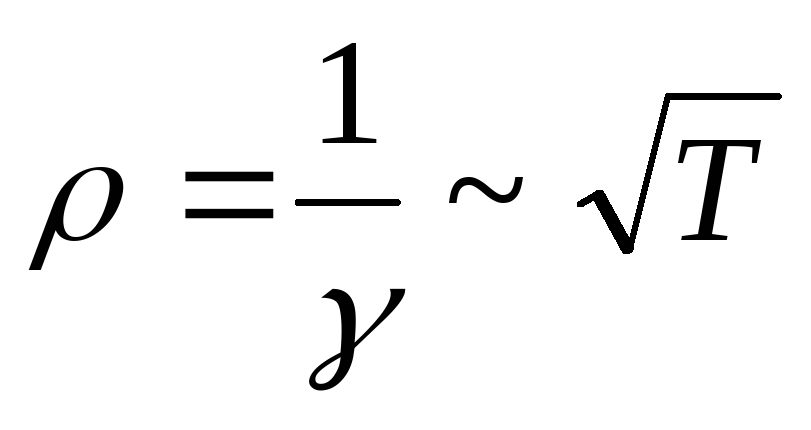 ,
тогда как опыт показывает, что
,
тогда как опыт показывает, что ~ Т .
Этот и другие недостатки классической
теории электропроводности металлов
устранила квантовая теория
электропроводности.
~ Т .
Этот и другие недостатки классической
теории электропроводности металлов
устранила квантовая теория
электропроводности.
4. Закон Ома для неоднородного участка цепи
На неоднородном участке цепи плотность тока пропорциональна сумме напряжен -ностей электростатического поля и поля сторонних сил, т.е.
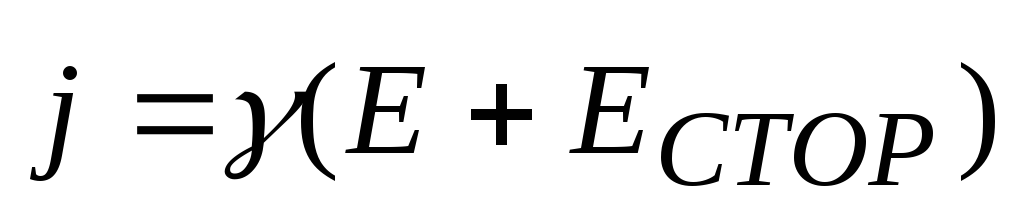 .
(19)
.
(19)
Рассмотрим цилиндрический проводник длиной / с площадью поперечного сечения S. Умножим обе части равенства (19) на перемещение dl вдоль оси проводника и проинтегрируем получившееся соотношение по длине проводника от 0 до l:
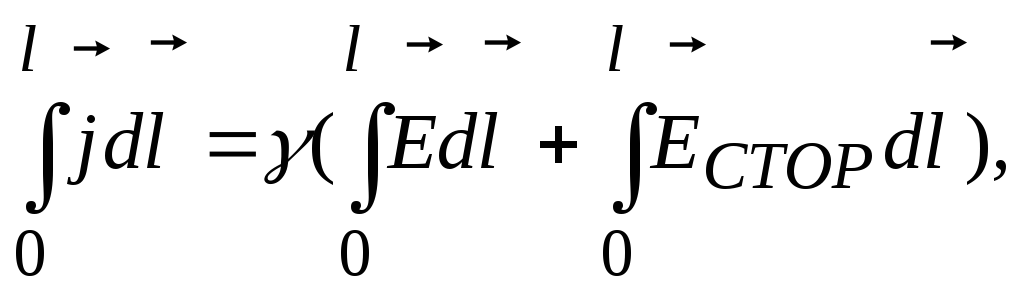
что
дает j l =  (
(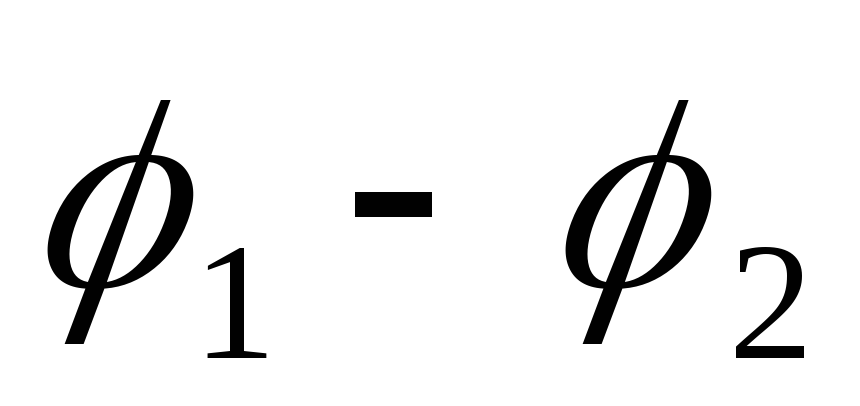 +
+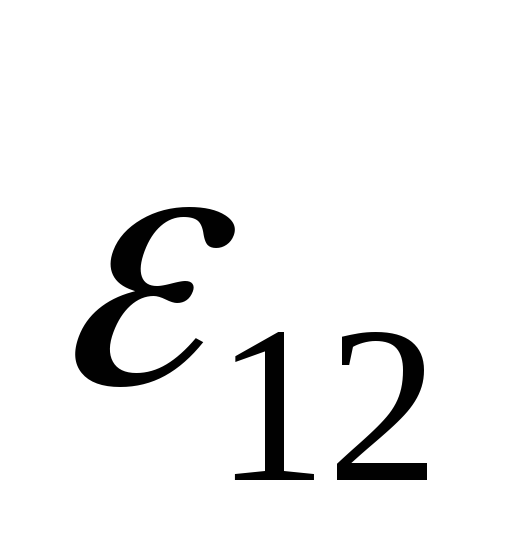 ). (20)
). (20)
Заменив j на I/S,
а  на
на 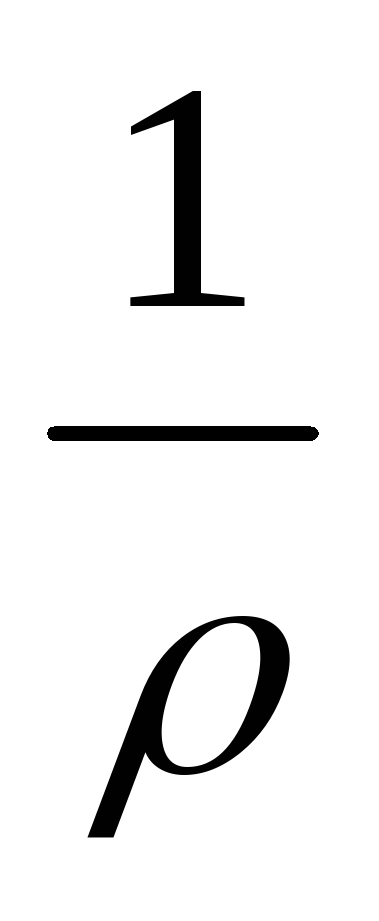 ,
из
(20)
получим I
,
из
(20)
получим I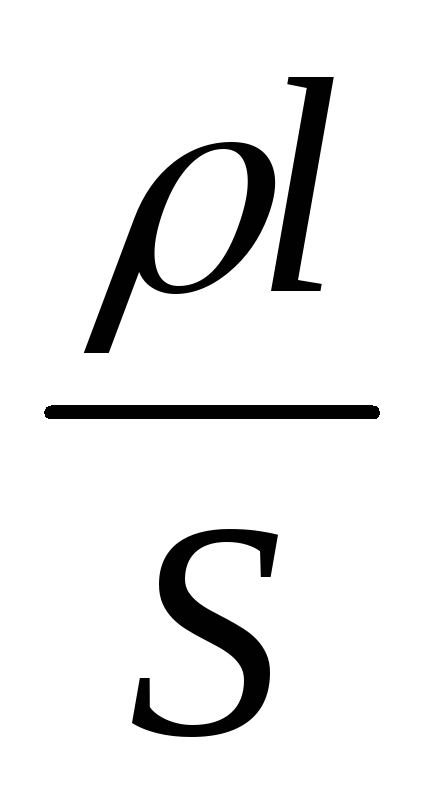 =
= +
+ 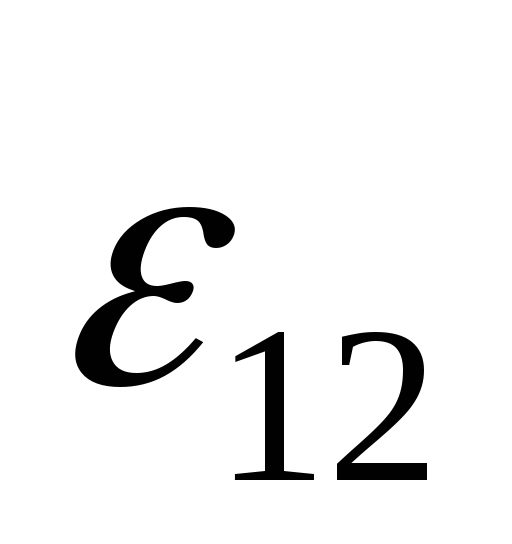 , откуда следует закон Ома для неоднородного
участка цепи I =
(
, откуда следует закон Ома для неоднородного
участка цепи I =
(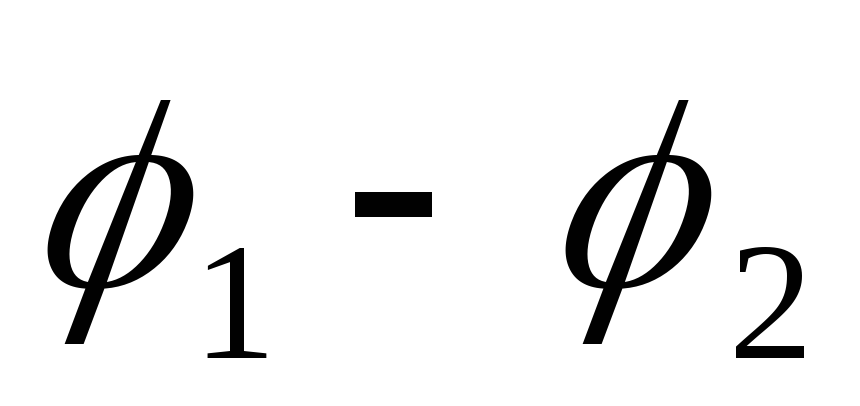 +
+ 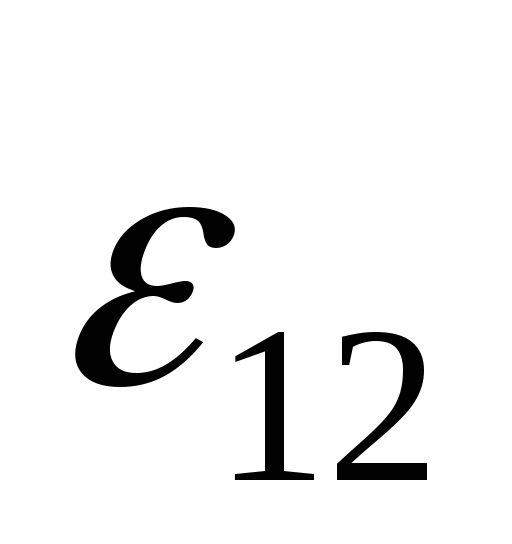 )
/ R
)
/ R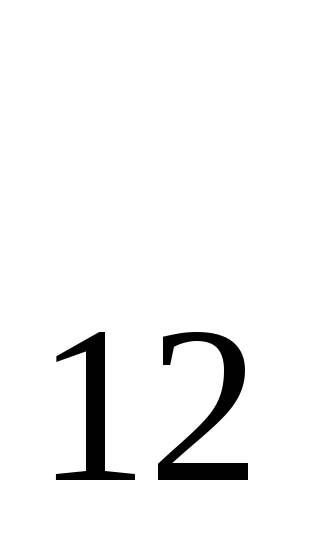 (21)
(21)
где R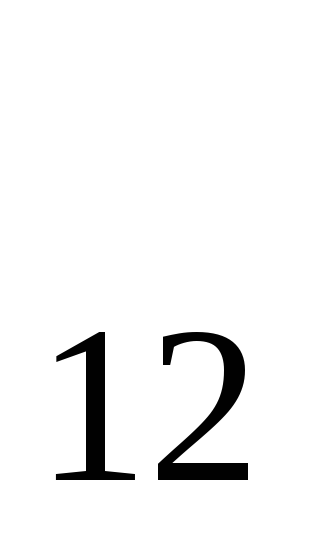 =
=  l / S — сопротивление участка цепи
12. Для
замкнутой цепи
l / S — сопротивление участка цепи
12. Для
замкнутой цепи 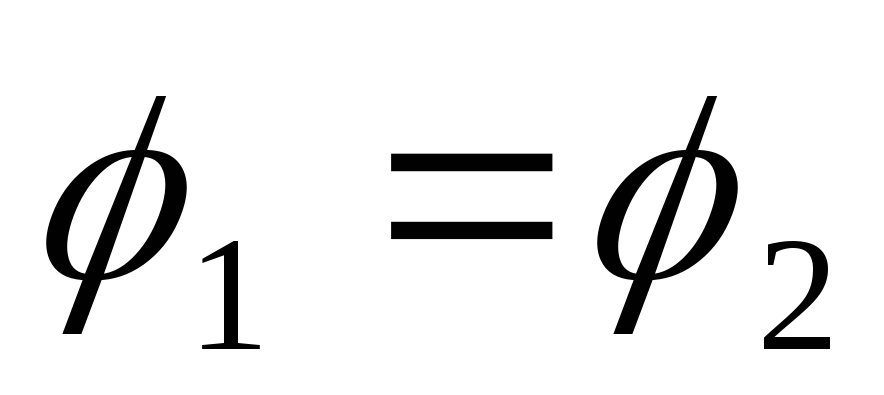 формула
(21)
запишется в виде I =
формула
(21)
запишется в виде I =  / R
/ R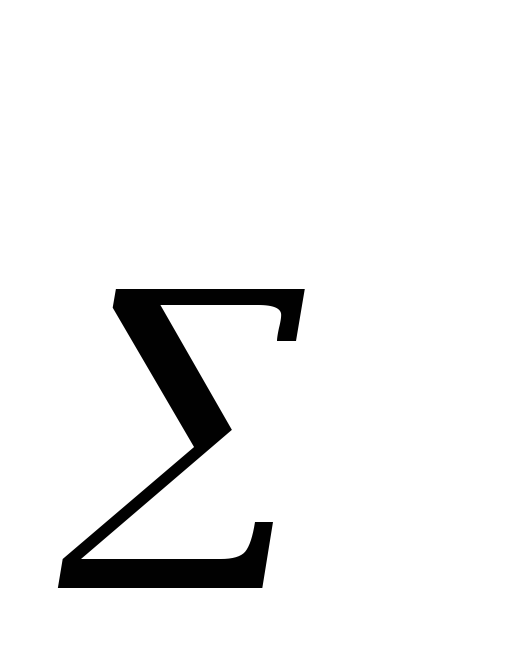 (22)
(22)
где R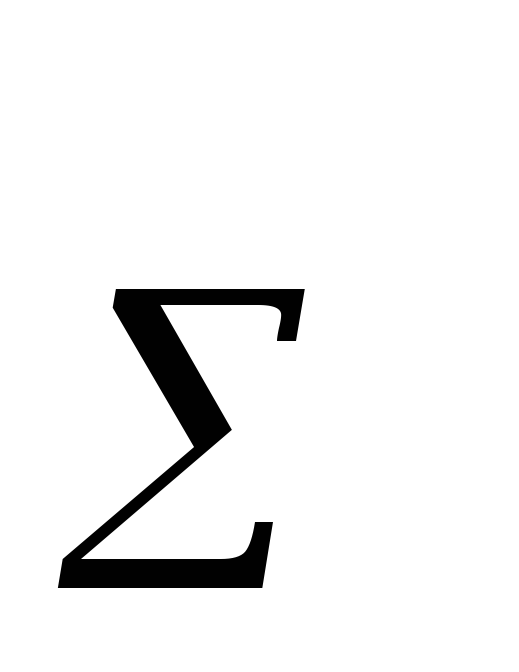 — суммарное сопротивление всей цепи;
— суммарное сопротивление всей цепи;  — ЭДС источника.
— ЭДС источника.
Пусть
замкнутая цепь состоит из источника
электрической энергии с ЭДС  и внутренним сопротивлением r ,а также внешней цепи потребителя,
имеющей сопротивление R.
Согласно
(22) I =
и внутренним сопротивлением r ,а также внешней цепи потребителя,
имеющей сопротивление R.
Согласно
(22) I =  /
(R + r). (23)
/
(R + r). (23)
Р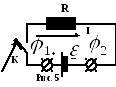 азность
потенциалов на электродах источника,
рис. 5, равна напряжению на внешнем
участке цепи: U =
азность
потенциалов на электродах источника,
рис. 5, равна напряжению на внешнем
участке цепи: U =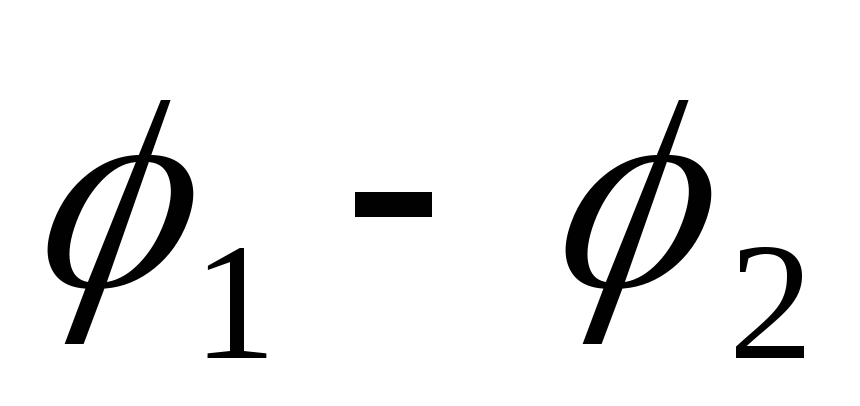 = IR =
= IR = —
Ir. (24)
—
Ir. (24)
Е  сли
цепь разомкнуть, то ток в ней прекратится
и напряжение
U
на зажимах источника станет равным его
ЭДС, т.е. U =
сли
цепь разомкнуть, то ток в ней прекратится
и напряжение
U
на зажимах источника станет равным его
ЭДС, т.е. U =  .
.
Таким
образом, напряжение на внешнем участке
цепи, рис.
5,
будет равно U = IR =  R / (R + r). (25)
R / (R + r). (25)
В
пределе, когда R  0 (источник тока замкнут накоротко), то
в этом случае, в соответствии с
(23),
ток максимален
0 (источник тока замкнут накоротко), то
в этом случае, в соответствии с
(23),
ток максимален
I =
I
=
I =
=  /
R, (26)
/
R, (26)
а напряжение во внешней цепи равно нулю.
В
противоположном предельном случае, R ,
цепь разомкнута и ток отсутствует: I=lim
,
цепь разомкнута и ток отсутствует: I=lim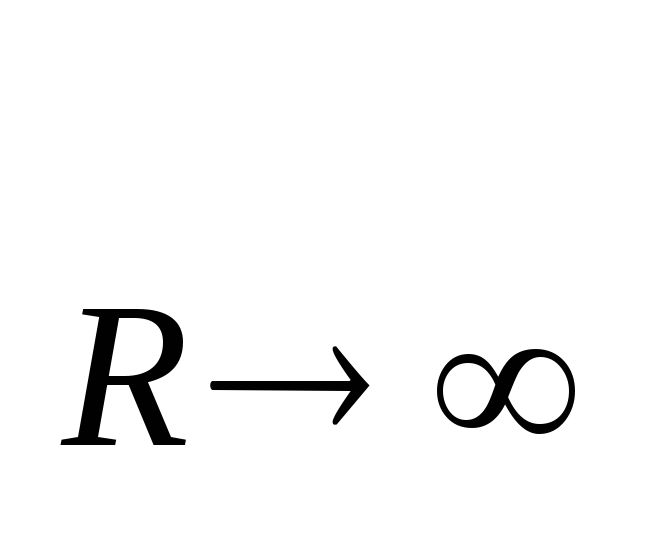 [
[ / (R+r)]=0, а
напряжение на зажимах источника
максимально и равно его ЭДС: U
/ (R+r)]=0, а
напряжение на зажимах источника
максимально и равно его ЭДС: U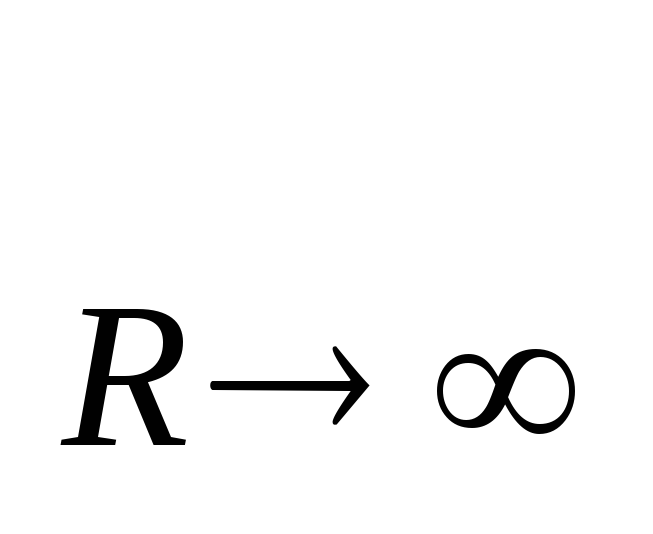 =
=  R / (R + r)=
R / (R + r)=  ,
т. к. lim
,
т. к. lim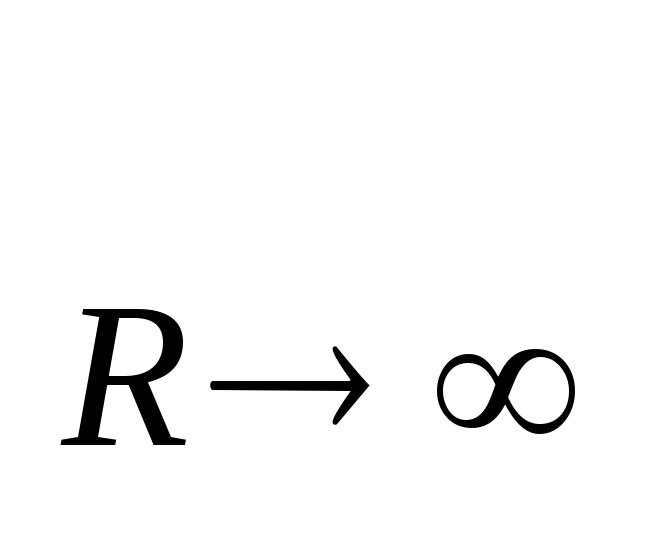 R / (R + r)
= 1. (27)
R / (R + r)
= 1. (27)
2.1.1. Закон Ома
ГЛАВА 2 ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
ПОСТОЯННОГО ТОКА
Всхемах замещения цепей постоянного тока только один вид приемников – резистивный элемент. Все электрические величины обозначают заглавными печатными буквами: I, U, E, кроме тока источника тока, который обозначают буквой J. Линейные электрические цепи состоят из линейных элементов, параметры которых не зависят от тока и напряжения.
2.1.Основныезаконы
Внастоящее время под законом Ома понимают все соотношения, связывающие между собой напряжение и ток. По закону Ома напряжение на резистивном элементе пропорционально току в нем. Коэффициент про-
порциональности назван сопротивлением: U R = RI . Закон | Ома можно | |||
сформулировать и относительно тока: |
|
|
| |
| I = GU , |
|
|
|
|
|
| 1 |
|
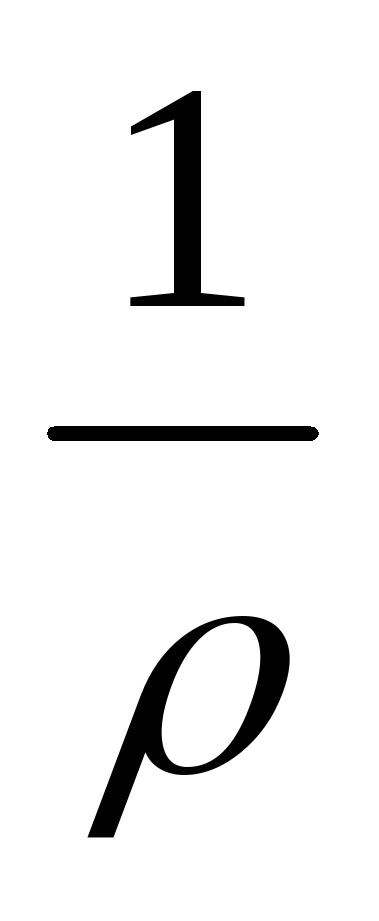
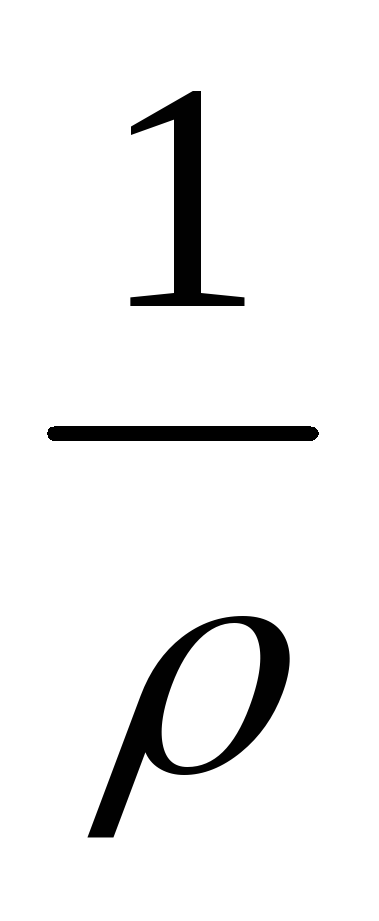
где G | – проводимость, величина, обратная сопротивлению G = |
| . | |
| ||||
|
|
| R | |
Проводимость измеряют в сименсах (См).
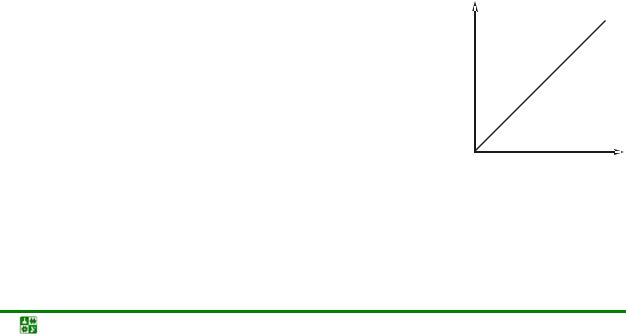
Геометрической интерпретацией закона Ома является вольтамперная характеристика (ВАХ). Для линейного элемента она имеет вид прямой линии (рис. 2.1).
История создания закона Ома показывает | U |
| |
роль личности и интернационализм в науке. |
| ||
|
| ||
В 1802 г. профессор физики петербургской |
|
| |
Медико-хирургической академии, академик В. В. |
|
| |
Петров впервые установил зависимость тока в про- |
|
| |
воднике от площади поперечного сечения проводни- |
|
| |
ка. Он первым ввел термин «сопротивление». |
|
| |
В. В. Петрова можно считать первым русским |
| I | |
электротехником, так как им впервые была показана | Рис. 2.1 | ||
| |||
и доказана возможность практического применения |
|
|
электричества для целей освещения. Свои разнообразные опыты В. В. Петров подробно описал в книге «Известие о гальвани-вольтовских опытах», которая вышла в С.-Петербурге в 1803 г. Это была первая книга на русском язы-
Теоретические основы электротехники. Учеб. пособие | -15- |

ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2.1. Основные законы
ке, посвященная исследованиям явлений электрического тока.
В1821 г. англичанин Х. Дэви установил, что проводимость проводника зависит от материала и температуры.
В1820–1825 гг. немецкий физик Георг Сименс Ом более глубоко исследовал эти явления и сформулировал свой закон.
2.1.2. Первый закон Кирхгофа
Первый закон Кирхгофа сформулирован для узла. Узел – это точка в схеме, где сходятся не менее трех ветвей. При использовании ЭВМ для ввода исходных данных узлами выделяют каждый элемент схемы замещения. Эти узлы называют ложными или устранимыми. В дальнейшем речь будет идти о неустранимых узлах.
Алгебраическая сумма токов в узле равна нулю:
n
∑I j = 0.
j=1
Правило знаков: токи, одинаково направленные относительно узла, записывают с одинаковыми знаками.
2.1.3. Второй закон Кирхгофа
Второй закон Кирхгофа относится к контуру. Алгебраическая сумма напряжений на приемниках в любом контуре равна алгебраической сумме ЭДС, действующих в этом же контуре:
С учетом закона Ома
Правило знаков: со знаком плюс записывают напряжения и ЭДС, направления которых совпадают с выбранным направлением обхода контура.
В 1845 г. Густав Роберт Кирхгоф, будучи студентом, написал работу, в примечании к которой были сформулированы два закона, являющиеся фундаментальными законами теоретической электротехники. Они были выведены в результате опытов.
Теоретические основы электротехники. Учеб. пособие | -16- |

ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2.1.Основные законы
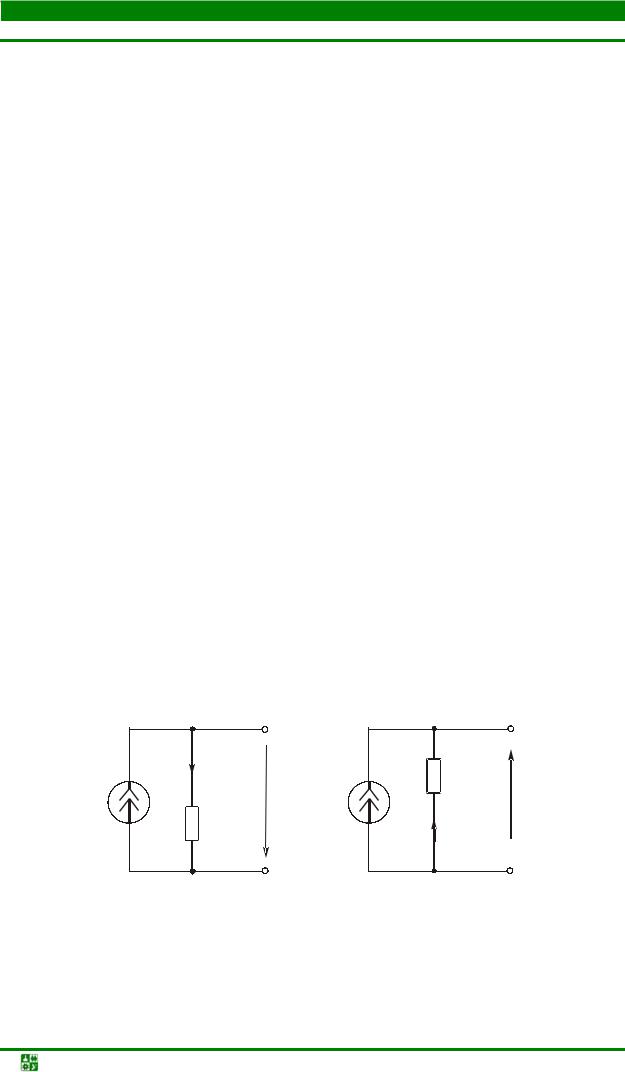
2.1.4.Закон Ома для активной ветви
Активная ветвь, названная так из-за наличия источника ЭДС, изобра-
жена на рис. 2.2. |
|
|
|
|
|
|
| |
Между выходными | зажимами |
|
|
|
| E | ||
ветви возникает напряжение Uab . Ин- | I | R |
| c _ | ||||
дексация | показывает | направление ко a |
|
| + b | |||
|
| |||||||
второму индексу. Напряжение – это |
|
|
|
|
| |||
разность | потенциалов | между двумя |
|
|
| Ua |
| |
точками, т. е. Uab =Va −Vb . |
|
|
|
|
| |||
точки а, |
|
|
| b |
| |||
Определим потенциал |
|
| Рис. 2.2 |
| ||||
исходя из | потенциала | Vb . Рассчитаем |
|
|
| |||
|
|
|
|
| ||||
изменение потенциала промежуточной точки с (см. рис. 2.2) по сравнению с Vb . Между точками b и c расположен источник ЭДС, поэтому потенциал
точки с отличается от потенциала точки b на величину Е. Стрелка источника показывает направление увеличения потенциала. Следовательно, потенциал точки с ниже потенциала точки b. Между точками с и а находится резистор сопротивлением R. Потенциал Va отличается от потенциала Vc величиной
напряжения на резисторе RI . Ток направлен от большего потенциала к меньшему, поэтому потенциал Va выше потенциала Vc .
Таким образом,
Va =Vb − E + RI,
Va −Vb = −E + RI.
Но Va −Vb =Uab , т. е. Uab = −E + RI .
Можно определить напряжение между двумя любыми точками, рассчитав изменение потенциалов между ними. При этом нужно вести расчет в сторону увеличения потенциала, т. е. от второго индекса напряжения к первому.
Решим уравнение относительно тока:
I = UabR+ E = G(Uab + E),
где G = R1 – проводимость ветви.
Это выражение называют законом Ома для активной ветви. Последнее выражение можно составить, исходя из следующих рассуж-
дений. Для появления тока в ветви (см. рис. 2.2) есть два условия: наличие разности потенциалов между концами ветви и действие источника ЭДС. Если направления ЭДС и напряжения Uаb совпадают с направлением тока, они
Теоретические основы электротехники. Учеб. пособие | -17- |
ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2.1. Основные законы
способствуют его появлению и должны быть записаны в уравнение со знаком плюс. В противном случае – со знаком минус. Рассуждая таким образом, получим для тока ветви прежнее выражение.
2.1.5. Баланс мощностей
Баланс мощностей – это интерпретация | закона сохранения энергии | |||
в электротехнике. |
|
|
|
|
Мощность генераторов энергии в электрической цепи равна мощности | ||||
потребителей: Pг = Рн, причем |
|
|
|
|
n | m |
|
|
|
Рг = ∑Ei Ii + ∑U j | J j , |
| ||
i=1 | j=1 |
|
|
|
n |
|
| m |
|
где ∑Ei Ii – мощность источников ЭДС; |
| ∑U j J j | – мощность источни- | |
i=1 |
|
| j=1 |
|
ков тока; J j – токи источников тока, U j – напряжения на зажимах источников
тока.
Эти суммы алгебраические. Источник может как вырабатывать, так и потреблять (заряд аккумулятора) электрическую энергию.
Если направления ЭДС и тока через источник ЭДС совпадают, мощность источника записывают в уравнении баланса мощностей с положительным знаком. Он работает в режиме генератора.
При противоположных направлениях ЭДС и тока мощность в уравнении баланса учитывают с отрицательным знаком (режим потребителя).
Определение знака мощности источника тока поясняет рис. 2.3, на котором показана разметка зажимов источника тока, вырабатывающего (а) или потребляющего (б) электрическую энергию.
+ |
|
| _ | |
| Iвн |
| R вн | |
J | U | J | ||
U | ||||
|
|
| ||
| Rвн |
| I вн | |
|
|
| ||
_ |
|
| + | |
а |
|
| ||
|
| б |
Рис. 2.3
Ток Iвн и напряжение U направлены в сторону уменьшения потенциала, что и позволяет разметить зажимы источника.
Теоретические основы электротехники. Учеб. пособие | -18- |
ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2.1. Основные законы
Мощность потребителей (нагрузок)
Эта сумма арифметическая.
Погрешность расчета не должна превышать (1–3) %.
2.2. Взаимноепреобразованиесхемзамещения источниковэнергии
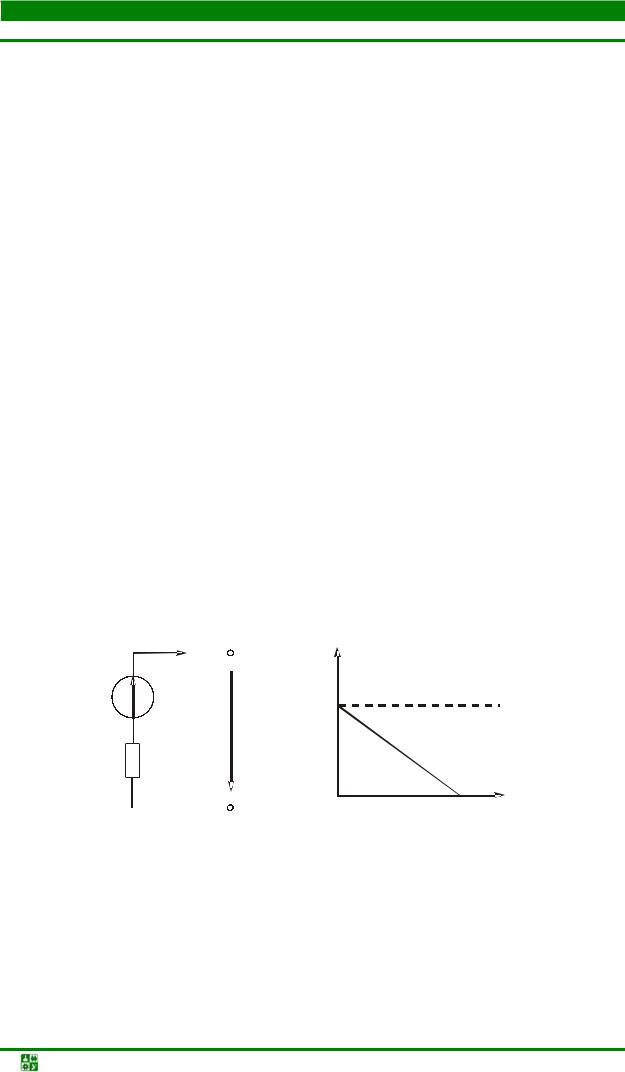
В некоторых случаях для упрощения расчетов токов рационально заменить источники тока эквивалентными источниками ЭДС или сделать обратное преобразование.
У идеального источника ЭДС (идеального источника напряжения – ИИН) напряжение на зажимах не зависит от изменения нагрузки и равно ЭДС Е. Напряжение на зажимах реального источника ЭДС (РИН) меньше Е на величину падения напряжения на резисторе, учитывающем внутреннее сопротивление источника (рис. 2.4), т. е.
Uab = E − RвнI . | (2.1) |
Чтобы получить это уравнение, нужно рассчитать изменение потенциалов между точками b и а.
График, иллюстрирующий эту зависимость, изображен на рис. 2.5. Его называют внешней вольт-амперной характеристикой (ВАХ).
|
|
| I | a | Uab |
|
|
|
| ||
|
|
|
|
| |
E |
| ВАХ ИИН | |||
|
|
|
| Uab | E |
|
|
|
| ВАХ РИН | |
Rвн |
|
|
|
| |
|
|
|
| Iкз | |
|
|
|
| b | |
|
|
|
| I | |
|
|
|
| ||
|
|
| Рис. 2.4 |
| Рис. 2.5 |
Ток идеального источника тока (ИИТ) не меняется при изменении нагрузки. У реального источника тока (РИТ), схема замещения которого изображена на рис. 2.6, ток приемника связан с напряжением на зажимах источника тока следующей зависимостью:
I = J −GвнUab , | (2.2) |
Теоретические основы электротехники. Учеб. пособие | -19- |
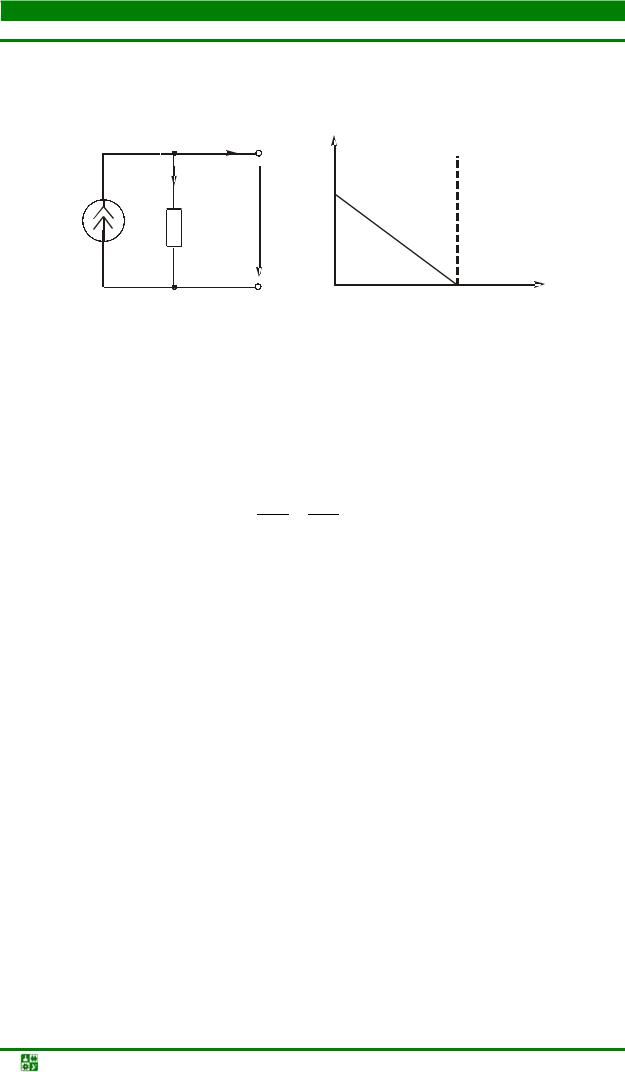
ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2.2. Взаимное преобразование схем замещения источников энергии
так как I = J − Iвн , а Iвн = GвнUab .
Внешняя ВАХ реального источника тока представлена на рис. 2.7.
| + | I | Uab ВАХ РИТ |
|
| Iвн |
| ВАХ ИИТ | |
|
| Uхх |
| |
|
|
|
| |
J | Gвн |
| Uab |
|
|
|
|
| |
| _ |
| J | I |
| Рис. 2.6 |
| Рис. 2.7 | |
Сопоставив рис. 2.5 и рис. 2.7, видим, что внешние ВАХ реальных источников ЭДС и тока аналогичны, поэтому возможна замена источника электрической энергии одного типа другим. Чтобы замена была эквивалентной, уравнения внешних ВАХ для источников должны быть одинаковыми.
Разделим уравнение (2.1) почленно на Rвн . Тогда
Uab = E − I ,
Rвн Rвн
отсюда
I = | E | − | Uab | . | (2.3) |
R |
| ||||
|
| R |
| ||
| вн |
| вн |
| |
Сравнивая уравнения (2.2) и (2.3), делаем вывод, что замена источников будет эквивалентной, если
E = R J ; | J = | E | ; | G |
| = | 1 | ; | R |
| = | 1 | . | ||
R |
| R |
|
|
| ||||||||||
вн |
|
|
| вн |
| вн |
|
| вн |
| G | вн | |||
|
| вн |
|
|
|
|
|
|
|
|
|
| |||
Воспользовавшись последними соотношениями, можно заменить источник тока эквивалентным источником ЭДС или сделать обратное преобразование.
Следует учесть, что эквивалентные источники энергии должны быть одинаково направлены относительно соответствующих узловых точек (см.
рис. 2.4 и рис. 2.6).
2.3. Потенциальнаядиаграмма
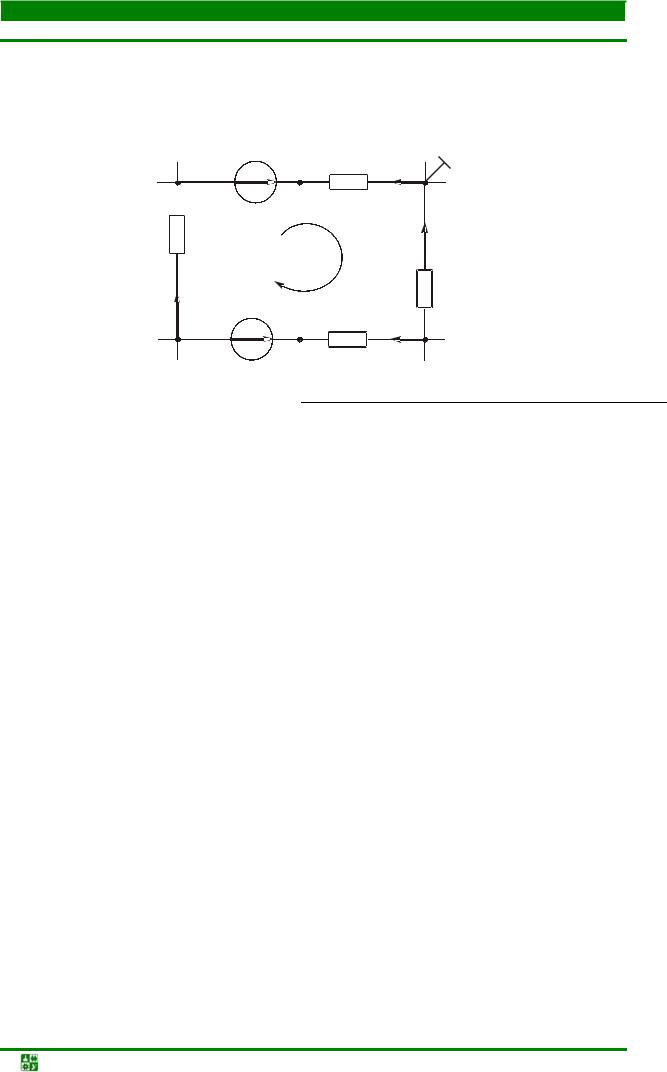
Потенциальная диаграмма дает картину распределения потенциалов в контуре.
Построим потенциальную диаграмму для одного из контуров сложной
Теоретические основы электротехники. Учеб. пособие | -20- |
ГЛАВА 2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2.3. Потенциальная диаграмма
схемы (рис. 2.8). Потенциал одной из точек контура принимаем равным нулю. Пусть Va = 0 . Выбираем направление обхода контура по часовой стрел-
ке.
д 
R 3
I3
г
E4 | + | R 4 | I 4 |
| |||
| e | a | |
|
| ||
|
|
| I 1 |
E 2 |
|
| R 1 |
| R2 | I 2 б | |
|
|
+ в
Рис. 2.8
Между точками а и б находится резистор сопротивлением R1. Потенциал Vб точки б отличается от потенциала Va на величину напряжения на этом резисторе R1I1 . Ток направлен от большего потенциала к меньшему, значит на пути от точки а к точке б потенциал увеличивается: Vб =Va + R1I1 . Потенциал Vв отличается от потенциала Vб на величину напряжения на резисторе сопротивлением R2 . Ток направлен от точки б к точке в, т. е. потенциал точки в меньше потенциала точки б: Vв =Vб − R2 I2 .
Потенциал Vг отличается от потенциала Vв на величину ЭДС Е2 .
Стрелка источника показывает направление увеличения потенциала, т. е. потенциал Vг <Vв :
Vг =Vв − E2 .
Вычислим потенциалы остальных точек на основании аналогичных рассуждений:
Vд =Vг − R3I3 ; Vе =Vд + Е4 ; Va =Vе + R4 I4 .
Если расчет токов и потенциалов произведен верно, потенциал последней точки должен быть равен нулю, что дает возможность проверить правильность решения.
По результатам расчетов строят потенциальную диаграмму. По оси абсцисс откладывают друг за другом в соответствующем масштабе сопротивления вдоль контура, начиная с заземленной точки. По оси ординат – потенциалы. Потенциальная диаграмма для контура на рис. 2.8 приведена на
Теоретические основы электротехники. Учеб. пособие | -21- |
Электрический ток. Закон Ома
При помещении изолированного проводника в электрическое поле E→ на свободные заряды q в проводнике будет действовать сила F→=qE→. Это провоцирует возникновение кратковременных перемещений свободных зарядов. Процесс завершается, когда собственное поле электрических зарядов будет компенсировано внешним. Электростатическое поле внутри проводника станет равным нулю.
Определение 1Существуют определенные условия, при которых возникает непрерывное упорядоченное движение свободных носителей заряда. Оно получило название электрического тока.
За направление электрического тока принято брать направление движения положительных свободных зарядов. При наличии электрического поля произойдет возникновение электрического тока в проводнике.
Определение 2Силой тока называют скалярную физическую величину I, равняющуюся отношению заряда ∆q, протекающего по сечению проводника за время ∆t:
I=∆q∆t
При неизменяемых силе тока и направлении за промежуток времени ток называют постоянным. Следует обращать внимание на его характеристики.

Рисунок 1.8.1. Упорядоченное движение электронов в металлическом проводнике и ток I. S – площадь поперечного сечения проводника, – электрическое поле.
Определение 3В системе СИI измеряется в амперах (А), а единица измерения 1 А устанавливается по магнитному взаимодействию двух параллельных проводников.
Законы постоянного тока. Формулы
Определение 4Постоянный электрический ток создается в замкнутой цепи, где свободные носители заряда проходят по замкнутым траекториям.
Разные точки цепи обладают неизменным по времени электрическим полем, исходя из основных законов постоянного тока. То есть в такой цепи оно ассоциируется с замороженным электростатическим полем. Когда электрический заряд перемещается по замкнутой траектории, то работа сил равняется нулю.
Определение 5Чтобы постоянный ток имел место на существование, нужно наличие такого устройства в цепи, которое будет создавать и поддерживать разности потенциалов разных участков цепи при помощи работы сил неэлектростатического происхождения. Их называют источниками постоянного тока. Такие силы, действующие на свободные носители заряда со стороны источников тока, получили название сторонних сил.
Их природа различна. Гальванические элементы или аккумуляторы обладают сторонними силами, возникающими по причине электрохимических процессов. В генераторах это обстоит по-другому: появление сторонних сил возможно при движении проводников в магнитном поле. Источник тока сравним с насосом, перекачивающим жидкость замкнутой гидравлической системы. Электрические зар
2.4.2. Законы ома и кирхгофа в комплексном виде
Закон Ома в комплексном виде:
Ỉ=Ủ/Zили Ỉ=Y∙Ủ, (2.26)
где Ỉ – ток, протекающий в электрической цепи,
Ủ – напряжение. приложенное к электрической цепи,
Y– комплексная проводимость электрической цепи,
Z– комплексное сопротивление электрической цепи.
Первый закон Кирхгофа. Сумма токов в проводах, сходящихся в узле электрической цепи равна нулю:
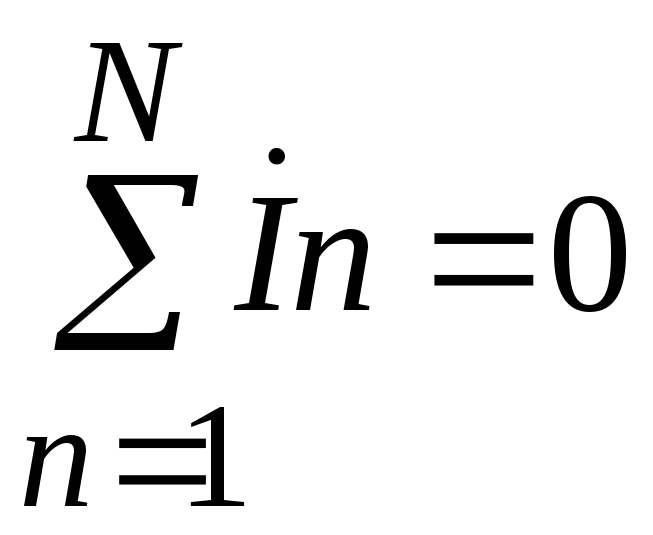 .
(2.27)
.
(2.27)
Второй закон Кирхгофа. Сумма комплексных э.д.с. или напряжений, действующих в замкнутом контуре, равна сумме падений напряжений на элементах этого контура.
 (2.28)
(2.28)
Законы Ома и Кирхгофа справедливы как для мгновенных, так и для действующих значений э.д.с. напряжений и токов.
Действующие(эффективное или среднеквадратическое напряжение) определяется выражением:
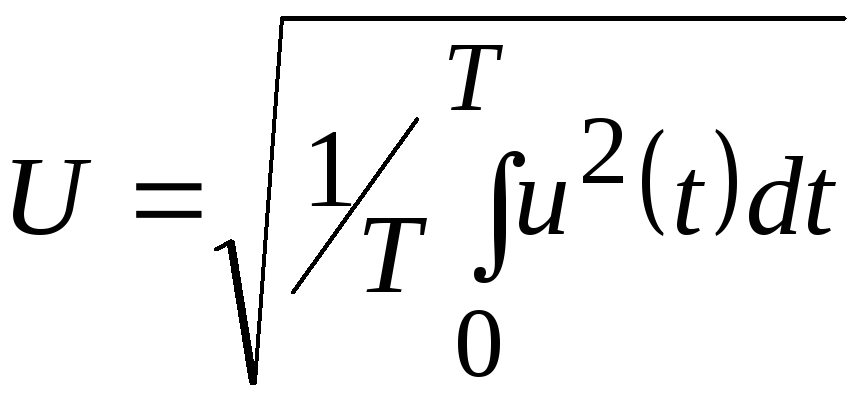 ,
(2.29)
,
(2.29)
где T – период колебаний напряжения, равный 1/f,
f – частота колебаний напряжения.
При
строго синусоидальной форме колебаний
действующее напряжение, равно:
U=Um/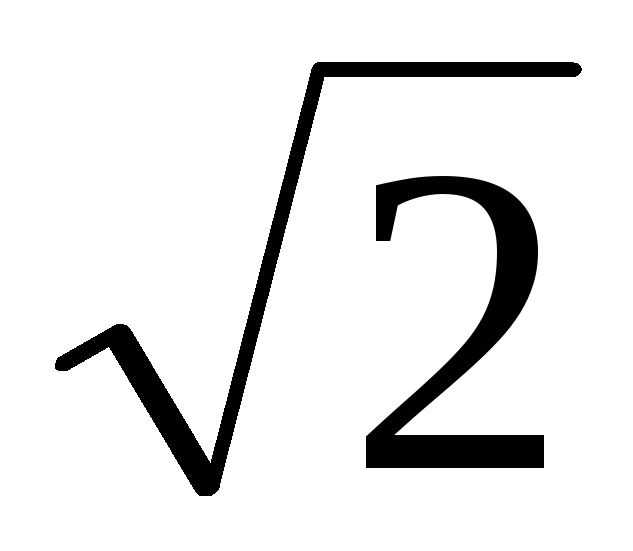 ,
(2.30)
,
(2.30)
где Um-максимальное значение напряженияu(t).
Аналогично определяются действующие значения э.д.с. и токов.
2.4.3. Построение векторных диаграмм на вращающейся комплексной плоскости
Для облегчения построения векторных диаграмм на вращающейся плоскости необходимо запомнить следующие основные положения:
а) В цепи с активным сопротивлением ток и напряжение совпадают по фазе.
б) В идеализированной цепи только с индуктивным сопротивлением без потерь напряжение по фазе опережает ток на угол, равный 90 градусов
в) В цепи с чисто емкостным сопротивлением без потерь ток опережает по фазе напряжение на угол +90 градусов.
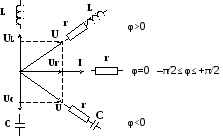
Рис.2.1.Мнемоническая схема, поясняющая возможные повороты
радиусов-векторов при различном включении r-L-Cэлементов.
При построении векторных диаграмм надо начинать построение с вектора напряжения или тока общего для всей анализируемой цепи. В частности при последовательном включение элементов цепи надо начинать с построения вектора тока, протекающего через все элементы цепи. При параллельном включении элементов цепи построение векторной диаграммы надо начинать с вектора общего приложенного напряжения, а затем строить вектора токов, протекающих через каждую из ветвей электрической цепи. Возможные сдвиги фаз векторов напряжения в электрических цепях, состоящих из различных комбинаций r-L-C элементов, приведены на мнемонической схеме (см. рис.2.1.).
Радиус-вектора на схеме и ниже выделяются жирным шрифтом или точками (черточками) над ними.
2.4.4. Резонанс напряжений в цепи, состоящей из последовательно включеных катушки индуктивности и конденсатора
Рассмотрим примеры такого анализа в предположении, что величины сопротивления, емкости и индуктивности не изменяются во времени и не зависят от приложенного напряжения и токов (см. рис.2.2).
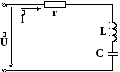
Рис.2.2.Электрическая схема последовательно включенных r-L-C- элементов.
Процессы, происходящие в исследуемой цепи (в соответствии со вторым законом Кирхгофа) описываются (при постоянстве величин элементов во времени и независимости их от величины протекающего тока) линейным интегрально-дифференциальным уравнением:
u(t)=ri(t)+Ldi(t)/dt+1/C ∫i(t)dt, (2.31)
где u(t) – переменное напряжение, подаваемое от источника на колебательный контур,
i(t) – переменный ток, протекающий в цепи,
L – индуктивность,
r – активное сопротивление катушки индуктивности,
С – емкость конденсатора.
Сопротивление (r), индуктивность (L) и емкость (C) образуют колебательный контур, в котором возможен резонанс напряжений. Термин «резонанс напряжения» подразумевает, что при равенстве Хl=Хc, переменные напряжения на элементах контура L и C увеличивается в Q раз по сравнению с напряжением подаваемым от источника на контур. Под величиной Q понимается добротность контура, равная Q=Хс/r.
При принятых предположениях уравнение (2.31) может быть представлено в следующем виде:
u(t)=i(t)*{r+j[Xl+Xc]}. (2.32)
Откуда следует выражение для комплексного сопротивления контура
Z=r+j{Xl–Xc}.
При резонансе напряжений, когда Хl=Хс, Z=r, то есть сопротивление контура оказывается активным, а ток, протекающий через контур, достигает максимальной величины, равной i(t)макс=u(t)/r.
В данном случае построение векторной диаграммы надо начинать с общего для цепи вектора тока (Ỉ), затем строятся векторы напряжений. При последовательном соединении катушки индуктивности и емкости общее реактивное сопротивление цепи X равно алгебраической разности индуктивного и емкостного сопротивлений Xl и Хc. Приложенное к такой цепи напряжение можно представить в виде векторной суммы вектора падения напряжения на активном сопротивлении (U r), совпадающего по фазе с вектором тока; вектора падения напряжения на индуктивности (Ul), опережающего ток по фазе на угол 90° и вектора падения напряжения на емкости (Uc), отстающего по фазе от вектора тока на угол 90°.При этом возможны следующие случаи:
а) Индуктивное сопротивление больше емкостного (Хl>ХС). В этом случае входное напряжение будет опережать ток по фазе на угол φ (см. рис. 2.3.).
б) Емкостное сопротивление больше индуктивного (Хl<Хс). При этом ток опережает напряжение на угол φ. Векторная диаграмма тока и напряжений показана на рис. 2.4.
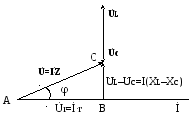

Uс–UL
Рис. 2.3 Рис. 2.4
в). Индуктивное сопротивление равно емкостному (Хl=Xс). Соответственно полное реактивное сопротивление цепи (Х) равно нулю, а полное сопротивление цепиZ=r, т.е. достигает своего минимального значения. При этом ток будет по фазе совпадать с напряжением, т.е. уголφ=0.Векторная диаграмма токов и напряжений для этого случая приведена на рис. 2.5.

Явление резонанса напряжений происходит также в кварцевых резонаторах, которые широко используются в автогенераторах колебаний.


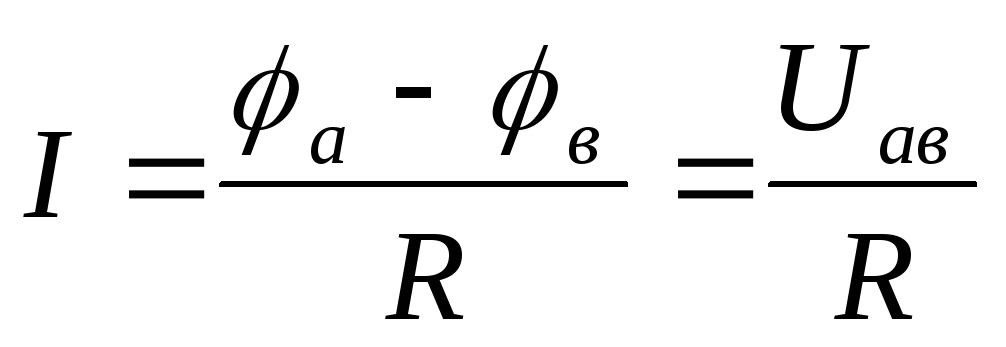 ,
,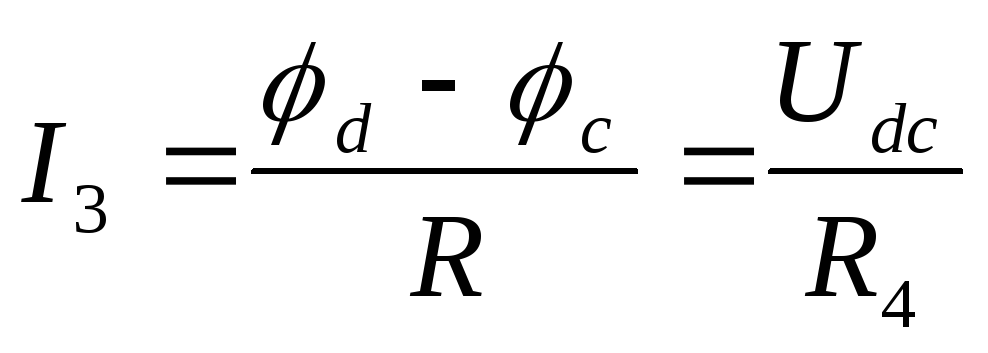 .
.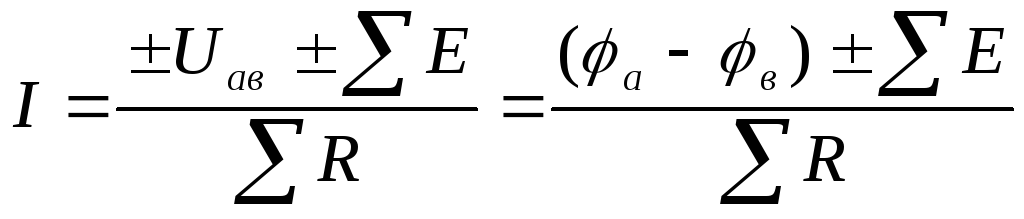 .
.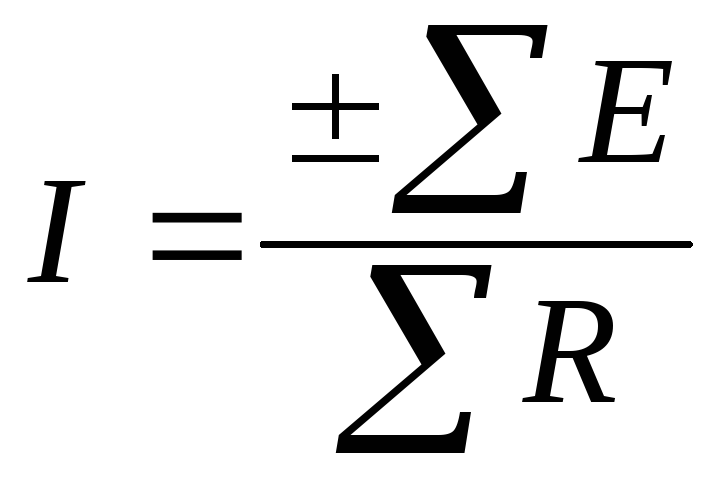 ,
,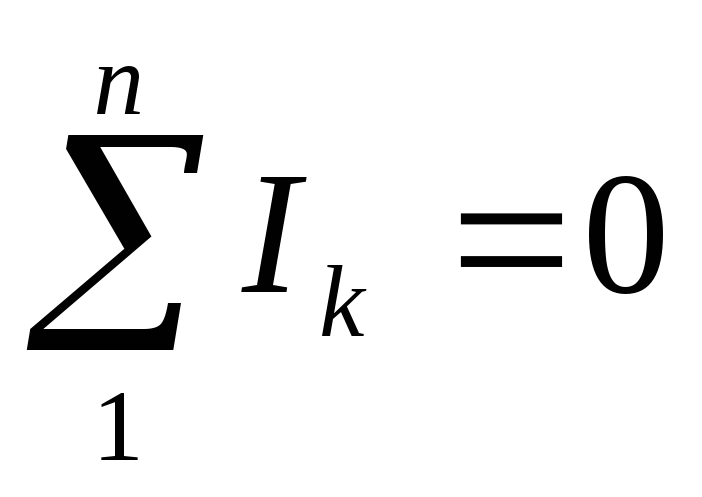 ,
,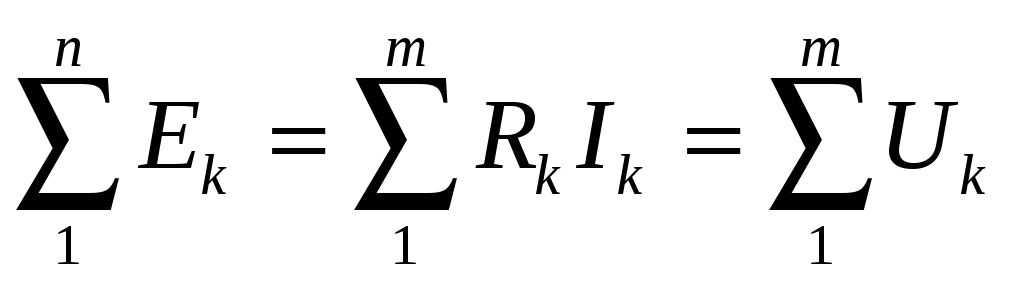 ,
,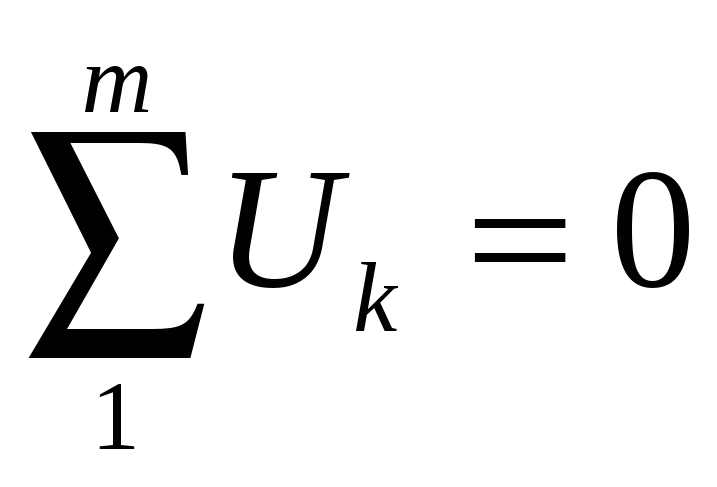 .
.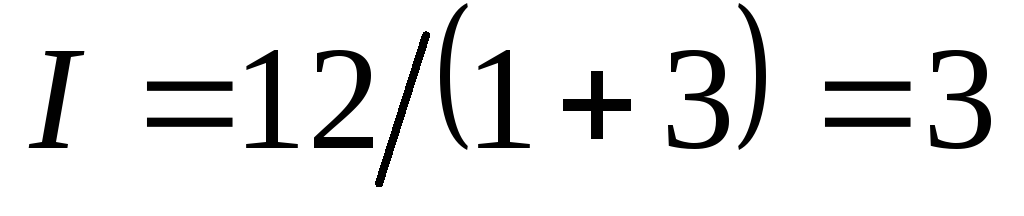 А.
А.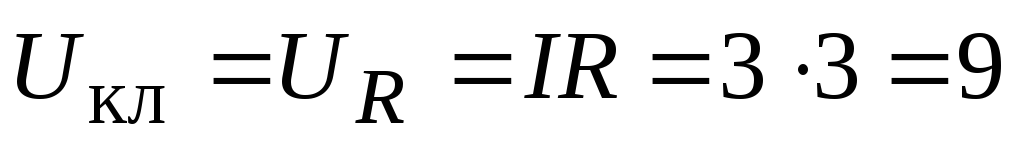 В. Естественно то же самое получается
и по формуле (2.15).
В. Естественно то же самое получается
и по формуле (2.15).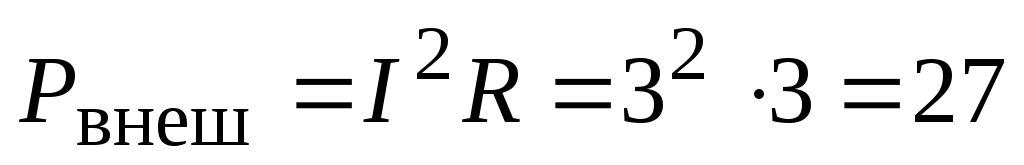 Вт.
Вт.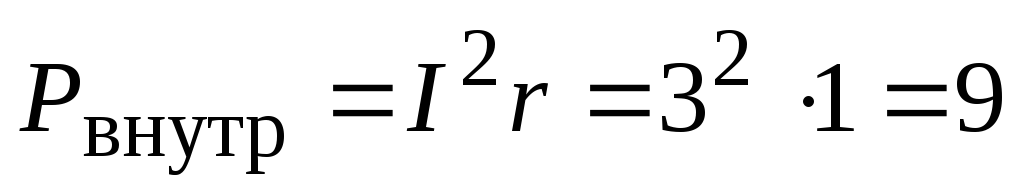 Вт.
Вт. Вт. Можно рассуждать и по-другому,
опираясь на уравнение (2.13):
Вт. Можно рассуждать и по-другому,
опираясь на уравнение (2.13):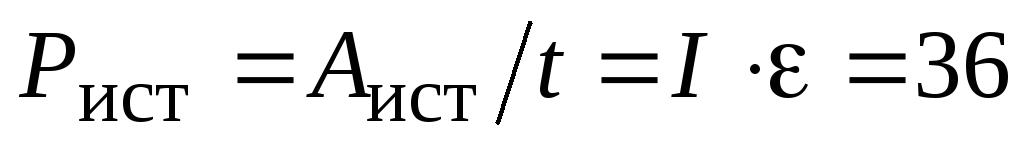 Вт.
Вт.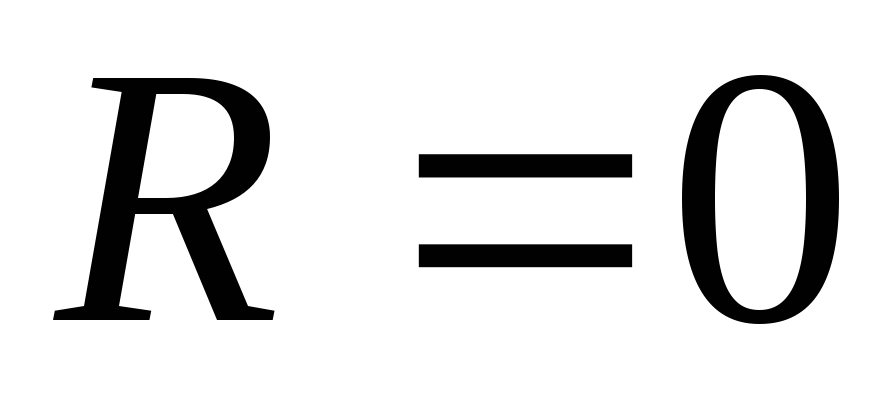 ):
):