Cистемы счисления, Двоичные (бинарные системы)
Степени точности
Системы счисления, которые вы используете, влияют на точность некоторых расчетов. Один из примеров можно увидеть в извлечении квадратного корня из 3 в десятичной системе. Используйте метод из второй части для извлечения квадратного корня из 2.
ПРИБЛИЖЕНИЯ
Обратите внимание, что каждое «место» в десятичной системе дает лучшее приближение к квадратному корню из 3. Чтобы проверить это, посмотрите, как возведение в квадрат извлаченного корня приблизит вас к значенbю, с которого вы извлекали корень: 3.
На первом месте 1, что в квадрате даст только 1 — ошибка на 2 единицы по сравнению с истинным значением — 3. Если бы использовалось 2, ответ был бы точнее: квадрат 2 это 4 — ошибка только на 1. Но наше правило, приведенное внизу, остается верным.
Второе «место» дает более точный результат. Квадрат 1.7 равен 2.89, что уменьшает ошибку до 0.11. Третье «место», 1.73 в квадрате дает 2.
9929 — ошибка в 0.0071. Четвертое место, 1.732 еще ближе к истине, так как это число, возведенное в квадрат дает 2.999824 — ошибка в 0.000176.
Дроби в расширенных системах счисления
Если вы использовали семеричную сисему, дробь 1/7 была бы 0.1 — полностью точным с только одной цифрой после запятой (не десятичной запятой, если эта система семеричная). В десятичной системе дробь, что получается в результате деления на 7, не является такой простой.
Дроби и десятичные числа
Эти задачи должны заставить вас задуматься о точности и надежности цифр. Что означает ошибка в одну миллионную? Будете ли Вы использовать (что маловероятно) семеричную систему вместо десятичной, чтобы проверить как точно 1/7?
Порядки величин
Порядки величин начинают собой совершенно новую концепцию в области математики. Чтобы показать другую сторону этой концепции, предположим, что Вам необходимо получить область, состоящую из идеального квадрата.
Вы можете расширить этот подход к аналогичным изменениям кубического объема. Теперь, начиная с большого куба, имеющего стороны L, необходимо добавить или вычесть 3 плитки с размерами L х L x S, три длинных параллелепипеда с размерами L х S х S, и один маленький куб со стороной S. Если S равно 1/10 от L (или гораздо меньше), то S в кубе составляет 1/1000 от L в кубе.
ПОРЯДКИ ВЕЛИЧИН
Вы можете продемонстрировать такую же самую прогрессию алгебраически. Чтобы сделать это, если a есть малой частью, тогда степени a, a2, a3, a4, и т.
д., состоит из ряда с уменьшающимися порядками величин. Обратите внимание, что последовательные степени имеют ряд коэффициентов, которые, если взять четвертую степень, есть 1, 4, 6, 4 и 1.
Тем не менее, продолжая работать в нашей знакомой десятичной системе, Вы заменяете различные значения a и показываете, как меняется его изменения последовательных степеней (1 +a). Если это 0.1, последовательные степени начинают «перетекать» в предыдущие «места». До 4-й степени, первые две цифры есть 1.1, 1.2, 1.3, но в 4-й степени 1,5 будет ближе.
Если a равно 0,01, более высокие степени не влияют на первый член, который в настоящее время во втором знаке после запятой. Оставьте его за вторым местом, первые два места есть 1,01, 1,02, 1,03 и 1,04. Дальнейшие члены 4-й степени только достигают 1,0406 на 4-м месте.
Однако, если a равно 0.2, следующие члены влияют на более ранние. Цифры в квадратиках демонстрируют это.
Системы счисления
Перед изобретением электронных цифровых устройств использовались счетные машины.
Числа, которые можно было видеть через окошко, были похожи на те, которые мы сейчас видим на дисплее калькуляторов. Если бы Вы подняли крышку счетной машины, Вы бы увидели, как работает механизм счетной машины, что могло бы помочь Вам понять в общем системы счисления.
Самое правое колесико ведет отсчет 0 до 9 в десятичной системе. Когда оно доходит 9, оно перейдет от 9 до 0 и одновременно передвинет следующее колесико с 0 до 1. Каждый раз, когда первое колесо переходит от 9 до 0, следующее колесико будет переходить на 1 больше, пока оно не возвратиться к 9. Тогда, два колесика будут означать 99. Когда в этот раз первое колесико перейдет от 9 до 0, следующее колесико также перейдет от 9 до 0, а третье колесико передвинется от 0 до 1, и таким образом счетная машина покажет 100.
Двенадцатеричная система
Десятеричная система не единственная, которую Вы можете использовать. Давно, некоторые народы использовали двенадцатеричную систему, считая до 12 вместо десяти.
Первые шесть букв алфавита вместе с однозначными числами полностью формируют ряд до числа 15.
Десятичная
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Шестнадцатеричная
0 1 2 3 4 5 6 7 8 9 A B C D E F
В десятичной системе «10» (один ноль) означает десять. В двенадцатеричной системе «10» означает двенадцать. В шестнадцатеричной «10» означает шестнадцать. Чтобы получить немного практики в различных системах счисления, попробуйте пользоваться некоторое время двенадцатеричной системой. Вы увидите, почему калькуляторы или компьютеров используют шестнадцатеричную систему, хотя результат высвечивается в десятичной системе счисления.
Преобразование из десятичной системы в двенадцатеричную
Зачем работать в двенадцатеричной системе, когда она никогда не используется? Потому что что-то незнакомое заставляет вас думать, оно помогает вам понять почему это не используется. Шестнадцатеричная система основана на двоичной (основание два), но ее не так просто использовать в системах, использующих большие базы чисел. Итак, посмотрим на преобразование десятичной системы в двенадцатеричную.
Чтобы узнать, скольки раз по двенадцать состоит число, Вы делите число (например 143131, как показано на рисунке ниже) на 12 в в знакомой Вам десятичной системе. Остаток после деления на 12 записывается слева в двенадцатеричной система. Затем разделите число на 12 еще раз. На этот раз остаток равен одиннадцать. В двенадцатеричной систем все числа до одиннадцати должны использовать одну цифру, так что для 11 используется буква е. Вы можете сами далее проследить за правильностью вычислений в остальной части этого преобразования.
Преобразование десятичного числа 143131 в двенадцатеричное
Переход от двенадцатеричной системы в десятичную
Как преобразовать число из двенадцатеричной системы в десятичную? Просто сделать обратный процесс. Двенадцатеричное число разделить на десять столько раз, сколько необходимо. Вам потребуется, как минимум колонка десяти из двенадцатеричной таблицы умножения. Вы, вероятно, были знакомы с двенадцатью колонками, чтобы сделать это довольно легко. Тем не менее, таким образом Вы должны использовать колонку десяти в двенадцатиричной системе счисления. Эта система не знакома, и поэтому заставит вас думать.
Пойдем ниже по колонке десяти. Десять раз по два есть 18. Это означает, что 1 двенадцать и 8, что вы обычно называете двадцать. Двенадцать и восемь в сумме дают двадцать, не так ли? Далее, десять раз по 3 есть 26, что означает 2 двенадцать и 6. Два на двенадцать дает 24 и с шестью дает результат, который обычно называют 30.
Пройдите до конца самостоятельно.
ДВЕНАДЦАТИРИЧНАЯ ТАБЛИЦА УМНОЖЕНИЯ
Преобразование двенадцатеричного 6 +9e7 в десятичное
Двоичное счисление
Трудность в работе с двоичной системой состоит в том, что каждое место имеет только два «значения»: 0 и 1. Вы не можете посчитать «до» чего-то, а затем перейти к следующему месту. Если у вас уже есть 1, следующая цифра 1 преобразует его обратно в 0, и даст 1 следующему месту. Если у вас есть ряд единиц, то добавление еще одной единицы преобразует все единицы обратно в 0, и присвоит следующему месту 1 (справа налево).
В панели окошек ниже, десятичный эквивалент числа заменен двоичными числами. В двоичной системе в любом месте будет либо 1, либо 0.
Преобразование десятичных чисел в двоичные
Здесь значения места в двоичном системе, которые имеют 1 вместо 0, приведены в виде десятичных чисел. Начнем с числа в десятичной форме, 1546. Во-первых, 11-я двоичная колонка является 1024, что ставит 1 в 11-м столбце двоичного файла.
Для завершения предыдущего раздела в следующей таблице приведены двоичные эквиваленты десятичных чисел от 1 до 30.
Умножение в двоичной системе
Хотя Вы вводите данные в калькулятор или компьютер в знакомой десятичной системе счисления, все они используют двоичную систему для выполнения математических функций. Попробуем проделать умножение чисел, как делает это калькулятор. Предположим, вы умножаете 37 на 27. Во-первых, необходимо преобразовать каждое число в двоичную систему, что и делает калькулятор, когда вы вводите цифры.
Я буду упрощать этот процесс, преобразовав числа в настоящие двоичные, а не в би-пятеричные, которые облегчают задачу для калькулятора, но делают ее более трудной для понимания. Но с этим разберемся позже.
Ниже приведено преобразование 37 в 27 в чистой двоичной системе.
Здесь есть умножение в двоичной системе, изложенное также, как обычные способы умножения, но в системе, где не допускаются цифры больше чем 1. Каждая цифра должна быть равно 1 или 0. И в действительности процесс сводится к тому, чтобы сложить последовательности цифр, которые представляют 37, и последовательность где 1-цифра есть 27.
Четыре единицы в 27, и поэтому три единицы в 37 (с «вкраплениями» нулей) вводятся 4 раза в нужных местах (для представления «27 раз») и слагаются. Вы можете их все добавить сразу. Тем не менее, калькулятор делает это последовательно. Каждые две сложенные единицы превращаются в 0 и добавляют 1 до следующего места слева.
Двигаясь справа налево, видно, что у первых трёх позиций в сумме есть только одна единица.
На четвёртой позиции есть две единицы, которые в сумме дают 0 этой позиции и добавляют единицу к пятой позиции, у которой уже есть собственная единица, так что здесь ставится 0 и единица переходит на шестую позицию. Но у этой позиции уже есть две единицы, поэтому здесь остается единица, которая также добавляется к единице на седьмом месте, где снова есть две единицы. Эта позиция теперь также имеет единицу, которая перемещается на восьмое место. На восьмой позиции эта единица остается и это окончательное перемещение, спровоцированное перемещением справа налево. Оставшиеся две позиции имеют по единице, которые и занимают их. Таким образом, получился результат — двоичное число 1111100111.
Преобразуйте двоичное число назад в десятичное, подставляя десятичный эквивалент каждой позиции, где есть единица. Для проверки, умножьте 37 на 27 старым длинным способом.
«Каким длинным путем?» спросите Вы. Двоичный путь и так кажется довольно длинный. Единственная причина, того, что калькулятор делает это так быстро, это то, что он выполняет миллионы операций в секунду.
Поэтому, этим долгим методом калькулятор считает быстрее, чем вы считаете методом, который гораздо короче.
Умножение 37 на 27 двоичным способом
ДВОИЧНОЕ УМНОЖЕНИЕ
Альтернативное двоичное преобразование
Вот еще один способ преобразования десятичных чисел в двоичные. Он использует таблицу двоичных эквивалентов чисел от 1 до 9 для каждого десятичного места. Для иллюстрации этого способа два числа для деления, приведенного ниже, преобразованы в двоичные (см. таблицы ниже).
Обратите внимание, что двоичные эквиваленты для конкретной цифры не имеют никакого отношения друг к другу — от одной колонки к другой. Вы не можете передвинуть десятичную точку или умножить на десять, как Вы делаете подобный сдвиг в двоичной системе. Я вернусь к тому как калькуляторы или компьютеры справляются с этой проблемой чуть позже.
Деление двоичных чисел
Деление двоичных чисел на самом деле есть повторяющееся вычитание.
37 в двоичной системе 1000001.
Для преобразования двоичного числа обратно в десятичное, используйте вычитание в двоичной системе и применяйте таблицы из предыдущего раздела. Первое вычитание есть двоичное число 100-а, что оставляет 11101. Для двоичного числа 20-ти, что оставляет 1001, вычитается двоичное 9. Работая так через двоичные, после деления 4773 на 37 частное есть 129.
АЛЬТЕРНАТИВНОЕ ДВОИЧНОЕ ПРЕОБРАЗОВАНИЕ
ДЕЛЕНИЕ 4773 на 37
1001010100101 на 100101
Специальная двоичная система для калькуляторов
Вы заметили, что двоичные числа для различных чисел в десятичной системе меняются на каждой позиции, что делает преобразование сложным. При вводе цифры на калькуляторе, первая цифра появляется справа. При вводе следующей цифры, первая цифра перемещается влево и новая цифра появляется справа от нее. Если бы калькулятор преобразовывал бы двоичную последовательность в новую с получением следующей цифры, система была бы очень сложной.
Так, калькулятор выделяет 4 двоичных места для каждого десятичного знака, для чего требуется немного больше «пространства» в памяти калькулятора, чем потребовался бы чистый двоичный код.
По сути дела, калькулятор теперь «работает» в десятичной системе, но использует 4 «бита» двоичной системы для каждой десятичной позиции.
Показатели степеней
В любой системе счисления — двоичной, восьмеричной, десятичной или шестнадцатеричной (или даже в других, которые используются в очень узких сферах), место цифры указывает степень числа, на котором основывается эта система. В двоичной системе, позиция, где появляется единица, представляет некоторую степень числа 2. На 4-й позиции это третья степень числа 2, что равно 8. Вот сравнение степеней 2 и степеней 10.
На этом примере Вы можете увидеть некоторые правила использования показателей степеней, которые помогают нам идти короткими путями в умножении и делении. Во-первых, помните, что умножение и деление это укороченные методы выполнения повторяющихся операция сложения и вычитания. Теперь, степени являются укороченными методами для многократного умножения и деления.
Предположим, что Вы должны умножить xa на xb.
Произведение равно x(a+b). Вы можете легко это увидеть, если Вы напишите x умноженное на само себя a раз, и тогда умножить результат на x, умноженной само на сабя b раз. Общее число раз, которое Вы умножали x само на себя, равно (a + b) раз. Для иллюстрации, предположим, что a равно 3 и b равно 2; x3 умноженное на x2 дает x5. В численном значении, 23 равно 8, 22 равно 4, и 25 равно 32. 8 x 4 = 32. Это проверка.
Теперь попробуем деление. Разделяя xa на xb, частное есть xa-b. Вы можете проверить этот ответ, умножая x само на себя a раз как числитель дроби и используя x умноженное само на себя b раз в знаменателе. Вы можете сократить b раз в знаменателе и оставить остаток х-ов в знаменателе, что равно (a — b) раз. Для иллюстрации, пусть a = 5 и b = 2. x5 разделенное на x2 равняется x3. Если вы использовали 2 для x, x5 равно 32, x2 равно 4, и x3 равно 8.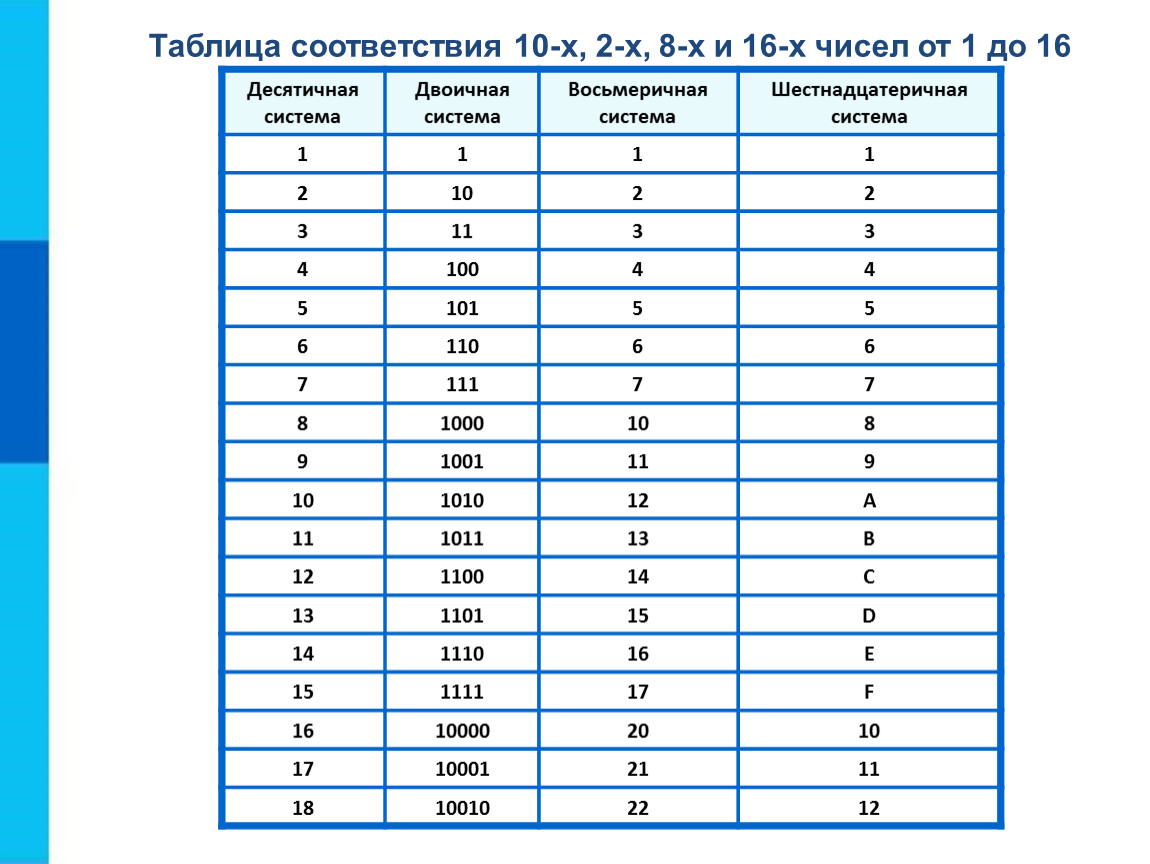
32 разделенное на 4 равно 8.
Арифметические корни: инверсия степеней
Здесь вы должны понимать разницу между инверсией числа и инверсией степени. Отрицательная степеннь есть инверсией или обратной величиной числа, возведенного в степень, определенную индексом. Арифметические корни есть противоположность возведению в степень. Например, из-за того, что 22 равно 4, то 41/2 равно 2; 23 равно 8, а 81/3 равно 2; 24 равно 16, а 161/4 равно 2 и так далее.
Дробные показатели степеней означают арифметические корни. Степень 3/2 четырех есть 8 — квадратный корень 4 есть 2, и 23 равно 8. Обратный процесс, 82/3 равно 4. Вы можете найти другие корни чисел используя квадратные корни. Например, 21/2 (квадратный корень двух) равно 1.414 и так далее; 81/2 равно удвоенному значению предыдущего. Почему? Так как 41/2 равно 2 и 21/2 равно 1.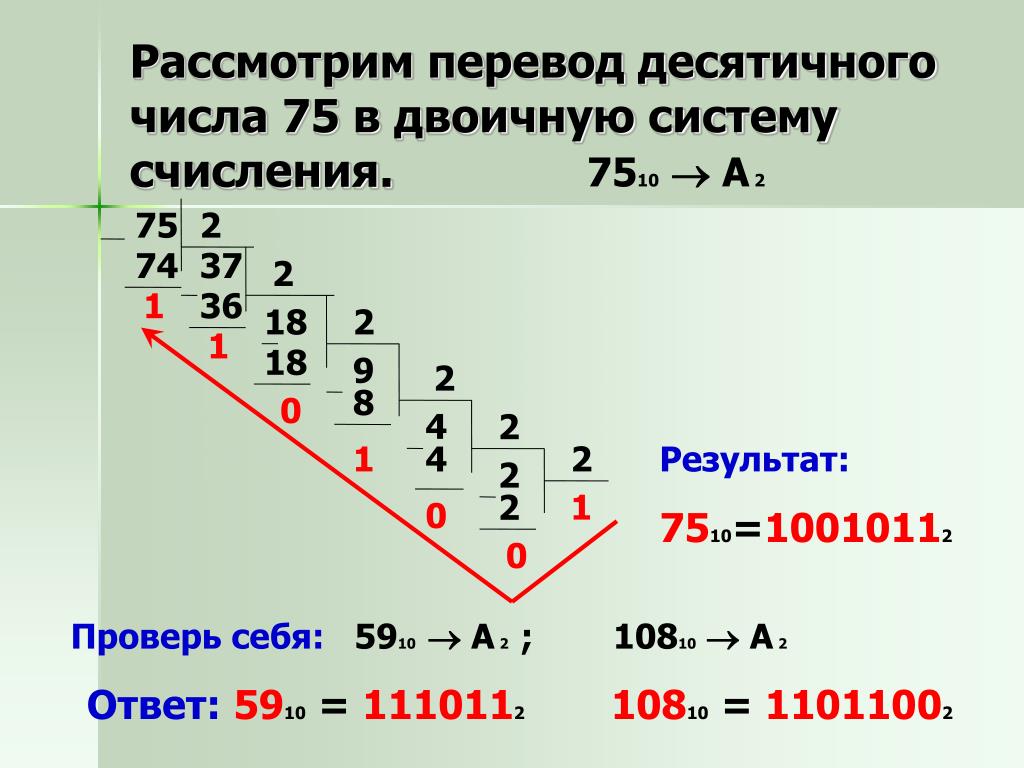
414, (2 раза по 4)1/2 равно 81/2 (удвоенное 1.414), что равно 2.828.
Вообще, Вы не ограничены квадратными корнями, да и вообще какими-либо конкретными корнями. Теперь, совершенно новая область чисел открыта для Вас.
Арифметический корень n-й степени и степени чисел
Представление арифметических корней n-й степени есть возвращением к практически устаревшему способу написания арифметических корней. Перед тем, как описанные в предыдущем разделе обозначения дробных степеней вошли в моду, было принято использовать число на знаком квадратного корня, для указания значения корня. Таким образом, просто знак корня перед х представлял собой квадратный корень из х, такой же, как х /. Написание цифры 3 над знаком корня означало кубический корень из х. Написание небольших n или любой другой буквы или цифры над знаком корня также обозначало конкретный корень.
Если число под знаком корня имело степень b и значение a стояло над знаком корня, это могло бы быть записано как: xb/a.
Длинный знак корня над членами a2 + b2 есть корнем всего выражения. Это выражение может быть записано как: (a2 + b2)1/2.
Вопросы и задачи
Примечание: эти вопросы и задачи расположены в случайном порядке. Если у Вас есть трудности с какой-то задачей, попробуйте решить другую, а затем вернуться к нерешенной задаче. Задачи составлены таким образом, что Вы должны проявлять определенную инициативу в применении принципов, которые были рассмотрены ранее.
1. Найдите десятичный эквивалент дроби 1/37. Определите ошибку преобразования, которая возникает, когда десятичный эквивалент преобразуется до трех значащих цифр.
2. Используя двойную систему, умножьте 15 на 63 и преобразуйте результат обратно в десятичное число. Проверьте свой результат непосредственно умножением десятичных чисел.
3. Используя двоичную систему, разделите 1922 на 31 и преобразовать результат обратно в десятичной число. Проверьте свой результат непосредственно умножением десятичных чисел.
4. Найдите значения следующих выражений:
(a) 163/4 (b) 2430,8 (c) 251,5
(d) 642/3 (e) 3434/3
5. Преобразуйте следующие числа из десятичных в двоичные. В качестве проверки, преобразуйте их также обратно в десятичные.
(a) 62 (b) 81 (c) 111
(d) 49 (e) 98 (f) 222
(g) 650 (h) 999 (i) 2000
6. Преобразуйте следующие числа из десятичных в двоичные. В качестве проверки, преобразуйте их также обратно в десятичные.
(a) 101 (b) 1111 (c) 10101
(d) 111100 (e) 110111000110
7.
Умножьте 129 на 31 в десятичной системе. Умножьте двоичные эквиваленты этих чисел. Предположим, что была сделана ошибка во второй цифре справа во втором числа в десятичном результате, поэтому 129 умножается на 41, а не на 31. Предположим, что подобная ошибка произошла в двоичной системе, поэтому вторая цифра справа во втором числе меняется на противоположную.
Сравните относительную погрешность в десятичной системе с ошибкой в двоичной системе счисления.
8. Подсчитайте значение выражения (a2 + b2)1/2 для следующих значений:
(a) a = 4 и b = 3 (b) a = 12 и b = 5
(c) a = 24 и b = 7 (d) a = 40 и b = 9
(e) a = 60 и b = 11 (f) a = 84 и b = 13
(g) a= 112 и 6= 15
Что общего имеет каждая пара?
9. Подсчитайте значение выражения (a2 + b2)1/2 для следующих значений:
(a) a = 8 и b = 6 (b) a = 15 и b = 8
(c) a = 24 и b = 10 (d) a = 35 и b = 12
(e) a = 48 и b = 14 (f) a = 63 и b = 16
Что общего имеет каждая пара?
10. Запишите как простые десятичные числа, без дробей, следующие выражения:
(a) 1002 (b) 1001/2
(c) 100-2 (d) 100-1/2
Из этих четырёх значений, найдите значения следующих выражений методом сложения и вычитания степеней:
(e) 1003/2 (f) 1005/2
(g) 100-3/2 (h) 100-5/2
11.
Используя на калькуляторе только клавишу вычисления квадратного корня, найдите следующие значения по крайней мере с тремя цифрами после запятой:
(a) 1001/4 (b) 1001/8
(c) 1001/16 (d) 1001/32
12. Если значение степени в d) предыдущей задачи делить пополам, то есть 1/64, 1/128, 1/256, 1/512, и так далее, к какому числу будет стремиться выражение? Почему?
13. Найдите значения до трех верных десятичных цифр после запятой для следующих:
(a) 320,1 (b) 320,2 (c) 320,3
(d) 320,4 (e) 320,5 (f)320,6
(g) 320,7 (h) 320,8 (i) 320,9
14. Посчитайте значения следующих выражений, используя калькулятор, если Вы хотите. Где возможно, посчитайте значения выражений хотя бы до трёх десятичных цифр после запятой:
(a) (102 — 26)1/2 (b) (362 — 83)1/2 (c) (282 — 212)1/3
(d) (52 — 32)1/4 (e) (172 — 152)1/6 (f) 65611/2
(g) 6561-1/2 (h) 65611/4 (i) 6561-1/4
(j) 65611/8 (k) 6561-1/8
Двоичная система счисления: пресловутые нолики и единички
О чем речь? Можно с уверенностью назвать двоичную систему счисления одной из основных, которые используются в вычислительной технике.
А значит, привычные нам компьютер и смартфон применяют 0 и 1 для расчетов.
На что обратить внимание? Стоит отметить, что такая «популярность» – это дань традиции, заложенной праотцом вычислительных машин Блезом Паскалем. И все же, порой, нужно переводить показатели двоичной системы в 10-ю или 16-ю. Как же это сделать?
В статье рассказывается:- Общепринятые системы счисления
- Числа, используемые в двоичной системе счисления
- Сложение, вычитание и умножение в двоичной системе счисления
- Как переводить числа в двоичной системе счисления в десятичную
- Алгоритм перевода из двоичной системы счисления в шестнадцатеричную
-
Пройди тест и узнай, какая сфера тебе подходит:
айти, дизайн или маркетинг.Бесплатно от Geekbrains
Общепринятые системы счисления
Человечество в ходе своего развития со временем стало нуждаться в способах подсчета.
Нужно было считать, например, количество добычи или убитых врагов из других племен. И эта нужда у древних людей только возрастала. Поначалу пользовались абстрактными понятиями типа «нисколько», «один», «много». Затем в употребление вошла «пара», означающая два каких-то предмета. Уже одно это нововведение существенно упростило жизнь древнему человеку.
В дальнейшем люди стали считать единицами, используя в качестве таковых пальцы на руках и ногах, зарубки на деревьях, кости зверей, узелки на веревках. Благодаря изобретению таких примитивных счетных машин человечество спустя тысячелетия смогло понять, что в древности люди умели не только считать, но также фиксировать результаты счета.
С течением времени возникла необходимость в символьном обозначении любого количества больше единицы. В итоге древними египтянами были впервые придуманы знаки, обозначающие 1, 5 и 10.
Система чисел, состоящая из определенных знаков (цифр), фактически и является системой счисления.
Другими словами, это способ численного выражения с помощью принятых правил и специальных знаков, называемых цифрами.
Любая система счисления принадлежит к одной из двух категорий:
Позиционные СС
Конкретное значение числа определяется не только цифрами, но и их позицией. Сюда относят арабскую систему, где первый разряд справа отведен для единиц, второй разряд справа — для десятков, третий разряд справа — для сотен и т. д. Таким образом, для записи числа 475 необходимо в крайней правой позиции расположить пятерку (пять единиц), после нее — семерку (семь десятков) и затем — четверку (четыре сотни). Позиционными считаются также системы счисления с основаниями (2, 8, 16).
Непозиционные СС
Значение числа определяется только знаком (цифрой). Для обозначения единиц, десятков, сотен и тысяч используются отдельные символы. Наиболее показательным представителем данной группы является римская система счисления. Здесь имеется еще одна отличительная особенность. Для записи очень больших чисел необязательно использовать весь набор знаков — на такие случаи существуют функции сложения и вычитания.
К примеру, число 475 римскими цифрами может выглядеть как CCCCXXXXXXXIIIII либо, в сокращенном виде, как CDLXXV. В последнем варианте используются именно вычитание и прибавление. Значение цифры, стоящей слева от большего числа, отнимается соответственно от этого числа. Если эта цифра стоит справа, то значение прибавляется.
Впервые позиционная система счисления была введена в Вавилоне. Примечательно, что она была шестнадцатеричная. К 19 веку распространение получила двенадцатеричная система.
Прежде чем разбирать, как записывается двоичная система счисления, определимся с терминами. Алфавит любой СС состоит из знаков, обозначающих отдельные цифры. Основанием называют значение, равное количеству знаков для кодирования чисел и представляющее собой целое число от 2 и выше.
Непозиционные ССКогда рассматривается несколько разных СС, тип каждой из них обычно обозначается подстрочным знаком. По умолчанию, если не указано основание, число является десятичным. Позиция цифры в числе называется разрядом.
Числа, используемые в двоичной системе счисления
Состав двоичной системы счисления — цифры 0 и 1. Основание равно 2. В крайней правой позиции числа указывается количество единиц, левее — количество двоек, затем количество четверок и т. д.
Таким образом, любое натуральное число кодируется в последовательный ряд из нулей и единиц — это и будет являться двоичной системой счисления. Решение такой задачи покажем на примере ниже.
10112 = 1*23 + 0*2*2+1*21+1*20 =1*8 + 1*2+1=1110
Как известно, двоичная система счисления используется вычислительной техникой для хранения информации, а также для преобразования данных в графические изображения. В свою очередь обработка двоичного кода требует предварительного размещения каждой цифры внутри особой электронной схемы (триггера). Эта схема может пребывать в одном из двух состояний — «ноль» или «единица».
Отдельное число, состоящее из нескольких цифр, сохраняется группой триггеров — регистром. Оперативная память компьютера фактически является совокупностью таких регистров.
Топ-30 самых востребованных и высокооплачиваемых профессий 2023
Поможет разобраться в актуальной ситуации на рынке труда
Подборка 50+ ресурсов об IT-сфере
Только лучшие телеграм-каналы, каналы Youtube, подкасты, форумы и многое другое для того, чтобы узнавать новое про IT
ТОП 50+ сервисов и приложений от Geekbrains
Безопасные и надежные программы для работы в наши дни
pdf 3,7mb
doc 1,7mb
Уже скачали 21130С точки зрения вычислительной техники любое сохраняемое число представляет собой машинное слово, арифметические и логические операции над которым выполняет арифметико-логическое устройство (АЛУ). Чтобы компьютеру было проще работать с регистрами, они нумеруются (или наделяются адресами).
Так, для сложения двух чисел используются адреса регистров, где они расположены, а не сами эти числа. Данные записываются в восьмеричной и шестнадцатеричной системах для более быстрого и простого перевода чисел в двоичный формат.
Тем не менее, конечный пользователь видит всю числовую информацию в привычном ему десятичном виде. Почему так происходит? Изначально, нажимая на клавишу, пользователь передает компьютеру соответствующую последовательность электрических сигналов (нулей и единиц). Для каждого символа определен конкретный набор этих импульсов.
Специальные программы (драйверы клавиатуры и экрана) преобразуют эти сигналы в читаемый вид путем обращения к кодовой таблице. Например, стандарт Unicode позволяет закодировать таким образом 65536 символов. Именно так используется двоичная система счисления в информатике — нули и единицы преобразуются программным способом в текст и изображения на экране.
исла, используемые в двоичной системе счисленияДалее приведем очевидные достоинства использования двоичного способа представления информации.
- От технических устройств требуется лишь два устойчивых состояния (например, наличие тока и отсутствие тока и т. д.).
- Вычислительной технике значительно проще выполнять операции с двоичными данными, чем с десятичными.
- Таблицы сложения и умножения в двоичной системе имеют гораздо меньший размер по сравнению с такими же таблицами для десятичной системы.
Недостатки:
- возможное превращение конечных десятичных дробей в бесконечные двоичные;
- большее количество занимаемых разрядов по сравнению с десятичной записью;
- сложность с восприятием записи чисел, поскольку двоичная система счисления — этопредставление только в виде нулей и единиц.
Сложение, вычитание и умножение в двоичной системе счисления
Для того, чтобы складывать числа, пользуются следующей таблицей:
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 10 (переход в старший разряд) |
Таблица вычитания в двоичной системе счисления выглядит так:
| — | 0 | 1 |
| 0 | 0 | 1 |
| 1 | (взятие из старшего разряда) 1 | 0 |
Только до 8.
06
Скачай подборку тестов, чтобы определить свои самые конкурентные скиллы
Список документов:
Тест на определение компетенцийЧек-лист «Как избежать обмана при трудоустройстве»Инструкция по выходу из выгоранияЧтобы получить файл, укажите e-mail:
Подтвердите, что вы не робот,
указав номер телефона:
Умножение выполняется по следующей таблице:
| * | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
Как переводить числа в двоичной системе счисления в десятичную
Сперва приведем алфавиты трех используемых систем — двоичной, десятичной и шестнадцатеричной.
| Основание | Наименование системы | Алфавит |
| 2 | Двоичная | 0, 1 |
| 10 | Десятичная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
| 16 | Шестнадцатеричная | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Как уже упоминалось, двоичная система счисления имеет основание 2.
Чтобы перевести число в десятичный формат, можно воспользоваться такой таблицей степеней данного основания:
| 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
Здесь ряд начинается с единицы, а каждая последующая цифра является результатом умножения предыдущей на двойку. После 1 ставится так называемая двоичная точка.
В качестве примера переведем число 1011011 двоичной системы счисления в 10-ный формат (число 91):
0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>>11*2+0=22>>22*2+1=45>> 45*2+1=91.
А конвертация 101111 в десятичную систему даст число 47:
0*2+1=1>>1*2+0=2>>2*2+1=5>>5*2+1=11>> 11*2+1=23 >> 23*2+1=47
НУЖНА КАРТИНКА
Таким же образом можно переводить и дробные числа. Для примера возьмем 1011010, 101 в двоичной системе счисления. Перевод чисел в десятичную можно осуществлять в таком виде:
1*26 + 0*25 + 1*24 + 1*2 + 0 *22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 0 * 2-2 + 1 * 2-3 = 90,625
Иначе говоря, расчет будет следующим:
1*64+0*32+1*16+1*8+0*4+1*2+0*1+1*0,5+0*0,25+1*0,125 = 90,625
Полученное значение в десятичной системе также высчитывается по таблице:
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0,5 | 0,25 | 0,125 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0. | .1 | 0 | 1 |
| +64 | +0 | +16 | +8 | +0 | +2 | +0 | +0.5 | +0 | +1.125 |
Алгоритм перевода из двоичной системы счисления в шестнадцатеричную
Здесь необходимо выполнить 2 шага:
- Перевод числа из двоичной системы в десятичную
- Преобразование полученного значения в шестнадцатеричный формат
К примеру, имеется число 1011101 в двоичной системе счисления. Запись чисел для выполнения первого шага осуществляется по формуле:
A2 = an-1 ∙ 2n-1 + an-2 ∙ 2n-2 + ∙∙∙ + a0 ∙ 20
Подставляем значения:
10111012=1 ∙ 26 + 0 ∙ 25 + 1 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 1 ∙ 20 = 1 ∙ 64 + 0 ∙ 32 + 1 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 1 ∙ 1 = 64 + 0 + 16 + 8 + 4 + 0 + 1 = 9310
Теперь полученное десятичное число необходимо преобразовать в шестнадцатеричное. Для этого 93 многократно последовательно делим на 16 до тех пор, пока остаток не станет меньше 16.
В процессе деления остатки нужно записывать в обратном порядке. Результатом всех операций будет число 9310=5D16.
НУЖНА КАРТИНКА
Перевод дробных чисел в шестнадцатеричный формат выполняется аналогичным образом — через промежуточный этап перевода в десятичную систему.
Вновь покажем это на примере. Преобразуем двоичное число 10001100.110 сначала в десятичную систему по формуле:
An = an-1 ∙ qn-1 + an-2 ∙ qn-2 + ∙∙∙ + a0 ∙ q0 + a-1 ∙ q-1 + ∙∙∙ + a-m ∙ q-m
Подставляем наши значения:
10001100.1102=1 ∙ 27 + 0 ∙ 26 + 0 ∙ 25 + 0 ∙ 24 + 1 ∙ 23 + 1 ∙ 22 + 0 ∙ 21 + 0 ∙ 20 + 1 ∙ 2-1 + 1 ∙ 2-2 + 0 ∙ 2-3 = 1 ∙ 128 + 0 ∙ 64 + 0 ∙ 32 + 0 ∙ 16 + 1 ∙ 8 + 1 ∙ 4 + 0 ∙ 2 + 0 ∙ 1 + 1 ∙ 0.5 + 1 ∙ 0.25 + 0 ∙ 0.125 = 128 + 0 + 0 + 0 + 8 + 4 + 0 + 0 + 0.5 + 0.25 + 0 = 140.7510
Следует отметить сильное сходство формул расчетов дробного и целого десятичных чисел. Тем не менее, отличия также имеются.
Вторым этапом переводим число 140,75 в шестнадцатеричный формат.
Это делается в два подэтапа:
- Перевод отдельно целой части числа.
- Перевод отдельно дробной части числа.
Итак, нам необходимо сначала преобразовать 140 в шестнадцатеричную систему счисления, последовательно деля это число на 16, пока остаток не станет меньше делителя.
После записи остатков в обратном порядке получаем результат: 14010=8C16
Операции с дробной частью отличаются тем, что мы многократно и последовательно умножаем ее, пока она не станет равной нулю (или значению в соответствии с заданной точностью).
В нашем случае это будет выглядеть так: 0.75 * 16 = 12.0 (C).
Поскольку после первого же умножения дробная часть обнулилась, дальнейшие итерации прекращаем. Итоговый результат: 0.12 (0.С) или, иначе, 0.75 ∙ 16 = 12.0 (C)
Остался последний этап — соединение преобразованных целой и дробной частей: 140.7510=8C.C16. Это и будет общим решением всей задачи.
Сперва может показаться, что изложенный здесь материал слишком сложен и запутан для простого обывателя.
На самом деле двоичная арифметика предельно логична и понятна. Пользование таблицами сложения и умножения не представляет сложности, если в них разобраться.
Продвижение блога — Генератор продаж
Рейтинг: 3( голосов 2 )
Поделиться статьей2 в двоичном формате — Как преобразовать 2 из десятичного в двоичный?
ОБЕЩАНИЕ НА 30 ДНЕЙ | ПОЛУЧИТЕ 100% ВОЗВРАТ ДЕНЕГ*
*T&C Apply 2 в двоичной системе счисления равно 10. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты).
Мы использовали 2 бита для представления 2 в двоичном формате. В этой статье давайте узнаем, как преобразовать десятичное число 2 в двоичное.
Как преобразовать 2 в двоичный код?
Шаг 1: Разделите 2 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0.
| Дивиденд | Остаток |
|---|---|
| 2/2 = 1 | 0 |
| 1/2 = 0 | 1 |
Шаг 2: Запишите остаток снизу вверх, т.е. в обратном хронологическом порядке. Это даст двоичный эквивалент 2,
Таким образом, двоичный эквивалент десятичного числа 2 равен 10.
☛ Калькулятор преобразования десятичного числа в двоичный
Давайте посмотрим на значение десятичного числа 2 в различных системах счисления.
- 2 в двоичном формате: 2₁₀ = 10₂
- 2 в восьмеричной системе: 2₁₀ = 2₈
- 2 в шестнадцатеричном формате: 2₁₀ = 2₁₆
- 10₂ в десятичном формате: 2₁₀
Условия задачи:
Часто задаваемые вопросы о 2 в двоичном формате
Что такое 2 в двоичном формате?
2 в двоичном формате равно 10.
Чтобы найти десятичный эквивалент в двоичном, разделите 2 последовательно на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.
☛ Двоичное преобразование в десятичное
Какой двоичный эквивалент 2 + 98?
2 в двоичной системе счисления равно 10, а 98 равно 1100010. Мы можем сложить двоичный эквивалент 2 и 98 с использованием правил двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 — это перенос на следующий бит]. Таким образом, (10)₂ + (1100010)₂ = (1100100)₂, что есть не что иное, как 100.
☛ Калькулятор двоично-десятичных чисел
Сколько бит имеет 2 в двоичном виде?
Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 2 в двоичном формате, т. е. 10. Таким образом, мы использовали 2 бита для представления 2 в двоичном формате.
Как преобразовать 2 в двоичный эквивалент?
Мы можем разделить 2 на 2 и продолжать деление, пока не получим 0.
Записывайте остаток на каждом шаге.
- 2 mod 2 = 0 — LSB (младший значащий бит)
- 1 mod 2 = 1 — MSB (старший бит)
Записать остатки от MSB до LSB. Следовательно, десятичное число 2 в двоичной форме можно представить как 10.
Найдите значение 8 × 2 в двоичной форме.
Мы знаем, что 2 в двоичном формате равно 10, а 8 равно 1000. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0 , 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 10 × 1000 = 10000, что равно 16 в десятичной системе счисления. [2 × 8 = 16]
☛ Также проверьте:
- 45 в двоичном формате — 101101
- 24 в двоичном формате — 11000
- 50 в двоичном формате — 110010
- 1000 в двоичном формате — 1111101000
- 170 в двоичном формате — 10101010
- 19 в двоичном формате — 10011
- 150 в двоичном формате — 10010110
Рабочие листы по математике и визуальные учебные программы
Преобразователь двоичного кода в десятичный
Преобразователь двоичного кода в десятичныйГлавная›Преобразование›Преобразование чисел›Двоичный код в десятичный
От BinaryDecimalOctalHexadecimalText
Кому BinaryDecimalOctalHexadecimalText
Введите двоичное число Десятичное число Десятичное число из дополнения до 2 со знаком Шестнадцатеричный номерДесятичные шаги вычисления
Преобразователь десятичного числа в двоичное ►
Преобразование двоичного числа в десятичное 2
d 1 d 0Десятичное число равно сумме двоичных цифр (d n ), умноженных на их степень 2 (2 n ):
десятичное = d 0 ×2 0 + d 1 × 2 1 + d 2 × 2 2 + .
..
Пример
90 002 Найти десятичное значение 111001 2 :| двоичное номер: | 1 | 1 | 1 | 0 | 0 | 1 |
|---|---|---|---|---|---|---|
| степень двойки: | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
111001 2 = 1⋅2 5 +1⋅2 4 +1⋅2 3 +0⋅2 2 +0 ⋅2 1 +1⋅2 0 = 57 10
Таблица преобразования двоичного кода в десятичный
| Двоичный Число | Десятичный Число | Шестнадцатеричный Число |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 10 | 2 | 2 |
| 11 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
| 1000 | 8 | 8 |
| 1001 | 9 | 9 |
| 1010 | 10 | А |
| 1011 | 11 | Б |
| 1100 | 12 | С |
| 1101 | 13 | Д |
| 1110 | 14 | Е |
| 1111 | 15 | Ф |
| 10000 | 16 | 10 |
| 10001 | 17 | 11 |
| 10010 | 18 | 12 |
| 10011 | 19 | 13 |
| 10100 | 20 | 14 |
| 10101 | 21 | 15 |
| 10110 | 22 | 16 |
| 10111 | 23 | 17 |
| 11000 | 24 | 18 |
| 11001 | 25 | 19 |
| 11010 | 26 | 1А |
| 11011 | 27 | 1Б |
| 11100 | 28 | 1С |
| 11101 | 29 | 1Д |
| 11110 | 30 | 1Э |
| 11111 | 31 | 1F |
| 100000 | 32 | 20 |
| 1000000 | 64 | 40 |
| 10000000 | 128 | 80 |
| 100000000 | 256 | 100 |
См.
