Обратный и дополнительный коды числа
Назначение сервиса. Онлайн-калькулятор предназначен для представления чисел в обратном и дополнительном коде.- Решение онлайн
- Видеоинструкция
- Также решают
Число
Найти: прямой код обратный код дополнительный код
Вместе с этим калькулятором также используют следующие:
Операции с двоичными числами (сложение и вычитание)
Умножение двоичных чисел
Формат представления чисел с плавающей запятой
Пример №1. Представить число 133,54 в форме числа с плавающей точкой.
Решение. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*102 = 1.3354*exp102
Число 1.3354*exp102 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp10=2
Если мантисса находится в диапазоне 1 ≤ M

Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp103
Пример №2. Представить двоичное число 101.102 в нормализованном виде, записать в 32-битом стандарте IEEE754.
Таблица истинности
Алгебра и геометрия
Целые числа в ЭВМ могут быть представлены в виде:- прямого кода. Прямой код двоичного числа совпадает по изображению с записью самого числа.
- обратного кода
- дополнительного кода. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.

Прямой код числа кодирует только знаковую информацию и используется для хранения положительных и отрицательных чисел в ЭВМ. Прямой код двоичного числа совпадает по изображению с записью самого числа, но в знаковом разряде ставится 0, если число положительное и, 1 если число отрицательное.
Следует помнить, что положительные числа в обратном и дополнительном коде совпадают с прямым кодом.
1) Прямой код числа (кодируется только знаковая информация), “+”=0; ”-”=1.
Для прямого кода возможны два представления нуля, машинный положительный ноль, т.е. +0,110=0,110, машинный отрицательный ноль, т.е. -0,111=1,111.
Пример перевода
x2=-11101-[x2]пр=111101
x3=0,101-[x3]пр=0,101
x4=-0,111-[x4]пр=1,111
2) Обратный код числа, используется для выполнения арифметических операций вычитания, умножения, деления, через сложение.
 Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
Обратный код положительного числа совпадает с его прямым кодом, обратный код отрицательного числа формируется по правилам: в знаковом разряде записывается “1”; цифровые значения меняются на противоположные.
Пример перевода
x2=-11101-[x2]обр=100010
x3=0,101-[x3]обр=0,101
x4=-0,111-[x4]обр=1,000
3) Дополнительный код числа, имеет такое же назначение, как и обратный код числа. Формируется по следующим правилам: положительные числа в дополнительном коде выглядят также как и в обратном и в прямом коде, т.е. не изменяются. Отрицательные числа кодируются следующим образом: к обратному коду отрицательного числа (к младшему разряду) добавляется 1, по правилу двоичной арифметики.
Пример перевода
x
x2=-11101-[x2]обр=100010+1-[x2]доп=100011
x3=0,101-[x3]доп=0,101
x4=-0,111-[x4]обр=1,000+1-[x4]доп=1,001
Для выявления ошибок при выполнении арифметических операций используются также модифицированные коды: модифицированный прямой; модифицированный обратный; модифицированный дополнительный, для которых под код знака числа отводится два разряда, т. е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
е. “+”=00; ”-”=11. Если в результате выполнения операции в знаковом разряде появляется комбинация 10 или 01 то для машины это признак ошибки, если 00 или 11 то результат верный.
Как определить, положительное или отрицательное число? Знак числа определяет старший бит: 0 — положительное число, 1 — отрицательное число. Например, для числа 1,001 сразу можно определить, что оно отрицательное (меньше нуля).
Пример. Представить в дополнительном коде десятичные числа: -4.
Решение. Представим число в двоичном коде.
4 = 00001002
Инвертируем все разряды числа, а в знаковый разряд заносим 1
.
Двоичное число 0000100 имеет обратный код 1,1111011
1.
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 |

| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 |
| 7 | 5 | 4 | 3 | 2 | 1 | 0 | |
| 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Число -4 представляется в двоичном дополнительном коде как
11111100
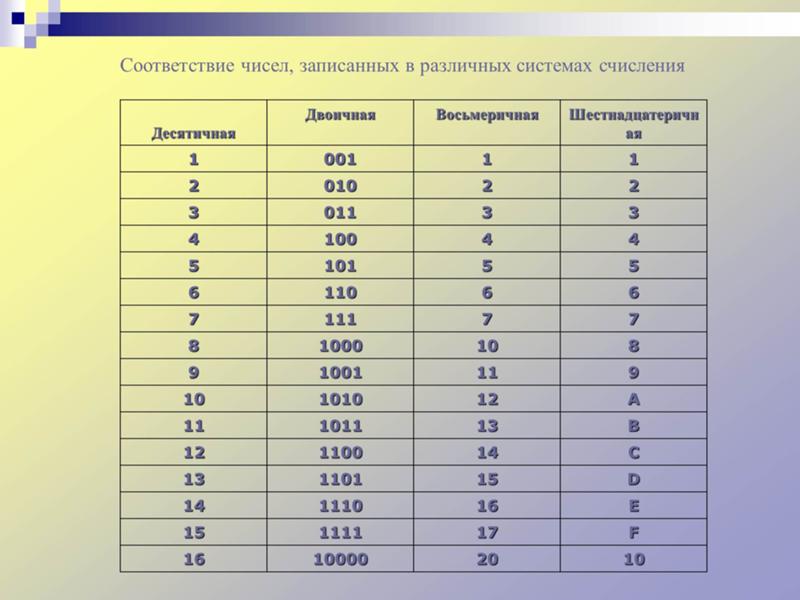
Перевод чисел из заданной системы в другую.
 Способы перевода чисел из одной системы счисления в другую
Способы перевода чисел из одной системы счисления в другуюИз 16 или 8 в 2
| Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр) (см. таблицу). | |||||||
| Двоичная (Основание 2) | Восьмеричная (Основание 8) | Десятичная (Основание 10) | Шестнадцатиричная (Основание 16) | ||||
| триады | тетрады | ||||||
| 0 1 | 0 1 2 3 4 5 6 7 | 000 001 010 011 100 101 110 111 | 0 1 2 3 4 5 6 7 8 9 | 0 1 2 3 4 5 6 7 8 9 A B C D E F | 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 |
Например :
а) Перевести 305.4 8 «2» с.с.
б) Перевести 7B2. E 16 «2» с.с.
E 16 «2» с.с.
16А 16 =1 0110 1010 2 345 8 =11 100 101 2
Из 2 в 16 или 8
Например :
а) Перевести 1101111001.1101 2 «8» с.с.
б) Перевести 11111111011.100111 2 «16» с.с.
1000101010010101 2 =1000 1010 1001 0101=8A95 16 = 1 000 101 010 010 101=105225 8
Из 16 в 8 и обратно
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Например :
Перевести 175.24 8 «16» с.с.
Результат: 175.24 8 = 7D.5 16 .
Из 10 в любую с.с.
Например :
а) Перевести 181 10 «8» с.с.
Результат: 181 10 = 265 8
б) Перевести 622 10 «16» с.с.
Результат: 622 10 = 26E 16
Перевод правильных дробей
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.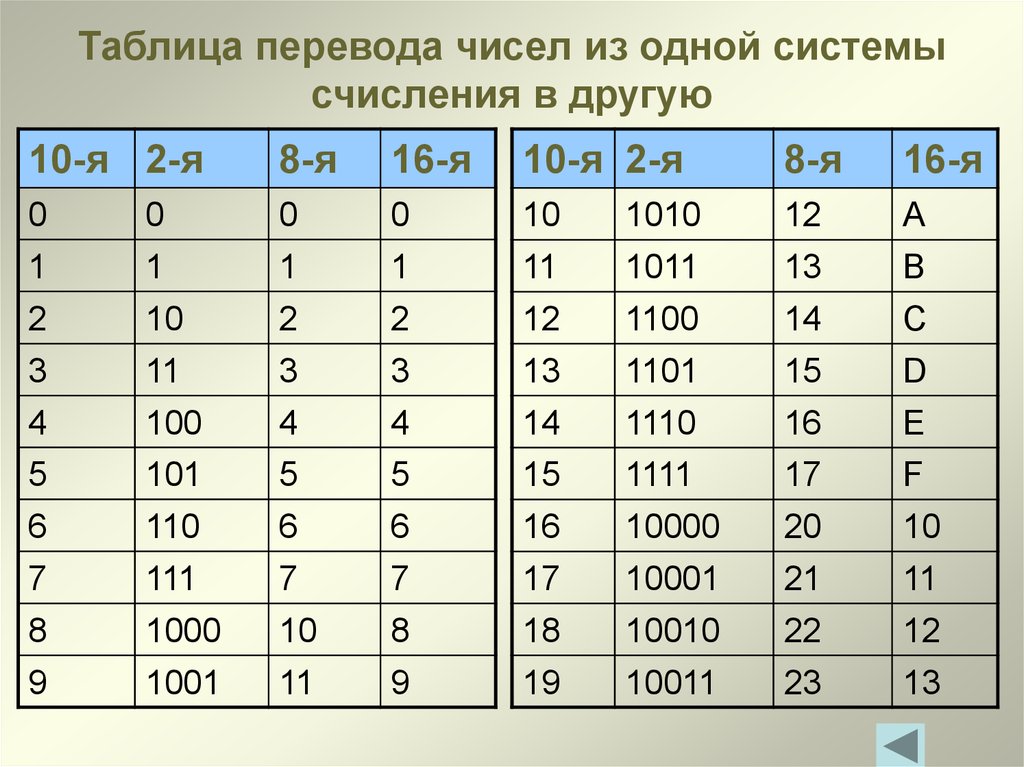
Например :
Перевести 0.3125 10 «8» с.с.
Результат: 0.3125 10 = 0.24 8
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Например :
Перевести 0.65 10 «2» с.с. Точность 6 знаков.
Результат: 0.65 10 0.10(1001) 2
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Например :
Перевести 23.125 10 «2» с.с.
Таким образом: 23 10 = 10111 2 ; 0.125 10 = 0.001 2 .
Результат: 23.125 10 = 10111.001 2 .
Необходимо отметить, что целые числа остаются целыми, а правильные дроби — дробями в любой системе счисления.
Из 2, 8 или 16 в 10
Например :
a)10101101.101 2 = 1 2 7 + 0 2 6 + 1 2 5 + 0 2 4 + 1 2 3 + 1 2 2 + 0 2 1 + 1 2 0 + 1 2 -1 + 0 2 -2 + 1 2 -3 = 173. 625 10
625 10
б) Перевести 703.04 8 «10» с.с.
703.04 8 = 7 8 2 + 0 8 1 + 3 8 0 + 0 8 -1 + 4 8 -2 = 451.0625 10
в) Перевести B2E.4 16 «10» с.с.
B2E.4 16 = 11 16 2 + 2 16 1 + 14 16 0 + 4 16 -1 = 2862.25 10
Схема перевода чисел из одной системы счисления в другую
Aрифметические операции в позиционных системах счисления
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
Сложение
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
Например :
Выполнить сложение двоичных чисел:
а) X=1101, Y=101;
Результат 1101+101=10010.
б) X=1101, Y=101, Z=111;
Результат 1101+101+111=11001.
Таблица сложения в 8-ой системе счисления
| 2+2=4 | 3+2=5 | 4+2=6 | 5+2=7 | 6+2=10 | 7+2=11 |
| 2+3=5 | 3+3=6 | 4+3=7 | 5+3=10 | 6+3=11 | 7+3=12 |
| 2+4=6 | 3+4=7 | 4+4=10 | 5+4=11 | 6+4=12 | 7+4=13 |
| 2+5=7 | 3+5=10 | 4+5=11 | 5+5=12 | 6+5=13 | 7+5=14 |
| 2+6=10 | 3+6=11 | 4+6=12 | 5+6=13 | 6+6=14 | 7+6=15 |
| 2+7=11 | 3+7=12 | 4+7=13 | 5+7=14 | 6+7=15 | 7+7=16 |
Таблица сложения в 16-ой системе счисления
| + | A | B | C | D | E | F | ||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | B | C | D | E | F | |||||||||||
| A | A | B | C | D | E | F | ||||||||||
| B | B | C | D | E | F | 1A | ||||||||||
| C | C | D | E | F | 1A | 1B | ||||||||||
| D | D | E | F | 1A | 1B | 1C | ||||||||||
| E | E | F | 1A | 1B | 1C | 1D | ||||||||||
| F | F | 1A | 1B | 1C | 1D | 1E |
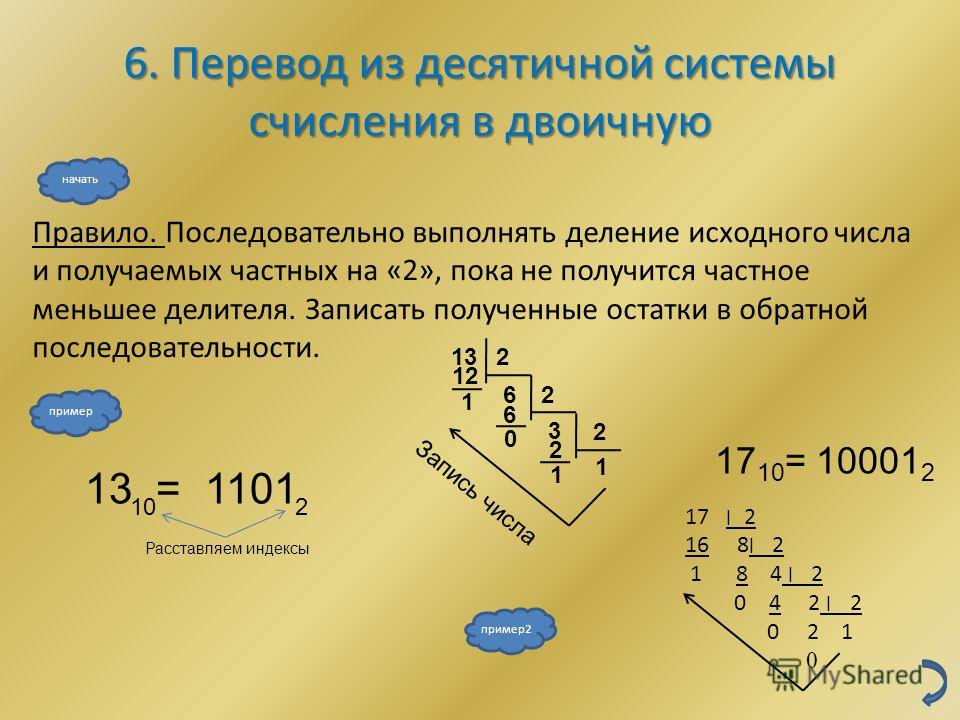
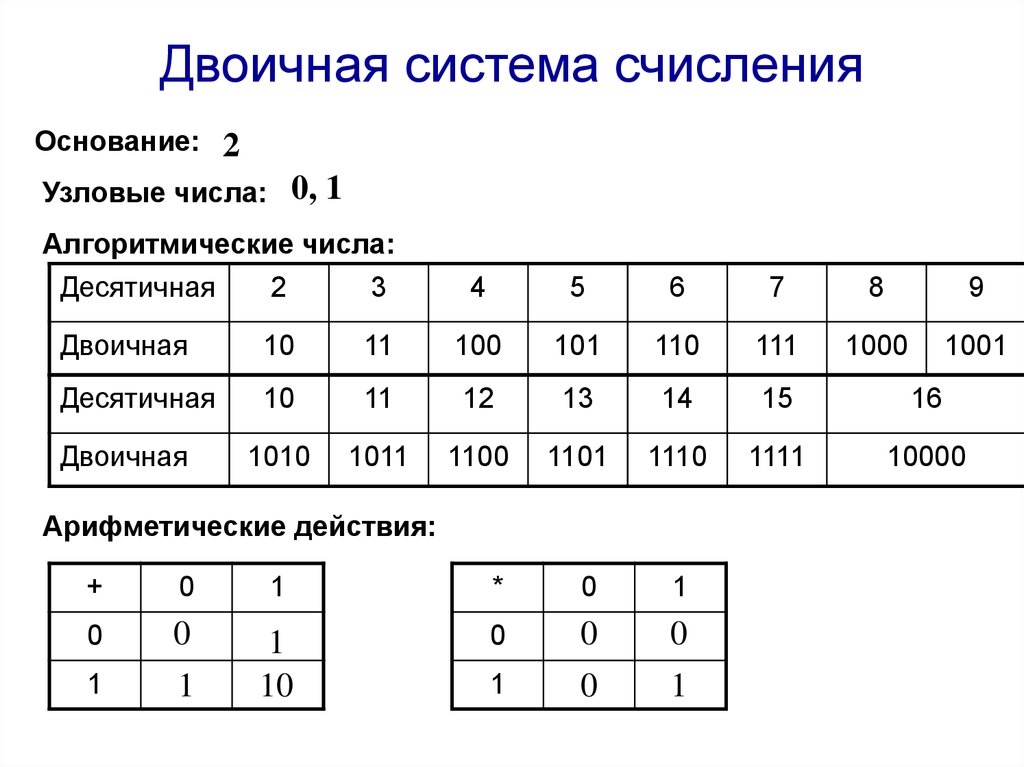
Рассмотрим способы перевода чисел из одной системы счисления в другую.
а) Перевод двоичного числа в десятичное.
Необходимо сложить двойки в степенях, соответствующих позициям, где в двоичном стоят единицы. Например:
Возьмем число 20. В двоичной системе оно имеет следующий вид: 10100.
Итак (считаем слева направо, считая от 4 до 0; число в нулевой степени всегда равно единице)
10100 = 1*2 4 + 0*2 3 + 1*2 2 + 0*2 1 + 0*2 0 = 20
16+0+4+0+0 = 20.
б) Перевод десятичного числа в двоичное.
Необходимо делить его на два, записывая остаток справа налево:
20/2 = 10, остаток 0
10/2=5, остаток 0
5/2=2, остаток 1
2/2=1, остаток 0
1/2=0, остаток 1
В результате получаем: 10100 = 20
в) Перевод шестнадцатеричного числа в десятичное.
В шестнадцатеричной системе номер позиции цифры в числе соответствует степени, в которую надо возвести число 16:
8A = 8*16 + 10 (0A) = 138
Напоследок приведем алгоритм перевода в двоичную и из двоичной системы, предлагаемый Л. Радюком.
Пусть А(цд) — целое десятичное число. (n-3) + … + a(1), а остаток равен a(0).
(n-3) + … + a(1), а остаток равен a(0).
На втором шаге целое частное опять разделим на 2, остаток от деления будет теперь равен a(1).
Если продолжать этот процесс деления, то после n-го шага получим последовательность остатков:
a(0), a(1),…, a(n-1).
Легко заметить, что их последовательность совпадает с обратной последовательностью цифр целого двоичного числа, записанного в свёрнутой форме:
A(2) = a(n-1)…a(1)a(0).
Таким образом, достаточно записать остатки в обратной последовательности, чтобы получить искомое двоичное число.
Тогда сам алгоритм будет следующим:
1. Последовательно выполнять деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор, пока не получится частное, меньшее делителя, то есть меньше 2.
2. Записать полученные остатки в обратной последовательности, а слева добавить последнее частное.
Для перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трёх двоичных цифр триаду, а при преобразовании шестнадцатеричного числа в группу из четырёх цифр тетраду.
Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трёх двоичных цифр триаду, а при преобразовании шестнадцатеричного числа в группу из четырёх цифр тетраду.
Подводя итоги работы, можно сделать следующие выводы.
Позиционная система счисления состоит в использовании ограниченного числа цифр, зато позиция каждой цифры в числе обеспечивает значимость (вес) этой цифры. Позиция цифры в числе на математическом языке называется разрядом.
Основание позиционной системы счисления это количество различных знаков или символов (цифр), используемых для отображения чисел в данной системе.
Для того чтобы двоичные числа, отличающиеся довольно значительной длиной, было легче воспринимать и отображать, их сжимают в восьмеричную и шестнадцатеричную системы счисления.
В компьютерных технологиях все виды информации кодируются только цифрами или, точнее, числами, которые представляются в двоичной системе счисления способе представления любых чисел с помощью двух знаков (цифр) по позиционному принципу.
Правила перевода чисел из одной системы счисления в другую
Поскольку одно и то же число может быть записано в различных системах счисления (например, ), то встает вопрос о переводе представления числа из одной системы в другую. Правила перевода для целых и дробных чисел отличаются.
Для перевода чисел из любой системы счисления в десятичную можно воспользоваться формулой (1).
Пример. Перевести в десятичную систему счисления числа
Решение:
Перевод целых чисел из одной системы счисления в другую
1. Делить заданное число на новое основание, записанное в виде числа со старым основанием до получения остатка.
2. Полученное частное следует вновь делить на новое основание, и этот процесс надо повторять до тех пор, пока частное не станет меньше делителя.
3. Полученные остатки от деления и последнее частное записываются в порядке обратном полученному при делении.
Решение:
Перевод дробных чисел из одной системы счисления в другую
Умножить заданное число на новое основание, записанное в виде числа со старым основанием. При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность полученного результата.
При каждом умножении целая часть произведения берется в виде очередной цифры соответствующего разряда, а оставшаяся дробная часть принимается за новое множимое. Число умножений определяет разрядность полученного результата.
Пример. Перевести число в двоичную, восьмеричную, шестнадцатеричную системы счисления.
Решение:
Решение: Переведем отдельно целую и дробную части числа в двоичную систему счисления.
.
Соединяя целую и дробную части, получим
Так как двоичная, восьмеричная и шестнадцатеричная системы счисления связаны друг с другом через степени 2, то преобразования между ними можно выполнять более простым способом.
1. Для перевода из шестнадцатеричной (восьмеричной) системы счисления в двоичную достаточно двоичным кодом записать шестнадцатеричные (восьмеричные) коды цифр тетрадами (триадами).
2.
Обратный перевод из двоичного кода производится в обратном порядке: двоичное число разбивается влево и вправо от запятой на тетрады для последующей записи цифр в шестнадцатеричном представлении и на триады – для записи их значений восьмеричными цифрами.
3. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно используется вспомогательный, двоичный код числа.
Пример. Перевести число в восьмеричную, шестнадцатеричную системы счисления.
Решение:
Пример. Перевести число в двоичную систему счисления.
Решение:
Способы перевода чисел из одной системы счисления в другую.
Перевод чисел из одной позиционной системы счисления в другую: перевод целых чисел.
Чтобы перевести целое число из одной системы счисления с основанием d1 в другую с основанием d2 необходимо последовательно делить это число и получаемые частные на основание d2 новой системы до тех пор, пока не получится частное меньше основания d2. Последнее частное — старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры — это остатки от деления, записываемые в последовательности, обратной их получению. Арифметические действия выполнять в той системе счисления, в которой записано переводимое число.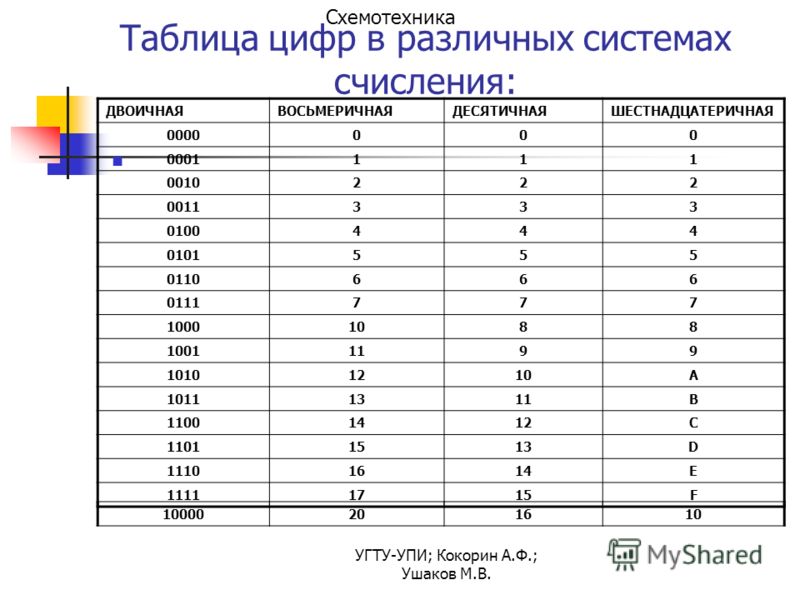
Пример 1. Перевести число 11(10) в двоичную систему счисления.
Ответ: 11(10)=1011(2).
Пример 2. Перевести число 122(10) в восьмеричную систему счисления.
Ответ: 122(10)=172(8).
Пример 3. Перевести число 500(10) в шестнадцатеричную систему счисления.
Ответ: 500(10)=1F4(16).
Перевод чисел из одной позиционной системы счисления в другую: перевод правильных дробей.
Чтобы перевести правильную дробь из системы счисления с основанием d1 в систему с основанием d2, необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание новой системы счисления d2. Правильная дробь числа в новой системе счисления с основанием d2 формируется в виде целых частей получающихся произведений, начиная с первого.
Если при переводе получается дробь в виде бесконечного или расходящегося ряда, процесс можно закончить при достижении необходимой точности.
При переводе смешанных чисел, необходимо в новую систему перевести отдельно целую и дробную части по правилам перевода целых чисел и правильных дробей, а затем оба результата объединить в одно смешанное число в новой системе счисления.
Пример 1. Перевести число 0,625(10) в двоичную систему счисления.
Ответ: 0,625(10)=0,101(2).
Пример 2. Перевести число 0,6(10) в восьмеричную систему счисления.
Ответ: 0,6(10)=0,463(8).
Пример 2. Перевести число 0,7(10) в шестнадцатеричную систему счисления.
Ответ: 0,7(10)=0,В333(16).
Перевод двоичных, восьмеричных и шестнадцатеричных чисел в десятичную систему счисления.
Для перевода числа P-ичной системы в десятичную необходимо использовать следующую формулу разложения:
аnan-1…а1а0=аnPn+ аn-1Pn-1+…+ а1P+a0 .
Пример 1. Перевести число 101,11(2) в десятичную систему счисления.
Ответ: 101,11(2)= 5,75(10) .
Пример 2. Перевести число 57,24(8) в десятичную систему счисления.
Ответ: 57,24(8) = 47,3125(10) .
Пример 3. Перевести число 7A,84(16) в десятичную систему счисления.
Ответ: 7A,84(16)= 122,515625(10) .
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления и обратно.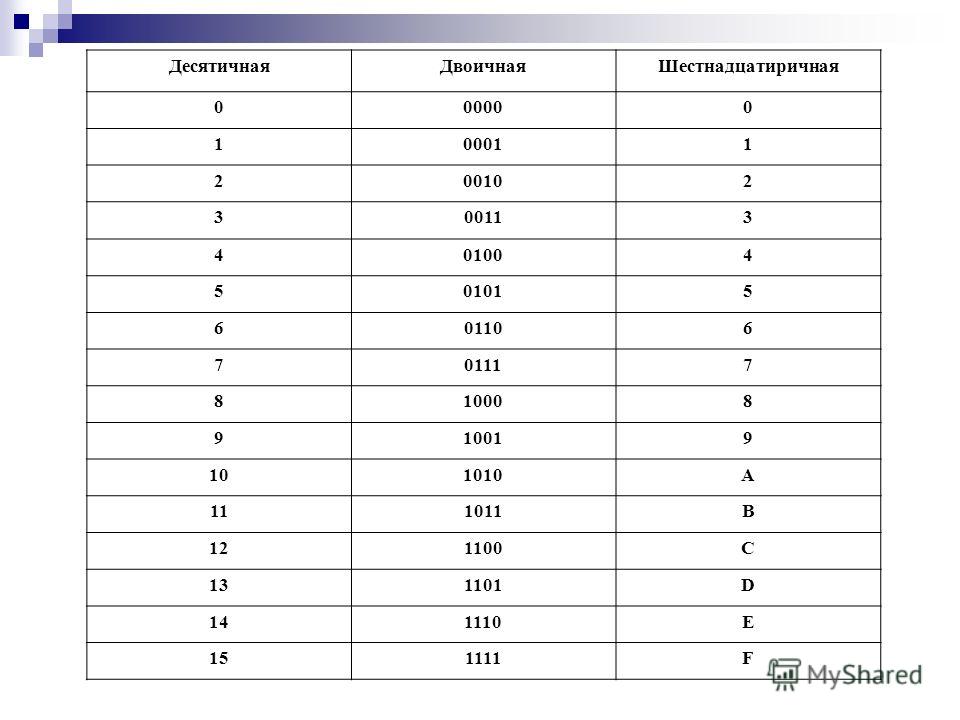
Для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа записать трехразрядным двоичным числом (триадой).
Пример: записать число 16,24(8) в двоичной системе счисления.
Ответ: 16,24(8)= 1110,0101(2) .
Для обратного перевода двоичного числа в восьмеричную систему счисления, необходимо исходное число разбить на триады влево и вправо от запятой и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1110,0101(2) в восьмеричной системе счисления.
Ответ: 1110,0101(2)= 16,24(8) .
Для перевода числа из шестнадцатеричной системы счисления в двоичную необходимо каждую цифру этого числа записать четырехразрядным двоичным числом (тетрадой).
Пример: записать число 7A,7E(16) в двоичной системе счисления.
Ответ: 7A,7E(16)= 1111010,0111111(2) .
Примечание: незначащие нули слева для целых чисел и справа для дробей не записываются.
Для обратного перевода двоичного числа в шестнадцатеричную систему счисления, необходимо исходное число разбить на тетрады влево и вправо от запятой и представить каждую группу цифрой в шестнадцатеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1111010,0111111(2) в шестнадцатеричной системе счисления.
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
n (степень) | |||||||||||
Пример.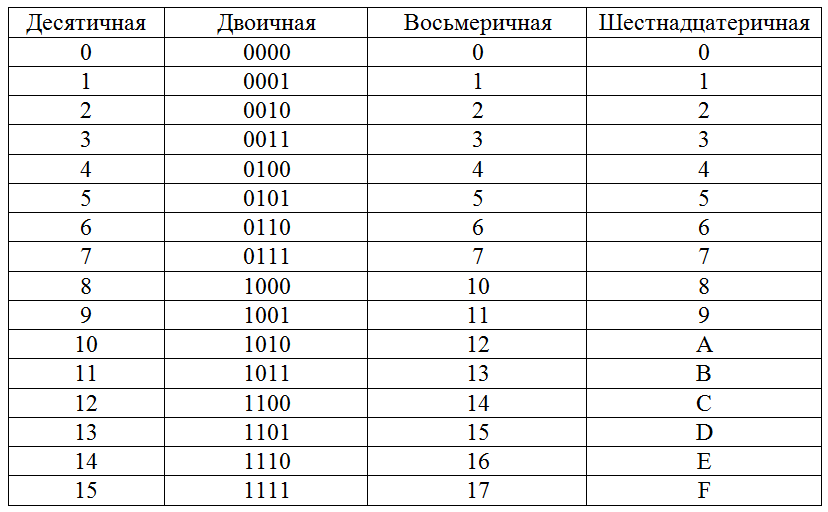
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
n (степень) | |||||||
Пример. Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
Степени числа 16
n (степень) | |||||||
Пример. Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
4.2.3. Перевод чисел в десятичную систему счисления
Для
перевода чисел из произвольной позиционной
системы счисления с основанием q в десятичную систему счисления необходимо
представить искомое десятичное число
в форме многочлена. Многочлен представляет
собой сумму n + 1 + m слагаемых, где n + 1 – количество
разрядов в целой части исходного числа, m – количество разрядов в дробной части
исходного числа:
Многочлен представляет
собой сумму n + 1 + m слагаемых, где n + 1 – количество
разрядов в целой части исходного числа, m – количество разрядов в дробной части
исходного числа:
.
Каждое слагаемое многочлена соответствует одному из разрядов исходного числа и равно весу цифры этого разряда. Слагаемое является произведением двух сомножителей. Первый сомножитель – десятичное число – равно собственному весу цифры соответствующего разряда. Второй сомножитель является степенью с основанием равным основанию системы счисления q и показателем, равным номеру разряда.
Пример 4.5. Дано двоичное число N2 = 1010100.012. Выполнить перевод числа в десятичную систему счисления:
10101002 = 1∙26 + 0∙25 + 1∙24 + 0∙23 + 1∙22 + 0∙21 + 0.20 + 0∙2-1 + 1∙2-2 =
=
64 + 0 + 16 + + 0 + 4 + 0 + 0 + 0 + 0. 25 = 84.2510.
25 = 84.2510.
Пример 4.6. Дано восьмеричное число N8 = 70203548. Выполнить перевод числа в десятичную систему счисления:
7020354.1118 = 7∙86 + 0∙85 + 2∙84 + 0∙83 + 3∙82 + 5∙81 + 4∙80 + 1∙8-1 + 1∙8-2 + 1∙8-3=
= 1835008 + 0 + 8192 + 0 + 256 + 40 +4 + 0.125 + 0.015625 + 0.001953125 =
= 1843500.14257812510.
Пример 4.7. Дано шестнадцатеричное число N16 = cf416. Выполнить перевод числа в десятичную систему счисления:
cf4.1116 = 12∙162 + 15∙161 + 4∙160 + 15∙16-1 + 4∙16-2 =
=
3072 + 240 + 4 + 0.0625 + 0.00390625 = 3316.0664062510.
Для перевода целых чисел из десятичной системы счисления в систему счисления с основанием q исходное число необходимо разделить на основание системы счисления q. При этом будет получено частное (целое число) и остаток от деления (целое число). На следующем шаге алгоритма необходимо полученное частное разделить на основание системы счисления. Будет получено очередное частное и остаток. Деление проводится до тех пор, пока очередное частное не окажется строго меньше основания системы счисления q. Запишем искомое число. Цифре старшего разряда будет соответствовать частное последнего деления. Цифре следующего разряда остаток последнего деления. Цифре следующего разряда остаток предпоследнего деления и т.д., цифре младшего разряда будет соответствовать остаток первого деления.
Пример 4.8. Дано десятичное число N10 = 41. Выполнить перевод числа в двоичную систему счисления (в скобках указан остаток от деления):
1) 41 : 2 = 20 (1), 20 > 2;
2) 20 : 2 = 10 (0), 10 > 2;
3) 10 : 2 = 5 (0), 5 > 2;
4) 5 : 2 = 2 (1), 2 > 2;
5) 2 : 2 = 1 (0), 1 <
2 – конец перевода.
Запишем искомое число: 4110 = 1010012.
Пример 4.9. Дано десятичное число N10 = 141. Выполнить перевод этого числа в восьмеричную систему счисления (в скобках указан остаток от деления):
1) 141 : 8 = 17 (5), 17 > 8;
2) 17 : 8 = 2 (1), 2 < 8 – конец перевода.
Запишем искомое число: 14110 = 2158.
Пример 4.10. Дано десятичное число N10 = 541. Выполнить перевод этого числа в шестнадцатеричную систему счисления (в скобках указан остаток от деления):
1) 541 : 16 = 33 (13), 33 > 16;
2) 33 : 16 = 2 (1), 2 < 16 – конец перевода.
Запишем искомое число: 54110 = 21d16.
Вопросы
Понятие системы счисления.

Значение числа и его запись.
Позиционные и непозиционные системы счисления.
Представление чисел в позиционной системе счисления.
Представление с фиксированной точкой.
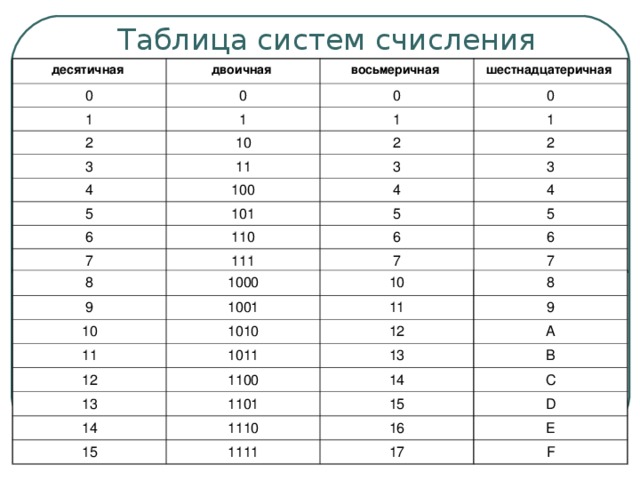
Понятие 2-й, 8-й, 16-й системы счисления.
Перевод чисел из 2-й системы счисления в 8-ю и 16-ю.
Перевод чисел из 16-й системы в 8-ю и 2-ю.
Перевод из 2-й 8-й и 16-й систем счисления в 10-ю систему счисления.
Перевод целых чисел из десятичной системы счисления в 2-ю систему счисления.
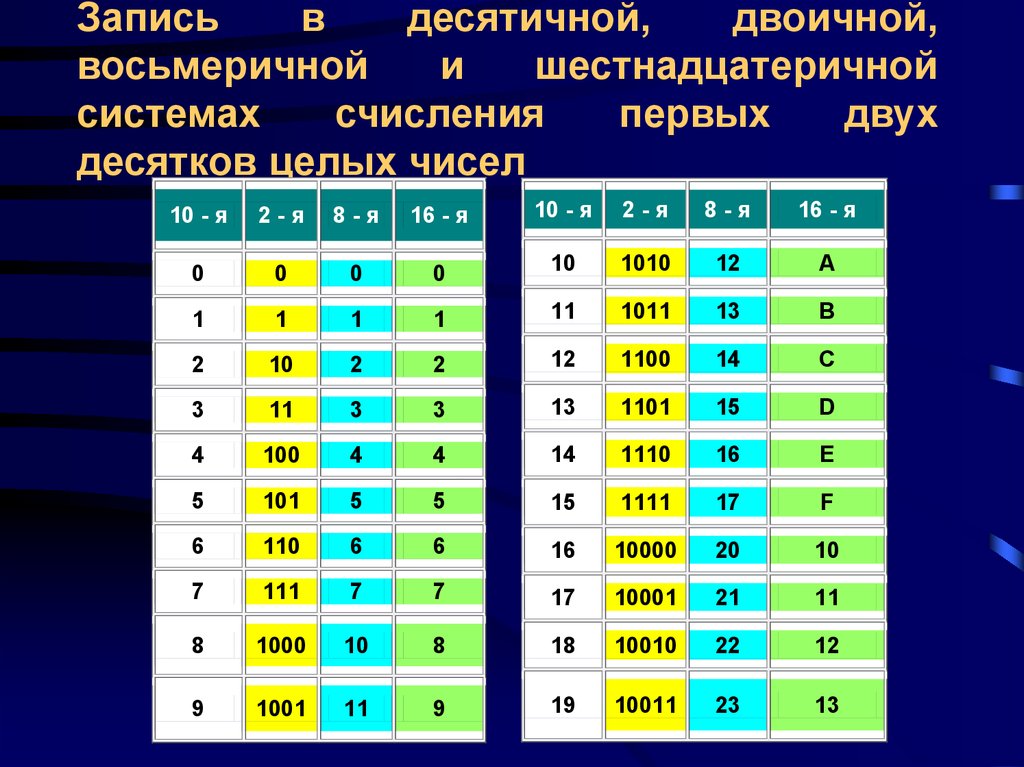
Системы счисления — Идем на урок информатики
| Перевод в десятичную систему счисления Задание 1. Решение. 2416 = 2 * 161 + 4 * 160 = 32 + 4 = 36 Ответ. 2416 = 3610 Задание 2. Известно, что X = 124 + 45 + 1012. Чему равно число X в десятичной системе счисления? Решение. Переведем каждое слагаемое в десятичную систему счисления: Ответ. X = 1510 Задание 3. Вычислите значение суммы 102 + 458 + 1016 в десятичной системе счисления. Решение. Переведем каждое слагаемое в десятичную систему счисления: Задание 1. Решение. Можно выполнить преобразование делением на 2 и комбинацией остатков в обратном порядке. Другой способ – это разложить число на сумму степеней двойки, начиная со старшей, вычисляемый результат которой меньше данного числа. При преобразовании пропущенные степени числа следует заменять нулями: 3710 = 32 + 4 + 1 = 25 + 22 + 20 = 1 * 25 + 0 * 24 + 0 * 23 + 1 * 22 + 0 * 21 + 1 * 20 = 100101 Ответ. 3710 = 1001012. Задание 2. Сколько значащих нулей в двоичной записи десятичного числа 73? Решение. Разложим число 73 на сумму степеней двойки, начиная со старшей и умножая пропущенные степени в дальнейшем на нули, а существующие на единицу: 7310 = 64 + 8 + 1 = 26 + 23 + 20 = 1 * 26 + 0 * 25 + 0 * 24 + 1 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 1001001 Ответ. Задание 3. Вычислите сумму чисел x и y при x = D216, y = 378. Результат представьте в двоичной системе счисления. Решение. Вспомним, что каждая цифра шестнадцатеричного числа формируется четырьмя двоичными разрядами, каждая цифра восьмеричного числа – тремя: D216 = 1101 0010 Сложим полученные числа: 11010010
11111
--------
11110001
Ответ. Сумма чисел D216 и y = 378, представленная в двоичной системе счисления равна 11110001. Задание 4. Дано: a = D716, b = 3318. Какое из чисел c, записанных в двоичной системе счисления, отвечает условию a < c < b?
Решение. Переведем числа в двоичную систему счисления: D716 = 11010111 Первые четыре разряда у всех чисел совпадают (1101). Первое число из перечня равно числу b, следовательно, не подходит. Второе число больше как b. Третье число равно a. Только четвертое число подходит: 0111 < 1000 < 1001. Ответ. Четвертый вариант (11011000) отвечает условию a < c < b. Задания на определение значений в различных системах счисления и их основанийЗадание 1. Для кодирования символов @, $, &, % используются двухразрядные последовательные двоичные числа. Первому символу соответствует число 00. С помощью данных символов была закодирована такая последовательность: $%&&@$. Декодируйте данную последовательность и переведите результат в шестнадцатеричную систему счисления. Решение. 1. Сопоставим двоичные числа кодируемым ими символам: 2. Декодируем заданную последовательность: 3. Ответ. 7A116. Задание 2. В саду 100x фруктовых деревьев, из которых 33x – яблони, 22x – груши, 16x – сливы, 17x — вишни. Чему равно основание системы счисления (x). Решение. 1. Заметим, что все слагаемые – двузначные числа. В любой системе счисления их можно представить так: 2. Условие задачи таково: 3. Решим квадратное уравнение: 4. Отрицательное число не может быть основанием системы счисления. Поэтому x может быть равен только 9. Ответ. Искомое основание системы счисления равно 9. Задание 3. В системе счисления с некоторым основанием десятичное число 12 записывается как 110. Найдите это основание. Решение. Сначала распишем число 110 через формулу записи чисел в позиционных системах счисления для нахождения значения в десятичной системе счисления, а затем найдем основание методом перебора. 110 = 1 * x2 + 1 * x1 + 0 * x0 = x2 + x Нам надо получить 12. Пробуем 2: 22 + 2 = 6. Пробуем 3: 32 + 3 = 12. Значит основание системы счисления равно 3. Ответ. Искомое основание системы счисления равно 3. Задание 4. В какой системе счисления десятичное число 173 будет представлено как 445? Решение. Задачи на нахождение нескольких оснований систем счисления Есть группа задач, в которых требуется перечислить (в порядке
возрастания или убывания) все основания систем счисления, в которых
представление данного числа заканчивается на заданную цифру. Эта задача
решается довольно просто. Пример Решение |
Преобразование дробей в десятичные числа
Преобразование дробей в десятичные числа| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
Таблицы преобразования дробей в десятичные числаВажное примечание: любой диапазон чисел, равный , подчеркнутый означает, что эти числа повторяются. Например, 0, 09 означает 0,09.0909…. Например, 0, 09 означает 0,09.0909…. Перечислены только дроби в наименьшем выражении. Например, чтобы найти 2/8, сначала упростите его до 1/4, а затем выполните поиск.
в таблице ниже.
Нужно преобразовать повторяющуюся десятичную дробь в дробь? Следуйте этим примерам: ПРИМЕЧАНИЕ Образец, если нули, предшествующие повторному десятичному делу: Чтобы преобразовать десятичную дробь, которая начинается с неповторяющейся части , например
как 0,21 456 456456456456…, до дроби, запишите в виде суммы
неповторяющаяся часть и повторяющаяся часть. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
Что такое 3/16 в виде десятичной дроби? (Преобразовать 3/16 в десятичную)
Преобразование 3/16 в десятичную, возможно, является одним из самых простых вычислений, которые вы можете сделать. В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
Хотите быстро узнать или показать учащимся, как преобразовать 3/16 в десятичную дробь? Включи это очень быстрое и веселое видео прямо сейчас!
Прежде всего, если вы не знаете, что такое числитель и знаменатель в дроби, нам нужно повторить это:
3 (числитель) / 16 (знаменатель)
Вот маленький секрет, с помощью которого можно мгновенно преобразовать любую дробь в десятичную: Просто разделите числитель на знаменатель:
= 3/16
= 3 ÷ 16
= 0,1875
Вот и все! 3/16 в виде десятичной дроби равно 0,1875.
Хотел бы я рассказать вам больше о преобразовании дроби в десятичную, но это действительно так просто, и мне больше нечего об этом сказать.
Если вы хотите попрактиковаться, возьмите ручку и блокнот и попробуйте самостоятельно вычислить некоторые дроби в десятичном формате. Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Почему вы хотите преобразовать 3/16 в десятичную дробь?
Отличный вопрос. У нас есть много расчетов на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно?
Ну, во-первых, это просто хороший способ представить дробь в лучшем виде, который позволяет вам выполнять с ними обычные арифметические действия (такие как сложение, вычитание, деление и умножение).
В реальной жизни мы в основном имеем дело с десятичными дробями (например, с валютой), и, поскольку наш мозг с юных лет приучен понимать и сравнивать десятичные дроби чаще, чем дроби, проще понимать и сравнивать дроби, если они сначала преобразовать в десятичную!
Вот небольшой пример из реальной жизни преобразования дроби в десятичную при использовании количества. Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Надеюсь, это руководство помогло вам понять, как преобразовать дробь в десятичное число. Теперь вы можете идти вперед и преобразовывать дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Калькулятор преобразования дроби в десятичную дробь
Дробь в виде десятичной дроби
Введите числитель и знаменатель
Вычисление следующей дроби в десятичную дробь
- Что такое 3/17 в виде десятичной дроби?
Случайная дробь в десятичные числа
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите преобразовывать дроби в десятичные? Ниже приведена куча случайно сгенерированных вычислений для вашего удовольствия от десятичной любви:
Что такое 283/475 как десятичная
Десятичное число 421/895
Десятичное число 816/926
Десятичное число 307/337
Десятичное число 611/810
Что такое десятичное число 199/210?
Что такое десятичное число 626/819?
Что такое десятичное число 757/785?
Что такое десятичное число 441/610?
Что такое 935/962 в виде десятичного числа
Что такое 313/843 в виде десятичного числа
Десятичное число 194/416
Десятичное число 454/872
Десятичное число 331/964
Десятичное число 86/808
Десятичное число 84/921
Десятичное число 633/810
Десятичное число 391/893
Десятичное число 525/643
Десятичное число 224/7
Что такое 479/896 в виде десятичного числа
Что такое 224/888 в виде десятичного числа
Десятичное число 884/985
Десятичное число 916/933
Десятичное число 649/972
Десятичное число 230/548
Десятичное число 6
Десятичное число 950/966
Десятичное число 767/803
Десятичное число 220/304
Десятичное число 183/271
Десятичное число 226/271
Что такое 817/844 в виде десятичного числа
Что такое 100/472 в виде десятичного числа
Десятичное число 309/579
Десятичное число 402/757
Десятичное число 927/997
Десятичное число 215/628
Десятичное число 846/987
Десятичное число 613/910
Десятичное число 539/752
Десятичное число 834/933
Что такое 904/986 в виде десятичного числа
Что такое 211/772 в виде десятичного числа
Что такое десятичное число 892/976?
Что такое десятичное число 617/651?
Что такое десятичное число 596/842?
Что такое десятичное число 857/875?
Десятичное число 834/850
Десятичное число 626/738
Десятичное число 195/687
Десятичное число 581/682
Что такое 828/927 в виде десятичного числа
Что такое 895/900 в виде десятичного числа
Десятичное число 848/937
Десятичное число 498/970
Десятичное число 334/469
Десятичное число 167/936
Десятичное число 76/399
Десятичное число 213/291
Десятичное число 242/997
Десятичное число 923/987
Десятичное число 1 201/7
Что такое 55/370 в виде десятичного числа
Что такое 906/955 в виде десятичного числа
Десятичное число 39/812
Десятичное число 973/1000
Десятичное число 946/979
Десятичное число 787/918
Десятичное число 6 918/9
Десятичное число 432/515
Десятичное число 321/874
Десятичное число 586/786
Десятичное число 530/888
Десятичное число 856/86
Что такое 17/102 в виде десятичного числа
Что такое 778/784 в виде десятичного числа
Десятичное число 800/855
Десятичное число 656/714
Десятичное число 480/873
Десятичное число 692/846
Десятичное число 5
Десятичное число 283/372
Десятичное число 375/852
Десятичное число 677/920
Десятичное число 869/934
Десятичное число 4 660/920
Что такое 536/741 в виде десятичного числа
Что такое 997/999 в виде десятичного числа
Десятичное число 11/151
Десятичное число 881/965
Десятичное число 836/958
Десятичное число 849/899
Десятичное число 1/16 ? (Преобразовать 1/16 в десятичную)
Преобразование 1/16 в десятичную, возможно, является одним из самых простых вычислений, которые вы можете сделать. В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
Хотите быстро узнать или показать учащимся, как преобразовать 1/16 в десятичную дробь? Включи это очень быстрое и веселое видео прямо сейчас!
Прежде всего, если вы не знаете, что такое числитель и знаменатель в дроби, нам нужно повторить это:
1 (числитель) / 16 (знаменатель)
Вот небольшой секрет, с помощью которого можно мгновенно преобразовать любую дробь в десятичную: Просто разделите числитель на знаменатель:
= 1/16
= 1 ÷ 16
= 0,062555
Вот буквально все! 1/16 в виде десятичной дроби составляет 0,0625.
Хотел бы я рассказать вам больше о преобразовании дроби в десятичную, но это действительно так просто, и мне больше нечего об этом сказать.
Если вы хотите потренироваться, возьмите ручку и блокнот и попробуйте самостоятельно вычислить некоторые дроби в десятичном формате.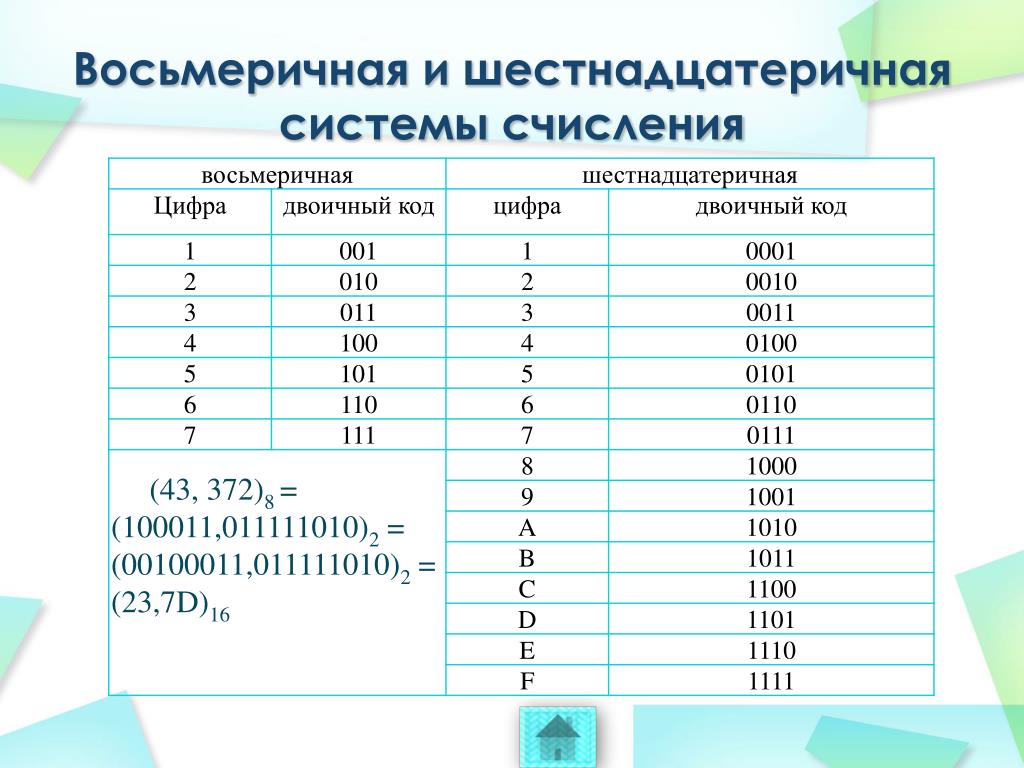 Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Зачем нужно преобразовывать 1/16 в десятичную дробь?
Отличный вопрос. У нас есть много расчетов на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно?
Ну, во-первых, это просто хороший способ представить дробь в лучшем виде, который позволяет вам выполнять с ними обычные арифметические действия (такие как сложение, вычитание, деление и умножение).
В реальной жизни мы в основном имеем дело с десятичными дробями (например, с валютой), и, поскольку наш мозг с раннего возраста приучают понимать и сравнивать десятичные дроби чаще, чем дроби, проще понимать и сравнивать дроби, если они сначала преобразовать в десятичную!
Вот небольшой пример из реальной жизни преобразования дроби в десятичную при использовании количества. Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Надеемся, что это руководство помогло вам понять, как преобразовать дробь в десятичное число. Теперь вы можете идти вперед и преобразовывать дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 1/16 в виде десятичной дроби?». VisualFractions.com . По состоянию на 3 октября 2022 г.
 http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-16-as-a-decimal/.
http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-16-as-a-decimal/.«Что такое 1/16 в виде десятичной дроби?». VisualFractions.com , http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-16-as-a-decimal/. По состоянию на 3 октября 2022 г.
Что такое 1/16 в виде десятичной дроби?. VisualFractions.com. Получено с http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-16-as-a-decimal/.
Калькулятор преобразования дроби в десятичную дробь
Дробь в виде десятичной дроби
Введите числитель и знаменатель
Вычисление следующей дроби в десятичную дробь
- Что такое 1/17 в виде десятичной дроби?
Случайная дробь в десятичные числа
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите преобразовывать дроби в десятичные? Ниже приведена куча случайно сгенерированных вычислений для вашего удовольствия от десятичной любви:
Десятичное число 820/823
Десятичное число 455/792
Десятичное число 806/960
Десятичное число 808/909
Десятичное число 610/943
Что такое десятичное число 434/805
Что такое десятичное число 883/905
Что такое десятичное число 509/888
Что такое десятичное число 927/943
Что такое десятичное число 475/763
Что такое 63/726 в виде десятичного числа
Что такое 564/852 в виде десятичного числа
Десятичное число 411/857
Десятичное число 60/505
Десятичное число 424/603
Десятичное число 807/890
Десятичное число 673/718
962/984
Что такое 85/431 в виде десятичного числа
Что такое 909/910 в виде десятичного числа
Что такое 938/991 в виде десятичного числа
Что такое 163/179 в виде десятичного числа
Что такое 294/773 в виде десятичного числа
Что такое 618/647 в виде десятичного числа
Что такое 969/990 в виде десятичного числа
Что такое десятичное число 120/765
Что такое десятичное число 661/859
Что такое десятичное число 487/614
Что такое десятичное число 906/977
Что такое десятичное число 619/983
Что такое 176/825 в виде десятичного числа
Что такое 586/799 в виде десятичного числа
Что такое десятичное число 999/1000
Что такое десятичное число 446/627
Что такое десятичное число 215/605
Что такое десятичное число 178/640
Что такое десятичное число 445/974 9103
611/690 Что такое 279/740 в виде десятичного числа
Что такое 421/575 в виде десятичного числа
Десятичное число 696/797
Десятичное число 433/840
Десятичное число 414/903
Десятичное число 174/708
Десятичное число 754/769 0
Десятичное число 651/925
Десятичное число 722/807
Десятичное число 815/832
Десятичное число 527/562
Десятичное число 68/3191
Что такое 307/724 в виде десятичного числа
Что такое 271/521 в виде десятичного числа
Что такое 926/939 в виде десятичного числа
Что такое 924/957 в виде десятичного числа
Что такое 809/997 в виде десятичного числа
Что такое 466/578 в виде десятичного числа
Что такое 853/946 в виде десятичного числа
Десятичное число 532/620
Десятичное число 22/380
Десятичное число 898/968
Десятичное число 987/999
Десятичное число 227/437
Что такое 318/351 в виде десятичного числа
Что такое 734/831 в виде десятичного числа
Что такое 969/978 как десятичное число
Что такое 419/627 как десятичное число
Что такое 911/977 как десятичное число
Что такое 353/863 как десятичное число
Что такое 522/730 как десятичное число 0
Десятичное число 687/908
Десятичное число 444/821
Десятичное число 137/473
Десятичное число 50/605
Десятичное число 271/709 0
Что такое 248/971 в виде десятичного числа
Что такое 107/728 в виде десятичного числа
Десятичное число 352/894
Десятичное число 321/723
Десятичное число 543/967
Десятичное число 347/426
Десятичное число 536/651
Десятичное число 614/662
Десятичное число 579/710
Десятичное число 211/613
Десятичное число 813/991
Десятичное число 214/749
Что такое 383/871 в виде десятичного числа
Что такое 480/789 в виде десятичного числа
Десятичное число 527/588
Десятичное число 750/944
Десятичное число 479/674
Десятичное число 582/680
Десятичное число 600/7891
Инструмент для преобразования десятичных чисел с основанием 16
Число с основанием
Число с основанием 10
Число с основанием 10 эквивалентно десятичному.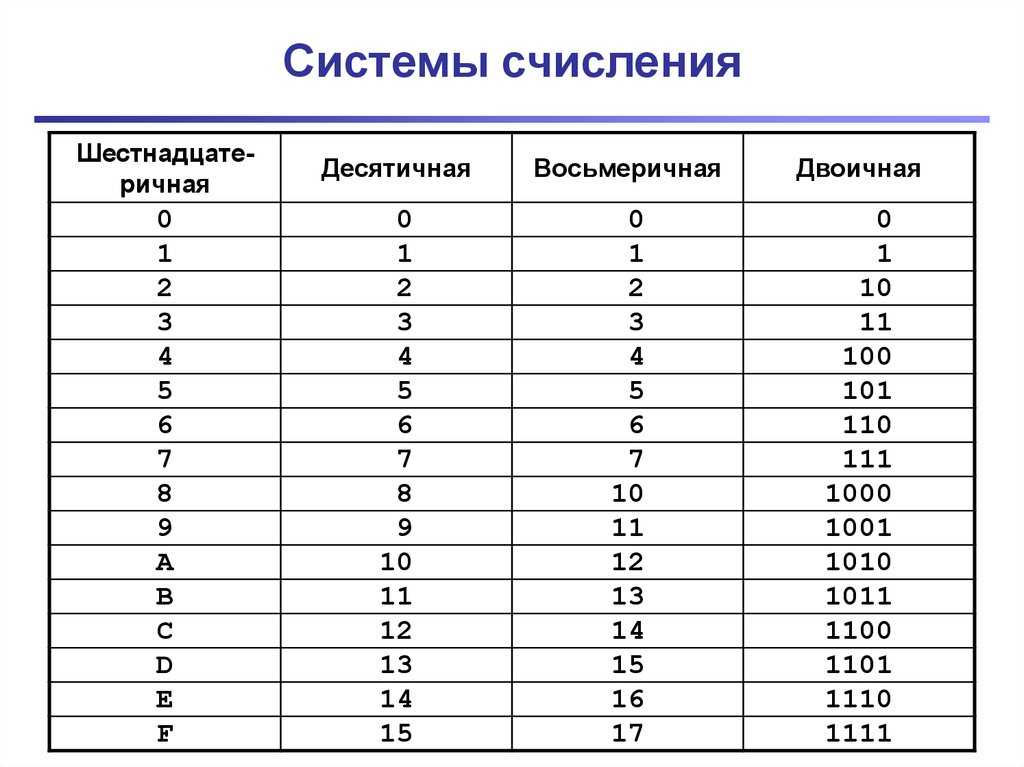
База-11
Десятичная (база-11) позиционная система счисления основана на числе одиннадцать. Для десятичной дроби требуется одиннадцать символов от 0 до 9.и A.
Base-12
Двенадцатеричная система (также известная как base-12 или дюжина) представляет собой позиционную систему счисления с основанием двенадцать. Для двенадцатеричной системы требуется двенадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A и B. позиционная система счисления с тринадцатью в основе. Он использует 13 различных цифр для представления чисел. Цифры для основания 13 могут быть 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B и C.
Основание-14
Тетрадесятеричная (основание-14) позиционная система счисления основана на числе четырнадцать. Для тетрадесятичного числа требуется четырнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D. Система обозначений основана на числе пятнадцать. Для пятидесятичного числа требуется пятнадцать символов, таких как: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E.
Base-16
Base-16 эквивалентно в шестнадцатеричный.
База-17
База 17 или семеричная система счисления — это позиционная система счисления с основанием 17. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A , B, C, D, E, F и G.
Основание-18
Основание 18 или восьмидесятеричное число основано на восемнадцати и требует 18 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G и H.
Основание-19
Основание 19 или недесятичное число основано на девятнадцати и требует 19 различных символов (0, 1, 2, 3, 4). , 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H и I.
Основание-2
Основание-2 эквивалентно двоичному.
Основание-20
Десятеричная система счисления или система счисления с основанием 20 основана на двадцати. Двадцать используемых символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I и J.
Base-21
База 21 или недесятичная система счисления основана на двадцати одном.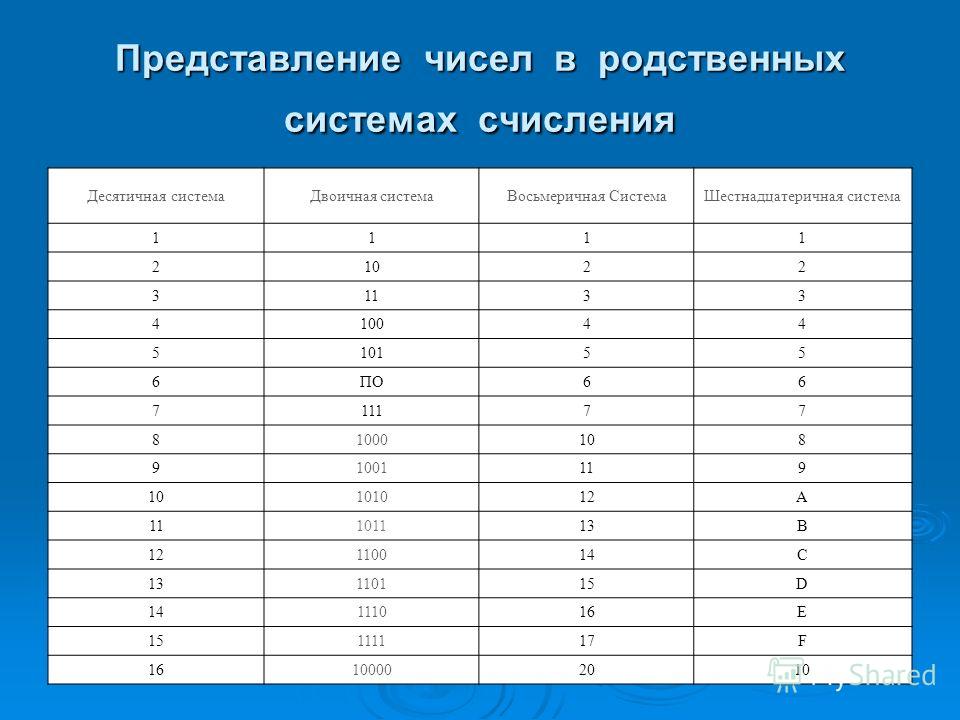 Используется двадцать один символ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J и K.
Используется двадцать один символ: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J и K.
База-22
База 22 или двенадцатидесятичная система счисления основана на двадцати двух. Используются двадцать два символа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K и L.
Основание-23
Основание 23 или десятичная система счисления основана на двадцати трех. Двадцать три используемых символа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L и M.
Основание-24
Система счисления с основанием 24 — это система счисления, основанная на 24. В этой системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K, L, M и N.
Основание-25
Система счисления с основанием 25 — это система счисления с числом 25. база. В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N и O.
Основание-26
Шестнадцатеричная система счисления имеет основание двадцать шесть.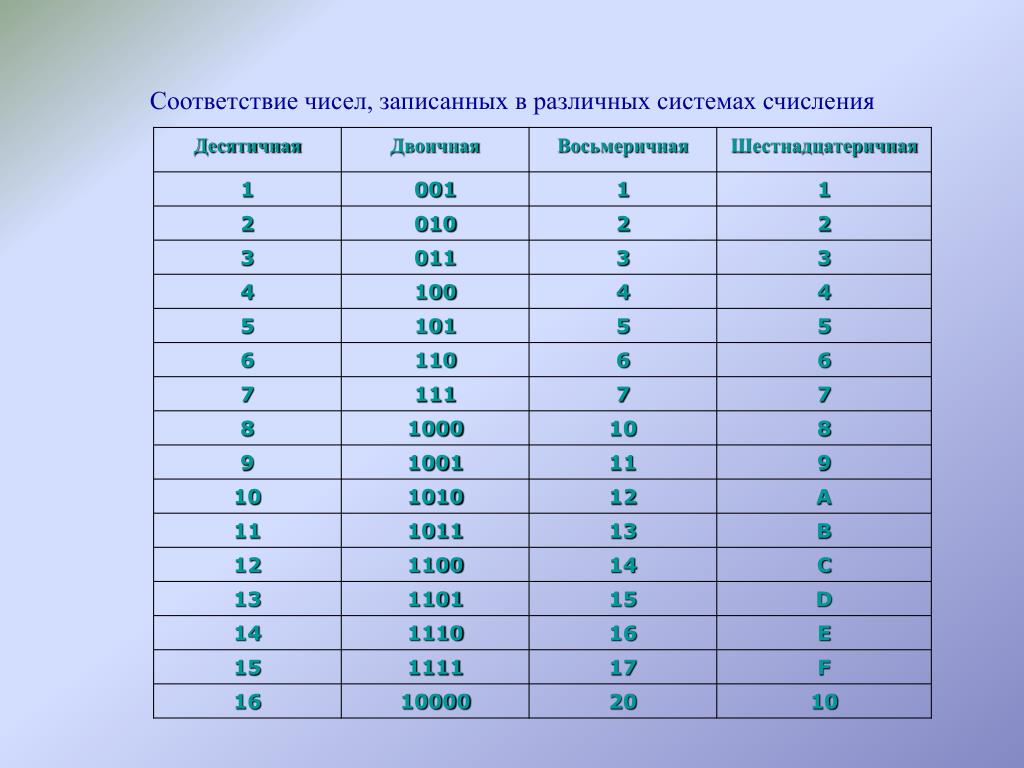 В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N, O и P.
В этой системе используются следующие символы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L. , M, N, O и P.
Основание-27
Семидесятичная система счисления имеет основание двадцать семь. В этой системе используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P и Q.
Base-28
Система счисления с основанием 28 основана на двадцать восемь и использует 28 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K , L, M, N, O, P, Q и R.)
Base-29
Система счисления с основанием 29 основана на двадцати девяти и использует 29 различных символов (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R и S.)
База-3
Терне или троица — это система счисления с основанием 3. Для троичной системы счисления требуется только три символа: 0, 1 и 2.
Основание-30
Тройная система счисления или основание 30 — это позиционная система счисления, использующая 30 в качестве основания.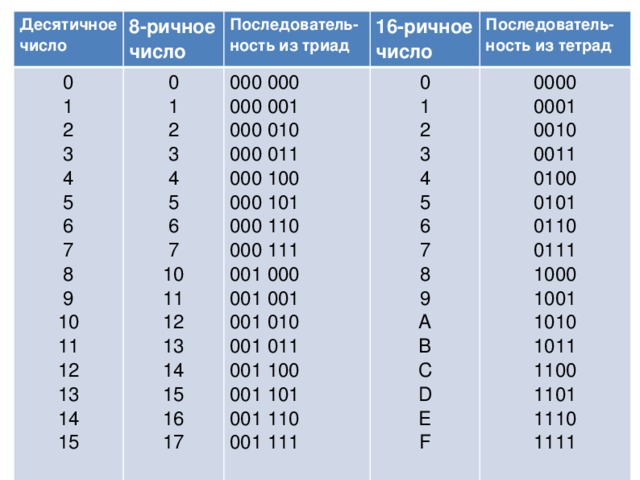 Цифры в этом основании могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-T.
Цифры в этом основании могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-T.
Основание-31
Нетроичная система счисления или основание 31 — это позиционная система счисления, использующая 31 в качестве основания. Цифры в этом основании могут быть представлены с помощью арабских цифр 0-9 и латинских букв A-U.
Основание-32
Двенадцатикратная или основание-32 — это система счисления, в основе которой лежит число 32. Цифры в этой базе могут быть представлены арабскими цифрами 0-9 и латинскими буквами A-V.
База-33
Система счисления с основанием 33 основана на 33 различных символах (числа 0-9 и буквы A-W).
База-34
Система счисления с основанием 34 основана на 34 различных символах (числа 0-9 и буквы A-X).
База-35
Система счисления с основанием 35 основана на 35 различных символах (числа 0-9и буквы А-У).
База-36
База 36 или шестнадцатеричная система счисления — это позиционная система счисления, использующая 36 в качестве основания. Выбор 36 удобен тем, что цифры можно представить с помощью арабских цифр 0-9 и латинских букв A-Z.
Выбор 36 удобен тем, что цифры можно представить с помощью арабских цифр 0-9 и латинских букв A-Z.
Основание 4
Четверка — это система счисления с основанием 4. Он использует цифры 0, 1, 2 и 3 для представления любого действительного числа.
База-5
Пятикратная система счисления с основанием пять. Базовая пятерка начинается с 0-4.
Основание-6
Сенарий (основание-6) — это система счисления с секс-символами (0, 1, 2, 3, 4, 5).
Основание-7
Семеричная система счисления является системой счисления с основанием 7 и использует цифры 0-6.
База-8
База-8 эквивалентно восьмеричной системе.
Base-9
Nonary — это система счисления с основанием 9, обычно использующая цифры 0-8.
Двоичная система счисления
Двоичная система счисления, или система счисления с основанием 2, представляет числовые значения с помощью двух символов: 0 и 1.
Десятичная система счисления
Десятичная система счисления (также называемая десятичной или иногда десятичной) имеет основание десять.
Шестнадцатеричная
Шестнадцатеричная (также с основанием 16 или шестнадцатеричная) — это позиционная система счисления с основанием 16. В ней используется шестнадцать различных символов, чаще всего символы 0–9 для представления значений от нуля до девяти, и А,Б,В,Г,Д,Ф.
Восьмеричная система счисления
Восьмеричная система счисления, или сокращенно восьмеричная, представляет собой систему счисления с основанием 8 и использует цифры от 0 до 7
Как преобразовать футы/дюймы/дроби в десятичный формат
Калькуляторы Спайка
Множество чисел, с которыми нужно иметь дело, и нет, не очень полезные для выбора лотерейных номеров. Но если вы понимаете основные понятия, это избавляет вас от необходимости конвертировать эти числа, и вы обязательно станете победителем.
| Дюйм | Десятичный фут | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 дюйм | 0,0833 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2 дюйма0005 | 0.167 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 3 inches | 0. 25 25 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 4 inches | 0.333 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5 inches | 0.417 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6 inches | 0.5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 inches | 0.583 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 8 дюймов | 0,667 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9 дюймов | 0,75 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 дюймов | 0,833
ПримерПреобразование 7′- 4 3/4″ в десятичное значение.
Конечно, вы не можете добавить десятичное значение фута к десятичному значению дюйма без преобразования десятичного значения дроби в дюймах в десятичное значение фута. Попробуем еще раз: Преобразование 7′-4 3/4″ в десятичное число.
Запишите 7′- 4 3/4″ в десятичном виде = 7,3955
Разделите количество дюймов на 12 Пример:2 дюйма ÷ 12 = 0,16667 5 дюймов ÷ 12 = 0,41667 Преобразование дюймов плюс дробь в десятичную Преобразуйте дюйм в дробь, используя тот же знаменатель, что и дробь, прибавьте дробь к этому количеству и разделите числитель на знаменатель. |


 Какому числу в десятичной системе счисления соответствует число 2416?
Какому числу в десятичной системе счисления соответствует число 2416? Чему равно число 37 в двоичной системе счисления?
Чему равно число 37 в двоичной системе счисления? В двоичной записи десятичного числа 73 присутствует четыре значащих нуля.
В двоичной записи десятичного числа 73 присутствует четыре значащих нуля. Поэтому сравнение упрощается до сравнения младших четырех разрядов.
Поэтому сравнение упрощается до сравнения младших четырех разрядов.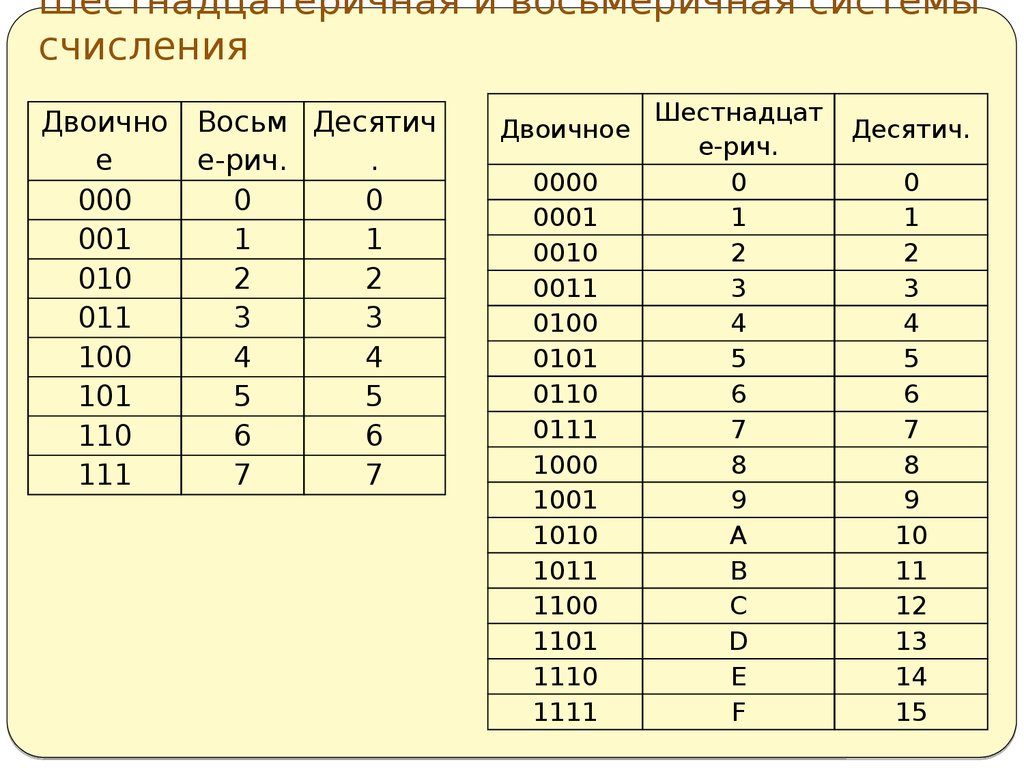 Переведем двоичное число в шестнадцатеричную систему счисления:
Переведем двоичное число в шестнадцатеричную систему счисления: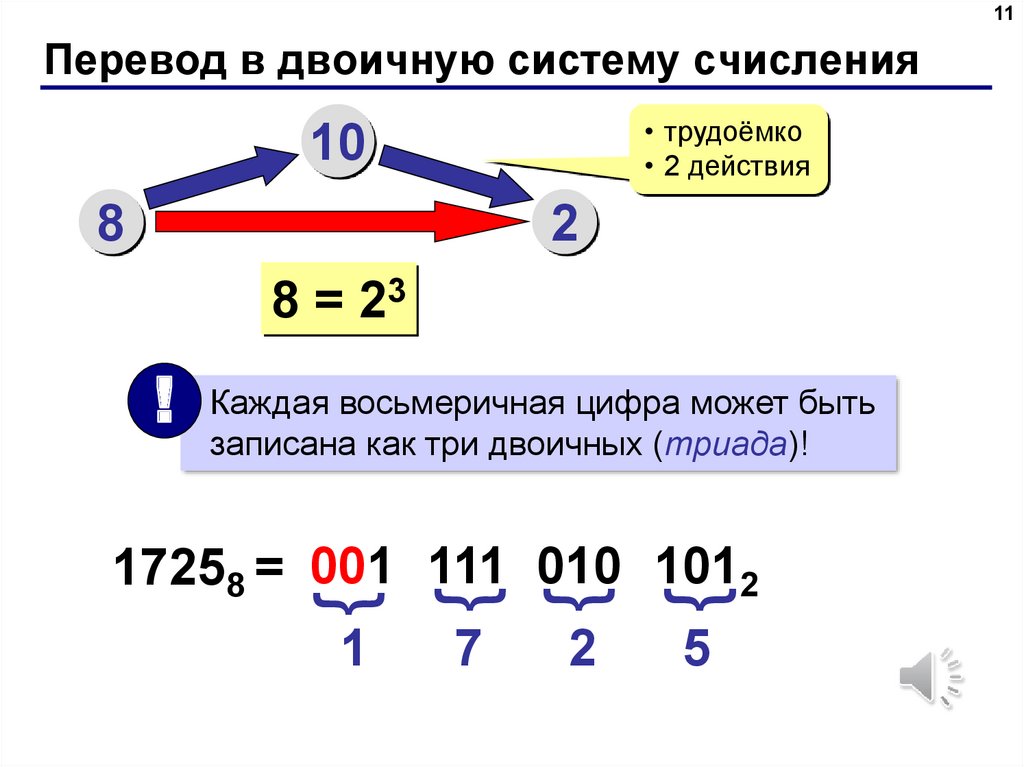 Квадратный корень из D равен 11.
Квадратный корень из D равен 11.
 Сначала нужно из исходного числа вычесть заданную цифру. Получившееся число и будет первым основанием системы счисления. А все
другие основания могут быть только делителями этого числа. (Данное
утверждение доказывается на основе правила перевода чисел из одной
системы счисления в другую – см. п.4). Помните только, что основание системы счисления не может быть меньше заданной цифры!
Сначала нужно из исходного числа вычесть заданную цифру. Получившееся число и будет первым основанием системы счисления. А все
другие основания могут быть только делителями этого числа. (Данное
утверждение доказывается на основе правила перевода чисел из одной
системы счисления в другую – см. п.4). Помните только, что основание системы счисления не может быть меньше заданной цифры! 142857
142857 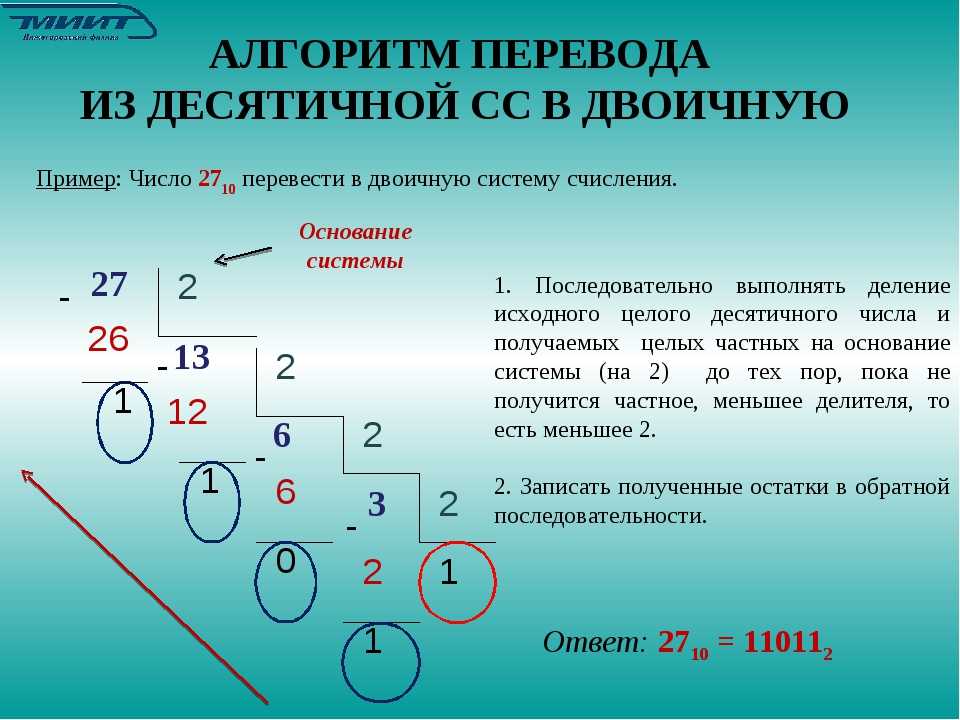 09
09  2 2222222… = 2/9
2 2222222… = 2/9 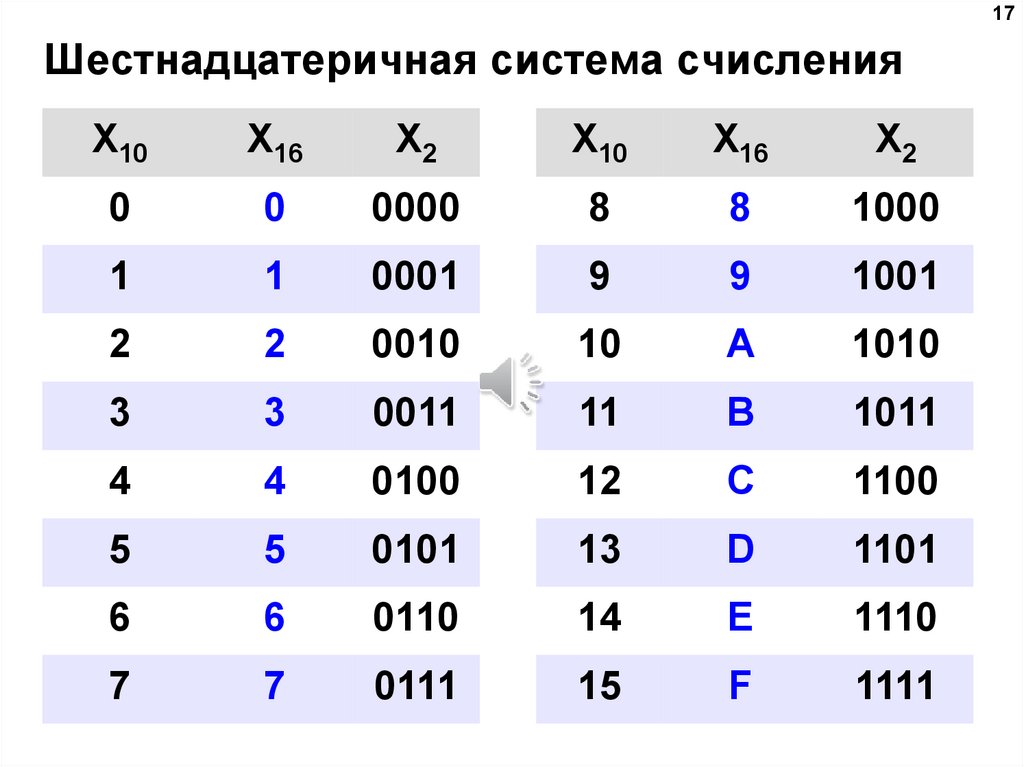 Второе десятичное число (которое повторяется) преобразуется
по приведенной выше схеме.
Второе десятичное число (которое повторяется) преобразуется
по приведенной выше схеме.  http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-16-as-a-decimal/.
http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-16-as-a-decimal/. 5
5
 4375
4375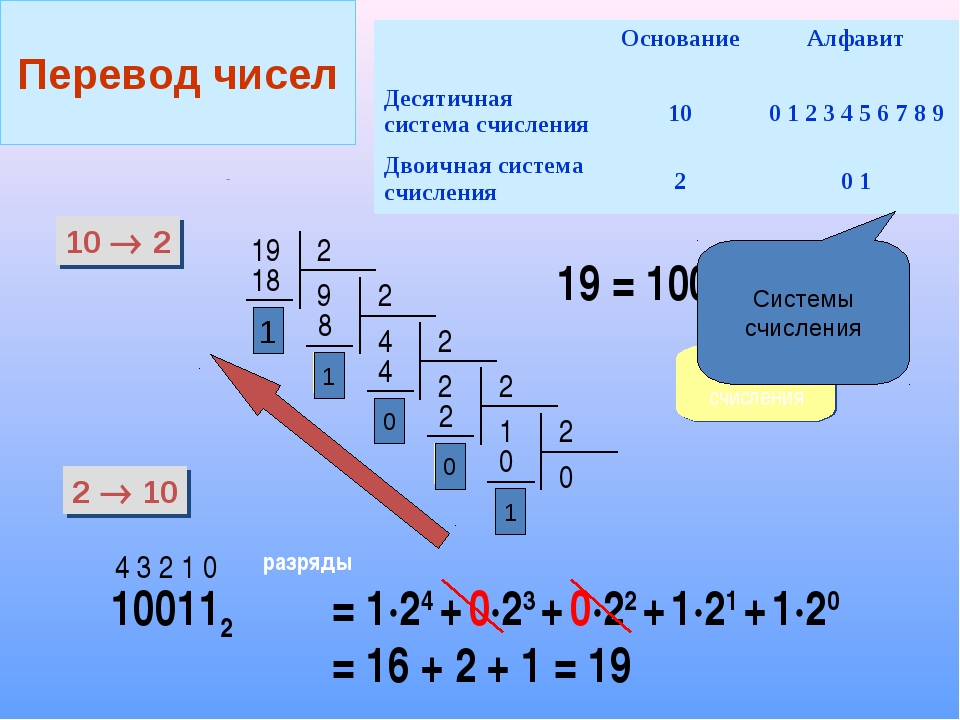 417
417