Таблица 16 ричной системы. Системы счисления
Для представления чисел в микропроцессоре используется двоичная система счисления
.
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число x=a n a n-1 ..a 1 a 0 ,a -1 a -2 …a -m запишется в двоичной системе счисления как
x = a n ·2 n +a n-1 ·2 n-1 +…+a 1 ·2 1 +a 0 ·2 0 +a -1 ·2 -1 +a -2 ·2 -2 +…+a -m ·2 -m
где a i — двоичные цифры (0 или 1).
Восьмеричная система счисления
В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:
10 10 = A 16 12 10 = C 16 14 10 = E 16
11 10 = B 16 13 10 = D 16 15 10 = F 16 .
Например, число 175 10 в шестнадцатеричной системе счисления запишется как AF 16 . Действительно,
10·16 1 +15·16 0 =160+15=175
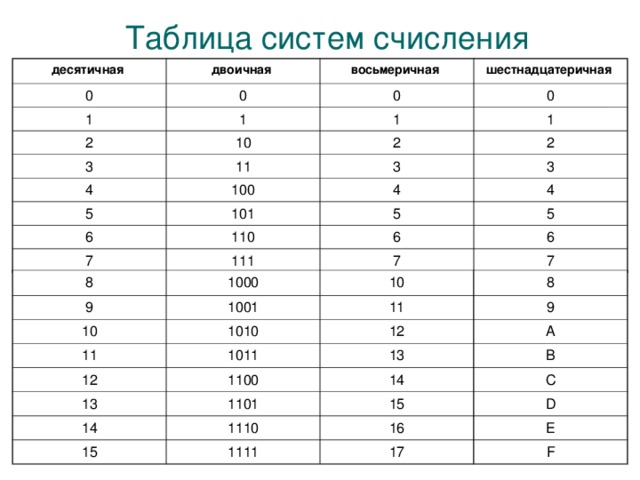
В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Двоично-восьмеричные и двоично-шестнадцатеричные преобразования
Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов.
Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Три разряда восьмеричной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.
Пример: Преобразовать число 1101110,01 2 в восьмеричную систему счисления.
Объединяем двоичные цифры в триады справа налево. Получаем
001 101 110,010 2 = 156,2 8 .
Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:
156,2 8 = 001 101 110,010 2 .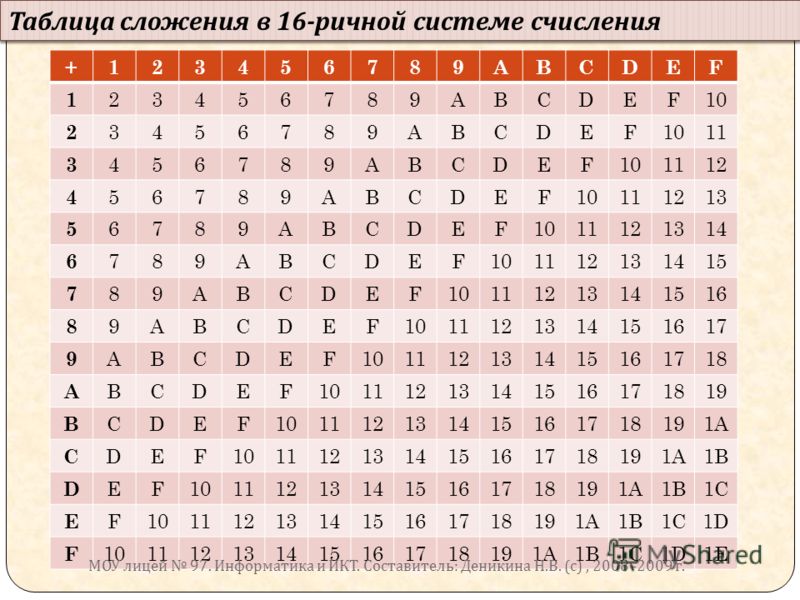
Четыре разряда шестнадцатеричной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.
Пример: Преобразовать число 1101110,11 2 в шестнадцатеричную систему счисления.
Объединяем двоичные цифры в тетрады справа налево. Получаем
0110 1110,1100 2 = 6E,C 16 .
Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом.
Шестнадцатеричная запись («Hex») — удобный способ представления двоичных значений.
Так же, как десятичная система счисления имеет основание десять, а двоичная — два, шестнадцатеричная система имеет основание шестнадцать.
Система счисления с основанием 16 использует числа от 0 до 9 и буквы от A до F. Рисунок показывает эквивалентные десятичные, двоичные и шестнадцатеричные значения для двоичных чисел от 0000 до 1111. Для нас легче выражать значение в виде одной шестнадцатеричной цифры, чем в виде четырех битов.
Понимание Байтов
Учитывая, что 8 битов (байт) являются стандартной двоичной группировкой, двоичные числа от 00000000 до 11111111 могут быть представлены в шестнадцатеричной записи как числа от 00 до FF. Начальные нули всегда отображаются, чтобы завершить 8-разрядное представление. Например, двоичное значение 0000 1010 в шестнадцатеричном виде будет 0A.
Представление Шестнадцатеричных Значений
Отметьте: Важно отличать шестнадцатеричные значения от десятичных значений для символов от 0 до 9, как показано на рисунке.
Шестнадцатеричные значения обычно представляются в тексте значением, которому предшествует 0x (например 0x73), или с помощью нижнего индекса 16.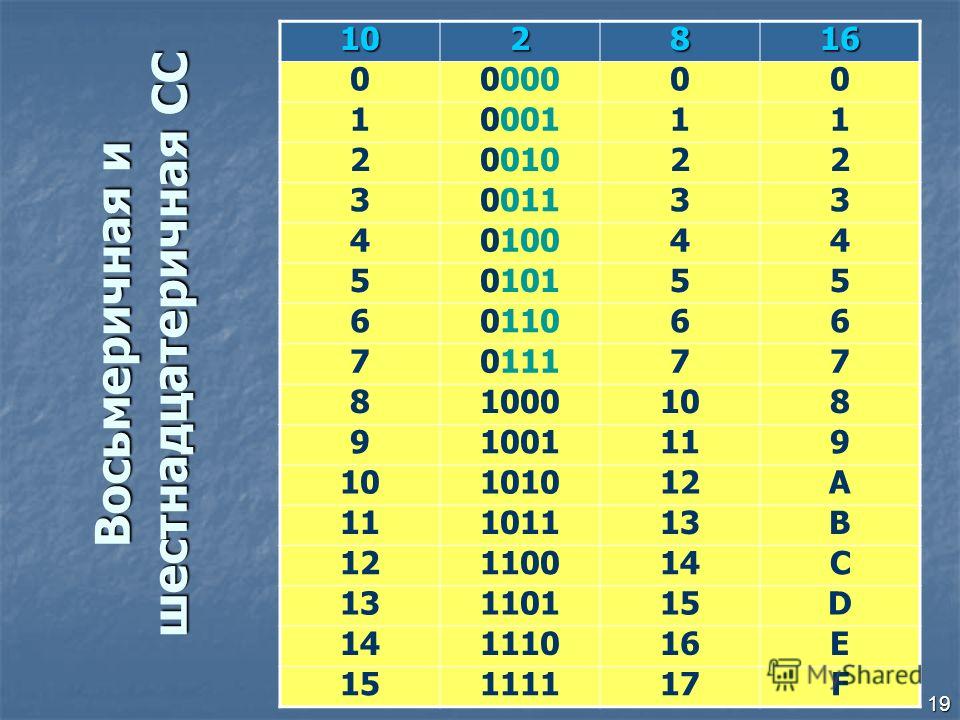
Реже, они могут сопровождаться буквой H, например 73H. Однако, поскольку текст нижнего индекса не распознается ни в командной строке, ни в средах программирования, в техническом представлении шестнадцатеричных чисел им предшествует «0x» (нуль X). Поэтому, примеры выше были бы показаны в виде 0x0A и 0x73 соответственно.
Шестнадцатеричная запись используется, чтобы представлять MAC-адреса Ethernet и адреса IP Версии 6.
Шестнадцатеричные Преобразования
Преобразования чисел между десятичными и шестнадцатеричными значениями являются простыми, но быстрое деление или умножение на 16 не всегда удобно. Если такие преобразования необходимы, обычно легче преобразовать десятичное или шестнадцатеричное значение в двоичное, а затем преобразовать двоичное значение в десятичное или шестнадцатеричное, в зависимости от того, что требуется получить.
С практикой возможно распознать двоичные шаблоны битов, которые соответствуют десятичным и шестнадцатеричным значениям. Рисунок показывает эти шаблоны для некоторых 8-разрядных значений.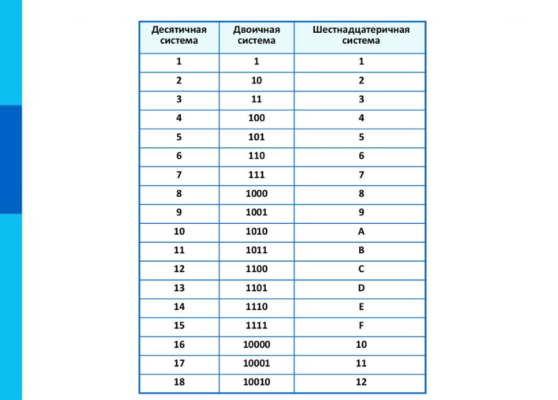
Шестнадцатеричная система счисления. аша первая программа.
Для написания программ на Ассемблере, необходимо разобраться с шестнадцатеричной системой счисления. Ничего сложного в ней нет. Мы используем в жизни десятичную систему. Уверен, что вы все ее знаете, поэтому я постараюсь объяснить шестнадцатеричную систему, проводя аналогию с десятичной.
Итак, в десятичной системе если мы к какому-нибудь числу справа добавим нуль, то это число увеличится в 10 раз. Например: 1 х 10 = 10; 10 х 10 = 100; 100 х 10 = 1000 и т.д. В этой системе мы используем цифры от 0 до 9, т.е. десять разных цифр (собственно, поэтому она и называется десятичная).
В
шестнадцатеричной системе мы
используем, соответственно,
шестнадцать «цифр». Я специально
написал слово «цифр» в кавычках,
т.к. в ней используются не только
цифры. Да и в самом деле как так?
Объясняю: от 0 до 9 мы считаем так же,
как и в десятичной, а вот дальше
будет так: A, B, C, D, E, F. Число F, как не
трудно
посчитать,
будет равно 15 в десятичной системе
(см.
Десятичное число | Шестнадцатеричное число |
Таблица 1. Десятичная и шестнадцатеричная системы.
Т.о., если мы к какому-нибудь числу в шестнадцатеричной системе добавим справа нуль, то это число увеличится в 16 раз.
Пример 1: 1 х 16 = 10; 10 х 16 = 100; 100 х 16 = 1000 и т.д.
Вы смогли
отличить в Примере 1
шестнадцатеричные числа от
десятичных? А из этого ряда: 10, 12, 45,
64, 12, 8, 19? Это могут быть как
шестнадцатеричные, так и
десятичные. Для того, чтобы не было
путаницы, и компьютер смог бы
однозначно отличить одни числа от
других, в Ассемблере принято после
шестнадцатеричного числа ставить
символ h или H (H это
сокращение от англ.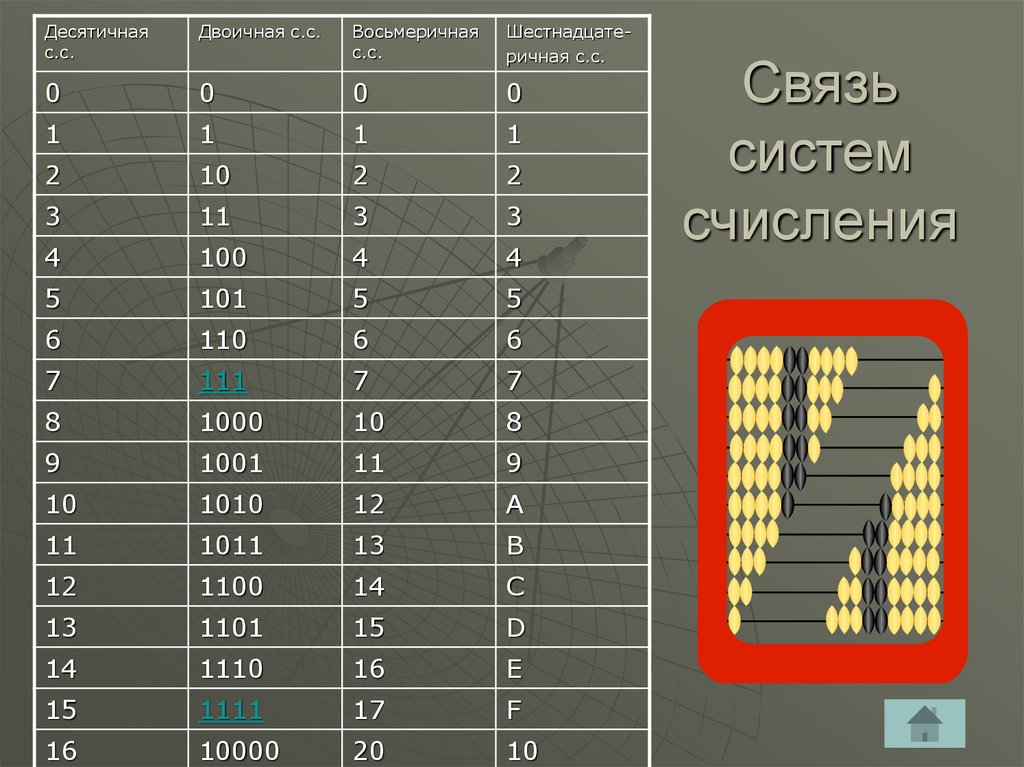
hexadecimal (шестнадцатеричное).
Для краткости его иногда называют
просто Hex )
Т.о. Пример 1 (см. выше) правильнее будет записать так: 1 х 16 = 10h; 10h x 16 = 100h; 100h x 16 = 1000h. Либо так: 1h x 10h = 10h; 10h x 10h = 100h; 100h x 10h = 1000h.
Для чего нужна шестнадцатеричная система, мы рассмотрим в последующих выпусках. А в данный момент для нашего примера программы, который будет рассмотрен ниже, нам необходимо знать о существовании шестнадцатеричных чисел.
Итак, подведем
итог. Шестнадцатеричная система
счисления состоит из 10 цифр (от 0 до
9) и 6 букв латинского алфавита (A, B, C,
D, E, F). Если к какому-нибудь числу в
шестнадцатеричной системе добавим
справа нуль, то это число
увеличится в 16 раз. Очень важно
уяснить данную тему , так как мы
будем постоянно использовать ее
при написании программ.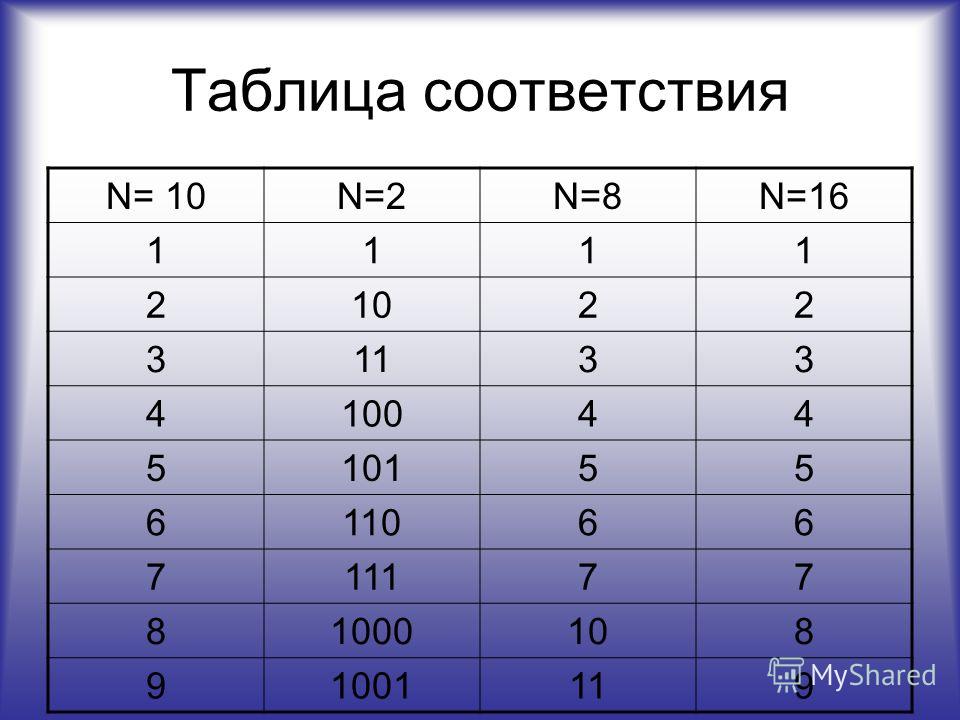
Теперь немного о том, как я буду строить примеры на Ассемблере. Не совсем удобно приводить их в HTML-формате, поэтому сперва будет сам код программы с пронумерованными строчками, а сразу же после него объяснения и примечания.
Примерно так:
| строк | Код программы |
| (1) | mov ah,9 |
Объяснения:
В строке (1) мы делаем то-то, а в строке (15) то-то.
Огромная просьба: НЕ копируйте программы со страницы в буфер, а затем не вставляйте их в Блокнот (или еще куда-нибудь)! Перепечатывайте их вручную в текстовом редакторе. Если есть принтер, то выделите программу, распечатайте выделенный фрагмент, а затем перебейте в редактор с бумаги. Все примеры нужно набирать самостоятельно! Это ускорит запоминание операторов.
И еще. Строчные и
ПРОПИСНЫЕ буквы в Ассемблере не
различаются.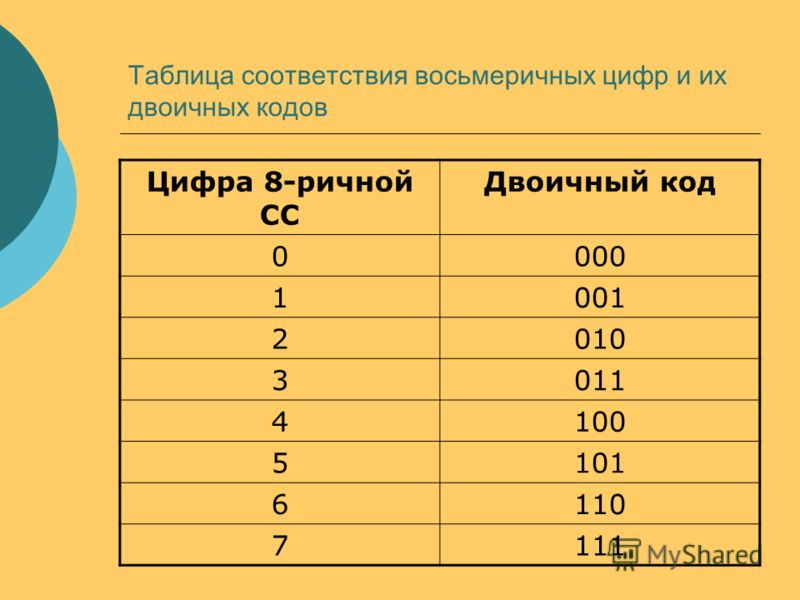
Записи вида:
Ассемблером воспринимаются одинаково. Можно, конечно, заставить Ассемблер различать строчные и ПРОПИСНЫЕ символы, но мы пока этого делать не будем. Для удобства чтения программы лучше всего операторы печатать строчными буквами, а названия подпрограмм и меток начинать с прописной. Но это как кому будет удобно.
Итак, переходим к нашей первой программе:
(1) CSEG segment
(2) org 100h
(4) Begin:
(6) mov ah,9
(7) mov dx,offset Message
(8) int 21h
(10) int 20h
(11)
(12) Message db «Hello, world!$»
(13) CSEG ends
(14) end Begin
Для того, чтобы объяснить все операторы данного примера, нам потребуется несколько выпусков. Поэтому описание некоторых команд мы просто опустим на данном этапе. Просто считайте, что так должно быть. В самое ближайшее время мы рассмотрим эти операторы подробно. Итак, строки с номерами (1), (2) и (13) вы просто игнорируете.
Строки (3), (5), (9) и
(11) остаются пустыми.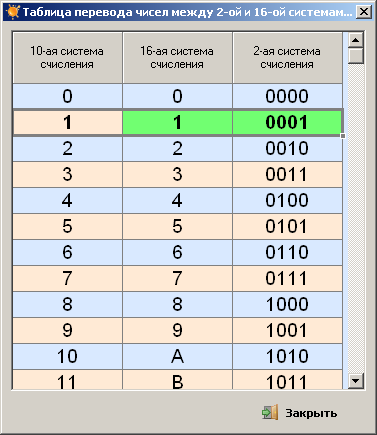
Это делается
для наглядности. Ассемблер их будет
просто опускать.
Теперь перейдем к рассмотрению остальных операторов. Со строки (4) начинается код программы. Это метка, указывающая Ассемблеру на начало кода. В строке (14) стоят операторы end Begin (Begin англ. начало; end конец). Это конец программы. Вообще вместо слова Begin можно было бы использовать что-нибудь другое. Например, Start:. В таком случае, нам пришлось бы и завершать программу End Start (14).
Строки (6) (8) выводят на экран сообщение Hello, world!. Здесь придется вкратце рассказать о регистрах процессора (более подробно эту тему мы рассмотрим в следующем выпуске).
Регистр процессора это специально отведенная память для хранения какого-нибудь числа.
Например:
Если мы хотим сложить два числа, то в математике запишем так:
A, B и
C это своего рода
регистры (если говорить о
компьютере), в которых могут
хранится некоторые данные. А=5 можно
прочитать как: Присваиваем А
число 5 .
Для присвоения регистру какого-нибудь значения, в Ассемблере существует оператор mov (от англ. move загрузить). Строку (6) следует читать так: Загружаем в регистр AH число 9 (проще говоря, присваиваем AH число 9). Ниже рассмотрим зачем это надо.
В строке (7) загружаем в регистр DX адрес сообщения для вывода (в данном примере это будет строка Hello, world!$ ).
Прерывания будут подробно рассматриваться в последующих выпусках. Здесь я скажу несколько слов.
Прерывание MS-DOS это своего рода подпрограмма (часть MS-DOS) , которая находится постоянно в памяти и может вызываться в любое время из любой программы.
Рассмотрим вышесказанное на примере (мелким шрифтом выделим примечания ):
Программа сложения двух чисел
НачалоПрограммы
A=5 в переменную A заносим значение 5
B=8 в переменную B значение 8
ВызовПодпрограммы Сложение
теперь С равно 13
A=10 тоже самое, только другие числа
B=25
ВызовПодпрограммы Сложение
теперь С равно 35
КонецПрограммы
Подпрограмма Сложение
C=A+B
ВозвратИзПодпрограммы возвращаемся в то место, откуда вызывали
КонецПодпрограммы
В данном примере
мы дважды вызвали подпрограмму Сложение ,
которая сложила два числа,
переданные ей в переменных
A и
B.
Результат помещается в переменную
С. Когда вызывается подпрограмма,
компьютер запоминает с какого
места она была вызвана, а затем,
когда закончила работу
подпрограмма, компьютер
возвращается в то место, откуда она
вызывалась. Т.о. можно вызывать
подпрограммы неопределенное
количество раз с любого места.
При выполнении
строки (8) программы на Ассемблере
мы вызываем подпрограмму (в данном
случае это называется прерывание),
которая выводит на экран строку.
Для этого мы, собственно, и помещаем
необходимые значения в регистры.
Всю необходимую работу (вывод
строки, перемещение курсора) берет
на себя подпрограмма. Эту строку
можно прочитать так: вызываем
двадцать первое прерывание (int от англ.
interrupt прерывание). Обратите
внимание, что после числа 21 стоит
буква
h. Это, как
мы уже знаем, шестнадцатеричное
число (33 в десятичной системе).
Конечно, нам ничего не мешает
заменить строку
int 21h на
int 33. Программа будет
работать корректно. Просто в
Ассемблере принято указывать номер
прерывания в шестнадцатеричной
системе.
В строке (10) мы, как вы уже догадались, вызываем прерывание 20 h. Для вызова данного прерывания не нужно указывать какие-либо значения в регистрах. Оно выполняет только одну задачу: выход из программы (выход в DOS). В результате выполнения прерывания 20h, программа вернется туда, откуда ее запускали (загружали, вызывали). Например, в Norton Commander или DOS Navigator.
Строка (12) содержит сообщение для вывода. Первое слово (message сообщение) название сообщения. Оно может быть любым (например, mess или string и пр.). Обратите внимание на строку (7), в которой мы загружаем в регистр DX адрес нашего сообщения.
Можно создать еще одну строку, которую назовем Mess2. Затем, начиная со строки (9) вставим следующие команды:
(10) mov dx,offset Mess2
(13) Message db «Hello, world!$»
(14) Mess2 db «Это Я! $»
и ассемблировать нашу программу заново. Надеюсь, что вы догадались, что произойдет
Обратите внимание
на последний символ в строках
Message
и
Mess2 — $.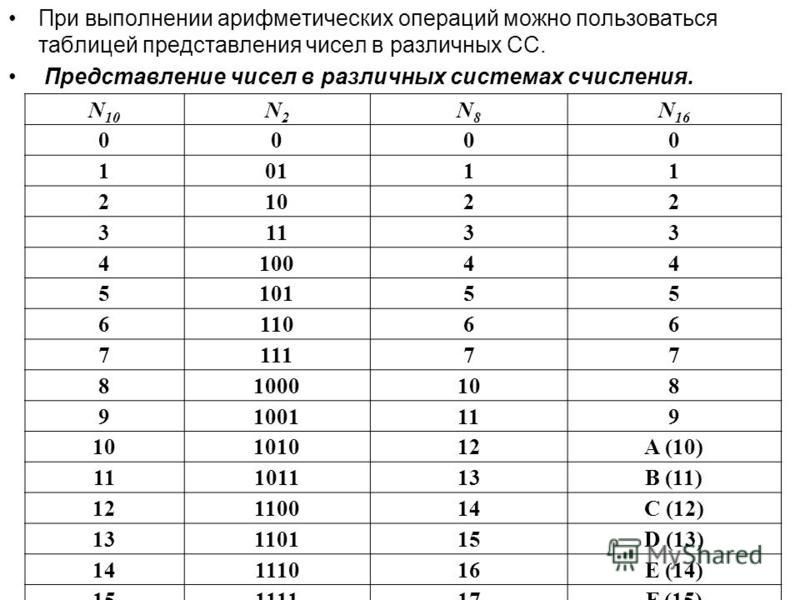
Он указывает на конец
строки. Если мы его уберем, то 21
h прерывание продолжит
вывод до тех пор, пока не встретится
где-нибудь в памяти символ
$. На экране мы увидим
мусор
.
Если у вас есть отладчик, то можно посмотреть как будет работать наша программа.
Целю настоящего выпуска не было разобраться подробно с каждым оператором . Это невозможно, т.к. у вас еще недостаточно знаний. Я полагаю, что уже через 3-4 выпуска вы поймете принцип и структуру программы на Ассемблере. Может быть, вам показался язык Ассемблера чрезвычайно сложным, но это, поверьте, с первого взгляда.
Теперь предстоит совсем легкая прогулка, связанная с шестнадцатеричной системой счисления. В этом случае, надеемся, вы подозреваете и, видимо, справедливо, что у нас должно теперь быть 16 различных цифр.
Но, как мы знаем, традиционных («арабских») цифр всего десять. А требуется шестнадцать. Получается, что не хватает шести знаков.
Замечание
Таким образом, возникает чисто дизайнерская задача по теме «Знаки» — придумать недостающие символы для цифр .
Значит, в свое время специалистам необходимо было придумать какие-нибудь новые знаки. Но когда-то, в начале компьютерной эры, особого выбора в знаках не было. Программисты располагали только знаками цифр и букв. Поэтому они пошли по элементарному пути: взяли первые буквы латинского алфавита в качестве цифр, тем более что исторически это не первый случай (мы уже упоминали, что первоначально вместо цифр многие народы использовали буквы).
Замечание
Надеемся, что всем понятно, почему в этом случае нельзя использовать, например, числа «10», «11», «12» и т. д.? Потому что, если мы говорим о шестнадцатеричной системе счисления, то должно быть шестнадцать цифр , а не чисел .
И десятичное число «10» стали обозначать латинской буквой «А» (точнее, «цифрой А»). Соответственно, дальше идут цифры «В», «С», «D», «Е» и «Р.
Поскольку мы намеревались построить шестнадцатеричную систему, то, начиная с нуля, здесь как раз и получится 16 цифр. Например, цифра «D» — это десятичное число «13», а цифра «F» — это десятичное число «15».
Когда к шестнадцатеричному числу «F» прибавляем единицу, то, поскольку эти цифры у нас кончились, в этом разряде ставим «О», а в следующий разряд переносим единицу, поэтому получается, что десятичное число «16» будет представлено в шестнадцатеричной системе счисления числом «10», т. е. получается «шестнадцатеричная десятка». Соединим десятичные и шестнадцатеричные числа в единую таблицу (табл. 4.5).
Таблица 4.5 . Соответствие десятичных и шестнадцатеричных чисел.
| Десятичное число | Шестнадцатеричное число | Десятичное число | Шестнадцатеричное число |
|---|---|---|---|
| 0-9 | 0-9 | 29 | 1D |
| 10 | А | 30 | 1Е |
| 11 | В | 31 | 1F |
| 12 | С | 32-41 | 20-29 |
| 13 | D | 42-47 | 2A-2F |
| 14 | Е | 48-255 | 30-FF |
| 15 | F | 256 | 100 |
| 16 | 10 | 512 | 200 |
| 17-25 | 11-19 | 1024 | 400 |
| 26 | 1А | 1280 | 500 |
| 27 | 1В | 4096 | 1000 |
| 28 | 1C |
Шестнадцатеричная система используется, чтобы более компактно записывать двоичную информацию.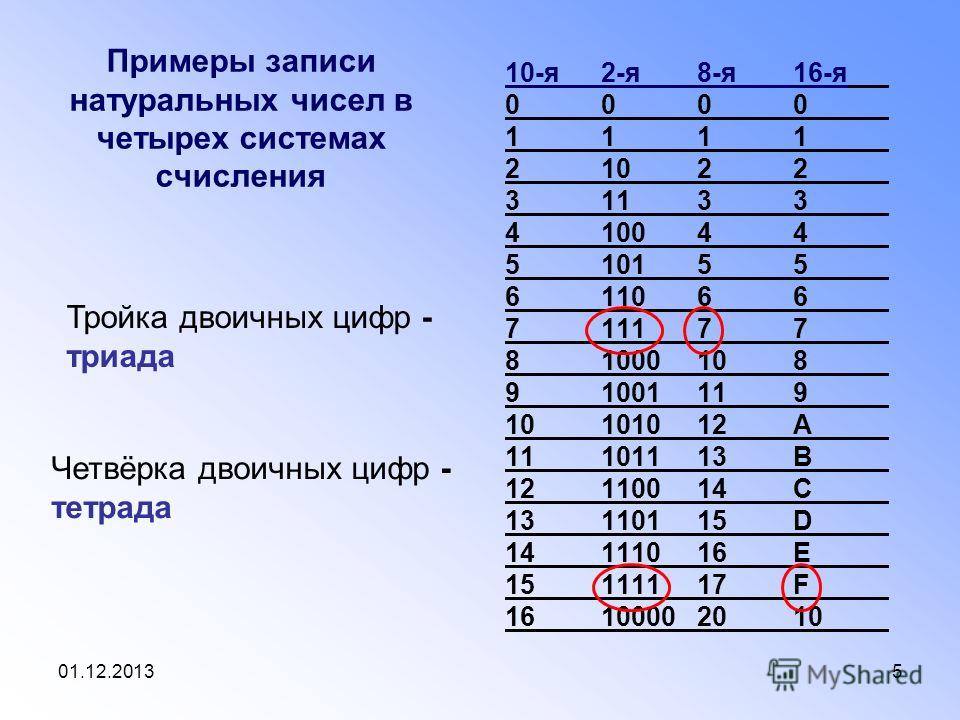
В самом деле, «шестнадцатеричная тысяча», состоящая из четырех разрядов, в двоичном виде занимает тринадцать разрядов (1000 16 = 1000000000000 2).
При обсуждении систем счисления неоднократно фигурировали «десятки», «сотни» и «тысячи», поэтому необходимо обратить внимание на так называемые «круглые» числа.
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
- * A —10;
- * B —11;
- * C —12;
- * D —13;
- * E — 14;
- * F — 15.
Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код , можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
Математический способ записи .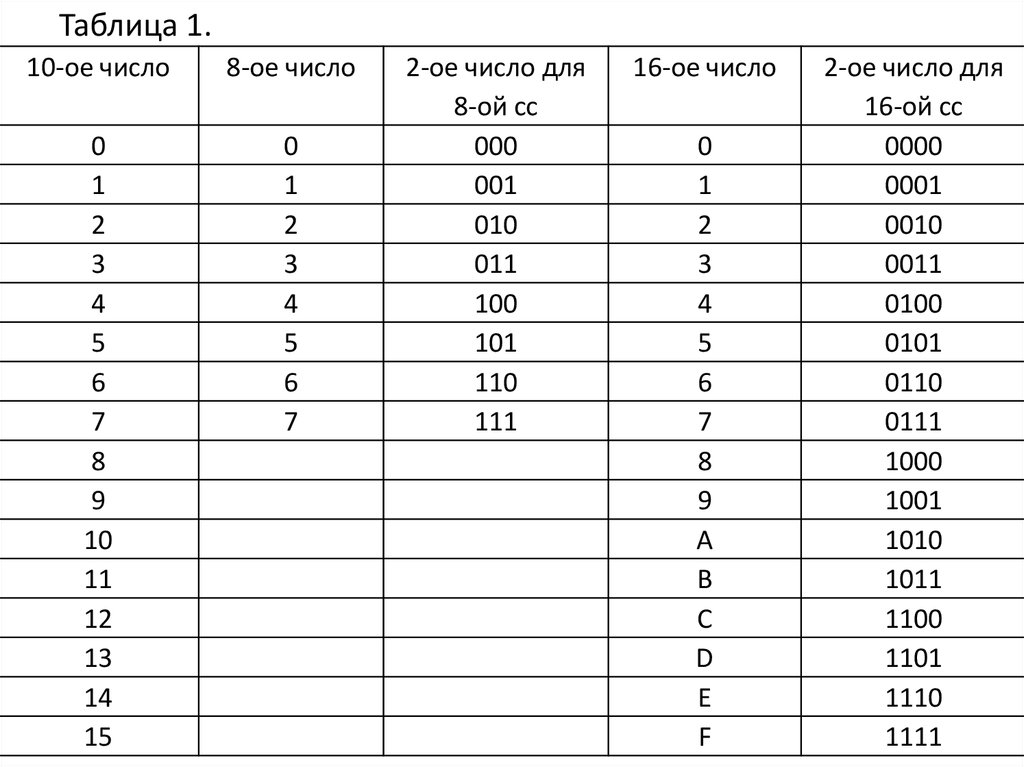
В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .
В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;
* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Двоичная СС | шестнадцатеричная СС |
Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры.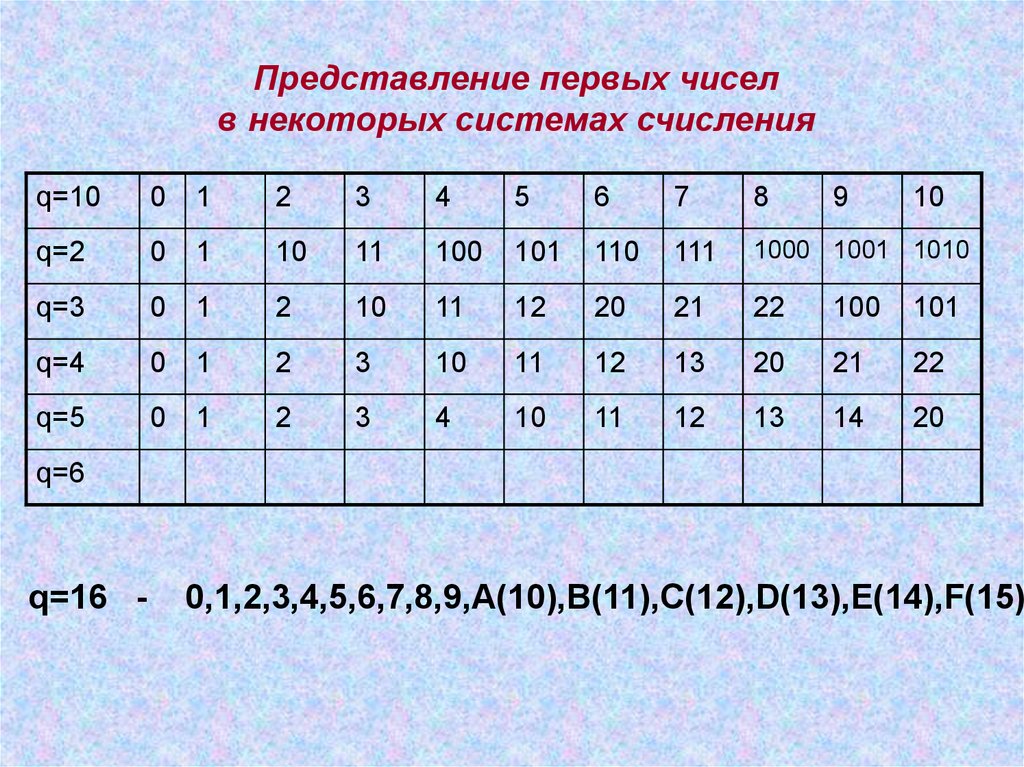
Используя правило, запишем его в виде суммы степеней с основанием 16:
A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10
Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.
Таблица тетрад для перевода.
Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.
Двоичная СС | Восьмеричная СС |
Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2
Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16
В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.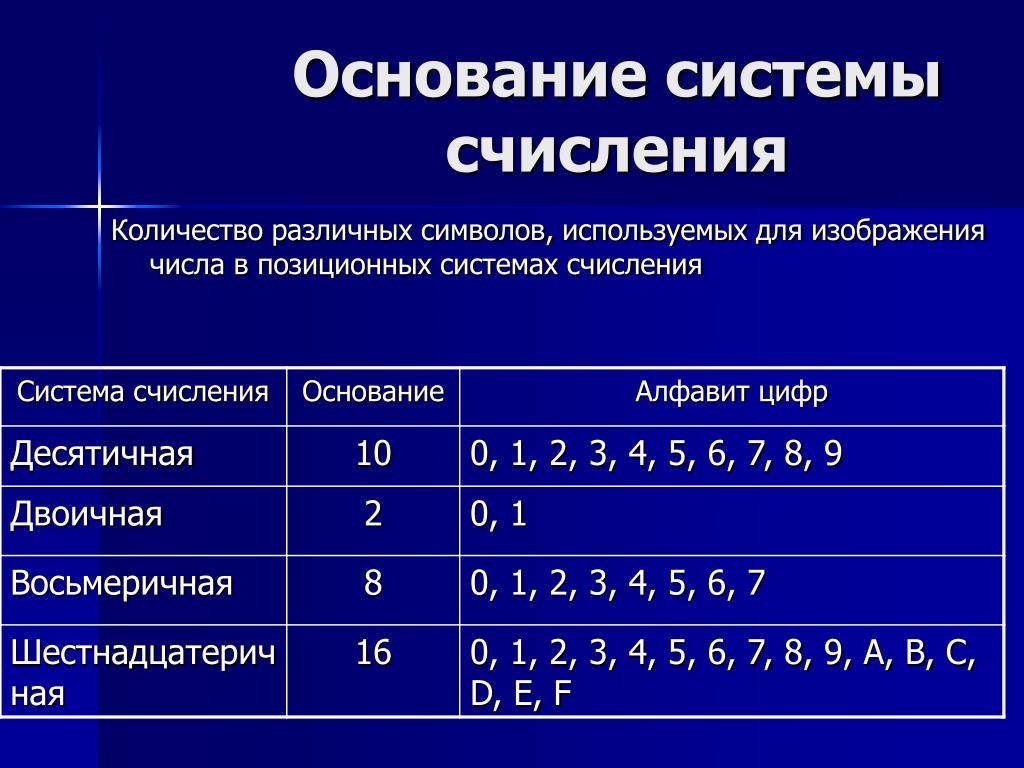
Автоматический перевод . Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (см. меню слева: Hex, Dec, Oct, Bin). При этом изменение текущей системы счисления автоматически производит перевод.
sistemschisleniya | Just another WordPress.com site
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Перевод чисел из шестнадцатеричной системы в десятичнуюДля перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.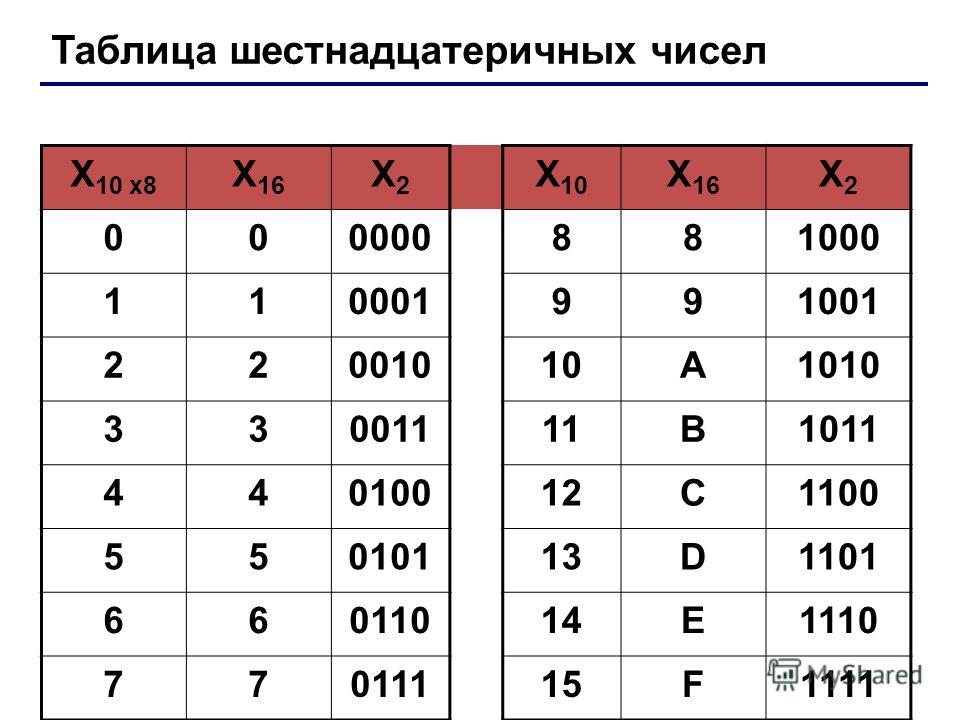
Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316 = 3·160+10·161+5·162
= 3·1+10·16+5·256 = 3+160+1280 = 144310
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например: 0101101000112 = 0101 1010 0011 = 5A316
Десяти́чная система счисления — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4,5, 6, 7, 8, 9, 0 (ноль), называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.
Десятичная непозиционная система счисления с единичным кодированием десятичных цифр возникла во второй половине третьего тысячелетия до н. э. в древнем Египте. В другой великой цивилизации — вавилонской— за две тысячи лет до н. э. внутри шестидесятеричных разрядов использовалась позиционная десятичная система счисления с единичным кодированием десятичных цифр.
Древнейшая известная запись позиционной десятичной системы обнаружена в Индии в 595 г. Нуль в то время применялся не только в Индии, но и в Китае. В этих старинных системах для записи одинакового числа использовались символы, рядом с которыми дополнительно помечали, в каком разряде они стоят. Потом перестали помечать разряды, но число всё равно можно прочитать, так как у каждого разряда есть своя позиция. А если позиция пустая, её нужно пометить нулём. В поздних вавилонских текстах такой знак стал появляться, но в конце числа его не ставили. Лишь в Индии нуль окончательно занял своё место, эта запись распространилась затем по всему миру.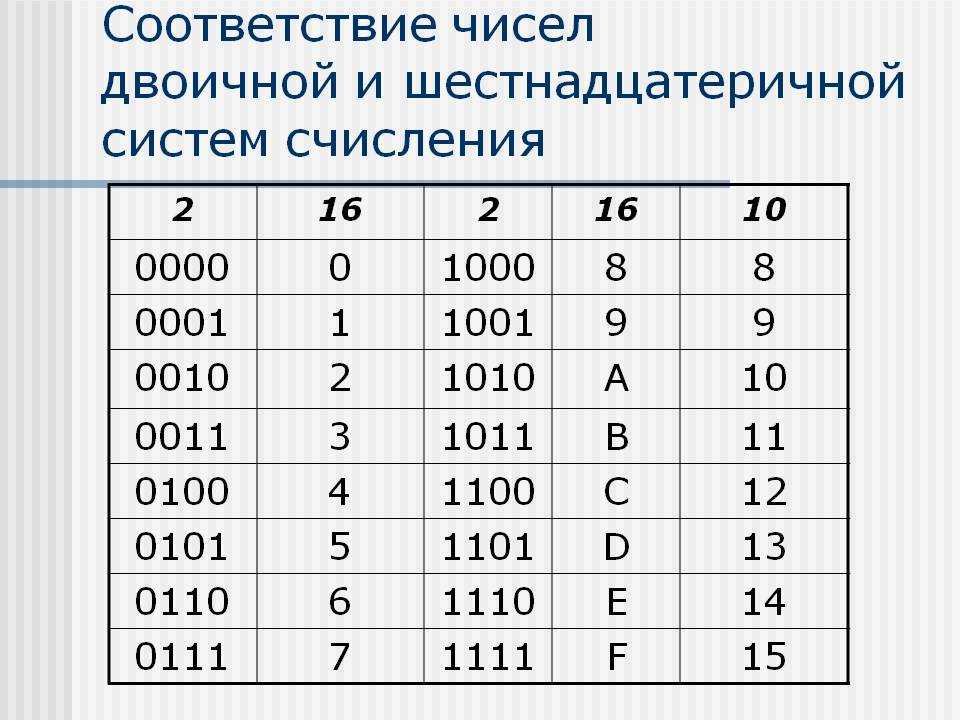
Индийская нумерация пришла сначала в арабские страны, затем и в Западную Европу. О ней рассказал среднеазиатский математик аль-Хорезми. Простые и удобные правила сложения и вычитания чисел, записанных в позиционной системе, сделали её особенно популярной. А поскольку труд аль-Хорезми был написан на арабском, то за индийской нумерацией в Европе закрепилось неправильное название — «арабская» (арабские цифры).
Восьмери́чная систе́ма счисле́ния — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры 0 до 7.
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Таблица перевода чисел
Tech Stuff — Hexadecimal, Decimal and Binary
Основной единицей, используемой в компьютерном мире, является байт (также известный как октет), байт (или октет) состоит из 8 битов (также известных как двоичные цифры).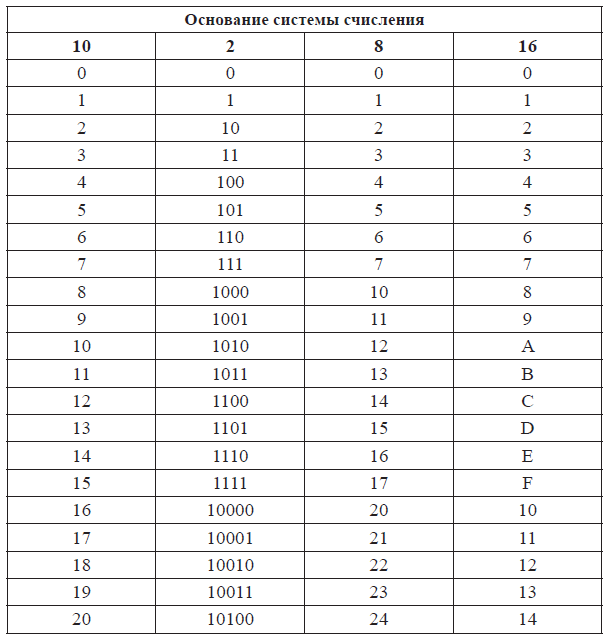
Большинство современных систем используют кратные байты, таким образом, 16-битная система состоит из 2 байтов (2 x 8 = 16), 32-битная система состоит из 4 байтов (4 x 8 = 32), а 64-битная система состоит из 2 байтов (4 x 8 = 32). имеет 8 байт (8 x 8 = 64). Термин слово , как и в описании 32-битное слово, в значительной степени исчез из технического лексикона.
Содержимое любого байта, например, в ячейке памяти или в сети, может быть выражено во многих системах нумерации . Наиболее часто используемые системы нумерации: Десятичная , Шестнадцатеричная и Двоичная :
| Система нумерации | База | Диапазон | Примечания |
| Десятичный | основание 10 | 0 — 1,2,3… | Самая распространенная система счисления — долларовая, метрическая и т.д. Байт (8 бит) имеет 256 возможных значений в диапазоне 0 — 255 |
| Двоичный | база 2 | 0 — 1 | Базовый уровень, на котором работает электронная схема компьютера — один бит. |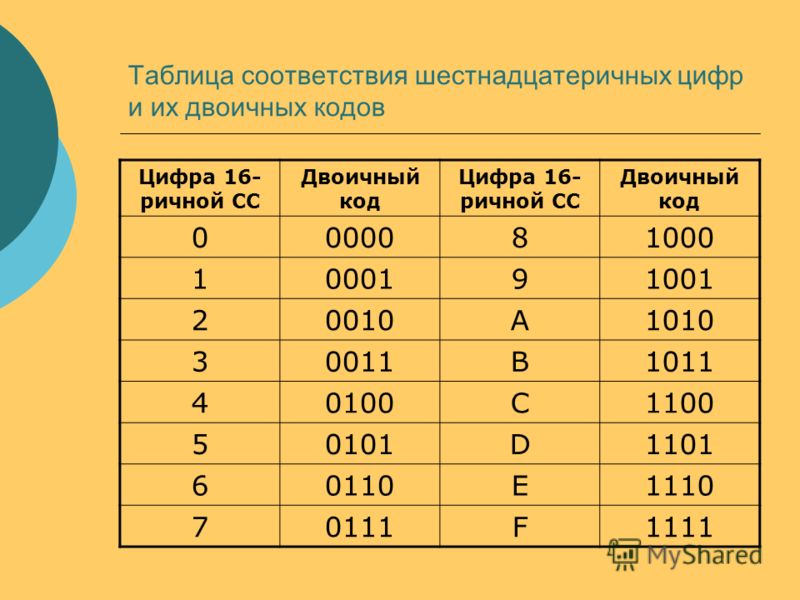
| Шестнадцатеричный | база 16 | 0-9, А-Ф | Каждый шестнадцатеричный символ представляет 4 бита (0 — 15 десятичных), которые называются полубайтом (маленький байт — честно!). Байт (или октет) состоит из 8 бит, поэтому он всегда представлен двумя шестнадцатеричными символами в диапазоне от 00 до FF. |
Историческая справка: Когда-то, когда мир и даже автор этой страницы были молоды, компьютеры были построены с 12-битными, 24-битными и даже 36-битными словами (в этом был какой-то смысл тогда просто выглядит странно сегодня). Каждый из этих размеров слова делится на 3 и использует восьмеричную систему счисления (с основанием 8). Каждый 3-битный элемент содержит 8 значений в диапазоне от 0 до 7. Таким образом, ячейка памяти с 12-битным двоичным значением 000.001.100.111 будет записана в восьмеричной форме как 0147.
Нумерация битов
При работе с двоичными данными каждый бит внутри байта (октета) может потребоваться идентифицировать с помощью метода, называемого нумерацией битов.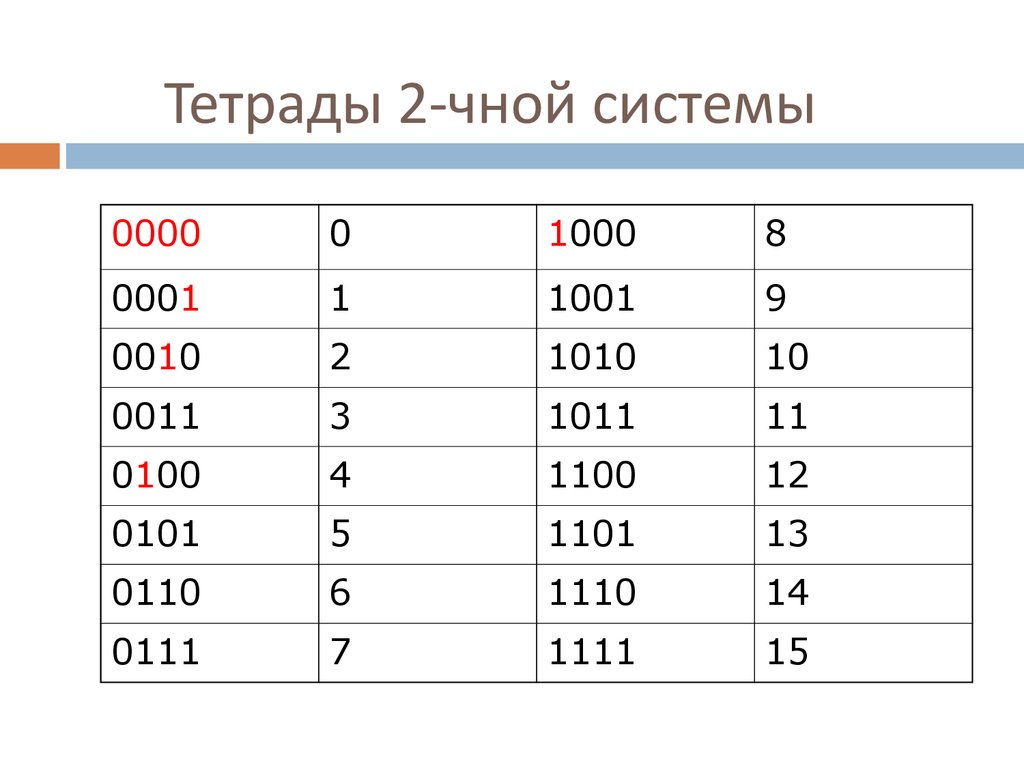
Нумерация битов может быть очень запутанной, поскольку различные стандартные органы принимают разные соглашения. Ниже приведены все допустимые и используемые соглашения о нумерации битов для описания 8-битного байта (октета).
| Содержимое памяти | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Правила нумерации битов | ||||||||
| Слева направо основание 0 (IETF) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Основание слева направо 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Справа налево основание 1 (ITU) | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Степень числа 2 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
Всегда проверяйте, какое соглашение используется в любой спецификации.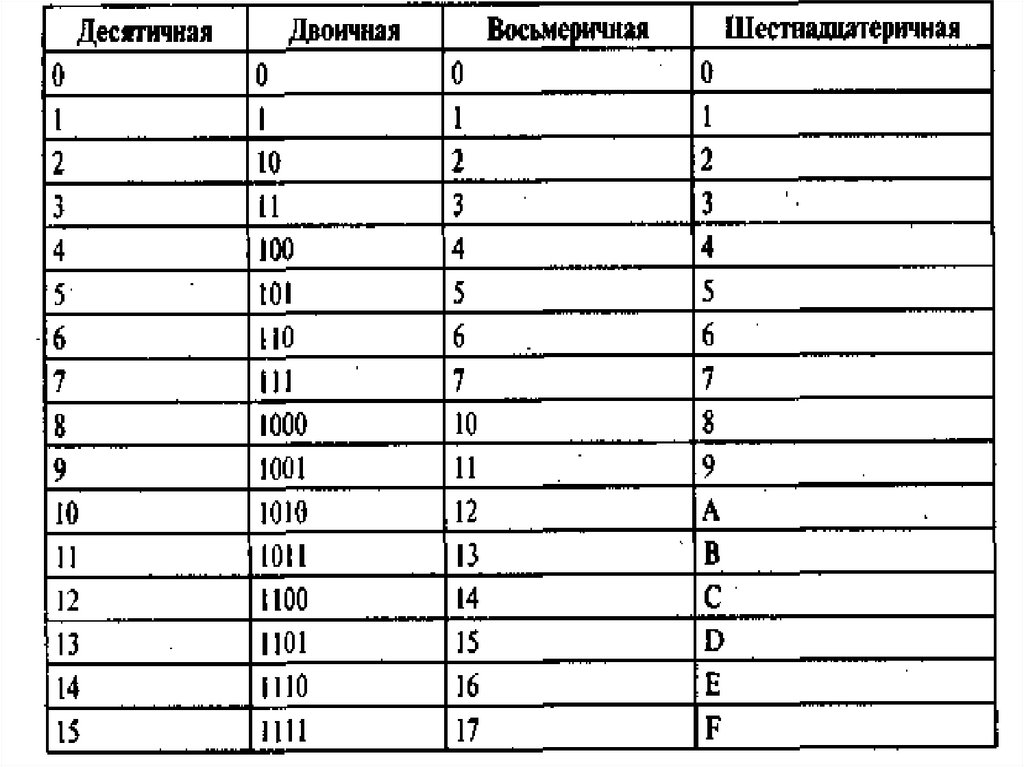
Мы смирились с неизбежным и используем стандарт слева направо с основанием 0 (IETF) , поскольку благодаря Интернету он широко используется и, надеюсь, столь же широко понятен. Обоснование IETF для этого стандарта заключается в том, что он также однозначно представляет то, что называется сетевым порядком , то есть бит 0 идет в сеть первым, бит 1 вторым и так далее. Биты также имеют тенденцию выходить из сети в том же порядке, в котором они были отправлены. Использование сетевого порядка необходимо, поскольку внутреннее (машинное) представление данных может сильно различаться (вся эта ерунда с обратным порядком байтов и прямым порядком байтов), но когда данные загружаются в сеть, они должны быть в согласованном порядке, который может быть использован любая система, независимо от ее внутреннего представления, которая хочет использовать данные.
Наконец, при работе с двоичными файлами вы часто будете сталкиваться с терминами «старший значащий бит» (MSB) и «наименее значащий бит» (LSB).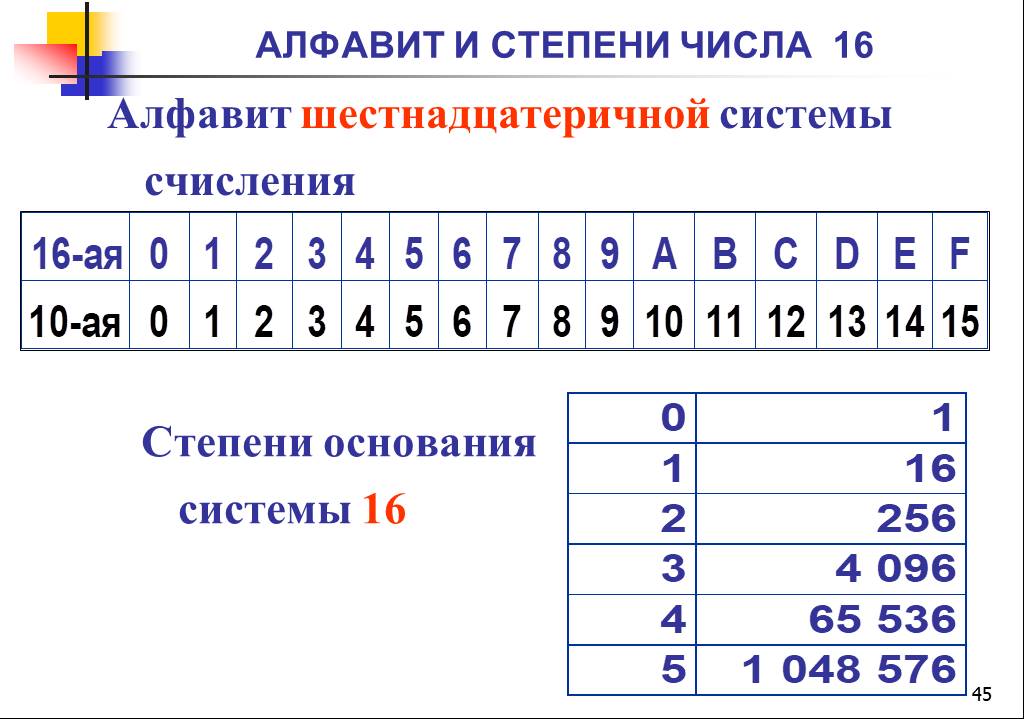
MSB всегда находится СЛЕВА, а LSB — СПРАВА. Таким образом, при использовании нумерации битов IETF старший бит — это бит 0, а младший бит — бит 7, тогда как при использовании нумерации битов ITU старший бит — это бит 8, а младший бит — бит 1. Совершенно ясно, верно?
8-битный байт (октет) Таблица преобразования:
Преобразование IPv4 из десятичного числа в шестнадцатеричное
| Десятичное число | Шестнадцатеричный | Двоичный | Десятичный | Шестнадцатеричный | Двоичный |
| 0 | 00 | 0000 0000 | 128 | 80 | 1000 0000 |
| 1 | 01 | 0000 0001 | 129 | 81 | 1000 0001 |
| 2 | 02 | 0000 0010 | 130 | 82 | 1000 0010 |
| 3 | 03 | 0000 0011 | 131 | 83 | 1000 0011 |
| 4 | 04 | 0000 0100 | 132 | 84 | 1000 0100 |
| 5 | 05 | 0000 0101 | 133 | 85 | 1000 0101 |
| 6 | 06 | 0000 0110 | 134 | 86 | 1000 0110 |
| 7 | 07 | 0000 0111 | 135 | 87 | 1000 0111 |
| 8 | 08 | 0000 1000 | 136 | 88 | 1000 1000 |
| 9 | 09 | 0000 1001 | 137 | 89 | 1000 1001 |
| 10 | 0А | 0000 1010 | 138 | 8А | 1000 1010 |
| 11 | 0Б | 0000 1011 | 139 | 8Б | 1000 1011 |
| 12 | 0С | 0000 1100 | 140 | 8С | 1000 1100 |
| 13 | 0Д | 0000 1101 | 141 | 8Д | 1000 1101 |
| 14 | 0Е | 0000 1110 | 142 | 8Е | 1000 1110 |
| 15 | 0Ф | 0000 1111 | 143 | 8Ф | 1000 1111 |
| 16 | 10 | 0001 0000 | 144 | 90 | 1001 0000 |
| 17 | 11 | 0001 0001 | 145 | 91 | 1001 0001 |
| 18 | 12 | 0001 0010 | 146 | 92 | 1001 0010 |
| 19 | 13 | 0001 0011 | 147 | 93 | 1001 0011 |
| 20 | 14 | 0001 0100 | 148 | 94 | 1001 0100 |
| 21 | 15 | 0001 0101 | 149 | 95 | 1001 0101 |
| 22 | 16 | 0001 0110 | 150 | 96 | 1001 0110 |
| 23 | 17 | 0001 0111 | 151 | 97 | 1001 0111 |
| 24 | 18 | 0001 1000 | 152 | 98 | 1001 1000 |
| 25 | 19 | 0001 1001 | 153 | 99 | 1001 1001 |
| 26 | 1А | 0001 1010 | 154 | 9А | 1001 1010 |
| 27 | 1Б | 0001 1011 | 155 | 9Б | 1001 1011 |
| 28 | 1С | 0001 1100 | 156 | 9С | 1001 1100 |
| 29 | 1Д | 0001 1101 | 157 | 9Д | 1001 1101 |
| 30 | 1Е | 0001 1110 | 158 | 9Е | 1001 1110 |
| 31 | 1F | 0001 1111 | 159 | 9Ф | 1001 1111 |
| 32 | 20 | 0010 0000 | 160 | А0 | 1010 0000 |
| 33 | 21 | 0010 0001 | 161 | А1 | 1010 0001 |
| 34 | 22 | 0010 0010 | 162 | А2 | 1010 0010 |
| 35 | 23 | 0010 0011 | 163 | А3 | 1010 0011 |
| 36 | 24 | 0010 0100 | 164 | А4 | 1010 0100 |
| 37 | 25 | 0010 0101 | 165 | А5 | 1010 0101 |
| 38 | 26 | 0010 0110 | 166 | А6 | 1010 0110 |
| 39 | 27 | 0010 0111 | 167 | А7 | 1010 0111 |
| 40 | 28 | 0010 1000 | 168 | А8 | 1010 1000 |
| 41 | 29 | 0010 1001 | 169 | А9 | 1010 1001 |
| 42 | 2А | 0010 1010 | 170 | АА | 1010 1010 |
| 43 | 2Б | 0010 1011 | 171 | АБ | 1010 1011 |
| 44 | 2С | 0010 1100 | 172 | АС | 1010 1100 |
| 45 | 2D | 0010 1101 | 173 | н. э. | 1010 1101 |
| 46 | 2Е | 0010 1110 | 174 | АЕ | 1010 1110 |
| 47 | 2F | 0010 1111 | 175 | АФ | 1010 1111 |
| 48 | 30 | 0011 0000 | 176 | В0 | 1011 0000 |
| 49 | 31 | 0011 0001 | 177 | В1 | 1011 0001 |
| 50 | 32 | 0011 0010 | 178 | В2 | 1011 0010 |
| 51 | 33 | 0011 0011 | 179 | В3 | 1011 0011 |
| 52 | 34 | 0011 0100 | 180 | В4 | 1011 0100 |
| 53 | 35 | 0011 0101 | 181 | В5 | 1011 0101 |
| 54 | 36 | 0011 0110 | 182 | В6 | 1011 0110 |
| 55 | 37 | 0011 0111 | 183 | В7 | 1011 0111 |
| 56 | 38 | 0011 1000 | 184 | В8 | 1011 1000 |
| 57 | 39 | 0011 1001 | 185 | В9 | 1011 1001 |
| 58 | 3А | 0011 1010 | 186 | БА | 1011 1010 |
| 59 | 3Б | 0011 1011 | 187 | ББ | 1011 1011 |
| 60 | 3С | 0011 1100 | 188 | до н.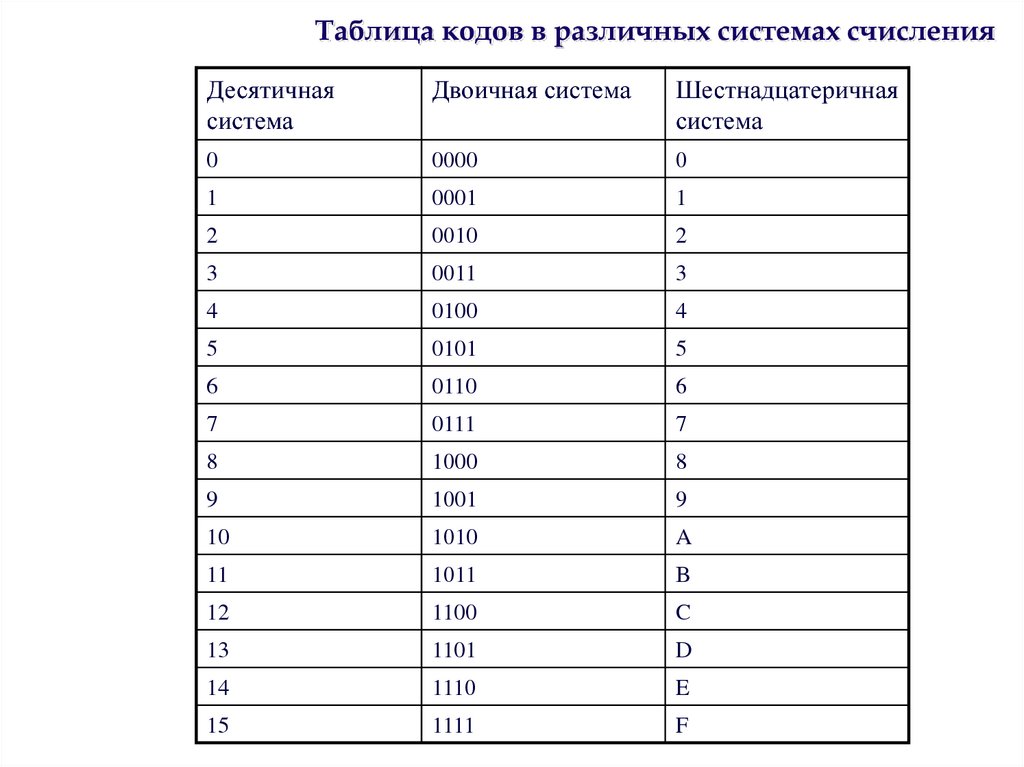 э. | 1011 1100 |
| 61 | 3D | 0011 1101 | 189 | БД | 1011 1101 |
| 62 | 3Е | 0011 1110 | 190 | БЭ | 1011 1110 |
| 63 | 3F | 0011 1111 | 191 | БФ | 1011 1111 |
| 64 | 40 | 0100 0000 | 192 | С0 | 1100 0000 |
| 65 | 41 | 0100 0001 | 193 | С1 | 1100 0001 |
| 66 | 42 | 0100 0010 | 194 | С2 | 1100 0010 |
| 67 | 43 | 0100 0011 | 195 | С3 | 1100 0011 |
| 68 | 44 | 0100 0100 | 196 | С4 | 1100 0100 |
| 69 | 45 | 0100 0101 | 197 | С5 | 1100 0101 |
| 70 | 46 | 0100 0110 | 198 | С6 | 1100 0110 |
| 71 | 47 | 1100 0111 | 199 | С7 | 1100 0111 |
| 72 | 48 | 0100 1000 | 200 | С8 | 1100 1000 |
| 73 | 49 | 0100 1001 | 201 | С9 | 1100 1001 |
| 74 | 4А | 0100 1010 | 202 | СА | 1100 1010 |
| 75 | 4Б | 0100 1011 | 203 | КБ | 1100 1011 |
| 76 | 4С | 0100 1100 | 204 | СС | 1100 1100 |
| 77 | 4Д | 0100 1101 | 205 | CD | 1100 1101 |
| 78 | 4Е | 0100 1110 | 206 | СЕ | 1100 1110 |
| 79 | 4F | 1100 1111 | 207 | КФ | 1100 1111 |
| 80 | 50 | 0101 0000 | 208 | Д0 | 1101 0000 |
| 81 | 51 | 0101 0001 | 209 | Д1 | 1101 0001 |
| 82 | 52 | 0101 0010 | 210 | Д2 | 1101 0010 |
| 83 | 53 | 0101 0011 | 211 | Д3 | 1101 0011 |
| 84 | 54 | 0101 0100 | 212 | Д4 | 1101 0100 |
| 85 | 55 | 0101 0101 | 213 | Д5 | 1101 0101 |
| 86 | 56 | 0101 0110 | 214 | Д6 | 1101 0110 |
| 87 | 57 | 1101 0111 | 215 | Д7 | 1101 0111 |
| 88 | 58 | 0101 1000 | 216 | Д8 | 1101 1000 |
| 89 | 59 | 0101 1001 | 217 | Д9 | 1101 1001 |
| 90 | 5А | 0101 1010 | 218 | DA | 1101 1010 |
| 91 | 5Б | 0100 1011 | 219 | ДБ | 1101 1011 |
| 92 | 5С | 0101 1100 | 220 | DC | 1101 1100 |
| 93 | 5Д | 0101 1101 | 221 | ДД | 1101 1101 |
| 94 | 5Е | 0101 1110 | 222 | ДЭ | 1101 1110 |
| 95 | 5F | 1101 1111 | 223 | ДФ | 1101 1111 |
| 96 | 60 | 0110 0000 | 224 | Э0 | 1110 0000 |
| 97 | 61 | 0110 0001 | 225 | Е1 | 1110 0001 |
| 98 | 62 | 0110 0010 | 226 | Е2 | 1110 0010 |
| 99 | 63 | 0110 0011 | 227 | Е3 | 1110 0011 |
| 100 | 64 | 0110 0100 | 228 | Е4 | 1110 0100 |
| 101 | 65 | 0110 0101 | 229 | Е5 | 1110 0101 |
| 102 | 66 | 0110 0110 | 230 | Е6 | 1110 0110 |
| 103 | 67 | 1110 0111 | 231 | Е7 | 1110 0111 |
| 104 | 68 | 0110 1000 | 232 | Е8 | 1110 1000 |
| 105 | 69 | 0110 1001 | 233 | Е9 | 1110 1001 |
| 106 | 6А | 0110 1010 | 234 | ЕА | 1110 1010 |
| 107 | 6Б | 0110 1011 | 235 | ЭБ | 1110 1011 |
| 108 | 6С | 0110 1100 | 236 | ЕС | 1110 1100 |
| 109 | 6Д | 0110 1101 | 237 | ЭД | 1110 1101 |
| 110 | 6Е | 0110 1110 | 238 | ЕЕ | 1110 1110 |
| 111 | 6F | 1110 1111 | 239 | ЭФ | 1110 1111 |
| 112 | 70 | 0111 0000 | 240 | Ф0 | 1111 0000 |
| 113 | 71 | 0111 0001 | 241 | Ф1 | 1111 0001 |
| 114 | 72 | 0111 0010 | 242 | Ф2 | 1111 0010 |
| 115 | 73 | 0111 0011 | 243 | Ф3 | 1111 0011 |
| 116 | 74 | 0111 0100 | 244 | Ф4 | 1111 0100 |
| 117 | 75 | 0111 0101 | 245 | Ф5 | 1111 0101 |
| 118 | 76 | 0111 0110 | 246 | Ф6 | 1111 0110 |
| 119 | 77 | 1111 0111 | 247 | Ф7 | 1111 0111 |
| 120 | 78 | 0111 1000 | 248 | Ф8 | 1111 1000 |
| 121 | 79 | 0111 1001 | 249 | Ф9 | 1111 1001 |
| 122 | 7А | 0111 1010 | 250 | ФА | 1111 1010 |
| 123 | 7Б | 0111 1011 | 251 | ФБ | 1111 1011 |
| 124 | 7С | 0111 1100 | 252 | ФК | 1111 1100 |
| 125 | 7Д | 0111 1101 | 253 | ФД | 1111 1101 |
| 126 | 7Е | 0111 1110 | 254 | ФЭ | 1111 1110 |
| 127 | 7Ф | 0111 1111 | 255 | ФФ | 1111 1111 |
Преобразование десятичного IPv4 в шестнадцатеричный
Чтобы преобразовать десятичный IPv4-адрес с точками в шестнадцатеричный, возьмите каждое десятичное значение с точками и преобразуйте его с помощью шестнадцатеричного калькулятора (подойдет стандартный калькулятор Windows в научном режиме или режиме программиста).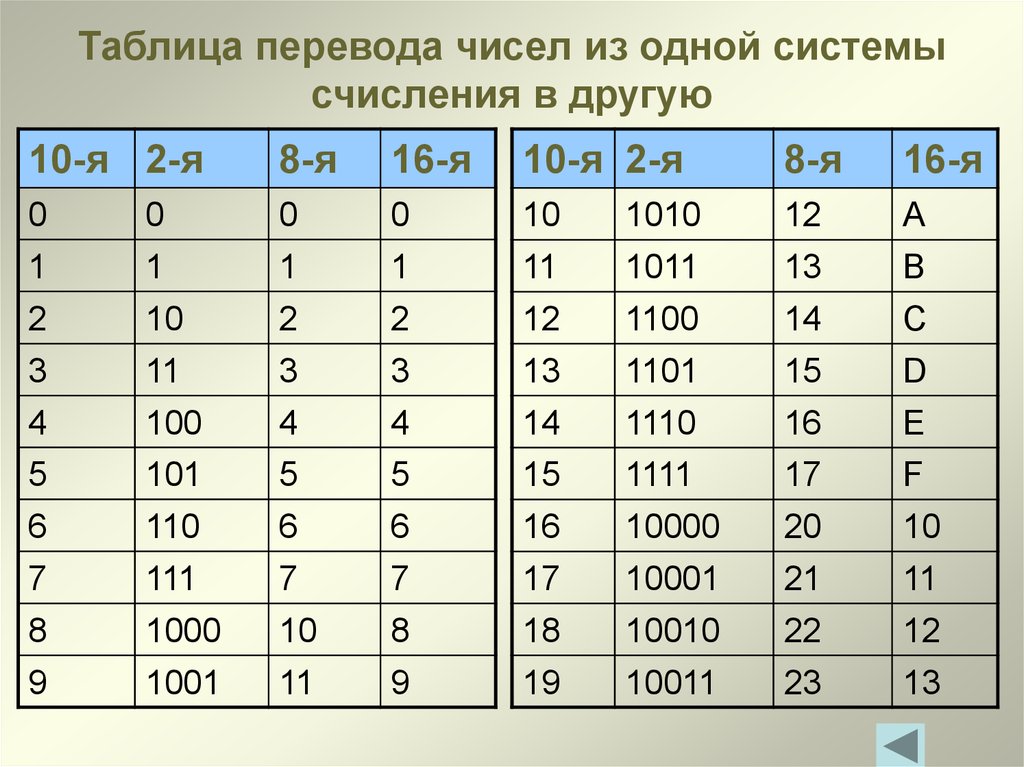
Это даст:
IP-адрес в десятичном формате с точками = 192.168.0.5 Десятичный 192 = Шестнадцатеричный = C0 Десятичный 168 = Шестнадцатеричный = A8 Десятичный 0 = Шестнадцатеричный = 00 Десятичный 5 = Шестнадцатеричный = 05 IP-адрес в шестнадцатеричном формате с точками = C0.A8.00.05
Проблемы, замечания, предложения, исправления (включая битые ссылки) или что-то добавить? Пожалуйста, найдите время от занятой жизни, чтобы «написать нам» (вверху экрана), веб-мастеру (ниже) или в информационную поддержку на zytrax. У вас будет теплое внутреннее сияние до конца дня.
Таблица преобразования десятичных чисел в двоичные — Изучение двоичных чисел
Автор Rick Regan 30 июня 2009 г.
Вот таблица, которую вы можете использовать для преобразования небольших целых чисел — целых чисел от 0 до 255 — непосредственно между десятичными и двоичными (в качестве альтернативы использованию десятичного/двоичного преобразователя):
| Декабрь | Двоичный | Декабрь | Двоичный | Декабрь | Двоичный | Декабрь | Двоичный | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 64 | 1000000 | 128 | 10000000 | 192 | 11000000 | |||
| 1 | 1 | 65 | 1000001 | 129 | 10000001 | 193 | 11000001 | |||
| 2 | 10 | 66 | 1000010 | 130 | 10000010 | 194 | 11000010 | |||
| 3 | 11 | 67 | 1000011 | 131 | 10000011 | 195 | 11000011 | |||
| 4 | 100 | 68 | 1000100 | 132 | 10000100 | 196 | 11000100 | |||
| 5 | 101 | 69 | 1000101 | 133 | 10000101 | 197 | 11000101 | |||
| 6 | 110 | 70 | 1000110 | 134 | 10000110 | 198 | 11000110 | |||
| 7 | 111 | 71 | 1000111 | 135 | 10000111 | 199 | 11000111 | |||
| 8 | 1000 | 72 | 1001000 | 136 | 10001000 | 200 | 11001000 | |||
| 9 | 1001 | 73 | 1001001 | 137 | 10001001 | 201 | 11001001 | |||
| 10 | 1010 | 74 | 1001010 | 138 | 10001010 | 202 | 11001010 | |||
| 11 | 1011 | 75 | 1001011 | 139 | 10001011 | 203 | 11001011 | |||
| 12 | 1100 | 76 | 1001100 | 140 | 10001100 | 204 | 11001100 | |||
| 13 | 1101 | 77 | 1001101 | 141 | 10001101 | 205 | 11001101 | |||
| 14 | 1110 | 78 | 1001110 | 142 | 10001110 | 206 | 11001110 | |||
| 15 | 1111 | 79 | 1001111 | 143 | 10001111 | 207 | 11001111 | |||
| 16 | 10000 | 80 | 1010000 | 144 | 10010000 | 208 | 11010000 | |||
| 17 | 10001 | 81 | 1010001 | 145 | 10010001 | 209 | 11010001 | |||
| 18 | 10010 | 82 | 1010010 | 146 | 10010010 | 210 | 11010010 | |||
| 19 | 10011 | 83 | 1010011 | 147 | 10010011 | 211 | 11010011 | |||
| 20 | 10100 | 84 | 1010100 | 148 | 10010100 | 212 | 11010100 | |||
| 21 | 10101 | 85 | 1010101 | 149 | 10010101 | 213 | 11010101 | |||
| 22 | 10110 | 86 | 1010110 | 150 | 10010110 | 214 | 11010110 | |||
| 23 | 10111 | 87 | 1010111 | 151 | 10010111 | 215 | 11010111 | |||
| 24 | 11000 | 88 | 1011000 | 152 | 10011000 | 216 | 11011000 | |||
| 25 | 11001 | 89 | 1011001 | 153 | 10011001 | 217 | 11011001 | |||
| 26 | 11010 | 90 | 1011010 | 154 | 10011010 | 218 | 11011010 | |||
| 27 | 11011 | 91 | 1011011 | 155 | 10011011 | 219 | 11011011 | |||
| 28 | 11100 | 92 | 1011100 | 156 | 10011100 | 220 | 11011100 | |||
| 29 | 11101 | 93 | 1011101 | 157 | 10011101 | 221 | 11011101 | |||
| 30 | 11110 | 94 | 1011110 | 158 | 10011110 | 222 | 11011110 | |||
| 31 | 11111 | 95 | 1011111 | 159 | 10011111 | 223 | 11011111 | |||
| 32 | 100000 | 96 | 1100000 | 160 | 10100000 | 224 | 11100000 | |||
| 33 | 100001 | 97 | 1100001 | 161 | 10100001 | 225 | 11100001 | |||
| 34 | 100010 | 98 | 1100010 | 162 | 10100010 | 226 | 11100010 | |||
| 35 | 100011 | 99 | 1100011 | 163 | 10100011 | 227 | 11100011 | |||
| 36 | 100100 | 100 | 1100100 | 164 | 10100100 | 228 | 11100100 | |||
| 37 | 100101 | 101 | 1100101 | 165 | 10100101 | 229 | 11100101 | |||
| 38 | 100110 | 102 | 1100110 | 166 | 10100110 | 230 | 11100110 | |||
| 39 | 100111 | 103 | 1100111 | 167 | 10100111 | 231 | 11100111 | |||
| 40 | 101000 | 104 | 1101000 | 168 | 10101000 | 232 | 11101000 | |||
| 41 | 101001 | 105 | 1101001 | 169 | 10101001 | 233 | 11101001 | |||
| 42 | 101010 | 106 | 1101010 | 170 | 10101010 | 234 | 11101010 | |||
| 43 | 101011 | 107 | 1101011 | 171 | 10101011 | 235 | 11101011 | |||
| 44 | 101100 | 108 | 1101100 | 172 | 10101100 | 236 | 11101100 | |||
| 45 | 101101 | 109 | 1101101 | 173 | 10101101 | 237 | 11101101 | |||
| 46 | 101110 | 110 | 1101110 | 174 | 10101110 | 238 | 11101110 | |||
| 47 | 101111 | 111 | 1101111 | 175 | 10101111 | 239 | 11101111 | |||
| 48 | 110000 | 112 | 1110000 | 176 | 10110000 | 240 | 11110000 | |||
| 49 | 110001 | 113 | 1110001 | 177 | 10110001 | 241 | 11110001 | |||
| 50 | 110010 | 114 | 1110010 | 178 | 10110010 | 242 | 11110010 | |||
| 51 | 110011 | 115 | 1110011 | 179 | 10110011 | 243 | 11110011 | |||
| 52 | 110100 | 116 | 1110100 | 180 | 10110100 | 244 | 11110100 | |||
| 53 | 110101 | 117 | 1110101 | 181 | 10110101 | 245 | 11110101 | |||
| 54 | 110110 | 118 | 1110110 | 182 | 10110110 | 246 | 11110110 | |||
| 55 | 110111 | 119 | 1110111 | 183 | 10110111 | 247 | 11110111 | |||
| 56 | 111000 | 120 | 1111000 | 184 | 10111000 | 248 | 11111000 | |||
| 57 | 111001 | 121 | 1111001 | 185 | 10111001 | 249 | 11111001 | |||
| 58 | 111010 | 122 | 1111010 | 186 | 10111010 | 250 | 11111010 | |||
| 59 | 111011 | 123 | 1111011 | 187 | 10111011 | 251 | 11111011 | |||
| 60 | 111100 | 124 | 1111100 | 188 | 10111100 | 252 | 11111100 | |||
| 61 | 111101 | 125 | 1111101 | 189 | 10111101 | 253 | 11111101 | |||
| 62 | 111110 | 126 | 1111110 | 190 | 10111110 | 254 | 11111110 | |||
| 63 | 111111 | 127 | 1111111 | 191 | 10111111 | 255 | 11111111 |
Имеется четыре столбца по 64 записи в каждой, всего 256 записей.
