НОУ ИНТУИТ | Лекция | Основы информатики
< Лекция 11 || Лекция 1: 12345678910
Аннотация: В этой лекции раскрывается базовая терминология информатики. Рассматриваются технические средства хранения информации, ее кодирование, системы счисления. Показывается история развития ЭВМ, говорится о принципах построения и управления компьютером, компьютерных вирусах. Значительное внимание уделено правовой охране программ и лицензии GPL.
Ключевые слова: свойства информации, группа, Теория информации, формальный язык, анализ, информатика, разделы, архитектура, операции, ПО, умозаключение, информация, определение, плоскость, достоверность, ясность, понятность, поиск, тип носителя, дерево, запись, floppy disk, ZIP, hard, диск, кодирование, компьютер, печать, вывод, знание, количество информации, бит, единица измерения, BIT, ложь, byte, байт, KOI8-R, пробел, килобайт, мегабайт, гигабайт, файл, хранилище данных, базы данных, поток, OS/2, произвольное, тип данных, standard, information, interchangeable, alt, кодировка, кодирование символов, диапазон, текстовые файлы, непозиционная система счисления, место, основание, сложение, вычитание, умножение, двоичная система счисления, binary digit, делимое, octal, hexadecimal, composability, максимальная степень, типы информации, обратный код, двоичное представление, мантисса, символ алфавита, таблица кодировки, векторная графика, picture element, растровая графика, электрический сигнал, память компьютера, ЦАП, MIDI, поколение ЭВМ, arithmetic, печатающее устройство, transistor, алгоритмический язык, algorithmic language, машинный язык, транслятор, многоязычность, artificial intelligence, expert system, типы задач, суперкомпьютер, вычислительная задача, файловый сервер, подкласс, архитектура компьютера, процесс обработки данных, внешнее запоминающее устройство, винчестер, запрос прерывания, CPU, storage device, input device, output device, communications device, процессор, память, арифметико-логическое устройство, мышь, controller, контроллер, производительность, RAM, random access, memory, ROM, read, разрядность, быстродействие, материнская плата, SIMM, DIMM, disc drive, последовательным доступом, keyboard, microphonics, scanner, лист, диаметр, знакоместо, шрифт, printer, множества, печатающая головка, Интернет, modem, скорость передачи, модем, сетевая карта, длина цепочки, компьютерные вирусы
intuit.ru/2010/edi»>Термином информатика обозначают совокупность дисциплин, изучающих свойства информации, а также способы представления, накопления, обработки и передачи информации с помощью технических средств. В англоязычных странах применяют термин computer science — компьютерная наука.Теоретическую основу информатики образует группа фундаментальных наук, которую в равной степени можно отнести как к математике, так и к кибернетике: теория информации, теория алгоритмов, математическая логика, теория формальных языков и грамматик, комбинаторный анализ и т. д. Кроме них информатика включает такие разделы, как архитектура ЭВМ, операционные системы, теория баз данных, технология программирования и многие другие.
Информационная технология есть совокупность конкретных технических и программных средств, с помощью которых мы выполняем разнообразные операции по обработке информации во всех сферах нашей жизни и деятельности. Иногда информационную технологию называют компьютерной технологией или прикладной информатикой.
Иногда информационную технологию называют компьютерной технологией или прикладной информатикой.
Информационные процессы
Термин информация ведет свое происхождение от латинского слова informatio, означающего разъяснение, изложение, осведомленность. Информацию мы передаем друг другу в устной и письменной форме, а также в форме жестов и знаков. Любую нужную информацию мы осмысливаем, передаем другим и делаем определенные умозаключения на ее основе.
Информацию мы извлекаем из учебников и книг, газет и журналов, телепередач и кинофильмов. Записываем ее в тетрадях и конспектах. В производственной деятельности информация передается в виде текстов и чертежей, справок и отчетов, таблиц и других документов. Такого рода информация может предоставляться и с помощью ЭВМ.
В любом виде информация для нас выражает сведения о ком-то или о чем-то. Она отражает происходящее или происшедшее в нашем мире, например, что мы делали вчера или будем делать завтра, как провели летний отпуск или каков будет характер будущей работы. При этом информация обязательно должна получить некоторую форму — форму рассказа, рисунка, статьи и т. д. Чертежи и музыкальные произведения, книги и картины, спектакли и кинофильмы — все это формы представления информации.
Она отражает происходящее или происшедшее в нашем мире, например, что мы делали вчера или будем делать завтра, как провели летний отпуск или каков будет характер будущей работы. При этом информация обязательно должна получить некоторую форму — форму рассказа, рисунка, статьи и т. д. Чертежи и музыкальные произведения, книги и картины, спектакли и кинофильмы — все это формы представления информации.
Информация, в какой бы форме она ни предоставлялась, является некоторым отражением реального или вымышленного мира. Поэтому информация — это отражение предметного мира с помощью знаков и сигналов.
Стоит отметить, что абсолютно точное определение информации дать невозможно, это такое же первичное понятие, как точка или плоскость в геометрии.
Получение информации — это получение фактов, сведений и данных о свойствах, структуре или взаимодействии объектов и явлений окружающего нас мира. Предметное содержание информации позволяет уяснить ее основные свойства — достоверность, полноту, ценность, актуальность, ясность и понятность.
Предметное содержание информации позволяет уяснить ее основные свойства — достоверность, полноту, ценность, актуальность, ясность и понятность.
- Информация достоверна, если она не искажает истинное положение дел. Недостоверная информация может привести к неправильному пониманию или принятию неправильных решений.
- Информация полна, если ее достаточно для понимания и принятия решений. Неполнота информации сдерживает принятие решений или может повлечь ошибки.
- Ценность информации зависит от того, какие задачи мы можем решить с ее помощью.
- При работе в постоянно изменяющихся условиях важно иметь актуальную, т. е. соответствующую действительности, информацию.
- Информация становится понятной, если она выражена языком, доступным людям, для которых она предназначена.

Информационная деятельность человека
Накопление человечеством опыта и знаний при освоении природы смешалось с освоением информации. Именно этот процесс и привел к образованию инфосферы. Такое понятие, как обработка информации, появилось совсем недавно, но обрабатывать информацию люди начали еще в древние времена.
Сначала из поколения в поколение информация передавалась устно. Это были сведения о профессиональных навыках, например, о приемах охоты, обработки охотничьих трофеев, способах земледелия и др. Но затем информацию стали фиксировать в виде графических образов окружающего мира. Первые наскальные рисунки, изображающие животных, растения и людей, появились примерно 20-30 тысяч лет назад.
Начатый поиск более современных способов фиксирования информации привел к появлению письменности. На чем только люди не писали! В Индии — на пальмовых листьях, в Вавилоне — на глиняных плитках, на Руси пользовались берестой. Как видим, письменность — новый шаг человечества в области хранения и передачи информации. Однако первым революционным явлением в этой сфере стало изобретение печатного станка, благодаря которому появилась книга и, таким образом, стало возможно массовое тиражирование профессиональных знаний, зафиксированных на материальном носителе.
Как видим, письменность — новый шаг человечества в области хранения и передачи информации. Однако первым революционным явлением в этой сфере стало изобретение печатного станка, благодаря которому появилась книга и, таким образом, стало возможно массовое тиражирование профессиональных знаний, зафиксированных на материальном носителе.
Сегодня потоки книг, сливаясь с потоками технической документации и многотомной справочной литературой, образуют океаны информации. Эту информацию необходимо хранить и передавать потребителю, для чего нужен мобильный и емкий носитель.
Но книга является неудобным, сложным, дорогим, а главное «медленным» носителем информации. Вся многогранность содержания раскрывается человеку при перелистывании, чтении и рассматривании книги. Она не может непосредственно влиять на производственный процесс. Сначала человеку необходимо найти нужную ему книгу, освоить накопленные в ней знания, которые позже смогут дать толчок дальнейшему развитию производства. Книга, как носитель информации, сегодня уже отстает от стремительного продвижения человечества по пути освоения природы.
Книга, как носитель информации, сегодня уже отстает от стремительного продвижения человечества по пути освоения природы.
Был и другой вид информационной деятельности. Отдельные государства, стремясь к расширению своих территорий, проводили агрессивную политику по отношению к своим соседям. Подготовка и ведение боевых действий требовали информации о военном потенциале противника. Ее добывали, например, через разведчиков. Тогда остро встал вопрос о защите информации от утечки в посторонние руки. Стали развиваться методы кодирования, разрабатываться способы быстрой и безопасной пересылки информации.
Шли годы, рос объем информации, которой обменивалось общество. Для сбора, переработки и распространения информации создавались издательства и типографии — родилась информационная промышленность. Газеты, журналы и другие издания, выпускаемые большими тиражами, зачастую кроме полезной информации обрушивали на человека огромное количество и ненужных, бесполезных сведений. Для обозначения таких лишних сведений придумали специальный термин — информационный шум. Помимо печати появились и другие средства массовой информации — радио и телевидение. И общество привыкло к тому, что когда говорят об информации, то речь идет о сведениях, полученных через радио, газеты и т. д.
Для обозначения таких лишних сведений придумали специальный термин — информационный шум. Помимо печати появились и другие средства массовой информации — радио и телевидение. И общество привыкло к тому, что когда говорят об информации, то речь идет о сведениях, полученных через радио, газеты и т. д.
Революционным изобретением XX века явилась электронная вычислительная машина (ЭВМ). Она является как носителем информации, так и средством доставки ее потребителю. В совокупности с линиями связи, такими, как проводная, радио, космическая и оптическая, ЭВМ делает доступной любую часть гигантского океана информации, которая без непосредственного воздействия на человека может влиять на работу производственного оборудования, например, на станки с программным управлением.
Дальше >>
< Лекция 11 || Лекция 1: 12345678910
Системы счисления — презентация онлайн
Похожие презентации:
Системы счисления. (9 класс)
(9 класс)
Системы счисления
Системы счисления
Системы счисления
Системы счисления (Лекция 02)
Системы счисления
Системы счисления
Системы счисления
Системы счисления
Теоретические основы информатики. Системы счисления
Тема
«Системы счисления»
2. Введение
Современный человек в повседневной жизнипостоянно сталкивается с числами и цифрами — они
с нами везде. Различные системы счисления
используются всегда, когда появляется потребность
в числовых расчётах, начиная с вычислений
учениками младших классов, выполняемых
карандашом на бумаге, заканчивая вычислениями,
выполняемыми на суперкомпьютерах.
3. История систем счисления
Система счисления – это определённый способпредставления чисел и соответствующие ему правила
действия над ними.
Системы счисления
Позиционные
Непозиционные
Цель создания системы счисления- выработка
наиболее удобного способа записи количественной
информации.

4. Древние системы счисления:
5. Позиционные и непозиционные системы счисления
Непозиционныесистемы
Позиционные
системы
От положения цифры в
записи числа не зависит
величина, которую она
обозначает.
Величина, обозначаемая
цифрой в записи числа,
зависит от ее позиции.
Основание – количество
используемых цифр.
Позиция – место каждой
цифры.
6. Запись числа в позиционной системе счисления
Любое целое число в позиционной системе можнозаписать в форме многочлена:
где — основание системы счисления, – цифры числа,
записанного в данной системе счисления, — количество
разрядов числа.
Так, например число 629310запишется в форме
многочлена следующим образом:
629310=6·103 + 2·102 + 9·101 + 3·100
7. Примеры позиционных систем счисления:
ДвоичнаяСистема счисления с основанием 2,
используются два символа — 0 и 1.
Восьмеричная
Система счисления с основанием 8,
используются цифры от 0 до 7.

Десятичная
Система с основанием 10, наиболее
распространённая система счисления в мире.
Двенадцатеричная
Система с основанием 12. Используются цифры
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B.
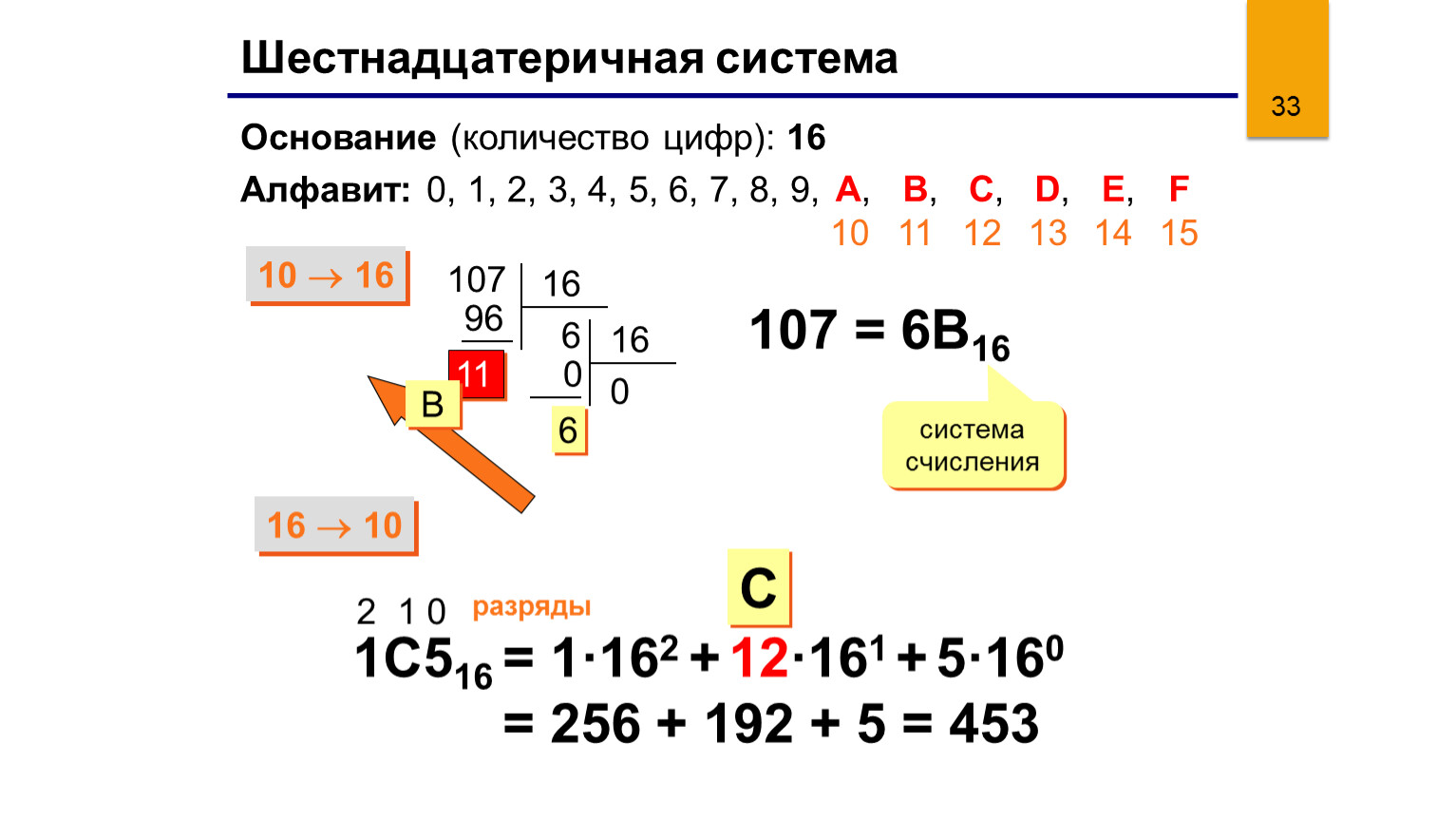
Шестнадцатеричная С основанием 16, используются цифры от 0 до 9
и латинские буквы от A до F для обозначения
цифр от 10 до 15.
Шестидесятеричная
Система с основанием 60, используется в
измерении углов и, в частности, долготы и
широты.
8. История двоичной системы счисления
Двоичная система счисления была придуманаматематиками и философами ещё до появления компьютеров
(XVII — XIX вв.).
Пропагандистом двоичной системы был знаменитый Г.В.
Лейбниц. Он отмечал особую простоту алгоритмов
арифметических действий в двоичной арифметике в
сравнении с другими системами и придавал ей
определенный философский смысл.
В 1936 — 1938 годах американский инженер и математик
Клод Шеннон нашёл замечательные применения двоичной
системы при конструировании электронных схем.
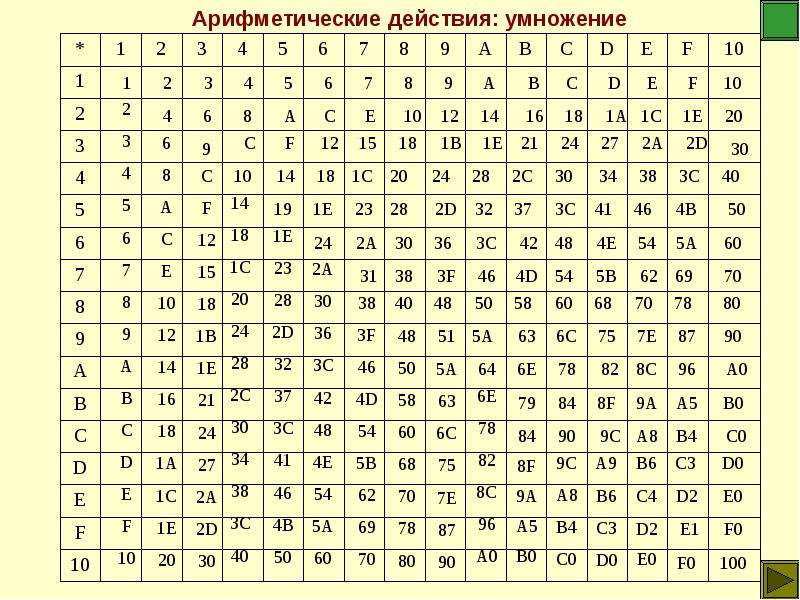
9. Двоичная система счисления
(бинарнаясистема счисления, binary) — позиционная
система счисления с основанием 2.
Неудобством этой системы счисления является
необходимость перевода исходных данных из десятичной
системы в двоичную при вводе их в машину и обратного
перевода из двоичной в десятичную при выводе
результатов вычислений.
Главное достоинство двоичной системы — простота
алгоритмов сложения, вычитания, умножения и деления.
10. Сложение, вычитание, умножение и деление в двоичной системе счисления
Сложение Вычитание Умножение Деление0 + 0 = 0;
0 + 1 = 1;
1 + 0 = 1;
1 + 1 = 10.
0 — 0 = 0;
1 — 0 = 1;
1 — 1 = 0;
10 — 1 = 1.
0 · 1 = 0;
1 · 1 = 1.
0 / 1 = 0;
1 / 1 = 1.
11. Двоичное кодирование в компьютере
В конце ХХ века, века компьютеризации,человечество пользуется двоичной системой
ежедневно, так как вся информация, обрабатываемая современными ЭВМ, хранится в них в
двоичном виде.

В современные компьютеры мы можем вводить
текстовую информацию, числовые значения, а также
графическую и звуковую информацию. Количество
информации, хранящейся в ЭВМ, измеряется ее
«длиной» (или «объемом»), которая выражается в битах
(от английского binary digit – двоичная цифра).
12. Перевод чисел из одной системы счисления в другую
13. Заключение
Высшим достижением древней арифметикиявляется открытие позиционного принципа
представления чисел.
Нужно признать важность не только самой
распространенной системы, которой мы пользуемся
ежедневно. Но и каждой по отдельности. Ведь в
разных областях используются разные системы
счисления, со своими особенностями и
характерными свойствами.
Десятичная
Двоичная
Восьмеричная
Шестнадцатеричная
1
001
1
1
2
010
2
2
3
011
3
3
4
100
4
4
5
101
5
5
6
110
6
6
7
111
7
7
8
1000
10
8
9
1001
11
9
10
1010
12
A
11
1011
13
B
12
1100
14
C
13
1101
15
D
14
1110
16
E
15
1111
17
F
16
10000
20
10
15.
 Перевод двоичного числа в десятичноеПеревод чисел
Перевод двоичного числа в десятичноеПеревод чиселДля перевода двоичного числа в десятичное
необходимо его записать в виде многочлена,
состоящего из произведений цифр числа и
соответствующей степени числа 2, и вычислить по
правилам десятичной арифметики:
16. Перевод восьмеричного числа в десятичное
Перевод чиселДля перевода восьмеричного числа в
десятичное необходимо его записать в виде
многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 8, и
вычислить по правилам десятичной
арифметики:
17. Перевод шестнадцатеричного числа в десятичное
Перевод чиселДля перевода шестнадцатеричного числа в
десятичное необходимо его записать в виде
многочлена, состоящего из произведений цифр
числа и соответствующей степени числа 16, и
вычислить по правилам десятичной
арифметики:
18. Перевод десятичного числа в двоичную систему
Перевод чиселДля перевода десятичного числа в двоичную
систему его необходимо последовательно делить на 2 до
тех пор, пока не останется остаток, меньший или равный
1.
 Число в двоичной системе записывается как
Число в двоичной системе записывается какпоследовательность последнего результата деления и
остатков от деления в обратном порядке.
Пример: Число
перевести в двоичную систему
счисления:
19. Перевод десятичного числа в восьмеричную систему
Перевод чиселДля перевода десятичного числа в восьмеричную
систему его необходимо последовательно делить на 8 до тех
пор, пока не останется остаток, меньший или равный 7.
Число в восьмеричной системе записывается как
последовательность цифр последнего результата деления и
остатков от деления в обратном порядке.
Пример: Число
перевести в восьмеричную систему
счисления:
20. Перевод десятичного числа в шестнадцатеричную систему
Перевод чиселДля перевода десятичного числа в шестнадцатеричную
систему его необходимо последовательно делить на 16 до тех
пор, пока не останется остаток, меньший или равный 15. Число
в шестнадцатеричной системе записывается как
последовательность цифр последнего результата деления и
остатков от деления в обратном порядке.

Пример: Число
перевести в шестнадцатеричную
систему счисления:
21. Перевод чисел из двоичной системы в восьмеричную
Перевод чиселЧтобы перевести число из двоичной системы в
восьмеричную, его нужно разбить на триады (тройки цифр),
начиная с младшего разряда, в случае необходимости
дополнив старшую триаду нулями, и каждую триаду заменить
соответствующей восьмеричной цифрой. При переводе
необходимо пользоваться двоично-восьмеричной таблицей:
2-ная
000
001
010
011
100
101
110
111
8-ная
0
1
2
3
4
5
6
7
Пример: Число
систему счисления:
перевести в восьмеричную
22. Перевод из двоичной системы в шестнадцатеричную
Перевод чиселЧтобы перевести число из двоичной системы в
шестнадцатеричную, его нужно разбить на тетрады
(четверки цифр).
Двоично-шестнадцатеричная таблица:
2-ная
0000
0001
0010
0011
0100
0101
0110
0111
16-ная
0
1
2
3
4
5
6
7
2-ная
1000
1001
1010
1011
1100
1101
1110
1111
16-ная
8
9
A
B
C
D
E
F
Пример: Число
перевести в
шестнадцатеричную систему счисления:
23.
 Перевод восьмеричного числа в двоичноеПеревод чисел
Перевод восьмеричного числа в двоичноеПеревод чиселДля перевода восьмеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной
ей двоичной триадой.
2-ная
000
001
010
011
100
101
110
111
8-ная
0
1
2
3
4
5
6
7
Пример: Число
счисления:
перевести в двоичную систему
24. Перевод шестнадцатеричного числа в двоичное
Перевод чиселДля перевода шестнадцатеричного числа в двоичное
необходимо каждую цифру заменить эквивалентной ей
двоичной тетрадой.
2-ная
0000
0001
0010
0011
0100
0101
0110
0111
16-ная 0
1
2
3
4
5
6
7
2-ная
1001
1010
1011
1100
1101
1110
1111
9
A
B
C
D
E
F
1000
16-ная 8
Пример: Число
счисления:
перевести в двоичную систему
25. Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
Перевод чиселПри переходе из восьмеричной системы счисления
в шестнадцатеричную и обратно, необходим
промежуточный перевод чисел в двоичную систему.

Пример 1: Число
перевести в восьмеричную
систему счисления:
Пример 2: Число
перевести в
шестнадцатеричную систему счисления:
26. Единичная система
Древние системы счислениячисел, количество предметов, изображалось нанесением
черточек или засечек на какой-либо твердой поверхности.
Археологами найдены такие «записи» при раскопках
культурных слоев, относящихся к периоду палеолита (10–11
тысяч лет до н.э.).
В такой системе применялся только один вид знаков –
палочка. Каждое число обозначалось с помощью строки,
составленной из палочек, количество которых равнялось
обозначаемому числу.
English Русский Правила
Преобразователь случайных чисел | Преобразование шестнадцатеричной системы счисления в основание 16 Конвертер длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (на массу)Конвертер удельной энергии, теплоты сгорания (на объем) температура Конвертер интервалов Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияКонвертер теплопроводностиКонвертер удельной теплоемкостиПлотность тепла, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиKine Конвертер вязкости maticПоверхностное натяжение КонвертерПроницаемость, проницаемость, паропроницаемость Конвертер скорости пропускания паров влаги Конвертер уровня звукаКонвертер чувствительности микрофонаКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с выбираемым эталонным давлениемКонвертер яркостиКонвертер силы светаКонвертер освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеОптическая мощность (диоптрий) Конвертер ) в увеличение (X)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаПреобразователь электрического токаКонвертер линейной плотности токаПреобразователь поверхностной плотности токаКонвертер напряженности электрического поляПреобразователь потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь проводимостиПреобразователь емкостиПреобразователь емкостиIn Преобразователь электрической проводимостиПреобразователь реактивной мощности переменного токаПреобразователь американского калибра проводовПреобразование Уровни в дБм, дБВ, Ваттах и других единицах измерения. двоично-десятичный шестнадцатеричный base-2base-3base-4base-5base-6base-7base-8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base -23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36 Volume Charge DensityЗнаете ли вы, что это одно и то же вакуумное устройство используется на вашей кухне и в радарах? Нажмите или коснитесь, чтобы узнать, что это за устройство! Обзор Различные способы представления чисел Индо-арабские цифры Римские Системы в других культурах Унарные Позиционная система Двоичная система Классификация чисел Отрицательные числа Рациональные числа Натуральные числа Целые числа Комплексные числа Простые числа Интересные факты о числах Цифры против мошенничества Современный счет в Коммерция Группировка цифр Несчастливые числа Изучайте технический английский с помощью этого видео! ОбзорПриложение-калькулятор для iPhone Число — это абстрактное математическое понятие, представляющее количество. Различные способы представления чиселНекоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания. Индийско-арабские цифры Индо-арабская система счисления сегодня является одной из наиболее широко используемых в мире. Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. Десять — обычное число для счета, потому что у людей десять пальцев, а части тела исторически часто использовались для счета. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках. Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне. Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910). РимскиеРимские цифры использовались в Римской империи и Европе до 14 века. Они до сих пор используются в некоторых контекстах, например, на часах, для обозначения часов. Римские цифры основаны на семи цифрах, записанных буквами латинского алфавита:
Порядок важен в римской системе, потому что большее число, за которым следует меньшее, означает, что два должны быть добавлены, но меньшее число перед большим означает, что меньшее число вычитается из большего. Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа. Системы в других культурахЛюди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв. Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа. В некоторых культурах используются более простые представления, такие как вавилонская система, которая имеет только два клинописных символа: один (немного напоминающий букву «Т») и десять (немного похожий на букву «С»). Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Унарная система счисления. Метки подсчета в различных культурах Унарная Унарная система представляет каждое число с тем же количеством символов, что и его значение. Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства. Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему. Позиционная системаПозиционная система работает с основанием. Например, в базе 10 у нас есть следующее:
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи. Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰ Двоичная система счисленияДвоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2. Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу: Художественное представление двоичных чисел
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию. Например: 11111 (31) В этом случае, работая справа налево:
Итак, складывая это вместе, мы получаем 101010. Вычитание работает по тому же принципу, только вместо переноса единиц мы «заимствуем» их. 101 (5) Деление и расчет квадратных корней также очень похожи на основание-10. Классификация номеровВсе номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются. Долг — отрицательное число Отрицательные числаОтрицательные числа — это числа, представляющие отрицательное значение. Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число. Рациональные числа Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число. Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами. Натуральные числаНатуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456. Целые числаЦелые числа включают нули, отрицательные и положительные числа, которые не являются дробями. Примеры включают -65 и 11 223. Комплексные числаКомплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательного числа. Простые числаПростые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге. Интересные факты о числахКитайские цифры для защиты от мошенничества Числительные для защиты от мошенничества Для предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать, добавив дополнительные штрихи. Современный счет в торговлеНекоторые языки в странах, где в настоящее время используется 10-кратная система счисления, свидетельствуют о том, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов. Группировка чисел И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000. Несчастливые числаЛеонардо да Винчи. Последний ужин. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия. В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году. В России и многих странах бывшего СССР все четных чисел считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны. В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае число 7 также является несчастливым, потому что оно представляет собой духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов. В Японии другое несчастливое число — 9.0016 9 , что имеет то же произношение, что и «страдание». В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «я жил». Это подразумевает, что жизнь окончена, и относится к смерти. 666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией. Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Ссылки Эта статья была написана Катериной Юрием Преобразование десятичного числа в восьмеричное Преобразование десятичного числа в двоичное с основанием 20 Преобразование восьмеричного в двоичное Преобразование десятичного числа в двоичное с основанием 36 в десятичное Преобразование десятичного числа в основание 4 Преобразование десятичного числа в основание 24 Преобразование шестнадцатеричного числа в десятичное Вам могут быть интересны другие конвертеры из группы «Общие преобразователи единиц измерения»:Конвертер длины и расстояния Конвертер массы Конвертер объема сухого вещества и единиц измерения общей кулинарной обработки Преобразователь площади Преобразователь объема и общей величины кулинарной обработки Преобразователь температуры Преобразователь давления, напряжения, модуля Юнга Энергия и рабочий преобразователь силовой преобразователь сила Преобразователь Преобразователь времени Преобразователь линейной скорости и скорости Преобразователь угла Преобразователь эффективности использования топлива, расхода топлива и экономии топлива Конвертер единиц информации и хранения данных Конвертер метрических префиксов Конвертер передачи данных Курсы валют Размеры мужской одежды и обуви Размеры женской одежды и обуви 9 0007 Компактный калькулятор Полный калькулятор Определения единиц измеренияDo у вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms  |
Преобразование чисел в другие системы счисления
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel для iPad Excel для iPhone Excel для планшетов Android Excel 2010 Excel 2007 Excel для Mac 2011 Excel для телефонов Android Больше. ..Меньше
..Меньше
Система счисления представляет собой систематический способ представления чисел с помощью символьных символов и использует базовое значение для удобной группировки чисел в компактной форме. Наиболее распространенной системой счисления является десятичная, имеющая базовое значение 10 и набор символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Однако существуют и другие системы счисления. , и их можно более эффективно использовать для определенной цели. Например, поскольку компьютеры используют логическую логику для выполнения вычислений и операций, они используют двоичную систему счисления, базовое значение которой равно 2.
Microsoft Office Excel имеет несколько функций, которые можно использовать для преобразования чисел в следующие системы счисления и из них:
Система счисления | Базовое значение | Набор символов |
Двоичный | 2 | 0,1 |
Восьмеричный | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
Десятичный | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 |
Шестнадцатеричный | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, Б, В, Г, Д, Ф |
Для выполнения этой задачи используйте функцию BIN2DEC.
|
Для выполнения этой задачи используйте функцию BIN2HEX.
|
|
Для выполнения этой задачи используйте функцию BIN2OCT.
|
|
Для выполнения этой задачи используйте функцию DEC2BIN.
|
Для выполнения этой задачи используйте функцию DEC2HEX.
|
Для выполнения этой задачи используйте функцию DEC2OCT.
|
Для выполнения этой задачи используйте функцию HEX2BIN.
|
|
Для выполнения этой задачи используйте функцию HEX2DEC.
|
|
Для выполнения этой задачи используйте функцию HEX2OCT.
|
|
Для выполнения этой задачи используйте функцию OCT2BIN.
|
Для выполнения этой задачи используйте функцию OCT2DEC.
|
Для выполнения этой задачи используйте функцию OCT2HEX.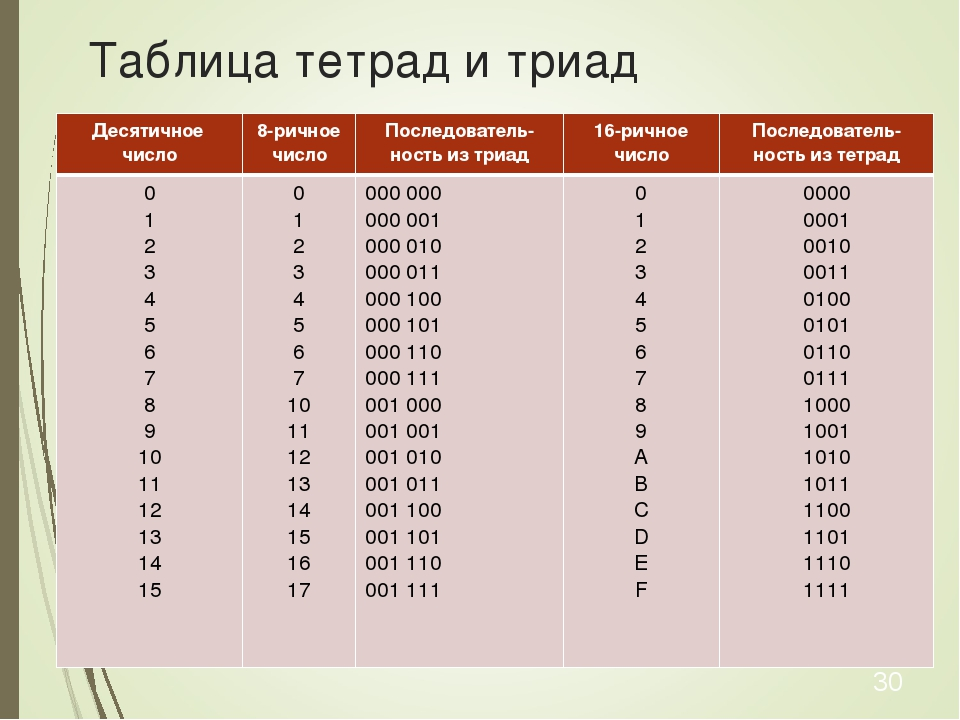



 Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются.
Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.

 Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.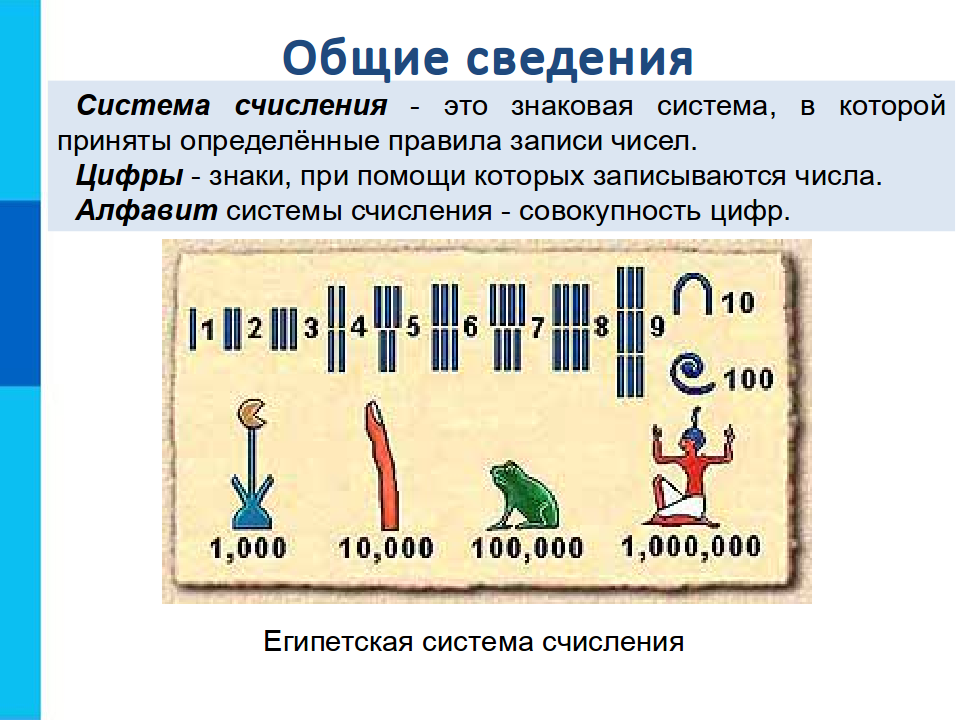

 Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например: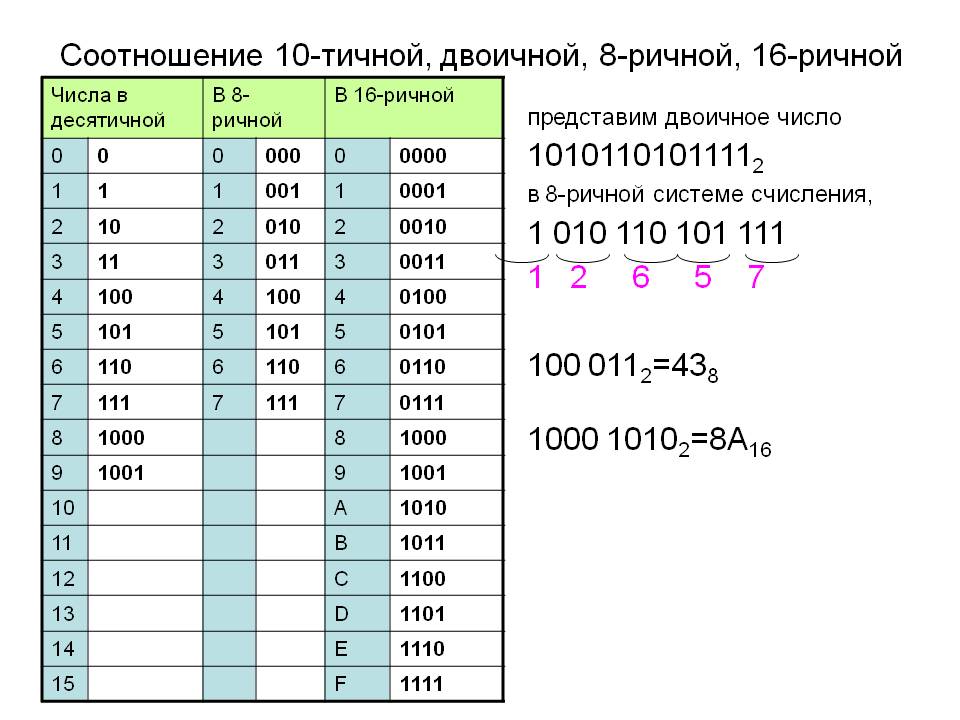
 Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи.

 Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками.
Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят. Это позиционная система с основанием 2, в которой числовые значения представлены двумя символами: 0 и 1.
Это позиционная система с основанием 2, в которой числовые значения представлены двумя символами: 0 и 1.

 2ШЕСТ.(11111011, 4)
2ШЕСТ.(11111011, 4)