Закон всемирного тяготения. Движение планет и спутников

Тема сегодняшнего урока: «Закон всемирного тяготения. Движение планет и спутников». Закон всемирного тяготения был сформулирован Ньютоном, который исходил из очень интересных соображений при выводе этого закона. Притча гласит о яблоке, упавшем ему на голову, но на деле все было не так просто. Ньютон понял, что притяжение тел к Земле и сила, с которой Луна притягивается к Земле, – это силы одной природы. Эта природа названа всемирным тяготением, и все небесные тела взаимодействуют друг с другом, так же, как и Земля взаимодействует с Луной.

Соображения Ньютона состояли в следующем.

— Если сила притяжения тела к Земле пропорциональна массе тела F_тяг = mg, а каждой силе действия есть сила противодействия F_1,2 = F_2,1 и если тело притягивается к Земле, то и Земля притягивается к телу. Тогда сила тяготения должна быть пропорциональна как массе одного тела, так и массе второго тела F_тяг ~ m₁m₂, то есть сила тяготения пропорциональна произведению масс, взаимодействующих тел.

— Ньютон заметил, что ускорение на планете Земля, ускорение свободного падения

g = F_тяг / m – это примерно 10 м/с², а ускорение, с которым движется Луна по своей орбите а_л = F_тяг / М_л = g / 3600, – это центростремительное ускорение, в 3600 раз меньше ускорения свободного падения. Ньютон догадался, почему такая разница в числах: дело в том, что расстояние от Земли до Луны составляет примерно шестьдесят земных радиусов r

з-л ≈ 60R_з. Их, а также ускорение 3600 Ньютон объединил следующим выводом: сила тяготения обратно пропорциональна квадрату расстояния между взаимодействующими телами F_тяг ~ 1 / r².

Учитывая эти два посыла, Ньютон дал общую формулировку: сила всемирного тяготения прямо пропорциональна массам взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними.

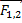  = γ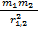

(-)

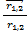γ – коэффициент пропорциональности (гамма), а направление силы – это сила притяжения друг к другу, и направление в этой формуле дается следующим образом: это единичный вектор, приведенный из первого тела ко второму, то есть отношение самого вектора к его модулю. Знак минус означает, что сила тяготения направлена не от первого тела ко второму, а от второго тела к первому.

Коэффициент пропорциональности измерил Кавендиш в своем эксперименте:

γ = G = 6,62 · 10^-11 Нм² / кг²

Из закона всемирного тяготения следуют формулы ускорения свободного падения:

1. Ускорение свободного падения у поверхности планеты:

g₀ = F_тяг / m = γmМ_з / R²_з · m = γ · М_з / R²_з.

Зная ускорение на планете Земля, радиус Земли, значение гравитационной постоянной, можно при необходимости вычислить массу Земли.

2. Ускорение свободного падения на каком-то расстоянии h от поверхности планеты:

g_h = γ· М_з / (R_з + h)² = (γ · М_з / R²_з) · R²_з / (R_з + h)².

Так как в такой форме ее трудно применить, то пользуются приведенной формулой:

g_h = g₀ · (R_з / R_з + h)²

3. Ускорение свободного падения на глубине: g_h↓ = g₀ · (R_з — h / R_з).

На основе закона всемирного тяготения можно рассчитать ск

Богданов К.Ю. — учебник по физике для 10 класса -§11

§ 11. ГРАВИТАЦИОННЫЕ СИЛЫ: ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ

Любые два тела притягиваются друг к другу с силой, которая прямо пропорциональна массам обоих тел и обратно пропорционально квадрату расстояния между ними.                                          

Этот закон, называемый законом всемирного тяготения

, в математической форме записывается следующим образом:

где m₁ и m₂ – массы тел, R – расстояние между ними (см. рис. 11а), а G — гравитационная постоянная, равная 6,67^.10^-11 Н^.м²/кг².

Закон всемирного тяготения был впервые сформулирован И. Ньютоном, когда он пытался объяснить один из законов И. Кеплера, утверждающий, что для всех планет отношение куба их расстояния R до Солнца к квадрату периода  T обращения вокруг него одинаково, т.е.

Выведем закон всемирного тяготения так, как сделал это Ньютон, считая, что планеты движутся по окружностям. Тогда по второму закону Ньютона на планету массой m_Пл, движущуюся по окружности радиуса R со скоростью v и центростремительным ускорением v²/R должна действовать сила F, направленная к Солнцу (см. рис. 11б) и равная:

 

Скорость v планеты можно выразить через радиус R орбиты и период обращения T:

Подставляя (11.4) в (11.3) получаем следующее выражение для F:

Из закона Кеплера (11.2) следует, что T² = const^.R³ . Следовательно, (11.5) можно преобразовать в:

Таким образом, Солнце притягивает планету с силой прямо пропорциональной массе планеты и обратно пропорционально квадрату расстояния между ними. Формула (11.6) очень похожа на (11.1), не хватает лишь массы Солнца в числителе дроби справа. Однако если сила притяжения между Солнцем и планетой зависит от массы планеты, то эта сила должна зависеть также и от массы Солнца, а значит, константа в правой части (11.6) содержит массу Солнца в качестве одного из сомножителей. Поэтому Ньютон выдвинул своё знаменитое предположение, что гравитационная сила должна зависеть от произведения масс тел и закон стал таким, каким мы его записали в (11.1).

Закон всемирного тяготения и третий закон Ньютона не противоречат друг другу. По формуле (11.1) сила, с которой тело 1 притягивает тело 2, равно силе, с которой тело 2 притягивает тело 1.   

Для тел обычных размеров гравитационные силы очень малы. Так, два рядом стоящих легковых автомобиля притягиваются друг к другу с силой, равной весу капли дождя. С тех пор, как Г. Кавендиш в 1798 г. определил значение гравитационной постоянной, формула (11.1) помогла совершить очень много открытий в «мире огромных масс и расстояний». Например, зная величину ускорения свободного падения (

g=9,8 м/с²) и радиус Земли (R=6,4^.10⁶ м), можно вычислить её массу m_З следующим образом. На каждое тело массой m₁ вблизи поверхности Земли (т.е. на расстоянии R от её центра) действует гравитационная сила её притяжения, равная m₁g, подстановка которой в (11.1) вместо F даёт:

откуда получаем, что m_З = 6^.10²⁴ кг.

Вопросы для повторения:

·        Сформулируйте закон всемирного тяготения?

·        Что такое гравитационная постоянная?

 

Рис. 11. (а) – к формулировке закона всемирного тяготения; (б) – к выводу закона всемирного тяготения из закона Кеплера.

11.Сила Всемирного тяготения

11. Сила всемирного тяготения

Для решения этих задач необходимо знать:

• формулы для расчета плотности вещества и силы тяжести;

• формулировку и математическую формулу закона всемирно­го тяготения.

1. Металлический брусок прямоугольной формы размером а х b х с подвешен к динамометру. Показания динамометра F. Плотность металла . Определите значение величины, обозначенной *. Во сколько раз изменятся показания динамометра, если все размеры бруска увели­чить в  раз?

Вариант	1	2	3	4	5	6	7	8	9	10	11	12
а, см	10	12	14	18	*	20	16	10	14	12	*	18
b, см	6,0	4,0	3,0	*	5,0	8,0	10	4,0	*	6,0	5,0	6,0
с, см	2,0	*	1,5	2,0	3,0	4,0	0,50	*	3,0	2,0	2,5	4,0
F, Н	5,3	3,8	*	25,1	23,6	55,2	*	4,2	17,3	12,6	23,6	*
, г/см3	*	2,7	7,8	8,9	7,3	*	11,3	7,2	7,0	*	19,3	2,7
	1,5	2	2,5	3	1,5	2	2,5	3	1,5	2	2,5	3

2. Два тела массами т₁ и т₂, находящиеся на расстоянии r друг от друга, взаимодействуют с силой гравитационного притяжения F. Опре­делите значение величины, обозначенной *. Как изменится сила грави­тационного взаимодействия, если расстояние между телами увеличить в  раз?

Вариант	1	2	3	4	5	6	7	8	9	10	11	12
m1, 106 кг	2,5	*	3	4	1,5	*	2	3	3	*	4	2
m2, 106 кг	2	2,5	*	3	4	1,5	*	2	2,5	3	*	4
r, км	1	1,5	2	*	1,5	2	2,5	*	2	2,5	1,5	*
F, мН	*	130	100	130	*	90	60	400	*	70	470	90
	3	2,5	2	1,5	3	2,5	2	1,5	3	2,5	2	1,5

3. Астронавты при облете некоторой планеты обнаружили, что ускорение свободного падения на высоте Н от ее поверхности равно g. Диаметр планеты D, масса планеты М. Определите значение величины, обозначенной *.

Вариант	1	2	3	4	5	6	7	8	9	10	11	12
H, км	*	400	300	200	*	200	400	300	*	100	200	400
g, м/с2	10	*	12	6,0	4,0	*	2,0	8,0	4,0	*	6,0	12
D, 103 км	8,0	13,8	*	6,8	4,0	9,6	*	11,4	20,0	7,8	*	7,2
М, 1024 кг	2,6	6,0	2,0	*	0,3	2,5	0,6	*	6,6	1,5	2,4	*

Закон всемирного тяготения. Сила тяжести (практика)

Данная тема посвящена решению задач на закон всемирного тяготения и силу тяжести.

Задача 1. Масса Юпитера равна 1,9 ∙ 10²⁷ кг, а его средний радиус — 70000 км. Определите ускорение свободного падения вблизи поверхности планеты. Какую минимальную скорость нужно сообщить телу на Юпитере, чтобы оно стало искусственным спутником?

Задача 2. Спутник движется вокруг Земли на высоте 1700 км над ее поверхностью. Считая орбиту спутника круговой, определите модуль его линейной скорости и период обращения спутника по орбите, если средний радиус Земли составляет 6400 км. (g = 10 м/с².)

Задача 3. На некоторой планете тела на экваторе невесомы. Определите среднюю плотность вещества планеты, если период ее обращения вокруг своей оси составляет 50000 с.

«Если запастись терпением и проявить старание,

 то посеянные семена знания непременно

дадут добрые всходы. Ученья корень горек,

да плод сладок»

Леонардо да Винчи

Закон всемирного тяготения. Ускорение свободного падения на Земле и других небесных телах

1612. Два астероида массой 10 т и 30 т приблизились друг к другу на расстояние 200 м. Какова сила их взаимного гравитационного притяжения?

1613. Найдите силу гравитационного притяжения Луны и Земли. Какие ускорения имеют Луна и Земля в результате действия этой силы?

1614. Искусственный спутник Земли массой 83,6 кг движется по круговой орбите вокруг нашей планеты. Расстояние от центра Земли до спутника равно 6600 км. Какова сила гравитационного притяжения между спутником и Землей. Какие ускорения имеют спутник и Земля благодаря этой силе?

1615. Как изменится сила гравитационного притяжения между двумя шариками, если расстояние между ними увеличить в 4 раза?

1616. Как изменится сила гравитационного притяжения между двумя шариками, находящимися на небольшом расстоянии друг от друга, если уменьшить массу каждого шарика в 3 раза?

1617. Космическая ракета удалилась от поверхности Земли на расстояние, равное радиусу Земли. Во сколько раз уменьшилась сила притяжения ракеты к Земле?

1618. Масса Земли в 81 раз больше массы Луны. Центры планет Земля и Луна находятся на расстоянии приблизительно 60 земных радиусов друг от друга. На каком расстоянии от центра Земли должен находиться предмет, чтобы сила притяжения к Земле была равна силе притяжения к Луне?

1619. Найдите ускорение свободного падения на планете Меркурий, если известно, что масса Меркурия меньше массы Земли в 18,18 раза, а радиус Земли в 2,63 раза больше радиуса Меркурия.

1620. Масса планеты Меркурий 3,29 • 1023 кг, а его радиус 2420 км. Найдите ускорение свободного падения на поверхности Меркурия.

1621. Зная радиус Земли и ускорение свободного падения на поверхности нашей планеты, вычислите массу Земли.

1622. Штангист на Земле может поднять груз массой 100 кг. Груз какой массы он мог бы поднять, находясь на полюсе Марса, если радиус Марса составляет 0,53 радиуса Земли, а масса Марса составляет 0,11 массы Земли?

1623. Каково ускорение свободного падения в космическом корабле, находящемся на высоте, равной трем радиусам Земли?

Задачи. Сила всемирного тяготения — PhysBook

Уровень А

1. С какой силой притягиваются:

а) два вагона массой по 80 т, если между ними расстояние 3,0 км;

б) Луна и Земля, массы которых равны 7,35·10²² кг и 5,98·10²⁴ кг соответственно, а среднее расстояние между ними 3,84·10⁸ м;

в) два протона массой 1,67·10^-27 кг, находящихся на расстоянии 1,00·10^-10 м друг от друга?

Решение

2. На каком расстоянии сила притяжения между двумя телами массой по 200 кг каждое будет равна 3,00·10^-14 Н?

Решение

3. Два шарика находятся на расстоянии 0,20 м друг от друга и притягиваются силой 6,0·10^-13 Н. Какова масса первого шарика, если масса второго равна 20 г?

Решение

4. Космический аппарат массой 750 кг достиг поверхности Луны. Найдите силу тяжести, действующую на аппарат:

а) на поверхности Земли;

б) на поверхности Луны.

Решение

5. Какова масса тела, если сила тяжести, действующая на него, равна 49 Н? Тело находится вблизи поверхности Земли.

Решение

6. Масса мальчика 50,0 кг. Определите силу тяжести, действующую на него на поверхности:

а) Меркурия;

б) Юпитера.

Решение

7. Тело имеет массу 10 кг. Какая сила тяжести действует на это тело на высоте трех земных радиусов от поверхности Земли?

Решение

8. Вычислите ускорение свободного падения тел вблизи поверхности Марса.

Решение

9. Каково ускорение свободного падения Земли на высоте, равной радиусу Земли?

Решение

10. Средний радиус планеты 2420 км, а ускорение свободного падения 3,72 м/с². Найдите массу планеты.

Решение

11. Найдите первую космическую скорость для следующих тел Солнечной системы:

а) Венера,

б) Земля,

в) Луна.

Решение

12. Какую скорость должен иметь спутник Земли, движущийся по круговой орбите, на высоте 1700 км от поверхности Земли?

Решение

Примеры решения задач по теме «Закон всемирного тяготения»

Примеры решения задач по теме «Закон всемирного тяготения»

«Физика — 10 класс»

При решении задач надо помнить, что сила тяготения действует между любыми телами, имеющими массу, но формула справедлива только для тел, которые можно считать материальными точками, а также для однородных тел шаровой формы. При этом расстояние r — это расстояние между центрами шаров.

Задача 1.

При опытной проверке закона всемирного тяготения сила взаимодействия между двумя свинцовыми шарами массами m₁ = 5 кг и m₂ = 500 г, расстояние между центрами которых r = 7 см, оказалась равной F = 34 нН. Вычислите по этим данным гравитационную постоянную.

Р е ш е н и е.

Согласно закону всемирного тяготения
Из этого выражения следует, что
Подставим в эту формулу результаты опыта, при этом все данные переведём в СИ: m₂ = 500 г = 5 • 10^-1 кг, r = 7 см = 7 • 10^-2 м, F = 34 нН = 3,4 • 10^-8 Н.

Получим
Уточнённое значение гравитационной постоянной, которое входит в таблицы:

Задача 2.

Определите равнодействующую силу, действующую на Луну, считая, что силы притяжения к Земле и Солнцу взаимно перпендикулярны. Массы Луны, Земли и Солнца соответственно равны m_Л = 7,36 • 10²² кг; m₃ = 5,98 • 10²⁴ кг; m_C = 1,99 • 10³⁰ кг; расстояния от Луны до Земли и от Луны до Солнца соответственно равны r_ЛЗ = 3,85 • 10⁸ м, r_ЛС = 1,5 • 10¹¹ м.

Р е ш е н и е.

По условию задачи силы гравитационного притяжения Луны к Земле и Солнцу взаимно перпендикулярны (рис. 3.6). Рассчитаем силу гравитационного притяжения Луны к Земле.

Сила притяжения Луны к Солнцу равна

По теореме Пифагора найдём равнодействующую силу, действующую на Луну,

Задача 3.

На поверхности Земли находятся два свинцовых шара радиусом R = 10 см каждый. В одном из них вырезана сферическая полость, как показано на рисунке 3.7. Радиус полости r = 5 см, центр полости находится на расстоянии l = 5 см от центра шара. Определите силу гравитационного притяжения шаров. Центры шаров находятся на расстоянии L = 40 см.

Р е ш е н и е.

Если бы у правого шара не было вырезанной полости, то сила гравитационного притяжения шаров была бы равна при этом Вырезав полость, мы уменьшаем эту силу притяжения на силу F₂, равную силе притяжения левого шара к вырезанной части:

Тогда

Заметим, что L = 4R = 8r; R = 2r, соответственно m = 8 m₁.

Подставив эти выражения в формулу (1), получим

Учтя, что получаем

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Динамика — Физика, учебник для 10 класса — Класс!ная физика

Основное утверждение механики — Сила — Инертность тела. Масса. Единица массы — Первый закон Ньютона — Второй закон Ньютона — Принцип суперпозиции сил — Примеры решения задач по теме «Второй закон Ньютона» — Третий закон Ньютона — Геоцентрическая система отсчёта — Принцип относительности Галилея. Инвариантные и относительные величины — Силы в природе — Сила тяжести и сила всемирного тяготения — Сила тяжести на других планетах — Примеры решения задач по теме «Закон всемирного тяготения» — Первая космическая скорость — Примеры решения задач по теме «Первая космическая скорость» — Вес. Невесомость — Деформация и силы упругости. Закон Гука — Примеры решения задач по теме «Силы упругости. Закон Гука» — Силы трения — Примеры решения задач по теме «Силы трения» — Примеры решения задач по теме «Силы трения» (продолжение) —