Законы Кирхгофа простыми словами: определения и формулы

По всем проводникам, которые являются частью электрической цепи, протекает электрический ток. При проведении расчётов не редкостью являются случаи, когда необходимо вычислить параметры тока и напряжения в цепях сложной формы, то есть в тех, где имеются разветвления. Для получения точных расчётов применяют правила Кирхгофа, которые иногда называют законами. Используя их вместе с законами Ома, можно с легкостью определять параметры независимых контуров в самых разветвленных и сложных цепях. Важным преимуществом данных законов является то, что не нужно использовать глубокие расчёты, благодаря приведенным алгоритмам посчитать сможет даже неопытный физик, сложные и многоуровневые расчёты превращаются в простые односложные сложения.

Закон Кирхгофа своими словами, кратко и понятно для чайников

История возникновения закона начинается с первого упоминания немецкого учёного Кирхгофа в XIX веке. В этот период в стране проходили репрессии, остро ощущалась нехватка новых технологий. Учёные искали решения, способные ускорить развитие промышленности. Вышеупомянутый учёный занимался исследованиями в области электричества. Он точно осознавал, что будущее за технологиями. Однако была проблема: как провести точные математические вычисления в цепях сложной формы. Тогда и возник закон.

К узлу подходят два провода, в то время как отходит всего один. Значение тока, который протекает по направлению от узла, равняется сумме протекающего по оставшимся двум проводникам, иными словами, идущим к нему. Правило, о котором идёт речь в статье, даёт понятное объяснение тому, что в противном случае происходило бы накопление заряда, однако такого никогда не бывает. Каждый физик на практике знает, что любую сложную цепь можно разделить на небольшие участки.

Возникает другая сложность: трудно определить путь, по которому он проходит. Более того, важно понимать, что на различных участках сопротивления разные, а из этого следует, что энергия будет распределяться неравномерно.

Первый закон Кирхгофа: определение

Первый закон, или, как он известен некоторым, правило, Густава Кирхгофа был выведен на основании другого закона – сохранения заряда. Как уже было упомянуто раннее, физик осознавал, что в узле надолго заряд задержаться не сможет, так как распределится по ветвям контура, которые образуют эти соединения.

Важно! У Кирхгофа было предположение, которое он впоследствии сумел доказать, благодаря проведенным экспериментам, что количество зарядов, оказавшихся в узле, равняется количеству тока, вытекающего из него.

Схема первого закона Кирхгофа

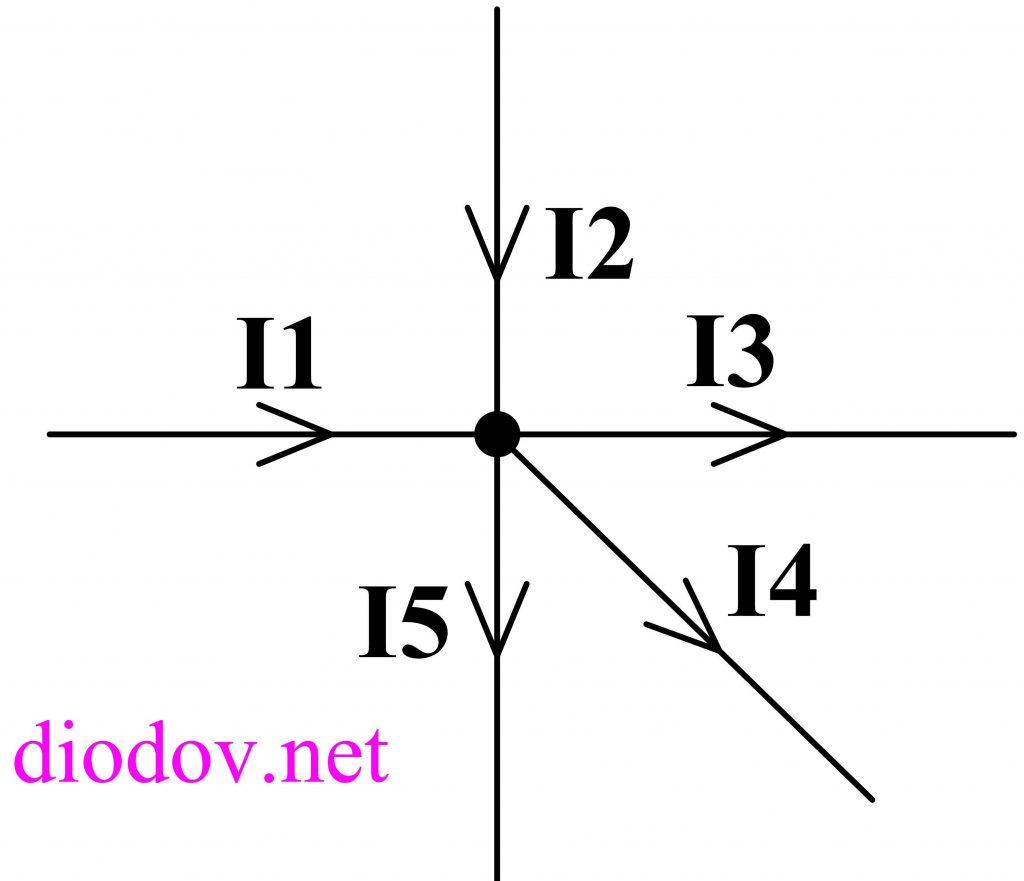
На рисунке показана схема, состоящая из нескольких контуров. Все части рисунка подписаны. Итак, закон № 1 утверждает, что сумма токов в любом узле абсолютно любой электрической цепи равняется нулю. Согласно правилу, входящий ток равен сумме выходящих, поэтому I₁ = I₂ + I₃. Узлами сети называются такие участки, в которых соединяются несколько проводников. Ток, который оказывается в узле, обозначается стрелкой, направленной к узлу, в то время вытекающий ток – стрелкой от узла. Таким образом, обозначение воспринимается проще в любой задаче.

Наглядно это показано на картинке.

Первый закон Кирхгофа

На основании вышесказанного запишем уравнение первого закона ученого:

I₁ + I₂ − I₃ − I₄ − I₅ = 0

Эта же формула может быть записана в более сокращенном виде:

I₁ + I₂ = I₃ + I₄ + I₅

Важно! Положительные или же противоположные – отрицательные – знаки токам присвоены в условном порядке. Их можно поменять, значение не поменяется.

Для примера разберём схему, изображённую на картинке выше.

Источник питания может быть абсолютно любой природы, им могут быть пальчиковые батарейки или же полноценный блок питания с возможностью регулировки. Итак, следуя первому закону, верным будет уравнение:

I₁ − I₂ − I₃ = 0 или же I₁ = I₂ + I₃

Чтобы продолжить измерения, необходимо в место на схеме, где указан амперметр, подключить мультиметр, который покажет, что закон полностью работает.

Формула для электрической и магнитной цепи

При проведении расчётов используют вышеупомянутые законы.

Первый закон для магнитных цепей вытекает из принципа непрерывности магнитного потока, который известен ещё из курса физики.

Второй же закон, если разобрать по частям, понятно, является иной формой записи закона полного тока. Прежде чем записать уравнения, необходимо в любом порядке остановить свой выбор на положительном направлении потоков в ветвях, аналогичное действие необходимо провести с напряжением обхода контуров. Если направление магнитного потока на определённом участке совпадает с направлением обхода, то магнитное напряжение на этом участке будет положительным, если же оно определяется как противоположное, то значение будет отрицательным.

Схожий случай, если МДС совпадает с направлением обхода, тогда знак положительный, в противном случае – отрицательный.

Закон для магнитных цепей

Для примера рассмотрим схему. Левая ветвь пусть будет первой, все относящиеся к ней величины будут записаны с индексом 1. Средняя весть будет второй, и величины получат индекс 2. Соответственно, величины правой ветви – индекс 3.

В произвольном порядке выберем направление потоков в ветвях. Предположим, что направление всех потоков будет вверх. Следуя первому закону, необходимо составить для каждого узла цепи уравнение. В цепи всего два узла, соответственно, составим всего одно уравнение:

Ф₁ + Ф₂ + Ф₃ = 0

Далее используем второй закон Кирхгофа, по которому нужно составить столько уравнений, сколько ветвей, не учитывая числа уравнений, составленных по первому закону.

Итак, запишем уравнения. Первое будет предназначено для контура, образованного первой и второй ветвями, второе – для контура, который будет образован первой и третьей ветвями.

Перед тем как составлять уравнения по второму закону, нужно выбрать положительное направление обхода контуров. Контуры будем обходить по часовой стрелке.

Итак, итоговое уравнение имеет вид:

H₁l₁ + Hδ₁δ₁ − H₂l₂ − Hδ₂δ₂ = I₁w₁ − I₂w₂

В левую часть уравнения были включены слагаемые со знаком плюс, потому что на первом участке поток направлен соответственно обходам контура, а слагаемые – с отрицательным знаком, потому что поток направлен в противоположную обходу контура сторону.

Второй закон Кирхгофа: определение

Второй закон вызывает у многих вопросы, так как он несколько труднее первого, но этот миф легко можно развеять, объяснив принцип работы. Для начала необходимо разобрать определение закона, который звучит таким образом: в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех пассивных элементах цепи.

Формулировка определения несколько затрудняет его понимание, поэтому можно упростить: сумма ЭДС в замкнутом контуре равняется сумме падений напряжений. Так намного проще и понятнее.

Закон напряжения и формула для магнитной цепи

Формула, которая выражает этот закон, примет такой вид:

Формула второго закон Кирхгофа

В качестве примера возьмём самый элементарный и понятный для всех случай. Нам понадобится взять батарейку и резистор – всё в одном экземпляре. Так как резистор в единичном количестве, так же как и батарейка, то ЭДС батарейки будет равняться 1,5 ватт, и это равно падению напряжения на резисторе.

Если для примера взять уже два резистора и подключить их к батарейке, то 1,5 ватт будут распределяться равномерно на обоих резисторах, то есть на каждом окажется по 0,75 ватт. Если взять уже три резистора по 1 кОм, то падение напряжения будет на них уже по 0,5 ватт. Логика расчётов сохраняется в любом случае. Формула примет вид:

Формула	Е1 = IR1 + IR2 + IR3
Преобразование	1,5 Вт = 0,5 Вт + 0,5 Вт + 0,5 Вт
Итог	1,5 Вт = 1,5 Вт

Важно! Второй закон будет работать независимо от того, сколько использовано источников питания и нагрузок. Не влияет на расчёты и место их расположения в контуре схемы. Так что даже у разных схем решение может быть одинаковым, но должно быть соблюдено условие – количество элементов должно быть идентичным.

Закон Кирхгофа для теплового излучения

Данный закон имеет другое название «третий закон». Сперва для лучшего понимания введем понятие теплового излучения. Принято называть тепловым излучение электромагнитное излучение, возникающее благодаря чужеродной энергии вращательного и колебательного движения атомов, молекул. Данное явление можно обнаружить абсолютно у всех тел, имеющих температуру не равняющуюся нулю или меньше. Основной количественной характеристикой теплового излучения выступает энергетическая светимость. Она должна быть вычислена одной из первых или же указана в условиях. Рассчитать её самостоятельно весьма проблематично. Её значение не постоянное, оно может меняться в зависимости от определенных характеристик: оказывает влияние температура окружающей среды, а также уровень нагретости тела. Имеет значение и длина, чем длиннее — тем значение меньше.

Формула выглядит таким образом:

R = E/(S·t), [Дж/(м2с)] = [Вт/м2]

Ещё одной характеристикой остаётся спектральная плотность энергетической светимости.

Важно ввести ещё одно понятие: коэффициент поглощения – это отношение поглощенной телом энергии к падающей энергии. Только теперь перейдем непосредственно к выделенному закону. Первое, что нужно сказать, что тепловое излучение является равновесной величиной. Это указывает на то, что сколько энергии будет излучаться телом, столько и им же и поглотится. При расчётах данное заявление имеет существенное значение. Можно сразу приравнивать оба значение. Таким образом, для трёх тел, которые находятся в замкнутой полости, формула примет вид:

Закон для теплового излучения

Раннее указанная формула будет верной даже тогда, когда какое-либо тело из указанных будет АЧ:

Закон звучит данным образом: отношение спектральной плотности энергетической светимости тела к его монохроматическому коэффициенту поглощения (при определенной температуре и для определенной длины волны) не зависит от природы тела и равно для всех тел спектральной плотности энергетической светимости при тех же самых температуре и длине волны.

Законы Кирхгофа в комплексной форме

Итак, для того, чтобы вывести математическую формулировку первого закона в комплексной формуле, необходимо представить все синусоидальные токи в комплексных значениях. Формула примет данный вид:

Комплексная форма первого закона Кирхгофа

Расшифровывая формулу получим, что алгебраическая сумма комплексных значений токов всех ветвей, которые сходятся в узле цепи, будет равняться нулю.

Закон №2 сформулирован не менее просто. Для контура замещения, который содержит лишь неактивные элементы и источники ЭДС, в каждую секунду алгебраическая сумма напряжений на данных элементах контура равняется числовой сумме ЭДС. Некоторым может показаться данная формулировка трудной, но при реальном разборе станет ясно, что все весьма просто и элементарно:

Комплексная форма второго закона Кирхгофа

Например, рассмотрим рисунок. Для выбранного на схеме замещения контура 1

u1-u2-u3+u4=0

Для второго контура:

ur-uL=e1-e2

В комплексной записи закон выглядит таким образом:

Контур 1

Контур 2

Задачи и примеры на законы Кирхгофа с решением

На картинках ниже подробно разобраны 2 задачи с применением законов Кирхгофа. Полное решение с наглядным примером на схемах и ответ.

Пример решения задачи по законам Кирхгофа

Законы Кирхгофа простыми словами ⋆ diodov.net

Два закона Кирхгофа вместе с законом Ома составляют тройку законов, с помощью которых можно определить параметры электрической цепи любой сложности. Законы Кирхгофа мы будем проверять на примерах простейших электрических схем, собрать которые не составит никакого труда. Для этого понадобится несколько резисторов, пара источников питания, в качестве которых подойдут гальванические элементы (батарейки) и мультиметр.

Первый закон Кирхгофа

Первый закон Кирхгофа говорит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая, аналогичная по смыслу формулировка: сумма значений токов, входящих в узел, равна сумме значений токов, выходящих из узла.

Давайте разберем сказанное более подробно. Узлом называют место соединения трех и более проводников.

Ток, который втекает в узел, обозначается стрелкой, направленной в сторону узла, а выходящий из узла ток – стрелкой, направленной в сторону от узла.

Согласно первому закону Кирхгофа

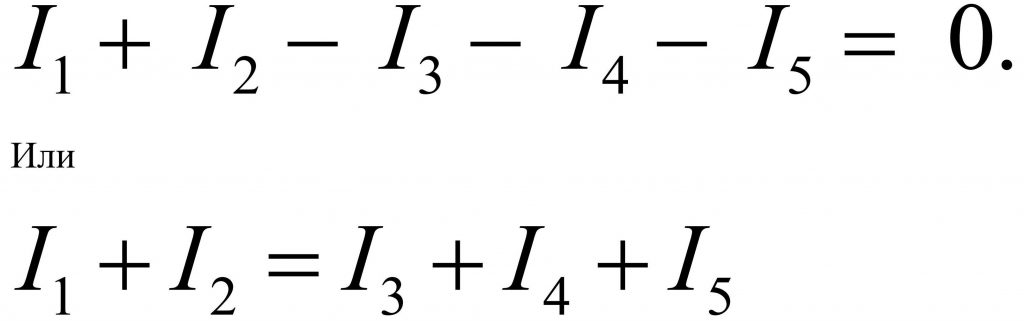
Условно присвоили знак «+» всем входящим токам, а «-» ‑ все выходящим. Хотя это не принципиально.

1 закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому, поступающие к узлу заряды покидают его.

Убедиться в справедливости 1-го закона Кирхгофа нам поможет простая схема, состоящая из источника питания, напряжением 3 В (две последовательно соединенные батарейки по 1,5 В), три резистора разного номинала: 1 кОм, 2 кОм, 3,2 кОм (можно применять резисторы любых других номиналов). Токи будем измерять мультиметром в местах, обозначенных амперметром.

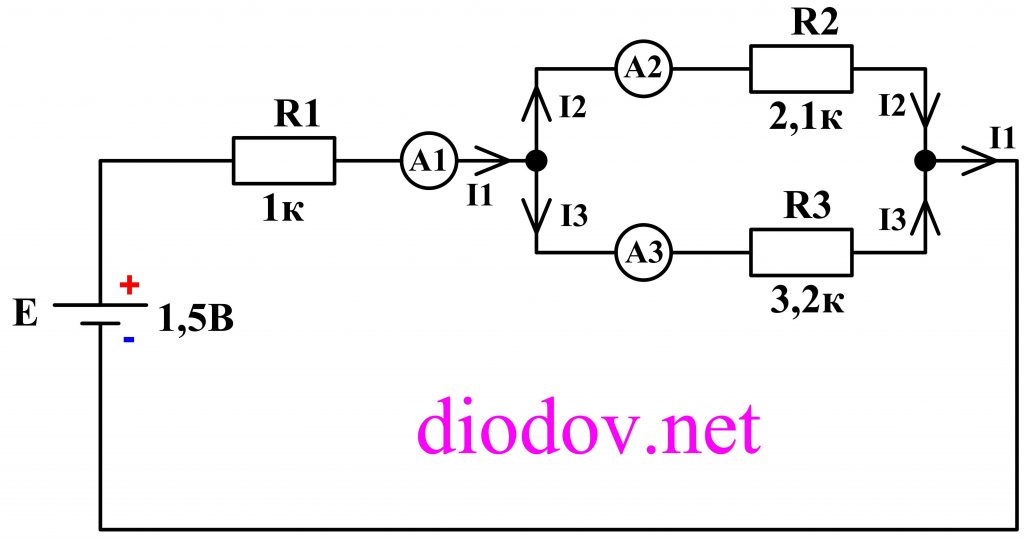
Если сложить показания трех амперметров с учетом знаков, то, согласно первому закону Кирхгофа, мы должны получить ноль:

I₁ — I₂ — I₃ = 0.

Или показания первого амперметра А1 будет равняться сумме показаний второго А2 и третьего А3 амперметров.

Второй закон Кирхгофа

Второй закон Кирхгофа воспринимается начинающими радиолюбителями гораздо сложнее, нежели первый. Однако сейчас вы убедитесь, что он достаточно прост и понятен, если объяснять его нормальными словами, а не заумными терминами.

Упрощенно 2 закон Кирхгофа говорит: сумма ЭДС в замкнутом контуре равна сумме падений напряжений

ΣE = ΣIR

Самый простой случай данного закона разберем на примере батарейки 1,5 В и одного резистора.

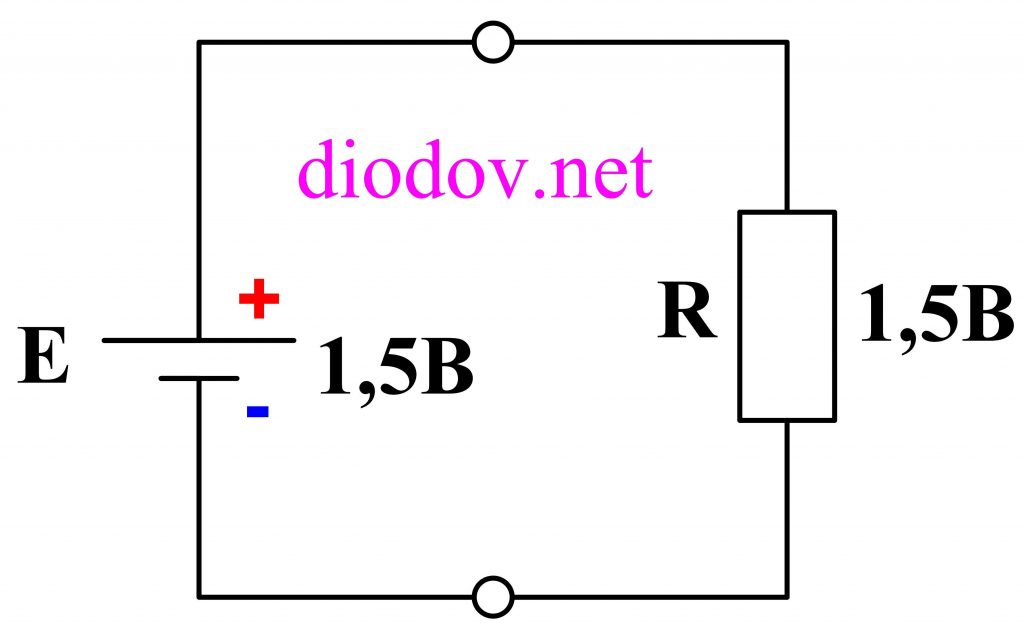
Поскольку резистор всего один и одна батарейка, то ЭДС батарейки 1,5 В будет равна падению напряжения на резисторе.

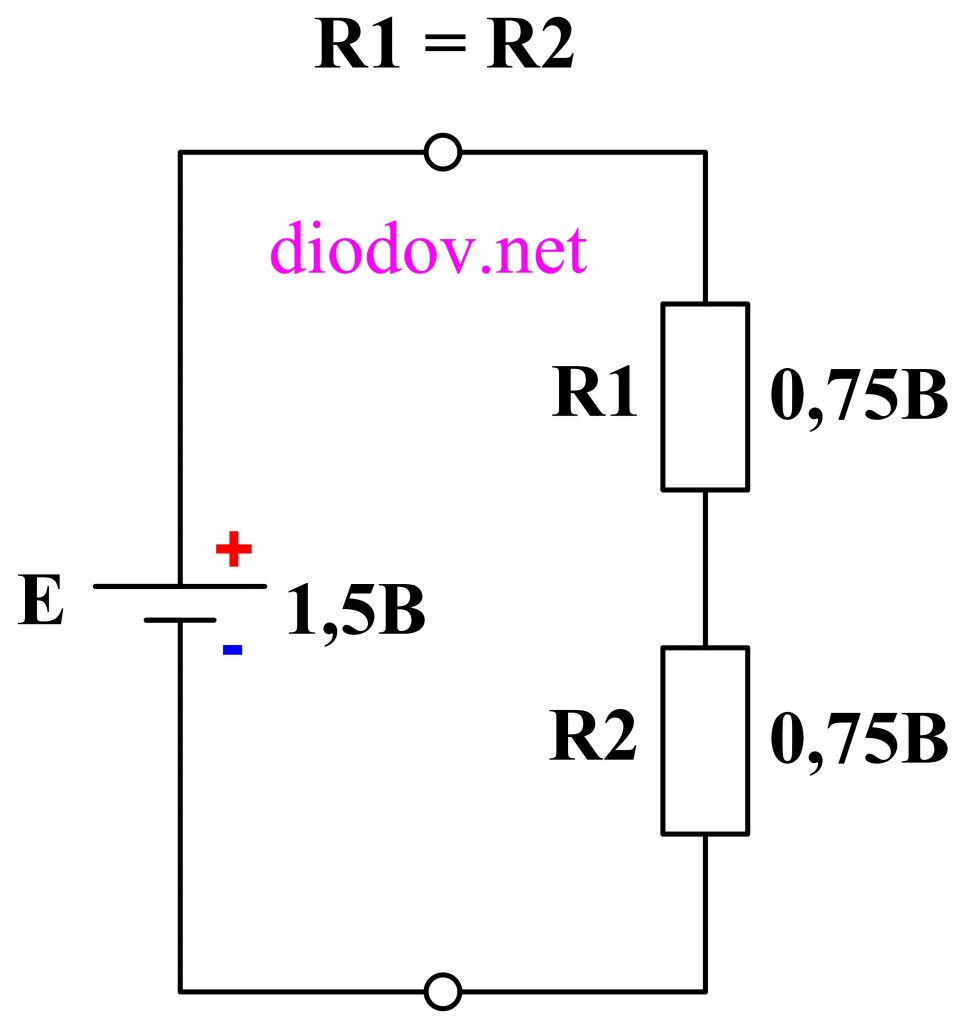
Если мы возьмем два резистора одинакового номинала и подключим к батарейке, то 1,5 В распределятся поровну на резисторах, то есть по 0,75 В.

Если возьмем три резистора снова одинакового номинала, например по 1 кОм, то падение напряжения на них будет по 0,5 В.

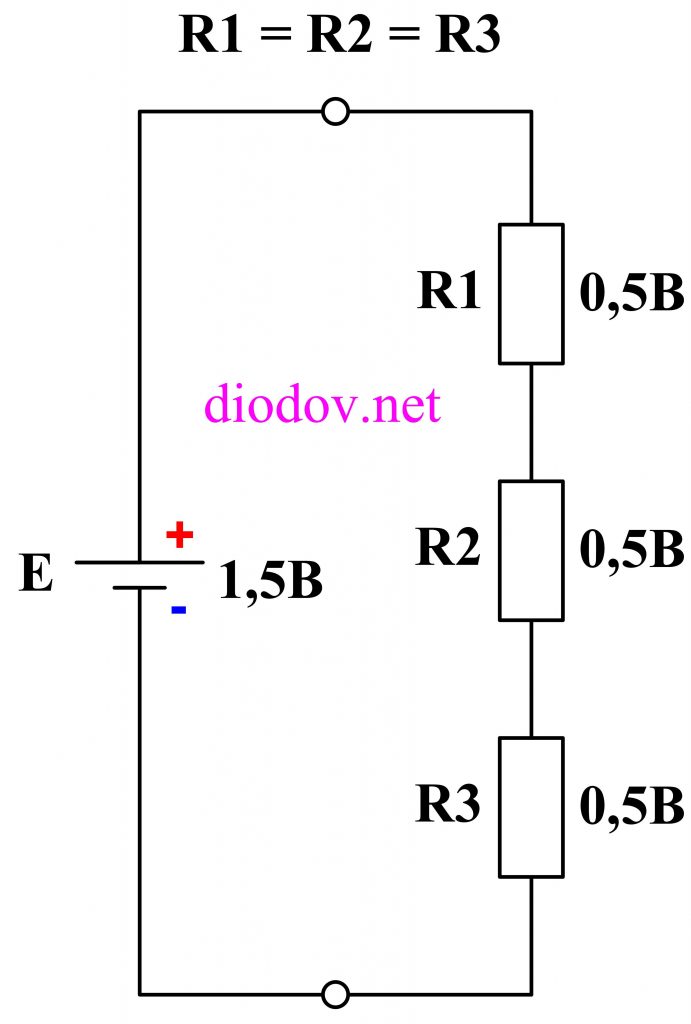
Формулой это будет записано следующим образом:

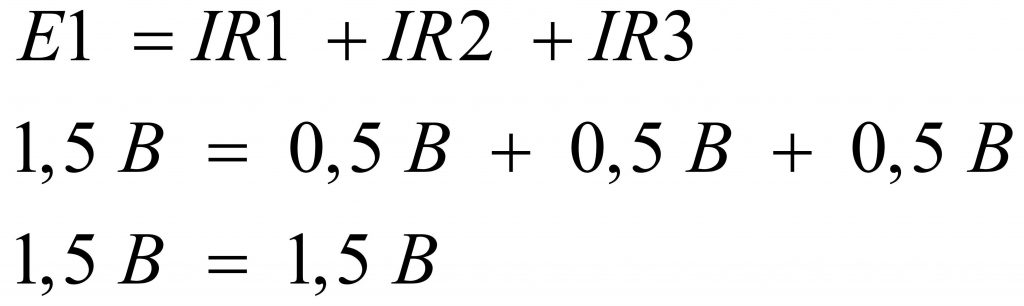
Рассмотрим условно более сложный пример. Добавим в последнюю схему еще один источник питания E2, напряжением 4,5 В.

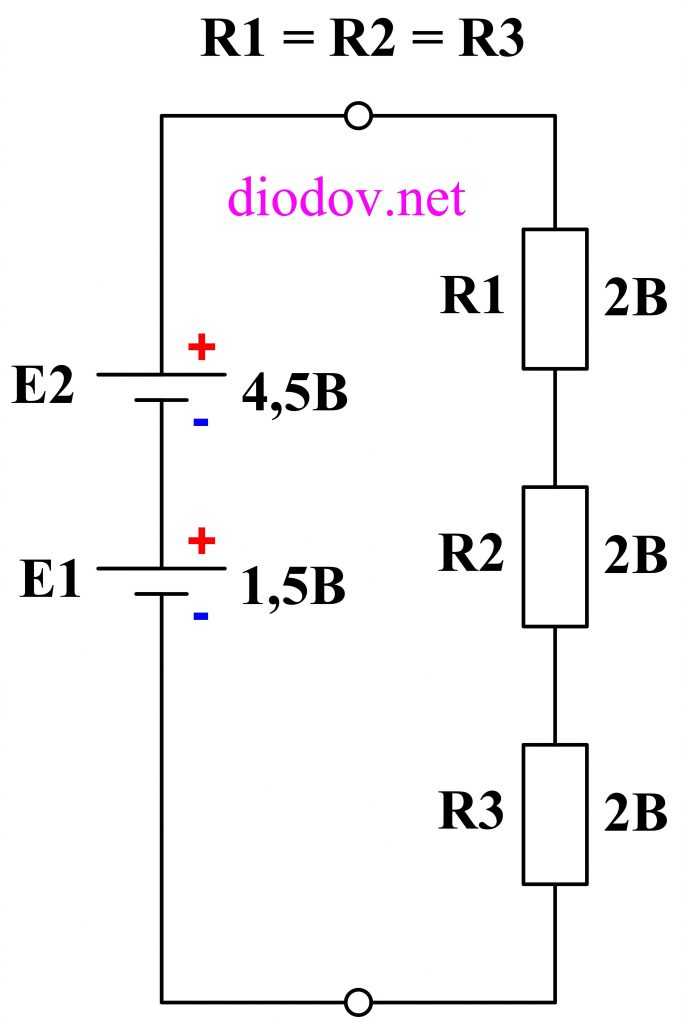
Обратите внимание, что оба источника соединены последовательно и согласно, то есть плюс одной батарейки соединяется с минусом другой батарейки или наоборот. При таком способе соединения гальванических элементов их электродвижущие силы складываются: E1 + E2 = 1,5 + 4,5 = 6 В, а падение напряжения на каждом сопротивлении составляет по 2 В. Формулой это описывается так:

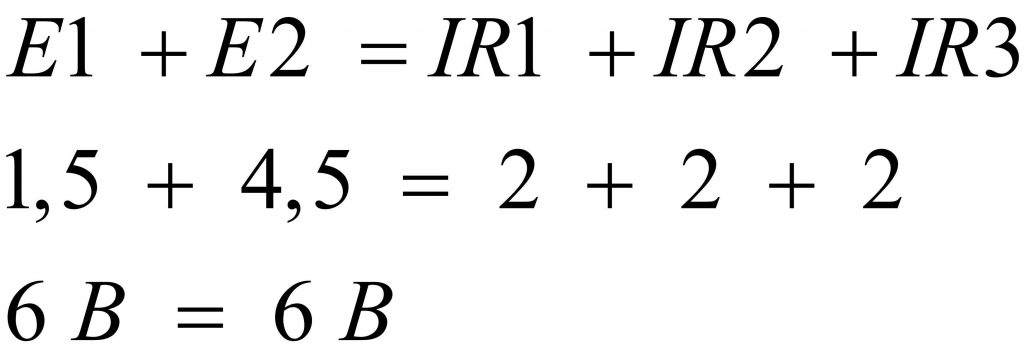
И последний отличительный вариант, который мы рассмотрим в данной статье, предполагает последовательное встречное соединение гальванических элементов. При таком соединении источников питания из большей ЭДС отнимается значение меньшей ЭДС. Следовательно к резисторам R1…R3 будет приложена разница E1 – E2, то есть 4,5 – 1,5 = 3 В, — по одному вольту на каждый резистор.

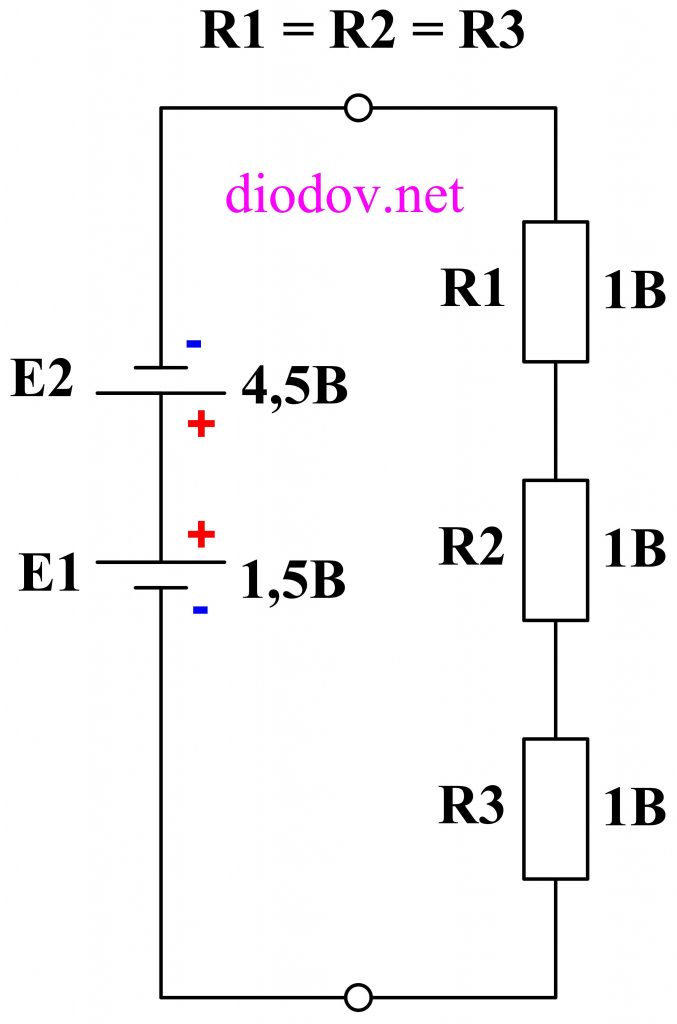
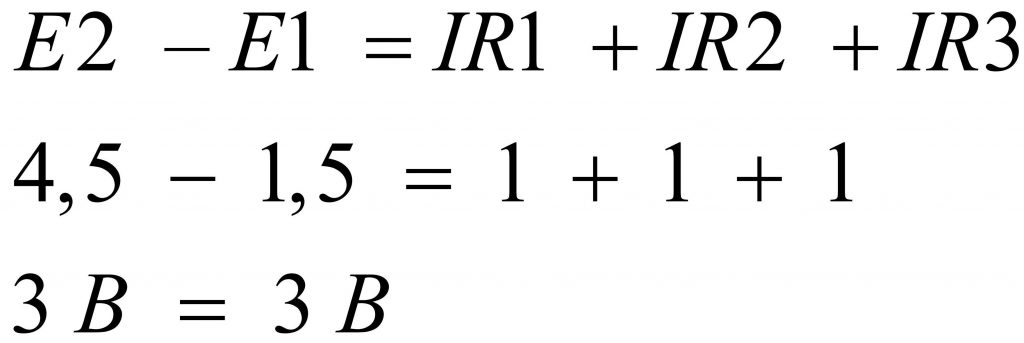
Второй закон Кирхгофа работает не зависимо от количества источников питания и нагрузок, а также независимо от места их расположения в контуре схемы. Полезно будет собрать рассмотренные схемы и выполнить соответствующие измерения с помощью мультиметра.

Законы Кирхгофа действуют как для постоянного, так и для переменного тока.

Еще статьи по данной теме

Постоянный ток: законы Кирхгофа

При решении задач на законы Кирхгофа лучше придерживаться определенного алгоритма: 1. определить число неизвестных токов – столько уравнений должно быть в системе ; 2. определить количество узлов – уравнений по первому закону тогда нужно составить на одно меньше; 3. проложить контуры и записать для них уравнения по второму закону. Кто хочет разобраться досконально – есть видео.

Задача 1. Два элемента с В и В соединены по схеме, показанной на рисунке . Сопротивление Ом. Внутреннее сопротивление элементов одинаково Ом. Определить силу тока, идущего через сопротивление .

К задаче 1

Обозначим токи в ветвях произвольно. По первому закону Кирхгофа сумма токов, сходящихся в узле, равна 0:

   

Будем обходить верхний контур против часовой стрелки. По второму закону Кирхгофа сумма падений напряжений в контуре равна сумме ЭДС:

   

   

Будем обходить второй контур по часовой стрелке:

   

   

Неизвестных токов – три, мы составили три уравнения. Этого достаточно, чтобы найти токи:

   

Выразим из второго уравнения, а – из третьего:

   

   

Подставим эти выражения в первое уравнение:

   

   

   

   

   

Тогда токи и

   

   

Ответ: A, A, A.
Задача 2. Найти силу тока на всех участках цепи‚ если В, В‚ В, Ом‚ Ом‚ Ом‚ Ом‚  Ом, Ом.

К задаче 2

Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас два узла, поэтому уравнение будет одно.  Затем, обходя контуры, составим два уравнения по второму закону: их нужно составить два, так как неизвестных токов в цепи три.

   

Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора):  , , .

Ответ: , , .

 

Задача 3. В схеме, показанной на рисунке, найти силу тока через гальванометр, если В, кОм; В, кОм.  Сопротивлением гальванометра пренебречь.

К задаче 3

Нам неизвестно сопротивление гальванометра, запишем для напряжения на нем два уравнения:

   

   

Приравнивая, получим

   

Заметим, что, если  , то равенство будет выполнено. Таким образом, ток через гальванометр не течет.

Ответ: .

Задача

4. В цепи   В‚ В, Ом,  Ом. Найти распределение токов в цепи. Внутреннее сопротивление источников тока не учитывать.

К задаче 4

Обозначаем токи в ветвях произвольно, выбираем направления обходов контуров и сами контуры. Составляем систему уравнений. Сначала составим уравнение по первому закону Кирхгофа – у нас три узла, поэтому уравнений будет два.  Затем, обходя контуры, составим три уравнения по второму закону: их нужно составить именно три, так как неизвестных токов в цепи шесть.

   

Решаем систему и находим ответ (я решала с помощью он-лайн калькулятора):  , , , , , .

Ответ: , , , , , .
Задача 5. Какую силу тока покажет амперметр в схеме, изображенной на рисунке? Сопротивлением амперметра пренебречь.

К задаче 5

Обозначим токи в цепи произвольно. Обозначим направления обхода контуров. Запишем систему уравнений: составим три уравнения по первому закону (на одно меньше, чем количество узлов) и три уравнения по второму закону, так как неизвестных токов шесть и система должна состоять из шести уравнений.

   

Чтобы воспользоваться калькулятором, я задала Ом и В.  В итоге получилось: , , , , , .

Минусы свидетельствуют о противоположном направлении тока в этой ветви тому, что мы нарисовали.

Теория по физике для ЕГЭ, пособия по подготовке и справочные материалы в Москве

Первое правило Кирхгофа

Алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю.

Также можно легко запомнить первый закон Кирхгофа следующим образом: сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Здесь ток \(I_1\) — ток, втекающий в узел, а токи \(I_2\) и \(I_3\) — токи, вытекающие из узла. Тогда можно записать:

\(I_1 = I_2 + I_3,\ (1)\)

Перенесем токи \(I_2\) и \(I_3\) в левую часть выражения (1), тем самым получим:

\(I_1 — I_2 — I_3 = 0,\ (2)\)

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «—».

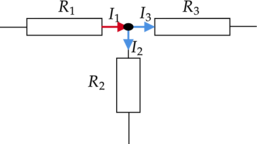
Второе правило Кирхгофа

Алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур.

Термин «алгебраическая сумма» означает, что как величина ЭДС, так и величина падения напряжения на элементах может быть как со знаком «+», так и со знаком «—». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта: либо по часовой стрелке, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

— ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура, записываются со знаком «+», в противном случае ЭДС записываются со знаком «—».

— напряжения, падающие на элементах цепи, записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «—».

Например, рассмотрим цепь на рисунке и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке и выбрав направление токов через резисторы, как показано на рисунке.

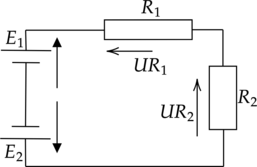
Получим:

\(E_1- E_2 = -UR_1 — UR_2\) или \(E_1 = E_2 — UR_1 — UR_2\)

Электричество и магнетизм

Приведем пример расчета токов в разветвленной цепи (рис. 4.25).

Рис. 4.25. Пример разветвленной цепи 

Направления действия ЭДС показаны синими стрелками. В этой цепи у нас имеется два узла — точки b и d (m = 2), и три ветви — участок b–а–d с током I₁, участок b–d с током I₂ и участок b–c–d с током I₃ (n = 3). Значит, мы можем написать одно (m – 1 = 2 – 1 = 1) уравнение на основе первого правила Кирхгофа и два (n – m + 1 = 3 – 2 + 1 = 2) уравнения на основе второго правила Кирхгофа. Как же это делается на практике? 

Шаг первый. Выберем направления токов, текущих в каждой из ветвей цепи. Как эти направления выбрать — совершенно неважно. Если мы угадали, в окончательном результате значение этого тока получится положительным, если нет и направление должно быть обратным — значение этого тока получится отрицательным. В нашем примере мы выбрали направления токов как показано на рисунке. Важно подчеркнуть, что направления действия ЭДС не произвольны, они определяются способом подключения полюсов источников тока (см. рис. 4.25). 

Шаг второй. Записываем первое правило Кирхгофа для всех узлов кроме одного (в последнем узле, выбор которого произволен, это правило будет выполняться автоматически). В нашем случае мы можем записать уравнение для узла b, куда входит ток I₂ и выходят токи I₁ и I₃

(4.45)

Шаг третий. Нам осталось написать уравнения (в нашем случае — два) для второго правила Кирхгофа. Для этого надо выбрать два независимых замкнутых контура. В рассматриваемом примере имеются три такие возможности: путь по левому контуру b–a–d–b, путь по правому контуру b–c–d–b и путь вокруг всей цепи b–a–d–c–b. Достаточно взять любые два из них, тогда для третьего контура второе правило Кирхгофа будет выполнено автоматически. Направление обхода контура роли не играет, но при обходе ток будет браться со знаком плюс, если он течет в направлении обхода, и со знаком минус, если ток течет в противоположном направлении. Это же относится к знакам ЭДС.

Возьмем для начала контур b–a–d–b. Мы выходим из точки b и движемся против часовой стрелки. На нашем пути встретятся два тока, I₁ и I₂, направления которых совпадают с выбранным направлением обхода. ЭДС также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как

(4.46)

В качестве второго замкнутого пути для разнообразия выберем путь b–a–d–c–b вокруг всей цепи. На этом пути мы встречаем два тока I₁ и I₃, из которых первый войдет со знаком плюс, а второй — со знаком минус. Мы встретимся также с двумя ЭДС, из которых  войдет в уравнения со знаком плюс, а  — со знаком минус. Уравнение для этого замкнутого пути имеет вид

(4.47)

 

Шаг четвертый. Мы нашли три уравнения для трех неизвестных токов в цепи. Решение произвольной системы линейных уравнений описывается в курсе математики. Для наших целей (цепь достаточна проста) можно просто выразить I₃ через I₁ из уравнения (4.47)

(4.48)

I₂ через I₁ с помощью уравнения (4.46)

(4.49)

и подставить (4.48), (4.49) в уравнение первого правила Кирхгофа (4.45). Это уравнение содержит лишь неизвестное I₁, которое находится без труда

(4.50)

Подставляя это выражение в (4.48), (4.49), находим соответственно токи I₂, I₃

(4.51)

Первый и второй закон Кирхгофа

При расчете режима работы электрической цепи очень часто необходимо определить токи, напряжения и мощности на всех ее участках при заданных ЭДС источников и сопротивлений участков цепи. Данный расчёт основан на применении законов Кирхгофа.

В этой статье предполагается, что вы знакомы с определениями узла, ветви и контура.

---

Содержание:

---

Первый закон Кирхгофа

Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю (токи входящие в узел считаются положительными, выходящие из узла отрицательными).

Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:

Рисунок 1 — Первый закон Кирхгофа

I1 + I2 − I3 + I4 − I5 − I6 = 0.

Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен. 

#1. Запишите выражение для узла В

#2. Найдите ток i

Результат

Отлично!

Попытайтесь снова(

Выбор направления токов

Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.

Например

 

Рисунок 2

На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).

Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:
1. Ток должен вытекать из узла через одну или несколько других ветвей;
2. Хотя бы один ток должен входить в узел.

Предположим, что после расчёта цепи получились следующие значения токов:

I1 = -5 А;
I2 = -2 A;
I3 = 3 А.

Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).

Рисунок 3 — действительное направление токов обозначено синими стрелками

• I1 − I2 + I3 = 0;
• -5  − (-2) +3 = 0;
• -I1 + I2 + I3 = 0;
• -5  + 2 +3 = 0.

Второй закон Кирхгофа.

Второй закон Кирхгофа: в контуре электрической цепи алгебраическая сумма эдс равна алгебраической сумме падений напряжения на всех сопротивлениях данного контура.

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; I_i, R_i – ток и сопротивление i-й ветви.

Применение второго закона Кирхгофа

Для контура ABСDE, изображенного на рисунке 4, стрелками указаны положительные направления токов (произвольно). Составим уравнение согласно второму закону Кирхгофа. Для этого произвольно зададимся направлением обхода контура по часовой или против часовой стрелки. В данном примере направление обхода контура выберем по часовой стрелке.

Рисунок 4

При составлении уравнений по второму закону Кирхгофа, ЭДС записывается со знаком “+”, если ее направление совпадает с направлением произвольно выбранного обхода контура. В противном случае ЭДС записывается со знаком “-”.

Падения напряжения записываются со знаком “+”, если направление тока в нем совпадает с направлением обхода.

Начнём с эдс E1, так как её направление совпадает с обходом контура — записываем её со знаком “+” перед знаком равно.

Контур ABСDE E1 =

E2 направленна против обхода контура записываем со знаком “-” перед знаком равно.

Контур ABСDE E1 − E2 =

Так как больше ЭДС в контуре ABСDЕ нет — левая часть уравнения готова.

В правой части уравнения указываются падения напряжения контура, так как направления токов I1 и I2 совпадает с обходом контура – записываем падения напряжения со знаком “+”.

Контур ABСDЕE E1 − E2 = I1*R1 + I2*R2

Направление тока I3 не совпадет с обходом контура:

Контур ABСDE E1 − E2 = I1*R1 + I2*R2 − I3*R3.

Уравнение для контура готово.

Законы Кирхгофа являются основой для расчета электрической цепи, вот несколько методов применяющие данные законы.

Правила Кирхгофа — Википедия

Пра́вила Кирхго́фа (часто в литературе ошибочно называются Зако́нами Кирхго́фа) — соотношения, которые выполняются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного, переменного и квазистационарного тока^[1]. Имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения многих задач в теории электрических цепей и практических расчётов сложных электрических цепей. Применение правил Кирхгофа к линейной электрической цепи позволяет получить систему линейных уравнений относительно токов или напряжений, и соответственно, найти значения токов на всех ветвях цепи и все межузловые напряжения.

Сформулированы Густавом Кирхгофом в 1845 году^[2].

Название «Правила» корректнее потому, что эти правила не являются фундаментальными законами природы, а вытекают из фундаментальных законов сохранения заряда и безвихревости электростатического поля (третье уравнение Максвелла при неизменном магнитном поле). Эти правила не следует путать с ещё двумя законами Кирхгофа в химии и физике.

Формулировка правил

Определения

Для формулировки правил Кирхгофа вводятся понятия узел, ветвь и контур электрической цепи. Ветвью называют участок электрической цепи с одним и тем же током, например, на рис. отрезок, обозначенный R₁, I₁ есть ветвь. Узлом называют точку соединения трех и более ветвей (на рис. обозначены жирными точками). Контур — замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи. Термин замкнутый путь означает, что, начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, можно вернуться в исходный узел. Ветви и узлы, проходимые при таком обходе, принято называть принадлежащими данному контуру. При этом нужно иметь в виду, что ветвь и узел могут принадлежать одновременно нескольким контурам.

В терминах данных определений правила Кирхгофа формулируются следующим образом.

Первое правило

Сколько тока втекает в узел, столько из него и вытекает.
i₂ + i₃ = i₁ + i₄

Первое правило Кирхгофа гласит, что алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. При этом направленный к узлу ток принято считать положительным, а направленный от узла — отрицательным: Алгебраическая сумма токов, направленных к узлу, равна сумме направленных от узла.

∑ j = 1 n I j = 0. {\displaystyle \sum \limits _{j=1}^{n}I_{j}=0.}

Иными словами, сколько тока втекает в узел, столько из него и вытекает. Это правило следует из фундаментального закона сохранения заряда.

Второе правило

Второе правило Кирхгофа (правило напряжений Кирхгофа) гласит, что алгебраическая сумма напряжений на резистивных элементах замкнутого контура равна алгебраической сумме ЭДС, входящих в этот контур. Если в контуре нет источников ЭДС (идеализированных генераторов напряжения), то суммарное падение напряжений равно нулю:

для постоянных напряжений ∑ k = 1 n E k = ∑ k = 1 m U k = ∑ k = 1 m R k I k ; {\displaystyle \sum _{k=1}^{n}E_{k}=\sum _{k=1}^{m}U_{k}=\sum _{k=1}^{m}R_{k}I_{k};}

для переменных напряжений ∑ k = 1 n e k = ∑ k = 1 m u k = ∑ k = 1 m R k i k + ∑ k = 1 m u L k + ∑ k = 1 m u C k . {\displaystyle \sum _{k=1}^{n}e_{k}=\sum _{k=1}^{m}u_{k}=\sum _{k=1}^{m}R_{k}i_{k}+\sum _{k=1}^{m}u_{L\,k}+\sum _{k=1}^{m}u_{C\,k}.}

Это правило вытекает из 3-го уравнения Максвелла, в частном случае стационарного магнитного поля.

Иными словами, при полном обходе контура потенциал, изменяясь, возвращается к исходному значению. Частным случаем второго правила для цепи, состоящей из одного контура, является закон Ома для этой цепи. При составлении уравнения напряжений для контура нужно выбрать положительное направление обхода контура. При этом падение напряжения на ветви считают положительным, если направление обхода данной ветви совпадает с ранее выбранным направлением тока ветви, и отрицательным — в противном случае (см. далее).

Правила Кирхгофа справедливы для линейных и нелинейных линеаризованных цепей при любом характере изменения во времени токов и напряжений.

Особенности составления уравнений для расчёта токов и напряжений

Если цепь содержит p {\displaystyle p} узлов, то она описывается p − 1 {\displaystyle p-1} уравнениями токов. Это правило может применяться и для других физических явлений (к примеру, система трубопроводов жидкости или газа с насосами), где выполняется закон сохранения частиц среды и потока этих частиц.

Если цепь содержит m {\displaystyle m} ветвей, из которых содержат источники тока ветви в количестве m i {\displaystyle m_{i}} , то она описывается m − m i − ( p − 1 ) {\displaystyle m-m_{i}-(p-1)} уравнениями напряжений.

• Правила Кирхгофа, записанные для p − 1 {\displaystyle p-1} узлов или m − ( p − 1 ) {\displaystyle m-(p-1)} контуров цепи, дают полную систему линейных уравнений, которая позволяет найти все токи и все напряжения.
• Перед тем, как составить уравнения, нужно произвольно выбрать:
  • положительные направления токов в ветвях и обозначить их на схеме, при этом не обязательно следить, чтобы в узле направления токов были и втекающими, и вытекающими, окончательное решение системы уравнений всё равно даст правильные знаки токов узла;
  • положительные направления обхода контуров для составления уравнений по второму закону, с целью единообразия рекомендуется для всех контуров положительные направления обхода выбирать одинаковыми (напр.: по часовой стрелке).
• Если направление тока совпадает с направлением обхода контура (которое выбирается произвольно), падение напряжения считается положительным, в противном случае — отрицательным.
• При записи линейно независимых уравнений по второму правилу Кирхгофа стремятся, чтобы в каждый новый контур, для которого составляют уравнение, входила хотя бы одна новая ветвь, не вошедшая в предыдущие контуры, для которых уже записаны уравнения по второму закону (достаточное, но не необходимое условие).
• В сложных непланарных графах электрических цепей человеку трудно увидеть независимые контуры и узлы, каждый независимый контур (узел) при составлении системы уравнений порождает ещё 1 линейное уравнение в определяющей задачу системе линейных уравнений. Подсчёт количества независимых контуров и их явное указание в конкретном графе развит в теории графов.

Пример

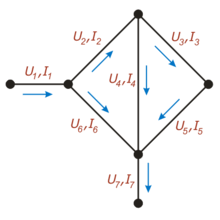На этом рисунке для каждой ветви обозначен протекающий по ней ток (буквой «I») и напряжение между соединяемыми ею узлами (буквой «U»)

Количество узлов: 3.

p − 1 = 2 {\displaystyle p-1=2}

Количество ветвей (в замкнутых контурах): 4. Количество ветвей, содержащих источник тока: 0.

m − m i − ( p − 1 ) = 2 {\displaystyle m-m_{i}-(p-1)=2}

Количество контуров: 2.

Для приведённой на рисунке цепи, в соответствии с первым правилом, выполняются следующие соотношения:

{ I 1 − I 2 − I 6 = 0 I 2 − I 4 − I 3 = 0 {\displaystyle {\begin{cases}I_{1}-I_{2}-I_{6}=0\\I_{2}-I_{4}-I_{3}=0\end{cases}}}

Обратите внимание, что для каждого узла должно быть выбрано положительное направление, например, здесь токи, втекающие в узел, считаются положительными, а вытекающие — отрицательными.

Решение полученной линейной системы алгебраических уравнений позволяет определить все токи узлов и ветвей, такой подход к анализу цепи принято называть методом контурных токов.

В соответствии со вторым правилом, справедливы соотношения:

{ U 2 + U 4 − U 6 = 0 U 3 + U 5 − U 4 = 0 {\displaystyle {\begin{cases}U_{2}+U_{4}-U_{6}=0\\U_{3}+U_{5}-U_{4}=0\end{cases}}}

Полученные системы уравнений полностью описывают анализируемую цепь, и их решения определяют все токи и все напряжения ветвей. Такой подход к анализу цепи принято называть методом узловых потенциалов.

О значении для электротехники

Правила Кирхгофа имеют прикладной характер и позволяют наряду и в сочетании с другими приёмами и способами (метод эквивалентного генератора, принцип суперпозиции, способ составления потенциальной диаграммы) решать задачи электротехники. Правила Кирхгофа нашли широкое применение благодаря простоте формулировки уравнений и возможности их решения стандартными способами линейной алгебры (методом Крамера, методом Гаусса и др.).

Закон излучения Кирхгофа

Закон излучения Кирхгофа гласит — отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты для равновесного излучения и не зависит от их формы, химического состава и проч.

Закон Кирхгофа в химии

Закон Кирхгофа гласит — температурный коэффициент теплового эффекта химической реакции равен изменению теплоёмкости системы в ходе реакции.

Примечания

Литература

• Матвеев А. Н. Электричество и магнетизм : учебное пособие. — М.: Высшая школа, 1983. — 463 с.
• Калашников С. Г. Электричество : учебное пособие. — М.: Физматлит, 2003. — 625 с.
• Бессонов Л. А. Теоретические основы электротехники. Электрические цепи. — 11-е издание. — М.: Гардарики, 2007.
• Герасимов В. Г., Кузнецов Э. В., Николаева О. В. Электротехника и электроника. Кн. 1. Электрические и магнитные цепи. — М.: Энергоатомиздат, 1996. — 288 с. — ISBN 5-283-05005-X.

Краткая информация о законах Кирхгофа с принципиальной схемой

В 1845 году Густав Кирхгоф (немецкий физик) вводит свод законов, касающихся тока и напряжения в электрических цепях. Законы Кирхгофа обычно называют KCL (Закон Кирхгофа по току) и KVL (Закон Кирхгофа по напряжению). KVL утверждает, что алгебраическая сумма напряжения в узле замкнутой цепи равна нулю. Закон KCL гласит, что в замкнутой цепи входящий ток в узле равен току, выходящему из узла.Когда мы наблюдаем в учебнике по резисторам, что одно эквивалентное сопротивление (RT) может быть найдено при последовательном или параллельном подключении нескольких резисторов, эти схемы подчиняются закону Ома. Но в сложных электрических цепях мы не можем использовать этот закон для расчета напряжения и тока. Для таких расчетов мы можем использовать KVL и KCL.

Законы Кирхгофа

Законы Кирхгофа в основном касаются напряжения и тока в электрических цепях. Эти законы можно понимать как результаты уравнений Максвелла в пределе низких частот.Они идеально подходят для цепей постоянного и переменного тока на частотах, где длины волн электромагнитного излучения очень велики по сравнению с другими цепями.

Законы Кирхгофа для цепей

Существуют различные отношения между напряжениями и токами в электрической цепи. Эти отношения определяются законами Кирхгофа, такими как KVL и KCL. Эти законы используются для определения полного сопротивления сложной сети или эквивалентного электрического сопротивления и токов, протекающих в нескольких ветвях н / в.

Закон Кирхгофа по току

Закон о токе KCL или Кирхгофа или первый закон Кирхгофа гласит, что полный ток в замкнутой цепи, входящий ток в узле равен току, выходящему в узле, или алгебраической сумме тока в узле в узле электронная схема равна нулю.

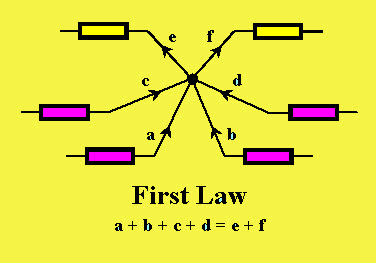
Закон Кирхгофа

На вышеприведенной диаграмме токи обозначены буквами a, b, c, d и e. Согласно закону KCL, входящие токи равны a, b, c, d, а выходящие токи — e и f с отрицательными значениями.Уравнение может быть записано как

a + b + c + d = e + f

Обычно в электрической цепи термин узел относится к стыку или соединению нескольких компонентов или элементов или токоведущих дорожек, например компоненты и кабели. В замкнутой цепи должен существовать ток, протекающий в полосе узла или из него. Этот закон используется для анализа параллельных цепей.

Закон Кирхгофа о напряжении

KVL или закон напряжения Кирхгофа или второй закон Кирхгофа гласит, что алгебраическая сумма напряжения в замкнутой цепи равна нулю или алгебраическая сумма напряжения в узле равна нулю.

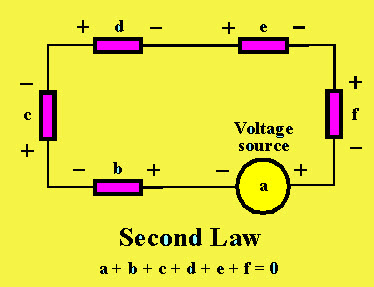
Закон Кирхгофа о напряжении

Этот закон касается напряжения. Например, объясняется приведенная выше схема. Источник напряжения «a» соединен с пятью пассивными компонентами, а именно b, c, d, e, f, имеющими разность напряжений на них. Арифметически разница напряжений между этими компонентами складывается, потому что эти компоненты соединены последовательно. Согласно закону KVL, напряжение на пассивных компонентах в цепи всегда равно и противоположно источнику напряжения.Следовательно, сумма разностей напряжений на всех элементах в цепи всегда равна нулю.

a + b + c + d + e + f = 0

Общие термины теории цепей постоянного тока

Общая цепь постоянного тока состоит из различных теоретических терминов:

Цепь: Цепь постоянного тока является проводящей с обратной связью полоса, по которой протекает электрический ток
Путь: Одна дорожка используется для подключения источников или элементов
Узел: Узел — это соединение в цепи, в которой несколько элементов соединены вместе, и обозначено точкой ,
Ветвь: Ветвь — это одиночный элемент или совокупность элементов, которые соединены между двумя узлами, такими как резисторы или источник
Петля: Петля в цепи — это замкнутый путь, где ни один элемент схемы или узел не встречается более чем один раз.
Сетка: Сетка не содержит замкнутого пути, но представляет собой единственный открытый цикл, и он не содержит никаких компонентов внутри сетки.

Пример законов Кирхгофа

Используя эту схему, мы можем рассчитать протекающий ток в резисторе 40 Ом

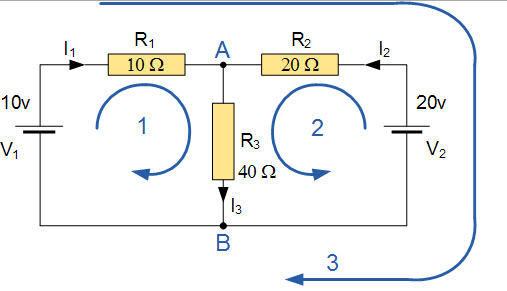
Пример схемы для KVL и KCL

Вышеупомянутая схема состоит из двух узлов, а именно A и B, трех ветвей и двух независимые петли.

Применив KCL к указанной выше схеме, мы можем получить следующие уравнения.

В узлах A и B мы можем получить уравнения

I1 + I2 = I2 и I2 = I1 + I2

Используя KVL, уравнения мы можем получить следующие уравнения

Из цикла 1: 10 = R1 X I1 + R2 X I2 = 10I1 + 40I2
Из цикла 2: 20 = R2 X I2 + R2 X I3 = 20I2 + 40I3
Из цикла 3: 10-20 = 10I1-20 I2

Уравнение I2 можно переписать как

Уравнение1 = 10 = 10I1 + 40 (I1 + I2) = 50 I1 + 40 I2
Уравнение 2 = 20 = 20I2 +40 (I1 + I2) = 40 I1 + 60 I2

Теперь у нас есть два параллельных уравнения, которые можно сократить до значений I1. и I2

Замена I1 на I2 дает значение I1 = -0.143 А
Замена I2 на I1 дает значение I2 = +0,429 А

Нам известно уравнение I3 = I1 + I2

Поток тока в резисторе R3 записывается как -0,143 + 0,429 = 0,286 А
Напряжение на резисторе R3 записывается как: 0,286 x 40 = 11,44 В

Знак –ve для «I» означает, что изначально предпочтительное направление протекания тока было неправильным. Фактически, аккумулятор на 20 В заряжает Аккумулятор 10 вольт.

Это все о законах Кирхгофа, которые включают KVL и KCL.Эти законы используются для расчета тока и напряжения в линейной цепи, и мы также можем использовать анализ контура для вычисления тока в каждом контуре. Кроме того, любые вопросы относительно этих законов, пожалуйста, дайте свои ценные предложения, комментируя в разделе комментариев ниже.

Фото:

.

Законы Кирхгофа

Законы Кирхгофа

Вперед: Проблемы Up: цепей предыдущий: резисторов, включенных параллельно

Хотя полезно иметь возможность уменьшить количество последовательных и параллельных резисторов в схемы, когда они возникают, схемы в целом не состоят исключительно таких комбинаций. Для таких случаев есть мощный набор отношения, называемые законы Кирхгофа , которые позволяют анализировать произвольные схемы.Таких законов два:

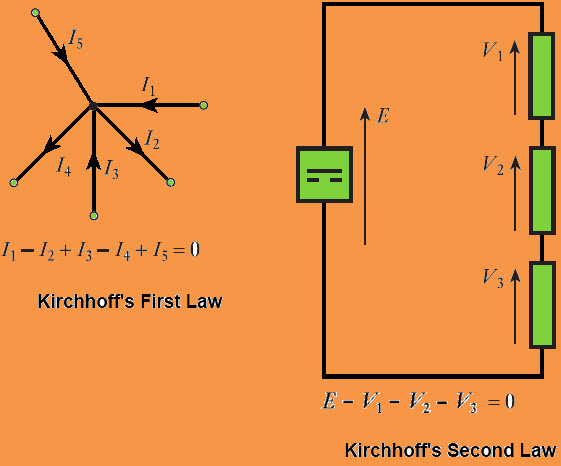
• 1 ^st law or the junction rule : для данного перекрестка или узла в цепи, сумма входящих токов равна сумме выходящих токов. Этот закон является утверждением сохранения заряда. Например, на рис. 17.6,
  

  Рисунок 17.6: Иллюстрация правила перекрестка Кирхгофа

  
  правило соединения говорит нам I ₁ = I ₂ + I ₃ .
• 2 ^{nd закон} или правило петли : вокруг любого замкнутого петля в цепи, сумма разностей потенциалов по всем элементам равно нулю. Этот закон — утверждение сохранения энергии, в этом любое обвинение, что начинается и заканчивается в одной точке с та же скорость должна была набрать столько же энергии, сколько и потерянный. Например, на рис. 17.7,
  

  Рисунок 17.7: Иллюстрация правила петли Кирхгофа

  
  , где прямоугольниками обозначен элемент схемы, правило цикла говорит нам 0 = ( V _b — V _a ) + ( V _c — V _b ) + ( V _d — V _c ) + ( В _d — В _a ).

Второй закон влечет за собой определенные условные обозначения для потенциальных различий. по элементам схемы. Для батарей и резисторов эти условные обозначения следующие: резюмировано на рис. 17.8. Обратите внимание, что в этих соглашениях ток всегда течет от высокого к низкому потенциалу.

Рисунок 17.8: Соглашения о знаках для правила петли Кирхгофа

При анализе схем с использованием законов Кирхгофа полезно иметь в виду следующие рекомендации.

1.

Нарисуйте схему и присвойте метки известным и неизвестным количества, включая токи в каждой ветви. Вы должны назначить направления течениям; не волнуйся, если ты неправильно угадать направление конкретного неизвестного тока, поскольку ответ в результате анализа в этом случае просто выйдет отрицательным, но с нужной величиной.

2.

Примените правило соединения к как можно большему количеству соединений в цепи для получения максимального количества независимых отношений.

3.

Примените правило цикла к необходимому количеству петель в схеме. чтобы решить неизвестное. Обратите внимание, что если у одного есть n неизвестных в схеме потребуется n независимых уравнений. В общем есть будет больше петель в цепи, чем нужно решить для всех неизвестные; отношения, возникающие из этих « лишних » циклов, могут быть использованы в качестве проверки последовательности ваших окончательных ответов.

4.

Решите полученную систему одновременных уравнений для неизвестные количества.

Умение анализировать схемы по законам Кирхгофа, особенно с с учетом условных обозначений и решения одновременных уравнений, приходит с практикой.

---

Вперед: Проблемы Up: цепей предыдущий: резисторов, включенных параллельно

[email protected]
09.10.1997

,

Закон Кирхгофа о цепях для напряжения и тока

Сегодня мы узнаем о законе Кирхгофа о цепях. Прежде чем вдаваться в детали и теоретическую часть, давайте посмотрим, что это на самом деле.

В 1845 году немецкий физик Густав Кирхгоф описал взаимосвязь двух величин в токе и разности потенциалов (напряжения) внутри цепи . Это соотношение или правило называется Законом Кирхгофа.

Закон Кирхгофа состоит из двух законов: Закон Кирхгофа — , который связан с протекающим током, внутри замкнутой цепи и называется KCL , а второй — это закон Кирхгофа , который предназначен для работы с источниками напряжения цепь, известная как закон напряжения Кирхгофа или KVL .

Первый закон Кирхгофа / KCL

Первый закон Кирхгофа: « В любом узле (соединении) в электрической цепи сумма токов, протекающих в этот узел, равна сумме токов, вытекающих из этого узла ». Это означает, что , если мы рассматриваем узел как резервуар для воды, скорость потока воды, которая наполняет резервуар, равна скорости потока, который его опорожняет.

Итак, в случае электричества сумма токов, поступающих в узел, равна сумме выходных токов из узла.

Мы лучше поймем это на следующем изображении.

На этой схеме показано соединение, в котором несколько проводов соединены вместе . Синие провода подают ток в узел , а красные провода принимают токи из узла . Тремя входящими грузилами соответственно Iin1, Iin2 и Iin3 , а остальными исходящими грузилами соответственно Iout1, Iout2 и Iout3 .

Согласно закону общий входящий ток в этом узле равен сумме токов трех проводов (который равен Iin1 + Iin2 + Iin3), а также равен сумме токов трех исходящих проводов (Iout1 + Iout2 + Iout3).

Если вы преобразуете это в алгебраическое суммирование, сумма всех токов, входящих в узел, и сумма токов, выходящих из узла, будет равна 0. Для случая источника тока текущий поток будет положительным, а для случая при опускании тока текущий поток будет отрицательным.
Итак,

( Iin1  +  Iin2  +  Iin3 ) + ( -Iout1  +  -Iout2  +  -Iout3 ) =  0 .
 

Эта идея называется Сохранение заряда .

Второй закон Кирхгофа / KVL

Концепция второго закона Кирхгофа также очень полезна для анализа схем. В его Втором законе говорится, что « Для последовательной сети или пути с замкнутым контуром алгебраическая сумма произведений сопротивлений проводников и тока в них равна нулю или полной ЭДС, доступной в этом контуре. ».

Направленная сумма разностей потенциалов или напряжения на всем сопротивлении (сопротивление проводника в случае отсутствия других резистивных продуктов) равна нулю, 0.

Давайте посмотрим на схему.

На этой схеме 4 резистора подключены к источнику питания «vs». Ток течет внутри замкнутой сети от положительного узла к отрицательному через резисторы по часовой стрелке. Согласно закону Ома в теории цепей постоянного тока, на каждом резисторе будет некоторая потеря напряжения из-за соотношения сопротивления и тока. Если мы посмотрим на формулу, это В = IR , где I — ток, протекающий через резистор.В этой сети есть четыре точки на каждом резисторе. Первая точка — это A, который получает ток от источника напряжения и подает ток на R1. То же самое происходит с B, C и D.

Как согласно закону KCL , узлы A, B, C, D, где ток входит, а ток выходит, одинаковы. В этих узлах сумма входящего и исходящего тока равна 0, поскольку узлы являются общими между потребляющим и исходящим током.

Теперь падение напряжения на A и B составляет vAB , B и C — vBC , C и D — vCD , D и A — vDA .

Сумма этих трех разностей потенциалов составляет vAB + vBC + vCD, , а разность потенциалов между источником напряжения (между D и A) равна –vDA . Из-за того, что ток течет по часовой стрелке, источник напряжения перевернут, и по этой причине он имеет отрицательное значение.

Следовательно, сумма полных разностей потенциалов равна

.

  vAB + vBC + vCD + (-vDA) = 0  

Следует иметь в виду, что текущий поток должен идти по часовой стрелке в каждом узле и на каждом пути сопротивления, иначе расчет не будет точным.

Общая терминология в теории цепей постоянного тока:

Теперь мы уже знакомы с законом цепи Кирхгофа о напряжении и токе, KCL и KVL, но, как мы уже видели в предыдущем руководстве, с помощью закона Ома мы можем измерять токи и напряжение на резисторе. Но в случае сложной схемы, такой как мост и сеть, вычисление тока и падения напряжения становится более сложным, используя только закон Ома. В таких случаях закон Кирхгофа очень полезен для получения идеальных результатов.

В случае анализа используется несколько терминов для описания частей схемы. Эти условия следующие: —

Серия: —

Когда одинаковый ток протекает через все компоненты, соединенные один за другим на конце, это называется последовательным соединением

Параллельный: —

Когда одинаковая величина напряжения приложена ко всем компонентам, подключенным параллельно, когда оба конца всех компонентов соединены в двух точках, в комбинации один к одному, который имеет одинаковую разность потенциалов.

Филиал: —

Один или несколько компонентов подключаются между двумя узлами. Это могут быть резистивные компоненты или источники питания, называемые ответвлением.

Схема / схема: —

Замкнутый контур с проводящим путем (ами), по которому протекает ток.

Шлейф: —

Замкнутый путь в цепи, в которой ни один узел или соединение не встречается более одного раза.

Сетка: —

Одиночный открытый контур без замкнутого пути, внутри которого отсутствуют компоненты.

Узел: —

Это соединение или терминал в цепи, где два или более элемента электрически соединены и образуют две или более ответвлений. На схеме это точка, в которой выполняется минимум два соединения.

Переход: —

Junction является синонимом Node.

Путь: —

Соединительные элементы или источники питания в одну линию.

Пример решения схемы с использованием KCL и KVL:

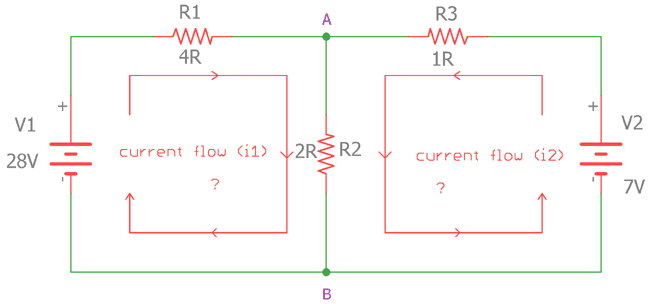
Вот двухконтурная схема.В первом контуре V1 — это источник напряжения, который подает 28 В через R1 и R2, а во втором контуре; V2 — это источник напряжения, обеспечивающий 7 В на R3 и R2. Вот два разных источника напряжения, обеспечивающих разные напряжения на двух контурах контура. Резистор R2 в обоих случаях общий. Нам нужно вычислить два потока тока, i1 и i2, используя формулу KCL и KVL , а также при необходимости применить закон Ома.

Давайте посчитаем для первого цикла.

Как описано ранее в KVL, , что в последовательном сетевом пути с замкнутым контуром, разность потенциалов всех резисторов равна 0.

Это означает, что разность потенциалов на R1, R2 и V1 в случае протекания тока по часовой стрелке равна нулю.

  VR1 + VR2 + (-V1) = 0  

Давайте выясним разность потенциалов на резисторах.

В случае VR1

В соответствии с законом сопротивления V = IR (I = ток и R = сопротивление в Ом)

  VR1 = (i1) x 4
VR1 = 4 (i1) 
 

В случае VR2

R2 является общим для обоих шлейфов. Таким образом, полный ток, протекающий через этот резистор, является суммой обоих токов, таким образом, I через R2 равно (i1 + i2).

Итак,

В соответствии с законом сопротивления V = IR (I = ток и R = сопротивление в Ом)

  VR2 = (i1 + i2) x 2
VR1 = 2 {(i1) + (i2)}  

В случае V1,

Поскольку ток течет по часовой стрелке , разность потенциалов будет отрицательной, поэтому она составляет -28В .

Таким образом, по КВЛ

  VR1 + VR2 + (-V1) = 0 
  VR1 + VR2 + (-V1) = 0 
  4 (i1) + 2 {(i1) + (i2)} - 28 =  

  4 (i1) + 2 (i1) + 2 (i2) - 28 = 0
6 (il) + 2 (i2) = 28 …………………… .. Уравнение 1  

Давайте вычислим второй цикл .

В этом случае ток течет в направлении против часовой стрелки .

То же, что и предыдущий, разность потенциалов на R3, R2 и V2 в случае протекания тока по часовой стрелке равна нулю.

  VR3 + VR2 + V1 = 0  

Давайте выясним разность потенциалов на этих резисторах.

В случае VR3

Будет отрицательным из-за направления против часовой стрелки.

В соответствии с законом сопротивления V = IR (I = ток и R = сопротивление в Ом)

 
VR3 = - (i2) x 1
VR3 = -1 (i2)  

В случае VR2,

Также будет отрицательным из-за направления против часовой стрелки ,

R2 является общим для обоих шлейфов .Таким образом, полный ток, протекающий через этот резистор, является суммой обоих токов, таким образом, I через R2 равно (i1 + i2) .

Итак,

  Согласно закону сопротивления V = IR (I = ток и R = сопротивление в Ом)

VR2 = - (i1 + i2) x 2
VR2 = -2 {(i1) + (i2)}  

В случае V2

Поскольку ток течет против часовой стрелки , разность потенциалов будет положительной, в точности противоположной V1, поэтому она составляет 7 В.

Так, по КВЛ

  VR3 + VR2 + V2 = 0 
  VR3 + VR2 + V2 = 0 
  -1 (i2) - 2 {(i1) + (i2)} + 7 = 0  

  -1 (i2) - 2 (i1) - 2 (i2) + 7 = 0
-2 (il) - 3 (i2) = -7 …………………… .. Уравнение 2  

Теперь решая эти два одновременных уравнений, мы получаем i1 равно 5A и i2 равно -1 А .

Теперь, , посчитаем значение тока, протекающего через резистор R2 .
Поскольку является разделяющим резистором для обоих контуров, трудно получить результат, используя только закон Ома .

Согласно правилу KCL, ток , поступающий в узел, равен току, выходящему из узла.

Так в случае протекания тока через резистор R2: —

  iR2 = i1 + i2 
  = 5А + (-1А)
= 4A  

Ток, протекающий через этот резистор R2, равен 4A .

Вот как KCL и KVL полезны для определения тока и напряжения в сложных схемах.

Шаги по применению закона Кирхгофа в сетях:

1. Маркировка всех источников напряжения и сопротивлений как V1, V2, R1, R2 и т. Д., Если значения допустимы, то необходимы предположения.
2. Обозначение каждой ветви или тока контура как i1, i2, i3 и т. Д.
3. Применение закона напряжения Кирхгофа (KVL) для каждого соответствующего узла.
4. Применение закона Кирхгофа (KCL) для каждого отдельного независимого контура в цепи.
5. При необходимости будут применяться линейные одновременные уравнения, чтобы узнать неизвестные значения.

.

Что такое закон Кирхгофа и закон напряжения Кирхгофа?

Закон Кирхгофа: Немецкий физик Густав Кирхгоф разработал два закона, позволяющих легко анализировать взаимосвязь любого количества элементов схемы. Первый закон имеет дело с протеканием тока и широко известен как Закон Кирхгофа ( KCL), а второй касается падения напряжения в замкнутой сети и известен как Закон Кирхгофа (KVL).

KCL утверждает, что сумма тока в переходе остается нулевой, и согласно KVL сумма электродвижущей силы и падения напряжения в замкнутой цепи остается нулевой.

При применении KCL входящий ток принимается как положительный, а исходящий — как отрицательный. Аналогичным образом, при применении KVL рост потенциала считается положительным, а падение потенциала — отрицательным.

KVL и KCL помогают найти аналогичное электрическое сопротивление и импедансы сложной системы. Он также определяет ток, протекающий через каждую ветвь сети.

В комплекте:

Эти два закона описаны ниже

Действующий закон Кирхгофа

Текущий закон Кирхгофа гласит, что «алгебраическая сумма всех токов в любой узловой точке или стыке цепи равна нулю».

Σ I = 0

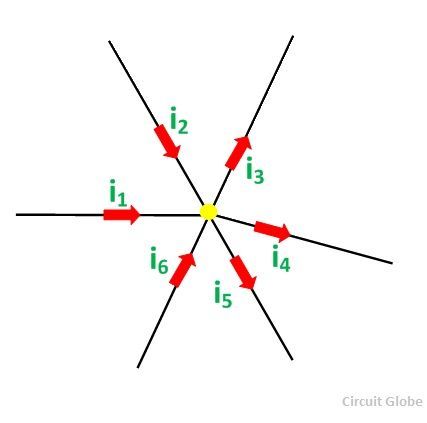Принимая во внимание приведенную выше цифру в соответствии с действующим законодательством Кирхгофа:

i ₁ + i ₂ — i ₃ — i ₄ — i ₅ + i ₆ = 0 ……… (1)

Направление входящих токов к узлу считается положительным, а исходящие токи — отрицательным. Также можно принять обратное, т.е. входящий ток как отрицательный, а исходящий как положительный. Это зависит от вашего выбора.

Уравнение (1) также можно записать как:

i ₁ + i ₂ + i ₆ = i ₃ + i ₄ + i ₅

Сумма входящих токов = Сумма исходящих токов

В соответствии с Законом Кирхгофа , алгебраическая сумма токов, входящих в узел, должна быть равна алгебраической сумме токов, покидающих узел в электрической сети.

Закон Кирхгофа о напряжении

Закон Кирхгофа о напряжении гласит, что алгебраическая сумма напряжений (или падений напряжения) на любом замкнутом пути сети, поперечной в одном направлении, равна нулю.Другими словами, в замкнутой цепи алгебраическая сумма всех ЭДС и алгебраическая сумма всех падений напряжения (произведение тока (I) и сопротивления (R)) равна нулю.

Σ E + Σ V = 0

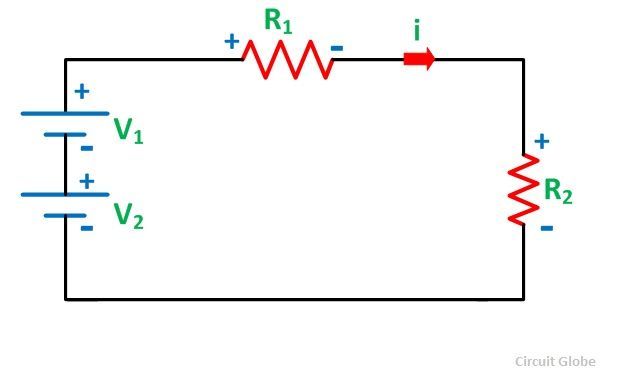На приведенном выше рисунке показан замкнутый контур, также называемый сеткой. В соответствии с законом Кирхгофа о напряжении:

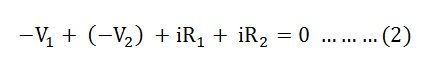
Здесь предполагаемый ток I вызывает положительное падение напряжения при переходе от положительного к отрицательному потенциалу, а отрицательное падение потенциала, когда ток течет от отрицательного к положительному потенциалу.

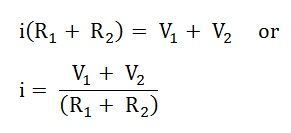
Принимая во внимание другой рисунок, показанный ниже, и принимая направление тока i

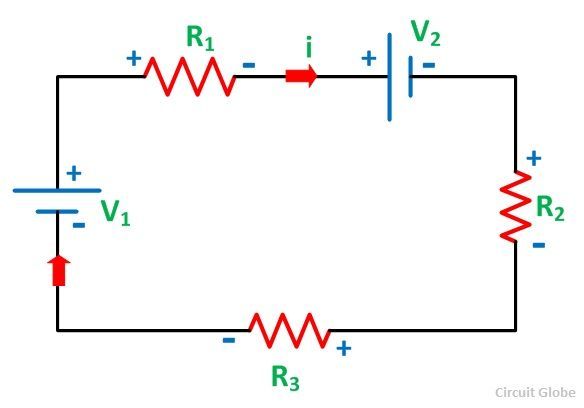
Следовательно,

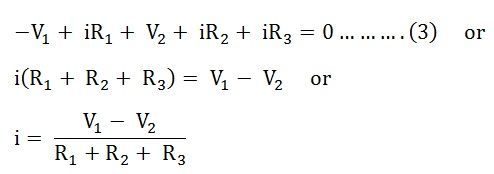
Видно, что напряжение V ₁ отрицательно как в уравнении (2), так и в уравнении (3), тогда как V ₂ отрицательно в уравнении (2), но положительно в уравнении (3). Это связано с изменением направления тока, принятым на обоих рисунках.

На рисунке A ток в обоих источниках V ₁ и V ₂ течет с отрицательной полярности на положительную, в то время как на рисунке B ток в источнике V ₁ отрицательный на положительный, но для V ₂ равен от положительной к отрицательной полярности.

Для зависимых источников в цепи также может применяться KVL. В случае расчета мощности любого источника, когда ток входит в источник, мощность поглощается источниками, в то время как источник подает мощность, если ток выходит из источника.

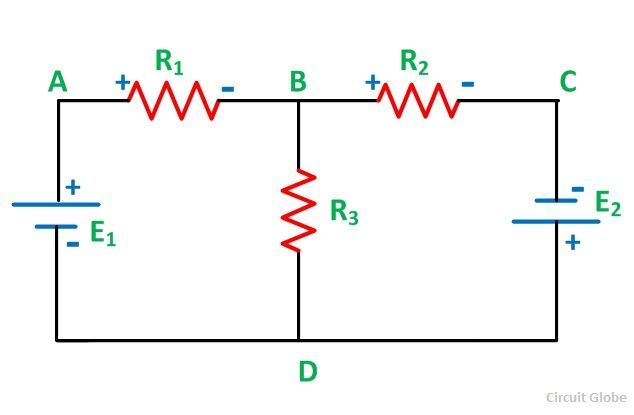
Важно знать некоторые термины, используемые в схеме при применении KCL и KVL, такие как узел, соединение, ветвь, петля, сетка. Они объясняются с помощью схемы, показанной ниже:

Узел

Узел — это точка в сети или цепи, где соединяются два или более элемента схемы.Например, на приведенной выше принципиальной схеме A и B — узловые точки.

Переход

Соединение — это точка в сети, в которой соединяются три или более элемента схемы. Это точка, где разделяется ток. В приведенной выше схеме B и D — это переходы.

Филиал

Часть сети, которая находится между двумя точками соединения, называется ветвью. В приведенной выше схеме DAB, BCD и BD являются ветвями схемы.

Петля

Замкнутый путь сети называется петлей.ABDA, BCDB — это петли на приведенной выше принципиальной схеме.

Сетка

Самая простая форма петли, которую нельзя разделить дальше, называется сеткой.

,