Законы Кирхгофа таковы. Что такое законы Кирхгофа?

Другими словами, в узел втекает одинаковое количество тока и из него вытекает одинаковое количество. Этот закон следует из закона сохранения заряда. Если схема содержит p узлов, тогда она описывается p – 1 уравнение тока. Этот закон можно применить и к другим физическим явлениям (например, к водопроводу), где существует закон сохранения величины и потока этой величины.

Содержание

Законы Кирхгофа

Законы Кирхгофа. (или Принципы Кирхгофа) – это соотношения, которые применяются между токами и напряжениями на участках любой электрической цепи. Правила Кирхгофа позволяют рассчитывать любые электрические цепи постоянного тока и квазистационарные электрические цепи. [1] Они имеют особое значение в электротехнике благодаря своей универсальности, поскольку подходят для решения многих задач теории электрических цепей. Применение правил Кирхгофа к линейной цепи дает систему линейных уравнений относительно токов и, следовательно, позволяет найти значение токов на всех ветвях цепи. Сформулирован Густавом Кирхгофом в 1845 году.

Второй закон Кирхгофа работает независимо от количества источников тока и нагрузок, а также от их расположения в цепи. Будет полезно собрать рассматриваемые схемы и провести соответствующие измерения с помощью мультиметра.

Первый закон Кирхгофа

Первый закон Кирхгофа гласит, что сумма токов в любом узле электрической цепи равна нулю. Существует и другая похожая формулировка: сумма токов, входящих в узел, равна сумме токов, вытекающих из узла.

Давайте рассмотрим это более подробно. Узел – это место соединения трех или более проводников.

Ток, втекающий в узел, обозначен стрелкой, направленной к узлу, а ток, вытекающий из узла, обозначен стрелкой, направленной от узла.

Согласно первому закону Кирхгофа

Мы условно присваиваем знак “+” всем входящим токам и знак “-” всем выходящим токам. Хотя это не является принципиальным вопросом.

1-й закон Кирхгофа согласуется с законом сохранения энергии, поскольку электрические заряды не могут накапливаться в узлах, поэтому входящие заряды покидают узел.

Простая схема, состоящая из источника тока напряжением 3 В (две последовательно соединенные батарейки по 1,5 В) и трех резисторов разной величины, поможет нам проверить закон Кирхгофа: 1 кОм, 2 кОм и 3,2 кОм (можно использовать резисторы любой другой величины). Токи будут измерены мультиметром в точках, указанных амперметром.

Если сложить показания трех амперметров с учетом их знаков, то, согласно первому закону Кирхгофа, получится ноль:

Или показания первого амперметра А1 будет равна сумме показаний второго А2 и третий А3 амперметр.

В параллельно В отличие от этого, провода соединены таким образом, что на каждый элемент цепи подается одинаковое напряжение от источника питания, что означает, что каждый элемент цепи имеет разный ток в зависимости от его сопротивления. Примером параллельной схемы является подключение ламп на лестничной клетке: напряжение подается на шины, а лампы устанавливаются на перекладины. Токи, протекающие через каждый узел в такой цепи, определяются первым законом Кирхгофа.

Закон Кирхгофа

Алгебраическая сумма токов в любом узле электрической цепи равна нулю (т.е. число зарядов, вытекающих через этот узел, должно быть равно числу зарядов, входящих в него).

Сумма напряжений в любой замкнутой электрической цепи равна нулю.

Карьера Густава Кирхгофа во многом типична для немецкой физики XIX века. Германия присоединилась к промышленной революции позже, чем ее западные соседи, и поэтому испытывала большую потребность в передовых технологиях для стимулирования промышленного развития. Благодаря этому ученые, особенно естествоиспытатели, пользовались большим уважением в Германии. В год окончания университета Кирхгоф женился на дочери профессора, “выполнив, таким образом”, по словам одного из его биографов, “два необходимых условия для успешной научной карьеры”. Но еще раньше, в возрасте двадцати одного года, он сформулировал основные законы расчета токов и напряжений в электрических цепях, которые сегодня носят его имя.

Середина XIX века стала периодом активных исследований свойств электрических цепей, и результаты этих исследований вскоре нашли практическое применение. Основные принципы расчета простых цепей, такие как закон Ома, были уже хорошо известны. Проблема заключалась в том, что уже технически было возможно создавать очень сложные и разветвленные цепи из проводов и различных элементов схемы – но никто не знал, как смоделировать их математически, чтобы рассчитать их свойства. Кирхгоф смог сформулировать правила, которые позволили относительно легко анализировать самые сложные схемы, и законы Кирхгофа до сих пор являются важным инструментом для специалистов по электронике и электротехнике.

Оба закона Кирхгофа сформулированы достаточно просто и имеют понятную физическую интерпретацию. Первый закон гласит, что если вы рассматриваете любой узел сумма электрических токов, втекающих в цепь, будет равна сумме электрических токов, вытекающих из цепи, что, вообще говоря, является следствием закона сохранения электрического заряда. Например, если у нас есть узел T в электрической цепи и два провода подают в него ток, третий провод будет подавать ток в направлении от этого узла, и он будет равен сумме двух входящих токов. Физический смысл этого закона прост: если бы он не выполнялся, в узле происходило бы непрерывное накопление электрического заряда, чего никогда не происходит.

Второй закон не менее прост. Если у нас есть сложная, разветвленная цепь, ее можно мысленно разложить на ряд простых, замкнутых цепей. Токи в цепи могут по-разному распределяться по этим контурам, и самое сложное – определить, в какую сторону потекут токи в сложной цепи. В любой цепи электроны могут либо получить дополнительную энергию (например. от батареи), или потерять его (например, на резисторе или другом элементе). Второй закон Кирхгофа гласит, что чистая приращенная энергия электронов в любой замкнутой цепи равна нулю. Этот закон также имеет простую физическую интерпретацию. Если бы это было не так, то каждый раз, когда электроны проходят через замкнутую цепь, они приобретали бы или теряли энергию, и сила тока постоянно увеличивалась бы или уменьшалась. В первом случае можно было бы получить вечный двигатель, что запрещено первым законом термодинамики; во втором случае неизбежно исчезли бы все токи в электрических цепях, чего мы не наблюдаем.

Наиболее частое применение законов Кирхгофа наблюдается в так называемых последовательных и параллельных цепях. В в последовательных цепях (Ярким примером такой схемы является елочная гирлянда, состоящая из последовательно соединенных лампочек) Электроны от источника питания проходят последовательно через все лампочки с помощью ряда проводов, и напряжение падает через сопротивление каждой лампочки в соответствии с законом Ома.

В параллельно В отличие от этого, провода соединены таким образом, что на каждый элемент цепи подается одинаковое напряжение от источника питания, что означает, что каждый элемент цепи имеет разный ток в зависимости от его сопротивления. Примером параллельной схемы является подключение ламп на лестничной клетке: напряжение подается на шины, а лампы устанавливаются на перекладины. Токи, протекающие через каждый узел в такой цепи, определяются первым законом Кирхгофа.

Немецкий физик. Он родился в Кенигсберге (современный Калининград). Он сформулировал законы расчета электрических цепей, еще будучи студентом Кенигсбергского университета. Он продолжил свою блестящую карьеру в различных немецких университетах, последним из которых был Берлинский, где он был профессором теоретической физики с 1875 года до своей смерти. Работая в университете Бреслау (на территории современной Польши), вместе с Робертом Бунзеном он разработал основы спектроскопии (ср. Открытие Кирхгофа-Бунсена). Он также открыл еще одну серию законов Кирхгофа, описывающих поглощение и тепловое излучение. Хотя вторую половину своей жизни Кирхгоф провел в инвалидном кресле в результате несчастного случая, все современники считали его очень приятным человеком и убежденным оптимистом.

Физически второй закон Кирхгофа описывает баланс напряжений в любой цепи.

Законы Кирхгофа – формулы и приложения

Законы Кирхгофа определяют взаимосвязь между токами и напряжениями в разветвленных электрических цепях любого типа. Законы Кирхгофа особенно важны в электротехнике благодаря своей универсальности. Законы Кирхгофа справедливы для линейных и нелинейных цепей для постоянных и переменных напряжений и токов.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Она заключается в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

Где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 – I2 + I3 – I4 + I5 = 0

В этом уравнении токи, направленные к узлу, предполагаются положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма напряжений, падающих на отдельные части замкнутой цепи, произвольно выделенные в сложной разветвленной цепи, равна алгебраической сумме ЭДС в цепи

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i ветви.

Таким образом, для замкнутого контура (рис. 2) E1 – E2 + E3 = I1R1 – I2R2 + I3R3 – I4R4

Обратите внимание на знаки полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением любого обхода цепи;

2) падение напряжения на резисторе положительно, если направление тока в резисторе совпадает с направлением тока в шунте.

Физически второй закон Кирхгофа описывает баланс напряжений в любой цепи.

Расчет разветвленной электрической цепи с использованием законов Кирхгофа

Метод законов Кирхгофа предполагает решение системы уравнений, состоящей из первого и второго законов Кирхгофа.

Этот метод предполагает составление уравнений в соответствии с первым и вторым законами Кирхгофа для узлов и контуров электрической цепи и решение этих уравнений для определения неизвестных токов в ветвях и напряжений на них. Таким образом, число неизвестных равно числу ветвей b , следовательно, первый и второй принципы Кирхгофа требуют одинакового числа независимых уравнений.

Число уравнений, которые можно вывести из первого закона, равно числу узлов в цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбираются таким образом, чтобы каждый последующий узел отличался от соседних узлов хотя бы одной ветвью. Остальные уравнения располагаются согласно второму закону Кирхгофа для независимых контуров, т.е. количество уравнений b – (y – 1) = b – y +1 .

Цикл называется независимым, если он содержит хотя бы одну ветвь, которая не содержится в других циклах.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3). Схема содержит четыре узла и шесть ветвей.

Таким образом, из первого закона Кирхгофа получаем y – 1 = 4 – 1 = 3 уравнения, а из второго b – y + 1 = 6 – 4 + 1 = 3 , также три уравнения.

Выберем случайным образом положительные направления токов во всех ветвях (рис. 4). Направление обхода контуров – по часовой стрелке.

Приведите необходимое количество уравнений в соответствии с первым и вторым законами Кирхгофа

Полученная система уравнений решается относительно токов. Если в результате расчета в ветви возникает отрицательный ток, то его направление – против часовой стрелки.
Потенциальная диаграмма – это графическое представление второго закона Кирхгофа, которое используется для проверки правильности расчетов в линейных резистивных цепях. Потенциальный график строится для цепи без источников тока, и потенциалы точек в начале и конце графика должны быть одинаковыми.

Рассмотрим цепь abcda схемы, показанной на рис. 4. Отметим дополнительную точку k в ветви ab между резистором R1 и ЭДС E1.

Рис. 4 Контур для построения графика потенциала

Берем потенциал любого узла равным нулю (например, ?a= 0), выбираем обход контура и строим потенциалы точек контура: ?a = 0, ?k = ?a – I1R1 , ? b = ? k + E1, ?c = ? b – I2R2 , ? d = ?c – E2 , ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы учитывайте, что сопротивление ЭДС равно нулю (рис. 5 ).

Рис. 5 Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Законы Кирхгофа для цепей синусоидального тока формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа: “алгебраическая сумма комплексных токов в узле цепи равна нулю”.

Второй закон Кирхгофа: “В любой замкнутой электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этой цепи”.

Если вам понравилась эта статья, пожалуйста, поделитесь ею в социальных сетях. Это поможет нашему сайту сильно вырасти!

Запишем первый закон Кирхгофа в комплексной форме:

1-й закон Кирхгофа

В цепях, состоящих из источника и приемника энергии, соединенных последовательно, соотношения между током, сопротивлением и ЭДС цепи в целом или любого ее участка определяются законом Ома. На практике, однако, в цепях токи в любой точке идут по разным путям (рис. 1). В связи с этим были введены новые правила расчета схем.

Рисунок 1: Схема параллельного соединения проводников.

Таким образом, при параллельном соединении проводников начала всех проводников соединяются в одной точке, а концы проводников – в другой. Начало цепи подключено к одному полюсу источника напряжения, а конец цепи – к другому полюсу.

На рисунке показано, что при параллельном соединении проводников существует несколько путей, по которым может протекать ток. Ток, текущий в точку A, проходит через три резистора и равен сумме токов, выходящих из этой точки: I = I1 + I2 + I3.

Согласно первому закону Кирхгофа, алгебраическая сумма токов ветвей, сходящихся в каждом узле любой цепи, равна нулю. Ток, направленный к узлу, считается положительным, а ток, направленный от узла, считается отрицательным.

Запишем первый закон Кирхгофа в комплексной форме:

Первый закон Кирхгофа гласит, что алгебраическая сумма токов, направленных к узлу, равна сумме токов, направленных от узла. Это означает, что в узел втекает столько же тока, сколько вытекает из него (что следует из закона сохранения электрического заряда). Алгебраическая сумма – это сумма знаков плюс и минус.

Рисунок 2. i_1+i_4=i_2+i_3.

Рассмотрим применение 1-го закона Кирхгофа на следующем примере:

• I1 – общий ток, втекающий в узел A, а I2 и I3 – токи, вытекающие из узла A.
• Тогда мы можем написать: I1 = I2 + I3.
• Аналогично для узла B: I3 = I4 + I5.
• Пусть I4 = 5 A и I5 = 1 A, получаем: I3 = 5 + 1 = 6 (A).
• Пусть I2 = 10 A, получаем: I1 = I2 + I3 = 10 + 6 = 16 (A).
• Запишем аналогичное соотношение для узла C: I6 = I4 + I5 = 5 + 1 = 6 A.
• И для узла D: I1 = I2 + I6 = 10 + 6 = 16 A
• Таким образом, мы можем ясно видеть справедливость первого закона Кирхгофа.

Здесь мы имеем полную аналогию с распределением потоков воды во взаимосвязанных трубопроводах.

Второй закон

Для расчетов сложных электрических цепей с несколькими источниками энергии применяется второй закон Кирхгофа, который можно сформулировать следующим образом В любой замкнутой электрической цепи алгебраическая сумма всех ЭДС равна алгебраической сумме падений напряжения на последовательно соединенных в цепи резисторах, т.е..

В этом случае эти положительные значения должны рассматриваться как э.д.с. и токи, направление которых совпадает с направлением цепи.
Если в электрическую цепь включены два источника энергии, направление э.д.с. которых одинаково (рис. 20, а), то э.д.с. всей цепи равна сумме э.д.с. этих источников, т.е. E = E₁ + E₂. Однако если э.ф. источников в цепи имеют противоположные направления, то результирующая э.ф. источников равна разности э.ф. источников, т.е.

Когда несколько источников энергии разного направления соединены последовательно в электрическую цепь, общая а.к. равна алгебраической сумме а.к. всех источников. При суммировании а.к. одного направления берется со знаком плюс, а а.к. противоположного направления – со знаком минус. При составлении уравнений направление контура выбирается, а направления токов определяются произвольно.

Замкнутая цепь изображается буквами а, б, в и г. Из-за наличия ветвей в точках а, б, в, г токи I₁, I₂, I₃ и I₄Контур может иметь разные направления вращения, с разными силами.

Для такой цепи, согласно второму закону Кирхгофа, можно записать:

где r₀₁, r₀₂, r₀₃ – внутреннее сопротивление энергии
r₁, r₂, r₃, r₄ – Сопротивление потребителей энергии.
В особом случае отсутствия ответвлений и последовательного соединения проводников общее сопротивление равно сумме всех сопротивлений.
Если внешняя цепь источника энергии с внутренним сопротивлением r состоит, например, из трех последовательно соединенных проводников с соответствующими сопротивлениями

r₁, r₂, r₃то, исходя из второго закона Кирхгофа, можно записать следующее уравнение:

В случае нескольких источников тока левая часть этого равенства будет алгебраической суммой ЭДС этих источников.

Читайте далее:

• Топология электрической цепи (Лекция N 2).
• Разветвленные цепи. Правило обхода цепи – Электричество и магнетизм – Киберфорум.
• Как найти напряжение источника.
• Значение слова ЭЛЕКТРОТЕХНИКАЦИЯ. Что такое ЭЛЕКТРОТЕХНИКА?.
• 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
• Электричество. Сила электричества.
• 5 причин, почему лампочки часто перегорают в вашей квартире и что делать?.

Закон Кирхгофа (страница 1)

Применение закона Кирхгофа к расчету линейных электрических цепей постоянного тока

1. В цепи (рисунок 10) известны значения токов ; величины сопротивлений . Определить напряжение U на входных зажимах цепи, сопротивление и величину Е источника ЭДС.

Решение:
По закону Ома определим напряжение между узлами 3-2:

Из уравнения, составленного по первому закону Кирхгофа для узла 3:

определим ток :

Тогда, по закону Ома для ветви с сопротивлением :

откуда выражаем величину Е источника ЭДС:

Напряжение можно выразить из уравнения, записанного по II закону Кирхгофа для контура 1-3-2-1:

Зная величины напряжения и тока , определим величину сопротивления :

Напряжение на входных зажимах цепи определится:

Ток определим из уравнения, записанного по первому закону Кирхгофа для 1 узла:

тогда

2. В цепи (рисунок 11) известны величины сопротивлений резистивных элементов ; мощность, изменяемая ваттметром Р=320 Вт. Определить токи ветвей, напряжение на зажимах цепи.

Решение:
Из формулы для расчета мощности выражаем ток :

Затем определяем напряжение на зажимах параллельных ветвей:

По закону Ома определяем ток в ветви с сопротивлением :

Значение тока в неразветвленной части цепи определим из уравнения, записанного по первому закону Кирхгофа для узла 1:

Напряжение на входных зажимах цепи можно представить как сумму падений напряжений на сопротивлениях :

где
тогда

3. На рисунке 12 показана часть сложной цепи. Задано: . Найти напряжение .

Решение:
Уравнение по второму закону Кирхгофа для данного контура, при выбранном направлении обхода контура, запишется следующим образом:

откуда выражаем напряжение :

4. В схеме (рисунок 13) известны: . Определить напряжения .

Решение:
Считаем направления обходов контуров совпадающими с направлениям искомых напряжений. Запишем уравнения по второму закону Кирхгофа для каждого контура и выразим напряжения:
контур 1-2-6-5-1

контур 3-4-6-5-3

контур 1-3-5-1

контур 2-4-6-2

контур 1-4-6-5-1

контур 2-3-5-6-2

5. Определить показание амперметра (рисунок 14), если .

Решение:
По закону Ома определим значения токов в ветвях:

Запишем уравнение по первому закону Кирхгофа для узла b:

откуда

6. На рисунке 15 показана часть сложной цепи. Найти напряжения , если .

Решение:
По закону Ома определим ток на участке с-d:

Запишем уравнение по второму закону Кирхгофа для контура a-b-c-d:

откуда выразим напряжение :

7. В схеме электрической цепи, приведенной на рисунке 16, определить токи в ветвях пользуясь законами Кирхгофа. Параметры элементов цени: .

Решение:
Выбираем произвольно положительные направления искомых токов ветвей и обозначаем их на схеме. Составляем уравнение по первому закону Кирхгофа для узла 1. Выбрав направления обходов контуров, составляем уравнения по второму закону Кирхгофа. Получаем систему из трех уравнений:

Решаем полученную систему уравнений с помощью определителей:

Находим значения токов:

Для проверки правильности расчета составим уравнение баланса мощностей:

Мощность источников:

Мощность потребителей:

8. Определить токи ветвей цепи (рисунок 17), если: .

Решение:
Произвольно задаемся положительными направлениями токов в ветвях с сопротивлениями . В ветви с источником тока направление тока уже определено полярностью источника. Составляем уравнение по первому закону Кирхгофа для узла 1. Количество контурных уравнений зависит от количества ветвей с неизвестными токами, т.е. ветвей, не содержащих источники тока. Для данной цепи количество контурных уравнений равно 1. Составим систему уравнений:

Решаем систему уравнений с помощью определителей:

Определяем значения токов:

Первый закон Кирхгофа: определение, формула, вывод, преимущество

Дом »Физика

Дивья Каре | Обновлено: 7 ноября 2022 г. 13:36 IST

0

Сохранить

Скачать публикацию в формате PDF

Законы Кирхгофа помогают в разработке сложных схем с различными электрическими компонентами, которые используются в повседневной жизни. Это также помогает в исследовании любых электрических цепей, например, сколько тока протекает в различных участках электрической цепи.

Законы Кирхгофа были названы в честь Густава Роберта Кирхгофа, немецкого физика. Он также помог продвинуть наше понимание излучения черного тела и спектроскопии. В 1845 году он впервые нашел закон. Это основа сетевого анализа и обычно используется во временной и частотной областях цепей. Закон Кирхгофа представляет собой комбинацию закона тока Кирхгофа и закона напряжения Кирхгофа.

Закон Кирхгофа — это другое название первого закона Кирхгофа.

В этой статье по физике мы более подробно обсудим первый закон Кирхгофа.

Первый закон Кирхгофа

Первый закон Кирхгофа гласит, что в любом узле (узле) цепи сумма токов, проходящих в этот узел, эквивалентна сумме токов, вытекающих из этого узла. Это означает, что если мы думаем об узле как о резервуаре для воды, скорость потока воды, заполняющего резервуар, равна скорости его опорожнения.

В случае электричества сумма токов, входящих в узел, равна сумме токов, выходящих из узла.

Формула

Токи, втекающие в точку (A) = Токи, вытекающие из точки (A)

\( \sum l_{\text {(in)}}=\sum l_{\text {( out) }}\)

Ток, втекающий в точку, а также вытекающий из нее, имеет положительный знак (+) в месте соединения (узла).

\( I_1+I_2+I_3=I_4+I_5+I_6\)

В замкнутой цепи алгебраическая сумма токов в переходе равна нулю.

\( \sum l=0\)

Ток, втекающий в точку, имеет положительный знак (+) в узле, тогда как ток, вытекающий из точки, имеет отрицательный знак (-).

\( I_1+I_2+I_3-I_4-I_5-I_6=0\)

Первый закон Кирхгофа и сохранение заряда

Первый закон Кирхгофа для электрических цепей основан на сохранении заряда, а второй закон Кирхгофа для электрических цепей — на основе энергосбережения. Концепция Кирхгофа известна как закон сохранения заряда, потому что ток сохраняется вокруг перехода без потери тока.

Поскольку сила электрического тока в (Амперах) соответствует количеству электрических зарядов в (Кулонах), пересекающих площадь поперечного сечения за одну секунду, первый закон Кирхгофа является применением принципа сохранения заряда (количество заряда втекающий в узел эквивалентен количеству заряда, вытекающему из этого узла).

Преимущества и недостатки Законы Кирхгофа

Преимущества

Законы Кирхгофа применяются для определения:

• Значения тока, напряжения и внутреннего сопротивления в цепях постоянного тока.
• Мы также можем использовать этот закон, чтобы найти неизвестное сопротивление в цепи.
• Законы Кирхгофа широко используются при строительстве моста Уитстона. Это полезно для анализа сетки и узлов.

Недостатки

• Законы Кирхгофа неприменимы к высокочастотным цепям переменного тока. Закон тока применяется только тогда, когда электрический заряд в цепи постоянен.
• КВЛ используется в предположении, что магнитные поля в замкнутом контуре не изменяются. В результате мы не можем использовать КВЛ при флуктуациях магнитного поля внутри цепи.

Решенные примеры для первого закона Кирхгофа

Пример 1. Найдите текущий \(i_3\) в узле, показанном ниже.

Решение 1. В узел втекают токи \(i_1\) и \(i_2\), а из него вытекают токи \(i_3\) и \(i_4\). Примените текущий закон Кирхгофа к указанному узлу.

\(i_1+i_2 = i_3+i_4\)

Подставить известные значения

\(2+9=i_3+4\)

\(i_3=7 A\)

Сразу установить приложение Testbook воспользоваться их всеобъемлющими и надежными учебными материалами, а также помощью экспертов Testbook, чтобы успешно сдать желаемый конкурсный экзамен. Воспользуйтесь невероятной экономией прямо сейчас, установив бесплатное приложение Testbook.

Часто задаваемые вопросы о первом законе Кирхгофа

В.1 Что такое первый закон Кирхгофа?

Ответ 1 Первый закон Кирхгофа или правило соединения Кирхгофа утверждает, что сумма токов, втекающих в любой узел (соединение) электрической цепи, равна сумме токов, вытекающих из этого узла.

Q.2 Применим ли первый закон Кирхгофа к цепям переменного тока?

Ответ 2 Да, закон Кирхгофа применим к цепям переменного тока.

Q.3 Какова формула действующего закона Кирхгофа?

Ответ 3 \(\sum l _{\text {(in)}}=\sum l_{\text {(out)}}\)

Q.4 Каково значение Первый закон Кирхгофа?

Ответ 4 Первый закон Кирхгофа выражает сохранение зарядов.

В.5 Что такое закон Кирхгофа для тока и закон напряжения?

Ответ 5 Анализ цепей с сосредоточенными параметрами основан на законе тока Кирхгофа и законе напряжения Кирхгофа. Эти правила в сочетании с вольтамперными характеристиками частей схемы системы позволяют проводить систематический анализ любой электрической сети.

Скачать публикацию в формате PDF

Read More Posts

Learn the Young’s Double-Slit Experiment Derivation
Hubble’s Law: Statement, Formula, Derivation, Applications & Limitations
Radiation Detector: Definition, Types, Advantages, Disadvantages & Приложения
Центростремительная и центробежная сила: определение, формула, различия, примеры и приложения
Фазовые изменения: узнайте значение, примеры и характеристики

Правило соединения Кирхгофа: определение и уравнение

Правило соединения Кирхгофа: определение и уравнение | StudySmarter

Выберите язык

Предлагаемые языки для вас:

Немецкий (DE)

Дойч (Великобритания)

Европа

• английский (DE)
• английский (Великобритания)

StudySmarter — универсальное учебное приложение.

4.8 • Рейтинг +11k

Более 3 миллионов загрузок

Бесплатно

Правило соединения Кирхгофа

СОДЕРЖАНИЕ :

ОГЛАВЛЕНИЕ

Lerne mit deinen Freunden und bleibe auf dem richtigen Kurs mit deinen persönlichen Lernstatistiken

Jetzt kostenlos anmelden

Nie wieder prokastinieren mit unseren Lernerinnerungen.

Jetzt kostenlos anmelden

При первом изучении основ принципиальных схем мы обычно рассматриваем простые последовательные и параллельные схемы. Однако, если бы вы открыли любой старый бытовой прибор, вы бы, скорее всего, увидели, казалось бы, неразборчивую путаницу проводов и электрических компонентов. Большинство приборов состоят из чрезвычайно сложных цепей, которые не являются ни последовательными, ни параллельными цепями, где вычисление величин с помощью \(V=IR\) заняло бы слишком много времени.

Итак, как такие схемы разрабатываются и анализируются на практике? К счастью, есть два закона схемотехники, известные как законы Кирхгофа, которые можно применить к любой принципиальной схеме, какой бы сложной она ни была. В этой статье мы подробно рассмотрим первый из этих законов, известный как правило соединения Кирхгофа.

Определение первого закона Кирхгофа

В 1845 году студент-физик из Пруссии Густав Кирхгоф исследовал поведение токов и разностей потенциалов в цепях, содержащих множество петель и узлов или соединений. Применив закон Ома к этим цепям, он сумел обобщить результаты в два простых закона, которые и по сей день невероятно полезны в области электротехники. Их основное применение — преобразование невероятно сложных принципиальных схем в наборы простых алгебраических выражений.

Рис. 1. Густав Кирхгоф (1824–1887) был прусским физиком, который внес важный вклад в понимание электрических цепей, в первую очередь в свои два закона.

Первый из этих законов, известный как Правило соединения Кирхгофа , касается тока, втекающего и выходящего из соединения цепи, и будет в центре внимания этой статьи. Напомним, что ток в проводе — это просто скорость, с которой заряд течет по этому проводу. Обычно цепи включают соединения, как показано на рисунке 2, в результате чего ток в проводе разделяется на два или более провода. Правило соединения Кирхгофа гарантирует, что ток, втекающий в соединение, всегда совпадает с током, выходящим из соединения.

Правило соединения Кирхгофа гласит, что сумма токов, встречающихся в соединении цепи, всегда должна быть равна нулю.

Рис. 2 – Пример соединения в цепи. Правило соединения Кирхгофа гласит, что \(i_2+i_3=i_1+i_4\).

Уравнение, описывающее правило соединения Кирхгофа

Если набор токов \(I_1,I_2,\dots,I_k\) встречается в соединении, то правило соединения Кирхгофа можно выразить алгебраически, присвоив знак \(\pm\) знаку каждый ток в зависимости от того, входят ли они в соединение или выходят из него. По соглашению токи, входящие в соединение, получают знак \(+\), а выходящие — знак \(-\). Тогда правило соединения Кирхгофа может быть выражено уравнением

\[\sum_{k,\text{входящий}} I_k-\sum_{l,\text{выходящий}}I_l=0\,\mathrm{A}. \]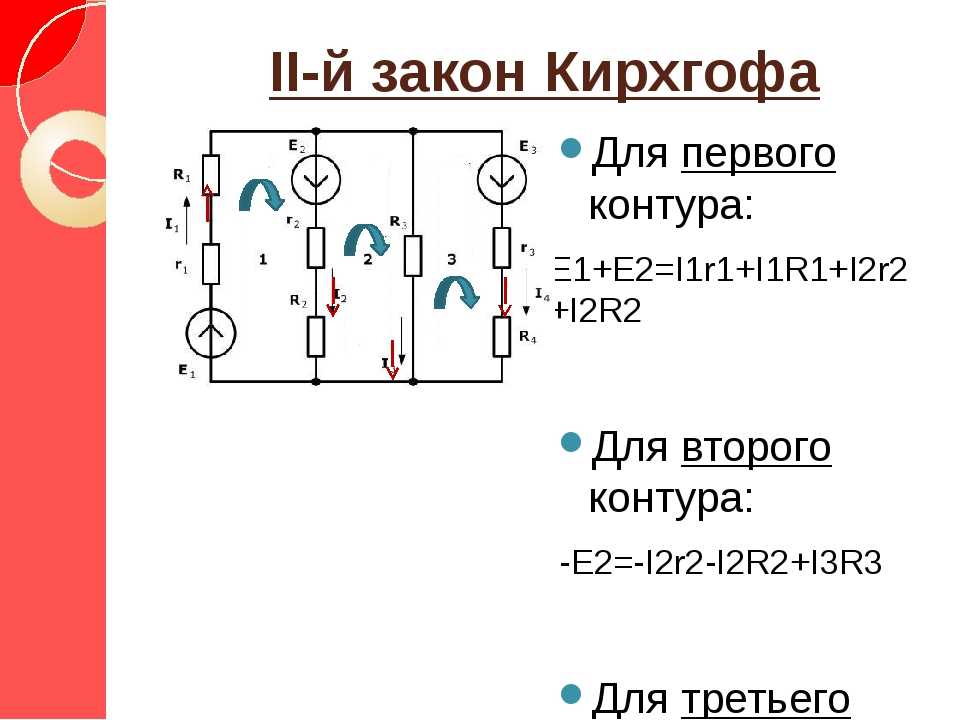

Например, на рис. 2, \(i_2\) и \(i_3\) входят в перекресток, а \(i_1\) и \(i_4\) выходят из него, поэтому

\[\begin{align}&i_2+i_3-i_1-i_4= 0\,\mathrm{A}\,\\\iff &i_2+i_3=i_1+i_4,\end{align}\]

демонстрируя, что сумма токов, входящих в соединение, должна быть равна сумме токов выезд с развязки. И наоборот, если направление тока неизвестно, его можно определить по правилу соединения Кирхгофа, предполагая, что он входит или выходит из соединения и находит его знак. Если его значение отрицательное, предположение было неверным.

В качестве простого примера рассмотрим токи в последовательной цепи, как показано на рисунке 3. Мы должны помнить о том, как мы определяем знак тока в каждом соединении, поскольку один и тот же ток может иметь разный знак в зависимости от того, в каком соединении мы считаем. Если ток течет по часовой стрелке от положительной клеммы к отрицательной, то мы можем присвоить положительный знак токам, входящим в соединение, и отрицательные знаки тем, которые выходят из соединения. На рисунке 3 мы можем сказать, что каждый угол является соединением, поэтому каждое «соединение» имеет только один текущий вход и один текущий выход, поэтому правило соединения Кирхгофа говорит нам, что должно выполняться следующее:\[\begin{align} &I_1-I_2= 0\,\mathrm{A},\\ &I_2-I_3=0\,\mathrm{A},\\ &I_3-I_4=0\,\mathrm{A},\\&I_4-I_1=0\,\mathrm {A},\\\ подразумевает &I_1=I_2=I_3=I_4.\end{align}\]

Другими словами, ток в последовательной цепи одинаков во всех точках цепи.




Рис. 3. Правило соединения Кирхгофа требует, чтобы ток в последовательной цепи был везде одинаковым, т. е. \(I_1=I_2=I_3=I_4\) в приведенной выше схеме.

Примеры правила соединения Кирхгофа

Давайте рассмотрим некоторые способы использования правила соединения Кирхгофа для анализа принципиальных схем и расчета недостающих токов.

Рис. 4. Правило соединения Кирхгофа позволяет нам решать схемы, подобные приведенной выше, не зная напряжения батареи.

Рассмотрим схему, приведенную выше, где мы хотим найти недостающие токи ветвей \(I_1,I_2,I_3\). Каждая ветвь содержит резистор разного сопротивления. Немедленно правило Кирхгофа о соединении говорит нам, что \(I_1=5\,\mathrm{A}\), поскольку ток, втекающий в батарею, должен быть таким же, как и ток, вытекающий из батареи (мы можем выбрать батарею в качестве соединения). и увидеть это непосредственно). Далее нам нужно найти токи \(I_2\) и \(I_3\). Глядя на правое соединение и предполагая, что оба тока \(I_2\) и \(I_3\) идут справа налево, правило соединения гласит, что \[\begin{align}I_1-I_2-I_3&=0\,\mathrm {A},\\\подразумевает I_2+I_3&=5\,\mathrm{A}.\end{align}\]

Мы можем использовать \(V=IR\), отметив, что потенциал в параллельных цепях одинаков во всех ветвях, чтобы найти долю тока, протекающего в каждой ветви. Поскольку ток обратно пропорционален сопротивлению, через резистор \(2\,\mathrm{\Omega}\) будет протекать вдвое больший ток, чем через резистор \(4\,\mathrm{\Omega}\). Следовательно, \(I_3=2I_2\) и, таким образом, \[\begin{align}3I_2&=5\,\mathrm{A},\\\ подразумевает I_2&=\frac{5}{3}\,\mathrm{A} ,\\\ подразумевает I_3&=\frac{10}{3}\,\mathrm{A}. \end{align}\]

Поскольку мы получаем положительные значения для неизвестных токов, мы знаем, что наше предположение об их направлении было правильным, поэтому мы заключаем, что токи действительно текут справа налево.

Рис. 5. Правило соединения Кирхгофа особенно полезно для более сложных схем, где \(V=IR\) становится сложнее использовать.

В то время как использование \(V=IR\) для нахождения пропущенных величин обычно является самым простым методом решения схем, если схема особенно сложна, как показано на рис. 5, то правило соединения Кирхгофа является наиболее эффективным методом. Давайте применим его, чтобы найти недостающие токи \(I_1,I_2,I_3\). Во-первых, мы можем применить правило соединения, чтобы найти \(I_1\). Поскольку \(I_1\) выходит из соединения, в которое входят потоки \(3\,\mathrm{A}\) и \(6\,\mathrm{A}\), мы знаем, что \[\begin{align} &-I_1+3\,\mathrm{A}+6\,\mathrm{A}=0\,\mathrm{A},\\\ подразумевает &I_1=9\,\mathrm{A}.\end{align}\]

Как и ожидалось, положительное значение, которое мы получаем для \(I_1\), говорит нам, что наше предположение было правильным, так что ток \(I_1\) должен вытекать перекрестка, справа налево.

На следующем перекрестке, применяя правильный знак для направления тока, как указано на принципиальной схеме, мы находим \[\begin{align}I_1-I_2-2\,\mathrm{A}&=0\,\mathrm {A},\\\ подразумевает I_2=I_1-2\,\mathrm{A}&=7\,\mathrm{A}.\end{align}\]

Опять же, как и ожидалось, положительное значение подтверждает, что \(I_2\) вытекает из соединения вниз.

Есть два перекрестка, которые мы можем найти \(I_3\), давайте выберем нижний перекресток. Может показаться, что мы не знаем, каков третий ток на этом стыке вместе с \(I_2\) и \(I_3\). Однако обратите внимание, что между этим током и током \(3\,\mathrm{A}\), поступающим от нижней батареи, нет дальнейших соединений, поэтому это третий задействованный ток. Применение правила соединения, предполагающее, что \(I_3\) расположено слева направо (как показано на изображении), дает \[\begin{align}I_2+I_3-3\,\mathrm{A}&=0\,\mathrm{A },\\\подразумевает, что I_3=3\,\mathrm{A}-7\,\mathrm{A}&=-4\,\mathrm{A}.\end{align}\]

Подождите, мы получили отрицательное значение! Это означает, что наше предположение о направлении \(I_3\) было неверным. Мы заключаем, что \(I_3=4\,\mathrm{A}\), но его направление на самом деле справа налево. Изображение неправильное!

Это одно из самых полезных свойств законов Кирхгофа: они могут исправить любые неверные исходные предположения о направлении тока.

Правило соединения Кирхгофа: сохранение тока

Правило соединения Кирхгофа — это просто утверждение о сохранении тока в цепи. Сохранение тока само по себе является следствием основного закона сохранения заряда. Согласно фундаментальному закону сохранения, ни одна система не может нарушать закон сохранения заряда.

Закон сохранения тока гласит, что при фиксированных напряжении и сопротивлении ток не может создаваться или уничтожаться в цепи.

Закон сохранения электрического заряда гласит, что общий электрический заряд изолированной системы, т. е. сумма всех отрицательных и положительных зарядов в системе, всегда должен оставаться постоянным. Например, общий заряд во Вселенной оставался постоянным с момента Большого взрыва.

Чтобы проиллюстрировать взаимосвязь между сохранением заряда и правилом соединения Кирхгофа, давайте представим сценарий, в котором правило соединения не выполняется.

Рассмотрим три потока \(I_1,I_2,I_3\), встречающиеся на узле, где \(I_1,I_2\) входят в узел и \(I_3\) выходят из него. Допустим,

\[I_1+I_2-I_3=x\,\mathrm{A},\text{ где } x\neq 0\,\mathrm{A}.\]

По определению тока это означает что каждую секунду \(x\,\mathrm{C}\) заряда самопроизвольно разрушается на стыке. Ясно, что это нарушает фундаментальный закон сохранения заряда, поэтому всегда должно выполняться правило соединения Кирхгофа.

Первый и второй закон Кирхгофа

Второй закон Кирхгофа, известный как правило цикла Кирхгофа, касается суммы разностей потенциалов вокруг контура в замкнутой цепи. При использовании в тандеме с правилом соединения Кирхгофа оно становится мощным инструментом для анализа сложных цепей и поиска неизвестных величин, таких как разности потенциалов, сопротивления и токи.

Правило петли Кирхгофа гласит, что сумма разностей потенциалов вокруг любой петли в цепи должна быть равна нулю: \[\sum_kV_k=0\,\mathrm{V}.\]

Правило петли Кирхгофа можно рассматривать как следствие закона сохранения энергии. Поскольку большинство параллельных цепей содержат несколько циклов, существует свобода выбора самого простого цикла для применения правила цикла Кирхгофа, которое часто значительно упрощает задачи. Чтобы применить правило контура, мы рассматриваем батареи как источники положительной разности потенциалов, в то время как компоненты, такие как резисторы, являются источниками отрицательной разности потенциалов. Давайте рассмотрим пример задачи, в которой мы можем применить оба правила для поиска недостающих величин. 9{-9}\,\mathrm{F}\) — емкость, а \(V\) — напряжение, которое нам пока неизвестно.

Мы можем применить оба закона Кирхгофа, чтобы найти отсутствующие разности потенциалов и токи в приведенной выше цепи, что также позволит нам найти заряд конденсатора.

Во-первых, правило соединения Кирхгофа говорит нам, что токи \(I_1\) и \(I_2\), входящие и текущие \(I_3\), выходящие из узла справа, должны удовлетворять \[\begin{align}I_1+I_2 -I_3&=0\,\mathrm{A},\\\ подразумевает I_1+I_2&=I_3.\end{align}\]

Левый узел — тот же самый случай, только знаки токов меняются местами, что приводит к эквивалентному уравнению.

Правило цикла Кирхгофа дает нам еще два условия, из которых мы можем найти все неизвестные переменные. Мы можем выбрать несколько разных контуров, но самый простой вариант — разделить цепь на два основных контура, верхний и нижний, оба в обход конденсатора. Мы знаем, что сумма разностей потенциалов вокруг каждой петли должна быть равна нулю, что дает следующие уравнения. \\3\,\mathrm{V}-V_2-V_3&=0\,\mathrm{V}.\end{align}\]

Мы можем выразить неизвестные разности потенциалов через токи и сопротивления резисторов, используя \(V=IR\), что в сочетании с уравнениями из правила соединения Кирхгофа образует набор решаемых одновременных уравнений.

\[\begin{align}&I_1+I_2=I_3\tag{1},\\&5\,\mathrm{V}-(3\,\mathrm{\Omega})I_1-(1\,\mathrm {\Omega})I_3=0\,\mathrm{V}\tag{2},\\&3\,\mathrm{V}-(1\,\mathrm{\Omega})I_3-(4\,\ mathrm{\Omega})I_2=0\,\mathrm{V}\tag{3}.\end{align}\]

Если мы разделим последние два уравнения на единицу \(\Omega\), мы получим три текущих уравнения:

\[\begin{align}&I_1+I_2=I_3\tag{1},\\&5\,\ mathrm{A}-3I_1-I_3=0\,\mathrm{A}\tag{2},\\&3\,\mathrm{A}-I_3-4I_2=0\,\mathrm{A}\tag{3 }.\end{align}\]

Подстановка \(I_3\) из первого уравнения в два других уравнения дает \[\begin{align}&5\,\mathrm{A}-4I_1-I_2=0 \,\mathrm{A}\tag{4},\\&3\,\mathrm{A}-I_1-5I_2=0\,\mathrm{A}\tag{5}.\end{align}\]

Мы можем изолировать \(I_2\), объединив \((4)\) и \((5)\) следующим образом\[\begin{align}(4)-4\times (5)&\ подразумевает -7\,\mathrm{A}+19I_2=0\,\mathrm{A},\\&\ подразумевает, что I_2=0,4\,\mathrm{A}.\end{align}\]Подставляя это в \(( 4)\) дает\[\begin{align}I_1=1.2\,\mathrm{A}.\end{align}\]

Соединяя все вместе в уравнение \((1)\), получаем, что все три тока равны \[I_1=1,2\,\mathrm{A},\, I_2=0,4\,\mathrm{A},\, I_3=1,5\,\mathrm{A}. {-9}\,\mathrm{F}=7.6\,\mathrm{nC}.\]

Правило соединения Кирхгофа — основные выводы

• Соединение в цепи — это точка, в которой ток разделяется на несколько ветвей.
• Правило соединения Кирхгофа гласит, что сумма токов в соединении всегда должна быть равна нулю.
• По соглашению, токи, входящие в соединение, получают знак \(+\), а токи, выходящие из соединения, получают знак \(-\).
• Правило соединения — это просто следствие сохранения тока, которое само по себе является следствием сохранения заряда.
• Правило петли Кирхгофа гласит, что сумма разностей потенциалов вокруг любой петли цепи всегда должна быть равна нулю. Его можно использовать в тандеме с правилом соединений для решения сложных схем.

Ссылки

1. Рис. 1 — Густав Роберт Кирхофф (https://commons.wikimedia.org/wiki/File:Gustav_Robert_Kirchhoff.jpg) Смитсоновских библиотек находится в общественном достоянии.
2. Рис. 2 — Законы KCL-Kirchhoff’s Circuit Laws (https://commons. wikimedia.org/wiki/File:KCL_-_Kirchhoff%27s_circuit_laws.svg) от Pflodo под лицензией CC BY-SA 3.0 (https://creativecommons .org/licenses/by-sa/3.0/deed.en)
3. Рис. 3 — Серийная схема, StudySmarter Originals.
4. Рис. 4 – Параллельная схема, StudySmarter Originals.
5. Рис. 5 – Комплексная схема, StudySmarter Originals.
6. Рис. 6 — Схема конденсатора, StudySmarter Originals.

Часто задаваемые вопросы о правиле соединения Кирхгофа

Законы тока и напряжения Кирхгофа используются при анализе цепей для нахождения недостающих токов и напряжений. Они особенно полезны для анализа сложных схем, где В = ИК не подходит.

Правило соединения Кирхгофа гласит, что сумма токов, встречающихся в соединении цепи, всегда должна быть равна нулю.

Правило соединения Кирхгофа дает уравнение для множества токов {I_k}, встречающихся в соединении.

ΣI_k=0

Это можно изменить, чтобы найти отсутствующие токи, если другие известны.

Есть два закона Кирхгофа. Правило соединения и правило цикла.

Для набора токов {I_k}, встречающихся на стыке,
ΣI_k=0.

Заключительный опрос по правилу перекрестков Кирхгофа

Тест по правилу перекрестков Кирхгофа — Teste dein Wissen

Вопрос

Укажите правило перекрестков Кирхгофа.

Показать ответ

Ответ

Сумма токов в узле всегда равна нулю с учетом их знаков в зависимости от того, идет ли ток в узел или от него.

Показать вопрос

Вопрос

Укажите правило петли Кирхгофа.

Показать ответ

Ответ

Сумма разностей потенциалов вокруг любого контура цепи равна нулю.

Показать вопрос

Вопрос

Три потока пересекаются на стыке. Если \(I_1=5\,\mathrm{A}\) и \(I_2=-3\,\mathrm{A}\), что такое \(I_3\)?

Показать ответ

Ответ

\(2\,\mathrm{A}\).

Показать вопрос

Вопрос

Ток \(10\,\mathrm{A}\) течет по проводу, который разделяется на две ветви. Если сопротивления ветвей равны \(R_1=1\,\mathrm{\Omega}\) и \(R_2=4\,\mathrm{\Omega}\) соответственно, каков ток через каждую ветвь?

Показать ответ

Ответ

\(I_1=8\,\mathrm{A}\) и \(I_2=2\,\mathrm{A}\).

Показать вопрос

Вопрос

Рассмотрим соединение с тремя токами \(I_1,\,I_2,\,I_3\). Первые два тока входят в узел и \(I_3\) выходят из него. Если \(I_1=I_3\), то что такое \(I_2\)?

Показать ответ

Ответ

\(I_2=0\,\mathrm{A}\).

Показать вопрос

Вопрос

Какое из этих утверждений верно для последовательных цепей?

Показать ответ

Ответ

Ток постоянен для всех компонентов.

Показать вопрос

Вопрос

Рассмотрим перекресток, содержащий четыре ответвления. Что из перечисленного не является возможной комбинацией токов?

Показать ответ

Ответ

\(+I,\,\frac{+I}{2},\,\frac{-I}{2},\,2I\).

Показать вопрос

Вопрос

Рассмотрим ответвление цепи с соединением на обоих концах. Если знак тока через ветвь \(+\) в одном переходе, то каков знак тока через другой переход?

Показать ответ

Ответ

\(-\).

Показать вопрос

Вопрос

Рассмотрим узел, в котором пересекаются 5 токов. Возможно ли, чтобы все токи имели одинаковую величину?

Показать ответ

Ответ

Показать вопрос

Вопрос

Следствием какого фундаментального закона сохранения является правило соединения Кирхгофа?

Показать ответ

Ответ

Сохранение электрического заряда.

Показать вопрос

Вопрос

Правило петли Кирхгофа является следствием какого фундаментального закона сохранения?

Показать ответ

Ответ

Сохранение энергии.

Показать вопрос

Вопрос

Количество ответвлений, несущих ток в узел, должно быть равно количеству ответвлений, отводящих ток от узла.

Показать ответ

Ответ

Неверно.

Показать вопрос

Подробнее о правиле соединения Кирхгофа

Откройте для себя подходящий контент для ваших предметов

Не нужно обманывать, если у вас есть все необходимое для успеха! Упаковано в одно приложение!

Учебный план

Будьте идеально подготовлены вовремя с индивидуальным планом.