Закон Фарадея для электролиза – формула и примеры

4.3

Средняя оценка: 4.3

Всего получено оценок: 260.

4.3

Средняя оценка: 4.3

Всего получено оценок: 260.

В 1836 году Майкл Фарадей опубликовал выведенные математически количественные характеристики электролиза. Обнаруженные взаимосвязи между количеством прошедшего через электролит электричества и количеством выделившегося при этом вещества впоследствии были названы законами Фарадея для электролиза.

Первый закон

Если пропускать через раствор медного купороса электрический ток в течение определённого количества времени, то на катоде выделяется небольшое количество меди. Однако если пустить ток большей силы, за такое же количество времени на катоде образуется большее количество меди. При увеличении времени и одинаковой силе тока также увеличивается количество меди.

Рис. 1. Майкл Фарадей.

Фарадей установил взаимосвязь массы вещества, силы тока и времени. Математически эта взаимосвязь выражается следующим образом:

m = kIt,

где:

• m – масса вещества;
• k – электрохимический эквивалент;
• I – сила тока;
• t – время.

Электрохимический эквивалент – это масса вещества, образованная при прохождении через электролит тока в 1 А за одну секунду. Выражается как соотношение массы вещества к количеству электричества или г/Кл.

Произведение силы тока и времени выражает количество электричества: q = It. Это электрический заряд, измеряемый в кулонах (один ампер к одной секунде). Электрический заряд отражает способность тела быть источником электромагнитного поля и принимать участие в электромагнитном взаимодействии.

Соответственно, уравнение Фарадея приобретает вид:

m = kq.

Рис. 2. Первый закон Фарадея.

Первый закон электролиза Фарадея: масса вещества, выделившегося при электролизе, прямо пропорциональна количеству электрического тока, пропущенного через электролит.

Второй закон

Фарадей, пропуская электрический ток одинаковой силы через различные электролиты, заметил, что массы веществ на электродах неодинаковы. Взвесив выделившиеся вещества, Фарадей сделал вывод, что вес зависит от химической природы вещества. Например, на каждый грамм выделенного водорода приходилось 107,9 г серебра, 31,8 г меди, 29,35 г никеля.

На основе полученных данных Фарадей вывел второй закон электролиза: для определённого количества электричества масса химического элемента, образовавшегося на электроде, прямо пропорциональна эквивалентной массе элемента. Она равна массе одного эквивалента – количеству вещества, реагирующему или замещающему 1 моль атомов водорода в химических реакциях:

μ_eq = μ/z,

где:

• μ – молярная масса вещества;
• z – число электронов на один ион (валентное число ионов).

Для выделения одного моля эквивалента затрачивается одинаковое количество электричества – 96485 Кл/моль. Это число называется числом Фарадея и обозначается буквой F.

Согласно второму закону, электрохимический эквивалент прямо пропорционален эквивалентной массе вещества:

k = (1/F) μ_eq или k = (1/zF)μ.

Рис. 3. Второй закон Фарадея.

Два закона Фарадея можно привести к общей формуле: m = (q / F) ∙ (μ/z).

Что мы узнали?

Фарадей, проводя реакцию электролиза разных веществ, вывел два закона. Согласно первому закону, масса вещества, осевшего на электрод, прямо пропорциональная количеству электричества, пропущенного через электролит: m = kq. Второй закон отражает взаимосвязь электрохимического эквивалента и эквивалентной массы вещества: k = (1/F) μ

eq. Электрохимический эквивалент – количество выделившегося вещества при прохождении единицы электричества. Эквивалентная масса – количество вещества, реагирующее с 1 молем водорода.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Лиза Шифр

  4/5

• Евгений Пшеничный

  5/5

• Татьяна Батарон

  4/5

Оценка доклада

4.3

Средняя оценка: 4.3

Всего получено оценок: 260.

---

А какая ваша оценка?

Законы электролиза Фарадея • Джеймс Трефил, энциклопедия «Двести законов мироздания»

200 законов мироздания > Химия

При электролизе масса превращенного вещества прямо пропорциональна количеству электричества, прошедшего через электролитическую ячейку.

При прохождении через электролит одного и того же количества электричества масса превращенного вещества зависит от массы и заряда ионов вещества.

Два закона электролиза — это всего лишь небольшая часть вклада Майкла Фарадея в науку. Электролиз — это совокупность процессов, происходящих при пропускании электрического тока через электролит — плавленое ионное вещество (например, плавленая соль) или раствор, в котором присутствуют ионы. Электрический ток проходит через электролит от одного электрода к другому. Положительно заряженные ионы при этом движутся к отрицательному электроду,

катоду, а отрицательно заряженные — к положительному электроду, аноду. Химические реакции происходят на электродах. Фарадей провел фундаментальные исследования электролитов и создал законы, в которых говорится, что химические превращения связаны с потоком электронов (то есть электрическим током): чем больше электронов, тем больше химических превращений.

Электролиз — это важный промышленный процесс, используемый как при получении определенных металлов, так и при конечной обработке поверхностей методом нанесения гальванического покрытия. Примером электролиза в действии может быть электролитическое рафинирование меди после ее выделения из руды. Выступающие в качестве катода тонкие листы чистой меди опускают в электролит, содержащий раствор сульфата меди и серную кислоту, а слитки неочищенной меди подвешивают в этом же растворе, и они действуют как анод. При пропускании электрического тока анод начинает растворяться, и ионы меди, вместе с некоторым количеством ионов железа и цинка, поступают в электролит. Остальные спутники меди, содержавшиеся в слитках (включая значительное количество серебра, золота и платины), выпадают в осадок и накапливаются на дне электролитической ванны. Ионы меди через электролит направляются к катоду и осаждаются на нем. Цинк и железо остаются в растворе.

В промышленных масштабах в подобных ваннах за месяц можно очистить всего несколько тонн меди, но при этом получается продукт 99,96-процентной чистоты. Более того, благодаря извлечению из осадка благородных металлов окупается весь процесс очистки. Кроме меди, электролитическим методом в промышленных масштабах очищаются также магний, натрий и алюминий.

В описанном выше процессе рафинирования меди атом меди переходит в электролит в виде иона, теряя два электрона. Следовательно, на аноде он принимает два электрона, и ион снова превращается в нейтральный атом меди (можно представить себе, что эти два электрона бегут по проводу, как электрический ток). Согласно первому закону Фарадея, для того чтобы очистить в два раза больше меди, необходимо в два раза больше электронов.

---

2

Показать комментарии (2)

Свернуть комментарии (2)

---

• Ilnar  25.05.2006  23:37 Ответить

  Положительно заряженные ионы при этом движутся к отрицательному электроду, аноду, а отрицательно заряженные — к положительному электроду, катоду.
  По-моему все наоборот, Катод(-), Анод(+). К катоду движутся катионы, к аноду — анионы.

  Ответить

• a_b  24.12.2009  12:42 Ответить

  Следует заметить, что при помощи электролиза магний, натрий и алюминий не очищаются (рафинируются), а извлекаются.

  Ответить

Написать комментарий

---

1834	Законы электролиза Фарадея

---

1831

Законы электромагнитной индукции Фарадея

1687

Законы механики Ньютона

Новостная рассылка  

«Элементы» в соцсетях: 

8.3: Закон Фарадея — Технические LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

3946

• Стивен У. Эллингсон
• Политехнический институт Вирджинии и Государственный университет через Инициативу открытых образовательных библиотек штата Вирджиния

Закон Фарадея описывает генерацию электрического потенциала изменяющимся во времени магнитным потоком. Это форма электромагнитной индукции .

Для начала рассмотрим сценарий, показанный на рисунке \(\PageIndex{1}\). Одиночная проволочная петля в присутствии приложенного магнитного поля \({\bf B}\). По причинам, объясненным позже, мы вводим небольшой зазор и определяем \(V_T\) как разность потенциалов, измеренную через зазор в соответствии с указанным соглашением о знаках. Сопротивление \(R\) может быть любым значением больше нуля, включая бесконечность; то есть буквальный разрыв.

Рисунок \(\PageIndex{1}\): Одиночная проволочная петля в присутствии приложенного магнитного поля.

Пока \(R\) не бесконечно, мы знаем из закона Ленца (раздел 8.2), что переменное во времени магнитное поле вызовет протекание тока в проводе. Закон Ленца также говорит нам, в каком направлении будет течь ток. Однако закон Ленца не говорит нам о величине тока и обходит некоторые важные физические аспекты, которые имеют большое значение для анализа и проектирования электрических устройств, включая генераторы и трансформаторы.

Более полную картину дает закон Фарадея. Что касается сценария на рисунке \(\PageIndex{1}\), закон Фарадея связывает потенциал \(V_T\), индуцированный изменением во времени \({\bf B}\). Затем \(V_T\) приводит к току, указанному в законе Ленца. Величина этого тока просто \(V_T/R\). Без дальнейших церемоний, вот закон Фарадея для этого сценария с одной петлей:

.

\[V_T = — \frac{\partial}{\partial t} \Phi ~~\mbox{(один цикл)} \label{m0055_eVT} \] 92\)) и \(d{\bf s}\) — вектор площади дифференциальной поверхности.

Чтобы продвинуться вперед с законом Фарадея, нужно четко понимать значения \(\mathcal{S}\) и \(d{\bf s}\). Если проволочная петля в данном сценарии лежит в плоскости, то хорошим выбором для \(\mathcal{S}\) будет просто плоская область, ограниченная петлей. Однако любая поверхность , ограниченная петлей, будет работать, включая неплоские поверхности, которые простираются выше и/или ниже плоскости петли. Все, что требуется, это чтобы каждая линия магнитного поля, проходящая через петлю, также проходила через \(\mathcal{S}\). Это происходит автоматически, если петле соответствует кривая \(\mathcal{C}\), определяющая край открытой поверхности \(\mathcal{S}\). Следовательно, величина \(d{\bf s}\) является элементом дифференциальной поверхности \(ds\), а направление \(d{\bf s}\) является единичным вектором \(\hat{\bf n}\) перпендикулярно каждой точке на \(\mathcal{S}\), поэтому \(d{\bf s}=\hat{\bf n}ds\).

Остается только одна проблема — ориентация \(\hat{\bf n}\). Это показано на рисунке \(\PageIndex{2}\). Вектор может быть перпендикулярен поверхности двумя возможными способами, и направление, выбранное для \(\hat{\bf n}\), повлияет на знак \(V_T\). Следовательно, \(\hat{\bf n}\) должно быть как-то связано с полярностью, выбранной для \(V_T\). Рассмотрим это отношение. Пусть \(\mathcal{C}\) начинается с терминала «\(-\)» \(V_T\) и проходит по всему периметру цикла, заканчиваясь на терминале «\(+\)». Тогда \(\hat{\bf n}\) определяется следующим «правилом правой руки»: \(\hat{\bf n}\) указывает в направлении согнутых пальцев правой руки, когда большой палец правой руки выровнен в направлении \(\mathcal{C}\). Стоит отметить, что именно это соглашение используется для связи \(\hat{\bf n}\) и \(\mathcal{C}\) в теореме Стокса.

Рисунок \(\PageIndex{2}\): связь между полярностью \(V_T\) и ориентациями \(\mathcal{C}\) и \(\hat{\bf{n}}\) в плоскости одноконтурный сценарий.

Теперь давайте вспомним, как закон Фарадея применяется к сценарию с одним контуром на рисунке [m0055_fFaradaySingleLoop]:

1. Назначить клеммы «\(+\)» и «\(-\)» на напряжение промежутка \(V_T\).
2. Ориентация \(\hat{\bf n}\) определяется по правилу правой руки, принимая направление \(\mathcal{C}\) за периметр цикла, начинающегося в «\(-\ )» и заканчивается на «\(+\)»
3. \({\bf B}\) дает магнитный поток \(\Phi\), связанный с контуром согласно уравнению \ref{m0055_ePhi}. \(\mathcal{S}\) — это любая открытая поверхность, которая пересекает все силовые линии магнитного поля, проходящие через петлю (поэтому вы также можете выбрать \(\mathcal{S}\) таким образом, чтобы получить простейшую из возможных интеграция).
4. По закону Фарадея (уравнение \ref{m0055_eVT}), \(V_T\) является производной по времени от \(\Phi\) со сменой знака.
5. Ток \(I\), протекающий в контуре, равен \(V_T/R\), при этом опорное направление (т.е. направление положительного тока) находится в диапазоне от «\(+\)» до «\(-\)» через резистор. Думайте о контуре как об источнике напряжения, и вы получите правильное опорное направление для \(I\).

Здесь повторим, что электромагнитная индукция, описываемая законом Фарадея, индуцирует потенциала (в данном случае \(V_T\)) , а не тока . Ток в контуре — это просто наведенное напряжение, деленное на сопротивление контура. Этот момент легко упустить из виду, особенно в свете закона Ленца, который, по-видимому, подразумевает, что индуцируется ток, а не потенциал.

Вас интересует значение знака минус в уравнении \ref{m0055_eVT}? В частности, это закон Ленца: ток \(I\), который в конце концов циркулирует в петле, создает собственное магнитное поле («\({\bf B}_{ind}\)» в разделе 8.2), которое отличается от приложенное магнитное поле \({\bf B}\) и которое имеет тенденцию противодействовать изменению \({\bf B}\). Таким образом, мы видим, что закон Фарадея включает в себя закон Ленца.

Часто интересуют структуры, состоящие из множества одинаковых петель. Мы имеем в виду нечто вроде катушки с \(N\ge1\) витками, плотно упакованными вместе. В этом случае закон Фарадея равен

.

\[\boxed{ V_T = — N\frac{\partial}{\partial t} \Phi} \label{m0055_eVTN} \]

Обратите внимание, что разница заключается просто в том, что потенциал промежутка \(V_T\) больше на \(N\). Другими словами, каждая обмотка катушки вносит потенциал, заданный уравнением \ref{m0055_eVT}, и эти потенциалы складываются последовательно.

Закон Фарадея, представленный в общем виде уравнением \ref{m0055_eVTN}, утверждает, что потенциал, индуцированный в катушке, пропорционален производной по времени магнитного потока через катушку.

Наведенный потенциал \(V_T\) часто называют «ЭДС», что является сокращением термина электродвижущая сила – конечно, неправильное название, поскольку не подразумевается фактическая сила, а только потенциал. Тем не менее термин «ЭДС» часто используется в контексте применения закона Фарадея по историческим причинам.

Ранее в этом разделе мы рассмотрели генерацию ЭДС изменением во времени \({\bf B}\). Однако уравнение \ref{m0055_eVT} показывает, что на самом деле происходит то, что ЭДС является результатом изменения во времени магнитного потока \(\Phi\). Магнитный поток представляет собой плотность магнитного потока, проинтегрированную по площади, поэтому оказывается, что ЭДС также можно генерировать, просто изменяя \(\mathcal{S}\), независимо от любого изменения во времени \({\bf B}\). Другими словами, ЭДС может генерироваться даже тогда, когда \({\bf B}\) постоянна, вместо этого изменяя форму или ориентацию катушки. Итак, у нас есть множество схем, по которым мы можем генерировать ЭДС. Вот они:

1. Изменяющийся во времени \({\bf B}\) (как мы рассмотрели ранее в этом разделе). Например, \({\bf B}\) может быть связано с постоянным магнитом, который перемещается (например, перемещается или вращается) вблизи катушки, как описано в разделе 8.2. Или, что чаще, \({\bf B}\) может быть связано с другой катушкой, по которой протекает переменный во времени ток. Эти механизмы вместе именуются ЭДС трансформатора . ЭДС трансформатора лежит в основе принципа работы трансформаторов; подробнее об этом см. Раздел 8.5.
2. Периметр \(\mathcal{C}\) и, следовательно, поверхность \(\mathcal{S}\), по которой определяется \(\Phi\), могут изменяться во времени. Например, проволочная петля может поворачиваться или изменять форму в присутствии постоянного магнитного поля. Этот механизм называется ЭДС движения и является основным принципом работы генераторов (раздел 8.7).
3. Трансформатор и ЭДС движения могут существовать в различных комбинациях. С точки зрения закона Фарадея, трансформатор и ЭДС движения одинаковы в том смысле, что в любом случае \(\Phi\) изменяется во времени, а это все, что требуется для создания ЭДС.

Наконец, комментарий к общему закону Фарадея. Выше мы ввели закон Фарадея, как если бы он был специфичен для петель и катушек проволоки. Однако правда в том, что закон Фарадея — это фундаментальная физика. Если вы можете определить замкнутый путь — с током или без него — тогда вы можете вычислить разность потенциалов, полученную при пересечении этого пути, используя закон Фарадея. Значение, которое вы вычисляете, представляет собой потенциал, связанный с электромагнитной индукцией, и существует независимо и в дополнение к разности потенциалов, связанной со статическим электрическим полем (например, раздел 5.12). Другими словами:

Закон Фарадея показывает вклад электромагнитной индукции (генерация ЭДС изменяющимся во времени магнитным потоком) в разность потенциалов, достигаемую при пересечении замкнутого пути.

В разделе 8.8 это понимание используется для преобразования статической формы закона напряжения Кирхгофа (раздел 5.10), который дает разность потенциалов, связанную только с электрическим полем, в уравнение Максвелла-Фарадея (раздел 8.8), которое является общее положение о связи между мгновенным значением электрического поля и производной магнитного поля по времени.

---

Эта страница под названием 8.3: Закон Фарадея распространяется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Стивеном В. Эллингсоном (Инициатива открытого образования технических библиотек штата Вирджиния) посредством исходного контента, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Стивен В. Эллингсон

   Лицензия

   CC BY-SA

   Версия лицензии

   4,0

   Программа OER или Publisher

   Инициатива открытого образования технических библиотек Вирджинии

   Показать оглавление

   нет

2. Теги

   1. Закон Фарадея
   2. индукция
   3. источник@https://doi.org/10.21061/electromagnetics-vol-1

Закон Фарадея

Введение

Этот эксперимент исследует закон электромагнитной индукции Фарадея. Это явление связано с наведенными напряжениями и токами из-за изменения магнитных полей. (Не путайте этот закон с законами электролиза Фарадея, которые совершенно различны.) Вы будете непосредственно измерять напряжение, индуцированное изменяющимся во времени магнитным полем, и исследовать несколько эффектов, возникающих в результате индуцированных ЭДС. Этот эксперимент разработан, чтобы следовать эксперименту с магнитными полями, поскольку зонд Холла и поля катушек и магнитов подробно исследуются в этом эксперименте. Вы должны быть знакомы с более ранним экспериментом, прежде чем приступать к этому (сначала прочтите описание магнитных полей, если вы не смогли провести этот эксперимент). Из нашего исследования изменяющегося во времени магнитного поля и индуцированных ЭДС мы знаем, что связь между этими величинами может быть выражена следующим соотношением:

( 1 )

ЭДС _{индуцированная} = − .

Отрицательный знак в уравнении (1) дает направление ЭДС индукции.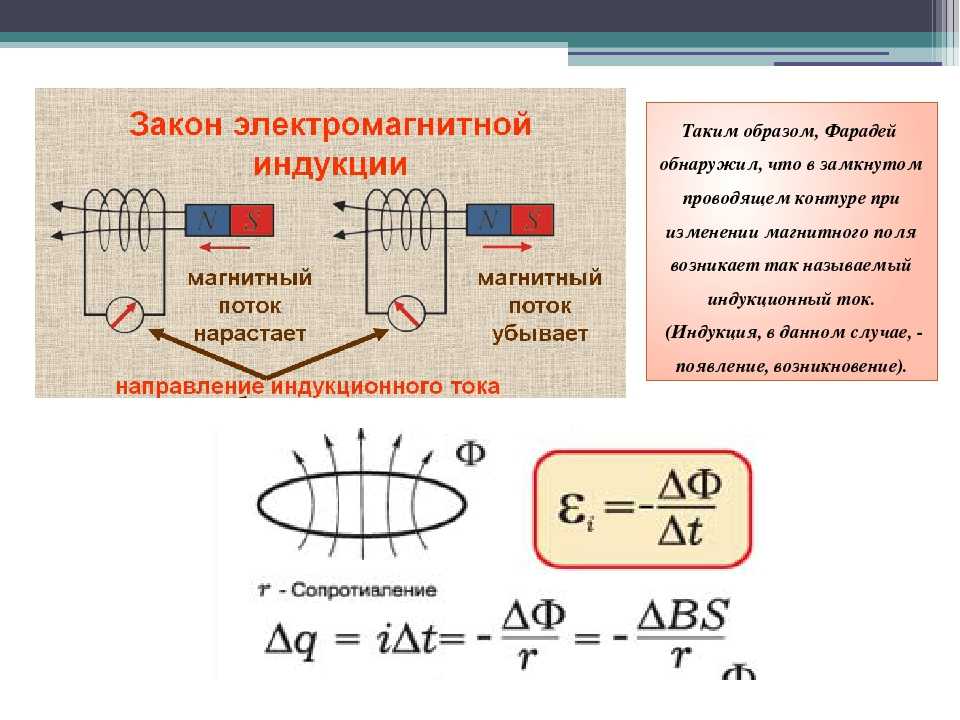 Для замкнутого контура можно выбрать или направление вокруг контура как «положительное». Поток считается положительным, если он продевает петлю в направлении большого пальца правой руки, когда пальцы указывают в положительном направлении петли (направление d s ). ЭДС также измеряется в положительном направлении контура, так что для положительной ЭДС E _{индуцированный} имеет тенденцию указывать вдоль d s . С этими соглашениями о знаках (как на рисунке 1) закон Фарадея указывает, что петлевая ЭДС будет отрицательной, если магнитный поток увеличивается со временем, и наоборот.

Рисунок 1 : Относительные направления согласно закону Фарадея

Другой способ запомнить знак ЭДС использует закон Ленца, который гласит, что индуцированные токи имеют направление, которое противостоит изменениям во внешнем магнитном поле. Наведенные токи могут противодействовать изменениям потока, создавая меньший поток, который частично компенсирует изменение потока. Это работает для проводящих петель или вихревых токов в твердых проводниках, где циркулирующие индуцированные токи управляются ЭДС закона Фарадея. Кроме того, эту идею можно использовать для нахождения направления ЭДС для любого контура, даже для тех, которые не содержат проводника, поскольку направление тока в проводящем контуре совпадает с направлением ЭДС независимо от проводимости. позволено. Для ЭДС из-за изменяющихся полей простейшим случаем является случай N — поворотная петля площадью A , которая остается перпендикулярной к изменяющемуся приложенному полю B . Если B пространственно однородна, поток для этого случая будет

( 2 )

Φ = N

А · В

91858 4, 1858 так что по закону Фарадея ЭДС равна

( 3 )

ЭДС _{индуцированная} = −NA.

Если приложенное поле синусоидальное, ЭДС индукции также будет синусоидальной. Для иллюстрации снова рассмотрим катушку N с витком, перпендикулярным однородному полю, в данном случае с величиной

( 4 )

В = В _o sin ω t.

Поскольку

= B _o ω cos ω t,

ЭДС будет равна

( 5 )

ЭМП _{индуцированный} = −NAB _o ω cos ω t.

Результирующее напряжение имеет фазовый сдвиг ~ 90 ° от приложенного поля (косинус по сравнению с синусоидальным) и больше для более высоких частот (из-за коэффициента ω ). Это встречается при приеме радиосигналов петлевой катушкой и при работе трансформаторов.

Объектив

Цель этого эксперимента состоит в том, чтобы вы создали изменяющиеся во времени магнитные поля в определенной области и наблюдали ЭДС, создаваемую в такой катушке. Тщательно измерив эти индуцированные поля, а также меняющиеся во времени магнитные поля, которые их создают, мы сможем проверить закон Фарадея.

Аппаратура

• Генератор функций
• Осциллограф
• Коробка датчика Холла
• Большая круглая катушка (намотана на черный ПВХ)
• Маленькая круглая катушка (намотана на белый нейлон)
• Соленоид со стальным сердечником
• Подковообразный магнит (с ниткой на нем)
• Цилиндрический магнит
• Алюминиевый блок (толщиной 1 см)
• Пластиковый блок (толщиной 1 см)
• Кусок медной проволоки
• Деревянная мормышка

Рисунок 2 : Оборудование

Процедура

Пожалуйста, распечатайте рабочий лист для этой лабораторной работы. Этот лист понадобится вам для записи ваших данных.

ЭДС от движущегося магнита

1

Подключите соленоидную катушку к входу канала 1 осциллографа с помощью кабеля BNC-банан, как показано на рис. 3. Настройте осциллограф следующим образом:

• •

  триггер [АВТО]

• •

  сек/дел.: 1 мс

• •

  В/дел.: 0,2 В (1 щуп)

• •

  муфта [постоянный ток]

2

Вы увидите небольшие колебания на осциллограмме. (Если вы видите большой сигнал 60 Гц, 0,1 В или больше, возможно, один из выводов подключен неправильно.) Небольшие колебания вызваны небольшими фоновыми полями переменного тока в лаборатории. Помимо этого, среднее напряжение должно быть равно нулю. Проверьте это, переключив вход осциллографа на «землю». (Совпадает ли среднее напряжение с землей?) Отрегулируйте вертикальное положение осциллографа так, чтобы линия кривой сигнала находилась в центре экрана. (Примечание: типичные фоновые поля составляют около 10 мГс.)

Рис. 3 : Соленоид и осциллограф

3

С соленоидом на лабораторном столе исследуйте его взаимодействие с цилиндрическим магнитом (см. рис. 3). Убедитесь, что вы можете индуцировать напряжение соленоида (видимое на осциллографе), перемещая магнит рядом с ним. Продвиньте северный полюс магнита к верхней части соленоида. Повторите, используя южный полюс магнита. Одинаковы ли знаки индуцированных напряжений или поменялись местами? Опишите результаты.

4

Переверните катушку соленоида (нижней стороной вверх) и снова сдвиньте северный полюс магнита к катушке. Знаки индуцированных напряжений для этого случая такие же или обратные по сравнению с шагом 3?

5

Держите полюс магнита устойчиво напротив одного конца катушки. Создается ли стабильное напряжение?

6

Убедитесь, что ЭДС создается путем перемещения катушки к магниту и от него (который находится на лабораторном столе). Опишите результаты.

7

Земля имеет постоянное магнитное поле около 0,5 Гс (5 × 10 ^–5 Тл) в лаборатории. Тем не менее, в отсутствие магнита вы не должны были бы видеть индуцированное напряжение на катушке. Почему это? Свяжите свой ответ с законом Фарадея.

8

При перемещении северного полюса магнита к катушке величина магнитного потока в катушке будет увеличиваться или уменьшаться? (Подумайте о том, как силовые линии исходят от полюса магнита.)

9

Являются ли признаки реакции, записанные вами на шагах 3 и 4, теми, которые вы ожидаете от закона Фарадея? Объяснять.

10

Объясните наблюдение ЭДС, которое вы сделали, удерживая полюс магнита неподвижно напротив одного конца катушки. Возникает ли в этой ситуации магнитный поток в катушке?

Движущийся провод в магнитном поле

Пример: гитарный звукосниматель.

1

Аккуратно выпрямите около 10 см медной проволоки и оберните ее вокруг деревянного приспособления (вам нужно будет обернуть концы этой проволоки вокруг двух кнопок с обеих сторон приспособления, чтобы проволока была достаточно натянута для этого эксперимента. ) Сделайте отрезок провода относительно натянутым и поместите подковообразный магнит в ярмо так, чтобы его отверстие было направлено вверх, а провод находился между наконечниками его полюсов.

2

Теперь соедините концы этого провода с концами кабеля BNC-банан, используя два коротких провода с зажимами типа «крокодил» на каждом конце. Подсоедините кабель BNC-банан к входу канала 1 осциллографа, как показано на рис. 4.

Рис. 4 : Сегмент провода и осциллограф

3

Установите осциллограф на:

• •

  триггер [АВТО]

• •

  по горизонтали сек/дел. : 20 мс

• •

  вертикальное В/дел.: 5 мВ (1 x датчик)

• •

  муфта [постоянный ток]

Отрегулируйте отображение осциллографа так, чтобы кривая линии располагалась ближе к центру экрана.

Осторожно:
На концах измерительного провода имеются открытые коннекторы; следите за тем, чтобы они не соприкасались друг с другом, и сокращайте свое наблюдение.

4

Теперь у вас есть магнитный звукосниматель, как в электрогитаре (провод — это гитарная струна). Передерните провод и посмотрите на результат на осциллографе. Какую максимальную амплитуду напряжения можно получить таким образом?

5

Попробуйте медленно покачать провод вперед и назад; амплитуда одинаковая?

6

Если бы вы хотели улучшить свою схему датчика, чтобы получить более сильные сигналы, какие изменения могли бы помочь: большее магнитное поле, более толстый провод, меньшее сопротивление провода? Почему?

Измерения с полями, зависящими от времени

1

Найдите коробку с датчиком Холла на лабораторном столе. Установите усиление на коробке на xl00. Выключите фильтр. Подключите выход датчика Холла к входу Ch2 осциллографа. Настройки осциллографа должны быть:

• триггер [АВТО]
• сек/дел.: 2,5 мс
• В/дел.: 2 мВ (1 x датчик)
• муфта [AC]

2

Подсоедините большую круглую катушку к выходу функционального генератора. Установите частоту на 100 Гц (синусоиду), а выход на максимальное значение. Поместите катушку горизонтально на столешницу.

3

Держите зонд Холла в центре большой катушки. Обратите внимание, что осциллограф показывает напряжение, пропорциональное зависящему от времени полю, для каждой из трех функций (синусоидальная, треугольная, квадратная). (Шум присущ датчику Холла; вы должны стремиться найти центр кривой, поскольку флуктуации одинаково положительны и отрицательны.)

В последующих процедурах датчик и большая круглая катушка должны удерживаться на одной линии друг с другом для получения точных показаний. Как вы помните, силовые линии для круглой катушки, наблюдаемые на оси, лежат параллельно оси (в данном случае вверх и вниз).

4

Отложите большую катушку и найдите маленькую круглую катушку. Подключите его к входу осциллографа (вместо выхода коробки пробника Холла). Удерживая маленькую катушку в центре большой катушки, наблюдайте на осциллографе формы сигналов для каждой из трех функций функционального генератора (рис. 5). Нарисуйте формы сигналов для каждого случая, используя прилагаемый шаблон экрана и программу Paint. Эквивалентны ли они производным форм волны магнитного поля?

Примечание. Возможно, вам потребуется отрегулировать уровень запуска, чтобы стабилизировать форму волны на экране осциллографа. Уровень запуска должен быть около середины амплитуды сигнала для достижения наилучших результатов в состоянии покоя.

Рисунок 5 : Катушки и осциллограф

5

Снова подключите коробку пробника Холла к осциллографу. Держите датчик Холла устойчиво в центре катушки. Установите генератор функций для треугольной волны. Измерьте рост напряжения (Δ V ) и прошедшее время (Δ t ) для части волны из коробки датчика Холла.

6

Отсюда вычислите наклон

.

Используйте калибровку на коробке датчика Холла, чтобы преобразовать это в скорость изменения магнитного поля,

.

7

Сделав это, снова подключите малую катушку к осциллографу, поместите катушку в центр большой катушки и измерьте амплитуду ЭДС индукции в вольтах непосредственно с помощью осциллографа. (Амплитуда составляет половины от пикового значения.)

8

Повторите эту последнюю процедуру: подключите коробку пробника Холла к осциллографу, измените генератор функций на синусоидальную волну и измерьте амплитуду волны (половину размаха напряжения). Частота должна быть по-прежнему 100 Гц, а датчик Холла должен находиться в центре катушки. Преобразуйте измеренную осциллографом амплитуду в магнитное поле в Тл, используя калибровку на коробке датчика Холла. Теперь подключите маленькую катушку к осциллографу и держите приемную катушку в центре большой катушки. Запишите амплитуду синусоидальной ЭДС, наблюдаемую на осциллографе.

9

Малая круглая катушка содержит 50 витков. Примите средний диаметр равным 2,05 см. С помощью этой информации и скорости изменения поля

, которую вы измерили на шаге 6, рассчитайте устойчивую ЭДС, предсказанную по закону Фарадея. Соответствует ли расчетный результат измеренному вами ЭДС?

10

Для синусоидального магнитного поля закон Фарадея предсказывает

ЭДС _{индуцированная} = -NAB ω cos ω t,

как описано выше. По амплитуде синусоидального поля, которую вы только что измерили, рассчитайте прогнозируемую амплитуду ЭДС. Вы должны сначала преобразовать Гц в радианы/с. Соответствует ли это значению, которое вы наблюдали?

Магнитный тормоз и вихревые токи

Магнитный тормоз

1

Подвесьте подковообразный магнит на веревке над лабораторным столом. Снимите удерживающую планку магнита, если она еще не снята.

2

Вращайте магнит вокруг своей оси на конце струны. С некоторой осторожностью это можно сделать так, чтобы магнит вращался на месте с небольшим колебанием. Обратите внимание, что магнит некоторое время будет вращаться без остановки, попеременно наматывая и разматывая струну. Наблюдайте за этим поведением вращающегося магнита в течение нескольких циклов.

3

Теперь поднесите алюминиевый блок к полюсам вращающегося магнита, не касаясь его, подсунув под вращающийся магнит. Есть ли эффект? Запишите свои наблюдения.

4

Повторите с пластиковым блоком. Есть ли разница?

Вихретоковый двигатель

5

Держите подвешенный магнит в покое на сантиметр или два выше алюминиевого блока, лежащего на столешнице.

6

Будьте осторожны, чтобы не коснуться магнита, и пусть один из ваших партнеров по лаборатории осторожно потянет алюминий в горизонтальном направлении. Наблюдайте и записывайте воздействие на магнит.

7

Что произойдет, если вы измените направление движения алюминиевого блока?

8

Теперь попробуйте это с пластиковым блоком и обратите внимание, что эффект не может быть вызван воздушными потоками.

9

Реальная форма вихревых токов в этой части весьма сложна.