Двоичная система счисления, 0 и 1, двоичные числа

Содержание:

1. Общая форма записи двоичных чисел
2. Правила сложения двоичных чисел
3. Вычитание методом заимствования
4. Вычитание методом дополнения
5. Правила умножения двоичных чисел

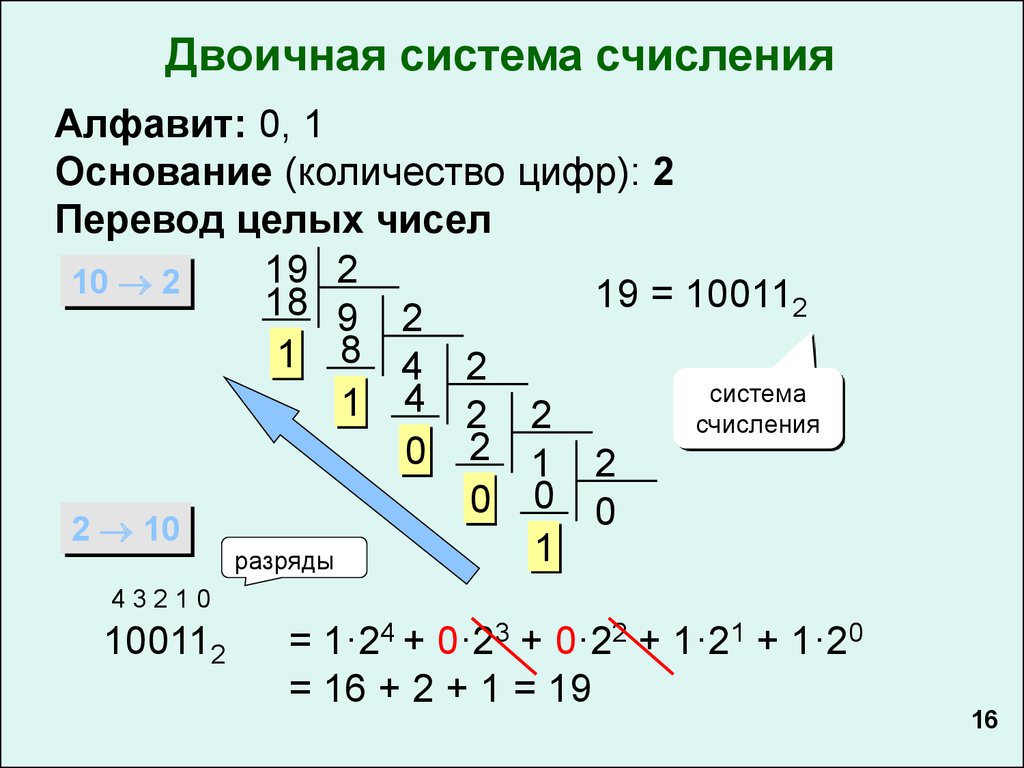
Вспомним материал по системам счисления. В нём говорилось, что наиболее удобной системой счисления для компьютерных систем является двоичная система. Дадим определение этой системе:

Двоичной системой счисления называется позиционная система счисления, у которой основанием является число 2.

Для записи любого числа в двоичной системе счисления используются всего лишь 2 цифры: 0 и 1.

Общая форма записи двоичных чисел

Для целых двоичных чисел можно записать:

a_n−1a_n−2…a₁a₀=a_n−1⋅2ⁿ⁻¹+a_n−2⋅2ⁿ⁻²+…+a₀⋅2⁰

Данная форма записи числа «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: требуется вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.

Правила сложения двоичных чисел

Основные правила сложения однобитовых чисел

0+0=0
0+1=1
1+0=1
1+1=10

Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.

Пример сложения двоичных чисел

Правила вычитания двоичных чисел

0-0=0
1-0=0
10-1=1

Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.

Вычитание методом заимствования

Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.

Вот несколько простых примеров:

1 — 0 = 1
11 — 10 = 1
1011 — 10 = 1001

Рассмотрим более сложную задачу. Вы должны запомнить только одно правило, чтобы решать задачи на вычитание двоичных чисел. Это правило описывает заимствование цифры слева, чтобы вы могли вычесть 1 из 0 (0 — 1).

110 — 101 = ?

В первом столбце справа вы получаете разность 0 — 1. Для ее вычисления необходимо позаимствовать цифру слева (из разряда десятков).

Во-первых, зачеркните 1 и замените ее на 0, чтобы получить такую задачу: 1010 — 101 = ?
Вы вычли («позаимствовали») 10 из первого числа, поэтому вы можете написать это число вместо цифры, стоящей справа (в разряд единиц). 101100 — 101 = ?
Вычтите цифры в правом столбце. В нашем примере:

101100 — 101 = ?

Правый столбец: 10 — 1 = 1.
102 = (1 x 2) + (0 x 1) = 210 (цифры нижнего регистра обозначают систему счисления, в которой записаны числа).

12 = (1×1) = 110.

Таким образом, в десятичной системе эта разность записывается в виде: 2 — 1 = 1.

Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):

101100 — 101 = __1 = _01 = 001 = 1.

Вычитание методом дополнения

Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.

Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).

Рассмотрим пример: 101100₂ — 11101₂= ?

Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.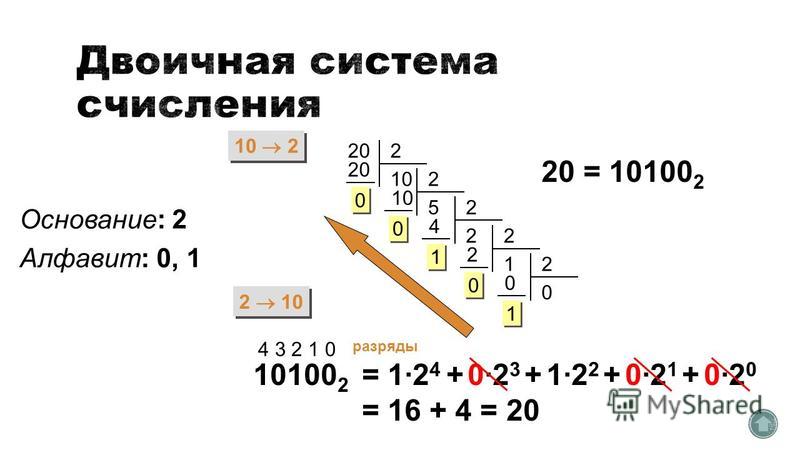

101100₂ — 011101₂= ?

В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.

011101₂ → 100010₂.

На самом деле мы «забираем дополнение у единицы», то есть вычитаем каждую цифру из 1. Это работает в двоичной системе, так как у такой «замены» может быть только два возможных результата: 1 — 0 = 1 и 1 — 1 = 0.

К полученному вычитаемому прибавьте единицу.

100010₂+ 1₂ = 100011₂

Теперь вместо вычитания сложите два двоичных числа.

101100₂ +100011₂= ?

Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.

1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 101101₂ нужно вычесть 11011₂

2) Обозначим как A число 101101₂ и как B число 11011₂.

3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).

Разр.	6	5	4	3	2	1	0
A		1	0	1	1	0	1
B			1	1	0	1	1

 

4) Вычтем разряд за разрядом из числа A число B записывая результат в C начиная с младших разрядов. Правила поразрядного вычитания, для двоичной системы счисления представлены в таблице ниже.

Заем из текущего разряда Oi-1	Ai	Bi	Ci	Заем из следующего разряда Oi+1
	0	0	0
	0	1	1	1
	1	0	1
	1	1	0
1	0	0	1	1
1	0	1	0	1
1	1	0	0
1	1	1	1	1

 

Весь процесс сложения наших чисел выглядит следующим образом:

(красным шрифтом показаны заёмы из соответствующего разряда)

Получилось 101101₂ — 11011₂ = 10010₂
или в десятичной системе счисления: 45₁₀ — 27₁₀ = 18₁₀

Правила умножения двоичных чисел.

В целом эти правила очень просты и понятны.

0*0=0
0*1=0
1*0=0
1*1=1

Умножение многоразрядных двоичных чисел происходит точно также как и обычных. Каждое значащий разряд умножаем на верхнее число по приведенным правилам, соблюдая позиции. Умножать просто — так как умножение на единицу даёт одно и тоже число.

×				1	1	1	0
					1	0	1
+				1	1	1	0
		1	1	1	0
	1	0	0	0	1	1	0

 

Система счисления Методы перевода десятичного числа в двоичное

Перевод в восьмеричную систему счисления

Пример №1. Перевести число 132,267₁₀ в восьмеричное представление.
Решение находим с помощью калькулятора. Переводим целую часть числа, т.е. 132.

Целая часть от деления	Остаток от деления
132 div 8 = [16].5 = 16	132 mod 8 = 4 (132 — 16*8)
16 div 8 = 2	16 mod 8 = 0	2 div 8 = 0	2 mod 8 = 2	0 div 8 = 0	0 mod 8 = 0

Остаток от деления записываем в обратном порядке. Получаем число в 8-ой системе счисления: 0204
132 = 0204₈

Для перевода дробной части числа последовательно умножаем дробную часть на основание 8. В результате каждый раз записываем целую часть произведения.
0.267*8 = 2.136 (целая часть 2)
0.136*8 = 1.088 (целая часть

1)
0.088*8 = 0.704 (целая часть 0)
0.704*8 = 5.632 (целая часть 5)
Получаем число в 8-ой системе счисления: 2105
0. 267 = 2105₈

Таким образом, число 132,267 записывается в восьмеричной системе счисления как 204,2105₈

Пример №2. Перевести число 1000000010,1001₂ в восьмеричное представление.
Переводим целую часть числа. Для этого разделим исходный код на группы по 3 разряда.
1000000010₂ = 001 000 000 010 ₂
Затем заменяем каждую группу на код из таблицы.

Двоичная СС	Восьмеричная СС
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Получаем число: 001 000 000 010 ₂ = 1002₈

Переводим дробную часть числа. Для этого разделим исходный код на группы по 3 разряда.
1001₂ = 100 100

2
Затем заменяем каждую группу на код из таблицы.
Получаем число: 100 100₂ = 44₈
Таким образом, число 1000000010,1001₂ в восьмеричной системе счисления записывается как 1002,44.

Пример №3. Перевести число 132,267₁₀ в восьмеричное представление.
Переводим целую часть числа. Заменяем каждый разряд на код из таблицы.

Двоичная СС	Шестнадцатеричная СС
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Получаем число: A5F₁₆ = 101001011111₂

Переводим дробную часть числа.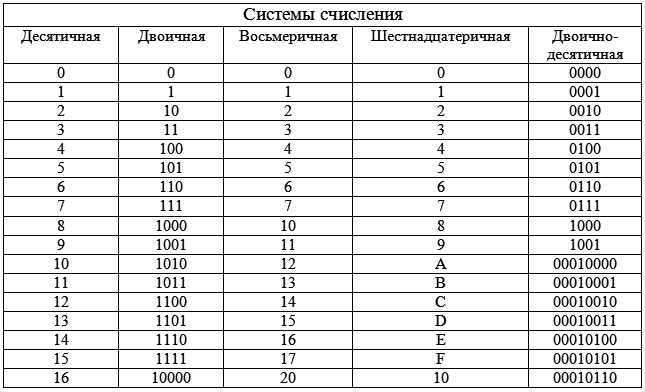

Получаем число: 3B₁₆ = 00111011₂
Переводим целую часть числа. Для этого разделим исходный код на группы по 3 разряда.
101001011111₂ = 101 001 011 111 ₂
Затем заменяем каждую группу на код из таблицы.

Двоичная СС	Восьмеричная СС
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Получаем число: 101 001 011 111 ₂ = 5137₈

Переводим дробную часть числа. Для этого разделим исходный код на группы по 3 разряда.
00111011₂ = 001 110 110₂
Затем заменяем каждую группу на код из таблицы.
Получаем число: 001 110 110₂ = 166₈
Таким образом, число A5F,3B₁₆ в восьмеричной системе счисления записывается как 5137,166.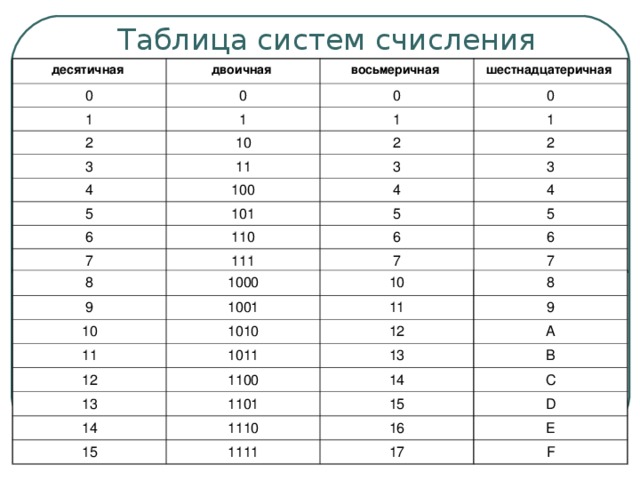

Перейти к онлайн решению своей задачи

1 в двоичном формате — Как преобразовать 1 из десятичного в двоичный?

1 в двоичной системе равно 1. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, равные 0 и 1 (биты). Мы использовали 1 бит для представления 1 в двоичном виде. В этой статье мы покажем, как преобразовать десятичное число 1 в двоичное.

• 1 в двоичном виде: 1₁₀ = 1₂
• 1 в восьмеричной системе: 1₁₀ = 1₈
• 1 в шестнадцатеричном формате: 1₁₀ = 1₁₆
• 1₂ в десятичном формате: 1₁₀

Как преобразовать 1 в двоичный код?

Шаг 1: Разделите 1 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0.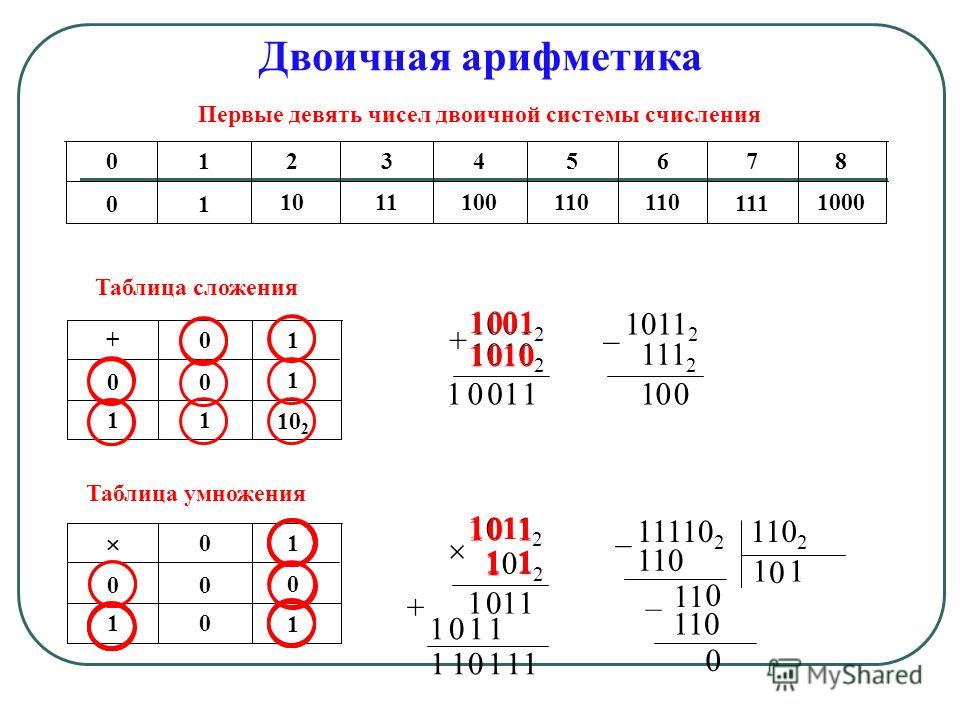

Дивиденд	Остаток
1/2 = 0	1

Шаг 2: Запишите остаток снизу вверх, т.е. в обратном хронологическом порядке. Это даст двоичный эквивалент 1.

Следовательно, двоичный эквивалент десятичного числа 1 равен 1.

☛ Калькулятор преобразования десятичной дроби в двоичную

Постановка задачи:

Часто задаваемые вопросы о 1 в двоичной системе

Что такое 1 in Бинарный?

1 в двоичном формате равен 1. Чтобы найти десятичный эквивалент в двоичном, последовательно делите 1 на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.

☛ Двоичный код в десятичный

Сколько бит имеет 1 в двоичном формате?

Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 1 в двоичном формате, т. е. 1. Таким образом, мы использовали 1 бит для представления 1 в двоичном формате.

Что такое двоичный эквивалент 1 + 5?

1 в двоичной системе счисления равно 1, а 5 равно 101. Мы можем сложить двоичный эквивалент 1 и 5, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (1)₂ + (101)₂ = (110)₂, что есть не что иное, как 6,9.0003

☛ Двоично-десятичный калькулятор

Найдите значение 3 × 1 в двоичной форме.

Мы знаем, что 1 в двоичном формате равно 1, а 3 равно 11. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0 ; 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 1 × 11 = 11, что равно 3 в десятичной системе счисления. [1 × 3 = 3]

Как преобразовать 1 в двоичный эквивалент?

Мы можем разделить 1 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге. 1 по модулю 2 = 1. Следовательно, десятичное число 1 в двоичном виде можно представить как 1.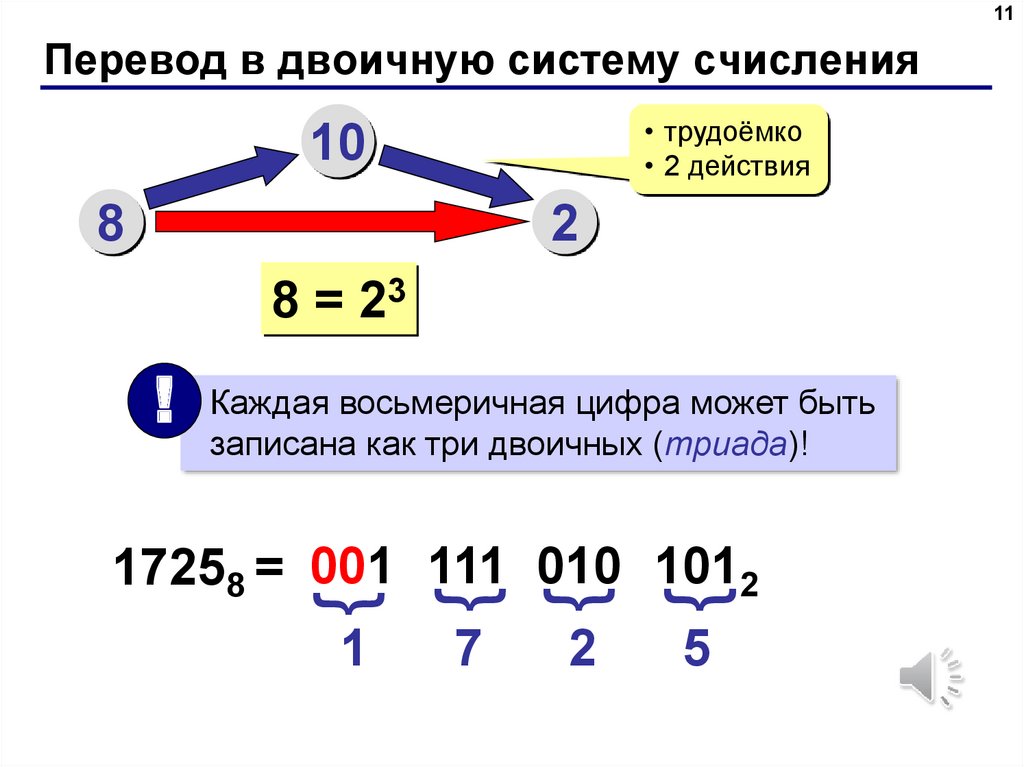

☛ Также проверьте:

• 73 в двоичном формате — 1001001
• 225 в двоичном формате — 11100001
• 3000 в двоичном формате — 101110111000
• 69 в двоичном формате — 1000101
• 120 в двоичном формате — 1111000
• 5 в двоичном формате — 101
• 222 в двоичном формате — 11011110

Рабочие листы по математике и визуальный учебный план

Почему 0,1 не существует в числах с плавающей запятой

Многие новые программисты узнают о двоичных числах с плавающей запятой, увидев, что их программы дают странные результаты: «Почему моя программа печатает 0,100000000000000001, когда я ввожу 0,1 ?»; «Почему 0,3 + 0,6 = 0,89999999999999991?»; «Почему 6 * 0,1 не равно 0,6?» Подобные вопросы задаются каждый день на онлайн-форумах, таких как stackoverflow.com.

Ответ заключается в том, что большинство десятичных дробей имеют бесконечное число представлений в двоичном виде. Возьмем, к примеру, 0,1.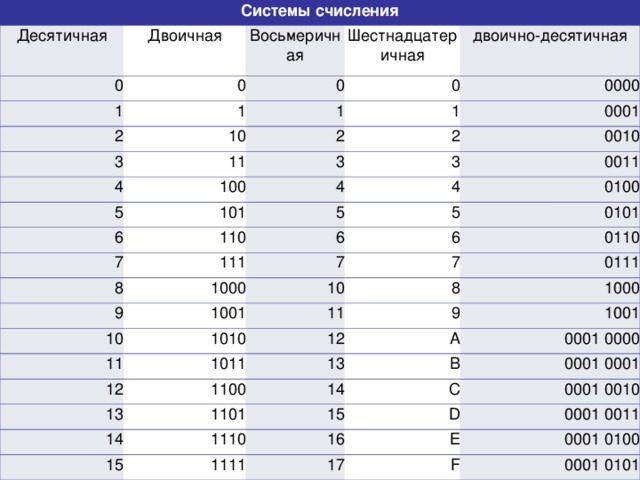 Это одно из самых простых десятичных чисел, которое только можно придумать, и все же оно выглядит таким сложным в двоичном виде:

Десятичный 0,1 В двоичном (до 1369 разрядов)

Биты продолжаются вечно; независимо от того, сколько из этих битов вы храните в компьютере, вы никогда не получите двоичный эквивалент десятичного числа 0,1.

0,1 В двоичном формате

0,1 составляет одну десятую или 1/10. Чтобы показать его в двоичном виде, то есть в виде бицимального числа, разделите двоичную единицу на двоичное число 1010, используя длинное двоичное деление:

Вычисление одной десятой в двоичном виде

Процесс деления будет повторяться вечно — и цифры в частном — тоже, потому что 100 («один-ноль-ноль») снова появляется как рабочая часть дивиденда. Зная это, мы можем прервать деление и записать ответ в повторяющейся двоичной системе счисления как 0,00011.

0,1 В с плавающей запятой

0,00011 — конечное представление бесконечного числа цифр. Это не поможет нам с плавающей запятой. Число с плавающей запятой не представляет числа с помощью повторяющихся полос; он представляет их фиксированным числом битов. Например, в числах с плавающей запятой двойной точности используются 53 бита, поэтому бесконечное в противном случае представление округляется до 53 значащих битов.

Давайте посмотрим, как выглядит 0,1 с двойной точностью. Во-первых, давайте запишем его в двоичном формате, усеченном до 57 значащих бит:

0.000110011001100110011001100110011001100110011001100110011001…

Bits 54 and beyond total to greater than half the value of bit position 53, so this rounds up to

0.0001100110011001100110011001100110011001100110011001101

In decimal, this is

0.1000000000000000055511151231257827021181583404541015625

which is slightly greater than 0.1.

Если вы распечатаете это число до 17 значащих десятичных цифр, вы получите 0,10000000000000001 (печать также округляет результат). Обратите внимание, что если бы вы печатали менее 17 цифр, ответ был бы 0,1.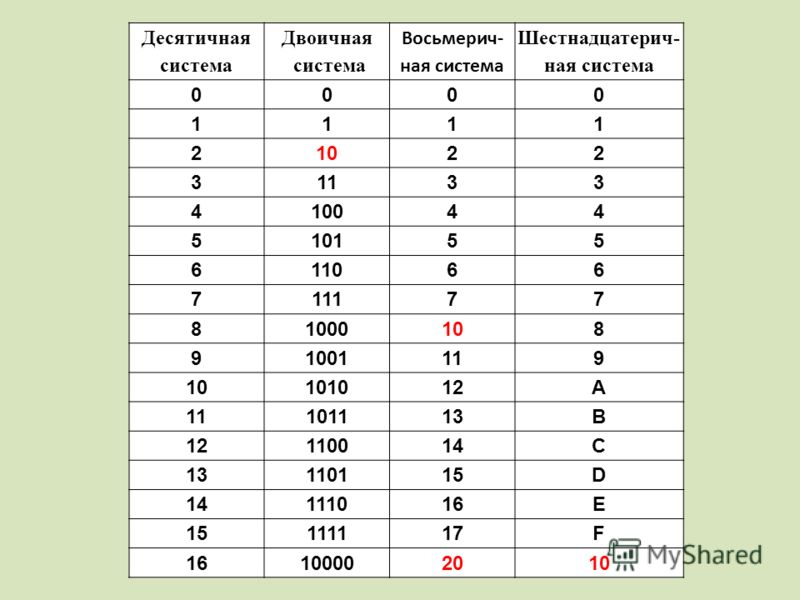 Хотя это всего лишь иллюзия — компьютер не сохранил 0,1.

Может быть чуть больше или чуть меньше 0,1

В зависимости от того, сколько битов точности используется, приближение 0,1 с плавающей запятой может быть меньше 0,1. Например, в половинной точности, которая использует 11 значащих бит, 0,1 округляется до 0,0001100110011 в двоичном формате, что составляет 0,0999755859375 в десятичном виде.

0.1 — это всего лишь один из многих примеров

0.1 — наиболее часто используемый пример в дискуссиях о «неточностях» с плавающей запятой — вот почему я выбрал его. Но есть много, много других примеров. Как узнать, есть ли у произвольной десятичной дроби эквивалентная двузначная дробь, которая заканчивается или повторяется?

Конечно, вы можете сделать то, что я сделал выше: преобразовать десятичную дробь в целое число в степени десяти, а затем выполнить двоичное деление. Если вы получаете остаток от нуля, двухзначное число завершается; если вы столкнетесь с рабочим делимым, которое вы видели раньше, двухзначное число повторяется. Этот метод великолепен, потому что вы видите, как бинарное представление разворачивается перед вашими глазами. Однако это утомительно. Двоичное деление сложно, даже если вы знаете, как это сделать.

Существует более простой тест: десятичная дробь имеет эквивалентную завершающую двузначную дробь тогда и только тогда, когда десятичная дробь, записанная в виде правильной дроби в наименьших терминах, имеет знаменатель, являющийся степенью двойки. (Нужно немного теории чисел, чтобы понять, почему это работает, но объяснение аналогично тому, почему десятичные дроби заканчиваются только для дробей со степенью двойки и/или степенью пятерки в знаменателе.) По этому правилу вы можете видеть, что 0,1 имеет бесконечную двузначную дробь: 0,1 = 1/10, а 10 не является степенью двойки. 0,5, с другой стороны, заканчивается: 0,5 = 5/10 = 1/2. Если спросить, есть ли у десятичной дроби соответствующая двузначная дробь, которая завершается или повторяется, следует использовать этот тест.

Некоторые завершающие двоичные числа не существуют в числах с плавающей запятой

Важно отметить, что некоторые десятичные числа с завершающими двоичными числами также не существуют в числах с плавающей запятой.