Светильник линейный Gauss WLF-1 40W 3600lm 4000K 185-265V IP20 1192*75*25мм алюминий LED 1/20
Характеристики 144125236
CRI
CRI (индекс цветопередачи) параметр, характеризующий соответствие естественного цвета тела видимому, при освещении его источником света. Проще говоря, лампа имеющая низкий CRI будет искажать цвет предметов. Хорошим показателем является цветопередача от 80 и выше. Средний показатель 70-80. При индексе цветопередачи ниже 70 светодиодную лампу для жилого помещения брать не стоит.
70
Световой поток
Этот параметр характеризует самый важный показатель современной светотехники, количество света от источника. Чем выше цифра, тем свет ярче.
3600 Лм
Угол освещения
Угол освещения очень важен при выборе лампы. Чем больше угол тем большую площадь освещает светильник. Угол освещения лампы накаливания обычно составляет 250 градусов. У точечных светильников он составляет порядка 120 градусов.
У точечных светильников он составляет порядка 120 градусов.
120°
Цветовая температура
Цветовая температура — характеристика цвета света испускаемого лампой. Чем ниже цифра тем теплее свет. Выражена в Кельвинах.
4000 К
Свет
Характеристика Свет — это описание понятным языком характеристики Цветовая температура.
Теплый: 2500K — 3500K
Дневной: 3600K — 4600K
Белый: 5000K — 6000K
Холодный: 6200K — 8000K
дневной
Питание
Допустимое напряжение подаваемое на устройство для его нормальной работы.
220 В
Мощность
Параметр отображает энергопотребление устройства, выраженное в Ваттах.
40 Вт
Рабочее напряжение
Характеристика отображает при каком напряжении возможна работа лампы или светильника.
185-265 В
Производитель
Фирма производящая товар.
Gauss
Тип
Тип устройства, опеределяет его набор функций.
светильник линейный
Диммирование
С помощью диммера (светорегулятора) вы имеете возможность плавного управления яркостью света лампы. Но для этого вам нужны специальные светодиодные лампы с функцией диммирования.
Обычные светодиодные лампы диммировать нельзя.
нет
Срок службы
Это период времени, в течение которого изготовитель обязуется обеспечивать потребителю возможность использовать прибор по назначению и несет ответственность за существенные недостатки, которые могут возникнуть.
35000 ч
Гарантия
Гарантия – это срок, предоставляемый потребителю продавцом или производителем, в течение которого покупатель может обратиться по вопросам качества изделия, а также по обслуживанию устройства за счет магазина.
2 года
Класс защиты
Степень защиты светильников от пыли и влаги определяется международной системой классификации Ingress Protection, сокращено IP. К примеру IP66 означает: пыленепроницаемое устройство с защитой от сильных водяных струй.
IP20
Вес Брутто
Вес товара с упаковкой.
350 гр.
Вес Нетто
Вес товара без упаковки.
330 гр
Высота
Размер лампы, светильника или прожектора.
25 мм
Ширина
Размер лампы, светильника или прожектора.
75 мм
Длина
Размер лампы, светильника, прожектора или светодиодной.
1192 мм
Найти похожие
Довольны качеством товара
- Продано: 18
- Возвращено: 0
- Возвращено по причине — Не работает (вышла из строя/брак): 0
- Процент довольных качеством: 100%
Список
Карта
Обухово
Удаленный склад
Срок поставки с удаленного склада составляет в среднем 4 рабочих дня
Доступность: 1000
Чехов
Основной склад
Комсомольская д. 15
15
Время самовывоза 8:00-20:00. Требуется предварительное согласование.
+7 495 409-03-57
При заказе: +4 дня к срокам доставки
По вашему запросу ничего не найдено
Удаленный склад
Срок поставки с удаленного склада составляет в среднем 4 рабочих дня
Основной склад
Комсомольская д. 15
+7 495 409-03-57
Время самовывоза 8:00-20:00. Требуется предварительное согласование.
Двигайте карту двумя пальцами
Отзывы не найдены
Светильник линейный Gauss WLF-1 50W 4550lm 6500K 185-265V IP20 1492*75*25мм алюминий LED 144126350
Название:
Артикул:
Текст:
Выберите категорию: Все Светодиодные лампы » Лампы Vintage Filament » Общего назначения » Свечи » Шары » Софитные лампы » Лампы GX53, GX70 » Зеркальные Лампы » Капсульные лампы G4, G9 » Диммируемые лампы »» Диммируемые LED лампы Gauss SMD »» Диммируемые LED лампы Gauss Filament »» Диммируемые LED лампы Gauss step dimmable » Flame » Шары G95/G125 » Filament »» Лампы Gauss LED Filament Basic »» Лампы Gauss LED Filament Clear »» Лампы Gauss LED Filament OPAL »» Лампы Gauss LED Black Filament Artline » LOFT » Комплекты » GAUSS elementary » Линейные лампы Т8 » Мощные лампы Т100-160 » Фито Филамент » Аккумуляторные лампы » Пульты » Gauss Basic Светодиодные светильники » Светильники с декоративным стеклом » Линейный LED светильник IP20 » Линейный LED светильник IP65 » Офисные панели » Светильники сауна, ЖКХ, IP65, IP54, UFO » Даунлайты » Даунлайты StepDim » Светильники Fito TL » Светильники TL » Светильники OVERHEAD » Светильники ФРИСБИ » Ультратонкие светильники » Слимы с подсветкой » Кухонные панели » Светильники с подсветкой » Многофункциональные автономные светильники » Светильники Фито-Сады » Светильники на солнечных батареях » Светильники-ночники » Кольцевые светильники Ring Light » Точечные светильники »» Белые точечные светильники »» Черные точечные светильники »» Точечные светильники GX53 »» Круглые точечные светильники »» Квадратные точечные светильники » Офисные панели Gauss MiR » Светильники Серия HALL IP40 » Светильники Серия СПП-Т8-G13 / ДПО-Т8-G13 » Уличные консольные светильники »» Avenue КСС «Д» »» Avenue КСС «Ш» »» Qplus »» Кронштейн Gauss для уличных светильников » Трековые светильники Gauss »» Трековые светильники »» Белые трековые светильники »» Черные трековые светильники »» Трековые светильники 4000K »» Однофазные трековые светильники »» Аксессуары к трековым светильникам » Настольные светильники Gauss »» Белые настольные лампы »» Черные настольные лампы »» Красные настольные лампы »» Зеленые настольные лампы »» Желтые настольные лампы » Светильники садово-парковые »» Серия Aura »» Серия Clio »» Серия Cube »» Серия Electra »» Серия Enigma »» Серия Sigma »» Серия Sonata »» Серия Vega » Светильник Gauss Basic Space » Праздничное освещение » Светильники для ванной комнаты » Даунлайты New » Светильники настольные декоративные » Сенсорные светильники » Белые светодиодные светильники » Черные светодиодные светильники » Светодиодные светильники 6500К » Светодиодные светильники 4000К » Круглые светодиодные светильники » Квадратные светодиодные светильники » Декоративные подвесы Светодиодная лента » Лента Gauss » Лента Gauss Elementary » Умная подсветка SmartLight » Блоки питания и контроллеры » Аксессуары для Led ленты » Лента LED Комплект Gauss » Лента Gauss 24V » Лента Gauss Basic Умный свет » Лампы »» Лампы SMD »» Лампы Filament »» Прожекторы » Светильники »» Даунлайты »» Настенно-потолочные » Светодиодная лента » Аксессуары Светодиодные прожекторы » Прожекторы Elementary » Прожекторы Elementary с датчиком » Прожекторы Qplus » Прожекторы EVO 6500K » Аккумуляторные светодиодные прожекторы » Прожекторы Qplus Графитовый серый корпус » Прожекторы Elementary зеленого свечения Очистители воздуха Стаканы с подсветкой Новогодняя продукция Фонари Gauss
Производитель: ВсеGauss
Новинка: Вседанет
Спецпредложение: Вседанет
Результатов на странице: 5203550658095
Светильник светодиодный ДПО-36 Вт 3010 Лм 6500K IP20 1192*75*25 мм алюминий WLF-1 GAUSS 144125336
Главная >Светотехника >Светильники настенно-потолочные >Светильник настенно-потолочный накладной >Gauss >Светильник светодиодный ДПО-36 Вт 3010 Лм 6500K IP20 1192*75*25 мм алюминий WLF-1 GAUSS 144125336 (#539300)
| Наименование | Наличие | Цена
опт с НДС |
Дата обновления |
Добавить в корзину |
Срок поставки |
|---|---|---|---|---|---|
| Светильник светодиодный WLF-1 40Вт 6500К IP20 3630лм 1192х75х25 ДПО алюм. (аналог ЛПО) GAUSS 144125336 | 231 | 1 001.94 р. | 04.10.2022 | От 1 дня | |
| Светильник светодиодный линейный WLF-1 IP20 1192*75*25мм 36W 3010Лм 6500K алюминий 1/20 | 144125336 | Gauss | 175 | 1 100.45 р. | 04.10.2022 | От 1 дня | |
| Светильник светодиодный ДПО-36 Вт 3010 Лм 6500K IP20 1192*75*25 мм алюминий WLF-1 GAUSS — 144125336 | Под заказ |
1 097. 87
р. 87
р.
|
03.10.2022 | От 30 дней | |
| … … … … … … … … … … | |||||
Условия поставки светильника светодиодного ДПО-36 Вт 3010 Лм 6500K IP20 1192*75*25 мм алюминий WLF-1 GAUSS 144125336
Купить светильники светодиодные ДПО-36 Вт 3010 Лм 6500K IP20 1192*75*25 мм алюминий WLF-1 GAUSS 144125336 могут физические и юридические лица, по безналичному и наличному расчету, отгрузка производится с пункта выдачи на следующий день после поступления оплаты.
Цена светильника светодиодного ДПО-36 Вт 3010 Лм 6500K IP20 1192*75*25 мм алюминий WLF-1 GAUSS 144125336 LED 36W 2650Лм 1209х75х25 ЛПО) зависит от общей суммы заказа, на сайте указана оптовая цена.
Доставим светильник светодиодного ДПО-36 Вт 3010 Лм 6500K IP20 1192*75*25 мм алюминий WLF-1 GAUSS 144125336 на следующий день после оплаты, по Москве и в радиусе 200 км от МКАД, в другие регионы РФ отгружаем транспортными компаниями.
Похожие товары
Светильник светодиодный встраиваемый ДВО-12 Вт 880 Лм 3000К круг IP20 монтажный d155 мм 170х22 180-265 В Slim Gauss 939111112 | 4 | от 525.44 р. | 2 варианта |
Светильник светодиодный встраиваемый ДВО-12 Вт 880 Лм 3000К круг IP20 монтажный d155 мм 170х22 мм 180-265 В Slim Gauss — 939111112 | 4 | 567.23 р. | |
Светильник светодиодный 12Вт 2700К IP20 встраив. | Под заказ | 525.44 р. | |
Светильник светодиодный встраиваемый ДВО-9 Вт 660 Лм 4000К квадрат IP20 монтажный d130х130 мм 145х145х22 180-265 В Slim Gauss 940111209 | 11 | от 420.10 р. | 2 варианта |
Светильник светодиодный встраиваемый ДВО-9 Вт 660 Лм 4000К квадрат IP20 монтажный d130х130 мм 145х145х22 мм 180-265 В Slim Gauss — 940111209 | 11 | 460. 31 р. 31 р. | |
Светильник светодиодный 9Вт 4100К IP20 встраив. ультратонкий квадрат. Gauss 940111209 | Под заказ | 420.10 р. | |
Светильник светодиодный встраиваемый ДВО-12 Вт 880 Лм 4000К круг IP20 монтажный d155 мм 170х22 180-265 В Slim Gauss 939111212 | 19 | 525.44 р. | |
Светильник светодиодный промышленный линейный ДПО LED 3017 Народный 2х9Вт 6500К IP20 опал | SQ0329-0129 TDM ELECTRIC | Под заказ | 525. 02 р. 02 р. | |
Светильник светодиодный встраиваемый ДВО-6 Вт 400 Лм 4000К круг IP20 монтажный d105 мм 120х22 180-265 В Slim Gauss 939111206 | Под заказ | 319.77 р. | |
Преобразовать Гс в Тл (гаусс в тесла)
Категории измерений:Активность катализатораБайт / Битвес ткани (текстиль)ВремяВыбросы CO2Громкость звукаДавлениеДинамическая вязкостьДлина / РасстояниеЁмкостьИндуктивностьИнтенсивность светаКинематическая вязкостьКоличество веществаКулинария / РецептыМагнитный потокмагнитодвижущая силаМасса / ВесМассовый расходМолярная концентрацияМолярная массаМолярный объемМомент силыМощностьМощностью эквивалентной дозыМузыкальный интервалНапряжённость магнитного поляНефтяной эквивалентОбъёмОбъёмный расход жидкостиОсвещенностьПлоский уголПлотностьПлотность магнитного потокаПлощадьПоверхностное натяжениеПоглощённая дозаПриставки СИпроизведение дозы на длинупроизведения дозы на площадьПроизводительность компьютера (флопс)Производительность компьютера (IPS)РадиоактивностьРазмер шрифта (CSS)Световая энергияСветовой потокСилаСистемы исчисленияСкоростьСкорость вращенияСкорость передачи данныхТекстильные измеренияТелесный уголТемператураУскорениеЧастей в . ..ЧастотаЭквивалентная дозаЭкспозиционная дозаЭлектрическая эластичностьЭлектрический дипольный моментЭлектрический зарядЭлектрический токЭлектрическое напряжениеЭлектрическое сопротивлениеЭлектрической проводимостиЭнергияЯркостьFuel consumption
..ЧастотаЭквивалентная дозаЭкспозиционная дозаЭлектрическая эластичностьЭлектрический дипольный моментЭлектрический зарядЭлектрический токЭлектрическое напряжениеЭлектрическое сопротивлениеЭлектрической проводимостиЭнергияЯркостьFuel consumption
Изначальное значение:
Изначальная единица измерения:В·с/м²Вб/m²гамма [γ]гаусс [Гс]гигатесла [ГТл]килотесла [кТл]мегатесла [МТл]микротесла [мкТл]миллигаусс [мГс]миллитесла [мТл]нанотесла [нТл]пикотесла [пТл]тератесла [ТТл]тесла [Тл]
Требуемая единица измерения:В·с/м²Вб/m²гамма [γ]гаусс [Гс]гигатесла [ГТл]килотесла [кТл]мегатесла [МТл]микротесла [мкТл]миллигаусс [мГс]миллитесла [мТл]нанотесла [нТл]пикотесла [пТл]тератесла [ТТл]тесла [Тл]
Числа в научной записи
Прямая ссылка на этот калькулятор:
https://www.preobrazovaniye-yedinits.info/preobrazovat+gauss+v+tesla.php
1 гаусс [Гс] = 0,000 1 тесла [Тл] — Калькулятор измерений, который, среди прочего, может использоваться для преобразования гаусс в тесла.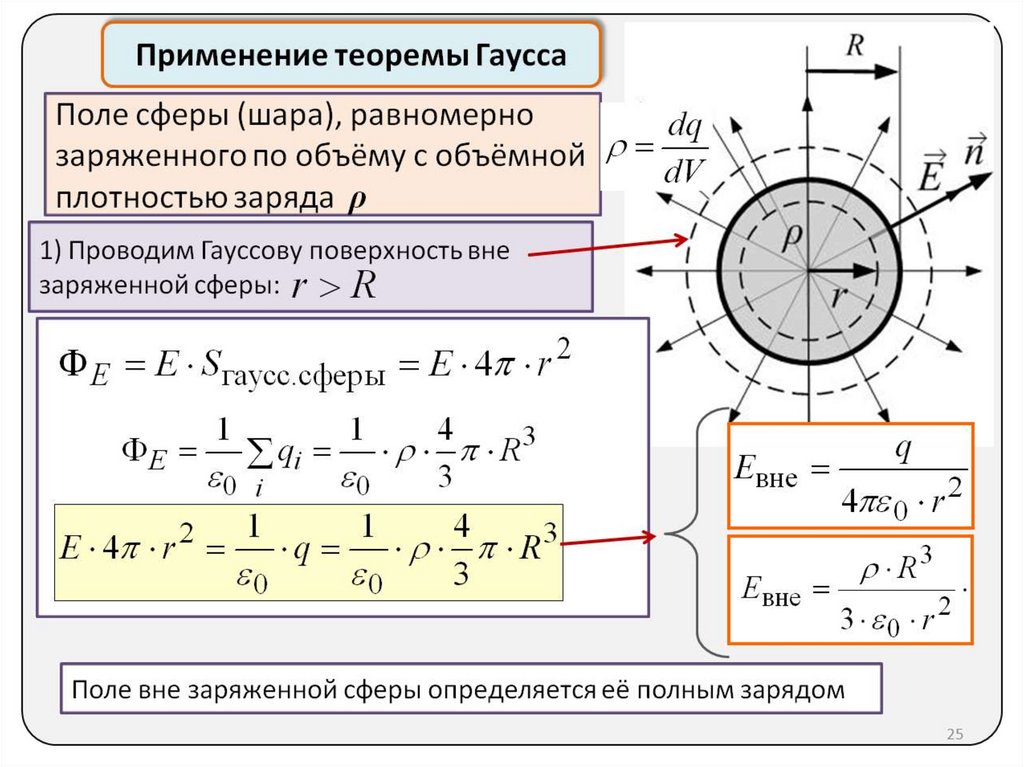 ), скобки и π (число пи), уже поддерживаются на настоящий момент.
), скобки и π (число пи), уже поддерживаются на настоящий момент.
С помощью этого калькулятора можно ввести значение для конвертации вместе с исходной единицей измерения, например, ‘132 гаусс’. При этом можно использовать либо полное название единицы измерения, либо ее аббревиатуруНапример, ‘гаусс’ или ‘Гс’. После ввода единицы измерения, которую требуется преобразовать, калькулятор определяет ее категорию, в данном случае ‘Плотность магнитного потока’. После этого он преобразует введенное значение во все соответствующие единицы измерения, которые ему известны. В списке результатов вы, несомненно, найдете нужное вам преобразованное значение. Как вариант, преобразуемое значение можно ввести следующим образом: ’75 Гс в Тл‘ или ’16 Гс сколько Тл‘ или ’12 гаусс -> тесла‘ или ’16 Гс = Тл‘ или ’39 гаусс в Тл‘ или ’35 Гс в тесла‘ или ’88 гаусс сколько тесла‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения нужно преобразовать исходное значение. Независимо от того, какой из этих вариантов используется, исключается необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Все это за нас делает калькулятор, который справляется со своей задачей за доли секунды.
Как вариант, преобразуемое значение можно ввести следующим образом: ’75 Гс в Тл‘ или ’16 Гс сколько Тл‘ или ’12 гаусс -> тесла‘ или ’16 Гс = Тл‘ или ’39 гаусс в Тл‘ или ’35 Гс в тесла‘ или ’88 гаусс сколько тесла‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения нужно преобразовать исходное значение. Независимо от того, какой из этих вариантов используется, исключается необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Все это за нас делает калькулятор, который справляется со своей задачей за доли секунды.
Кроме того, калькулятор позволяет использовать математические формулы. В результате, во внимание принимаются не только числа, такие как ‘(22 * 59) Гс’. Можно даже использовать несколько единиц измерения непосредственно в поле конверсии. 3′. Объединенные таким образом единицы измерения, естественно, должны соответствовать друг другу и иметь смысл в заданной комбинации.
3′. Объединенные таким образом единицы измерения, естественно, должны соответствовать друг другу и иметь смысл в заданной комбинации.
Если поставить флажок рядом с опцией ‘Числа в научной записи’, то ответ будет представлен в виде экспоненциальной функции. Например, 3,841 599 965 041 4×1025. В этой форме представление числа разделяется на экспоненту, здесь 25, и фактическое число, здесь 3,841 599 965 041 4. В устройствах, которые обладают ограниченными возможностями отображения чисел (например, карманные калькуляторы), также используется способ записи чисел 3,841 599 965 041 4E+25. В частности, он упрощает просмотр очень больших и очень маленьких чисел. Если в этой ячейке не установлен флажок, то результат отображается с использованием обычного способа записи чисел. В приведенном выше примере он будет выглядеть следующим образом: 38 415 999 650 414 000 000 000 000. Независимо от представления результата, максимальная точность этого калькулятора равна 14 знакам после запятой. Такой точности должно хватить для большинства целей.
Пересчет координат (МСК, СК 63, СК 64, СК 47, WGS 84, ПЗ 90) онлайн
Пересчет координат (МСК, СК 63, СК 64, СК 47, WGS 84, ПЗ 90) онлайн — GeoBridgeРучной ввод каталога координат
Введите координаты в текстовое окно «N,E исходные» через запятую.
Загрузка каталога координат из таблицы
Скопируйте 2 колонки с координатами из таблицы (например Excel) и вставьте их в окно «N,E исходные». При этом табуляция разделяющая колонки с координатами будет автоматически заменена на запятую.
Подойдет любая таблица, главное чтобы разделителем колонок была «табуляция», а разделителем строк «перевод строки».
Загрузка каталога координат из AutoCad
Выделите объекты в AutoCad координаты которых хотите пересчитать.
В командной строке введите _list и нажмите Enter.
Скопируйте каталог из появившегося окна и вставьте его в окно «N,E исходные».
После этого необходимо нажать кнопку
чтобы поменять координаты местами.
Внимание! Данный сервис создан для определения приблизительного местоположения точек в различных системах координат. Результаты пересчета нельзя использовать в геодезических работах любого вида.
MapBasic.RU
Утилиты и параметры для ГИС MapInfo http://mapbasic.ru/
| {{ ucs.source.title }} | {{ ucs. target.title }} target.title }} |
N,E — исходные г.ггг г°м’с»
N,E — результат
Разделитель целой и дробной части «точка». Разделитель между координатами «запятая».
градусы (десятичные)
градусы
минуты
секунды
{{ tr.
 str }}
str }}Зона СК-1942: | {{ tr.zone42 }} |
Осевой меридиан: | {{ tr.osm }}° |
| # | N | E | N | E | |
|---|---|---|---|---|---|
| {{ $index + 1 }} | {{ t. SourceNorth }} SourceNorth }} | {{ t.SourceEast }} | {{ t.TargetNorth }} | {{ t.TargetEast }} |
ссылка на контур: {{ contour.title }}
Копировать данные
Копировать в AutoCad:
точками
полилинией
Копировать таблицу:
как есть
реверс N,E
Только результат:
как есть
реверс N,E
KML (полигон):
исходные
результат
исходные R
результат R
Комментарии для сайта Cackle
Как пополнить базу проекций?
Если вы не нашли требуемую систему координат в списке проекций, мы можем ее создать.
Для этого необходимо прислать 4-6 точек в исходной системе и любой другой из списка (в идеале СК-1942, СК-95 или WGS84).
Если у вас уже есть параметры пересчета, то такие данные мы добавим значительно быстрей.
— Выделите содержимое текстового окна (Ctrl+A).
— Скопируйте его в буфер обмена (Ctrl+C).
— Для того что бы отобразить данные в AutoCAD (или другой совместимой системе) поместите курсор в командную строку и нажмите сочетание клавиш Ctrl-V.
— При этом важно чтобы курсор мыши находился в пределах командной строки.
Разделитель: табуляция ; ,
Общее число проекций {{ ucses.length }}. пополнить базу
пополнить базу
{{ u.title }}
Проекции пользователей
Общее число проекций {{ ucses.length }}. пополнить базу
{{ u.title }}
Проекции пользователей
Если вы не нашли требуемую систему координат в списке проекций, мы можем ее создать.
Для этого необходимо прислать 4-6 точек в исходной системе и любой другой из списка (в идеале СК-1942, СК-1963 или WGS84).
Если у вас уже есть параметры пересчета, то такие данные мы добавим значительно быстрей.
Решение любых систем уравнений
Системы уравнений/ Любые
Примеры
Для графика:
: [, ]
: [, ]
Решим систему уравнений!
Что умеет калькулятор?
- Решает системы уравнений различными методами:
- Метод Крамера
- Метод Гаусса
- Численный метод
- Графический метод
- Подробное решение тремя способами:
- Методами Крамера и Гаусса
- Прямой способ подстановки переменных
Примеры
Система линейных уравнений с двумя неизвестными
x + y = 5 2x - 3y = 1
Система линейных ур-ний с тремя переменными
2*x = 2 5*y = 10 x + y + z = 3
Система дробно-рациональных уравнений
x + y = 3 1/x + 1/y = 2/5
Система нелинейных уравнений
x^2 - 1 = 1 + y/2 n1 - y^2 = 2 + x
Система четырёх уравнений
x1 + 2x2 + 3x3 - 2x4 = 1 2x1 - x2 - 2x3 - 3x4 = 2 3x1 + 2x2 - x3 + 2x4 = -5 2x1 - 3x2 + 2x3 + x4 = 11
Система линейных уравнений с четырьмя неизвестными
2x + 4y + 6z + 8v = 100 3x + 5y + 7z + 9v = 116 3x - 5y + 7z - 9v = -40 -2x + 4y - 6z + 8v = 36
Система показательных и логарифмических уравнений
y - log(x)/log(3) = 1 x^y = 3^12
Система трёх нелинейных ур-ний, содержащая квадрат и дробь
2/x = 11 x - 3*z^2 = 0 2/7*x + y - z = -3
Система двух ур-ний, содержащая куб (3-ю степень)
x = y^3 x*y = -5
Система ур-ний c квадратным корнем
x + y - sqrt(x*y) = 5 2*x*y = 3
Система тригонометрических ур-ний
x + y = 5*pi/2 sin(x) + cos(2y) = -1
Метод Гаусса
x - y - 1 = 0 nx + y + 2 = 0
Метод Крамера
2*x - 3*y = 5 n5*x + y = 4
Прямой метод
2*x - y = 3 n2*x + y = 9
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):
- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- DiracDelta(x)
- Дельта-функция Дирака
- Heaviside(x)
- Функция Хевисайда
Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Единица измерения: терминология, принципы и значения
В системе СГС или системе сантиметр-грамм-секунд различных физических единиц гаусс является единицей магнитной индукции. Как правило, электродвижущая сила будет индуцироваться приложением плотности магнитного потока. Один гаусс эквивалентен, когда из-за плотности магнитного потока в каждом линейном участке или сантиметре провода индуцируется один абвольт или 10 -8 вольт электродвижущей силы. Предположим, что провод движется со скоростью один сантиметр в секунду вбок под углом девяносто градусов к магнитному потоку. Все магниты обычно измеряются в гауссах. Символ G используется для обозначения этой единицы измерения, которая измеряет плотность магнитного потока или магнитную индукцию.
Символ G используется для обозначения этой единицы измерения, которая измеряет плотность магнитного потока или магнитную индукцию.
Терминология Гаусса
Как мы уже знаем, гаусс является единицей магнитной индукции. Единица была названа в честь немецкого ученого по имени Карл Фридрих Гаусс. Ранее этот конкретный термин применялся для обозначения напряженности магнитного поля до 1932 года. Теперь единица измерения напряженности магнитного поля переведена в систему сантиметр-грамм-секунда. Но и сейчас некоторые говорят, что напряженность магнитного поля Земли составляет около одного гаусса. Карл Фридрих Гаусс был известным математиком девятнадцатого века. Он внес большой вклад в исследования и разработку магнитометра.
Гаусс и Тесла
Для всех, кто изучает физику, очень важно знать взаимное преобразование гаусса в тесла и наоборот. Но перед этим важно понять эти два термина. Гаусс происходит от гауссовой системы единиц, которая была унаследована от системы сантиметр-грамм-секунда. Кроме того, система СГС неоднократно менялась, чтобы окончательно заменить ее Международной системой единиц или системой СИ. Следовательно, все стандартные органы не одобряли использование гаусса в качестве единицы измерения. Хотя до сих пор используется в различных областях науки. Тесла — это единица измерения магнитной индукции в системе СИ. Преобразование из гаусса в тесла довольно просто. Все, что вам нужно сделать, это разделить на 10000. Один тесла эквивалентен 10000 гаусс. Там же указано, что 1 гаусс равен 10 -4 тесла.
Кроме того, система СГС неоднократно менялась, чтобы окончательно заменить ее Международной системой единиц или системой СИ. Следовательно, все стандартные органы не одобряли использование гаусса в качестве единицы измерения. Хотя до сих пор используется в различных областях науки. Тесла — это единица измерения магнитной индукции в системе СИ. Преобразование из гаусса в тесла довольно просто. Все, что вам нужно сделать, это разделить на 10000. Один тесла эквивалентен 10000 гаусс. Там же указано, что 1 гаусс равен 10 -4 тесла.
Гаусс и магнетизм
Один максвелл на квадратный сантиметр равен одному гауссу. 1 Гаусс равен 10 -4 Вебера на квадратный метр. Напряженность поля любого магнитного материала можно определить с помощью датчика Гаусса. Напряженность магнитного поля часто измеряется в теслах, а не в гауссах. Но это технически не правильно. Это связано с тем, что определения напряженности магнитного поля и плотности магнитного потока не совпадают. Хотя оба они обозначаются одной и той же буквой B. Единицы намагниченности ферромагнитного вещества или остаточной намагниченности любого постоянного магнита также измеряются в единицах тесла и гаусса. Остаточная намагниченность также известна как сила любого магнита.
Хотя оба они обозначаются одной и той же буквой B. Единицы намагниченности ферромагнитного вещества или остаточной намагниченности любого постоянного магнита также измеряются в единицах тесла и гаусса. Остаточная намагниченность также известна как сила любого магнита.
Гаусс Единицы Физические принципы
Вместе с Вильгельмом Эдуардом Вебером, одним из известных физиков, Гаусс создал систему сантиметр-грамм-секунду или систему СГС. Она очень похожа на современную систему СИ и известна как стандартная единица измерения. Основные единицы системы СГС образуют гауссовую единицу магнитного потока. Для длины используется сантиметр, для времени — секунда, а для массы — грамм. В Германии до 1970 года гаусс не был какой-либо юридической единицей или объектом в метрологии. Однако гаусс широко используется в астрофизике. Законной единицей плотности магнитного потока в системе СИ является тесла, и соотношение между гауссами и теслами также довольно простое и важное. Один ньютон на метр-ампер также равен одному тесла.
Один ньютон на метр-ампер также равен одному тесла.
Некоторые типичные значения в гауссах
Давайте посмотрим на некоторые типичные значения в гауссах.
Поверхностное магнитное поле Земли — от 0,25 до 0,60 Гс.
Ядро магнитного поля Земли — 25G.
Сила магнита СИБ — от 10000 до 13000G.
Электродинамический квантовый порог магнитной силы — 4×10 13 Г.
Магнитное поле новорожденных магнитаров — 10 15 G.
Напряженность магнитного поля внутри аппарата МРТ или магнитно-резонансной томографии — от 3000 до 70000G.

Напряженность магнитного поля в пределах пятна – 1500 Гс.
Для трансформаторов требуются сплавы железа с высокой проницаемостью, которые имеют насыщение от 16000 до 22000G.
Знаете ли вы?
Сила магнитного поля обычного магнита на холодильник составляет около 50 Гс.
Метрические префиксы можно легко комбинировать с гауссами, такими как миллигаусс.
4π × 10 -3 эрстед эквивалентен одному амперу на метр.
Плотность магнитного потока — это количество силовых линий, проходящих через определенную замкнутую поверхность.

Гаусс Определение и значение | Dictionary.com
- Основные определения
- Викторина
- Примеры
- Британский
- Медицинский
- Научная
Показывает уровень сложности слова.
[ gous ]
/ gaʊs /
Сохрани это слово!
Показывает уровень оценки в зависимости от сложности слова.
Определение Гаусса
существительное Электричество.
сантиметр-грамм-секунда единица магнитной индукции, равная магнитной индукции магнитного поля, в котором заряд в один абкулон, движущийся с компонентой скорости, перпендикулярной полю и равной одному сантиметру в секунду, действует на силой в одну дину; 1 максвелл на квадратный сантиметр или 10-4 вебера на квадратный метр. Символ: G
Символ: G
(ранее) Эрстед (по умолчанию 1).
ВИКТОРИНА
Сыграем ли мы в «ДОЛЖЕН» ПРОТИВ. «ДОЛЖЕН» ВЫЗОВ?
Следует ли вам пройти этот тест на «должен» или «должен»? Это должно оказаться быстрым вызовом!
Вопрос 1 из 6
Какая форма используется для указания обязательства или обязанности кого-либо?
Происхождение гаусса
Впервые записано в 1880–1885 гг.; имени К. Ф. Гаусса
Слова рядом gauss
gauntry, gaup, gaur, закон Гауза, принцип Гауза, gauss, gaussian, кривая Гаусса, распределение Гаусса, изображение Гаусса, целое число Гаусса
Другие определения для Гаусса (2 из 2)
GAUSS
[GOUS]
/ GAʊS /
SUM
KARL FRIE · DRICH [KAHRL FEER-DRIH], / KɑRL ˈFRI DRɪX / 1775555555555555555555 года. , немецкий математик и астроном.
ДРУГИЕ СЛОВА ОТ Gauss
Gauss·i·an, прилагательное Dictionary.com Unabridged
На основе Random House Unabridged Dictionary, © Random House, Inc. , 2022
, 2022
Как использовать gauss в предложении
Вы можете подумать, что Гаусс просто гений математики, так что он очень быстро складывал числа в уме.
Что не так с ярлыками? (Эп. 483)|Стивен Дж. Дубнер|18 ноября 2021 г.|Фрикономика
Мы прорвались через стаю менее чем в двадцати пяти милях к северу от того места, где зимовал «Гаусс» (Германская экспедиция, 1902 г.).
Дом Снежной бури|Дуглас Моусон
Гаусс решил задачу на своей доске и положил ее лицевой стороной вниз на стол, выкрикивая: «Вот она!», согласно обычаю.
Герои Телеграфа|Дж. Мунро
Из приходской школы Гаусс поступил в Екатерининскую гимназию, хотя его отец сомневался, сможет ли он позволить себе такие деньги.
Герои Телеграфа|Дж. Мунро
Он подружился с Гауссом и покупал математические книги, которые они вместе читали.
Герои Телеграфа|Дж. Мунро
Слава Гаусса путешествовала туда, но герцог сопротивлялся всем попыткам привести или заманить его в университет этого места.

Герои Телеграфа|Дж. Манро
Определения гаусса в Британском словаре (1 из 2)
гаусс
/ (ɡaʊs) /
существительное во множественном числе гаусс
единица измерения плотности магнитного потока в единицах измерения плотности магнитного потока; плотность потока, вызывающая ЭДС величиной 1 абвольт (10–8 вольт) на сантиметр в проводе, движущемся поперек поля со скоростью 1 сантиметр в секунду. 1 гаусс эквивалентен 10 –4 тесла
Происхождение слова гаусс
после Карла Гаусса
Определения гаусса в Британском словаре (2 из 2)
Гаусс
/ (нем. ɡaus) /
существительное
Карл Фридрих (karl ˈfriːdrɪç). 1777–1855, немецкий математик: разработал теорию чисел и применил математику к астрономии, электричеству, магнетизму и геодезии.
Производные формы Гаусса © William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012
Медицинские определения гаусса
гаусса
[gous]
n. пл. гаусс
пл. гаусс
Единица измерения магнитной индукции сантиметр-грамм-секунда.
Медицинский словарь Стедмана The American Heritage® Copyright © 2002, 2001, 1995, компания Houghton Mifflin. Опубликовано компанией Houghton Mifflin.
Научные определения гаусса (1 из 2)
гаусс
[ gous ]
Единица плотности магнитного потока в системе сантиметр-грамм-секунда, равная одному максвеллу на квадратный сантиметр, или 10-4 тесла.
Научные определения гаусса (2 из 2)
Гаусс
Карл Фридрих 1777-1855
Немецкий математик, астроном и физик, внесший значительный и быстрый вклад в математику своим вкладом в алгебру, геометрию, статистику и теоретическую математику . Он также правильно рассчитал орбиту астероида Церера в 1801 году и изучил электричество и магнетизм, разработав магнитометр в 1832 году. В его честь названа гауссовая единица плотности магнитного потока.
Научный словарь American Heritage®
Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Модели Гаусса — MATLAB & Simulink
Модели Гаусса
О моделях Гаусса
Модель Гаусса соответствует пикам и задается как
y=∑i=1naie[−(x−bici)2]
амплитуда, б центроид (местоположение), c относится к ширине пика, n — количество пиков, которые должны соответствовать, и 1 ≤ n ≤ 8.
Гауссовы пики встречаются во многих областях науки и техники. За Например, пики Гаусса могут описывать линейчатые спектры излучения и химические вещества. анализы концентрации.
Подгонка моделей Гаусса в интерактивном режиме
Откройте приложение Curve Fitter, введя
кривая монтажникв командной строке MATLAB ® . Либо на вкладке Приложения , в Математика, статистика и оптимизация щелкните Curve Fitter .
Либо на вкладке Приложения , в Математика, статистика и оптимизация щелкните Curve Fitter .В приложении Curve Fitter выберите данные кривой. На Вкладка Curve Fitter в Раздел данных , нажмите Выбрать Данные . В выберите фитинг В диалоговом окне Data выберите X данные и Y данные или просто Y данные по индексу.
Щелкните стрелку в разделе Fit , чтобы откройте галерею и нажмите Gaussian в 9Группа 0304 Модели регрессии .

Вы можете указать следующие параметры в Fit Панель параметров :
Укажите количество терминов в виде положительного целого числа в диапазон [1 8]. Просмотрите панель результатов . увидеть условия модели, значения коэффициентов и статистика соответствия.
Опционально, в дополнительных параметрах укажите начальные значения коэффициентов и ограничения или изменить настройки алгоритма. Приложение рассчитывает оптимизированные начальные точки для Gaussian подходит, исходя из набор данных. Вы можете переопределить начальные точки и указать ваши собственные ценности в Варианты установки панель.

Подгонка по Гауссу имеет параметр ширины
c1ограничено нижней границей0. Нижние границы по умолчанию для большинства библиотечные модели-Inf, которые указывает, что коэффициенты не ограничены.
Дополнительные сведения о настройках см. в разделе «Указание параметров подгонки и оптимизированных начальных точек».
Подгонка гауссовских моделей с помощью функции подгонки
Открытие сценария Live
В этом примере показано, как использовать функцию подгонки для подгонки гауссовой модели к данным.
Модель библиотеки Гаусса является входным аргументом для функций fit и fittype . Укажите тип модели gauss , а затем число термов, например, 92)
Коэффициенты (с доверительной вероятностью 95%):
а1 = 1,47 (1,426, 1,515)
b1 = 897,7 (897, 898,3)
с1 = 27,08 (26,08, 28,08)
а2 = 0,6994 (0,6821, 0,7167)
b2 = 810,8 (790, 831,7)
с2 = 592,9 (500,1, 685,7)
plot(f,x,y)
См.
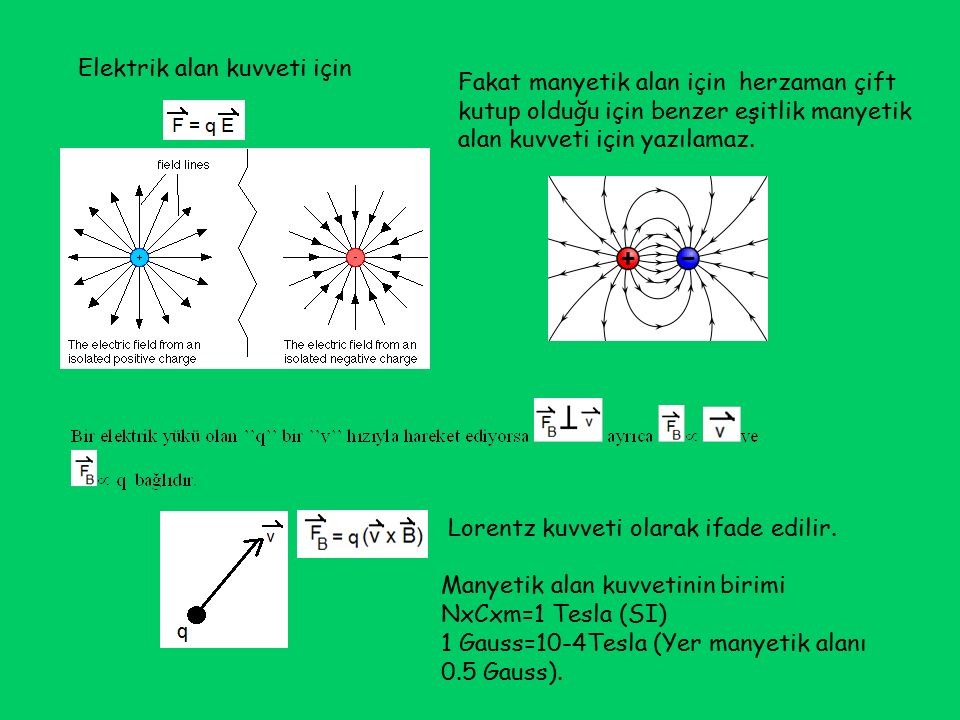 также
такжеПриложения
- Curve Fitter
Функции
-
fit|фиттип|фитопций
Связанные темы
- Подгонка по Гауссу с экспоненциальным фоном
- Укажите параметры подгонки и оптимизированные начальные точки
У вас есть модифицированная версия этого примера. Хотите открыть этот пример со своими правками?
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
Пушка Гаусса |
Пушка Гаусса0005
Технологический университет Чалмерса,
Гётеборг, Швеция
* электронная почта: akean@student. chalmers.se
chalmers.se
Получено:
2
Август
2017
Принято:
4
Август
2017
Abstract
В этом отчете исследуются различные свойства гауссовой пушки. Скорость выстрела пушки измеряется для различного количества стальных шаров, различной входной скорости и различной геометрии пушки. Измеряя силу притяжения магнита к шарам, можно получить карту потенциальной энергии для процесса выстрела. Обнаружено, что стрельбу из гауссовой пушки можно смоделировать как последовательные столкновения магнита с соседними шарами и между последовательными шарами. Чтобы достичь максимально возможной скорости выброса спускового крючка, выпущенного из состояния покоя, следует использовать цепную пушку. Оптимальное количество шаров на каждой отдельной пушке зависит от энергий намагничивания и коэффициентов восстановления.
Ключевые слова: пушка Гаусса / пушка / магнит / динамика / цепь
© Å. Andersson et al., Опубликовано EDP Sciences, 2017 г.
Это статья с открытым доступом, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (http://creativecommons. org/licenses/by/4.0), которая разрешает неограниченное использование. , распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
org/licenses/by/4.0), которая разрешает неограниченное использование. , распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
1 Введение
Пушка Гаусса является популярным устройством для обучения, поскольку она проста в изготовлении и доступна по цене. Он устроен так, как показано на рисунке 1. Линия стальных шариков прикреплена к сильному магниту. Если дополнительный шарик сталкивается с магнитом, самый крайний шарик может быть выброшен с высокой скоростью. В присутствии магнитного поля сталкивающийся шар, или спусковой крючок, теряет магнитную потенциальную энергию и приобретает кинетическую энергию. Помещая больше шариков на стреляющую сторону магнита, потенциальная энергия, теряемая спусковым шариком, становится меньше, чем потенциальная энергия, приобретаемая выброшенным шариком. Следовательно, выброшенный шар может достигать более высоких скоростей, чем спусковой крючок. Однако из-за потерь энергии при столкновениях скорость выброса не будет увеличиваться до бесконечности. Таким образом, пушка Гаусса является хорошим примером системы, которую можно оптимизировать.
Таким образом, пушка Гаусса является хорошим примером системы, которую можно оптимизировать.
Хотя гауссовую пушку легко сконструировать, тщательный анализ далеко не тривиален из-за огромного количества параметров. В этом отчете основное внимание уделяется определению скорости выброшенного мяча в зависимости от параметров системы и тому, как максимизировать эту скорость. Настраиваемые параметры включают количество шаров на огневой стороне пушки, размер магнита, радиус шаров и скорость попадания спускового крючка. В более ранних работах измерялась сила, действующая на стальные шары, как функция расстояния, чтобы вычислить потенциальную энергию пускового шара и выброшенного шара, тем самым оценивая полученную кинетическую энергию системы [1,2]. В этом отчете мы представляем более подробный анализ процесса обжига и новый подход к определению коэффициентов реституции. Структура IMRaD плюс модель, тупик и заключение. Тупик содержит заброшенные эксперименты и бесполезные мысли.
| рисунок 1 Процесс стрельбы из пушки Гаусса. |
2 Модель
Процесс обжига моделируется следующим образом: на шарики действует магнитная сила от магнита, гравитационная сила от земли и сила трения и нормальная сила от дорожки. На рисунке 1 представлены четыре различных шага, которые мы рассматриваем в нашей модели. (а) Спусковой крючок притягивается магнитом и катится ко дну потенциальной ямы с начальной скоростью v 0 . Предполагая, что катится без проскальзывания, сумма поступательной и вращательной энергии равна , а магнитная потенциальная энергия равна 0. (b) Когда целевой шар ударяется о магнит, его магнитная потенциальная энергия равна E 0 и его скорость v в . Если мяч все еще катится без проскальзывания, его вращательная энергия равна . Однако мяч может также начать скользить при приближении, и в этом случае энергия вращения будет меньше этого значения. Предполагая, что вращение не может уменьшиться по сравнению с начальным движением, нижняя граница вращательной энергии определяется выражением . (c) Поскольку кинетическая энергия целевого мяча передается стреляющему мячу в результате столкновений, последний мяч линии с магнитной потенциальной энергией E n , выбрасывается. Его скорость v out выражается как функция полного коэффициента восстановления v out = ε tot v
Если мяч все еще катится без проскальзывания, его вращательная энергия равна . Однако мяч может также начать скользить при приближении, и в этом случае энергия вращения будет меньше этого значения. Предполагая, что вращение не может уменьшиться по сравнению с начальным движением, нижняя граница вращательной энергии определяется выражением . (c) Поскольку кинетическая энергия целевого мяча передается стреляющему мячу в результате столкновений, последний мяч линии с магнитной потенциальной энергией E n , выбрасывается. Его скорость v out выражается как функция полного коэффициента восстановления v out = ε tot v

Таким образом, мы получаем следующую систему уравнений из сохранения энергии и определения коэффициента восстановления: (1) (2) (3)
с описанием неизвестной энергии вращения спускового крючка. соответствует вращению без проскальзывания, т.е. v дюймов = rω дюймов . Наименьшее возможное значение для α (без углового ускорения). Из уравнения (1) и ω 0 < ω в , мы можем доказать
Следовательно, если , то v 0 ≈ v в и . Это также будет доказано экспериментально. До тех пор составная формула для v 1 ( v 0 ) будет следующей: уравнения (1), (2) и (3) вместе дают: (4)
Это соотношение предполагает линейную зависимость между квадратами скоростей и зависит от трех параметров, описывающих кинетическую энергию спускового крючка α , потеря энергии при передаче энергии ε и потенциальная энергия шаров E n . Далее мы экспериментально оценим эти члены, чтобы лучше понять проблему, и проверим линейную зависимость между и .
Далее мы экспериментально оценим эти члены, чтобы лучше понять проблему, и проверим линейную зависимость между и .
3 метода
3.1 Измерение скорости
Экспериментальная установка для измерения скорости состояла из пушки Гаусса на деревянной дорожке (из породы пихты). Чтобы измерить скорость, лазеры были направлены поперек дорожки, а осциллограф регистрировал каждый раз, когда мяч прерывал лазерный луч, и выдавал время между прерываниями. Поскольку ожидалось, что скорость уменьшится из-за трения, было использовано несколько лазеров. На рис. 2 представлено аннотированное изображение используемой установки. Всего два лазерных луча пересекли траекторию в пяти различных точках, ближайшая из которых находилась на расстоянии 10 мм от выбрасываемого шара, т. е. на расстоянии x = 10 мм. The speed was obtained from v = ( x − x ′ )/( t − t ′ ) where x − x ′ denotes the distance between two близлежащие лучи и t и t ′ обозначают соответствующие моменты времени, когда лучи были разрушены выпущенным шаром. Поскольку x − x ′ является постоянным и t − t ′ измеряется с точностью до наносекунды, погрешность измерения определяется случайным характером срабатывания. То, как рано мяч коснется дорожки, имеет значение, и мы не могли полностью это контролировать. Для борьбы с этим все эксперименты с контролируемыми параметрами повторялись пять раз. Для таких измерений стандартная ошибка среднего отображается в виде планок погрешностей.
Поскольку x − x ′ является постоянным и t − t ′ измеряется с точностью до наносекунды, погрешность измерения определяется случайным характером срабатывания. То, как рано мяч коснется дорожки, имеет значение, и мы не могли полностью это контролировать. Для борьбы с этим все эксперименты с контролируемыми параметрами повторялись пять раз. Для таких измерений стандартная ошибка среднего отображается в виде планок погрешностей.
Магнит был изготовлен из нескольких соединенных цилиндрических неодимовых магнитов радиусом 10 мм и высотой 2,5 мм, намагниченных вдоль оси симметрии [3]. Использовались как большие, так и малые шарики диаметром 12,0 мм и диаметром 9 мм.0,5 мм (погрешности менее 1 мкм) и масса 7,10 г и 3,51 г соответственно (погрешности менее 0,01 г). Деревянная дорожка имела U-образную форму с немного большим радиусом, чем у шариков. Для крепления магнита использовался клей-расплав.
Рис. 2 2Экспериментальная установка для измерения скорости. Пушка Гаусса стоит на деревянной гусенице. Спусковой крючок приближается к пушке справа, а слева расположены лазеры для измерения скорости стрельбы. |
3.2 Измерение силы и определение энергии
Для определения энергии — E n необходимой для полного выталкивания шара из системы, состоящей из магнита и n других прилипших к нему шаров, сила притяжения F ( d ) было измерено для различных расстояний d . E n можно вычислить путем интегрирования F н ( д ) с 2 р по ∞ . Фактические измерения проводились двумя немного разными способами.
Для больших расстояний, d > 3 мм, шарик приклеивался к немагнитной горизонтальной пластине, высота которой y могла регулироваться с точностью Δ y < 0,01 мм. Под пластиной находился магнит и другие шарики, прикрепленные к грузу, что составляло общий вес M . Эта система опиралась на шкалу, показывающую значение 9.0480 м с точностью Δ м < 0,01 g. Сила притяжения F была рассчитана как F = ( M − м ) г . Этот метод имеет хорошую точность как для d , так и для F , но для d < 3 мм F становится настолько большим, что пластина изгибается, и поэтому точность y и d становится слишком низкой.
Эта система опиралась на шкалу, показывающую значение 9.0480 м с точностью Δ м < 0,01 g. Сила притяжения F была рассчитана как F = ( M − м ) г . Этот метод имеет хорошую точность как для d , так и для F , но для d < 3 мм F становится настолько большим, что пластина изгибается, и поэтому точность y и d становится слишком низкой.
Для малых расстояний, d < 3 мм, полоски ленты общей толщиной d были наклеены на пушку, и шар изначально лежал поверх уложенных полос. Пушка была прижата к весу тяжелыми грузами. Затем мяч вытягивали, поднимая ту же пластину, что и выше, как показано на рис. 3. По мере подъема пластины отображаемая масса м постепенно опускалась, пока не достигла определенного значения м c , при котором мяч оторвался, в результате чего м быстро увеличились. F рассчитывали как максимальное снижение веса, F = ( M − м c ) г . Этот метод имеет большую точность для d , но большую ошибку для F , Δ F < 0,1 N.
Этот метод имеет большую точность для d , но большую ошибку для F , Δ F < 0,1 N.
| Рис. 3 Установка для измерения силы, приложенной магнитами к одному стальному шарику. Мяч подвешен над магнитами, которые прикреплены к грузам. Взаимная сила, действующая на магниты, уменьшает вес, отображаемый на весах, что позволяет рассчитать магнитную силу как функцию разницы отображаемого веса. Способ, которым мяч был подвешен на этом изображении, мы использовали для очень малых расстояний ( d < 3 мм) между шаром и магнитами. |
3.3 Определение COR
COR ε to определяется как
Эти скорости трудно измерить, так как магнитное поле быстро ускоряет шарики на коротком расстоянии очень близко к магниту или близко к линии шариков. Поэтому мы измерили v 0 и v 1 и использовали уравнения (1) и (3), чтобы получить в в и в из . Это было сделано для количества шаров n = 1, …, 7. Количество цилиндрических магнитов также варьировалось в интервале 3–9.
Это было сделано для количества шаров n = 1, …, 7. Количество цилиндрических магнитов также варьировалось в интервале 3–9.
4 результатов
4.1 Сила и энергия
Обычно мы определяем E n как магнитную потенциальную энергию между магнитом и стреляющим шаром, между которым и магнитом находится n шаров. Для рисунка 1 n = 1. Обратите внимание, что мы определяем термины магнитной потенциальной энергии E 0 , E 1 , … чтобы они всегда были отрицательными.
Сила F n ( d ) измерялась для малых и больших шаров. Для краткости показан график только для больших шаров (рис. 4). Сюжеты были качественно схожи. Энергии E n в таблице 1 были определены путем интегрирования кубического интерполянта F n ( d ). Высшее n приводит к тому, что для выхода из пушки требуется меньше энергии, что увеличивает v 1 .
| Рис. 4 Тяговые усилия F 0 , F 1 и F 2 для больших мячей в зависимости от расстояния d между магнитом и краем мяча. Обратите внимание, что d определяется самим магнитом, поэтому F n определяется только для d ≥ n ⋅ 12 мм. E n получен интегрированием кубического интерполянта (сплошная линия). |
Таблица 1
Значения E n в мДж для больших и малых шаров.
4.2 Скорость
При измерении конечной скорости v 1 варьировались следующие параметры:
На рис. 5 показано изменение двух первых параметров. Набор данных из 13 магнитов показывает, что скорость выброса не увеличивается монотонно с увеличением количества магнитов. Было обнаружено, что оптимальное количество магнитов равно 6, добавление большего количества приводит к слишком большому рассеиванию энергии, чтобы окупить дополнительный магнитный поток. Поэтому все последующие пушки будут состоять из 6 магнитов, чтобы максимизировать скорость.
Поэтому все последующие пушки будут состоять из 6 магнитов, чтобы максимизировать скорость.
Влияние размера шара можно увидеть на рисунке 6. Меньший размер шара позволяет увеличить v 1 и увеличить оптимальное n . В большинстве последующих экспериментов использовались маленькие шарики.
Наконец, параметр v 0 варьировался практически для каждой точки данных на рис. 6. Результат был качественно одинаковым для каждого случая, поэтому представлен только один такой график (рис. 7).
| Рис. 5 Скорости выброса v 1 для маленьких шариков с v 0 как можно меньшими в зависимости от количества шариков и магнитов. |
| Рис. 6 Скорости выброса v 1 для шаров различных размеров, когда v 0 = 0, в зависимости от числа шаров, находящихся между магнитом и выброшенным шаром n . |
4.3 COR
log ( ε tot ) как функция n показана на рисунке 8 с шестью магнитами. Экспоненциальное соотношение предполагает, что , где ε bm — это COR между шариком и магнитом, а ε bb — это COR между шариками. В таблице 2 показаны ε bb и ε bm для разного количества магнитов. Значение α влияет на то, как v в вычисляется из v 0 и, в свою очередь, ε to . Чем выше n , тем больше рассеивается энергии, что снижает v 1 .
| Рис. 8 Логарифм значений COR показан на оси y , а количество шаров показано на x — ось. |
Таблица 2
Значения COR, полученные в результате линеаризации рисунка 8, в предположении .
5 Обсуждение
5.1
n зависимостьОбщая качественная зависимость от n соответствовала предсказанию теории. Для маленьких n , выброшенный мяч передает значительное количество энергии, покидая магнит. Для больших n значительное количество энергии рассеивается при столкновениях между шарами.
5.2 Линейность
Еще одной сильной стороной модели была предсказанная (при условии постоянной α ) и измеренная линейность между и . Уравнения (1), (2) и (3) вместе дают линейную зависимость между v 1 и v 0 , явно указанное в уравнении (4). Линейная зависимость между квадратами скоростей проверена для больших и малых шаров с n = 3, 4, …, 7. На рис.
На рис.
Квадрат скорости выброса как функция скорости срабатывания , для маленьких шаров и n = 5. Каждый кружок соответствует одному выброшенному шару. Линейная зависимость является общей чертой, независимо от выбора размера мяча и н . Цепная пушка : Когда пушки соединены вместе, квадрат скорости соответствует сходящемуся ряду, представленному зеленой пунктирной линией. При большом количестве пушек конечная скорость соответствует фиолетовому кресту перекрестка.
5.3 Цепная пушка
Когда две пушки соединены вместе так, что v 1 первой становится v 0 второй, в результате получается лучшая пушка. Какова конечная скорость при сколь угодно длинной цепи пушек?
Известно, что для одной пушки является линейной функцией от , в частности уравнения (4). В общем, последовательность x n +1 = Ax n + B сходится к если | А | < 1. Для нашей системы . Это положительно и меньше 1, потому что ε tot < 1 и 2 α > 1. На рисунке 7 показана сходимость ряда.0480 v 0 = v 1 (фиолетовая точка на рис. 7) к расчетным значениям, . Сравнение можно увидеть на рисунке 9. Оно не только дает нам ожидаемое значение α = 0,7, но также может рассматриваться как проверка уравнения (4), если предполагается, что α = 0,7.
Для нашей системы . Это положительно и меньше 1, потому что ε tot < 1 и 2 α > 1. На рисунке 7 показана сходимость ряда.0480 v 0 = v 1 (фиолетовая точка на рис. 7) к расчетным значениям, . Сравнение можно увидеть на рисунке 9. Оно не только дает нам ожидаемое значение α = 0,7, но также может рассматриваться как проверка уравнения (4), если предполагается, что α = 0,7.
Из рисунка 9 видно, что α = 0,7 является хорошим приближением, которое позволило бы упростить уравнения (1) и (4). Анализ оптимальных значений α показывает, что они имеют среднее значение 0,68 и расчетное стандартное отклонение 0,028. Таким образом, 0,7 — это 0,74 стандартного отклонения от α , что соответствует невозможности отбросить нулевую гипотезу α = 0,7 с p < 0,5. Таким образом, мы можем принять приближение α = 0,7. Интересное наблюдение на Рисунке 9 состоит в том, что оптимальные n ниже, чем если бы использовалась одна пушка. Это связано с повышенной важностью рассеяния энергии в цепной системе.
Это связано с повышенной важностью рассеяния энергии в цепной системе.
| Рис. 9 Сравнение точек пересечения линейных регрессий (желтая линия на рис. 7) и точек пересечения нашей модели (фиксированные точки уравнения (4)). Поскольку уравнение (4) зависит от α , который пока неизвестен, делается несколько графиков в зависимости от выбора α . |
6 Тупик
Ранее мы рассматривали возможность сравнения измеренной силы тяги с силой, рассчитанной по уравнениям поля B . От этого подхода отказались из-за повышенной сложности и неизвестности магнитного дипольного момента.
Мы попытались заснять выброшенный мяч, чтобы узнать о его вращении, но временное разрешение оказалось недостаточным для количественного анализа. Иногда шары вращались вокруг вертикальной оси из-за соприкосновения с бортом огневой дорожки, что делало невозможным определение угловой скорости.
7 Заключение
Канон Гаусса — это простое устройство, которое представляет собой глубокую проблему оптимизации. Выброс стреляющего шара происходит из-за большой кинетической энергии, передаваемой при столкновениях от пускового шара, и из-за ограничения магнитной потенциальной энергии распорными шарами. В то время как большое количество промежуточных шаров уменьшает глубину потенциальной ямы, из которой должен вылететь стреляющий шар, это также увеличивает потери энергии, происходящие во время передачи энергии. Эти два конкурирующих поведения приводят к существованию оптимального количества дистанционирующих мячей.
Выброс стреляющего шара происходит из-за большой кинетической энергии, передаваемой при столкновениях от пускового шара, и из-за ограничения магнитной потенциальной энергии распорными шарами. В то время как большое количество промежуточных шаров уменьшает глубину потенциальной ямы, из которой должен вылететь стреляющий шар, это также увеличивает потери энергии, происходящие во время передачи энергии. Эти два конкурирующих поведения приводят к существованию оптимального количества дистанционирующих мячей.
Мы представили простую модель, основанную на законе сохранения энергии, чтобы связать скорость стреляющего шара со скоростью спускового крючка, и нашли линейную зависимость между квадратами этих двух величин. Наша модель опирается на три параметра, а именно вращательный кинетический член α , коэффициент восстановления ε tot и магнитную потенциальную энергию E n , из которых последние два были исследованы экспериментально. Для α , мы протестировали все возможные значения и в каждом случае обнаружили, что при α = 0,7 модель согласуется с экспериментами. То, что α = 0,7, также помогло лучше понять физику процесса выброса. Линейное поведение было подтверждено экспериментами и пролило свет на конечную скорость, достигаемую последовательностью гауссовского канона. Это и составляет основной результат настоящей работы.
Для α , мы протестировали все возможные значения и в каждом случае обнаружили, что при α = 0,7 модель согласуется с экспериментами. То, что α = 0,7, также помогло лучше понять физику процесса выброса. Линейное поведение было подтверждено экспериментами и пролило свет на конечную скорость, достигаемую последовательностью гауссовского канона. Это и составляет основной результат настоящей работы.
В дополнение к представленному здесь исследованию оптимизации канон Гаусса демонстрирует многочисленные особенности, заслуживающие внимания. Например, симметрия между количеством спускового крючка и стреляющего шара (один и один в данной работе) можно рассматривать как обобщение колыбели Ньютона, но также изучать как распространение солитонной волны через дистанционирующие шары [4]. Неупругие столкновения, приводящие к конечным потерям коэффициента восстановления, также представляют интерес. Поэтому мы считаем, что гауссовский канон является мощным инструментом не только для стрельбы металлическими шарами, но и для обучения и понимания физики.
Каталожные номера
- Дж.А. Рабчук, Винтовка Гаусса и магнитная энергия, Phys. Учить. 41, 158 (2003) [Перекрестная ссылка] [Google ученый]
- Д. Каган, Энергия и импульс в ускорителе Гаусса, Phys. Учить. 42, 24 (2004) [Перекрестная ссылка] [Google ученый]
- Неодиммагнит, номер продукта 31-1467, http://www.
 clasohlson.com
[Google ученый]
clasohlson.com
[Google ученый] - Модель синус-гордона и ее приложения (2014 г.), http://www.springer.com/in/book/97833116. [Google ученый]
Цитируйте эту статью как : Оке Андерссон, Карл-Йоар Карлссон, Хампус Лейн, Пушка Гаусса, Emergent Scientist 1 , 6 (2017)
Все таблицы
Таблица 1
Значения E n в мДж для больших и малых шаров.
В тексте
Таблица 2
Значения COR, полученные в результате линеаризации рисунка 8, в предположении .
В тексте
Все фигурки
| рисунок 1 Процесс стрельбы из пушки Гаусса. (a) Спусковой крючок движется к магниту и линии стальных шариков. (b) Спусковой крючок сталкивается с магнитом со скоростью 90 480 v 90 481 90 499 дюймов 90 500 . Энергия столкновения передается через магнит и шарики в линии. (c) Крайний правый шар выброшен с начальной скоростью v out . (d) Выброшенный мяч достигает скорости v 1 905:00 . | |
| В тексте | |
| Рис. 2 Экспериментальная установка для измерения скорости. Пушка Гаусса стоит на деревянной гусенице. Спусковой крючок приближается к пушке справа, а слева расположены лазеры для измерения скорости стрельбы. | |
| В тексте | |
| Рис. 3 Установка для измерения силы, приложенной магнитами к одному стальному шарику. | |
| В тексте | |
| Рис. 4 Тяговые усилия F 0 , F 1 и F 2 для больших мячей в зависимости от расстояния d между магнитом и краем мяча. Обратите внимание, что d определяется самим магнитом, поэтому F n определяется только для d ≥ n ⋅ 12 мм. E n получен интегрированием кубического интерполянта (сплошная линия). | |
| В тексте | |
Рис. 5 5Скорости выброса v 1 для маленьких шариков с v 0 как можно меньшими в зависимости от количества шариков и магнитов. | |
| В тексте | |
| Рис. 6 Скорости выброса v 1 для шаров различных размеров, когда v 0 = 0, в зависимости от числа шаров, находящихся между магнитом и выброшенным шаром n . n = 0 не учитывается, так как выброса не происходит. Для маленьких шариков оптимально n = 5. Для больших шаров это n = 1, наименьшее из возможных n . | |
| В тексте | |
| Рис. 8 Логарифмы значений COR показаны на оси y , а количество шаров показано на оси x . Диаметр шара 12 мм, количество магнитов 6 и α = 0,7. Линейная регрессия y = −0,12 n − 0,08 показана сплошной красной линией. | |
| В тексте | |
| Рис. 7 Квадрат скорости выброса как функция скорости срабатывания , для маленьких шаров и n = 5. Каждый кружок соответствует одному выброшенному шару. Линейная зависимость является общей характеристикой, независимо от выбора размера шара и n . Цепная пушка : Когда пушки соединены вместе, квадрат скорости соответствует сходящемуся ряду, представленному зеленой пунктирной линией. При большом количестве пушек конечная скорость соответствует фиолетовому кресту перекрестка. | |
| В тексте | |
| Рис. 9 Сравнение точек пересечения линейных регрессий (желтая линия на рис. 7) и точек пересечения нашей модели (фиксированные точки уравнения (4)). Поскольку уравнение (4) зависит от α , которое пока неизвестно, построено несколько графиков в зависимости от выбора α . | |
| В тексте | |
определение гаусса по The Free Dictionary
Также найдено в: Тезаурусе, Медицине, Финансах, Сокращениях, Энциклопедии, Википедии.
Связано с гауссом: исключение Гаусса
gauss
(gous)n. пл. гаусс или гаусс·с Сокр. G
Единица измерения плотности магнитного потока сантиметр-грамм-секунда, равная одному максвеллу на квадратный сантиметр.
[По имени Карла Фридриха Гаусса .]
Словарь английского языка American Heritage®, пятое издание. Авторские права © 2016, издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.
Гаусс
( немецкий ɡaus)n
(биография) Карл Фридрих (karl ˈfriːdrɪç). 1777–1855, немецкий математик: разработал теорию чисел и прикладной математики к астрономии, электричеству и магнетизму, а также геодезию
1777–1855, немецкий математик: разработал теорию чисел и прикладной математики к астрономии, электричеству и магнетизму, а также геодезию
Гаусса прил.
GAUSS
(ɡAWʊS)9048
GAUSS
(ɡAWʊS)9048 8 89818104818981898181818181818181818181818181818181818181818181818181818
.
(Единицы) единица плотности магнитного потока в сгс; плотность потока, которая индуцирует ЭДС в 1 абвольт (10 –8 вольт) на сантиметр в проводе, движущемся по полю со скоростью 1 сантиметр в секунду. 1 Гаусс эквивалентен 10 –4 Tesla
Collins English Dictionary — Complete и Unabridged, 12th Edition 2014 © Harpercollins Publishers 1991, 1994, 1998, 2000, 2003, 2006, 2009, 2011, 2014
, 2000, 2003, 2006, 2009, 2011, 2014
, 2000, 2003, 2006, 2009, 2011, 2014
, 2000, 2003, 2007, 2009, 2011, 2014
.
 (gaʊs)
(gaʊs)сущ.
единица измерения напряженности магнитного поля сантиметр-грамм-секунда, равная 10 −4 тесла. Символ: G
[1880–85; после К. Френч. Gauss]
Gauss
(gaʊs)сущ.
Карл Фридрих, 1777–1855, немецкий математик и астроном.
Гауссьян, прил.
Рэндом Хаус Словарь колледжа Кернермана Вебстера, © 2010 K Dictionaries Ltd. Авторские права Random House, Inc., 2005, 1997, 1991. Все права защищены.
ТезаурусАнонимыРодственные словаСинонимы Легенда:
Переключение на новый тезаурус
| Существительное | 1. | GAUSS — Подразделение Magnetic Flus Dewelles Define. величина магнитного потока на единицу площади поперечного сечения микрогаусс — единица плотности магнитного потока, равная одной миллионной части гаусса тесла — единица плотности магнитного потока, равная одному веберу на квадратный метр |
2. | Гаусс — немецкий математик, разработавший теорию чисел и применивший математику к электричеству и магнетизму, а также астрономию и геодезию (1777-1855) 409090 Карл Фридрихс Гаусс |
На основе WordNet 3.0, коллекции клипартов Farlex. © 2003-2012 Принстонский университет, Farlex Inc.
Переводы
Упоминается в ?
- degauss
- degausser
- degaussing
- flux density unit
- flux unit
- G
- gamma
- Gauss Carl Friedrich
- Gauss Karl Friedrich
- Gauss sign
- Gaussage
- Gaussian
- Gaussian distribution
- Логарифмы Гаусса
- Гиперболическая геометрия
- Карл Фридрих Гаусс
- Карл Гаусс
- килогаусс
- единица магнитного потока
Ссылки в архиве периодических изданий ?
Гаусс, величайший судебный детектив из всех.
Что мы читаем сегодня: главные подозреваемые
Ван добавил: «База данных Gauss DB с искусственным интеллектом поможет расширить возможности HUAWEI CLOUD и полностью раскрыть мощь диверсифицированных вычислений, включая вычисления x86, ARM, GPU и NPU.
Huawei запускает базу данных с поддержкой искусственного интеллекта
Gauss — технологическая компания из Силиконовой долины, впервые внедрившая модель беспроводной доставки медицинских технологий9.0005
Gauss обеспечивает финансирование в размере 20 млн долларов США в рамках серии C для платформы с поддержкой ИИ для операционных залов
Поскольку оптимальные размеры составляли от 0 до 150 микрон, а оптимальная напряженность магнитного поля составляла 2000 Гаусс, для этих размеров и поля была проведена дополнительная магнитная сепарация. интенсивность.
Характеристика магнетитовой железной руды Band-E Narges для переработки минерального сырья/Caracterizacion del yacimiento de hierro Band-E Narges (Иран) para el procesamiento Mineral
Гаусс, чье имя пишется как GauA на его родном немецком языке, родился в 1777 г. он умер в 1855 году.
он умер в 1855 году.
Кем был Иоганн Карл Фридрих Гаусс? Немецкий математик с необычным пожеланием на могиле отмечен дудлом Google на 241-й день рождения; Гаусса называют «принцем математиков» — он внес свой вклад в такие области, как алгебра, статистика, анализ, геометрия, механика и астрономия
«Кроме того, этим летом Калининград станет одним из городов, принимающих чемпионат мира по футболу 2018 года. а новое сообщение через Ригу предложит удобные варианты перелета для тех, кто планирует посетить чемпионат», — добавил Гаусс.
AirBaltic начинает полеты в новый российский город
Сари, «Оценка производительности искаженного сигнала, вызванного случайной точкой пути и моделью мобильности Гаусса Маркова по стандартам IEEE 1609.4», 4th Int.
Анализ влияния мобильности на производительность стандарта IEEE 802.11ah со схемой схемы трафика
Свойство момента согласования в теореме 1. 4 также можно интерпретировать как матричную формулировку обобщенной квадратуры Гаусса для аппроксимации квазиопределенных линейных функционалов; см. [45, 49].
4 также можно интерпретировать как матричную формулировку обобщенной квадратуры Гаусса для аппроксимации квазиопределенных линейных функционалов; см. [45, 49].
АЛГОРИТМ ЛАНЧОСА И КОМПЛЕКСНАЯ КВАДРАТУРА ГАУССА
То, что я хотел бы назвать «воображаемой печатностью» в цифровых издательских проектах Troll Thread и Gauss PDF (с косым взглядом на журнал Triple Canopy и Ugly Duckling Presse), позволяет этим издателям расширить определения «поэзии», «журнала», «книги» и «публикации» в их перекрывающихся современных сообществах мелкой прессы и авангарда.
Думая о непечатном в современных постцифровых публикациях
Немецкая компания Heidelberg Engineering, занимающаяся офтальмологическими ИТ-решениями, и американский производитель медицинского оборудования Gauss Medical создали совместное предприятие в Китае.
Снимок сделки: HEIDELBERG ENGINEERING, GAUSS MEDICAL ESTABLISH CHINA JV
В [16] сравниваются точности аппроксимации различных методов разреженных сеток, включая правило трапеций, правило Креншоу-Кертиса и правило Гаусса-Паттерсона.
Новое разреженное кубатурное правило Гаусса-Эрмита, основанное на соотношениях относительного веса для отслеживания цели по азимуту и дальности
Изначально выбранная ими функция ядра является функцией Гаусса.
Ядро мексиканского вейвлета ELM для мультиклассовой классификации
Браузер словарей ?
- ▲
- gaulter
- Gaultheria
- Gaultheria hispidula
- Gaultheria procumbens
- Gaultheria shallon
- Gaultier
- gaum
- gaumless
- gaumy
- gaun
- gaunt
- gauntlet
- gauntleted
- Gauntletted
- gauntly
- gauntness
- Gauntree
- gauntry
- gaup
- gauper
- gaur
- gaure
- Gauri
- Gause’s law
- Gause’s principle
- gauss
- Гаусс Карл Фридрих
- Гаусс Карл Фридрих
- Знак Гаусса
- Гаусса
- Гауссиан
- Кривая Гаусса
- Gaussian distribution
- Gaussian shape
- gaussmeter
- Gauss’s logarithms
- Gautama
- Gautama Buddha
- Gautama Siddhartha
- Gauteng
- Gautier
- Gautier Théophile
- gauze
- gauze bandage
- Gauze dresser
- gauzelike
- марлевый
- сетчатый
- сетчатый
- желудочный
- гаварный
- ▼
Полный браузер ?
Полевые индикаторы | 1 Гаусс
Доступные опции
Полевые индикаторы | 20 Гаусс | РБ Аннис Полевые индикаторы | 10 Гаусс | РБ Аннис Полевые индикаторы | 5 Гаусс | РБ Аннис Полевые индикаторы | 50 Гаусс | РБ Аннис Полевые индикаторы | 2 Гаусса | РБ Аннис Полевые индикаторы | 100 Гаусс | РБ Аннис Полевые индикаторы | 1 Гаусс | РБ Аннис Полевые индикаторы | 0,5 Гаусса | РБ Аннис Полевые индикаторы | 200 Гаусс | РБ Аннис Полевые индикаторы | 300 Гаусс | РБ Аннис Полевые индикаторы | 400 Гаусс | РБ Аннис
Серийный выпуск и сертификация
Сериализация и сертификация (+$66,00)
Покупаете оптом? Узнать больше Да, запросить ценовое предложение.
 Нет, количество закупок меньше 5 единиц.
Нет, количество закупок меньше 5 единиц.- Описание
R.B. Индикаторы поля Анниса Гаусса
Карманный считыватель Гаусса, используемый для определения наличия остаточного магнетизма в детали после ее намагничивания и осмотра. Это надежные и недорогие инструменты для обеспечения успешного размагничивания детали.
Индикаторы поля являются важной частью процессов магнитопорошкового контроля, поскольку остаточные магнитные поля могут:
- Влиять на обработку, вызывая прилипание стружки к компоненту
- Создание помех для жизненно важного электронного оборудования
- Создать в процессе сварки состояние, известное как «дуга дуги», которое может вызвать отталкивание присадочного металла от сварного шва
- Вызывает прилипание абразивных частиц к подшипникам или поверхностям обшивки
Стандартные варианты изделия — некалиброванные
| НОМЕР ПРОДУКТА | ОПИСАНИЕ | ДИАПАЗОН ГАУССА |
| Модель 25/0,5-0-0,5 | Некалиброванный индикатор магнитного поля | 0,5 — 0 — 0,5 |
Модель 25/1-0-1 | Некалиброванный индикатор магнитного поля | 1 — 0 — 1 |
Модель 25/2-0-2 | Некалиброванный индикатор магнитного поля | 2 — 0 — 2 |
Модель 25/5-0-5 | Некалиброванный индикатор магнитного поля | 5 — 0 — 5 |
Модель 25/10-0-10 | Некалиброванный индикатор магнитного поля | 10 — 0 — 10 |
Модель 25/20-0-20 | Некалиброванный индикатор магнитного поля | 20 — 0 — 20 |
Модель 25/50-0-50 | Некалиброванный индикатор магнитного поля | 50 — 0 — 50 |
Модель 25/100-0-100 | Некалиброванный индикатор магнитного поля | 100 — 0 — 100 |
Варианты изделия High Gauss — некалиброванные
| НОМЕР ПРОДУКТА | ОПИСАНИЕ | ДИАПАЗОН ГАУССА |
| Модель 25-H/200-0-200 | Некалиброванный индикатор магнитного поля | 200 — 0 — 200 |
Модель 25-H/300-0-300 | Некалиброванный индикатор магнитного поля | 300 — 0 — 300 |
Модель 25-H/400-0-400 | Некалиброванный индикатор магнитного поля | 400 — 0 — 400 |
Стандартные варианты изделия — калиброванные
| НОМЕР ПРОДУКТА | ОПИСАНИЕ | ДИАПАЗОН ГАУССА |
| Модель 25/0,5-0-0,5Cal | Индикатор калиброванного магнитного поля | 0,5 — 0 — 0,5 |
Модель 25/1-0-1Cal | Индикатор калиброванного магнитного поля | 1 — 0 — 1 |
Модель 25/2-0-2Cal | Индикатор калиброванного магнитного поля | 2 — 0 — 2 |
Модель 25/5-0-5Cal | Индикатор калиброванного магнитного поля | 5 — 0 — 5 |
Модель 25/10-0-10Cal | Индикатор калиброванного магнитного поля | 10 — 0 — 10 |
Модель 25/20-0-20Cal | Индикатор калиброванного магнитного поля | 20 — 0 — 20 |
Модель 25/50-0-50Cal | Индикатор калиброванного магнитного поля | 50 — 0 — 50 |
Модель 25/100-0-100Кал. | Индикатор калиброванного магнитного поля | 100 — 0 — 100 |
Варианты изделия с высоким гауссом — калиброванные
| НОМЕР ПРОДУКТА | ОПИСАНИЕ | ДИАПАЗОН ГАУССА |
Модель 25-H/200-0-200Cal | Индикатор калиброванного магнитного поля | 200 — 0 — 200 |
Модель 25-H/300-0-300Cal | Индикатор калиброванного магнитного поля | 300 — 0 — 300 |
Модель 25-H/400-0-400Cal | Индикатор калиброванного магнитного поля | 400 — 0 — 400 |
Сопутствующие товары
Теги поиска:
неразрушающий контроль неразрушающий контроль не разрушительный тестирование осмотр материалы р.


 ультратонкий круглый Gauss 939111112
ультратонкий круглый Gauss 939111112 3
3 14159..
14159..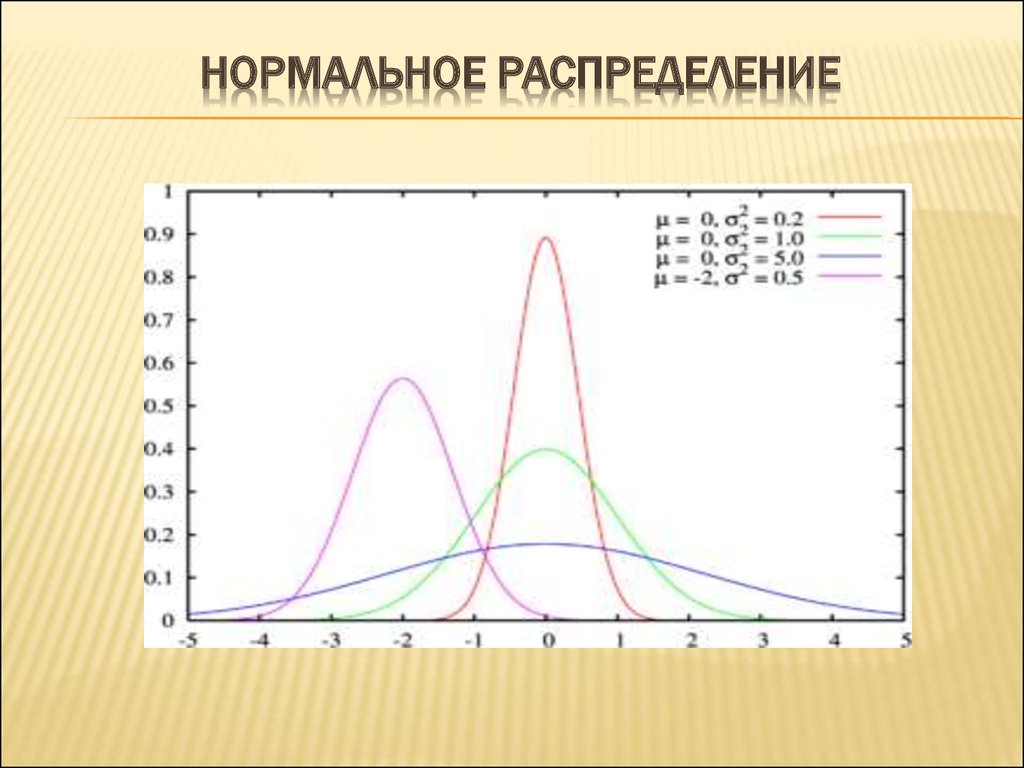


 Либо на вкладке Приложения , в Математика, статистика и оптимизация щелкните Curve Fitter .
Либо на вкладке Приложения , в Математика, статистика и оптимизация щелкните Curve Fitter .

 (a) Спусковой крючок движется к магниту и линии стальных шариков. (b) Спусковой крючок сталкивается с магнитом со скоростью 90 480 v 90 481 90 499 дюймов 90 500 . Энергия столкновения передается через магнит и шарики в линии. (c) Крайний правый шар выброшен с начальной скоростью v out . (d) Выброшенный мяч достигает скорости v 1 .
(a) Спусковой крючок движется к магниту и линии стальных шариков. (b) Спусковой крючок сталкивается с магнитом со скоростью 90 480 v 90 481 90 499 дюймов 90 500 . Энергия столкновения передается через магнит и шарики в линии. (c) Крайний правый шар выброшен с начальной скоростью v out . (d) Выброшенный мяч достигает скорости v 1 . n = 0 не учитывается, так как выброса не происходит. Для маленьких мячей, n = 5 является оптимальным. Для больших шаров это n = 1, наименьшее из возможных n .
n = 0 не учитывается, так как выброса не происходит. Для маленьких мячей, n = 5 является оптимальным. Для больших шаров это n = 1, наименьшее из возможных n . Диаметр шара 12 мм, количество магнитов 6 и α = 0,7. Линейная регрессия y = −0,12 n − 0,08 показана сплошной красной линией.
Диаметр шара 12 мм, количество магнитов 6 и α = 0,7. Линейная регрессия y = −0,12 n − 0,08 показана сплошной красной линией. clasohlson.com
[Google ученый]
clasohlson.com
[Google ученый] Мяч подвешен над магнитами, которые прикреплены к грузам. Взаимная сила, действующая на магниты, уменьшает вес, отображаемый на весах, что позволяет рассчитать магнитную силу как функцию разницы отображаемого веса. Способ, которым мяч был подвешен на этом изображении, мы использовали для очень малых расстояний ( d < 3 мм) между шаром и магнитами.
Мяч подвешен над магнитами, которые прикреплены к грузам. Взаимная сила, действующая на магниты, уменьшает вес, отображаемый на весах, что позволяет рассчитать магнитную силу как функцию разницы отображаемого веса. Способ, которым мяч был подвешен на этом изображении, мы использовали для очень малых расстояний ( d < 3 мм) между шаром и магнитами.

