Объясняем 4 главных закона логики на простых примерах
21 декабря 2019 Жизнь Колонка
Это знание необходимо, чтобы не допускать ошибок в рассуждениях и замечать, когда их совершают другие.
Катя Анисимова
Студент-химик, выпускница мастерской прикладной рациональности «Летней школы» и автор «Общества скептиков».
Мы часто слышим фразы вроде «это нелогично» и «где тут логика». Интуитивно понятно, что логика — это что-то про наши рассуждения, выводы, структуру мыслей. В целом так и есть. Логика — это наука, которая появилась в V веке до нашей эры и изучает законы и форму мышления.
Под формой мышления понимают структуру мысли, а не её содержание. Например, с точки зрения логики выражение «Все шмумрики хжуют тофц с штецеллой на фафлак. Финкус — шмумрик. Финкус хжует тофц с штецеллой на фафлак» абсолютно верно, а «Все планеты Солнечной системы вращаются вокруг Солнца. Земля вращается вокруг Солнца. Следовательно, Земля — планета Солнечной системы» — нет.
Вся логика «живёт» на четырёх законах. Разберёмся, какие это законы и как они работают.
1. Закон тождества
Каждая мысль должна быть равна самой себе, не должна иметь больше одного значения.
В чём суть
Еще до нашей эры Аристотель говорил: «…Иметь не одно значение — значит не иметь ни одного значения; если же у слов нет (определённых) значений, тогда утрачена всякая возможность рассуждать друг с другом, а в действительности и с самим собой, ибо невозможно ничего мыслить, если не мыслить каждый раз что-нибудь одно».
Примеры нарушения
Самый популярный пример нарушения закона тождества — фраза «студенты прослушали лекцию». Слово «прослушали» можно понять в двух значениях: то ли студенты внимательно слушали преподавателя, то ли всё пропустили.
Примером нарушения закона тождества будет и эта шутка:
— Я сломал руку в двух местах.
— Больше не ходи в эти места.
В результате немного более сложных нарушений закона тождества получаются софизмы.
Софизм — это внешне правильное доказательство ложной мысли с помощью преднамеренного нарушения логических законов.
Что лучше: вечное блаженство или бутерброд? Конечно же, вечное блаженство. А что может быть лучше вечного блаженства? Конечно же, ничто! Но бутерброд ведь лучше, чем ничто, поэтому бутерброд лучше вечного блаженства.
Подвох здесь в том, что слово «ничто» употребилось сначала в значении «ни один предмет или явление», а потом в значении «отсутствие чего-либо»
Как применять в жизни
Первый закон логики поможет распознать софизмы. Первое, на что стоит обращать внимание, — неоднозначные слова.
2. Закон противоречия
Высказывание и его отрицание не могут быть одновременно истинными.
В чём суть
Если одно суждение что-то утверждает, а другое то же самое отрицает об одном и том же объекте в одно и то же время и в одном и том же отношении, то они не могут одновременно быть истинными.
Например, два суждения — «котик чёрный» и «котик белый» — не могут одновременно быть истинными, если речь идёт об одном и том же котике, в одно и то же время и в одном и том же отношении.
То есть цвет котика сравнивается с одной и той же палитрой.
Примеры нарушения
«Этот рыжий кот оставил по всему ковру чёрные шерстинки». И из детства — «Закрой рот и ешь».
Как применять в жизни
Самое сложное — выявить противоречие. Фраза «в детстве у меня не было детства» не нарушает закон противоречия, а «сделал устный доклад в письменной форме» нарушает. Так что, главное — понять, имеет место противоречие или игра слов.
3. Закон исключённого третьего
Два противоречащих суждения об одном и том же предмете в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными
В чём суть
Суждения бывают противоположными и противоречащими.
Противоположные суждения всегда предполагают некий третий, промежуточный вариант. Например, для суждений «дом большой» и «дом маленький» промежуточным будет «дом среднего размера». Для противоречащих суждений нет никакого третьего варианта.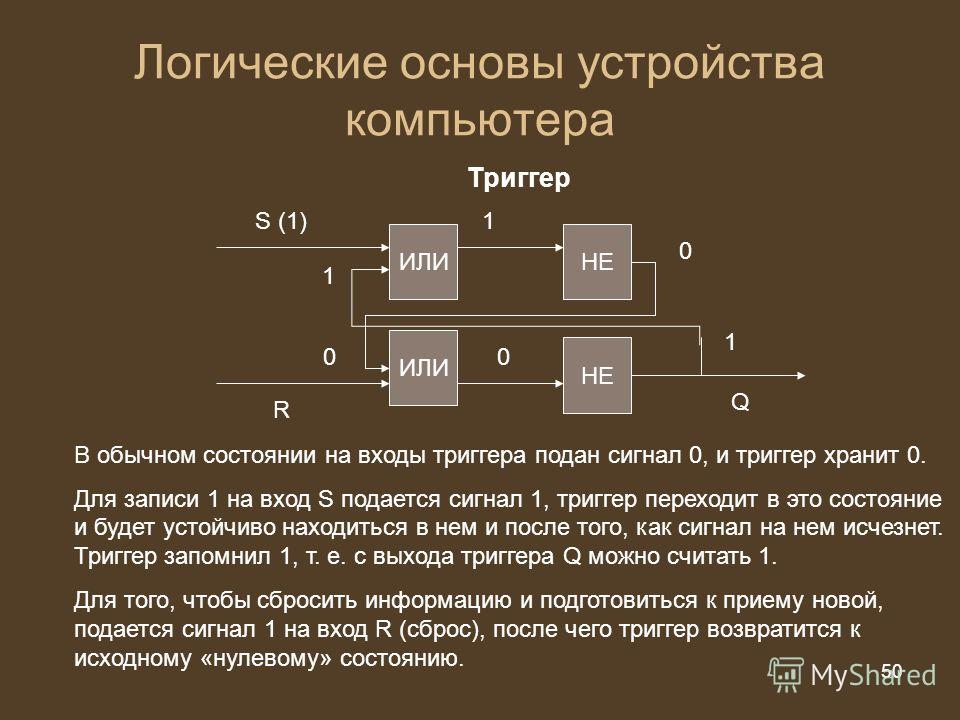
Например, для суждений «дом большой» и «дом небольшой» третьего верного варианта не предполагается.
Итак, два противоречащих суждения об одном и том же предмете, в одно и то же время и в одном и том же отношении не могут быть одновременно истинными и не могут быть одновременно ложными.
Пример нарушения
Суждения «кот старый» и «кот нестарый» об одном и том же котике в одно и то же время не могут быть одновременно верными.
Как применять в жизни
Примеры простые до безобразия, но в жизни закон противоречия нарушается скорее так: между противоречащими суждениями есть ещё часть монолога, да и сами суждения могут быть высказаны не очень явно. Как с этим быть? Внимательно вслушиваться в то, что говорит собеседник, и следить за мыслью. Если все остальные законы не нарушаются, присмотритесь ещё раз к формулировкам. Возможно, тут замаскированные противоречащие суждения.
4. Закон достаточного основания
Любая мысль (тезис) для того, чтобы иметь силу, обязательно должна быть доказана какими-либо аргументами, причём эти аргументы должны быть достаточными для основания исходной мысли, то есть она должна вытекать из них.
В чём суть
Помните, что такое презумпция невиновности? Она основана на законе достаточного основания. Принцип презумпции невиновности предписывает считать человека невиновным, даже если он даёт показания против себя, до тех пор, пока его вина не будет достоверно доказана какими-либо фактами. Другими словами, признание вины не гарантирует, что человек действительно совершил преступление, а вот улики и доказательства — вполне могут. То есть признание вины — недостаточное основание, а факты и улики, указывающие на преступника, — достаточное.
Пример нарушения
«Не ставьте мне двойку. Я прочитал весь учебник и, возможно, что-то отвечу». Вывод не вытекает из основания: студент мог прочитать весь учебник, но из этого не следует, что он сможет что-то ответить.
Как применять в жизни
Закон достаточного основания предостерегает от поспешных выводов. Если мы помним о том, что любое утверждение должно быть подкреплено фактами, это поможет распознавать дешёвые сенсации и небылицы.
Читайте также 🧐
- 10 задач на логику и сообразительность
- 26 ошибок мышления, из-за которых мы ничего не понимаем
- Как философия помогает в повседневной жизни
Логика скрипта
Логика скрипта – это функция, позволяющая создавать файлы, которые называются скриптами логики и содержат инструкции по выполнению расчетов с данными планирования и консолидации.
Функции
Расчеты логики можно выполнять только на элементах базового уровня. Кроме того, логика специфична для каждой модели.
Приложение Business Planning and Consolidation содержит библиотеку формул MDX, а образец среды EnvironmentShell – ряд логических функций.
Примечание
В ключевых словах логики не учитывается регистр. Однако во всех именах сред, моделей, измерений и элементов в K2 регистр учитывается.
Для каждого создаваемого участка логики скрипта предоставляются следующие два файла:
Файл .LGF, являющийся файлом ASCII, который создается и редактируется при настройке логических расчетов. Доступ к файлу .LGF осуществляется через редактор логики.
Файл .LGX, являющийся скомпилированным файлом логики, который создается системой при проверке и сохранении логики. Это исполняемая версия файла .LGF, которая не хранится в Business Planning and Consolidation.
Логикой по умолчанию является специальный логический оператор, который выполняется при каждой обратной записи в модель. Вся логика в файле 
LGF выполняется после отправки данных. Сначала данные фиксируются в модели, а затем файл Default.LGF выполняется для данных модели. Если вся логика находится в файле Default.LGF, файл логики может стать неуправляемым. Поэтому можно создать другие файлы логики, например FXTrans.LGF для пересчета иностранных валют и ICElim.LGF для межфирменных исключений. Логика по умолчанию может содержать оператор INCLUDE для выполнения определенной логики в реальном времени, например пересчета валюты, если это необходимо, вместо выполнения отдельного пакетного процесса.
Для получения доступа к файлам логики служит подкаталог логики скрипта в иерархии модели.
Библиотека логики
В Business Planning and Consolidation имеется библиотека стандартных логических функций, которые доступны для использования. Этот файл имеет расширение .LGF, и его можно вызвать при проверке с помощью функции INCLUDE в файле логики. Модуль логики производит поиск в файле библиотеки соответствующих формул, которые будут использоваться, на основании информации в файле .
LGF.
Ниже приведены примеры логики, поставляемой с Business Planning and Consolidation.
Allocation.lgf: выполнение распределения
Calcaccount.lgf: для подготовки денежного потока; выполнение бизнес-правила расчета счета
Consolidation.lgf: для выполнения бизнес-правила консолидации согласно законодательству
Copy_Opening.lgf: для выполнения бизнес-правила переноса сальдо
FX_Trans.lgf: для выполнения пересчета валют
ICBooking.lgf: для выполнения межфирменного согласования и проводки разницы
ICData.lgf: для выполнения межфирменного согласования
ICElim.lgf: для выполнения межфирменного согласования
MDXlib.lgf: библиотека финансовых функций MDX
System_Constants.lgf: хранение констант для использования в логике скрипта. Дополнительные сведения см. в следующем разделе Файл системных констант.
System_Library.lgf: основные примеры набора ключевых слов
Validation.lgf: для выполнения правила проверки
Файл системных констант
Файл системных констант – это файл логики, который сопоставляет имена измерений для модели со стандартной логикой Business Planning and Consolidation. Если обновлять файл констант измерениями, то можно не изменять и не перезаписывать никакие стандартные функции, включенные в Business Planning and Consolidation.
Файл системных констант находится в папке \\root\Webfolders\ <Environment>\systemlibrary\logiclibrary. Этот файл можно редактировать, используя функции выгрузки и загрузки из транзакции UJFS в интерфейсе ABAP.
Выполнение логики скрипта
Логику скрипта можно вызывать автоматически при каждой отправке данных системой в базу данных. Инструкции, содержащиеся в файле логики по умолчанию, выполняются сразу после отправки данных, и результаты можно просмотреть немедленно.
Операции
На экране администрирования Planning and Consolidation можно просмотреть все скрипты логики для модели, выбрав Скрипты логики в разделе Правила. Выберите модель и нажмите Открыть. Отображаются все скрипты логики, настроенные для этой модели.
Можно создать новый скрипт логики для выбранной модели, нажав Создать и присвоив скрипту логики имя. Имя можно ввести прямо в редакторе логики. Также можно вставить ключевые слова Business Planning and Consolidation, ключевые слова MDX, имена измерений и имена элементов из раскрывающихся списков, при необходимости заменив переменные в ключевых словах. Для добавления ключевого слова из раскрывающихся списков в строку скрипта можно дважды щелкнуть ключевое слово, выбрать ключевое слово и нажать Вставить ключевое слово или перетащить ключевое слово из раскрывающегося списка в строку в редакторе логики.
В редакторе логики можно вставлять и отменять комментарии для блоков логики скрипта и для отдельных строк.
При создании нового скрипта логики или изменении существующего скрипта можно проверить его синтаксис. Найденные в логике ошибки отображаются в нижней части редактора логики с номерами строк, что облегчает их поиск и устранение.
Можно скопировать существующий скрипт логики, выбрав файл, введя имя для нового скрипта и изменив его по необходимости.
Можно использовать в редакторе логики следующее цветовое кодирование для облегчения написания скриптов логики и устранения в них ошибок:
Ключевые слова выводятся синим
Значения констант выводятся зеленым
Комментарии выводятся серым
Ошибки в синтаксисе, такие как неправильные скобки, неверно написанные ключевые слова и имена измерений, а также нераспознанные слова, выводятся красным
Ошибки в логике скрипта легко можно исправить с помощью строк с ошибками в нижней части окна редактора логики.
Ошибки выводятся с номерами строк.
Дополнительная информация
r — логический (0) в операторе if
спросил
Изменено 2 года, 9 месяцев назад
Просмотрено 46 тысяч раз
Эта строка:
which(!is.na(c(NA,NA,NA))) == 0
производит логический(0)
В то время как эта строка
если(что(!is.na(c(NA,NA,NA))) == 0){print('ИСТИНА')}
генерирует:
Ошибка в if (what(!is.na(c(NA, NA, NA))) == 0) { :
аргумент имеет нулевую длину
Почему возникает ошибка? Что логично(0)
- r
- if-statement
- нет данных
3
logical(0) — вектор базового логического типа с нулевой длиной.
> !is.na(c(NA, NA, NA)) [1] ЛОЖЬ ЛОЖЬ ЛОЖЬ > which(!is.na(c(NA, NA, NA))) == 0 логический(0)
В следующей строке вы спрашиваете, равен ли этот вектор нулевой длины logical(0) 0, а это не так. Вы получаете ошибку, потому что не можете сравнить вектор нулевой длины со скаляром.
Вместо этого вы можете проверить, равна ли длина этого первого вектора 0:
if(length(what(!is.na(c(NA,NA,NA)))) == 0){print('TRUE' )}
4
Вызов который для проверки того, является ли вектор логики ложным, является плохой идеей. , который дает вам вектор индексов для ИСТИННЫХ значений. Если их нет, этот вектор имеет длину 0. Лучше использовать любой .
> любой(!is.na(c(NA,NA,NA))) ЛОЖНЫЙ
Во-первых, logical(0) указывает, что у вас есть вектор, который должен содержать логические значения, но вектор имеет нулевую длину.
В первом подходе вы делаете
!is.na(c(NA, NA, NA)) # ЛОЖЬ, ЛОЖЬ, ЛОЖЬ
Использование which() для этого вектора создаст пустой целочисленный вектор ( integer(0) ). Таким образом, проверка того, равен ли пустой набор нулю, приведет к пустому логическому вектору.
Во втором подходе вы пытаетесь увидеть, является ли вектор which(!is.na(c(NA,NA,NA))) == 0 TRUE или FALSE . Однако это не так, потому что он пуст. Оператору if требуется либо ИСТИНА или ЛОЖЬ . Вот почему он выдает ошибку , аргумент имеет нулевую длину
Просто используйте length() вот так:
foo <- logical(0)
if(length(foo) == 0) { } # ИСТИНА
if(length(foo) != 0) { } # ЛОЖЬ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Статья о логике+0 от The Free Dictionary
Логика+0 | Статья о логике+0 от The Free DictionaryЛогика+0 | Статья о логике+0 от The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
