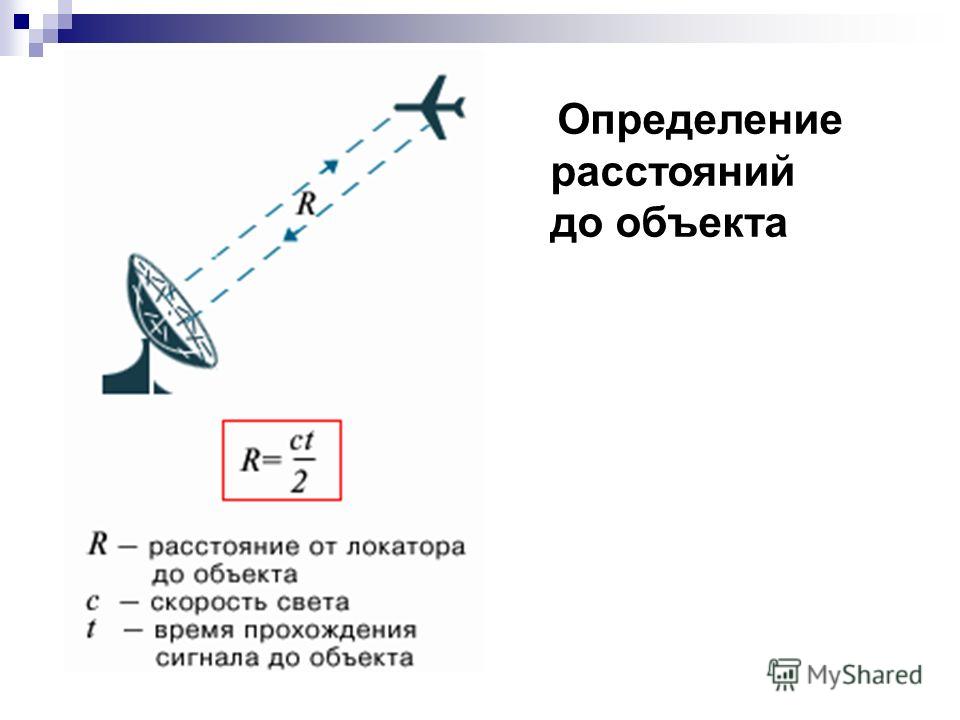
Уравнение радиосвязи, Дальность действия радиолокатора Радиотехнические системы
Сразу хочу сказать, что здесь никакой воды про уравнение радиосвязи, и только нужная информация. Для того чтобы лучше понимать что такое уравнение радиосвязи, дальность действия радиолокатора , настоятельно рекомендую прочитать все из категории Радиотехнические системы.
Основное уравнение радиолокации — формула, описывающая дальность действия радиолокатора , через расчет мощности радиосигналов и различных потерь. Для большинства активных радиолокаторов, являющихся моностатическими (передающая и приемная антенны находятся вблизи или совмещены), мощность принимаемого сигнала обратно пропорциональна 4-й степени расстояния до цели, для пассивных локаторов мощность сигнала обратно пропорциональна 2-й степени расстояния.
Какова дальность радиосвязи и от чего она зависит? Для ответа на этот вопрос необходимо вспомнить о том какую роль выполняет антенна передатчика и приемника.
Количество энергии, перехваченной антенной радиоприемного устройства, зависит от площади приемной антенны Sa. Та же, в свою очередь тоже связана с коэффициентом усиления и длиной волны 
Уравнение максимальной дальности действия РЛС в свободном пространстве
Максимальная дальность действия РЛС – это предельное расстояние до цели, при котором обеспечивается обнаружение отраженного сигнала от цели на фоне шумов с заданной вероятностью.
Дальность действия РЛС в свободном пространстве (не учитывая влияния земли и атмосферы) в первую очередь зависит от основных ее параметров, отражающих свойств и размеров облучаемого объекта, т.е. цели.
Параметры РЛС
|
— мощность передатчика в импульсе |
— |
Pu |
|
— чувствительность приемника |
— |
Pпр. |
|
— коэффициент усиления антенны |
— |
G |
|
— эффективная площадь антенны |
— |
Sа |
Параметры цели
|
— эффективная отражающая поверхность цели |
σ |
Рис.
КНД = 360о 360о / [Qaα o Qaβo]; Ga= КНД *η ; Sa = Ga λ2 / (4π) (1)
Ga≈ (10-25) 103 / (
Примеры:
| Тип антенны | коэффициент усиления |
| Зеркальная 1,5х3,5 град 2см | 3500 |
| Полуволновый вибратор | 1,5 |
| Четвертьволновый вибратор | 1 |
Важным показателем дальности радиосвязи является плотность потока мощности γ.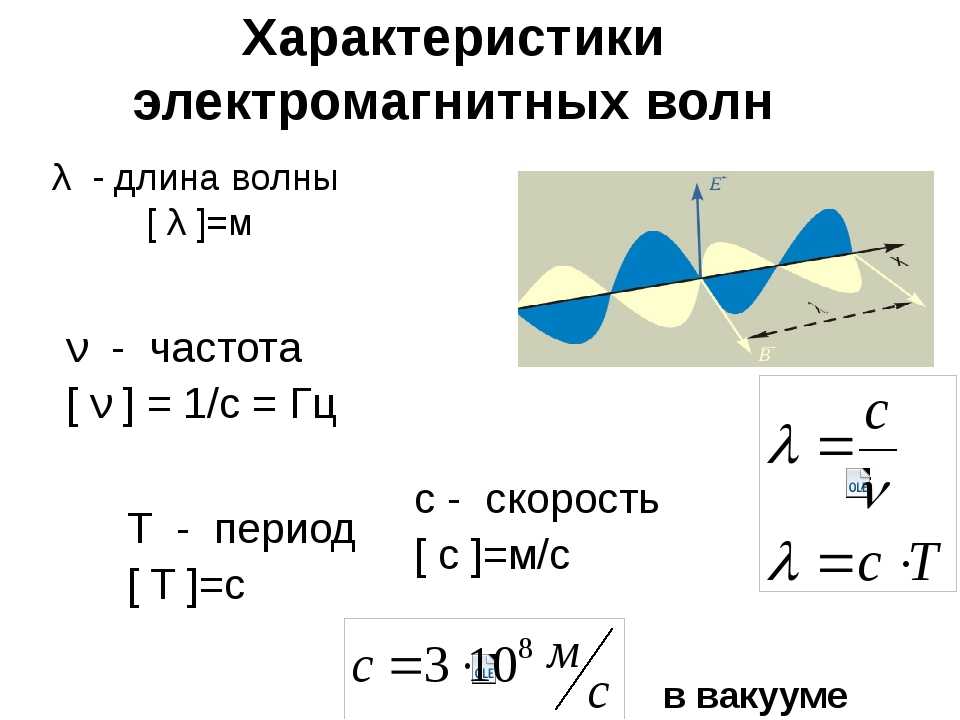 Он показывает, сколько мощности радиоволны в ваттах приходится на один квадратный метр поверхности сферы излучении.
Он показывает, сколько мощности радиоволны в ваттах приходится на один квадратный метр поверхности сферы излучении.
Рис. 2. О выводе уравнения радиосвязи
Точечный излучатель излучает сферические радиоволны. На расстоянии R от него мощность сигнала передатчика в антенне
Антенна приемника перехватит часть потока и в ней образуется мощность принимаемого сигнала рпр = γпSaпр . Об этом говорит сайт https://intellect.icu . Отсюда можно рассчитать мощность принимаемого сигнала с учетом зависимости площади антенны от коэффициента усиления из равенств (1):
рпр = Sa
Отношение (2) является первой формой уравнения радиосвязи. По нему можно рассчитать мощность сигнала на входе приемника принимающей станции. Но нельзя забывать, что в приемнике образуются электрические шумы. Их мощность может быть приведена ко входу, как было ранее показано в лекции LekzRT1.3 . Мощность приведенных шумов
По нему можно рассчитать мощность сигнала на входе приемника принимающей станции. Но нельзя забывать, что в приемнике образуются электрические шумы. Их мощность может быть приведена ко входу, как было ранее показано в лекции LekzRT1.3 . Мощность приведенных шумов
рш = nш2 ∆Fпр ; рш = NkT ∆Fпр (3)
В равенствах (3)  N – коэффициент шума приемника, kT — постоянная Больцмана и условная шумовая температура приемника в град. Кельвина.
N – коэффициент шума приемника, kT — постоянная Больцмана и условная шумовая температура приемника в град. Кельвина.
Спектральную плотность мощности nш2 можно найти в справочниках по приемным устройствам, так же как и шумовую температуру. Коэффициенты шума приемных устройств так же являются одними из важных характеристик и указаны в паспортах на изделия.
Вернемся к вероятностям обнаружения и ложной Роб тревоги Рлт . Ни завися от отношения сигнал / шум и уровня порога Uп автоматического обнаружителя. Инженеры оптимизировали уровень порога для различных требований по Роби Рлт и получили так называемые рабочие характеристики приемника. Их вид дан на рис. 3.
рис. 3. Рабочие характеристики приемника
Потенциальные возможности качественного приема информации зависят от коэффициента различимости kр (Роб,Рлт) сигнала на фоне шумов, то есть от того отношения сигнал/шум, которое обеспечено каналом радиопередачи. На рис. 3 дан пример того, как оценивается требуемое отношение сигнал/шум в зависимости от заданных величин Роб,Рлт. Таким образом, мощность передатчика Рп при известных характеристиках антенн и длине волны должна быть такой, чтобы был обеспечен найденный по кривым рис. 3 kр. То есть выполнялось условие рпр >= kр pш.С учетом последнего можно получить вторую форму уравнения радиосвязи, по которому можно рассчитать дальность действия радиосвязи.
На рис. 3 дан пример того, как оценивается требуемое отношение сигнал/шум в зависимости от заданных величин Роб,Рлт. Таким образом, мощность передатчика Рп при известных характеристиках антенн и длине волны должна быть такой, чтобы был обеспечен найденный по кривым рис. 3 kр. То есть выполнялось условие рпр >= kр pш.С учетом последнего можно получить вторую форму уравнения радиосвязи, по которому можно рассчитать дальность действия радиосвязи.
Чувствительность приемника характеризует способность его принимать слабые сигналы (чем меньше мощность принимаемых сигналов, тем лучше чувствительность). Коэффициент усиления и эффективная площадь антенны характеризует ее фокусирующие свойства.
Определение максимальной дальности РЛС
Предположим, передатчик РЛС находится в точке «О» (рис. 2.1 ), а цель находится на расстоянии Д в точке «О».
рис. 2.1
Тогда плотность потока мощности Пц на расстоянии Д (в точке О1) при ненаправленной передающей антенне РЛС можно найти, разделив излучаемую мощность Ри на поверхность сферы с радиусом Д, равную 4πД2
.
При направленном излучении плотность потока мощности у цели Пц возрастает в G раз. Следовательно, Пц в направлении максимального излучения будет равна:
.
Если в направлении максимального излучения антенны находится цель с эффективной отражающей поверхностью (м2), то отраженная от цели мощность Ротр получается равной:
.
Под эффективной отражающей поверхностью цели понимают такую поверхность, которая при равномерном рассеивании энергии по всем направлениям дает такую же интенсивность отраженного сигнала в месте приема, как и реальная цель.
Плотность потока отраженной мощности Потр на расстоянии Д от станции можно получить, разделив величину отраженной мощности Ротр на поверхность сферы радиусом Д
.
Таким образом установили, что на единицу площади приемной антенны РЛС приходится плотность потока отраженной мощности, равная Потр.
Учитывая, что эффективная площадь антенны равна Sa, м2, то полная величина мощности отраженного сигнала, принятая антенной РЛС Рпр, будет равна
.
Из последней формулы определим дальность действия РЛС
.
Максимальная дальность действия РЛС определяется минимально необходимой мощностью отраженного сигнала Рпр на входе приемника, при которой возможно различить на экране индикатора отраженный импульс. А это есть не сто иное, как чувствительность приемника РЛС Рпр.мин. Подставив это значение в уравнение дальности действия РЛС, получим
(1)
Данное выражение называют основным уравнением радиолокации для свободного пространства. Оно показывает зависимость дальности действия РЛС от параметров станции и характера цели.
Рассмотрим влияние технических параметров РЛС и эффективной отражающей поверхности цели на дальность действия радиолокатора.
А. Влияние параметров передатчика (Ри)
Из уравнения (1) следует, что
,
т.е. дальность действия радиолокатора тем больше, чем больше мощность излучения Ри. Однако корень четвертой степени показывает, что существенное увеличение дальности может быть получено только за счет очень большого увеличения мощности передатчика. Так, для увеличения Дmax в два раза мощность излучения необходимо увеличить в 16 раз (24 = 16).
Б. Влияние параметров антенны (G и Sa)
В РЛС для излучения и приема энергии используется одна антенна, для которой коэффициент усиления G и эффективная площадь Sa взаимосвязаны следующим отношением
или .
Подставив в уравнение (1) значение Sa , получим
или Д max ~ .
Отсюда следует, что увеличение G является более эффективным способом увеличения Д max.
При неизменной длине волны λ увеличение G достигается увеличением эффективной площади антенны Sa, которая пропорциональна геометрическим размерам антенны Sr:
где – коэффициент использования геометрической площади антенны.
Для многовибраторных антенн k = (0,3…0,4), для параболических антенн k = (0,5…0,7).
Увеличение Sr ограничено конструктивными соображениями.
В. Влияние параметров приемника (Рпр.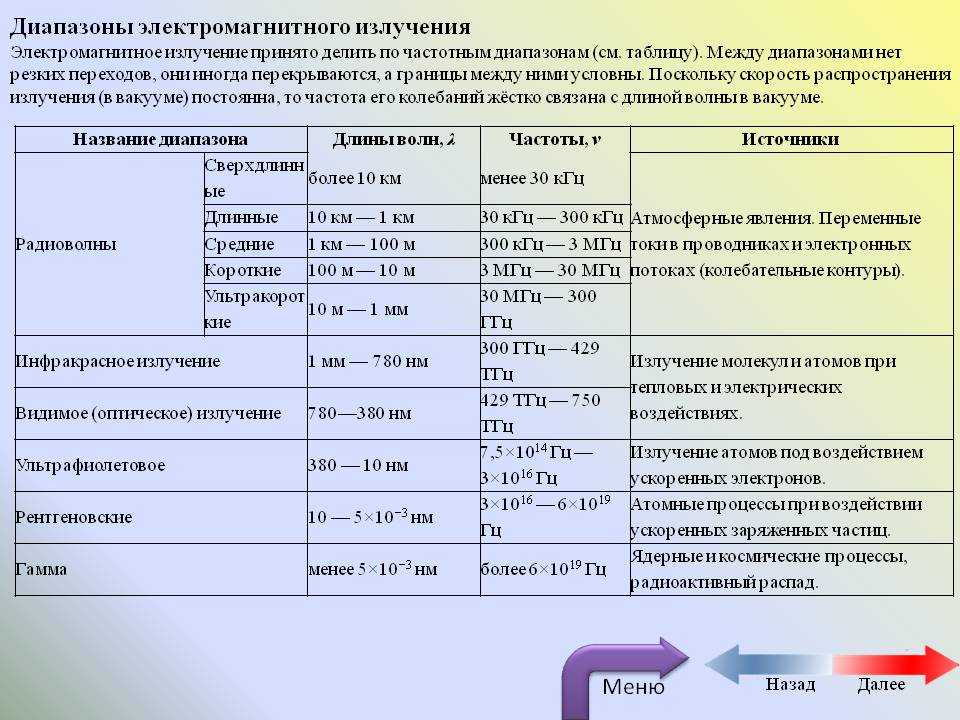 min)
min)
Чувствительность приемника Рпр.min определяет минимальную мощность отраженного сигнала на входе приемника, при которой на выходе приемника сигнал различим на фоне шумов. Она связана с дальностью действия соотношением
из которого следует, что Дmax тем больше, чем выше чувствительность приемника (то есть меньше абсолютная величина Рпр.min..
Г. Влияние эффективной отражающей поверхности цели (σ)
Эффективная отражающая поверхность цели σ учитывает:
величину поверхности цели, ориентированной относительно диаграммы направленности антенны РЛС;
длину волны РЛС λ;
коэффициент отражения материала, из которого выполнена цель;
форму цели.
Поскольку σ сложного объекта (ракеты, самолета и т.п.) рассчитать достаточно трудно, то практически ее определяют экспериментальным путем. При расчетах можно использовать следующие данные в м2.
При расчетах можно использовать следующие данные в м2.
|
Объекты |
РЛС «см» |
РЛС «м» |
|
Тяжелый стратегический бомбардировщик |
30 |
70 |
|
Истребитель-бомбардировщик |
5…8 |
15…20 |
|
Ракета класса «воздух-земля»: |
||
|
СРЭМ |
0,01…0,1 |
0,5…2,5 |
|
СКЭД |
0,1. |
1,0…5,0 |
|
Беспилотный самолет-разведчик |
0,1…0,2 |
|
|
Автоматический аэростат |
0,5…0,7 |
|
Соотношение дальности действия РЛС и параметров цели показывает
, что с увеличением σ дальность обнаружения увеличивается, так как увеличивается мощность отраженного сигнала.
Примечание. Указать студентам, что вероятный противник при разработке новых самолетов стремится уменьшить эффективную отражающую поверхность.
В настоящее время РЛС ПВО обнаруживают цели с минимальной отражающей поверхностью.
Принимаемая мощность
Мощность принимаемого отклика радиосигнала задается уравнением :
Обозначения:
- Pr — мощность сигнала приемной антенны;
- Pt — мощность радиопередатчика;
- Gt — коэффициент усиления передающей антенны;
- Ar (иногда S) — эффективная площадь (апертура) приемной антенны, Ar = Gr*λ²/4π, где Gr — коэффициент усиления приемной антенны, λ — длина волны.

- σ — эффективная площадь рассеяния цели в данном ракурсе;
- F — коэффициент потерь при распространении сигнала;
- Rt — расстояние от передающей антенны до цели;
- Rr — расстояние от цели до приемной антенны.
В случае, когда передающая и приемная антенны располагаются на одинаковом расстоянии от цели, то есть во всех моностатических РЛС (Однопозиционных радиолокационных системах, ОПРЛС) и иногда, в других типах, формула упрощается за счет Rt = Rr = R, что приводит к коэффициенту R4:
Таким образом, принимаемая мощность уменьшается пропорционально 4-й степени расстояния.
Коэффициент F можно принять равным 1, если считать, что волна распространяется в вакууме без потерь и без интерференции.
Минимальная чувствительность приемника
Минимальная мощность, при получении которой приемник может обнаружить отраженный от цели сигнал, задается формулой
- k — постоянная Больцмана;
- T — абсолютная температура приемника;
- Δfr — полоса пропускания приемника;
- kn — коэффициент шума приемника;
- kd — коэффициент различимости (отношение энергий сигнал/шум на входе приемника, при котором обеспечивается прием сигналов с заданными параметрами).

Дальность действия радиолокатора с пассивным ответом
,
где:
— мощность передатчика;
— коэффициент направленного действия антенны;
— эффективная площадь антенны
— эффективная площадь рассеяния цели
— минимальная чувствительность приемника.
Дальность действия радиолокатора с активным ответом
Активный ответ приходит от радиолокационного ответчика (ретранслятора), установленного на цели.
Максимальная дальность действия по каналу запроса
Максимальная дальность действия по каналу ответа
При работе с активным ответом, расстояние входит в формулы со степенью 2, а не 4, так как мощность ответчика является фиксированной и не зависит от мощности падающего на «цель» излучения радара. В случае же пассивного ответа, цель, согласно принципу Гюйгенса-Френеля, представляет собой вторичный переизлучатель, мощность которого прямо пропорциональна падающему на него излучению радара. Таким образом, при пассивной радиолокации сигнал от передатчика радара по пути к цели ослабевает в раз, отражается, а затем по пути от цели до приемника радара ослабевает еще в . В результате получаем коэффициент , и в случае, когда Rt = Rr = R, этот коэффициент равен .
В результате получаем коэффициент , и в случае, когда Rt = Rr = R, этот коэффициент равен .
Расчет дальности действия РЛС на фоне мешающих отражений от объемно распределенных отражателей
Дальность действия на фоне мешающих отражений при редкоимпульсном излучении существенно снижается. Причем, наиболее заметно такое снижение на фоне мешающих отражений от поверхностно распределенных помех.
Переход к квазинепрерывному излучению предпочтителен, когда цель находится в зоне мешающих отражений на дальностях до радиогоризонта.
На больших дальностях или при наблюдении цели вне зоны мешающих отражений предпочтительнее использование импульсного сигнала.
ВЫВОДЫ
Дальность действия РЛС тем больше, чем больше мощность излучения Ри, коэффициент усиления G и эффективная площадь антенны Sa, эффективная отражающая поверхность цели σ и чем меньше абсолютная величина чувствительности приемника Рпр. min.
min.
Наибольший эффект для увеличения Дmaxдает увеличение геометрических размеров антенны G и Sa, где для увеличения Дmax в два раза достаточно увеличить площадь антенны в 4 раза. Но геометрические размеры ограничиваются конструктивными особенностями антенных устройств. Наименьший эффект для увеличения Дmaxдает увеличение Ри ,σ, Рпр.min , так как для увеличения Дmax в два раза их надо увеличивать в 16 раз.
См. также
- предельная дальность прямой радиовидимости , влияние кривизны земли , влияние рефракции на дальность работы рлс , рефракция и сверхрефракция ,
- Радиолокация
- Радиолокационная станция , РЛС
- Предельная дальность прямой радиовидимости, кривизна Земли
- Телеграфное уравнение
- Уравнение Максвелла
Статью про уравнение радиосвязи я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое уравнение радиосвязи, дальность действия радиолокатора
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Радиотехнические системы
Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое уравнение радиосвязи, дальность действия радиолокатора
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Радиотехнические системы
Основы радиолокации — Основные принципы радиолокации — Уравнение дальности радиолокации
Уравнение дальности радиолокации
Уравнение дальности радиолокации (часто для краткости — уравнение радиолокации)
в простой и наглядной форме связывает между собой максимальную дальность действия радиолокатора,
его параметры, а также параметры цели. В зависимости от требуемого результата уравнение радиолокации может быть записано относительно
максимальной дальности действия радиолокатора или относительно мощности электромагнитной волны на входе приемной антенны.
Во втором случае мощность Pe
у приемной антенны радиолокатора выражается зависимостью от излучаемой мощности PS,
дальности цели R и отражающих характеристик цели,
описываемых ее эффективной поверхностью рассеяния σ.
Если известна чувствительность радиолокационного приемника,
то с помощью уравнения радиолокации можно определить максимальную теоретически достижимую дальность действия радиолокатора.
Таким образом, уравнение радиолокации может использоваться для оценки тактико-технических характеристик радиолокатора.
В зависимости от требуемого результата уравнение радиолокации может быть записано относительно
максимальной дальности действия радиолокатора или относительно мощности электромагнитной волны на входе приемной антенны.
Во втором случае мощность Pe
у приемной антенны радиолокатора выражается зависимостью от излучаемой мощности PS,
дальности цели R и отражающих характеристик цели,
описываемых ее эффективной поверхностью рассеяния σ.
Если известна чувствительность радиолокационного приемника,
то с помощью уравнения радиолокации можно определить максимальную теоретически достижимую дальность действия радиолокатора.
Таким образом, уравнение радиолокации может использоваться для оценки тактико-технических характеристик радиолокатора.
Вывод уравнения радиолокации
Прежде всего предположим, что распространение радиоволн происходит в идеальных условиях, то есть без потерь.
Рисунок 1. Плотность мощности, излучаемая ненаправленным излучателем,
уменьшается при геометрическом расширении луча (при удалении от излучателя)
Плотность мощности, излучаемая ненаправленным излучателем,
уменьшается при геометрическом расширении луча (при удалении от излучателя)
Рисунок 1. Плотность мощности, излучаемая ненаправленным излучателем, уменьшается при геометрическом расширении луча (при удалении от излучателя)
Если высокочастотная энергия излучается изотропным излучателем, то она распространяется равномерно во всех направлениях. Следовательно, поверхности с одинаковой плотностью мощности представляют собой сферы, площадь которых в зависимости от расстояния от излучателя определяется как (A= 4 π R²). Одно и то же количество энергии с увеличением радиуса сферы распределяется на все большую площадь ее поверхности. Это означает, что плотность мощности электромагнитной волны на поверхности сферы обратно пропорциональна квадрату радиуса сферы. Таким образом, можно записать уравнение для вычисления плотности мощности Su, излучаемой ненаправленным излучателем
(1)
- PS = излучаемая мощность [Вт]
- R1 = расстояние от передающей антенны до цели [м]
коэффициент
усиления антенны
Рисунок 2: Усиление антенны, умноженное на плотность мощности, дает направленную плотность мощности.
коэффициент
усиления антенны
Рисунок 2: Усиление антенны, умноженное на плотность мощности, дает направленную плотность мощности.
Если же передающая антенна является направленной, то это приводит к увеличению плотности мощности, излучаемой в определенном направлении. Этот эффект называют усилением антенны. Таким образом, выражение для плотности мощности направленного излучателя Sg можно записать в виде
(2)
- G = коэффициент усиления антенны.
Конечно, в действительности антенны радиолокаторов не являются «частично излучающими» изотропными излучателями. К антеннам радиолокаторов предъявляют требования малой ширины луча и коэффициента усиления на уровне 30 или 40 дБ (например, зеркальная параболическая антенна или фазированная антенная решетка).
Обнаружение цели зависит не только от плотности мощности в районе цели, а также от того,
какая часть этой мощности отражается в направлении на радиолокатор. Для того, чтобы определить полезную отраженную мощность, необходимо знать
эффективную поверхность рассеяния σ
цели.
Ее значение зависит от многих факторов, однако можно утверждать, что цель с большей площадью отражает больше мощности, чем цель с меньшей площадью.
Это означает, что, при одинаковых условиях наблюдения пассажирский авиалайнер обладает большей площадью рассеяния, чем спортивный самолет.
Для того, чтобы определить полезную отраженную мощность, необходимо знать
эффективную поверхность рассеяния σ
цели.
Ее значение зависит от многих факторов, однако можно утверждать, что цель с большей площадью отражает больше мощности, чем цель с меньшей площадью.
Это означает, что, при одинаковых условиях наблюдения пассажирский авиалайнер обладает большей площадью рассеяния, чем спортивный самолет.
Из приведенного выше следует, что отраженная от цели мощность Pr зависит от плотности мощности Su, коэффициента усиления антенны G и изменяющейся эффективной поверхности рассеяния σ:
(3)
У упрощенном виде цель может рассматриваться как излучатель. При таком подходе отраженная мощность Pr рассматривается как излученная мощность.
Применив к отраженной мощности те же рассуждения, что и к излученной, по аналогии с формулой (1), можем записать выражение для плотности мощности Se у приемной антенны:
Рисунок 3. Связь между выражениями (3) и (4)
Связь между выражениями (3) и (4)
(4)
- R2 = расстояние между целью и приемной антенной.
Рисунок 3. Связь между выражениями (3) и (4)
Принятая в приемной антенне мощность Pe зависит от плотности мощности в точке приема Se и эффективной площади антенны AW.
Pe = Se · AW
(5)
Очевидно, что значение эффективной площади антенны характеризует ту часть мощности,
которую антенна может «собрать» из всего потока мощности, отраженной от цели.
Чем больше площадь антенны, тем больше мощности она может на себя «собрать».
Кроме того, этот параметр обусловлен наличием потерь в антенне.
По этой причине принятая антенной мощность не равна падающей на нее мощности.
Эффективность антенны количественно описывают при помощи коэффициента эффективности Ka,
значение которого для реальных антенн, как правило, составляет около 0,6 … 0,7.
Коэффициент эффективности антенны связывает между собой ее геометрическую и эффективную площадь, то есть
AW = A · Ka
(6)
- A = геометрическая площадь антенны [м²]
С учетом введенных величин выражение для принятой мощности Pe может быть записано в виде:
В приведенных выше выражениях излученная и отраженная волны рассматривались по отдельности. Следующим шагом является получение выражения, связывающего их параметры вместе. Для этого подставим выражение для отраженной мощности (3) в формулу для принятой мощности (8). В дальнейшем учтем, что для случая совмещенного радиолокатора R1 = R2.
Коэффициент усиления антенны G может быть выражен через длину волны λ. Не приводя здесь вывода этого выражения, запишем окончательную формулу:
(10)
Выразив из (10) геометрическую площадь антенны А и подставив полученное выражение в (9), после упрощения получим:
(11)
Решая полученное уравнение относительно дальности цели R, мы получим классическое уравнение дальности радиолокации:
(12)
В полученном уравнении учитываются все величины, оказывающие влияние на распространение радиолокационных сигналов. Перед тем, как попробовать применить уравнение радиолокации на практике, например, для оценки эффективности радиолокатора,
необходимо привести некоторые дополнительные соображения.
Перед тем, как попробовать применить уравнение радиолокации на практике, например, для оценки эффективности радиолокатора,
необходимо привести некоторые дополнительные соображения.
Для конкретного радиолокатора большинство параметров (в частности, Ps, G, λ) можно считать постоянными, поскольку их значения изменяются в небольших пределах. С другой стороны, эффективная поверхность рассеяния изменяется достаточно сильно. Однако, для практических задач ее часто полагают равной 1 м².
Наименьшую принимаемую мощность, при которой отраженный сигнал может быть обнаружен, обозначают PEmin. Сигналы меньшей, чем PEmin мощности, не могут использоваться, поскольку они будут потеряны в шумах приемника. Поэтому PEmin еще называют чувствительностью приемника. Значение PEmin определяет максимальную дальность действия Rmax радиолокатора:
(13)
Использование этого уравнения радиолокации позволяет легко объяснить влияние той или иной характеристики радиолокатора на дальность его действия.
Учет потерь
Приведенный выше вывод уравнения радиолокации выполнен в предположении идеальных условий распространения электромагнитных волн, то есть распространения без потерь. В реальности необходимо учитывать разнообразные потери, поскольку они могут существенно влиять на эффективность радиолокатора. С этой целью уравнение радиолокации дополняется коэффициентом потерь Lges.
(14)
Этот коэффициент учитывает следующие потери:
- L D = внутренние потери в передающем и приемном трактах радиолокатора;
- L f = флуктуационные потери во время отражения от цели;
- L Atm = атмосферные потери — потери на поглощение электромагнитных волн при распространении их в атмосфере от радиолокатора до цели и обратно.
В высокочастотных компонентах радиолокатора, таких как
волноводы,
фильтры, а также в
антенных обтекателях
также возникают внутренние потери. Для конкретного радиолокатора эти потери относительно постоянны и могут быть легко измерены.
Для конкретного радиолокатора эти потери относительно постоянны и могут быть легко измерены.
Атмосферное ослабление и отражение от поверхности Земли являются постоянными факторами.
Влияние Земной поверхности
Расширенная, однако реже используемая, форма записи уравнения радиолокации учитывает дополнительные факторы, такие как поверхность Земли, однако не учитывает чувствительность приемника и атмосферное ослабление.
В этом выражении, помимо уже известных величин, появляются следующие:
- Kα — коэффициент потерь вместо Lges.;
- Az — эффективная поверхность отражения вместо σ;
- ti — длительность импульса;
- nR — коэффициент шума приемника;
- d — коэффициент четкости экрана индикаторного устройства;
- Re — толщина слоя поглощающей среды;
- γ — угол отражения луча;
- K — постоянная Больцмана;
- T0 — абсолютная температура в К;
- δR — коэффициент ослабления в поглощающей среде.

Отражение от плоской земной поверхности
Геометрическое представление (Рисунок 4) поясняет влияние поверхности Земли.
Плоскость Земли вблизи антенны радиолокатора оказывает существенное влияние на диаграмму направленности антенны в вертикальной плоскости.
Взаимодействие прямой и переотраженной от поверхности грунта волн изменяет диаграмму направленности антенны на передачу и на прием.
Это влияние значительно в диапазоне очень высоких частот (ОВЧ, VHF), к которому относятся частоты 30 … 300 МГц.
С увеличением частоты такое влияние уменьшается.
Для обнаружения маловысотных целей использование отражения от земной поверхности является необходимым.
Однако это возможно, только если размеры неровностей поверхности в
первой зоне Френеля
(радиуса RF) относительно антенны не превышают значения
0,001·RF (то есть,
если радиус первой зоны Френеля RF = 1000 м,
то на этом расстоянии от антенны радиолокатора не должно быть неровностей больше 1 м!).
Рисунок 4. Геометрия отражений от земной поверхности
Рисунок 4. Геометрия отражений от земной поверхности
Специализированные радиолокаторы, работающие в диапазоне
ОВЧ (VHF),
используют отражение от земной поверхности для увеличения дальности действия на малых высотах.
На больших высотах влияние этого отражения приводит к нежелательным эффектам,
а именно, к изрезанности зоны обзора в вертикальной плоскости.
На Рисунке 5 показано изменение формы диаграммы направленности антенны под влиянием отражения от земной поверхности.
Изрезанность зоны обзора приводит к пропаданию сигнала от цели во время ее нахождения между лепестками.
Указанный эффект использовался в наземных радиолокаторах управления воздушным движением,
при этом лучшие результаты наблюдались на более низких частотах,
где лепестки получались довольно широкими и обеспечивали достаточное покрытие на больших высотах.
С увеличением рабочей частоты радиолокатора влияние отражения от земной поверхности на форму
диаграммы направленности антенны в вертикальной плоскости ослабевает.
Вертикальное сечение диаграммы
направленности в свободном пространстве
Влияние отражений от земли
«Сера, дорогой друг, вся теория»(Гёте, «Фауст»):
Вот идеализированная
Косекансная диаграмма направленности!
Рисунок 5. Диаграмма направленности антенны в вертикальной плоскости с учетом влияния отражений от земной поверхности.
Вертикальное сечение диаграммы
направленности в свободном пространстве
Влияние отражений от земли
«Сера, дорогой друг, вся теория»(Гёте, «Фауст»):
Вот идеализированная
Косекансная диаграмма направленности!
Рисунок 5. Диаграмма направленности антенны в вертикальной плоскости с учетом влияния отражений от земной поверхности.
Вертикальное сечение диаграммы
направленности в свободном пространстве
Влияние отражений от земли
«Сера, дорогой друг, вся теория»(Гёте, «Фауст»):
Вот идеализированная
Косекансная диаграмма направленности!
Рисунок 5. Диаграмма направленности антенны в вертикальной плоскости с учетом влияния отражений от земной поверхности.
Диаграмма направленности антенны в вертикальной плоскости с учетом влияния отражений от земной поверхности.
Увеличение высоты антенны приводит к тому, что количество лепестков увеличивается и они становятся более узкими, тем самым уменьшается количество пропаданий сигнала от цели, двигающейся на постоянной высоте. Однако вместе с этим, увеличение высоты антенны приводит к увеличению размеров первой зоны Френеля, то есть зоны, существенной для формирования диаграммы направленности антенны. А это, в свою очередь, ужесточает требования к позиции радиолокатора.
Таким образом, отражение от земной поверхности может оказывать как позитивное,
так и негативное влияние на эффективность функционирования радиолокатора.
Степень этого влияния зависит от многих факторов, таких как длина волны,
высота подъема антенны, наличие и размер неровностей поверхности позиции на расстоянии, соответствующем первой зоне Френеля.
Отсюда следует, что для конкретного радиолокатора, когда на первые два фактора влиять не представляется возможным,
особое значение приобретает выбор и подготовка позиции.
Формула радиоволн — GeeksforGeeks
Радиоволны определяются как волны с большой длиной волны, которые могут распространяться вдоль кривизны земли. Они являются частью спектра с частотами ниже видимого света, что делает их незаметными для невооруженного глаза. Радиоволны распространяются по-разному в зависимости от их частоты. Это волны широкого спектра, которые могут передаваться и приниматься передатчиками и приемниками. Частота меняется в зависимости от того, как они взаимодействуют с различными средами, особенно от того, проникают ли они в материалы и как они взаимодействуют с ионосферой Земли. Они также известны как земные или поверхностные волны. Они работают на частотах от 300 ГГц до 3 кГц.
Что такое радиоволны?Концепция радиоволн объясняется формулой их скорости. Скорость радиоволны рассчитывается путем вычисления произведения ее длины волны и частоты.
- Обозначается символом v r .
- Стандартная единица измерения — метры в секунду (м/с).

- И размерная формула задается как [M 0 L 1 T -1 ].
Радиоволны Формула
Примеры задачФормула для расчета радиоволн определяется,
V R = λV
, где
- V R — скорость,
- λ — это волна и
- vfore,
- . это частота радиоволн.
Задача 1. Рассчитайте скорость радиоволны с длиной волны 280 м и частотой 1 МГц.
Решение:
У нас есть
λ = 280
V = 1 × 10 6
Используя формулу, которую мы имеем,
V R = λV
= 280 (10 6 )
= = 280 (10 6 ) 2,8 × 10 7 м/с
Задача 2. Рассчитайте скорость радиоволны с длиной волны 35 м и частотой 2 МГц.
Решение:
Имеем,
λ = 35
v = 2 × 10 6
Using the formula we have,
v r = λv
= 35 (2 × 10 6 )
= 7 × 10 7 m/s
Problem 3: Рассчитайте скорость радиоволны с длиной волны 150 м и частотой 1,5 кГц.
Решение:
Имеем,
λ = 150
v = 1,5 × 10 3
9 По формуле имеем,0012 R = λV
= 150 (1,5 × 10 3 )
= 2,25 × 10 5 м/с
Проблема 4: Рассчитывайте длину волны радиотех × 10 6 м/с и частоте 1,5 МГц.
Решение:
Мы имеем,
V R = 3 × 10 6
V = 1,5 × 100018 6
Использование формулы, которую мы имеем,
9002 V R.0013 = λv
λ = (3 × 10 6 )/(1,5 × 10 6 )
= 2 м
Задача 5: Рассчитать длину волны радиоволны × 10
6 м/с и частоте 2 кГц.Решение:
Мы имеем,
λ = 4 × 10 6
В = 2 × 10 3
Используя Формулу,
V R = λV,
V R = λV.
λ = (4 × 10 6 )/(2 × 10 3 )
= 2000 м
500 м.
Решение:
. = (5 × 10 6 )/500
= 10 кГц
Задача 7. Рассчитайте частоту радиоволны, имеющей скорость 2,5 × 10 7 м/с и длину волны 800 м.
Решение:
. = (2,5 × 10 7 )/800
= 31,2 кГц
Распространение радиоволн и моделирование параболическим уравнением
Выбранный тип: Мягкая обложка
Количество:
62,25 $
Цифровая пробная копия
Запросить цифровую оценочную копиюГекхан Апайдин, Левент Севги
ISBN: 978-1-119-43211-1
Октябрь 2017 г. Wiley-IEEE Press
152 страницы
Wiley-IEEE Press
152 страницы
Электронная книга
Всего от 50 долларов США
Распечатать
Всего от 62,25 долл. США
О-бук
Электронная книга com are delivered on the VitalSource platform. To download and read them, users must install the VitalSource Bookshelf Software.</li><li>E-books have DRM protection on them, which means only the person who purchases and downloads the e-book can access it.</li><li>E-books are non-returnable and non-refundable.</li><li>To learn more about our e-books, please refer to our <a href="https://www.wiley.com/wiley-ebooks" target="_blank">FAQ</a>.</li></ul>» data-original-title=»» title=»»/>
50,00 $
Мягкая обложка
62,25 $
O-Book </p>» data-original-title=»» title=»»/>
Загрузить рекламный проспект
Загрузить рекламный проспект
Загрузить флаер продукта для загрузки PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание.
Описание
Важный вклад в литературу, который представляет новые мощные методы моделирования и имитации распространения радиоволн
Полное понимание распространения электромагнитных волн имеет основополагающее значение для разработки сложных технологий связи и обнаружения. Мощные численные методы, описанные в этой книге, представляют собой большой шаг вперед в нашей способности точно моделировать распространение электромагнитных волн, чтобы устанавливать и поддерживать надежные каналы связи, обнаруживать цели в радиолокационных системах и поддерживать надежные сети мобильной связи и радиовещания.
Первая новая книга по моделированию и моделированию распространения направленных волн, появившаяся почти за два десятилетия, Распространение радиоволн и моделирование с помощью параболических уравнений рассматривает основы распространения электромагнитных волн в целом, уделяя особое внимание распространению радиоволн через различные среды. Авторы исследуют множество новых приложений и подробно описывают различные виртуальные электромагнитные инструменты для решения нескольких часто встречающихся проблем распространения электромагнитных волн. Все описанные методы представлены в контексте реальных сценариев, отражающих различное влияние различных сред на распространение радиоволн. Этот ценный текст:
- Рассматривает распространение земных и поверхностных волн
- Объясняет применение радаров с точки зрения моделирования параболических уравнений и подходов к моделированию
- Вводит несколько простых и сложных сценариев MATLAB
- Обучает приложениям, которые работают с широким диапазоном распространения электромагнитных, акустических и оптических волн моделирование
- Представляет материал в формате краткого справочника, идеально подходящего для занятых исследователей и инженеров
Распространение радиоволн и моделирование параболических уравнений — важный ресурс для инженеров по электротехнике, электронике, связи и вычислительной технике, работающих над промышленными и военными приложениями, основанными на направленном распространении радиоволн. Это также полезный справочник для продвинутых студентов инженерных специальностей и академических исследователей.
Это также полезный справочник для продвинутых студентов инженерных специальностей и академических исследователей.
Связанные ресурсы
Об авторе
ГЁХАН АПАЙДИН, BSEE, MSEE, P H D, — внештатный инженер-электрик и электронщик. Его исследовательские интересы включают аналитические и численные методы в электромагнетизме, особенно электромагнитные расчеты распространения волн, моделирование дифракции, рассеяние и смежные области.
ЛЕВЕНТ СЕВГИ, BSEE, MSEE, P H D, — профессор кафедры электротехники и электроники Университета Окан, Стамбул, Турция. Его исследования были сосредоточены на распространении в сложных средах, моделировании и измерениях ЭМС/БЭМ, аналитических и численных методах в электромагнетизме и радиолокационных системах.
Соглашение о таблице
ПРЕДИСЛОВИЕ IX
АРЕМЕНТЫ XI
Коды MATLAB XIII
ГЛАВА 1: Введение 1
1. 1 Электромагнитные проблемы и классификация 1
1 Электромагнитные проблемы и классификация 1
1.2 Уравнения максимального.
1.4 Двумерное уравнение Гельмгольца 5
1.5 Валидация, проверка и процедура калибровки 6
1.6 Преобразование Фурье, ДПФ и БПФ 7
Глава 2: РАСПРОСТРАНЕНИЕ ВОЛН НАД ПЛОСКОЙ ЗЕМЛЕЙ 15
2.1 Плоская Земля и двухлучевая модель GO 15
2.2 Задача с одним ножом и четырехлучевая модель 2 2 930 0 16 Вертикальный линейный профиль рефракции и суммирование мод 19
Глава 3. МОДЕЛИРОВАНИЕ ПАРАБОЛИЧЕСКИМ УРАВНЕНИЕМ 23
3.1 Введение 23
3.2 Форма уравнения параболической волны 24
70003
3.4 Инжекция антенны/источника 28
3.5 Модель параболического уравнения с разделенным шагом (SSPE) 29
3.5.1 Узкоугольный и широкоугольный SSPE 30
3.5.2 A MATLAB-Based3 Simple 900 Code 0 0 900 Code 0 3,6 модель параболического уравнения на основе FEM 32
3.7 Эффекты атмосферной рефракции 40
Глава 4: Распространение волн на коротких диапазонах 43
4. 1 Введение 43
1 Введение 43
4.2 Точное источник модели 44
4.3 Волновые Продюсеры.0003
4.3.1 Плоская Земля и двухлучевая модель 47
4.3.2 PE-распространитель волны на основе МКЭ 49
4.3.3 PE-распространитель волны на основе SSPE 49
4.3.4 Метод моментного моделирования 39 900 49 904 Край ножа и четыре лучи модель 49
4.5 Канонические тесты и калибровка 50
Глава 5: Моделирование PE и местности 53
5.1 нерегулярная местность PEC 53
5.2 Преобразование Фурье (DMFT) 56
5.3 Численные результаты и сравнение 57
Глава 6: Аналитические точные и приблизительные модели 65
6.1 Распространение волн в параллельной пластинке волновода 65
6.2 Функция Грина с точки зрения суммирования режима 68
6.3. Наклонный источник Гаусса 70
6.4 Гибридный луч + метод изображения 71
6.5 Численные модели 73
6.5.1 Модели параболических уравнений: SSPE и FEMPE 73
6. 5.2 Метод моментов 75
5.2 Метод моментов 75
Глава 7: Распространение волн внутри трехмерного прямоугольного волновода 79
7.1 Введение 79
7,2 Трехмерная модель прямоугольной волновойгида 80
7,3 Трехмерные модели параболических уравнений 81
7.3.1 SSP
7.3.2 Модель FEMPE 82
7.3.3 Модель ADIPE 82
7.4 Испытания и калибровка 83
8.2 Формулировка двухстороннего метода SSPE 91
8.3 Плоская Земля с бесконечной стенкой 91
8.4 Плоская Земля с одинарными и двойными остроконечными кромками 91
8.5 Моделирование двухстороннего распространения в волноводах Split-Stepmen 96
8.6002 — и модели параболических уравнений на основе конечных элементов 968.7 Испытания и калибровка 97
Глава 9: ПАКЕТ ВИРТУАЛЬНОГО РАСПРОСТРАНЕНИЯ PETOOL 101
9.1 Введение 101
.2 Petool Software 103
9.3 Характерные примеры 107
Глава 10: Фырк-виртуальный пакет распространения 113
10.


 ..1,0
..1,0