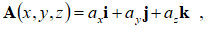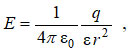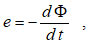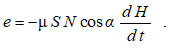«Как радиоволны распространяются в вакууме?» – Яндекс.Кью

Вот интерпретация двух из четырех уравнений Максвелла, определяющая рождение и распространение электромагнитной (ЭМ) волны:

• Всякое изменение магнитного поля (B) порождает в окружающем пространстве вихревое электрическое поле (E), силовые линии которого замкнуты.
• Изменяющееся во времени электрическое поле порождает в окружающем пространстве магнитное поле.
  Простейший рисунок, иллюстрирующий рождение и распространение ЭМ волны, приведен ниже, где каждая пара векторов (Е, B) рождается одновременно, перпендикулярно друг к другу и  перпендикулярно направлению движения волны V.

Вот более реальная 3-х мерная картинка эволюции и распространения ЭМ волны, где для наглядности магнитная компонента поля искусственно сдвинута вниз вдоль пунктирных линий, а желтая полоса — излучатель электрического поля (антенна). 

А этот рисунок показывает изменение амплитуд векторов электрического и магнитного полей в процессе распространения ЭМ волны в 3-мерном пространстве.

Надо учесть, что приведённые (или любые другие) рисунки лишь приближенно и грубо описывают реальное рождение и распространение ЭМ волны, точное описание которых задаётся только уравнениями Максвелла. 

А теперь можно и ответить на вопрос о распространении ЭМ волны в вакууме. Именно в вакууме распространение ЭМ волны происходит с максимально возможной скоростью, предоставленной природой, c ≈ 300000 км/сек. Определяется это опять из уравнений Максвелла, где скорость света зависит от поляризационных свойств среды: c = 1/√(ε₀μ₀), где ε₀ и μ₀ − электрическая и магнитная проницаемости вакуума, определяющие его динамические поляризационные свойства. Дело в том, что любая среда (и ваше тело тоже) противодействует прохождению чего-либо постороннего сквозь неё. Исходя из квантовой физики, вакуум не является исключением. В среднем он нейтрален и пуст, но из принципа неопределенности следует, что в интервалах очень малых времен, Δt → 0, в вакууме рождаются и исчезают виртуальные пары заряженных частиц (е⁺е⁻), поляризующих вакуум на время Δt. Именно поляризационные свойства вакуума и определяют скорость света. Если бы поляризации вакуума не было бы вообще (ε₀=0, μ₀=0), скорость света была бы бесконечной. Если бы эта поляризация отличалась от известных на сегодня значений, то Вселенная была бы другой, и скорее всего нас не было бы там (см. Антропный принцип ). 

Как следует из уравнений Максвелла, движение ЭМ волны в веществе (воздух, вода, металл, плазма) происходит с меньшей скоростью, из-за дополнительных поляризационных свойств вещества (ε, μ), и равна: c = 1/√(εε₀μμ₀), где ε >1 и μ >1 — относительные электрическая и магнитная проницаемости вещества. Есть еще одна точка зрения, которая предполагает, что на самом деле скорость света в веществе остается постоянной (равной скорости в вакууме) и «видимое» уменьшение его значения, связано задержкой времени на переизлучения парциальных ЭМ волн зарядами (электронами, ионами) внутри вещества. Лично мне импонирует последняя интерпретация. Хочется чего-то постоянного в этой жизни.

Электромагнитные волны

Дж. Максвелл доказал существование электромагнитных волн еще в 1864 после того, как решил применить их к изменяющимся во времени электромагнитным полям. Проанализировав все известные на тот момент законы электродинамики, увидел связь и асимметрию между электрическими и магнитными полями.

Понятие вихревого электрического поля

Максвеллом было введено понятие вихревого электрического поля, после чего он предложил иную формулировку закона электромагнитной индукции, которая была открыта в 1831 году Фарадеем:

Определение 1

Всякое изменение магнитного поля может стать причиной порождения в окружающем пространстве вихревого электрического поля с замкнутыми силовыми линиями.

Максвелл показал гипотезу, которая говорит совсем об обратном, а именно:

Определение 2

Электрическое поле, изменяющееся во времени, является причиной появления в окружающем пространстве магнитного поля.

Рисунки 2.6.1 и 2.6.2 показывают взаимное преобразование электрического и магнитного полей.

Рисунок 2.6.1. Закон электромагнитной индукции по определению Максвелла.

Рисунок 2.6.2. Гипотеза Максвелла об изменяющемся электрическом поле, порождающим магнитное поле.

Свойства уравнений Максвелла

Вначале данная гипотеза не имела экспериментального подтверждения, а выступала как теоретическое предположение. Основываясь на ней, Максвеллу смог зафиксировать непротиворечивую систему уравнений, которые описывали взаимные превращения электрического и магнитного полей. Данная запись называлась системой уравнений электромагнитного поля, иначе говоря, уравнениями Максвелла. Исходя из теории, используются выводы:

1. Электромагнитные волны существуют. Они могут распространяться как в пространстве, так и во времени электромагнитного поля. Электромагнитные полны поперечные, а векторы E→ и
   B→ располагаются перпендикулярно друг другу в одной плоскости, которая перпендикулярна относительно направления распространения волны. Это отчетливо видно на приведенном ниже изображении.

Рисунок 2.6

10 Электромагнитные волны в вакууме

Лекция № 10

Электромагнитные волны в вакууме.

1. Свободное электромагнитное поле в вакууме

Переменное электрическое поле создает вокруг себя переменное магнитное поле. В свою очередь, переменное магнитное поле создает вокруг себя электрическое поле, которое также переменно. Возникает вопрос: не могут ли переменные электрическое и магнитное поля, поддерживая друг друга, существовать в вакууме без зарядов и токов? Математически вопрос сводится к тому, имеют ли уравнения Максвелла для полей в вакууме

E rotB = 0 0 t ;

rotE = — B ;

t

divE = 0; divB = 0

решения, отличающиеся от тривиального B = 0, E = 0? Ответ гласит, что такие решения существуют и их бесконечно много.

Чтобы убедиться в этом, исключим из уравнений одно из полей, например, индукцию B. Применим для этого операцию rot к обеим частям второго уравнения:

rotrotE = — rotB.

t

Используя далее первое уравнение, получим rotrotE = — 0

0

2E

или

t2

2

2E

graddivE —

E = —

.

t2

0

0

Так как divE = 0, то мы окончательно получим

2

E =

2E

2

E =

1 2E

или

,

0 t2

c

t2

0

2

где c2 = 1/( 0 0). Такому же уравнению удовлетворяет в вакууме и индукция B

2B = 1 2B . c2 t2

Эти уравнения называются волновыми. Покажем теперь, что волновое уравнение имеет бесчисленное множество нетривиальных решений. Для простоты рассмотрим случай, когда поля зависят только от одной декартовой координаты х. Тогда одномерное волновое уравнение имеет вид

2f		1		2f	0.
x2		c2		t2

Решение этого уравнения имеет вид

f(x,t) F1(x ct) F2 (x ct),

где F1 и F2 произвольные функции. При этом функция F1(x-ct) описывает волну, распространяющуюся со скоростью с вдоль положительной оси х, а функция F2(x+ct) — волну, распространяющуюся с той же скоростью в противоположном направлении.

Электромагнитные волны в вакууме

2

________________________________________________________________________________

Величина с равна скорости света в вакууме. Скорость электромагнитных волн совпадает со скоростью света в вакууме.

Электромагнитная волна в вакууме обладает свойством поперечности. Это немедленно вытекает из уравнений divE = 0; divВ = 0. Действительно, подставляя в них

E E(x ct), B B(x ct), мы получим Ex Bx 0,

x x

откуда Ex = const, Bx = const. Но мы рассматриваем переменные, а не статические поля. Поэтому следует считать Ex =0, Bx=0, т.е. переменные поля не имеют составляющих вдоль направления распространения волны и являются, следовательно, поперечными. Отличными от нуля в них могут быть только y- и z- составляющие.

Мы показали, что одномерное волновое уравнение имеет бесчисленное множество нетривиальных решений. Этим же свойством обладает и трехмерное волновое уравнение, и все эти решения имеют вид волн, распространяющихся в разных направлениях со скоростью света с.

Существование нетривиальных решений уравнений Максвелла в отсутствие токов и зарядов имеет фундаментальное значение. Оно означает, что переменные поля могут существовать в вакууме без зарядов и токов. Это значит, что электромагнитное поле следует рассматривать как физическую реальность, а не как атрибут зарядов.

Ранее нами было показано, что электромагнитное поле обладает энергией, импульсом и моментом импульса. Это свидетельствует о том, что электромагнитное поле действительно материально.

Свободное электромагнитное поле не может быть статическим и обязательно представляет собой волну. Проще всего анализировать плоскую волну.

2. Плоские монохроматические волны

Электромагнитная волна называется плоской, если векторы напряженности электромагнитного поля одинаковы во всех точках любой плоскости, перпендикулярной направлению распространения волн. Поверхностями постоянной фазы в плоской волне являются плоскости, расположенные перпендикулярно направлению распространения волны. Волна называется монохроматической, если векторы напряженности электромагнитного поля изменяются во времени по гармоническому закону с определенной частотой.

Если плоская электромагнитная волна распространяется вдоль оси Z, то векторы напряженности поля такой волны могут быть записаны в виде

E(z,t) E(z)ei t

H(z,t) H(z)ei t

Волновые уравнения для напряженностей электромагнитного поля.

	2	E =				2E
					0 t2
			0

22H

H = 0 0 t2

Напряженность электрического и магнитного полей удовлетворяет одному и тому же волновому уравнению с одной и той же скоростью распространения c 1/ 0 0 .

Совместим ось Z с направлением распространения электромагнитной волны. Рассмотрим, например, уравнение (3) для вектора Е. Подставим выражение (1) в (3) и сокращая после дифференцирования на экспоненциальный множитель, получим

0 0

Электромагнитные волны в вакууме

3

________________________________________________________________________________

e

i t

2E(z)

0 0(i )

2

E(z)e

i t

z2

d2E(z)

2

E(z)

2

E(z)

0

0 (i )

0 0

dz2

2E(z)

d

2

E(z) 0

0

0

dz2

d2E(z)

2

E(z) 0

k

(5)

dz2

k2

2 0 0

(6)

k — волновое число, равное

2

2

k =

= /c=

.

(7)

0 0

Общее решение уравнения (5) имеет вид

cT

подставляя (8) в (1), находим

E(z) a1e ikz a2eikz ,

(8)

E(z,t) a1ei( t kz) a2ei( t kz)

(9)

Первый член в правой части (9) представляет собой волну, распространяющуюся в

положительном направлении оси Z. Это следует из того, что точка постоянной фазы

(10)

t kz const

движется в направлении возрастающих значений z, т.е. z в (10) при увеличении t также увеличивается. Второй член равенства (9) описывает волну, распространяющуюся в отрицательном направлении оси Z.

Решения уравнения (2) находятся аналогично. Поэтому для векторов напряженностей электромагнитной волны, распространяющейся в положительном направлении оси Z, можно

написать следующие выражения:
E(z,t) E0ei( t kz),	H(z,t) H0ei( t kz),	(11)

где E0 и H0 — амплитуды напряженности поля.

Формулы (11) показывают, что плоские волны в вакууме распространяются без изменения амплитуды, т.е. без затухания. Фазовая скорость волны находится с помощью дифференцирования уравнения (10) по времени

vф= dz 1 =с. dt k

Выражение (7), записанное как =ck, определяет закон дисперсии электромагнитных волн в вакууме. Из него следует, что групповая скорость волны

d vгр= d =с.

Это значит, что скорости распространения vф и vгр не зависят от частоты , а волновые пакеты (суперпозиции плоских монохроматических волн с разными частотами) распространяются в вакууме без изменения формы.

Формулы (11) записаны при специальном выборе системы координат, когда ось Z совпадает с направлением распространения волны. От этого ограничения можно освободиться, введя волновой вектор k, который по направлению совпадает с распространением волны, а по значению определяется выражением (6). Для плоской волны, распространяющейся вдоль оси Z, модуль векторов E и H в любой точке плоскости, перпендикулярной оси Z, один и тот же. Пусть r — радиус-вектор некоторой точки на такой

Электромагнитные волны в вакууме

4

________________________________________________________________________________

плоскости постоянной фазы. Очевидно, что kz = kr и, следовательно, вместо (11) можно написать

E(r,t) E0ei( t kr), H(r,t) H0ei( t kr). (12)

Эти формулы описывают напряженность электрического и магнитного полей плоской электромагнитной волны, распространяющейся в направлении вектора k . Частота волны равна , а длина волны дается формулой = 2 /k.

3. Свойства плоских монохроматических волн

Для исследования свойств плоских волн запишем уравнения Максвелла в комплексном виде.

Предварительно выведем несколько математических преобразований

divE0ei( t kr) ei tE0div(e ikr) ei tE0 (e ikr) ei tE0 ( ik)(e ikr) ikE, divE E ikE,

rotE0ei( t kr) ei tE0rot(e ikr) ei tE0 (e ikr) ei t( ik) E0 (e ikr) ik E, rotE E ik E,

E E0ei( t kr) i E.t t

Итак, применение дифференциальных операторов div, rot, / t к экспоненциальным функциям не меняет их вида. Измеряемыми физическими величинами являются при этом действительные части соответствующих комплексных выражений.

Теперь применим эти преобразования к уравнениям Максвелла

rotH= 0	E		;		H = 0	E		;
	t					t
rotE = — 0		H		;	E= — 0		H		;
divE = 0;		t			E = 0;		t
divH = 0					H = 0
-ik H= 0i E					k H=- 0 E
-ik E=- 0i H					k E= 0 H
-ikE=0					kE=0
-ikH=0					kH=0

Равенство нулю скалярных произведений kE и kH означает, что векторы напряженностей электрического и магнитного полей в случае плоской волны лежат в плоскости, перпендикулярной направлению распространения волны. Если ввести единичный вектор n = k/k, направленный по распространению волны, то уравнение k E= 0 H

приобретает вид

kn E= 0 H,			k 0 0
		n E		H	(13)
	0		0

Отсюда видно, что векторы E и H перпендикулярны друг другу. Ранее было показано, что они оба перпендикулярны n. Из равенства (13) следует, что векторы E, H, n составляют правовинтовую тройку взаимно перпендикулярных векторов.

Электромагнитные волны в вакууме

5

________________________________________________________________________________

E

n

H

Взяв от обеих частей равенства (13) модули, получаем
			0		E		0	H.	(14)
Умножив обе части (14) на		, получим				E 0H или
	0			0 0
					Е=сВ.				(15)

Из (14) можно заключить, что векторы Е и Н в плоской волне в вакууме изменяются в одной фазе.

Найдем объемную плотность энергии электромагнитного поля

2

2

0E 0

0H 0

1

1

0 0

w=( 0E

+ 0H )/2=

H +

E=EH

=

EH

S,

2 0

2 0

c

c

где учтено равенство (14).

Выражение для вектора Пойнтинга можно записать в виде

S=cw, S=wc .

Таким образом, скорость движения энергии в вакууме равна фазовой скорости волны — скорости света.

Все приведенные выше рассуждения остаются в силе и при рассмотрении распространения плоской монохроматической волны в диэлектрике. Только вместо скорости

света с во всех выражениях будет фигурировать скорость v = c/ , а там, где стоят значения постоянных 0 и 0 , появятся произведения 0 и o .

4.Поляризация плоской волны

Вплоской монохроматической волне электрическое и магнитное поля направлены перпендикулярно направлению распространения волны. В таких случаях говорят о волне с поперечной поляризацией, или просто о поперечной волне.

Подробнее изучим свойства амплитуды Е0 плоской монохроматической волны. При

комплексном описании поля Е=Eo ei 0 — комплексный вектор, который может быть разложен на два действительных вектора

где E1, E2 — два вещественных вектора, ортогональные к направлению распространения волны.

Выберем E1 и E2 так, чтобы они были взаимно перпендикулярны. Формула

E= Re{E0expi( t-kr)}

означает тогда, что электрическое поле монохроматической волны всегда можно представить в виде суперпозиции двух полей, направленных вдоль двух взаимно перпендикулярных постоянных векторов и изменяющихся, как cos( t-kr) и sin( t-kr), т.е. со сдвигом по фазе на В случае вещественного Eo (т.е. E2=0) говорят о линейной

Электромагнитные волны в вакууме

6

________________________________________________________________________________

поляризации волны. Таким образом, можно сказать, что в общем случае поле плоской монохроматической волны представляет собой суперпозицию двух взаимно перпендикулярных полей, соответствующих двум линейно поляризованным волнам, причем разность фаз полей равна .

Наличие трех взаимно перпендикулярных векторов k, E1, E2 позволяет естественным образом выбрать декартову систему координат, орты которой направлены вдоль этих векторов. А именно: направим ось z вдоль k (на нас), ось х — вдоль E1 и ось у — вдоль E2 (правовинтовая система координат).

Y

E2		E
		X
		E1

Ex E1 cos ,					Ey		= E2 sin ,
		E	x	2			Ey	2
Тогда									1. Мы видим, что конец вектора Е в каждой точке пространства
		E1					E2

описывает с течением времени эллипс, полуоси которого равны E1 и E2. Вращение этого вектора происходит либо по часовой стрелке (если вектор E2 параллелен оси У), либо против нее (если вектор -E2 параллелен оси У). В первом случае говорят о правополяризованной волне, а во втором — о левополяризованной.

Магнитный вектор также описывает эллипс, оси которого повернуты относительно осей электрического вектора на , а направления вращения Е и Н совпадают.

В частном случае, когда Е1=Е2, эллиптическая поляризация вырождается в круговую, которая также может иметь два направления вращения. При Е1 0, Е2=0 или Е1=0, Е2 0 поляризация называется линейной — электрический и магнитный векторы колеблются вдоль фиксированных взаимно перпендикулярных направлений.

Отметим, что при фиксированном k возможны две независимые поляризации плоской монохроматической волны — эллиптическая (в частном случае круговая) с правым и левым направлениями вращения или две линейные поляризации во взаимно перпендикулярных направлениях.

Электромагнитные волны и свет. Часть 2. Как происходит распространение электромагнитных волн

Механические волны – это распространение смещения атомов вещества, поэтому наличие этих атомов обязательно, без вещества они распространяться не могут.

Электромагнитные волны – это распространение изменений характеристик поля. Поэтому наличие или отсутствие вещества может повлиять только на сами изменения характеристик поля, но не на сам факт распространения электромагнитных волн. Так что связь посредством электромагнитных волн будет работать и в вакууме, и наоборот при наличии плотных преград.

---

 

Есть ли у поля граница?

Когда мы описываем взаимодействие зарядов, мы говорим о поле вблизи заряда. Речь пойдет об электрическом поле, но оно является проявлением электромагнитного, так что к нему применимы те же выводы.

Если поднести два заряда друг к другу, они притянутся или оттолкнутся. Вокруг заряда есть поле, и мы часто говорим об ограниченной области вблизи заряда, именно туда нужно поместить второй заряд, чтобы наблюдать взаимодействие.

А есть ли границы у этой области, внутри которых поле есть, а дальше – нет? По закону Кулона, сила электростатического взаимодействия зарядов равна:

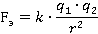
Сила обратно пропорциональна квадрату расстояния между зарядами. На больших расстояниях сила 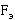 будет мала, она не будет заметно влиять на движение тел, ее не зарегистрируют доступные нам приборы, поэтому ею можно пренебречь и считать ее нулевой. Однако считать, что поле где-то заканчивается, неправильно (см. рис. 2).

Рис. 2. Зависимость силы взаимодействия от расстояния

 

Мы разобрали модель: заряд в свободном пространстве, и его поле есть везде, на любом исчислимом расстоянии от заряда. В реальном мире такого нет: бесконечное свободное пространство и в нем одно заряженное тело. В реальном мире множество заряженных тел, вещество состоит из заряженных протонов и электронов. Поэтому можно рассматривать такую модель: не поле есть вблизи заряда, а поле есть везде, как некая материя, пронизывающая все пространство. И поэтому электромагнитные волны могут распространяться так же по всему пространству. А заряды и то, как они расположены, влияет на параметры этого поля в разных точках. Вдали от зарядов поле слабее, вблизи заряда поле сильнее, вблизи другого заряда – еще сильнее. Где-то заряды распределены так, что их поля в сумме дают ноль или почти ноль, например внутри проводника. Как эти неоднородности влияют на распространение волны – это отдельная задача: где-то меняют направление, где-то отражаются и т. д. Но принципиальное отличие от механических волн, для распространения которых нужно вещество, мы увидели.

---

Чтобы использовать какое-то явление, в том числе электромагнитные волны, нужно их описать, нужна модель. Причем модель должна быть простой, нет смысла рассматривать процессы подробнее, чем нужно для решения прикладных задач: построить прибор, предсказать ход процесса с требуемой точностью. Эту точность мы определяем сами, здесь важен наш опыт и способность принимать решения, об этом – в ответвлении.

---

 

Как мы выбираем точность модели?

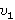Навстречу друг другу катятся два шара, даны их массы  и  и скорости  и . Найдите скорости шаров после упругого столкновения.

Как вы решите такую задачу? Здесь все просто: столкновение, скорее всего, лобовое, применим закон сохранения импульса и закон сохранения энергии (см. рис. 3).

Рис. 3. Столкновение тел

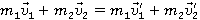
и так далее, останется только решить записанные уравнения.

Но так ли все просто? По шарам при ударе распространится механическая волна, раздастся звук удара. Они могут нагреться, так как абсолютно упругий удар – это модель, такого идеального удара в реальности быть не может. Никто не отменял гравитацию, шары притягиваются. Плюс могло быть вращение шаров, проскальзывание при качении. Это все могло повлиять на скорости шаров, а мы этого не учли, записали только простые уравнения.

Как же правильно, до какой точности нужно описывать процессы? Как правильно – решаем мы сами, в зависимости от задачи, которую решаем. Если нам достаточно примерно понять, в каком направлении и приблизительно с какой скоростью будут двигаться шары и не остановится ли один из них – выбранной модели с двумя уравнениями достаточно. Если речь о бильярде, то важную роль играет вращение и нелобовые столкновения под разными углами, там это надо учесть.

Мы сами выбираем точность модели в зависимости от решаемой задачи. В задачах, которые мы решаем на уроках физики, чаще всего этот выбор уже сделал за нас автор задачи. В самом условии подразумевается, как ее правильно решать и в рамках какой модели. В задаче о шариках прямо сказано, что столкновение упругое, даны массы и скорости шариков, намекая нам на то, какие уравнения применять.

---

Пока рассмотрим самую простую модель: электромагнитную волну, которая представляет собой распространение синусоидальных колебаний поля. Когда мы рассматривали механические волны, мы тоже начинали с распространения синусоидальных колебаний вещества.

Что такое колебания поля? То же, что и в случае с веществом: периодически повторяющиеся изменения физических параметров. Здесь это параметры поля: напряженность, магнитная индукция (см. рис. 4).

Рис. 4. Электромагнитная индукция

Как эти изменения распространяются? Давайте рассмотрим это в моделях электрического и магнитного поля, которые мы уже хорошо изучили.

Магнитная составляющая электромагнитного поля проявляется при движении заряда в данной системе отсчета. Но при движении заряда меняется электрическое поле, поэтому можно считать, что магнитное поле возникает при изменении электрического поля. Поскольку все эти формулировки эквивалентны, выберем в качестве модели последнюю: при изменении электрического поля возникает магнитное поле.

При движении заряда с постоянной скоростью возникает постоянное магнитное поле – мы изучали магнитное поле проводника с постоянным током. А что, если заряд движется с ускорением? Скорость движения заряда изменяется, значит, изменяется магнитное поле вокруг этого заряда. А что происходит при изменении магнитного поля? Один такой случай мы описали как электромагнитную индукцию: изменение магнитного поля. Его мы рассматривали как изменение магнитного потока через контур, которое вызывает ток в этом контуре. Вообще ток по проводнику просто так не течет, заряды движутся под действием электрического поля. Поэтому можно описать это так: при изменении магнитного поля возникает вихревое электрическое поле. Почему вихревое – потому что оно не направлено от положительного заряда к отрицательному, оно замкнуто, и под его действием заряды движутся по кругу (см. рис. 5).

Рис. 5. Возникновение электромагнитной волны

Так вот, изменение электрического поля создает вихревое магнитное поле (оно всегда вихревое, линии магнитного поля замкнуты), а изменение магнитного поля создает вихревое электрическое поле. А его изменение, в свою очередь, создает магнитное поле, и так далее – таким образом можно описать распространение электромагнитной волны.

Мы увидели на качественном уровне, каким образом возмущение в одной области вызывает возмущение в соседней. Такая связь – это необходимое условие распространения волны. В случае с механическими волнами есть силы, возникающие при деформации вещества, сила натяжения веревки и т. д. В случае с электромагнитными волнами мы проследили такую цепочку: при ускоренном движении заряда изменение электрического поля вызывает появление магнитного, а изменение магнитного поля вызывает появление электрического.

Если описать эти процессы математически, как это сделал Максвелл, то получится система уравнений, простейшим решением которой действительно будет синусоидальная волна. Эта волна поперечная, то есть возникающие при ее распространении поля направлены перпендикулярно направлению ее распространения. Математика там достаточно сложная, ею мы сейчас заниматься не будем. Воспользуемся готовым результатом: система уравнений решается, решение представляет собой волну, и экспериментально подтвердилось, что это решение достаточно точно описывает реальные электромагнитные волны (см. рис. 6).

Рис. 6. Электромагнитная волна

Какие у нас уже есть инструменты для описания волн? Длина волны, скорость распространения волны, а так как распространяются колебания, то и частота. Эти понятия применимы и к электромагнитным волнам, и означают они то же, что и для других волн. Скорость распространения волны – это скорость перемещения возмущения. Длина волны – это расстояние между соседними точками пространства, в которых параметры поля колеблются в одинаковой фазе. Частота – это частота колебаний параметров поля в данной точке (см. рис. 7).

Рис. 7. Характеристики электромагнитных волн

Для электромагнитных волн справедливо уравнение, полученное для механических волн:

Скорость электромагнитных волн в вакууме постоянна и равна приблизительно 300 000 км/с, эту постоянную обычно обозначают отдельной буквой, . В веществе эта скорость немного уменьшается, при этом уменьшается длина волны, а частота остается неизменной, об этом чуть позже. А скорость распространения электромагнитных волн – это вообще максимально возможная в природе скорость, ни один материальный объект не может двигаться с большей скоростью.

Урок 10. электромагнитные волны — Физика — 11 класс

В процессе эволюции у многих животных и даже у растений появились «приборы», улавливающие лучи от 300 до 900 нм, среди них – глаза. Электромагнитные волны в этой области спектра стали называть светом. Правда, с 300 нм видит только пчела, это ультрафиолетовый свет. Сколько бы мы ни рассматривали мельчайшие организмы, как бы тщательно ни изучали более крупных животных и человека, специальных рецепторов, воспринимающих радиочастотные электромагнитные волны, нам не найти. Мы не ощущаем их, хотя они и влияют на общее состояние человека. Видимо, сами живые клетки становятся приемниками волн различной длины. Чем меньше длина волны, тем отчетливее реагирует на них организм. У людей, в отличие от некоторых животных, которых природа наделила прекрасными термолокаторами, нет живых «приборов» ночного видения, способных воспринимать инфракрасные лучи, идущие от всего живого, даже от растений. А вот кровососущим, к примеру, в любое время дня и ночи нужно искать и находить добычу. Для них большое значение играют не видимые лучи, а инфракрасные, позволяющие дистанционно находить тела своих будущих жертв. Самый обычный постельный клоп обнаруживает объекты, имеющие температуру тела, на расстоянии нескольких метров. Другой кровосос – клещ – вооружен более совершенным термолокатором. Забравшись на кончик листа дерева или куста, он поднимает передние ножки и начинает ими водить в разные стороны. На ножках можно различить округлые образования – это и есть термолокаторы. Они воспринимают лучи за несколько метров от источника. Достаточно человеку высунуть голову из автомобиля, как клещ на расстоянии нескольких метров обнаруживает его и начинает двигаться в его сторону. В глубинах океана есть тоже много животных, пользующихся «приборами» ночного видения. Последние отблески света в воде гаснут на глубине 200 м, а жизнь продолжается на 10-километровой глубине. Одни существа зажигают в кромешной тьме свои биолюминесцентные «фонарики», другие предпочитают, оставаясь невидимыми, улавливать инфракрасный свет, идущий от всех живых существ. Глубоководные кальмары, кроме своих обычных глаз имеют ещё термоскопические глаза, улавливающие инфракрасные лучи. Каждый термоскопический глаз снабжён специальным светофильтром, задерживающим все лучи, кроме инфракрасных. Самое интересное то, что термоскопические глаза расположены у кальмара на хвосте. Вращая им, как головой, кальмар высматривает животных, которыми можно полакомиться. В Америке водятся чрезвычайно ядовитые гремучие змеи, а в Средней Азии щитомордники. У них на голове четыре ноздри. С каждой стороны одна нормальная, а вторая большая. Это большое углубление между глазом и ноздрей – термолокатор – своеобразный глаз – инфракрасная камера-обскура. Даже если её глаза закрыты, ямкоголовая змея, нанося удары по добыче, ошибается не более чем на 5 градусов. Казалось бы, термолокаторы, построенные человеком, более чувствительны, чем созданные природой. Но живой «прибор» на единицу термолоцирующей площади в несколько тысяч раз чувствительней.

Почему распространяются электромагнитные волны — Страна Знаний

Часть 1. О трёх силах, действующих в природе

В XIX веке было известно о трёх силах, действующих в природе: электрической, магнитной и гравитационной.

Вот что писал об этом в одной из своих работ основатель теории электромагнитного поля Джеймс Максвелл: «Уже древним был известен тот факт, что некоторые тела, будучи натерты, начинают притягивать другие тела…»

Джеймс Клерк Максвелл
(1831–1879)

Это явление было названо электричеством, так как янтарь – по-гречески электрон – был первым веществом, на котором наблюдалось такое явление.

Другие тела, в частности магнитный железняк и куски железа и стали, подвергнутые определённому воздействию, также с давнего времени известны как вещества, способные к действию на расстоянии.

Было установлено, что эти явления, включая и другие, связанные с ними, отличаются от электрических, они получили название магнитных – по названию Фессалийской Магнезии магнитного железняка».

Итак, о существовании электрической и магнитной сил в природе было известно с древних времён. Но неразрывная связь между ними была установлена только на рубеже XVIII и XIX веков экспериментальным путем тремя физиками – Эрстедом, Ампером и Фарадеем.

Опираясь на эти экспериментальные исследования, Дж. Максвелл сформулировал теорию электромагнитного поля сначала в статье «Динамическая теория электромагнитного поля» (1864 г.), а затем в обширном труде «Трактат об электричестве и магнетизме», опубликованном в 1873 году. Теория объяснила взаимодействие между электрическими и магнитными явлениями и установила связь оптики с электродинамикой.

Независимо от двух сил – электрической и магнитной – было известно и о третьей силе – гравитационной. Теорию гравитации, объяснившей движение планет и других тел Солнечной системы, в завершающем виде в 1686 году изложил Исаак Ньютон в фундаментальном труде «Математические начала натуральной философии».

Генрих Рудольф Герц
(1857–1894)

Понятие «гравитация», т.е. взаимное тяготение материальных тел, и сопутствующее ему понятие «гравитационные волны» родились примерно на 100 лет раньше понятий «электромагнитное поле» и «электромагнитные волны».

Но если с физическим понятием «электромагнитные волны» учёным удалось досконально разобраться, проверить их существование экспериментальным путем и использовать для самых разнообразных нужд, то с понятием «гравитационные волны» дело обстоит значительно сложнее. Причина здесь состояла в том, что мощность гравитационных волн ничтожно мала по сравнению с электромагнитными.

Считается, что экспериментально гравитационные волны удалось обнаружить только в сентябре 2016 года, подтвердив тем самым общую теорию относительности Эйнштейна о возможности существования гравитационных волн при ускоренном движении материи.

 Электрическое и магнитное поля. Радиотехника есть наука о методах и средствах передачи и приёма информации на расстоянии посредством электромагнитных волн, распространяющихся в свободном пространстве.

Поэтому одним из «краеугольных камней» фундамента радиотехники является теория электромагнитного поля, зародившаяся в середине XIX века. С экспериментального обоснования и изучения физических основ этой теории, объясняющей такие явления, как излучение и распространение электромагнитных волн, и началось становление радиотехники.

Итак, электромагнитные волны существуют, их научились генерировать, излучать, измерять, принимать, извлекать из них передаваемую с их помощью информацию и использовать для самых разнообразных нужд.

Электромагнитное поле разделяется на два взаимосвязанных поля: электрическое и магнитное. Одной из центральных проблем физики XIX века была проблема изучения свойств этих полей и их взаимодействия между собой.

Электрическое поле воздействует как на неподвижные, так и движущиеся электрические заряды, магнитное – только на движущиеся заряды. Силы, воздействующие на электрические заряды со стороны электромагнитного поля, являются направленными, и поэтому могут быть описаны с помощью векторов.

Напомним, что в математике вектором называют отрезок, имеющий определённую длину и направление. В трёхмерной декартовой системе координат вектор описывается тремя проекциями на оси 0x, 0y, 0z (Рис. 1) :

(1)

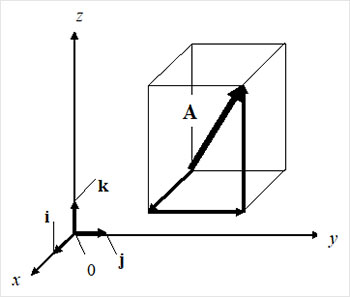Рис. 1

где i, j, k – единичные векторы (орты) вдоль осей,

a_x , a_y , a_z – скаляры, прямоугольные декартовые координаты вектора A , являющиеся проекциями этого вектора на координатные оси 0x, 0y, 0z.

Совокупность векторов образует векторное поле, которое графически изображается с помощью силовых линий – пространственных кривых, в каждой точке которых вектор направлен вдоль касательной.

Скалярное поле, определённое только для точек некоторой плоскости, называется плоским.

Введём величины, известные из школьного курса физики, определяющие электрическое и магнитное поля, которыми нам дальше придётся пользоваться:
E – напряжённость электрического поля, размерность В/м;
H – напряжённость магнитного поля, размерность А/м;
q – электрический заряд, размерность Кл = А∙с.

Напомним обозначения, принятые в практической системе единиц СИ:
В – вольт; А – ампер; Кл– кулон; м – метр; с – секунда.

Электрические свойства среды характеризуются абсолютной диэлектрической постоянной:

где ε₀ =8,85∙10^–12   Кл / (В∙м) – электрическая постоянная,

ε_М –относительная диэлектрическая электрическая постоянная среды, в вакууме ε_М=1.

Магнитные свойства среды характеризуются абсолютной магнитной постоянной:

где μ₀ =1,257∙10^–6   В∙ с/ (А∙м )=Гн/м – магнитная постоянная;

μ_М – относительная магнитная постоянная среды, в вакууме μ_М =1.

В каждый момент времени в любой точке пространства электромагнитное поле описывается вектором напряжённости электрического поля E и магнитного поля H

Результаты опытов позволили установить закономерности, связанные с электромагнитными явлениями, и описать электрические и магнитные поля. В этих полях линии вектора E называются электрическими силовыми линиями, а линии вектора H – магнитными. Рассмотрим несколько примеров электрических и магнитных полей.

Электрическое поле неподвижных зарядов. Такое поле является электростатическим, т.е. не изменяющимся во времени.

а) Электростатическое поле одиночного положительного и отрицательного заряда представлено на рис. 2,а. Численное значение напряжённости такого поля определяется выражением:

(4)

где q – величина заряда, r – расстояние от заряда до исследуемой точки поля.

б) Электростатическое поле между двумя плоскими металлическими пластинами с зарядами разной полярности приведено на рис. 2,б. Линии в таком однородном электрическом поле параллельны.

в) Электростатическое поле двух равных по величине разноимённых зарядов +q и —q приведено на рис. 2, в.

г) Электростатическое поле электрического диполя, т.е. звена из двух близлежащих равных по величине точечных разноименных зарядов +q и —q , приведено на рис. 2, г.

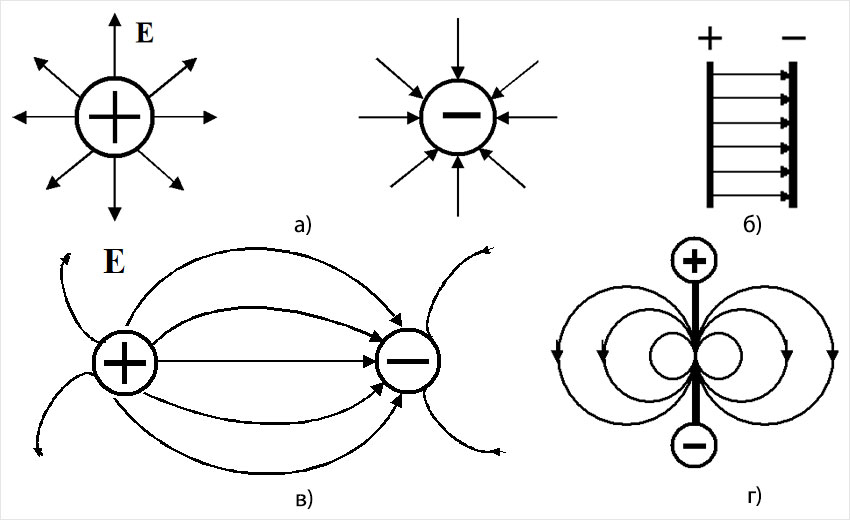Рис. 2

Магнитное поле постоянного магнита. Такое поле стержневого магнита представлено на рис. 3. Оно является магнитостатическим, т.е. не изменяющимся во времени. Магнитные силовые линии всегда замкнуты, и вне магнита они направлены от северного полюса к южному.

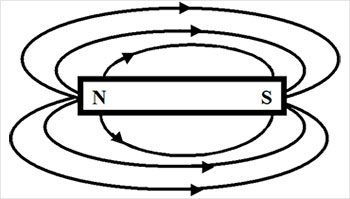Рис. 3

Экспериментальные исследования показывают, что электростатическое поле не влияет на магнитное, а статическое магнитное – на электрическое. Образно говоря, они «сохраняют свою индивидуальность независимо от других».

Магнитное поле проводника с током. Об электричестве и магнетизме было известно с древних времён. Так, янтарь был первым материалом, на котором были обнаружены электрические заряды. По его имени («янтарь» по-гречески звучит как «электрон») и было названо данное физическое явление.

Другие вещества, как, например, куски железной руды, обнаруживали свойство действовать на расстоянии, притягивая к себе другие подобные тела. Данное явление получило название «магнетизм». Но связь между электричеством и магнетизмом была установлена только в начале XIX века физиком Хансом Кристианом Эрстедом (1777–1851).

Последний экспериментально установил, что протекание по проводнику электрического тока сопровождается возникновением в окружающем пространстве магнитного поля, что было обнаружено им случайно по отклонению магнитной стрелки компаса, находящегося вблизи провода.

Далее другой физик – Андре-Мария Ампер (1775–1836) – разработал теорию такого магнетизма, а в 1822 году открыл существование магнитного поля соленоида.

В случае прямолинейного проводника силовые линии магнитного поля имеют вид концентрических окружностей (рис. 4,а), в случае соленоида, т.е. спирали из проволоки, – замкнутых искривленных линий (рис. 4,б).

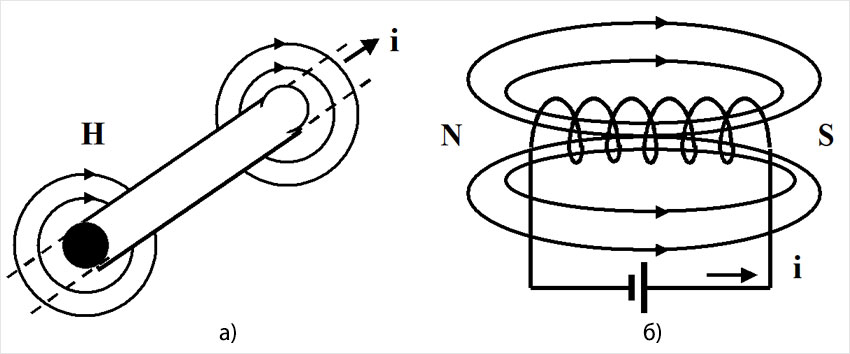Рис. 4

Таким образом, опытным путём было установлено, что:

1. Пока электрический заряд неподвижен, существует только электростатическое поле (рис. 2),
2. Движение тех же зарядов, обуславливающих электрический ток, всегда сопровождается возникновением магнитного поля (рис. 4). Первым данное явление открыл датский физик Ханс Кристиан Эрстед.

Майкл Фарадей
(1791–1867)

Опыты Фарадея и закон электромагнитной индукции. На основании изложенного можно предположить, что поскольку движение заряда и связанное с ним изменение электрического поля приводят к образованию магнитного поля, то должно существовать и противоположное явление: образование электрического поля при изменении магнитного.

Именно этой идеей руководствовался великий английский физик-экспериментатор Майкл Фарадей (1791–1867), приступая к своим опытам по обнаружению взаимосвязи электрического и магнитного полей.

Вот что он писал по поводу взаимодействия электрических и магнитных сил: «Было бы чрезвычайно важно решить вопрос о том, тождественны или различны силы этих двух видов, и установить их истинное взаимоотношение. Этот вопрос, по-видимому, вполне доступен опыту и сулит богатую награду тому, кто попытается её разрешить».

Сам же Фарадей и нашёл ответ на поставленную им задачу, проведя серию опытов. Здесь уместно заметить, что Фарадей, как сотрудник Королевского института Великобритании, результаты проводимых им опытов по зародившейся в XIX веке науке об электричестве и магнетизме регулярно публиковал в журнале «Philosophical Transaction», а затем собрал воедино изданные им статьи в одну книгу с названием «Experimental Researches in Electricity by Michael Faraday, D.C.L.F.P.S», полностью изданной в Великобритании в 1931 г.

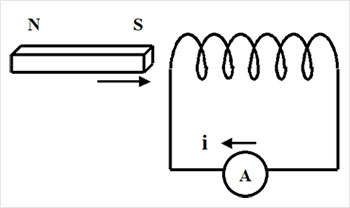Рис. 5а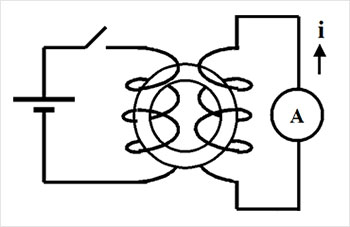Рис. 5б

Этот величайший по своему значению для науки фундаментальный труд в течение десяти лет, с 1947 по 1957 гг., был издан в трёх томах на русском языке под названием «Экспериментальные исследования по электричеству».

В этих трёх томах собрано и описано в общей сложности 7192 опыта, объединённых в виде 14 серий, четыре из которых посвящены электромагнитной индукции. В книгу включены и письма Фарадея к разным учёным.

Два обстоятельства поражают при чтении дневника Фарадея – его исключительная работоспособность и преданность физике и тщательное, буквально филигранное проведение каждого опыта с его подробным описанием.

Вот как сам Фарадей описывает свой опыт (см. рис. 5,а), приведший к открытию закона электромагнитной индукции: «Я взял цилиндрический магнитный брусок (3/4 дюйма в диаметре и 8,5 дюйма длиной) и ввёл один его конец внутрь спирали из медной проволоки (220 футов длиной), соединённой с гальванометром. Потом я быстрым движением втолкнул магнит внутрь спирали на всю его длину, и стрелка гальванометра испытала толчок. Затем я так же быстро вытащил магнит из спирали, и стрелка опять качнулась, но в противоположную сторону. Эти качания стрелки повторялись всякий раз, как магнит вталкивался или выталкивался».

На основании полученного экспериментальным путём результата Фарадей приходит к следующему заключению: «…электрическая волна возникает только при движении магнита, а не в силу свойств, присущих ему в покое».

Таким образом, Фарадеем было установлено: всякий раз при изменении положения магнита – его вводе или выводе из соленоида – в замкнутой электрической цепи возникает ток, регистрируемый амперметром (в XIX веке такой прибор называли гальванометром) (рис. 5,а). Следовательно, изменение магнитного поля, обусловленное движением магнита, приводит к возникновению тока в замкнутой цепи, т.е. образованию электрического поля.

Данное явление, которому была придана математическая форма, получило название закона электромагнитной индукции.

Согласно ему, в случае размещения в магнитном поле разомкнутого проволочного витка, индуцируемое в нём напряжение электродвижущей силы (ЭДС) численно равно и противоположно по знаку скорости изменения магнитного потока Ф сквозь поверхность, ограниченную этим витком (рис. 6,а):

(5)

где F= m H S cos α – магнитный поток, пронизывающий виток, S – площадь поперечного сечения витка.

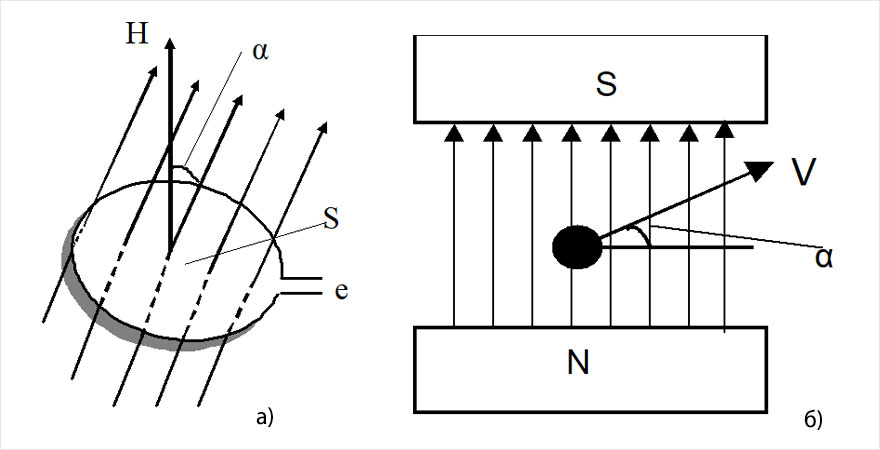Рис. 6

Согласно (5), только при изменении магнитного поля, когда производная dF ∕dt ≠ 0, происходит появление электрического поля. В случае размещения в магнитном поле спирали из N витков, напряжение ЭДС увеличится в то же число раз, и формула (5) принимает вид:

(6)

В постоянном магнитном поле индуцировать напряжение в проводе можно только путём его перемещения (рис. 6,б). Поскольку проводник длиной l при движении с постоянной скоростью V в магнитном поле за время Δt покроет площадь Δ S = l V Δt, то, согласно (5), получим:

Наряду с индукцией Фарадей открыл и явление самоиндукции, состоящее в наведении ЭДС напряжения в проводнике при изменении тока в другом близлежащем проводнике, например, за счёт периодического замыкания и размыкания цепи (рис. 5,б).

Всякий раз при замыкании и размыкании ключа в первой цепи, т.е. при изменении в ней тока, во второй цепи по отклоняющейся стрелке амперметра регистрировалось кратковременное протекание тока.

Чем сильнее была связь между цепями – двумя изолированными друг от друга отрезками проводов, намотанных на железное кольцо, тем больший ток протекал во второй цепи. Объяснение данного явления состоит в том, что изменяющееся магнитное поле в электрической цепи с ключом индуцирует ЭДС напряжения в другом проводнике.

Таким образом, в данном случае имеют место оба явления взаимодействия электрического и магнитного полей: в цепи с ключом изменяющееся электрическое поле создаёт изменяющееся магнитное поле, которое, в свою очередь, в индуцирует в расположенной рядом цепи электрическое поле.

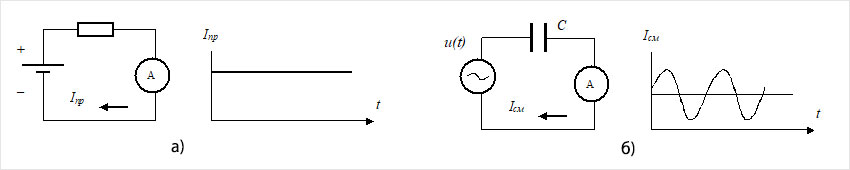Рис. 7

Максвелл и теория электромагнитного поля. Проведём опыт с измерением тока в двух электрических цепях: с резистором и конденсатором (рис. 7).

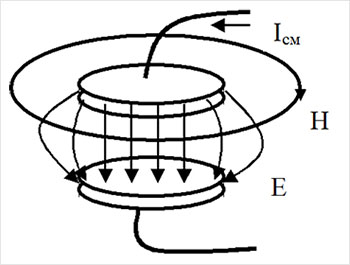Рис. 8

В первой из цепей (рис. 7,а) протекает ток проводимости I_пр, представляющий собой упорядоченное движение электрических зарядов. Вторя цепь разорвана (рис. 7,б) и поэтому в ней невозможно непрерывное движение электрических зарядов, т.е. нет тока проводимости I_пр.

Однако, опытным путем можно установить, что в такой цепи с конденсатором все же возможно протекание тока, но только переменного и, следовательно, отличного от тока проводимости.

Как было сказано выше, протекание тока проводимости сопровождается образованием магнитного поля, силовые линии которого в виде колец образуют своеобразную оболочку вокруг проводника (рис. 4,а). Однако, такая «оболочка» не обрывается у пластин конденсатора, а продолжает существовать, окружая линии переменного электрического поля конденсатора кольцевыми линиями магнитного поля (рис. 8).

Часть 2 в следующем номере

В.И. Каганов, доктор технических наук, профессор МИРЭА

электромагнитные волны (билет 10)

Квинтэссенции рефератов для подготовки к экзамену по ФОЗИ.

Выполнил студент группы ЗИ-22 Сахау Азат.

7) Электромагнитные волны.

Электромагнитная волна представляет собой процесс распространения в пространстве изменяющихся электрического и магнитного полей.

Существование электромагнитных волн было теоретически предсказано Максвеллом. Экспериментально электромагнитные волны были открыты и изучены Герцем.

Основными свойствами электромагнитных волн являются:

.

1. поглощение;

2. рассеяние;

3. преломление;

4. отражение;

5. интерференция;

6. дифракция;

7. поляризация;

Электромагнитные волны и их характеристика.

Электромагнитная волна представляет собой процесс распространения в пространстве изменяющихся электрического и магнитного полей.

Существование электромагнитных волн было предсказано английским физиком Майклом Фарадеем. В 1831 году Фарадей открыл явление электромагнитной индукции — возбуждение электрического тока в замкнутом проводящем контуре, находящемся в переменном магнитном поле. Он является основоложником учения об электромагнитных явлениях, в котором электрические и магнитные явления рассматриваются с единой точки зрения. С помощью многочисленных опытов Фарадей доказал, что действие электрических зарядов и токов не зависит от способа их получения.

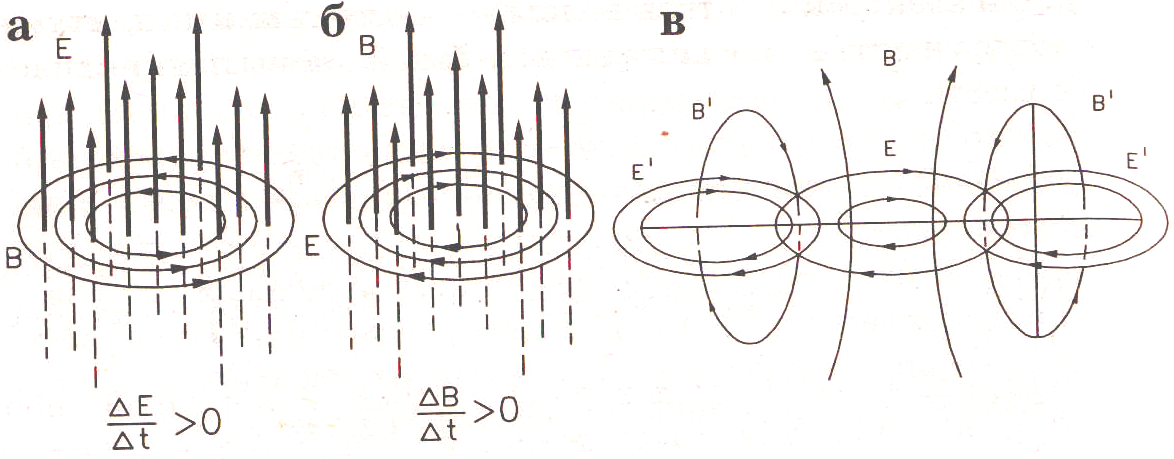
Взаимопревращения электрического и магнитного полей

 Согласно теории Максвелла, в каждой точке пространства изменение электрического поля создает переменное вихревое магнитное поле, вектора В магнитной индукции которого лежат в плоскости, перпендикулярной к вектору Е напряженности электрического поля. Механическое уравнение, выражающее эту закономерность, называется первым уравнением Максвелла. Изменение во времени индукции магнитного поля создает переменное вихревое электрическое поле, векторы Е напряженности которого лежат в плоскости, перпендикулярной к вектору В. Математическое уравнение, описывающее эту закономерность, называется вторым уравнением Максвелла. Из уравнения Максвелла следует, что возникшее в какой-либо точке изменение во времени магнитного (или электрического) поля будет перемещаться от одноц точки к другой, при этом будут происходить взаимные превращения этих полей, т.е. будет происходить распространение электромагнитных взаимодействий в пространстве.

В 1865 году Дж. Максвелл теоретически доказал, что электромагнитные колебания распространяются в вакууме с конечной скоростью, равной скорости света: с = 3 * 10^8 м/с.

В 1888 году электромагнитные волны были впервые экспериментально обнаружены немецким физиком Генрихом Герцем (1857-1894), что сыграло решающую роль для утверждения максвелловской теории электромагнитных волн.

Таким образом, электромагнитные волны — это электромагнитные колебания, распространяющиеся в пространстве с конечной скоростью.

Длина электромагнитной волны — расстояние между двумя ближайшими точками, в которых колебания происходят в одинаковых фазах.

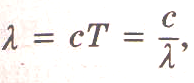где — длина волны; с — скорость света в вакууме; Т — период колебаний; v — частота колебаний. Скорость света в вакууме с= 3 * 10^8 м/с.

При распространении электромагнитных волн в какой-либо другой среде скорость волны изменяется и длина волны , где u — скорость волны в среде. В атмосфере скорость практически можно принять равной скорости света в вакууме.

Скорость u электромагнитной волны в среде определяется из формулы Максвелла:

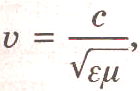где е — относительная диэлектрическая проницаемость среды, — относительная магнитная проницаемость среды.

Скорость распространения электромагнитных волн в данной среде совпадает со скоростью света в этой среде, что является одним из обоснований электромагнитной природы света.

Основная характеристика электромагнитных волн — это частота их колебаний v (или период Т). Длина волны л меняется при переходе из одной среды в другую, в то время как частота остается неизменной. Электромагнитные волны являются поперечными волнами.

Распространение электромагнитных волн связано с переносом энергии электромагнитного поля волны, которая переносится в направлении распространения волны, т.е. в направлении вектора v. Наряду с энергией электромагнитная волна обладает импульсом. Если волна поглощается, то ее импульс передается тому объекту, который ее поглощает.

 Отсюда следует, что при поглощении электромагнитная волна оказывает давление на преграду.

Плотностью потока электромагнитного излучения I (интенсивностью электромагнитной волны) называют отношение электромагнитной энергии W, проходящей за время t через перпендикулярную лучам поверхность площадью S, к произведению площади S на время t:

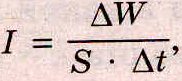где W — электромагнитная энергия, прошедшая за время t через поверхность площадью S.

Единицей измерения интенсивности электромагнитного излучения I является ватт на м [вт/м ].

Плотность потока излучения (интенсивность электромагнитной волны) равна произведению плотности электромагнитной энергии на скорость её распространения:

где — магнитная постоянная в СИ.

Интенсивность электромагнитной волны пропорциональна среднему значению произведения модулей векторов Е и В электромагнитного поля, т.е. пропорциональны квадрату напряженности Е: