1. Трехмерное пространство. Векторы. Линейные операции над векторами.
1
Определение. Вектором AB называется направленный отрезок с началом в точке А и с концом в точке В.
Краткости ради, будем обозначать вектор одной буквой; например,
a = AB (рис.2), и называть его, когда это необходимо, одномерным при n=1, двумерным при n=2 и трехмерным при n=3.
Начало вектора называют также его точкой приложения. Вектор BA называется противоположным вектору AB и обозначается − a
|
| B |
|
|
| A |
|
|
|
| − |
|
|
a |
| a | ||||
A | B |
|
| Рис. | ||
|
|
|
|
|
| |
Длиной вектора AB называется длина отрезка АВ и обозначается AB
или |
| a |
| . Длина вектора называется также модулем вектора. |
|
|
| |||||||||||||||||||||||
|
|
|
|
|
| Если точки А и В совпадают, то вектор называется нулевым |
| и обо- | ||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
| =1, то вектор |
| называется единичным. |
|
|
| ||||||||||||
значается |
| . Если |
| a |
|
|
|
|
| |||||||||||||||||||||
|
|
| a |
|
|
| ||||||||||||||||||||||||
0 |
|
|
| |||||||||||||||||||||||||||
|
|
|
|
|
| Два вектора |
| и |
| называются коллинеарными, если они лежат на | ||||||||||||||||||||
|
|
|
|
|
| a | b | |||||||||||||||||||||||
одной прямой или параллельны одной прямой (рис. |
|
|
| |||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
| l1 |
|
|
|
|
|
|
|
|
|
| a |
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| b |
|
|
| |||||||
|
|
|
|
|
|
|
| l2 |
|
|
| |||||||||||||||||||
|
|
| b |
|
|
|
|
|
|
| ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| b | |||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| Рис | c | . |
|
|
|
|
|
|
|
| Рис4. |
|
| Рис.5 |
|
|
| ||||
|
|
|
|
| Два вектора называются одинаково направленными | ( про- | ||||||||||||||||||||||||
тивоположно |
| направленными ) , | если они коллинеарны и распола- | |||||||||||||||||||||||||||
гаются по одну сторону (по разные стороны) прямой, проходящей через начала этих векторов (рис.4), (рис.5).
Определение. Два вектора a и b называются равными, если они имеют равные длины и одинаковые направления; при этом пишут: a =b .
Из этого определения вытекает, что если вектор a перемещать в Rn параллельно самому себе, сохраняя его длину и направление, то получим тот же
вектор a .
В частности, коллинеарные векторы всегда можно расположить на одной прямой.
2
Определение. Три вектора называются компланарными, если они лежат в одной плоскости или параллельны одной плоскости.
Очевидно, компланарные векторы всегда можно расположить в одной плоскости (рис.6).
a
b
c
Рис.6
|
|
|
| Определение. Суммой двух | векторов | a | и | b |
| называется вектор | |||||
| c | = | a | + | b | , идущий из начала вектора | a |
| в конец вектора | b | , при условии, что | ||||
вектор b приложен к концу вектора a (рис.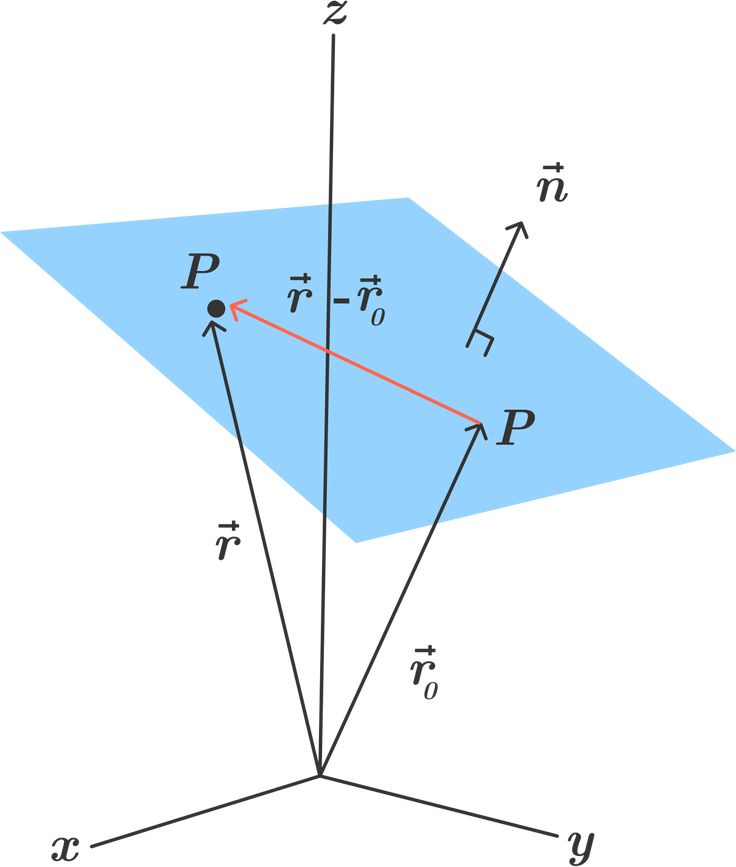 7) (правило треугольника). a
7) (правило треугольника). a
|
| a + |
|
| b | b |
b
a
Рис.7
Очевидно, если векторы a и b приложить к общему началу, то вектор a +b есть диагональ параллелограмма, построенного на этих векторах как на сторонах, выходящих из общего начала векторов a и b (рис.7) (правило параллелограмма).
Легко проверить следующие свойства суммы векторов:
1)a +b =b + a ; 2) (a +b) + с = a + (b + c) ; 3)a + 0 = a ; 4)a + (−a) = 0 .
Сумма любого числа векторов может быть построена при помощи следующего правила, вытекающего из определения суммы двух векторов.
Общее правило сложения векторов. Чтобы построить сумму векторов а1,а2,…,ап, нужно к концу вектора а1 приложить вектор а2, затем к концу вектора а2 приложить вектор а3 и так далее, пока не дойдем до вектора ап. Тогда суммой а1+а2+. ..+ап будет вектор, идущий из начала вектора а1 в конец вектора аn (рис.8).
..+ап будет вектор, идущий из начала вектора а1 в конец вектора аn (рис.8).
a4
a3
a5
3
Рис. 8
Определение. Вектор с = в-а называется разностью векторов в и а, если а+с = в
b | b − a |
|
a
(рис.9).
Из рис.9 видно, что разность двух векторов, приведенных к общему началу, есть вектор, идущий из конца вектор-вычитаемого в конец векторуменьшаемого.
Определение. Произведением вектора а на вещественное числоα называется вектор b = αa , который имеет длину b = αa , одинаково направ-
лен с вектором а, еслиα >0, и противоположно направлен вектору а, если
α <0 .
Итак, вектор αa — это вектор, коллинеарный вектору а и растянутый в α раз («растянутый» в широком смысле этого слова). При этом под вектором 0а понимается нулевой вектор 0.
Теорема. Если вектор в коллинеарен ненулевому вектору а, то существует вещественное число α такое, что в = αа.
Операции сложения векторов и произведения вектора на число связаны следующими условиями:
5)(α +β) а = αа+βа;
6)α(βа) = (αβ)а;
7)α(а+в) = αа+αв.
Свойства 5)-7) геометрически очевидны.
Рассмотрим вектор (-1)а. На основании свойства 5) имеем: а+(-1)а=0; из свойства (4) следует, что вектор (-1)а есть вектор -а, противоположный вектору а.
3. Базис. Разложение вектора по базису.
4
Определение. Упорядоченная пара (а,в) двух ненулевых двумерных векторов а и в называются базисом числовой плоскости R2, если для любого вектора с R2 существуют такие числа αи β, что справедливо представле-
ние |
|
c = αa +βb | (1) |
|
При этом числа α и β называются аффинными координатами вектора с в базисе (а,в), а равенство (1) называется разложением вектора с по базису (а,в).
Определение. Упорядоченная тройка (а,в,с) трех ненулевых трехмерных векторов а,в,с называется базисом числового пространства R3 , если для любо-
Упорядоченная тройка (а,в,с) трех ненулевых трехмерных векторов а,в,с называется базисом числового пространства R3 , если для любо-
го вектора с R3 существуют такие вещественные числа α,β,γ , что спра-
ведливо равенство |
|
d = αа+βв+ γ c | (2) |
При этом числа α,β,γ называются аффинными координатами вектора d в базисе (а, в, с), а равенство (2) называется разложением вектора d по базису (а, в,
с).
Рассмотрим важные частные случаи базиса.
1. Пусть i,j — единичные двумерные векторы, лежащие на осях координат соответственно OX и OY. Так как они неколлинеарны, то (i,j) — базис пространства R2. Тогда, для любого вектора с R2 существуют такие числа с1 и с2, что имеет место равенство
с = с1i+c2j,
которое записывается короче: с = (с1,с2).
Найдем координаты векторов i и j в базисе (i,j).
Пусть i = (i1,i2), j = (j1,j2). Тогда
Тогда
i = i1i+i2j, j = j1i+j2j.
Откуда получаем: i1 = 1, i2 = 0, j1 = 0, j2 = 1; то есть i = (1,0), j = (0,1).
Базис (i,j) называется прямоугольным базисом в пространстве R2. 2. Пусть i,j,k — единичные трехмерные векторы, лежащие на осях ко-
ординат соответственно OX,OY,OZ. Так как они некомпланарны, то (i,j,k) — базис пространства R3. Тогда, для любого вектора с R3 существуют такие числа с1,с2,с3, что имеет место равенство
с = с1i+c2j+с3k,
которое записывается короче: с = (с1,с2,с3).
Аналогично, для координат векторов i,j,k в базисе (i,j,k) имеем: i = (1,0,0), j = (0,1,0), k = (0,0,1).
Базис (i,j,k) называется прям оугольным базисом в пространстве R3. Основное значение базиса состоит в том, что линейные операции над векторами при задании базиса становятся обычными арифметическими операциями над числами — координатами этих векторов. Именно справедлива следующая
теорема.
Теорема. При сложении двух векторов, разложенных по одному и тому же базису, их координаты складываются. При умножении вектора на число все его координаты умножаются на это число.
При умножении вектора на число все его координаты умножаются на это число.
5
Например, в прямоугольном базисе для векторов а=(2,3,-1), в=(3,0,1) име-
ем: 2а+3в=(13, 6, 1).
Пусть в некотором пространстве заданы произвольная ось Т и вектор АВ. Обозначим буквами А1 и В1 основания перпендикуляров, опущенных на ось т из точек А и В соответственно (рис.13).
B B
A A
T
O
B1 | A1 | A1 | B1 |
Рис.13
Определение. Проекцией вектора АВ на ось т называется величина вектора А1В1, то есть длина вектора А1В1, если ось т и вектор А1В1 одинаково направлены и длина вектора А1В1, взятая со знаком минус, если ось т и вектор А1В1 противоположно направлены.
Пусть а=АВ. Проекцию вектора а на ось т обозначают символом — прmа. Выясним геометрический смысл координат вектора в прямоугольном ба-
зисе.
Пусть a вектор из пространства R2 , в котором задана прямоугольная сис-
тема координат OXY, и пусть а1 | = прха и а2 = пруа проекции вектора а на оси | |||
OX и OY соответственно. |
|
| ||
|
| а = а1i+а2j |
| (9) |
y |
|
|
|
|
B2 |
| B |
|
|
|
|
|
| |
a2j |
|
|
|
|
A2 |
| A |
|
|
|
|
|
| |
j |
| a1i |
|
|
| i | A1 | B1 | x |
|
| Рис. |
|
|
Аналогично, если а — трехмерный вектор и а1 | = прха, а2 = пруа, а3 = прzа | |||
проекции этого вектора на оси OX, OY, OZ соответственно, то имеем (рис.15): | ||||
| а = а1i+a2j+a3k |
| (10) | |
|
| 6 |
|
| z |
| C1 |
|
|
| A |
| O | y |
|
| B1 |
x | A1 |
|
Рис. 15 Из формул (9) и (10) вытекает геометрический смысл координат вектора:
координаты вектора в прямоугольном базисе являются проекциями этого вектора на соответствующие оси.
Из теоремы Пифагора вытекают формулы для длины вектора:
|
|
|
| a |
| = | a1 | 2 +a2 | 2 — для двумерного вектора; | (11) | |
|
|
|
|
| |||||||
| a |
| = a 2 | +a 2 | +а 2 | — для трехмерного случая. | (12) | ||||
|
| ||||||||||
|
|
| 1 |
|
|
| 2 | 3 |
|
| |
Определение. Углом наклона вектора а к оси m называется уголϕ
Углом наклона вектора а к оси m называется уголϕ
между двумя выходящими из произвольной точки М лучами, один из которых имеет направление вектора а, другой — направление оси m (рис16).
B
ϕ
A
M
m
Рис.16
Теорема. Проекция вектора а на ось m равна длине вектора а, умноженной на косинус ϕ угла наклона вектора а к оси m, то есть
прmа = |
| асosϕ. | (13) |
|
Определение. Направляющими косинусами вектора а называются косинусы углов наклона α,β, γ к осям соответственно OX, OY, OZ, то
есть числа cosα,cosβ,cosγ.
Для трехмерного вектора а=(а1,а2,а3), заданного прямоугольными координатами, формула (13) дает формулы, выражающие координаты вектора а
через его длину и направляющие косинусы: |
|
a1 = a cosα, a2 = a cosβ, a3 = a cos γ. | (14) |
Вектор — трехмерное пространство — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Векторы трехмерного пространства ( а также векторы плоскости, определяемые аналогично) можно складывать между собой и умножать на числа. [1]
Все векторы трехмерного пространства, концы которых не лежат на данной прямой. [2]
Кольцо Ли образуют векторы трехмерного пространства с обычным сложением и векторным умножением. Кольцом Ли является и всякое кольцо с нулевым умножением. Оба эти утверждения проверяются непосредственным подсчетом. [3]
Пространственные составляющие 4-вектора образуют некоторый вектор трехмерного пространства, так как преобразование Лоренца с коэффициентами а / а а 4 0, а44 1 есть обычный пространственный поворот, влияющий только на пространственные составляющие 4-вектора. Обратное утверждение будет, однако, неверным: составляющие вектора трехмерного пространства не обязательно преобразуются как пространственные составляющие 4-вектора. Составляющие обычного вектора можно умножить на любую функцию р, не изменяя характера их преобразования при пространственном повороте. Но при этом существенно меняется характер того преобразования, которому подвергаются эти составляющие при преобразовании Лоренца.
[4]
Составляющие обычного вектора можно умножить на любую функцию р, не изменяя характера их преобразования при пространственном повороте. Но при этом существенно меняется характер того преобразования, которому подвергаются эти составляющие при преобразовании Лоренца.
[4]
Фундаментальным математическим понятием, обобщающим понятие множества векторов трехмерного пространства, является линейное пространство, — понятие более общее и абстрактное, чем n — мерное координатное линейное пространство. Однако при первоначальном изучении полезно иметь дело с n — мерным координатным линейным пространством, поскольку это понятие, с одной стороны, проще и, с другой стороны, достаточно для исследования широкого круга проблем. [5]
Понятие равенства, а также линейные операции над векторами трехмерного пространства, если их записать через координаты, полностью совпадают с соответствующими понятием и действиями над строками из трех элементов ( см. гл.
[6]
гл.
[6]
Цветовое уравнение (2.15) показывает, что цвет может быть представлен как вектор SS трехмерного пространства. Проекции вектора на оси координат, задаваемые единичными векторами R, G, В, соответственно равны R, G, В. [7]
Разумеется, речь идет лишь о некоторых условных понятиях, аналогичных по своим свойствам длине вектора трехмерного пространства и углу между векторами в трехмерном пространстве. [8]
В основе учения о цвете ( см. § 2.8) лежит представление о его математическом выражении как векторе трехмерного пространства, а о цветности, отражающей только цветовые ощущения, — как двумерном числе, которое может быть отображено точкой на плоскости. [9]
Результаты, полученные в п п 2 — 7, дают нам право в дальнейшем оперировать с плоскостями, прямыми и векторами комплексного трехмерного пространства так, как если бы это были обыкновенные плоскости, прямые и векторы обыкновенного ( вещественного) пространства. [10]
[10]
На плоскости можно найти два линейно независимых вектора, но уже всякие три вектора линейно зависимы. Если R — совокупность векторов трехмерного пространства, то три линейно независимых вектора в R найти можно, но всякие четыре вектора линейно зависимы. [11]
Если в некотором множестве G для любых двух элементов а, Ъ определен элемент а — — Ь, удовлетворяющий свойствам 1 — 4, то говорят, что задана абелгва группа. Таким образом, множество L3 векторов трехмерного пространства является абелевой группой. [12]
Пространственные составляющие 4-вектора образуют некоторый вектор трехмерного пространства, так как преобразование Лоренца с коэффициентами а / а а 4 0, а44 1 есть обычный пространственный поворот, влияющий только на пространственные составляющие 4-вектора. Обратное утверждение будет, однако, неверным: составляющие вектора трехмерного пространства не обязательно преобразуются как пространственные составляющие 4-вектора.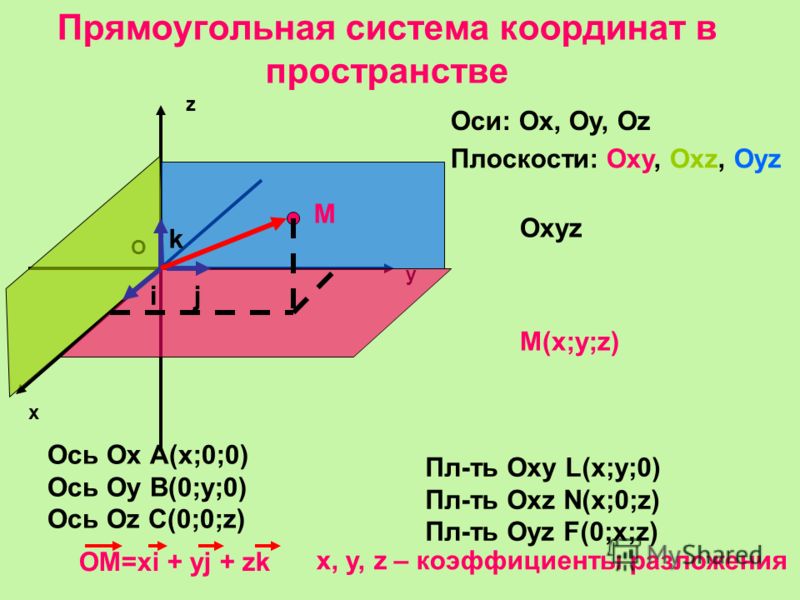 Составляющие обычного вектора можно умножить на любую функцию р, не изменяя характера их преобразования при пространственном повороте. Но при этом существенно меняется характер того преобразования, которому подвергаются эти составляющие при преобразовании Лоренца.
[13]
Составляющие обычного вектора можно умножить на любую функцию р, не изменяя характера их преобразования при пространственном повороте. Но при этом существенно меняется характер того преобразования, которому подвергаются эти составляющие при преобразовании Лоренца.
[13]
Например, все столбцовые матрицы третьего порядка изоморфны по сложению с векторами трехмерного пространства. Сложение векторов определено по правилу параллелограмма. [14]
Эти примеры указывают на целесообразность рассмотрения совокупности всевозможных упорядоченных систем из п действительных чисел. Эта совокупность после введении в нее операций сложения и умножения на число ( что будет сделано ниже по аналогии с соответствующими операциями над векторами трехмерного пространства, выраженными через компоненты) и носит название л-мер-ного векторного пространства. Таким образом, л-мерное пространство есть лишь алгебраическое образование, сохраняющее некоторые простейшие свойства совокупности векторов трехмерного пространства, выходящих из начала координат. [15]
[15]
Страницы: 1 2
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному… Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории… Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов. Мероприятия для защиты от морозного пучения грунтов: Инженерная защита от морозного (криогенного) пучения грунтов необходима для легких малоэтажных зданий и других сооружений… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 5 из 5 Полагая, что понятия плоскости и трехмерного пространства известны читателю из школьного курса геометрии, обобщим, а в некоторых случаях уточним, начальные сведения о векторах. Векторомназывается направленный отрезок с начальной точкой A и конечной точкой B, который можно перемещать параллельно самому себе. Обозначение: или . Длиной (модулем, нормой) вектора называется число, равное длине отрезка AB, изображающего вектор. Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых, и компланарными, если их количество равно трем и они лежат в одной плоскости или на параллельных плоскостях. Если точки начала и конца вектора совпадают, например, то такой вектор называется нулевым вектором и обозначается: . Длина нулевого вектора равна нулю, т.е. . Поскольку направление нулевого вектора не определено, то его считают коллинеарным любому вектору. Произведением вектора на число λ называется вектор: имеющий длину и направление, совпадающее с направлением вектора если λ > 0, и противоположное ему, если λ < 0. Противоположным вектором вектору называется произведение этого вектора на число (− 1), т.е. .
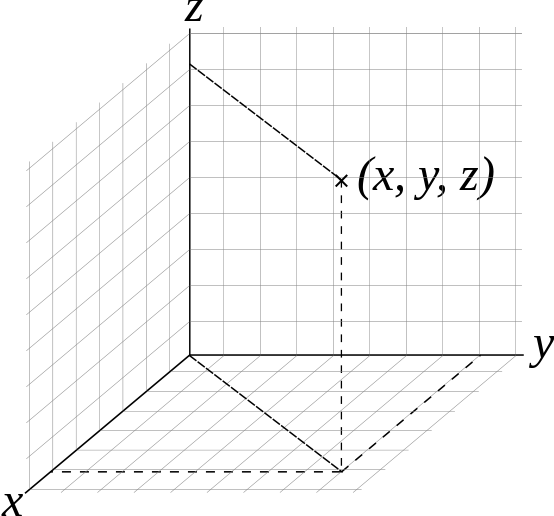
Перенесем вектор параллельно самому себе таким образом, чтобы его начальная точка совпала с началом координат. Тогда можно ввести понятие координат вектора. Координатами вектора называются координаты его конечной точки, если его начальная точка помещена в начало координат. При этом координатами вектора на плоскости являются числа , где M(x, y), а в трехмерном пространстве – соответственно – числа , где M(x, y, z).
В соответствии с приведенными определениями не трудно показать, что суммой векторов и будет вектор с координатами: , произведением вектора на число l будет вектор с координатами: . Из тех же определений следует, что длина вектора равна квадратному корню из суммы квадратов его координат: или . соответственно, на плоскости и в трехмерном пространстве.
Скалярным произведением двух векторов называется число (скаляр), равное произведению длин этих векторов на косинус угла j между ними, т.е.: . Скалярное произведение векторов можно выразить и через координаты этих векторов: или . соответственно, на плоскости и в трехмерном пространстве. Если , то очевидно угол между векторами и будет равен нулю, следовательно: , т.е. скалярный квадрат вектора равен квадрату его длины. Очевидно, что косинус угла между векторами будет определяться выражением:
3.2. N-мерный вектор и векторное пространство Определение. N-мерным вектором называется упорядоченная совокупность n действительных чисел: а каждое число хi называется i-ой компонентой(координатой) вектора.
По аналогии с векторами на плоскости (двухмерными векторами) и в трехмерном пространстве (трехмерными векторами) можно сформулировать следующие правила, которые следует рассматривать как аксиомы.
Два n-мерных вектора равнытогда и только тогда, когда равны их соответствующие компоненты, т.е. , если для всех . Суммой двух n-мерных векторов называется n-мерный вектор, компоненты которого равны сумме соответствующих компонент слагаемых векторов, т.е. если то для всех . Произведением n-мерного вектора на действительное число называется n-мерный вектор, компоненты которого равны произведению этого числа на соответствующие компоненты этого вектора, т.е. если , то для всех .
Операции над векторами, установленные этими правилами, принято называть линейными операциями. Линейные операции над векторами должны удовлетворять целому ряду свойств, рассматриваемых как аксиомы.
1. — коммутативное свойство суммы. 2. — ассоциативное свойство суммы. 3. — ассоциативное свойство относительно числового множителя. 4. — дистрибутивное свойство относительно суммы векторов. 5. — дистрибутивное свойство относительно суммы числовых множителей. 6. Существует нулевой вектор такой, что для любого вектора , в этом – особая роль нулевого вектора. 7. Для любого вектора существует противоположный вектор такой, что . 8. Для любого вектора справедливо , в этом – особая роль числового множителя 1.
Определение. Векторным (линейным) пространством называется множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведенным восьми аксиомам,
ПРИМЕР:Для заданной матрицы А размера mxnстроки этой матрицы можно рассматривать как множество n-мерных векторов.
⇐ Предыдущая12345 Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим. Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
Объяснение урока: Величина вектора в 3D
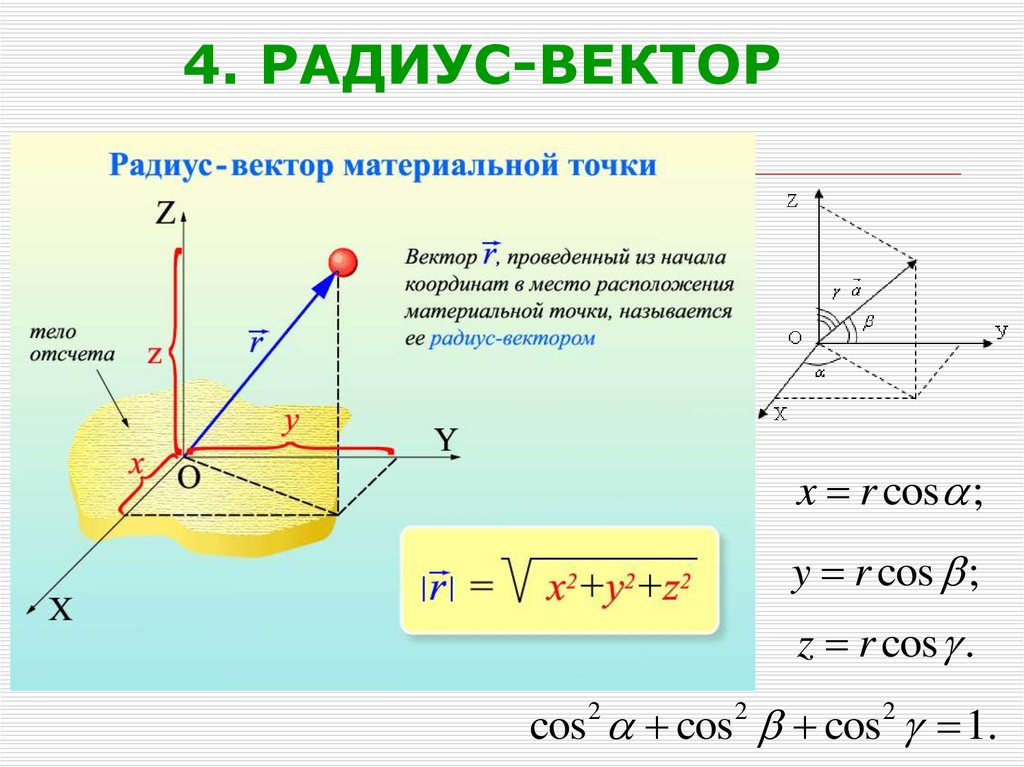
В этом объяснении мы узнаем, как найти величину вектора положения в пространстве.
Существует несколько способов выражения трехмерного вектора, однако мы сосредоточимся на форме компонента. и форма единичного вектора.
Определение: Представление компонентов и единичных векторов
Рассмотрим следующую точку 𝑃 в трехмерном пространстве.
Координаты точки 𝑃
𝑃(𝑥,𝑦,𝑧) и 𝑂𝑃
описывает вектор из начала координат 𝑂 в точку 𝑃.
Этот вектор можно представить двумя способами: Componentform:UnitVectorform:𝑂𝑃=(𝑥,𝑦,𝑧)𝑂𝑃=𝑥⃑𝑖+𝑦⃑𝑗+𝑧⃑𝑘.
Обратите внимание, что это просто разные формы записи. В последней форме используются единичные векторы ⃑𝑖, ⃑𝑗 и ⃑𝑘, которые векторы величины 1 в 𝑥-, 𝑦- и 𝑧-направления соответственно: ⃑𝑖=(1,0,0),⃑𝑗=(0,1,0),⃑𝑘=(0,0,1).
Мы должны знать, что единичный вектор имеет величину (или длина) 1. Мы также должны быть знакомы с нахождением величины вектора в 2D, используя Теорема Пифагора сформулирована ниже: 𝑎+𝑏=𝑐𝑐=√𝑎+𝑏.
Обратите внимание, что это практически та же проблема, что и нахождение величины вектора в 2D. Напомним, что по некоторому вектору ⃑𝐴, его величину часто представляют с помощью обозначение |⃑𝐴| или иногда ‖⃑𝐴‖: ⃑𝐴=(𝑥,𝑦)‖‖⃑𝐴‖‖=𝑥+𝑦.
Возможно, менее известный факт о теореме Пифагора
заключается в том, что его можно обобщить до стольких измерений, сколько
мы требуем. Мы можем использовать этот факт, чтобы расширить наш 2D-метод, чтобы охватить 3D.
Мы можем использовать этот факт, чтобы расширить наш 2D-метод, чтобы охватить 3D.
Вместо нахождения длинной диагонали прямоугольника, как показано в нашем двумерном примере, мы можем использовать теорему Пифагора. в 3D, чтобы найти длинную диагональ прямоугольного параллелепипеда:
𝑎+𝑏+𝑐=𝑑𝑑=√𝑎+𝑏+𝑐.
Сначала можно предположить, что, поскольку в двумерной теореме используются квадраты (или квадратные корни), то трехмерное теореме потребуются кубы (или кубические корни). К счастью, это не так!
Для этого объяснителя мы не будем вдаваться в доказательство теоремы, но достаточно признать, что нахождение длина длинной диагонали прямоугольного параллелепипеда — это, по сути, та же проблема, что и нахождение величины вектора в 3D.
Это ключевое понимание, которое нам нужно для нашего определения.
Определение: Величина вектора в 3D
Рассмотрим вектор ⃑𝐴
в трехмерном пространстве, где вектор может быть выражен как:
⃑𝐴=(𝑥,𝑦,𝑧)⃑𝐴=𝑥⃑𝑖+𝑦⃑𝑗+𝑧⃑𝑘. или
или
Величина ⃑𝐴 определяется выражением ‖‖⃑𝐴‖‖=𝑥+𝑦+𝑧.
Обратите внимание, что обычно просто используются переменные 𝑥, 𝑦 и 𝑧 в расчетах величины: ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧.
В нашем вычислении величины каждый компонент вектора возводится в квадрат до того, как сумма будет извлечена из квадратного корня. Этот значит будем всегда в конечном итоге берут квадратный корень из положительного число, которое корректно определено, но имеет два решения. Например, √25 может быть 5 или -5.
Стоит отметить, что величина вектора определяется как неотрицательный. Это означает, что мы можем смело игнорировать отрицательное решение для всех величин в этом объяснителе.
Теперь, когда мы понимаем, как найти величину общего вектор в 3D, давайте попрактикуемся в применении этих знаний в Некоторые примеры.
Пример 1. Нахождение величины трехмерного вектора
Если ⃑𝐴=(2,−5,2), найдите ‖‖⃑𝐴‖‖.
Ответ
Этот вопрос дает нам вектор ⃑𝐴 в компонентной форме. С вектор имеет 3 компонента, мы признаем, что он существует в трехмерном пространстве.
Альтернативный способ выразить ⃑𝐴 использование единичных векторов ⃑𝐴=2⃑𝑖−5⃑𝑗+2⃑𝑘.
Нас попросили найти ‖‖⃑𝐴‖‖, который представляет величину (или длину) вектора. Чтобы решить эту вопрос, мы помним, что величина вектора в трехмерном пространстве определяется как ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧, где 𝑥, 𝑦 и 𝑧 представляют компоненты вектора в соответствующих сторонах света.
Наш вектор состоит из следующих компонентов: 𝑥=2, 𝑦=−5, 𝑧=2.
Чтобы найти его величину, подставляем эти значения в формулу: ‖‖⃑𝐴‖‖=2+(−5)+2‖‖⃑𝐴‖‖=√4+25+4‖‖⃑𝐴‖‖=√33.
С небольшим упрощением получаем наш ответ.
Для вопросов такого типа иногда может быть полезно найти десятичное приближение для вашего ответа.
(возможно, если нужно для сравнения). В этом случае не нужно, и поскольку нет возможности услужливо
уменьшать
√33, мы можем оставить наш ответ радикальным.
В этом случае не нужно, и поскольку нет возможности услужливо
уменьшать
√33, мы можем оставить наш ответ радикальным.
Пример 2. Нахождение величины трехмерного вектора, выраженного через единичные векторы
Если ⃑𝐴=2⃑𝑖+3⃑𝑗−⃑𝑘, найти ‖‖⃑𝐴‖‖.
Ответ
Этот вопрос имеет очень похожую форму на наш предыдущий пример; однако на этот раз мы работаем с 3D вектор, ⃑𝐴, который был задан в терминах единичных векторов.
Опять же, нас попросили найти величину этого вектора, ‖‖⃑𝐴‖‖ и поэтому мы можем использовать формулу для величина вектора в 3D: ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧.
Наш вектор состоит из следующих компонентов: 𝑥=2, 𝑦=3, 𝑧=−1.
Стоит отметить, что хотя единичный вектор ⃑𝑘
не имеет коэффициента, тот факт, что он
присутствие в нашем векторе говорит об обратном. Мы всегда должны
будьте осторожны, чтобы не игнорировать коэффициенты 1, или в этом
случае −1 при работе с векторами, выраженными в виде суммы
единичные векторы.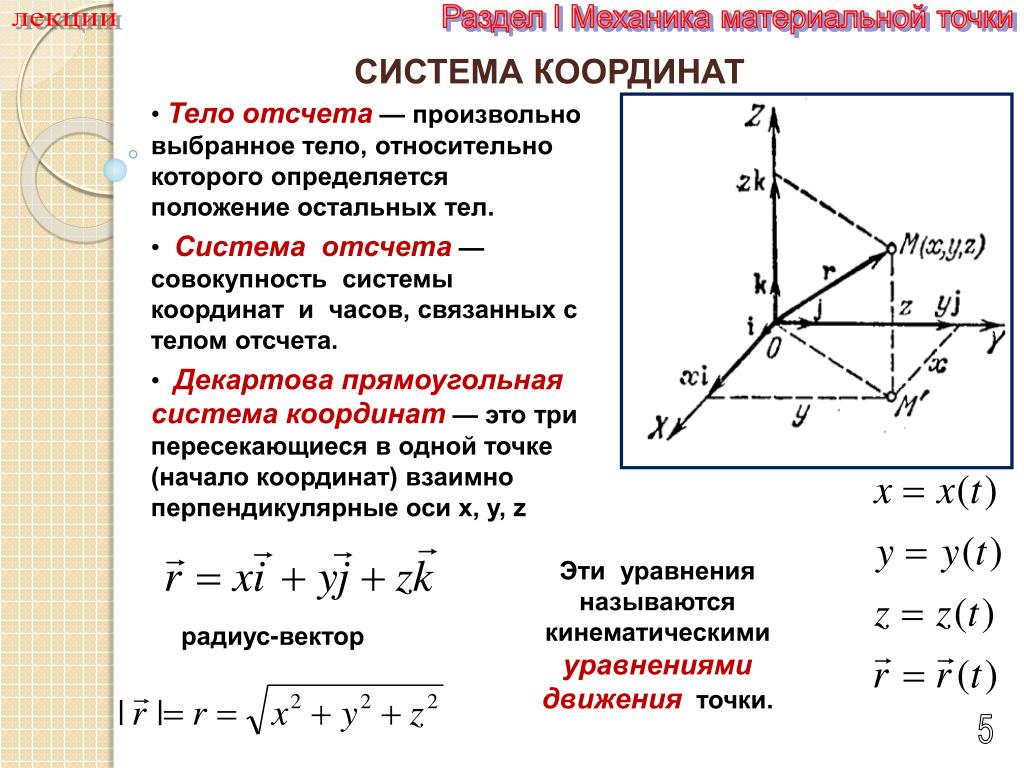 Снова подставляем наши значения в
формулу и упростить, чтобы найти
‖‖⃑𝐴‖‖:
‖‖⃑𝐴‖‖=2+3+(−1)‖‖⃑𝐴‖‖=√4+9+1‖‖⃑𝐴‖‖=√14.
Снова подставляем наши значения в
формулу и упростить, чтобы найти
‖‖⃑𝐴‖‖:
‖‖⃑𝐴‖‖=2+3+(−1)‖‖⃑𝐴‖‖=√4+9+1‖‖⃑𝐴‖‖=√14.
Как и в предыдущем примере, вполне нормально оставить наша величина в форме радикала.
Формула, которую мы использовали, не только помогает нам найти величина вектора, но также может использоваться для найти недостающий компонент вектора, если нам дана величина.
Давайте рассмотрим пример.
Пример 3. Нахождение значения неизвестного компонента вектора по его модулю
Если ⃑𝐴=𝑎⃑𝑖+⃑𝑗−⃑𝑘 и ‖‖⃑𝐴‖‖=√6, найдите все возможные значения 𝑎.
Ответ
В этом примере нам дана величина трехмерного вектора, и мы должны использовать эту информацию, чтобы найти неизвестный компонент. Коэффициент для единичного вектора ⃑𝑖 задается параметром 𝑎. это неизвестно что мы должны работать над поиском.
Наш вектор состоит из следующих компонентов:
𝑥=𝑎,𝑦=1,𝑧=−1.
Мы можем подставить эти значения в формулу для величины вектора в 3D: ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧‖‖⃑𝐴‖‖=𝑎+(1)+(−1).
В этом случае у нас есть другая информация. Величина вектора ‖‖⃑𝐴‖‖=√6. Чтобы решить для нашего неизвестного нам также нужно будет подставить это в наше уравнение: √6=𝑎+(1)+(−1).
Чтобы продолжить, мы можем возвести обе стороны в квадрат, а затем упростить: 6=𝑎+(1)+(−1)6=𝑎+1+14=𝑎.
На этом этапе у нас есть уравнение для 𝑎. Здесь мы можем взять квадратный корень из обеих частей уравнения: 𝑎=√4𝑎=±2.
Мы должны помнить, что извлечение квадратного корня из числа имеет как положительное, так и отрицательное решение. С мы находим коэффициент вектора (а не величины), мы не можем игнорировать отрицательное решение.
Наш ответ состоит в том, что возможные значения для 𝑎 равны 2 и −2.
В качестве примечания к предыдущему примеру учтите, что, зная величину вектора, мы можем найти только
значение одной неизвестной компоненты того же вектора.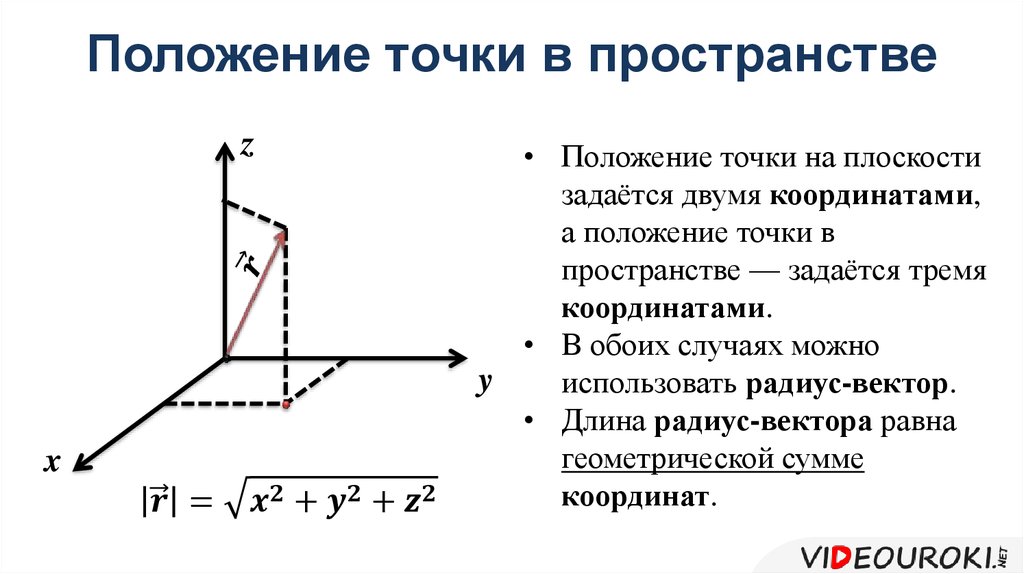 Если бы было более одного неизвестного компонента, наш
уравнение могло бы выглядеть примерно так:
√6=𝑎+𝑏+(−1)6=𝑎+𝑏+15=𝑎+𝑏.
Если бы было более одного неизвестного компонента, наш
уравнение могло бы выглядеть примерно так:
√6=𝑎+𝑏+(−1)6=𝑎+𝑏+15=𝑎+𝑏.
Поскольку в приведенном выше уравнении два неизвестных, бесконечное число решений, и поэтому мы не были бы в состоянии найти уникальную пару значений для 𝑎 и 𝑏.
Переходя к нашему следующему примеру, мы помним, что при работе с векторами такие операции, как сложение и вычитание являются важными инструментами. Чтобы найти величину вектора, нам может понадобиться сначала использовать эти операции для найти его составляющие.
Пример 4. Решение задач на величину вектора
Учитывая, что ⃑𝐴+⃑𝐵=(−2,4,3) и ⃑𝐴=(3,5,3), определить ‖‖⃑𝐵‖‖.
Ответ
Напомним, что при сложении двух векторов отдельные компоненты
просто сложить вместе. Данное выражение
⃑𝐴+⃑𝐵 сам по себе является вектором, и нам даны его компоненты,
вместе с компонентами одинокого вектора
⃑𝐴. Так как компоненты
⃑𝐵 неизвестны, будем
представить их с помощью 𝑥, 𝑦,
и 𝑧:
⃑𝐵=(𝑥,𝑦,𝑧).
Так как компоненты
⃑𝐵 неизвестны, будем
представить их с помощью 𝑥, 𝑦,
и 𝑧:
⃑𝐵=(𝑥,𝑦,𝑧).
Это позволяет составить уравнение (⃑𝐴+⃑𝐵)=⃑𝐴+⃑𝐵(−2,4,3)=(3,5,3)+(𝑥,𝑦,𝑧).
Чтобы изолировать наши неизвестные, мы можем вычесть вектор ⃑𝐴, или (3,5,3), с обеих сторон этого уравнения, оставив нам только вектор ⃑𝐵, или (𝑥,𝑦,𝑧), справа сторона: (−2,4,3)−(3,5,3)=(𝑥,𝑦,𝑧).
Теперь мы можем составить три отдельных уравнения для ⃑𝑖, ⃑𝑗 и ⃑𝑘 направления; однако это было бы ненужный. Вспоминая свойства векторного сложения и вычитания, мы можем упростить левую часть напрямую, обрабатывая каждый компонент отдельно: ((−2−3), (4−5), (3−3))=(𝑥,𝑦,𝑧)(−5,−1,0)=(𝑥,𝑦,𝑧).
Так как мы определили (𝑥,𝑦,𝑧) для представления вектора ⃑𝐵, мы обнаружили, что ⃑𝐵=(−5,−1,0).
Теперь, когда мы нашли компоненты вектора
⃑𝐵,
мы можем найти его величину:
‖‖⃑𝐵‖‖=(−5)+(−1)+0‖‖⃑𝐵‖‖=√25+1+0‖‖⃑𝐵‖‖=√26.
Теперь мы ответили на вопрос . Поскольку никаких полезных упрощений для выполнения нет, мы можем оставить наш ответь в суровой форме.
Обратите внимание, что свойства сложения и вычитания векторов можно использовать при работе с системами, включающими координаты точки.
Рассмотрим систему с двумя точками 𝐴(𝑥,𝑦,𝑧) и 𝐵(𝑥,𝑦,𝑧). Представьте, что мы хотим найти расстояние между эти две точки.
Эта задача аналогична поиску величины вектора между точками 𝐴 и 𝐵, другими словами, ‖‖𝐴𝐵‖‖.
Мы знаем, что 𝑂𝐴=(𝑥,𝑦,𝑧),𝑂𝐵=(𝑥,𝑦,𝑧).
Вектор 𝐴𝐵 можно легко найти с помощью напоминая, что 𝐴𝐵=𝑂𝐵−𝑂𝐴.
Затем мы могли бы найти расстояние между двумя точками, применив нашу величину формула: ‖‖𝐴𝐵‖‖=‖‖𝑂𝐵−𝑂𝐴‖‖.
Одно очень важное отличие, которое мы увидим, состоит в том, что величина суммы или разности не обязательно совпадает с сумма или разность двух величин: Величина различия: Разность величин: ‖‖𝑂𝐵−𝑂𝐴‖‖‖‖𝑂𝐵‖‖−‖‖𝑂𝐴‖‖
В следующем примере мы увидим, почему это так.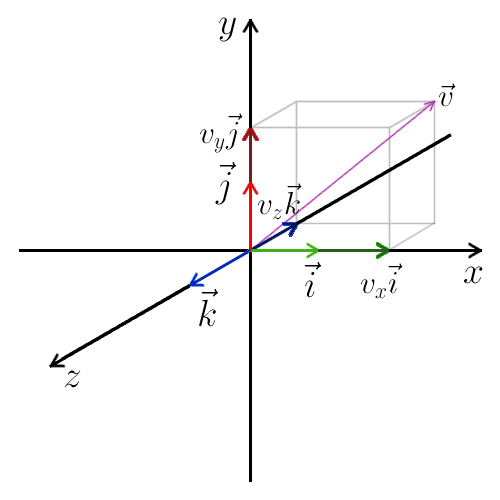
Пример 5. Решение задач на величину вектора и сложение векторов
If ⃑𝐴=⃑𝑖+3⃑𝑗+4⃑𝑘 и ⃑𝐵=2⃑𝑗−⃑𝑘, определить ‖‖⃑𝐴+⃑𝐵‖‖ и ‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖.
Ответ
Вопрос дал нам два трехмерных вектора и попросил нас найти величина суммы векторов, ‖‖⃑𝐴+⃑𝐵‖‖, вместе с суммой величин векторов, ‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖. Хотя эти две вещи могут выглядеть очень похожими, мы должны быть осторожны, чтобы не предполагать, что они эквивалентны.
Начнем с ‖‖⃑𝐴+⃑𝐵‖‖. Сначала нам нужно найти компоненты вектора ⃑𝐴+⃑𝐵, добавив наши два заданные векторы: ⃑𝐴+⃑𝐵=⃑𝑖+3⃑𝑗+4⃑𝑘+2⃑𝑗-⃑𝑘=⃑𝑖+(3+2)⃑𝑗+(4−1)⃑𝑘=⃑𝑖+5⃑𝑗+3⃑𝑖
С некоторым упрощением находим наши компоненты. Коэффициенты для каждого из наших единичных векторов теперь могут быть подставляется в формулу модуля вектора: ‖‖⃑𝐴+⃑𝐵‖‖=√1+5+3=√1+25+9=√35.
А что насчет ‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖? В этот момент нахождение величины
известный вектор должен быть знакомым. Мы начинаем
найдя ‖‖⃑𝐴‖‖:
‖‖⃑𝐴‖‖=√1+3+4=√1+9+16=√26.
Мы начинаем
найдя ‖‖⃑𝐴‖‖:
‖‖⃑𝐴‖‖=√1+3+4=√1+9+16=√26.
Тогда находим ‖‖⃑𝐵‖‖: ‖‖⃑𝐵‖‖=√2+(−1)=√4+1=√5.
Объединив эти две части информации, мы получим ответ: ‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖=√26+√5.
Для сравнения мы можем найти десятичную аппроксимацию для этих двух величин: ‖‖⃑𝐴+⃑𝐵‖‖=√35≈5,91…,‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖=√26+√5≈7,33….
Конечно, в этом случае мы показали, что ‖‖⃑𝐴+⃑𝐵‖‖≠‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖.
Если мы решим изучить ‖‖⃑𝐴+⃑𝐵‖‖ и ‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖ присмотревшись, мы можем понять, что это, по сути, треугольник неравенство, как показано ниже!
Величина суммы двух векторов никогда не может быть больше суммы величин: ‖‖⃑𝐴+⃑𝐵‖‖≤‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖.
Обратите внимание, что есть единственный случай, когда эти количества равны, что происходит, когда векторы ⃑𝐴 и ⃑𝐵 указывают на то же направление. Другими словами, ⃑𝐴 и ⃑𝐵 параллельны.
Эту логику также можно применить для сравнения ‖‖⃑𝐴−⃑𝐵‖‖ с ‖‖⃑𝐴‖‖−‖‖⃑𝐵‖‖. Это приводит к аналогичному результату, который резюмируется в
ключевые моменты ниже.
Это приводит к аналогичному результату, который резюмируется в
ключевые моменты ниже.
Ключевые точки
- Величина вектора представляет его длину и определяется как всегда положительное число.
- Член ‖‖⃑𝐴‖‖ представляет величину вектора ⃑𝐴.
- Учитывая, что ⃑𝐴=𝑥⃑𝑖+𝑦⃑𝑗+𝑧⃑𝑘, его величину можно найти по следующей формуле: ‖‖⃑𝐴‖‖=√𝑥+𝑦+𝑧.
- Если два вектора ⃑𝐴 и ⃑𝐵 имеют одинаковое направление, то ‖‖⃑𝐴+⃑𝐵‖‖=‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖,‖‖⃑𝐴−⃑𝐵‖‖=‖‖⃑𝐴‖‖−‖‖⃑.
- Если два вектора ⃑𝐴 и ⃑𝐵 не имеют одинакового направления, то ‖‖⃑𝐴+⃑𝐵‖‖≠‖‖⃑𝐴‖‖+‖‖⃑𝐵‖‖,‖‖⃑𝐴-⃑𝐵‖‖≠‖‖⃑𝐴‖‖‖‑𝐵‖‖‑‑.
Исчисление III — Трехмерное пространство
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. 3}\)). Это очень важная тема для Исчисления III, поскольку значительная часть Исчисления III выполняется в трехмерном (или более высоком) пространстве.
3}\)). Это очень важная тема для Исчисления III, поскольку значительная часть Исчисления III выполняется в трехмерном (или более высоком) пространстве.
Мы будем рассматривать уравнения графиков в трехмерном пространстве, а также векторные функции и методы исчисления с ними. Мы также рассмотрим пару новых систем координат для трехмерного пространства.
Это единственная глава, которая существует в двух местах в примечаниях. Когда мы изначально писали эти заметки, все эти темы были затронуты в исчислении II, однако с тех пор мы переместили некоторые из них в исчисление III. Таким образом, вместо того, чтобы разделить главу на части, мы сохранили ее в примечаниях к Calculus II, а также поместили копию в примечания к Calculus III. Многие из разделов, не охваченных в Calculus III, все равно будут иногда использоваться там, и поэтому они служат кратким справочником, когда они нам понадобятся. Кроме того, это позволяет тем, кто преподает тему в любом месте, иметь быстрый доступ к заметкам.
Вот список тем этой главы.
Трехмерная система координат. В этом разделе мы представим стандартную трехмерную систему координат, а также некоторые общие обозначения и понятия, необходимые для работы в трех измерениях.
Уравнения линий. В этом разделе мы получим векторную форму и параметрическую форму уравнения линий в трехмерном пространстве. Мы также приведем симметричные уравнения линий в трехмерном пространстве. Также обратите внимание, что хотя эти формы также могут быть полезны для линий в двухмерном пространстве.
Уравнения плоскостей – В этом разделе мы выведем векторное и скалярное уравнения плоскости. Мы также покажем, как написать уравнение плоскости из трех точек, лежащих на плоскости.
Quadric Surfaces – В этом разделе мы рассмотрим несколько примеров квадратичных поверхностей. Некоторыми примерами поверхностей квадратного сечения являются конусы, цилиндры, эллипсоиды и эллиптические параболоиды.
Функции нескольких переменных. В этом разделе мы дадим краткий обзор некоторых важных тем о функциях нескольких переменных. В частности, мы обсудим нахождение области определения функции нескольких переменных, а также кривых уровня, поверхностей уровня и следов.
В этом разделе мы дадим краткий обзор некоторых важных тем о функциях нескольких переменных. В частности, мы обсудим нахождение области определения функции нескольких переменных, а также кривых уровня, поверхностей уровня и следов.
Векторные функции. В этом разделе мы вводим понятие векторных функций, основное внимание уделяя кривым в трехмерном пространстве. Однако мы кратко коснемся и поверхностей. Мы покажем, как найти область определения векторной функции и как построить график векторной функции. Мы также покажем простую связь между векторными функциями и параметрическими уравнениями, которая иногда будет очень полезна.
Исчисление с векторными функциями. В этом разделе мы обсудим, как выполнять базовое исчисление, т. е. пределы, производные и интегралы, с векторными функциями.
Касательные, нормальные и бинормальные векторы. В этом разделе мы определим касательные, нормальные и бинормальные векторы.
Длина дуги с помощью векторных функций. В этом разделе мы расширим формулу длины дуги, которую мы использовали в начале материала, чтобы включить нахождение длины дуги векторной функции. Как мы увидим, новая формула на самом деле является почти естественным расширением той, которую мы уже видели.
Как мы увидим, новая формула на самом деле является почти естественным расширением той, которую мы уже видели.
Кривизна – В этом разделе мы приводим две формулы для вычисления кривизны ( т.е. насколько быстро функция меняется в данной точке) векторной функции.
Скорость и ускорение. В этом разделе мы вернемся к стандартному применению производных, скорости и ускорения объекта, функция положения которого задается векторной функцией. Для ускорения мы приводим формулы как для нормального ускорения, так и для тангенциального ускорения.
Цилиндрические координаты. В этом разделе мы определим цилиндрическую систему координат, альтернативную систему координат для трехмерной системы координат. Как мы увидим, цилиндрические координаты на самом деле не что иное, как очень естественное расширение полярных координат в трехмерном пространстве.
Сферические координаты. В этом разделе мы определим сферическую систему координат, еще одну альтернативную систему координат для трехмерной системы координат. Эта система координат очень удобна для работы со сферическими объектами. Мы выведем формулы для преобразования между цилиндрическими координатами и сферическими координатами, а также между декартовыми и сферическими координатами (более полезными из двух).
Эта система координат очень удобна для работы со сферическими объектами. Мы выведем формулы для преобразования между цилиндрическими координатами и сферическими координатами, а также между декартовыми и сферическими координатами (более полезными из двух).
Трехмерные векторы – объяснение и примеры
Векторы очень полезны в повседневной жизни. Однако в реальном мире все происходит в трех измерениях. Обычно мы учимся решать векторы в двумерном пространстве. Тем не менее, чтобы расширить и развить использование векторов в более реалистичных приложениях, важно объяснить векторы с точки зрения трехмерных плоскостей.
Трехмерный вектор определяется как:
«Трехмерный вектор — это отрезок, нарисованный в трехмерной плоскости, имеющий начальную точку, называемую хвостом, и конечную точку, называемую глава. Подобно нормальному вектору в двумерной плоскости, трехмерный вектор также имеет некоторую величину и направление».
В этой теме мы подробно обсудим следующие моменты:
- Что такое трехмерный вектор?
- Как найти величину трехмерного вектора?
- Как рассчитать угол между двумя трехмерными векторами?
- Как нарисовать трехмерный вектор?
- Примеры
- Проблемы
Что такое трехмерный вектор?
Трехмерный вектор — это вектор, представленный в трехмерной плоскости с тремя координатами; х, у и г.
Как и в предыдущих разделах, мы изучили и обсудили векторы в 2-мерном пространстве. Чтобы избежать вычислительной сложности и упростить идею, чтобы мы могли легко понять концепцию, пришло время узнать о трехмерных векторах.
Например, если нам нужно указать направление любого твердого объекта или тела, такого как автомобили, самолеты, роботы и т. д., обычно можно подумать, что ему нужны три координаты для определения положения объектов x, y , и ось z, и это совершенно правильно. Итак, чтобы описать влияние всех признаков, нам нужно использовать трехмерное пространство.
Точно так же, если мы рассмотрим карту в 2-D, она полезна только для навигации от одной точки к другой. Тем не менее, если нам нужно указать различные ландшафты и окружение, одного двухмерного описания карты недостаточно. Вот почему необходимо понимать концепцию трехмерных векторов в трехмерной системе координат и их свойства.
Трехмерный вектор похож на двухмерный во всех аспектах, но в случае с трехмерным вектором нам нужно отслеживать еще одно направление. Трехмерные векторные операции аналогичны двухмерным операциям только с добавлением вычислительного шага. Мы можем выполнять различные вычисления, такие как нахождение угла между двумя векторами, скалярное умножение и т. д.
Трехмерные векторные операции аналогичны двухмерным операциям только с добавлением вычислительного шага. Мы можем выполнять различные вычисления, такие как нахождение угла между двумя векторами, скалярное умножение и т. д.
Теперь первый вопрос: «Что такое трехмерная система координат?» Трехмерная система координат имеет 3 измерения или может рассматриваться как имеющая 3 перпендикулярные оси: оси x, y и z. Такая система называется трехмерной прямоугольной системой координат.
Вектор, нарисованный в трехмерной плоскости и имеющий три точки координат, определяется как трехмерный вектор. Теперь есть три оси, значит, есть три пересекающиеся пары осей. Каждая пара образует плоскость, плоскость xy, плоскость yz и плоскость xz. Трехмерный вектор может быть представлен как u (ux, uy, uz) или
Величина трехмерных векторов вычисляется аналогичным образом с добавлением еще одной координаты. 9 2 )
9 2 )
Где ux, uy и uz — величины координатных осей.
Как мы уже говорили, концепция трехмерного вектора не отличается от концепции двумерного вектора, за исключением того, что теперь в трехмерном векторе есть еще одно измерение. Величина вектора всегда положительна, так как распространенной ошибкой при вычислении величины вектора является то, что мы забываем абсолютный знак. Только величина нулевого вектора равна нулю.
Давайте лучше разберемся с концепцией на примере.
Пример 1
Рассчитайте величину следующих трехмерных векторов.
- U = (3,4,5)
- V = <2,5,6,>
- S = 3 I + K = 3 I + K = 3 I + K = 3 I + K = 3 I + K = 3 I + K = 3 I + K = 3 I + . сначала рассмотрим уравнение 1:
u = (3,4,5)
| у | = √ ((3)2 + (4)2 + (5)2)
| и | = √ (9 + 16 + 25)
| и | = 7,07
Теперь рассмотрим уравнение 2 :
v = <2,5,6,>
| против | = √ ((2)2 + (5)2 + (6)2)
| против | = √ (4 + 25 + 36)
| против | = 8,06
Вычислим для уравнение 3:
| с | = √ ((3)2 + (0)2 + (8)2)
| с | = √ (9 + 0 + 64)
| с | = 9,05
Итак, в приведенных выше примерах мы вычислили величины трехмерных векторов.
Что такое вектор смещения?
Вектор смещения определяется как:
» Вектор, объясняющий изменение положения объекта, называется вектором смещения.»
Рассмотрим вектор AB , начальная точка которого — A (x1, y1, z1), а конечная точка — B (x2, y2, z2). Он имеет некоторую величину и направление, и в этом случае направление определяется как направление от А к В. 92)
| АВ | = √ (9 + 4 + 16)
| АВ | = √ (29)
| АБ | = 5,38
Расстояние между двумя точками равно 5,38 м.
Направление вектора, определяемое единичным векторомЕдиничный вектор определяется как тип вектора, величина которого всегда равна 1. Таким образом, единичный вектор описывает направление вектора v при условии, что величина вектора равна |v|.
Тогда вектор направления задается как
Û = U / | У |
Давайте решим несколько примеров, чтобы применить эту концепцию к трехмерным векторам.

Пример 3
Узнать направление и величину заданного трехмерного вектора PQ (3,5,6).
Решение
Величина данного вектора определяется как:
|PQ| = √ ((3)2 + (5)2 + (6)2)
|PQ| = √ (9 + 25 + 36)
|PQ| = 8,366
Направление трехмерного вектора задается единичным вектором следующим образом:
UPQ = PQ / | PQ |
UPQ = [3, 5, 6] / 8.366
Example 4
Find out the direction and magnitude of the given vector AB = 5 i + 3 j + 2 k
Решение
Величина данного вектора определяется как:
|AB| 92)
|АВ| = √ (25 + 9 + 4)
|AB| = 6,166
Направление вектора задается единичным вектором следующим образом:
UAB = AB / | АВ |
UAB = (5 i + 3 j + 2 k ) / 6,166
Угол между двумя трехмерными векторами скалярное произведение двух векторов в трехмерном пространстве задается как:у.
 в = |у| |v|.cos θ
в = |у| |v|.cos θ где |u| и |v| — величины двух векторов u и v, а θ — угол между двумя векторами.
Чтобы понять понятие угла между двумя трехмерными векторами, давайте пересмотрим понятие скалярного произведения или скалярного произведения. Скалярное произведение определяется как произведение двух трехмерных векторов, которое дает взамен скалярную величину.
Таким образом, угол между двумя трехмерными векторами задается как скалярное произведение двух векторов, деленное на произведение величин двух векторов.
Для вычисления угла между двумя трехмерными векторами необходимо выполнить следующие шаги:
- Во-первых, вычислить величину двух векторов.
- Теперь начнем с рассмотрения обобщенной формулы скалярного произведения и сделаем угол θ основным предметом уравнения и соответствующим образом смоделируем его,
u . v = |и| |v|.cosθ
cosθ = u .
 против / |и| |в|
против / |и| |в|θ = arccos ( u . v / |u| |v|)
- Используйте стандартную алгебраическую формулу для вычисления скалярного произведения двух векторов.
Точно так же угол между двумя трехмерными векторами также можно рассчитать с помощью векторного произведения, выполнив те же действия, что обсуждались выше, с той лишь разницей, что он будет иметь sin вместо cos и обобщенную формулу кросс- продукт для того, чтобы два узнать результат.
Давайте разберемся с концепцией на примере.
Пример 5
Учитывая, что существуют два вектора U = 2 I + 2 J + 3 K и V = 6 I и V = 6 I и V = 6 I и V = 6 I и V = 6 . . по формуле скалярного произведения вычислить угол между двумя векторами.
Решение
Выполните следующие шаги, чтобы вычислить угол между двумя векторами.

- Начните с формулы скалярного произведения.
- Найдите величину двух векторов. 92)
|в| = √ (36 + 9 + 1)
|v| = √ (46)
Теперь, вычисляя скалярное произведение двух векторов,
u.v = (2 i + 2 j + 3 k ). (6 i + 3 j + 1 k )
u.v = ((2.6)(1) + (2.3)(1) + (3.1)(1))
4 u.8v = 12 + 6 +3u.v = 21
Теперь, в качестве последнего шага, поместите все значения в формулу, чтобы вычислить значение θ.
θ = arccos ( u . v / |u| |v|)
θ = arccos (21 /√ (17).√ (46) )
θ = arccos (21 / (4.12) (6.78) )
θ = arccos (0,75)
θ = 0,7227 рад
Итак, переводя угол в градусы,
θ = 41,36°
Чтобы построить трехмерный вектор, рассмотрим следующую аналогию.
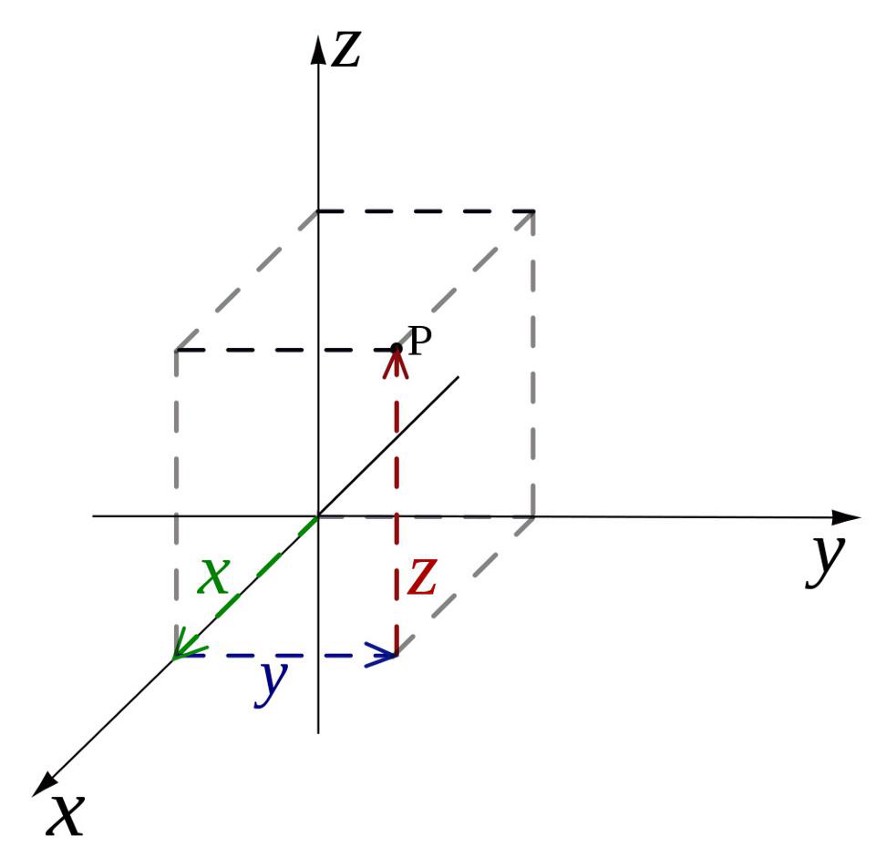
Рассмотрим трехмерную систему координат с 3 осями x, y и x, которые также можно обозначить в стандартных единичных векторах, таких как i, j, и к .
 Как показано на рисунке, стороны с метками являются положительными осями x, положительными осями y и положительной осью z, а стороны без меток считаются отрицательными осями. Пересечение трех перпендикулярных осей называется началом О. Итак, с этими осями любой точке А в пространстве можно поставить в соответствие три координаты А = (А1, А2, А3).
Как показано на рисунке, стороны с метками являются положительными осями x, положительными осями y и положительной осью z, а стороны без меток считаются отрицательными осями. Пересечение трех перпендикулярных осей называется началом О. Итак, с этими осями любой точке А в пространстве можно поставить в соответствие три координаты А = (А1, А2, А3).Давайте рассмотрим человека, стоящего в углу комнаты и смотрящего вниз в точку, где стены соприкасаются с полом. Таким образом, это пересечение можно визуализировать как трехмерную ось. Пол и стену слева от человека, пересекающие друг друга по прямой, можно рассматривать как положительные оси абсцисс. Пол и стена, пересекающиеся по направлению к правой стороне человека, являются осью Y. Стены, пересекающиеся по вертикальной линии, имеют положительную ось z. Противоположная часть каждого рассматривается как отрицательная часть каждой оси.
Вектор отображается синим цветом, его конец фиксируется в начале координат, а наконечник указывает направление, показанное на рисунке ниже.
 Теперь нарисуйте проекцию вектора на три оси, показанные красным цветом, которые являются координатами данного вектора.
Теперь нарисуйте проекцию вектора на три оси, показанные красным цветом, которые являются координатами данного вектора.Так же, как и в двумерном, мы также можем обозначить трехмерный вектор через единичный вектор i, j, и k. Это единичные векторы в вышеуказанных положительных осях. Трехмерный вектор можно представить как A = A1 i + A2 j + A3 k , где A1, A2 и A3 — координаты трехмерного вектора.
Существуют различные программы для построения трехмерных векторов и графиков, которые можно использовать для визуализации и рисования трехмерных векторов и правильного понимания их характеристик.
Практические задачи- Рассчитайте величину следующих трехмерных векторов: U = 5 I + 10 j + 8 K AB = 1 I + 2 J + 5 K <3,5,8>
- дано дано, что это координат. (5,0,8) и Б (9,5,4). Найдите расстояние между двумя точками.
- Найти угол между заданными векторами и <-8,7,2> и v <-6,4,3>.



 3).
3).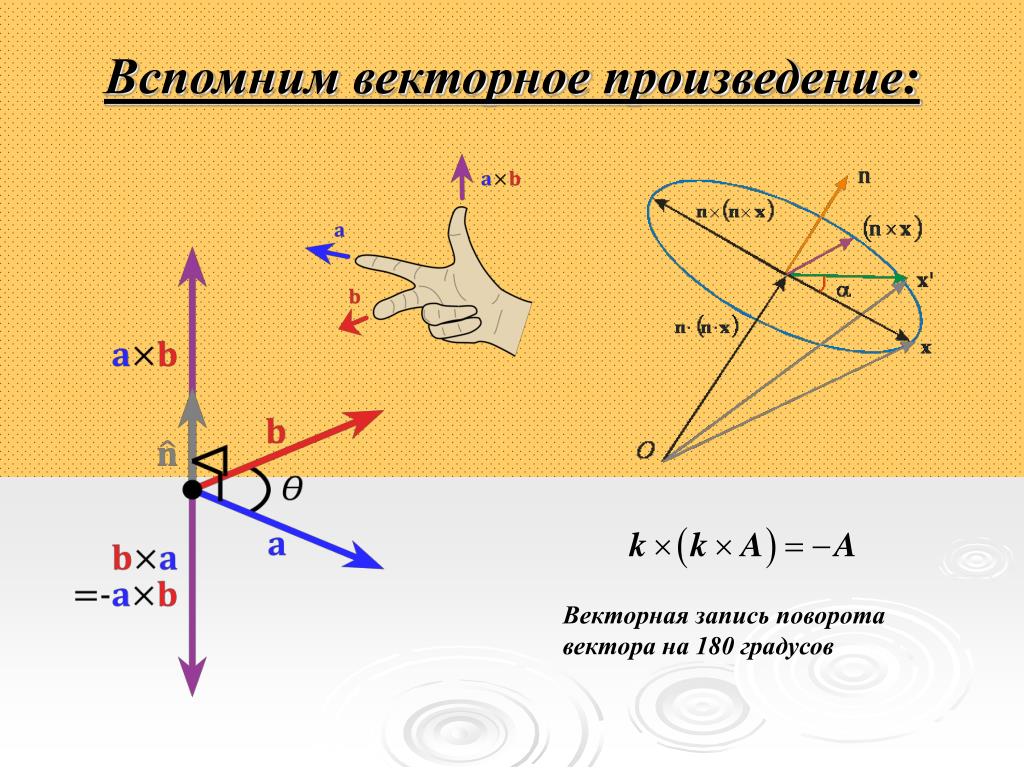 3
3 Тогда (рис.14)
Тогда (рис.14) 14
14
 ..
..


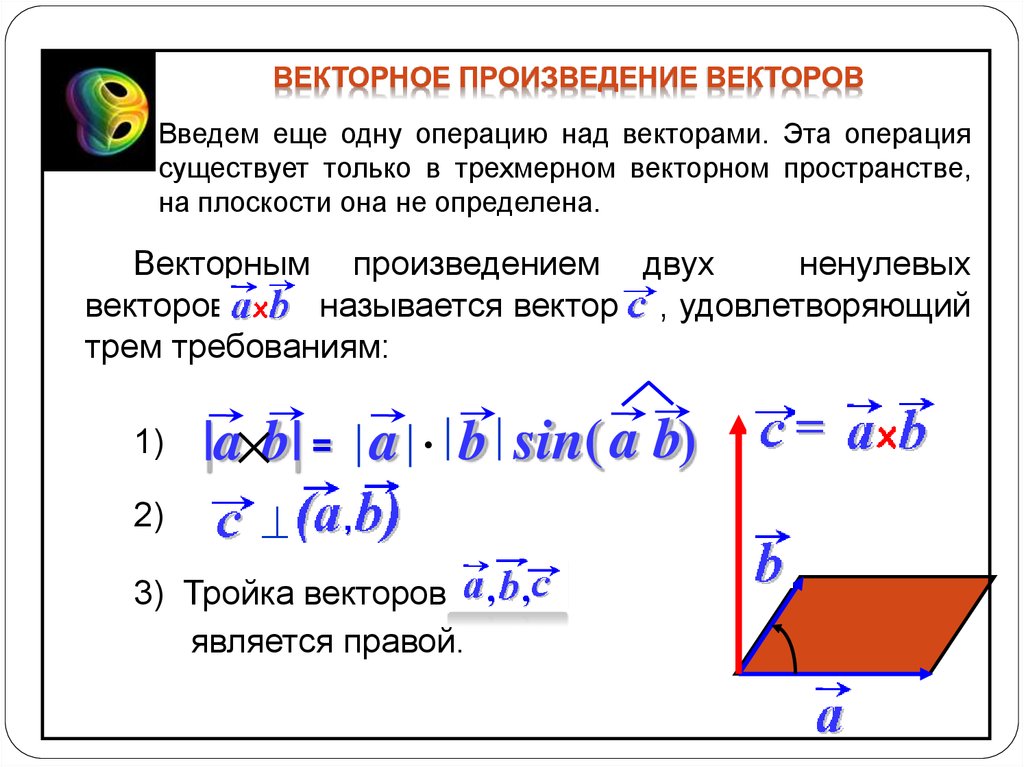


 в = |у| |v|.cos θ
в = |у| |v|.cos θ  против / |и| |в|
против / |и| |в|
 Как показано на рисунке, стороны с метками являются положительными осями x, положительными осями y и положительной осью z, а стороны без меток считаются отрицательными осями. Пересечение трех перпендикулярных осей называется началом О. Итак, с этими осями любой точке А в пространстве можно поставить в соответствие три координаты А = (А1, А2, А3).
Как показано на рисунке, стороны с метками являются положительными осями x, положительными осями y и положительной осью z, а стороны без меток считаются отрицательными осями. Пересечение трех перпендикулярных осей называется началом О. Итак, с этими осями любой точке А в пространстве можно поставить в соответствие три координаты А = (А1, А2, А3). Теперь нарисуйте проекцию вектора на три оси, показанные красным цветом, которые являются координатами данного вектора.
Теперь нарисуйте проекцию вектора на три оси, показанные красным цветом, которые являются координатами данного вектора.