Скорость ⚠️ распространения магнитного поля в вакууме: что характеризует интенсивность, формулы
Содержание:
- Распространение магнитного поля
- Эмпирический способ нахождения скорости электромагнитных волн
- Вывод скорости распространения электромагнитных волн из теории Максвелла
Содержание
- Распространение магнитного поля
- Эмпирический способ нахождения скорости электромагнитных волн
- Вывод скорости распространения электромагнитных волн из теории Максвелла
Распространение магнитного поля
Определение
Магнитным полем называют одну из форм проявления электромагнетизма: поле, оказывающее воздействие на заряды, которые перемещаются, а также на намагниченные тела в разных состояниях.
Магнитное поле создают источники в виде:
- проводников, по которым протекает электрический ток;
- зарядов и заряженных тел, находящихся в движении;
- тел, которые намагничены;
- переменных электрических тел.
Интенсивность магнитного поля определяют с помощью магнитной индукцией. Эта величина соответствует приложенной силе, с которой она оказывает воздействие на проводник длиной один метр с протекающим по нему током в 1 А. Единица измерения магнитной индукции является 1 Тл (тесла).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: infonotes.ruВ формуле:
F – является наибольшей силой, которая оказывает действие на проводник;
L – представляет собой длину проводника;
I – определяет силу тока заряженных частиц в металле.
Эмпирический способ нахождения скорости электромагнитных волн
Скорость, с которой распространяются электромагнитные волны, можно определить эмпирическим методом.
При этом изучают неподвижные волны, полученные в цепи. К примеру, такую картину можно наблюдать, когда выход генератора подсоединен к проводам линии через конденсаторы. Во время работы генератора между проводами возникают колебания напряжения, что свидетельствует о наличии колебаний электрического поля. Таким образом образуется электромагнитная волна.
Понять интенсивность колебаний в разных точках линии можно, если включить лампы накаливания. Благодаря подобному опыту, удается выяснить, что возникновение стоячих волн в линии обусловлено определенной частотой генератора, совпадающей с частотой собственных колебаний линий.
Проводя измерения расстояния (△x), на которое удалены соседние узлы в стоячей волне, можно сделать вывод о том, что данная величина равна 1/2 длины волны (λ). Если измерить ν, то есть частоту колебаний генератора, то можно определить скорость распространения электромагнитной волны по формуле:
V = λ * v
Вывод скорости распространения электромагнитных волн из теории Максвелла
После того, как Максвеллом было установлено существование единого электромагнитного поля, которое можно наблюдать, независимо от наличия источника, ученому удалось определить скорость распространения данного электромагнитного поля.
Магнитное поле, которое образовано заряженными частицами или телами, перемещающимися в вакуумной среде со скоростью \(\vec{v}\) согласно закону Био-Савара-Лапласа, определяется, как:
Источник: ens.tpu.ruСледует отметить, что точечным зарядом создается электрическое поле на расстоянии r:
Источник: ens.tpu.ruДалее необходимо умножить первое уравнение на \(\frac{\varepsilon _{0}}{\varepsilon _{0}}\):
Источник: ens.tpu.ruС другой стороны, можно отметить, что путем перемещения магнитное поле формирует вихревое электрическое поле:
Источник: ens.tpu.ruВ том случае, когда электрическое и магнитное поля образуют друг друга, то скорость их движения будет одинаковой.
Таким образом:
Примечание
С помощью знака ‘ демонстрируют тот факт, что одно поле порождает другое и наоборот.
Векторные величины будут перпендикулярны друг другу.
Источник: ens.tpu.ruС помощью всех трех векторов будет образована правовинтовая система в направлении распространения:
Источник: ens.tpu.ruИсходя из взаимной перпендикулярности векторов, можно записать выражение:
Источник: ens.tpu.ruВ таком случае, можно записать абсолютные значения векторов:
Источник: ens.tpu.ru Источник: ens.tpu.ru Источник: ens.tpu.ruВ такой форме будет записана скорость распространения электромагнитного поля в вакууме, которая совпадает со скоростью света.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
как узнать скорость / Справочник :: Бингоскул
Распространение электромагнитных волн в различных средах: как узнать скоростьдобавить в закладки удалить из закладок
Содержание:
Электромагнитной волной называется возмущение среды, распространяющееся с определённой скоростью. Где и как она распространяется, описывают законы Максвелла для магнитных и электрических явлений. Её источниками или переизлучателями являются практически все окружающие нас вещи. Рассмотрим законы, по которым распространяются электромагнитные волны (ЭМВ). Разберёмся, как определяется их скорость в вакууме, воздухе и прочих средах.
Особенности распространения электромагнитных волн в разных средах
Возмущение электромагнитного поля (ЭМВ) перемещается в вакууме – безвоздушной среде – со скоростью c = 299 992 458 м/с = ~300 тыс.
км/с или свыше 1,08 млрд км/ч. Иные среды оказывают заметное влияние на скорость распространения электромагнитных полей. Их структурные элементы – атомы и молекулы – частично поглощают, отражают или рассеивают ЭМВ, создают препятствие на пути их движения. Вследствие, амплитуда волны снижается. Например, свет. Он замедляется и искажается практически любой преградой, даже прозрачным стеклом. Иные излучения ведут себя по-другому.
Фазовая скорость электромагнитной волны в среде вычисляется по формуле:
\nu = \frac { c } { \sqrt {εμ } } , где, ε и μ – электрическая и магнитная проницаемость среды (вещества) для рассматриваемого излучения. Поведение электромагнитного излучения зависит от его характеристик: частоты и длины волны.
Обычно величина \sqrt {εμ } указывается в таблицах или даётся в условиях задач, поэтому формула упрощается до:
\nu = \frac { c } { n }, где n – коэффициент преломления среды.
Низкочастотное излучение
Радиоволны в частотном диапазоне до 104 Гц в атмосфере распространяются на многие километры.
Из-за большой длины (сотни – десятки километров) неплохо огибают препятствия, не задерживаются в водной толще, распространяются в земной коре.
Радиоволны
Это широкий спектр излучений, у которых при повышении частоты снижается способность огибать препятствия. Излучение радиодиапазона лучше НЧ поглощается и отражается препятствиями, особенно верхними слоями атмосферы.
Световой диапазон
Излучение в терагерцовом диапазоне (видимый свет и ультрафиолет) почти прозрачны для атмосферы Земли, стекла, в воде заметно искажаются (замедляются). Ультрафиолет практически непрозрачен даже для обычного стекла. Большинство остальных сред для них – диэлектрики. У инфракрасных большая проницательная способность, чем у оптических.
Рентгеновские и γ-лучи
Излучения в частотном диапазоне от 1016 Гц всё лучше преодолевают препятствия с ростом частоты, ведь длина волны становится сравнимой с молекулами и атомами. Это позволяет лучам свободно распространяться даже в плотных материалах.
8 км/с.
Тесты
В вакууме скорость распространения электромагнитной волны равна:
- 300 тыс. км/ч.
- 299,9 тыс. км/с.
- 1 млрд м/ч.
Поделитесь в социальных сетях:
19 сентября 2022, 07:49
Физика
electronic_wave_equation
где c — скорость света в среде. В вакууме c = 299792458 метров в секунду, это скорость света в свободном пространстве.
Уравнение электромагнитной волны выводится из уравнений Максвелла.
Следует также отметить, что в большей части старой литературы B называется «плотностью магнитного потока» или «магнитной индукцией».
Дополнительные рекомендуемые знания
Содержимое
|
2 Решения для плоских волнСкорость распространения
В вакууме
Если волна распространяется в вакууме, то
- метров в секунду
это скорость света в вакууме. Магнитная постоянная и диэлектрическая проницаемость вакуума являются важными физическими константами, играющими ключевую роль в электромагнитной теории.
| Символ | Имя | Числовое значение | Единица измерения СИ | Тип |
|---|---|---|---|---|
| Скорость света в вакууме | метра в секунду | определенный | ||
| диэлектрическая проницаемость вакуума | Фарад на метр | производный | ||
| магнитная постоянная | Генри на метр | определенный |
В материальном носителе
Скорость света в линейной, изотропной и недисперсионной материальной среде равна
где
– показатель преломления среды, – магнитная проницаемость среды, – электрическая проницаемость среды.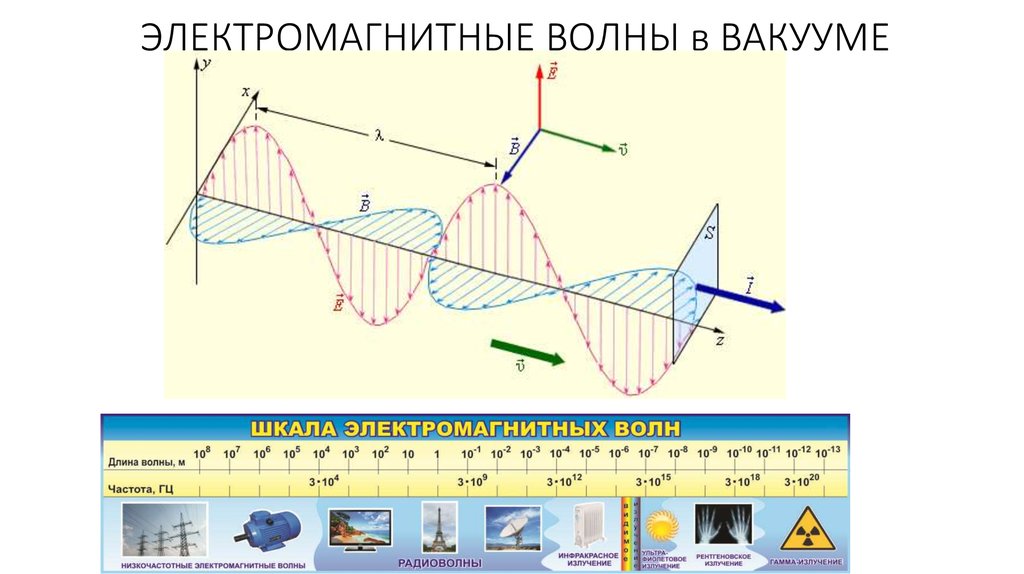
Происхождение уравнения электромагнитной волны
Сохранение заряда
Сохранение заряда требует, чтобы скорость изменения во времени общего заряда, заключенного в объеме V , была равна чистому току, протекающему через поверхность S , охватывающую объем:
где j — плотность тока (в амперах на квадратный метр), протекающего через поверхность, а ρ — плотность заряда (в кулонах на кубический метр) в каждой точке объема.
Из теоремы о дивергенции это соотношение можно преобразовать из интегральной формы в дифференциальную:
Закон Ампера до исправления Максвелла
В своей первоначальной форме закон Ампера связывает магнитное поле B с плотностью тока j :
, которые можно преобразовать в дифференциальную форму, используя теорему Стокса:
Несоответствие между схемным законом Ампера и законом сохранения заряда
Взятие дивергенции обеих частей окружного закона Ампера дает:
Дивергенция ротора любого векторного поля, в том числе и магнитного поля B , всегда равна нулю:
Объединение этих двух уравнений означает, что
Поскольку отлична от нуля константа, отсюда следует, что
Однако закон сохранения заряда говорит, что
Следовательно, как и в случае с законами Кирхгофа, закон Ампера действует только в ситуациях, связанных с постоянной плотностью заряда.
Это исключило бы ситуацию, возникающую в пластинах заряжающего или разряжающегося конденсатора.
Поправка Максвелла к окружному закону Ампера
Закон Гаусса в интегральной форме гласит:
, которые можно преобразовать в дифференциальную форму с помощью теоремы о расходимости:
Взяв производную по времени от обеих частей и изменив порядок дифференцирования в левой части на обратный, получим:
Этот последний результат, наряду с законом Ампера и уравнением сохранения заряда, предполагает, что на самом деле существует два происхождения магнитного поля: плотность тока j , как уже установил Ампер, и так называемый ток смещения :
Таким образом, исправленная форма кругового закона Ампера принимает вид:
Гипотеза Максвелла о том, что свет представляет собой электромагнитную волну
В своей статье 1864 года, озаглавленной «Динамическая теория электромагнитного поля», Максвелл использовал поправку к циркулярному закону Ампера, которую он сделал в части III своей статьи 1861 года «О физических силовых линиях».
В ЧАСТИ VI своей статьи 1864 года, озаглавленной «ЭЛЕКТРОМАГНИТНАЯ ТЕОРИЯ СВЕТА». [1] (стр. 497 статьи и стр. 9 ссылки в формате pdf) Максвелл объединил ток смещения с некоторыми другими уравнениями электромагнетизма и получил волновое уравнение со скоростью, равной скорости света. Он прокомментировал:
- Совпадение результатов, по-видимому, показывает, что свет и магнетизм являются проявлениями одной и той же субстанции и что свет представляет собой электромагнитное возмущение, распространяющееся через поле в соответствии с электромагнитными законами.
(см. [2], стр. 499 статьи и стр. 1 ссылки на pdf)
Максвелловский вывод уравнения электромагнитной волны был заменен в современной физике гораздо менее громоздким методом, включающим комбинирование исправленной версии амперовского закона замыкания с законом индукции Фарадея.
Чтобы получить уравнение электромагнитной волны в вакууме с использованием современного метода, мы начнем с современной формы «Хевисайда» уравнений Максвелла.
В вакууме эти уравнения таковы:
Принятие уравнения завитка дает:
Используя идентификатор вектора
где любая векторная функция пространства, она превращается в волновые уравнения:
где
- метров в секунду
— скорость света в свободном пространстве.
Ковариантная форма однородного волнового уравнения
Эти релятивистские уравнения можно записать в ковариантной форме как
где электромагнитный четырехпотенциал
с условием датчика Лоренца:
- .
Здесь
- — оператор Даламбера. Квадратная рамка не является типографской ошибкой; это правильный символ для этого оператора.
Однородное волновое уравнение в искривленном пространстве-времени
Основная статья: уравнения Максвелла в искривленном пространстве-времени
Уравнение электромагнитной волны модифицируется двумя способами: производная заменяется ковариантной производной и появляется новый член, зависящий от кривизны.
где
— тензор кривизны Риччи, а точка с запятой указывает на ковариантное дифференцирование.
Предполагается обобщение условия калибровки Лоренца в искривленном пространстве-времени:
- .
Уравнение неоднородной электромагнитной волны
Основная статья: Уравнение неоднородной электромагнитной волны
Локализованные изменяющиеся во времени плотности заряда и тока могут действовать как источники электромагнитных волн в вакууме. Уравнения Максвелла можно записать в виде волнового уравнения с источниками. Добавление источников к волновым уравнениям делает уравнения в частных производных неоднородными.
Решения уравнения однородной электромагнитной волны
Основная статья: Волновое уравнение
Общее решение уравнения электромагнитных волн представляет собой линейную суперпозицию волн вида
и
практически любая корректная функция g безразмерного аргумента φ, где
- — угловая частота (в радианах в секунду), а
- — волновой вектор (в радианах на метр).
Хотя функция g может быть и часто является монохроматической синусоидой, она не обязательно должна быть синусоидальной или даже периодической. На практике g не может иметь бесконечную периодичность, потому что любая реальная электромагнитная волна всегда должна иметь конечную протяженность во времени и пространстве. В результате и на основании теории разложения Фурье реальная волна должна состоять из суперпозиции бесконечного набора синусоидальных частот.
Кроме того, для правильного решения волновой вектор и угловая частота не являются независимыми; они должны соответствовать дисперсионному соотношению:
, где k — волновое число, а λ — длина волны.
Монохроматический, синусоидальный установившийся режим
Простейший набор решений волнового уравнения получается из предположения о синусоидальных формах сигналов одной частоты в раздельной форме:
где
- — воображаемая единица,
- — угловая частота в радианах в секунду,
- — это частота в герцах, а
- это формула Эйлера.
Решения для плоских волн
Основная статья: Синусоидальные плоские решения уравнения электромагнитных волн
Рассмотрим плоскость, определяемую единичным вектором нормали
- .
Тогда решения волновых уравнений в виде плоской бегущей волны
и
где
- — вектор положения (в метрах).
Эти решения представляют собой плоские волны, распространяющиеся в направлении вектора нормали. Если мы определим направление z как направление, а направление x как направление , то по закону Фарадея магнитное поле лежит в направлении y и связано с электрическим полем соотношением
- .
Поскольку расхождения электрического и магнитного полей равны нулю, поля в направлении распространения отсутствуют.
Это решение является линейно поляризованным решением волновых уравнений. Существуют также решения с круговой поляризацией, в которых поля вращаются вокруг вектора нормали.
Спектральное разложение
Из-за линейности уравнений Максвелла в вакууме решения можно разложить на суперпозицию синусоид. На этом основан метод преобразования Фурье для решения дифференциальных уравнений. Синусоидальное решение уравнения электромагнитных волн принимает вид
и
где
- — время (в секундах),
- — угловая частота (в радианах в секунду),
- — волновой вектор (в радианах на метр), а
- — фазовый угол (в радианах).
Волновой вектор связан с угловой частотой соотношением
, где k — волновое число, а λ — длина волны.
Электромагнитный спектр представляет собой график величин поля (или энергий) в зависимости от длины волны.
Другие растворы
Возможны также сферически-симметричные и цилиндрически-симметричные аналитические решения уравнений электромагнитных волн.
В цилиндрических координатах волновое уравнение можно записать следующим образом:
и
Каталожные номера
Электромагнетизм
Журнальные статьи
- Джеймс Клерк Максвелл, «Динамическая теория электромагнитного поля», Philosophical Transactions of the Royal Society of London 155 , 459-512 (1865). (Эта статья сопровождала презентацию Максвелла Королевскому обществу от 8 декабря 1864 г.)
http://www.zpenergy.com/downloads/Maxwell_1864_1.pdf http://www.zpenergy.com/downloads/Maxwell_1864_2.pdf http://www.zpenergy.com/downloads/Maxwell_1864_3.pdf http://www.zpenergy.com/downloads/Maxwell_1864_4.pdf http://www.zpenergy.com/downloads/Maxwell_1864_5.pdf http://www.zpenergy.com/downloads/Maxwell_1864_6.pdf
Учебники для бакалавриата
- Гриффитс, Дэвид Дж. (1998). Введение в электродинамику (3-е изд.) . Прентис Холл. ISBN 0-13-805326-X .
- Типлер, Пол (2004). Физика для ученых и инженеров: электричество, магнетизм, свет и элементарная современная физика (5-е изд.) . WH Freeman. ISBN 0-7167-0810-8 .
- Эдвард М. Перселл, Электричество и магнетизм (Макгроу-Хилл, Нью-Йорк, 1985). ISBN 0-07-004908-4 .
- Герман А. Хаус и Джеймс Р. Мелчер, Электромагнитные поля и энергия (Прентис-Холл, 1989) ISBN 0-13-249020-X .
- Банеш Хоффманн, Относительность и ее корни (Фриман, Нью-Йорк, 1983). ISBN 0-7167-1478-7 .
- Дэвид Х. Стаэлин, Энн В. Моргенталер и Джин Ау Конг, Электромагнитные волны (Прентис-Холл, 1994) ISBN 0-13-225871-4 .
- Чарльз Ф. Стивенс, Шесть основных теорий современной физики , (MIT Press, 1995) ISBN 0-262-69188-4 .
ISBN 0-13-805326-X . Учебники для выпускников
- Джексон, Джон Д. (1998). Классическая электродинамика (3-е изд.) . Уайли. ISBN 0-471-30932-X .
- Ландау, Л. Д., Классическая теория поля (Курс теоретической физики: Том 2), (Баттерворт-Хайнеманн: Оксфорд, 1987). ISBN 0-08-018176-7 .
- Максвелл, Джеймс С. (1954). Трактат об электричестве и магнетизме . Дувр. ISBN 0-486-60637-6 .
- Чарльз В. Мизнер, Кип С. Торн, Джон Арчибальд Уиллер, Гравитация , (1970) В.Х. Фриман, Нью-Йорк; ISBN 0-7167-0344-0 . (Обработка уравнений Максвелла в терминах дифференциальных форм.)
Классическая электродинамика (3-е изд.) . Уайли. ISBN 0-471-30932-X . Векторное исчисление
- HM Schey, Div Grad Curl и все такое: неофициальный текст по векторному исчислению , 4-е издание (WW Norton & Company, 2005) ISBN 0-393-92516-1 .
См. также
Теория и эксперимент
- Уравнения Максвелла
- Волновое уравнение
- Электромагнитное моделирование
- Электромагнитное излучение
- Сохранение заряда
- Свет
- Электромагнитный спектр
- Оптика
- Специальная теория относительности
- Общая теория относительности
- Динамика фотонов в двухщелевом эксперименте
- Фотонная поляризация
- Силовая формула Лармора
- Теоретическое и экспериментальное обоснование уравнения Шрёдингера
Приложения
- Радуга
- Космическое микроволновое фоновое излучение
- Лазер
- Лазерный синтез
- Фотография
- рентген
- Рентгеновская кристаллография
- РАДАР
- Радиоволны
- Оптические вычисления
- Микроволновая печь
- Голография
- Микроскоп
- Телескоп
- Гравитационная линза
- Излучение черного тела
Биографии
- Андре Мари Ампер
- Альберт Эйнштейн
- Майкл Фарадей
- Генрих Герц
- Оливер Хевисайд
- Джеймс Клерк Максвелл
Скорость электромагнитных волн Важные понятия для JEE
Электромагнитные волны, как следует из названия, представляют собой комбинацию электрических и магнитных сигналов.
Как правило, когда одновременно присутствуют электрическое поле и магнитное поле, это приводит к возникновению электромагнитных волн. При этом как поля электрического, так и магнитного токов перпендикулярны друг другу, образуя угол 90 градусов. Эти волны могут создаваться в таких средах, как вакуум, воздух, вода или твердый материал. Нет необходимости в среде для распространения электромагнитных волн. Длина волны и амплитуда этих волн обычно учитываются при измерении других их свойств. Поэтому их часто называют поперечными волнами.
Давайте подробно рассмотрим понятие скорости электромагнитных волн в вакууме и скорости электромагнитных волн в среде.
Распространение электромагнитных волн
Источником электромагнитных волн являются заряды, которые ускоряются и могут излучать энергию в виде волн. Важно отметить, что скорость электромагнитной волны зависит от источника ее излучения. Предположим, что заряд колеблется в среде, и он может создавать колеблющееся электрическое поле, вызывая тем самым колеблющееся магнитное поле.
Эти два колеблющихся электрического и магнитного поля продолжают двигаться и распространяются в пространстве в виде электромагнитных волн.
Давайте узнаем о некоторых характеристиках электромагнитных волн. ЭМ-волны распространяются со скоростью света, т. е. 3 x 10 8 м/с, и электрическое поле E, и магнитное поле B имеют одинаковую частоту, поскольку они продолжают колебаться и остаются в фазе друг с другом на протяжении всего распространения. . Имея эти характеристики, мы можем изобразить, как ЭМ волна распространяется в среде в плоскости XYZ. Скажем, если электромагнитная волна распространяется в положительном направлении по оси x, электрическое поле будет колебаться параллельно оси y, а магнитное поле, которое должно быть перпендикулярно электрическому полю, будет колебаться параллельно оси z. ось. Тогда мы сможем изобразить эти электрические и магнитные поля как синусоидальные функции положения x и времени t, как показано ниже.
Электромагнитная волна в плоскости XYZ
Таким образом, на изображении выше мы видим, что E и B перпендикулярны друг другу.
Эти два поля могут быть записаны как синусоидальные функции, как показано ниже.
$E=E_{0} \operatorname{Sin}(k x-\omega t)$ и $B=B_{0} \operatorname{Sin}(k x-\omega t)$
Эти два функции положения, x и времени, t.
Где k известно как волновое число, которое определяется уравнением
9{8}~\dfrac{m}{s}$.В приведенных выше функциях электрического и магнитного полей 𝜔 — угловая частота ЭМ волны, которая определяется формулой $\omega=2\pi f$, где f — частота ЭМ волны в среде .
And, Bo и Eo — амплитуды магнитного и электрического полей, распространяющихся в электромагнитной волне, отношение которых определяется выражением Eo = CBo, где c — скорость света.
Теперь давайте узнаем о диэлектрической и магнитной проницаемости электрических и магнитных полей, чтобы определить скорость электромагнитных волн в среде.
Скорость электромагнитной волны в среде
Чтобы вывести формулу скорости электромагнитной волны, мы должны узнать о таких терминах, как диэлектрическая проницаемость и проницаемость электрических и магнитных полей.
{-12}~\dfrac{Farad}{meter}$. Отношение диэлектрической проницаемости среды к диэлектрической проницаемости вакуума называется относительной диэлектрической проницаемостью и обозначается $\epsilon_r$ 9{8} \dfrac{\mathrm{~m} }{ \mathrm{s}}$
Скорость электромагнитной волны в среде, если это не вакуум, можно записать как
$\mathbf{c}_ {\text {med}}=\dfrac{1}{\sqrt{\mu \varepsilon}}$ — — — — — (1)
Из определений диэлектрической и магнитной проницаемости мы знаем, что
${\ mu}=\mu_{\mathrm{o}} \mu_{\mathrm{r}}$ и $\varepsilon=\varepsilon_{\mathrm{o}} \varepsilon_{\mathrm{r}}$
два значения в уравнении 1, мы получаем
$\mathbf{C}_{\text{med}}=\dfrac{1}{\sqrt{\mu_{o} \varepsilon_{o} \mu_{r} \varepsilon_{r}}}$
Где $C_{o}=\dfrac{1}{\sqrt{\varepsilon_{o} \mu_{o}}}$ и приведенное выше уравнение становится следующим:
$C_{\text {medium}}= \dfrac{C_{0}}{\sqrt{\mu_{r} \varepsilon_{r}}}$
Это соотношение между скоростью электромагнитных волн в среде и скоростью электромагнитных волн в свободном пространстве.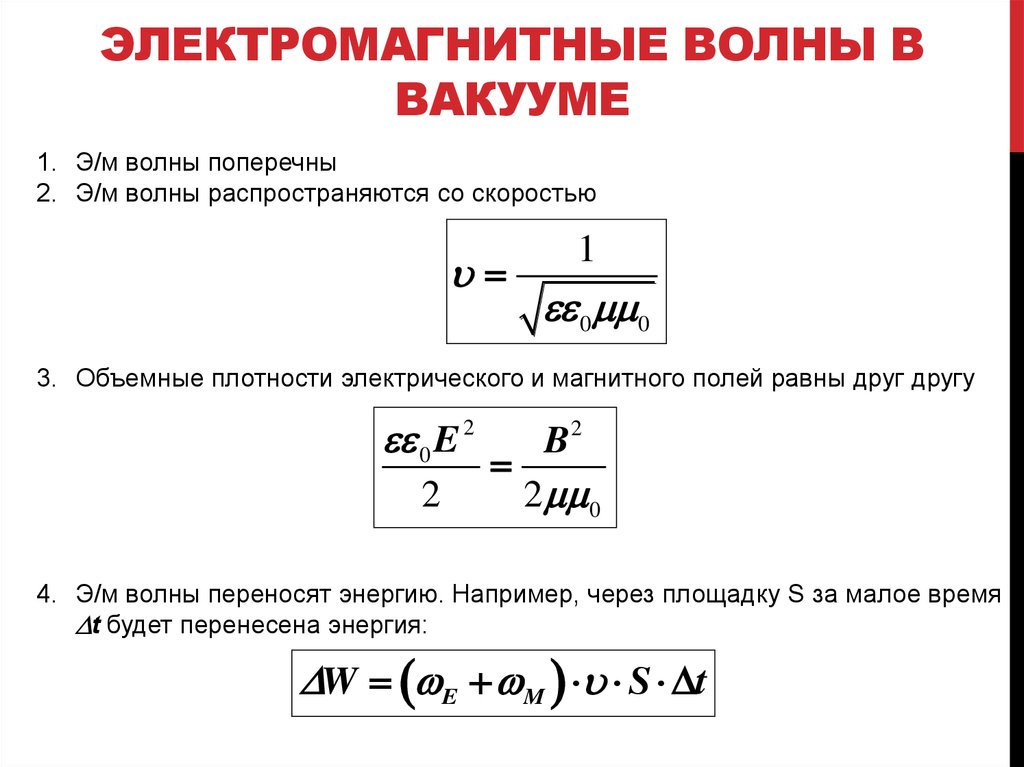
Здесь $\sqrt{\mu_{r} \varepsilon_{r}}=\dfrac{C_{0}}{C_{\text {medium}}}=n$
Где n — показатель преломления среды.
Примечание. Скорость электромагнитных волн в вакууме одинакова, даже если они имеют разную длину волны. Решим некоторые задачи, связанные со скоростью электромагнитных волн в воздухе или среде.
Решенные примеры скорости электромагнитной волны
Пример 1. Электромагнитная волна распространяется в среде, относительная диэлектрическая проницаемость которой равна 2,25, а относительная проницаемость равна 1. Найдите скорость электромагнитной волны в этой среде. 98~\dfrac{m}{s}$.
Пример 2. Электромагнитная волна распространяется через среду, уравнения электрического и магнитного полей которой имеют вид E = 35sin(kx-wt) и B = Bosin(kx-wt). Найдите значение Бо.
Решение:
Учитывая, что
E = 35sin(kx-wt), где Eo = 35 Ньютон/Кулон
CBo где
$B_{o}=\dfrac{E_{o}}{C}=\dfrac{35}{3 \times 10^{8}}=11,67 \times 10^{-8}~\text { Тесла } $ 9{-8}$ Тесла
Подведем итог тому, что мы узнали до сих пор.
