8$ м/с.

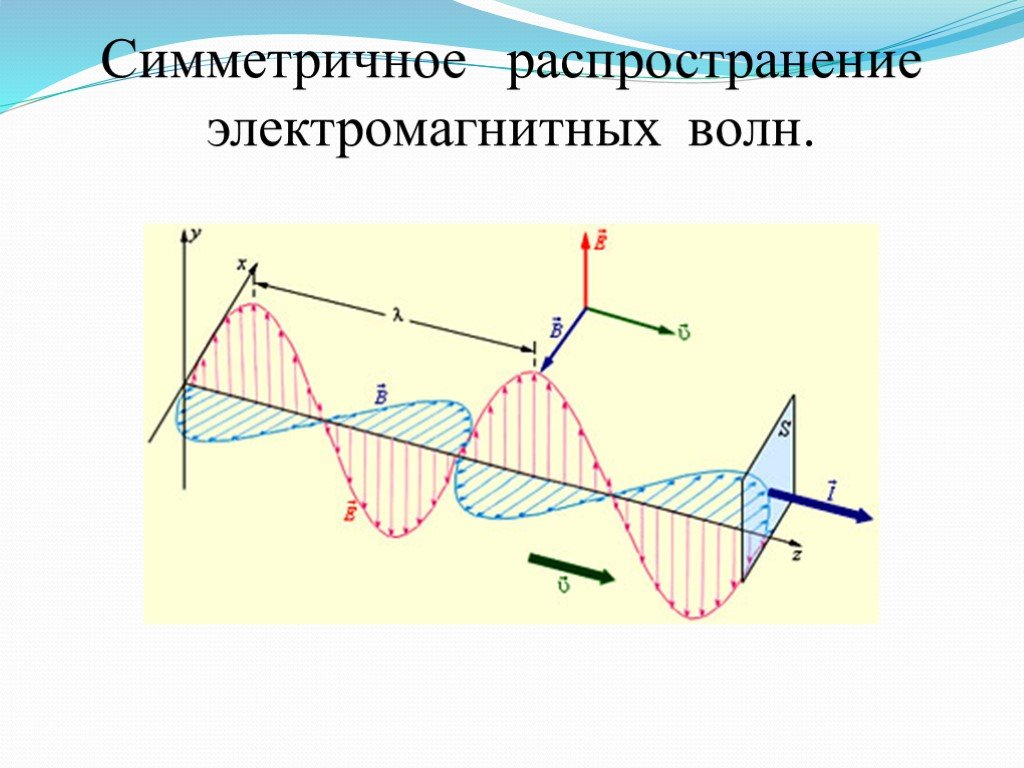
Однако, если заряд движется в некоторой среде, то эта среда оказывает на процесс распространения электромагнитной волны очень заметное влияние.

Любая среда в какой-то степени поглощает энергию электромагнитной волны, и амплитуда вектора ее напряженности падает. Наблюдать такое поглощение можно, вспомнив, что свет также является электромагнитной волной, и существуют прозрачные и непрозрачные для света вещества. Другие электромагнитные излучения в различных средах также поглощаются по-разному.

Возможность получения рентгеновских снимков обусловлена тем, что различные ткани по-разному поглощают рентгеновские лучи. Там, где лучи, пройдя через биологическую ткань, не ослабли – воздействие на чувствительный слой экрана будет сильнее, чем там, где лучи были сильно поглощены.

Рис. 1. Примеры рентгеновских снимков.

Скорость распространения электромагнитной волны в среде меньше, чем в вакууме, и это приводит к частичному отражению волны на границе сред, и преломлению ее при переходе из одной среды в другую.

{18}$ Гц начинают все лучше проникать сквозь различные, и даже проводящие среды, за счет того, что длина волны становится сравнима с размерами атомов, а для гамма-диапазона даже сравнима с размерами ядер. Кроме того, малая длина волны обуславливает слабое отражение волн этого диапазона от границ различных сред.

Рис. 3. Таблица шкалы электромагнитных волн.

Что мы узнали?

В вакууме электромагнитная волна свободно распространяется во все стороны от заряда, движущегося с ускорением. Любая среда в какой-то степени поглощает энергию, и амплитуда волны по мере распространения падает. Кроме того, скорость распространения в среде меньше, чем в вакууме, это приводит к частичному отражению волны на границе сред и к преломлению ее при переходе из одной среды в другую.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4. 6

Средняя оценка: 4.6

Всего получено оценок: 147.

---

А какая ваша оценка?

Основы радиолокации — Распространение электромагнитных волн

Распространение электромагнитных волн

Рисунок 1. Ионосферная, земная и прямая волны

Рисунок 1. Ионосферная, земная и прямая волны

Распространение электромагнитных волн

Распространение электромагнитных волн между передающей и приемной антеннами представляет собой очень сложное явление. Различают три типа распространения электромагнитных волн в земной атмосфере:

• земные (поверхностные) волны;
• ионосферные волны;
• прямые волны.

Земная (поверхностная) волна

Земные волны распространяются вблизи земной поверхности. Земная волна является предпочтительным типом распространения для радиосвязи на большие расстояния с использованием частот ниже 3 МГц (земля ведет себя как проводник для частот ниже 5 МГц). Земная волна также используется для радиосвязи на коротких расстояниях с использованием частот от 3 до 30 МГц.

Из-за того, что земля не обладает бесконечной электрической проводимостью, земная волна при распространении над поверхностью испытывает потери энергии, что влияет на дальность распространения волны. Чем ниже проводимость поверхности, над которой распространяется волна, тем меньше дальность ее распространения. По этой причине дальность распространения земной волны над морской поверхностью больше, чем над поверхностью земли (проводимость морской воды выше, чем проводимость земли).

Следует отметить, что в диапазоне частот радиолокационных устройств земная волна не возникает.

Ионосферная волна

Ионосферная радиоволна — это волна, которая при распространении однократно или многократно отражается от ионосферы. Благодаря этому радиоволны могут распространяться на значительные расстояния и даже огибать земной шар.

Различают два механизма возникновения ионосферных волн: рефракция в тропосфере и отражение от ионосферы.

Рефракция в тропосфере

Тропосфера, самый нижний слой атмосферы Земли, простирается от поверхности Земли до высоты чуть более 11 км. Практически все погодные явления происходят в этом слое. Как правило, тропосфера характеризуется устойчивым снижением как температуры, так и давления воздуха по мере увеличения высоты. Однако многочисленные изменения погодных явлений вызывают колебания влажности и неравномерный нагрев земной поверхности. В результате воздух в тропосфере находится в постоянном движении. Это движение вызывает образование небольших турбулентностей или завихрений, проявляющихся в скачкообразных изменениях траекторий самолетов, входящих в турбулентные области атмосферы. Эти турбулентности наиболее интенсивны у поверхности Земли и постепенно уменьшаются с высотой. В областях турбулентности радиоволны с короткими длинами волн преломляются или рассеиваются.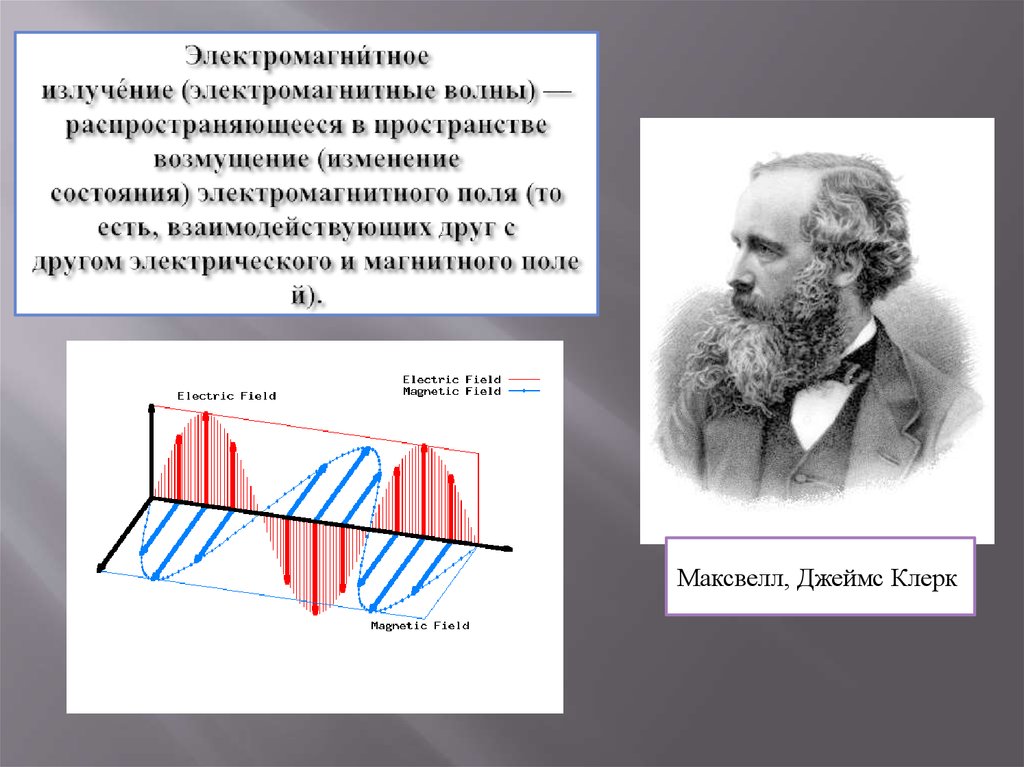

В случаях, когда распространение радиоволны происходит под небольшими углами, траектория волны может изменяться вплоть до направления обратно к земле. Такое рассеяние обеспечивает улучшенную связь на более высоких частотах.

Отражение от ионосферы

Для радиоволн на частотах от 3 МГц до 30 МГц («коротковолновые») ионосфера действует как отражатель. Более высокие частоты проникают в ионосферу, более низкие настолько гасятся слоями D и E, что лишь изредка (в основном ночью) отражаются.

Поскольку переходы между отдельными слоями плавные, принцип зеркального отражения применим только в ограниченной степени. Кроме того, слои находятся в движении и колеблются по интенсивности, поэтому условия отражения постоянно меняются. Поскольку ионосферная волна также отражается землей, многократные отражения приводят к тому, что такие коротковолновые излучения распространяются на очень большие расстояния. Однако такие частоты, как правило, не используются в радиолокации, за исключением радиолокаторов особого типа, называемых загоризонтными (OTH-B).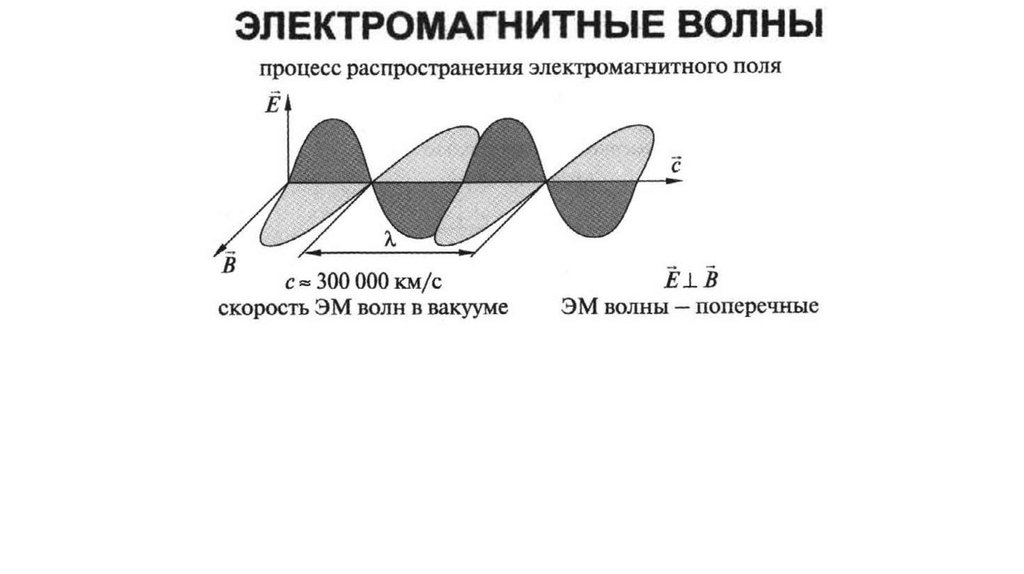

Прямая волна

На частотах выше 100 МГц обычно электромагнитные волны не отражаются от ионосферы, а продолжают распространяться в начальном направлении. Такие волны называются прямыми волнами. Для большинства задач радиолокации характерен именно этот тип распространения электромагнитных волн. Поскольку в данном случае волны распространяются приблизительно прямолинейно и, таким образом, ведут себя подобно световым лучам, их называют квазиоптическими волнами. Электромагнитная волна, излученная передающей антенной, достигнет приемной антенны только в случае прямой видимости между этими антеннами. По этой причине, а также из-за кривизны земной поверхности возможная дальность действия радиотехнической системы зависит от высот антенн передатчика и приемника. Теоретически эта дальность ограничена так называемой радиовидимостью (радиогоризонтом).

Одностороннее спиральное распространение электромагнитных волн, поддерживаемое намагниченной плазмой

Стремление к одностороннему переносу света с защитой от рассеяния недавно стало горячей темой исследований не в последнюю очередь из-за явных технологических преимуществ возможности манипулировать электромагнитными волнами при сохранении идеальная передача. Ее кажущимся носителем является поверхностная волна, по определению это волна, ограниченная границей раздела двух полубесконечных сред. Традиционная поверхностная волна обычно терпит неучтенные потери на рассеяние при столкновении с какими-либо поверхностными нарушениями, такими как резкий изгиб. Недавно было предложено много видов фотонных нетривиальных поверхностных волн, которые демонстрируют устойчивое свойство односторонней нерассеивающей транспортировки, посредством имитации топологической электронной системы 9.0003 1,2 . Определяющей чертой топологических фаз является соответствие объем-ребро. Соответствие объемного края, относящееся к удивительной зависимости граничных возбуждений от характеристик объемных распространяющихся мод, а не от локальных свойств границы, перестраивает наши представления о зонной теории энергий. После того, как Холдейн предложил фотонный аналог квантового эффекта Холла в 2008 году ^3,4 , появилось несколько важных статей, разъясняющих топологические граничные состояния как теоретически, так и 9. 0003 5,6,7,8,9 и экспериментально ^{10,11,12,13,14,15} бросили совершенно новый вызов традиционной оптике. В то же время намагниченные метаматериалы с почти нулевым эпсилоном ¹⁶ также были предложены для доказательства односторонних фотонных состояний в двумерной плоскости. Очевидно, возникла совершенно новая полевая топологическая фотоника ¹⁷ . Тем не менее, что нельзя игнорировать, так это то, что изготовление и сборка, особенно трехмерный случай объемного фотонного кристалла или метаматериалов, по-прежнему сложны и требуют много времени. Здесь мы предлагаем простую естественную системно-намагниченную плазму для реализации винтового одностороннего распространения по поверхности. Что еще более важно, топологическую транспортировку электромагнитных поверхностных волн можно реконфигурировать, просто регулируя внешнее магнитное поле или плотность плазмы.

Недавнее исследование намагниченной плазмы показало интересные электромагнитные свойства, такие как субдифракционная визуализация ¹⁸ и прозрачность, индуцированная магнитным полем ¹⁹ . В сильном магнитном поле движение свободных электронов в холодной плазме ограничивается плоскостью, перпендикулярной приложенному магнитному полю. С другой стороны, электроны могут свободно двигаться вдоль направления магнитного поля. Ранее было показано, что при чрезвычайно сильном магнитном поле волна может распространяться почти без дифракции вдоль направления магнитного поля подобно тому, как волна распространяется внутри гиперболических метаматериалов ^20,21 , который в настоящее время является очень активной темой исследований, включая субволновую визуализацию ^22,23,24 , отрицательное преломление ²⁵ , усиление спонтанного излучения с большим фактором Перселла ²⁶ и даже топологически упорядоченные метаматериалы ⁹ .

При распространении электромагнитной волны с угловой частотой ω в плазме без потерь плазма без потерь ведет себя как модель свободных электронов, электромагнитный отклик которой можно описать диэлектрической проницаемостью Друде , где – плазменная частота, являющаяся концентрацией электронов, e и m обозначают элементарный заряд электрона и массу электрона соответственно. Как показано ранее ¹⁸ , приложенное внешнее постоянное магнитное поле приводит к тому, что изотропная плазма становится чрезвычайно анизотропной средой из-за того, что электроны движутся по циклотронным орбитам в плоскости, перпендикулярной полю. Если магнитное поле выровнено в направлении z, электромагнитный отклик намагниченной плазмы без потерь может быть описан следующим локальным однородным тензором диэлектрической проницаемости ^18,27,28 ,

где , и . Циклотронная частота определяется приложенным постоянным магнитным полем.

Рассматривая волну, распространяющуюся вдоль направления  + z с круговыми поляризациями в качестве основных состояний, эту относительную диэлектрическую проницаемость замагниченной плазмы можно привести к диагональному тензору , где , ‘’ соответствуют правополяризованным и левополяризованным состояниям соответственно. Чтобы удовлетворить наше гиперболическое требование в направлении z, параллельном статическому магнитному полю, рабочая частота должна удовлетворять условиям без потерь.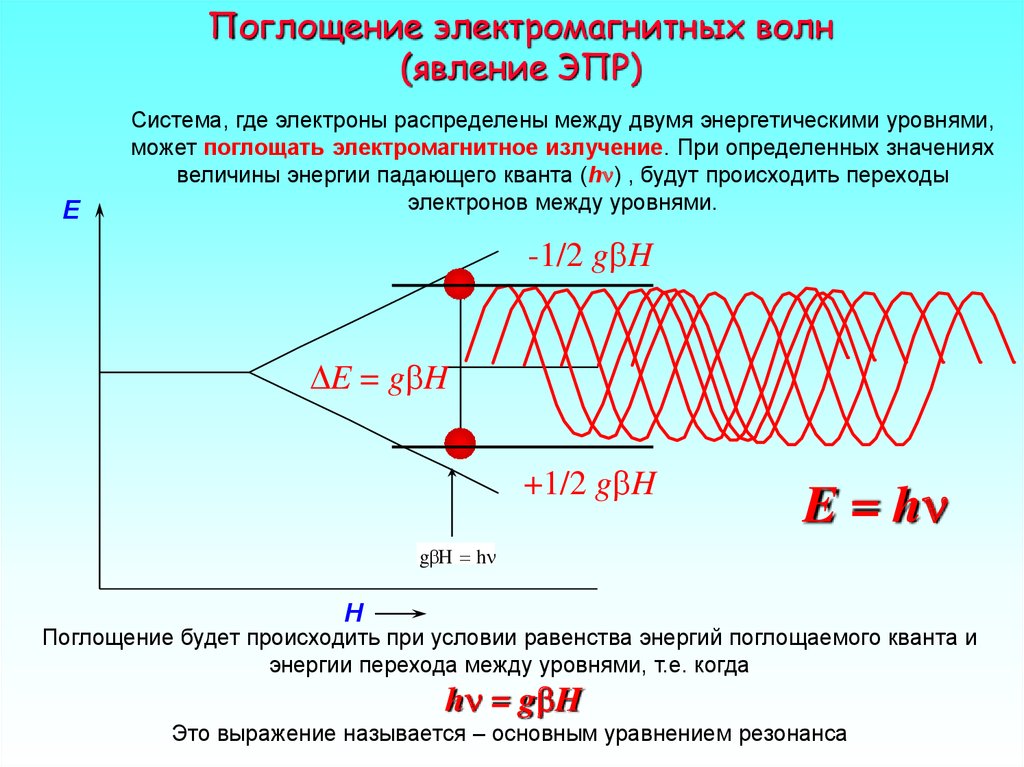 В то время как приложенное магнитное поле втягивает недиагональные компоненты в относительную диэлектрическую проницаемость, намагниченная плазма показывает две запрещенные зоны в k-пространстве с условием . Таким образом, рабочая угловая частота должна быть меньше и удовлетворять . Исходя из этих ограничений, мы можем найти , что означает, что КЭП вакуума находится в запрещенных зонах КЭП замагниченной плазмы, как показано на рис. 1. Другими словами, эти два материала имеют перекрывающиеся запрещенные зоны в пространстве k, т.е. необходимое условие для реализации односторонней устойчивой к рассеянию транспортировки. На рис. 1 показаны соответствующие гиперболические свойства и ширина запрещенной зоны замагниченной плазмы, ее можно рассматривать как результат нетривиального преобразования из нормальных гиперболических метаматериалов.

Рисунок 1

ЭТХ замагниченной плазмы и вакуума.

Обычный режим заворачивается вакуумом (указано). Существует большой разрыв между экстраординарным режимом и вакуумом. В минимальной точке верхней псевдогиперболической ветви свет распространяется со строгими состояниями левой круговой поляризации. Однако при приближении к бесконечности состояния поляризации становятся линейными. Пиковая точка верхней обычной полусферы показывает строгую правую круговую поляризацию, противоположную минимальной точке, потому что эти два состояния поднимаются из точки вырождения во время нетривиального преобразования из нормальных гиперболических метаматериалов. В отрицательном случае поляризация представляет противоположные свойства. В плоскости z-компонента электрического поля снова равна нулю, но его поляризация немного эллиптична по сравнению с этими положениями полюсов. Диэлектрическая проницаемость рассчитывается относительно . Волновые векторы выражены в единицах .

Увеличить

Перейдем теперь к изучению того, как эти топологические особенности проявляются на границе замагниченной плазмы. В дальнейшем мы исследуем системы с непрерывной трансляционной инвариантностью в направлении z, тем самым сохраняя .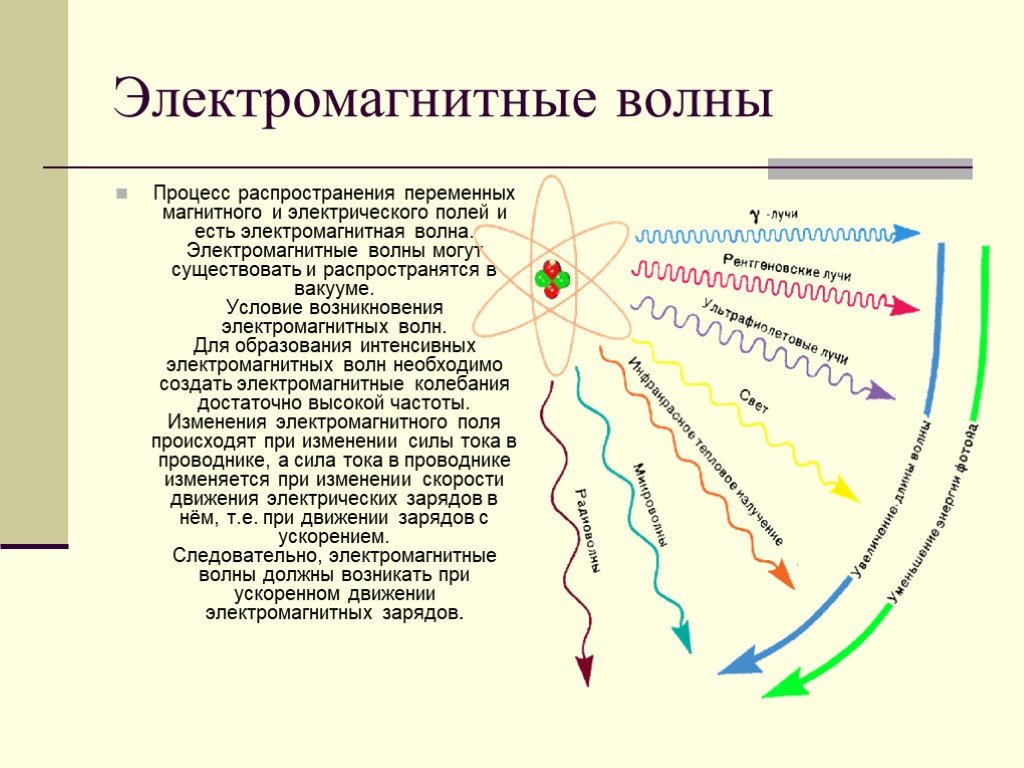 Здесь, предполагая, что поверхностная волна экспоненциально затухает в любом направлении от плоскости y-z (т. е. полупространство занято изотропными средами, такими как вакуум, а замагниченная плазма находится в ), мы используем метод, предложенный Дьяконовым в 1988 ²⁹ для краткого расчета этих поверхностных волн. Со стороны вакуума есть две ортогональные собственные моды, которые можно выразить как

, где — мнимая, представляющая постоянную затухания вдоль положительного направления x, а q — абсолютное значение волнового вектора распространения в плоскости. Точно так же мы можем также записать постоянную затухания на стороне замагниченной плазмы как функцию вектора . Из двух независимых собственных мод замагниченной плазмы его можно получить, решая уравнения Максвелла,

, которые по-прежнему являются функциями . До сих пор мы нашли четыре собственных моды, которые локализованы по обе стороны поверхности. Их объединяет электромагнитное граничное условие. Постулирование того, что тангенциальные компоненты этих полей непрерывны на границе раздела, дает нам детерминантную задачу матрицы ограничений,

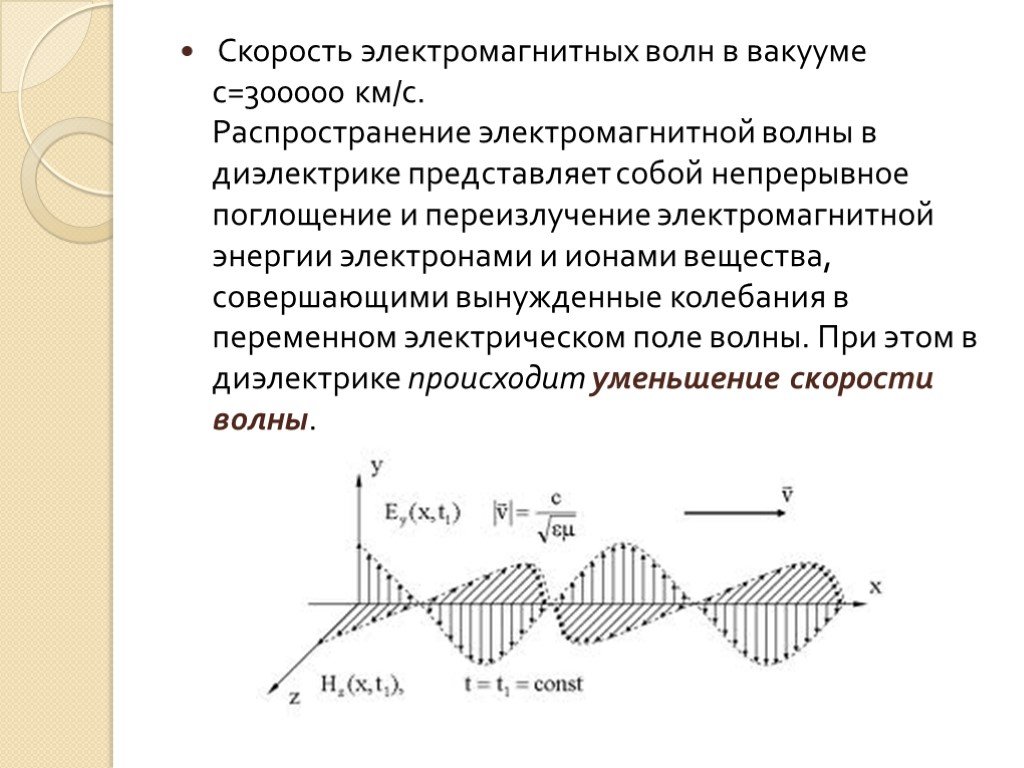. После ее решения на рис. режим, что означает, что пространственное разделение левой и правой движущихся поверхностных волн в определенной степени предотвращает возникновение обратного рассеяния от любого z-инвариантного беспорядка, как показано на рис. 2б. Топологический порядок для замагниченной плазмы объясняется наличием нового типа плазмонных точек Вейля, возникающих на плазменной частоте системы ³⁰ .

Рисунок 2

Объемные и поверхностные состояния.

( a ) Объемные и поверхностные состояния этой системы. Верх/Низ относится к конфигурации, в которой вакуум расположен сверху/снизу намагниченной плазмы. ( b ) Схематическое изображение спирального одностороннего обратного рассеяния в 3D. Киральное поверхностное состояние, распространяющееся вокруг замагниченной плазмы с добавленной цилиндрической формой, окруженной вакуумом, несмотря на наличие приподнятого цилиндра, обратное рассеяние запрещено из-за отсутствия мод против часовой стрелки.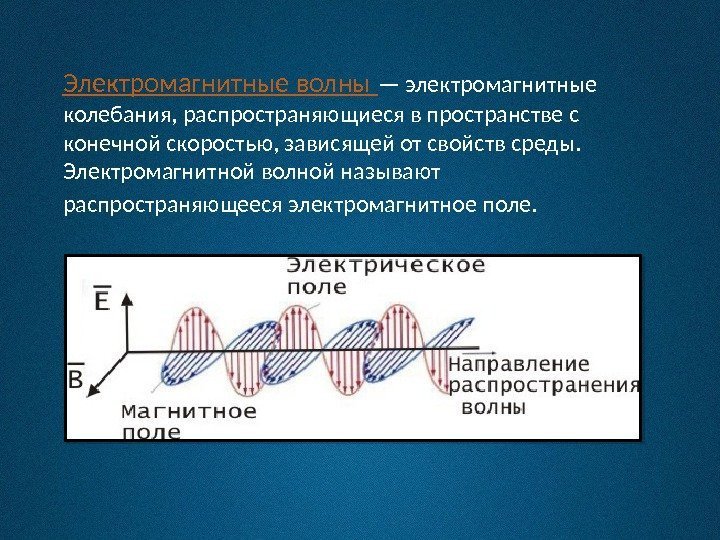

Изображение в натуральную величину

Невосприимчивость к обратному рассеянию также была подтверждена с помощью полноволнового моделирования, показанного на рис. 3b, в котором правая поверхностная волна плавно распространяется вокруг острого дефекта. Моделирование выполняется в плоскости x-y для трех различных постоянных распространения в области тени, обозначенных буквами «A», «B» и «C» на рис. 3a. Для точек «А» и «С», поскольку они не находятся в области щели, электромагнитная волна может рассеиваться в объемные состояния z-инвариантными рассеивателями. С другой стороны, в точке «В», где находится середина зазора, поверхностная волна не подвержена рассеянию на острых краях, и поэтому численное моделирование подтверждает, что это топологически нетривиальное поверхностное состояние. Как и ожидалось, при изменении направления магнитного поля распространение поверхностной волны также переключается на противоположное направление. Это может обеспечить топологические состояния поверхности с динамически реконфигурируемыми свойствами. Поскольку частота столкновений на несколько порядков ниже рабочей частоты, этот реальный случай все же можно считать 9 без потерь.0003 18 .

Рис. 3

Моделирование топологически защищенных поверхностных состояний на границе раздела магнитной плазмы и вакуума.

( a ) Увеличенная область тени на рис. 2(а). ( b ) Распределение поля смоделировано с помощью коммерческого модуля Comsol RF. Параметр намагниченной плазмы равен , а рабочая частота .

Изображение в полный размер

Интересно, что после увеличения точки «С», показанной на рис. 3а, где состояние поверхности очень близко к КЭС вакуума, обнаруживается, что состояние поверхности не сливается с КЭС вакуума, скорее, она конформно огибает КЭП вакуума и идет параллельно другой ветви КЭП замагниченной плазмы. Это указывает на то, что даже при на каждой поверхности существует однонаправленное поверхностное состояние с дисперсионным соотношением, выражающимся как ¹⁶ ,

где и обозначает верхний и нижний регистр соответственно. Важно то, что эта поверхностная мода может быть возбуждена только магнитным током. После подстановки реалистичных параметров в уравнение. 5 мы получаем упомянутый тонкий разрыв между поверхностным состоянием и объемным состоянием вакуума в точке «C». Однако, поскольку поверхностные состояния не попадают в щель, они не защищены от z-инвариантных дефектов.

Для полноты картины мы показываем состояния поляризации этих нетривиальных поверхностных волн на рис. 4. В соответствии с граничными условиями тангенциальные компоненты электрического (E) и магнитного поля (H) непрерывны на границе раздела. Однако вертикальные компоненты полей E и H прерывисты. В частности, они связаны . Поэтому состояния поляризации со стороны вакуума и со стороны замагниченной плазмы различны. Состояния поляризации по обе стороны интерфейса обычно эллиптически поляризованы. Интересно, что эллипс поляризации лежит в плоскости, перпендикулярной поверхности. Другое интересное наблюдение заключается в том, что эллипс поляризации обычно не перпендикулярен вектору Пойнтинга.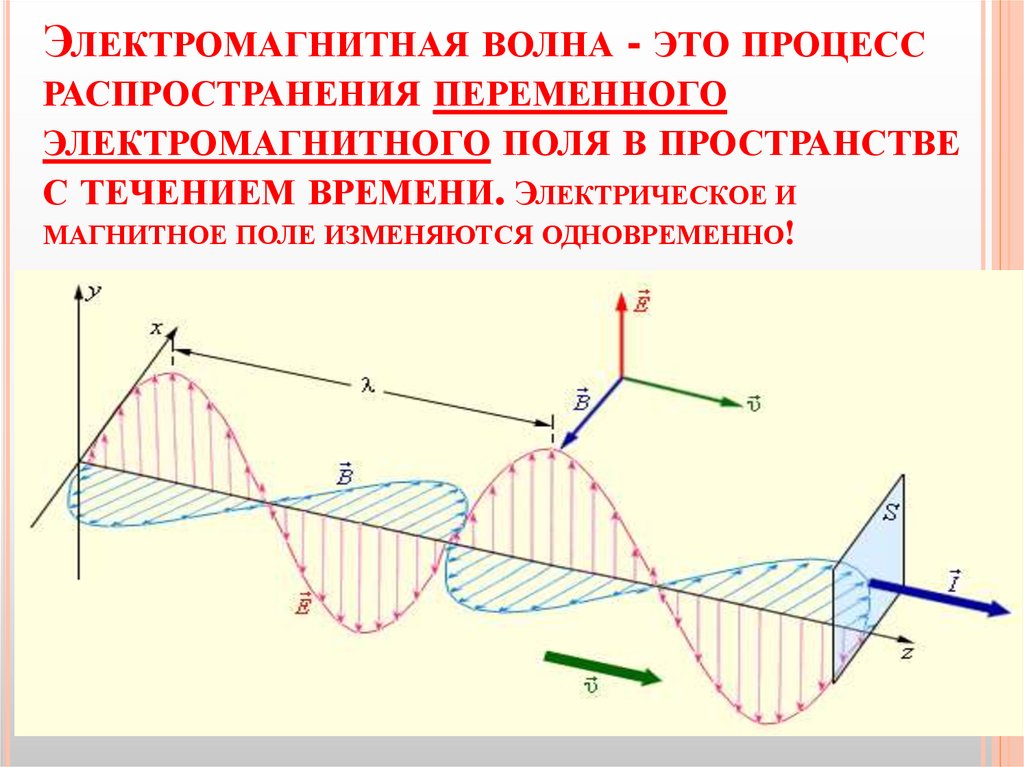 Угол, образующийся между ними, монотонно изменяется от 0° в течение k _z  = 0 до 90° для k приближается к бесконечности, как показано на рис. 4б. Более того, график эллиптичности показывает, что когда k приближается к бесконечности, электрическое поле в вакуумной стороне становится поляризованным по кругу.

Рисунок 4

Поляризация поверхностных состояний электрическим полем.

( a ) Поляризационное состояние поверхностных волн в вакууме и в замагниченной плазме. Плоскость поляризации перпендикулярна границе раздела, поэтому при виде сверху она проецируется на границу раздела в виде линейного вектора. Насекомое показывает, что состояния поляризации эллиптические. ( b ) и ( c ) Направление плоскости поляризации и эллиптичности () состояний поляризации в вакууме и в замагниченной плазме. Этот рисунок соответствует рис. 3(а) для поверхностных состояний при .

Увеличить

В заключение мы теоретически исследовали существование однонаправленно распространяющейся поверхностной волны между вакуумом и замагниченной плазмой. Моделирование подтверждает наличие однонаправленного, невосприимчивого к обратному рассеянию распространения поверхностной волны на основе простой природной системы – намагниченной плазмы. Хотя исследование было сосредоточено на намагниченной плазме в свободном пространстве для управления электромагнитными волнами в микроволновом режиме, оно может быть распространено на терагерцовый режим, работая с полупроводниками с очень малой эффективной массой, такими как InSb. Таким образом, эти нетривиальные краевые состояния можно наблюдать и в терагерцовом диапазоне при использовании намагниченных полупроводников ³¹ .

Учебник по микроскопии молекулярных выражений: свет и цвет — распространение электромагнитных волн

gif»> Праймер для микроскопии Свет и цвет Основы микроскопа Специальные методы Цифровая визуализация Конфокальная микроскопия Визуализация живых клеток Микрофотография Музей микроскопии Виртуальная микроскопия Флуоресценция Веб-ресурсы Информация о лицензии Использование изображения Пользовательские фотографии Партнеры Информация о сайте Свяжитесь с нами Публикации Главная Галереи: gif»> Фотогалерея Кремниевый зоопарк Фармацевтика Чип-шоты Фитохимикаты Галерея ДНК Микроскейпы Витамины Аминокислоты Камни Религиозная коллекция Пестициды пивные шоты Коктейльная коллекция Заставки Выиграть обои Mac Обои Киногалерея

Интерактивные учебные пособия Распространение электромагнитных волн Электромагнитные волны могут генерироваться различными способами, такими как разрядная искра или колеблющийся молекулярный диполь. Видимый свет является широко изучаемой формой электромагнитного излучения и демонстрирует колеблющиеся электрические и магнитные поля, амплитуды и направления которых представлены векторами, которые колеблются по фазе в виде синусоидальных волн в двух взаимно перпендикулярных (ортогональных) плоскостях. В этом руководстве исследуется распространение виртуальной электромагнитной волны и рассматривается ориентация векторов магнитного и электрического поля. Чтобы повернуть модель волны, щелкните и перетащите в любом месте окна. Учебник начинается с электромагнитной волны, генерируемой разрядной искрой виртуального конденсатора. Искровой ток колеблется с частотой, характерной для цепи, и результирующее электромагнитное возмущение распространяется с векторами электрического ( E ) и магнитного ( B ) полей, колеблющимися перпендикулярно друг другу и направлению распространения ( Z ). Длина волны, излучаемая разрядом виртуального конденсатора, может быть изменена (в пределах диапазона видимого света) с помощью ползунка Длина волны . Перед дальнейшим обсуждением явления анизотропии необходимо сделать базовый обзор нескольких принципов физической оптики, необходимых для последующих дискуссий. Как упоминалось ранее, видимый свет представляет собой форму электромагнитной волны. Если зарядить конденсатор (рис. 1) и через два электрода разрядить искру, ток, индуцированный искрой, на короткое время стекает вниз, замедляется, но из-за индуктивности цепи течет обратно вверх, перезаряжая снова конденсатор. Распространение электромагнитной волны, генерируемой разряжающимся конденсатором или колеблющимся молекулярным диполем, показано на рисунке 1. Искровой ток колеблется с частотой ( n ), которая является характеристикой цепи. Возникающие в результате электромагнитные возмущения распространяются электронным ( E ) и магнитным ( B ) векторами, колеблющимися перпендикулярно друг другу, а также направлению распространения ( Z ). Частота n определяется осциллятором, а длина волны определяется частотой колебаний, деленной на скорость волны.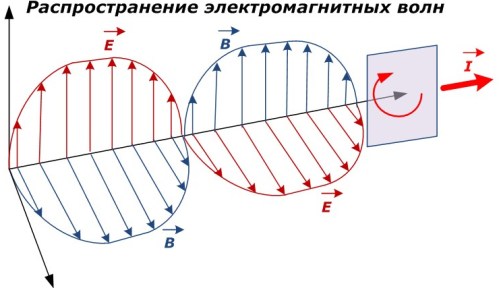 Когда ток колеблется вверх и вниз в искровом промежутке с характеристической частотой цепи ( n ), создается магнитное поле, которое колеблется в горизонтальной плоскости. Изменяющееся магнитное поле, в свою очередь, индуцирует электрическое поле, так что серия электрических и магнитных колебаний объединяется, создавая образование, которое распространяется как электромагнитная волна. Электрическое поле в электромагнитной волне колеблется, его векторная сила то усиливается, то ослабевает, указывая то в одном, то в другом направлении, чередуясь по синусоидальному закону (рис. 1). На той же частоте магнитное поле колеблется перпендикулярно электрическому полю. Электрический и магнитный векторы, отражающие амплитуду и направления колебаний двух волн, ориентированы перпендикулярно друг другу и направлению распространения волны. Скорость результирующей электромагнитной волны может быть выведена из соотношений, определяющих взаимодействие электрического и магнитного полей. Уравнения Максвелла доказывают, что скорость равна скорости света в вакууме ( c ; равно 300 000 километров в секунду), деленной на квадратный корень из диэлектрической проницаемости ( x ) среды, умноженной на магнитную проницаемость ( м ). ) среды. Таким образом, (1) Для большинства материалов, встречающихся в живых клетках (некоторые из которых непроводящие), магнитная проницаемость равна единице, так что : (2) Эмпирически известно, что скорость света обратно пропорциональна показателю преломления ( n ) материала, через который он распространяется, поэтому: и = б/н (3) Из уравнений (2) и (3) можно сделать вывод, что показатель преломления равен квадратному корню из диэлектрической проницаемости этого материала, если измерения производятся на той же частоте : (4) Уравнение (4) показывает, что оптические измерения фактически являются измерениями электрических свойств материала. Диэлектрические свойства, в свою очередь, непосредственно отражают пространственное трехмерное расположение атомов и молекул, определяющих структуру вещества. Вектор, описывающий взаимодействие между электромагнитным полем и веществом, лежит в том же направлении, что и электрический вектор. Это верно независимо от того, рассматриваются ли электрические или магнитные векторы, поскольку важно влияние электрических или магнитных полей на электроны в материальной среде (магнитное поле воздействует на те электроны, которые движутся в плоскости, перпендикулярной магнитному полю). ). Соавторы Кеннет Р. Спринг — Научный консультант, Лусби, Мэриленд, 20657. Shinya Inoué — Морская биологическая лаборатория, 7 MBL Street, Woods Hole, Massachusetts, 02543. Брайан О. Флинн , Роберт Т. Саттер и Майкл В. Дэвидсон — Национальная лаборатория сильных магнитных полей, 1800 Ист Пол Дирак Доктор, Университет штата Флорида, Таллахасси, Флорида, 32310. alexxlab Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт Рубрики Прост Радио Разное Своими руками Советы Схем Схемы Транзист Транзисторы Электрон Электроника